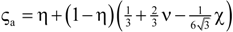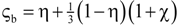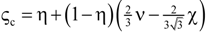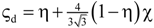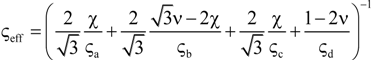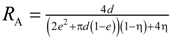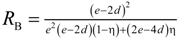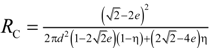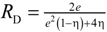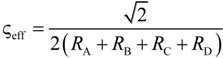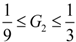Morphological Characterization and Effective Thermal Conductivity of Dual-Scale Reticulated Porous Structures
Abstract
:1. Introduction

2. Experimental
2.1. RPC Synthesis
2.2. Synchrotron Submicrometer Tomography
2.3. Micrometer Tomography

3. Morphological Characterization
3.1. Porosity
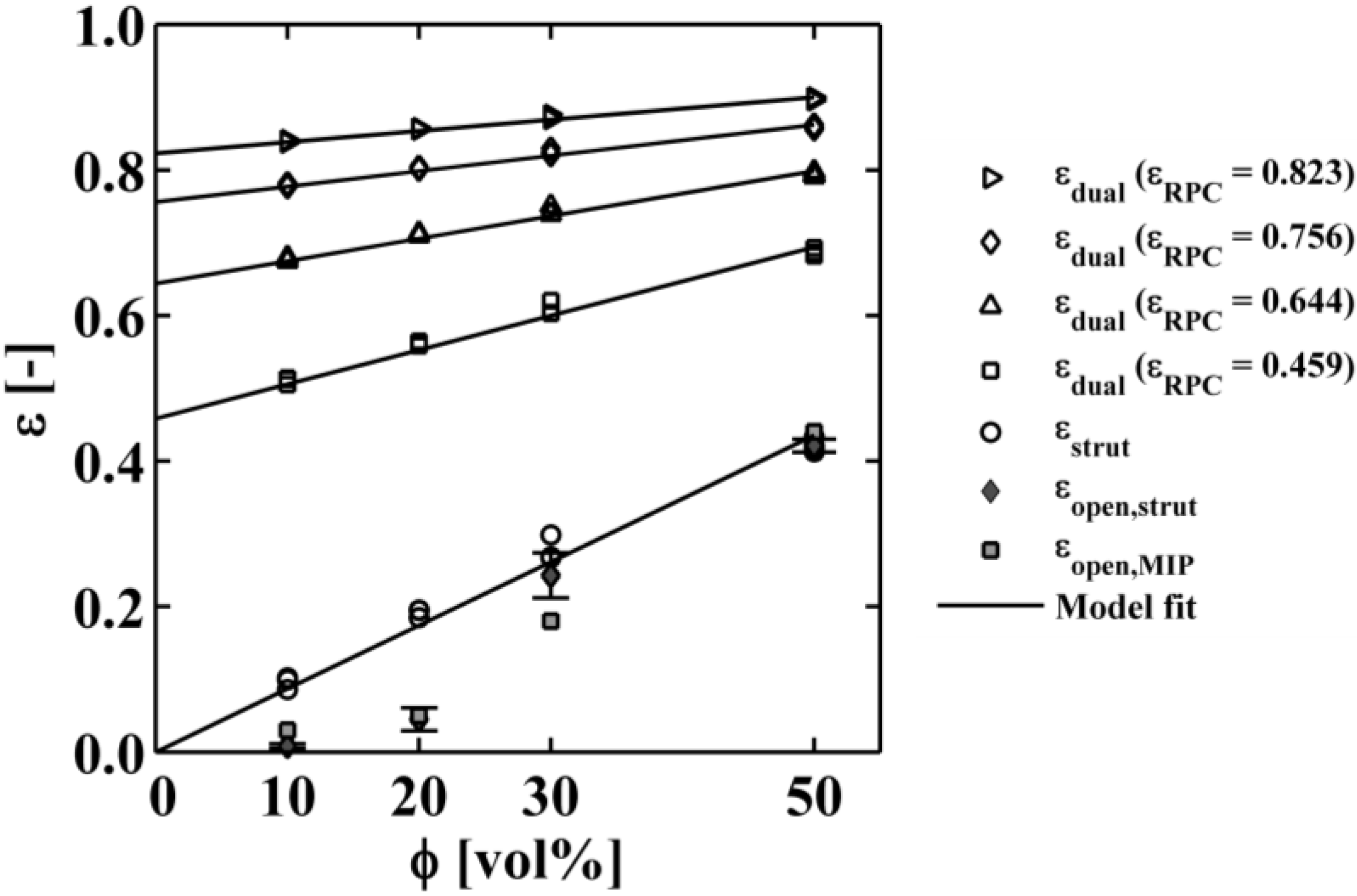
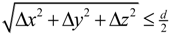 . Table 1 lists the dilation radius, digital porosity, and mean pore diameter of the original RPC reconstruction and of the digitally altered RPC for 3 increasing strut thicknesses, and the corresponding digital section cut and 3D rendering. As expected, porosity and mean pore diameter of the RPC decrease with increasing strut dilation because the thicker struts consume void space.
. Table 1 lists the dilation radius, digital porosity, and mean pore diameter of the original RPC reconstruction and of the digitally altered RPC for 3 increasing strut thicknesses, and the corresponding digital section cut and 3D rendering. As expected, porosity and mean pore diameter of the RPC decrease with increasing strut dilation because the thicker struts consume void space.| rdil (voxel) | 0 | 2 | 5 | 10 |
| rdil (mm) | 0 | 0.071 | 0.179 | 0.357 |
| εRPC (–) | 0.823 | 0.756 | 0.644 | 0.459 |
| dmean (mm) | 2.32 | 2.21 | 1.98 | 1.64 |
| Digital section cut through 3D structure at h = 50% |  |  |  |  |
| 3D rendering of RPC with mm-sized pores |  |  |  |  |
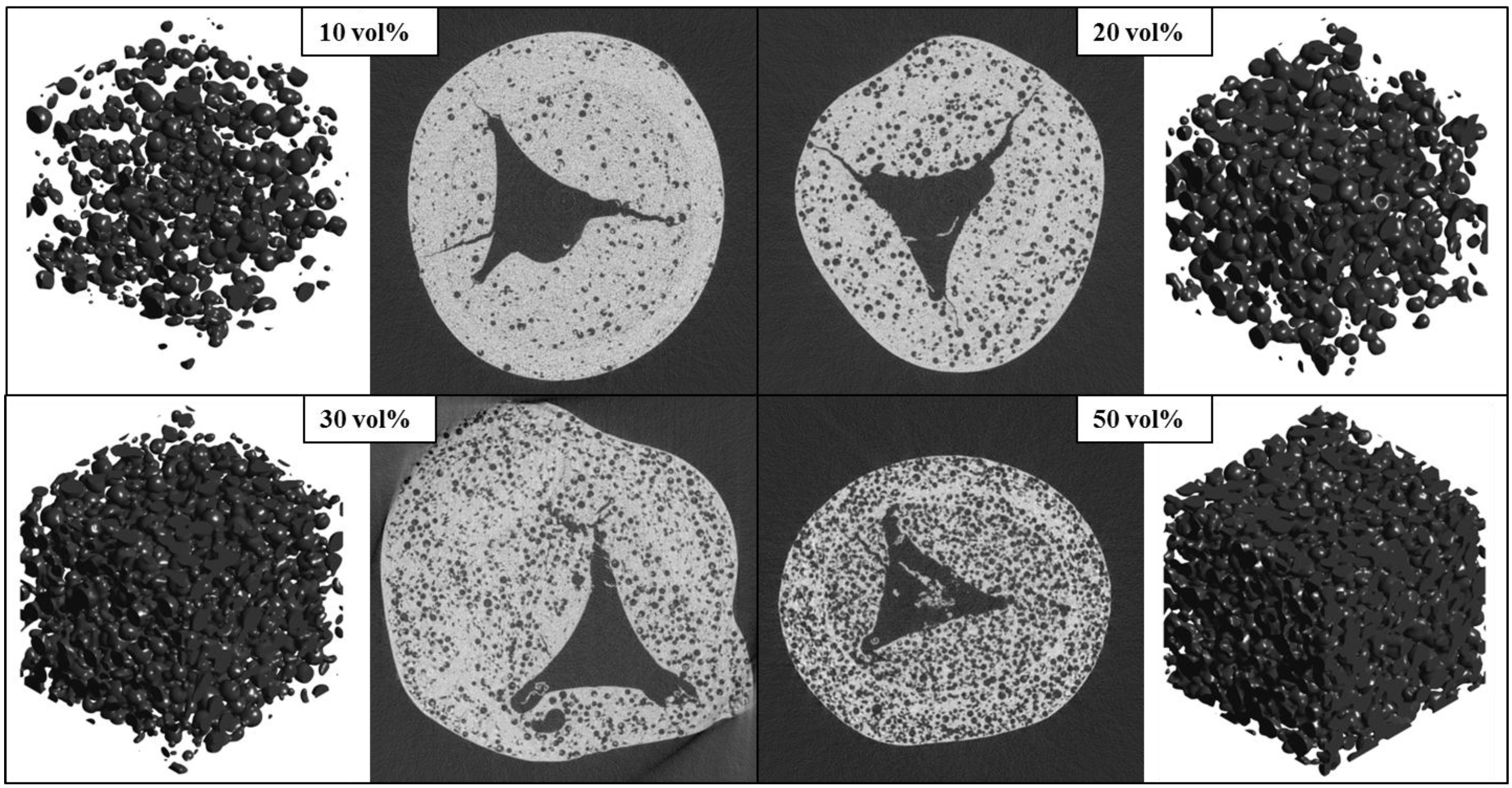
| ϕ (vol%) | 10 | 20 | 30 | 50 |
| εstrut (–) | 0.1195 | 0.1797 | 0.2605 | 0.4436 |
| εopen (–) | 0.0095 | 0.0102 | 0.2167 | 0.4423 |
| dmean (µm) | 9.22 | 11.50 | 9.62 | 9.12 |
| 3D rendering of connected pore space | 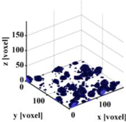 | 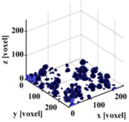 |  |  |

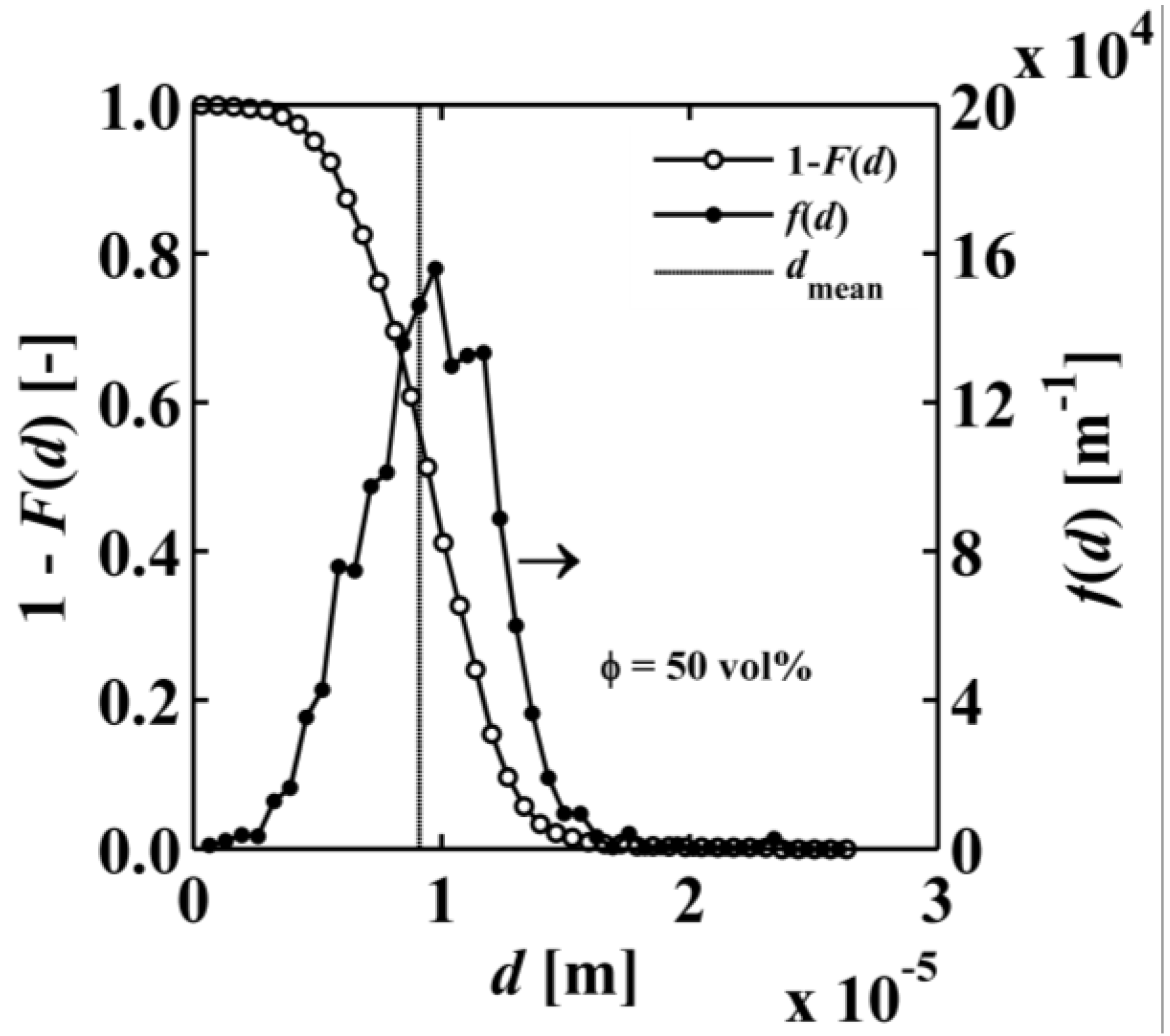
3.2. Pore Size Distribution
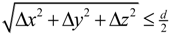 . In a last step, the algorithm inverts back the solid and void space. The cumulative pore size distribution 1 − F(d) is defined as the ratio of the opening-closing porosity, εoc(d), and the original porosity [27]:
. In a last step, the algorithm inverts back the solid and void space. The cumulative pore size distribution 1 − F(d) is defined as the ratio of the opening-closing porosity, εoc(d), and the original porosity [27]:
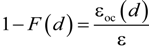
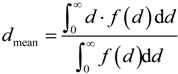
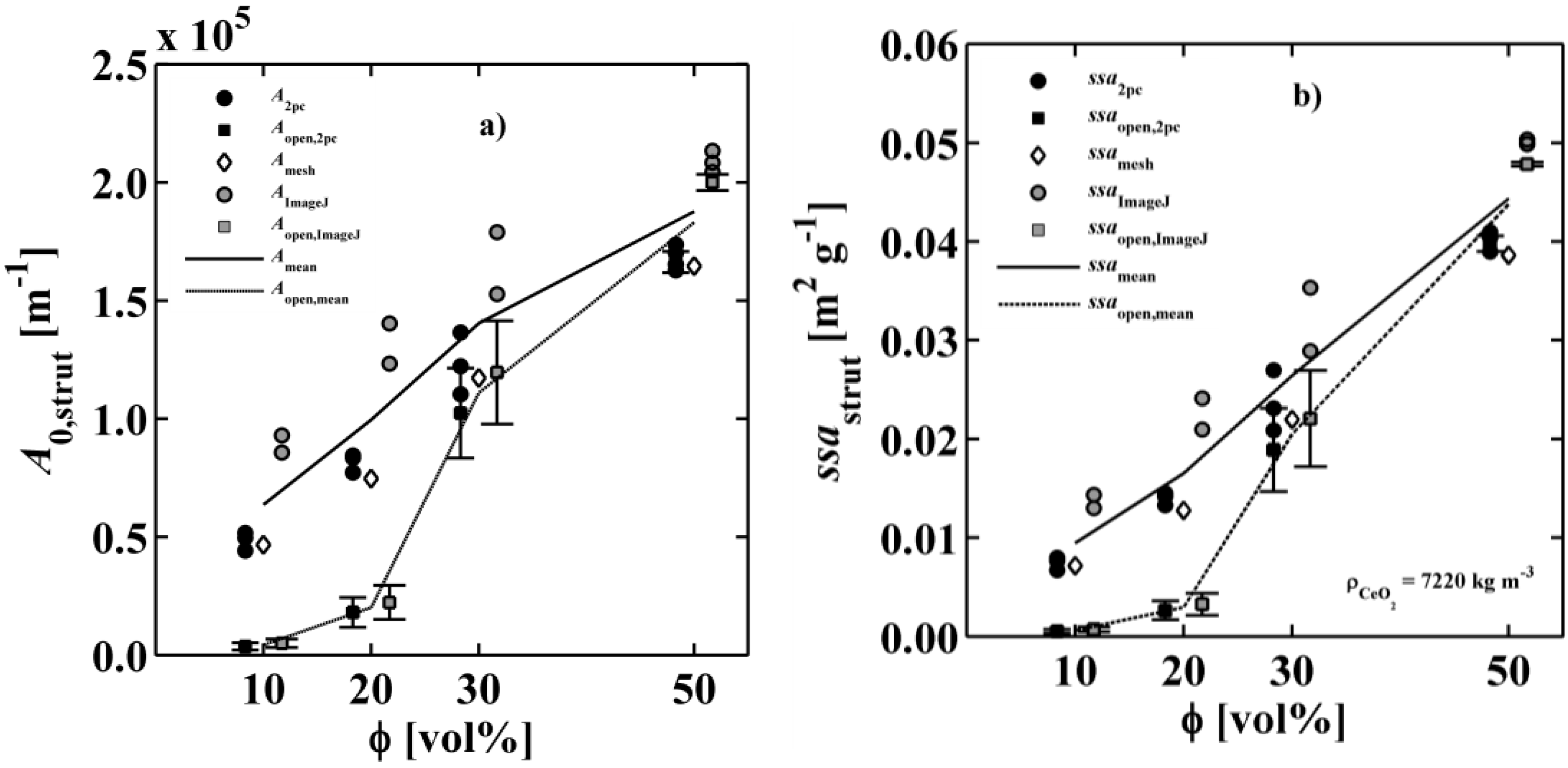
3.3. Specific Surface Area
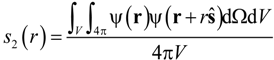
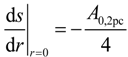
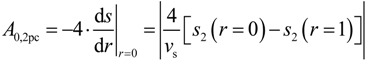
| rdil (voxel) | 0 | 2 | 5 | 10 |
| rdil (mm) | 0 | 0.071 | 0.179 | 0.357 |
| ssaRPC,2pc (m2·g−1) | 9.06 × 10−4 | 5.89 × 10−4 | 4.07 × 10−4 | 2.62 × 10−4 |
| ssaRPC.mesh (m2·g−1) | 6.39 × 10−4 | 4.98 × 10−4 | 3.75 × 10−4 | 2.64 × 10−4 |
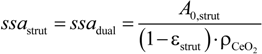
4. Heat Conduction Modelling
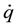 = 0
= 0
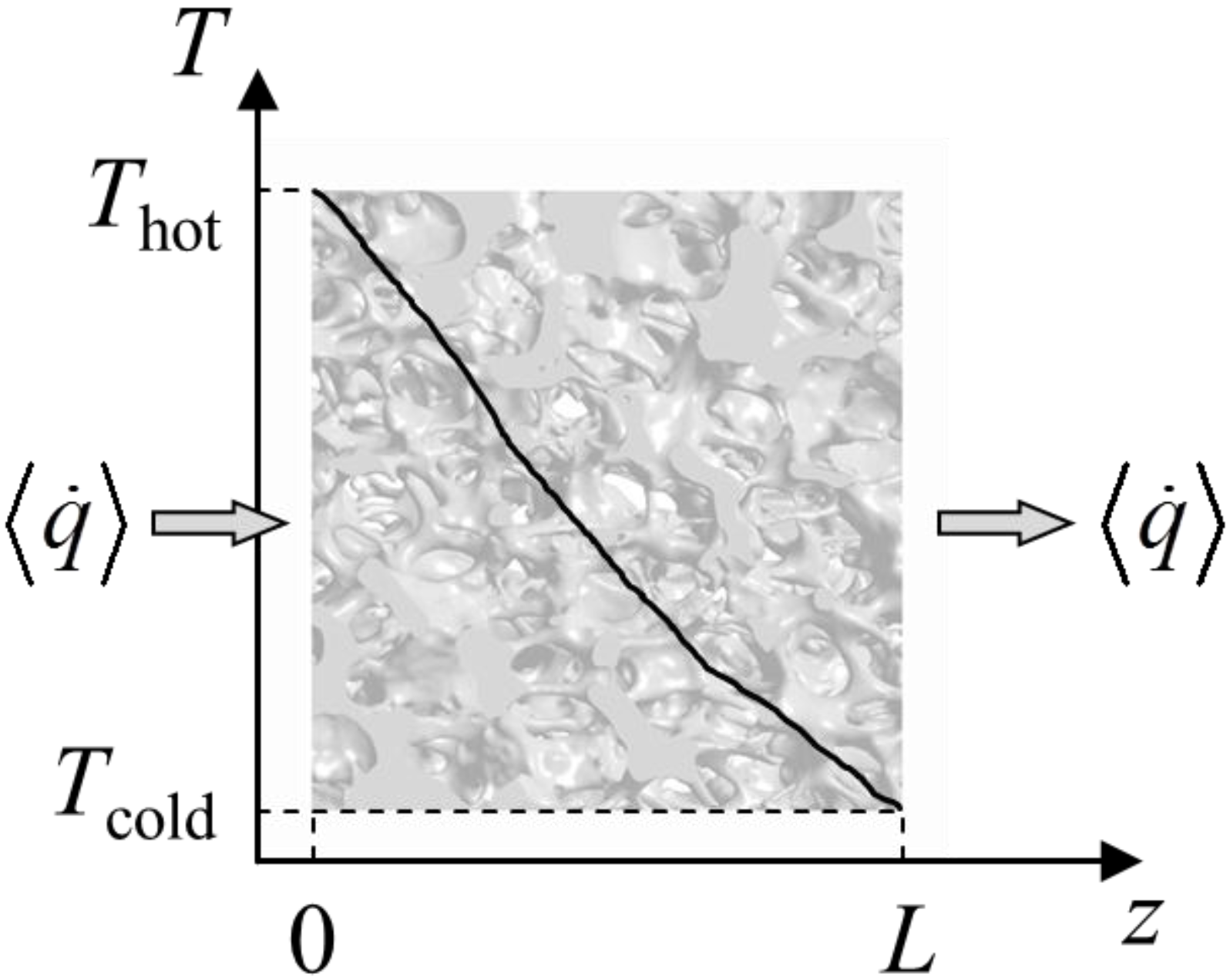
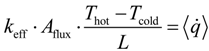
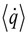 the effective heat flux at the inlet or outlet, and Aflux = L2 is the inlet or outlet area constraint with Thot or Tcold, respectively. The methodology for determination of keff for dual-scale porous structures is schematically shown in Figure 9. In a first step, keff of the strut with µm-sized pores (keff,strut) is determined according Equation (19). In a second step, this keff,strut serves as an input for the solid domain of a further simulation performed with the mm-sized pores of the RPC.
the effective heat flux at the inlet or outlet, and Aflux = L2 is the inlet or outlet area constraint with Thot or Tcold, respectively. The methodology for determination of keff for dual-scale porous structures is schematically shown in Figure 9. In a first step, keff of the strut with µm-sized pores (keff,strut) is determined according Equation (19). In a second step, this keff,strut serves as an input for the solid domain of a further simulation performed with the mm-sized pores of the RPC.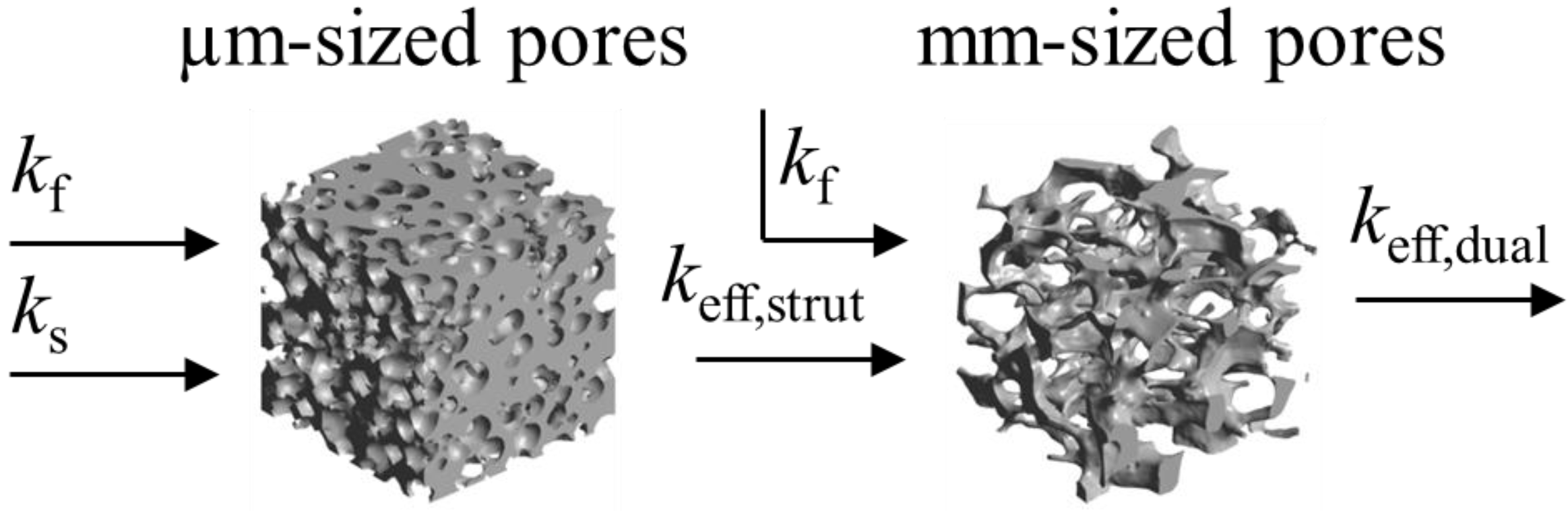
| Model ID | Model | Analytical Expression  | Fitting Parameter |
|---|---|---|---|
| 1 | Parallel slabs [43,44,46] | ςeff = εη + (1 − ε) | None |
| 2 | Serial slabs [43,44,46] | 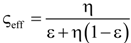 | None |
| 3 | Hashin and Shtrikman upper bound [47] | 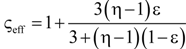 | None |
| 4 | Hashin and Shtrikman lower bound [47] | 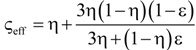 | None |
| 5 | Woodside & Messmer [48] | 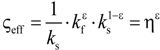 | None |
| 6 | Russell [49] | 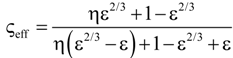 | None |
| 7 | Loeb [50] | 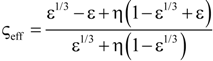 | None |
| 8 | Maxwell model [45,51,52,53] | 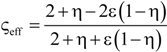 | None |
| 9 | Schuetz-Glicksmann [54,55] | 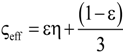 | None |
| 10 | Bhattacharya et al. [56] | 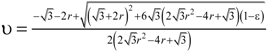 | r |
| 11 | Boomsma and Poulikakos [57] | 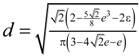 | e |
| 12 | Hamilton [58] | 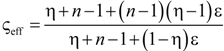 | n |
| 13 | Miller bound [59] | 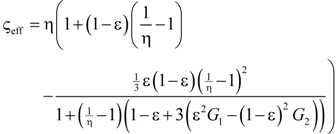 | 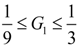 |
| 14 | Calmidi and Mahajan [60] | ςeff = εη + A(1 − ε)n | A |
| 15 | Dul’nev and Zarichnyak [22,30,61,62] | 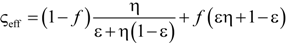 | f |
| 16 | Extended three-resistor model (this work) | f = c0 + c1ε + c2ε2 | c0 |
| 17 | Scalable three-resistor model (this work) | 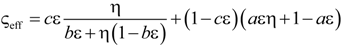 | a |
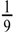 ) up to platelike (number
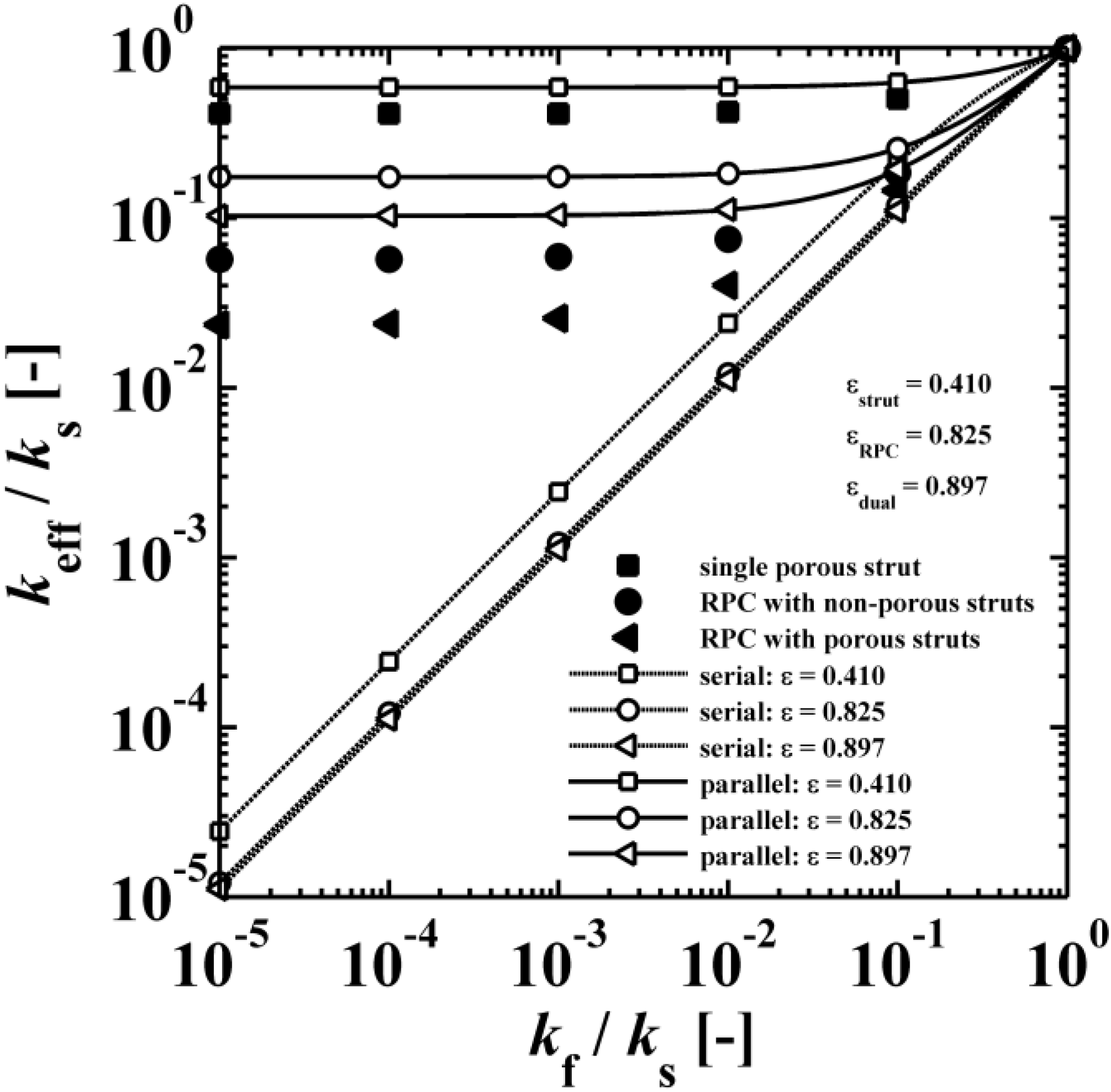
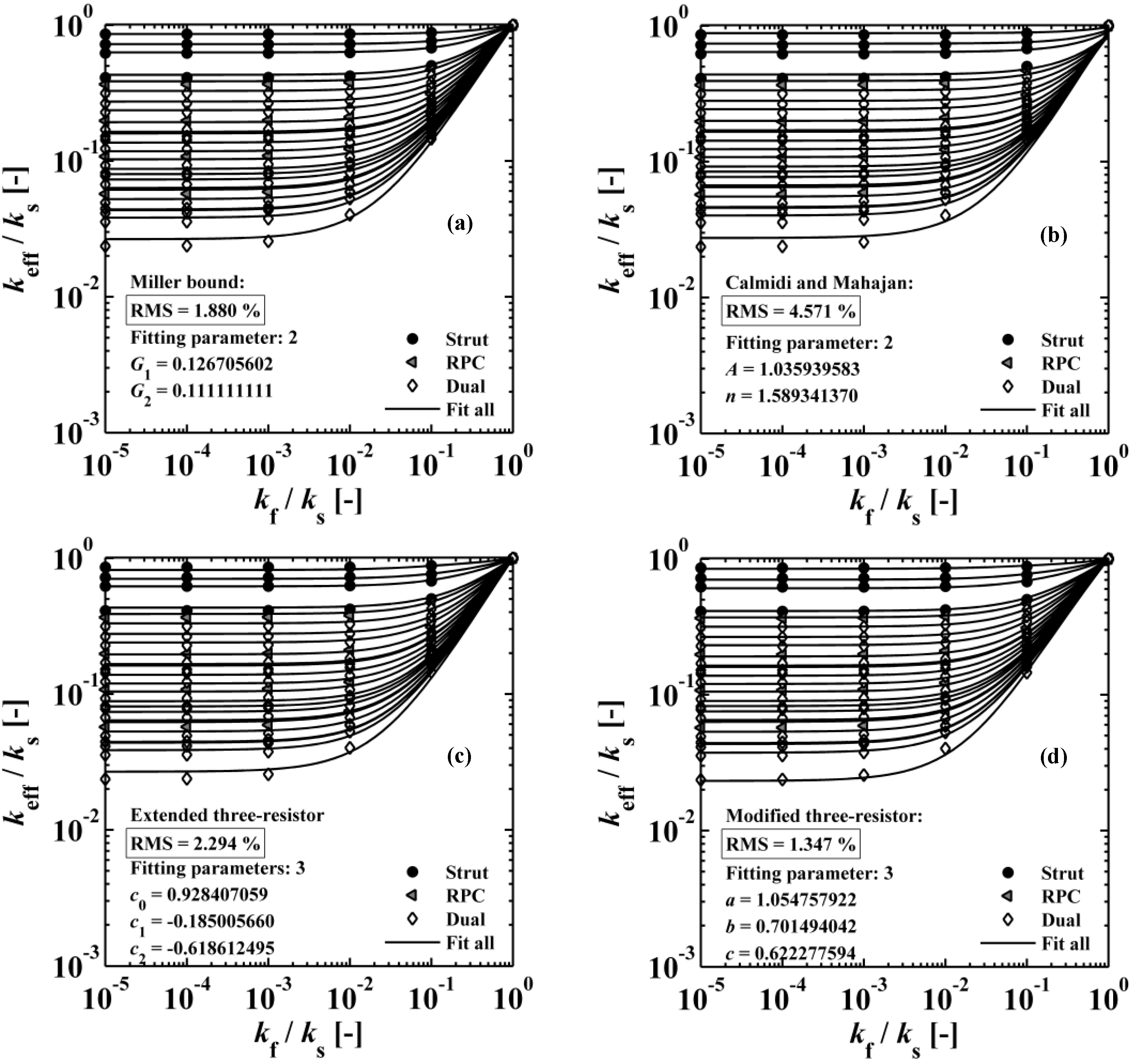
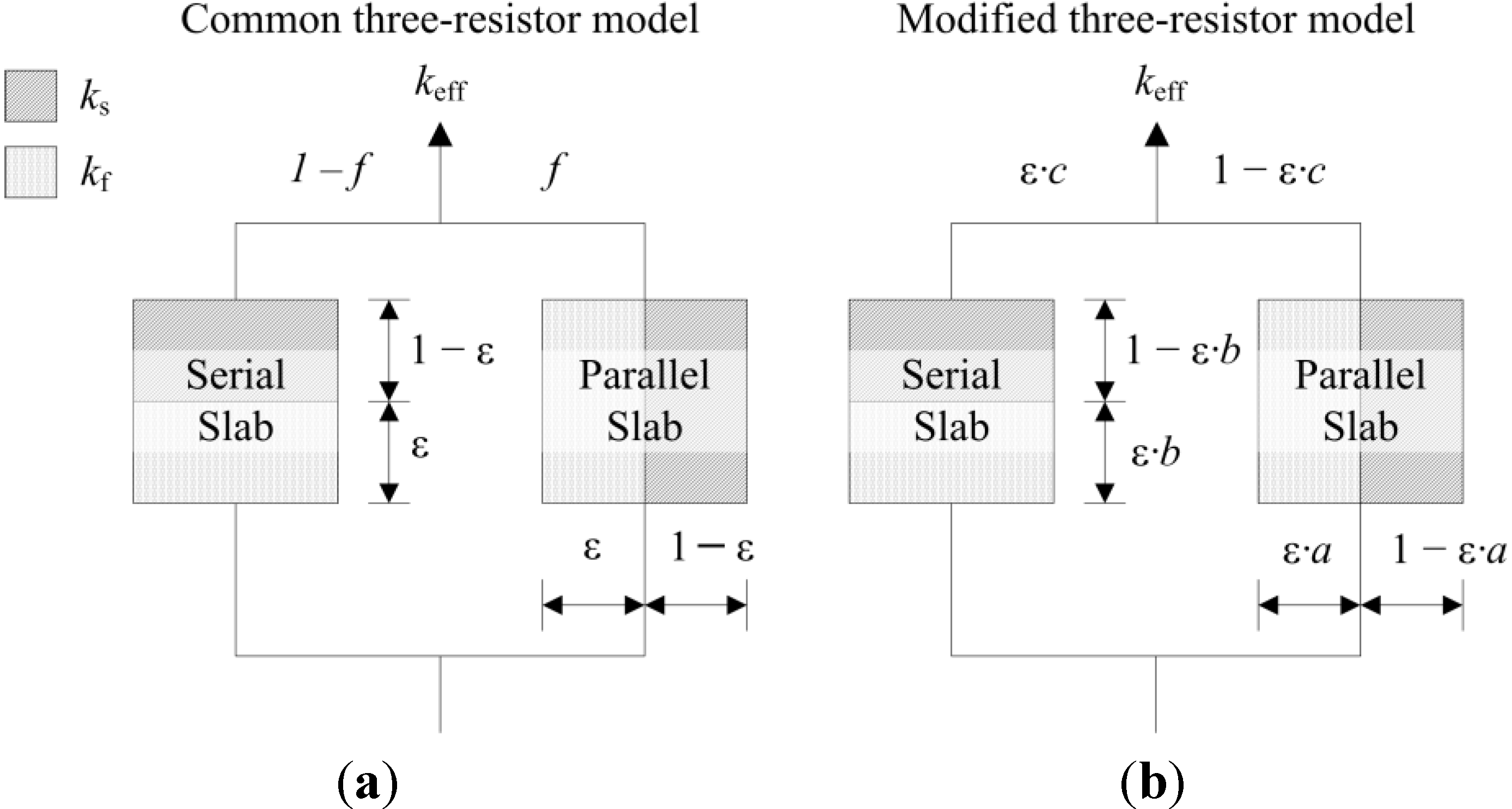
) up to platelike (number 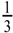 ) void and solid shapes. Miller’s bound model is restricted within the upper and lower bound of Hashin and Shtrikman [59] for all fitting parameters. The empirical model of Calmidi and Mahajan [60], shown in Figure 11b, is capable of predicting all three data sets and an overall data sets with a RMS < 5%. The model of Dul’nev and Zarichnyak [62] gives only keff,strut with a RMS < 5%. Dul’nev and Zarichnyak [22,30,61,62] propose a model using a linear combination of the Wiener lower and upper bounds with empirical fitting parameter, f, for weighting linear combination which is also called three-resistor model. However, if keff is fitted individually for each structure (porosity), an inverse trend of f is observed with porosity. Therefore, the three-resistor model is then extended by describing f as a 2nd-order polynomial function with porosity. Such extended three-resistor model, shown in Figure 11c, predicts keff,strut with RMS = 0.3% instead of 3.9%, keff,RPC with RMS = 1.6% instead of 9.2%, keff,dual with RMS = 2.2% instead of 9.8%, and keff,all with RMS = 2.3% instead of 12.6%. The three fitting parameters describing f with a 2nd-order polynomial function (c0, c1, c2) are replaced to allow the serial and parallel resistance, as well as their combination, to linearly scale with porosity, as shown schematically in Figure 12. Least-squares fitting of this modified three-resistor model, shown in Figure 11d, delivers the most accurate predictions: keff,strut with RMS = 0.1%, keff,RPC with RMS = 1.1%, keff,dual with RMS = 1.4%, and keff,all with RMS = 1.3%. The modified three-resistor model shows the best performance in prediction of keff with overall RMS < 1.5%. Fitting parameter a and b allow the lumped fluid and solid parts to deviate from actual ε within the parallel and serial slabs, respectively. Fitting parameter c allows linear combination of the serial and parallel slab to deviate from ε. This gives some degree of freedom for capturing different tortuous regions for a high porosity range (0.09 < ε < 0.9) and predicts the effective thermal conductivity more accurately compared to linear (or non-linear) combination of parallel/serial bounds and to Miller’s bound model.
) void and solid shapes. Miller’s bound model is restricted within the upper and lower bound of Hashin and Shtrikman [59] for all fitting parameters. The empirical model of Calmidi and Mahajan [60], shown in Figure 11b, is capable of predicting all three data sets and an overall data sets with a RMS < 5%. The model of Dul’nev and Zarichnyak [62] gives only keff,strut with a RMS < 5%. Dul’nev and Zarichnyak [22,30,61,62] propose a model using a linear combination of the Wiener lower and upper bounds with empirical fitting parameter, f, for weighting linear combination which is also called three-resistor model. However, if keff is fitted individually for each structure (porosity), an inverse trend of f is observed with porosity. Therefore, the three-resistor model is then extended by describing f as a 2nd-order polynomial function with porosity. Such extended three-resistor model, shown in Figure 11c, predicts keff,strut with RMS = 0.3% instead of 3.9%, keff,RPC with RMS = 1.6% instead of 9.2%, keff,dual with RMS = 2.2% instead of 9.8%, and keff,all with RMS = 2.3% instead of 12.6%. The three fitting parameters describing f with a 2nd-order polynomial function (c0, c1, c2) are replaced to allow the serial and parallel resistance, as well as their combination, to linearly scale with porosity, as shown schematically in Figure 12. Least-squares fitting of this modified three-resistor model, shown in Figure 11d, delivers the most accurate predictions: keff,strut with RMS = 0.1%, keff,RPC with RMS = 1.1%, keff,dual with RMS = 1.4%, and keff,all with RMS = 1.3%. The modified three-resistor model shows the best performance in prediction of keff with overall RMS < 1.5%. Fitting parameter a and b allow the lumped fluid and solid parts to deviate from actual ε within the parallel and serial slabs, respectively. Fitting parameter c allows linear combination of the serial and parallel slab to deviate from ε. This gives some degree of freedom for capturing different tortuous regions for a high porosity range (0.09 < ε < 0.9) and predicts the effective thermal conductivity more accurately compared to linear (or non-linear) combination of parallel/serial bounds and to Miller’s bound model.| Model | RMS | keff,strut (n = 24) | keff,RPC (n = 24) | keff,dual (n = 96) | keff,all (n = 144) |
|---|---|---|---|---|---|
| 1 | RMS (%) | 7.516 | 26.861 | 32.158 | 28.620 |
| 2 | RMS (%) | 233.780 | 223.485 | 213.144 | 218.449 |
| 3 | RMS (%) | 3.010 | 16.561 | 20.992 | 18.466 |
| 4 | RMS (%) | 204.379 | 207.200 | 200.080 | 202.003 |
| 5 | RMS (%) | 63.012 | 139.992 | 148.175 | 136.255 |
| 6 | RMS (%) | 4.772 | 17.828 | 22.024 | 19.497 |
| 7 | RMS (%) | 2.611 | 15.241 | 19.916 | 17.443 |
| 8 | RMS (%) | 3.010 | 16.561 | 20.992 | 18.466 |
| 9 | RMS (%) | 7.516 | 26.861 | 32.158 | 21.621 |
| 10 | r | 0.2912 | 0.1972 | 0.1254 | 0.2684 |
| 11 | RMS (%) | N/A 1 | N/A 1 | N/A 1 | N/A 1 |
| 12 | n | 2.1985 | 1.6343 | 1.5325 | 1.5701 |
| 13 | G1 | 1/9 | 0.1262 | 0.1268 | 0.1267 |
| 14 | A | 1.0285 | 1.0482 | 1.0709 | 1.0360 |
| 15 | f | 0.8377 | 0.4954 | 0.4217 | 0.4865 |
| 16 | c0 | 0.9972 | 0.3336 | 0.2581 | 0.9284 |
| 17 | a | 1.3194 | 1.0823 | 1.0541 | 1.0548 |
5. Summary and Conclusions
Acknowledgments
Nomenclature
| A0,(.) | Volumetric specific surface area (m−1) |
| Aflux | Cross sectional inlet/outlet area of cubic sample for heat flux (m2) |
| ssa(.) | Physical specific surface area (Index: strut, RPC, dual) (m2 g−1) |
| d | Diameter of spherical structuring elements (m) |
| dmean | Mean pore diameter (m) |
| f(d) | Pore size distribution (–) |
| F(d) | Cumulative pore size distribution (–) |
| ks | Solid thermal conductivity (W m−1 K−1) |
| kf | Fluid thermal conductivity (W m−1 K−1) |
| keff,(.) | Effective thermal conductivity of porous structure (W m−1 K−1) |
| lREV | Cube edge length of representative elementary volume (m) |
| L | Cube edge length (m) |
| n | Number of simulation data points (–) |
 | Heat flux through sample (W m−2 ) |
| s2(r) | Two point correlation function (–) |
| Tcold | Cold side temperature (K) |
| Tf | Fluid temperature (K) |
| Thot | Hot side temperature (K) |
| Ts | Solid temperature (K) |
| vs | Voxel size (m) |
| V | Total sample cube volume (m3) |
| Vf | Void volume (m3) |
| ε(.) | Porosity (–) |
| γ | Error band of porosity (–) |
| ςeff | Ratio of effective to solid thermal conductivity (–) |
| η | Ratio of fluid to solid thermal conductivity (–) |
| ϕ | Pore former concentration (vol%) |
Subscripts
| 2pc | 2-point correlation |
| mesh | 3D-mesh generated from digitally segmented structures |
| ImageJ | Calculated using open source software ImageJ |
| strut | Morphological property of porous strut |
| RPC | Morphological property of RPC with non-porous struts |
| dual | Morphological property of RPC with porous struts (dual-scale) |
| open | Open morphological property excluding closed pores |
| oc | Morphological property after applying opening-closing algorithm |
Conflicts of Interest
References
- Bear, J.; Buchlin, J.M. Modelling and Applications of Transport Phenomena in Porous Media; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1991; p. 380. [Google Scholar]
- Ho, C.K.; Webb, S.W. Gas Transport in Porous Media; Springer: Dordrecht, The Netherlands, 2006; p. 44. [Google Scholar]
- Vadász, P.T. Emerging Topics in Heat and Mass Transfer in Porous Media: From Bioengineering and Microelectronics to Nanotechnology; Springer: Dordrecht, The Netherlands, 2008; p. 328. [Google Scholar]
- Verruijt, A. An Introduction to Soil Dynamics; Springer: Dordrecht, The Netherlands, 2010; p. 433. [Google Scholar]
- Bear, J.; Verruijt, A. Modeling Groundwater Flow and Pollution: With Computer Programs for Sample Cases; D. Reidel Pub. Co.: Dordrecht, The Netherlands, 1987; p. 414. [Google Scholar]
- Dhamrat, R.S.; Ellzey, J.L. Numerical and experimental study of the conversion of methane to hydrogen in a porous media reactor. Combust. Flame 2006, 144, 698–709. [Google Scholar] [CrossRef]
- Pantangi, V.K.; Mishra, S.C.; Muthukumar, P.; Reddy, R. Studies on porous radiant burners for lpg (liquefied petroleum gas) cooking applications. Energy 2011, 36, 6074–6080. [Google Scholar] [CrossRef]
- Zermatten, E.; Vetsch, J.R.; Ruffoni, D.; Hofmann, S.; Müller, R.; Steinfeld, A. Micro-computed tomography based computational fluid dynamics for the determination of shear stresses in scaffolds within a perfusion bioreactor. Ann. Biomed. Eng. 2014, 42, 1085–1094. [Google Scholar] [CrossRef]
- Fend, T.; Hoffschmidt, B.; Pitz-Paal, R.; Reutter, O.; Rietbrock, P. Porous materials as open volumetric solar receivers: Experimental determination of thermophysical and heat transfer properties. Energy 2004, 29, 823–833. [Google Scholar] [CrossRef]
- Hischier, I.; Leumann, P.; Steinfeld, A. Experimental and numerical analyses of a pressurized air receiver for solar-driven gas turbines. J. Sol. Energy Eng. 2012, 134, 1–8. [Google Scholar]
- Hischier, I.; Poživil, P.; Steinfeld, A. A modular ceramic cavity-receiver for high-temperature high-concentration solar applications. J. Sol. Energy Eng. 2011, 134. [Google Scholar] [CrossRef]
- Romero, M.; Steinfeld, A. Concentrating solar thermal power and thermochemical fuels. Energy Environ. Sci. 2012, 5, 9234–9245. [Google Scholar] [CrossRef]
- Miller, J.E.; McDaniel, A.H.; Allendorf, M.D. Considerations in the design of materials for solar-driven fuel production using metal-oxide thermochemical cycles. Adv. Energy Mater. 2014, 4. [Google Scholar] [CrossRef]
- Furler, P.; Scheffe, J.; Gorbar, M.; Moes, L.; Vogt, U.; Steinfeld, A. Solar thermochemical CO2 splitting utilizing a reticulated porous ceria redox system. Energy Fuels 2012, 26, 7051–7059. [Google Scholar]
- Furler, P.; Scheffe, J.; Marxer, D.; Gorbar, M.; Bonk, A.; Vogt, U.; Steinfeld, A. Thermochemical CO2 splitting via redox cycling of ceria reticulated foam structures with dual-scale porosities. PCCP 2014, 16, 10503–10511. [Google Scholar] [CrossRef]
- Furler, P.; Scheffe, J.R.; Steinfeld, A. Syngas production by simultaneous splitting of H2O and CO2 via ceria redox reactions in a high-temperature solar reactor. Energy Environ. Sci. 2012, 5, 6098–6103. [Google Scholar] [CrossRef]
- Ackermann, S.; Scheffe, J.R.; Steinfeld, A. Diffusion of oxygen in ceria at elevated temperatures and its application to H2O/CO2 splitting thermochemical redox cycles. J. Phys. Chem. C 2014, 118, 5216–5225. [Google Scholar] [CrossRef]
- Chueh, W.C.; Falter, C.; Abbott, M.; Scipio, D.; Furler, P.; Haile, S.M.; Steinfeld, A. High-flux solar-driven thermochemical dissociation of CO2 and H2O using nonstoichiometric ceria. Science 2010, 330, 1797–1801. [Google Scholar] [CrossRef]
- Venstrom, L.J.; Petkovich, N.; Rudisill, S.; Stein, A.; Davidson, J.H. The effects of morphology on the oxidation of ceria by water and carbon dioxide. J. Sol. Energy Eng. 2012, 134. [Google Scholar] [CrossRef]
- Gibbons, W.T.; Venstrom, L.J.; de Smith, R.M.; Davidson, J.H.; Jackson, G.S. Ceria-based electrospun fibers for renewable fuel production via two-step thermal redox cycles for carbon dioxide splitting. Phys. Chem. Chem. Phys. 2014, 16, 14271–14280. [Google Scholar] [CrossRef]
- Keene, D.J.; Davidson, J.H.; Lipiński, W. A model of transient heat and mass transfer in a heterogeneous medium of ceria undergoing nonstoichiometric reduction. J. Heat Transfer 2013, 135. [Google Scholar] [CrossRef]
- Kaviany, M. Principles of Heat Transfer in Porous Media, 2nd ed.; Springer-Verlag: New York, NY, USA, 1995; p. 708. [Google Scholar]
- Whitaker, S. The Method of Volume Averaging; Series: Theory and Applications of Transport in Porous Media); Kluwer Academic: Dordrecht, The Netherlands, 1999; p. 219. [Google Scholar]
- Bodla, K.K.; Weibel, J.A.; Garimella, S.V. Advances in fluid and thermal transport property analysis and design of sintered porous wick microstructures. J. Heat Transf. 2013, 135. [Google Scholar] [CrossRef]
- Krishnan, S.; Murthy, J.Y.; Garimella, S.V. Direct simulation of transport in open-cell metal foam. J. Heat Transf. 2006, 128, 793–799. [Google Scholar] [CrossRef]
- Petrasch, J.; Meier, F.; Friess, H.; Steinfeld, A. Tomography based determination of permeability, dupuit-forchheimer coefficient, and interfacial heat transfer coefficient in reticulate porous ceramics. 2008, 29, 315–326. [Google Scholar]
- Petrasch, J.; Wyss, P.; Stämpfli, R.; Steinfeld, A. Tomography-based multiscale analyses of the 3D geometrical morphology of reticulated porous ceramics. J. Am. Ceram. Soc. 2008, 91, 2659–2665. [Google Scholar] [CrossRef]
- Bodla, K.K.; Murthy, J.Y.; Garimella, S.V. Microtomography-based simulation of transport through open-cell metal foams. Numer. Heat Transf. A Appl. 2010, 58, 527–544. [Google Scholar] [CrossRef]
- Petrasch, J.; Wyss, P.; Steinfeld, A. Tomography-based monte carlo determination of radiative properties of reticulate porous ceramics. J. Quant. Spectrosc. Radiat. Transf. 2007, 105, 180–197. [Google Scholar] [CrossRef]
- Haussener, S.; Coray, P.; Lipinski, W.; Wyss, P.; Steinfeld, A. Tomography-based heat and mass transfer characterization of reticulate porous ceramics for high-temperature processing. J. Heat Transf. 2010, 132. [Google Scholar] [CrossRef]
- Petrasch, J.; Schrader, B.; Wyss, P.; Steinfeld, A. Tomography-based determination of the effective thermal conductivity of fluid-saturated reticulate porous ceramics. ASME J. Heat Transf. 2008, 130. [Google Scholar] [CrossRef]
- Karl, S.; Somers, A.V. Method of Making Porous Ceramic Articles. U.S. Patent 3090094 A, 21 May 1963. [Google Scholar]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Sezgin, M.; Sankur, B.L. Survey over image thresholding techniques and quantitative performance evaluation. ELECTIM 2004, 13, 146–168. [Google Scholar]
- Zamel, N.; Li, X.; Shen, J. Correlation for the effective gas diffusion coefficient in carbon paper diffusion media. Energy Fuels 2009, 23, 6070–6078. [Google Scholar] [CrossRef]
- Giesche, H. Mercury porosimetry: A general (practical) overview. Part. Part. Syst. Charact. 2006, 23, 9–19. [Google Scholar] [CrossRef]
- Webb, P.A. An Introduction to the Physical Characterization of Materials by Mercury Intrusion Porosimetry with Emphasis on Reduction and Presentation of Experimental Data; Micromeritics Instrument Corp.: Norcross, GA, USA, 2001. [Google Scholar]
- Abràmoff, M.D.; Magalhães, P.J.; Ram, S.J. Image processing with imageJ. Biophoton. Int. 2004, 11, 36–43. [Google Scholar]
- Doube, M.; Kłosowski, M.M.; Arganda-Carreras, I.; Cordelières, F.P.; Dougherty, R.P.; Jackson, J.S.; Schmid, B.; Hutchinson, J.R.; Shefelbine, S.J. Bonej: Free and extensible bone image analysis in imageJ. Bone 2010, 47, 1076–1079. [Google Scholar] [CrossRef]
- Friess, H.; Haussener, S.; Steinfeld, A.; Petrasch, J. Tetrahedral mesh generation based on space indicator functions. Int. J. Numer. Methods Eng. 2013, 93, 1040–1056. [Google Scholar] [CrossRef]
- Berryman, J.G.; Blair, S.C. Use of digital image analysis to estimate fluid permeability of porous materials: Application of two-point correlation functions. J. Appl. Phys. 1986, 60, 1930–1938. [Google Scholar] [CrossRef]
- Mogensen, M.; Sammes, N.M.; Tompsett, G.A. Physical, chemical and electrochemical properties of pure and doped ceria. Solid State Ion. 2000, 129, 63–94. [Google Scholar] [CrossRef]
- Bruggeman, D.A.G. Berechnung verschiedener physikalischer konstanten von heterogenen substanzen. I. Dielektrizitätskonstanten und leitfähigkeiten der mischkörper aus isotropen substanzen. Ann. Phys. 1935, 416, 636–664. (In German) [Google Scholar] [CrossRef]
- Deissler, R.G.; Boegli, J.S. An investigation of effective thermal conductivities of powders in various gases. Trans. ASME 1958, 80, 1417–1425. [Google Scholar]
- Wang, M.; Pan, N. Predictions of effective physical properties of complex multiphase materials. Mater. Sci. Eng. R Rep. 2008, 63, 1–30. [Google Scholar] [CrossRef]
- DeVera, A.L.; Strieder, W. Upper and lower bounds on the thermal conductivity of a random, two-phase material. J. Phys. Chem. 1977, 81, 1783–1790. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the effective magnetic permeability of multiphase materials. J. Appl. Phys. 1962, 33, 3125–3131. [Google Scholar] [CrossRef]
- Woodside, W.; Messmer, J.H. Thermal conductivity of porous media. II. Consolidated rocks. J. Appl. Phys. 1961, 32, 1699–1706. [Google Scholar] [CrossRef]
- Russell, H.W. Principles of heat flow in porous insulators. J. Am. Ceram. Soc. 1935, 18, 1–5. [Google Scholar] [CrossRef]
- Loeb, A.L. Thermal conductivity: VIII, a theory of thermal conductivity of porous materials. J. Am. Ceram. Soc. 1954, 37, 96–99. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism, 3rd ed.; Dover Publications: New York, NY, USA, 1954. [Google Scholar]
- Choy, T.C. Effective Medium Theory: Principles and Applications; Oxford University Press: Oxford, UK, 1999; p. 182. [Google Scholar]
- Sattler, K.D. Handbook of Nanophysics. Nanoparticles and Quantum Dots; Taylor & Francis: Boca Raton, FL, USA, 2011. [Google Scholar]
- Kamiuto, K. Modeling of composite heat transfer in open-cellular porous materials at high temperatures. In Cellular and Porous Material Thermal Properties Simulation Prediction; Wiley-VCH: Weinheim, Germany, 2008; pp. 165–198. [Google Scholar]
- Coquard, R.; Loretz, M.; Baillis, D. Conductive heat transfer in metallic/ceramic open-cell foams. Adv. Eng. Mater. 2008, 10, 323–337. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Calmidi, V.V.; Mahajan, R.L. An analytical-experimental study for the determination of the effective thermal conductivity of high porosity fibrous foams. ASME Appl. Mech. Divis. Pupl. AMD 1999, 233, 13–20. [Google Scholar]
- Boomsma, K.; Poulikakos, D. On the effective thermal conductivity of a three-dimensionally structured fluid-saturated metal foam. Int. J. Heat Mass Transf. 2001, 44, 827–836. [Google Scholar] [CrossRef]
- Hamilton, R.L.; Crosser, O.K. Thermal conductivity of heterogeneous two-component systems. Ind. Eng. Chem. Fundam. 1962, 1, 187–191. [Google Scholar] [CrossRef]
- Miller, M.N. Bounds for effective electrical, thermal, and magnetic properties of heterogeneous materials. J. Math. Phys. 1969, 10, 1988–2004. [Google Scholar] [CrossRef]
- Calmidi, V.V.; Mahajan, R.L. The effective thermal conductivity of high porosity fibrous metal foams. J. Heat Transf. 1999, 121, 466–471. [Google Scholar] [CrossRef]
- Matsushita, M.; Monde, M.; Mitsutake, Y. Predictive calculation of the effective thermal conductivity in a metal hydride packed bed. Int. J. Hydrog. Energy 2014, 39, 9718–9725. [Google Scholar] [CrossRef]
- Dul’Nev, G.N.; Zarichnyak, Y.P. A study of the generalized conductivity coefficients in heterogeneous systems. Heat Transf. Sov. Res. 1970, 2, 89–107. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ackermann, S.; Scheffe, J.R.; Duss, J.; Steinfeld, A. Morphological Characterization and Effective Thermal Conductivity of Dual-Scale Reticulated Porous Structures. Materials 2014, 7, 7173-7195. https://doi.org/10.3390/ma7117173
Ackermann S, Scheffe JR, Duss J, Steinfeld A. Morphological Characterization and Effective Thermal Conductivity of Dual-Scale Reticulated Porous Structures. Materials. 2014; 7(11):7173-7195. https://doi.org/10.3390/ma7117173
Chicago/Turabian StyleAckermann, Simon, Jonathan R. Scheffe, Jonas Duss, and Aldo Steinfeld. 2014. "Morphological Characterization and Effective Thermal Conductivity of Dual-Scale Reticulated Porous Structures" Materials 7, no. 11: 7173-7195. https://doi.org/10.3390/ma7117173
APA StyleAckermann, S., Scheffe, J. R., Duss, J., & Steinfeld, A. (2014). Morphological Characterization and Effective Thermal Conductivity of Dual-Scale Reticulated Porous Structures. Materials, 7(11), 7173-7195. https://doi.org/10.3390/ma7117173