2.1. Sample Geometry
Two different sample geometries were investigated: one is a flat pure shear (PS) geometry with a thickness of 4 mm, and the other one is a so-called “faint waist pure shear” (FWPS) geometry with a nominal thickness of 2 mm. In [
5], this investigation has been performed for an engineering material. Now, this investigation is resumed for a model material. The corresponding cross-sections can be found in
Figure 1. It further shows the major strain distributions for the two geometries at equal displacement evaluated with 2D digital image correlation. As is also described in [
5], the strain distribution is uniform for flat PS geometry, whereas it shows enhanced strain in the middle of the sample for FWPS geometry. Thus, the strain is constant along the height of the specimen for PS samples and equals a mean strain value, ε
mean. For FWPS geometry, two strain values can be evaluated: a mean strain value averaged along the height, ε
mean, and an enhanced strain, ε
max.
Figure 1.
Strain distribution for flat pure shear (PS) and faint waist pure shear (FWPS) samples at equal displacement and corresponding cross-sections.
Figure 1.
Strain distribution for flat pure shear (PS) and faint waist pure shear (FWPS) samples at equal displacement and corresponding cross-sections.
In
Figure 2a, FCG curves of an SBR blend with 50 phr (parts per hundred parts rubber) carbon black can be found in dependence of the tearing energy for the two geometries. The crack growth rates for the FWPS geometry are larger than for the PS geometry. Yet, the crack growth curves of the two overlap if crack growth rates are plotted against the major strain and if the enhanced strain, ε
max, is taken into account for FWPS geometry (
Figure 2b). The crack is affected by ε
max; however, the tearing energy evaluated from force-displacement curves does not account for this enhanced strain, but is related to the mean strain, ε
mean [
5].
Figure 2.
(a) Fatigue crack growth (FCG) curves in dependence of tearing energy for FWPS and PS samples [SBR 100 filled with 50 phr carbon black (CB)]; (b) FCG curves in dependence of major strain for FWPS and PS samples [SBR 100 filled with 50 phr carbon black (CB)].
Figure 2.
(a) Fatigue crack growth (FCG) curves in dependence of tearing energy for FWPS and PS samples [SBR 100 filled with 50 phr carbon black (CB)]; (b) FCG curves in dependence of major strain for FWPS and PS samples [SBR 100 filled with 50 phr carbon black (CB)].
One disadvantage of PS samples is that the crack sometimes grows out of the plane of the notch, especially at higher tearing energies. An additional manual evaluation of the crack images is needed to obtain the actual crack length. This is undesirable, because an additional evaluation increases the user effort. Crack growth out of the plane of the notch was mainly observed with the engineering blend [
5] and seldom with the SBR blend. The major advantage of the PS geometry is that the tearing energy concept was developed for flat pure shear geometries [
2,
5]. Besides, the thicker PS geometry is more suitable for supporting tensional-compressional loads without buckling, which are of major interest in this study. Thus, PS geometry is used for the investigations described in the following subsections.
2.2. Frequency
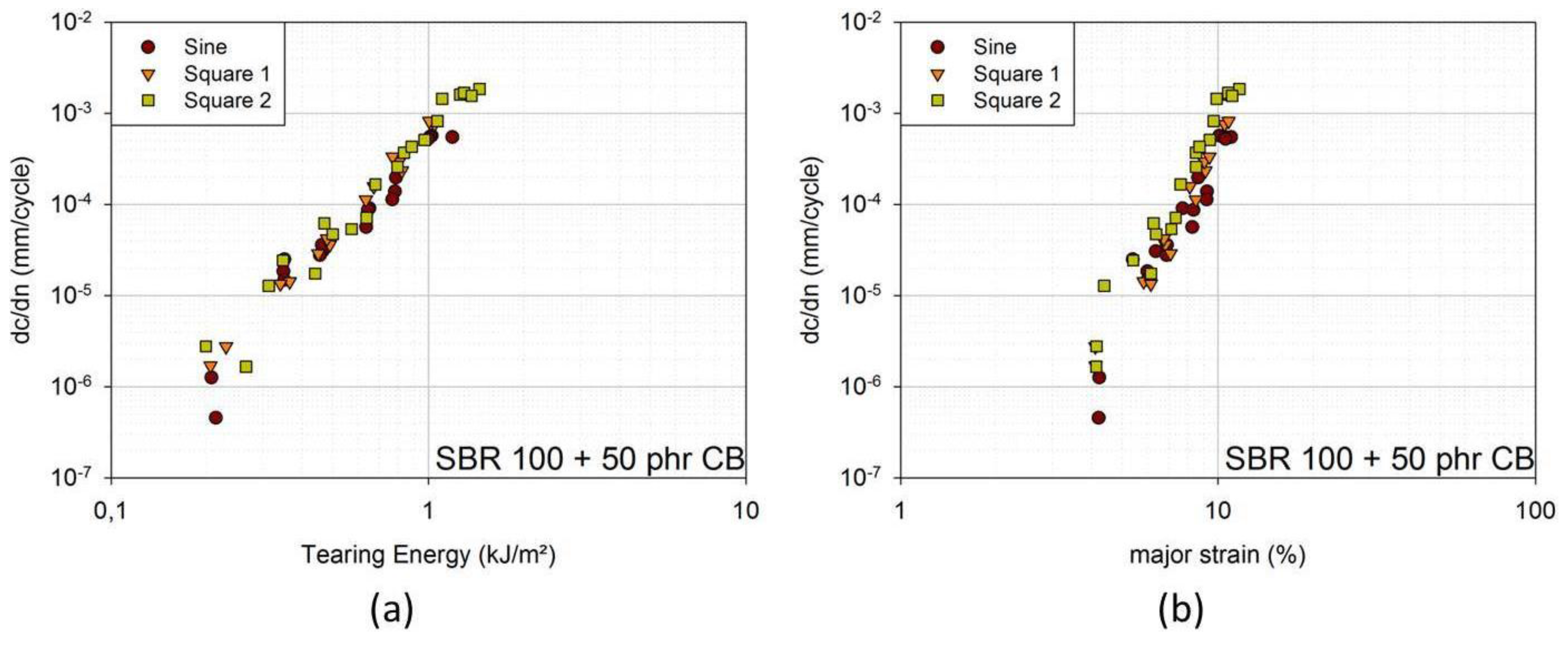
To determine the influence of frequency, the maximum and minimum amplitude were kept constant, and the frequency and, therefore, the rate of strain were changed. Three frequencies were chosen as 1 Hz, 3 Hz and 5 Hz. These cover the frequency range that is of interest for handrails on test facilities.
Figure 3 shows the results for the engineering material (NR/SBR 20/80 with 80 phr carbon black). Up to tearing energies of approximately 1.5 kJ/m², no differences can be identified between the FCG curves of 1 Hz, 3 Hz and 5 Hz. Above approximately 1.5 kJ/m², the curves of 3 Hz and 5 Hz still overlap, whereas the curves of 1 Hz lie at lower crack growth rates.
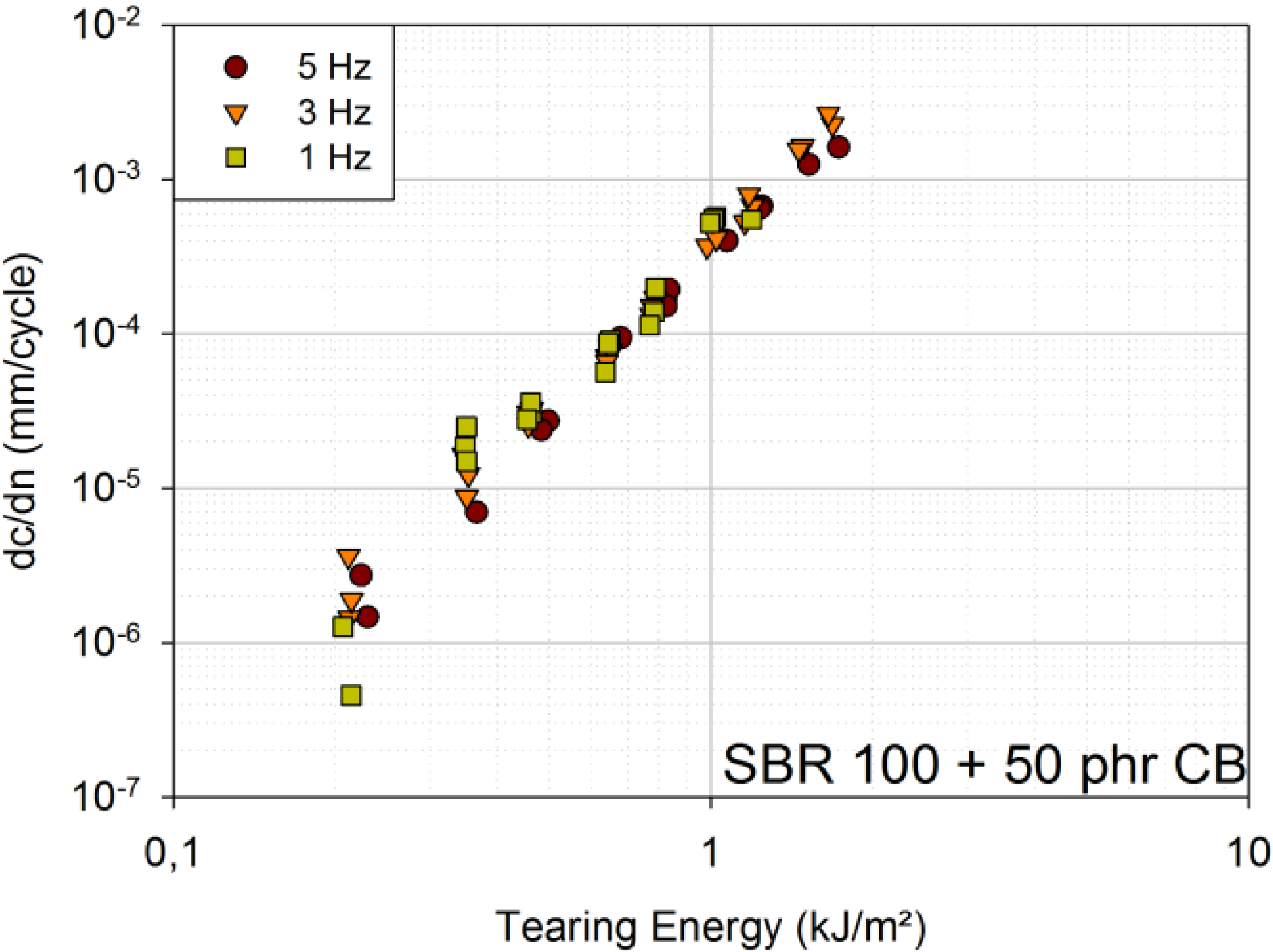
For the SBR blend with 50 phr carbon black, the curves for 1 Hz, 3 Hz and 5 Hz overlap over the whole tearing energy range tested (
Figure 4).
Upon the first impression, these results are inconsistent with the literature. In [
6,
8], it is stated that amorphous rubbers, like SBR, show a very large influence of frequency, whereas rubbers that can strain-crystallize, like NR, show no influence of frequency. For amorphous rubbers, the dependency on frequency is attributed to time-dependent steady crack growth, which is inhibited by strain-induced crystallization (NR). However, it is also stated that time-dependent steady crack growth is mainly critical for frequencies below 0.2 Hz. As the lowest frequency in this study is 1 Hz, time-dependent crack growth should not be significant. Besides, time-dependent crack growth is substantially reduced by the addition of fillers, like carbon black [
6].
Figure 3.
FCG curves for 1 Hz, 3 Hz and 5 Hz [engineering material: NR/SBR 20/80 filled with 80 phr carbon black (CB)].
Figure 3.
FCG curves for 1 Hz, 3 Hz and 5 Hz [engineering material: NR/SBR 20/80 filled with 80 phr carbon black (CB)].
Figure 4.
FCG curves for 1 Hz, 3 Hz and 5 Hz [model material: SBR 100 filled with 50 phr carbon black (CB)].
Figure 4.
FCG curves for 1 Hz, 3 Hz and 5 Hz [model material: SBR 100 filled with 50 phr carbon black (CB)].
It can be concluded that time-dependent crack growth, and, hence, frequency dependence, is smaller in filled amorphous rubbers than in unfilled ones. Nevertheless, time-dependent crack growth is significant mainly for very small frequencies. The FCG curves for different frequencies overlap, because the SBR blend is filled with 50 phr carbon black, and only frequencies down to 1 Hz are investigated. The same is true for the engineering material, but at tearing energies above 1.5 kJ/m², another effect seems to become more important: heat build-up due to cyclic loads. At 1.5 kJ/m², the plateau temperature is approximately 39 °C for 3 Hz and even approximately 47 °C for 5 Hz, whereas it is only approximately 28 °C for 1 Hz (tested under laboratory conditions). This large heat build-up represents another failure mechanism, and thermal failure is assumed to be added to the present mechanical failure [
8].
For SBR with 50 phr carbon black, the temperature rise is far smaller (at 1.5 kJ/m² and 5 Hz only approximately 35.5 °C), due to the lower level of carbon black filler content. Samples of SBR with 50 phr carbon black have not been loaded up to the same tearing energies as the engineering material, due to far larger crack growth rates, even at small loads.
2.3. Ratio
The amplitude ratio equates to the minimum amplitude divided by the maximum amplitude and is therefore dimensionless. The investigation of the NR/SBR blend with 80 phr carbon black is of major importance, because it represents an actual engineering material. Thus, five different ratios were chosen for the engineering material [ratio −1; ratio −0.5; ratio 0; ratio +0.1; ratio +0.5]. For the two model materials (SBR with 50 phr carbon black and BR/SBR 50/50 with 50 phr carbon black), three ratios were investigated [ratio −0.5; ratio 0; ratio +0.5].
The results for the NR/SBR blend are presented in
Figure 5. Compared to ratio 0, FCG curves for ratio +0.1 lie at slightly smaller crack growth rates, and for ratio +0.5, they lie at significantly smaller crack growth rates. The measurements with ratio +0.5 show quite a large scatter, because sometimes, no crack growth was detectable at all. In order to display such points in a double-logarithmic diagram, they were associated with a crack growth rate of 10
−8 mm/cycle.
Compared to ratio 0, ratio −0.5 shows similar crack growth rates; only at higher tearing energies, the crack growth rates of −0.5 are slightly larger. This can be attributed to the fact that there is a small compressional region, even for ratio 0, due to the permanent set [
11].
The FCG curves for ratio −1 clearly lie at the largest crack growth rates. This is also described in the literature [
12], where increased fatigue crack growth for ratio −1 is associated with a chemical degradation at the crack tip caused by large compressional loads.
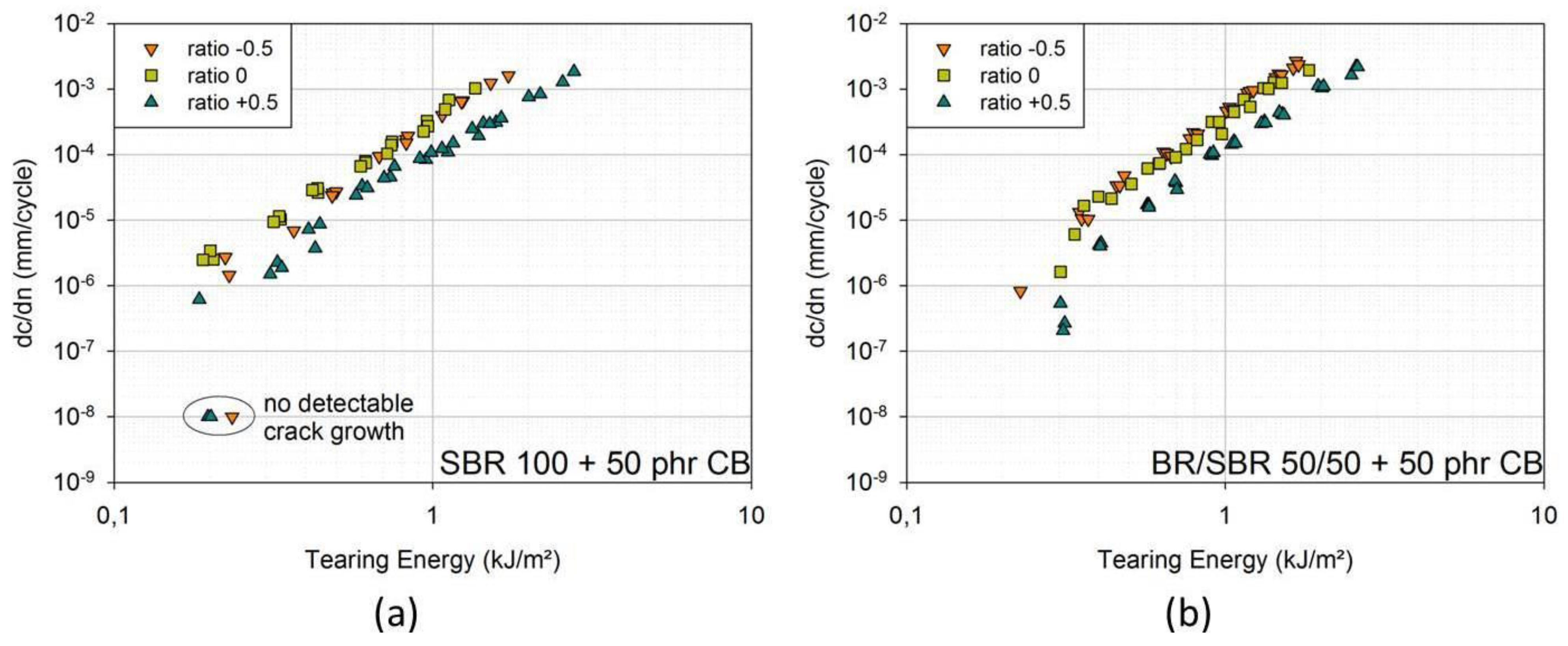
In
Figure 6a,b, one can see the results for SBR with 50 phr carbon black and BR/SBR 50/50 with 50 phr carbon black. In both cases, FCG curves for ratio +0.5 lie at significantly smaller crack growth rates. FCG curves for ratio 0 and −0.5 overlap. For BR/SBR, the curves for ratio 0 lie at slightly smaller crack growth rates than for ratio −0.5, though the differences are small.
All results indicate a beneficial effect of a positive loading ratio. Usually, this effect is attributed to strain-crystallizing rubbers [
6]. However, the beneficial effect of an increased minimum strain has been also described in [
13] for filler reinforced non-strain-crystallizing rubbers and is attributed to the filler-polymer system.
Figure 5.
FCG curves for ratio −1; ratio −0.5; ratio 0; ratio +0.1; and ratio +0.5 [engineering material: NR/SBR 20/80 filled with 80 phr carbon black (CB)]; a non-detectable crack growth corresponds to a crack growth rate of 10−8 mm/cycle.
Figure 5.
FCG curves for ratio −1; ratio −0.5; ratio 0; ratio +0.1; and ratio +0.5 [engineering material: NR/SBR 20/80 filled with 80 phr carbon black (CB)]; a non-detectable crack growth corresponds to a crack growth rate of 10−8 mm/cycle.
Figure 6.
(a) FCG curves for ratio −0.5; ratio 0; ratio +0.5; (model material: SBR 100 filled with 50 phr carbon black (CB)); (b) FCG curves for ratio +0.5; ratio 0; ratio −0.5; (model material: BR/SBR 50/50 filled with 50 phr carbon black (CB)). Non-detectable crack growth corresponds to a crack growth rate of 10−8 mm/cycle.
Figure 6.
(a) FCG curves for ratio −0.5; ratio 0; ratio +0.5; (model material: SBR 100 filled with 50 phr carbon black (CB)); (b) FCG curves for ratio +0.5; ratio 0; ratio −0.5; (model material: BR/SBR 50/50 filled with 50 phr carbon black (CB)). Non-detectable crack growth corresponds to a crack growth rate of 10−8 mm/cycle.
2.5. Heat Build-Up
According to [
6], the heat generation per second during cyclic loading is given by the dissipated energy per cycle, times the frequency. For the current investigation, the heat generation is divided by the cross-section area of the sample in order to take into account sample geometry. Thus, it is suggested to display resulting plateau temperatures in dependence of dissipated energy per time and per unit area.
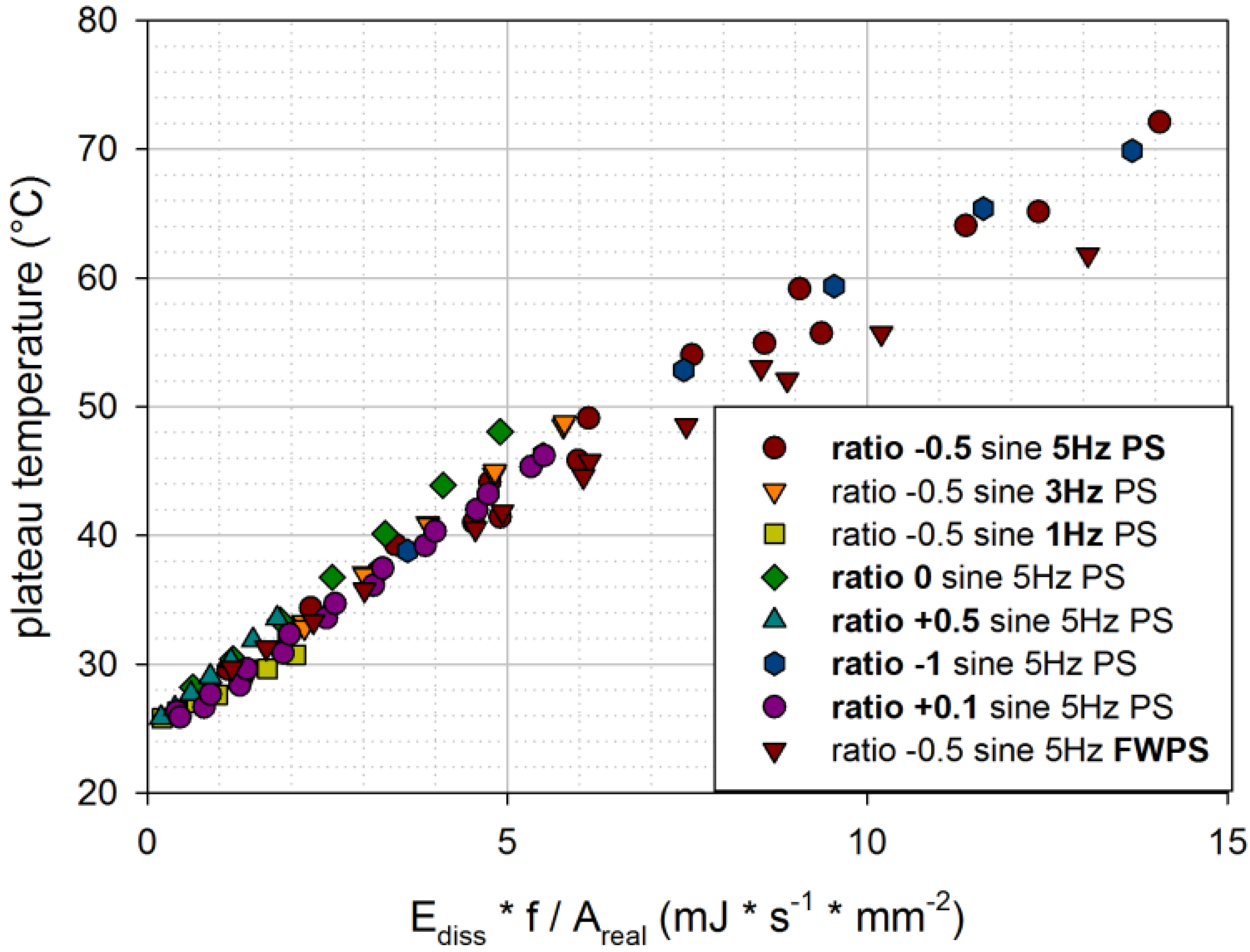
In
Figure 9, plateau temperatures for the engineering material (NR/SBR 20/80 with 80 phr carbon black) are plotted against dissipated energy per second and per unit area. Plateau temperatures are obtained for various loading conditions (various amplitude ratios, frequencies and sample geometries). Though there is quite a large scatter, a linear trend can be observed. At higher tearing energies, plateau temperatures of FWPS are lower compared to PS, probably because of buckling during compression.
For SBR with 50 phr carbon black and BR/SBR 50/50 with 50 phr carbon black, the results from fatigue crack growth measurements cannot be used to determine plateau temperatures, because the crack growth is very large, and therefore, the number of cycles was substantially reduced. Thus, measurements of plateau temperatures were performed separately on non-cut samples.
Approximately linear relationships can be observed also for SBR with 50 phr carbon black and BR/SBR 50/50 with 50 phr carbon black for the variation of frequency and amplitude ratio. Though, especially for SBR with 50 phr carbon black, there is quite a large scatter.
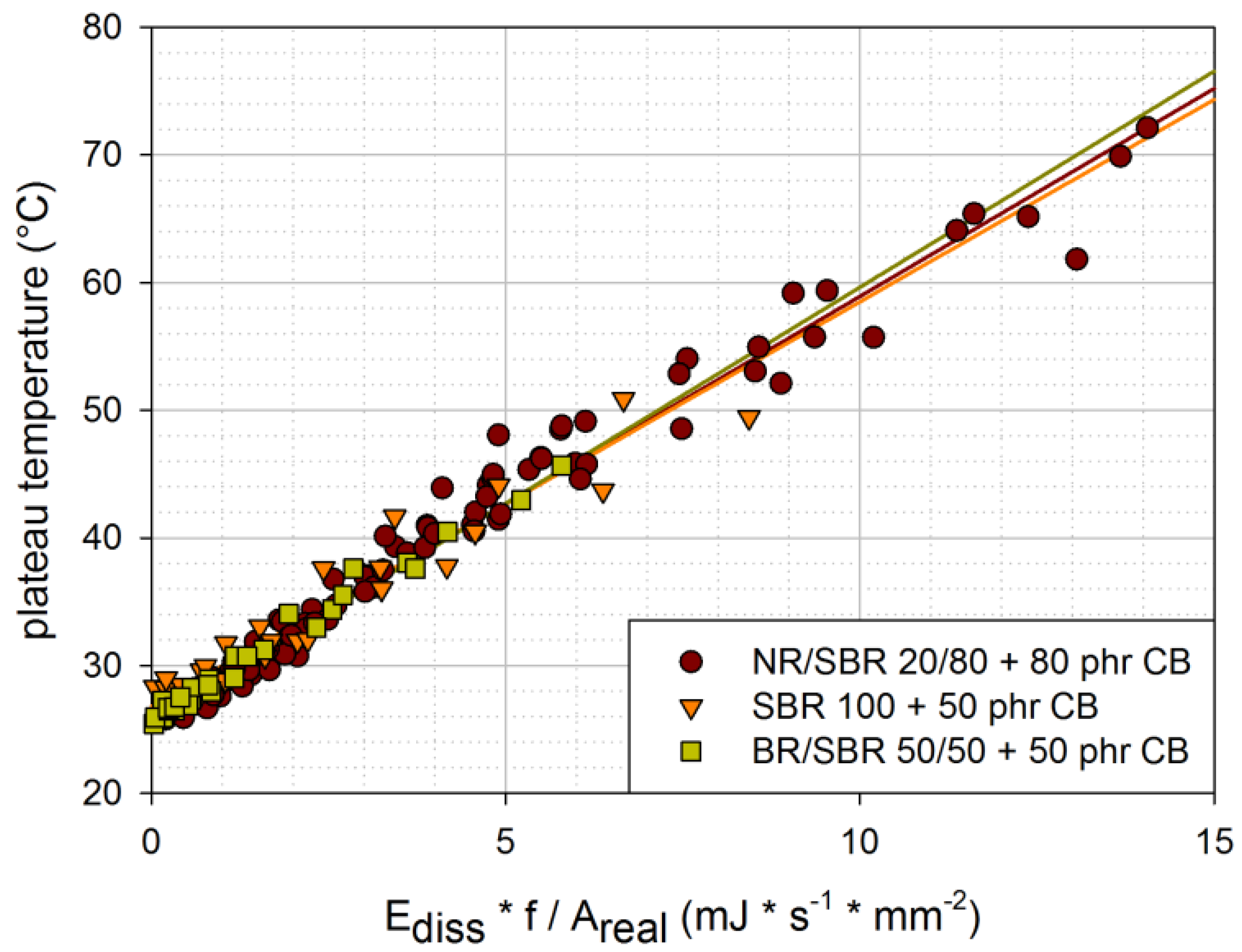
In
Figure 10, the plateau temperatures determined under various loading conditions are plotted for the three investigated materials. The linear fits nearly overlap for all three materials. The differences in material behavior seem to be covered by the dissipated energy, which is determined from force-displacement curves. Furthermore, all investigated rubber blends seem to have similar coefficients of thermal conduction. This is in accordance with [
6], where it is stated that thermal conductivity in rubber is fairly independent of the elastomer.
Figure 9.
Plateau temperatures for various loading conditions in dependence of the dissipated energy per second and per unit area [engineering material: NR/SBR 20/80 filled with 80 phr carbon black (CB)].
Figure 9.
Plateau temperatures for various loading conditions in dependence of the dissipated energy per second and per unit area [engineering material: NR/SBR 20/80 filled with 80 phr carbon black (CB)].
Figure 10.
Plateau temperatures for various loading conditions in dependence of the dissipated energy per second and per unit area [engineering material: NR/SBR 20/80 filled with 80 phr carbon black; model material: SBR 100 filled with 50 phr carbon black; model material: BR/SBR 50/50 filled with 50 phr carbon black (CB)].
Figure 10.
Plateau temperatures for various loading conditions in dependence of the dissipated energy per second and per unit area [engineering material: NR/SBR 20/80 filled with 80 phr carbon black; model material: SBR 100 filled with 50 phr carbon black; model material: BR/SBR 50/50 filled with 50 phr carbon black (CB)].
Nevertheless, it has to be emphasized that the scatter of the results in
Figure 10 is quite large. Thus, the dissipated energy per time and unit area only gives an idea of the plateau temperature reached. There are probably other influence factors that are not considered in this very simple relationship.
In order to further test this quite simple relationship, additional dynamic mechanical analysis measurements were performed. Temperature differences were calculated from the plateau temperature and the sample temperature before loading. Very few measurements led to evaluable data, as sometimes, the sample shifted within the fixtures or the resulting loads exceeded the load limit. For BR/SBR 50/50 filled with 50 phr carbon black, only two measurements were evaluable.
However, the temperature differences in dependence of dissipated energy per second and per unit area show, again, a linear relationship. Yet, it has to be emphasized that the heat build-up within the sample is very small compared to the results of usual fatigue measurements. This can be attributed to the far smaller sample size and the lower loads applied.