Material–Structural Synergy in Ultra-High-Performance Concrete-Optimized Prestressed Concrete Cylinder Pipes: Achieving Lightweight Design for Sustainable Infrastructure
Abstract
1. Introduction
2. Validation of Numerical Model
2.1. Element Discretization and Parameters
2.2. Constitutive and Contact Model
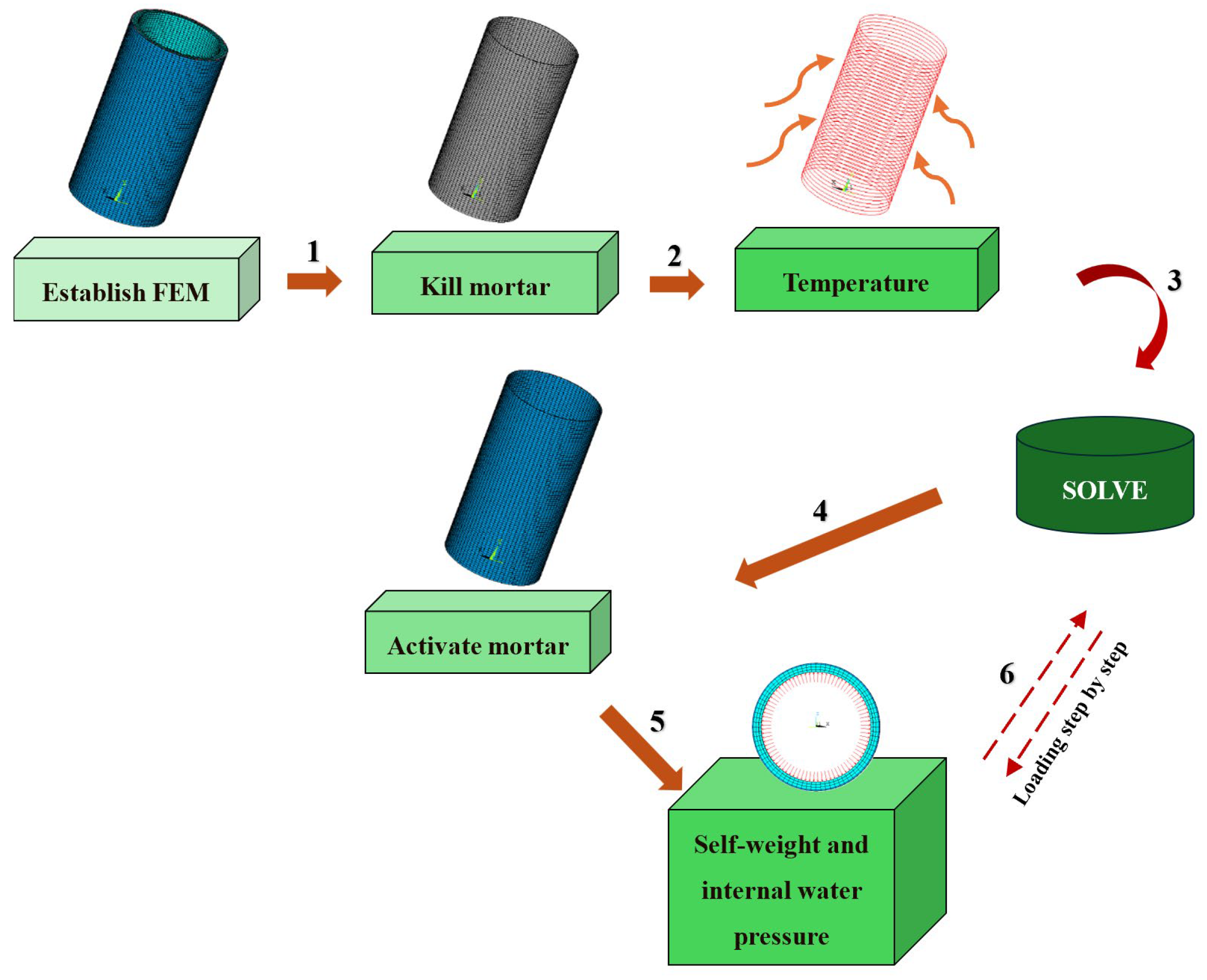
2.3. Analysis Procedure
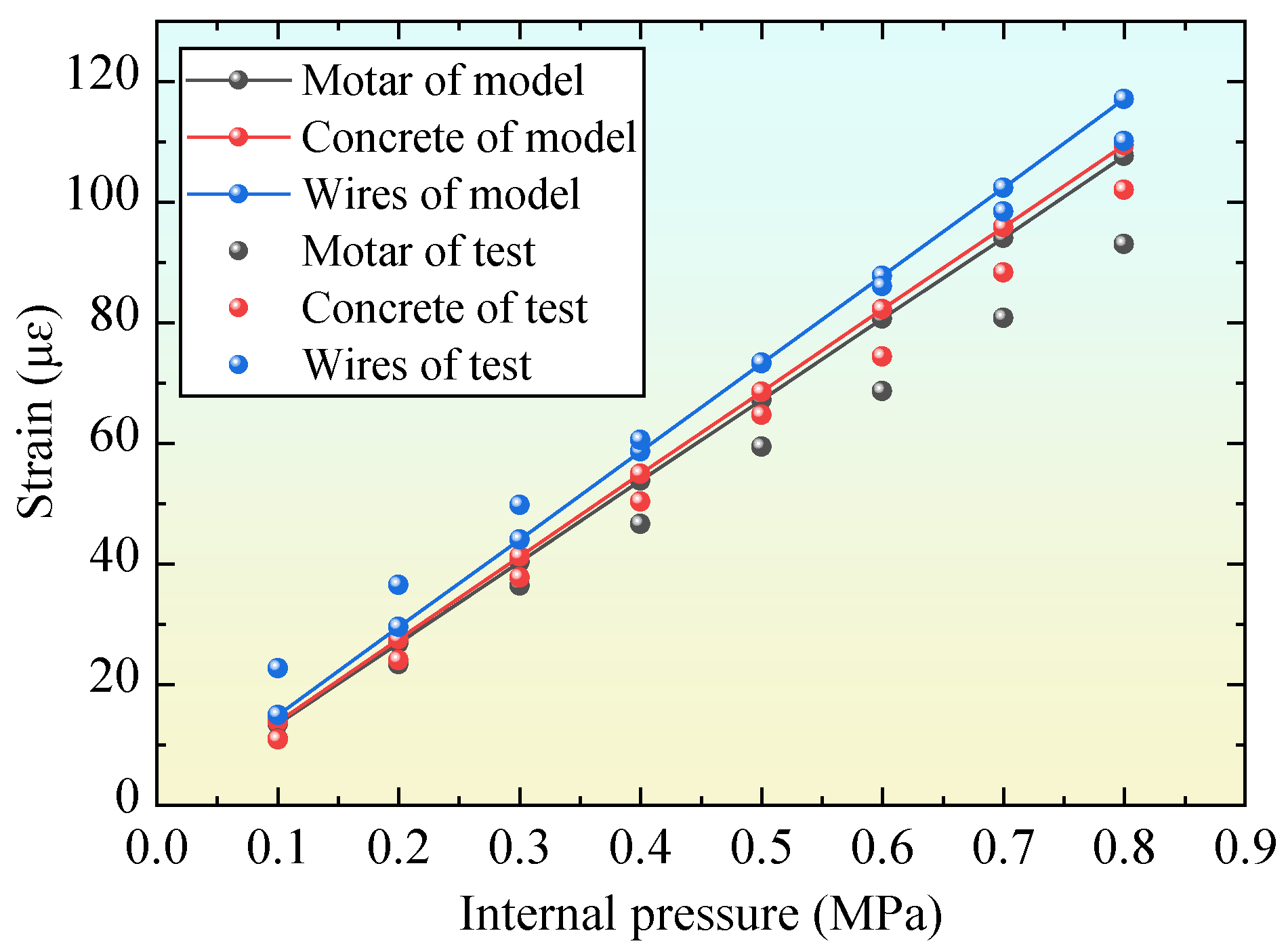
2.4. Model Evaluation
3. Modeling
4. Calculated Results and Analysis
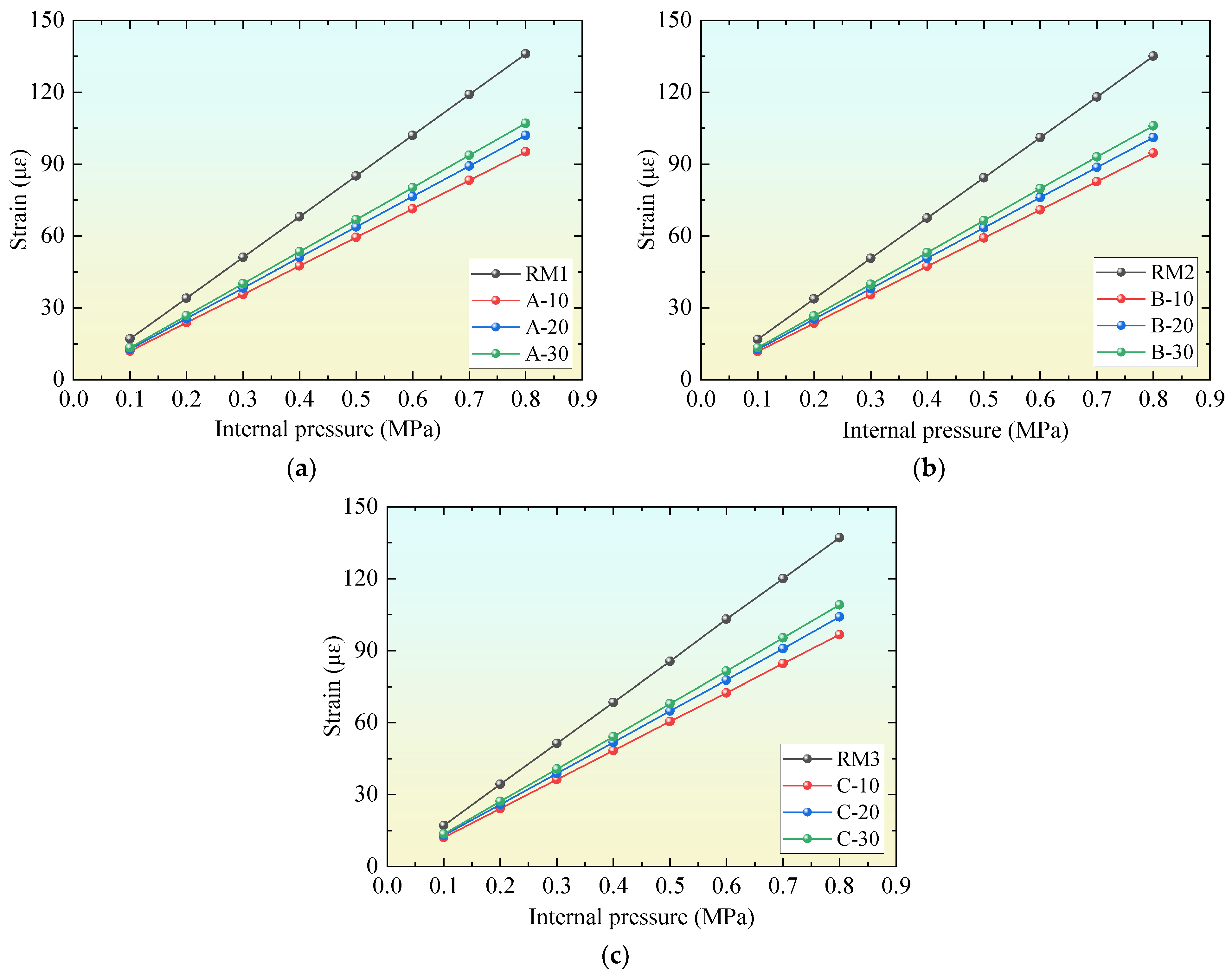
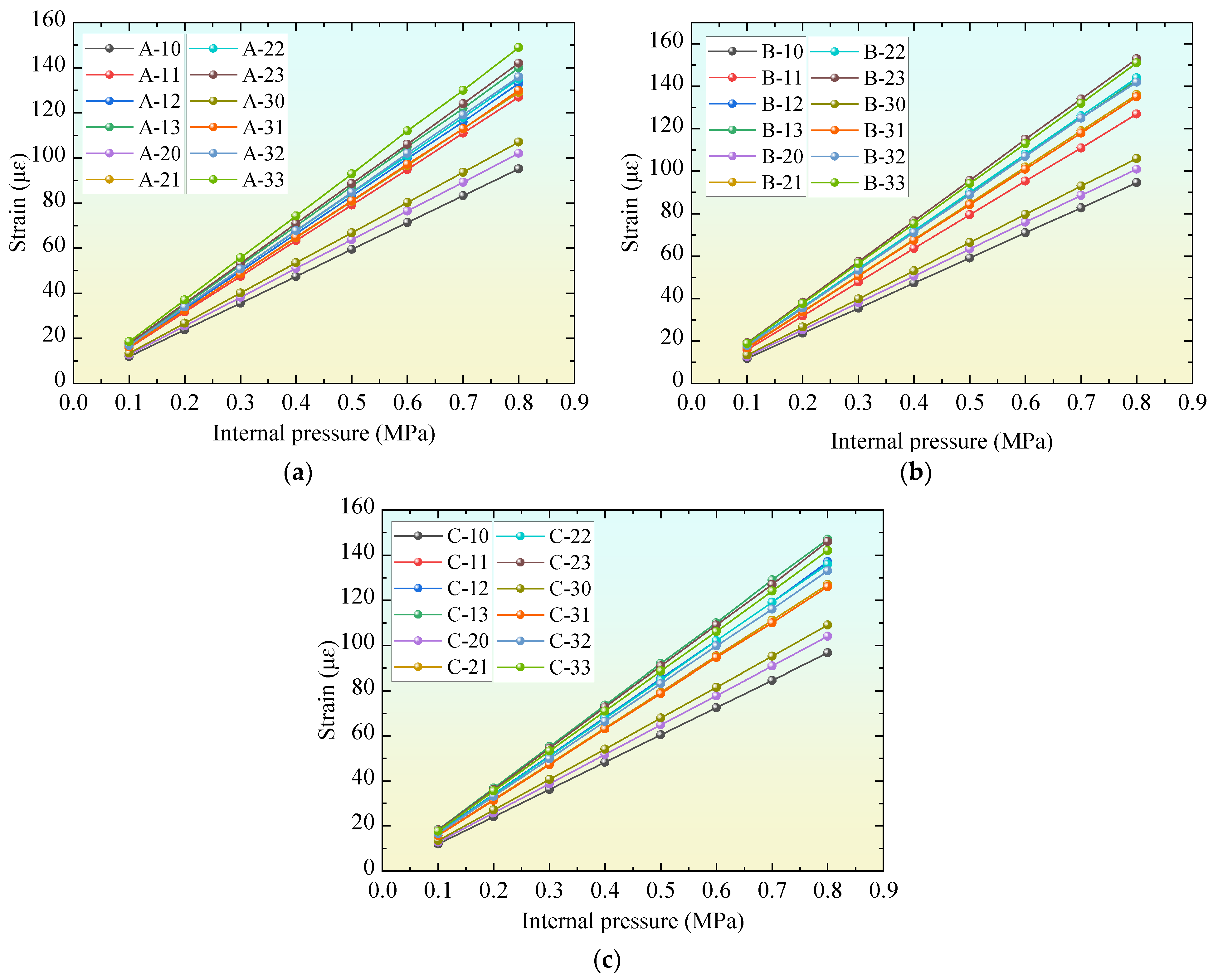
4.1. Effect of UHPC on Strain of Mortar Coating
4.2. Influence of UHPC on Thickness of Concrete Core
4.3. Establishing the Optimization Formula for Hc
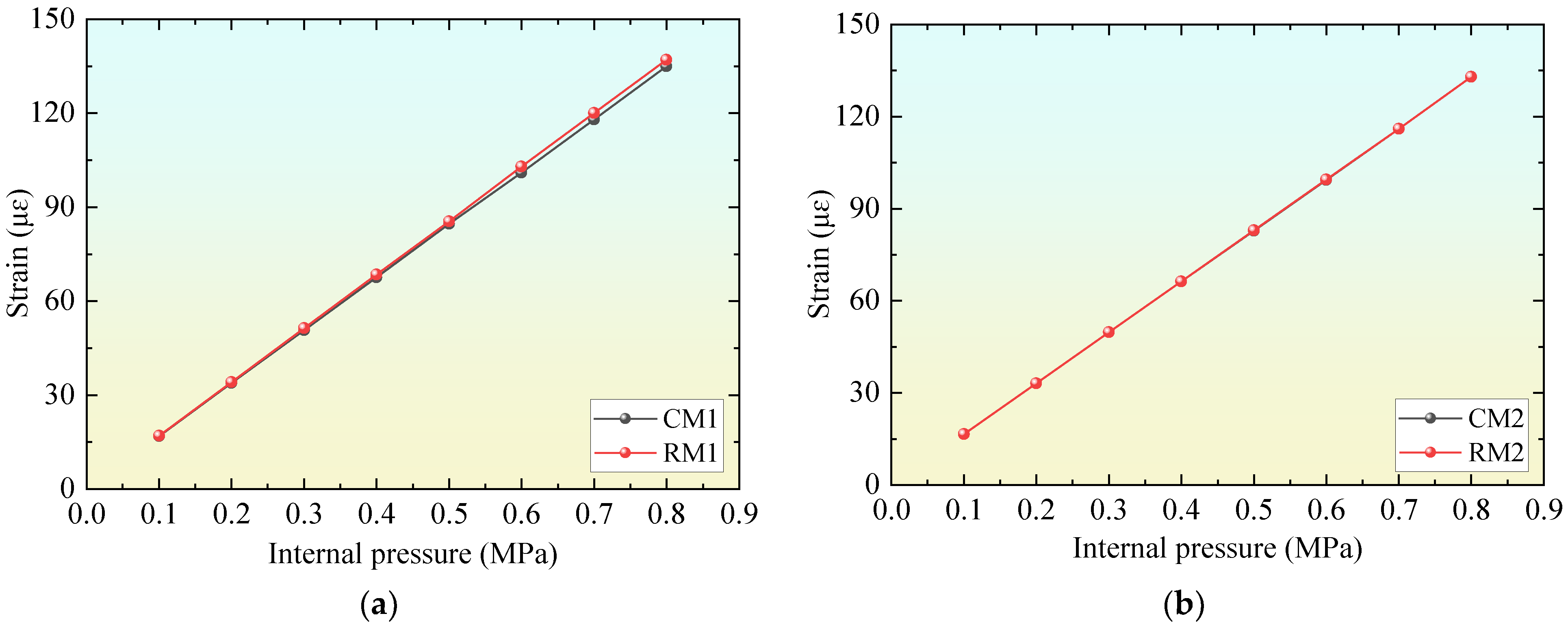
4.4. Formula Validation
5. Conclusions and Suggestions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- American Water Works Association. Design of Prestressed Concrete Cylinder Pipe (AWWAC304-14); American Water Works Association: Denver, CO, USA, 2019. [Google Scholar]
- Tong, D.; Sun, L. Research on compactness measurement method for deep backfill soil of PCCP construction. Chin. J. Undergr. Space Eng. 2018, 14, 1157–1165. [Google Scholar]
- Zarghamee, M.; Fok, K. Analysis of prestressed concrete pipe under combined loads. J. Struct. Eng. 1990, 116, 2022–2039. [Google Scholar] [CrossRef]
- Zarghamee, M.; Ojdrovic, R.; Dana, W. Coating delamination by radial tension in prestressed concrete pipe. I: Experiments. J. Struct. Eng. 1993, 119, 2701–2719. [Google Scholar] [CrossRef]
- Zarghamee, M.; Ojdrovic, R.; Dana, W. Coating delamination by radial tension in prestressed concrete pipe. II: Analysis. J. Struct. Eng. 1993, 119, 2720–2732. [Google Scholar] [CrossRef]
- Zarghamee, M.; Moharrami, M. Experimental study and numerical simulation of three-edge bearing test of large diameter prestressed concrete cylinder pipes. Cond. Assess. Constr. Rehabil. 2018, 776–787. [Google Scholar]
- Zai, K.; Fang, H.; Guo, C.; Li, B.; Wang, N.; Yang, K.; Zhang, X.; Du, X.; Di, D. Using EPS and CFRP liner to strengthen prestressed concrete cylinder pipe. Constr. Build. Mater. 2024, 412, 134860. [Google Scholar] [CrossRef]
- Zarghamee, M.S.; Eggers, D.W.; Ojdrovic, R.; Rose, B. Risk analysis of prestressed concrete cylinder pipe with broken wires. In Proceedings of the Pipeline Engineering & Construction International Conference, Baltimore, MD, USA, 13–16 July 2003; pp. 599–609. [Google Scholar]
- Zhai, K.; Fang, H.; Fu, B.; Wang, F.; Hu, B. Mechanical response of externally bonded CFRP on repair of PCCPs with broken wires under internal water pressure. Constr. Build Mater. 2020, 239, 117878. [Google Scholar] [CrossRef]
- Zhai, K.; Guo, C.; Fang, H.; Li, B.; Wang, F. Stress distribution and mechanical response of PCCP with broken wires. Eng. Struct. 2021, 245, 112858. [Google Scholar] [CrossRef]
- Zhai, K.; Fang, H.; Guo, C.; Fu, B.; Ni, P.; Ma, H.; Fang, H.; Wang, F. Mechanical properties of CFRP-strengthened prestressed concrete cylinder pipe based on multifield coupling. Thin-Walled Struct. 2021, 162, 107629. [Google Scholar] [CrossRef]
- Xiang, T.; Chen, X.; Guo, Z.; Wang, J.; Cui, L.; Qiang, Y.; Zhang, S. Robust solid slippery surface for anti-corrosion: Experimental and simulation. Prog. Org. Coat. 2024, 188, 108250. [Google Scholar] [CrossRef]
- Zarghamee, M.S. Hydrostatic pressure testing of prestressed concrete cylinder pipe with broken wires. In Proceedings of the Pipeline Engineering & Construction International Conference, Baltimore, MD, USA, 13–16 July 2003; pp. 294–303. [Google Scholar]
- Liu, X.; Feng, X. A near-wall acoustic wave-based localization method for broken wires in a large diameter PCCP using an FBG sensor array. Measurement 2022, 205, 112154. [Google Scholar] [CrossRef]
- Zhai, K.; Fang, H.; Yang, M.; Sun, M.; Zhang, X.; Zhao, X.; Xue, B.; Lei, J.; Yao, X. The impacts of CFRP widths and thicknesses on the strengthening of PCCP Failure experiment on CFRP-strengthened prestressed concrete cylinder pipe with broken wires. Structures 2023, 56, 104856. [Google Scholar] [CrossRef]
- Hu, H.; Niu, F.; Dou, T.; Zhang, H. Rehabilitation Effect Evaluation of CFRP-Lined Prestressed Concrete Cylinder Pipe under Combined Loads Using Numerical Simulation. Math. Probl. Eng. 2018, 2018, 3268962. [Google Scholar] [CrossRef]
- Hu, H.; Dou, T.; Niu, F.; Zhang, H.; Su, W. Experimental and numerical study on CFRP-lined prestressed concrete cylinder pipe under internal pressure. Eng. Struct. 2019, 190, 480–492. [Google Scholar] [CrossRef]
- Beijing Municipal Engineering Design and Research Institute. Specification for Structural Design of Buried Prestressed Concrete Pipeline and Prestressed Concrete Cylinder Pipeline of Water Supply and Sewerage Engineering; Beijing Municipal Engineering Design and Research Institute: Beijing, China, 2011. [Google Scholar]
- Huawei, Z. Structure Optimization Design of Prestressed Ultra High Performance Concrete Pip; Harbin Institute of Technology: Harbin, China, 2020. [Google Scholar]
- Sheng, Z. Study on Structural Analysis and Safety Evaluation of Large Diameter Buried Pipeline; Dalian University of Technology: Dalian, China, 2017. [Google Scholar]
- Lv, Y.; Chen, Y.; Dai, W.; Yang, H.; Jiang, L.; Li, K.; Jin, W. Preparation and properties of porous concrete based on geopolymer of red mud and yellow river sediment. Materials 2024, 17, 923. [Google Scholar] [CrossRef]
- Cui, L.; Xiang, T.; Hu, B.; Lv, Y.; Rong, H.; Liu, D.; Zhang, S.; Guo, M.; Lv, Z.; Chen, D. Design of monolithic superhydrophobic concrete with excellent anti-corrosion and self-cleaning properties. Colloid Surf. A 2024, 685, 133345. [Google Scholar] [CrossRef]
- Lv, Y.; Zhang, W.; Wu, F.; Wu, P.; Zeng, W.; Yang, F. Static mechanical properties and mechanism of C200 ultra-high-performance concrete (UHPC) containing coarse aggregates. Sci. Eng. Compos. Mater. 2020, 27, 186–195. [Google Scholar]
- Liu, Y.; Wei, Y. Effect of calcined bauxite powder or aggregate on the shrinkage properties of UHPC. Cem. Concr. Comp. 2021, 118, 103967. [Google Scholar] [CrossRef]
- Deng, F.; Xu, L.; Chi; Chen, Q. Effect of steel-polypropylene hybrid fiber and coarse aggregate inclusion on the stress-strain behavior of ultra-high-performance concrete under uniaxial compression. Compos. Struct. 2020, 252, 112685. [Google Scholar] [CrossRef]
- Wu, F.; Xu, L.; Chi, Y.; Zeng, Y.; Deng, F.; Chen, Q. Compressive and flexural properties of ultra-high-performance fiber-reinforced cementitious composite: The effect of coarse aggregate. Compos. Struct. 2020, 236, 111810. [Google Scholar] [CrossRef]
- Haile, B.F.; Jin, D.W.; Yang, B.; Park, S.; Lee, H.K. Multilevel homogenization for the prediction of the mechanical properties of ultra-high-performance concrete. Constr. Build. Mater. 2019, 229, 116797. [Google Scholar] [CrossRef]
- Yoo, D.; Kang, S.; Lee, J.; Yoon, Y.S. Effect of shrinkage reducing admixture on tensile and flexural behaviors of UHPFRC considering fiber distribution characteristics. Cem. Concr. Res. 2013, 54, 180–190. [Google Scholar] [CrossRef]
- Makita, T.; Brühwiler, E. Tensile fatigue behaviour of ultra-high performance fibre reinforced concrete (UHPFRC). Mater. Struct. 2014, 47, 475–491. [Google Scholar] [CrossRef]
- Liu, Y.; Wei, Y. Internal curing efficiency and key properties of UHPC influenced by dry or prewetted calcined bauxite aggregate with different particle size. Constr. Build. Mater. 2021, 312, 125406. [Google Scholar] [CrossRef]
- Zhang, H.; Ji, T.; Zeng, X.; Yang, Z.; Lin, X.; Liang, Y. Mechanical behavior of ultra-high-performance concrete (UHPC) using recycled fine aggregate cured under different conditions and the mechanism based on integrated microstructural parameters. Constr. Build. Mater. 2018, 192, 489–507. [Google Scholar] [CrossRef]
- Yu, L.; Huang, L.; Ding, H. Rheological and mechanical properties of ultra-high-performance concrete containing fine recycled concrete aggregates. Materials 2019, 12, 3717. [Google Scholar] [CrossRef]
- Shao, X.; Qiu, M.; Yan, B.; Luo, J. A review on the research and application of ultra-high-performance concrete in bridge engineering around the world. Chin. J. Mater. Rep. 2017, 31, 33–43. [Google Scholar]
- Zhai, K.; Fang, H.; Li, B.; Guo, C.; Yang, K.; Du, X.; Du, M.; Wang, N. Failure experiment on CFRP strengthened prestressed concrete cylinder pipe with broken wires. Tunn. Undergr. Sp. Technol. 2023, 135, 105032. [Google Scholar] [CrossRef]
- Zhai, K.; Fang, H.; Guo, C.; Ni, P.; Zhang, C. Strengthening of PCCP with broken wires using prestressed CFRP. Constr. Build. Mater. 2021, 267, 120903. [Google Scholar] [CrossRef]
- Zhai, K.; Fang, H.; Guo, C.; Ni, P.; Wu, H.; Wang, F. Full-scale experiment and numerical simulation of prestressed concrete cylinder pipe with broken wires strengthened by prestressed CFRP. Tunn. Undergr. Sp. Tech. 2021, 115, 104021. [Google Scholar] [CrossRef]
- Hu, B.; Fang, H.; Wang, F.; Zhai, K. Full-scale test and numerical simulation study on load-carrying capacity of prestressed concrete cylinder pipe (PCCP) with broken wires under internal water pressure. Eng. Fail. Anal. 2019, 104, 513–530. [Google Scholar] [CrossRef]
- Zhang, W.G.; Goh, A.T.C. Numerical study of pillar stresses and interaction effects for twin rock caverns. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 193–206. [Google Scholar] [CrossRef]
- Fang, H.; Li, B.; Wang, F.; Wang, Y.; Cui, C. The mechanical behaviour of drainage pipeline under traffic load before and after polymer grouting trenchless repairing. Tunn. Undergr. Sp. Technol. 2018, 74, 185–194. [Google Scholar] [CrossRef]
- Thompson, M.K.; Thompson, J.M. ANSYS Mechanical APDL for Finite Element Analysis; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Ouyang, X. Calculation Model and Experimental Investigation of Modulus of Elasticity in Ultra-High Performance Concrete; Hunan University: Changsha, China, 2022. [Google Scholar]
- Zhang, R.; Zhang, W.G.; Goh, A.T.C. Numerical investigation of pile responses caused by adjacent braced excavation in soft clays. Int. J. Geotech. Eng. 2018, 15, 783–797. [Google Scholar] [CrossRef]
- Hajar, Z.; Lecointre, D.; Simon, A. Design and construction of the world first ultra-high performance concrete road bidges. In Proceedings of the International Symposium on Ultra-High Performance Concrete, Kassel, Germany, 13–15 September 2004; Kassel University Press: Kassel, Germany, 2004. [Google Scholar]
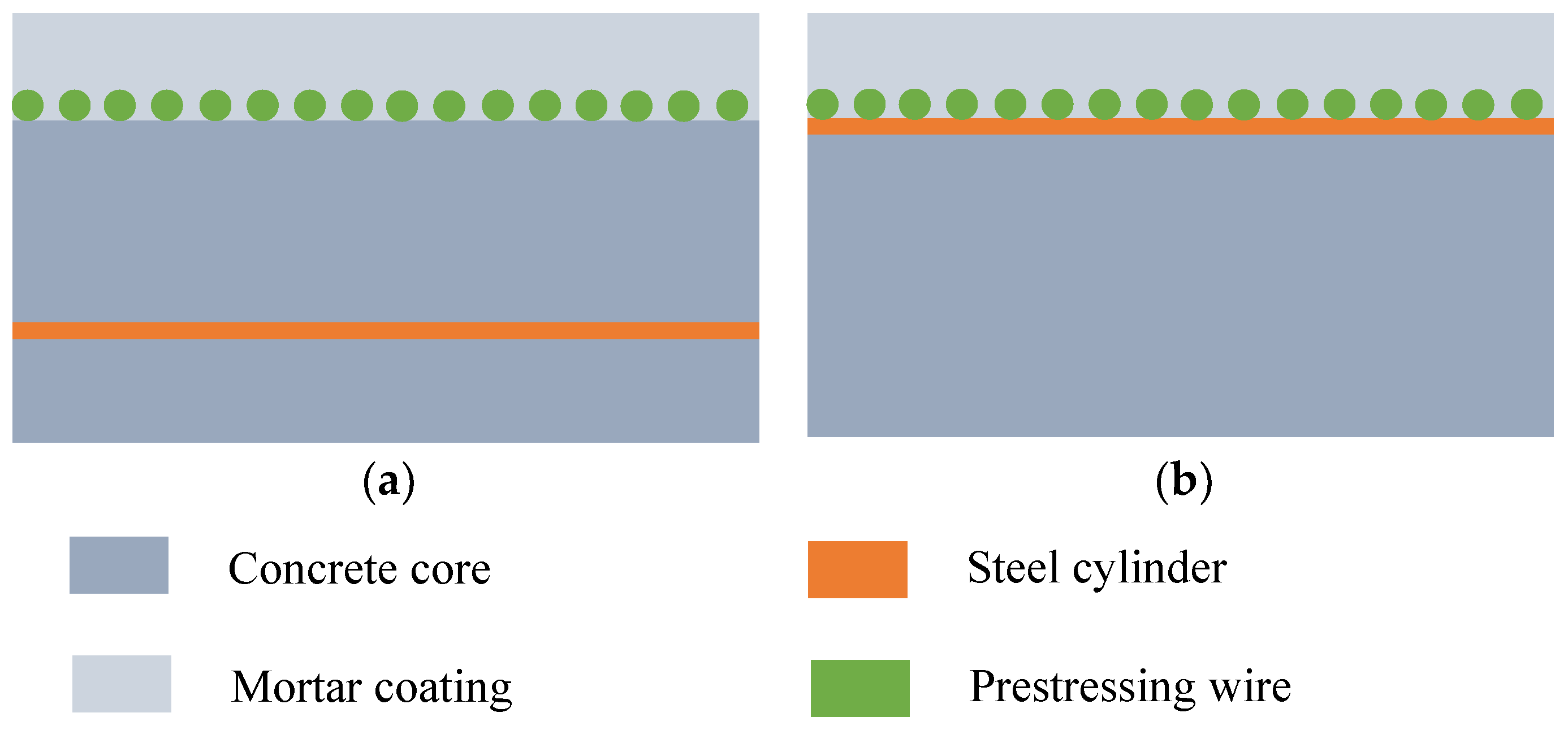


| Material | Density (kg/m3) | Modulus of Elasticity (GPa) | Poisson’s Ratio | Value (mm) |
|---|---|---|---|---|
| Concrete core | 2500 | 34.5 | 0.2 | 200 |
| Prestressing wire | 7850 | 205 | 0.3 | 7 |
| Mortar coating | 2400 | 24.165 | 0.2 | 32 |
| Steel cylinder | 7850 | 206 | 0.3 | 1.5 |
| D1 | Esi | Hc1 | NUM | D2 | Esi | Hc1 | NUM | D3 | Esi | Hc1 | NUM |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 m | Es1 = 53 GPa | 260 mm | A-10 | 3.4 m | Es1 = 53 GPa | 220 mm | B-10 | 2.8 m | Es1 = 53 GPa | 175 mm | C-10 |
| 190 mm | A-11 | 160 mm | B-11 | 130 mm | C-11 | ||||||
| 180 mm | A-12 | 150 mm | B-12 | 120 mm | C-12 | ||||||
| 170 mm | A-13 | 140 mm | B-13 | 110 mm | C-13 | ||||||
| Es2 = 48 GPa | 260 mm | A-20 | Es2 = 48 GPa | 220 mm | B-20 | Es2 = 48 GPa | 175 mm | C-20 | |||
| 200 mm | A-21 | 160 mm | B-21 | 140 mm | C-21 | ||||||
| 190 mm | A-22 | 150 mm | B-22 | 130 mm | C-22 | ||||||
| 180 mm | A-23 | 140 mm | B-23 | 120 mm | C-23 | ||||||
| Es3 = 45 GPa | 260 mm | A-30 | Es3 = 45 GPa | 220 mm | B-30 | Es3 = 45 GPa | 175 mm | C-30 | |||
| 210 mm | A-31 | 170 mm | B-31 | 150 mm | C-31 | ||||||
| 200 mm | A-32 | 160 mm | B-32 | 140 mm | C-32 | ||||||
| 180 mm | A-33 | 150 mm | B-33 | 130 mm | C-33 |
| D | Es1 | Es2 | Es3 |
|---|---|---|---|
| 4 | 30.2% | 25% | 21.3% |
| 3.4 | 29.6% | 25.2% | 21.5% |
| 2.8 | 29.5% | 24.1% | 20.4% |
| Hc | NUM | σm,∆ | Hc | NUM | σm,∆ | Hc | NUM | σm,∆ |
|---|---|---|---|---|---|---|---|---|
| 260 mm | A-10 | −1 | 220 mm | B-10 | −0.97 | 175 mm | C-10 | −0.98 |
| 190 mm | A-11 | −0.24 | 160 mm | B-11 | −0.19 | 130 mm | C-11 | −0.24 |
| 180 mm | A-12 | −0.1 | 150 mm | B-12 | 0 | 120 mm | C-12 | −0.01 |
| 170 mm | A-13 | 0.08 | 140 mm | B-13 | 0.21 | 110 mm | C-13 | 0.25 |
| 260 mm | A-20 | −0.84 | 220 mm | B-20 | −0.81 | 175 mm | C-20 | −0.8 |
| 200 mm | A-21 | −0.18 | 160 mm | B-21 | 0.03 | 140 mm | C-21 | −0.24 |
| 190 mm | A-22 | −0.03 | 150 mm | B-22 | 0.22 | 130 mm | C-22 | −0.03 |
| 180 mm | A-23 | 0.1 | 140 mm | B-23 | 0.44 | 120 mm | C-23 | 0.21 |
| 260 mm | A-30 | −0.7 | 220 mm | B-30 | −0.69 | 175 mm | C-30 | −0.68 |
| 210 mm | A-31 | −0.16 | 170 mm | B-31 | 0 | 150 mm | C-31 | −0.26 |
| 200 mm | A-32 | −0.03 | 160 mm | B-32 | 0.18 | 140 mm | C-32 | −0.1 |
| 180 mm | A-33 | 0.3 | 150 mm | B-33 | 0.34 | 130 mm | C-33 | 0.12 |
| Name | D | Es | Hc | |
|---|---|---|---|---|
| Example 1 | RM1 | 3.8 m | 34.5 GPa | Hc0 = 245 mm |
| CM1 | 3.8 m | 48 GPa | Hc1 = 180 mm | |
| Example 2 | RM2 | 2 m | 34.5 GPa | Hc0 = 125 mm |
| CM2 | 2 m | 53 GPa | Hc1 = 85 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Yuan, C.; Lv, Y.; Bai, W.; Zhang, Y. Material–Structural Synergy in Ultra-High-Performance Concrete-Optimized Prestressed Concrete Cylinder Pipes: Achieving Lightweight Design for Sustainable Infrastructure. Materials 2025, 18, 2144. https://doi.org/10.3390/ma18092144
Xie Y, Yuan C, Lv Y, Bai W, Zhang Y. Material–Structural Synergy in Ultra-High-Performance Concrete-Optimized Prestressed Concrete Cylinder Pipes: Achieving Lightweight Design for Sustainable Infrastructure. Materials. 2025; 18(9):2144. https://doi.org/10.3390/ma18092144
Chicago/Turabian StyleXie, Yunfei, Chenyang Yuan, Yajun Lv, Weifeng Bai, and Yizhen Zhang. 2025. "Material–Structural Synergy in Ultra-High-Performance Concrete-Optimized Prestressed Concrete Cylinder Pipes: Achieving Lightweight Design for Sustainable Infrastructure" Materials 18, no. 9: 2144. https://doi.org/10.3390/ma18092144
APA StyleXie, Y., Yuan, C., Lv, Y., Bai, W., & Zhang, Y. (2025). Material–Structural Synergy in Ultra-High-Performance Concrete-Optimized Prestressed Concrete Cylinder Pipes: Achieving Lightweight Design for Sustainable Infrastructure. Materials, 18(9), 2144. https://doi.org/10.3390/ma18092144





