Topological Analysis of Electron Density in Graphene/Benzene and Graphene/hBN
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
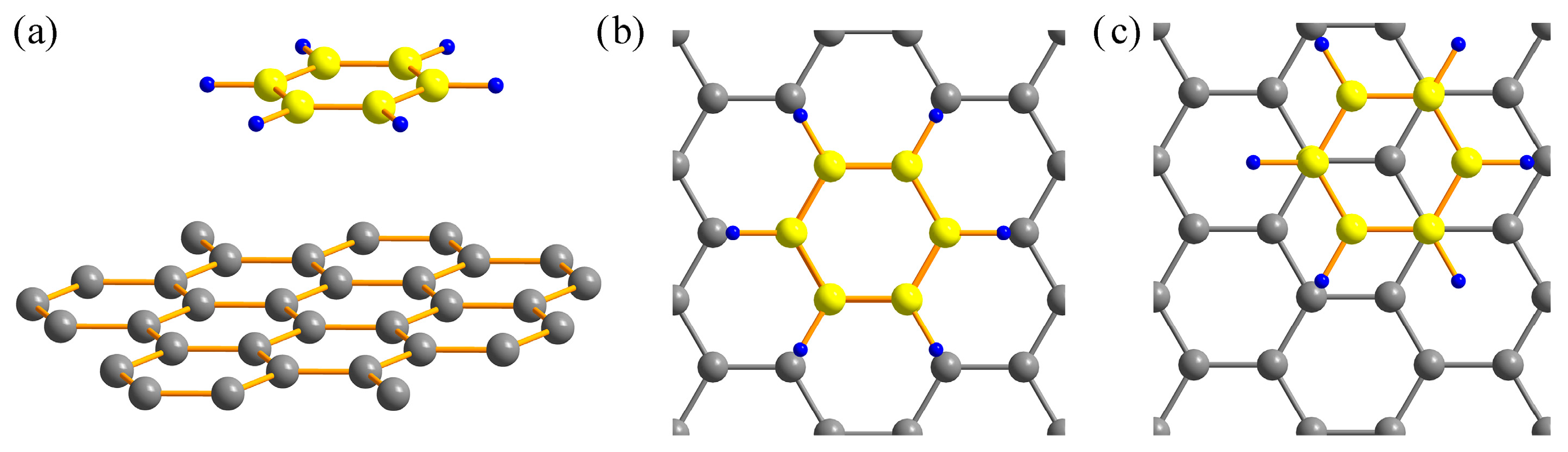
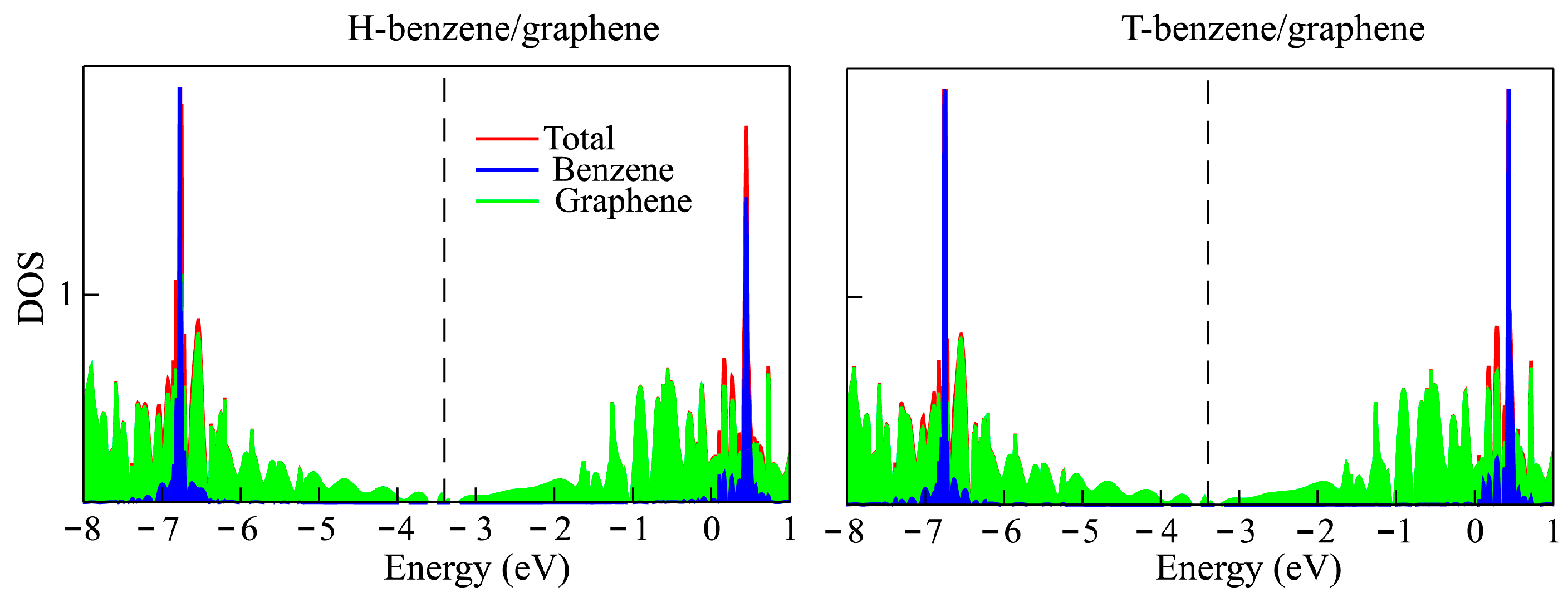
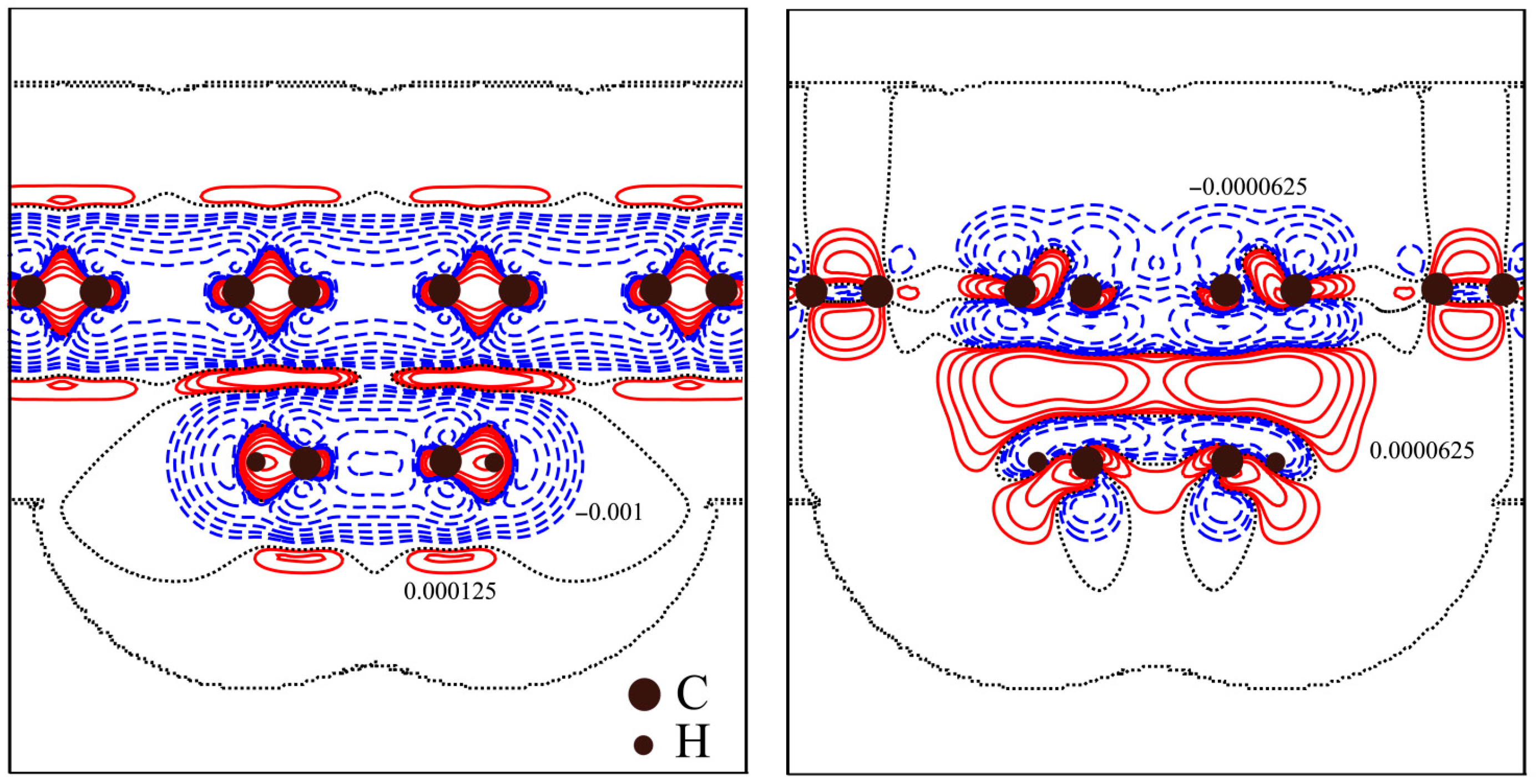
3.1. Benzene Molecule on a Graphene
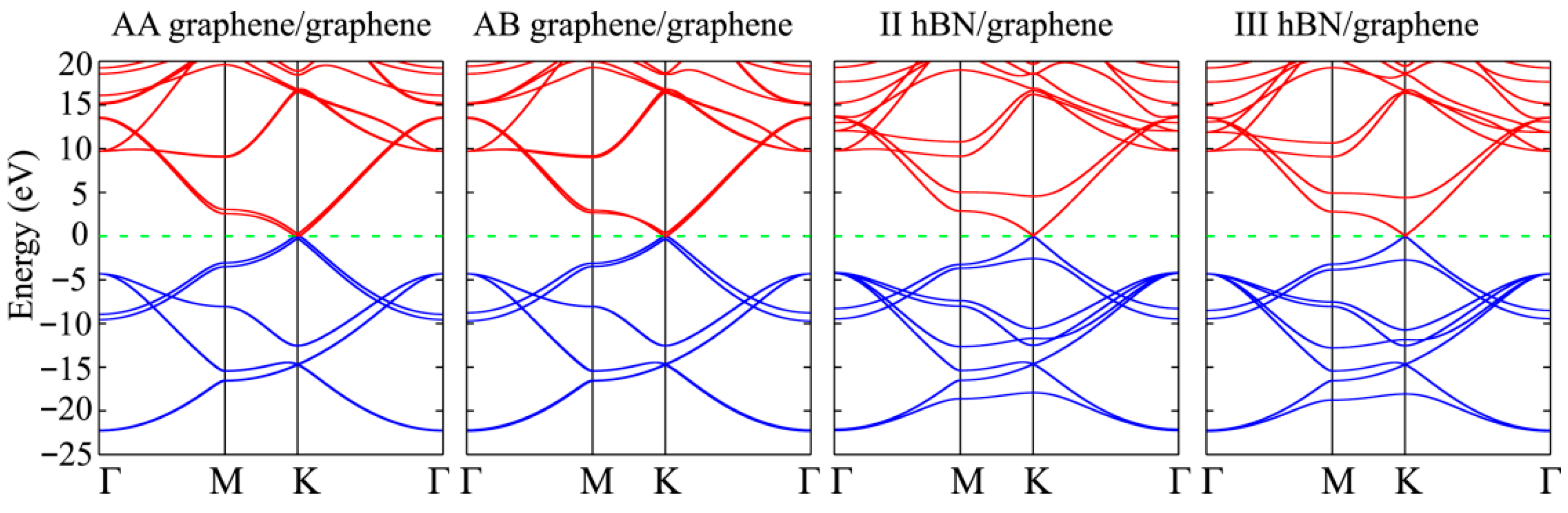
3.2. Graphene/Graphene Van Der Waals Heterostructure
3.3. Graphene/hBN Van Der Waals Heterostructure
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Mao, H.Y.; Lu, Y.H.; Lin, J.D.; Zhong, S.; Wee, A.T.S.; Chen, W. Manipulating the Electronic and Chemical Properties of Graphene via Molecular Functionalization. Prog. Surf. Sci. 2013, 88, 132–159. [Google Scholar] [CrossRef]
- Dong, X.; Fu, D.; Fang, W.; Shi, Y.; Chen, P.; Li, L. Doping Single-Layer Graphene with Aromatic Molecules. Small 2009, 5, 1422–1426. [Google Scholar] [CrossRef] [PubMed]
- Gobbi, M.; Orgiu, E.; Samorì, P. When 2D Materials Meet Molecules: Opportunities and Challenges of Hybrid Organic/Inorganic van Der Waals Heterostructures. Adv. Mater. 2018, 30, 1706103. [Google Scholar] [CrossRef]
- Liu, J.; Bao, S.; Wang, X. Applications of Graphene-Based Materials in Sensors: A Review. Micromachines 2022, 13, 184. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Y.; Yang, Z.; Hu, N. Review of Recent Progress on Graphene-Based Composite Gas Sensors. Ceram. Int. 2021, 47, 16367–16384. [Google Scholar] [CrossRef]
- He, S.; Ma, Y.; Maulik, G.; Jellicoe, M.; Nag, A.; Powell, W.; Deng, S.; Fang, J.; Wu, Y. A Review on Graphene-Based Sensors for Tactile Applications. Sens. Actuators A Phys. 2024, 372, 115363. [Google Scholar] [CrossRef]
- Wang, S.; Qi, X.; Hao, D.; Moro, R.; Ma, Y.; Ma, L. Review—Recent Advances in Graphene-Based Field-Effect-Transistor Biosensors: A Review on Biosensor Designing Strategy. J. Electrochem. Soc. 2022, 169, 027509. [Google Scholar] [CrossRef]
- Hwang, M.T.; Heiranian, M.; Kim, Y.; You, S.; Leem, J.; Taqieddin, A.; Faramarzi, V.; Jing, Y.; Park, I.; van der Zande, A.M.; et al. Ultrasensitive Detection of Nucleic Acids Using Deformed Graphene Channel Field Effect Biosensors. Nat. Commun. 2020, 11, 1543. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Mishchenko, A.; Carvalho, A.; Castro Neto, A.H. 2D Materials and van Der Waals Heterostructures. Science 2016, 353, aac9439. [Google Scholar] [CrossRef]
- Vu, T.V.; Hieu, N.V.; Phuc, H.V.; Hieu, N.N.; Bui, H.D.; Idrees, M.; Amin, B.; Nguyen, C.V. Graphene/WSeTe van Der Waals Heterostructure: Controllable Electronic Properties and Schottky Barrier via Interlayer Coupling and Electric Field. Appl. Surf. Sci. 2020, 507, 145036. [Google Scholar] [CrossRef]
- Nguyen, S.-T.; Nguyen, C.Q.; Ang, Y.S.; Van Hoang, N.; Hung, N.M.; Nguyen, C.V. Understanding Electronic Properties and Tunable Schottky Barriers in a Graphene/Boron Selenide van Der Waals Heterostructure. Langmuir 2023, 39, 6637–6645. [Google Scholar] [CrossRef] [PubMed]
- Fedorov, I.A.; Voroshilin, R.A.; Prosekov, A.Y. Theoretical Study of the Interaction of Lactose with Collagen, the Electronic and Mechanical Properties of Crystalline Lactose. Materialia 2022, 25, 101537. [Google Scholar] [CrossRef]
- Fedorov, I.A. Elastic Properties of the Molecular Crystals of Hydrocarbons from First Principles Calculations. J. Phys. Condens. Matter 2020, 32, 085704. [Google Scholar] [CrossRef]
- Mondal, S.; Ayadi, T.; Lebègue, S.; Gupta, M.K.; Mittal, R.; Vaitheeswaran, G. Lattice Dynamics and Pressure Induced Metallization of Solid Iodanil (C6I4O2) Studied Using Density Functional Theory. Phys. Scr. 2023, 98, 075918. [Google Scholar] [CrossRef]
- Geim, A.K.; Grigorieva, I.V. Van Der Waals Heterostructures. Nature 2013, 499, 419–425. [Google Scholar] [CrossRef]
- Castellanos-Gomez, A.; Duan, X.; Fei, Z.; Gutierrez, H.R.; Huang, Y.; Huang, X.; Quereda, J.; Qian, Q.; Sutter, E.; Sutter, P. Van Der Waals Heterostructures. Nat. Rev. Methods Prim. 2022, 2, 58. [Google Scholar] [CrossRef]
- Liu, Y.; Weiss, N.O.; Duan, X.; Cheng, H.-C.; Huang, Y.; Duan, X. Van Der Waals Heterostructures and Devices. Nat. Rev. Mater. 2016, 1, 16042. [Google Scholar] [CrossRef]
- Carr, S.; Massatt, D.; Fang, S.; Cazeaux, P.; Luskin, M.; Kaxiras, E. Twistronics: Manipulating the Electronic Properties of Two-Dimensional Layered Structures through Their Twist Angle. Phys. Rev. B 2017, 95, 075420. [Google Scholar] [CrossRef]
- Kashiwaya, S.; Shi, Y.; Lu, J.; Sangiovanni, D.G.; Greczynski, G.; Magnuson, M.; Andersson, M.; Rosen, J.; Hultman, L. Synthesis of Goldene Comprising Single-Atom Layer Gold. Nat. Synth. 2024, 3, 744–751. [Google Scholar] [CrossRef]
- Zhao, J.; Li, L.; Li, P.; Dai, L.; Dong, J.; Zhou, L.; Wang, Y.; Zhang, P.; Ji, K.; Zhang, Y.; et al. Realization of 2D Metals at the Ångström Thickness Limit. Nature 2025, 639, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Tau, O.; Lovergine, N.; Prete, P. Adsorption and Decomposition Steps on Cu(111) of Liquid Aromatic Hydrocarbon Precursors for Low-Temperature CVD of Graphene: A DFT Study. Carbon 2023, 206, 142–149. [Google Scholar] [CrossRef]
- Tau, O.; Lovergine, N.; Prete, P. Molecular decomposition reactions and early nucleation in CVD growth of graphene on Cu and Si substrates from toluene. In Low-Dimensional Materials and Devices; SPIE: San Diego, CA, USA, 2024; Volume 13114, p. 1311409. [Google Scholar] [CrossRef]
- Yu, W.; Sisi, L.; Haiyan, Y.; Jie, L. Progress in the Functional Modification of Graphene/Graphene Oxide: A Review. RSC Adv. 2020, 10, 15328–15345. [Google Scholar] [CrossRef] [PubMed]
- Georgakilas, V.; Otyepka, M.; Bourlinos, A.B.; Chandra, V.; Kim, N.; Kemp, K.C.; Hobza, P.; Zboril, R.; Kim, K.S. Functionalization of Graphene: Covalent and Non-Covalent Approaches, Derivatives and Applications. Chem. Rev. 2012, 112, 6156–6214. [Google Scholar] [CrossRef] [PubMed]
- Sherrill, C.D. Computations of Noncovalent π Interactions. In Reviews in Computational Chemistry; Lipkowitz, K.B., Cundari, T.R., Boyd, D.B., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; pp. 1–38. [Google Scholar]
- Sinnokrot, M.O.; Sherrill, C.D. Highly Accurate Coupled Cluster Potential Energy Curves for the Benzene Dimer: Sandwich, T-Shaped, and Parallel-Displaced Configurations. J. Phys. Chem. A 2004, 108, 10200–10207. [Google Scholar] [CrossRef]
- Jurečka, P.; Šponer, J.; Černý, J.; Hobza, P. Benchmark Database of Accurate (MP2 and CCSD(T) Complete Basis Set Limit) Interaction Energies of Small Model Complexes, DNA Base Pairs, and Amino Acid Pairs. Phys. Chem. Chem. Phys. 2006, 8, 1985–1993. [Google Scholar] [CrossRef]
- Klimeš, J.; Michaelides, A. Perspective: Advances and Challenges in Treating van Der Waals Dispersion Forces in Density Functional Theory. J. Chem. Phys. 2012, 137, 120901. [Google Scholar] [CrossRef]
- Burke, K. Perspective on Density Functional Theory. J. Chem. Phys. 2012, 136, 150901. [Google Scholar] [CrossRef]
- Becke, A.D. Perspective: Fifty Years of Density-Functional Theory in Chemical Physics. J. Chem. Phys. 2014, 140, 18A301. [Google Scholar] [CrossRef]
- Hermann, J.; DiStasio, R.A.; Tkatchenko, A. First-Principles Models for van Der Waals Interactions in Molecules and Materials: Concepts, Theory, and Applications. Chem. Rev. 2017, 117, 4714–4758. [Google Scholar] [CrossRef]
- Tsuzuki, S.; Honda, K.; Uchimaru, T.; Mikami, M. High-Level Ab Initio Computations of Structures and Interaction Energies of Naphthalene Dimers: Origin of Attraction and Its Directionality. J. Chem. Phys. 2004, 120, 647–659. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Dion, M.; Rydberg, H.; Schröder, E.; Langreth, D.C.; Lundqvist, B.I. Van Der Waals Density Functional for General Geometries. Phys. Rev. Lett. 2004, 92, 246401. [Google Scholar] [CrossRef] [PubMed]
- Sabatini, R.; Gorni, T.; de Gironcoli, S. Nonlocal van Der Waals Density Functional Made Simple and Efficient. Phys. Rev. B 2013, 87, 041108. [Google Scholar] [CrossRef]
- Thonhauser, T.; Cooper, V.R.; Li, S.; Puzder, A.; Hyldgaard, P.; Langreth, D.C. Van Der Waals Density Functional: Self-Consistent Potential and the Nature of the van Der Waals Bond. Phys. Rev. B-Condens. Matter Mater. Phys. 2007, 76, 125112. [Google Scholar] [CrossRef]
- Thonhauser, T.; Zuluaga, S.; Arter, C.A.; Berland, K.; Schröder, E.; Hyldgaard, P. Spin Signature of Nonlocal Correlation Binding in Metal-Organic Frameworks. Phys. Rev. Lett. 2015, 115, 136402. [Google Scholar] [CrossRef]
- Berland, K.; Cooper, V.R.; Lee, K.; Schröder, E.; Thonhauser, T.; Hyldgaard, P.; Lundqvist, B.I. Van Der Waals Forces in Density Functional Theory: A Review of the vdW-DF Method. Rep. Progr. Phys. 2015, 78, 066501. [Google Scholar] [CrossRef]
- Langreth, D.C.; Lundqvist, B.I.; Chakarova-Käck, S.D.; Cooper, V.R.; Dion, M.; Hyldgaard, P.; Kelkkanen, A.; Kleis, J.; Kong, L.; Li, S.; et al. A Density Functional for Sparse Matter. J. Phys. Condens. Matter 2009, 21, 084203. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Van Voorhis, T. Nonlocal van Der Waals Density Functional: The Simpler the Better. J. Chem. Phys. 2010, 133, 244103. [Google Scholar] [CrossRef]
- Ambrosetti, A.; Reilly, A.M.; DiStasio, R.A.; Tkatchenko, A. Long-Range Correlation Energy Calculated from Coupled Atomic Response Functions. J. Chem. Phys. 2014, 140, 18A508. [Google Scholar] [CrossRef]
- Tkatchenko, A.; Scheffler, M. Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 073005. [Google Scholar] [CrossRef] [PubMed]
- Kong, L.; Enders, A.; Rahman, T.S.; Dowben, P.A. Molecular Adsorption on Graphene. J. Phys. Condens. Matter 2014, 26, 443001. [Google Scholar] [CrossRef] [PubMed]
- Yeung, C.S.; Liu, L.V.; Wang, Y.A. Adsorption of Small Gas Molecules onto Pt-Doped Single-Walled Carbon Nanotubes. J. Phys. Chem. C 2008, 19, 7401–7411. [Google Scholar] [CrossRef]
- Zhang, Y.-H.; Zhou, K.-G.; Xie, K.-F.; Zeng, J.; Zhang, H.-L.; Peng, Y. Tuning the Electronic Structure and Transport Properties of Graphene by Noncovalent Functionalization: Effects of Organic Donor, Acceptor and Metal Atoms. Nanotechnology 2010, 21, 065201. [Google Scholar] [CrossRef]
- Chakarova-Käck, S.D.; Schröder, E.; Lundqvist, B.I.; Langreth, D.C. Application of van Der Waals Density Functional to an Extended System: Adsorption of Benzene and Naphthalene on Graphite. Phys. Rev. Lett. 2006, 96, 146107. [Google Scholar] [CrossRef]
- Hassan, M.; Walter, M.; Moseler, M. Interactions of Polymers with Reduced Graphene Oxide: Van Der Waals Binding Energies of Benzene on Graphene with Defects. Phys. Chem. Chem. Phys. 2014, 16, 33–37. [Google Scholar] [CrossRef]
- Otyepková, E.; Lazar, P.; Čépe, K.; Tomanec, O.; Otyepka, M. Organic Adsorbates Have Higher Affinities to Fluorographene than to Graphene. Appl. Mater. Today 2016, 5, 142–149. [Google Scholar] [CrossRef]
- AlZahrani, A.Z. First-Principles Study on the Structural and Electronic Properties of Graphene upon Benzene and Naphthalene Adsorption. Appl. Surf. Sci. 2010, 257, 807–810. [Google Scholar] [CrossRef]
- Tournus, F.; Charlier, J.-C. Ab Initio Study of Benzene Adsorption on Carbon Nanotubes. Phys. Rev. B 2005, 71, 165421. [Google Scholar] [CrossRef]
- Hernández, J.M.G.; Anota, E.C.; de la Cruz, M.T.R.; Melchor, M.G.; Cocoletzi, G.H. First Principles Studies of the Graphene-Phenol Interactions. J. Mol. Model. 2012, 18, 3857–3866. [Google Scholar] [CrossRef]
- Berland, K.; Hyldgaard, P. Analysis of van Der Waals Density Functional Components: Binding and Corrugation of Benzene and C60 on Boron Nitride and Graphene. Phys. Rev. B 2013, 87, 205421. [Google Scholar] [CrossRef]
- de Moraes, E.E.; Tonel, M.Z.; Fagan, S.B.; Barbosa, M.C. Density Functional Theory Study of π-Aromatic Interaction of Benzene, Phenol, Catechol, Dopamine Isolated Dimers and Adsorbed on Graphene Surface. J. Mol. Model. 2019, 25, 302. [Google Scholar] [CrossRef] [PubMed]
- Yankowitz, M.; Ma, Q.; Jarillo-Herrero, P.; LeRoy, B.J. Van Der Waals Heterostructures Combining Graphene and Hexagonal Boron Nitride. Nat. Rev. Phys. 2019, 1, 112–125. [Google Scholar] [CrossRef]
- Wang, J.; Ma, F.; Sun, M. Graphene, Hexagonal Boron Nitride, and Their Heterostructures: Properties and Applications. RSC Adv. 2017, 7, 16801–16822. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, X.; Ma, T.; Liu, D.; Gao, L.; Li, X.; Zhang, J.; Hu, Y.; Wang, H.; Dai, Y.; et al. Superlubricity of a Graphene/MoS2 Heterostructure: A Combined Experimental and DFT Study. Nanoscale 2017, 9, 10846–10853. [Google Scholar] [CrossRef]
- Wang, K.; Wang, Y.; Liu, Y.; Wang, H.; Luo, J. The Relationship between Surface Microstructure and Super-Lubrication Performance Based on 2D LDHs. Mater. Today Nano 2023, 23, 100361. [Google Scholar] [CrossRef]
- Fan, Y.; Zhao, M.; Wang, Z.; Zhang, X.; Zhang, H. Tunable Electronic Structures of Graphene/Boron Nitride Heterobilayers. Appl. Phys. Lett. 2011, 98, 083103. [Google Scholar] [CrossRef]
- Zhong, X.; Yap, Y.K.; Pandey, R.; Karna, S.P. First-Principles Study of Strain-Induced Modulation of Energy Gaps of Graphene/BN and BN Bilayers. Phys. Rev. B 2011, 83, 193403. [Google Scholar] [CrossRef]
- Kan, E.; Ren, H.; Wu, F.; Li, Z.; Lu, R.; Xiao, C.; Deng, K.; Yang, J. Why the Band Gap of Graphene Is Tunable on Hexagonal Boron Nitride. J. Phys. Chem. C 2012, 116, 3142–3146. [Google Scholar] [CrossRef]
- Bader, R.R.W. Atoms in Molecules; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Zhikol, O.A.; Shishkin, O.V.; Lyssenko, K.A.; Leszczynski, J. Electron Density Distribution in Stacked Benzene Dimers: A New Approach towards the Estimation of Stacking Interaction Energies. J. Chem. Phys. 2005, 122, 144104. [Google Scholar] [CrossRef]
- Fedorov, I.; Korabel’nikov, D.; Nguyen, C.; Prosekov, A. Physicochemical Properties of L- and Dl-Valine: First-Principles Calculations. Amino Acids 2020, 52, 425–433. [Google Scholar] [CrossRef] [PubMed]
- Da Silva, N.A.; Bruns, R.E.; Haiduke, R.L.A. Topological Electron Density Properties at Critical Points along Aromatic Rings as Reactivity and Regioselectivity Descriptors in Electrophilic Substitutions. J. Phys. Org. Chem. 2021, 34, e4252. [Google Scholar] [CrossRef]
- Zhurova, E.A.; Stash, A.I.; Tsirelson, V.G.; Zhurov, V.V.; Bartashevich, E.V.; Potemkin, V.A.; Pinkerton, A.A. Atoms-in-Molecules Study of Intra- and Intermolecular Bonding in the Pentaerythritol Tetranitrate Crystal. J. Am. Chem. Soc. 2006, 128, 14728–14734. [Google Scholar] [CrossRef] [PubMed]
- Zhurov, V.V.; Zhurova, E.A.; Stash, A.I.; Pinkerton, A.A. Characterization of Bonding in Cesium Uranyl Chloride: Topological Analysis of the Experimental Charge Density. J. Phys. Chem. A 2011, 115, 13016–13023. [Google Scholar] [CrossRef]
- Katan, C.; Rabiller, P.; Lecomte, C.; Guezo, M.; Oison, V.; Souhassou, M. Numerical Computation of Critical Properties and Atomic Basins from Three-Dimensional Grid Electron Densities. J. Appl. Crystallogr. 2003, 36, 65–73. [Google Scholar] [CrossRef]
- Espinosa, E.; Souhassou, M.; Lachekar, H.; Lecomte, C. Topological Analysis of the Electron Density in Hydrogen Bonds. Acta Crystallogr. Sect. B Struct. Sci. 1999, B55, 563–572. [Google Scholar] [CrossRef]
- Rajalakshmi, G.; Hathwar, V.R.; Kumaradhas, P. Topological Analysis of Electron Density and the Electrostatic Properties of Isoniazid: An Experimental and Theoretical Study. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2014, 70, 331–341. [Google Scholar] [CrossRef]
- Gajda, R.; Stachowicz, M.; Makal, A.; Sutuła, S.; Parafiniuk, J.; Fertey, P.; Woźniak, K. Experimental Charge Density of Grossular under Pressure—A Feasibility Study. IUCrJ 2020, 7, 383–392. [Google Scholar] [CrossRef]
- Contreras-García, J.; Johnson, E.R.; Keinan, S.; Chaudret, R.; Piquemal, J.-P.; Beratan, D.N.; Yang, W. NCIPLOT: A Program for Plotting Noncovalent Interaction Regions. J. Chem. Theory Comput. 2011, 7, 625–632. [Google Scholar] [CrossRef]
- Tantardini, C.; Michalchuk, A.A.L.; Samtsevich, A.; Rota, C.; Kvashnin, A.G. The Volumetric Source Function: Looking Inside van Der Waals Interactions. Sci. Rep. 2020, 10, 7816. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced Capabilities for Materials Modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Rappe, A.M.; Rabe, K.M.; Kaxiras, E.; Joannopoulos, J.D. Optimized Pseudopotentials. Phys. Rev. B 1990, 41, 1227–1230. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, R. Practical Methods of Optimization; Wiley: New York, NY, USA, 1980; Volume 1. [Google Scholar]
- Monkhorst, H.; Pack, J. Special Points for Brillouin Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Johnson, E.R.; Becke, A.D. A Post-Hartree–Fock Model of Intermolecular Interactions. J. Chem. Phys. 2005, 123, 024101. [Google Scholar] [CrossRef]
- Johnson, E.R.; Becke, A.D. A Post-Hartree-Fock Model of Intermolecular Interactions: Inclusion of Higher-Order Corrections. J. Chem. Phys. 2006, 124, 174104. [Google Scholar] [CrossRef]
- Fedorov, I.A.; Nguyen, C.V.; Prosekov, A.Y. Study of the Elastic Properties of the Energetic Molecular Crystals Using Density Functionals with van Der Waals Corrections. ACS Omega 2021, 6, 642–648. [Google Scholar] [CrossRef]
- Korabel’nikov, D.V.; Fedorov, I.A. Negative Linear Compressibility of Molecular and Ionic-Molecular Crystals. Phys. Chem. Chem. Phys. 2025, 27, 2232–2239. [Google Scholar] [CrossRef]
- Dovesi, R.; Erba, A.; Orlando, R.; Zicovich-Wilson, C.M.; Civalleri, B.; Maschio, L.; Rérat, M.; Casassa, S.; Baima, J.; Salustro, S.; et al. Quantum-Mechanical Condensed Matter Simulations with CRYSTAL. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1360. [Google Scholar] [CrossRef]
- Dovesi, R.; Saunders, V.R.; Roetti, C.; Orlando, R.; Zicovich-Wilson, C.M.; Pascale, F.; Civalleri, B.; Doll, K.; Harrison, N.M.; Bush, I.J.; et al. CRYSTAL17 User’s Manual; University of Torino: Torino, Italy, 2017. [Google Scholar]
- Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6169. [Google Scholar] [CrossRef]
- Vilela Oliveira, D.; Laun, J.; Peintinger, M.F.; Bredow, T. BSSE-correction Scheme for Consistent Gaussian Basis Sets of Double- and Triple-zeta Valence with Polarization Quality for Solid-state Calculations. J. Comput. Chem. 2019, 40, 2364–2376. [Google Scholar] [CrossRef]
- Gatti, C.; Casassa, S. TOPOND14 User’s Manual; CNR-ISTM Milano: Milano, Italy, 2014. [Google Scholar]
- Sozykin, S. CritPlot. Available online: https://github.com/sozykinsa/CritPlot (accessed on 30 March 2025).
- Momma, K.; Izumi, F. VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Zacharia, R.; Ulbricht, H.; Hertel, T. Interlayer Cohesive Energy of Graphite from Thermal Desorption of Polyaromatic Hydrocarbons. Phys. Rev. B 2004, 69, 155406. [Google Scholar] [CrossRef]
- Hirshfeld, F.L. Bonded-Atom Fragments for Describing Molecular Charge Densities. Theor. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Whitten, A.E.; Radford, C.J.; McKinnon, J.J.; Spackman, M.A. Dipole and Quadrupole Moments of Molecules in Crystals: A Novel Approach Based on Integration over Hirshfeld Surfaces. J. Chem. Phys. 2006, 124, 074106. [Google Scholar] [CrossRef] [PubMed]
- Usachov, D.; Adamchuk, V.K.; Haberer, D.; Grüneis, A.; Sachdev, H.; Preobrajenski, A.B.; Laubschat, C.; Vyalikh, D.V. Quasifreestanding Single-Layer Hexagonal Boron Nitride as a Substrate for Graphene Synthesis. Phys. Rev. B 2010, 82, 075415. [Google Scholar] [CrossRef]
- Roth, S.; Matsui, F.; Greber, T.; Osterwalder, J. Chemical Vapor Deposition and Characterization of Aligned and Incommensurate Graphene/Hexagonal Boron Nitride Heterostack on Cu(111). Nano Lett. 2013, 13, 2668–2675. [Google Scholar] [CrossRef]
- Chen, C.; Avila, J.; Wang, S.; Yang, R.; Zhang, G.; Asensio, M.C. Electronic Structure of Graphene/Hexagonal Boron Nitride Heterostructure Revealed by Nano-ARPES. J. Phys. Conf. Ser. 2017, 864, 012005. [Google Scholar] [CrossRef]
- Torres-Rojas, R.M.; Contreras-Solorio, D.A.; Hernández, L.; Enciso, A. Band Gap Variation in Bi, Tri and Few-Layered 2D Graphene/HBN Heterostructures. Solid State Commun. 2022, 341, 114553. [Google Scholar] [CrossRef]



| DFT-D3(BJ) | rVV10 | MBD | vdw-df2-b86r | |
|---|---|---|---|---|
| H-benzene/graphene | 3.48 | 3.45 | 4.18 | 3.45 |
| T-benzene/graphene | 3.37 | 3.38 | 4.13 | 3.35 |
| rs, a.u. | VS, Å3 | QS, |e| | |
|---|---|---|---|
| Gr-like dimer benzene | 1.3 | 2.42 | 0.0268 |
| T-benzene/graphene | 1.3 | 6.45 | 0.1089 |
| H-benzene/graphene | 1.5 | 6.28 | 0.0950 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fedorov, I. Topological Analysis of Electron Density in Graphene/Benzene and Graphene/hBN. Materials 2025, 18, 1790. https://doi.org/10.3390/ma18081790
Fedorov I. Topological Analysis of Electron Density in Graphene/Benzene and Graphene/hBN. Materials. 2025; 18(8):1790. https://doi.org/10.3390/ma18081790
Chicago/Turabian StyleFedorov, Igor. 2025. "Topological Analysis of Electron Density in Graphene/Benzene and Graphene/hBN" Materials 18, no. 8: 1790. https://doi.org/10.3390/ma18081790
APA StyleFedorov, I. (2025). Topological Analysis of Electron Density in Graphene/Benzene and Graphene/hBN. Materials, 18(8), 1790. https://doi.org/10.3390/ma18081790







