Double Domes of Mesoscopic Localized Anisotropic Lattice Strain in HCP–Ag75Al25 Under Uniaxial Compression
Abstract
1. Introduction
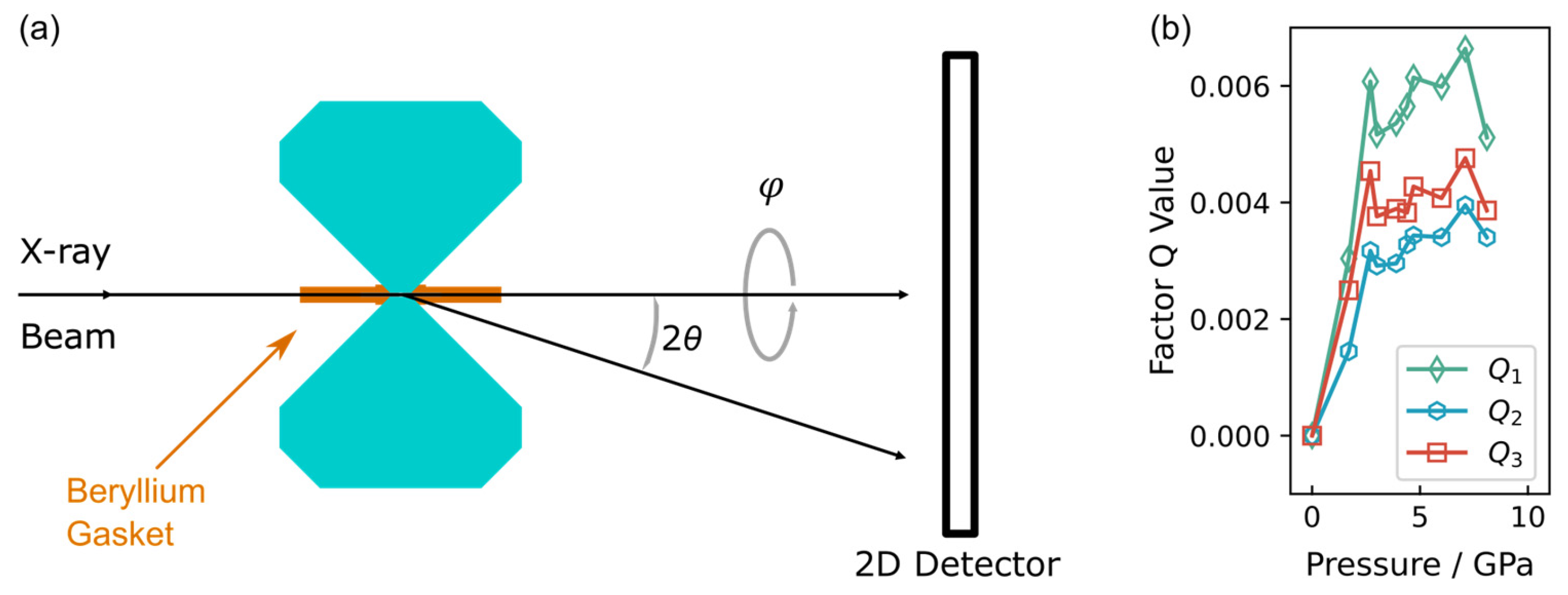
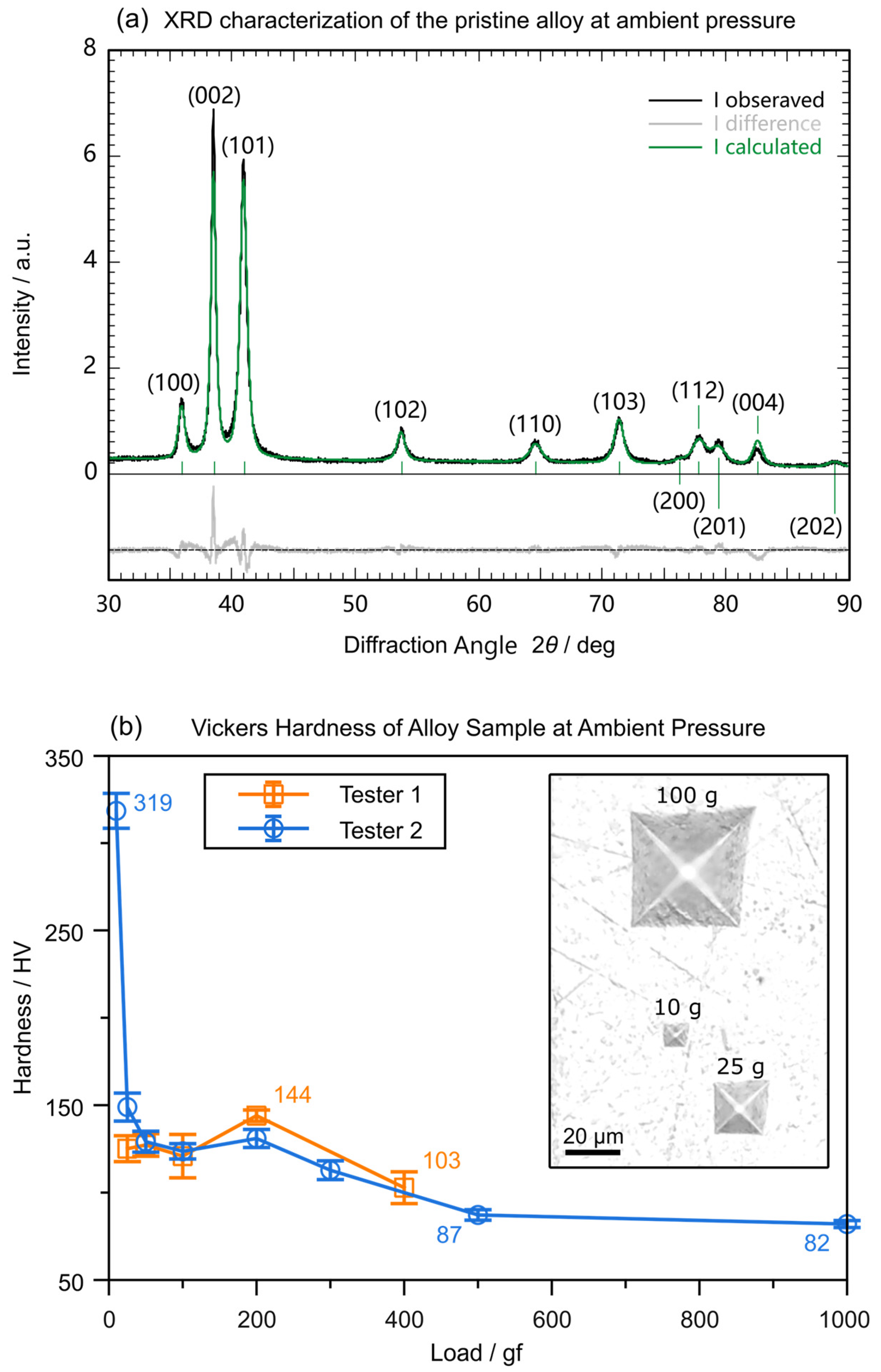
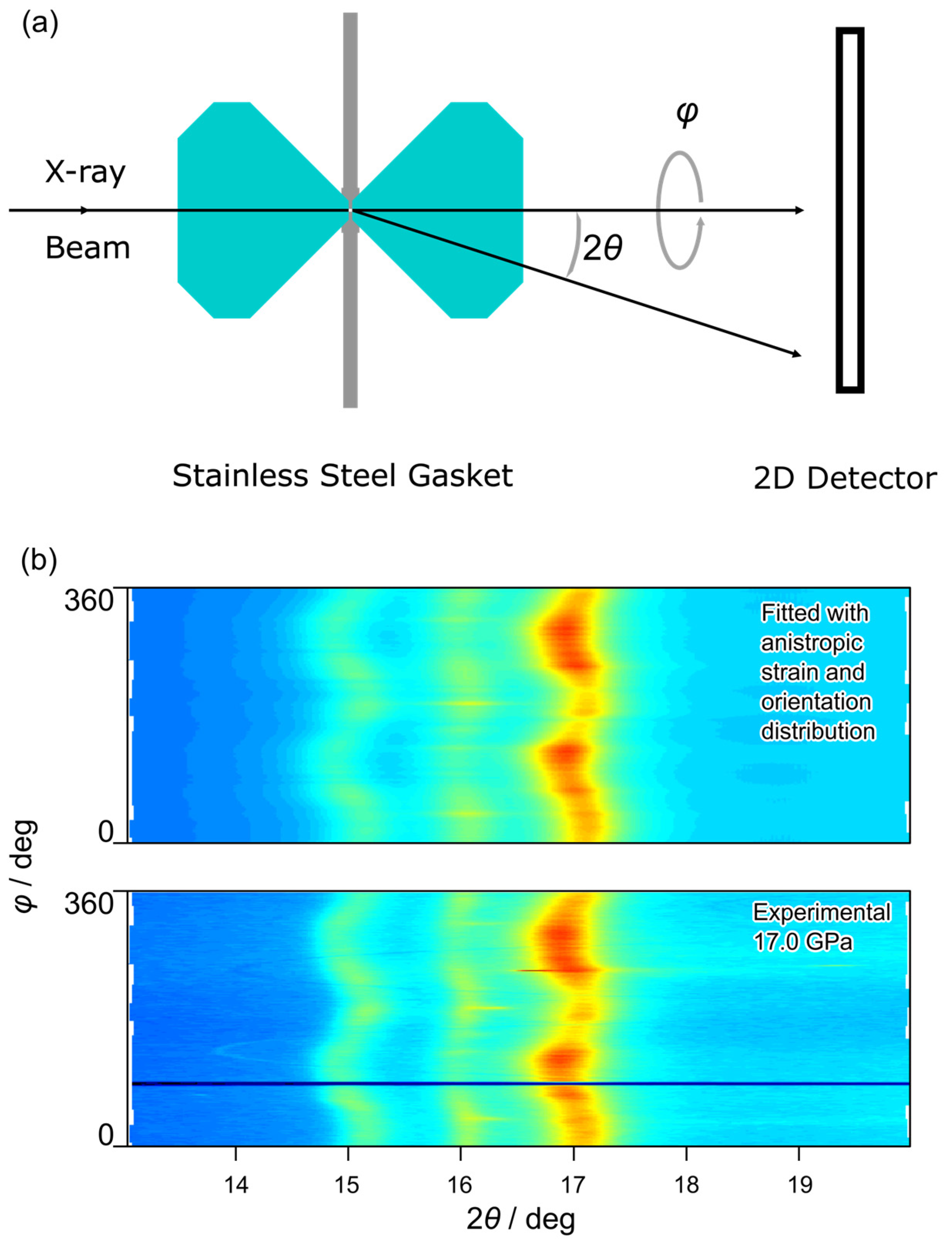
2. Materials and Methods
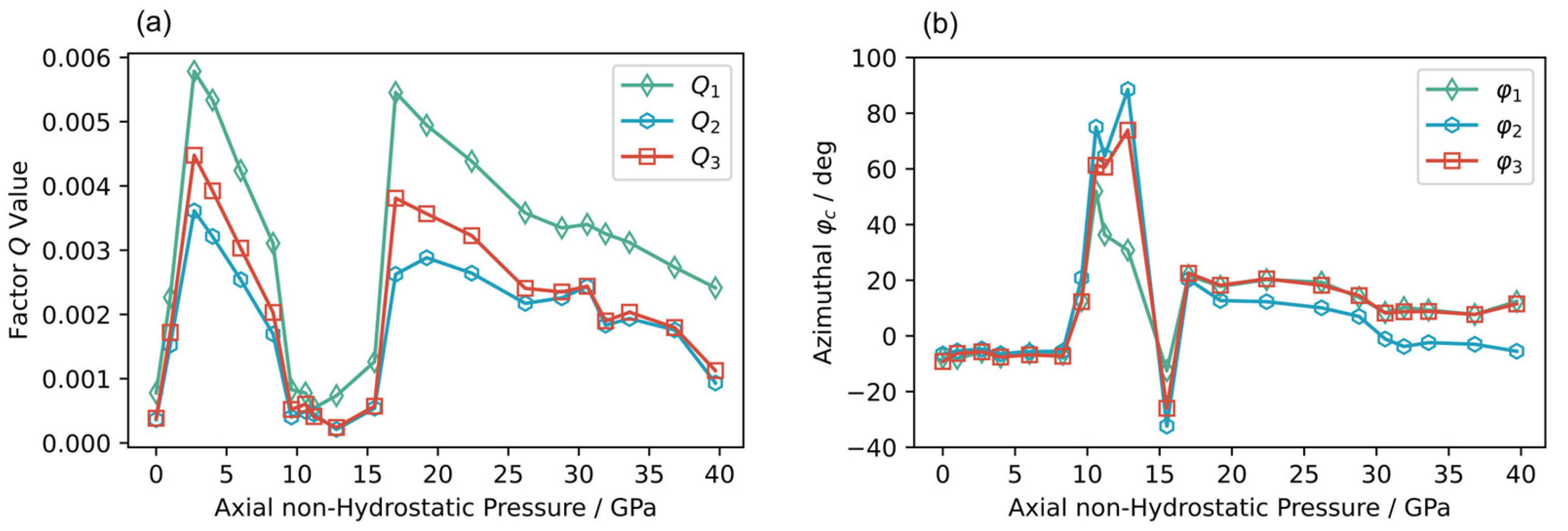
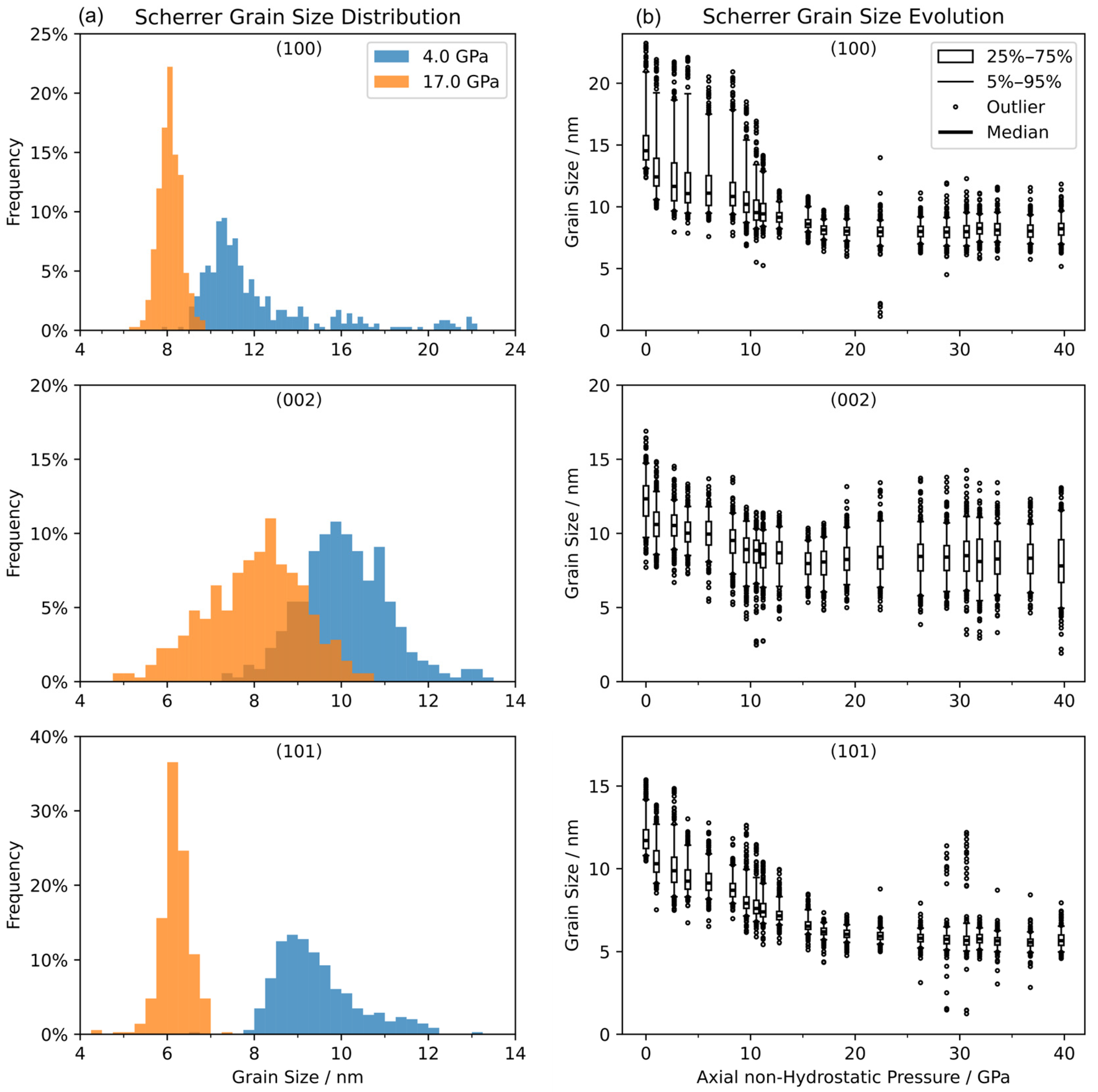
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DAC | Diamond anvil cell |
| EDS | Energy dispersive spectrometer |
| FWHM | Full width at half maximum |
| HCP | Hexagonal close-packed |
| LPO | Lattice-preferred orientation |
| PTM | Pressure-transmitting medium |
| XRD | X-ray diffraction |
Appendix A

Appendix B

References
- Kocks, U.F. The Relation between Polycrystal Deformation and Single-Crystal Deformation. Metall. Trans. 1970, 1, 1121–1143. [Google Scholar] [CrossRef]
- Cambou, B.; Dubujet, P.; Nouguier-Lehon, C. Anisotropy in Granular Materials at Different Scales. Mech. Mater. 2004, 36, 1185–1194. [Google Scholar] [CrossRef]
- Hutchinson, B. Critical Assessment 16: Anisotropy in Metals. Mater. Sci. Technol. 2015, 31, 1393–1401. [Google Scholar] [CrossRef]
- Nishihara, Y.; Ohuchi, T.; Kawazoe, T.; Seto, Y.; Maruyama, G.; Higo, Y.; Funakoshi, K.; Tange, Y.; Irifune, T. Deformation-Induced Crystallographic-Preferred Orientation of Hcp-Iron: An Experimental Study Using a Deformation-DIA Apparatus. Earth Planet. Sci. Lett. 2018, 490, 151–160. [Google Scholar] [CrossRef]
- Merkel, S.; Yagi, T. Effect of Lattice Preferred Orientation on Lattice Strains in Polycrystalline Materials Deformed under High Pressure: Application to Hcp-Co. J. Phys. Chem. Solids 2006, 67, 2119–2131. [Google Scholar] [CrossRef]
- Wang, Y.N.; Huang, J.C. Texture Analysis in Hexagonal Materials. Mater. Chem. Phys. 2003, 81, 11–26. [Google Scholar] [CrossRef]
- Barton, N.; Quadros, E. Anisotropy Is Everywhere, to See, to Measure, and to Model. Rock Mech. Rock Eng. 2015, 48, 1323–1339. [Google Scholar] [CrossRef]
- Koneva, N.A.; Trishkina, L.I.; Popova, N.A.; Kozlov, É.V. Accumulation of Defects During Plastic Deformation of Polycrystals of the Meso- and Microscale Grain Size. Russ. Phys. J. 2014, 57, 187–196. [Google Scholar] [CrossRef]
- Panin, V.E.; Egorushkin, V.E.; Elsukova, T.F.; Surikova, N.S.; Pochivalov, Y.I.; Panin, A.V. Multiscale Translation-Rotation Plastic Flow in Polycrystals. In Handbook of Mechanics of Materials; Schmauder, S., Chen, C.-S., Chawla, K.K., Chawla, N., Chen, W., Kagawa, Y., Eds.; Springer: Singapore, 2019; pp. 1255–1292. ISBN 978-981-10-6884-3. [Google Scholar]
- Yang, G.; Park, S.-J. Deformation of Single Crystals, Polycrystalline Materials, and Thin Films: A Review. Materials 2019, 12, 2003. [Google Scholar] [CrossRef]
- Koneva, N.A.; Potekaev, A.I.; Trishkina, L.I.; Cherkasova, T.V.; Klopotov, A.A. Critical Grain Size at Meso-Level after Deformation of Polycrystalline Metals and Alloys in Low-Stability State. Russ. Phys. J. 2020, 63, 773–778. [Google Scholar] [CrossRef]
- McAlister, A.J. The Ag−Al (Silver-Aluminum) System. Bull. Alloy Phase Diagr. 1987, 8, 526–533. [Google Scholar] [CrossRef]
- Zarkevich, N.A.; Johnson, D.D. Predicted Hcp Ag-Al Metastable Phase Diagram, Equilibrium Ground States, and Precipitate Structure. Phys. Rev. B 2003, 67, 064104. [Google Scholar] [CrossRef]
- Terlicka, S.; Dębski, A.; Gierlotka, W.; Wierzbicka-Miernik, A.; Budziak, A.; Sypien, A.; Zabrocki, M.; Gąsior, W. Structural and Physicochemical Properties of Silver-Rich Ag–Al Alloys. Calphad 2020, 68, 101739. [Google Scholar] [CrossRef]
- Guo, N.; Zhao, J. The Signature of Shear-Induced Anisotropy in Granular Media. Comput. Geotech. 2013, 47, 1–15. [Google Scholar] [CrossRef]
- Kumar, N.; Imole, O.I.; Magnanimo, V.; Luding, S. Effects of Polydispersity on the Micro–Macro Behavior of Granular Assemblies under Different Deformation Paths. Particuology 2014, 12, 64–79. [Google Scholar] [CrossRef]
- Messner, M.C.; Rhee, M.; Arsenlis, A.; Barton, N.R. A Crystal Plasticity Model for Slip in Hexagonal Close Packed Metals Based on Discrete Dislocation Simulations. Model. Simul. Mater. Sci. Eng. 2017, 25, 044001. [Google Scholar] [CrossRef]
- Imole, O.I.; Wojtkowski, M.; Magnanimo, V.; Luding, S. Micro-Macro Correlations and Anisotropy in Granular Assemblies under Uniaxial Loading and Unloading. Phys. Rev. E 2014, 89, 042210. [Google Scholar] [CrossRef]
- Capolungo, L.; Beyerlein, I.J.; Wang, Z.Q. The Role of Elastic Anisotropy on Plasticity in Hcp Metals: A Three-Dimensional Dislocation Dynamics Study. Model. Simul. Mater. Sci. Eng. 2010, 18, 085002. [Google Scholar] [CrossRef]
- Kondori, B.; Madi, Y.; Besson, J.; Benzerga, A.A. Evolution of the 3D Plastic Anisotropy of HCP Metals: Experiments and Modeling. Int. J. Plast. 2019, 117, 71–92. [Google Scholar] [CrossRef]
- Antonangeli, D.; Merkel, S.; Farber, D.L. Elastic Anisotropy in Hcp Metals at High Pressure and the Sound Wave Anisotropy of the Earth’s Inner Core. Geophys. Res. Lett. 2006, 33, L24303. [Google Scholar] [CrossRef]
- Antonangeli, D.; Occelli, F.; Requardt, H.; Badro, J.; Fiquet, G.; Krisch, M. Elastic Anisotropy in Textured Hcp-Iron to 112 GPa from Sound Wave Propagation Measurements. Earth Planet. Sci. Lett. 2004, 225, 243–251. [Google Scholar] [CrossRef]
- Wenk, H.-R.; Matthies, S.; Hemley, R.J.; Mao, H.-K.; Shu, J. The Plastic Deformation of Iron at Pressures of the Earth’s Inner Core. Nature 2000, 405, 1044–1047. [Google Scholar] [CrossRef] [PubMed]
- Stixrude, L.; Cohen, R.E. High-Pressure Elasticity of Iron and Anisotropy of Earth’s Inner Core. Science 1995, 267, 1972–1975. [Google Scholar] [CrossRef]
- Sokolov, A.S.; Trusov, P.V. Evaluation of the Effect of Considering Elastic Anisotropy on the Response of Polycrystals with Tetragonal and HCP Lattices. AIP Conf. Proc. 2021, 2371, 050009. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Creep and Plasticity of Hexagonal Polycrystals as Related to Single Crystal Slip. Metall. Trans. A 1977, 8, 1465–1469. [Google Scholar] [CrossRef]
- Zhang, Z.; Jun, T.-S.; Britton, T.B.; Dunne, F.P.E. Intrinsic Anisotropy of Strain Rate Sensitivity in Single Crystal Alpha Titanium. Acta Mater. 2016, 118, 317–330. [Google Scholar] [CrossRef]
- Barannikova, S.A.; Kolosov, S.V. Localized Plastic Deformation Patterns in FCC Single Crystals. Russ. Phys. J. 2023, 66, 8–15. [Google Scholar] [CrossRef]
- Park, Y.; Wakamatsu, T.; Azuma, S.; Nishihara, Y.; Ohta, K. Characterization of the Lattice Preferred Orientation of Hcp Iron Transformed from the Single-Crystal Bcc Phase in Situ at High Pressures up to 80 GPa. Phys. Chem. Miner. 2024, 51, 31. [Google Scholar] [CrossRef]
- Bočan, J.; Maňák, J.; Jäger, A. Anisotropic Mechanical Properties of Pure Magnesium Analyzed by In Situ Nanoindentation. Key Eng. Mater. 2015, 662, 11–14. [Google Scholar] [CrossRef]
- Ma, Z.-C.; Tang, X.-Z.; Mao, Y.; Guo, Y.-F. The Plastic Deformation Mechanisms of Hcp Single Crystals with Different Orientations: Molecular Dynamics Simulations. Materials 2021, 14, 733. [Google Scholar] [CrossRef]
- Mao, W.L.; Struzhkin, V.V.; Baron, A.Q.R.; Tsutsui, S.; Tommaseo, C.E.; Wenk, H.-R.; Hu, M.Y.; Chow, P.; Sturhahn, W.; Shu, J.; et al. Experimental Determination of the Elasticity of Iron at High Pressure. J. Geophys. Res. Solid Earth 2008, 113, B09213. [Google Scholar] [CrossRef]
- Kádas, K.; Vitos, L.; Ahuja, R. Elastic Properties of Iron-Rich Hcp Fe–Mg Alloys up to Earth’s Core Pressures. Earth Planet. Sci. Lett. 2008, 271, 221–225. [Google Scholar] [CrossRef]
- Niu, Z.; Zeng, S.; Tang, M.; Yang, Z. Elastic Properties of Disordered Binary Hcp-Fe Alloys under High Pressure: Effects of Light Elements. ChemPhysMater 2023, 2, 155–163. [Google Scholar] [CrossRef]
- Antonangeli, D.; Krisch, M.; Fiquet, G.; Badro, J.; Farber, D.L.; Bossak, A.; Merkel, S. Aggregate and Single-Crystalline Elasticity of Hcp Cobalt at High Pressure. Phys. Rev. B 2005, 72, 134303. [Google Scholar] [CrossRef]
- Goncharov, A.F.; Crowhurst, J.; Zaug, J.M. Elastic and Vibrational Properties of Cobalt to 120 GPa. Phys. Rev. Lett. 2004, 92, 115502. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Prescher, C.; Prakapenka, V.B. DIOPTAS: A Program for Reduction of Two-Dimensional X-ray Diffraction Data and Data Exploration. High Press. Res. 2015, 35, 223–230. [Google Scholar] [CrossRef]
- Singh, A.K.; Balasingh, C.; Mao, H.; Hemley, R.J.; Shu, J. Analysis of Lattice Strains Measured under Nonhydrostatic Pressure. J. Appl. Phys. 1998, 83, 7567–7575. [Google Scholar] [CrossRef]
- Duffy, T.S.; Shen, G.; Heinz, D.L.; Shu, J.; Ma, Y.; Mao, H.-K.; Hemley, R.J.; Singh, A.K. Lattice Strains in Gold and Rhenium under Nonhydrostatic Compression to 37 GPa. Phys. Rev. B 1999, 60, 15063–15073. [Google Scholar] [CrossRef]
- Merkel, S. Radial Diffraction in the Diamond Anvil Cell: Methods and Applications. In High-Pressure Crystallography; Springer: Dordrecht, The Netherlands, 2010; pp. 111–122. [Google Scholar]
- Hu, J.Z.; Mao, H.K.; Shu, J.F.; Guo, Q.Z.; Liu, H.Z. Diamond Anvil Cell Radial X-ray Diffraction Program at the National Synchrotron Light Source. J. Phys. Condens. Matter 2006, 18, S1091. [Google Scholar] [CrossRef]
- Lutterotti, L. Maud: A Rietveld Analysis Program Designed for the Internet and Experiment Integration. Acta Crystallogr. A 2000, 56, s54. [Google Scholar] [CrossRef]
- Yan, X.; Dong, H.; Li, Y.; Lin, C.; Park, C.; He, D.; Yang, W. Phase Transition Induced Strain in ZnO under High Pressure. Sci. Rep. 2016, 6, 24958. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; He, D.; Liu, J.; Li, Y.; Peng, F.; Li, Z.; Wang, J.; Bai, L. High-Pressure Radial X-ray Diffraction Study of Osmium to 58 GPa. Eur. Phys. J. B 2010, 73, 321–326. [Google Scholar] [CrossRef]
- Xiong, L.; Li, B.; Tang, Y.; Li, Q.; Hao, J.; Bai, L.; Li, X.; Liu, J. Radial X-ray Diffraction Study of the Static Strength and Texture of Tungsten to 96 GPa. Solid State Commun. 2018, 269, 83–89. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Li, M.; Li, N.; Yang, W. Double Domes of Mesoscopic Localized Anisotropic Lattice Strain in HCP–Ag75Al25 Under Uniaxial Compression. Materials 2025, 18, 1650. https://doi.org/10.3390/ma18071650
Sun Z, Li M, Li N, Yang W. Double Domes of Mesoscopic Localized Anisotropic Lattice Strain in HCP–Ag75Al25 Under Uniaxial Compression. Materials. 2025; 18(7):1650. https://doi.org/10.3390/ma18071650
Chicago/Turabian StyleSun, Zhexin, Mingtao Li, Nana Li, and Wenge Yang. 2025. "Double Domes of Mesoscopic Localized Anisotropic Lattice Strain in HCP–Ag75Al25 Under Uniaxial Compression" Materials 18, no. 7: 1650. https://doi.org/10.3390/ma18071650
APA StyleSun, Z., Li, M., Li, N., & Yang, W. (2025). Double Domes of Mesoscopic Localized Anisotropic Lattice Strain in HCP–Ag75Al25 Under Uniaxial Compression. Materials, 18(7), 1650. https://doi.org/10.3390/ma18071650







