Controlled Dry Adhesion of Bio-Inspired Fibrillar Polymers: Mechanics, Strategies, and Recent Advances
Abstract
1. Introduction
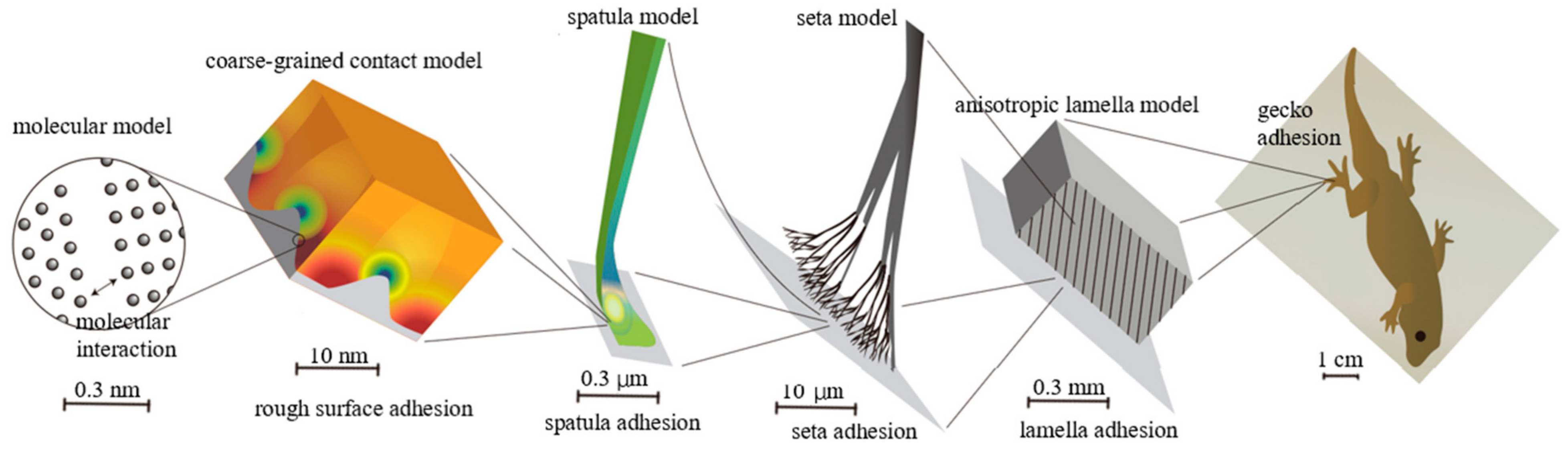
2. Interface Mechanics Between Microfibrils and Substrate
2.1. Contact Mechanics and Contact Splitting Efficiency
2.1.1. Pull-Off Force and Peel Force
2.1.2. Contact Splitting Efficiency
2.2. Fracture Mechanics of the Interface Between Microfibrils and Substrate
2.2.1. Total Energy of System and Fiber Deformation Equations
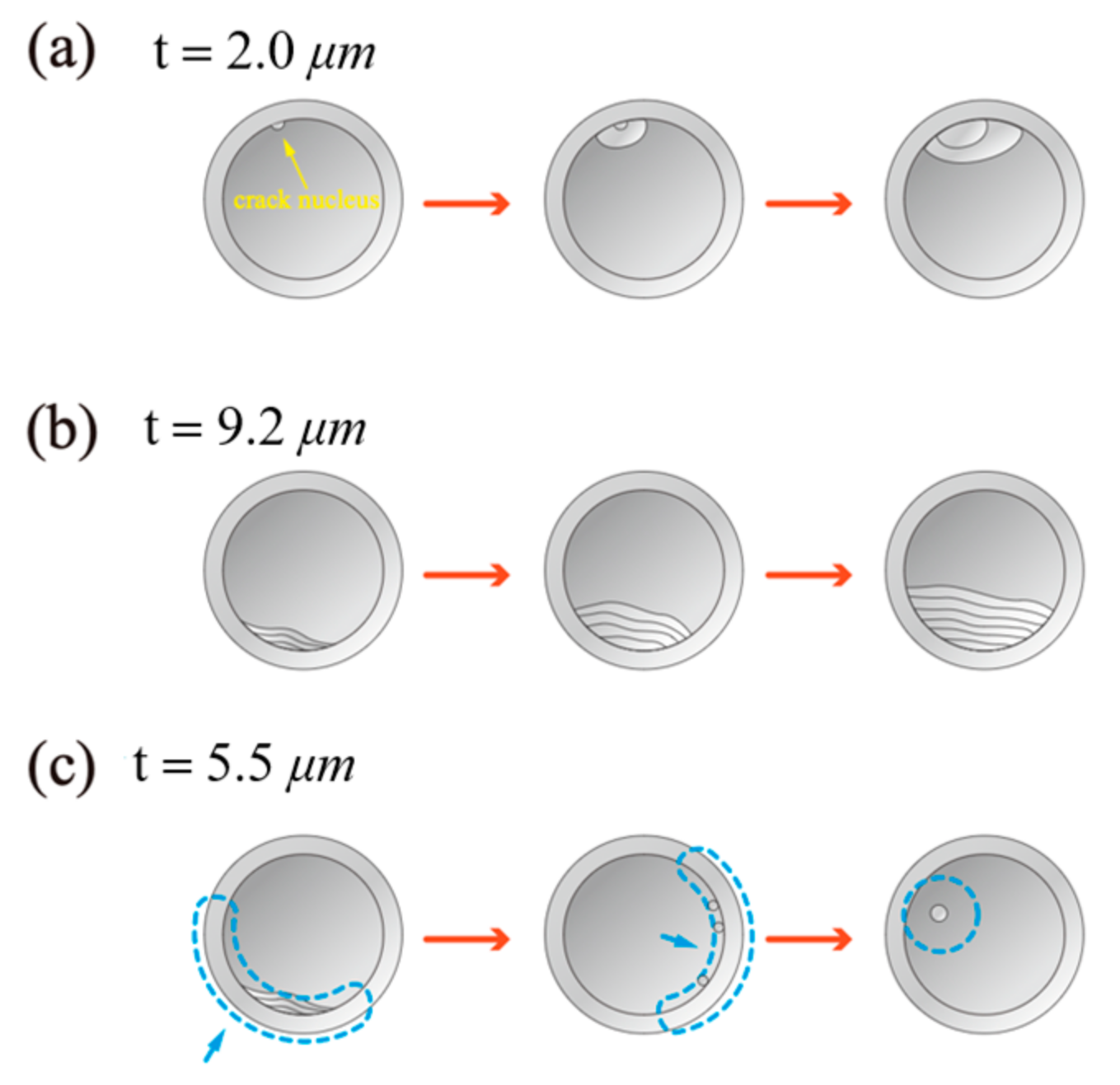
2.2.2. Stress Intensity Factor in Microfibril Arrays and Effective Energy Release Rate
2.2.3. Critical Force Scaling and Predicting Adhesive Behaviors
2.3. Coupled Adhesion and Friction
3. Effective Adhesion Strength of Artificial Fibrillar Adhesives
3.1. Contact Geometry and Stiffness of Microfibrils and Backing Layer
3.2. Substrate Roughness
3.3. Environmental Factors and Pull-Off Dynamics
| Research Approaches | Key Methods/Models | Key Research Focus | System Studied | Example Applications |
|---|---|---|---|---|
| Fracture Mechanics and Numerical Simulations | Linear Elastic Fracture Mechanics (LEFM) [60,61,99,103,115,118,146,147] | Stress distribution, crack initiation and propagation | Single fibril and arrays | Predicting detachment in adhesive systems |
| Cohesive Zone Modeling [68,71,72,73,74,107] | Interfacial energy dissipation and failure | Fibril–substrate interface | Enhanced control over detachment mechanics | |
| Hybrid Dynamic Fracture Mechanics [101,141,142,143,144,145] | Dynamic adhesion characteristics and rate-dependent work of adhesion | Single-fibril, micropatterned surfaces | Rate effects in synthetic adhesive structures | |
| Contact Mechanics | Contact Splitting [24,41], Peeling and Pull- Off [44,63,96,131], Equal Load Sharing [114,146], Traction–Separation Relation [50,100,102] | Load distribution and contact area scaling, enhancing adhesion on rough surfaces, backing-layer | Single fibril or arrays | High-strength adhesion with load-sharing, roughness effects |
| Elasticity Models | Spring Models [67,128] | Compliance and load-sharing | Single fibril or arrays | Designing optimal adhesion under loading |
| Statistical Models | Weibull Statistics, Probabilistic Models [40,69,70] | Variability in adhesion due to defects | Fibril array | Robust adhesion performance with defects |
| Coupled Adhesion and Friction | Frictional Adhesion Modeling [83,85,86,87] | Effects of shear force on adhesion | Arrays | Applications in robotic grippers |
| Buckling and Bending Analysis | Analytical or Numerical [48,148] | Stability under compressive loads, self-adhesion | Single fibril or array | Enhanced adaptability to uneven surfaces |
| Data-Driven Modeling | Supervised Machine Learning [65,66,117,149] | Prediction of adhesion strength, pattern recognition | Micropatterned surfaces | Performance optimization in adhesion design |
4. Enhancing or Tuning Adhesion: Case Studies
4.1. Innovative Design and Optimization of Fibrillar Adhesives
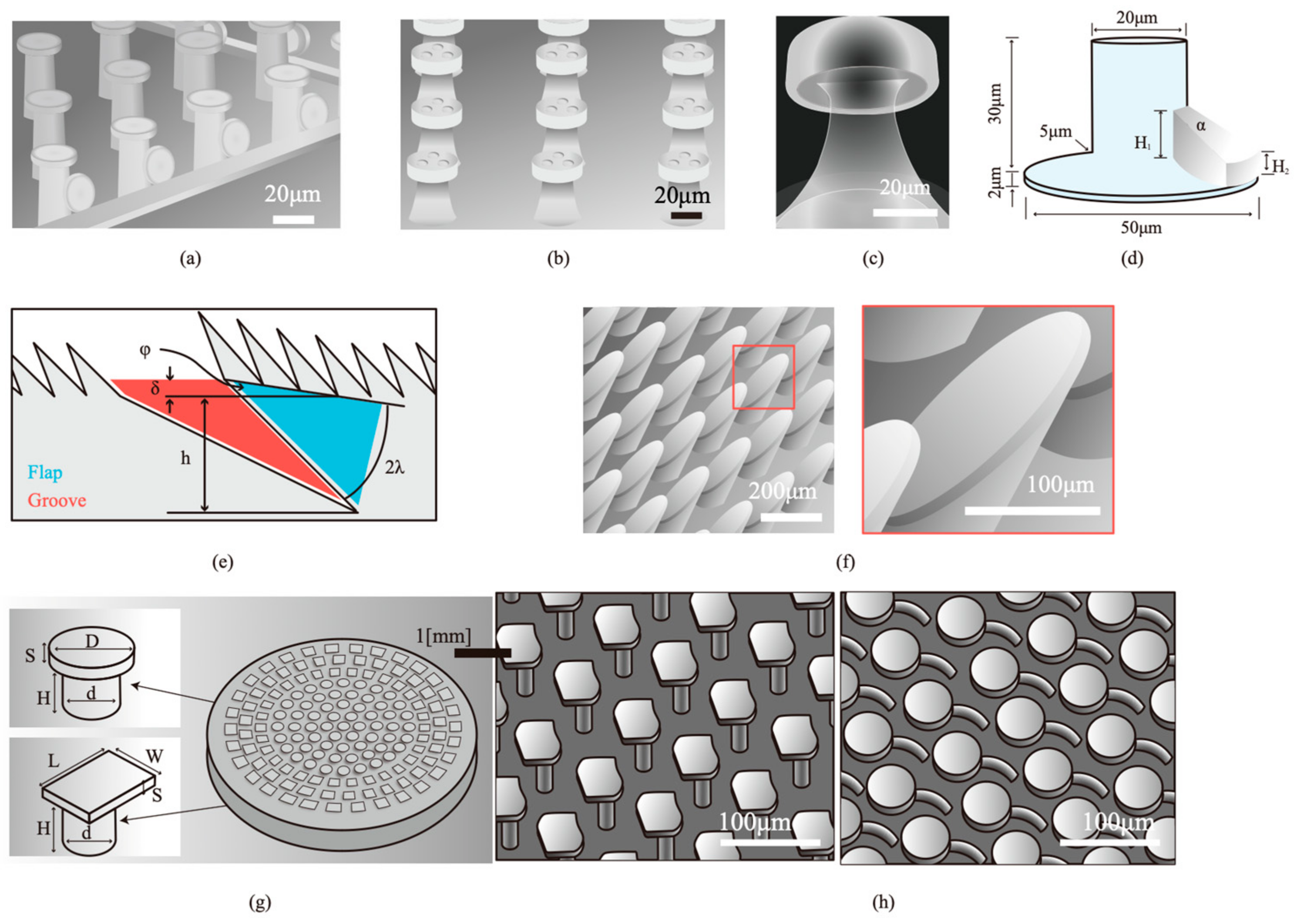
| Design Strategy | Applications | Advantages/Innovations |
|---|---|---|
| Dry-adhesive microstructure for rough surfaces [7] | Material handling on Mars | 392.94× increase in pull-off stress; enables low-energy handling of rough, additively manufactured surfaces |
| Springtail-, gecko-, and octopus-inspired 3D microstructures [153] | Medical devices, robotics, wearable adhesives | Strong reversible adhesion; super-repellency on wet and dry surfaces; versatile for synthetic/biological surfaces |
| Mushroom-shaped fibrillar arrays with double re-entrant tips [154] | Robotics, medical devices, underwater adhesives | Retains adhesion in presence of water, oil, and other liquids; robust, stretchable, and highly deformable |
| Trapezoidal-prism + mushroom-shaped microstructure [155] | Pick-and-place for microelectronics, transfer printing | Strong adhesion (87.8 kPa); low detachment strength (<0.07 kPa); works in dry and wet conditions |
| Gecko-inspired adhesive with spatial variation [156] | Robotics, climbing devices | 100× stronger adhesion in preferred direction; enhances control and mimics natural adhesive asymmetry |
| Anisotropic dry-adhesive microstructures produced via two-photon polymerization [157] | Space debris capture, high-anisotropy applications | High anisotropic adhesion factor (7.52:1); strong adhesion (up to 1105.29 mN/cm2); suitable for mass production |
| Combined microfibril textures (micro-spatulae and micro-mushroom) [159] | Robotics, adaptive gripping systems | Optimized adhesion and friction under varying loads and velocities; adaptable to environmental conditions |
| Off-center spatula-shaped microfiber caps [161] | Pick-and-place, robotics | 3–5× reduction in adhesion for easy detachment; 3× increase in shear with lateral drag; versatile directional control |
| Mushroom-like PDMS microline arrays with directional patterns [162] | Silicon wafer transportation | High shear adhesion in parallel direction; low peeling force, enabling easy detachment and directional control |
| Elastomeric mushroom-shaped microfibers with PSA layer [163] | Wearable medical devices, transfer printing, robotic manipulation | High adhesion strength (300 kPa); 35× durability improvement on smooth surfaces |
| T-shaped PDMS micropillars with modulus gradient [164] | Robotics, gripping systems | 4.6× increase in adhesion; 2.4× increase in friction compared to pure PDMS arrays |
| Fiber-reinforced adhesive with bio-inspired soft backings [167] | Soft robotic grippers, curved surfaces | Enhanced conformability and friction on curved substrates; scalable contact area inversely with backing stiffness |
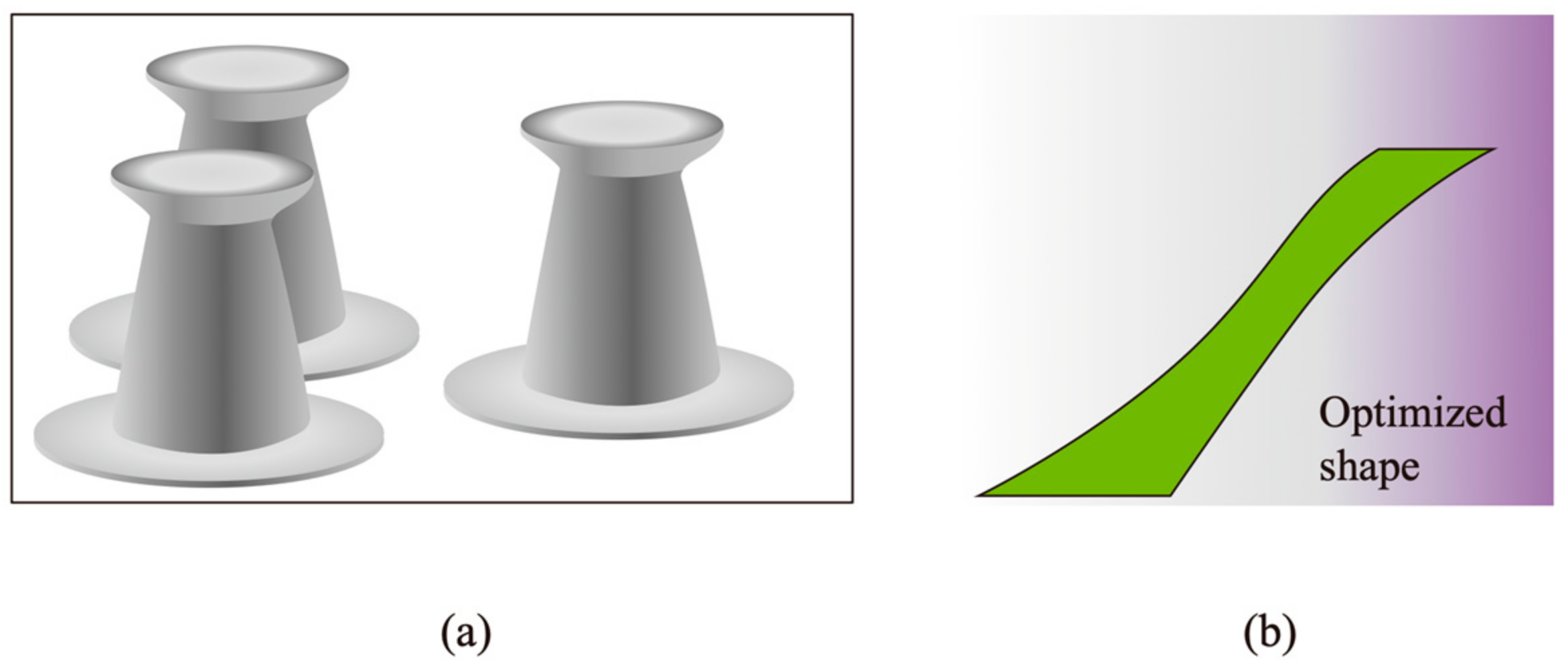
| Mushroom-like adhesive pillars with optimized geometry [168] | Robotic grasping, microtransfer printing | 2× adhesion enhancement; reduced edge stress concentration; crack initiation shifted to pillar center |
| Machine learning-optimized composite pillars [169] | Robotics, adhesive interfaces | 11× increase in detachment force; high adhesion under varied loading conditions; 1.7× improvement over rectangular core design |
| Gecko-inspired micropillars with asymmetrical tilt [170] | Robotics, gripping systems | 4× stronger adhesion than plain surface; 2× stronger in gripping direction than release direction |
| Machine learning-optimized gecko-inspired fibrils [171] | Robotics, medical devices | 77% improvement in adhesion; sensitivity to fibril shape and deformation considered |
| Free-form optimized adhesive pillar shapes [172] | Robotics, adhesive interfaces | Improved uniformity in stress distribution without stress peaks |
| Directional adhesive pillars with anisotropic properties [173] | Wall-climbing robots, grippers | Superior directionality and adhesion strength |
| In-plane combination of micropillars with different aspect ratios [175] | Space capture and docking | Maintains 85% adhesion after large deformation; resists overload-induced adhesion failure; adaptable to dynamic capture |
4.2. Strategies of Reversibly Controlled Adhesion and Latest Advances
4.2.1. Controlling the Amount of True Surface Contact
4.2.2. Controlled Adhesion by Shear Force
5. Discussion
5.1. Key Mechanisms and Innovations
5.2. Challenges in Interface Mechanics
5.3. Precision, Repeatability, and Practical Applications
5.4. Expanding the Application Range
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Arzt, E.; Quan, H.; McMeeking, R.M.; Hensel, R. Functional surface microstructures inspired by nature—From adhesion and wetting principles to sustainable new devices. Prog. Mater. Sci. 2021, 120, 100823. [Google Scholar] [CrossRef]
- Shintake, J.; Cacucciolo, V.; Floreano, D.; Shea, H. Soft robotic grippers. Adv. Mater. 2018, 30, 1707035. [Google Scholar] [CrossRef]
- Hajj-Ahmad, A.; Kaul, L.; Matl, C.; Cutkosky, M. GRASP: Grocery robot’s adhesion and suction picker. IEEE Robot. Autom. Lett. 2023, 8, 6419–6426. [Google Scholar] [CrossRef]
- Ben-Larbi, M.K.; Hensel, R.; Atzeni, G.; Arzt, E.; Stoll, E. Orbital debris removal using micropatterned dry adhesives: Review and recent advances. Prog. Aerosp. Sci. 2022, 134, 100850. [Google Scholar] [CrossRef]
- Spenko, M. Making Contact: A review of robotic attachment mechanisms for extraterrestrial applications. Adv. Intell. Syst. 2023, 5, 2100063. [Google Scholar] [CrossRef]
- Chen, T.G.; Cauligi, A.; Suresh, S.A.; Pavone, M.; Cutkosky, M.R. Testing gecko-inspired adhesives with Astrobee aboard the international space station: Readying the technology for space. IEEE Robot. Autom. Mag. 2022, 29, 24–33. [Google Scholar] [CrossRef]
- Mensching, N.; Krüger, M.L.; Kvaratskheliya, A.; Meyer, D.; Tracht, K.; Okulov, I.; Mädler, L. Dry-adhesive microstructures for material handling of additively manufactured and deep-rolled metal surfaces with reference to Mars. Materials 2023, 16, 4170. [Google Scholar] [CrossRef]
- Linghu, C.; Wang, C.; Cen, N.; Wu, J.; Lai, Z.; Song, J. Rapidly tunable and highly reversible bio-inspired dry adhesion for transfer printing in air and a vacuum. Soft Matter 2019, 15, 30–37. [Google Scholar] [CrossRef]
- Raut, H.K.; Baji, A.; Hariri, H.H.; Parveen, H.; Soh, G.S.; Low, H.Y.; Wood, K.L. Gecko-inspired dry adhesive based on micro-nanoscale hierarchical arrays for application in climbing devices. ACS Appl. Mater. Interfaces 2018, 10, 1288–1296. [Google Scholar] [CrossRef]
- Borijindakul, P.; Ji, A.; Dai, Z.; Gorb, S.; Manoonpong, P. Mini review: Comparison of bio-inspired adhesive feet of climbing robots on smooth vertical surfaces. Front. Bioeng. Biotechnol. 2021, 9, 765718. [Google Scholar] [CrossRef]
- Hawkes, E.W.; Eason, E.V.; Christensen, D.L.; Cutkosky, M.R. Human climbing with efficiently scaled gecko-inspired dry adhesives. J. R. Soc. Interface 2015, 12, 20140675. [Google Scholar] [CrossRef] [PubMed]
- Hensel, R.; Moh, K.; Arzt, E. Engineering micropatterned dry adhesives: From contact theory to handling applications. Adv. Funct. Mater. 2018, 28, 1800865. [Google Scholar] [CrossRef]
- Croll, A.B.; Hosseini, N.; Bartlett, M.D. Switchable adhesives for multifunctional interfaces. Adv. Mater. Technol. 2019, 4, 1900193. [Google Scholar] [CrossRef]
- Meiners, F.; Tracht, K. Releasing principles for dry-adhesive handling of microobjects. Procedia CIRP 2020, 91, 503–507. [Google Scholar] [CrossRef]
- Duan, W.; Yu, Z.; Cui, W.; Zhang, Z.; Zhang, W.; Tian, Y. Bio-inspired switchable soft adhesion for the boost of adhesive surfaces and robotics applications: A brief review. Adv. Colloid Interface Sci. 2023, 313, 102862. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Li, J.; Li, P.; Li, S. Gecko-inspired controllable adhesive: Structure, fabrication, and application. Biomimetics 2024, 9, 149. [Google Scholar] [CrossRef]
- Zhao, J.; Xia, N.; Zhang, L. A review of bioinspired dry adhesives: From achieving strong adhesion to realizing switchable adhesion. Bioinspir. Biomim. 2024, 19, 051003. [Google Scholar] [CrossRef]
- Sauer, R.A. Advances in the computational modeling of the gecko adhesion mechanism. J. Adhes. Sci. Technol. 2014, 28, 240–255. [Google Scholar] [CrossRef]
- Autumn, K.; Niewiarowski, P.H.; Puthoff, J.B. Gecko adhesion as a model system for integrative biology, interdisciplinary science, and bioinspired engineering. Annu. Rev. Ecol. Evol. Syst. 2014, 45, 445–470. [Google Scholar] [CrossRef]
- Russell, A.P.; Stark, A.Y.; Higham, T.E. The integrative biology of gecko adhesion: Historical review, current understanding, and grand challenges. Integr. Comp. Biol. 2019, 59, 101–116. [Google Scholar] [CrossRef]
- Autumn, K.; Peattie, A.M. Mechanisms of adhesion in geckos. Integr. Comp. Biol. 2002, 42, 1081–1090. [Google Scholar] [CrossRef] [PubMed]
- Johnson, K.L.; Kendall, K.; Roberts, A.D. Surface energy and the contact of elastic solids. Proc. R. Soc. A Math. Phys. Eng. Sci. 1971, 324, 301–313. [Google Scholar]
- Kendall, K. Thin-film peeling-the elastic term. J. Phys. D Appl. Phys. 1975, 8, 1449–1452. [Google Scholar] [CrossRef]
- Kim, J.K.; Varenberg, M. Contact splitting in dry adhesion and friction: Reducing the influence of roughness. Beilstein J. Nanotechnol. 2019, 10, 1–8. [Google Scholar] [CrossRef]
- Chen, B.; Wu, P.; Gao, H. Pre-tension generates strongly reversible adhesion of a spatula pad on substrate. J. R. Soc. Interface 2009, 6, 529–537. [Google Scholar] [CrossRef]
- Collino, R.R.; Philips, N.R.; Rossol, M.N.; McMeeking, R.M.; Begley, M.R. Detachment of compliant films adhered to stiff substrates via Van Der Waals interactions: Role of frictional sliding during peeling. J. R. Soc. Interface 2014, 11, 20140453. [Google Scholar] [CrossRef]
- Dalbe, M.-J.; Villey, R.; Ciccotti, M.; Santucci, S.; Cortet, P.-P.; Vanel, L. Inertial and stick-slip regimes of unstable adhesive tape peeling. Soft Matter 2016, 12, 4537–4548. [Google Scholar] [CrossRef]
- Labonte, D.; Federle, W. Biomechanics of shear-sensitive adhesion in climbing animals: Peeling pre-tension and sliding-induced changes in interface strength. J. R. Soc. Interface 2016, 13, 20160373. [Google Scholar] [CrossRef]
- Skopici, B.H.; Schniepp, H.C. Peeling in biological and bioinspired adhesive systems. JOM 2020, 72, 1509–1522. [Google Scholar] [CrossRef]
- Spolenak, R.; Gorb, S.; Gao, H.; Arzt, E. Effects of contact shape on the scaling of biological attachments. Proc. R. Soc. A Math. Phys. Eng. Sci. 2005, 461, 305–319. [Google Scholar] [CrossRef]
- Labonte, D.; Federle, W. Scaling and biomechanics of surface attachment in climbing animals. Philos. Trans. R. Soc. B Biol. Sci. 2015, 370, 20140027. [Google Scholar] [CrossRef] [PubMed]
- Varenberg, M.; Murarash, B.; Kligerman, Y.; Gorb, S. Geometry-controlled adhesion: Revisiting the contact splitting hypothesis. Appl. Phys. A Mater. Sci. Process. 2011, 103, 933–938. [Google Scholar] [CrossRef]
- Gao, H.; Yao, H. Shape insensitive optimal adhesion of nanoscale fibrillar structures. Proc. Natl. Acad. Sci. USA 2004, 101, 7851–7856. [Google Scholar] [CrossRef] [PubMed]
- Federle, W. Why are so many adhesive pads hairy? J. Exp. Biol. 2006, 209, 2611–2621. [Google Scholar] [CrossRef]
- Jagota, A.; Bennison, S.J. Mechanics of adhesion through a fibrillar microstructure. Integr. Comp. Biol. 2002, 42, 1140–1145. [Google Scholar] [CrossRef]
- Peressadko, A.; Gorb, S.N. When less is more: Experimental evidence for tenacity enhancement by division of contact area. J. Adhes. 2004, 80, 247–261. [Google Scholar] [CrossRef]
- Tang, T.; Hui, C.Y.; Glassmaker, N.J. Can a fibrillar interface be stronger and tougher than a non-fibrillar one? J. R. Soc. Interface 2005, 2, 505–516. [Google Scholar] [CrossRef]
- Carbone, G.; Pierro, E. Sticky bio-inspired micropillars: Finding the best shape. Small 2012, 8, 1449–1454. [Google Scholar] [CrossRef]
- Wang, L.; Jiang, Q.; Weng, Z.; Yuan, Q.; Wang, Z. Effects of flexural rigidity on soft actuators via adhering to large cylinders. Actuators 2022, 11, 286. [Google Scholar] [CrossRef]
- Booth, J.A.; Hensel, R. Perspective on statistical effects in the adhesion of micropatterned surfaces. Appl. Phys. Lett. 2021, 119, 230502. [Google Scholar] [CrossRef]
- Hu, H.; Tian, H.; Gao, Y.; Wan, Z.; Wang, L.; Xu, H.; Wang, C.; Shao, J.; Zheng, Z. Revisiting the contact splitting hypothesis: An effective route for enhancing adhesion on rough surface. J. Mech. Phys. Solids 2023, 170, 105121. [Google Scholar] [CrossRef]
- Glassmaker, N.J.; Himeno, T.; Hui, C.-Y.; Kim, J. Design of biomimetic fibrillar interfaces: 1, Making contact. J. R. Soc. Interface 2004, 1, 23–33. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, S.; Menon, C. A new model for predicting fiber clumping phenomenon in bio-inspired dry adhesives. J. Adhes. 2014, 90, 135–155. [Google Scholar] [CrossRef]
- Grill, M.J.; Meier, C.; Wall, W.A. Investigation of the peeling and pull-off behavior of adhesive elastic fibers via a novel computational beam interaction model. J. Adhes. 2021, 97, 730–759. [Google Scholar] [CrossRef]
- Filippov, A.E.; Gorb, S.N. Spatial model of the gecko foot hair: Functional significance of highly specialized non-uniform geometry. Interface Focus 2015, 5, 20140065. [Google Scholar] [CrossRef]
- Bhushan, B.; Peressadko, A.G.; Kim, T.W. Adhesion analysis of two-level hierarchical morphology in natural attachment systems for ‘smart adhesion’. J. Adhes. Sci. Technol. 2006, 20, 1475–1491. [Google Scholar] [CrossRef]
- Kim, T.W.; Bhushan, B. Effect of stiffness of multilevel hierarchical attachment system on adhesion enhancement. Ultramicroscopy 2007, 107, 902–912. [Google Scholar] [CrossRef]
- Kong, A.; Bacca, M. A self-adhesion criterion for slanted micropillars. Extreme Mech. Lett. 2022, 52, 101663. [Google Scholar] [CrossRef]
- Calahan, K.N.; Qi, Y.; Johannes, K.G.; Rentschler, M.E.; Long, R. Local lateral contact governs shear traction of micropatterned surfaces on hydrogel substrates. Sci. Adv. 2022, 25, eabn2728. [Google Scholar] [CrossRef]
- Calahan, K.N.; Johannes, K.G.; Yang, X.; Long, R.; Rentschler, M.E. Density of micropillar array influences shear traction of individual pillars on soft substrates. ACS Appl. Eng. Mater. 2024, 2, 1–9. [Google Scholar] [CrossRef]
- Bartlett, M.D.; Croll, A.B.; King, D.R.; Paret, B.M.; Irschick, D.J.; Crosby, A.J. Looking beyond fibrillar features to scale gecko-like adhesion. Adv. Mater. 2012, 24, 1078–1083. [Google Scholar] [CrossRef]
- Tian, Y.; Zhao, Z.; Zaghi, G.; Kim, Y.; Zhang, D.; Maboudian, R. Tuning the friction characteristics of gecko-inspired polydimethylsiloxane micropillar arrays by embedding Fe3O4 and SiO2 particles. ACS Appl. Mater. Interfaces 2015, 7, 13232–13237. [Google Scholar] [CrossRef]
- Simaite, A.; Karimi, M.A.; Spenko, M. Crosslinker and catalyst as silicone elastomer bonding enhancers: Applications to fabrication of hybrid electrostatic/gecko-like adhesives. J. Micromech. Microeng. 2019, 29, 077001. [Google Scholar] [CrossRef]
- Alizadehyazdi, V.; Simaite, A.; Spenko, M. Evaluation of material properties for practical microstructured adhesives: Low dust adhesion and high shear strength. ACS Appl. Mater. Interfaces 2019, 11, 8654–8666. [Google Scholar] [CrossRef]
- Simaite, A.; Spenko, M. Evaluation of silicone elastomers as structural materials for microstructured adhesives. Bioinspir. Biomim. 2019, 14, 046005. [Google Scholar] [CrossRef]
- King, D.R.; Bartlett, M.D.; Nalbach, M.; Irschick, D.J.; Crosby, A.J. High strength reversible adhesive closures. J. Polym. Sci. B Polym. Phys. 2017, 55, 1783–1790. [Google Scholar] [CrossRef]
- Kim, S.; Sitti, M.; Hui, C.-Y.; Long, R.; Jagota, A. Effect of backing layer thickness on adhesion of single-level elastomer fiber arrays. Appl. Phys. Lett. 2007, 91, 161905. [Google Scholar] [CrossRef]
- Gillies, A.G.; Puthoff, J.; Cohen, M.J.; Autumn, K.; Fearing, R.S. Dry self-cleaning properties of hard and soft fibrillar structures. ACS Appl. Mater. Interfaces 2013, 5, 6081–6088. [Google Scholar] [CrossRef]
- Khaderi, S.N.; Fleck, N.A.; Arzt, E.; McMeeking, R.M. Detachment of an adhered micropillar from a dissimilar substrate. J. Mech. Phys. Solids 2015, 75, 159–183. [Google Scholar] [CrossRef]
- Hensel, R.; McMeeking, R.M.; Kossa, A. Adhesion of a rigid punch to a confined elastic layer revisited. J. Adhes. 2019, 95, 44–63. [Google Scholar] [CrossRef]
- Kumar, N.; Khaderi, S.N. The detachment of an inclined micro-pillar adhered to a dissimilar substrate. J. Appl. Mech. 2021, 88, 101010. [Google Scholar] [CrossRef]
- Swift, M.D.; Haverkamp, C.B.; Stabile, C.J.; Hwang, D.; Plaut, R.H.; Turner, K.T.; Dillard, D.A.; Bartlett, M.D. Active membranes on rigidity tunable foundations for programmable, rapidly switchable adhesion. Adv. Mater. Technol. 2020, 5, 2000676. [Google Scholar] [CrossRef]
- Wahdat, H.; Elzière, P.; Chan, N.; Crosby, A.J. Mechanics of adhesives under annular confinement: Internal pressure, force, and interfacial area. Soft Matter 2021, 17, 5540–5547. [Google Scholar] [CrossRef]
- Luo, H.; Li, C.; Shi, C.; Nie, S.; Song, J. Switchable dry adhesive based on shape memory polymer with hemispherical indenters for transfer printing. Theor. Appl. Mech. Lett. 2021, 11, 100308. [Google Scholar] [CrossRef]
- Marulli, M.R.; Heepe, L.; Gorb, S.N.; Paggi, M. A finite element framework for the simulation of bio-inspired adhesives with mushroom-shaped microstructures. Mech. Res. Commun. 2022, 125, 103963. [Google Scholar] [CrossRef]
- Samri, M.; Thiemecke, J.; Hensel, R.; Arzt, E. Application of machine learning to object manipulation with bio-inspired microstructures. J. Mater. Res. Technol. 2023, 27, 1406–1416. [Google Scholar] [CrossRef]
- Sudersan, P.; Kappl, M. Mechanisms of detachment in fibrillar adhesive systems. J. Theor. Biol. 2023, 557, 111315. [Google Scholar] [CrossRef]
- Skondras-Giousios, D.; Karkalos, N.E.; Markopoulos, A.P. Finite element simulation of friction and adhesion attributed contact of bio-inspired gecko-mimetic PDMS micro-flaps with SiO2 spherical surface. Bioinspir. Biomim. 2020, 15, 066004. [Google Scholar] [CrossRef]
- Booth, J.A.; Tinnemann, V.; Hensel, R.; Arzt, E.; McMeeking, R.M.; Foster, K.L. Statistical properties of defect-dependent detachment strength in bioinspired dry adhesives. J. R. Soc. Interface 2019, 16, 20190239. [Google Scholar] [CrossRef]
- Hensel, R.; Thiemecke, J.; Booth, J.A. Preventing catastrophic failure of microfibrillar adhesives in compliant systems based on statistical analysis of adhesive strength. ACS Appl. Mater. Interfaces 2021, 13, 19422–19429. [Google Scholar] [CrossRef]
- Hwang, D.; Lee, C.; Yang, X.; Pérez-González, J.M.; Finnegan, J.; Lee, B.; Markvicka, E.J.; Long, R.; Bartlett, M.D. Metamaterial adhesives for programmable adhesion through reverse crack propagation. Nat. Mater. 2023, 22, 1030–1038. [Google Scholar] [CrossRef]
- Li, Q.; Liu, W.; Yang, C.; Rao, P.; Lv, P.; Duan, H.; Hong, W. Kirigami-inspired adhesion with high directional asymmetry. J. Mech. Phys. Solids 2022, 169, 105053. [Google Scholar] [CrossRef]
- Cen, J.; Komvopoulos, K. A cohesive-zone-based contact mechanics analysis of delamination in homogeneous and layered half-spaces subjected to normal and shear surface tractions. J. Appl. Mech. 2023, 90, 071011. [Google Scholar] [CrossRef]
- Li, G.; Tan, K.H.; Fung, T.C.; Yu, Q.J.; May, M. A coupled dynamic cohesive zone model for FRP-concrete mixed-mode separation. Compos. Struct. 2021, 268, 113872. [Google Scholar] [CrossRef]
- Autumn, K.; Dittmore1, A.; Santos, D.; Spenko, M.; Cutkosky, M. Frictional adhesion: A new angle on gecko attachment. J. Exp. Biol. 2006, 209, 3569–3579. [Google Scholar] [CrossRef]
- Federle, W.; Labonte, D. Dynamic biological adhesion: Mechanisms for controlling attachment during locomotion. Philos. Trans. R. Soc. B Biol. Sci. 2019, 374, 20190199. [Google Scholar] [CrossRef]
- Jagota, A.; Hui, C.-Y. Adhesion, friction, and compliance of bio-mimetic and bio-inspired structured interfaces. Mater. Sci. Eng. R Rep. 2011, 72, 253–292. [Google Scholar] [CrossRef]
- Zhao, B.; Pesika, N.; Rosenberg, K.; Tian, Y.; Zeng, H.; McGuiggan, P.; Autumn, K.; Israelachvili, J. Adhesion and friction force coupling of gecko setal arrays: Implications for structured adhesive surfaces. Langmuir 2008, 24, 1517–1524. [Google Scholar] [CrossRef]
- Hill, G.C.; Soto, D.R.; Peattie, A.M.; Full, R.J.; Kenny, T.W. Orientation angle and the adhesion of single gecko setae. J. R. Soc. Interface 2011, 8, 926–933. [Google Scholar] [CrossRef]
- Wu-Bavouzet, F.; Cayer-Barrioz, J.; Bot, A.L.; Brochard-Wyart, F.; Buguin, A. Effect of surface pattern on the adhesive friction of elastomers. Phys. Rev. E 2010, 82, 031806. [Google Scholar] [CrossRef]
- Nosonovsky, M.; Bhushan, B. Multiscale friction mechanisms and hierarchical surfaces in nano- and bio-tribology. Mater. Sci. Eng. R Rep. 2007, 58, 162–193. [Google Scholar] [CrossRef]
- Zeng, H.; Pesika, N.; Tian, Y.; Zhao, B.; Chen, Y.; Tirrell, M.; Turner, K.L.; Israelachvili, J.N. Frictional adhesion of patterned surfaces and implications for gecko and biomimetic systems. Langmuir. 2009, 25, 7486–7495. [Google Scholar] [CrossRef]
- Mergel, J.C.; Sahli, R.; Scheibert, J.; Sauer, R.A. Continuum contact models for coupled adhesion and friction. J. Adhes. 2019, 95, 1101–1133. [Google Scholar] [CrossRef]
- Eason, E.V.; Hawkes, E.W.; Windheim, M.; Christensen, D.L.; Libby, T.; Cutkosky, M.R. Stress distribution and contact area measurements of a gecko toe using a high-resolution tactile sensor. Bioinspir. Biomim. 2015, 10, 016013. [Google Scholar] [CrossRef]
- Gouravaraju, S.; Sauer, R.A.; Gautam, S.S. Investigating the normal and tangential peeling behaviour of gecko spatulae using a coupled adhesion-friction model. J. Adhes. 2021, 97, 952–983. [Google Scholar] [CrossRef]
- Gouravaraju, S.; Sauer, R.A.; Gautam, S.S. On the presence of a critical detachment angle in gecko spatula peeling—A numerical investigation using an adhesive friction model. J. Adhes. 2021, 97, 1234–1254. [Google Scholar] [CrossRef]
- Mergel, J.C.; Scheibert, J.; Sauer, R.A. Contact with coupled adhesion and friction: Computational framework, applications, and new insights. J. Mech. Phys. Solids 2021, 146, 104194. [Google Scholar] [CrossRef]
- Sahli, R.; Pallares, G.; Ducottet, C.; Ben Ali, I.E.; Al Akhrass, S.; Guibert, M.; Scheibert, J. Evolution of real contact area under shear and the value of static friction of soft materials. Proc. Natl. Acad. Sci. USA 2018, 115, 471–476. [Google Scholar] [CrossRef]
- Khajeh Salehani, M.; Irani, N.; Nicola, L. Modeling adhesive contacts under mixed-mode loading. J. Mech. Phys. Solids 2019, 130, 320–329. [Google Scholar] [CrossRef]
- McMeeking, R.M.; Ciavarella, M.; Cricrì, G.; Kim, K.-S. The interaction of frictional slip and adhesion for a stiff sphere on a compliant substrate. J. Appl. Mech. 2020, 87, 031016. [Google Scholar] [CrossRef]
- Menga, N.; Carbone, G.; Dini, D. Do uniform tangential interfacial stresses enhance adhesion? J. Mech. Phys. Solids 2018, 112, 145–156. [Google Scholar] [CrossRef]
- Lengiewicz, J.; De Souza, M.; Lahmar, M.A.; Courbon, C.; Dalmas, D.; Stupkiewicz, S.; Scheibert, J. Finite deformations govern the anisotropic shear-induced area reduction of soft elastic materials. J. Mech. Phys. Solids 2020, 143, 104056. [Google Scholar] [CrossRef]
- Papangelo, A.; Ciavarella, M. On mixed-mode fracture mechanics models for contact area reduction under shear load in soft materials. J. Mech. Phys. Solids 2019, 124, 159–171. [Google Scholar] [CrossRef]
- Sahli, R.; Pallares, G.; Papangelo, A.; Ciavarella, M.; Ducottet, C.; Ponthus, N.; Scheibert, J. Shear-induced anisotropy in rough elastomer contact. Phys. Rev. Lett. 2019, 122, 214301. [Google Scholar] [CrossRef]
- Wang, J.; Tiwari, A.; Persson, B.N.J.; Sivebæk, I. Sphere and cylinder contact mechanics during slip. J. Mech. Phys. Solids 2020, 143, 104094. [Google Scholar] [CrossRef]
- Chu, Z.; Wang, C.; Hai, X.; Deng, J.; Cui, J.; Sun, L. Analysis and measurement of adhesive behavior for gecko-inspired synthetic microwedge structure. Adv. Mater. Interfaces 2019, 6, 1900283. [Google Scholar] [CrossRef]
- Simaite, A.; Temple, B.; Karimi, M.A.; Alizadehyazdi, V.; Spenko, M. Understanding the influence of silicone elastomer properties on wedge-shaped microstructured dry adhesives loaded in shear. J. R. Soc. Interface 2018, 15, 20180551. [Google Scholar] [CrossRef]
- Seale, M.; Cummins, C.; Viola, I.M.; Mastropaolo, E.; Nakayama, N. Design principles of hair-like structures as biological machines. J. R. Soc. Interface 2018, 15, 20180206. [Google Scholar] [CrossRef]
- Areyano, M.; Booth, J.A.; Brouwer, D.; Gockowski, L.F.; Valentine, M.T.; McMeeking, R.M. Suction-controlled detachment of mushroom-shaped adhesive structures. J. Appl. Mech. 2021, 88, 031017. [Google Scholar] [CrossRef]
- Zhao, R.R.; Turner, K.T.; Bassani, J.L. Exploiting interface patterning for adhesion control. J. Mech. Phys. Solids 2022, 160, 104740. [Google Scholar] [CrossRef]
- Li, R.; Li, D.; Zhang, W. Modeling of Rate Effects in Detachment of Mushroom-Shaped Adhesive Structures. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition 2023, New Orleans, LA, USA, 29 October–2 November 2023. IMECE2023-112383. [Google Scholar]
- Linghu, C.; Du, Z.; Sun, Y.; Chen, W.; Hsia, K.J. On shear adhesion of adhesive fibrils. Extreme Mech. Lett. 2023, 64, 102092. [Google Scholar] [CrossRef]
- Ni, K.; Wang, Z. Theoretical optimization of micropillar arrays for structurally stable bioinspired dry adhesives. Theor. Appl. Mech. Lett. 2024, 14, 100512. [Google Scholar] [CrossRef]
- Wu, X.; Wang, X.; Mei, T.; Sun, S. Mechanical analyses on the digital behaviour of the Tokay gecko (Gekko gecko) based on a multi-level directional adhesion model. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20150085. [Google Scholar] [CrossRef]
- Bartlett, M.D.; Case, S.W.; Kinloch, A.J.; Dillard, D.A. Peel tests for quantifying adhesion and toughness: A review. Prog. Mater. Sci. 2023, 137, 101086. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Akamine, A.; Sawae, Y. On/off switching of adhesion in gecko-inspired adhesives. Biosurf. Biotribol. 2021, 7, 83–89. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Hensel, R.; Arzt, E. A design strategy for mushroom-shaped microfibrils with optimized dry adhesion: Experiments and finite element analyses. J. Appl. Mech. 2021, 88, 031015. [Google Scholar] [CrossRef]
- Carbone, G.; Pierro, E.; Gorb, S.N. Origin of the superior adhesive performance of mushroom-shaped microstructured surfaces. Soft Matter 2011, 7, 5545–5552. [Google Scholar] [CrossRef]
- Aksak, B.; Sahin, K.; Sitti, M. The optimal shape of elastomer mushroom-like fibers for high and robust adhesion. Beilstein J. Nanotechnol. 2014, 5, 630–638. [Google Scholar] [CrossRef]
- Balijepalli, R.G.; Begley, M.R.; Fleck, N.A.; McMeeking, R.M.; Arzt, E. Numerical simulation of the edge stress singularity and the adhesion strength for compliant mushroom fibrils adhered to rigid substrates. Int. J. Solids Struct. 2016, 85–86, 160–171. [Google Scholar] [CrossRef]
- Bacca, M.; Booth, J.A.; Turner, K.L.; McMeeking, R.M. Load sharing in bioinspired fibrillar adhesives with backing layer interactions and interfacial misalignment. J. Mech. Phys. Solids 2016, 96, 428–444. [Google Scholar] [CrossRef]
- Booth, J.A.; Bacca, M.; McMeeking, R.M.; Foster, K.L. Benefit of backing-layer compliance in fibrillar adhesive patches—Resistance to peel propagation in the presence of interfacial misalignment. Adv. Mater. Interfaces 2018, 5, 1800272. [Google Scholar] [CrossRef]
- Khungura, H.; Bacca, M. The role of interfacial curvature in controlling the detachment strength of bioinspired fibrillar adhesives. Mech. Mater. 2021, 160, 103914. [Google Scholar] [CrossRef]
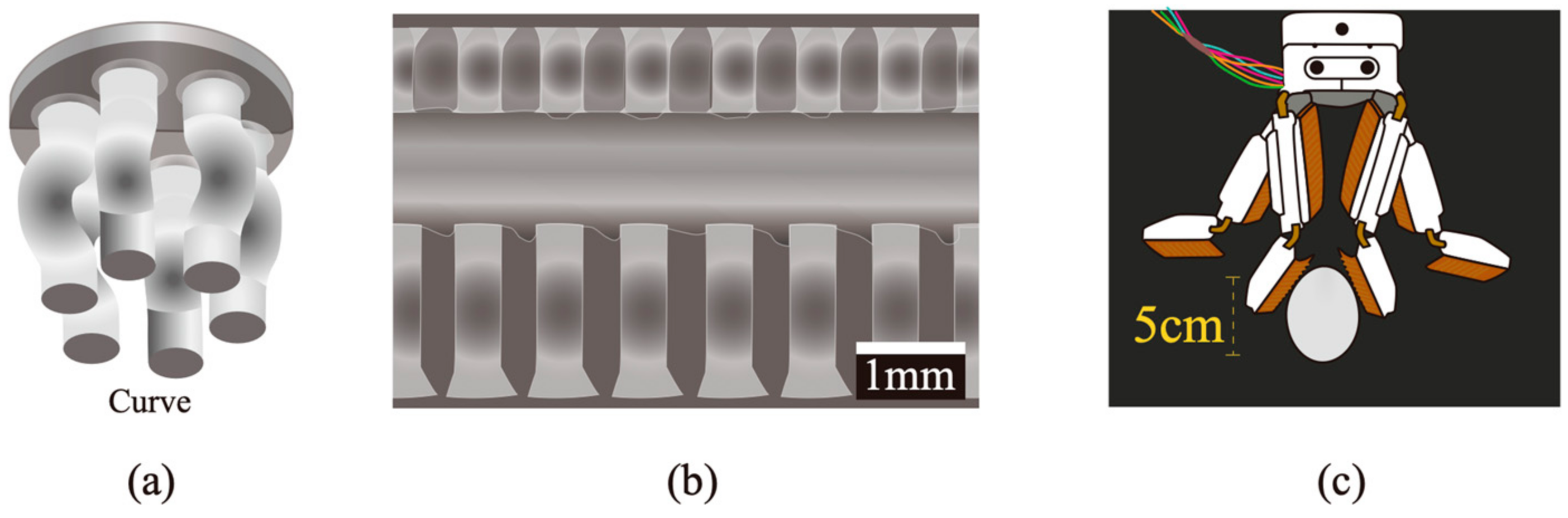
- Li, X.; Li, X.; Li, L.; Meng, Y.; Tian, Y. Load sharing design of a multi-legged adaptable gripper with gecko-inspired controllable adhesion. IEEE Robot. Autom. Lett. 2021, 6, 8482–8489. [Google Scholar] [CrossRef]
- Benvidi, F.H.; Bacca, M. Theoretical limits in detachment strength for axisymmetric bi-material adhesives. J. Appl. Mech. 2021, 88, 121007. [Google Scholar] [CrossRef]
- Samri, M.; Kossa, A.; Hensel, R. Effect of subsurface microstructures on adhesion of highly confined elastic films. J. Appl. Mech. 2021, 88, 031009. [Google Scholar] [CrossRef]
- Samri, M.; Thiemecke, J.; Prinz, E.; Dahmen, T.; Hensel, R.; Arzt, E. Predicting the adhesion strength of micropatterned surfaces using supervised machine learning. Mater. Today 2022, 53, 41–50. [Google Scholar] [CrossRef]
- Tarpey, R.; Ronan, W. The influence of substrate stiffness on interfacial stresses for adhesive microfibrils. J. Mech. Phys. Solids 2023, 172, 105175. [Google Scholar] [CrossRef]
- Niewiarowski, P.H.; Dhinojwala, A.; Garner, A.M. A physical model approach to gecko adhesion opportunity and constraint: How rough could it be? Integr. Comp. Biol. 2019, 59, 203–213. [Google Scholar] [CrossRef]
- Persson, B.N.J. Biological adhesion for locomotion on rough surfaces: Basic principles and a theorist’s view. MRS Bull. 2007, 32, 486–490. [Google Scholar] [CrossRef]
- Gillies, A.G.; Fearing, R.S. Simulation of synthetic gecko arrays shearing on rough surfaces. J. R. Soc. Interface 2014, 11, 20140021. [Google Scholar] [CrossRef]
- Kovalev, A.; Filippov, A.E.; Gorb, S.N. Critical roughness in animal hairy adhesive pads: A numerical modeling approach. Bioinspir. Biomim. 2018, 13, 066004. [Google Scholar] [CrossRef] [PubMed]
- Ozer, A. Mechanics of bio-inspired attachment systems contacting with rough surface: Effect of spring orientation angle on hierarchical spring model. J. Adhes. Sci. Technol. 2016, 30, 2710–2724. [Google Scholar] [CrossRef]
- Fischer, S.C.L.; Arzt, E.; Hensel, R. Composite pillars with a tunable interface for adhesion to rough substrates. ACS Appl. Mater. Interfaces 2017, 9, 1036–1044. [Google Scholar] [CrossRef]
- Pepelyshev, A.; Borodich, F.M.; Galanov, B.A.; Gorb, E.V.; Gorb, S.N. Adhesion of soft materials to rough surfaces: Experimental studies, statistical analysis and modelling. Coatings 2018, 8, 350. [Google Scholar] [CrossRef]
- Brely, L.; Bosia, F.; Pugno, N.M. The influence of substrate roughness, patterning, curvature, and compliance in peeling problems. Bioinspir. Biomim. 2018, 13, 026004. [Google Scholar] [CrossRef]
- Higham, T.E.; Russell, A.P.; Niewiarowski, P.H.; Wright, A.; Speck, T. The ecomechanics of gecko adhesion: Natural surface topography, evolution, and biomimetics. Integr. Comp. Biol. 2019, 59, 148–167. [Google Scholar] [CrossRef]
- Hui, C.-Y.; Liu, Z.; Bain, N.; Jagota, A.; Dufresne, E.R.; Style, R.W.; Kiyama, R.; Gong, J.P. How surface stress transforms surface profiles and adhesion of rough elastic bodies. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20200477. [Google Scholar] [CrossRef]
- Klittich, M.R.; Wilson, M.C.; Bernard, C.; Rodrigo, R.M.; Keith, A.J.; Niewiarowski, P.H.; Dhinojwala, A. Influence of substrate modulus on gecko adhesion. Sci. Rep. 2017, 7, 43647. [Google Scholar] [CrossRef]
- Pillai, R.; Nordberg, E.; Riedel, J.; Schwarzkopf, L. Nonlinear variation in clinging performance with surface roughness in geckos. Ecol. Evol. 2020, 10, 2597–2607. [Google Scholar] [CrossRef]
- Materzok, T.; Boer, D.D.; Gorb, S.; Müller-Plathe, F. Gecko adhesion on flat and rough surfaces: Simulations with a multi-scale molecular model. Small 2022, 18, 2201674. [Google Scholar] [CrossRef]
- Niewiarowski1, P.H.; Lopez, S.; Ge, L.; Hagan, E.; Dhinojwala, A. Sticky gecko feet: The role of temperature and humidity. PLoS ONE 2008, 3, e2192. [Google Scholar] [CrossRef] [PubMed]
- Peng, Z.; Yang, Y.; Chen, S. Coupled effects of the temperature and the relative humidity on gecko adhesion. J. Phys. D Appl. Phys. 2017, 50, 315402. [Google Scholar] [CrossRef]
- Mitchell, C.T.; Dayan, C.B.; Drotlef, D.-M.; Sitti, M.; Stark, A.Y. The effect of substrate wettability and modulus on gecko and gecko-inspired synthetic adhesion in variable temperature and humidity. Sci. Rep. 2020, 10, 19748. [Google Scholar] [CrossRef]
- Stark, A.Y.; Mitchell, C.T. Stick or slip: Adhesive performance of geckos and gecko-inspired synthetics in wet environments. Integr. Comp. Biol. 2019, 59, 214–226. [Google Scholar] [CrossRef]
- Russell, A.P.; Gamble, T. Evolution of the gekkotan adhesive system: Does digit anatomy point to one or more origins? Integr. Comp. Biol. 2019, 59, 131–147. [Google Scholar] [CrossRef]
- Büscher, T.H.; Gorb, S.N. Physical constraints lead to parallel evolution of micro- and nanostructures of animal adhesive pads: A review. Beilstein J. Nanotechnol. 2021, 12, 725–743. [Google Scholar] [CrossRef]
- Materzok, T.; Gorb, S.N.; Müller-Plathe, F. Gecko adhesion: A molecular-simulation perspective on the effect of humidity. Soft Matter 2022, 18, 1247. [Google Scholar] [CrossRef]
- Ringenwald, B.E.; Bogacki, E.C.; Narvaez, C.A.; Stark, A.Y. The effect of variable temperature, humidity, and substrate wettability on Gecko (Gekko gecko) locomotor performance and behavior. J. Exp. Zool. A Ecol. Integr. Physiol. 2021, 335, 454–463. [Google Scholar] [CrossRef]
- Palecek, A.M.; Garner, A.M.; Klittich, M.R.; Stark, A.Y.; Scherger, J.D.; Bernard, C.; Niewiarowski, P.H.; Dhinojwala, A. An investigation of gecko attachment on wet and rough substrates leads to the application of surface roughness power spectral density analysis. Sci. Rep. 2022, 12, 11556. [Google Scholar] [CrossRef]
- Li, R.; Sun, J.; Li, D.; Li, X.; Zhang, X.; Zhang, W. Rate-dependent adhesion in dynamic contact of spherical-tip fibrillar structures. Int. J. Solids Struct. 2022, 259, 111997. [Google Scholar] [CrossRef]
- Li, D.; Li, R.; Zhang, W. Combined effects of viscoelasticity and surface roughness on the adhesion behavior of a flat-end cylindrical microstructure. Int. J. Solids Struct. 2022, 251, 111753. [Google Scholar] [CrossRef]
- Li, R.; Li, D.; Zhang, W. Rate effects in detachment of a spherical probe from fibrillar adhesive surfaces. J. Mech. Phys. Solids 2023, 171, 105130. [Google Scholar] [CrossRef]
- Liang, C.; Wang, F.; Huo, Z.; Shi, B.; Tian, Y.; Zhao, X.; Zhang, D. Pull-off force modeling and experimental study of PDMS stamp considering preload in micro transfer printing. Int. J. Solids Struct. 2020, 193–194, 134–140. [Google Scholar] [CrossRef]
- Li, R.; Li, D.; Sun, J.; Zhang, X.; Zhang, W. Pull-off dynamics of mushroom-shaped adhesive structures. J. Mech. Phys. Solids 2024, 183, 105519. [Google Scholar] [CrossRef]
- Khungura, H.; Bacca, M. Optimal load sharing in bioinspired fibrillar adhesives: Asymptotic solution. J. Appl. Mech. 2021, 88, 031004. [Google Scholar] [CrossRef]
- Tong, Z.; Benvidi, F.H.; Bacca, M. Multimaterial topology optimization of adhesive backing layers via J-integral and strain energy minimizations. J. Appl. Mech. 2023, 90, 111002. [Google Scholar] [CrossRef]
- Meiners, F.; Tuitje, C.; Hogreve, S.; Tracht, K. Model-based prediction of the detachment of microspheres from dry adhesive gripper surfaces by bending. Procedia CIRP 2022, 115, 101–106. [Google Scholar] [CrossRef]
- Ekanayake, I.U.; Palitha, S.; Gamage, S.; Meddage, D.P.P.; Wijesooriya, K.; Mohotti, D. Predicting adhesion strength of micropatterned surfaces using gradient boosting models and explainable artificial intelligence visualizations. Mater. Today Commun. 2023, 36, 106545. [Google Scholar] [CrossRef]
- Hassan, A.; Kim, Y.; Ryu, S.; Hatton, B.; Filleter, T. Divisions in a fibrillar adhesive increase the adhesive strength. ACS Appl. Mater. Interfaces 2021, 13, 59478–59486. [Google Scholar] [CrossRef]
- Luo, A.; Turner, K.T. Achieving enhanced adhesion through optimal stress distributions. J. Mech. Phys. Solids 2021, 156, 104610. [Google Scholar] [CrossRef]
- Dong, X.; Zhao, H.; Wang, Z.; Ouzounian, M.; Hu, T.S.; Guo, Y.; Zhang, L.; Xu, Q. Gecko-inspired composite micro-pillars with both robust adhesion and enhanced dry self-cleaning property. Chin. Chem. Lett. 2019, 30, 2333–2337. [Google Scholar] [CrossRef]
- Dayan, C.B.; Chun, S.; Krishna-Subbaiah, N.; Drotlef, D.M.; Akolpoglu, M.B.; Sitti, M. 3D printing of elastomeric bioinspired complex adhesive microstructures. Adv. Mater. 2021, 33, 2103826. [Google Scholar] [CrossRef]
- Liimatainen, V.; Drotlef, D.-M.; Son, D.; Sitti, M. Liquid-superrepellent bioinspired fibrillar adhesives. Adv. Mater. 2020, 32, 2000497. [Google Scholar] [CrossRef]
- Pang, C.; Kim, J.-K.; Wu, Y.; Wang, M.Y.; Yu, H.; Sitti, M. Bioinspired microstructured adhesives with facile and fast switchability for part manipulation in dry and wet conditions. Adv. Funct. Mater. 2023, 33, 2303116. [Google Scholar] [CrossRef]
- Suresh, S.A.; Kerst, C.F.; Cutkosky, M.R.; Hawkes, E.W. Spatially variant microstructured adhesive with one-way friction. J. R. Soc. Interface 2019, 16, 20180705. [Google Scholar] [CrossRef]
- Busche, J.F.; Starke, G.; Knickmeier, S.; Dietzel, A. Controllable dry adhesion based on two-photon polymerization and replication molding for space debris removal. Micro Nano Eng. 2020, 7, 100052. [Google Scholar] [CrossRef]
- Badler, D.; Kasem, H. Synergetic effect of the simultaneous use of different biomimetic adhesive micro-structures on tribological performances. Biotribology 2020, 22, 100124. [Google Scholar] [CrossRef]
- Badler, D.; Goltsberg, R.; Ammar, A.A.; Kasem, H. Experimental study of adhesion, friction, and peeling of biomimetic combined micro-mushroom and micro-spatulae textures. Tribol. Int. 2023, 186, 108609. [Google Scholar] [CrossRef]
- Badler, D.; Kligerman, Y.; Kasem, H. Attachment ability of combined biomimetic adhesive micro-textures of different shapes. Friction 2023, 11, 1430–1441. [Google Scholar] [CrossRef]
- Geikowsky, E.; Aksak, B. Bioinspired fibrillar adhesives with shape-controlled off-center caps for switchable and directional adhesion. Bioinspir. Biomim. 2020, 15, 056007. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.H.; Jeong, H.E.; Kim, S.M.; Kang, S.M. Enhanced directional adhesion behavior of mushroom-shaped microline arrays. Int. J. Precis. Eng. Manuf. Green Technol. 2020, 7, 239–245. [Google Scholar] [CrossRef]
- Drotlef, D.-M.; Dayan, C.B.; Sitti, M. Bio-inspired composite microfibers for strong and reversible adhesion on smooth surfaces. Integr. Comp. Biol. 2019, 59, 227–235. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Tan, D.; Meng, F.; Yang, B.; Shi, Z.; Wang, X.; Li, Q.; Nie, C.; Liu, S.; Xue, L. Adhesion enhancement of micropillar array by combining the adhesive design from gecko and tree frog. Small 2021, 17, 2005493. [Google Scholar] [CrossRef]
- Shi, Z.; Tan, D.; Liu, Q.; Meng, F.; Zhu, B.; Xue, L. Tree frog-inspired nanopillar arrays for enhancement of adhesion and friction. Biointerphases 2021, 16, 021001. [Google Scholar] [CrossRef]
- Liu, Q.; Meng, F.; Tan, D.; Shi, Z.; Zhu, B.; Xiao, K.; Xue, L. Gradient micropillar array inspired by tree frog for robust adhesion on dry and wet surfaces. Biomimetics 2022, 7, 209. [Google Scholar] [CrossRef]
- Glaser, N.C.; Langowski, J.K.A. Stiff skin, soft core: Soft backings enhance the conformability and friction of fibre-reinforced adhesives. R. Soc. Open Sci. 2023, 10, 221263. [Google Scholar] [CrossRef]
- Pande, S.S.; Turner, K.T. Geometric optimization of pillars for enhanced adhesion. Extreme Mech. Lett. 2023, 59, 101969. [Google Scholar] [CrossRef]
- Luo, A.; Zhang, H.; Turner, K.T. Machine learning-based optimization of the design of composite pillars for dry adhesives. Extreme Mech. Lett. 2022, 54, 101695. [Google Scholar] [CrossRef]
- Shi, W.; Cheng, X.; Cheng, K. Gecko-inspired adhesives with asymmetrically tilting-oriented micropillars. Langmuir 2022, 38, 8890–8898. [Google Scholar] [CrossRef]
- Son, D.; Liimatainen, V.; Sitti, M. Machine learning-based and experimentally validated optimal adhesive fibril designs. Small 2021, 17, 2102867. [Google Scholar] [CrossRef]
- Kim, Y.; Yang, C.; Kim, Y.; Gu, G.X.; Ryu, S. Designing an adhesive pillar shape with deep learning-based optimization. ACS Appl. Mater. Interfaces 2020, 12, 24458–24465. [Google Scholar] [CrossRef]
- Kim, Y.; Yeo, J.; Park, K.; Destrée, A.; Qin, Z.; Ryu, S. Designing directional adhesive pillars using deep learning-based optimization, 3D printing, and testing. Mech. Mater. 2023, 185, 104778. [Google Scholar] [CrossRef]
- Dayan, C.B.; Son, D.; Aghakhani, A.; Wu, Y.; Demir, S.O.; Sitti, M. Machine learning-based shear optimal adhesive microstructures with experimental validation. Small 2023, 20, 2304437. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Li, R.; Yuan, K.; Chen, A.; Guo, N.; Xu, C.; Zhang, W. In-plane combination of micropillars with distinct aspect ratios to resist overload-induced adhesion failure. Adv. Sci. 2024, 11, 2400972. [Google Scholar] [CrossRef]
- Li, X.; Bai, P.; Li, X.; Li, L.; Li, Y.; Lu, H.; Ma, L.; Meng, Y.; Tian, Y. Robust scalable reversible strong adhesion by gecko-inspired composite design. Friction 2022, 10, 1192–1207. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Wang, B.; Yuan, Q.; Weng, Z.; Dai, Z. Reversible adhesive bio-toe with hierarchical structure inspired by gecko. Biomimetics 2023, 8, 40. [Google Scholar] [CrossRef]
- Barnefske, L.; Rundel, F.; Moh, K.; Hensel, R.; Zhang, X.; Arzt, E. Tuning the release force of microfibrillar adhesives by geometric design. Adv. Mater. Interfaces 2022, 9, 2201232. [Google Scholar] [CrossRef]
- Tinnemann, V.; Arzt, E.; Hensel, R. Switchable double-sided micropatterned adhesives for selective fixation and detachment. J. Mech. Phys. Solids 2019, 123, 20–27. [Google Scholar] [CrossRef]
- Nasab, A.M.; Luo, A.; Sharifi, S.; Turner, K.T.; Shan, W. Switchable adhesion via subsurface pressure modulation. ACS Appl. Mater. Interfaces 2020, 12, 27717–27725. [Google Scholar] [CrossRef]
- Wan, G.; Tang, Y.; Turner, K.T.; Zhang, T.; Shan, W. Tunable dry adhesion of soft hollow pillars through sidewall buckling under low pressure. Adv. Funct. Mater. 2022, 33, 2209905. [Google Scholar] [CrossRef]
- Ruotolo, W.; Brouwer, D.; Cutkosky, M.R. From grasping to manipulation with gecko-inspired adhesives on a multifinger gripper. Sci. Robot. 2021, 6, eabi9773. [Google Scholar] [CrossRef]
- Tu, C.; Ji, K.; Zhao, J.; Wang, X.; Wu, J.; Huo, T.; Ji, Y.; Chen, J.; Deng, K.; Dai, Z. Preload-induced switchable adhesion. Small 2024, 20, 2305091. [Google Scholar] [CrossRef]
- Wan, G.; Shan, W. Pneumatically tunable adherence of elastomeric soft hollow pillars with non-circular contacts. Int. J. Solids Struct. 2024, 294, 112736. [Google Scholar] [CrossRef]
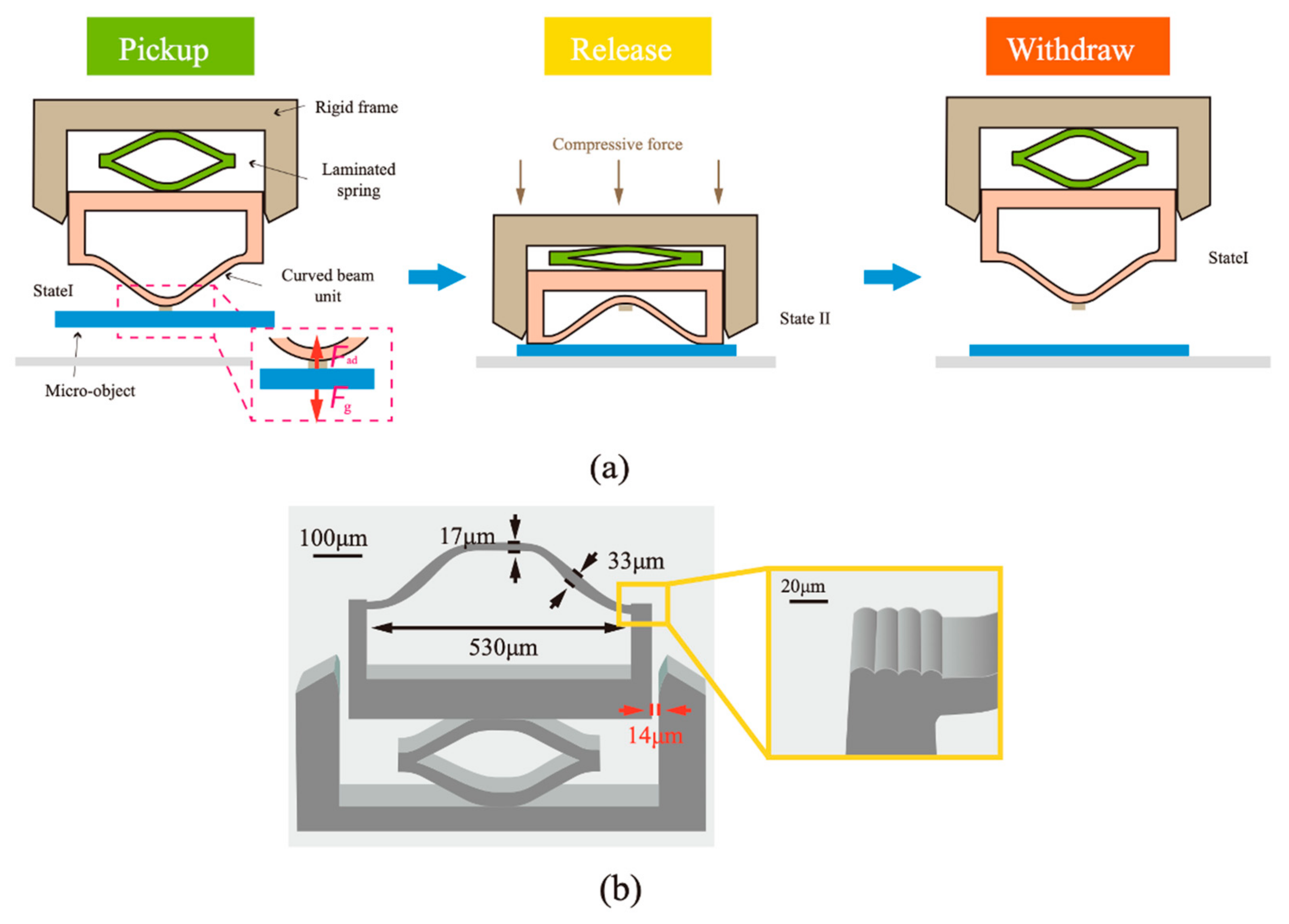
- Zhang, X.; Wang, Y.; Tian, Z.; Samri, M.; Moh, K.; McMeeking, R.M.; Hensel, R.; Arzt, E. A bioinspired snap-through metastructure for manipulating micro-objects. Sci. Adv. 2022, 8, eadd4768. [Google Scholar] [CrossRef] [PubMed]
- Paretkar, D.; Kamperman, M.; Martina, D.; Zhao, J.; Creton, C.; Lindner, A.; Jagota, A.; McMeeking, R.; Arzt, E. Preload-responsive adhesion: Effects of aspect ratio, tip shape and alignment. J. R. Soc. Interface 2013, 10, 20130171. [Google Scholar] [CrossRef]
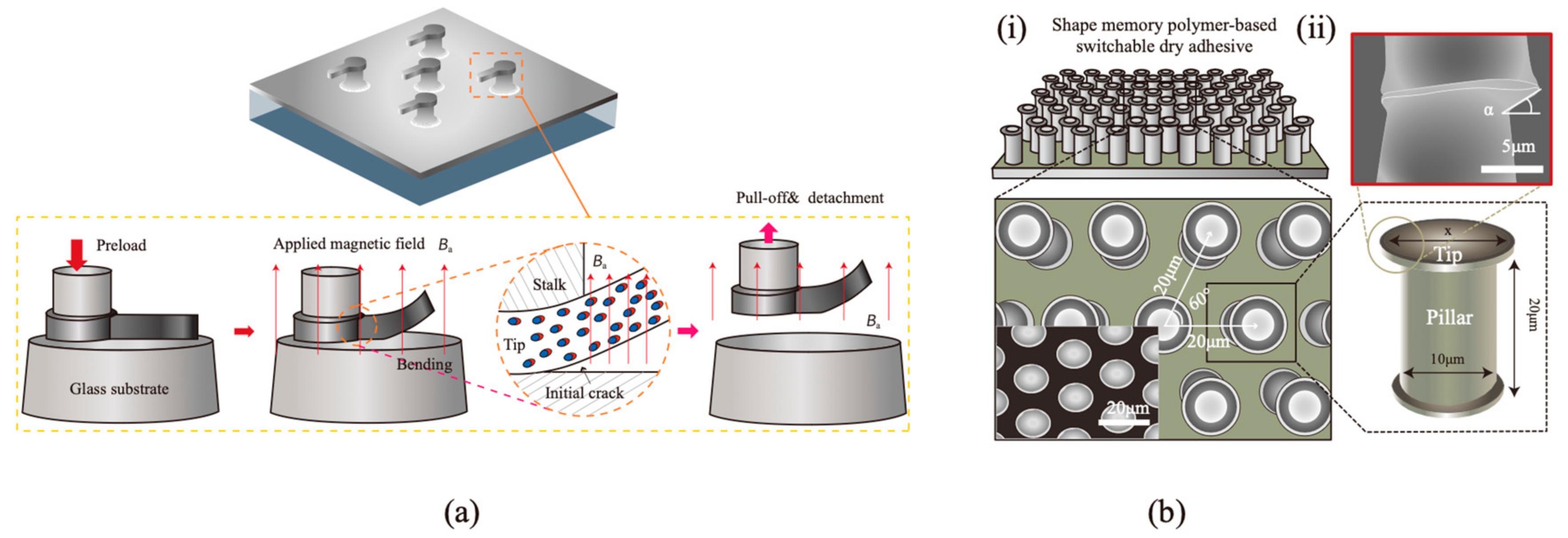
- Zhao, J.; Li, X.; Tan, Y.; Liu, X.; Lu, T.; Shi, M. Smart adhesives via magnetic actuation. Adv. Mater. 2022, 34, 2107748. [Google Scholar] [CrossRef]
- Lee, S.H.; Song, H.W.; Park, H.J.; Kwak, M.K. Surface adaptable and adhesion controllable dry adhesive with shape memory polymer. Macromol. Rapid Commun. 2022, 43, 2200012. [Google Scholar] [CrossRef]
- Tan, D.; Wang, X.; Liu, Q.; Shi, K.; Yang, B.; Liu, S.; Wu, Z.S.; Xue, L. Switchable adhesion of micropillar adhesive on rough surfaces. Small 2019, 15, 1904248. [Google Scholar] [CrossRef]
- Li, S.; Tian, H.; Shao, J.; Liu, H.; Wang, D.; Zhang, W. Switchable adhesion for nonflat surfaces mimicking geckos’ adhesive structures and toe muscles. ACS Appl. Mater. Interfaces 2020, 12, 39745–39755. [Google Scholar] [CrossRef]
- Luo, H.; Li, C.; Wang, S.; Zhang, S.; Song, J. Switchable adhesive based on shape memory polymer with micropillars of different heights for laser-driven noncontact transfer printing. ACS Appl. Mater. Interfaces 2024, 16, 9443–9452. [Google Scholar] [CrossRef]
- Wang, Y.; Lai, H.; Cheng, Z.; Zhang, H.; Zhang, E.; Lv, T.; Liu, Y.; Jiang, L. Gecko toe pads inspired in situ switchable superhydrophobic shape memory adhesive film. Nanoscale 2019, 11, 8984–8993. [Google Scholar] [CrossRef]
- Wang, D.; Hu, H.; Li, S.; Tian, H.; Fan, W.; Li, X.; Chen, X.; Taylor, A.C.; Shao, J. Sensing-triggered stiffness-tunable smart adhesives. Sci. adv. 2023, 9, eadf4051. [Google Scholar] [CrossRef] [PubMed]
- Son, C.; Jeong, S.; Lee, S.; Ferreira, P.M.; Kim, S. Tunable adhesion of shape memory polymer dry adhesive soft robotic gripper via stiffness control. Robotics 2023, 12, 59. [Google Scholar] [CrossRef]
- Tian, Y.; Pesika, N.; Zeng, H.; Rosenberg, K.; Zhao, B.; McGuiggan, P.; Autumn, K.; Israelachvili, J. Adhesion and friction in gecko toe attachment and detachment. Proc. Natl. Acad. Sci. USA 2006, 103, 19320–19325. [Google Scholar] [CrossRef] [PubMed]
- Dharmawan, A.G.; Xavier, P.; Hariri, H.H.; Soh, G.S.; Baji, A.; Bouffanais, R.; Foong, S.; Low, H.Y.; Wood, K.L. Design, modeling, and experimentation of a bio-inspired miniature climbing robot with bilayer dry adhesives. J. Mech. Robot. 2019, 11, 020902. [Google Scholar] [CrossRef]
- Kim, D.G.; Je, H.; Hart, A.J.; Kim, S. Additive manufacturing of flexible 3D surface electrodes for electrostatic adhesion control and smart robotic gripping. Friction 2023, 11, 1974–1986. [Google Scholar] [CrossRef]
- Hoang, T.T.; Quek, J.J.S.; Thai, M.T.; Phan, P.T.; Lovell, N.H.; Do, T.N. Soft robotic fabric gripper with gecko adhesion and variable stiffness. Sens. Actuators A Phys. 2021, 323, 112673. [Google Scholar] [CrossRef]
- Alizadehyazdi, V.; Spenko, M. A microstructured adhesive gripper with piezoelectric controlled adhesion, cleaning, and sensing. Smart Mater. Struct. 2019, 28, 115037. [Google Scholar] [CrossRef]
- Alizadehyazdi, V.; Bonthron, M.; Spenko, M. An electrostatic/gecko-inspired adhesives soft robotic gripper. IEEE Robot. Autom. Lett. 2020, 5, 4679–4686. [Google Scholar] [CrossRef]
- Shen, C.; Cheng, Y.; Peng, Z.; Chen, S. Switchable adhesion of gecko-inspired hierarchically wedge-mushroom-shaped surface. Chem. Eng. J. 2024, 488, 150900. [Google Scholar] [CrossRef]
- Gwon, M.; Park, G.; Hong, D.; Park, Y.-J.; Han, S.; Kang, D.; Koh, J. Soft directional adhesion gripper fabricated by 3D printing process for gripping flexible printed circuit boards. Int. J. Precis. Eng. Manuf. Green Technol. 2022, 9, 1151–1163. [Google Scholar] [CrossRef]
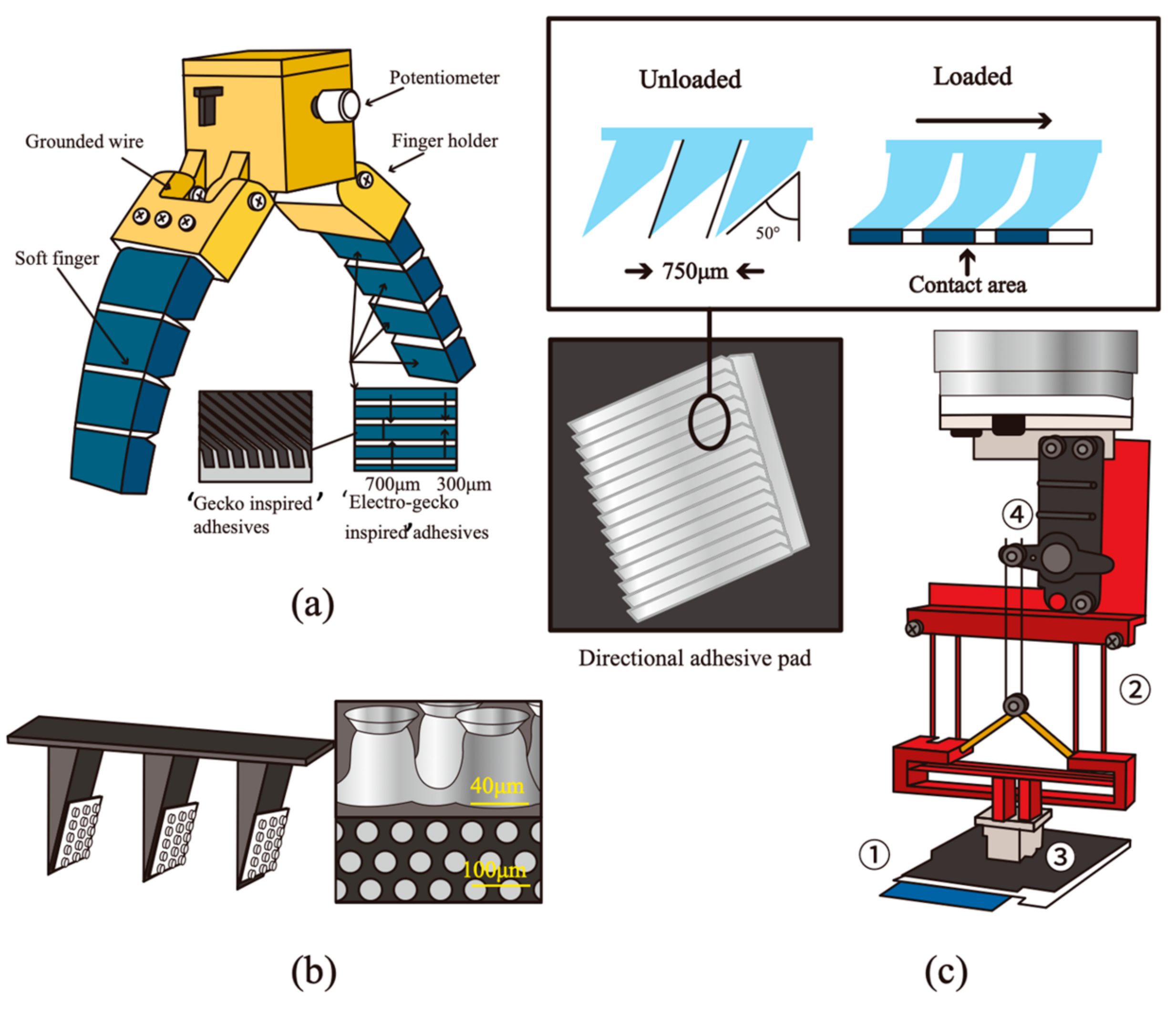
| Refrigerator | Table Desktop | Sputter Coater | 0.3 μm FibrMet disc | |
|---|---|---|---|---|
| Rq (μm) | 0.057 | 0.162 | 0.22 | 0.226 |
| Pull-off force (mN) (Original/Split) | 42/54.2 | 30/44.5 | 30.1/48.5 | 37/41.8 |
| Static friction force (mN) (Original/Split) | 360/398 | 280/374 | 250/308 | 335/310 |
| Design Strategy | Control Mechanism | Applications | Advantages/Innovations |
|---|---|---|---|
| Suction + gecko-inspired adhesion [3] | Suction for grip; nylon fabric with gentle airflow | Retail and warehouse robots | Lifts up to 2.3 kg; grips small items; conforms to irregular surfaces |
| Soft–hard–soft sandwiched composite for reversible adhesion [176] | Lateral shrinkage for uniform loading; stress concentration for easy detachment | Precision manufacturing, flexible electronics, climbing robots | Scalable adhesion (1.5 to 150 cm2); supports loads from 20 to 700 N; fast switching (~0.2 s); adhesion switching ratio of ~54 |
| Hierarchical bionic toe (bio-toe) with elastic actuator and bionic lamellae [177] | Bi-directional pressure for adhesion/release and non-linear deformation for adaptability | Robot grippers, wall-climbing robots, space, defense | High adaptability and load capacity; 100% release success; 12× shear adhesion force-to-preload ratio; contact rate of 60% even with contact tilt |
| Directional buckling micropatterned adhesives [178] | Compressive overload for elastic buckling and controlled release | Pick-and-place systems, micro-assembly | High switching ratio (~20); precise release of objects <1 mm; enhanced placement accuracy |
| Double-sided micropatterned PDMS adhesive pads [179] | Elastic buckling instabilities to switch adhesion states | Temporary double-sided fixation, micro-assembly | High switching efficiency (up to 83%); controlled detachment from one side |
| Soft hollow pillars (SHPs) with sidewall buckling [181] | Low-pressure control (negative for buckling, positive for bulging) | Microtransfer printing, selective pick-and-place | High adhesion tunability (up to 151×); versatile for varied surface textures and curvatures; low energy cost |
| Dry adhesive with multiphalange, multifinger design [182] | Buckling ribs for shear load sharing and normal compliance | Robotic manipulators, flexible grippers | High contact area; efficient shear load distribution; adaptable manipulation beyond pick-and-place |
| Multilayer adhesive with backing, middle, and bottom layers [183] | Preload adjustment for rapid adhesion switching via underside buckling | Transportation, handling applications | High switching ratio (up to 136×); rapid switching; dirt-resistant film-terminated structure |
| Trigger plant-inspired snap-action metastructure [185] | Tunable spring with snap-through mechanism for adhesion switching | Micro-object handling, pick-and-place systems | Extremely high switching ratio (>10,000); effective in dry/wet and smooth/rough environments |
| Mushroom-shaped adhesive with magnetized tip [187] | Magnetic actuation for morphology transformation and adhesion switching | Transfer technology, precision pick-and-place | Rapid and reversible adhesion control; noncontact switching for selective pickup and release |
| Gecko-inspired shape-memory polymer (SMP) adhesive [188] | Shape recovery for reversible adhesion switching | Glass transfer systems, precision assembly | High adhesion (≈332.8 kPa) with easy detachment (3.73 kPa); adaptable to various surfaces |
| Gecko- and creeper-inspired fibrillar adhesive with PU-GSMP layers [189] | UV-induced photothermal effect for phase change in GSMP micropillars | Robotics, handling rough surfaces | High adhesion strength (278 kPa); high switching ratio (29); fast switching (10 s); adaptable to surfaces with varied roughness |
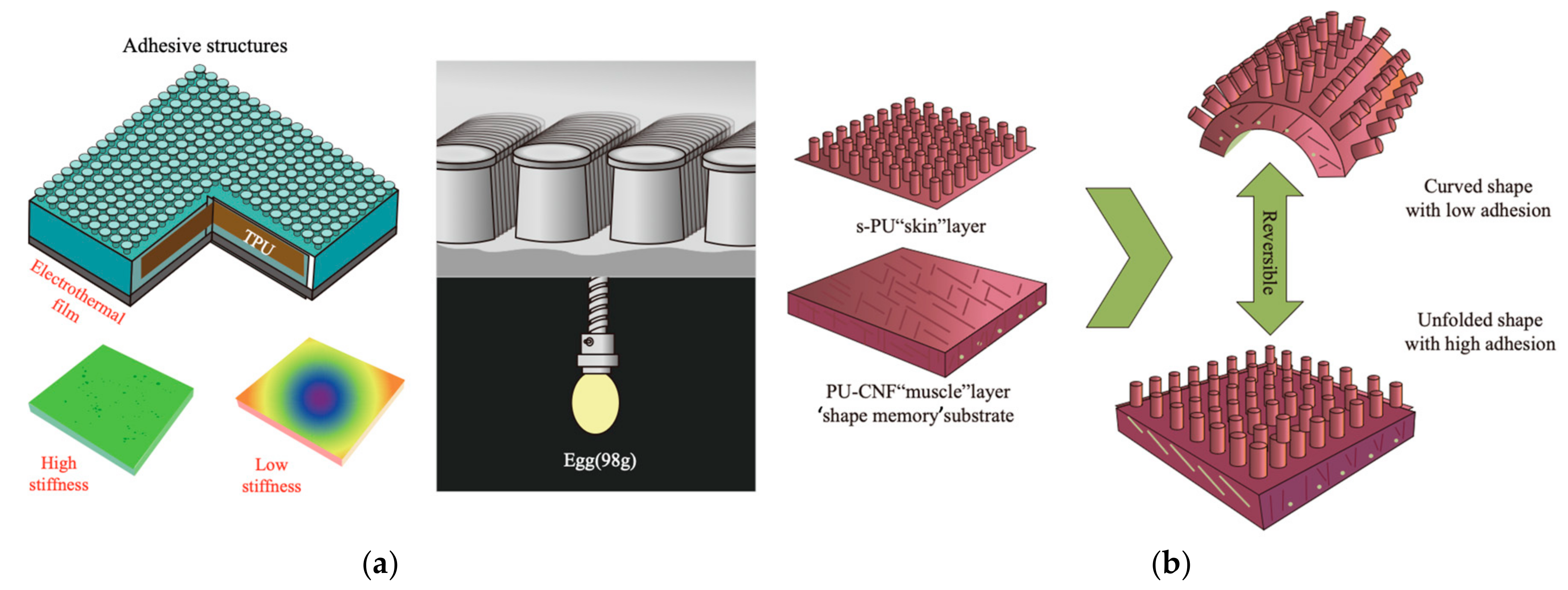
| Hierarchical structure with stiffness modulation [190] | Electrothermal film for adjustable stiffness in TPU layer | Soft grippers, wall-climbing robots | High and switchable adhesion on non-flat surfaces; adhesion increased by 10–100× with voltage control |
| Thermally responsive shape-memory polymer with micropillars [191] | Laser heating for shape recovery to switch adhesion | Noncontact transfer printing, electronics assembly | Strong adhesion for pick-up; laser-driven release for noncontact printing; adaptable to diverse surfaces (e.g., sandpaper, glass) |
| Superhydrophobic film with shape-memory polyurethane-cellulose nanofiber substrate [192] | Shape-memory effect for switching adhesion states | Controlled droplet manipulation, microfluidics | Captures/releases multiple droplets step-by-step |
| Shape-memory polymer (SMP) adhesive gripper [194] | Thermoelectric Peltier module for active heating and cooling to switch adhesion | Robotic pick-and-place, manipulation | Strong grip force (>2 atmospheres); minimal release force; works on flat, rough, and wet surfaces |
| Elastomeric 3D surface structures with conductive nanowire electrodes [197] | Combined shear and electrostatic adhesion, capacitive sensing for touch | Soft grippers, tactile sensors | 72% increase in gripping force with voltage; adaptable to various materials; multifunctional for adhesion and force sensing |
| Gripper with gecko adhesive and thermo-responsive filament [198] | Hydraulic-driven bending actuators, variable stiffness filament | High-load grasping, soft robotics, industrial handling | 655% increase in holding force; rapid cooling (31 s); cost-effective and scalable fabrication |
| Microstructured adhesive with integrated piezoelectric element [199] | Ultrasonic vibration for dust removal and adhesion tuning | Robotics, cleanroom applications | Removes 53–71% of contaminants; recovers 3–11% adhesion post-contamination; maintains performance over 1500 cycles |
| Combined electrostatic and gecko-inspired adhesive [200] | Tunable adhesion via electrostatic and microstructured adhesive layers | Grasping diverse materials, soft robotics | 100–168% increased gripping force across various materials; effective on rough surfaces; adaptable for soft and fragile objects |
| Hierarchical structure: asymmetric wedges + mushroom fibrils [201] | Loading–dragging–pulling and magnetic field actuation | Flexible devices, releasing ultra-light objects | Dual switchable adhesion modes; overcoming shear-induced adhesion limits; self-cleaning; ultra-light release |
| Soft gripper with 3D-printed directional adhesives and curved pillars [202] | Adhesion enhancement via additional coating for smoothness and tip deformation | Handling thin, flexible objects (e.g., films, FPCBs) | Cost-effective; environment-friendly; retains 95% adhesion after 10,000 cycles; adhesion recovery with cleaning |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Emami, A.; Khaleghian, M. Controlled Dry Adhesion of Bio-Inspired Fibrillar Polymers: Mechanics, Strategies, and Recent Advances. Materials 2025, 18, 1620. https://doi.org/10.3390/ma18071620
Xu S, Emami A, Khaleghian M. Controlled Dry Adhesion of Bio-Inspired Fibrillar Polymers: Mechanics, Strategies, and Recent Advances. Materials. 2025; 18(7):1620. https://doi.org/10.3390/ma18071620
Chicago/Turabian StyleXu, Shuo, Anahita Emami, and Meysam Khaleghian. 2025. "Controlled Dry Adhesion of Bio-Inspired Fibrillar Polymers: Mechanics, Strategies, and Recent Advances" Materials 18, no. 7: 1620. https://doi.org/10.3390/ma18071620
APA StyleXu, S., Emami, A., & Khaleghian, M. (2025). Controlled Dry Adhesion of Bio-Inspired Fibrillar Polymers: Mechanics, Strategies, and Recent Advances. Materials, 18(7), 1620. https://doi.org/10.3390/ma18071620






