Bending Performance of Alkali-Activated Concrete Beams Based on Digital Image Correlation Method
Abstract
1. Introduction
2. Experimental Programs
2.1. Specimen Preparations
2.2. Four-Point Bending Tests
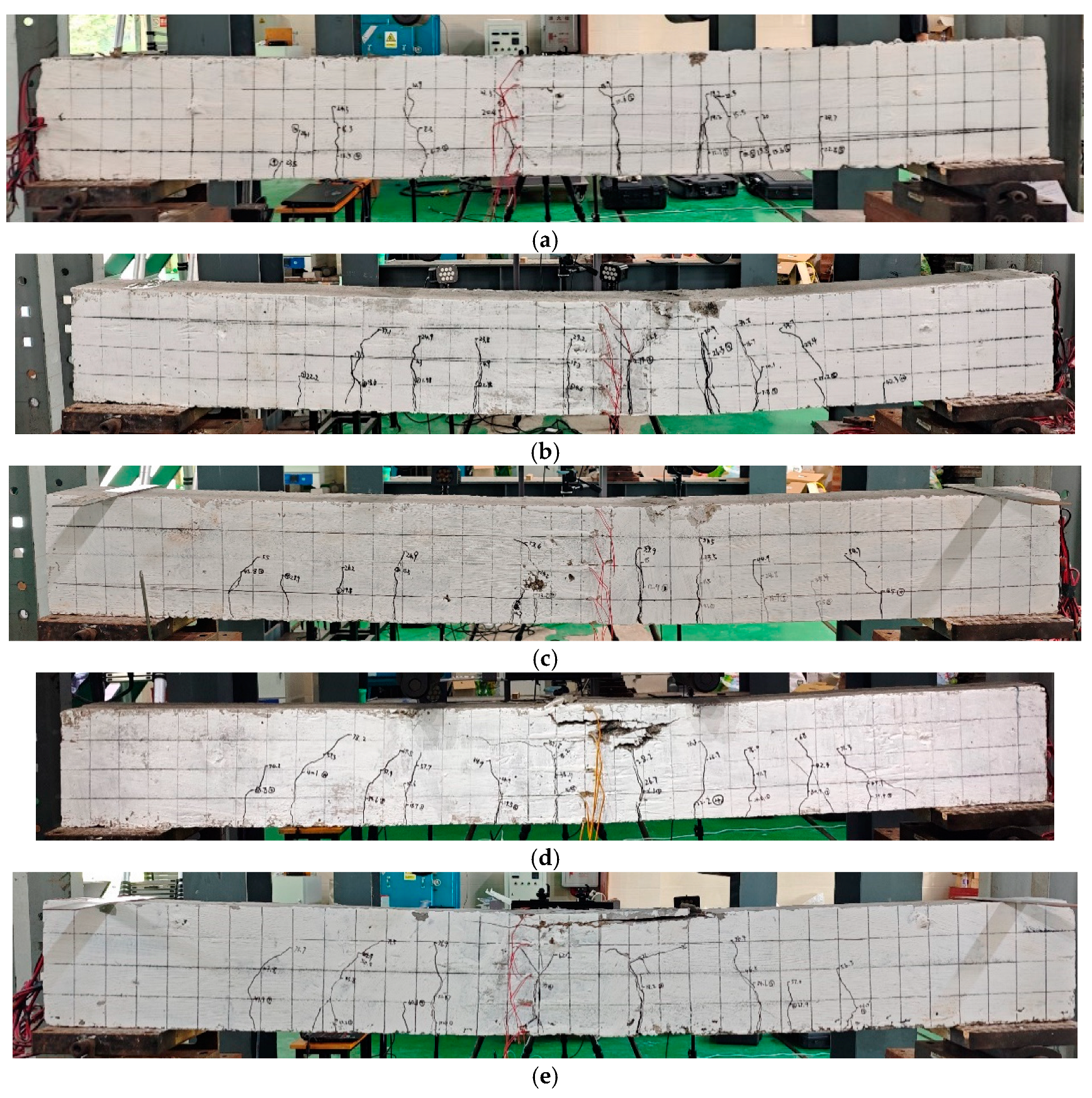
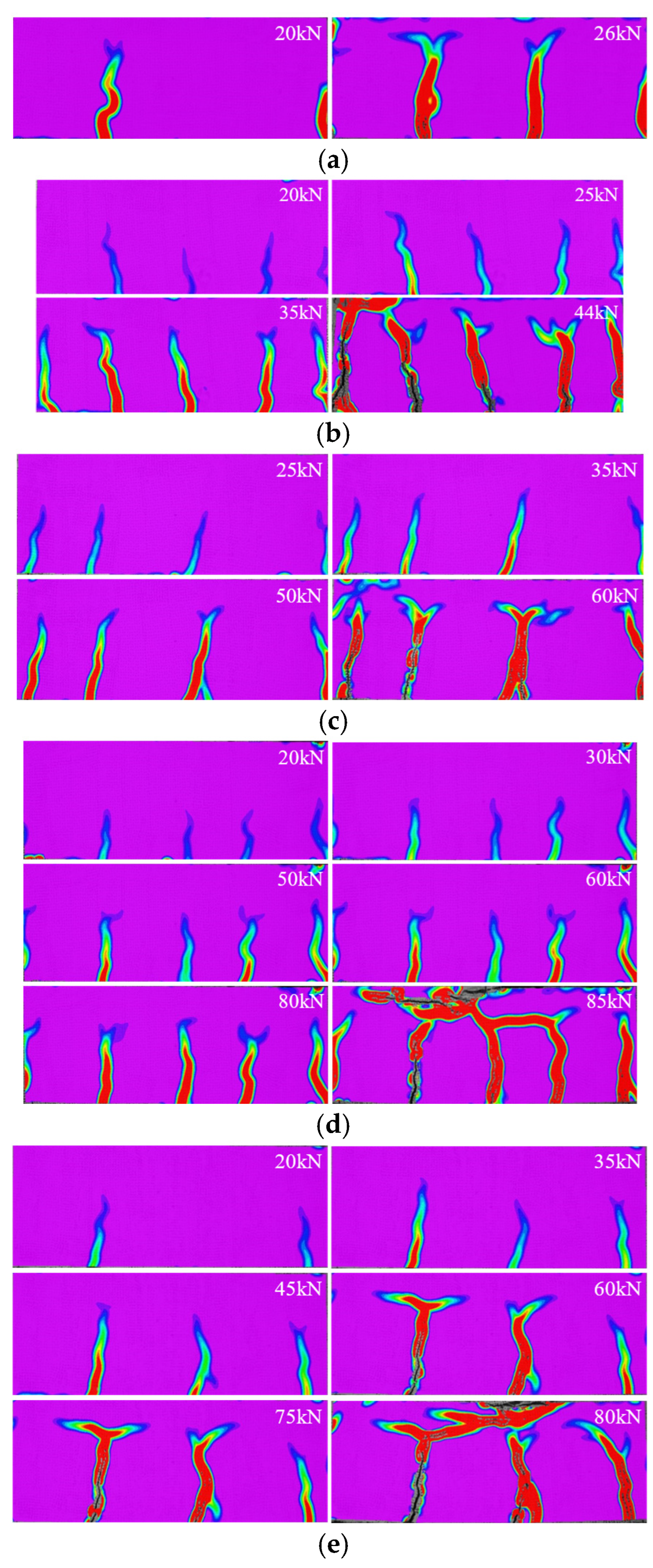
2.3. Failure Mode and Crack Propagation of Beams
3. Result Analysis
3.1. Cracking Load
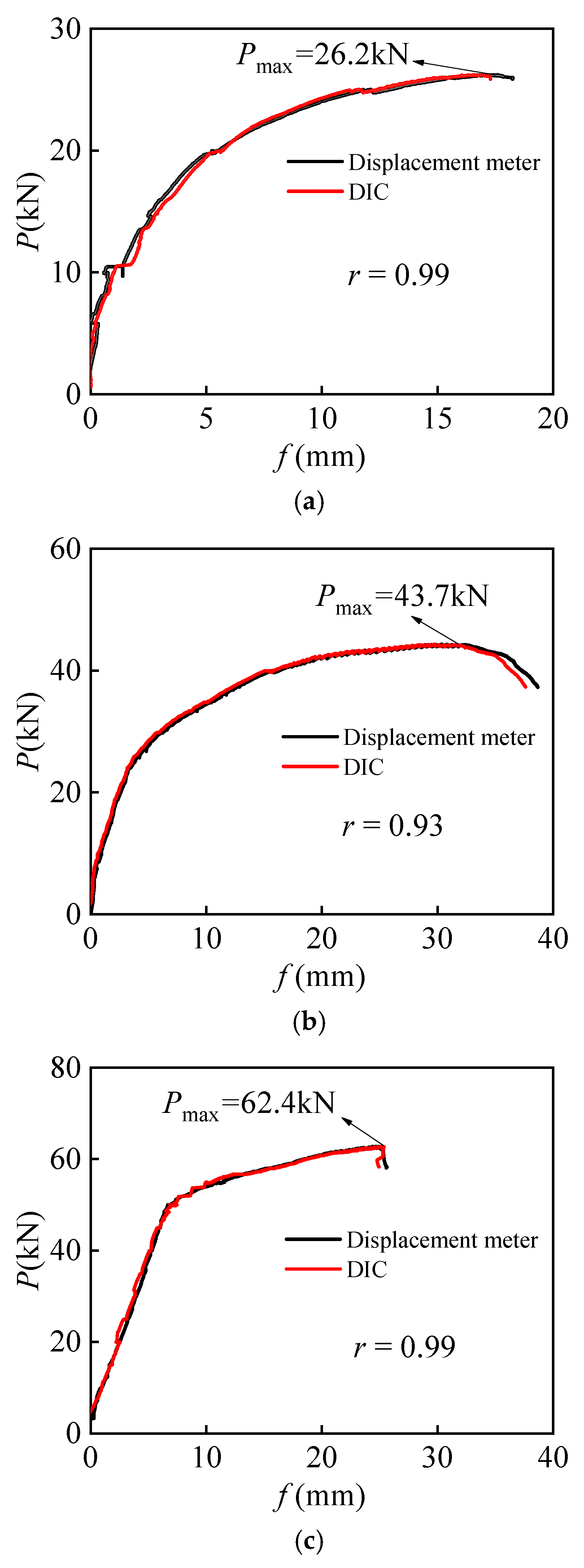
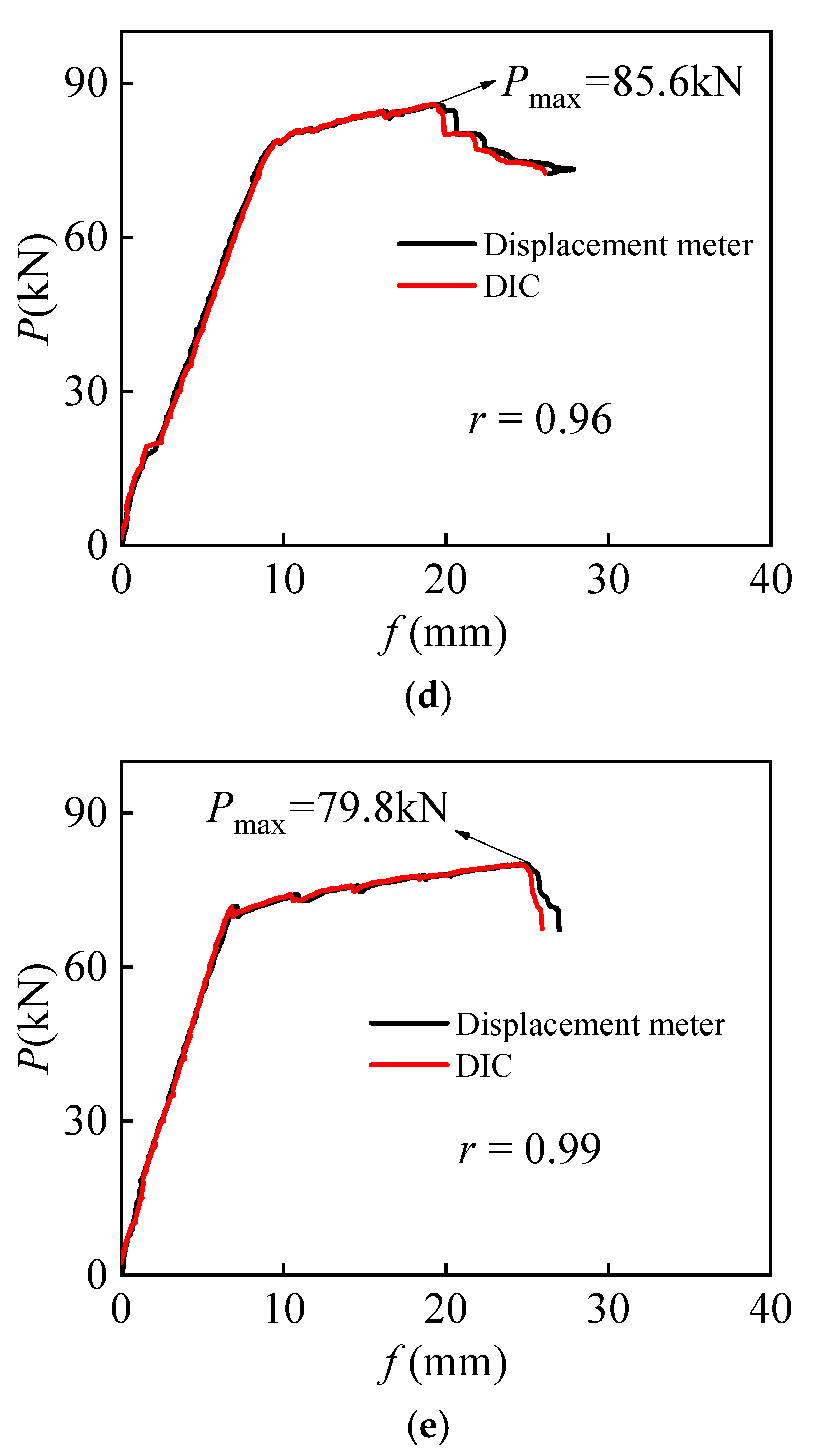
3.2. Load-Displacement Curve
3.3. Load-Crack Width Curve
4. Comparison Between Theoretical Calculation and Experimental Values
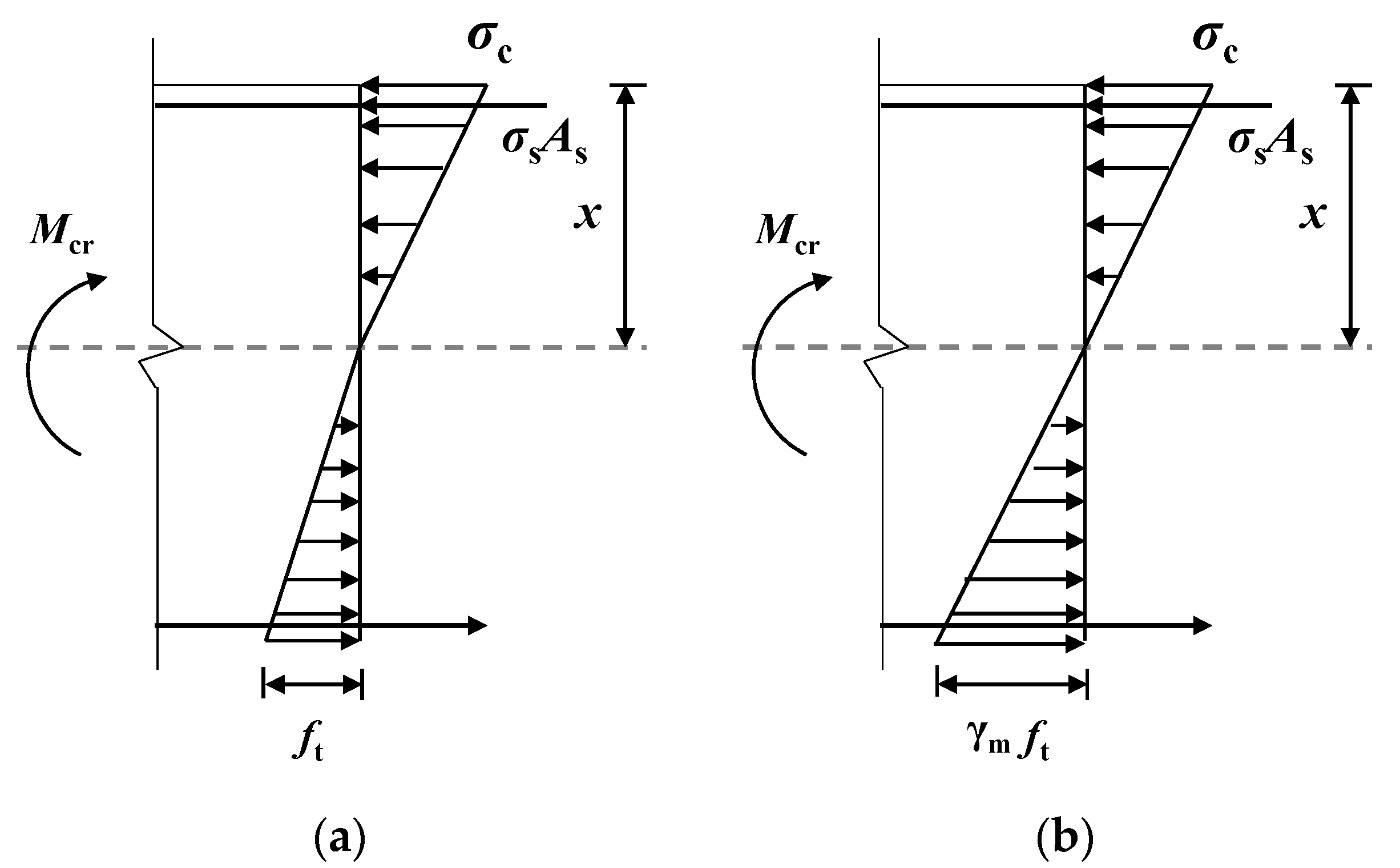
4.1. Cracking Moment
4.2. Mid-Span Displacement
4.3. Crack Width Calculation
5. Conclusions
- The DIC method outperforms traditional measurement techniques in assessing cracking load, displacement, and crack width. It offers precise, non-contact measurements of full-field deformations, enabling accurate determination of the cracking load and continuous tracking of crack propagation under different load conditions;
- For ALAC beams with different reinforcement ratios, the mid-span displacement corresponding to the peak load decreases as the reinforcement ratio increases, indicating that a higher reinforcement ratio enhances the stiffness of structures and reduces displacement. Furthermore, for the same reinforcement ratio, ALAC beams demonstrate higher ultimate bearing capacity and smaller maximum crack width compared to ordinary PCC beams, highlighting the superior mechanical properties of ALAC;
- For ALAC beams, the cracking load calculated using a plasticity coefficient of 1.17 for the section resistance moment aligns well with the experimental results. Additionally, the calculation formulas for mid-span displacement and maximum crack width, which are typically used for ordinary concrete beams, also provide accurate predictions for the corresponding properties of ALAC beams under normal service state. This indicates that existing design codes and calculation methods can, to some extent, be applied to ALAC, offering valuable theoretical support for engineering application.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yacob, N.S.; ElGawady, M.A.; Sneed, L.H.; Said, A. Shear strength of fly ash-based geopolymer reinforced concrete beams. Eng. Struct. 2019, 196, 109298. [Google Scholar] [CrossRef]
- Visintin, P.; Ali, M.M.; Albitar, M.; Lucas, W. Shear behaviour of geopolymer concrete beams without stirrups. Constr. Build. Mater. 2017, 148, 10–21. [Google Scholar] [CrossRef]
- Nguyen, K.T.; Ahn, N.; Le, T.A.; Lee, K. Theoretical and experimental study on mechanical properties and flexural strength of fly ash-geopolymer concrete. Constr. Build. Mater. 2016, 106, 65–77. [Google Scholar] [CrossRef]
- Zerfu, K.; Ekaputri, J.J. The effect of reinforcement ratio on the flexural performance of alkali-activated fly ash-based geopolymer concrete beam. Heliyon 2022, 8, e12015. [Google Scholar] [CrossRef] [PubMed]
- Akduman, Ş.; Kocaer, O.; Aldemir, A.; Şahmaran, M.; Yıldırım, G.; Almahmood, H.; Ashour, A. Experimental investigations on the structural behaviour of reinforced geopolymer beams produced from recycled construction materials. J. Build. Eng. 2021, 41, 102776. [Google Scholar] [CrossRef]
- Zheng, W.Z.; Zou, M.N.; Wang, Y. Literature review of alkali-activated cementitious materials. Jianzhu Jiegou Xuebao/J. Build. Struct. 2019, 40, 28–39. [Google Scholar]
- Amri, A.; Amartya, A.; Ilham, Y.; Sutikno, S.; Yenti, S.R.; Ibrahim, B.; Heltina, D.; Mondinos, N.; Altarawneh, M.; Jiang, Z.-T. The addition of low-cost few layers graphene (FLG) to improve flexural strength of coal fly ash based-geopolymer. J. Mater. Res. Technol. 2023, 24, 8849–8855. [Google Scholar] [CrossRef]
- Annappaswamy, G.M.; Channappa, T.M.; Prashanth, M.H. Numerical study on fracture behavior of alkali activated concrete mixes for different beam sizes. Mater. Today Proc. 2023, 88, 144–151. [Google Scholar] [CrossRef]
- Hasan, M.A.; Sheehan, T.; Ashour, A.; Elkezza, O. Flexural behaviour of geopolymer concrete T-Beams reinforced with GFRP bars. Structures 2023, 49, 345–364. [Google Scholar] [CrossRef]
- Thomas, R.J.; Peethamparan, S. Alkali-activated concrete: Engineering properties and stress—Strain behavior. Constr. Build. Mater. 2015, 93, 49–56. [Google Scholar] [CrossRef]
- Nath, P.; Sarker, P.K. Use of OPC to improve setting and early strength properties of low calcium fly ash geopolymer concrete cured at room temperature. Cem. Concr. Compos. 2015, 55, 205–214. [Google Scholar]
- Yang, C.; Xiong, L.X.; You, J.J.; JI, X.; Hu, R. Mechanical properties and microscopic characteristics of fly ash geopolymer concrete containing ordinary Portland cement. J. Civ. Environ. Eng. 2024, 46, 207–215. [Google Scholar]
- Bezemer, H.J.; Awasthy, N.; Luković, M. Multiscale analysis of long-term mechanical and durability behaviour of two alkaliactivated slag-based types of concrete. Constr. Build. Mater. 2023, 407, 133507. [Google Scholar]
- Liu, Y.F.; Fan, J.S.; Nie, J.G.; Kong, S.Y.; Qi, Y. Review and prospect of digital-image-based crack detection of structure surface. China Civ. Eng. J. 2021, 54, 20. [Google Scholar]
- Yang, L.; Hou, C.; Zhu, W.; Liu, X.; Yan, B.; Li, L. Monitoring the failure process of cemented paste backfill at different curing times by using a digital image correlation technique. Constr. Build. Mater. 2022, 346, 128487. [Google Scholar]
- Xie, Z.L.; Zhou, H.F.; Lu, L.J.; Chen, Z. An investigation into fracture behavior of geopolymer concrete with digital image correlation technique. Constr. Build. Mater. 2017, 155, 371–380. [Google Scholar]
- Jasiński, R.; Stebel, K.; Domin, J. Application of the DIC Technique to Remote Control of the Hydraulic Load System. Remote Sens. 2020, 12, 3667. [Google Scholar] [CrossRef]
- Yamaguchi, I. A laser-speckle strain gauge. J. Phys. E Sci. Instrum. 1981, 14, 1270–1273. [Google Scholar]
- Peters, W.H.; Ranson, W.F. Digital Imaging Techniques in Experimental Stress Analysis. Opt. Eng. 1982, 21, 427–431. [Google Scholar]
- Yan, B.F.; Kou, Y.H.; Qin, Y.Y.; Luo, L.; Li, S.K.; Li, S.S. Detection and Measurement Method for Full-field Crack Propagation of Concrete Structure Based on DIC Technology. China J. Highw. Transp. 2024, 37, 283–297. [Google Scholar]
- Xiong, E.G.; Gong, Z.W.; Luo, J.M.; Fan, T. Experiment on cracks in reinforced concrete beams based on digital image correlation technology. J. Jilin Univ. (Eng. Technol. Ed.) 2023, 53, 1094–1104. [Google Scholar]
- Pohoryles, D.A.; Melo, J.; Rossetto, T.; Fabian, M.; McCague, C.; Stavrianaki, K.; Lishman, B.; Sargeant, B. Use of DIC and AE for Monitoring Effective Strain and Debonding in FRP and FRCM-Retrofitted RC Beams. J. Compos. Constr. 2017, 21, 4016057. [Google Scholar] [CrossRef]
- Baietti, G.; Quartarone, G.; Carabba, L.; Manzi, S.; Carloni, C.; Bignozzi, M.C. Use of digital image analysis to determine fracture properties of alkali-activated mortars. Eng. Fract. Mech. 2020, 240, 107313. [Google Scholar]
- GB50010-2010; Code for Design of Concrete Structures. Ministry of Housing and Urban-Rural Development: Beijing, China, 2015.
- Drobiec, Ł.; Drobiec, R.; Mazur, W.; Jasiński, R. Safety of reinforced AAC structures. Cem. Wapno Beton. 2024, 29, 108–131. [Google Scholar]
- Li, J.; Dong, W.; Zhao, X.; Li, H. Investigation on fracture properties of concrete considering the viscoelastic characteristics. Constr. Build. Mater. 2024, 426, 136044. [Google Scholar]
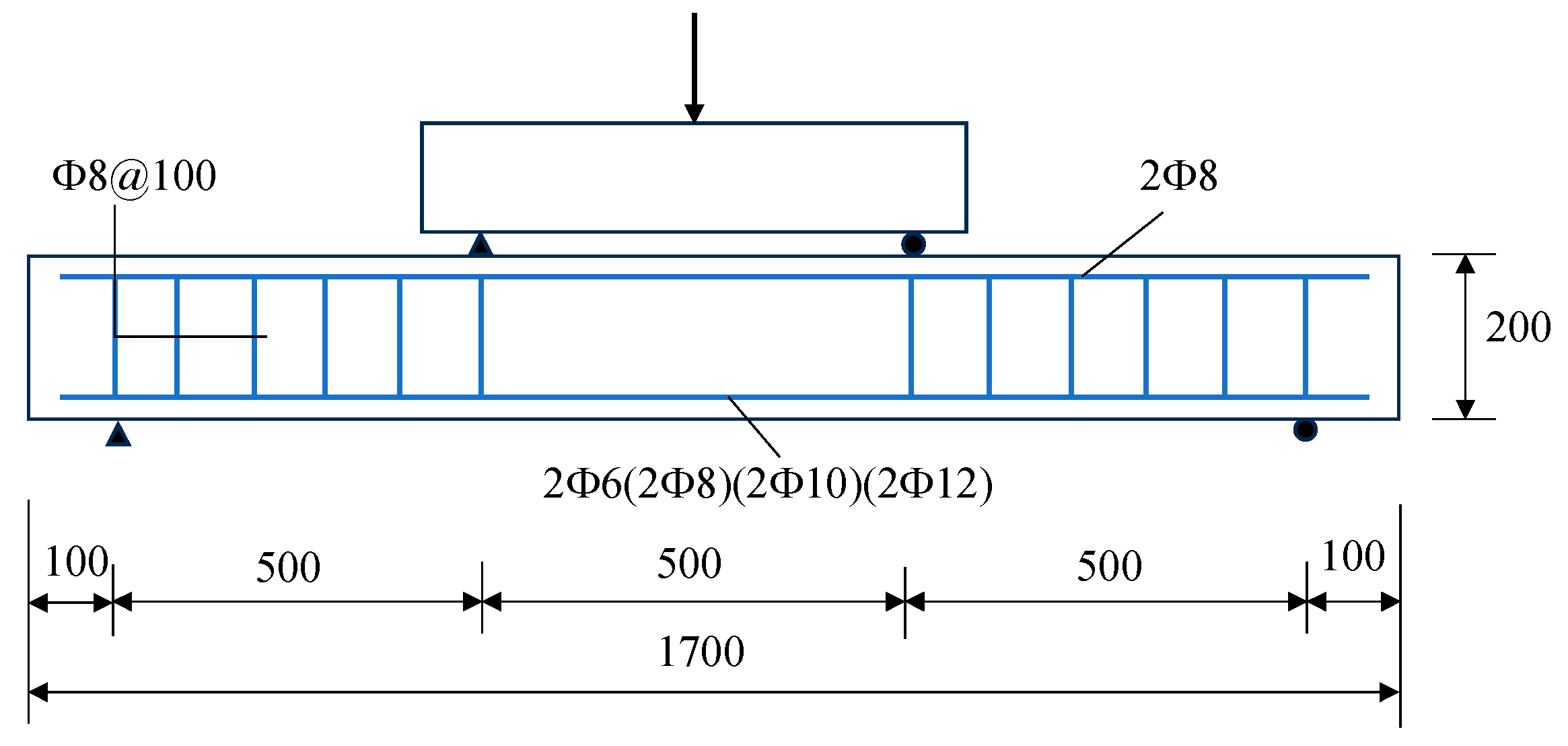

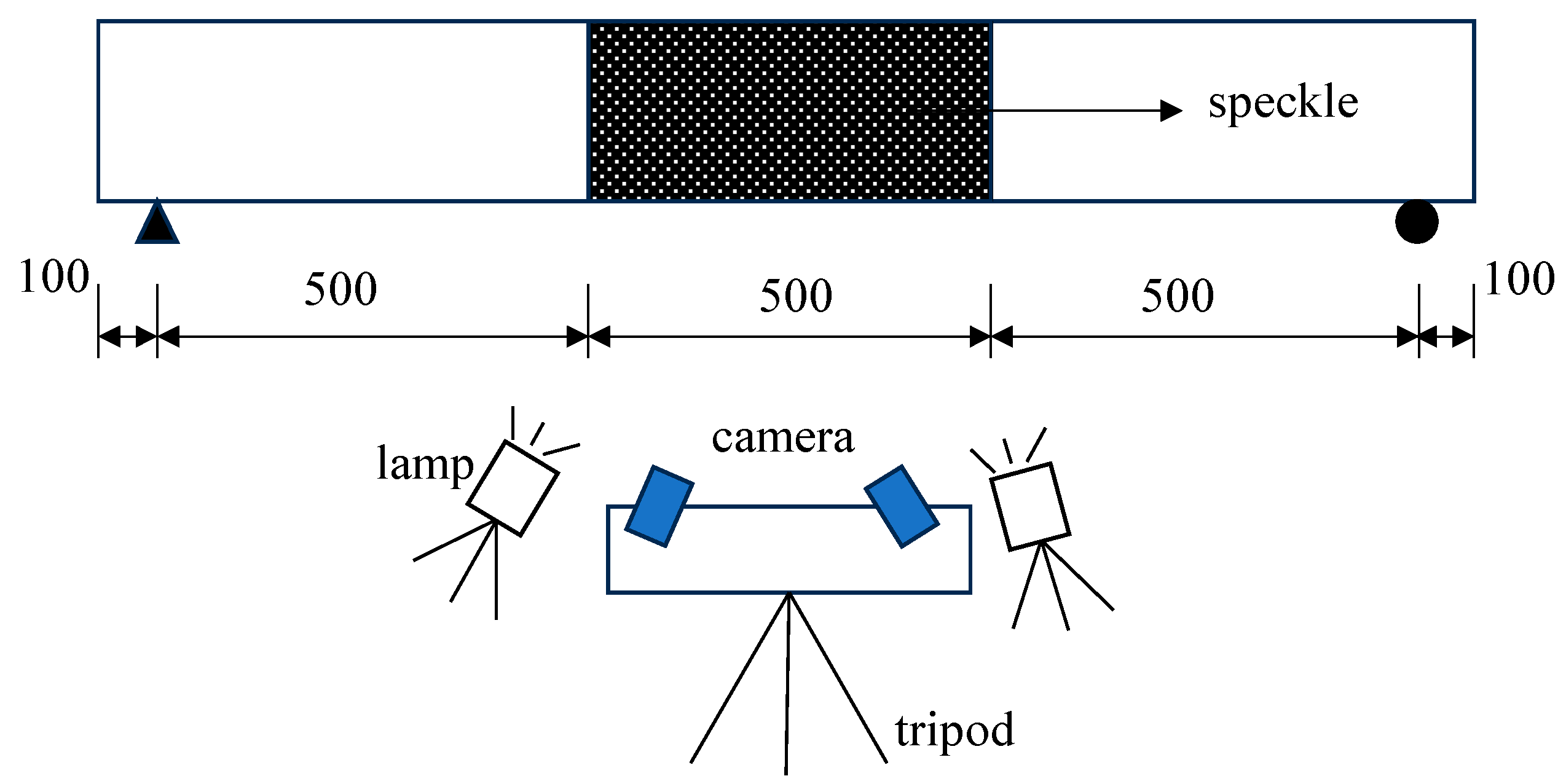

| Gravel | Sand | Mineral Powder | Fly Ash | Cement | NaOH | Na2SiO3 | Water | Superplasticizer | |
|---|---|---|---|---|---|---|---|---|---|
| ALAC | 1047 | 690 | 250 | 85 | 85 | 11 | 84 | 155 | 10 |
| PCC | 1047 | 690 | - | 70 | 350 | - | - | 190 | 10 |
| Material | Cube Compressive Strength fcu (MPa) | Axial Compressive Strength ftk (MPa) | Axial Tensile Strength ft (MPa) | Elastic Modulus Ec (GPa) |
|---|---|---|---|---|
| ALAC | 53.4 | 41.1 | 3.10 | 29.7 |
| PCC | 54.6 | 32.5 | 3.14 | 34.5 |
| Specimen | Type of Concrete | Diameter of Reinforcement (mm) | Ratio of Reinforcement (%) |
|---|---|---|---|
| A-6 | ALAC | 6 | 0.29 |
| A-8 | ALAC | 8 | 0.51 |
| A-10 | ALAC | 10 | 0.81 |
| A-12 | ALAC | 12 | 1.17 |
| P-12 | PCC | 12 | 1.17 |
| Specimen | Traditional Visual Observation Method (kN) | DIC Method (kN) |
|---|---|---|
| A-6 | 12.1 | 10.32 |
| A-8 | 13.6 | 10.90 |
| A-10 | 11.5 | 10.91 |
| A-12 | 14.0 | 12.04 |
| P-12 | 13.5 | 12.37 |
| Specimen | Measured Cracking Moment (DIC) (kN·m) | Calculated Cracking Moment (kN·m) | Ratio of Measured to Calculated Cracking Moment |
|---|---|---|---|
| A-6 | 2.58 | 2.93 | 0.88 |
| A-8 | 2.73 | 2.94 | 0.93 |
| A-10 | 2.73 | 2.95 | 0.93 |
| A-12 | 3.01 | 2.96 | 1.02 |
| P-12 | 3.09 | 2.98 | 1.04 |
| Specimen | Measured Displacement (DIC) (mm) | Calculated Displacement (mm) | Ratio of Measured to Calculated Displacement |
|---|---|---|---|
| A-6 | 3.21 | 2.11 | 1.52 |
| A-8 | 4.11 | 3.57 | 1.15 |
| A-10 | 4.70 | 4.06 | 1.16 |
| A-12 | 6.02 | 4.55 | 1.32 |
| P-12 | 4.31 | 4.02 | 1.07 |
| Specimen | Measured Crack Width (DIC) (mm) | Calculated Crack Width (mm) | Ratio of Measured to Calculated Crack Width |
|---|---|---|---|
| A-6 | 0.61 | 0.17 | 3.59 |
| A-8 | 0.46 | 0.35 | 1.31 |
| A-10 | 0.40 | 0.36 | 1.11 |
| A-12 | 0.36 | 0.35 | 1.03 |
| P-12 | 0.50 | 0.32 | 1.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Sun, H.; Wang, Z.; Han, X.; Li, X. Bending Performance of Alkali-Activated Concrete Beams Based on Digital Image Correlation Method. Materials 2025, 18, 1616. https://doi.org/10.3390/ma18071616
Gao H, Sun H, Wang Z, Han X, Li X. Bending Performance of Alkali-Activated Concrete Beams Based on Digital Image Correlation Method. Materials. 2025; 18(7):1616. https://doi.org/10.3390/ma18071616
Chicago/Turabian StyleGao, Hongbo, Hongna Sun, Zhaokun Wang, Xiaoyan Han, and Xinru Li. 2025. "Bending Performance of Alkali-Activated Concrete Beams Based on Digital Image Correlation Method" Materials 18, no. 7: 1616. https://doi.org/10.3390/ma18071616
APA StyleGao, H., Sun, H., Wang, Z., Han, X., & Li, X. (2025). Bending Performance of Alkali-Activated Concrete Beams Based on Digital Image Correlation Method. Materials, 18(7), 1616. https://doi.org/10.3390/ma18071616





