Comparison of Electron Compton Scattering with Positron Compton Scattering in Polyethylene
Abstract
1. Introduction
2. Theory
2.1. Theoretical Framework
2.2. Monte Carlo Method
2.3. Cross Sections
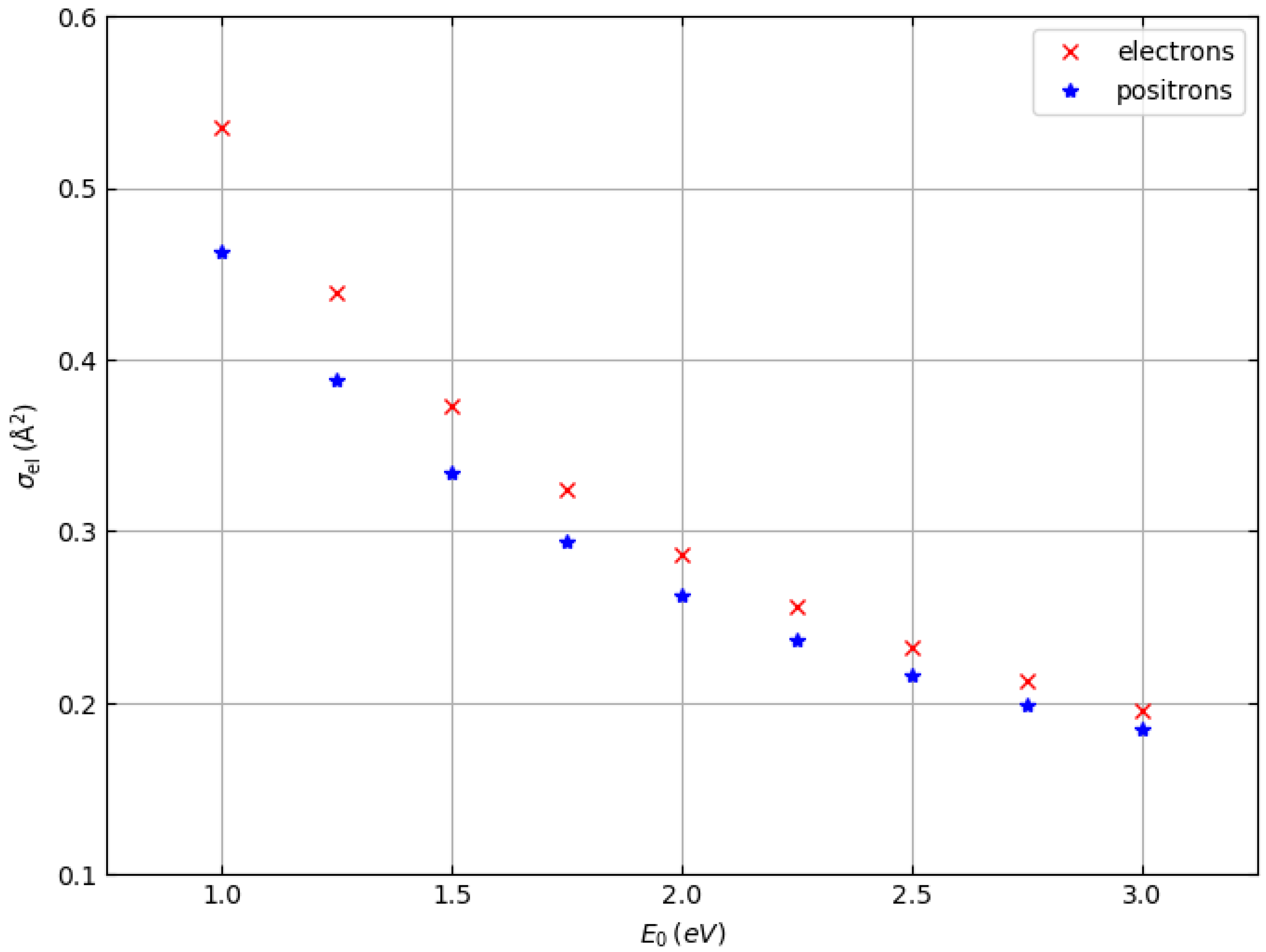
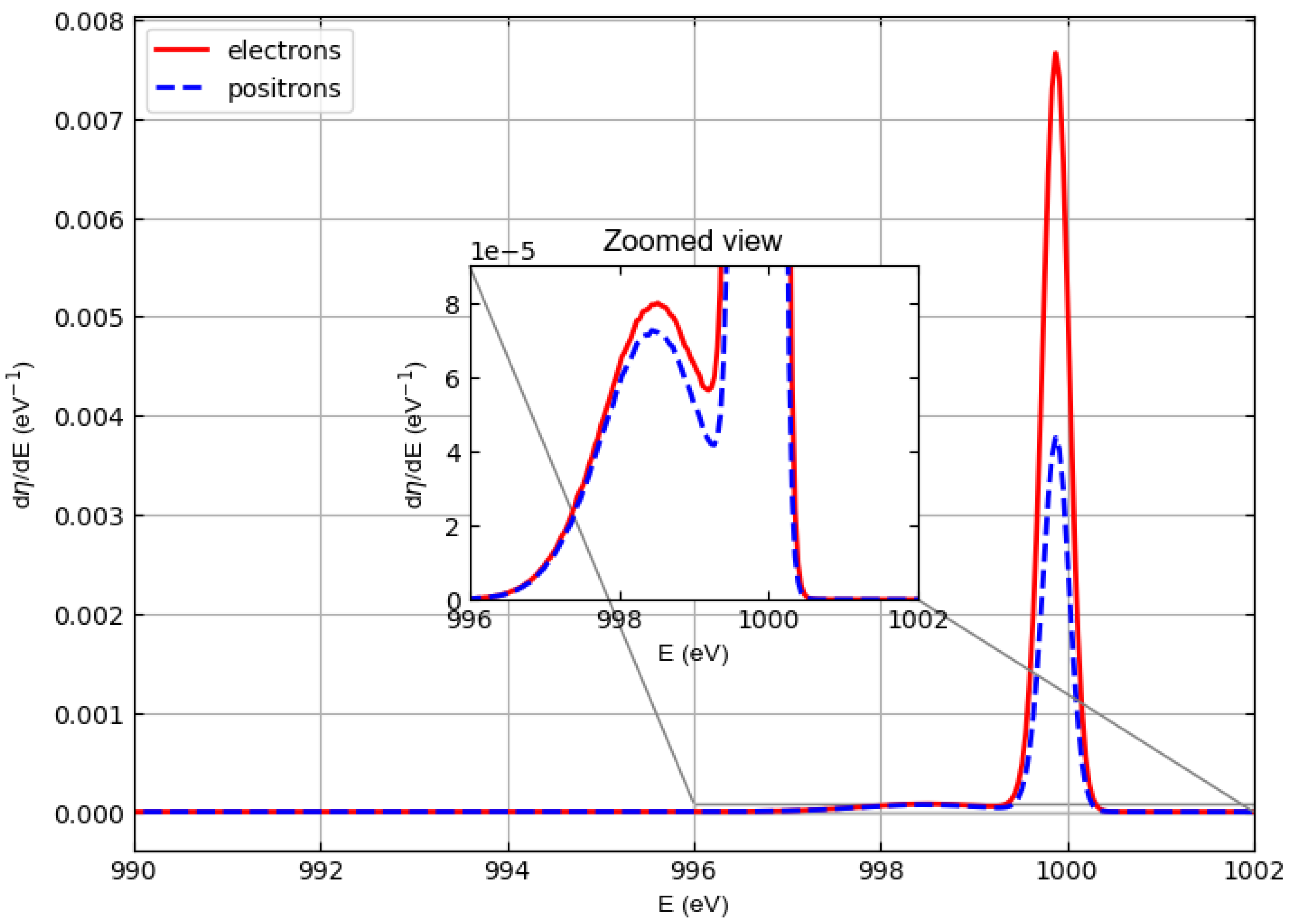
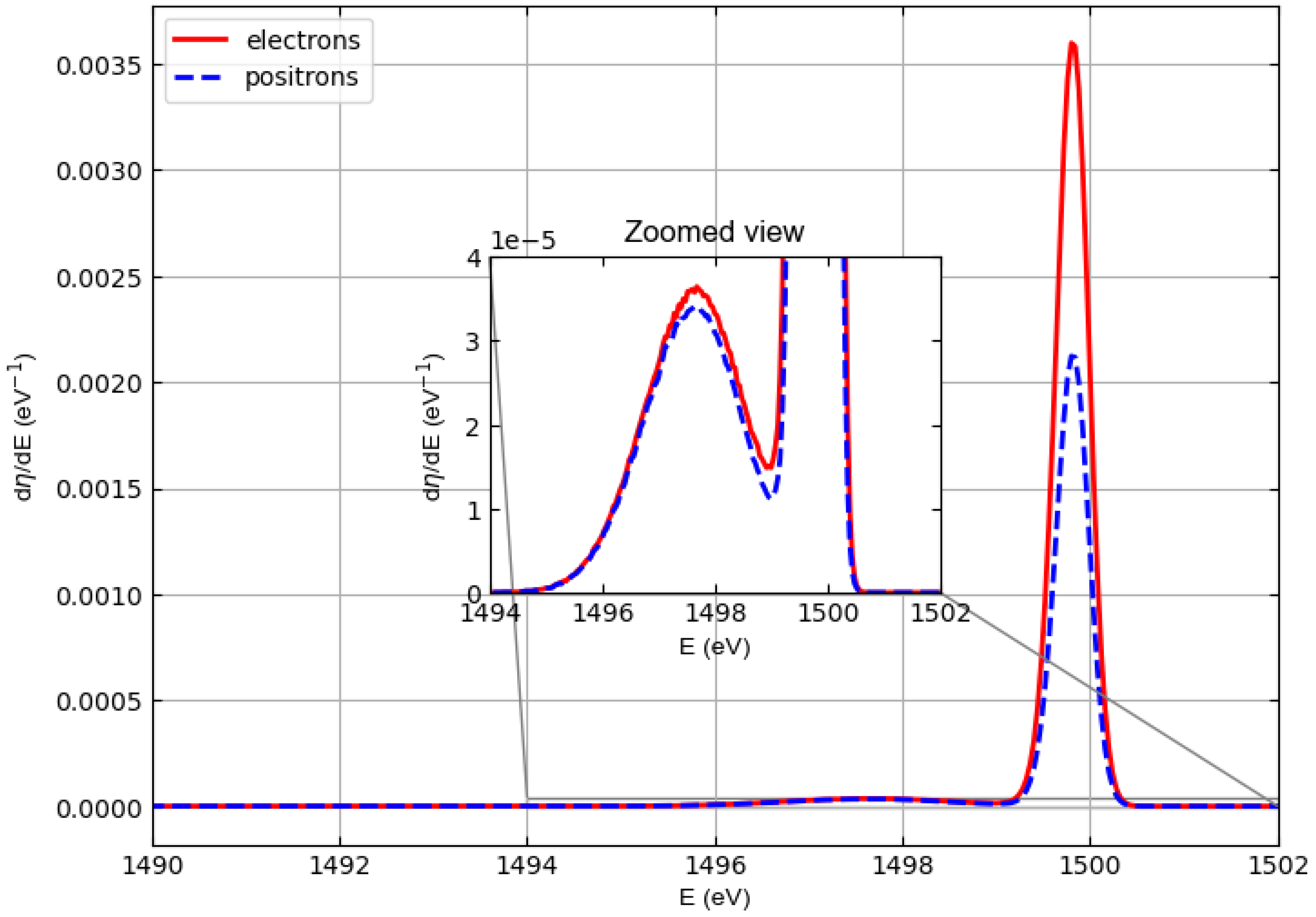
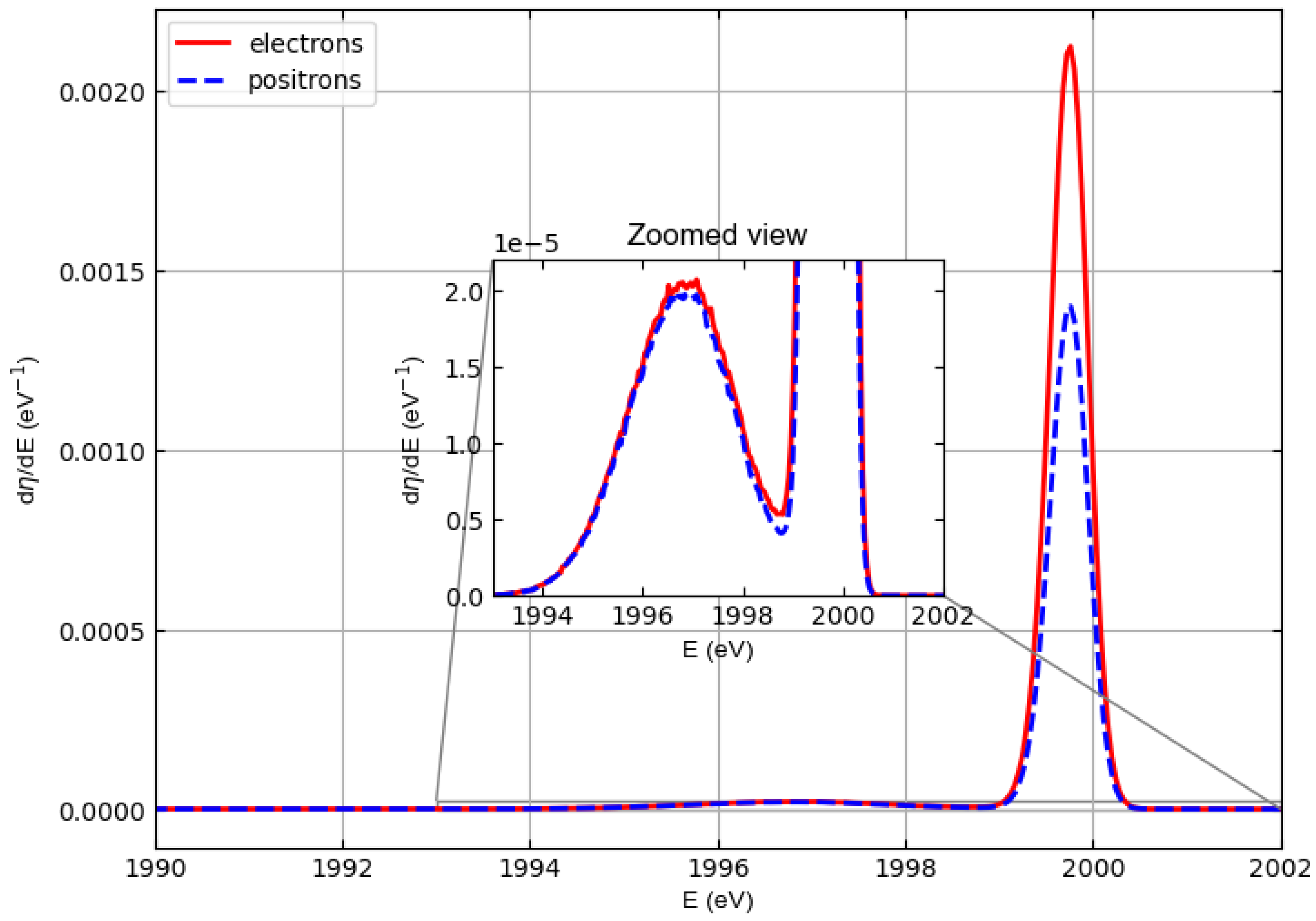
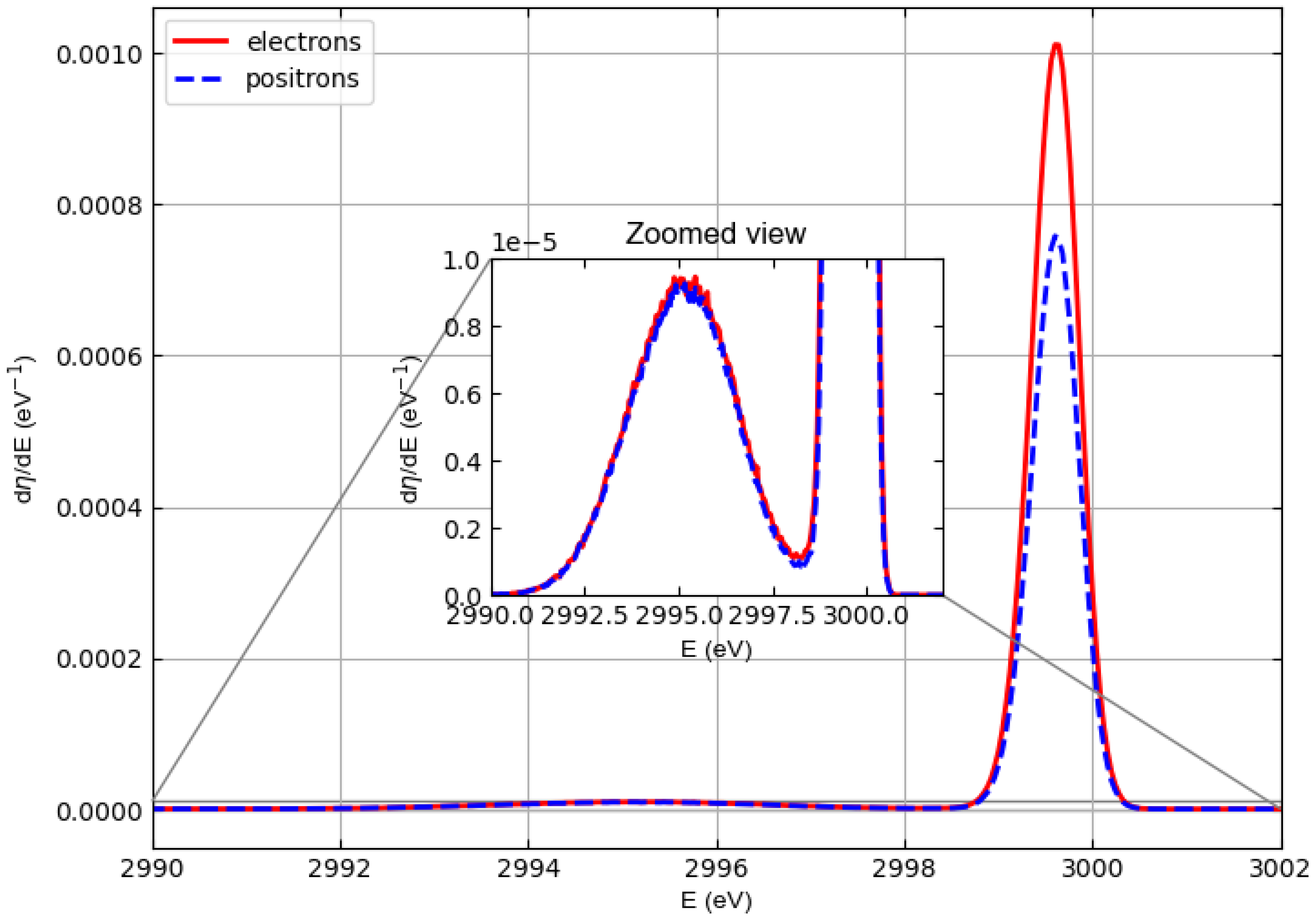
3. Results and Discussion
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Varga, D.; Tökési, K.; Berényi, Z.; Tóth, J.; Kövér, L.; Gergely, G.; Sulyok, A. Energy shift and broadening of the spectra of electrons backscattered elastically from solid surfaces. Surf. Interface Anal. 2001, 31, 1019–1026. [Google Scholar]
- Kwei, C.M.; Li, Y.C.; Tung, C.J. Energy spectra of electrons quasi-elastically backscattered from solid surfaces. J. Phys. D Appl. Phys. 2004, 37, 1394–1399. [Google Scholar]
- Vos, M. Observing atom motion by electron-atom compton scattering. Phys. Rev. A 2001, 65, 012703. [Google Scholar]
- Vos, M.; Went, M.R. Elastic electron scattering at high momentum transfer: A possible new analytic tool. J. Electron Spectrosc. Relat. Phenom. 2007, 155, 35–39. [Google Scholar]
- Vos, M.; Marmitt, G.G.; Grande, P.L. A Comparison of ERBS spectra of compounds with Monte Carlo simulations. Surf. Interface Anal. 2016, 48, 415–421. [Google Scholar]
- Yubero, F.; Rico, V.J.; Espinós, J.P.; Cotrino, J.; González-Elipe, A.R. Quantification of the H content in diamond-like carbon and polymeric thin films by reflection electron energy loss spectroscopy. Appl. Phys. Lett. 2005, 87, 084101. [Google Scholar]
- Yubero, F.; Pauly, N.; Dubus, A.; Tougaard, S. Test of validity of the V-type approach for electron trajectories in reflection electron energy loss spectroscopy. Phys. Rev. B 2008, 77, 245405. [Google Scholar]
- Alvarez, R.; Yubero, F. Interpretation of electron rutherford backscattering spectrometry for hydrogen quantification. Surf. Interface Anal. 2014, 46, 812–816. [Google Scholar]
- Filippi, M.; Calliari, L. On the use of elastic peak electron spectroscopy (EPES) to neasure the H content of hydrogenated amorphous carbon films. Surf. Interface Anal. 2008, 40, 1469–1474. [Google Scholar]
- Dapor, M. Electron-induced hydrogen desorption from selected polymers (polyacetylene, polyethylene, polystyrene, and polymethyl-methacrylate). Phys. Scr. 2024, 99, 0659b4. [Google Scholar]
- Dapor, M. Unveiling Doppler effects and charge phenomena in the elastic scattering of kev electrons on polystyrene. Phys. Scr. 2024, 99, 115976. [Google Scholar] [CrossRef]
- Dapor, M. Charge phenomena in the elastic backscattering of electrons from insulating polymers. Polymers 2024, 16, 2329. [Google Scholar] [CrossRef] [PubMed]
- Dapor, M. Analysis of the elastic peaks of hydrogen and oxygen from electron beams hitting liquid water. Phys. Scr. 2025, 100, 045409. [Google Scholar] [CrossRef]
- Vos, M. Electron scattering at high momentum transfer from methane: Analysis of line shapes. J. Chem. Phys. 2010, 132, 074306. [Google Scholar] [CrossRef]
- Lesiak, B.; Zemek, J.; Houdkova, J. Hydrogen detection and quantification at polymer surfaces investigated by elastic peak electron spectroscopy (EPES). Polymer 2008, 49, 4127–4132. [Google Scholar] [CrossRef]
- Orosz, G.T.; Gergely, G.; Menyhard, M.; Tóth, J.; Varga, D.; Lesiak, B.; Jablonski, A. Hydrogen and surface excitation in electron spectra of polyethylene. Surf. Sci. 2004, 566–568, 544–548. [Google Scholar] [CrossRef]
- Varga, D.; Tökési, K.; Berényi, Z.; Tóth, J.; Kövér, L. Observation of the hydrogen peak in the spectra of electrons backscattered from polyethylene. Surf. Interface Anal. 2006, 38, 544–547. [Google Scholar] [CrossRef]
- Paoli, M.P.; Holt, R.S. Anisotropy in the atomic momentum distribution of pyrolytic graphite. J. Phys. C Solid State Phys. 1988, 21, 3633–3639. [Google Scholar] [CrossRef]
- Shimizu, R.; Ding, Z.J. Monte Carlo modelling of electron-solid interactions. Rep. Prog. Phys. 1992, 55, 487–531. [Google Scholar] [CrossRef]
- Dapor, M. Transport of energetic electrons in solids; Springer Tracts in Modern Physics; Springer Nature: Cham, Switzerland, 2023; Volume 290. [Google Scholar]
- Taioli, S.; Dapor, M. Advancements in secondary and backscattered electron energy spectra and yields analysis: From theory to applications. Surf. Sci. Rep. 2025, 80, 100646. [Google Scholar] [CrossRef]
- Dapor, M. Electron-Atom Collisions. Quantum-Relativistic Theory and Exercises; De Gruyter: Berlin, Germany; Boston, MA, USA, 2022. [Google Scholar]
- Furness, J.B.; McCarthy, I.E. Semiphenomenological optical model for electron scattering on atoms. J. Phys. B Atom. Molec. Phys. 1973, 6, 2280–2291. [Google Scholar]
- Tanuma, S.; Powell, C.J.; Penn, D.R. Calculations of electron inelastic mean free paths. V. Data for 14 organic compounds over the 50-2000 eV range. Surf. Interface Anal. 1993, 21, 165–176. [Google Scholar]
- Shinotsuka, H.; Tanuma, S.; Powell, C.J. Calculations of electron inelastic mean free paths. XIII. Data for 14 organic compounds and water over the 50 eV to 200 keV range with the relativistic full Penn algorithm. Surf. Interface Anal. 2022, 54, 534–560. [Google Scholar]
- Ritchie, R.H. Plasma losses of fast electrons in thin films. Phys. Rev. 1957, 106, 874–881. [Google Scholar]
- Powell, C.J. Attenuation lengths of low-energy electrons in solids. Surf. Sci. 1974, 44, 29–46. [Google Scholar]
- Tung, C.J.; Ashley, J.C.; Ritchie, R.H. Electron inelastic mean free paths and energy losses in solids II: Electron gas statistical model. Surf. Sci. 1979, 81, 427–439. [Google Scholar]
- Penn, D.R. Quantitative chemical analysis by ESCA. J. Electron Spectrosc. Relat. Phenom. 1976, 9, 29–40. [Google Scholar]
- Penn, D.R. Electron mean-free-path calculations using a model dielectric function. Phys. Rev. B 1987, 35, 482–486. [Google Scholar] [CrossRef]
- Ashley, J.C. Energy loss rate and inelastic mean free path of low-energy electros and positrons in condensed matter. Nucl. Instrum. Methods Phys. Res. B 1990, 50, 323–334. [Google Scholar]
- Tanuma, S.; Powell, C.J.; Penn, D.R. Calculations of electron inelastic mean free paths. IX. Data for 41 elemental solids over the 50 eV to 30 keV range. Surf. Interface Anal. 2011, 43, 689–713. [Google Scholar]
- Shinotsuka, H.; Tanuma, S.; Powell, C.J.; Penn, D.R. Calculations of electron inelastic mean free paths. XII. Data for 42 inorganic compounds over the 50 eV to 200 keV range with the full Penn algorithm. Surf. Interface Anal. 2019, 51, 427–457. [Google Scholar]
- Mayers, J.; Burke, T.M.; Newport, R.J. Neutron compton scattering from amorphous hydrogenated carbon. J. Phys. Condens. Matter 1994, 6, 641–658. [Google Scholar]
- Jablonski, A. Elastic backscattering of electrons from surfaces. Surf. Sci. 1985, 151, 166–182. [Google Scholar]
- Gergely, G. Elastic peak electron spectroscopy for auger electron spectroscopy and electron energy loss spectroscopy. Surf. Interface Anal. 1981, 3, 201–205. [Google Scholar]
- Schmid, R.; Gaukler, K.H.; Seiler, H. Measurement of elastically reflected electrons (E < 2.5 kev) for imaging of surfaces in a simple ultra high vacuum “scanning electron microscope”. Scanning Electron Microsc. 1983, II, 501. [Google Scholar]


| Energy (eV) | IMFP | IMFP | IMFP | IMFP |
|---|---|---|---|---|
| (Electrons) | (Electrons) | (Electrons) | (Positrons) | |
| (Å) | (Å) | (Å) | (Å) | |
| Ref. [25] | Ref. [24] | Ref. [31] | Ref. [31] | |
| 1000 | - | 31.8 | 35.7 | 34.8 |
| 1096.6 | 35.2 | - | - | |
| 1500 | - | 44.0 | 48.9 | 48.0 |
| 1636.0 | 48.4 | - | - | |
| 2000 | - | 55.6 | 61.5 | 60.7 |
| 2208.3 | 61.7 | - | - | |
| 3000 | - | - | 85.6 | 84.8 |
| Incident Particle Energy | |||
|---|---|---|---|
| (keV) | (%) | ||
| 1.0 | 0.290 | 0.147 | 49 |
| 1.5 | 0.168 | 0.101 | 40 |
| 2.0 | 0.115 | 0.0770 | 33 |
| 3.0 | 0.0678 | 0.0514 | 24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dapor, M. Comparison of Electron Compton Scattering with Positron Compton Scattering in Polyethylene. Materials 2025, 18, 1609. https://doi.org/10.3390/ma18071609
Dapor M. Comparison of Electron Compton Scattering with Positron Compton Scattering in Polyethylene. Materials. 2025; 18(7):1609. https://doi.org/10.3390/ma18071609
Chicago/Turabian StyleDapor, Maurizio. 2025. "Comparison of Electron Compton Scattering with Positron Compton Scattering in Polyethylene" Materials 18, no. 7: 1609. https://doi.org/10.3390/ma18071609
APA StyleDapor, M. (2025). Comparison of Electron Compton Scattering with Positron Compton Scattering in Polyethylene. Materials, 18(7), 1609. https://doi.org/10.3390/ma18071609






