Fluid Flow and Stress Field During Laser Cladding-Based Surface Repair of Aluminum Alloy: Multi-Track Simulation
Abstract
1. Introduction
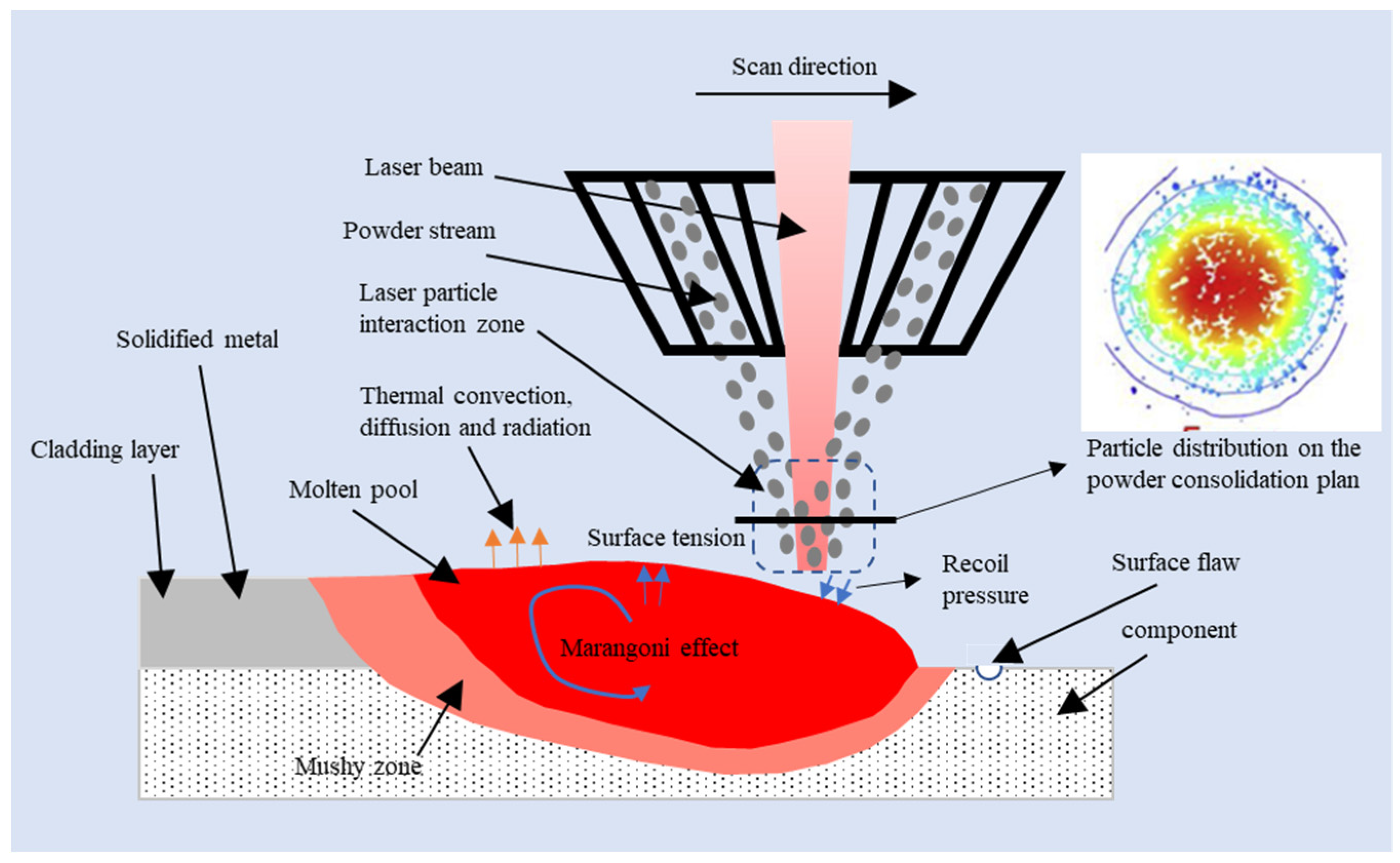
2. Fluid Flow Modeling During LC-Based Surface Repair Process
2.1. Mathematical Modeling of the Fluid Flow
2.1.1. Governing Equations
2.1.2. Mass Source Terms
2.1.3. Momentum Source Terms
2.1.4. Energy Source Terms
2.2. Numerical Implementation of the Fluid Flow Simulation
| Name | Value |
|---|---|
| Solidus density (kg/m3) | 2719 [5] |
| Liquidus density (kg/m3) | 2490 [5] |
| Solidus specific heat (J/(kg K)) | 906 [22] |
| Liquidus specific heat (J/(kg K)) | 1220 [22] |
| Solidus thermal conductivity (W/(m K)) | 202.4 [22] |
| Liquidus thermal conductivity (W/(m K)) | 61 [22] |
| Dynamic viscosity (kg/(m s)) | 0.004 [20] |
| Molecular mass (kg/kmol) | 26.982 |
| Reference temperature (K) | 298.15 |
| Latent heat of melting (J/kg) | 383,000 [22] |
| Latent heat of vaporization (J/kg) | 10,870,000 [22] |
| Solidus temperature (K) | 890 [22] |
| Liquidus temperature (K) | 929 [22] |
| Surface tension coefficient (N/m) | 0.914 − 0.35 × 10−3(T − 890) [23] |
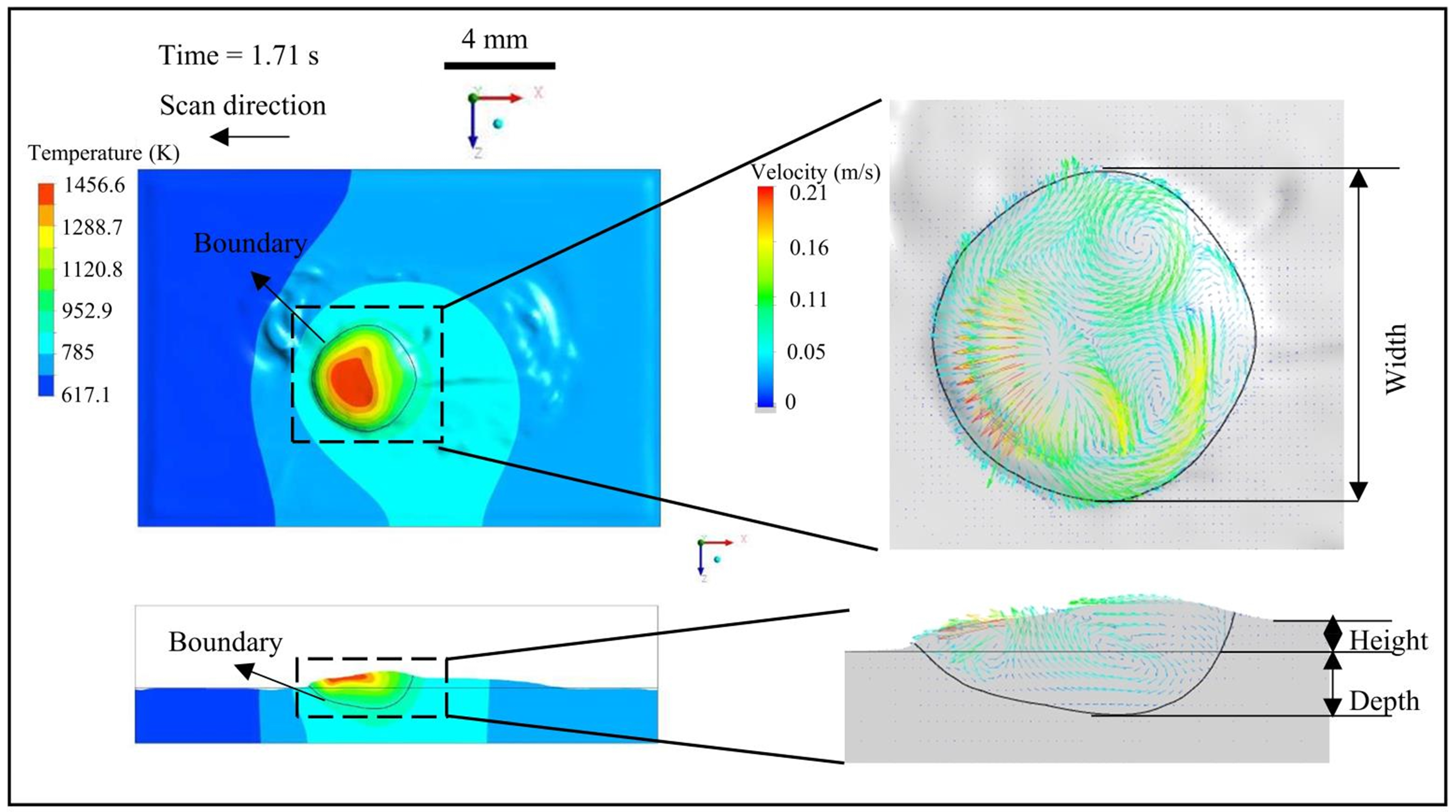
2.3. Results and Analysis
3. Stress Field Simulation During LC-Based Surface Repair Process
3.1. Mathematical Models of the Stress Field
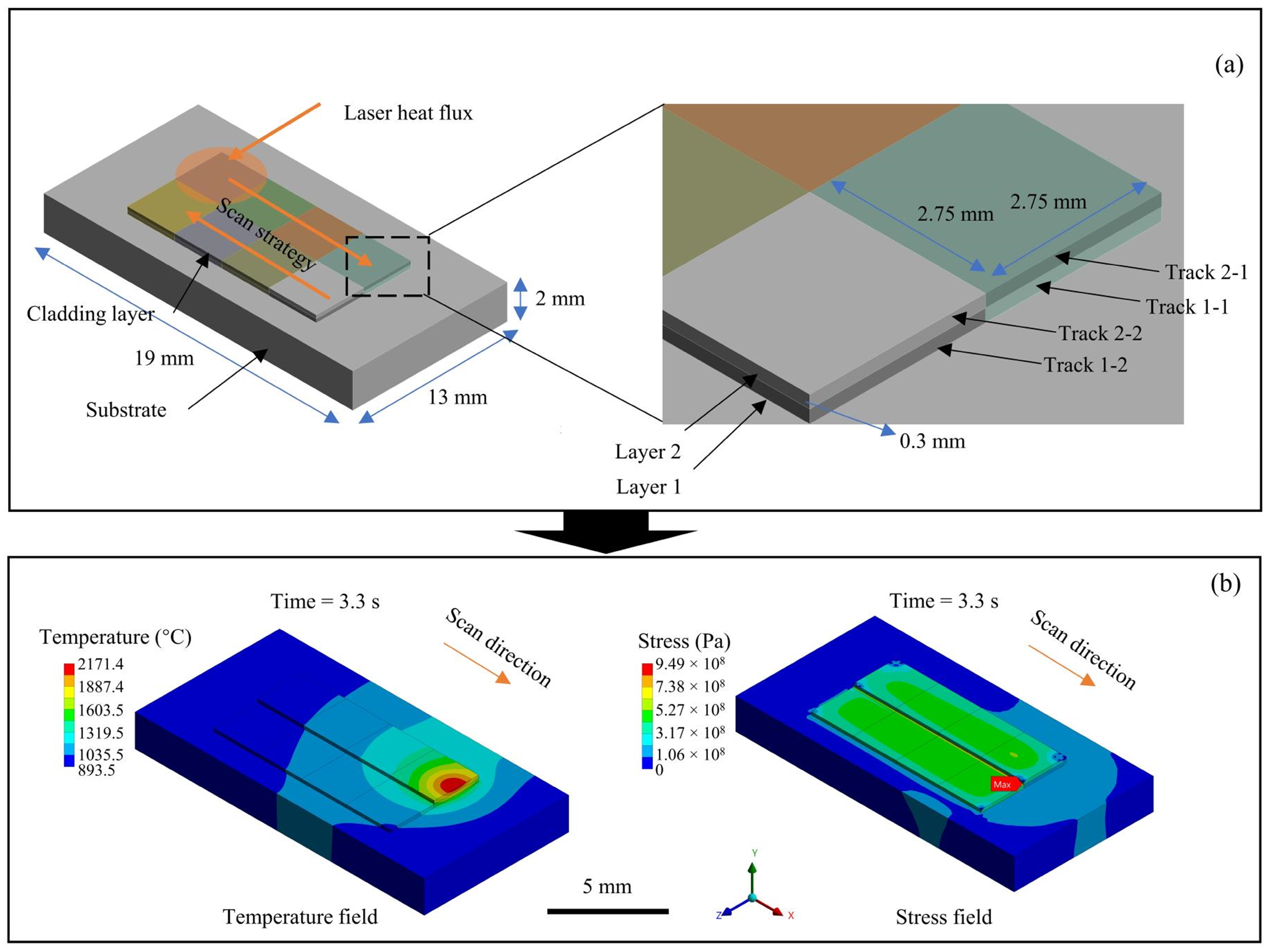
3.2. Numerical Implementation of the Stress Field Simulation
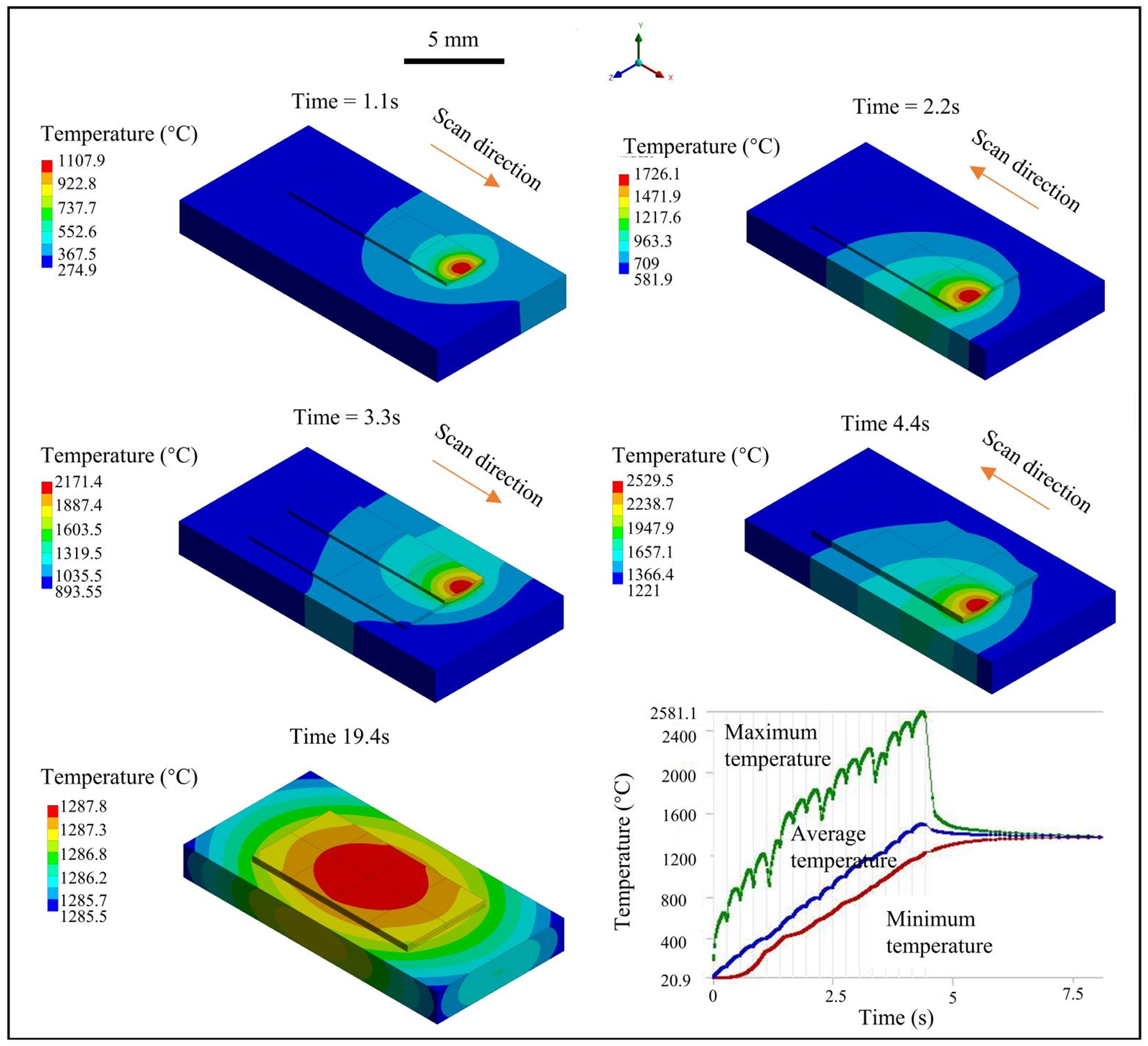
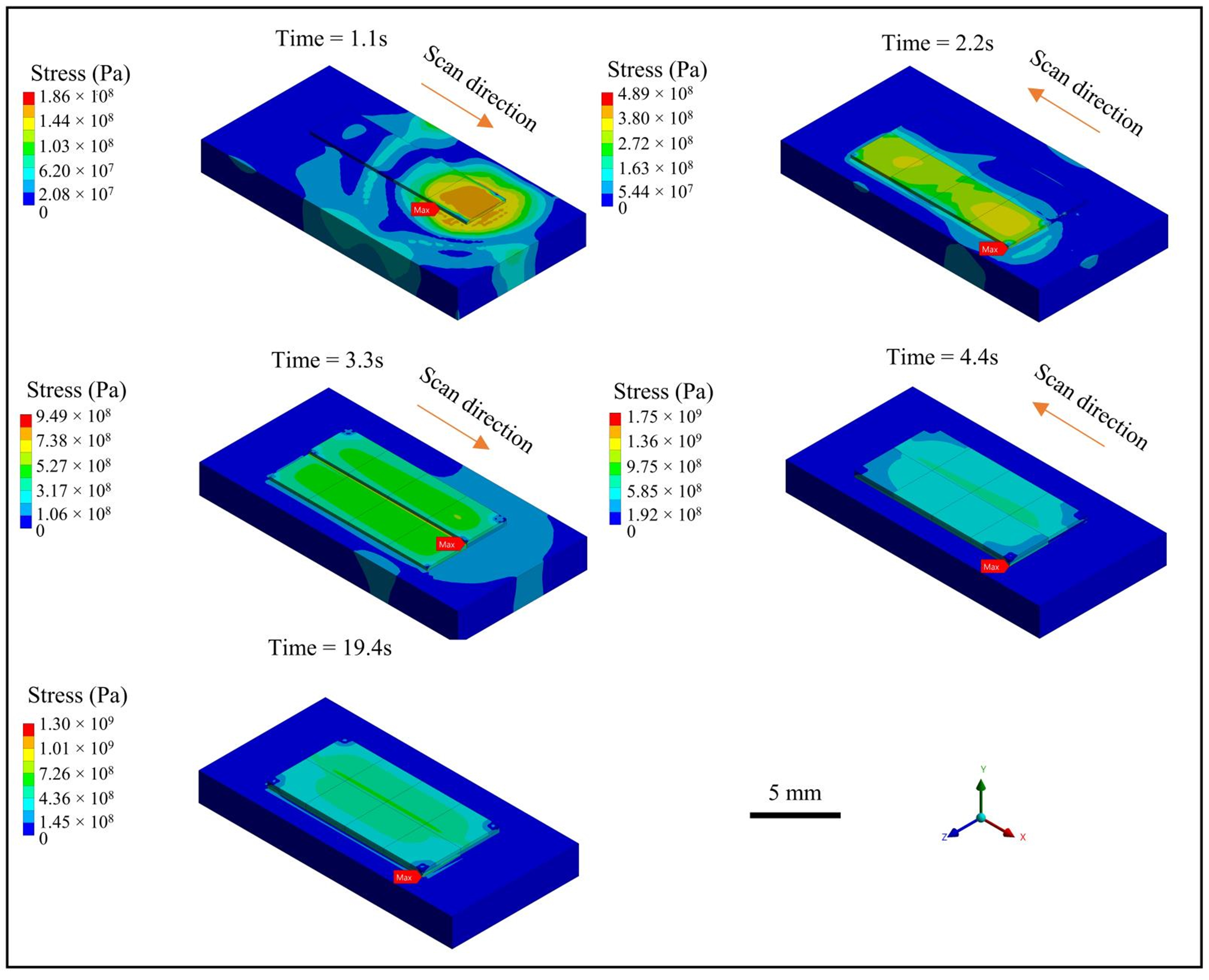
3.3. Results and Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, G.; Wang, Z.; Lu, Y.; Chen, M.; Yang, K.; Ni, Z. Underwater laser welding/cladding for high-performance repair of marine metal materials: A review. Chin. J. Mech. Eng. 2022, 35, 5. [Google Scholar] [CrossRef]
- Cheng, J.; Xing, Y.; Dong, E.; Zhao, L.; Liu, H.; Chang, T.; Chen, M.; Wang, J.; Lu, J.; Wan, J. An overview of laser metal deposition for cladding: Defect formation mechanisms, defect suppression methods and performance improvements of laser-cladded layers. Materials 2022, 15, 5522. [Google Scholar] [CrossRef] [PubMed]
- Torims, T. The application of laser cladding to mechanical component repair, renovation and regeneration. Daaam Int. Sci. Book 2013, 12, 587–608. [Google Scholar]
- Ge, H.; Xu, H.; Wang, J.; Li, J.; Yao, J. Investigation on composition distribution of dissimilar laser cladding process using a three-phase model. Int. J. Heat Mass Transf. 2021, 170, 120975. [Google Scholar] [CrossRef]
- Zhou, X.; Pei, Z.; Liu, Z.; Yang, L.; Yin, Y.; He, Y.; Wu, Q.; Nie, Y. Multiscale Simulation of Laser-Based Direct Energy Deposition (DED-LB/M) Using Powder Feedstock for Surface Repair of Aluminum Alloy. Materials 2024, 17, 3559. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, L.; Zhao, K.; Hao, Y.; Lyu, F.; Gao, Z.; Zhao, Y.; Zhan, X. Multiphysics modeling of flow characteristics and particulate migration behavior of titanium matrix composites by laser directed energy deposition. J. Manuf. Process. 2024, 131, 1014–1029. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, L.; Fuh, J.Y.H.; Zhang, H.; Yan, W. Multi-physics modeling and Gaussian process regression analysis of cladding track geometry for direct energy deposition. Opt. Lasers Eng. 2020, 127, 105950. [Google Scholar] [CrossRef]
- Sun, Z.; Guo, W.; Li, L. Numerical modelling of heat transfer, mass transport and microstructure formation in a high deposition rate laser directed energy deposition process. Addit. Manuf. 2020, 33, 101175. [Google Scholar] [CrossRef]
- Stender, M.E.; Beghini, L.L.; Sugar, J.D.; Veilleux, M.G.; Subia, S.R.; Smith, T.R.; San Marchi, C.W.; Brown, A.A.; Dagel, D.J. A thermal-mechanical finite element workflow for directed energy deposition additive manufacturing process modeling. Addit. Manuf. 2018, 21, 556–566. [Google Scholar] [CrossRef]
- Kiran, A.; Hodek, J.; Vavřík, J.; Urbánek, M.; Džugan, J. Numerical simulation development and computational optimization for directed energy deposition additive manufacturing process. Materials 2020, 13, 2666. [Google Scholar] [CrossRef]
- Gao, J.; Wu, C.; Hao, Y.; Xu, X.; Guo, L. Numerical simulation and experimental investigation on three-dimensional modelling of single-track geometry and temperature evolution by laser cladding. Opt. Laser Technol. 2020, 129, 106287. [Google Scholar] [CrossRef]
- Tamanna, N.; Kabir, I.; Naher, S. Thermo-mechanical modelling to evaluate residual stress and material compatibility of laser cladding process depositing similar and dissimilar material on Ti6Al4V alloy. Therm. Sci. Eng. Prog. 2022, 31, 101283. [Google Scholar] [CrossRef]
- Cook, P.S.; Murphy, A.B. Simulation of melt pool behaviour during additive manufacturing: Underlying physics and progress. Addit. Manuf. 2020, 31, 100909. [Google Scholar] [CrossRef]
- Pinkerton, A.J. An analytical model of beam attenuation and powder heating during coaxial laser direct metal deposition. J. Phys. D Appl. Phys. 2007, 40, 7323. [Google Scholar] [CrossRef]
- Nie, Y.; Low, K.W.; Liu, Z.; Yang, L.; Wang, Y.; Li, T.; Li, H.; He, Y. Mechanics insights into particle ejection during laser cutting of metal alloys. J. Adv. Manuf. Technol. 2025, 137, 1173–1187. [Google Scholar] [CrossRef]
- Tang, C.; Tan, J.L.; Wong, C.H. A numerical investigation on the physical mechanisms of single track defects in selective laser melting. Int. J. Heat Mass Transf. 2018, 126, 957–968. [Google Scholar] [CrossRef]
- Bayat, M.; Mohanty, S.; Hattel, J.H. Multiphysics modelling of lack-of-fusion voids formation and evolution in IN718 made by multi-track/multi-layer L-PBF. Int. J. Heat Mass Transf. 2019, 139, 95–114. [Google Scholar] [CrossRef]
- Sun, Z.; Chueh, Y.-H.; Li, L. Multiphase mesoscopic simulation of multiple and functionally gradient materials laser powder bed fusion additive manufacturing processes. Addit. Manuf. 2020, 35, 101448. [Google Scholar] [CrossRef]
- Pierron, N.; Sallamand, P.; Jouvard, J.-M.; Cicala, E.; Matteï, S. Determination of an empirical law of aluminium and magnesium alloys absorption coefficient during Nd: YAG laser interaction. J. Phys. D Appl. Phys. 2007, 40, 2096. [Google Scholar] [CrossRef]
- Pei, W.; Zhengying, W.; Zhen, C.; Junfeng, L.; Shuzhe, Z.; Jun, D. Numerical simulation and parametric analysis of selective laser melting process of AlSi10Mg powder. Appl. Phys. A 2017, 123, 540. [Google Scholar] [CrossRef]
- Gu, H.; Wei, C.; Li, L.; Han, Q.; Setchi, R.; Ryan, M.; Li, Q. Multi-physics modelling of molten pool development and track formation in multi-track, multi-layer and multi-material selective laser melting. Int. J. Heat Mass Transf. 2020, 151, 119458. [Google Scholar] [CrossRef]
- Valencia, J.J.; Quested, P.N. Thermophysical properties. In Metals Process Simulation; ASM International: Materials Park, OH, USA, 2010; pp. 18–32. [Google Scholar]
- Mills, K.C. Recommended Values of Thermophysical Properties for Selected Commercial Alloys; Woodhead Publishing: Sawston, UK, 2002. [Google Scholar]
- Toyserkani, E.; Khajepour, A.; Corbin, S. Three-dimensional finite element modeling of laser cladding by powder injection: Effects of powder feedrate and travel speed on the process. J. Laser Appl. 2003, 15, 153–160. [Google Scholar] [CrossRef]
- Park, S.J.; Heogh, W.; Yang, J.; Kang, S.; Jeong, W.; Lee, H.; Jang, T.-S.; Jung, H.-D.; Jahazi, M.; Han, S.C.; et al. Meta-structure of amorphous-inspired 65.1Co28.2Cr5.3Mo lattices augmented by artificial intelligence. Adv. Compos. Hybrid Mater. 2024, 7, 224. [Google Scholar] [CrossRef]




| Name | Value |
|---|---|
| Density (kg/m3) | 1.6288 |
| Specific heat (J/(Kg K)) | 520.64 |
| Heat conduction coefficient (W/(m K)) | 0.0158 |
| Dynamic viscosity (Kg/(m s)) | 2.125 × 10−5 |
| Molar mass (Kg/kmol) | 39.948 |
| Reference temperature (K) | 298.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Chu, H.; Liu, Z.; Yang, L.; Zhou, X.; He, Y.; Nie, Y. Fluid Flow and Stress Field During Laser Cladding-Based Surface Repair of Aluminum Alloy: Multi-Track Simulation. Materials 2025, 18, 1603. https://doi.org/10.3390/ma18071603
Wu Q, Chu H, Liu Z, Yang L, Zhou X, He Y, Nie Y. Fluid Flow and Stress Field During Laser Cladding-Based Surface Repair of Aluminum Alloy: Multi-Track Simulation. Materials. 2025; 18(7):1603. https://doi.org/10.3390/ma18071603
Chicago/Turabian StyleWu, Quan, Haiping Chu, Zhongkui Liu, Lihang Yang, Xiaosong Zhou, Yinfeng He, and Yi Nie. 2025. "Fluid Flow and Stress Field During Laser Cladding-Based Surface Repair of Aluminum Alloy: Multi-Track Simulation" Materials 18, no. 7: 1603. https://doi.org/10.3390/ma18071603
APA StyleWu, Q., Chu, H., Liu, Z., Yang, L., Zhou, X., He, Y., & Nie, Y. (2025). Fluid Flow and Stress Field During Laser Cladding-Based Surface Repair of Aluminum Alloy: Multi-Track Simulation. Materials, 18(7), 1603. https://doi.org/10.3390/ma18071603







