Influence of Rotational Speed on Accuracy in Measuring MIRS of Aerospace Aluminum Alloy by Incremental Hole-Milling Method
Highlights
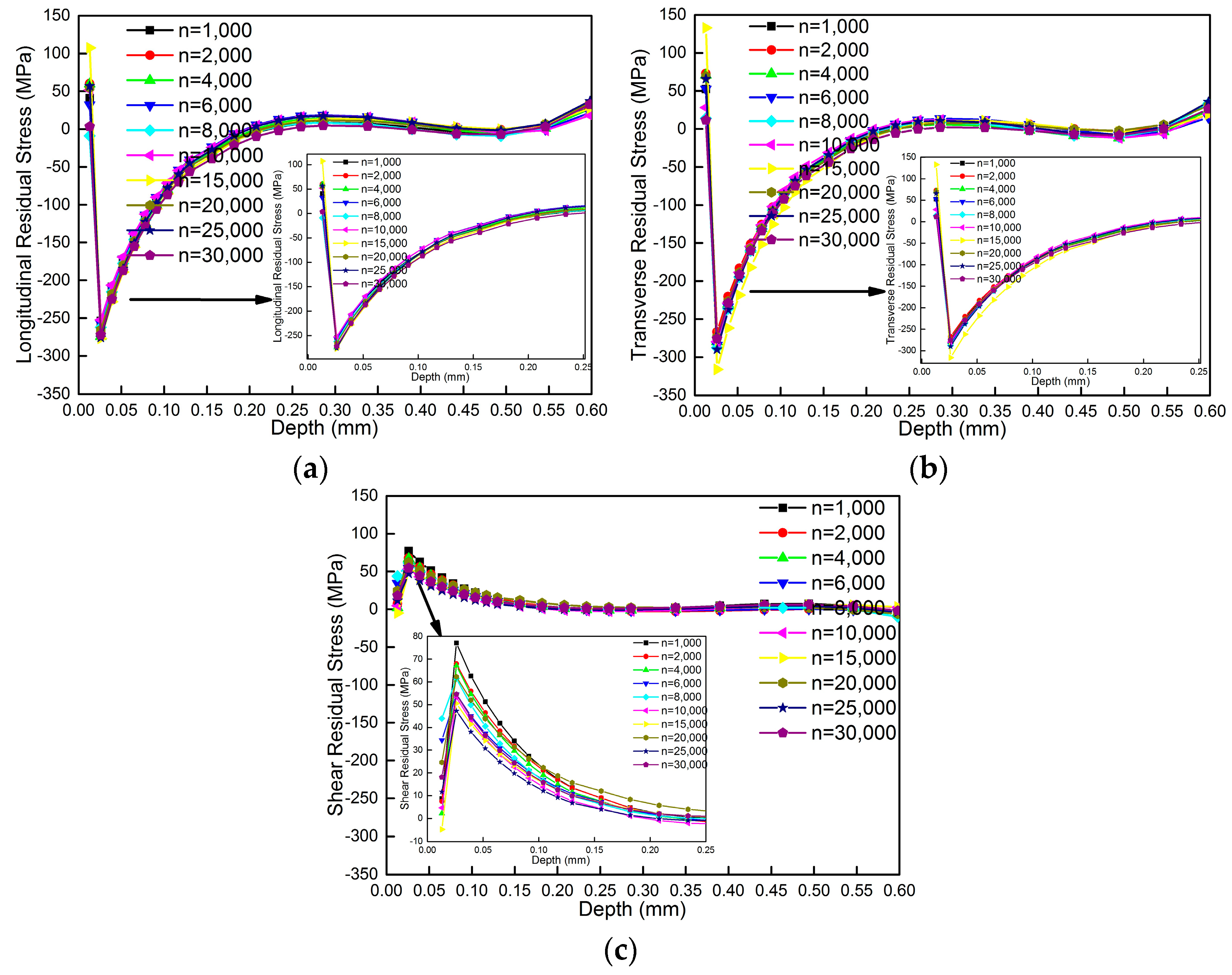
- The deviation of measured machining-induced residual stress can be controlled within 35 MPa when the rotational speed is more than 20,000 rpm;
- Shear stress increases by 63% when the rotational speed is below 10,000 rpm;
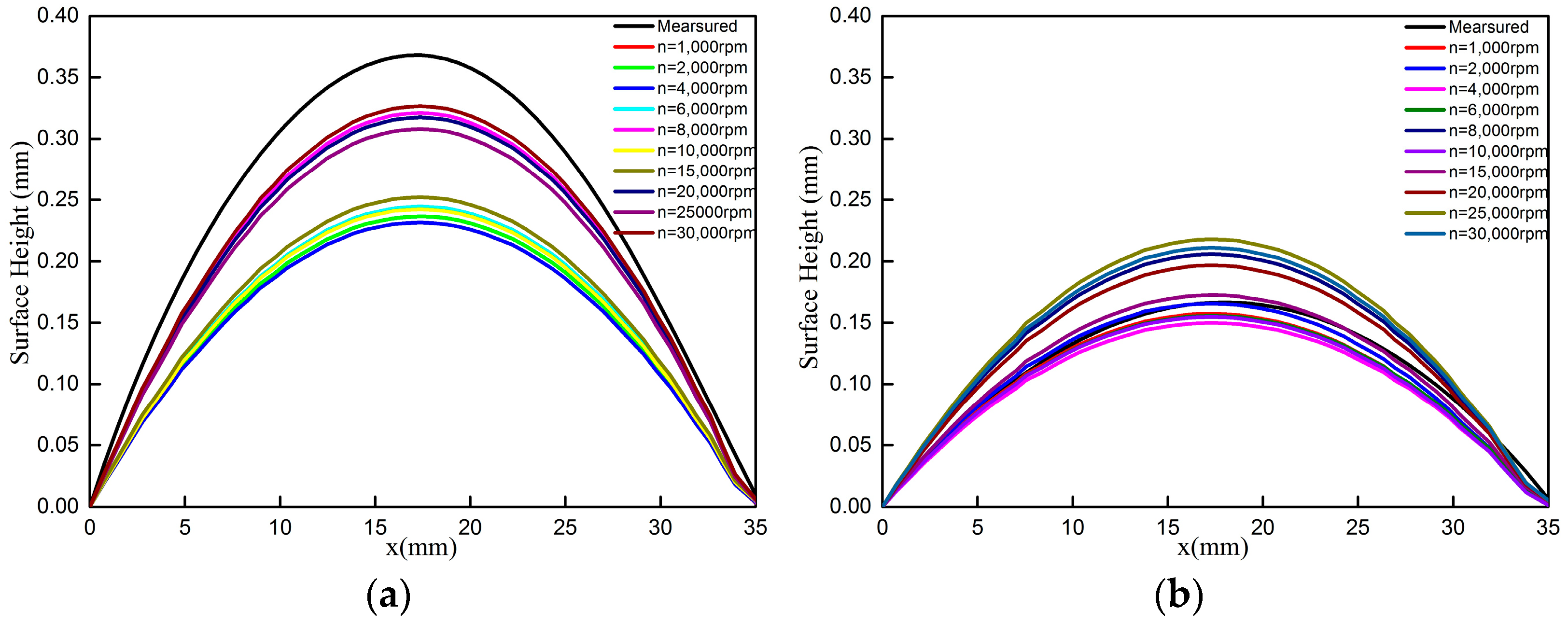
- The calculated maximum distortion on one of the diagonals of the samples can reach 89% of the measured maximum distortion of one diagonal when the rotational speed is more than 20,000 rpm.
Abstract
1. Introduction
2. Materials and Methods
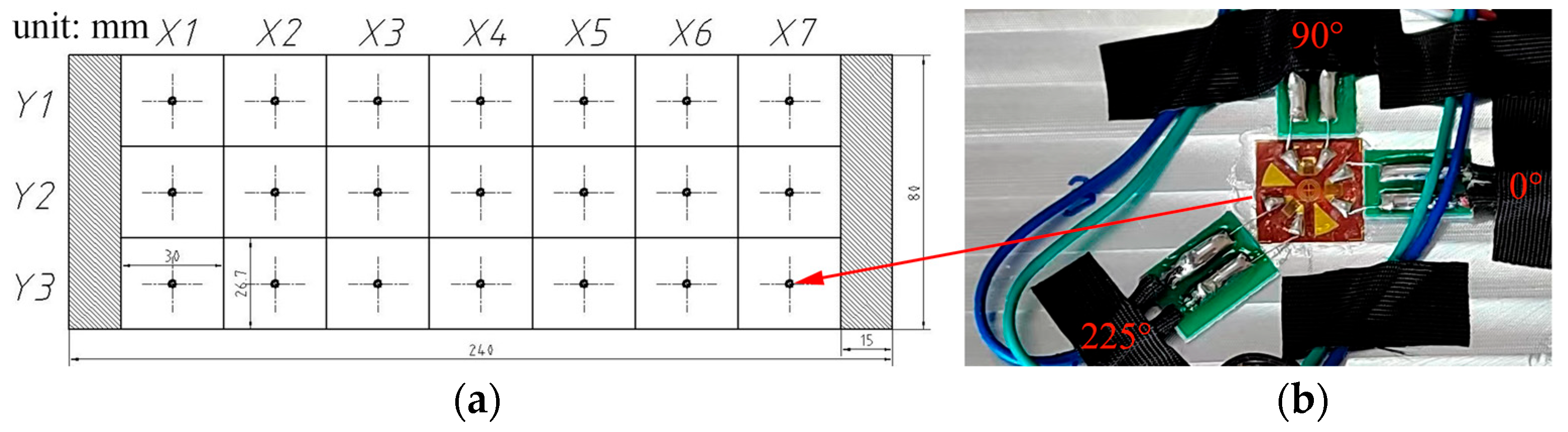
2.1. Sample Preparation
2.2. Machining Experiment
2.3. Residual Stress Measurement
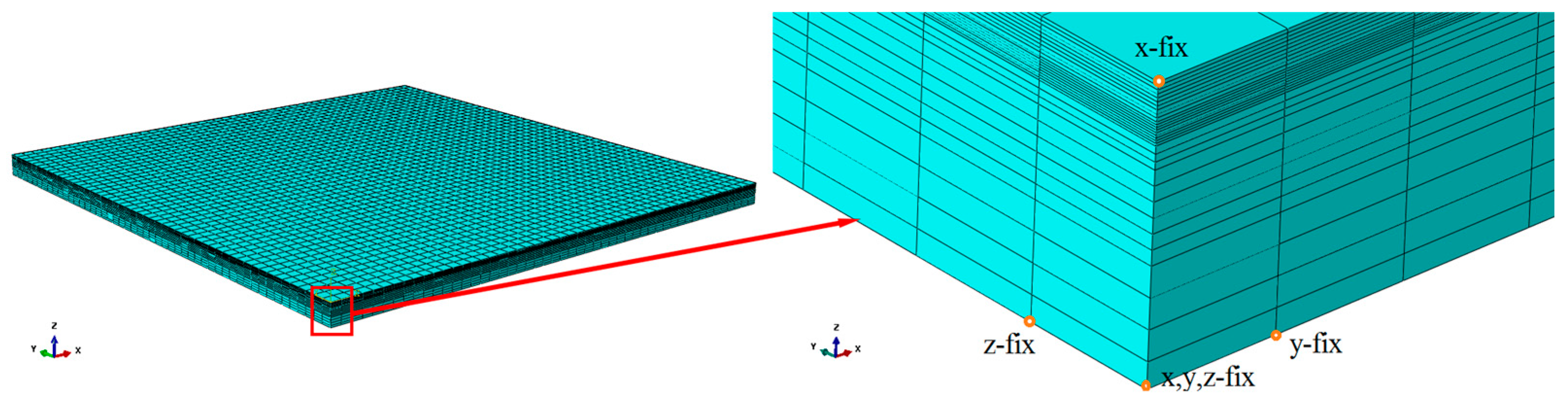
2.4. Experimental Verification
3. Results
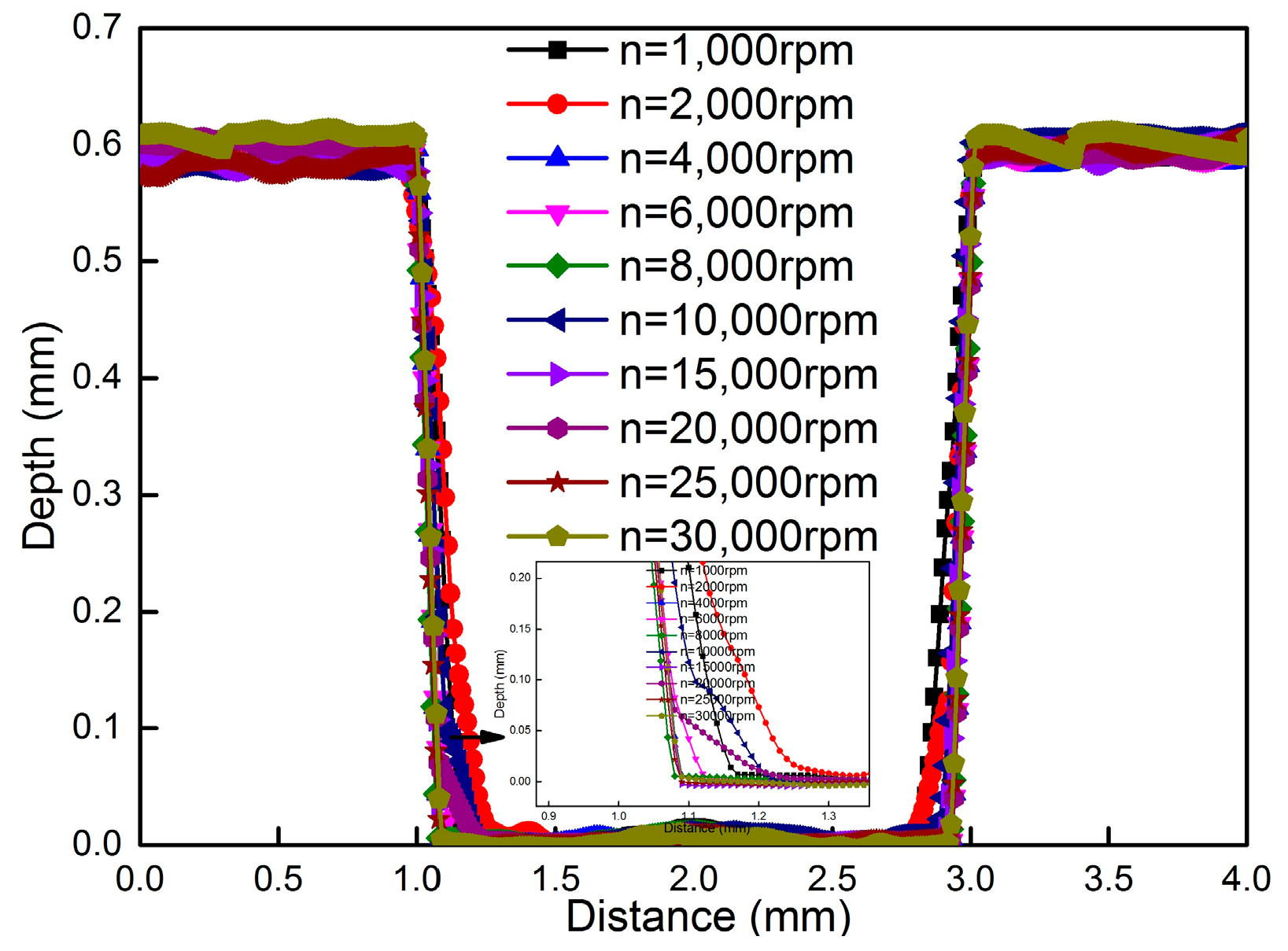
3.1. The Influence of Rotational Speed on Residual Stress Measurements
3.2. The Influence of Rotational Speed on Machining Distortion Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Weber, D.; Kirsch, B.; Chighizola, C.; Jonsson, J.; D’elia, C.; Linke, B.; Hill, M.; Aurich, J. Investigation on the scale effects of initial bulk and MIRS of thin walled milled monolithic aluminum workpieces on part distortions: Experiments and finite element prediction model. Procedia CIRP 2021, 102, 337–342. [Google Scholar]
- Mayer, M.M.; Ott, M.; Wimmer, M.; Hartl, R.; Volk, W.; Zaeh, M.F. Machining-induced distortion during peripheral milling of high strength aluminum parts. Procedia CIRP 2024, 126, 312–317. [Google Scholar] [CrossRef]
- Mathews, R.; Sunny, S.; Malik, A.; Halley, J. Coupling between inherent and machining-induced residual stresses in aluminum components. Int. J. Mech. Sci. 2022, 213, 106865. [Google Scholar] [CrossRef]
- Li, Y.; Gan, W.; Zhou, W.; Li, D. Review on residual stress and its effects on manufacturing of aluminum alloy structural panels with typical multi-processes. Chin. J. Aeronaut. 2023, 36, 96–124. [Google Scholar] [CrossRef]
- Viprey, F.; Fromentin, G.; Maurel, C.; Dorlin, T.; Karaouni, H. Effect of surface integrity on Inconel 718 thin part distortion during finish flank milling. Procedia CIRP 2024, 123, 107–112. [Google Scholar] [CrossRef]
- Mamane, A.I.; Giljean, S.; Pac, M.J.; L’hostis, G. Optimization of the measurement of residual stresses by the incremental hole drilling method. part I: Numerical correction of experimental errors by a configurable numerical–experimental coupling. Compos. Struct. 2022, 294, 115703. [Google Scholar] [CrossRef]
- Lu, W.; Chen, X.; Ho, D.C.W.; Wang, H. A novel analytical model for predicting the thin-walled workpiece deformation considering the effect of residual stress accumulation and redistribution in layer by layer milling. J. Manuf. Process. 2025, 141, 1444–1462. [Google Scholar] [CrossRef]
- Chighizola, C.R.; D’elia, C.R.; Weber, D.; Kirsch, B.; Aurich, J.C.; Linke, B.S.; Hill, M.R. Intermethod comparison and evaluation of measured near surface stress in milled aluminum. Exp. Mech. 2021, 61, 1309–1322. [Google Scholar] [CrossRef]
- Peral, D.; Correa, C.; Diaz, M.; Porro, J.; de Vicente, J.; Ocaña, J. Measured strains correction for eccentric holes in the determination of non-uniform residual stresses by the hole drilling strain gauge method. Mater. Des. 2017, 132, 302–313. [Google Scholar] [CrossRef]
- Nau, A.; Scholtes, B. Evaluation of the high-speed drilling technique for the incremental hole-drilling method. Exp. Mech. 2013, 53, 531–542. [Google Scholar]
- Steinzig, M.; Upshaw, D.; Rasty, J. Influence of drilling parameters on the accuracy of hole-drilling residual stress measurements. Exp. Mech. 2014, 54, 1537–1543. [Google Scholar]
- Schajer, G.S. Universal calibration constants for strain gauge hole-drilling residual stress measurements. Exp. Mech. 2022, 62, 351–358. [Google Scholar] [CrossRef]
- ASTM E837–20; Standard Test Method for Determining Residual Stresses by the Hole-Drilling Strain-Gage Method. ASTM International: West Conshohocken, PA, USA, 2020. [CrossRef]
- Wang, Z.; Sun, J.; Liu, L.; Wang, R.; Chen, W. An analytical model to predict the machining deformation of frame parts caused by residual stress. J. Mater. Process. Tech. 2019, 274, 116282. [Google Scholar] [CrossRef]
- Weber, D.; Kirsch, B.; Jonsson, J.E.; D’elia, C.R.; Linke, B.S.; Hill, M.R.; Aurich, J.C. Simulation based compensation techniques to minimize distortion of thin-walled monolithic aluminum parts due to residual stresses. CIRP J. Manuf. Sci. Technol. 2022, 38, 427–441. [Google Scholar] [CrossRef]
- Weber, D.; Kirsch, B.; Chighizola, C.R.; Jonsson, J.E.; D’Elia, C.R.; Linke, B.S.; Hill, M.R.; Aurich, J.C. Finite element simulation combination to predict the distortion of thin walled milled aluminum workpieces as a result of MIRS. In Proceedings of the 2nd International Conference of the DFG International Research Training Group 2057–Physical Modeling for Virtual Manufacturing (iPMVM 2020), Wadern, Germany, 16–18 November 2020; pp. 1–21. [Google Scholar]





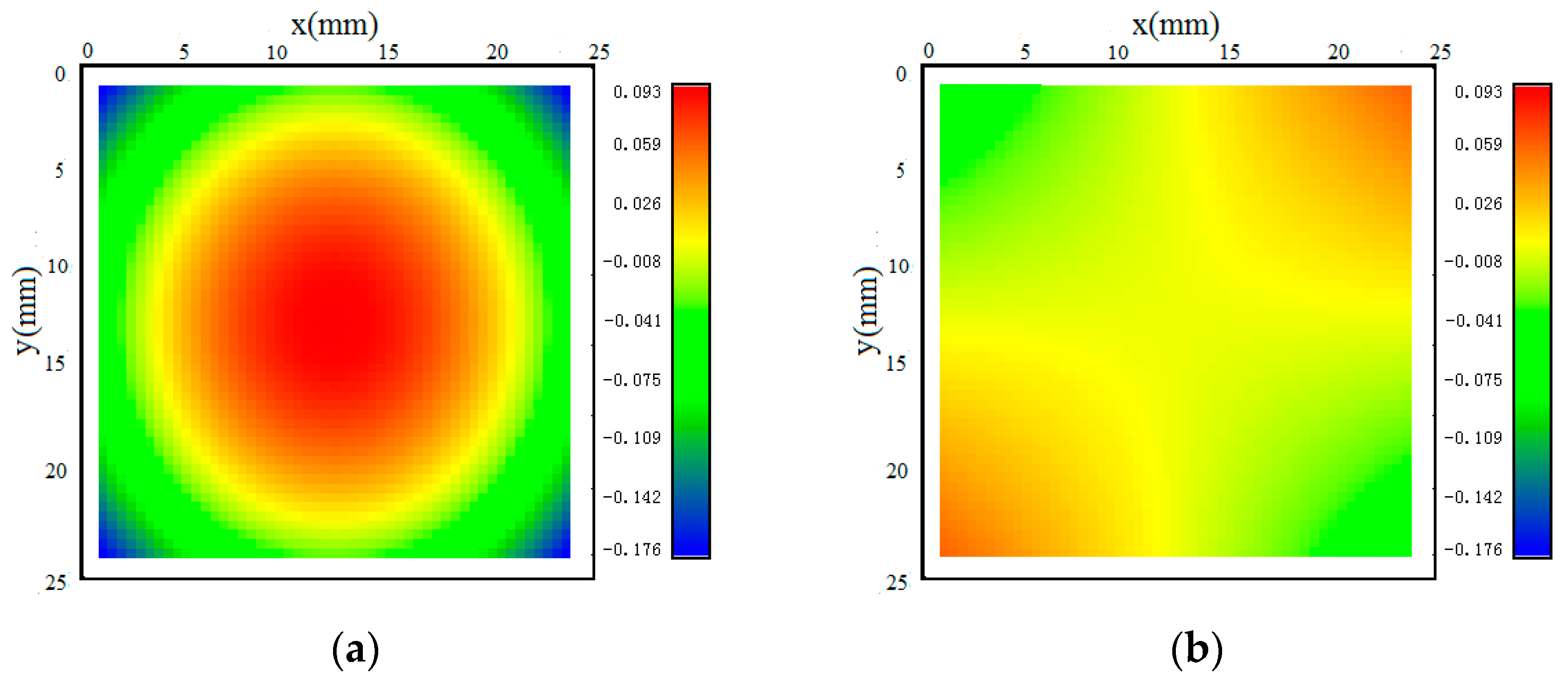


| Serial Number | Rotational Speed, rpm | Tool Diameter, mm | Hole Diameter, mm | Measurement Point Location |
|---|---|---|---|---|
| 1 | 1000 | 1.5 | 2.0 | X1Y1,X1Y2,X1Y3 |
| 2 | 2000 | 1.5 | 2.0 | X2Y1,X2Y2,X2Y3 |
| 3 | 4000 | 1.5 | 2.0 | X3Y1,X3Y2,X3Y3 |
| 4 | 6000 | 1.5 | 2.0 | X4Y1,X4Y2,X4Y3 |
| 5 | 8000 | 1.5 | 2.0 | X5Y1,X5Y2,X5Y3 |
| 6 | 10,000 | 1.5 | 2.0 | X6Y1,X6Y2,X6Y3 |
| 7 | 15,000 | 1.5 | 2.0 | X1Y1,X1Y2,X1Y3 |
| 8 | 20,000 | 1.5 | 2.0 | X2Y1,X2Y2,X2Y3 |
| 9 | 25,000 | 1.5 | 2.0 | X3Y1,X3Y2,X3Y3 |
| 10 | 30,000 | 1.5 | 2.0 | X4Y1,X4Y2,X4Y3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, J.; He, H.; Li, C.; Yi, Y.; Huang, S. Influence of Rotational Speed on Accuracy in Measuring MIRS of Aerospace Aluminum Alloy by Incremental Hole-Milling Method. Materials 2025, 18, 1582. https://doi.org/10.3390/ma18071582
Shen J, He H, Li C, Yi Y, Huang S. Influence of Rotational Speed on Accuracy in Measuring MIRS of Aerospace Aluminum Alloy by Incremental Hole-Milling Method. Materials. 2025; 18(7):1582. https://doi.org/10.3390/ma18071582
Chicago/Turabian StyleShen, Junbo, Hailin He, Chen Li, Youping Yi, and Shiquan Huang. 2025. "Influence of Rotational Speed on Accuracy in Measuring MIRS of Aerospace Aluminum Alloy by Incremental Hole-Milling Method" Materials 18, no. 7: 1582. https://doi.org/10.3390/ma18071582
APA StyleShen, J., He, H., Li, C., Yi, Y., & Huang, S. (2025). Influence of Rotational Speed on Accuracy in Measuring MIRS of Aerospace Aluminum Alloy by Incremental Hole-Milling Method. Materials, 18(7), 1582. https://doi.org/10.3390/ma18071582





