A Framework for the Estimation of Damping Ratio of Glued–Laminated Buildings by Use of Analysis in the Time Domain
Abstract
1. Introduction
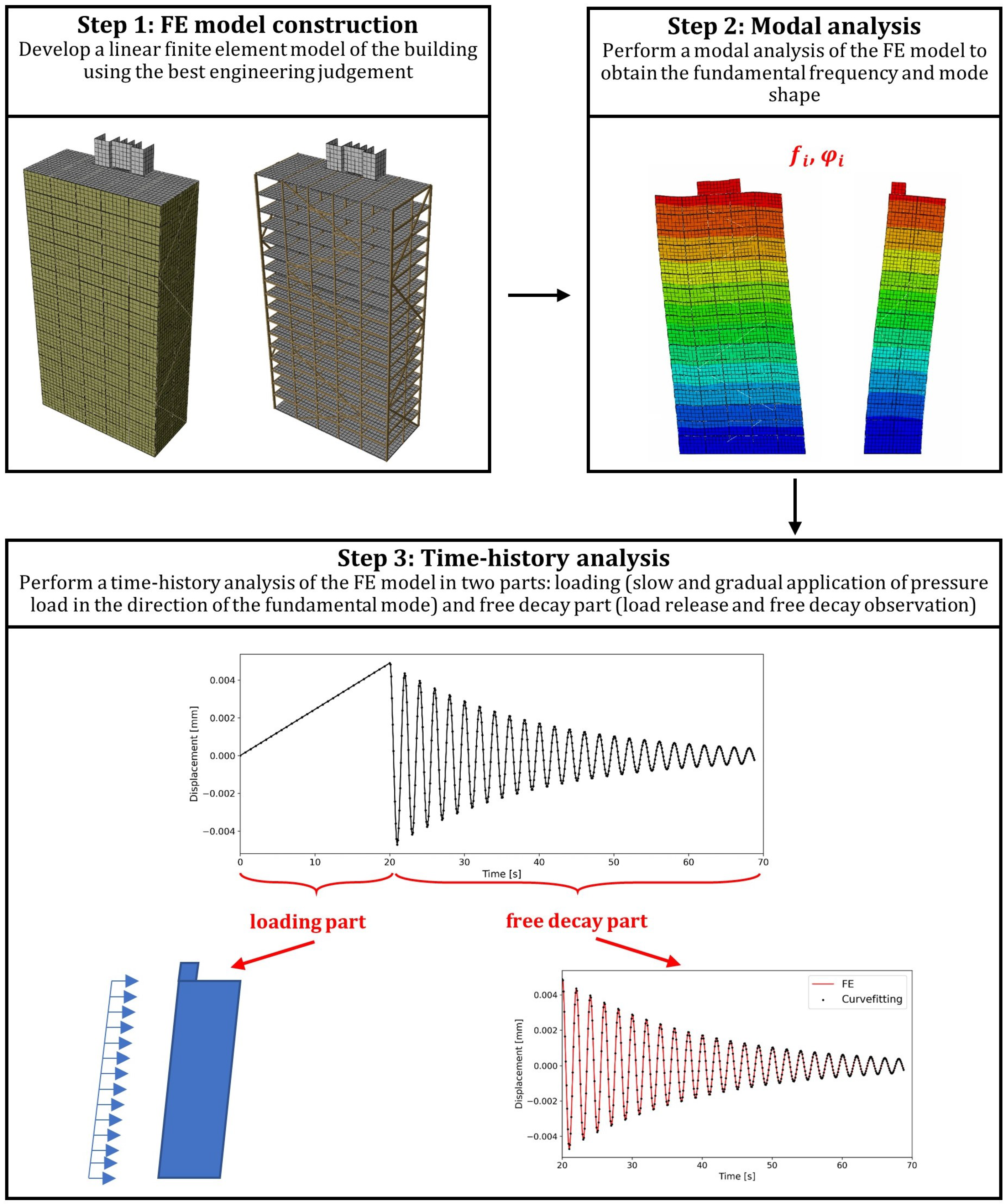
2. Proposed Framework
- Step 1: The framework depends on developing a linear-elastic finite element model. The numerical model should accurately represent the building’s actual design, incorporating the accurate geometry, structural components, and material properties. Stiffness and damping properties shall be assigned to the main timber elements and glulam connections.
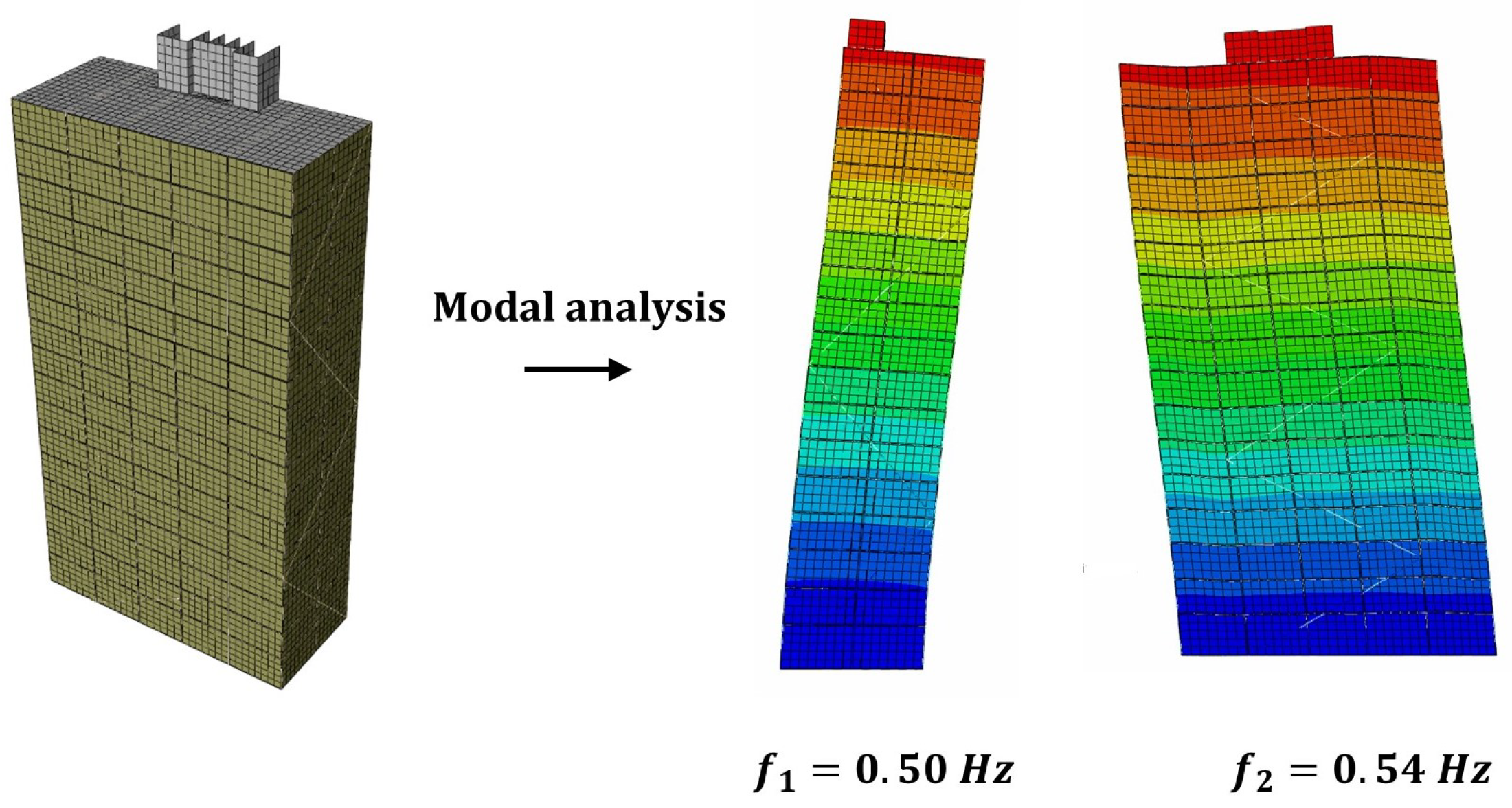
- Step 2: Once an accurate model has been developed, modal analysis is conducted to obtain the structure’s undamped natural frequencies and mode shapes.
- Step 3: The last step is to estimate the structure’s global damping ratio from dynamic analysis in the time domain. The process is carried out in three stages. In the first stage, uniform loading is gradually applied on one face of the structure. Then, in the second stage, the load is released, and the structure is allowed to vibrate freely. Finally, the damping ratio and fundamental frequency of the structure are calculated from free vibrations.
3. Case Study
3.1. Building Description
3.2. Laboratory Tests of Connections
3.3. Field Tests
3.4. Finite Element Modeling
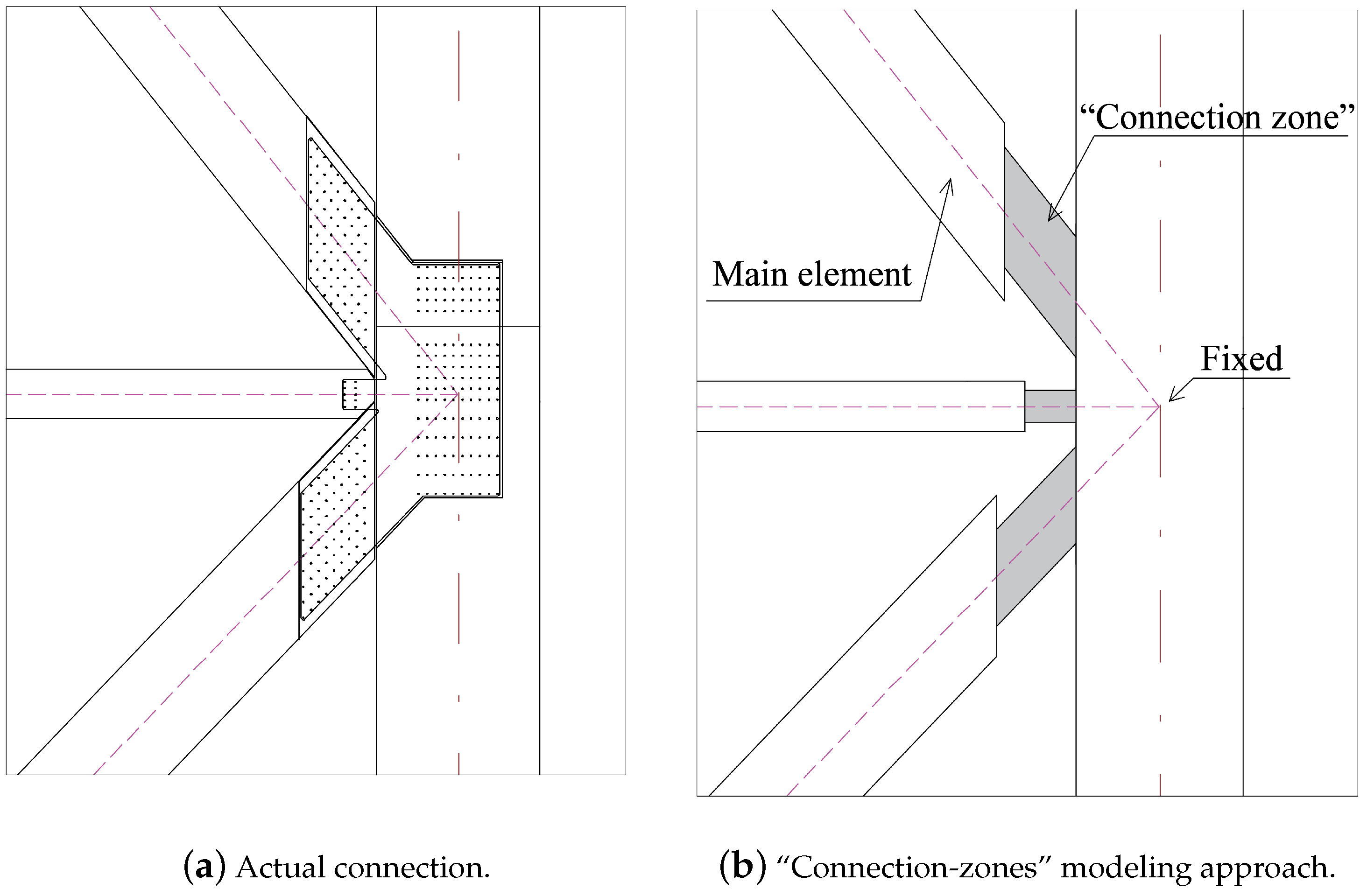
3.4.1. Glulam Connection Modeling
3.4.2. Damping Modeling
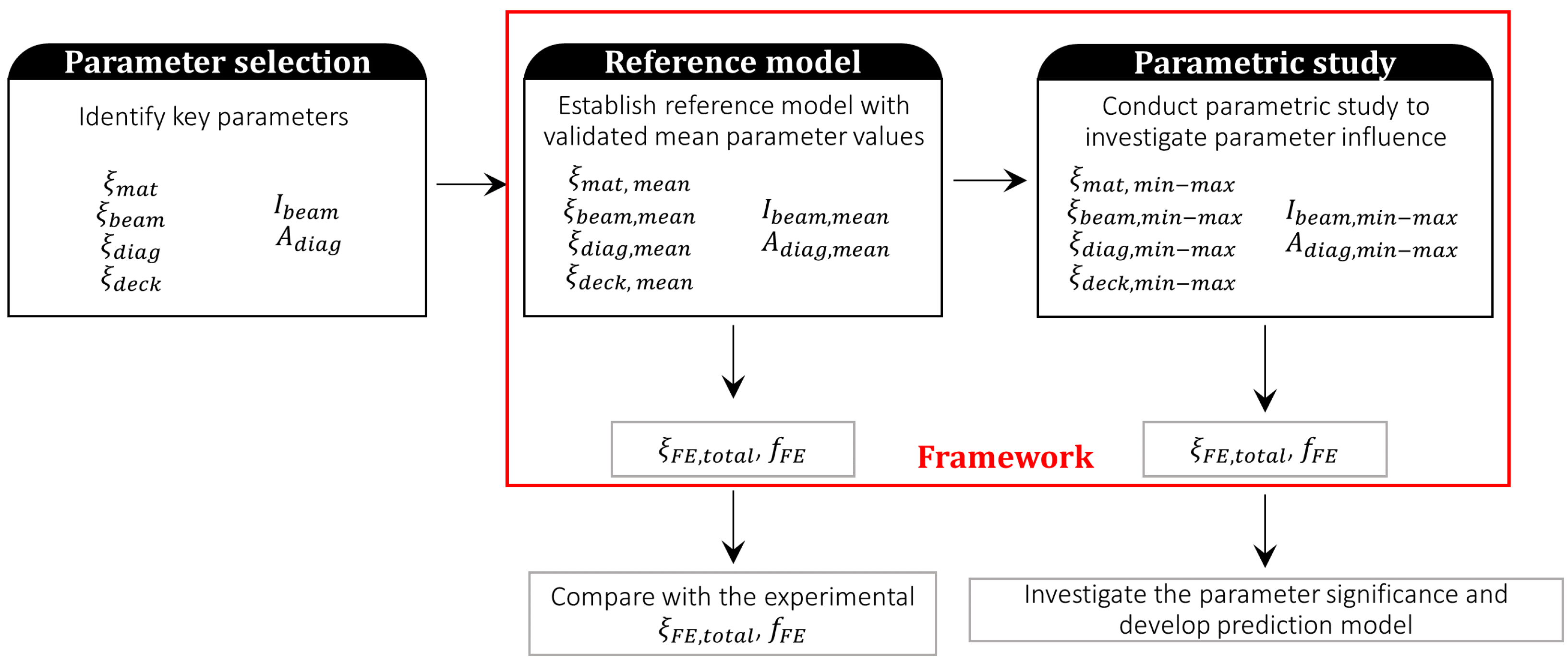
4. Parametric FE Study
4.1. Parameter Selection
4.2. Reference Model
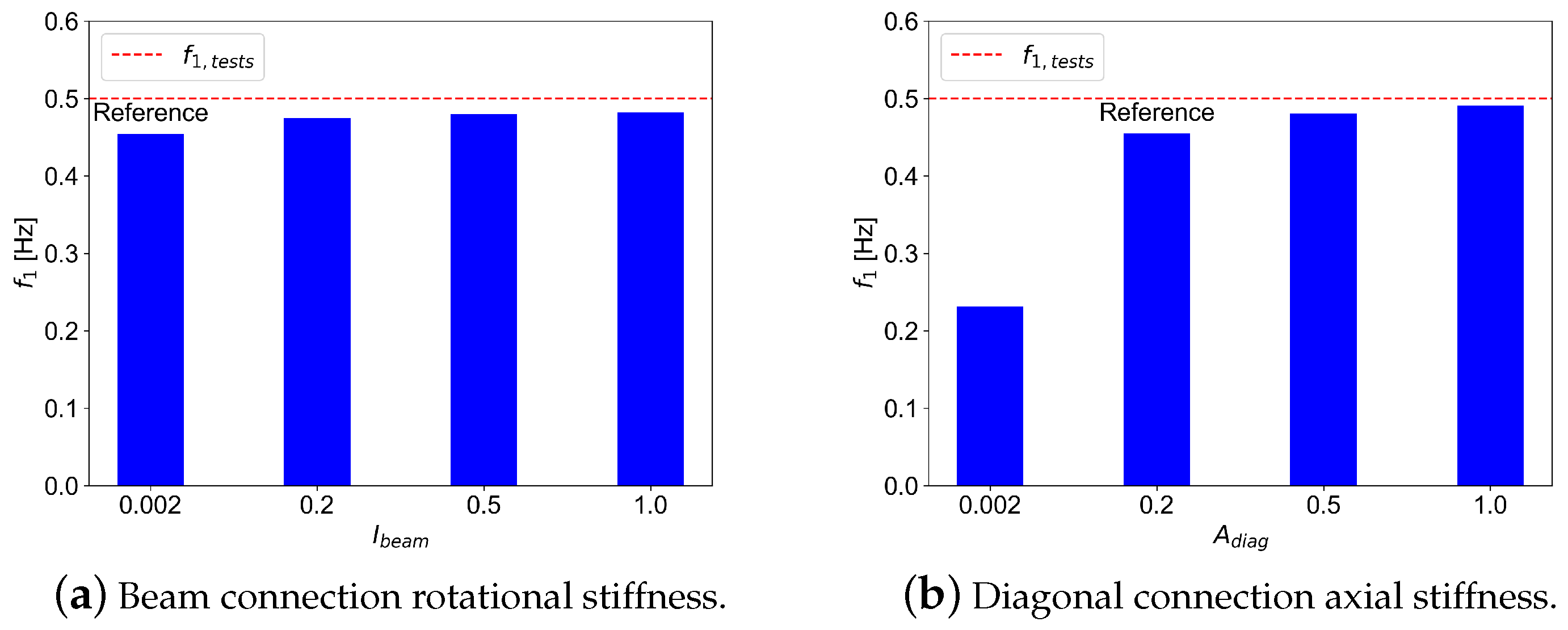
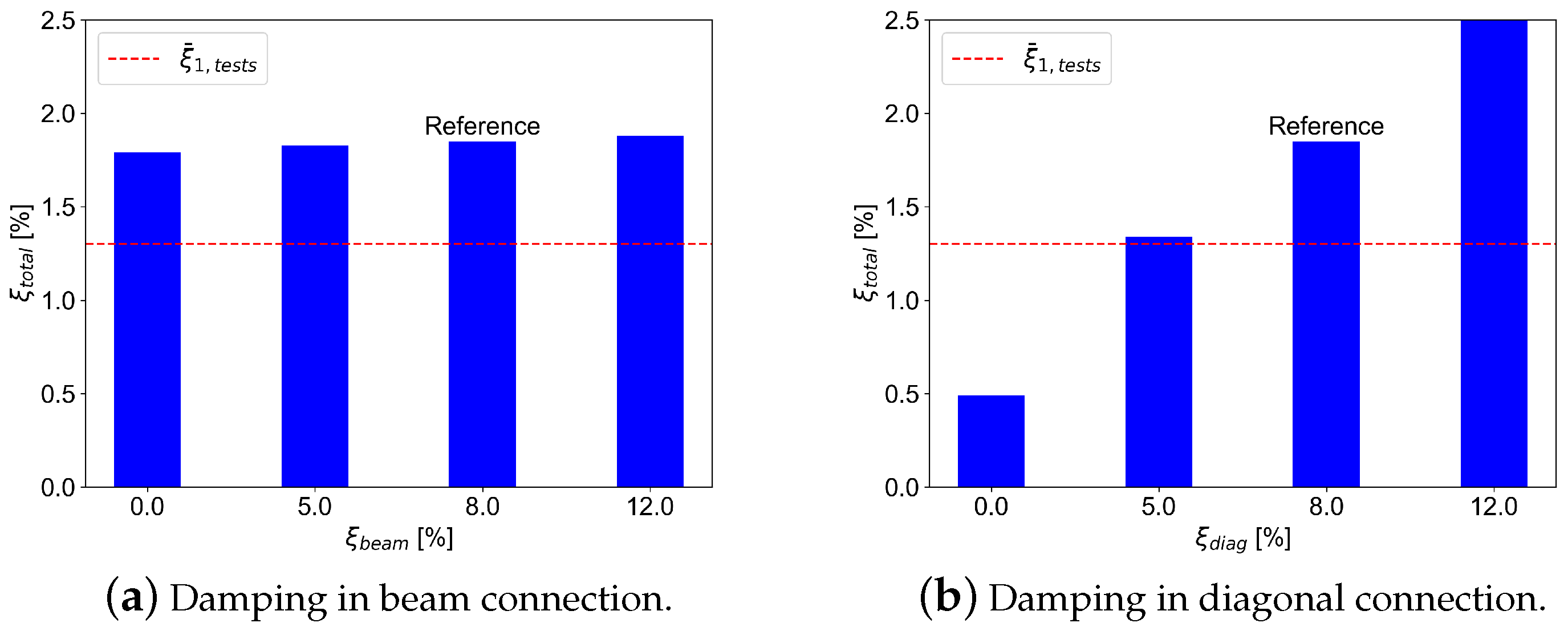
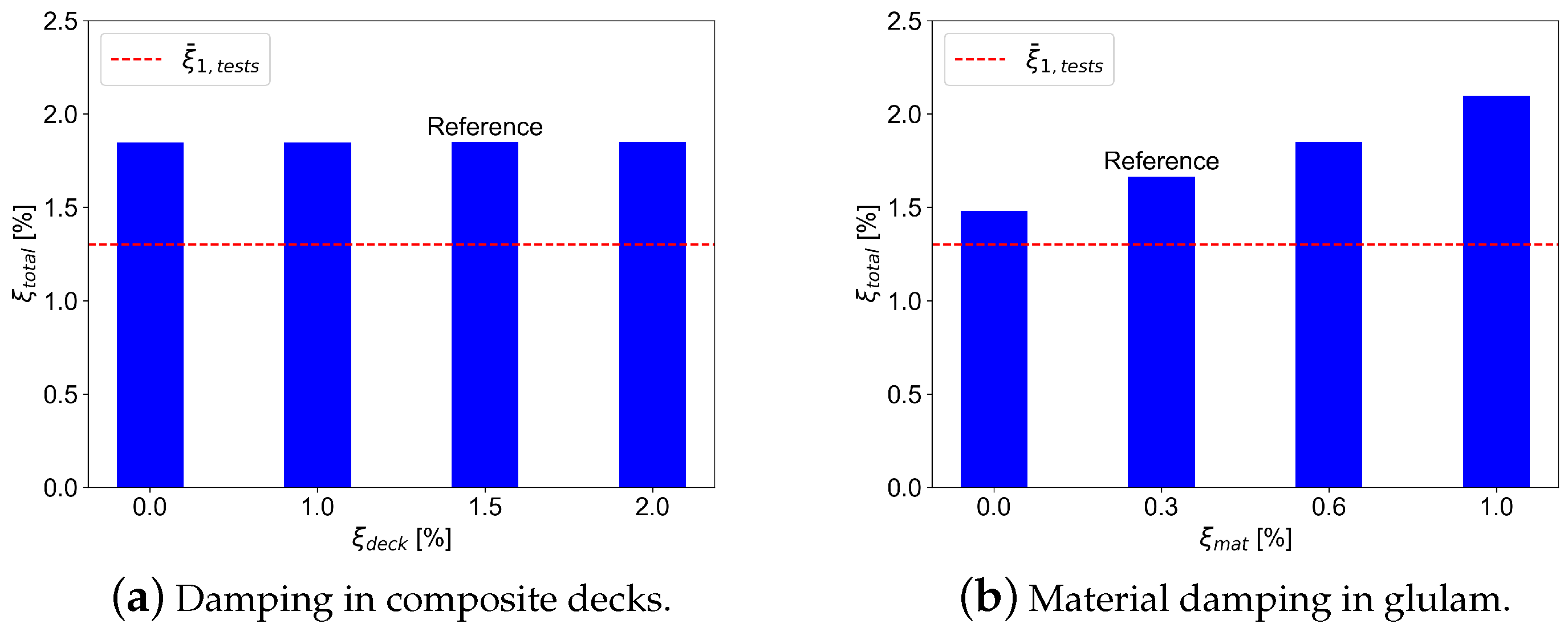
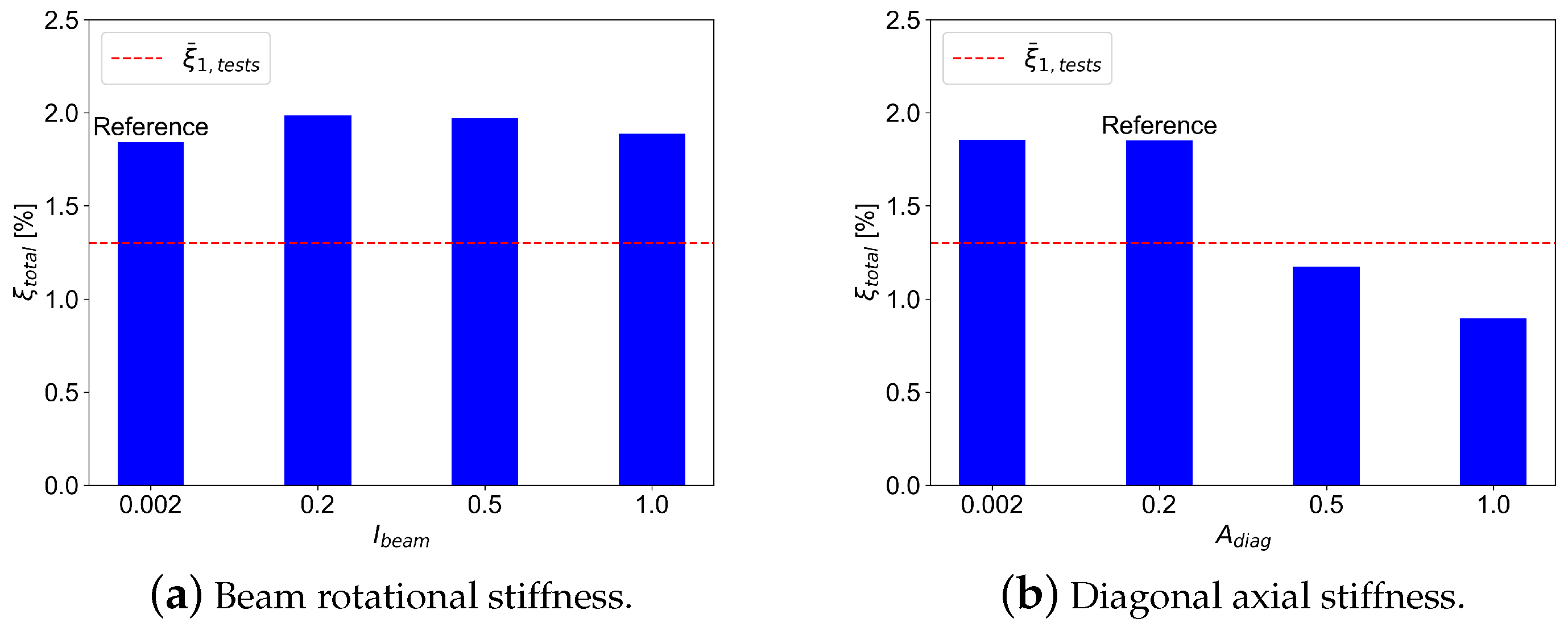
4.3. Parametric Study
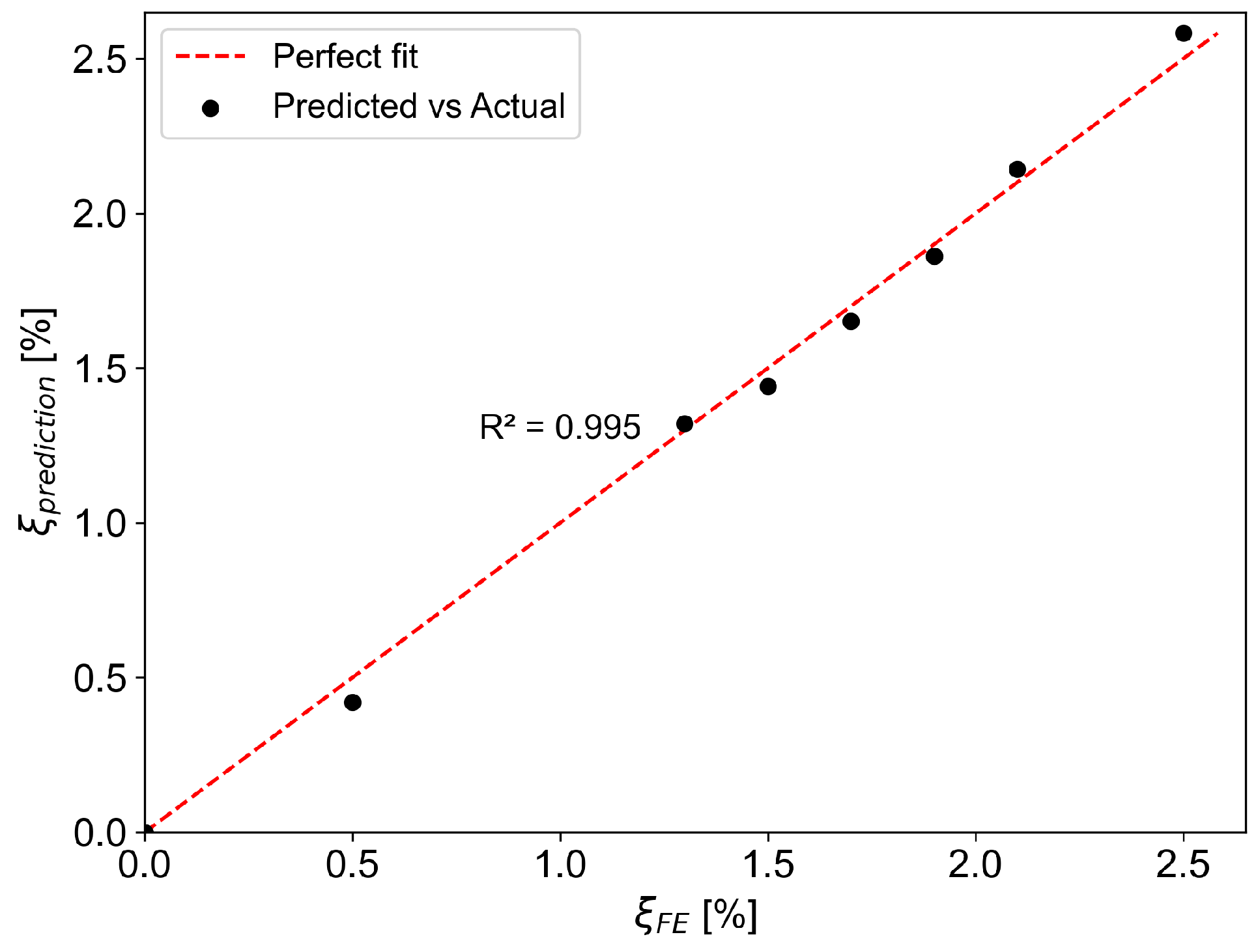
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reynolds, T.; Casagrande, D.; Tomasi, R. Comparison of multi-story cross-laminated timber and timber frame buildings by in situ modal analysis. Constr. Build. Mater. 2016, 102, 1009–1017. [Google Scholar] [CrossRef]
- Feldmann, A.; Huang, H.; Chang, W.S.; Harris, R.; Dietsch, P.; Grafe, M.; Hein, C. Dynamic properties of tall timber structures under wind-induced vibration. In Proceedings of the World Conference on Timber Engineering (WCTE) 2016, Vienna, Austria, 22–25 August 2016. [Google Scholar]
- Ao, W.K.; Pavic, A.; Kurent, B.; Perez, F. Novel FRF-based fast modal testing of multi-storey CLT building in operation using wirelessly synchronised data loggers. J. Sound Vib. 2023, 548, 117551. [Google Scholar] [CrossRef]
- Leyder, C. Monitoring-Based Performance Assessment of an Innovative Timber-Hybrid Building. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2018. [Google Scholar]
- Tulebekova, S.; Ao, W.K.; Pavic, A.; Malo, K.A.; Rønnquist, A. Identification of Modal Properties of a Tall Glue-Laminated Timber Frame Building under Long-Term Ambient Vibrations and Forced Vibrations. J. Struct. Eng. 2024, 150, 04024125. [Google Scholar] [CrossRef]
- Edskar, I. Modal Analysis, Dynamic Properties and Horizontal Stabilisation of Timber Buildings. Ph.D. Thesis, Lulea University of Technology, Lulea, Sweden, 2018. [Google Scholar]
- Mugabo, I.; Barbosa, A.R.; Riggio, M. Dynamic characterization and vibration analysis of a four-story mass timber building. Front. Built Environ. 2019, 5, 86. [Google Scholar]
- Aloisio, A.; Alaggio, R.; Fragiacomo, M. Equivalent Viscous Damping of Cross-Laminated Timber Structural Archetypes. J. Struct. Eng. 2021, 147, 04021012. [Google Scholar] [CrossRef]
- Kurent, B.; Brank, B.; Ao, W.K. Mode updating of seven-storey cross-laminated timber building designed on frequency-response-functions-based modal testing. Struct. Infrastruct. Eng. 2021, 19, 178–196. [Google Scholar]
- Tulebekova, S.; Malo, K.A.; Rønnquist, A.; Nåvik, P. Modeling stiffness of connections and non-structural elements for dynamic response of taller glulam timber frame buildings. Eng. Struct. 2022, 261, 114209. [Google Scholar]
- Cao, S.A.; Stamatopoulos, H. A Theoretical Study of the Dynamic Response of Planar Timber Frames with Semi-Rigid Moment-Resisting Connections Subjected to Wind Loads. Eng. Struct. 2021, 240, 112367. [Google Scholar] [CrossRef]
- CEN1991-1-4; Eurocode 1: Actions on Structures. Part 1-4: Wind actions. European Committee for Standardization: Brussels, Belgium, 2002.
- Larsson, C.; Abdeljaber, O.; Bolmsvik, Å.; Dorn, M. Long-term analysis of the environmental effects on the global dynamic properties of a hybrid timber-concrete building. Eng. Struct. 2022, 268, 114726. [Google Scholar]
- Tulebekova, S.; Malo, K.A.; Rønnquist, A.; Nåvik, P. Investigation of Long-Term Modal Properties of a Tall Glue-Laminated Timber Frame Building Under Environmental Variations. In Proceedings of the World Conference on Timber Engineering (WCTE) 2023, Oslo, Norway, 19–22 June 2023. [Google Scholar]
- Aloisio, A.; Pasca, D.P.; Kurent, B.; Tomasi, R. 2025. Long-term continuous dynamic monitoring of an eight-story CLT building. Mech. Syst. Signal Process. 2025, 224, 112094. [Google Scholar] [CrossRef]
- Labonnote, N.; Rønnquist, A.; Malo, K.A. Modified hysteretic damping model applied to Timoshenko timber beams. Comput. Struct. 2013, 121, 22–31. [Google Scholar] [CrossRef]
- Bjerve, J.; Sagerud, E.; Stamatopoulos, H.; Malo, K.A.; Rønnquist, A. Dynamic tests on a long-span, stressed-skin, timber floor. Wood Mater. Sci. Eng. 2023, 18, 1868–1877. [Google Scholar]
- Vilguts, A.; Nesheim, S.Ø.; Stamatopoulos, H.; Malo, K.A. A study on beam-to-column moment-resisting timber connections under service load, comparing full-scale connection testing and mock-up frame assembly. Eur. J. Wood Wood Prod. 2022, 80, 753–770. [Google Scholar]
- Abrahamsen, R. Mjøstårnet—Construction of an 81 m tall timber building. In 23rd International Holzbau-Forum IHF 2017. 2018. Available online: https://www.moelven.com/globalassets/moelven-limtre/mjostarnet/mjostarnet—Construction-of-an-81-m-tall-timber-building.pdf (accessed on 1 November 2024).
- Frette, E.; Heggheim, A.; Munkeby, T. An Experimental Investigation of Joints with Dowels and Slotted-In Steel Plates in Glulam Under Service Load. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2021. [Google Scholar]
- Council on Tall Buildings and Urban Habitat. Tallest All-Timber Building in the World. 2019. Available online: https://www.ctbuh.org/buildings-of-distinction/mjostarnet (accessed on 1 November 2024).
- Malo, K.A.; Stamatopoulos, H.; Massaro, F.M.; Tulebekova, S. Serviceability Stiffness of Timber Connections with Dowels and Slotted-in Steel Plates. In Proceedings of the World Conference on Timber Engineering (WCTE) 2023, Oslo, Norway, 19–22 June 2023. [Google Scholar]
- EN1995-1-1; Design of Timber Structures. Part 1–1: General-Common Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- EN14080; Timber Structures—Glued Laminated Timber and Glued Solid Timber—Requirements. European Committee for Standardization: Brussels, Belgium, 2013.
- EN 338; Structural Timber—Strength Classes. European Committee for Standardization: Brussels, Belgium, 2016.
- Chopra, A.K. (Ed.) Dynamics of Structures: Theory and Applications to Earthquake Engineering (SI Units); Pearson Education Limited: London, UK, 2020. [Google Scholar]
- Simulia. Abaqus FEA Software; Dassault Systèmes: Paris, France, 2017. [Google Scholar]



| Frequency [Hz] | Damping Ratio [%] * | |||
|---|---|---|---|---|
| Mode | AVT | FVT | AVT | FVT |
| 1 | 0.50 | 0.50 | 1.10–1.35 | 0.5–2.0 |
| 2 | 0.54 | 0.53 | 1.66–2.00 | 0.5–3.0 |
| 3 | 0.82 | 0.82 | 1.00–1.35 | - |
| Parameter | Experiment/EC | Connection Zone | Range |
|---|---|---|---|
| 2900 kNm/rad | 0.2% | 0.2–100% | |
| 1280 kN/mm | 20% | 0.2–100% |
| Parameter | Reference Value | Range |
|---|---|---|
| 0.6% | 0.3–1.0% | |
| 8% | 5–12.0% | |
| 8% | 5–12.0% | |
| 1.5% | 1.0–2.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tulebekova, S.; Stamatopoulos, H.; Malo, K.A. A Framework for the Estimation of Damping Ratio of Glued–Laminated Buildings by Use of Analysis in the Time Domain. Materials 2025, 18, 1545. https://doi.org/10.3390/ma18071545
Tulebekova S, Stamatopoulos H, Malo KA. A Framework for the Estimation of Damping Ratio of Glued–Laminated Buildings by Use of Analysis in the Time Domain. Materials. 2025; 18(7):1545. https://doi.org/10.3390/ma18071545
Chicago/Turabian StyleTulebekova, Saule, Haris Stamatopoulos, and Kjell A. Malo. 2025. "A Framework for the Estimation of Damping Ratio of Glued–Laminated Buildings by Use of Analysis in the Time Domain" Materials 18, no. 7: 1545. https://doi.org/10.3390/ma18071545
APA StyleTulebekova, S., Stamatopoulos, H., & Malo, K. A. (2025). A Framework for the Estimation of Damping Ratio of Glued–Laminated Buildings by Use of Analysis in the Time Domain. Materials, 18(7), 1545. https://doi.org/10.3390/ma18071545







