AI-Powered Very-High-Cycle Fatigue Control: Optimizing Microstructural Design for Selective Laser Melted Ti-6Al-4V
Abstract
1. Introduction
1.1. Machine Learning for Predicting Fatigue Properties in Additive Manufacturing
1.2. ML-Driven Microstructural Optimization in Titanium and Aluminum Alloys
1.3. ML-Enhanced Design of Fatigue-Resistant Metamaterials
1.4. Integration of ML in Additive Manufacturing for Process Optimization
2. Materials and Methods
2.1. Process Window
2.2. Very High Cycle Fatigue (VHCF) and Ultrasonic Fatigue Testing (USF)
- It performs eigenvalue extraction to calculate the natural frequencies and the corresponding mode shapes of a system.
- It accounts for initial stress and load stiffness effects due to preloads and initial conditions if geometric nonlinearity is included in the base state, allowing small vibrations of a preloaded structure to be modeled.
2.3. Model Build-Up and Training
3. Results and Discussion
3.1. Microstructural Heterogeneity for Strength Variability
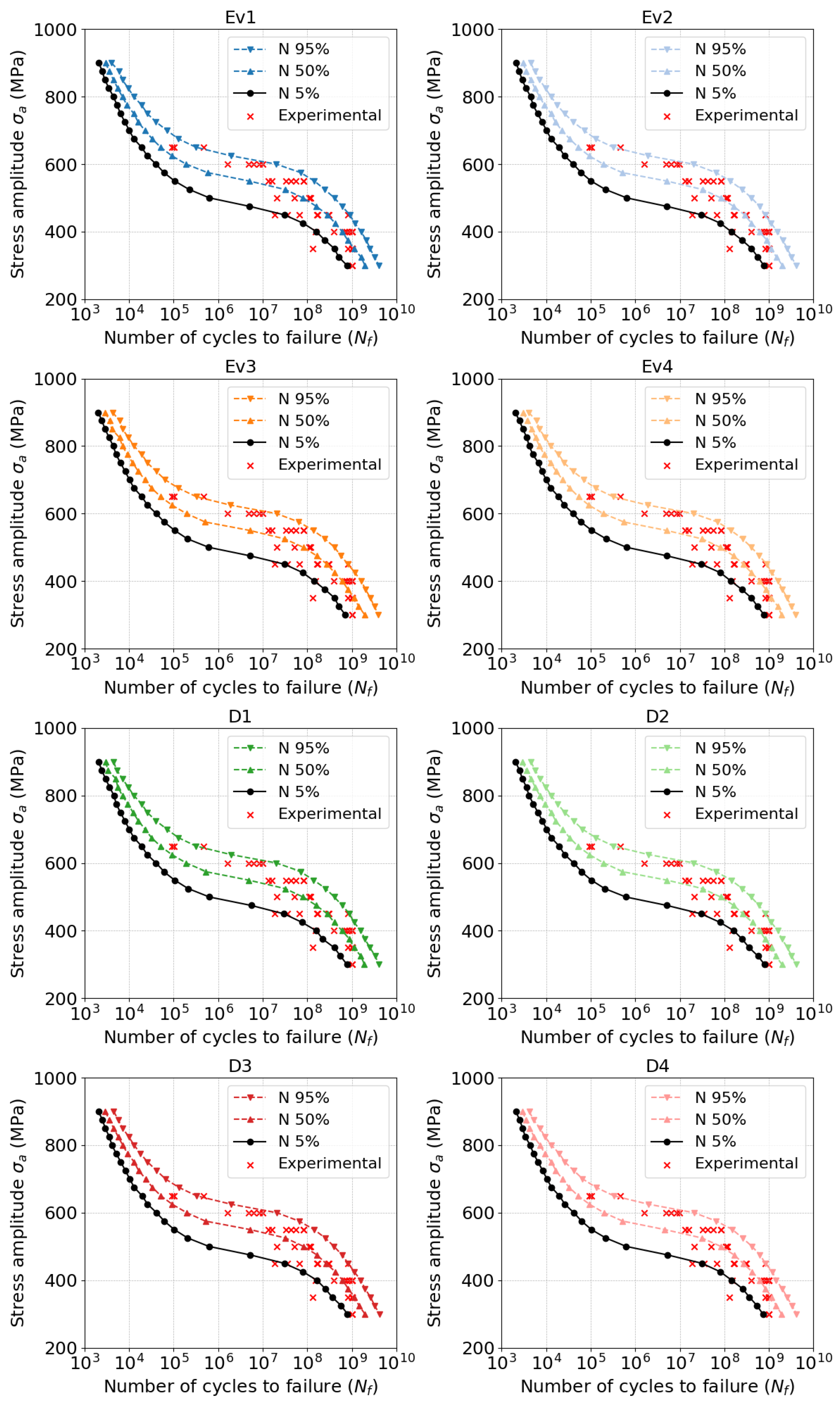
3.2. Model Predictions in VHCF for Different Microstructural Populations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AM | additive manufacturing |
| AI | Artificial Intelligence |
| BCC | Body-Centered Cubic |
| FEA | finite element analysis |
| HCP | Hexagonal Close-Packed |
| ID | internal damping |
| L-PBF | laser powder bed fusion |
| ML | machine learning |
| PDE | partial differential equation |
| PIML | physics-informed machine learning |
| PINN | physics-informed neural network |
| SLM | selective laser melting |
| USF | ultrasonic fatigue |
| VHCF | very high cycle fatigue |
References
- Awd, M. Machine Learning Algorithm for Fatigue Fields in Additive Manufacturing; Reports of Materials Science and Engineering; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2022. [Google Scholar] [CrossRef]
- Awd, M.; Münstermann, S.; Walther, F. Effect of microstructural heterogeneity on fatigue strength predicted by reinforcement machine learning. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 3267–3287. [Google Scholar] [CrossRef]
- Minerva, G.; Awd, M.; Tenkamp, J.; Walther, F.; Beretta, S. Machine learning-assisted extreme value statistics of anomalies in AlSi10Mg manufactured by L-PBF for robust fatigue strength predictions. Mater. Des. 2023, 235, 112392. [Google Scholar] [CrossRef]
- Awd, M.; Labanie, M.F.; Moehring, K.; Fatemi, A.; Walther, F. Towards deterministic computation of internal stresses in additively manufactured materials under fatigue loading: PartI. Materials 2020, 13, 2318. [Google Scholar] [CrossRef] [PubMed]
- Awd, M.; Saeed, L.; Münstermann, S.; Faes, M.; Walther, F. Mechanistic machine learning for metamaterial fatigue strength design from first principles in additive manufacturing. Mater. Des. 2024, 241, 112889. [Google Scholar] [CrossRef]
- Liu, Y.; Adande, S.; Britton, T.B.; Dunne, F.P.E. Cold dwell fatigue analyses integrating crystal-level strain rate sensitivity and microstructural heterogeneity. Int. J. Fatigue 2021, 151, 106398. [Google Scholar] [CrossRef]
- Fitzka, M.; Schönbauer, B.M.; Rhein, R.K.; Sanaei, N.; Zekriardehani, S.; Tekalur, S.A.; Carroll, J.W.; Mayer, H. Usability of ultrasonic frequency testing for rapid generation of high and very high cycle fatigue data. Materials 2021, 14, 2245. [Google Scholar] [CrossRef]
- Mukherjee, T.; Elmer, J.; Wei, H.; Lienert, T.; Zhang, W.; Kou, S.; DebRoy, T. Control of grain structure, phases, and defects in additive manufacturing of high-performance metallic components. Prog. Mater. Sci. 2023, 138, 101153. [Google Scholar] [CrossRef]
- Liu, W.; Huang, J.; Liu, J.; Wu, X.; Zhang, K.; Huang, A. Experimental and crystal plasticity modelling study on the crack initiation in micro-texture regions of Ti-6Al-4V during high cycle fatigue tests. Int. J. Fatigue 2021, 148, 106203. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Pramanik, A.; Basak, A.K.; Dong, Y.; Prakash, C.; Debnath, S.; Shankar, S.; Jawahir, I.S.; Dixit, S.; Buddhi, D. A critical review on additive manufacturing of Ti-6Al-4V alloy: Microstructure and mechanical properties. J. Mater. Res. Technol. 2022, 18, 4641–4661. [Google Scholar] [CrossRef]
- Hua, K.; Wan, Q.; Kou, H.; Zhang, F.; Zhang, Y.; Li, J. The interplay relationship between phase transformation and deformation behavior during hot compression in a metastable β titanium alloy. Mater. Des. 2021, 197, 109275. [Google Scholar] [CrossRef]
- Davis, A.E.; Caballero, A.E.; Biswal, R.; Williams, S.; Prangnell, P.B. Comparison of microstructure refinement in wire-arc additively manufactured Ti-6Al-2Sn-4Zr-2Mo-0.1Si and Ti-6Al-4V built with inter-pass deformation. Metall. Mater. Trans. A 2022, 53, 3833–3852. [Google Scholar] [CrossRef]
- Chen, K.; Fan, Q.; Yang, L.; Yao, J.; Xu, S.; Lei, W.; Gao, Y. Deciphering the microstructural evolution and adiabatic shearing behavior of the titanium alloy with stress-induced ω phase transformation during dynamic compression. Mater. Des. 2022, 221, 110939. [Google Scholar] [CrossRef]
- Schuch, M.; Hahn, T.; Herzig, N.; Bleckmann, M. The Mechanical Behavior and Microstructure of Additively Manufactured Ti6AI4V for Different Material States and Loading Conditions. J. Dyn. Behav. Mater. 2022, 8, 273–284. [Google Scholar] [CrossRef]
- Worsnop, F.F.; Lim, R.E.; Bernier, J.V.; Pagan, D.C.; Xu, Y.; McAuliffe, T.P.; Rugg, D.; Dye, D. The influence of alloying on slip intermittency and the implications for dwell fatigue in titanium. Nat. Commun. 2022, 13, 5949. [Google Scholar] [CrossRef]
- Awd, M.; Walther, F. Machine Learning of Fatigue Strength of Hybrid and Additively Manufactured Aluminum Alloys in VHCF Regime; ASTM International: West Conshohocken, PA, USA, 2023; pp. 262–276. [Google Scholar] [CrossRef]
- Sun, J.; Hensel, J.; Köhler, M.; Dilger, K. Residual stress in wire and arc additively manufactured aluminum components. J. Manuf. Process. 2021, 65, 97–111. [Google Scholar] [CrossRef]
- Böhm, C.; Werz, M.; Weihe, S. Practical approach to eliminate solidification cracks by supplementing AlMg4.5Mn0.7 with AlSi10Mg powder in laser powder bed fusion. Materials 2022, 15, 572. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Lane, R.; Kesler, M.S.; Brechtl, J.; Hu, X.; Mirzaeifar, R.; Rios, O.; Momen, A.M.; Nawaz, K. Experiment and non-local crystal plasticity finite element study of nanoindentation on Al-8Ce-10Mg alloy. Int. J. Solids Struct. 2021, 233, 111233. [Google Scholar] [CrossRef]
- Mason, C.J.T.; Avery, D.Z.; Phillips, B.J.; Jordon, J.B.; Allison, P.G. Strain rate dependent plasticity model for precipitate hardened aerospace aluminum alloy produced with solid-state additive manufacturing. J. Dyn. Behav. Mater. 2022, 8, 214–230. [Google Scholar] [CrossRef]
- Hu, Y.; Wu, S.; Guo, Y.; Shen, Z.; Korsunsky, A.M.; Yu, Y.; Zhang, X.; Fu, Y.; Che, Z.; Xiao, T.; et al. Inhibiting weld cracking in high-strength aluminium alloys. Nat. Commun. 2022, 13, 5816. [Google Scholar] [CrossRef]
- Lvov, V.; Senatov, F.; Stepashkin, A.; Veveris, A.; Pavlov, M.; Komissarov, A. Low-cycle fatigue behavior of 3D-printed metallic auxetic structure. Mater. Today Proc. 2020, 33, 1979–1983. [Google Scholar] [CrossRef]
- Kujawski, D. A new (ΔK+Kmax)0.5 driving force parameter for crack growth in aluminum alloys. Int. J. Fatigue 2001, 23, 733–740. [Google Scholar] [CrossRef]
- Farid, M. Data-driven method for real-time prediction and uncertainty quantification of fatigue failure under stochastic loading using artificial neural networks and Gaussian process regression. Int. J. Fatigue 2022, 155, 106415. [Google Scholar] [CrossRef]
- Salvati, E.; Tognan, A.; Laurenti, L.; Pelegatti, M.; De Bona, F. A defect-based physics-informed machine learning framework for fatigue finite life prediction in additive manufacturing. Mater. Des. 2022, 222, 111089. [Google Scholar] [CrossRef]
- Maleki, E.; Bagherifard, S.; Razavi, S.; Bandini, M.; du Plessis, A.; Berto, F.; Guagliano, M. On the efficiency of machine learning for fatigue assessment of post-processed additively manufactured AlSi10Mg. Int. J. Fatigue 2022, 160, 106841. [Google Scholar] [CrossRef]
- Sahar, T.; Rauf, M.; Murtaza, A.; Khan, L.A.; Ayub, H.; Jameel, S.M.; Ahad, I.U. Anomaly detection in laser powder bed fusion using machine learning: A review. Results Eng. 2023, 17, 100803. [Google Scholar] [CrossRef]
- Wang, H.; Li, B.; Xuan, F.Z. A dimensionally augmented and physics-informed machine learning for quality prediction of additively manufactured high-entropy alloy. J. Mater. Process. Technol. 2022, 307, 117637. [Google Scholar] [CrossRef]
- Falegnami, A.; Tomassi, A.; Gunella, C.; Amalfitano, S.; Corbelli, G.; Armonaite, K.; Fornaro, C.; Giorgi, L.; Pollini, A.; Caforio, A.; et al. Defining conceptual artefacts to manage and design simplicities in complex adaptive systems. Heliyon 2024, 10, e41033. [Google Scholar] [CrossRef]
- Chelikowsky, J.R. Introductory Quantum Mechanics with MATLAB: For Atoms, Molecules, Clusters, and Nanocrystals; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Bouchaud, E.; Jeulin, D.; Prioul, C.; Roux, S. (Eds.) Physical Aspects of Fracture; Springer: Dordrecht, The Netherlands, 2001. [Google Scholar] [CrossRef]
- Stephen, N.G. On energy harvesting from ambient vibration. J. Sound Vib. 2006, 293, 409–425. [Google Scholar] [CrossRef]
- Leonard, R.W.; Barone, A.; Truell, R.; Elbaum, C.; Noltingk, B.E. Akustik II/Acoustics II; Handbuch der Physik/Encyclopedia of Physics; Springer: Berlin/Heidelberg, Germany, 1962; Volume 3/11/2. [Google Scholar] [CrossRef]
- WES 1112; Standard Test Method for Ultrasonic Fatigue Testing of Metallic Materials. Japan Welding Engineering Society (JWES): Tokyo, Japan, 2017.
- Benenson, W. (Ed.) Handbook of Physics; Springer: New York, NY, USA, 2001. [Google Scholar]
- Mote, C.D. Global-local finite element. Int. J. Numer. Methods Eng. 1971, 3, 565–574. [Google Scholar] [CrossRef]
- Zhao, C.; Steven, G.; Xie, Y. A generalized evolutionary method for natural frequency optimization of membrane vibration problems in finite element analysis. Comput. Struct. 1998, 66, 353–364. [Google Scholar] [CrossRef]
- Stewart, J. Calculus, 7th ed.; Brooks/Cole, Cengage Learning: Belmont, CA, USA, 2012. [Google Scholar]
- Ellyin, F. Fatigue Damage, Crack Growth and Life Prediction; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Braga-Neto, U. Fundamentals of Pattern Recognition and Machine Learning; Springer International Publishing: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]
- Hoff, P.D. A First Course in Bayesian Statistical Methods; Springer Texts in Statistics; Springer: London, UK; New York, NY, USA, 2009. [Google Scholar]
- Cuzzolin, F. The Geometry of Uncertainty: The Geometry of Imprecise Probabilities; Artificial Intelligence: Foundations, Theory, and Algorithms; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Xiang, H.; Van Paepegem, W.; Kestens, L.A.I. Study of microstructural morphology of ti-6al-4v alloy by crystallographic analysis and phase field simulation. Materials 2022, 15, 5325. [Google Scholar] [CrossRef]
- Avateffazeli, M. Ultrasonic fatigue of laser beam powder bed fused metals: A state-of-the-art review. Eng. Fail. Anal. 2022, 134, 36. [Google Scholar] [CrossRef]
- Cao, M.; Liu, Y.; Dunne, F.P. A crystal plasticity approach to understand fatigue response with respect to pores in additive manufactured aluminium alloys. Int. J. Fatigue 2022, 161, 106917. [Google Scholar] [CrossRef]
- Hong, Y.; Hu, Y.; Zhao, A. Effects of loading frequency on fatigue behavior of metallic materials—A literature review. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 3077–3098. [Google Scholar] [CrossRef]
- Li, J.; Sun, J.; Qian, G.; Shi, L. Defect-induced cracking and fine granular characteristics in very-high-cycle fatigue of laser powder bed fusion AlSi10Mg alloy. Int. J. Fatigue 2022, 158, 106770. [Google Scholar] [CrossRef]
- Awd, M.; Siddique, S.; Walther, F. Microstructure-Based Assessment of Damage Mechanisms of Selective Laser Melted Al-Si Alloys Under Very High-Cycle Fatigue Loading. In Proceedings of the VHCF8—8th International Conference on Very High Cycle Fatigue, Online, 5–9 July 2021. [Google Scholar]
- Tenkamp, J.; Blinn, B.; Beck, T.; Walther, F. Microstructure- and plasticity-based fatigue and defect tolerance assessment of age-hardenable Al-Si cast alloys in LCF and HCF regime. Int. J. Fatigue 2023, 166, 107240. [Google Scholar] [CrossRef]
- Teixeira, M.; Awd, M.; Walther, F.; Pereira, M. Influence of the Loading Frequency on Very High Cycle Fatigue Behavior of Structural Steels. Fatigue Fract. Eng. Mater. Struct. 2025, 48, 751–763. [Google Scholar] [CrossRef]
- Bayat, M.; Zinovieva, O.; Ferrari, F.; Ayas, C.; Langelaar, M.; Spangenberg, J.; Salajeghe, R.; Poulios, K.; Mohanty, S.; Sigmund, O.; et al. Holistic computational design within additive manufacturing through topology optimization combined with multiphysics multi-scale materials and process modelling. Prog. Mater. Sci. 2023, 138, 101129. [Google Scholar] [CrossRef]
- Dharmadhikari, S.; Menon, N.; Basak, A. A reinforcement learning approach for process parameter optimization in additive manufacturing. Addit. Manuf. 2023, 71, 103556. [Google Scholar] [CrossRef]
- Nammalvar Raja Rajan, A.; Krochmal, M.; Wegener, T.; Biswas, A.; Hartmaier, A.; Niendorf, T.; Moeini, G. Micromechanical modeling of alsi10mg processed by laser-based additive manufacturing: From as-built to heat-treated microstructures. Materials 2022, 15, 5562. [Google Scholar] [CrossRef]
- Schimbäck, D.; Kaserer, L.; Mair, P.; Palm, F.; Leichtfried, G.; Pogatscher, S.; Hohenwarter, A. Deformation and fatigue behaviour of additively manufactured Scalmalloy® with bimodal microstructure. Int. J. Fatigue 2023, 172, 107592. [Google Scholar] [CrossRef]
- Mostafaei, A.; Zhao, C.; He, Y.; Reza Ghiaasiaan, S.; Shi, B.; Shao, S.; Shamsaei, N.; Wu, Z.; Kouraytem, N.; Sun, T.; et al. Defects and anomalies in powder bed fusion metal additive manufacturing. Curr. Opin. Solid State Mater. Sci. 2022, 26, 100974. [Google Scholar] [CrossRef]
- Awd, M.; Walther, F. Influence of fatigue testing frequency on fracture and crack propagation rate in additive manufactured metals using the extended finite element method. Rev. Española Mecánica Fract. 2022, 189–194. [Google Scholar]







| Parameter | Power | Spot Size | Scanning Velocity | Energy Density |
|---|---|---|---|---|
| Ti-6Al-4V Platform-Heated (PH) at 200 °C | ||||
| Batch | () | (; mm/s) | (; mm) | (Ev; J/mm3) |
| Standard | 240 | 1200 | 0.082 | 31.7 |
| 200 | 1000 | 0.082 | 31.7 | |
| 160 | 800 | 0.082 | 31.7 | |
| 120 | 600 | 0.082 | 31.7 | |
| 80 | 400 | 0.082 | 31.7 | |
| 80 | 1200 | 0.082 | 10.6 | |
| 160 | 1200 | 0.082 | 21.2 | |
| 320 | 1200 | 0.082 | 42.3 | |
| 400 | 1200 | 0.082 | 52.9 | |
| 240 | 3600 | 0.082 | 10.6 | |
| 240 | 1800 | 0.082 | 21.2 | |
| 240 | 900 | 0.082 | 42.3 | |
| 240 | 720 | 0.082 | 52.9 | |
| 240 | 1200 | 0.116 | 31.7 | |
| 240 | 1200 | 0.142 | 31.7 | |
| 240 | 1200 | 0.164 | 31.7 | |
| 240 | 1200 | 0.183 | 31.7 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Awd, M.; Walther, F. AI-Powered Very-High-Cycle Fatigue Control: Optimizing Microstructural Design for Selective Laser Melted Ti-6Al-4V. Materials 2025, 18, 1472. https://doi.org/10.3390/ma18071472
Awd M, Walther F. AI-Powered Very-High-Cycle Fatigue Control: Optimizing Microstructural Design for Selective Laser Melted Ti-6Al-4V. Materials. 2025; 18(7):1472. https://doi.org/10.3390/ma18071472
Chicago/Turabian StyleAwd, Mustafa, and Frank Walther. 2025. "AI-Powered Very-High-Cycle Fatigue Control: Optimizing Microstructural Design for Selective Laser Melted Ti-6Al-4V" Materials 18, no. 7: 1472. https://doi.org/10.3390/ma18071472
APA StyleAwd, M., & Walther, F. (2025). AI-Powered Very-High-Cycle Fatigue Control: Optimizing Microstructural Design for Selective Laser Melted Ti-6Al-4V. Materials, 18(7), 1472. https://doi.org/10.3390/ma18071472








