Vibration Characteristics Analysis of Boring Bar with Tunable Dynamic Vibration Absorber
Abstract
1. Introduction
2. Theoretical Model of the Boring Bar
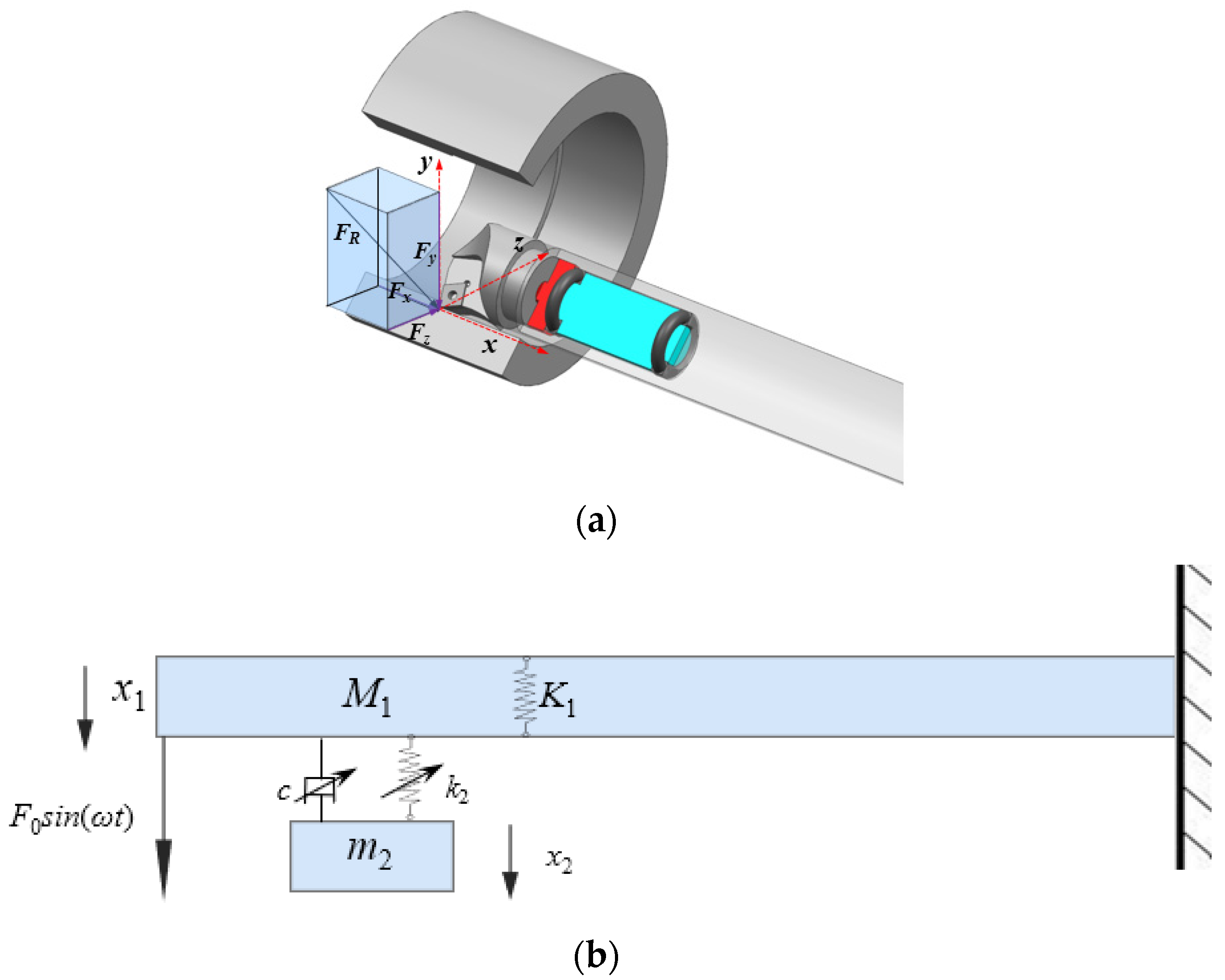
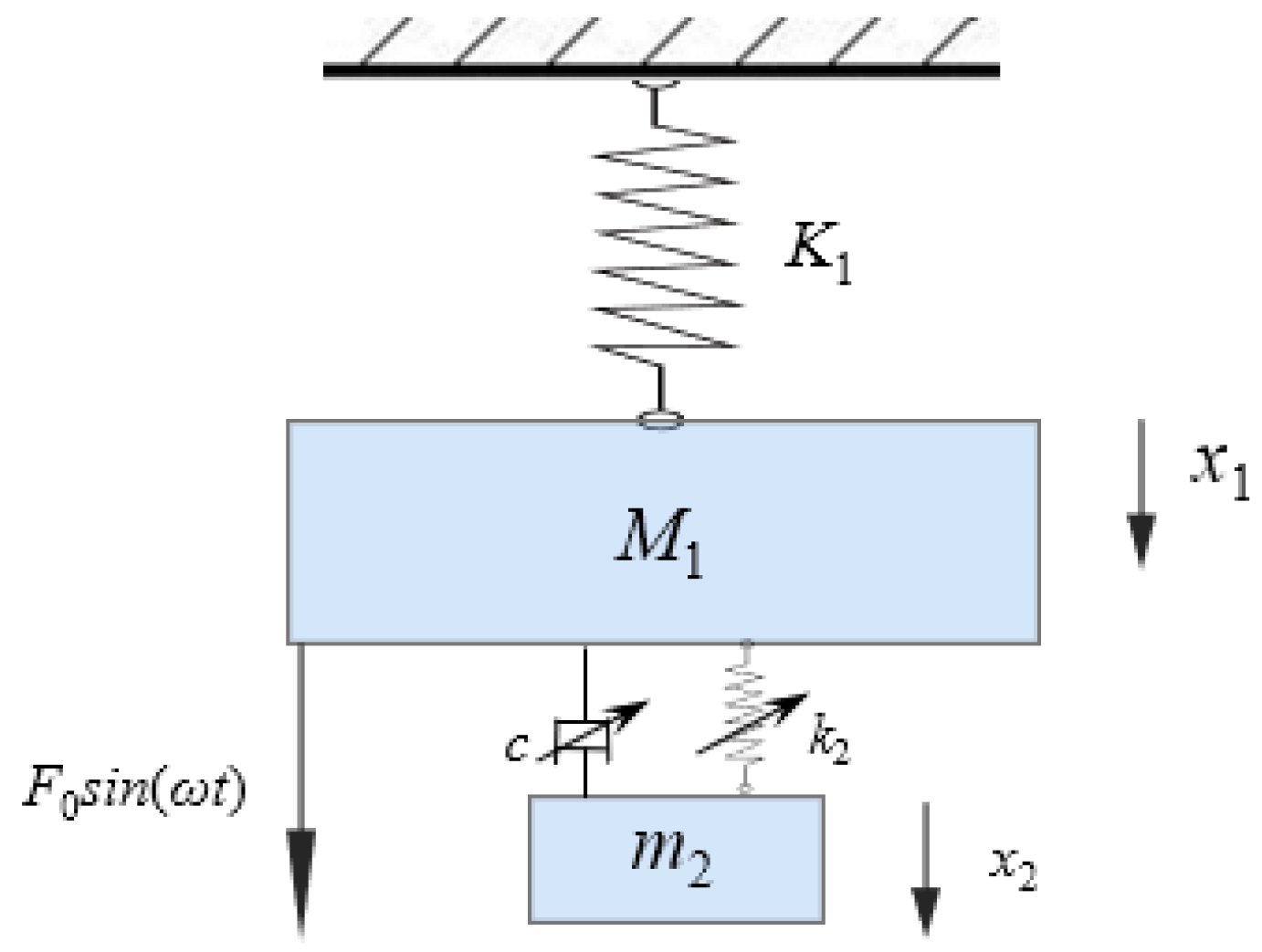
2.1. Vibration Model of Boring Bar
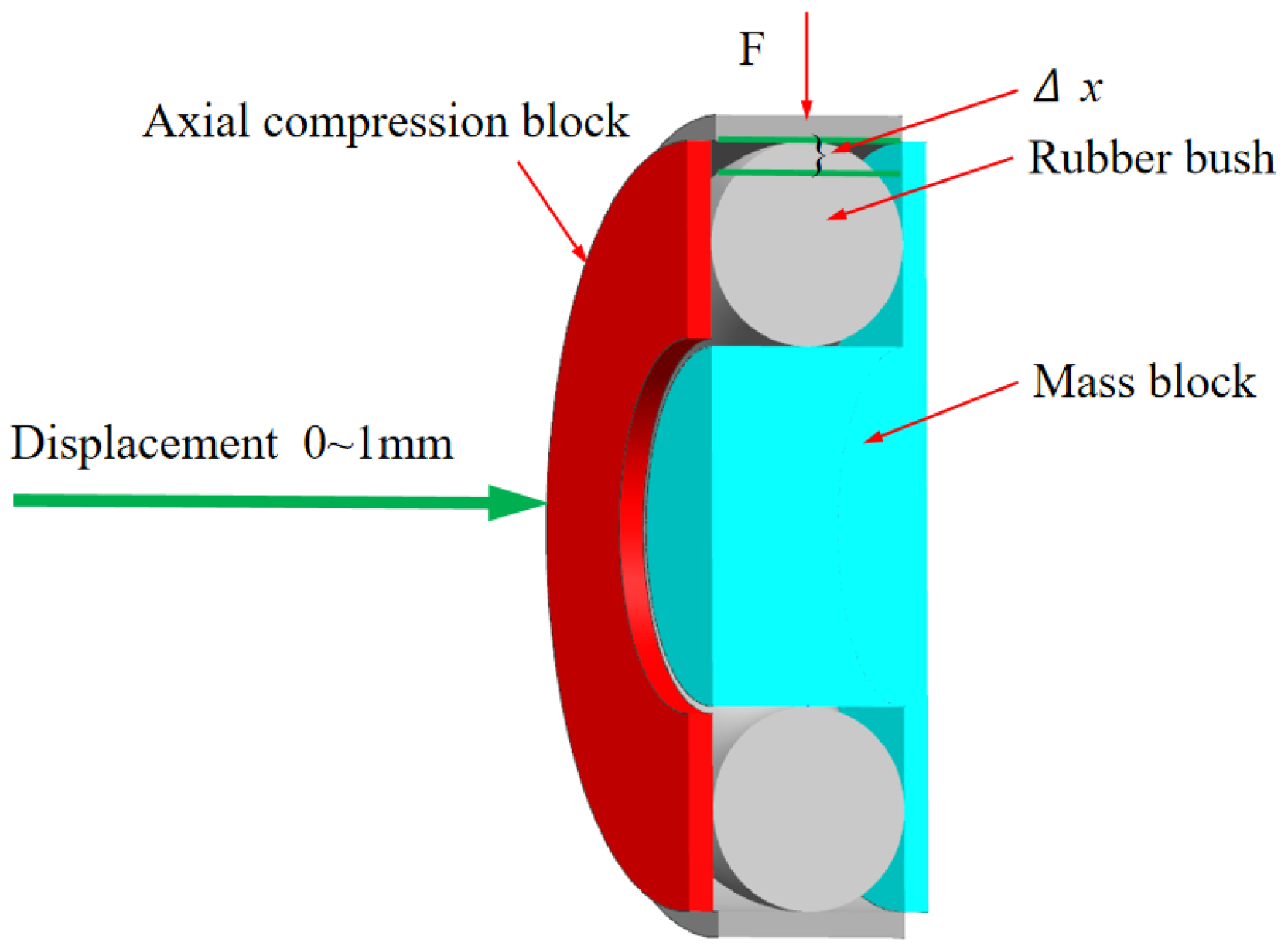
2.2. Design of Variable Parameter Boring Bar Structure
3. Analysis of Vibration Characteristics of Boring Bar
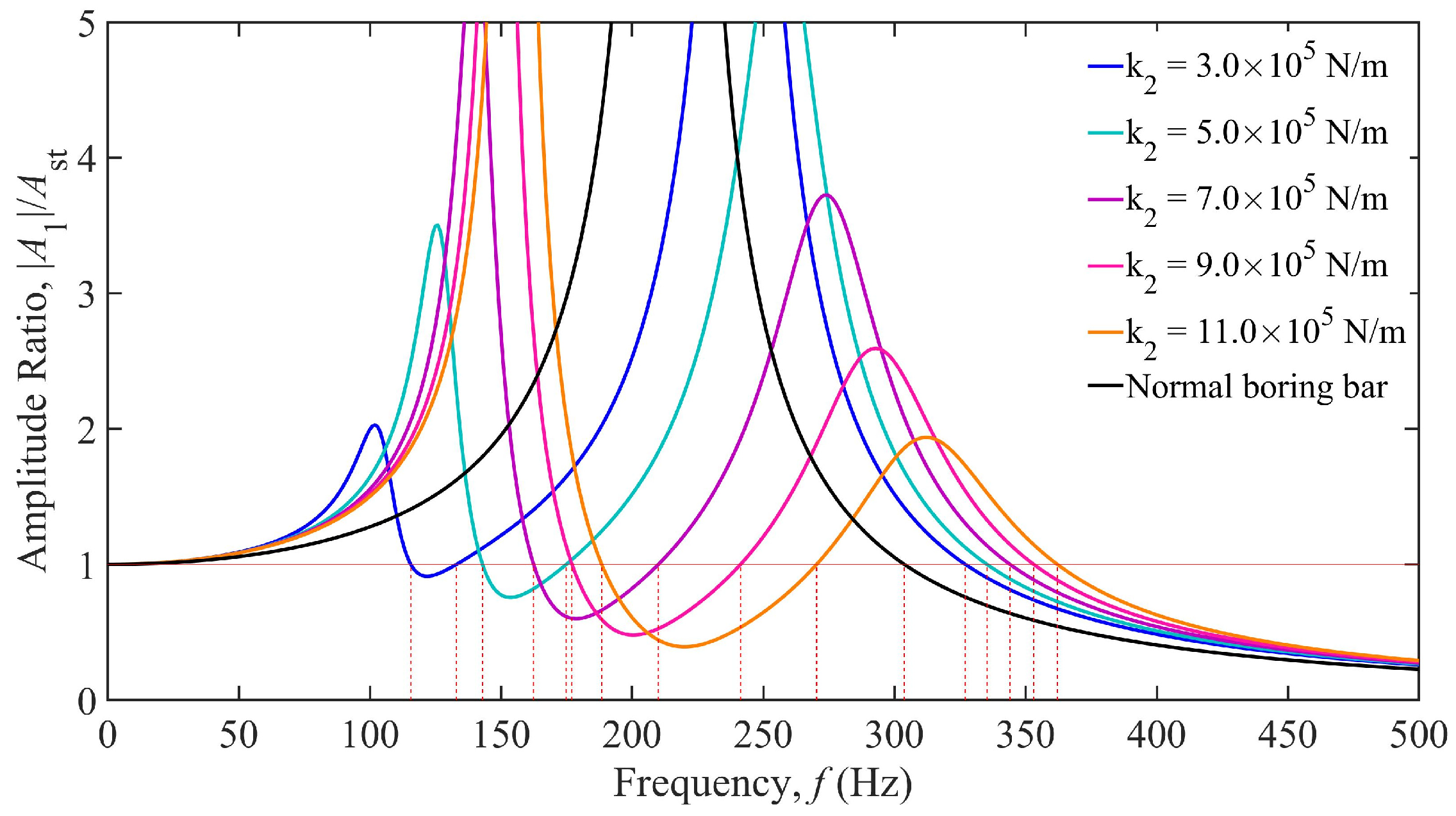
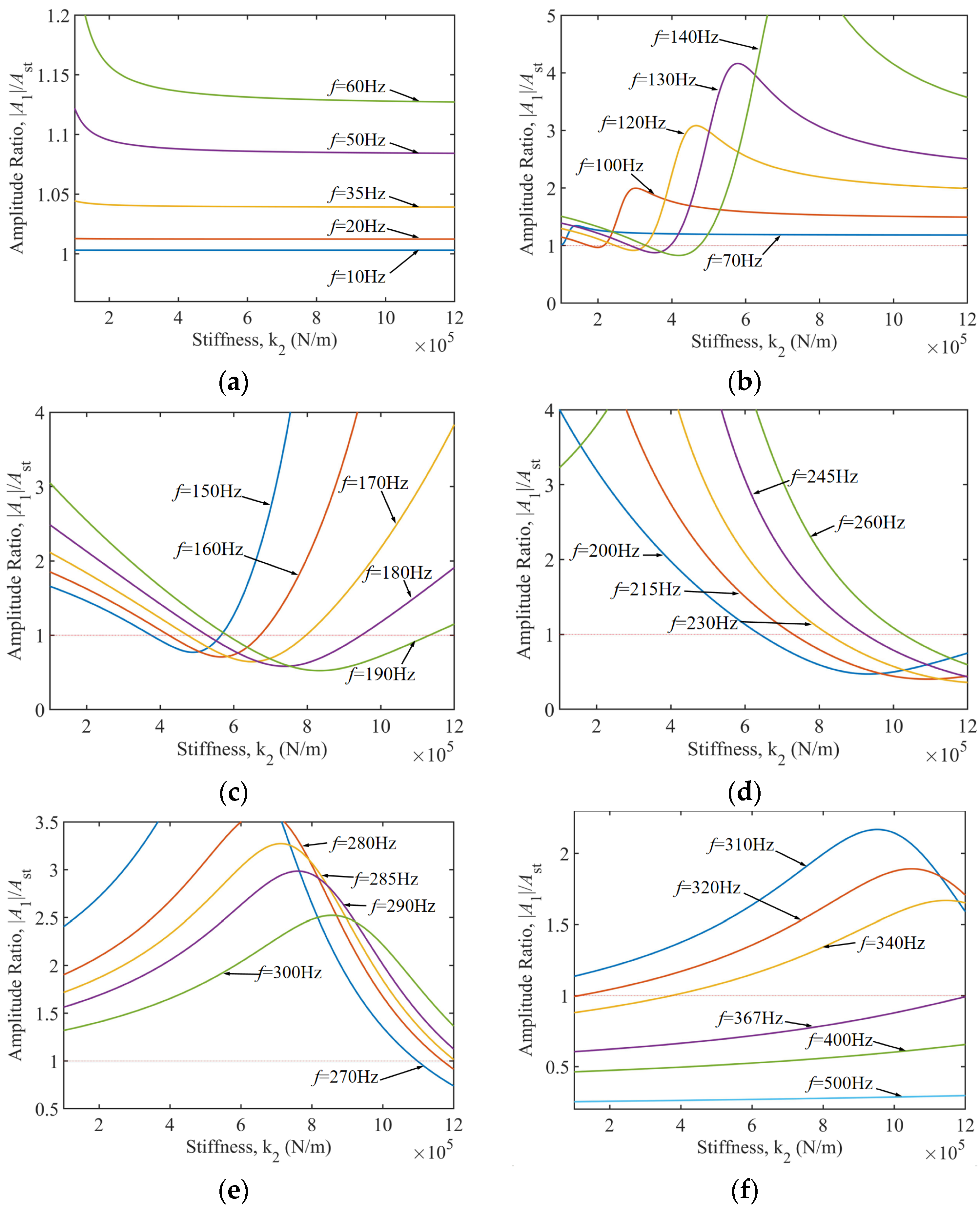
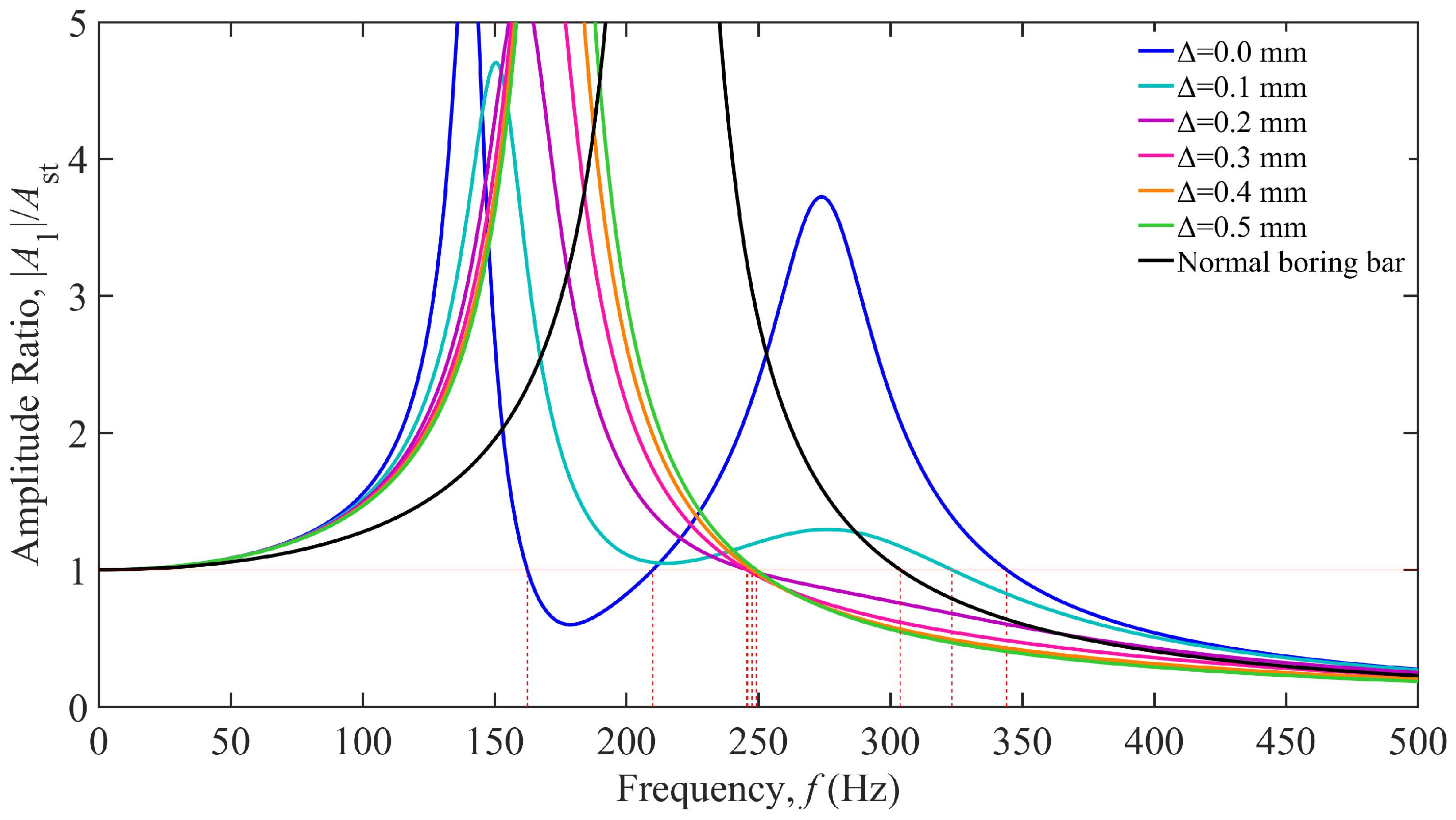
3.1. Influence of TDVA Stiffness on Boring Bar Vibration
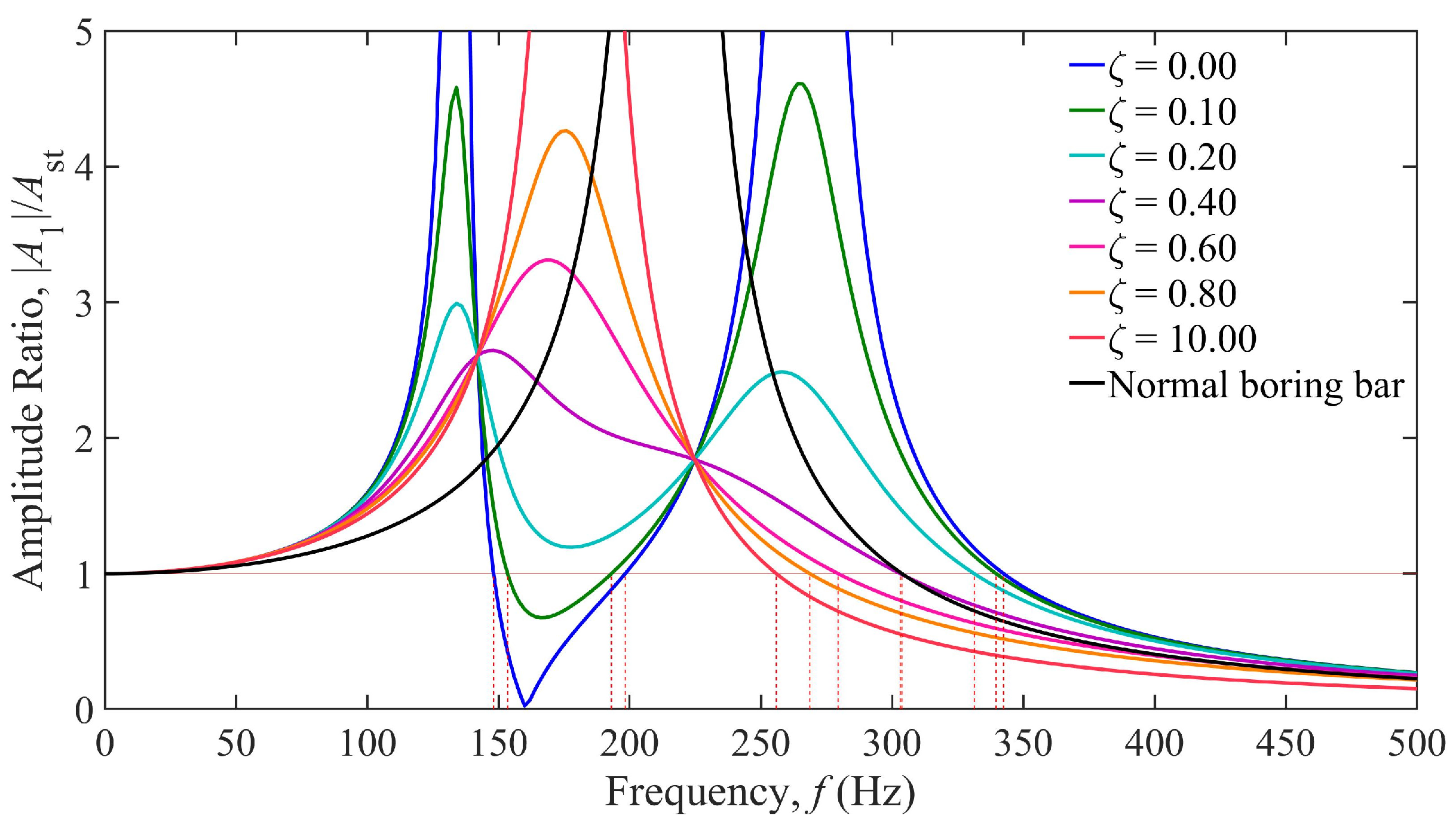
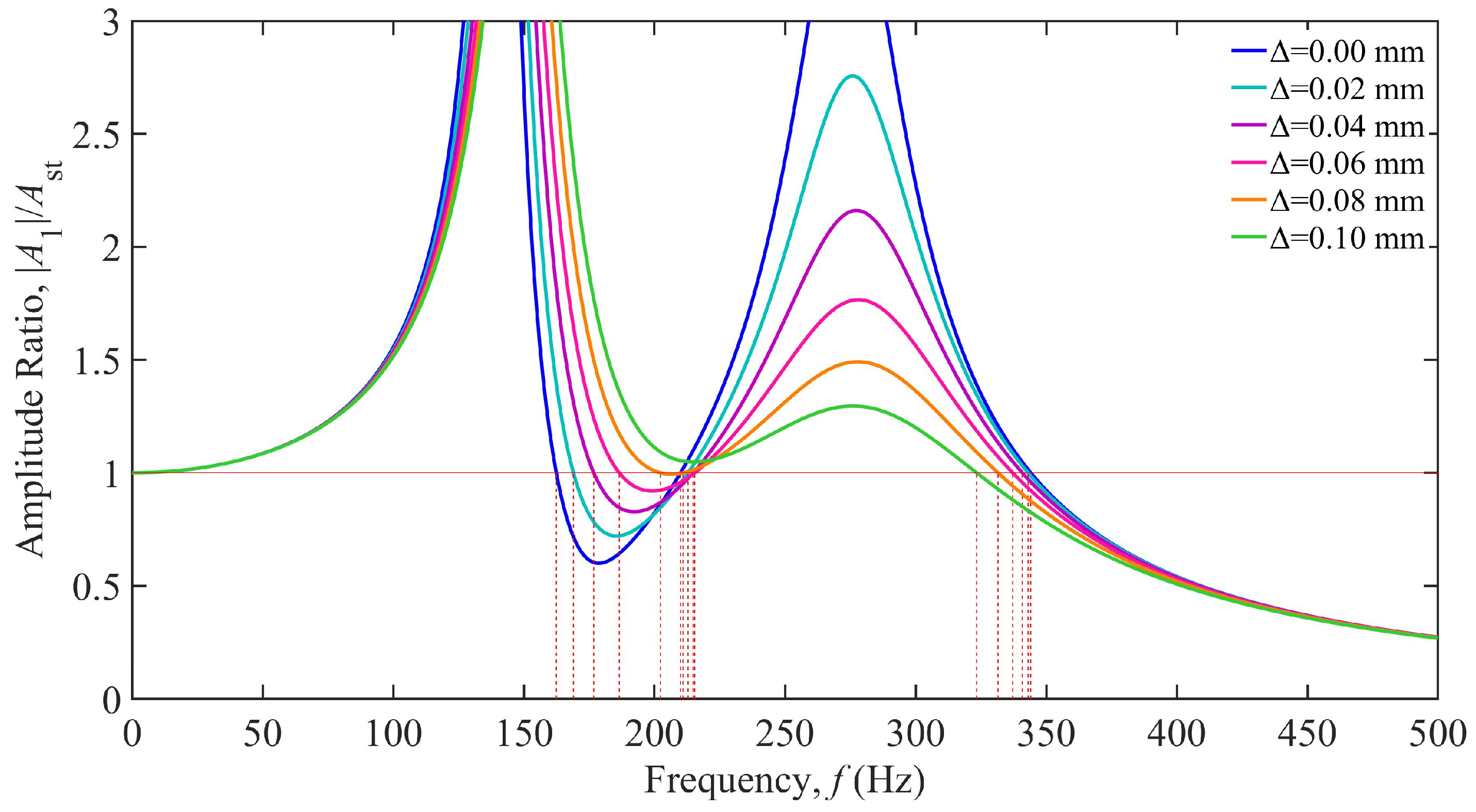
3.2. Influence of TDVA Damping on Boring Bar Vibration
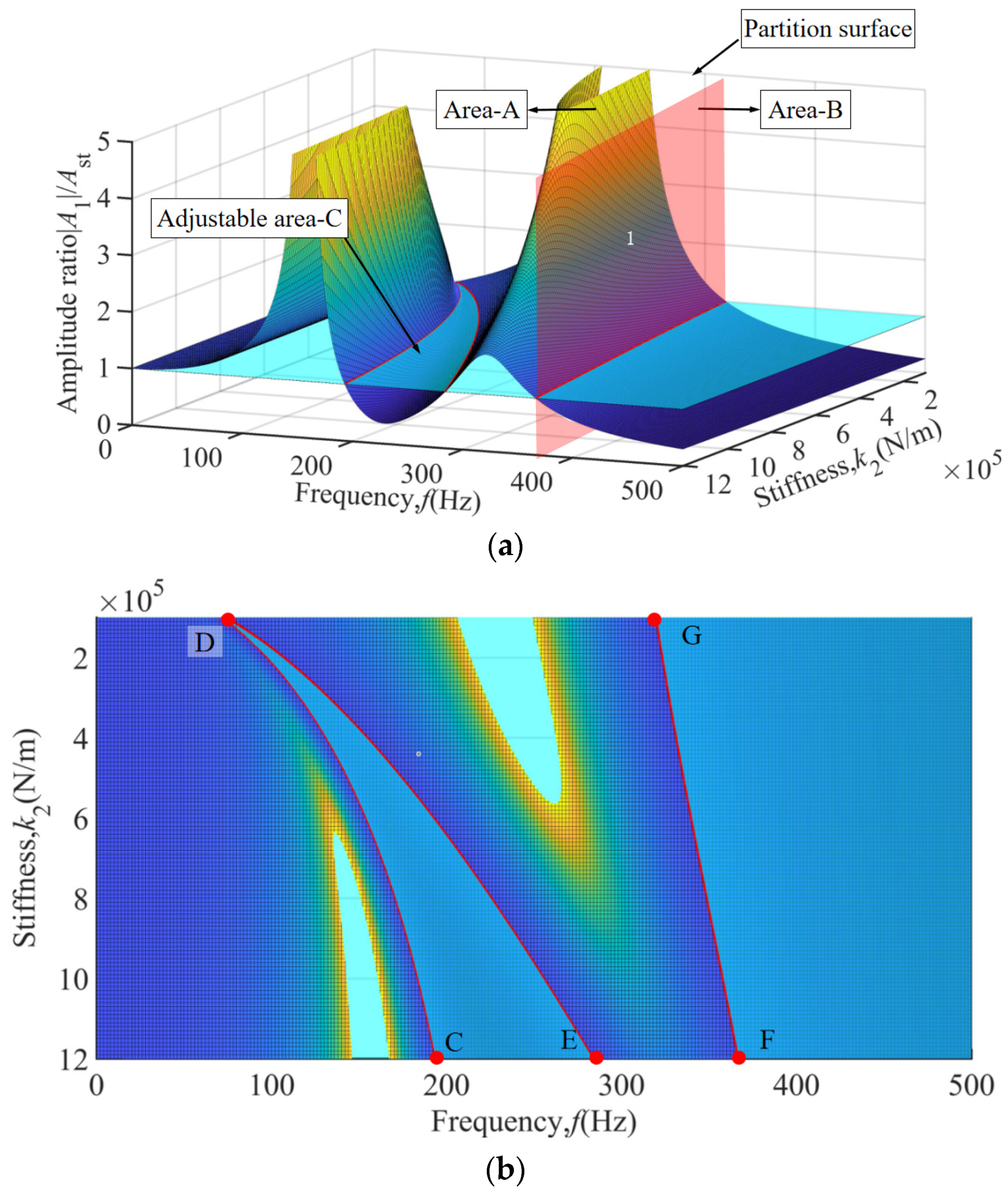
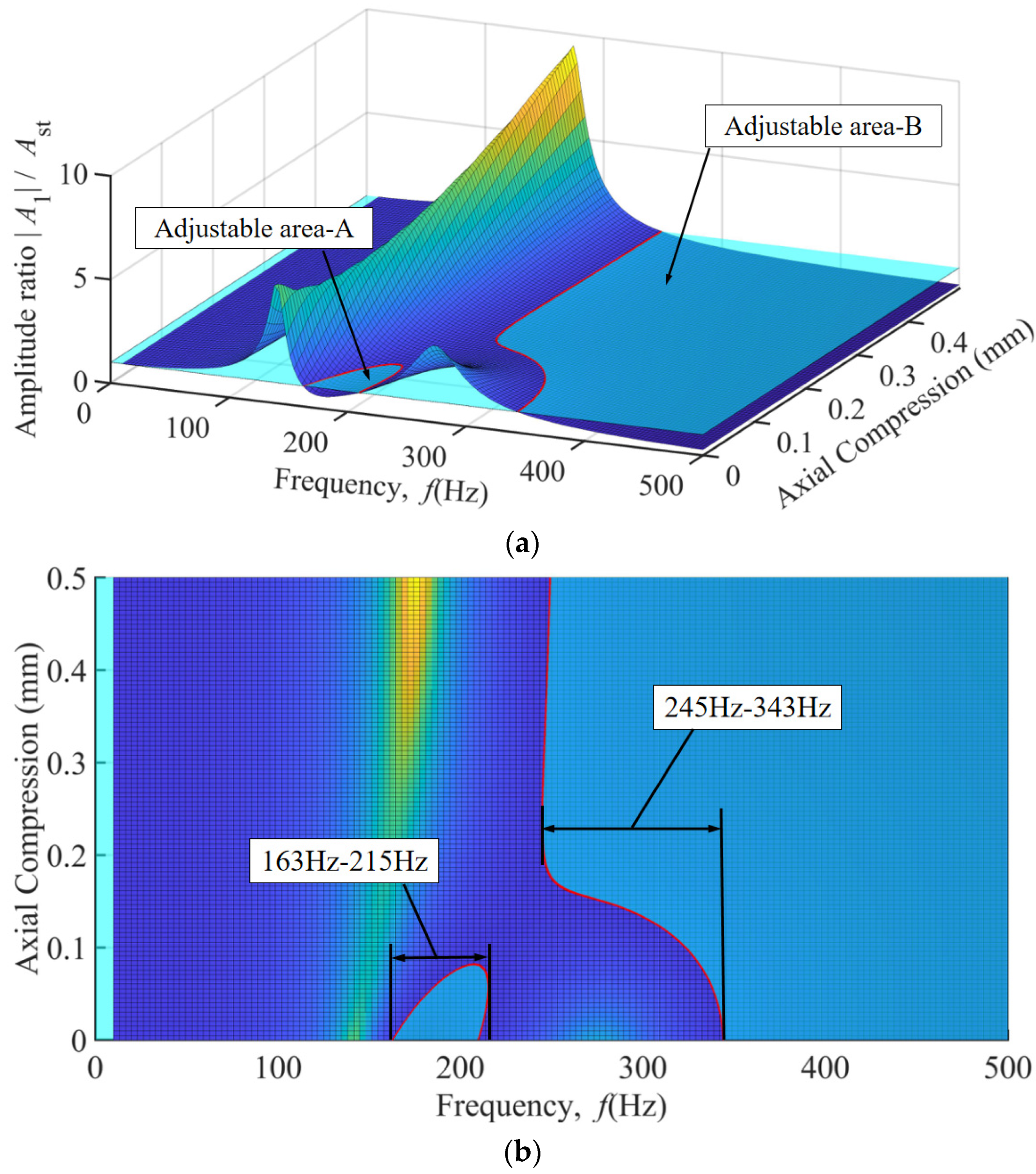
4. Analysis of Boring Bar Vibration Characteristics Under Combined Stiffness–Damping Effects of TDVA
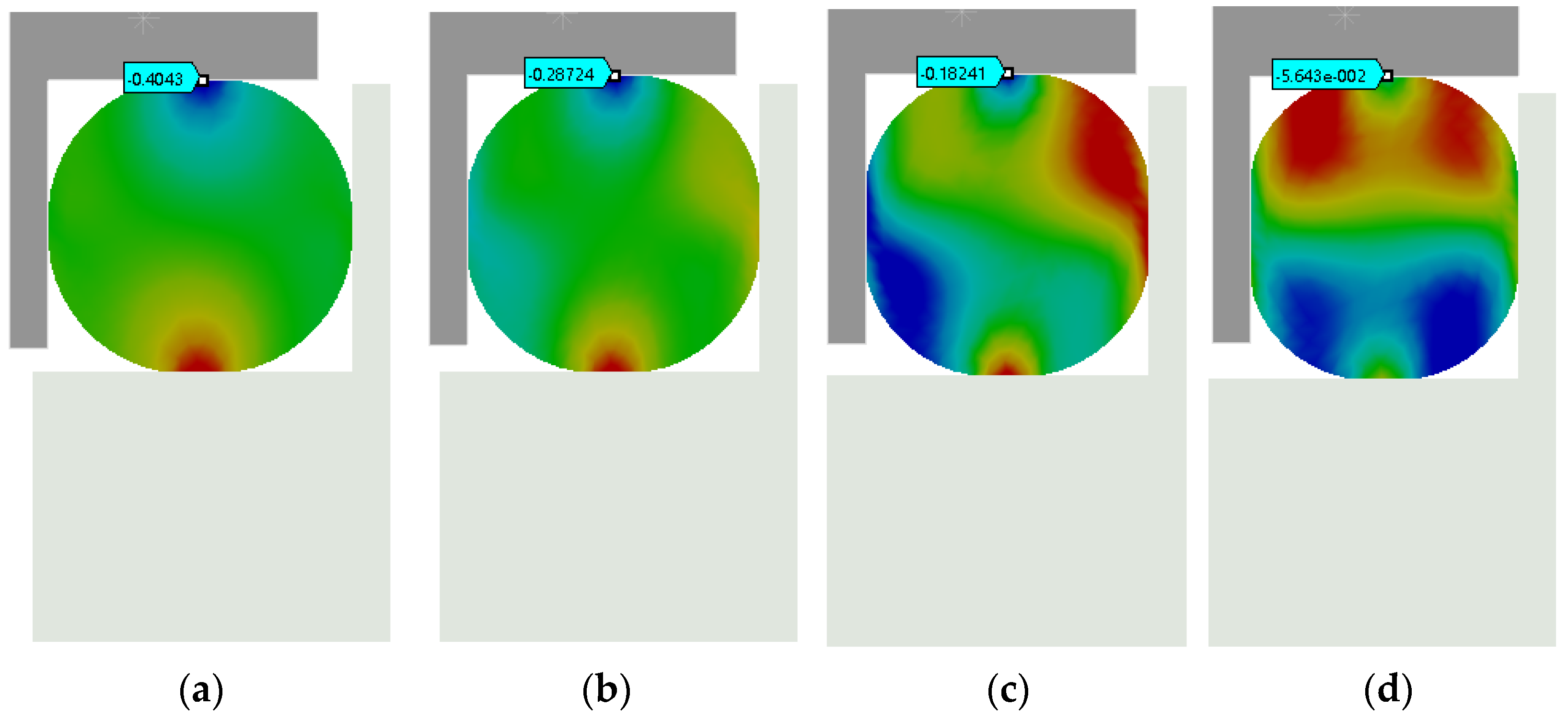
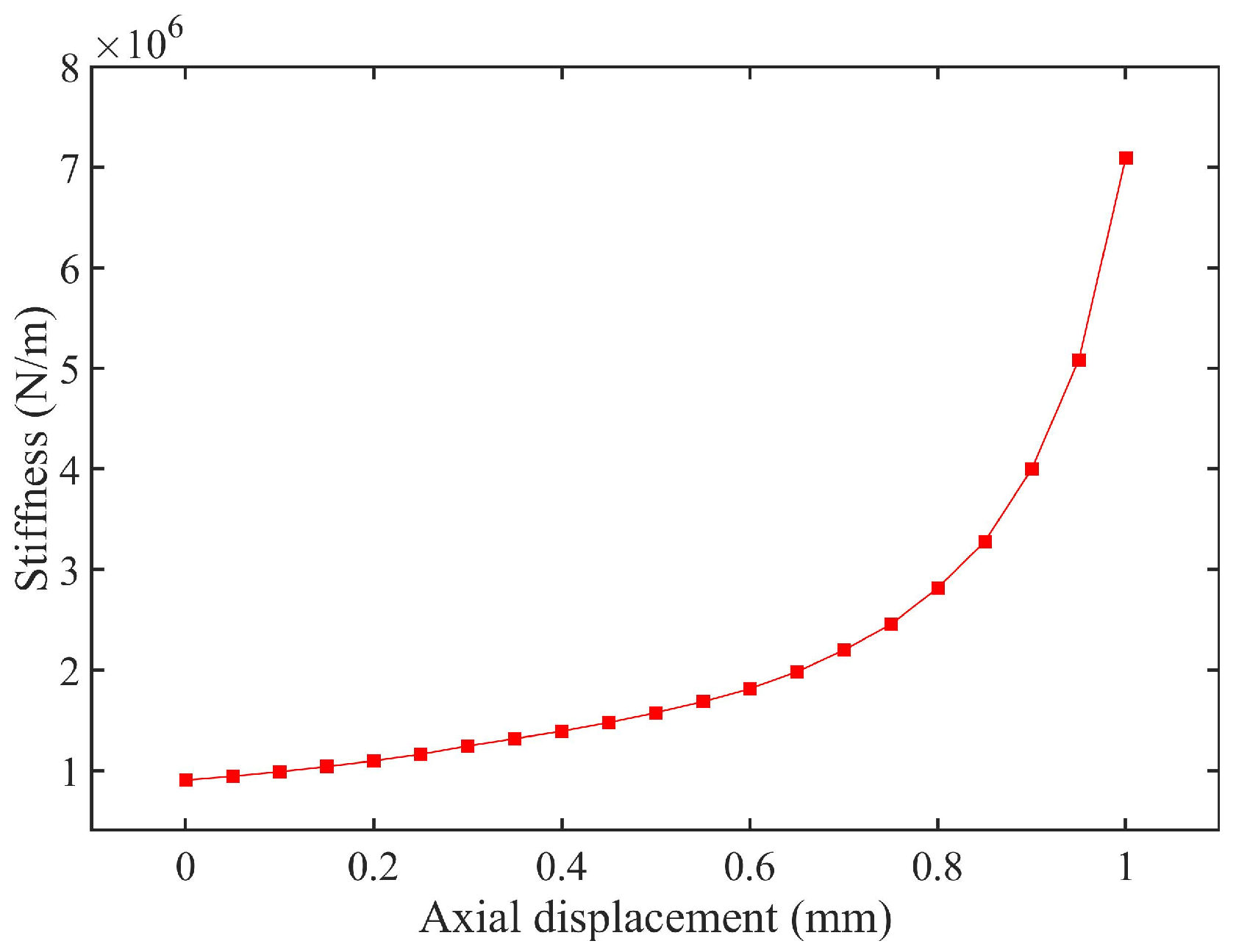
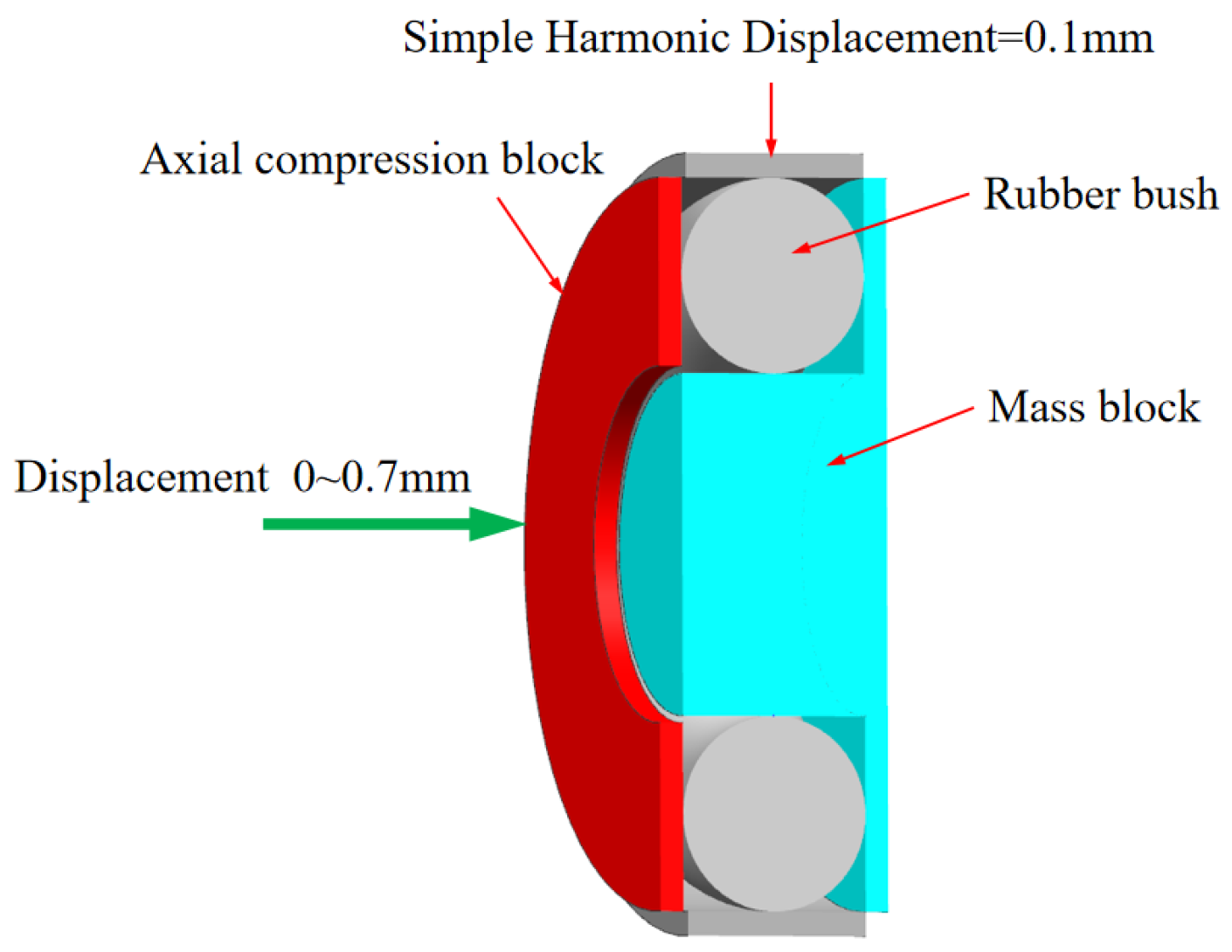
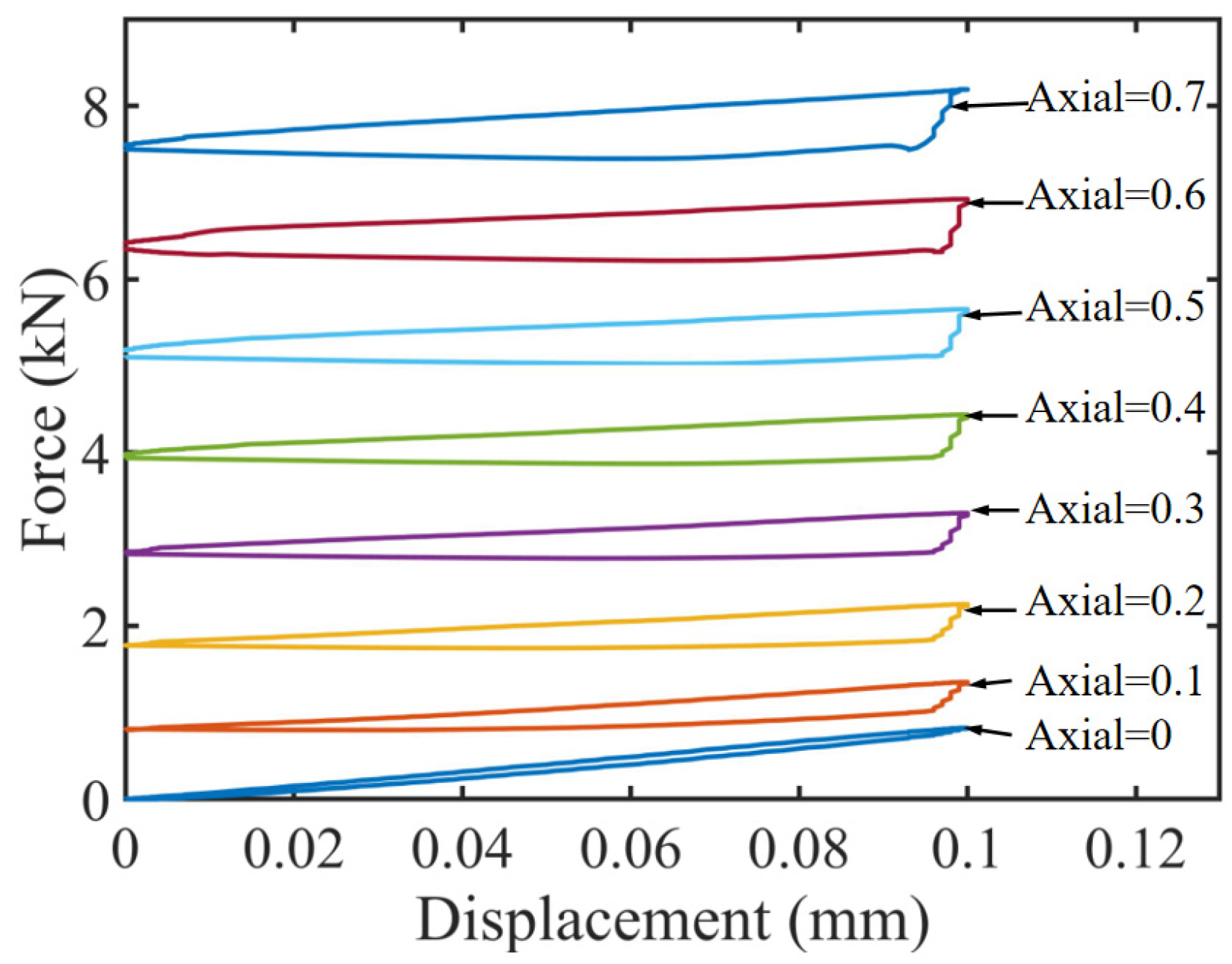
4.1. Stiffness Simulation Experiment of TDVA
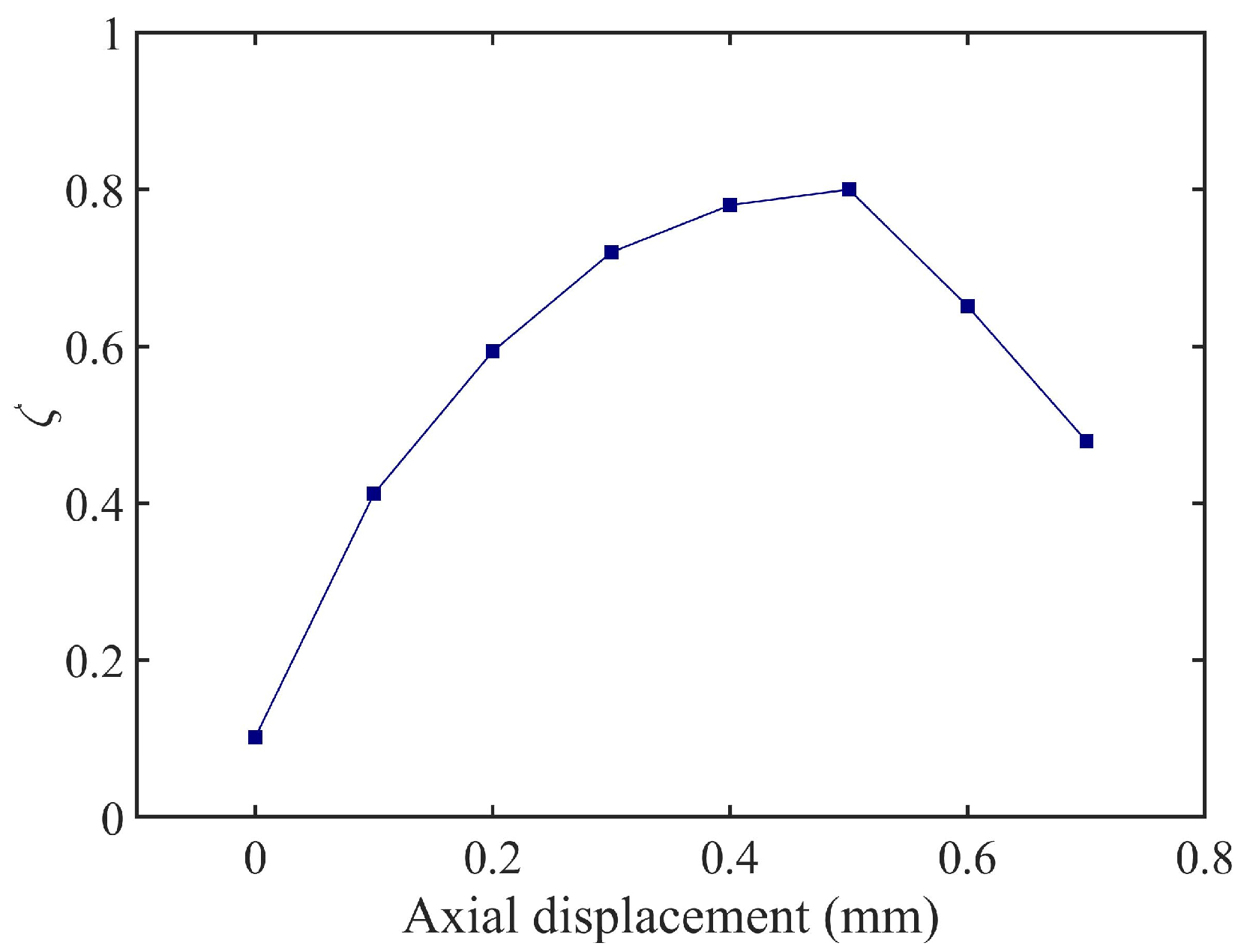
4.2. Damping Simulation Experiment of TDVA
5. TDVA Stiffness and Damping Combined Effect
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, J.; Sun, C.; Yan, Z. State-of-art, challenges, and outlook on deep hole boring: Chatter suppression, tool wear monitoring, and error measurement. Int. J. Adv. Manuf. Technol. 2025, 136, 2075–2105. [Google Scholar] [CrossRef]
- Li, H.; Xia, Y.; Su, B. Ultrasonic vibration-assisted chatter suppression for deep hole boring of stainless steel. Int. J. Adv. Manuf. Technol. 2024, 131, 1691–1703. [Google Scholar] [CrossRef]
- Suyama, D.; Diniz, A.; Pederiva, R. The use of carbide and particle-damped bars to increase tool overhang in the internal turning of hardened steel. Int. J. Adv. Manuf. Technol. 2016, 86, 2083–2092. [Google Scholar] [CrossRef]
- Matsubara, A.; Maeda, M.; Yamaji, I. Vibration suppression of boring bar by piezoelectric actuators and LR circuit. CIRP Ann.—Manuf. Technol. 2014, 63, 373–376. [Google Scholar] [CrossRef]
- Sajedi Pour, D.; Behbahani, S. Semi-active fuzzy control of machine tool chatter vibration using smart MR dampers. Int. J. Adv. Manuf. Technol. 2016, 83, 421–428. [Google Scholar] [CrossRef]
- Ghorbani, S.; Rogov, V.; Carluccio, A. The effect of composite boring bars on vibration in machining process. Int. J. Adv. Manuf. Technol. 2019, 105, 1157–1174. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Q.; Wu, S. Analysis of the vibration characteristics and adjustment method of boring bar with a variable stiffness vibration absorber. Int. J. Adv. Manuf. Technol. 2017, 98, 95–105. [Google Scholar] [CrossRef]
- Patel, A.; Yadav, A.; Law, M. Damped Chatter Resistant Boring Bar Integrated with an Absorber Working in Conjunction with an Eddy Current Damper. J. Vib. Eng. Technol. 2022, 11, 2013–2024. [Google Scholar] [CrossRef]
- Gourc, E.; Seguy, S.; Michon, G. Quenching chatter instability in turning process with a vibro-impact nonlinear energy sink. J. Sound Vib. 2015, 355, 392–406. [Google Scholar] [CrossRef]
- Li, L.; Sun, B.; Hua, H. Analysis of the Vibration Characteristics of a Boring Bar with a Variable Stiffness Dynamic Vibration Absorber. Shock Vib. 2019, 1–13. [Google Scholar] [CrossRef]
- Li, L.; Sun, B.; Hua, H. Nonlinear system modeling and damping implementation of a boring bar. Int. J. Adv. Manuf. Technol. 2019, 104, 921–930. [Google Scholar] [CrossRef]
- Li, L.; Yang, D.; Cui, Y. Optimization of machining performance in deep hole boring: A study on cutting tool vibration and dynamic vibration absorber design. Adv. Prod. Eng. Manag. 2023, 18, 371–380. [Google Scholar] [CrossRef]
- Iklodi, Z.; Barton, D.; Dombovari, Z. Bi-stability induced by motion limiting constraints on boring bar tuned mass dampers. J. Sound Vib. 2022, 517, 116538. [Google Scholar] [CrossRef]
- Houck, L.; Schmitz, T.; Smith, K. A tuned holder for increased boring bar dynamic stiffness. J. Manuf. Process. 2011, 13, 24–29. [Google Scholar] [CrossRef]
- Shi, H.; Ma, C.; Li, X.; Wang, G. Equivalent linearization of hyperelastic rubber rings in dynamic vibration absorber boring bar and simulation of its dynamic properties. Eng. Res. Express 2024, 6, 015517. [Google Scholar] [CrossRef]
- Rubio, L.; Loya, J.; Miguélez, M. Optimization of passive vibration absorbers to reduce chatter in boring. Mech. Syst. Signal Process. 2013, 41, 691–704. [Google Scholar] [CrossRef]
- Miguélez, M.; Rubio, L.; Loya, J. Improvement of chatter stability in boring operations with passive vibration absorbers. Int. J. Mech. Sci. 2010, 52, 1376–1384. [Google Scholar] [CrossRef]
- Liu, Q.; Li., J.; Ma, J. Structure design and vibration control of vibration reduction boring bar with variable damping. Int. J. Adv. Manuf. Technol. 2024, 134, 5301–5319. [Google Scholar] [CrossRef]
- Gokulu, T.; Defant, F.; Albertelli, P. Stability analysis of multi-insert rotating boring bar with stiffness variation. J. Sound Vib. 2024, 586, 118497. [Google Scholar] [CrossRef]
- Tian, J.; Wu, D.; Li, J. Design and Energy Dissipation Analysis of a Boring Bar Based on Particle Damping. J. Vib. Eng. Technol. 2025, 13, 51. [Google Scholar] [CrossRef]
- Guo, X.; Zhu, Y.; Luo, Z. Variable stiffness tuned particle dampers for vibration control of cantilever boring bars. Appl. Math. Mech. 2023, 44, 2163–2186. [Google Scholar] [CrossRef]
- Ramu, G.; Sundaramoorthy, K.; Singaravelu, C. A novel hybrid particle damping in boring bar for effective machining and chatter suppression. Sādhanā 2024, 49, 276. [Google Scholar] [CrossRef]
- Lawrance, G.; Paul, P.; Shylu, D. Effect of metallic substrate and rubber elastic materials over passive constrained layer damping on tool vibration during boring process. J. Low Freq. Noise Vib. Act. Control 2024, 43, 1139–1157. [Google Scholar] [CrossRef]
- Biju, C.; Shunmugam, M. Development of a boring bar with magneto rheological fluid damping and assessment of its dynamic characteristics. J. Vib. Control JVC 2018, 24, 3094–3106. [Google Scholar] [CrossRef]
- Chen, F.; Hanifzadegan, M.; Altintas, Y. Active Damping of Boring Bar Vibration with a Magnetic Actuator. IEEE/ASME Trans. Mechatron. 2015, 20, 2783–2794. [Google Scholar] [CrossRef]
- Yamada, K.; Matsuhisa, H.; Utsuno, H. Enhancement of efficiency of vibration suppression using piezoelectric elements and LR circuit by amplification of electrical resonance. J. Sound Vib. 2014, 333, 1281–1301. [Google Scholar] [CrossRef]
- Wang, X.; Yang, B.; Yu, H. Optimal Design and Experimental Study of a Multidynamic Vibration Absorber for Multifrequency Excitation. J. Vib. Acoust. 2017, 139, 031011. [Google Scholar] [CrossRef]
- Yang, Y.; Muñoa, J.; Altintas, Y. Optimization of multiple tuned mass dampers to suppress machine tool chatter. Int. J. Mach. Tools Manuf. 2010, 50, 834–842. [Google Scholar] [CrossRef]
- Febbo, M.; Vera, S. Optimization of a Two Degree of Freedom System Acting as a Dynamic Vibration Absorber. J. Vib. Acoust. 2008, 130, 011013. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, W.; Li, Y. Transverse vibration of the boring bar for BTA deep hole machining under stochastic excitation. J. Mech. Sci. Technol. 2023, 37, 5635–5648. [Google Scholar] [CrossRef]
- Kępczak, N.; Bechciński, G.; Rosik, R. Operating Properties of Deep Hole Boring Tools with Modified Design. Materials 2024, 17, 1551. [Google Scholar] [CrossRef] [PubMed]
- Saffury, J.; Altus, E. Optimized chatter resistance of viscoelastic turning bars. J. Sound Vib. 2009, 324, 26–39. [Google Scholar] [CrossRef]
- Zhang, Y.; Ren, Y.; Tian, J. Chatter stability of the constrained layer damping composite boring bar in cutting process. J. Vib. Control 2019, 25, 2204–2214. [Google Scholar]



| Equivalent Stiffness of the Boring Bar, K1 (106 N/m) | Equivalent Mass of the Boring Bar, M (kg) | Equivalent Mass of the TDVA, m2 (kg) | Damping Ratio of the TDVA, ζ | Equivalent Stiffness of the TDVA, K (106 N/m) | |
|---|---|---|---|---|---|
| TDVA boring bar | 2.2057 | 1.12 | 0.59 | variable | variable |
| Boring bar | 2.2134 | 1.216 |
| Boring Bar Type | Equivalent Stiffness (106 N/m) | Damping Ratio of the TDVA, ζ | Stiffness of the TDVA (106 N/m) | Processing Frequency Range (Hz) |
|---|---|---|---|---|
| TDVA boring bar | 2.2057 | 0-1-0.8 | 9-16 | 163–215, 245–500 |
| Normal boring bar | 2.2134 | - | - | 304–500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, Y.; Yu, G.; Hu, Q.; Xu, D.; Xu, J.; Lushchyk, P. Vibration Characteristics Analysis of Boring Bar with Tunable Dynamic Vibration Absorber. Materials 2025, 18, 1324. https://doi.org/10.3390/ma18061324
Guan Y, Yu G, Hu Q, Xu D, Xu J, Lushchyk P. Vibration Characteristics Analysis of Boring Bar with Tunable Dynamic Vibration Absorber. Materials. 2025; 18(6):1324. https://doi.org/10.3390/ma18061324
Chicago/Turabian StyleGuan, Yanqi, Guangbin Yu, Qingming Hu, Donghui Xu, Jiao Xu, and Pavel Lushchyk. 2025. "Vibration Characteristics Analysis of Boring Bar with Tunable Dynamic Vibration Absorber" Materials 18, no. 6: 1324. https://doi.org/10.3390/ma18061324
APA StyleGuan, Y., Yu, G., Hu, Q., Xu, D., Xu, J., & Lushchyk, P. (2025). Vibration Characteristics Analysis of Boring Bar with Tunable Dynamic Vibration Absorber. Materials, 18(6), 1324. https://doi.org/10.3390/ma18061324






