Dynamic Load Identification of Thin-Walled Cabin Based on CNN-LSTM-SA Neural Network
Abstract
1. Introduction
2. CNN-LSTM-SA Neural Network Load Identification Model Building
2.1. Load–Response Relationship in the Time Domain
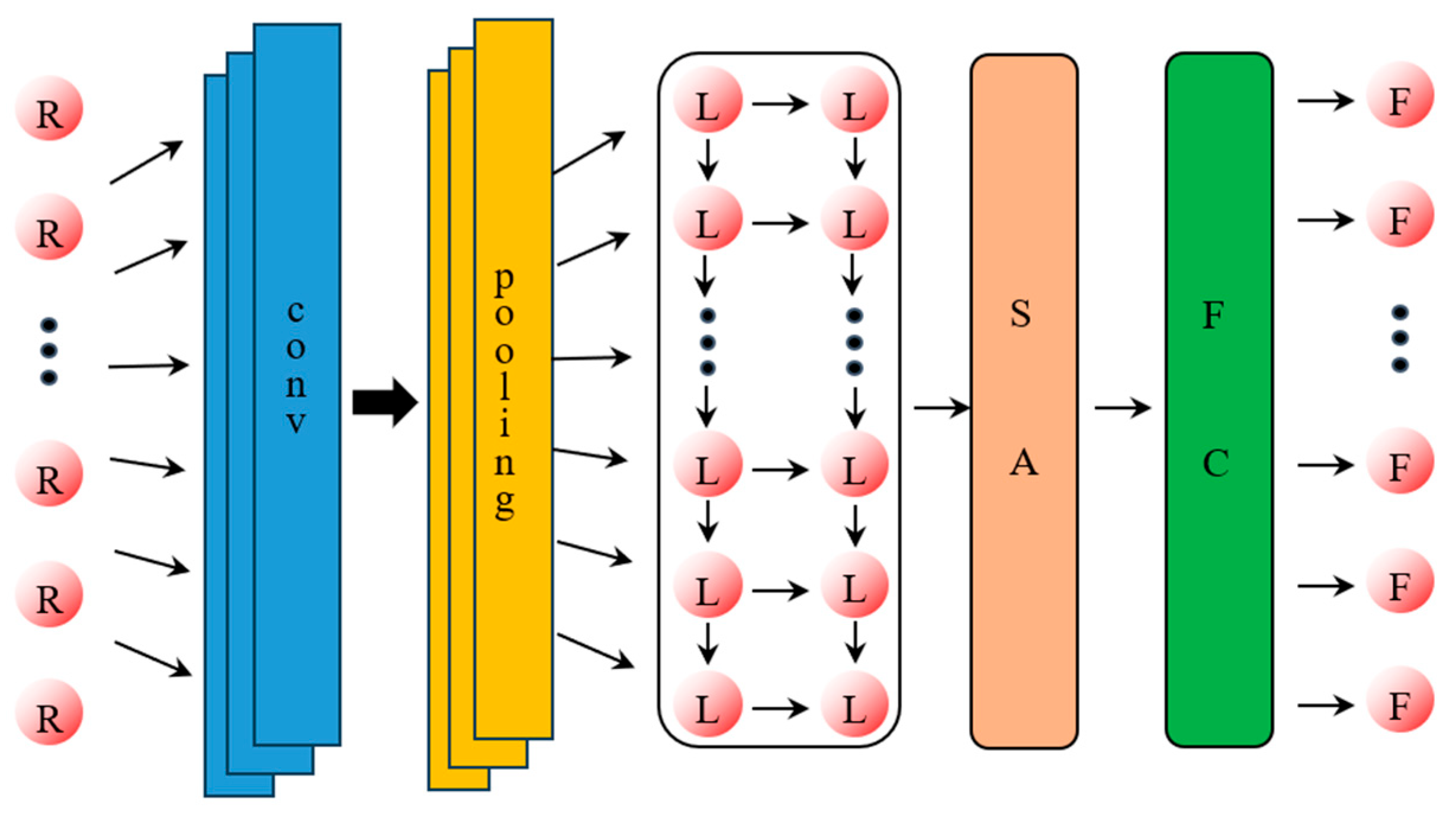
2.2. CNN-LSTM-SA Network Architecture
- (1)
- The forget gate generates an output value between 0 and 1 by reading the final output of the previous moment and the input of the current moment and using Equation (6), where 1 represents the complete retention of information and 0 represents the complete discarding of information.where is the weight matrix of the forget gate, is the bias term, and is the Sigmoid activation function;
- (2)
- The input gate generates the temporary state of the cell at the current moment by reading the final output of the previous moment and the input of the current moment and then updates the cell state in conjunction with the output of the forget gate to obtain the new cell state which taking the values from 0 to 1.where is the output value of the input gate at the current moment, which determines the extent to which the current input affects the update of the unit state . and are the weight matrix and bias terms for computing the temporary unit state . is the hyperbolic tangent activation function and denotes the matrix element-by-element multiplication;
- (3)
- The output gate extracts and outputs key information from the current unit state. It also reads the final output value of the cell at the previous moment and the input value of the cell at the current moment and calculates through Equation (10).where takes values from 0 to 1, is the weight of the output gate, and is the bias of the output gate;
- (4)
- Finally, the final output of the unit at the current moment is calculated from the output value of the output gate and the current state of the unit by Equation (11).
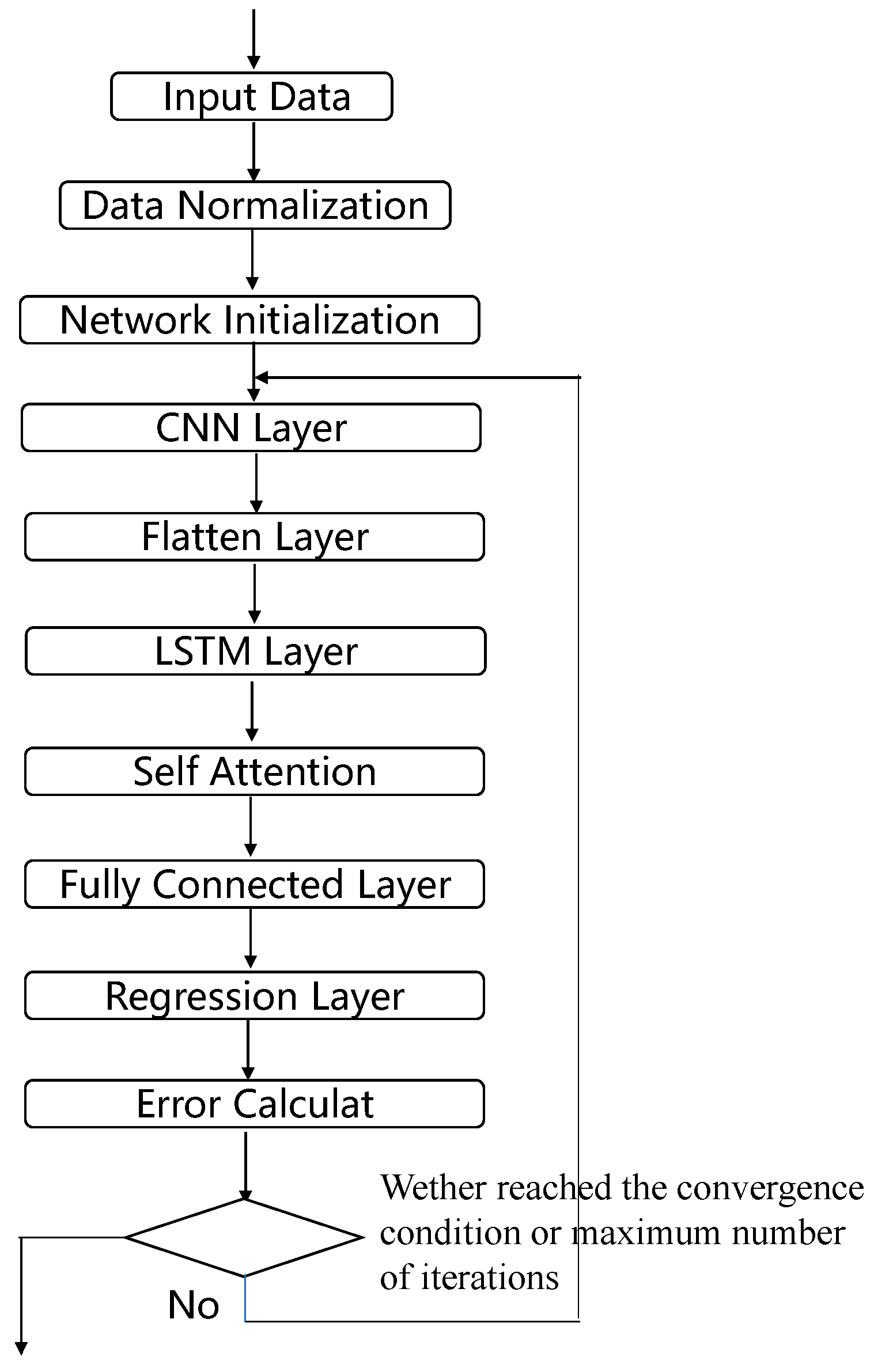
2.3. Constructing the CNN-LSTM-SA Load Identification Model
- (1)
- Segment the load and response data according to the method described above and perform data normalization as well as division of the training and test sets;
- (2)
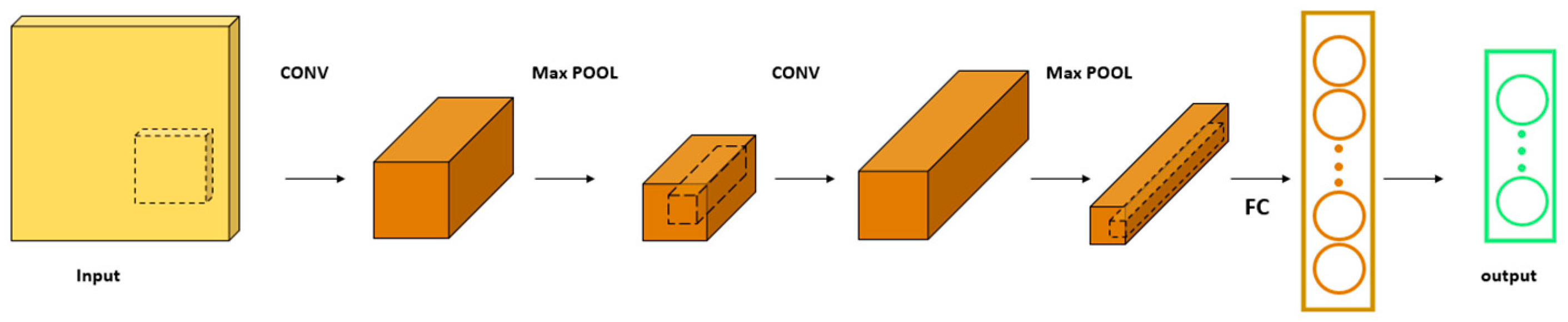
- After initialization of the network, the response data first pass through a one-dimensional convolutional CNN network for convolutional operation and average pooling operation to extract the high-dimensional features of the data;
- (3)
- In order to make the highly dimensional data adapt to the LSTM neural network, the data output from the CNN network need to be flattened. The flattening process consists of pulling the feature maps of each channel into one-dimensional vectors in order and then connecting the vectors of all channels;
- (4)
- The flattened data go sequentially through the LSTM neural network, the SA network, and the fully connected network, and finally the predicted load is generated;
- (5)
- Judge whether to terminate network training based on the error between the network’s predicted load and the actual load;
- (6)
- The trained network performs load identification on the test set to verify the recognition effect.
- (1)
- CNN layer: 1D convolutional kernel size, number of convolutional kernels, number of convolutional layers, and pooling size;
- (2)
- LSTM layer: number of LSTM units, number of LSTM layers, and dropout rate;
- (3)
- SA layer: number of attention heads, attention head dimension, and dropout rate;
- (4)
- Hyperparameters of the network: optimizer type, learning rate, learning rate decay, batch size, max epochs, etc.
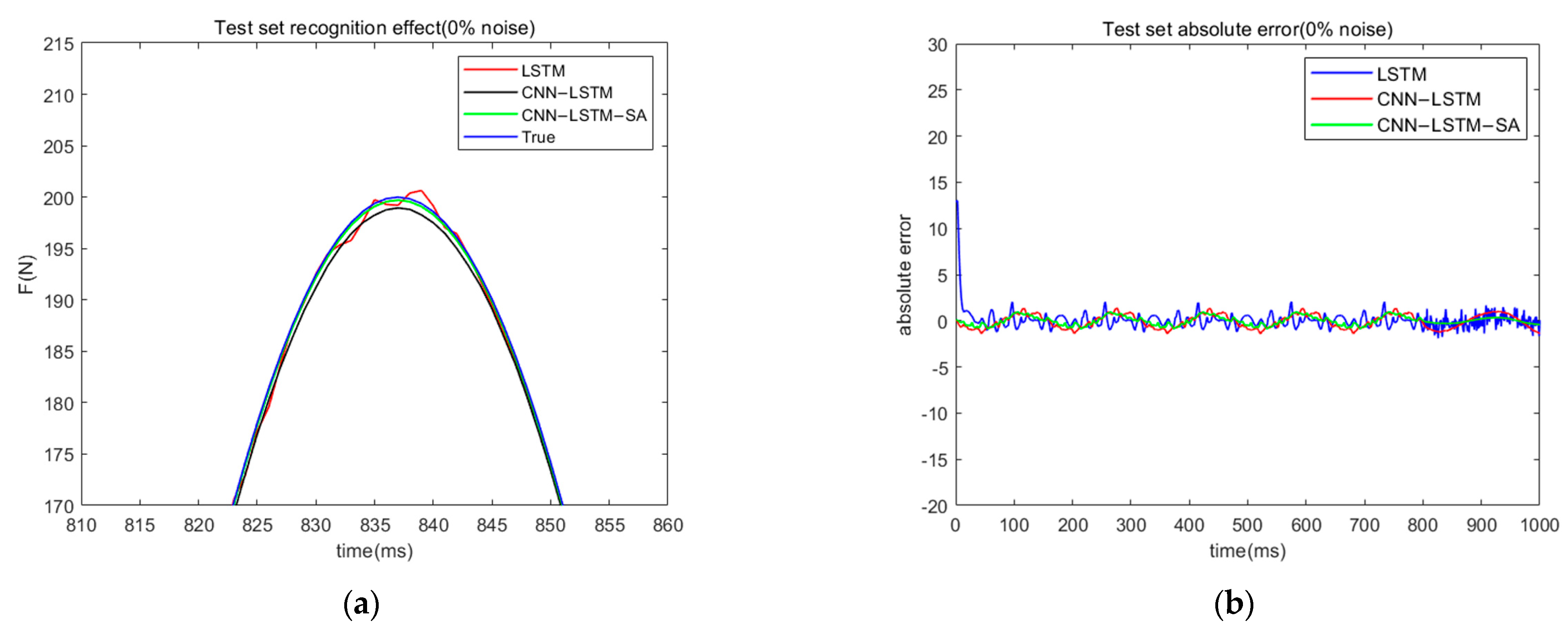
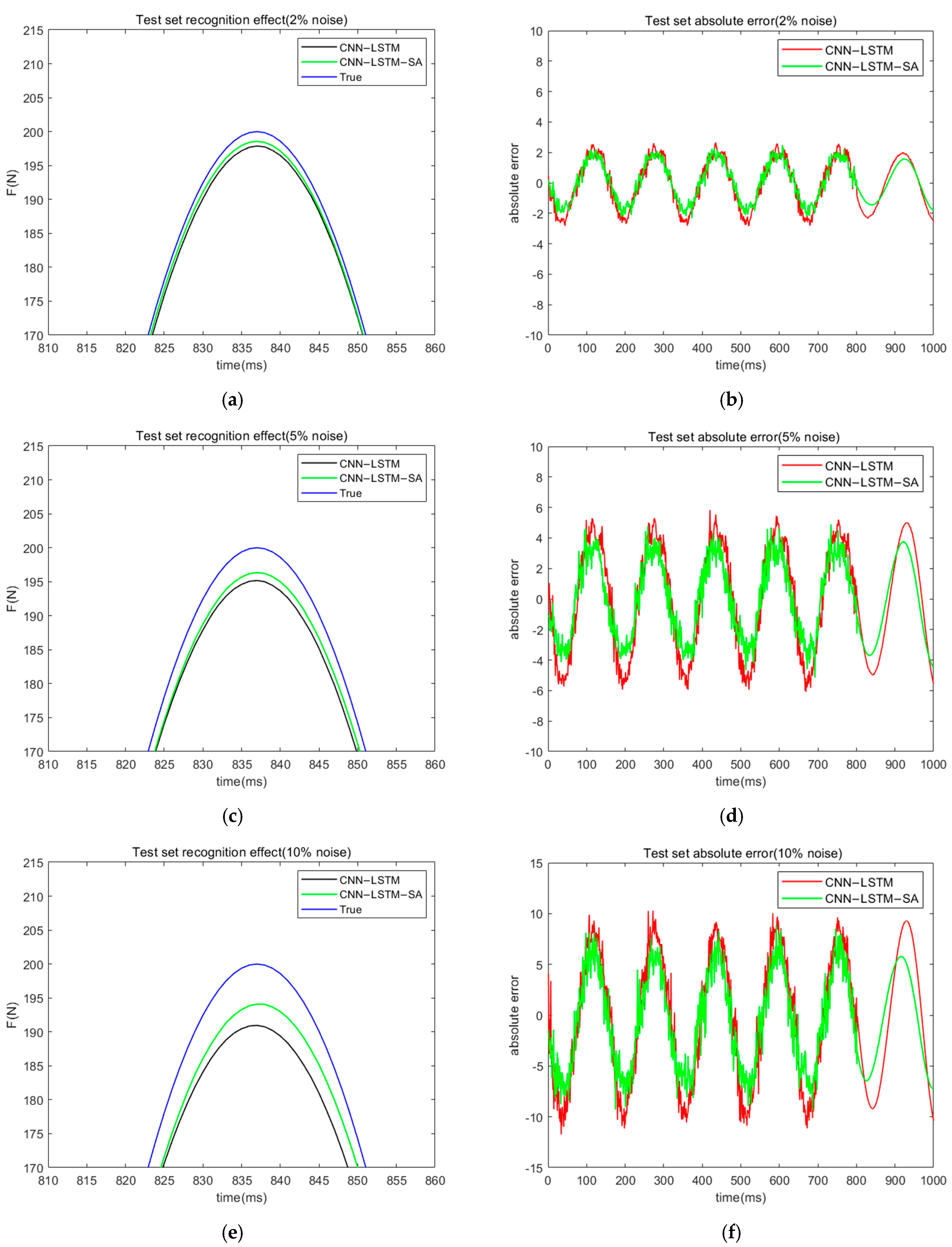
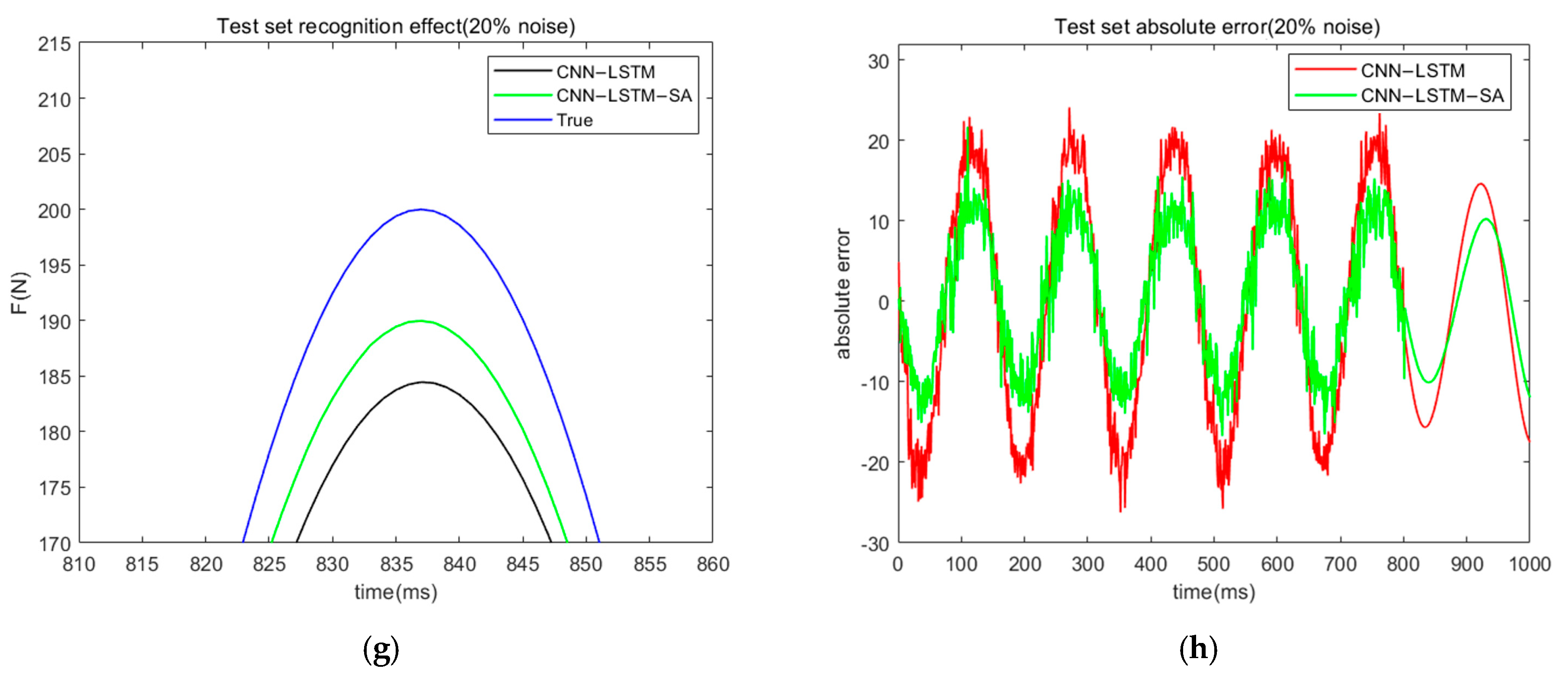
3. Numerical Simulation Study
4. Experimental Study
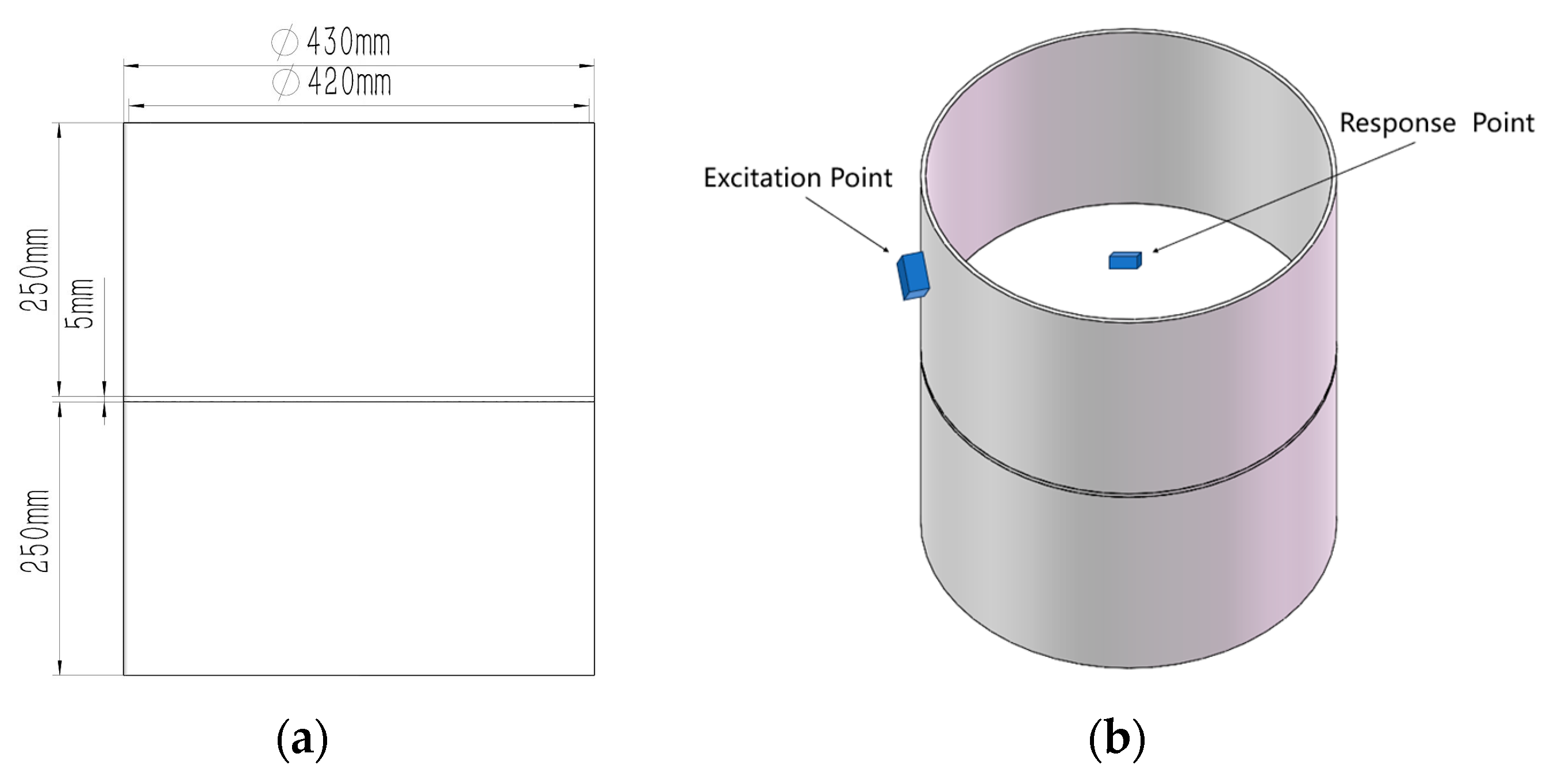
4.1. Test Object and Test System
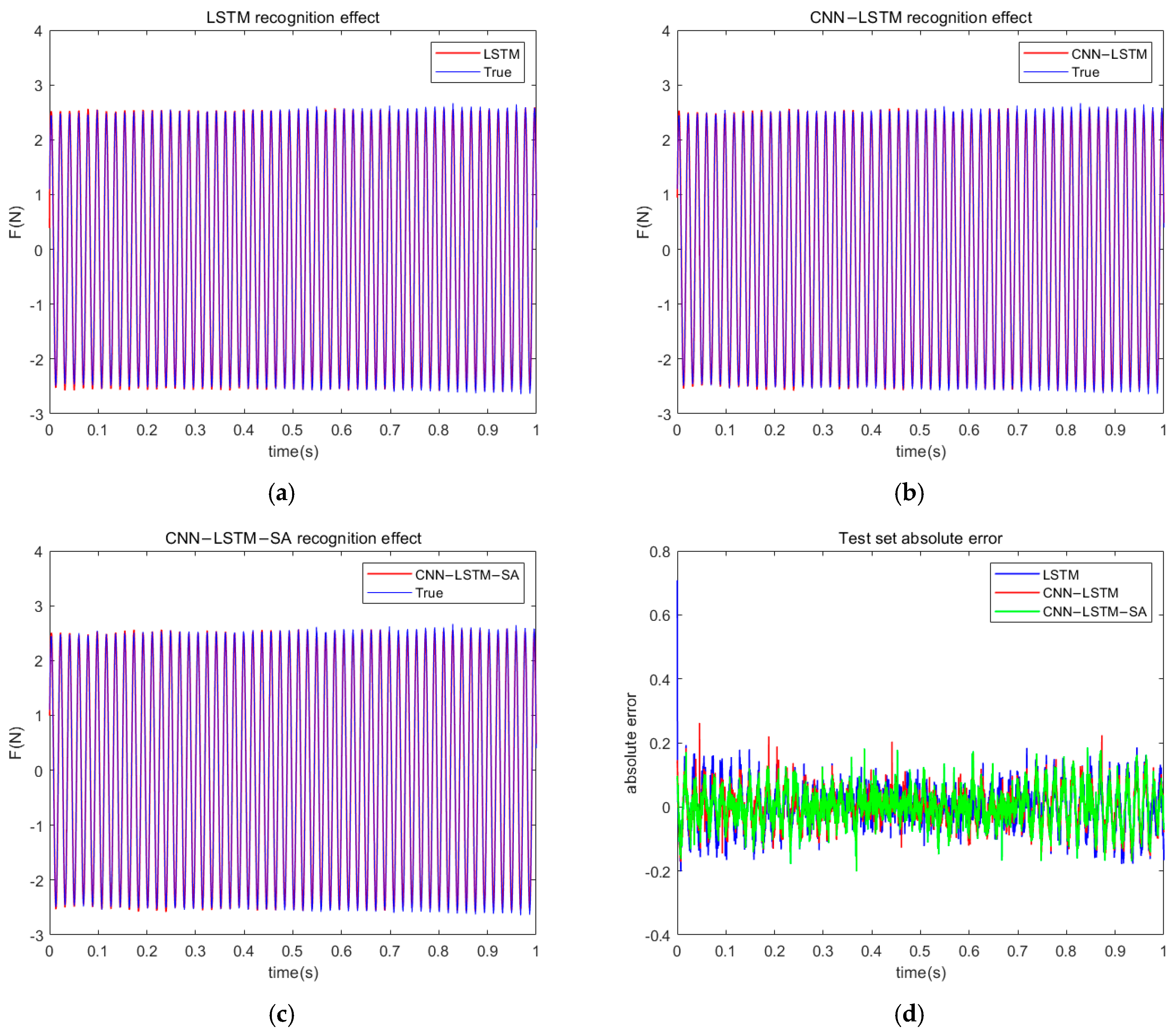
4.2. Time-Domain Identification of Sinusoidal Load
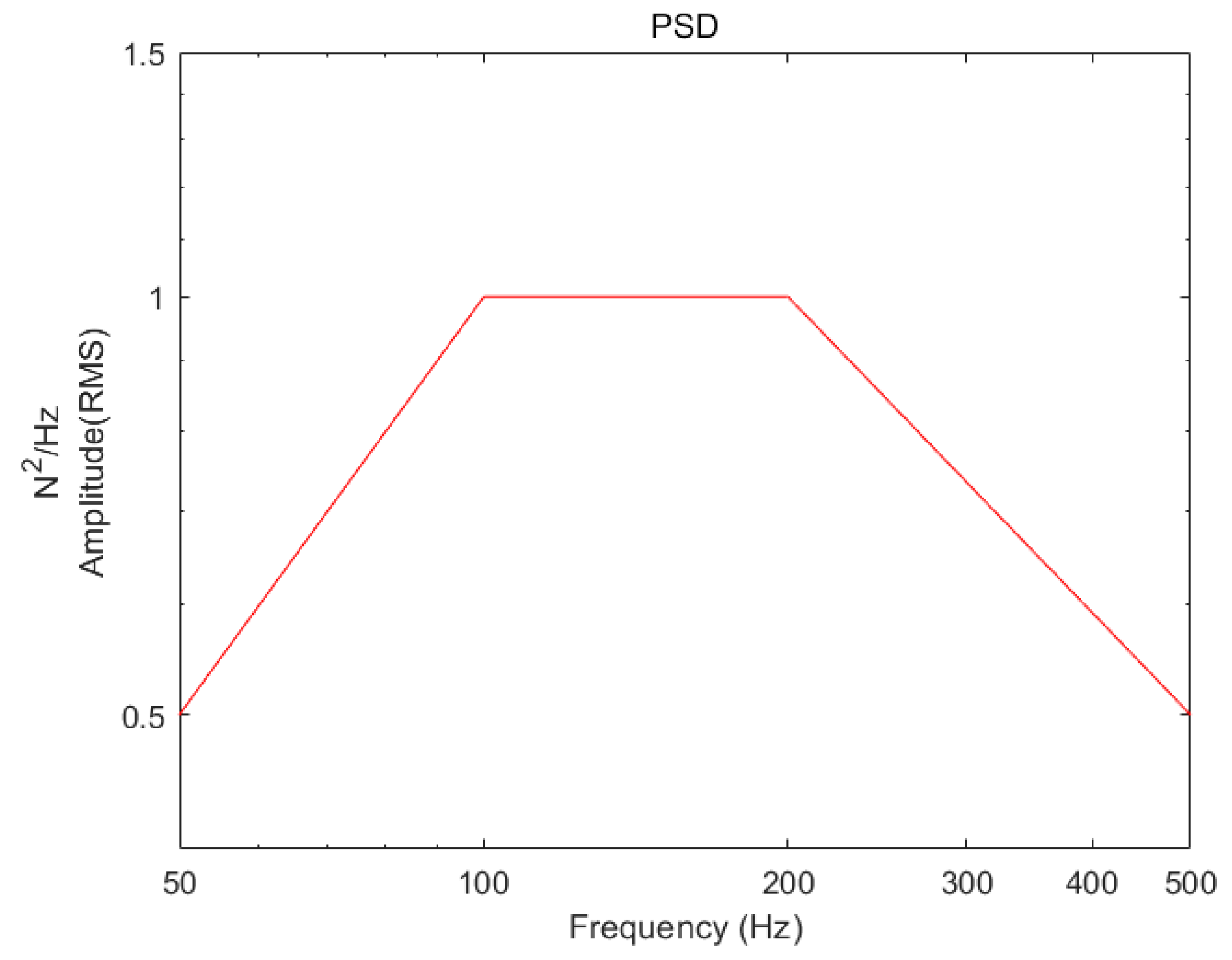
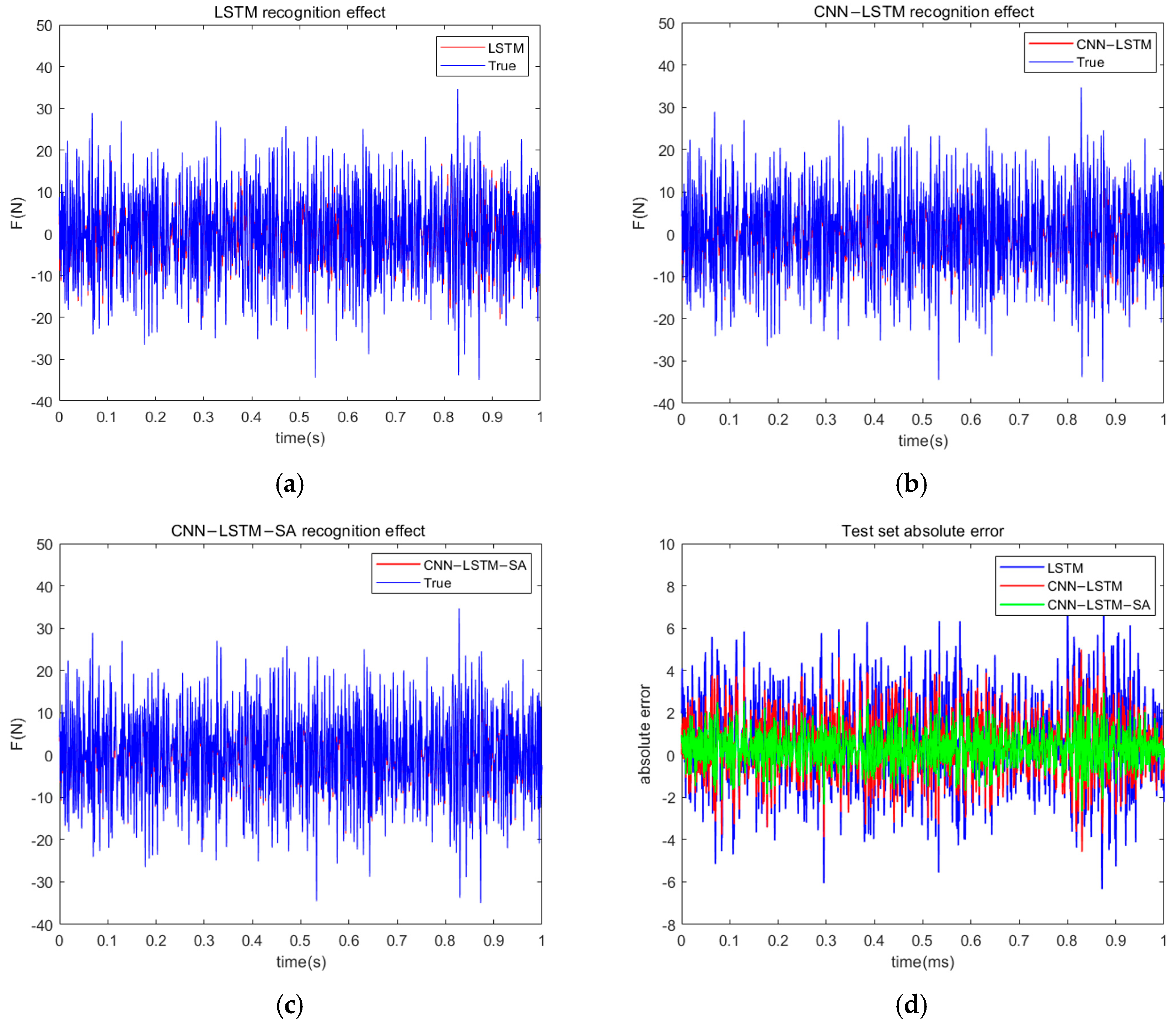
4.3. Time-Domain Identification of Random Load
5. Conclusions
- (1)
- Simulation results show that for sinusoidal load identification, the CNN-LSTM-SA network has obvious advantages in terms of recognition accuracy and noise immunity. The RMSE and MAE are 0.47 and 0.53 under 0% noise and 8.8 and 8.5 under 20% noise, respectively;
- (2)
- The experimental results show that the CNN-LSTM-SA network achieves high identification accuracies in both sinusoidal and random load identification tasks (RMSE of 0.08 and 0.83; R2 of 0.98 and 0.93, respectively);
- (3)
- The CNN-LSTM-SA-based load identification method provides researchers with a tool with higher accuracy and noise immunity, as well as a reliable method for structural health monitoring and optimal design.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, R.X.; Dobriban, E.; Hou, Z.C.; Qian, K. Dynamic Load Identification for Mechanical Systems: A Review. Arch. Comput. Methods Eng. 2022, 29, 831–863. [Google Scholar] [CrossRef]
- Bartlett, F.D.; Flannelly, W.G. Model Verification of Force Determination for Measuring Vibratory Loads. J. Am. Helicopter Soc. 1979, 24, 10–18. [Google Scholar] [CrossRef]
- Li, K.; Liu, J.; Wen, J.; Lu, C. Time domain identification method for random dynamic loads and its application on reconstruction of road excitations. Int. J. Appl. Mech. 2020, 12, 2050087. [Google Scholar] [CrossRef]
- Kazemi, M.; Hematiyan, M.; Ghavami, K. An efficient method for dynamic load identification based on structural response. In Proceedings of the International Conference on Engineering Optimization, Rio de Janeiro, Brazil, 1–5 June 2008; pp. 1–6. [Google Scholar]
- Liu, J.; Meng, X.; Zhang, D.; Jiang, C.; Han, X. An efficient method to reduce ill-posedness for structural dynamic load identification. Mech. Syst. Signal Process. 2017, 95, 273–285. [Google Scholar] [CrossRef]
- Roseiro, L.; Alcobia, C.; Ferreira, P.; Baïri, A.; Laraqi, N.; Alilat, N. Identification of the forces in the suspension system of a race car using artificial neural networks. In Computational Intelligence and Decision Making: Trends and Applications; Springer: Berlin, Germany, 2012; pp. 469–477. [Google Scholar]
- Tang, Q.; Xin, J.; Jiang, Y.; Zhou, J.; Li, S.; Chen, Z. Novel identification technique of moving loads using the random response power spectral density and deep transfer learning. Measurement 2022, 195, 111120. [Google Scholar] [CrossRef]
- Zhang, X.; He, W.; Cui, Q.; Bai, T.; Li, B.; Li, J.; Li, X. WavLoadNet: Dynamic Load Identification for Aeronautical Structures Based on Convolution Neural Network and Wavelet Transform. Appl. Sci. 2024, 14, 1928. [Google Scholar] [CrossRef]
- Zhou, J.; Dong, L.; Guan, W.; Yan, J. Impact load identification of nonlinear structures using deep Recurrent Neural Network. Mech. Syst. Signal Process. 2019, 133, 106292. [Google Scholar] [CrossRef]
- Yang, H.; Jiang, J.; Chen, G.; Mohamed, M.S.; Lu, F. A recurrent neural network-based method for dynamic load identification of beam structures. Materials 2021, 14, 7846. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Jiang, J.; Chen, G.; Zhao, J. Dynamic load identification based on deep convolution neural network. Mech. Syst. Signal Process. 2023, 185, 109757. [Google Scholar] [CrossRef]
- Wang, C.; Chen, D.; Chen, J.; Lai, X.; He, T. Deep regression adaptation networks with model-based transfer learning for dynamic load identification in the frequency domain. Eng. Appl. Artif. Intell. 2021, 102, 104244. [Google Scholar] [CrossRef]
- Lu, W.; Li, J.; Wang, J.; Qin, L. A CNN-BiLSTM-AM method for stock price prediction. Neural Comput. Appl. 2021, 33, 4741–4753. [Google Scholar] [CrossRef]
- Huy, T.H.B.; Vo, D.N.; Nguyen, K.P.; Huynh, V.Q.; Huynh, M.Q.; Truong, K.H. Short-term load forecasting in power system using CNN-LSTM neural network. In Proceedings of the 2023 Asia Meeting on Environment and Electrical Engineering (EEE-AM), Hanoi, Vietnam, 15 November 2023; pp. 1–6. [Google Scholar]
- Impraimakis, M. Deep recurrent-convolutional neural network learning and physics Kalman filtering comparison in dynamic load identification. Struct. Health Monit. 2024, 1, 31. [Google Scholar] [CrossRef]
- Zhang, J.; Luo, F.; Quan, X.; Wang, Y.; Shi, J.; Shen, C.; Zhang, C. Improving wave height prediction accuracy with deep learning. Ocean Model. 2024, 188, 102312. [Google Scholar] [CrossRef]
- Hu, X.; Yu, S.; Zheng, J.; Fang, Z.; Zhao, Z.; Qu, X. A hybrid CNN-LSTM model for involuntary fall detection using wrist-worn sensors. Adv. Eng. Inform. 2025, 65, 103178. [Google Scholar] [CrossRef]
- Venkateswaran, D.; Cho, Y. Efficient solar power generation forecasting for greenhouses: A hybrid deep learning approach. Alex. Eng. J. 2024, 91, 222–236. [Google Scholar] [CrossRef]
- Liu, J.; Meng, X.; Jiang, C.; Han, X.; Zhang, D. Time-domain Galerkin method for dynamic load identification. Int. J. Numer. Methods Eng. 2016, 105, 620–640. [Google Scholar] [CrossRef]
- Ilesanmi, A.E.; Ilesanmi, T.O. Methods for image denoising using convolutional neural network: A review. Complex Intell. Syst. 2021, 7, 2179–2198. [Google Scholar] [CrossRef]
- Wen, L.; Gao, L.; Li, X.; Zeng, B. Convolutional Neural Network with Automatic Learning Rate Scheduler for Fault Classification. IEEE Trans. Instrum. Meas. 2021, 70, 3509912. [Google Scholar] [CrossRef]
- Sang, S.; Li, L. A Novel Variant of LSTM Stock Prediction Method Incorporating Attention Mechanism. Mathematics 2024, 12, 945. [Google Scholar] [CrossRef]
- Uchida, K.; Tanaka, M.; Okutomi, M. Coupled convolution layer for convolutional neural network. Neural Netw. 2018, 105, 197–205. [Google Scholar] [CrossRef] [PubMed]



| RMSE | MAE | |
|---|---|---|
| LSTM | 1.10 | 0.61 |
| CNN-LSTM | 0.74 | 0.55 |
| CNN-LSTM-SA | 0.47 | 0.53 |
| Noise Level | 2% Noise | 5% Noise | 10% Noise | 20% Noise | ||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | |
| CNN-LSTM | 1.62 | 1.27 | 3.55 | 3.18 | 6.43 | 5.10 | 13.89 | 12.73 |
| CNN-LSTM-SA | 1.29 | 1.13 | 2.58 | 2.86 | 4.76 | 4.45 | 8.47 | 10.83 |
| RMSE | MAE | R2 | |
|---|---|---|---|
| LSTM | 0.12 | 0.14 | 0.97 |
| CNN-LSTM | 0.09 | 0.11 | 0.97 |
| CNN-LSTM-SA | 0.08 | 0.10 | 0.98 |
| RMSE | MAE | R2 | |
|---|---|---|---|
| LSTM | 2.07 | 3.42 | 0.88 |
| CNN-LSTM | 1.39 | 2.57 | 0.90 |
| CNN-LSTM-SA | 0.83 | 1.69 | 0.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Song, S.; Liu, C.; Zhao, Y. Dynamic Load Identification of Thin-Walled Cabin Based on CNN-LSTM-SA Neural Network. Materials 2025, 18, 1255. https://doi.org/10.3390/ma18061255
Wang J, Song S, Liu C, Zhao Y. Dynamic Load Identification of Thin-Walled Cabin Based on CNN-LSTM-SA Neural Network. Materials. 2025; 18(6):1255. https://doi.org/10.3390/ma18061255
Chicago/Turabian StyleWang, Jun, Shaowei Song, Chang Liu, and Yali Zhao. 2025. "Dynamic Load Identification of Thin-Walled Cabin Based on CNN-LSTM-SA Neural Network" Materials 18, no. 6: 1255. https://doi.org/10.3390/ma18061255
APA StyleWang, J., Song, S., Liu, C., & Zhao, Y. (2025). Dynamic Load Identification of Thin-Walled Cabin Based on CNN-LSTM-SA Neural Network. Materials, 18(6), 1255. https://doi.org/10.3390/ma18061255





