Hybrid Polypropylene Biocomposites Reinforced with Short Man-Made Cellulose Fibres and Softwood Flour—Optimisation of Properties Using Response Surface Methodology
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
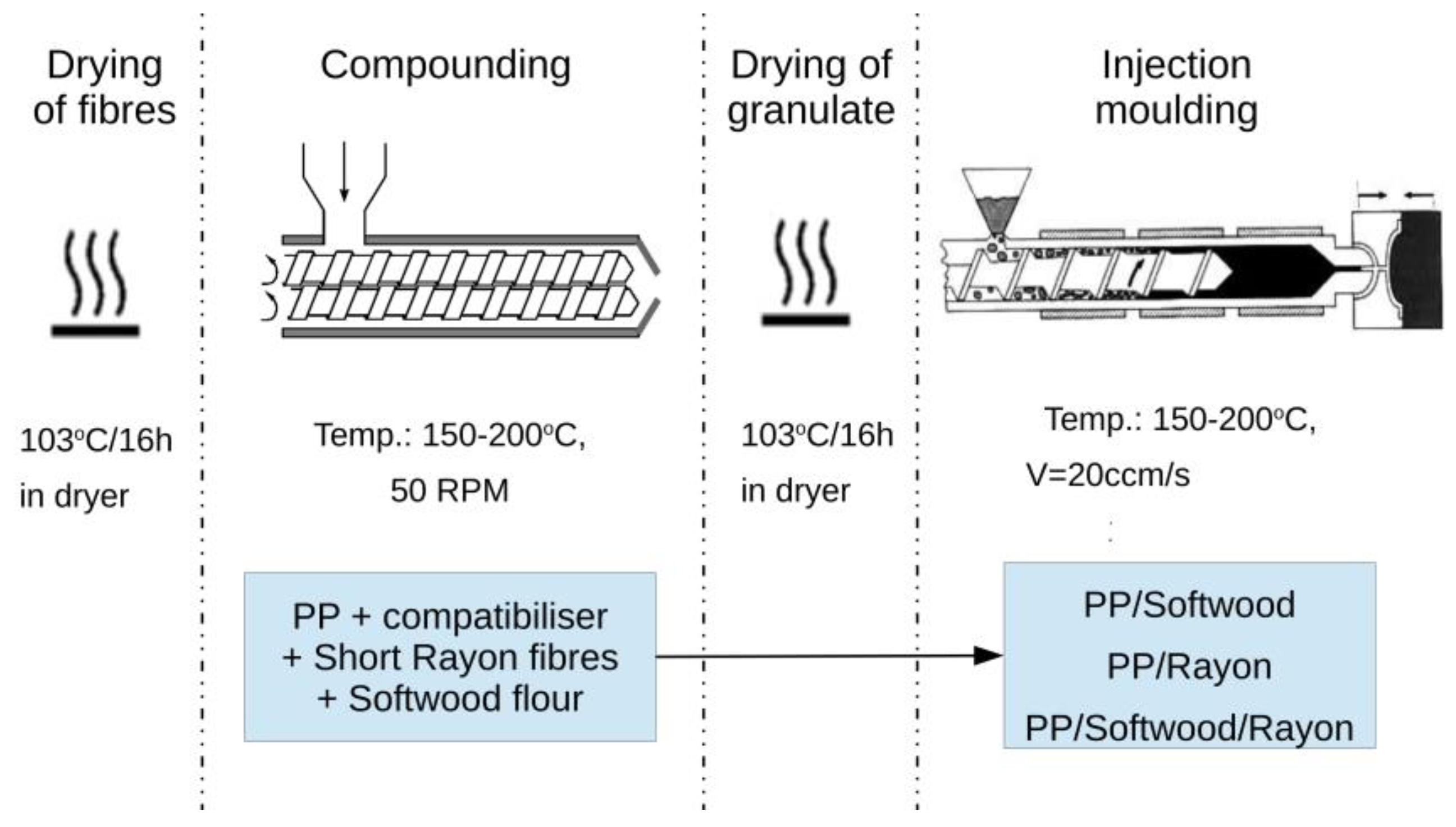
2.2.1. Manufacturing of Composites
2.2.2. Evaluation of Composite Properties
2.2.3. Design of Experiment
3. Results and Discussion
3.1. Influence of Hybridisation of Reinforcement on Manufacturing
3.2. Results of Experiments Overview
3.3. Adequacy of Approximations
3.4. Density and Porosity
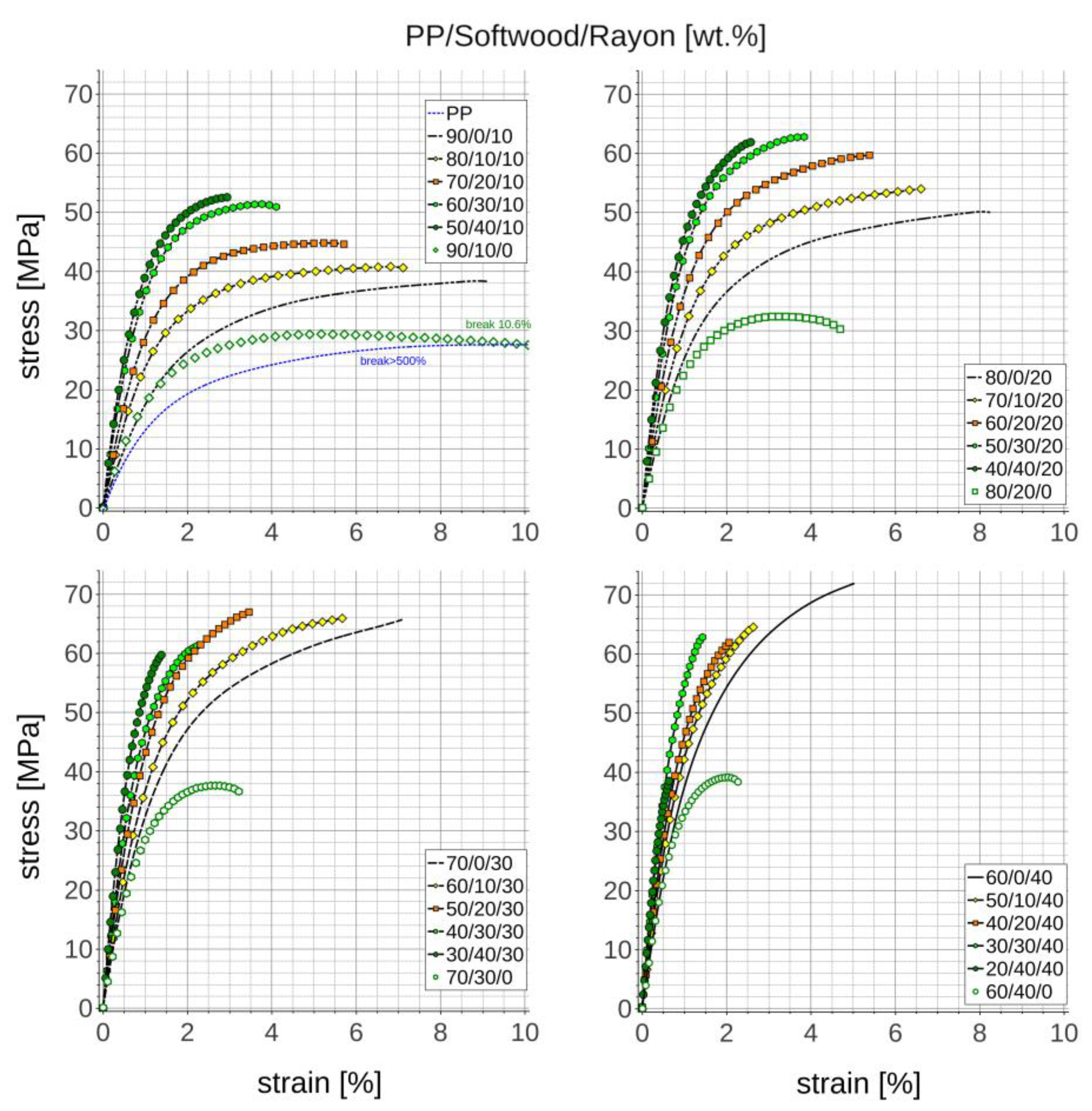
3.5. Tensile Properties
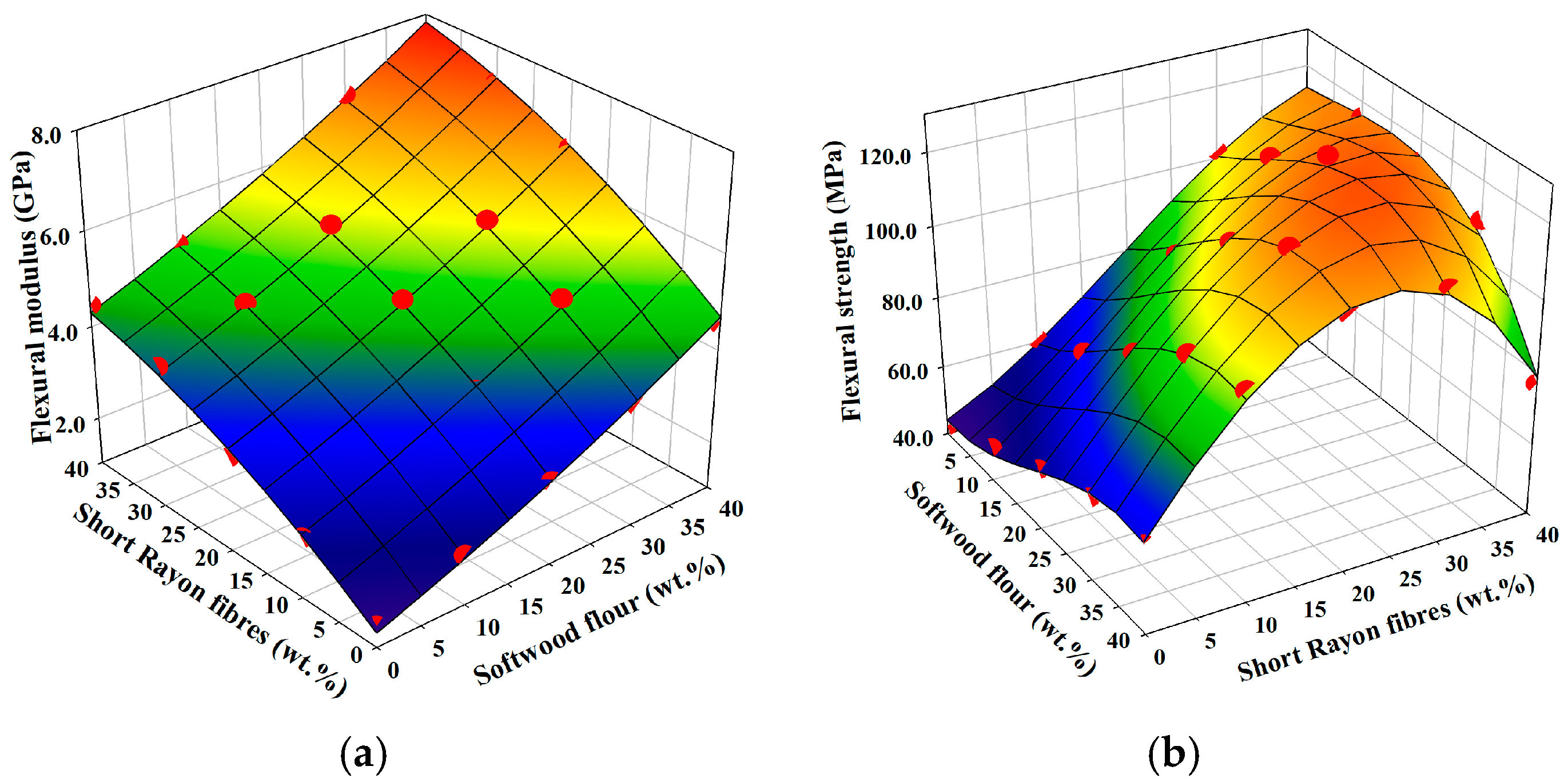
3.6. Flexural Properties
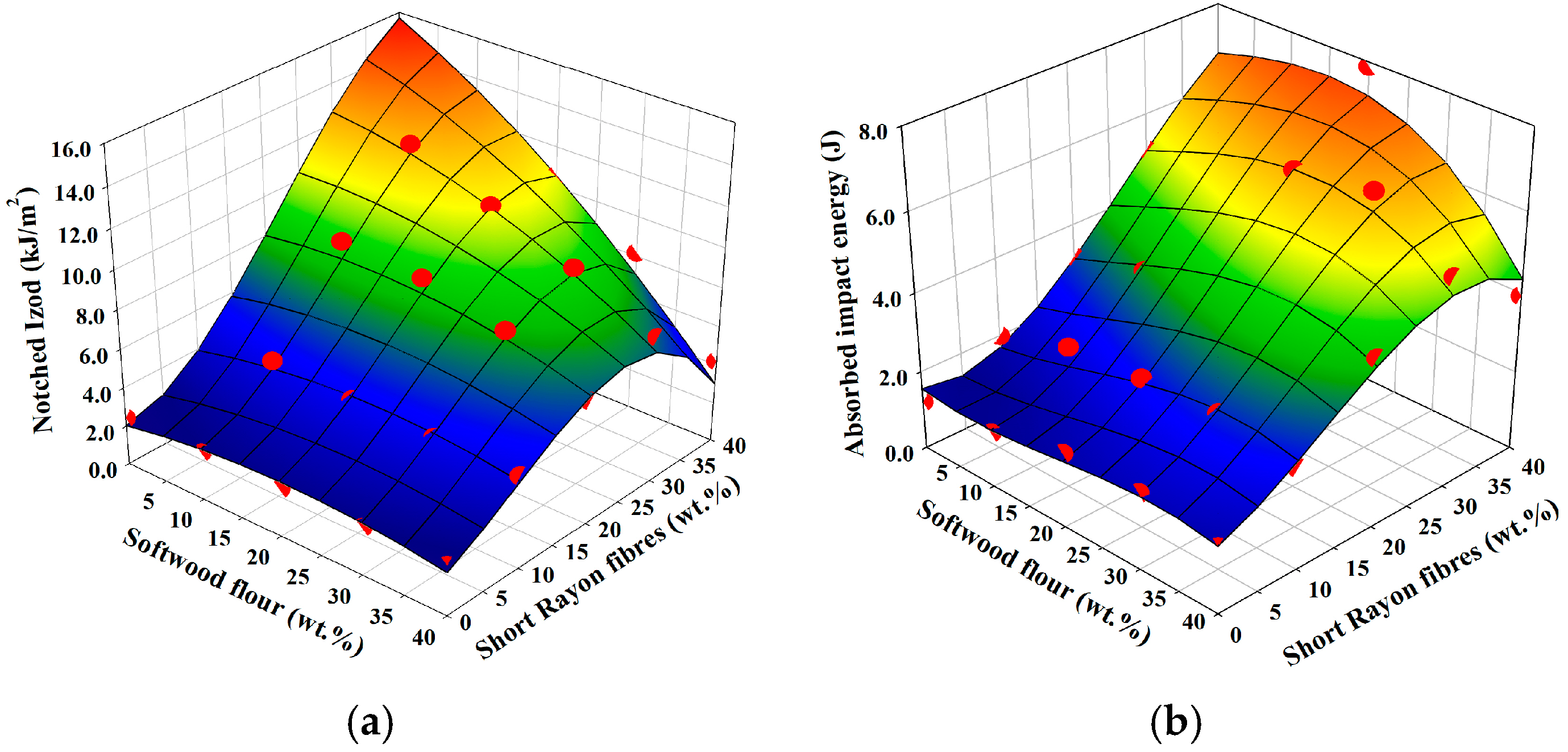
3.7. Impact Properties
4. Conclusions
- Tensile modulus is significantly increased by extra weight fractions of softwood flour added to short rayon fibre reinforcement;
- Tensile strength can be slightly increased by adding softwood flour in composites having up to 20 wt.% of short rayon fibres;
- Flexural strength can be significantly increased by adding softwood flour in composites having up to 30 wt.% of short rayon fibres;
- Impact resistance is slightly decreased by extra weight fractions of softwood flour added to short rayon fibre reinforcement and the decrease is more profound with respect to the notch sensitivity of composites;
- Weight fractions of reinforcement >70% hinder the process of injection moulding and significantly deteriorate strength and impact properties.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| WPC | Wood–polymer composites |
| NFC | Natural fibre composites |
| PP | Polypropylene |
| MA | Maleic anhydride |
| FFD | Full factorial design |
References
- Uddin, N. Developments in Fiber-Reinforced Polymer (FRP) Composites for Civil Engineering; Woodhead Publishing: Philadelphia, PA, USA, 2013; 560p. [Google Scholar]
- Market Analysis Report. Wood Plastics Composites Market Size, Share & Trends Analysis Report by Product (Polyethylene, Polypropylene), by Application (Automotive Components), by Region, and Segment Forecasts, 2025–2030. 198p. Available online: https://www.grandviewresearch.com/industry-analysis/wood-plastic-composites-market (accessed on 1 February 2025).
- Syduzzaman, M.; Al Faruque, M.A.; Bilisik, K.; Naebe, M. Plant-Based Natural Fibre Reinforced Composites: A Review on Fabrication, Properties and Applications. Coatings 2020, 10, 973. [Google Scholar] [CrossRef]
- Pickering, K. Properties and Performance of Natural-Fibre Composites, 1st ed.; Woodhead Publishing: Boca Raton, FL, USA, 2008; 576p. [Google Scholar]
- Pickering, K.L.; Efendy, M.G.A.; Le, T.M. A review of recent developments in natural fibre composites and their mechanical performance. Compos.-A Appl. Sci. Manuf. 2016, 83, 98–112. [Google Scholar] [CrossRef]
- Peças, P.; Carvalho, H.; Salman, H.; Leite, M. Natural Fibre Composites and Their Applications: A Review. J. Compos. Sci. 2018, 2, 66. [Google Scholar] [CrossRef]
- McKay, I.; Vargas, J.; Yang, L.; Felfel, R.M. A Review of Natural Fibres and Biopolymer Composites: Progress, Limitations, and Enhancement Strategies. Materials 2024, 17, 4878. [Google Scholar] [CrossRef] [PubMed]
- Bunsell, A.R. Handbook of Tensile Properties of Textile and Technical Fibres, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2018; 1054p. [Google Scholar]
- Kauffman, G.B. Rayon: The first semi-synthetic fiber product. J. Chem. Educ. 1993, 70, 887. [Google Scholar] [CrossRef]
- Chokshi, S.; Gohil, P.; Patel, D. Experimental investigations of bamboo, cotton and viscose rayon fiber reinforced Unidirectional composites. Mater. Today 2020, 28, 498–503. [Google Scholar] [CrossRef]
- Fu, S.-Y.; Lauke, B. Characterization of tensile behaviour of hybrid short glass fibre/calcite particle/ABS composites. Compos.-A Appl. Sci. Manuf. 1998, 29, 575–583. [Google Scholar] [CrossRef]
- Antonacci, J. Use of Coupled Mica Systems to Enhance Properties of Polypropylene Composites. In Handbook of Polypropylene and Polypropylene Composites; Karian, H.G., Ed.; Marcel Dekker: New York, NY, USA, 2003; pp. 554–571. [Google Scholar]
- Swolfs, Y.; Gorbatikh, L.; Verpoest, I. Fibre hybridisation in polymer composites: A review. Compos.-A Appl. Sci. Manuf. 2014, 67, 181–200. [Google Scholar] [CrossRef]
- Fu, S.-Y.; Lauke, B.; Mäder, E.; Yue, C.-Y.; Hu, X.; Mai, Y.-W. Hybrid effects on tensile properties of hybrid short glass fiber and short carbon fiber reinforced polypropylene composites. J. Mater. Sci. 2001, 36, 1243–1251. [Google Scholar] [CrossRef]
- Wollan, E. Glass & carbon fiber reinforcement combine in hybrid long fiber thermoplastic composites to bridge price & performance gap. J. Reinf. Plast. 2017, 61, 55–57. [Google Scholar] [CrossRef]
- Franciszczak, P.; Smoliński, J. Hybrid all-cellulose reinforcement in polypropylene matrix biocomposites for injection moulding—Influence of particle geometry and volume fraction on hybrid effect. Compos. Struct. 2023, 323, 117450. [Google Scholar] [CrossRef]
- Franciszczak, P.; Kalniņš, K.; Błędzki, A.K. Hybridisation of man-made cellulose and glass reinforcement in short-fibre composites for injection moulding—Effects on mechanical performance. Compos. B Eng. 2018, 145, 14–27. [Google Scholar] [CrossRef]
- Oksman, K.; Clemons, C. Mechanical properties and morphology of impact modified polypropylene-wood flour composites. J. Appl. Polym. Sci. 1998, 67, 1503–1513. [Google Scholar] [CrossRef]
- Khuri, A.I.; Mukhopadhyay, S. Response surface methodology. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 128–149. [Google Scholar] [CrossRef]
- Chelladurai, S.J.S.; Murugan, K.; Ray, A.P.; Upadhyaya, M.; Narasimharaj, V.; Gnanasekaran, S. Optimization of process parameters using response surface methodology: A review. Mater. Today 2020, 37, 1301–1304. [Google Scholar] [CrossRef]
- Marcuello, C.; Chabbert, B.; Berzin, F.; Bercu, N.B.; Molinari, M.; Aguié-Béghin, V. Influence of Surface Chemistry of Fiber and Lignocellulosic Materials on Adhesion Properties with Polybutylene Succinate at Nanoscale. Materials 2023, 16, 2440. [Google Scholar] [CrossRef]
- Bazan, P.; Rochman, A.; Mroczka, K.; Badura, K.; Melnychuk, M.; Nosal, P.; Weglowska, A. Composites Based on PLA/PHBV Blends with Nanocrystalline Cellulose NCC: Mechanical and Thermal Investigation. Materials 2024, 17, 6036. [Google Scholar] [CrossRef]
- Franciszczak, P.; Bledzki, A.K. Tailoring of dual-interface in high tenacity PP composites—Toughening with positive hybrid effect. Compos.-A Appl. Sci. Manuf. 2016, 83, 185–192. [Google Scholar] [CrossRef]
- Bledzki, A.K.; Franciszczak, P.; Osman, Z.; Elbadawi, M. Polypropylene biocomposites reinforced with softwood, abaca, jute, and kenaf fibers. Ind. Crops Prod. 2015, 70, 91–99. [Google Scholar] [CrossRef]
- Franciszczak, P.; Merijs-Meri, R.; Kalniņš, K.; Błędzki, A.K.; Zicans, J. Short-fibre hybrid polypropylene composites reinforced with PET and Rayon fibres—Effects of SSP and interphase tailoring. Compos. Struct. 2017, 181, 121–137. [Google Scholar] [CrossRef]
- Klyosov, A.A. Wood-Plastics Composites, 1st ed.; Wiley-Interscience: Hoboken, NJ, USA, 2007; 740p. [Google Scholar]
- Wang, Y.; He, X.; Deng, L.; Li, X.; Li, X. Preparation Optimization of Enhanced Poplar Wood by Organic–Inorganic Hybrid Treatment via Response Surface Methodology. Materials 2023, 16, 6718. [Google Scholar] [CrossRef]
- Beluns, S.; Gaidukovs, S.; Platnieks, O.; Barkane, A.; Gaidukova, G.; Grase, L.; Nabels-Sneiders, M.; Kovalovs, A.; Thakur, V.K. Clean manufacturing of cellulose nanopapers by incorporating lignin and xylan as sustainable additives. Carbohydr. Polym. Technol. Appl. 2022, 3, 100207. [Google Scholar] [CrossRef]
- Barkanov, E.; Akishin, P.; Namsone, E.; Auzins, J.; Morozovs, A. Optimization of Pultrusion Processes for an Industrial Application. Mech. Compos. Mater. 2021, 56, 697–712. [Google Scholar] [CrossRef]
- Yorukoglu, M.; Celik, A.N. A critical review on the estimation of daily global solar radiation from sunshine duration. Energy Convers. Manag. 2006, 47, 2441–2450. [Google Scholar] [CrossRef]
- Viana, F.A.C.; Haftka, R.T.; Steffen, V. Multiple surrogates: How cross-validation errors can help us to obtain the best predictor. Struct. Multidiscipl. Optim. 2009, 39, 439–457. [Google Scholar] [CrossRef]
- Tripathi, D. Practical Guide to Polypropylene, 1st ed.; Rapra Publishing: Shrewsbury, UK, 2002; 740p. [Google Scholar]
- Shenoy, A.V. Steady shear viscous properties. In Rheology of Filled Polymer Systems; Shenoy, A.V., Ed.; Springer-Science+Business Media: Dordrecht, The Netherlands, 1999; pp. 243–311. [Google Scholar]
- Zhang, T.; Evans, J.R.G. The solidification of large sections in ceramic injection molding: Part I. Conventional molding. J. Mater. Res. 1993, 8, 187–194. [Google Scholar] [CrossRef]
- Evans, K.E.; Gibson, A.G. Prediction of the maximum packing fraction achievable in randomly oriented short-fibre composites. Compos. Technol. 1986, 25, 149–162. [Google Scholar] [CrossRef]
- Madsen, B.; Lilholt, H. Physical and mechanical properties of unidirectional plant fibre composites—An evaluation of the influence of porosity. Compos. Technol. 2003, 63, 1265–1272. [Google Scholar] [CrossRef]
- Hagstrand, P.-O.; Bonjour, F.; Månson, J.-A.E. The influence of void content on the structural flexural performance of unidirectional glass fibre reinforced polypropylene composites. Compos.-A Appl. Sci. Manuf. 2005, 36, 705–714. [Google Scholar] [CrossRef]
- Hine, P.J.; Lusti, H.R.; Gusev, A.A. Numerical simulation of the effects of volume fraction, aspect ratio and fibre length distribution on the elastic and thermoelastic properties of short fibre composites. Compos. Technol. 2002, 62, 1445–1453. [Google Scholar] [CrossRef]
- Mortazavian, S.; Fatemi, A. Effects of fiber orientation and anisotropy on tensile strength and elastic modulus of short fiber reinforced polymer composites. Compos. B Eng. 2015, 72, 116–129. [Google Scholar] [CrossRef]
- Bernasconi, A.; Cosmi, F. Analysis of the dependence of the tensile behaviour of a short fibre reinforced polyamide upon fibre volume fraction, length and orientation. Procedia Eng. 2011, 10, 2129–2134. [Google Scholar] [CrossRef]
- Bledzki, A.K.; Franciszczak, P.; Mamun, A. The utilization of biochemically modified microfibers from grain by-products as reinforcement for polypropylene biocomposite. Express Polym. Lett. 2014, 8, 767–778. [Google Scholar] [CrossRef]
- Wiedenhoeft, A. Chapter 3—Structure and Function of Wood. In Wood Handbook; Forest Products Library: Madison, VA, USA, 2014; pp. 3.1–3.18. [Google Scholar]
- Joffre, T.; Miettinen, A.; Wernersson, E.L.G.; Isaksson, P.; Gamstedt, E.K. Effects of defects on the tensile strength of short-fibre composite materials. Mech. Mater. 2014, 75, 125–134. [Google Scholar] [CrossRef]
- Dilandro, L.; Dibenedetto, A.T.; Groeger, J. The effect of fiber matrix stress transfer on the strength of fiber-reinforced composite materials. Polym. Compos. 1988, 9, 209–221. [Google Scholar] [CrossRef]
- Sharma, A.; Anand Kumar, S.; Kushvaha, V. Effect of aspect ratio on dynamic fracture toughness of particulate polymer composite using artificial neural network. Eng. Fract. Mech. 2020, 228, 106907. [Google Scholar] [CrossRef]
- Sato, N.; Kurauchi, T.; Sato, S.; Kamigaito, O. Microfailure behaviour of randomly dispersed short fibre reinforced thermoplastic composites obtained by direct SEM observation. J. Mater. Sci. 1991, 26, 3891–3898. [Google Scholar] [CrossRef]
- Lin, G.M.; Lai, J.K.L. Fracture mechanism in short fibre reinforced thermoplastic resin composites. J. Mater. Sci. 1993, 28, 5240–5246. [Google Scholar] [CrossRef]
- Várdai, R.; Lummerstorfer, T.; Pretschuh, C.; Jerabek, M.; Gahleitner, M.; Pukánszky, B.; Renner, K. Impact modification of PP/wood composites: A new approach using hybrid fibers. Express Polym. Lett. 2019, 13, 223–234. [Google Scholar] [CrossRef]
- Rogers, M.G.; Plumtree, A. A comparison of Charpy and Izod test modes for polystyrene. Polym. Test. 1992, 11, 13–21. [Google Scholar] [CrossRef]
- Hartl, A.M.; Jerabek, M.; Lang, R.W. Effect of fiber orientation, stress state and notch radius on the impact properties of short glass fiber reinforced polypropylene. Polym. Test. 2015, 43, 1–9. [Google Scholar] [CrossRef]


| Design Factors: k = 2 (Reinforcement Type) | Levels: m = 5 (wt.%) | ||||
|---|---|---|---|---|---|
| Short rayon fibres | 0 | 10 | 20 | 30 | 40 |
| Softwood flour | 0 | 10 | 20 | 30 | 40 |
| Run | Factor X1 1 | Factor X2 2 | Weho 500 (wt.%) | Cordenka (wt.%) | PP Matrix (wt.%) | Real Density (g/ccm) | Std. Dev. | Theoretical Density (g/ccm) | Porosity—Void Content (vol.%) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 100.00 | 0.906 | 0.002 | - | - |
| 2 | 0 | 10 | 11.24 | 0 | 88.76 | 0.945 | 0.002 | 0.9470 | 0.19 |
| 3 | 0 | 20 | 19.98 | 0 | 80.02 | 0.982 | 0.001 | 0.9818 | −0.02 |
| 4 | 0 | 30 | 29.57 | 0 | 70.43 | 1.022 | 0.001 | 1.0231 | 0.11 |
| 5 | 0 | 40 | 39.11 | 0 | 60.89 | 1.056 | 0.019 | 1.0677 | 1.11 |
| 6 | 10 | 0 | 0 | 10.59 | 89.41 | 0.948 | 0.011 | 0.9503 | 0.29 |
| 7 | 10 | 10 | 0 | 20.44 | 79.56 | 0.985 | 0.001 | 0.9959 | 1.08 |
| 8 | 10 | 20 | 0 | 30.29 | 69.71 | 1.028 | 0.008 | 1.0461 | 1.73 |
| 9 | 10 | 30 | 0 | 40.22 | 59.78 | 1.072 | 0.002 | 1.1022 | 2.76 |
| 10 | 10 | 40 | 9.92 | 9.92 | 80.17 | 0.983 | 0.001 | 0.9870 | 0.37 |
| 11 | 20 | 0 | 9.92 | 19.84 | 70.23 | 1.025 | 0.002 | 1.0368 | 1.15 |
| 12 | 20 | 10 | 10.02 | 30.07 | 59.91 | 1.073 | 0.002 | 1.0941 | 1.96 |
| 13 | 20 | 20 | 10.00 | 39.98 | 50.02 | 1.115 | 0.003 | 1.1553 | 3.50 |
| 14 | 20 | 30 | 19.84 | 9.92 | 70.25 | 1.027 | 0.001 | 1.0303 | 0.36 |
| 15 | 20 | 40 | 19.60 | 19.60 | 60.80 | 1.071 | 0.002 | 1.0820 | 1.00 |
| 16 | 30 | 0 | 20.04 | 30.06 | 49.90 | 1.126 | 0.007 | 1.1479 | 1.91 |
| 17 | 30 | 10 | 20.00 | 39.99 | 40.01 | 1.165 | 0.004 | 1.2155 | 4.15 |
| 18 | 30 | 20 | 30.48 | 10.16 | 59.36 | 1.070 | 0.001 | 1.0824 | 1.11 |
| 19 | 30 | 30 | 30.18 | 20.12 | 49.70 | 1.121 | 0.001 | 1.1411 | 1.78 |
| 20 | 30 | 40 | 29.87 | 29.87 | 40.25 | 1.168 | 0.005 | 1.2049 | 3.10 |
| 21 | 40 | 0 | 30.04 | 40.06 | 29.90 | 1.225 | 0.007 | 1.2832 | 4.54 |
| 22 | 40 | 10 | 40.33 | 10.08 | 49.59 | 1.118 | 0.002 | 1.1338 | 1.37 |
| 23 | 40 | 20 | 40.40 | 20.20 | 39.40 | 1.175 | 0.001 | 1.2017 | 2.25 |
| 24 | 40 | 30 | 40.09 | 30.07 | 29.84 | 1.228 | 0.003 | 1.2736 | 3.60 |
| 25 | 40 | 40 | 39.76 | 39.76 | 20.47 | 1.273 | 0.012 | 1.3529 | 5.91 |
| Run | Factor X1 1 | Factor X2 2 | Tensile Modulus (GPa) | Tensile Strength (MPa) | Tensile Strain (%) | Flexural Modulus (GPa) | Flexural Strength (MPa) | Izod Impact Strength (kJ/m2) | Absorbed Energy in Impact (J) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1.55 ± 0.03 | 27.6 ± 0.1 | 10.4 ± 0.1 | 1.46 ± 0.02 | 42.3 ± 0.4 | 2.4 ± 0.1 | 1.2 ± 0.2 |
| 2 | 0 | 10 | 2.02 ± 0.13 | 38.4 ± 4.4 | 9.1 ± 0.4 | 2.29 ± 0.04 | 61.0 ± 0.5 | 3.8 ± 0.2 | 2.0 ± 0.5 |
| 3 | 0 | 20 | 3.08 ± 0.04 | 50.1 ± 0.9 | 8.2 ± 0.1 | 3.02 ± 0.05 | 79.4 ± 0.6 | 6.8 ± 0.4 | 3.2 ± 0.7 |
| 4 | 0 | 30 | 4.15 ± 0.07 | 65.8 ± 1.0 | 7.2 ± 0.5 | 4.02 ± 0.08 | 102.2 ± 0.8 | 11.7 ± 0.4 | 5.1 ± 0.6 |
| 5 | 0 | 40 | 4.85 ± 0.12 | 72.0 ± 1.0 | 5.0 ± 0.2 | 4.46 ± 0.10 | 113.8 ± 1.6 | 14.2 ± 0.4 | 6.8 ± 0.6 |
| 6 | 10 | 0 | 2.20 ± 0.05 | 29.4 ± 0.3 | 5.3 ± 0.1 | 2.07 ± 0.05 | 49.6 ± 0.7 | 2.5 ± 0.2 | 1.4 ± 0.5 |
| 7 | 10 | 10 | 3.10 ± 0.04 | 40.9 ± 0.7 | 7.0 ± 0.4 | 2.89 ± 0.03 | 69.8 ± 0.6 | 5.1 ± 0.2 | 2.6 ± 0.5 |
| 8 | 10 | 20 | 3.98 ± 0.08 | 54.4 ± 0.9 | 6.8 ± 0.8 | 3.77 ± 0.05 | 90.7 ± 0.6 | 9.3 ± 0.5 | 3.7 ± 0.5 |
| 9 | 10 | 30 | 4.82 ± 0.09 | 66.1 ± 1.1 | 5.6 ± 0.6 | 4.63 ± 0.11 | 111.1 ± 1.0 | 12.4 ± 0.6 | 5.5 ± 0.9 |
| 10 | 10 | 40 | 5.62 ± 0.16 | 64.5 ± 5.0 | 2.6 ± 0.6 | 5.07 ± 0.07 | 116.0 ± 2.2 | 11.0 ± 0.8 | 7.0 ± 1.0 |
| 11 | 20 | 0 | 2.96 ± 0.04 | 32.5 ± 0.1 | 3.3 ± 0.1 | 2.79 ± 0.11 | 57.2 ± 1.2 | 2.5 ± 0.2 | 1.9 ± 0.4 |
| 12 | 20 | 10 | 3.89 ± 0.08 | 45.1 ± 0.6 | 5.5 ± 0.4 | 3.79 ± 0.05 | 82.4 ± 0.9 | 4.9 ± 0.3 | 2.8 ± 0.2 |
| 13 | 20 | 20 | 4.89 ± 0.15 | 59.9 ± 0.8 | 5.3 ± 0.4 | 4.82 ± 0.04 | 105.6 ± 0.7 | 9.1 ± 0.4 | 3.7 ± 0.5 |
| 14 | 20 | 30 | 5.72 ± 0.09 | 67.2 ± 2.0 | 3.5 ± 0.5 | 5.58 ± 0.10 | 122.2 ± 1.1 | 10.8 ± 0.9 | 6.2 ± 1.2 |
| 15 | 20 | 40 | 6.24 ± 0.27 | 62.1 ± 5.1 | 2.1 ± 0.4 | 5.63 ± 0.23 | 114.3 ± 5.2 | 10.6 ± 1.2 | 7.9 ± 0.9 |
| 16 | 30 | 0 | 3.82 ± 0.05 | 37.7 ± 0.2 | 2.7 ± 0.1 | 3.60 ± 0.03 | 63.5 ± 0.5 | 2.5 ± 0.1 | 2.0 ± 0.2 |
| 17 | 30 | 10 | 4.98 ± 0.10 | 51.4 ± 0.4 | 3.8 ± 0.1 | 4.97 ± 0.04 | 94.9 ± 0.5 | 4.8 ± 0.4 | 2.9 ± 0.9 |
| 18 | 30 | 20 | 5.91 ± 0.12 | 62.8 ± 0.8 | 3.7 ± 0.1 | 5.79 ± 0.05 | 115.8 ± 0.8 | 8.1 ± 0.5 | 4.2 ± 0.6 |
| 19 | 30 | 30 | 6.42 ± 0.21 | 61.4 ± 1.9 | 2.2 ± 0.3 | 6.13 ± 0.21 | 117.2 ± 5.7 | 9.3 ± 1.0 | 6.5 ± 1.3 |
| 20 | 30 | 40 | 7.87 ± 0.25 | 63.3 ± 1.6 | 1.4 ± 0.1 | 6.92 ± 0.25 | 109.6 ± 6.8 | 8.2 ± 1.4 | 6.1 ± 1.5 |
| 21 | 40 | 0 | 4.77 ± 0.06 | 39.2 ± 0.2 | 2.0 ± 0.1 | 4.56 ± 0.05 | 65.2 ± 0.6 | 2.6 ± 0.1 | 1.7 ± 0.1 |
| 22 | 40 | 10 | 5.63 ± 0.06 | 52.4 ± 0.8 | 2.8 ± 0.1 | 5.70 ± 0.07 | 98.1 ± 1.0 | 4.8 ± 0.2 | 2.6 ± 0.5 |
| 23 | 40 | 20 | 6.66 ± 0.14 | 61.8 ± 1.5 | 2.6 ± 0.3 | 6.63 ± 0.28 | 110.3 ± 6.0 | 6.3 ± 0.8 | 4.3 ± 1.4 |
| 24 | 40 | 30 | 7.97 ± 0.21 | 60.0 ± 4.1 | 1.4 ± 0.2 | 7.28 ± 0.10 | 110.0 ± 3.4 | 7.4 ± 1.1 | 5.3 ± 1.2 |
| 25 | 40 | 40 | 8.13 ± 0.30 | 38.3 ± 3.1 | 0.6 ± 0.1 | 7.76 ± 0.74 | 77.2 ± 9.4 | 2.4 ± 1.1 | 3.9 ± 1.0 |
| Property | σcross, % | σ | σr, % | |
|---|---|---|---|---|
| First-order polynomial equation | ||||
| rcomp | 9.74 | 0.99 | 0.01 | 8.68 |
| VVol. | 35.05 | 0.89 | 0.50 | 31.91 |
| ETens | 11.72 | 0.99 | 0.19 | 10.79 |
| σTens | 72.84 | 0.58 | 8.59 | 64.99 |
| ɛTens | 48.52 | 0.80 | 1.15 | 44.63 |
| EFlex | 14.94 | 0.98 | 0.23 | 14.02 |
| σFlex | 67.01 | 0.67 | 14.69 | 60.33 |
| EIZOD | 59.89 | 0.71 | 2.21 | 59.89 |
| EImpact | 44.53 | 0.84 | 0.78 | 39.97 |
| Second-order polynomial equation | ||||
| rcomp | 4.94 | 0.99 | 0.01 | 3.76 |
| VVol. | 17.86 | 0.98 | 0.23 | 14.51 |
| ETens | 12.61 | 0.99 | 0.18 | 10.12 |
| σTens | 49.14 | 0.88 | 4.63 | 35.03 |
| ɛTens | 30.34 | 0.94 | 0.612 | 23.65 |
| EFlex | 9.99 | 0.99 | 0.147 | 8.77 |
| σFlex | 45.78 | 0.89 | 7.98 | 32.76 |
| EIZOD | 42.38 | 0.89 | 1.56 | 42.38 |
| EImpact | 43.23 | 0.89 | 0.64 | 32.59 |
| Third-order polynomial equation | ||||
| rcomp | 5.20 | 0.99 | 0.01 | 3.32 |
| VVol. | 19.96 | 0.98 | 0.22 | 14.29 |
| ETens | 16.35 | 0.99 | 0.19 | 10.63 |
| σTens | 30.93 | 0.96 | 2.63 | 19.91 |
| ɛTens | 39.84 | 0.95 | 0.57 | 22.15 |
| EFlex | 10.54 | 0.99 | 0.14 | 8.39 |
| σFlex | 13.83 | 0.99 | 2.30 | 9.44 |
| EIZOD | 36.96 | 0.95 | 1.36 | 36.96 |
| EImpact | 31.08 | 0.95 | 0.42 | 21.45 |
| Term | Coefficients | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ρcomp | VVol. | ETens | σTens | ɛTens | EFlex | σFlex | EIZOD | EImpact | |
| Constant | 0.91 | 0.41 | 1.36680 | 28.9018 | 9.07400 | 1.38280 | 44.0908 | 2.03794 | 0.42030 |
| X1 | 3.40 × 10−3 | −3.68 × 10−2 | 0.08696 | −0.53697 | −0.29183 | 0.08468 | −0.18528 | 0.07504 | 0.11780 |
| X2 | 4.03 × 10−3 | −2.05 × 10−2 | 0.08798 | 0.67296 | 0.07415 | 0.07744 | 1.07525 | 0.01891 | 0.15679 |
| X1·X1 | 1.25 × 10−5 | 1.19 × 10−3 | - | 0.05135 | 0.00260 | - | 0.06207 | −0.00155 | −0.00212 |
| X2·X2 | - | 2.15 × 10−3 | - | 0.04088 | −0.00442 | - | 0.05684 | 0.00498 | 0.00003 |
| X1·X2 | 3.37 × 10−5 | 1.40 × 10−3 | - | 0.04161 | 0.00194 | - | 0.10456 | 0.02009 | −0.00162 |
| X1·X1·X1 | - | - | - | −0.00079 | - | - | −0.00109 | −0.00001 | - |
| X1·X1·X2 | - | - | - | −0.00056 | - | - | −0.00111 | −0.00003 | - |
| X1·X2·X2 | - | - | - | −0.00111 | - | - | −0.00239 | −0.00026 | - |
| X2·X2·X2 | - | - | - | −0.00078 | - | - | −0.00099 | −0.00032 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Franciszczak, P.; Kovalovs, A.; Kwiatkowska, M. Hybrid Polypropylene Biocomposites Reinforced with Short Man-Made Cellulose Fibres and Softwood Flour—Optimisation of Properties Using Response Surface Methodology. Materials 2025, 18, 1239. https://doi.org/10.3390/ma18061239
Franciszczak P, Kovalovs A, Kwiatkowska M. Hybrid Polypropylene Biocomposites Reinforced with Short Man-Made Cellulose Fibres and Softwood Flour—Optimisation of Properties Using Response Surface Methodology. Materials. 2025; 18(6):1239. https://doi.org/10.3390/ma18061239
Chicago/Turabian StyleFranciszczak, Piotr, Andrejs Kovalovs, and Magdalena Kwiatkowska. 2025. "Hybrid Polypropylene Biocomposites Reinforced with Short Man-Made Cellulose Fibres and Softwood Flour—Optimisation of Properties Using Response Surface Methodology" Materials 18, no. 6: 1239. https://doi.org/10.3390/ma18061239
APA StyleFranciszczak, P., Kovalovs, A., & Kwiatkowska, M. (2025). Hybrid Polypropylene Biocomposites Reinforced with Short Man-Made Cellulose Fibres and Softwood Flour—Optimisation of Properties Using Response Surface Methodology. Materials, 18(6), 1239. https://doi.org/10.3390/ma18061239





