Nonstationary Stochastic Responses of Transmission Tower-Line System with Viscoelastic Material Dampers Under Seismic Excitations
Abstract
1. Introduction
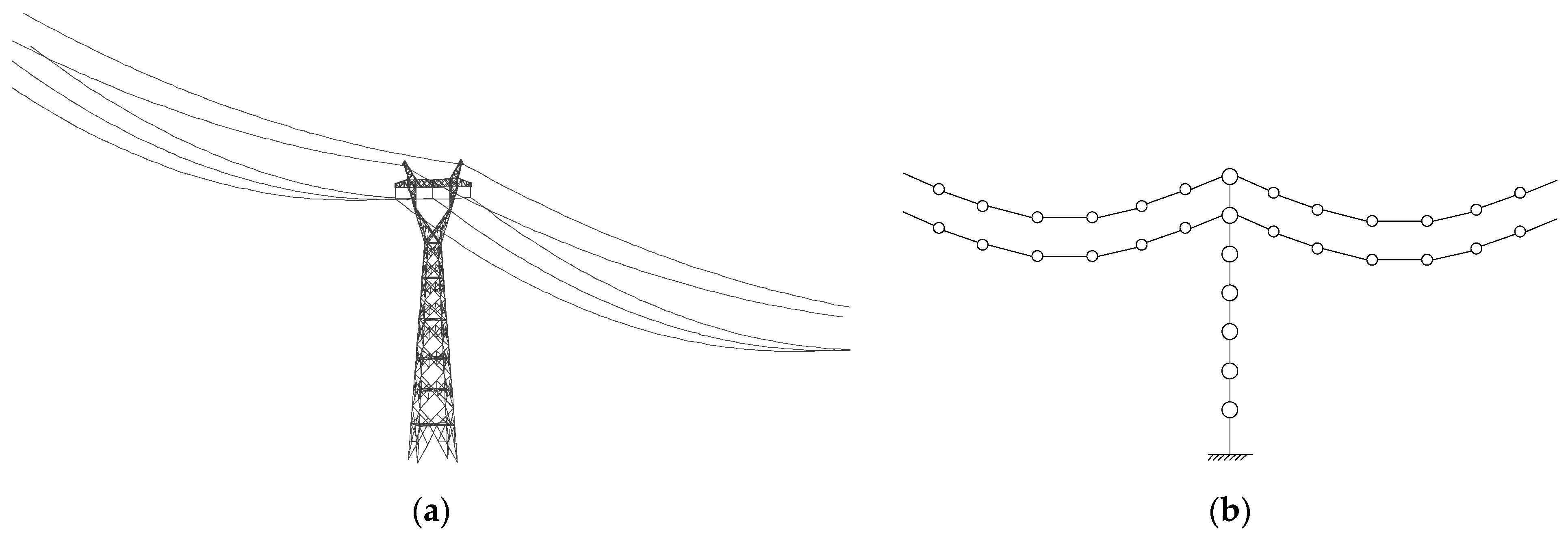
2. Model of TTL-VMD System
2.1. Mechanical Model of TTL
2.2. Mechanical Model of VMDs
3. Equation of Motion of TTL System with VMDs
4. Nonstationary Stochastic Seismic Responses of TTL-VMD System
4.1. Nonstationary Stochastic Seismic Excitation
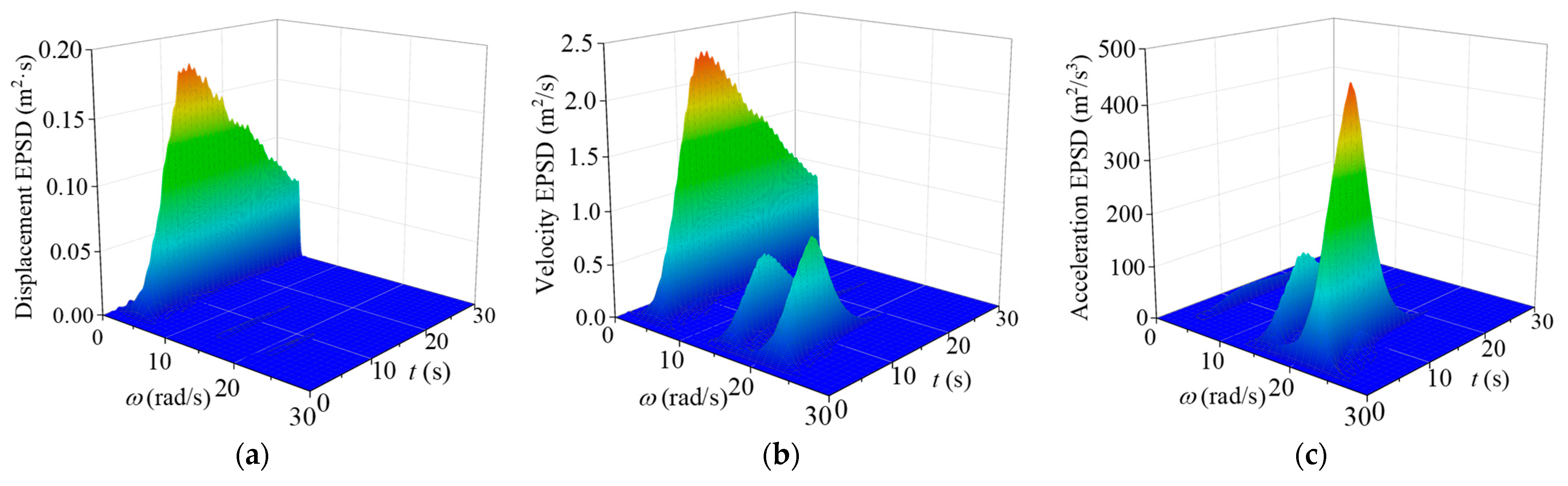
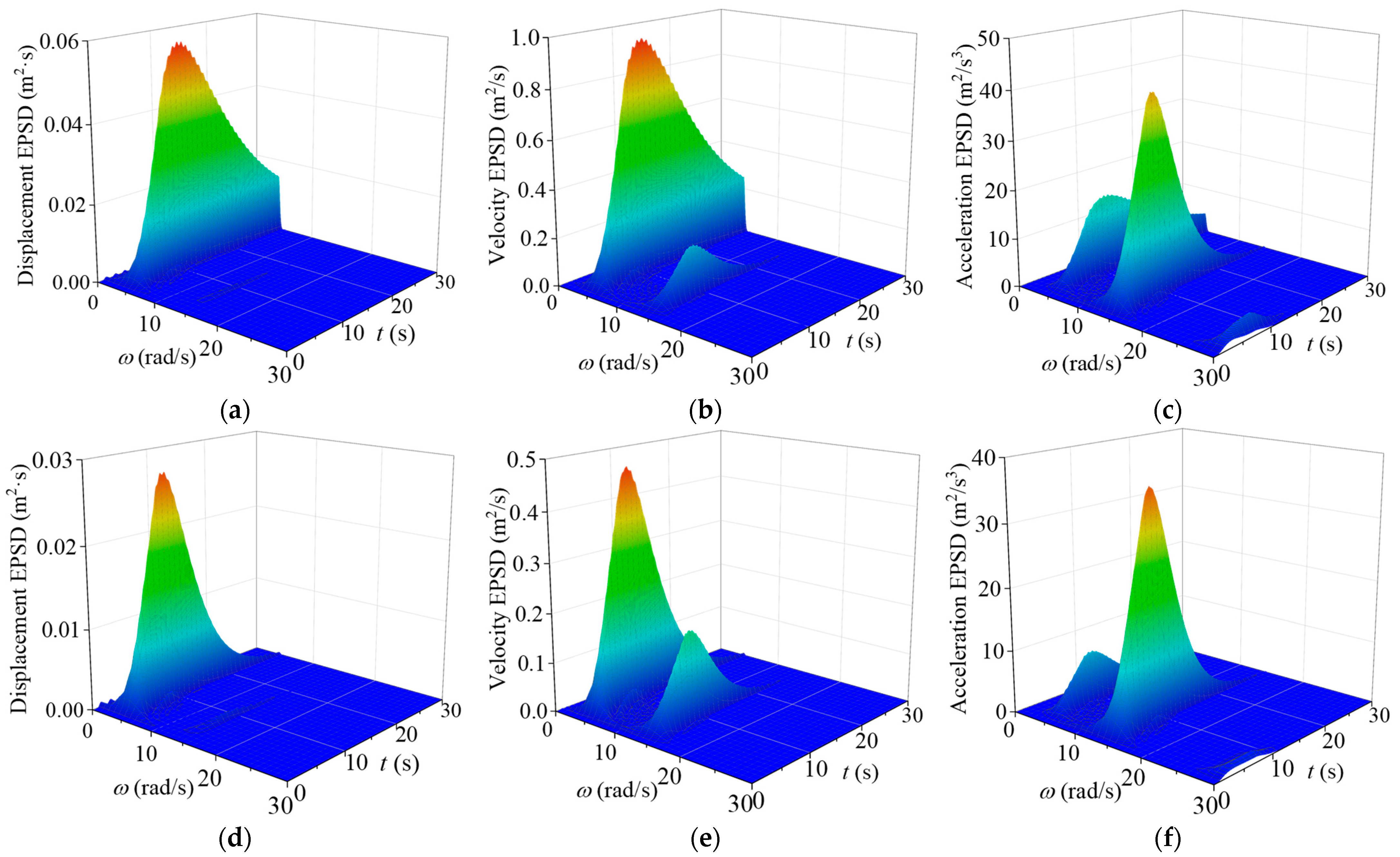
4.2. Nonstationary Stochastic Seismic Responses
4.3. Extreme Responses of Controlled System
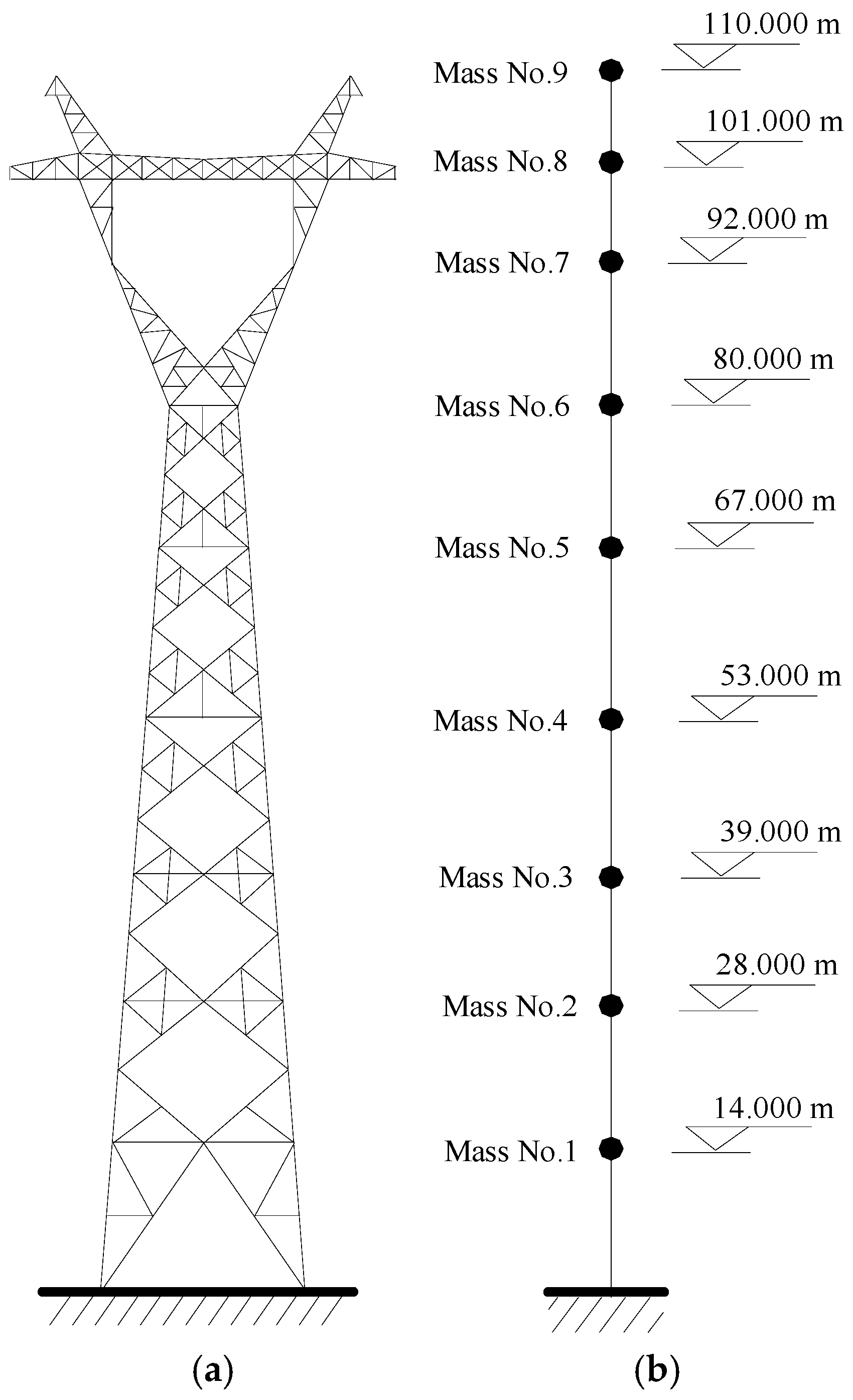
5. Case Study
5.1. Analytical Parameters
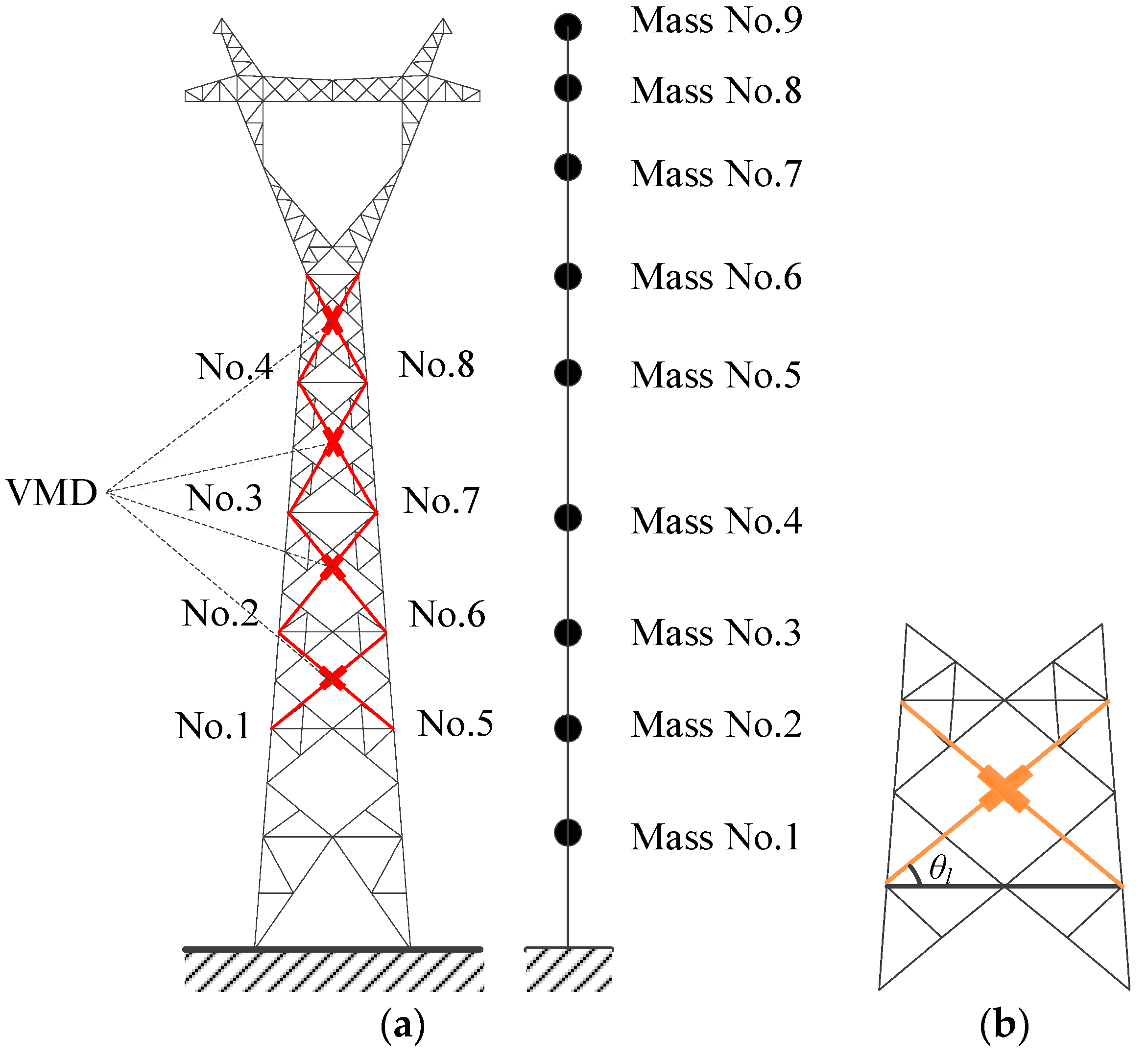
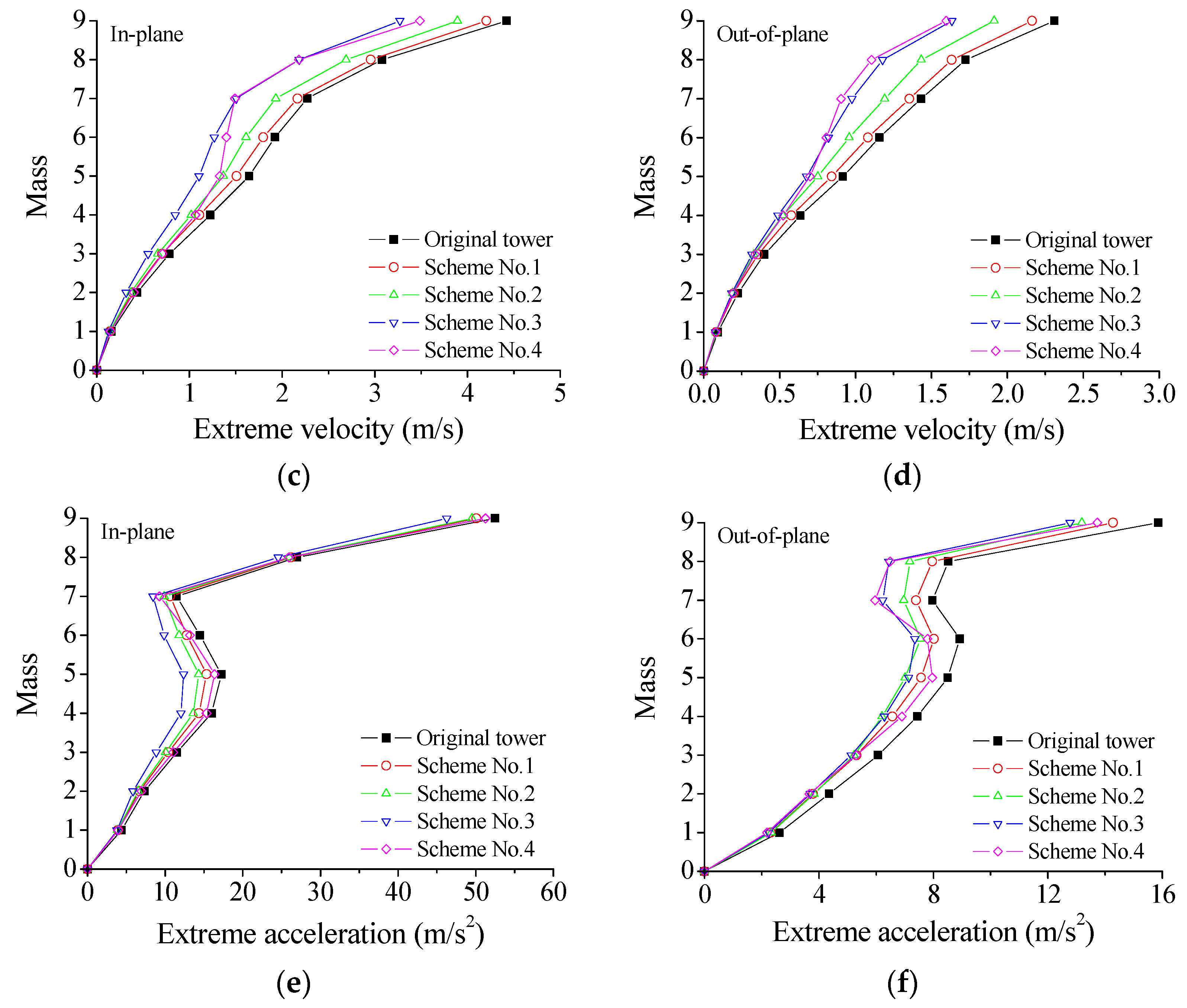
5.2. Damper Installation Schemes
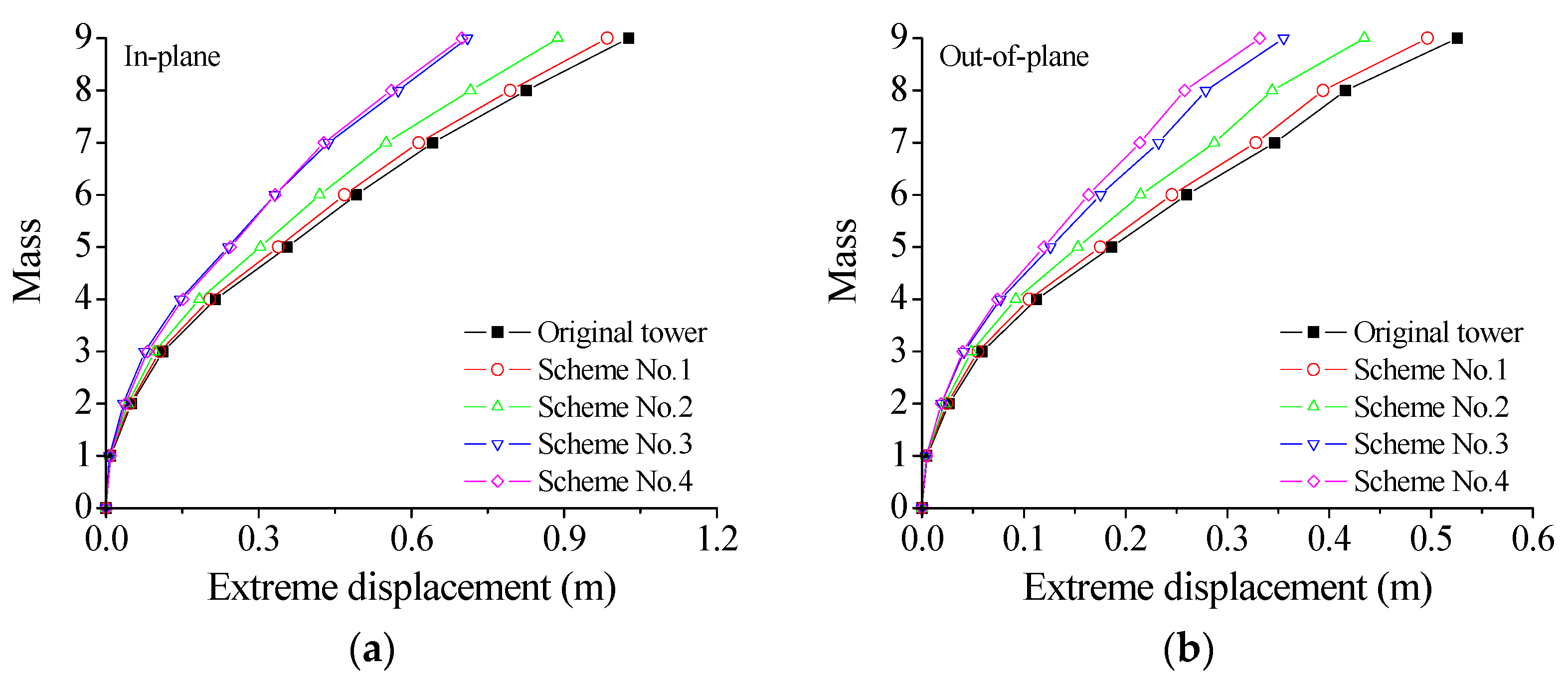
5.3. Control Performance
6. Parametric Study
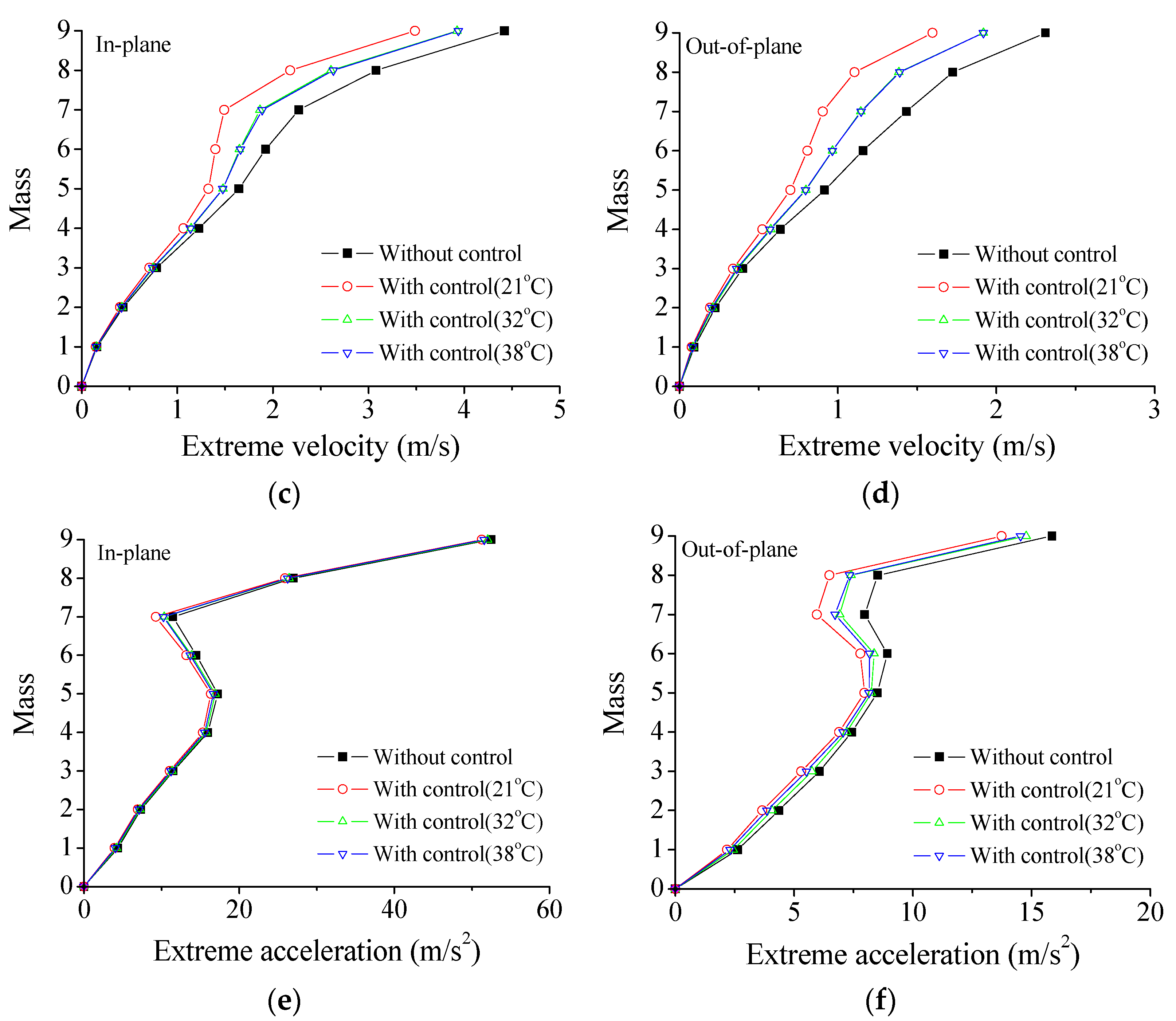
6.1. Effect of Service Temperature
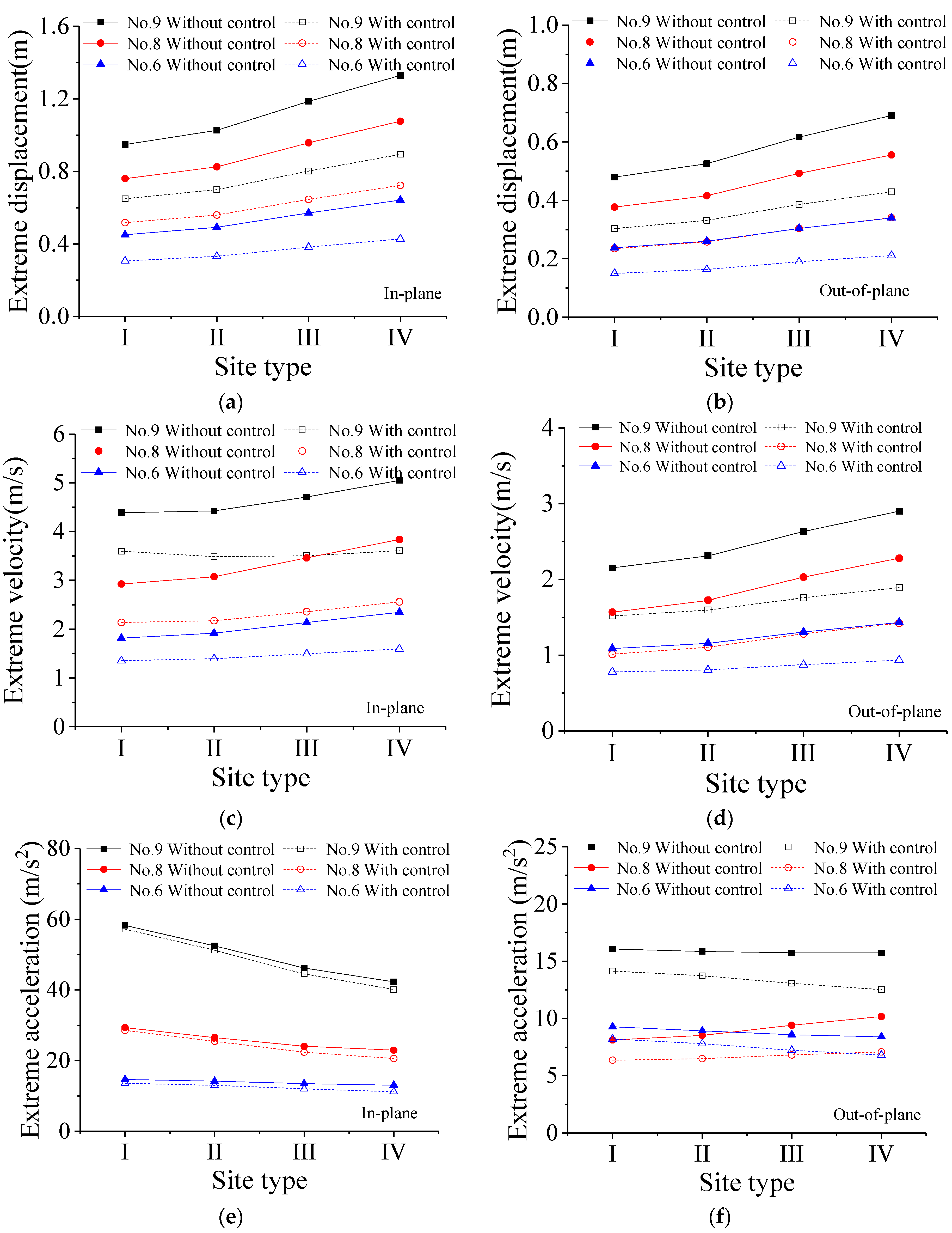
6.2. Effect of Site Type
7. Conclusions
- (1)
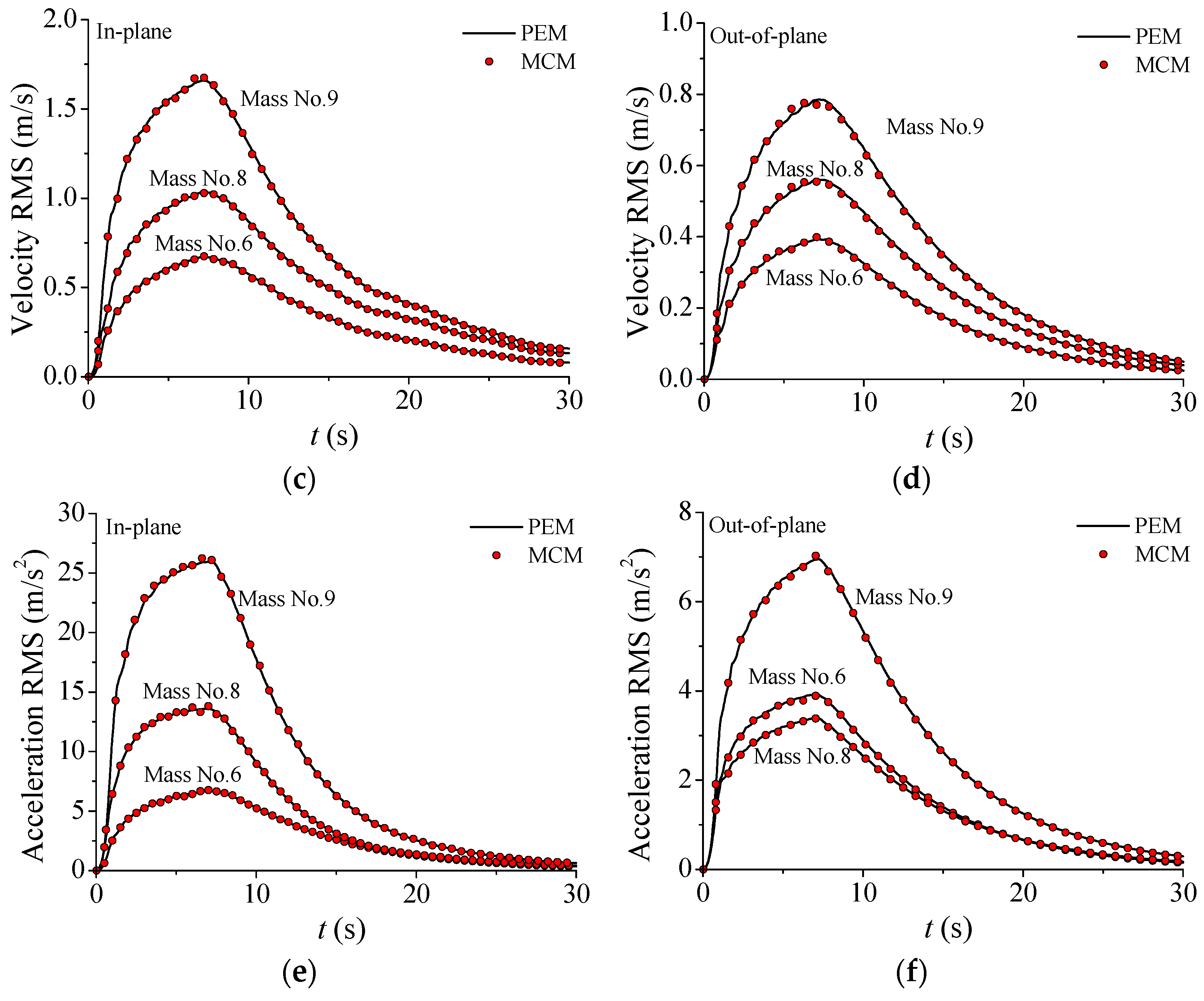
- The nonstationary stochastic responses of the TTL system are consistent with those based on MCM, validating the accuracy of the proposed analytical framework and demonstrating the effectiveness of VMDs in stochastic response reduction of the TTL system. The VMDs exhibit satisfactory control performance in reducing displacement, while the influence on acceleration is relatively minor.
- (2)
- All four damper installation schemes can mitigate the seismic responses of the TTL system. Scheme No. 4 exhibits the best control effectiveness in both directions in comparison with the other schemes.
- (3)
- Temperature significantly influences the control performance of VMDs, with optimal control effects observed at 21 °C. In contrast, higher temperatures result in a relatively lower reduction rate of stochastic dynamic responses.
- (4)
- The site type has a notable influence on the stochastic seismic responses of the TTL system. Under different site conditions, VMD is effective in controlling the extreme responses of transmission towers, with particularly stable control over displacement. As soil conditions become softer, both extreme displacement and velocity exhibit a significant increasing trend, while extreme acceleration shows a decreasing trend.
- (5)
- It is noted that the proposed comprehensive analytical framework is versatile and applicable to the seismic response analysis of other types of TTL systems with VMDs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbol | Description |
| a(t) | Uniform modulation function for t |
| a(ω,t) | Modulation function for t and ω |
| A, h | Total shear area/total thickness |
| c0, c1, c2 | Damping coefficients of the six-parameter model |
| c0l, c1l, c2l | Damping coefficients of the six-parameter model in the lth layer |
| C | Damping matrix of the transmission tower-line system |
| C0 | Damping matrix composed of all the parameters c0 in the VMD system |
| Cin, Cout | Damping matrix in the in-plane/out-of-plane direction |
| d; | Displacement/velocity of the damper |
| dl | Relative displacement between the lth layer and the (l − 1)th layer of the transmission tower |
| Fv | Damper force |
| Fv | Damper force vector |
| Damper force vector of the VMDs in the in-plane/out-of-plane direction | |
| Pseudo-excitation vector of the system | |
| Pseudo-damper force vector of the system | |
| g | Gravitational acceleration |
| Shear storage/loss modulus | |
| H | State matrix in the equation of state |
| I | Identity matrix |
| k0, k1, k2 | Stiffness coefficients of the six-parameter model |
| k0l, k1l, k2l | Stiffness coefficients of the six-parameter model in the lth layer |
| K′, K″ | Storage/loss stiffness |
| K | Stiffness matrix of the transmission tower-line system |
| K0, K1, K2 | Stiffness matrix composed of all the parameters k0/k1/k2 in the VMD system |
| Stiffness matrix of the transmission line in the in-plane/out-of-plane direction | |
| Kin, Kout | Stiffness matrix in the in-plane/out-of-plane direction |
| M | Number of frequency points with equal intervals |
| M | Mass matrix of the transmission tower-line system |
| Mass matrix of the transmission line in the in-plane/out-of-plane direction | |
| Min, Mout | Mass matrix of the transmission tower-line system in the in-plane/out-of-plane direction |
| n | Damper number in the tower |
| N(ω) | Orthogonal incremental process |
| p1, p2 | Damper forces of the Maxwell elements |
| P1(t), P2(t) | Damper force vectors of the Maxwell element |
| Pseudo-damper force vectors of the Maxwell element | |
| Excitation vector in the equation of state | |
| r0(ω,t), r1(ω,t) | Parameter vectors determined by r(ω,t) |
| R | Reduction rate of the extreme response |
| S0 | Spectral intensity coefficient |
| Power spectral density function of a stationary process | |
| Evolutionary power spectral density function of the nonstationary stochastic seismic excitation | |
| Equivalent stationary power spectral density function | |
| Power spectral density function of the state vector in the equation of state | |
| Tc, Uc | Kinetic/potential energy of the transmission line |
| t | Time variable |
| U1, U2 | Matrix composed of the reciprocal μ1/μ2 of the relaxation time of the Maxwell elements |
| Pseudo-state vector in the equation of state | |
| Wc(t) | Virtual work of the transmission line |
| Nonstationary seismic acceleration excitation | |
| y(t) | Nonstationary response |
| yl | Displacement of the transmission tower-line system in the lth layer |
| Equivalent stationary response | |
| Extreme value of the equivalent stationary response | |
| Extreme responses of the original/controlled system | |
| Displacement/velocity/acceleration responses vector | |
| yin(t), yout(t) | Displacement in the in-plane/out-of-plane direction |
| Pseudo-displacement/velocity | |
| Shear stress/strain | |
| Response variance of the system at time tm | |
| ω | Circular frequency |
| ωg | Ground filter frequency |
| ξg | Ground filter damping ratio |
| μ1, μ2 | Reciprocal of the relaxation time of the Maxwell elements |
| μ1l, μ1l | Reciprocal of the relaxation time of the Maxwell elements in the lth layer |
| θl | Angle between the damper installed in the lth layer |
| Π | Position matrix of the damper forces of the VMDs |
| 0th-order/2nd-order spectral moment | |
| τ | Duration during which the intensity exceeds 50% of the peak vibration |
| η | Ratio of extreme value and standard deviation of the equivalent stationary response |
| diag[·] | Diagonal matrix |
| P(·) | Probability distribution |
| Acronym | Description |
| EPSD | Evolutionary power spectral density |
| MCM | Monte Carlo Method |
| PEM | Pseudo-excitation method |
| PSD | Power spectral density |
| RMS | Root mean square |
| TTL | Transmission tower-line |
| TTL-VMD | Transmission tower-line and viscoelastic material damper |
| VMD | Viscoelastic material damper |
| 3D | Three-dimensional |
References
- Tian, L.; Ma, R.S.; Li, H.N.; Wang, Y. Progressive collapse of power transmission tower-line system under extremely strong earthquake excitations. Int. J. Struct. Stab. Dyn. 2016, 16, 1550030. [Google Scholar] [CrossRef]
- Chen, B.; Guo, W.H.; Li, P.Y.; Xie, W.P. Dynamic responses and vibration control of the transmission tower-line system: A state-of-the-art review. Sci. World J. 2014, 2014, 538457. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.W.; Kwak, M.K.; Kim, S.M.; Feeny, B.F. Slewing and active vibration control of a flexible single-link manipulator. Actuators 2025, 14, 43. [Google Scholar] [CrossRef]
- Hasheminejad, S.M.; Lissek, H.; Vesal, R. Energy harvesting and inter-floor impact noise control using an optimally tuned hybrid damping system. Acta Acust. 2024, 8, 42. [Google Scholar] [CrossRef]
- Xie, Q.; Sun, L. Failure mechanism and retrofitting strategy of transmission tower structures under ice load. J. Constr. Steel Res. 2012, 74, 26–36. [Google Scholar] [CrossRef]
- Chen, B.; Weng, S.; Zhi, L.H.; Li, D.M. Response control of a large transmission tower line system under seismic excitations using friction dampers. Adv. Struct. Eng. 2017, 20, 1155–1173. [Google Scholar] [CrossRef]
- Chen, B.; Sun, Y.Z.; Li, Y.L.; Zhao, S.L. Control of seismic response of a building frame by using hybrid system with magnetorheological dampers and isolators. Adv. Struct. Eng. 2014, 17, 1199–1215. [Google Scholar] [CrossRef]
- Versaci, M.; Palumbo, A. Magnetorheological fluids: Qualitative comparison between a mixture model in the Extended Irreversible Thermodynamics framework and a Herschel–Bulkley experimental elastoviscoplastic model. Int. J. Non-Linear Mech. 2020, 118, 103288. [Google Scholar] [CrossRef]
- Versaci, M.; Angiulli, G. A FEMs magnetic-thermal study for a MR automotive damper. In Proceedings of the Photonics & Electromagnetics Research Symposium (PIERS), Hangzhou, China, 21–25 November 2021. [Google Scholar] [CrossRef]
- Chen, B.; Zheng, J.; Qu, W.L. Control of wind-induced response of transmission tower-line system by using magnetorheological dampers. Int. J. Struct. Stab. Dyn. 2009, 9, 661–685. [Google Scholar] [CrossRef]
- Chen, B.; Yang, D.; Feng, K.; Ouyang, Y.Q. Response control of a high-rise television tower under seismic excitations by friction dampers. Int. J. Struct. Stab. Dyn. 2018, 18, 1850140. [Google Scholar] [CrossRef]
- Palmeri, A.; Ricciardelli, F.; De Luca, A.; Muscolino, G. State space formulation for linear viscoelastic dynamic systems with memory. J. Eng. Mech. ASCE 2003, 129, 715–724. [Google Scholar] [CrossRef]
- Palmeri, A.; Muscolino, G. A numerical method for the time-domain dynamic analysis of buildings equipped with viscoelastic dampers. Struct. Control Health Monit. 2011, 18, 519–539. [Google Scholar] [CrossRef]
- Tsai, C.S.; Lee, H.H. Applications of viscoelastic dampers to high-rise buildings. J. Struct. Eng. ASCE 1993, 119, 1222–1233. [Google Scholar] [CrossRef]
- Shu, Z.; You, R.; Zhou, Y. Viscoelastic materials for structural dampers: A review. Constr. Build. Mater. 2022, 342, 127955. [Google Scholar] [CrossRef]
- Chang, T.S.; Singh, M.P. Seismic analysis of structures with a fractional derivative model of viscoelastic dampers. Earthq. Eng. Eng. Vib. 2002, 2, 251–260. [Google Scholar] [CrossRef]
- Gan, F.L.; Jiang, H.L. Wind-induced vibration control for transmission system using steel-lead viscoelastic damper. Adv. Mater. Dev. Appl. Mech. 2014, 597, 376–379. [Google Scholar] [CrossRef]
- Zeng, C.; Hao, D.X.; Hou, L.Q. Research on calculation of equivalent damping ratio of electrical transmission tower line system with viscoelastic dampers. Adv. Mater. Res. 2014, 1064, 115–119. [Google Scholar] [CrossRef]
- Huang, G.P.; Hu, J.H.; He, Y.Z.; Liu, H.B.; Sun, X.G. Optimization of VEDs for vibration control of transmission line tower. Adv. Civ. Eng. 2021, 2021, 9060414. [Google Scholar] [CrossRef]
- Priestley, M.B. Evolutionary spectra and nonstationary processes. J. R. Stat. Soc. 1965, 27, 204–237. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Li, Q.S.; Lin, J.H.; Williams, F. W Random vibration analysis of long-span structures subjected to spatially varying ground motions. Soil Dyn. Earthq. Eng. 2009, 29, 620–629. [Google Scholar] [CrossRef]
- Jia, H.Y.; Zhang, D.Y.; Zheng, S.X.; Xie, W.C.; Pandey, M.D. Local site effects on a high-pier railway bridge under tridirectional spatial excitations: Nonstationary stochastic analysis. Soil Dyn. Earthq. Eng. 2013, 52, 55–69. [Google Scholar] [CrossRef]
- Zhao, Y.; Si, L.T.; Ouyang, H. Frequency domain analysis method of nonstationary random vibration based on evolutionary spectral representation. Eng. Comput. 2018, 35, 1098–1127. [Google Scholar] [CrossRef]
- Zhong, Y.L.; Li, S.; Jin, W.C.; Yan, Z.T.; Liu, X.P.; Li, Y. Frequency domain analysis of along-wind response and study of wind loads for transmission tower subjected to downbursts. Buildings 2022, 12, 148. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, D.; Sun, C.; Fu, X. Probabilistic study on non-stationary extreme response of transmission tower under moving downburst impact. Structures 2024, 68, 107179. [Google Scholar] [CrossRef]
- Li, H.N.; Shi, W.L.; Wang, G.X.; Jia, L.G. Simplified models and experimental verification for coupled transmission tower–line system to seismic excitations. J. Sound Vib. 2005, 286, 569–585. [Google Scholar] [CrossRef]
- Jamalabadi, M.Y.A. An improvement of port-hamiltonian model of fluid sloshing coupled by structure motion. Water 2018, 10, 1721. [Google Scholar] [CrossRef]
- Chen, B.; Song, X.X.; Li, W.P.; Wu, J.B. Vibration control of a wind-excited transmission tower-line system by shape memory alloy dampers. Materials 2022, 15, 1790. [Google Scholar] [CrossRef]
- Song, X.X.; Chen, Y.Z.; Chen, B.; Wu, J.B. Response control of a transmission tower-line system under wind excitations by electromagnetic inertial mass dampers. Adv. Struct. Eng. 2022, 25, 3334–3348. [Google Scholar] [CrossRef]
- Makris, N. Complex-parameter kelvin model for elastic foundations. Earthq. Eng. Struct. Dyn. 1994, 23, 251–264. [Google Scholar] [CrossRef]
- Singh, M.P.; Verma, N.P.; Moreschi, L.M. Seismic analysis and design with Maxwell dampers. J. Eng. Mech. ASCE 2003, 129, 273–282. [Google Scholar] [CrossRef]
- Singh, M.P.; Chang, T.S.; Nandan, H. Algorithms for seismic analysis of MDOF systems with fractional derivatives. Eng. Struct. 2011, 33, 2371–2381. [Google Scholar] [CrossRef]
- Renaud, F.; Dion, J.L.; Chevallier, G.; Tawfiq, I.; Lemaire, R. A new identification method of viscoelastic behavior: Application to the generalized Maxwell model. Mech. Syst. Signal Process. 2011, 25, 991–1010. [Google Scholar] [CrossRef]
- Mazza, F.; Vulcano, A. Control of the along-wind response of steel framed buildings by using viscoelastic or friction dampers. Wind Struct. 2007, 10, 233–247. [Google Scholar] [CrossRef]
- Mazza, F.; Vulcano, A. Control of the earthquake and wind dynamic response of steel-framed buildings by using additional braces and/or viscoelastic dampers. Earthq. Eng. Struct. Dyn. 2011, 40, 155–174. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Y.Y.; Zhang, Y.H.; Kennedy, D. Nonstationary seismic response analysis of long-span structures by frequency domain method considering wave passage effect. Soil Dyn. Earthq. Eng. 2018, 109, 1–9. [Google Scholar] [CrossRef]
- Song, G.; Lin, J.H.; Williams, F.W.; Wu, Z.G. Precise integration strategy for aseismic LQG control of structures. Int. J. Numer. Methods Eng. 2006, 68, 1281–1300. [Google Scholar] [CrossRef]
- GB 50011-2010; China Ministry of Construction. Code for Seismic Design of Buildings. Chinese Architectural Industry Press: Beijing, China, 2016. (In Chinese)





| T (°C) | k0 (kN/cm) | k1 (kN/cm) | k2 (kN/cm) | c0 (kN·s/cm) | c1 (kN·s/cm) | c2 (kN·s/cm) |
|---|---|---|---|---|---|---|
| 21 | 0.36 | 42.08 | 6.87 | 0.37 | 0.83 | 2.15 |
| 32 | 0.21 | 23.54 | 3.18 | 0 | 0.39 | 0.73 |
| 38 | 0.28 | 2327.46 | 3.28 | 0 | 0.57 | 0.18 |
| Direction | Location | Response | Reduction Rate (%) | |||
|---|---|---|---|---|---|---|
| Scheme No. 1 | Scheme No. 2 | Scheme No. 3 | Scheme No. 4 | |||
| In-plane | Mass No. 6 (top of tower body) | Displacement | 4.71 | 14.71 | 32.57 | 32.49 |
| Velocity | 6.55 | 16.29 | 34.08 | 27.25 | ||
| Acceleration | 11.51 | 18.47 | 31.92 | 8.76 | ||
| Mass No. 8 (cross arm) | Displacement | 3.86 | 13.30 | 30.53 | 32.17 | |
| Velocity | 3.98 | 12.62 | 29.00 | 29.14 | ||
| Acceleration | 2.75 | 3.66 | 8.95 | 3.85 | ||
| Mass No. 9 (Tower top) | Displacement | 4.08 | 13.54 | 30.85 | 31.90 | |
| Velocity | 4.97 | 12.02 | 26.08 | 21.17 | ||
| Acceleration | 4.59 | 5.69 | 11.89 | 2.35 | ||
| Out-of-plane | Mass No. 6 (top of tower body) | Displacement | 5.63 | 17.44 | 32.56 | 37.06 |
| Velocity | 6.62 | 17.27 | 28.99 | 30.25 | ||
| Acceleration | 10.06 | 15.33 | 17.56 | 12.64 | ||
| Mass No. 8 (cross arm) | Displacement | 5.24 | 17.26 | 32.96 | 37.97 | |
| Velocity | 5.30 | 16.93 | 31.67 | 35.89 | ||
| Acceleration | 6.57 | 15.72 | 24.40 | 23.84 | ||
| Mass No. 9 (tower top) | Displacement | 5.54 | 17.33 | 32.41 | 36.92 | |
| Velocity | 6.32 | 17.13 | 29.23 | 30.85 | ||
| Acceleration | 9.93 | 16.81 | 19.37 | 13.39 | ||
| Direction | Response | Freq. Order | Extreme Value | Reduction Rate (%) | |
|---|---|---|---|---|---|
| Original Tower | With Control | ||||
| In-plane | Displacement (m2·s) | 1 | 0.1833 | 0.1002 | 45.33 |
| 2 | 0.0035 | 0.0030 | 13.17 | ||
| Velocity (m2/s) | 1 | 2.3491 | 1.2569 | 46.50 | |
| 2 | 0.7019 | 0.6199 | 11.69 | ||
| Acceleration (m2/s3) | 1 | 30.5683 | 16.8119 | 45.00 | |
| 2 | 147.1099 | 130.4146 | 11.35 | ||
| Out-of-plane | Displacement (m2·s) | 1 | 0.0581 | 0.0280 | 51.71 |
| 2 | 0.0011 | 0.0010 | 12.28 | ||
| Velocity (m2/s) | 1 | 0.9676 | 0.4815 | 50.24 | |
| 2 | 0.2074 | 0.1841 | 11.24 | ||
| Acceleration (m2/s3) | 1 | 16.2968 | 8.3393 | 48.83 | |
| 2 | 40.9186 | 36.5927 | 10.57 | ||
| Direction | Location | Response | Reduction Rate (%) | ||
|---|---|---|---|---|---|
| 21 °C | 32 °C | 38 °C | |||
| In-plane | Mass No. 6 (top of tower body) | Displacement | 32.49 | 16.96 | 15.73 |
| Velocity | 27.25 | 14.24 | 13.71 | ||
| Acceleration | 8.76 | 4.03 | 5.24 | ||
| Mass No. 8 (cross arm) | Displacement | 32.17 | 17.45 | 16.19 | |
| Velocity | 29.14 | 17.89 | 16.85 | ||
| Acceleration | 3.85 | 9.72 | 10.73 | ||
| Mass No. 9 (tower top) | Displacement | 31.90 | 16.67 | 15.44 | |
| Velocity | 21.17 | 11.20 | 10.93 | ||
| Acceleration | 2.35 | 0.87 | 1.74 | ||
| Out-of-plane | Mass No. 6 (top of tower body) | Displacement | 37.06 | 20.12 | 19.58 |
| Velocity | 30.25 | 16.57 | 16.68 | ||
| Acceleration | 12.64 | 6.22 | 8.22 | ||
| Mass No. 8 (cross arm) | Displacement | 37.97 | 20.81 | 20.29 | |
| Velocity | 35.89 | 20.03 | 19.91 | ||
| Acceleration | 23.84 | 13.06 | 15.56 | ||
| Mass No. 9 (tower top) | Displacement | 36.92 | 20.08 | 19.56 | |
| Velocity | 30.85 | 16.95 | 16.99 | ||
| Acceleration | 13.39 | 6.86 | 8.36 | ||
| Site Type | ωg (Rad/s) | ξg | S0 (cm2/s3) |
|---|---|---|---|
| I | 15.71 | 0.64 | 215.19 |
| II | 12.57 | 0.72 | 250.57 |
| III | 8.98 | 0.80 | 323.85 |
| IV | 6.61 | 0.90 | 398.29 |
| Direction | Location | Response | Reduction Rate (%) | |||
|---|---|---|---|---|---|---|
| I | II | III | IV | |||
| In-plane | Mass No. 6 (top of tower body) | Displacement | 32.17 | 32.49 | 32.98 | 33.39 |
| Velocity | 25.43 | 27.25 | 30.06 | 32.04 | ||
| Acceleration | 7.34 | 8.76 | 11.16 | 14.26 | ||
| Mass No. 8 (cross arm) | Displacement | 31.94 | 32.17 | 32.56 | 32.87 | |
| Velocity | 26.83 | 29.14 | 31.78 | 33.23 | ||
| Acceleration | 2.60 | 3.85 | 7.08 | 10.34 | ||
| Mass No. 9 (tower top) | Displacement | 31.50 | 31.90 | 32.41 | 32.73 | |
| Velocity | 18.02 | 21.17 | 25.63 | 28.56 | ||
| Acceleration | 1.83 | 2.35 | 3.60 | 5.13 | ||
| Out-of-plane | Mass No. 6 (top of tower body) | Displacement | 36.83 | 37.06 | 37.54 | 37.92 |
| Velocity | 28.45 | 30.25 | 32.98 | 34.76 | ||
| Acceleration | 11.49 | 12.64 | 15.75 | 18.99 | ||
| Mass No. 8 (cross arm) | Displacement | 37.82 | 37.97 | 38.32 | 38.65 | |
| Velocity | 35.42 | 35.89 | 36.77 | 37.49 | ||
| Acceleration | 21.72 | 23.84 | 27.60 | 30.39 | ||
| Mass No. 9 (tower top) | Displacement | 36.72 | 36.92 | 37.39 | 37.81 | |
| Velocity | 29.41 | 30.85 | 33.18 | 34.81 | ||
| Acceleration | 12.00 | 13.39 | 16.94 | 20.46 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, M.; Chen, B.; Xiao, X.; Chen, Y. Nonstationary Stochastic Responses of Transmission Tower-Line System with Viscoelastic Material Dampers Under Seismic Excitations. Materials 2025, 18, 1138. https://doi.org/10.3390/ma18051138
Chang M, Chen B, Xiao X, Chen Y. Nonstationary Stochastic Responses of Transmission Tower-Line System with Viscoelastic Material Dampers Under Seismic Excitations. Materials. 2025; 18(5):1138. https://doi.org/10.3390/ma18051138
Chicago/Turabian StyleChang, Mingjing, Bo Chen, Xiang Xiao, and Yanzhou Chen. 2025. "Nonstationary Stochastic Responses of Transmission Tower-Line System with Viscoelastic Material Dampers Under Seismic Excitations" Materials 18, no. 5: 1138. https://doi.org/10.3390/ma18051138
APA StyleChang, M., Chen, B., Xiao, X., & Chen, Y. (2025). Nonstationary Stochastic Responses of Transmission Tower-Line System with Viscoelastic Material Dampers Under Seismic Excitations. Materials, 18(5), 1138. https://doi.org/10.3390/ma18051138







