Thin Cells of Polymer-Modified Liquid Crystals Described by Voronoi Diagrams
Abstract
1. Introduction
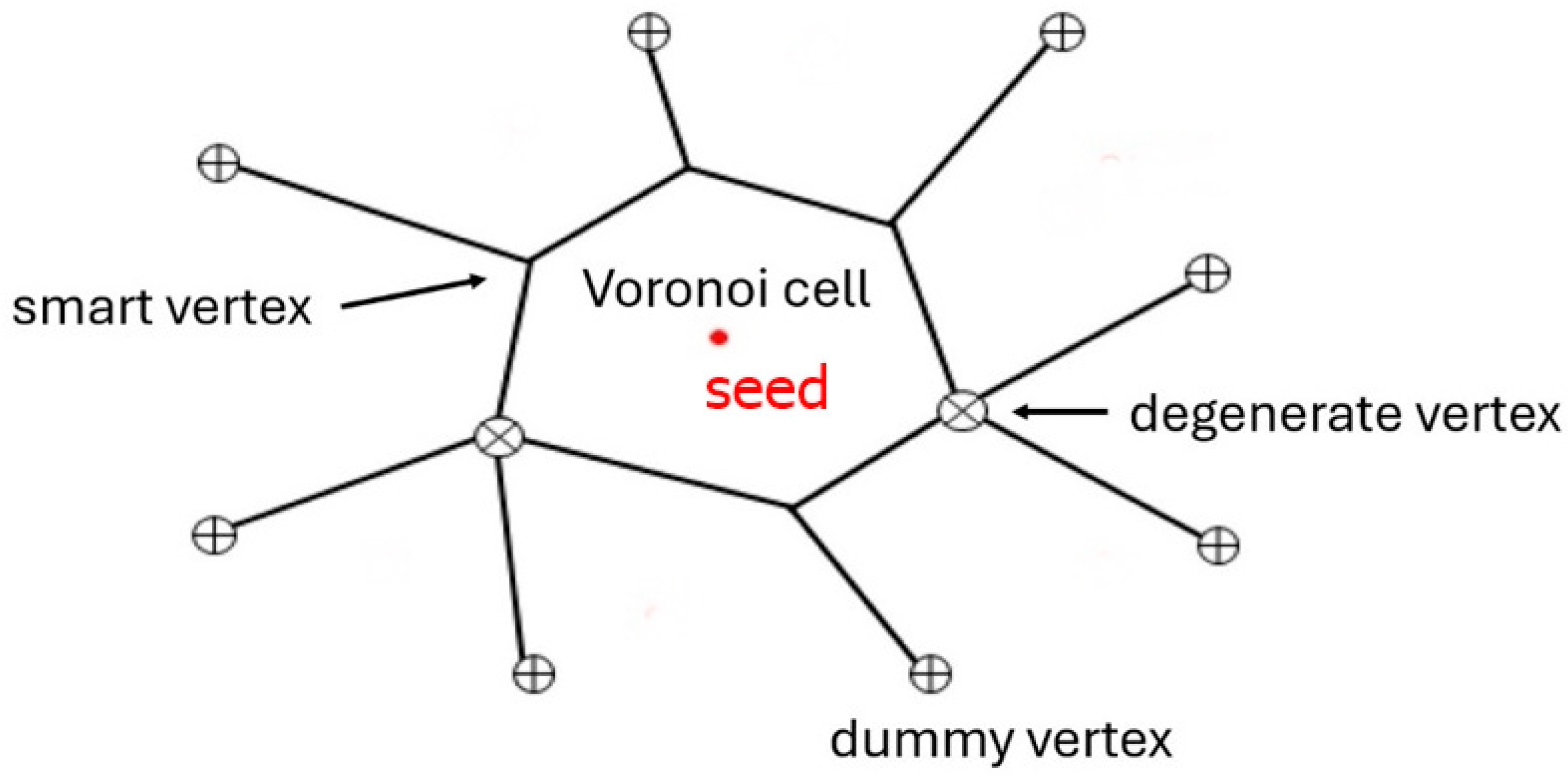
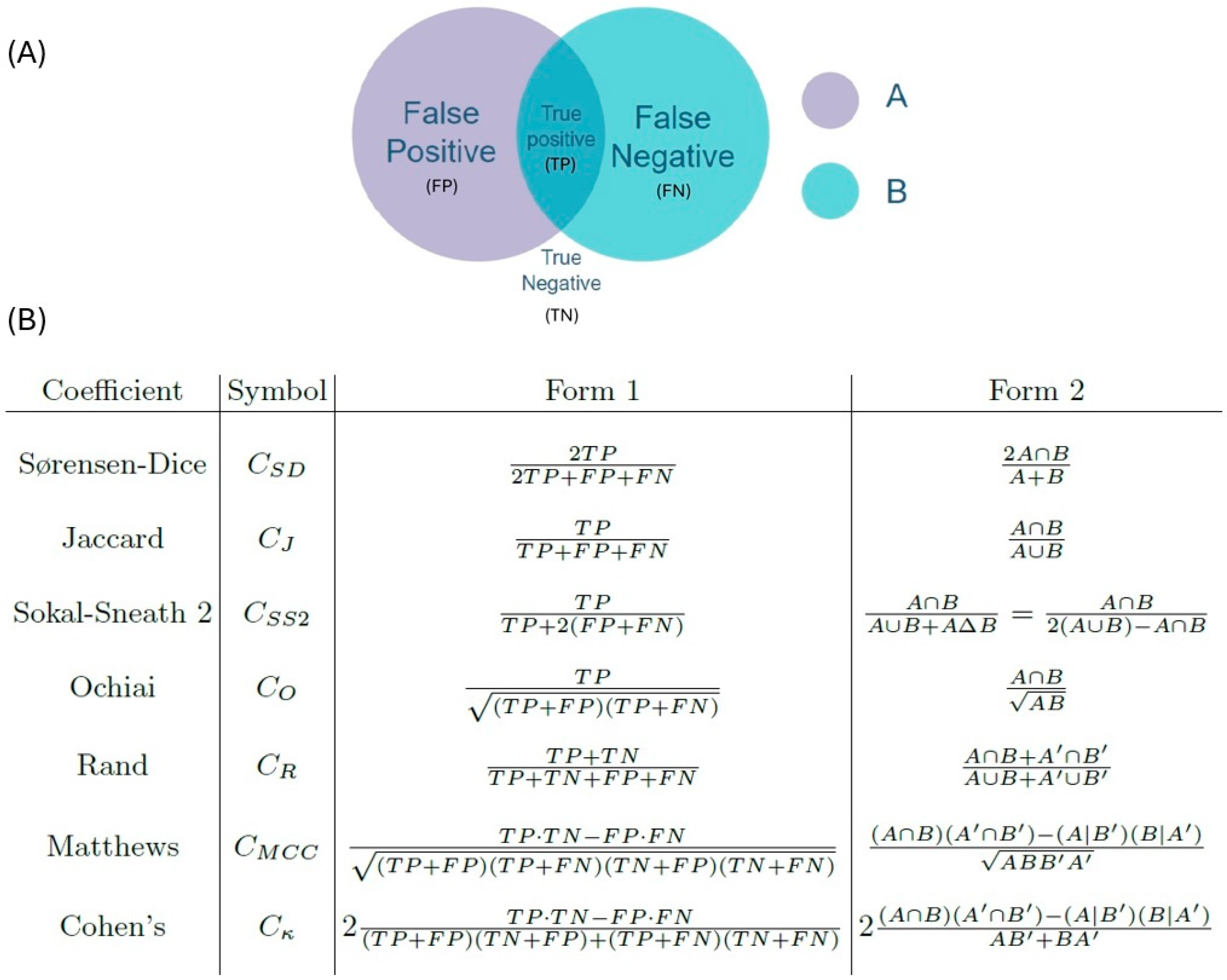
2. Methodology
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ball, P. The Self-Made Tapestry: Pattern Formation in Nature; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Cross, M.; Greenside, H. Pattern Formation and Dynamics in Non-Equilibrium Systems; Cambridge University Press: Cambridge, UK, 2009; Chapter 1. [Google Scholar]
- Walgraef, D. Spatio-Temporal Pattern Formation; Springer: New York, NY, USA, 1997. [Google Scholar]
- Camazine, S.; Deneubourg, J.-L.; Franks, N.R. Self-Organization in Biological Systems; Princeton University Press: Princeton, MA, USA, 2001. [Google Scholar]
- Ohta, S.; Inasawa, S.; Yamaguchi, Y. Size control of phase-separated liquid crystal droplets in a polymer matrix based on the phase diagram. J. Polym. Sci. Part B Polym. Phys. 2012, 50, 863–869. [Google Scholar] [CrossRef]
- Bronnikov, S.; Kostromin, S.; Zuev, V. Polymer-dispersed liquid crystals: Progress in preparation, investigation, and application. J. Macromol. Sci. Part B 2013, 52, 1718–1735. [Google Scholar] [CrossRef]
- Meng, Q.; Cao, H.; Kashima, M.; Liu, H.; Yang, H. Effects of the structures of epoxy monomers on the electro-optical properties of heat-cured polymer-dispersed liquid crystal films. Liq. Cryst. 2010, 37, 189–193. [Google Scholar] [CrossRef]
- Drzaic, P.S. Putting liquid crystal droplets to work: A short history of polymer dispersed liquid crystals. Liq. Cryst. 2006, 33, 1281–1296. [Google Scholar] [CrossRef]
- Khandelwal, H.; Schenning, A.; Debije, M. Infrared regulating smart window based on organic materials. Adv. Energy Mater. 2017, 7, 1602209. [Google Scholar] [CrossRef]
- Mouquinho, A.I.; Petrova, K.; Barros, M.T.; Sotomayor, J. New Polymer Networks for PDLC Films Application. In New Polymers for Special Applications; Ailton, D.S.G., Ed.; Intech Open: London, UK, 2012; Chapter 5. [Google Scholar] [CrossRef][Green Version]
- Dierking, I. (Ed.) Polymer-Modified Liquid Crystals; Royal Society of Chemistry: Cambridge, UK, 2019. [Google Scholar]
- Dirichlet, P.G.L. Über die Reduktion der positiven quadratischen Formen mit drei unbestimmten ganzen Zahlen. J. Für Die Reine Und Angew. Math. 1850, 40, 209–227. [Google Scholar]
- Voronoi, G.F. Nouvelles applications des paramètres continus à la théorie de formes quadratiques. J. Für Die Reine Und Angew. Math. 1908, 134, 198–287. [Google Scholar] [CrossRef]
- Aurenhammer, F.; Klein, R.; Lee, D.-T. Voronoi Diagrams and Delaunay Triangulations; World Scientific Publishing: Singapore, 2013. [Google Scholar]
- Okabe, A.; Boots, B.; Sugihara, K.; Chiu, S.N. Spatial Tessellations: Concepts and Applications of Voronoi Diagrams, 2nd ed.; Wiley: Chichester, UK, 2000. [Google Scholar]
- Ramella, M.; Boschin, W.; Fadda, D.; Nonino, M. Finding galaxy clusters using Voronoi tessellations. Astro. Astrophys. 2001, 368, 776–786. [Google Scholar] [CrossRef]
- Mulheran, P.A.; Blackman, J.A. Capture zones and scaling in homogeneous thin film growth. Phys. Rev. B 1996, 53, 10261–10267. [Google Scholar] [CrossRef]
- Pimpinelli, A.; Tumbek, L.; Winkler, A. Scaling and exponent equalities in island nucleation: Novel results and application to organic films. J. Phys. Chem. Lett. 2014, 5, 995–998. [Google Scholar] [CrossRef]
- Fanfoni, M.; Placidi, E.; Arciprete, F.; Orsini, E.; Patella, F.; Balzarotti, A. Sudden nucleation versus scale invariance of InAs quantum dots on GaAs. Phys. Rev. B 2007, 75, 245312. [Google Scholar] [CrossRef]
- Miyamoto, S.; Moutanabbir, O.; Haller, E.E.; Itoh, K.M. Spatial correlation of self-assembled isotopically pure Ge/Si(001) nano-islands. Phys. Rev. B 2009, 79, 165415. [Google Scholar] [CrossRef]
- Gomez, S.; Vlad, H.D.; Lopez, J.; Fernandez, E. Design and properties of 3D. scaffolds for bone tissue engineering. Acta Biomat. 2016, 42, 341–350. [Google Scholar] [CrossRef] [PubMed]
- Bock, M.; Tyagi, A.K.; Kreft, J.-U.; Alt, W. Generalized Voronoi tessellation as a model of two-dimensional cell tissue dynamics. Bull. Math. Bio. 2009, 72, 1696–1731. [Google Scholar] [CrossRef]
- Sanchez-Gutierrez, D.; Tozluoglu, M.; Barry, J.D.; Pascual, A.; Mao, Y.; Escudero, L.M. Fundamental physical cellular constraints drive self-organization of tissues. EMBO J. 2016, 35, 77–88. [Google Scholar] [CrossRef]
- Grujicic, M.; Zhang, Y. Determination of effective elastic properties of functionally graded materials using Voronoi cell finite element method. Mater. Sci. Eng. A 1998, 251, 64–76. [Google Scholar] [CrossRef]
- Zhang, K.S.; Wu, M.S.; Feng, R. Simulation of microplasticity-induced deformation in uniaxially strained ceramics by 3-D Voronoi polycrystal modelling. Int. J. Plast. 2005, 21, 801–834. [Google Scholar] [CrossRef]
- Zhu, H.X.; Hobdell, J.R.; Windle, A.H. Effects of cell irregularity on the elastic properties of 2D Voronoi honeycombs. J. Mech. Phys. Solids 2001, 49, 857–870. [Google Scholar] [CrossRef]
- Zhu, H.X.; Thorpe, S.M.; Windle, A.H. The effect of cell irregularity on the high strain compression of 2D Voronoi honeycombs. Int. J. Solids Struct. 2006, 43, 1061–1078. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, L.; Liu, Z.; Jiang, Z.; Liu, Y.; Wu, Y. Yield properties of closed-cell aluminum foam under triaxial loadings by a 3D Voronoi model. Mech. Mater. 2017, 104, 73–84. [Google Scholar] [CrossRef]
- Moorthy, S.; Ghosh, S. A Voronoi cell finite element model for particle cracking in elastic-plastic composite materials. Comput. Methods Appl. Mech. Eng. 1998, 151, 377–400. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, Q.; Xia, X. Voronoi-based peridynamics and cracking analysis with adaptive refinement. Int. J. Numer. Meth. Eng. 2017, 112, 2087–2109. [Google Scholar] [CrossRef]
- Li, S.; Ghosh, S. Extended Voronoi cell finite element model for multiple cohesive crack propagation in brittle materials. Int. J. Numer. Meth. Eng. 2006, 65, 1028–1067. [Google Scholar] [CrossRef]
- Fantini, M.; Curto, M. Interactive design and manufacturing of a Voronoi-based biomimetic bone scaffold for morphological characterization. Int. J. Interact. Des. Manuf. 2018, 12, 585–596. [Google Scholar] [CrossRef]
- Deering, J.; Dowling, K.I.; DiCecco, L.-A.; McLean, G.D.; Yu, B.; Grandfield, K. Selective Voronoi tessellation as a method to design anisotropic and biomimetic implants. J. Mech. Behav. Biomed. Mater. 2021, 116, 104361. [Google Scholar] [CrossRef]
- Sharma, N.; Ostas, D.; Rotar, H.; Brantner, P.; Thieringer, F.M. Design and Additive Manufacturing of a Biomimetic Customized Cranial Implant Based on Voronoi Diagram. Front. Physiol. 2021, 12, 647923. [Google Scholar] [CrossRef]
- Available online: https://imgur.com/a/1sofFc9 (accessed on 10 February 2025).
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 673. [Google Scholar] [CrossRef]
- Suzuki, A.; Iri, M. Approximation of a tessellation of the plane by a Voronoi diagram. J. Oper. Res. Soc. Jpn. 1986, 29, 69–97. [Google Scholar]
- Hartvigsen, D. Recognizing Voronoi diagrams with linear programming. J. Comput. 1992, 4, 369–374. [Google Scholar] [CrossRef]
- Aurenhammer, F. Recognising polytopical cell complexes and constructing projection polyhedra. J. Symb. Comput. 1987, 3, 249–255. [Google Scholar] [CrossRef]
- Dierking, I.; Flatley, A. Greenhalgh, Voronoi patterns in liquid crystal textures. J. Mol. Liq. 2021, 335, 116553. [Google Scholar] [CrossRef]
- Dierking, I.; Flatley, A. Greenhalgh, Can liquid crystal blue phase textures be described by Voronoi tessellations? Liq. Cryst. 2021, 48, 689–698. [Google Scholar] [CrossRef]
- Schoenberg, F.P.; Ferguson, T.; Li, C. Inverting Dirichlet tessellations. Comp. J. 2003, 46, 76–83. [Google Scholar] [CrossRef][Green Version]
- Rand, W.M. Objective criteria for the evaluation of clustering methods. J. Am. Stat. Assoc. 1971, 66, 846–850. [Google Scholar] [CrossRef]
- Jaccard, P. The distribution of the flora in the alpine zone.1. New Phytol. 1912, 11, 37–50. [Google Scholar] [CrossRef]
- Sørensen, T.J. A method of establishing groups of equal amplitude in plant sociology based on similarity of species content and its application to analyses of the vegetation on Danish commons, Kongelige Danske Videnskabernes Selskab. Biol. Skr. 1948, 5, 1–34. [Google Scholar]
- Dice, L.R. Measures of the amount of ecologic association between species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Matthews, B. Comparison of the predicted and observed secondary structure of T4 phage lysozyme. Biochim. Biophys. Acta (BBA)—Protein Struct. 1975, 405, 442–451. [Google Scholar] [CrossRef]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Ochiai, A. Zoogeographical studies on the soleoid fishes found in Japan and its neighbouring regions-II. Bull. Jpn. Soc. Sci. Fish. 1957, 22, 526–530. [Google Scholar] [CrossRef]
- Deza, M.M.D.E. Encyclopedia of Distances; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Gösgens, M.; Zhiyanov, A.; Tikhonov, A.; Prokhorenkova, L. Good classification measures and how to find them. In Advances in Neural Information Processing Systems, 35th Conference on Neural Information Processing Systems (NeurIPS 2021), Online, 6–14 December 2021; Beygelzimer, A., Dauphin, Y., Liang, P., Vaughan, J.W., Eds.; Neural Information Processing Systems Foundation, Inc. (NeurIPS): San Diego, CA, USA, 2021; Available online: https://proceedings.neurips.cc/ (accessed on 21 February 2025).
- Albatineh, A.N.K. On Similarity Measures for Cluster Analysis. Ph.D Thesis, Western Michigan University, Department of Statistics, Kalamazoo, MI, USA, 2004. [Google Scholar]
- Gower, J.C. A general coefficient of similarity and some of its properties. Biometrics 1971, 27, 857–871. [Google Scholar] [CrossRef]
- Yin, Y.; Yasuda, K. Similarity coefficient methods applied to the cell formation problem: A comparative investigation. Comput. Ind. Eng. 2005, 48, 471–489. [Google Scholar] [CrossRef]
- Seweryn, M.T.; Pietrzak, M.; Ma, Q. Application of information theoretical approaches to assess diversity and similarity in single-cell transcriptomics. Comput. Struct. Biotechnol. J. 2020, 18, 1830–1837. [Google Scholar] [CrossRef] [PubMed]
- Duarte, J.M.; Santos, J.B.D.; Melo, L.C. Comparison of similarity coefficients based on RAPD markers in the common bean. Genet. Mol. Biol. 1999, 22, 427–432. [Google Scholar] [CrossRef]
- Mir, M.A.; Mansoor, S.; Sugapriya, M.; Alyemeni, M.N.; Wijaya, L.; Ahmad, P. Deciphering genetic diversity analysis of saffron (Crocus sativus L.) using RAPD and ISSR markers. Saudi J. Biol. Sci. 2021, 28, 1308–1317. [Google Scholar] [CrossRef]
- Chao, A.; Chazdon, R.L.; Colwell, R.K.; Shen, T.-J. A new statistical approach for assessing similarity of species composition with incidence and abundance data. Ecol. Lett. 2004, 8, 148–159. [Google Scholar] [CrossRef]
- Kizhakidathazhath, R.; Nishikawa, H.; Okumura, Y.; Higuchi, H.; Kikuchi, H. High-performance polymer dispersed liquid crystal enabled by uniquely designed acrylate monomer. Polymers 2020, 12, 1625. [Google Scholar] [CrossRef]






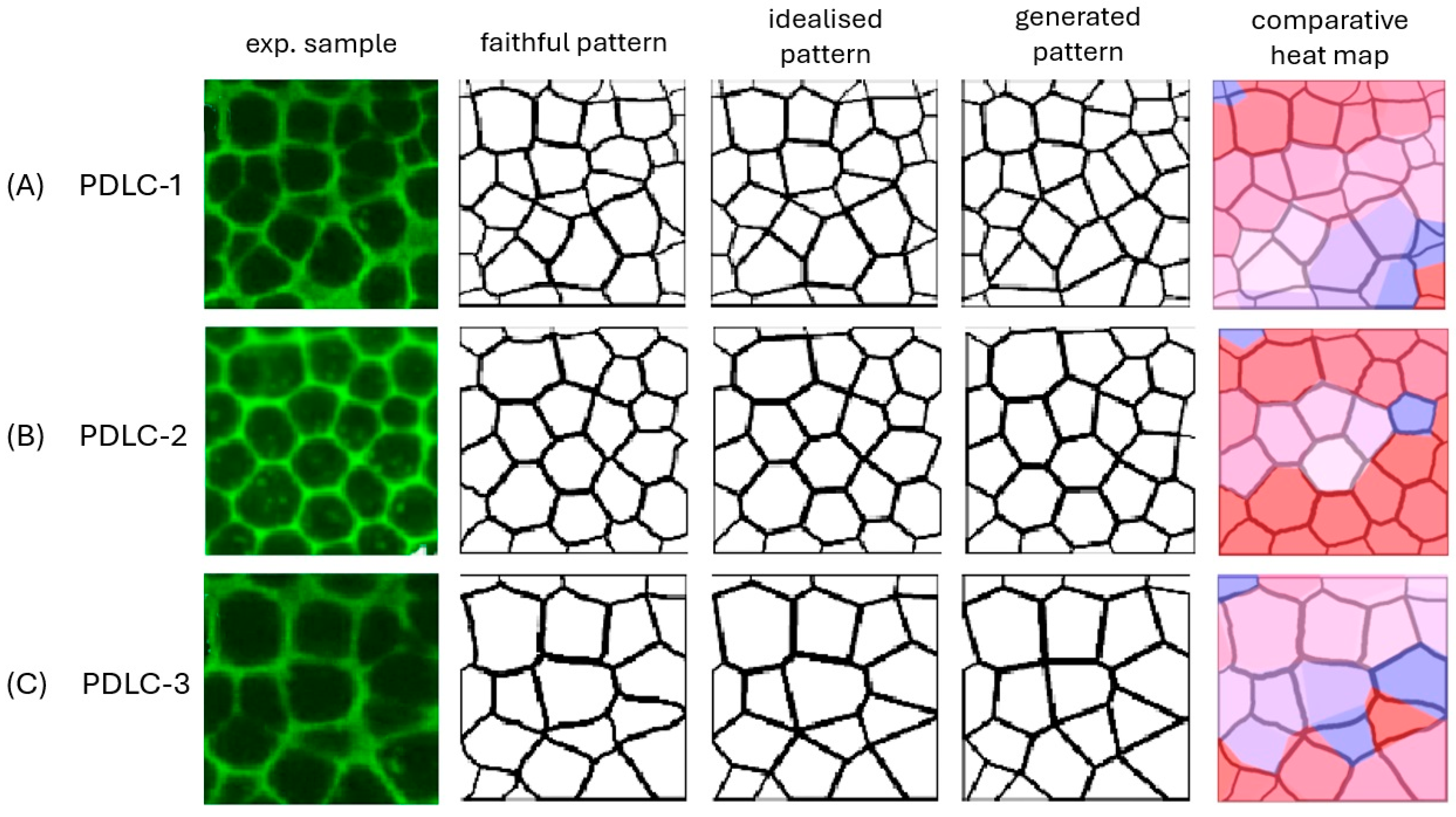


| Sample | Number of Cells | CIF | CGF | CGI | D | M | Δ | d | d′ |
|---|---|---|---|---|---|---|---|---|---|
| PDLC-1 | 37 | 97.6 | 81.0 | 81.2 | 0.21 | 82.9 | 1.74 | 2.10 | 2.15 |
| PDLC-2 | 30 | 98.8 | 92.5 | 92.1 | 0.48 | 93.7 | 1.62 | 1.73 | 1.76 |
| PDLC-3 | 22 | 97.7 | 89.8 | 92.2 | 2.39 | 91.9 | 0.31 | 0.34 | 0.34 |
| PSLC-1 | 34 | 99.0 | 94.3 | 94.9 | 0.66 | 95.2 | 0.29 | 0.31 | 0.31 |
| PSLC-2 | 33 | 98.1 | 89.0 | 90.2 | 1.25 | 90.6 | 0.43 | 0.48 | 0.48 |
| PSLC-3 | 30 | 99.1 | 93.6 | 94.7 | 1.15 | 94.4 | 0.30 | 0.32 | 0.32 |
| PSLC-4 | 36 | 99.6 | 92.1 | 92.3 | 0.27 | 92.5 | 0.11 | 0.12 | 0.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Woolhouse, F.; Dierking, I. Thin Cells of Polymer-Modified Liquid Crystals Described by Voronoi Diagrams. Materials 2025, 18, 1106. https://doi.org/10.3390/ma18051106
Woolhouse F, Dierking I. Thin Cells of Polymer-Modified Liquid Crystals Described by Voronoi Diagrams. Materials. 2025; 18(5):1106. https://doi.org/10.3390/ma18051106
Chicago/Turabian StyleWoolhouse, Felicity, and Ingo Dierking. 2025. "Thin Cells of Polymer-Modified Liquid Crystals Described by Voronoi Diagrams" Materials 18, no. 5: 1106. https://doi.org/10.3390/ma18051106
APA StyleWoolhouse, F., & Dierking, I. (2025). Thin Cells of Polymer-Modified Liquid Crystals Described by Voronoi Diagrams. Materials, 18(5), 1106. https://doi.org/10.3390/ma18051106







