Graph-Theory Algorithm for Prediction of Electrolyte Degradation Reactions in Lithium- and Sodium-Ion Batteries
Abstract
1. Introduction
2. Methodology
2.1. Basics of Graph Theory
2.2. Chemical Graph Theory
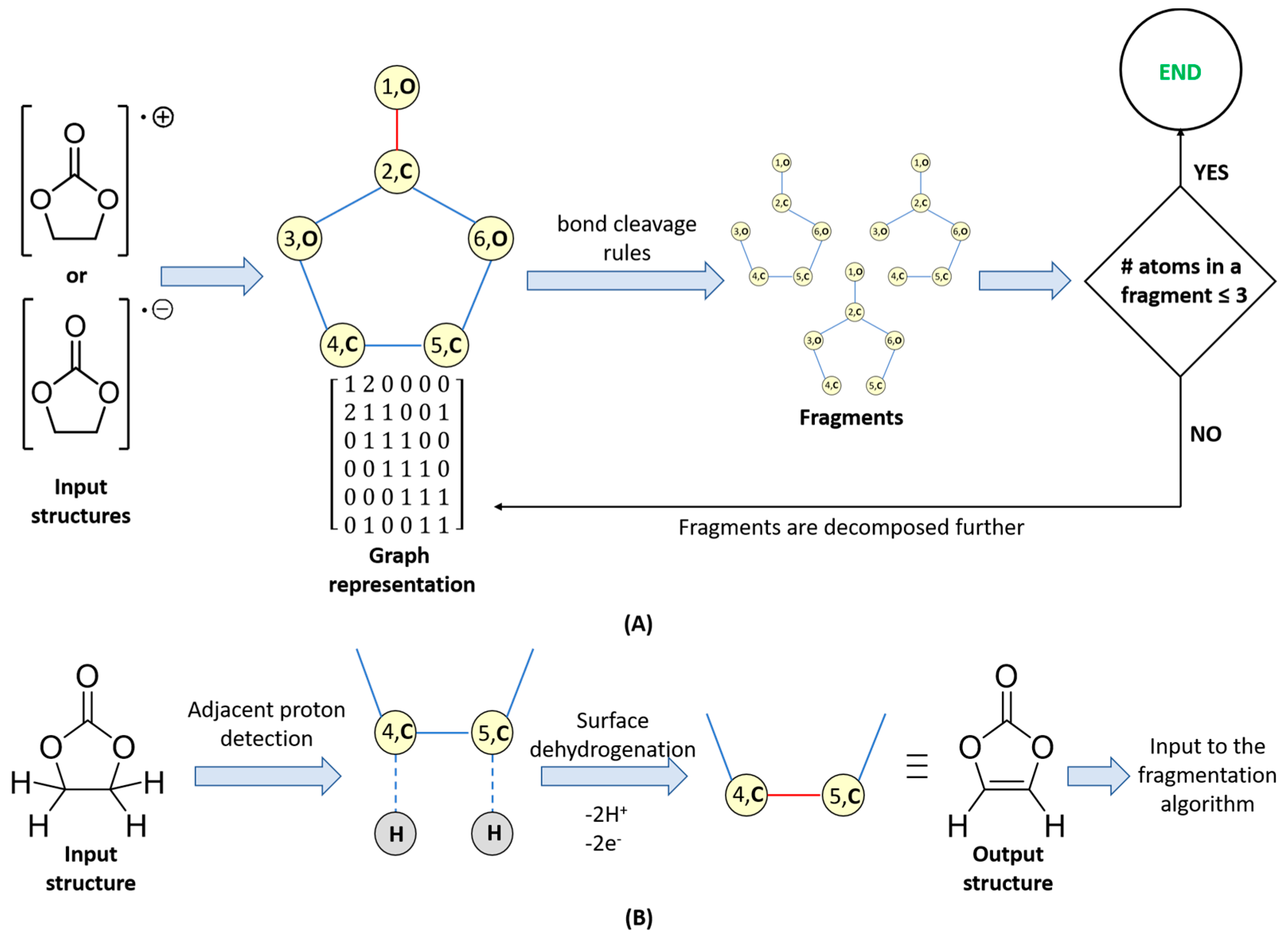
2.3. The Fragment-Generation Algorithm
- (i)
- Fragmentation: On anodes and cathodes anion-radicals and cation-radicals are formed, respectively. The polar bonds (e.g., C–O) in these species are known to undergo cleavage, so these types of fragmentations are considered (Figure 1A). In the present work, C–C bond cleavages are avoided since C–C bonds are essentially non-polar and, thus, are generally robust. Yet, the algorithm implementation is versatile enough to enable different user-defined bond cleavage rules.
- (ii)
- Surface dehydrogenation: Dehydrogenation of the electrolyte solvent may occur at inorganic electrode surfaces leading to the formation of unsaturated products (Figure 1B). For this step, an implicit surface presence is considered. The products generated are then fed to the fragmentation algorithm described in (i).
- (iii)
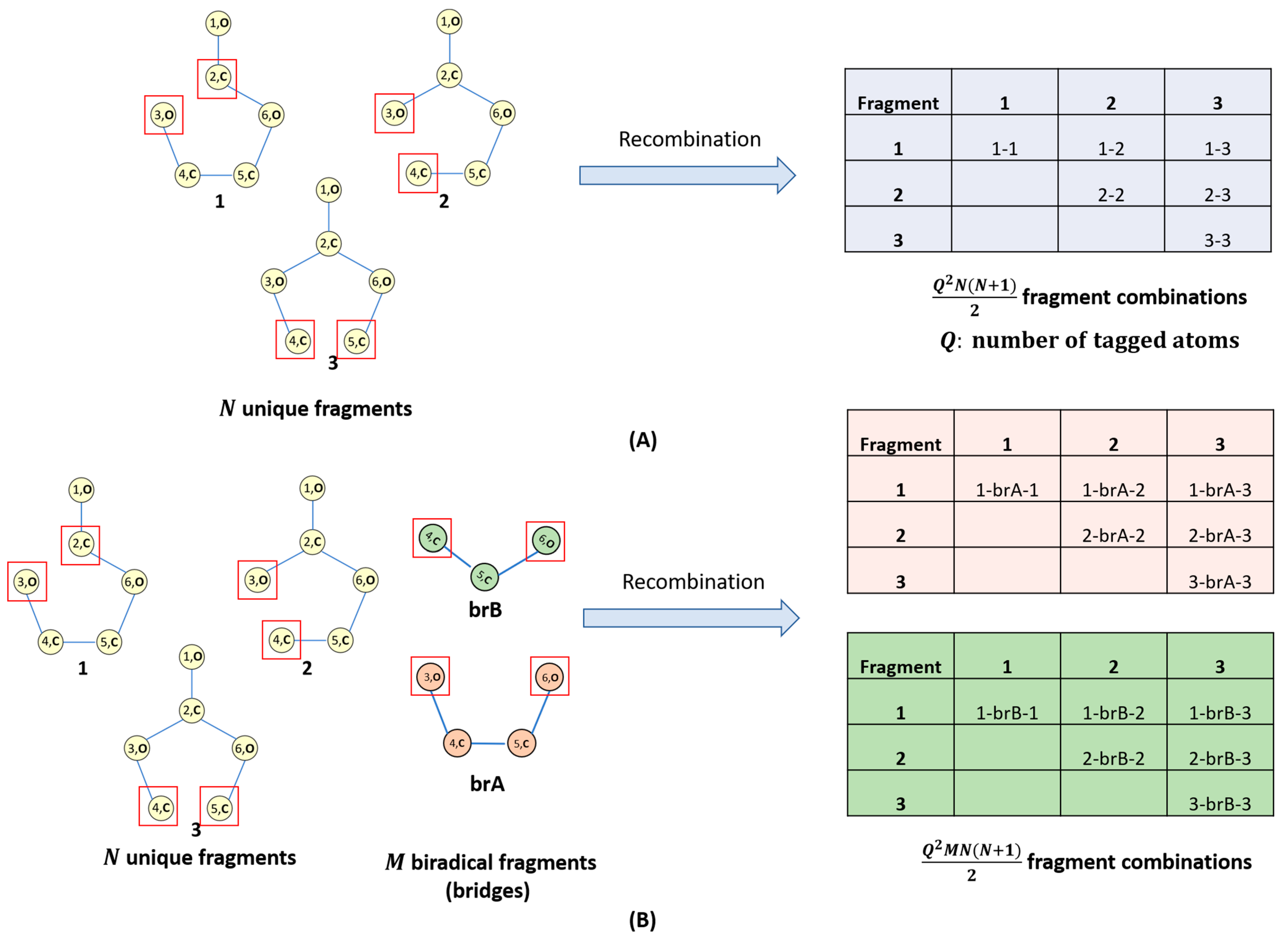
- Recombination and radical quenching: Radical species can recombine, forming different oligomer products (Figure 2A,B). Radicals can also be quenched by the presence of a trace amount of water in the electrolyte solvent. This can also be taken into account.
- (i)
- Atom types and connectivity information is extracted from the pseudograph and its adjacency matrix.
- (ii)
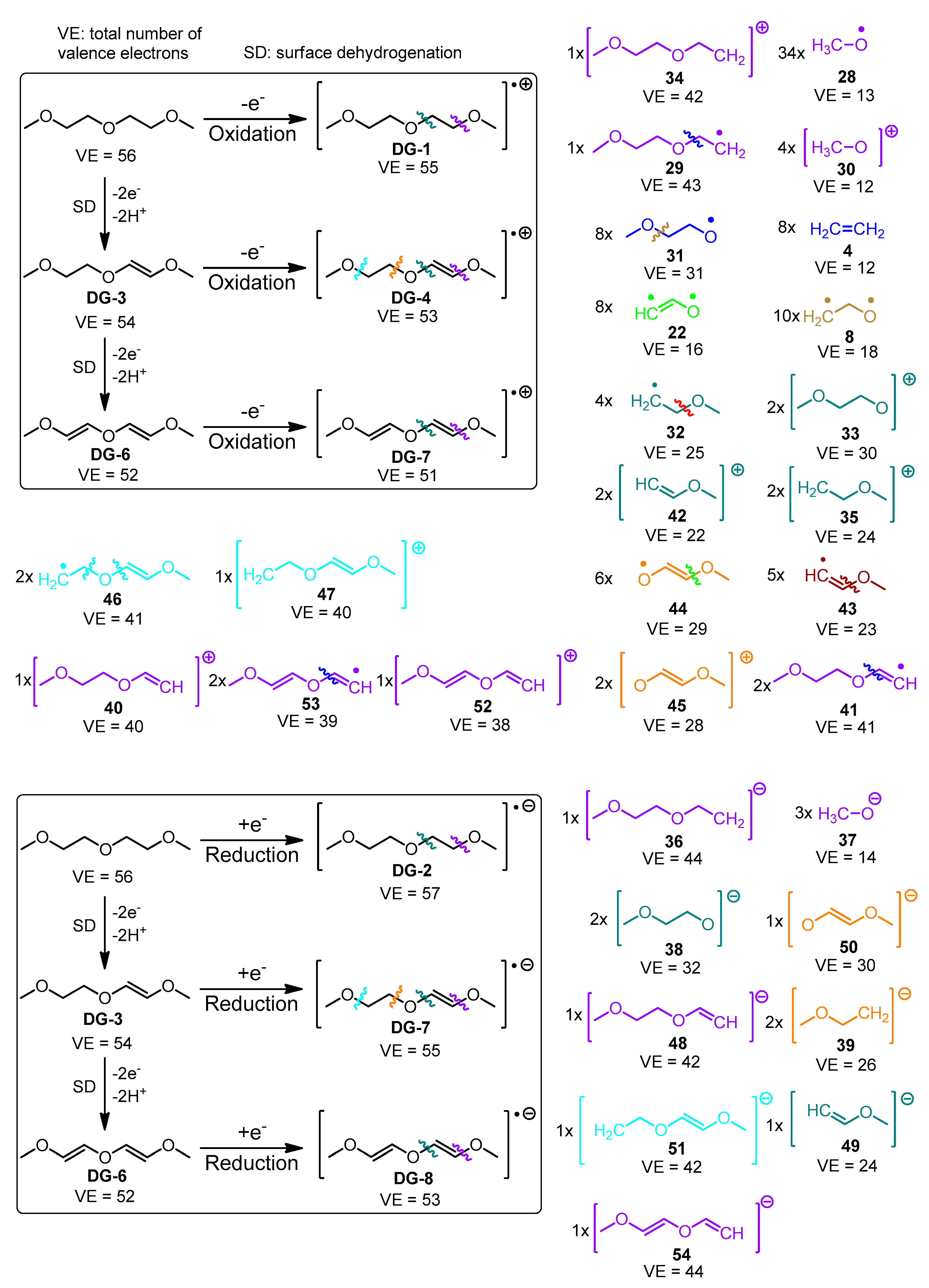
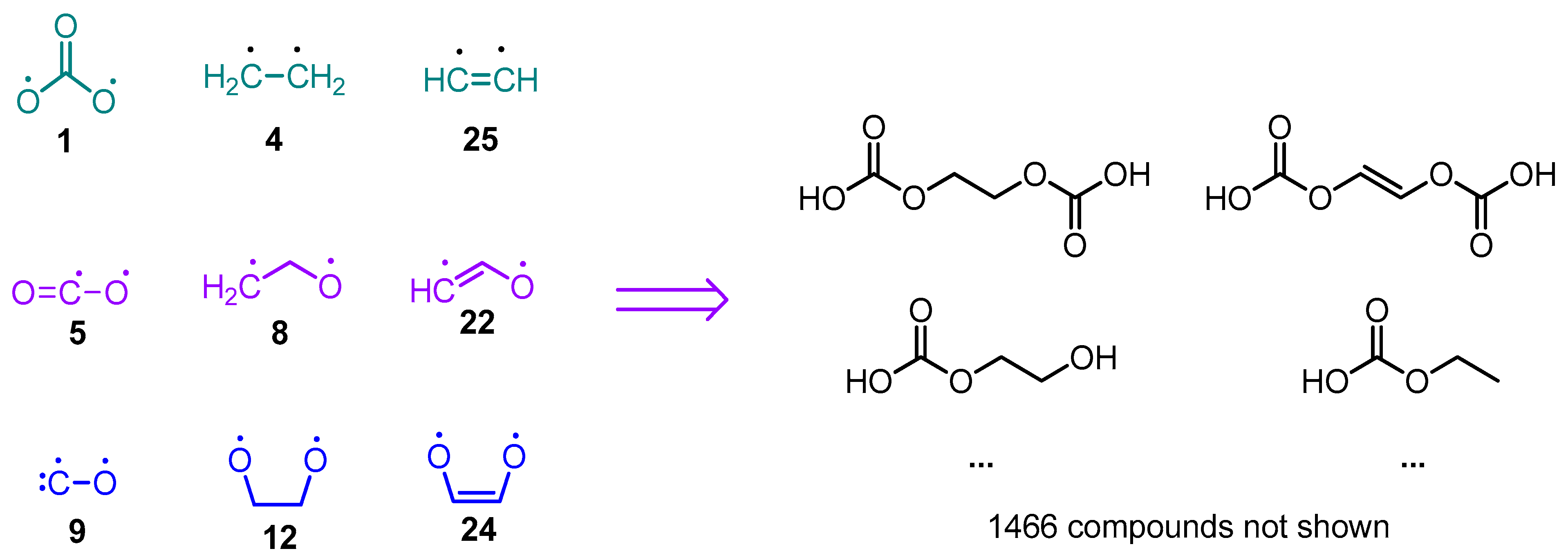
- Charge and multiplicity of the fragments, are estimated as follows: if a fragmentation step leads to the generation of two separate fragments (1) the number of valence electrons of both fragments is calculated; (2) the sum of valence electron numbers of both fragments is calculated and compared to the number of valence electrons in the parent structure; and (3) if needed, the valence electron numbers of the fragments are adjusted so that VE(first fragment) + VE(second fragment) = VE(total). The adjusted valence electron numbers of the fragments are used to assign charge and multiplicity to each fragment. Consider, for example, the cleavage of the cation-radical EC-2 (VE = 33, depicted in Figure S1, pathway III-o), leading to the formation of fragments 5 (CO2, VE5 = 4 + 2 × 6 = 16) and 8 (C2H4O, VE8 = 2 × 4 + 4 × 1 + 1 × 6 = 18). The sum of valence electrons of fragments 5 and 8 is VE5 + VE8 = 34, which is with one valence electron more than the number of valence electrons in EC-2 and, hence, the VE—numbers of the fragments—needs to be adjusted with 1. As a result, the following pairs of fragments are possible: (1) [CO2]•+ (fragment 7, VE7 = 15) and C2H4O (fragment 8, VE8 = 18) so that VE7 + VE8 = 33; (2) CO2 (fragment 5, VE5 = 16) and [C2H4O]•+ (fragment 6, VE8 = 17) so that VE6 + VE7 = 33.
- (i)
- Recombination of N radical fragments with Q-tagged atoms leading to the formation of maximum Q2N(N + 1)/2 recombination products (Figure 2A);
- (ii)
- Recombination of N radical fragments with Q-tagged atoms and M biradical bridges leading to the formation of up to Q2NM(N + 1)/2 recombination products (Figure 2B);
- (iii)
- Recombination resulting in organic peroxide bonds is currently excluded;
- (iv)
- Recombined centers are automatically untagged. Tagged atoms remaining after recombination are ‘quenched’ with hydrogen.
2.4. Enthalpy Estimation
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wulandari, T.; Fawcett, D.; Majumder, S.B.; Poinern, G.E.J. Lithium-based batteries, history, current status, challenges, and future perspectives. Battery Energy 2023, 2, 20230030. [Google Scholar] [CrossRef]
- Peters, J.P.; Baumann, M.; Binderd, J.R.; Weilce, M. On the environmental competitiveness of sodium-ion batteries under a full life cycle perspective—A cell-chemistry specific modelling approach. Sustain. Energy Fuels 2021, 5, 6414–6429. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Park, K.-S. The Li-Ion Rechargeable Battery: A Perspective. J. Am. Chem. Soc. 2013, 135, 1167–1176. [Google Scholar] [CrossRef]
- Ruan, H.; Barreras, J.V.; Engstrom, T.; Merla, Y.; Millar, R.; Wu, B. Lithium-ion battery lifetime extension: A review of derating methods. J. Power Sources 2023, 563, 232805. [Google Scholar] [CrossRef]
- Mansir, I.B.; Okonkwo, P.C. Component Degradation in Lithium-Ion Batteries and Their Sustainability: A Concise Overview. Sustainability 2025, 17, 1000. [Google Scholar] [CrossRef]
- Li, Y.; Guo, W.; Stroe, D.-I.; Zhao, H.; Kristensen, P.K.; Jensen, L.R.; Pedersen, K.; Gurevich, L. Evolution of aging mechanisms and performance degradation of lithium-ion battery from moderate to severe capacity loss scenarios. Chem. Eng. J. 2024, 498, 155588. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Ou, R.; Yang, J.; Xin, Y.; Singh, P.; Wu, F.; Qian, Y.; Gao, H. The safety aspect of sodium ion batteries for practical applications. J. Energy Chem. 2024, 95, 407–427. [Google Scholar] [CrossRef]
- Galatro, D.; Romero, D.A.; Freitez, J.A.; Da Silva, C.; Trescases, O.; Amon, C.H. Modeling degradation of lithium-ion batteries considering cell-to-cell variations. J. Energy Storage 2021, 44 Pt B, 103478. [Google Scholar] [CrossRef]
- Kabra, V.; Karmakar, A.; Vishnugopi, B.S.; Mukherjee, P.P. Quantifying the effect of degradation modes on Li-ion battery thermal instability and safety. Energy Storage Mater. 2025, 74, 103878. [Google Scholar] [CrossRef]
- Duan, C.; Guo, K.; Liu, F.; Pu, H.; Luo, J. Degradation prediction for mechanical components based on transfer learning and a multistage statistical model. Comput. Ind. Eng. 2024, 197, 110485. [Google Scholar] [CrossRef]
- Zhu, J.; Xu, W.; Knapp, M.; Dewi Darma, M.S.; Mereacre, L.; Su, P.; Hua, W.; Liu-Théato, X.; Dai, H.; Wei, X.; et al. A method to prolong lithium-ion battery life during the full life cycle. Cell Rep. Phys. Sci. 2023, 4, 101464. [Google Scholar] [CrossRef]
- Dreyer, S.L.; Kondrakov, A.; Janek, J.; Brezesinski, T. In situ analysis of gas evolution in liquid- and solid-electrolyte-based batteries with current and next-generation cathode materials. J. Mater. Res. 2022, 37, 3146–3168. [Google Scholar] [CrossRef]
- Spotte-Smith, E.W.C.; Blau, S.M.; Xie, X.; Patel, H.D.; Wen, M.; Wood, B.; Dwaraknath, S.; Persson, K.A. Quantum chemical calculations of lithium-ion battery electrolyte and interphase species. Sci. Data 2021, 5, 203. [Google Scholar] [CrossRef]
- Witt, D.; Röder, F.; Krewer, U. Analysis of Lithium-Ion Battery State and Degradation via Physicochemical Cell and SEI Modeling. Batter. Supercaps 2022, 5, e202200067. [Google Scholar] [CrossRef]
- Henschel, J.; Horsthemke, F.; Stenzel, Y.P.; Evertz, M.; Sabrina Girod, S.; Lürenbaum, C.; Kristina Kosters, K.; Wiemers-Meyer, S.; Winter, M.; Nowak, S. Lithium ion battery electrolyte degradation of field-tested electric vehicle battery cells—A comprehensive analytical study. J. Power Sources 2020, 447, 227370. [Google Scholar] [CrossRef]
- Lombardo, T.; Duquesnoy, M.; El-Bouysidy, H.; Årén, F.; Gallo-Bueno, A.; Jørgensen, P.B.; Bhowmik, A.; Demortière, A.; Ayerbe, E.; Alcaide, F.; et al. Artificial Intelligence Applied to Battery Research: Hype or Reality? Chem. Rev. 2021, 122, 10899–10969. [Google Scholar] [CrossRef] [PubMed]
- Kovács, D.P.; McCorkindale, W.; Lee, A.A. Quantitative interpretation explains machine learning models for chemical reaction prediction and uncovers bias. Nat. Comm. 2021, 12, 1695. [Google Scholar] [CrossRef]
- Ucak, U.V.; Ashyrmamatov, I.; Ko, J.; Lee, J. Retrosynthetic reaction pathway prediction through neural machine translation of atomic environments. Nat. Comm. 2022, 13, 1186. [Google Scholar] [CrossRef] [PubMed]
- Huber, F.; van der Burg, S.; van der Hooft, J.J.J.; Ridder, L. MS2DeepScore: A novel deep learning similarity measure to compare tandem mass spectra. J. Cheminform. 2021, 13, 84. [Google Scholar] [CrossRef] [PubMed]
- Kichev, I.; Borislavov, L.; Tadjer, A.; Stoyanova, R. Machine Learning Prediction of the Redox Activity of Quinones. Materials 2023, 16, 6687. [Google Scholar] [CrossRef] [PubMed]
- Amiri, M.N.; Håkansson, A.; Burheim, O.S.; Lamb, J.J. Lithium-ion battery digitalization: Combining physics-based models and machine learning. Renew. Sustain. Energy Rev. 2024, 200, 114577. [Google Scholar] [CrossRef]
- Thelen, A.; Huan, X.; Paulson, N.; Onori, S.; Hu, Z.; Hu, C. Probabilistic machine learning for battery health diagnostics and prognostics—Review and perspectives. npj Mater. Sustain. 2024, 2, 14. [Google Scholar] [CrossRef]
- Lundström, R.; Gogoi, N.; Melin, T.; Berg, E.J. Unveiling Reaction Pathways of Ethylene Carbonate and Vinylene Carbonate in Li-Ion Batteries. J. Phys. Chem. C 2024, 128, 8147–8153. [Google Scholar] [CrossRef]
- Tyagaraj, H.B.; Marje, S.J.; Ranjith, K.S.; Hwang, S.-K.; Al Ghaferi, A.; Chodankar, N.R.; Huh, Y.S.; Han, Y.-K. Sodium-ion batteries: Charge storage mechanisms and recent advancements in diglyme-based electrolytes. J. Energy Storage 2023, 74, 109411. [Google Scholar] [CrossRef]
- He, Y.-B.; Li, B.; Liu, M.; Zhang, C.; Lv, W.; Yang, C.; Li, J.; Du, H.; Zhang, B.; Yang, Q.-H.; et al. Gassing in Li4Ti5O12-based batteries and its remedy. Sci. Rep. 2012, 2, 913. [Google Scholar] [CrossRef]
- Rasheev, H.; Stoyanova, R.; Tadjer, A. Rivalry at the Interface: Ion Desolvation and Electrolyte Degradation in Model Ethylene Carbonate Complexes of Li+, Na+, and Mg2+ with PF6– on the Li4Ti5O12 (111) Surface. ACS Omega 2021, 6, 29735–29745. [Google Scholar] [CrossRef] [PubMed]
- Euler, L. Solutio problematis ad geometriam situs pertinentis. Comment. Acad. Sci. Petropolitanae 1741, 8, 128–140. [Google Scholar]
- Diestel, R. Graph Theory; Springer: New York, NY, USA, 1997, 2000. [Google Scholar]
- Balaban, A.T. Applications of graph theory in chemistry. J. Chem. Inf. Comput. Sci. 1985, 25, 334–343. [Google Scholar] [CrossRef]
- Trinajstic, N. Chemical Graph Theory; Routledge: London, UK, 2018; ISBN 9781351461573. [Google Scholar]
- García-Domenech, R.; Gálvez, J.; de Julián-Ortiz, J.V.; Pogliani, L. Some New Trends in Chemical Graph Theory. Chem. Rev. 2008, 108, 1127–1169. [Google Scholar] [CrossRef] [PubMed]
- Hagberg, A.A.; Schult, D.A.; Swart, P.J. Exploring Network Structure, Dynamics, and Function using NetworkX. In Proceedings of the 7th Python in Science Conference, Pasadena, CA, USA, 19–24 August 2008; Varoquaux, G., Vaught, T., Millman, J., Eds.; pp. 11–15. [Google Scholar]
- Landrum, G.; Tosco, P.; Kelley, B.; Rodriguez, R.; Cosgrove, D.; Vianello, R.; Sriniker; Gedeck, P.; Swain, M.; Scalfani, V.F.; et al. “Rdkit/rdkit: 2024_03_6 (Q1 2024) Release”. Open-Source Cheminformatics. Zenodo. Available online: https://www.rdkit.org (accessed on 29 August 2024).
- Heller, S.R.; McNaught, A.; Pletnev, I.; Stein, S.; Tchekhovskoi, D. InChI, the IUPAC International Chemical Identifier. J. Cheminform. 2015, 7, 23. [Google Scholar] [CrossRef]
- Warr, W.A. Many InChIs and quite some feat. J. Comput. Aided Mol. Des. 2015, 29, 681–694. [Google Scholar] [CrossRef]
- Rocha, G.; Freire, R.; Simas, A.; Stewart, J. RM1: A reparameterization of AM1 for H, C, N, O, P, S, F, Cl, Br, and I. J. Comp. Chem. 2006, 27, 1101–1111. [Google Scholar] [CrossRef]
- HyperChemTM; Professional 7.51. Hypercube, Inc.: Gainesville, FL, USA, 2003.
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6169. [Google Scholar] [CrossRef]
- Grimme, S.; Hansen, A.; Brandenburg, J.G.; Bannwarth, C. Dispersion-Corrected Mean-Field Electronic Structure Methods. Chem. Rev. 2016, 116, 5105–5154. [Google Scholar] [CrossRef]
- Kukeva, R.; Kalapsazova, M.; Rasheev, H.; Vassilev, G.; Tadjer, A.; Stoyanova, R. In Situ Electron Paramagnetic Resonance Monitoring of Predegradation Radical Generation in a Lithium Electrolyte. J. Phys. Chem. Lett. 2023, 14, 9633–9639. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Klein, E.; Lukeš, V.; Ilčin, M. DFT/B3LYP study of tocopherols and chromans antioxidant action energetics. Chem. Phys. 2007, 336, 51–57. [Google Scholar] [CrossRef]
- Shkrob, I.A.; Zhu, Y.; Marin, T.W.; Abraham, D. Reduction of Carbonate Electrolytes and the Formation of Solid-Electrolyte Interface (SEI) in Lithium-Ion Batteries. 1. Spectroscopic Observations of Radical Intermediates Generated in One-Electron Reduction of Carbonates. J. Phys. Chem. C 2013, 117, 38–19255. [Google Scholar] [CrossRef]
- Westman, K.; Dugas, R.; Jankowski, P.; Wieczorek, W.; Gachot, G.; Morcrette, M.; Irisarri, E.; Ponrouch, A.; Palacín, M.R.; Tarascon, J.-M.; et al. Diglyme Based Electrolytes for Sodium-Ion Batteries. ACS Appl. Energy Mater. 2018, 1, 2671–2680. [Google Scholar] [CrossRef]
- Dugas, R.; Ponrouch, A.; Gachot, G.; David, R.; Palacin, M.R.; Tarascon, J.M. Na Reactivity toward Carbonate-Based Electrolytes: The Effect of FEC as Additive. J. Electrochem. Soc. 2016, 163, A2333–A2339. [Google Scholar] [CrossRef]
- Gachot, G.; Grugeon, S.; Eshetu, G.G.; Mathiron, D.; Ribière, P.; Armand, M.; Laruelle, S. Thermal behaviour of the lithiated-graphite/electrolyte interface through GC/MS analysis. Electrochim. Acta 2012, 83, 402–409. [Google Scholar] [CrossRef]
- Du, H.; Wang, Y.; Kang, Y.; Zhao, Y.; Tian, Y.; Wang, X.; Tan, Y.; Liang, Z.; Wozny, J.; Li, T.; et al. Side Reactions/Changes in Lithium-Ion Batteries: Mechanisms and Strategies for Creating Safer and Better Batteries. Adv. Mater. 2024, 36, 2401482. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Wang, J.; Shao, H.; Xu, K.; Deng, Y. Gas Generation Mechanism in Li-Metal Batteries. Energy Environ. Mater. 2021, 5, 327–336. [Google Scholar] [CrossRef]
- Jung, R.; Strobl, P.; Maglia, F.; Stinner, C.; Gasteiger, H.A. Temperature Dependence of Oxygen Release from LiNi0.6Mn0.2Co0.2O2 (NMC622) Cathode Materials for Li-Ion Batteries. J. Electrochem. Soc. 2018, 165, A2869–A2879. [Google Scholar] [CrossRef]
- Jin, Y.; Kneusels, N.-J.H.; Grey, C.P. NMR Study of the Degradation Products of Ethylene Carbonate in Silicon–Lithium Ion Batteries. J. Phys. Chem. Lett. 2019, 10, 6345–6350. [Google Scholar] [CrossRef] [PubMed]


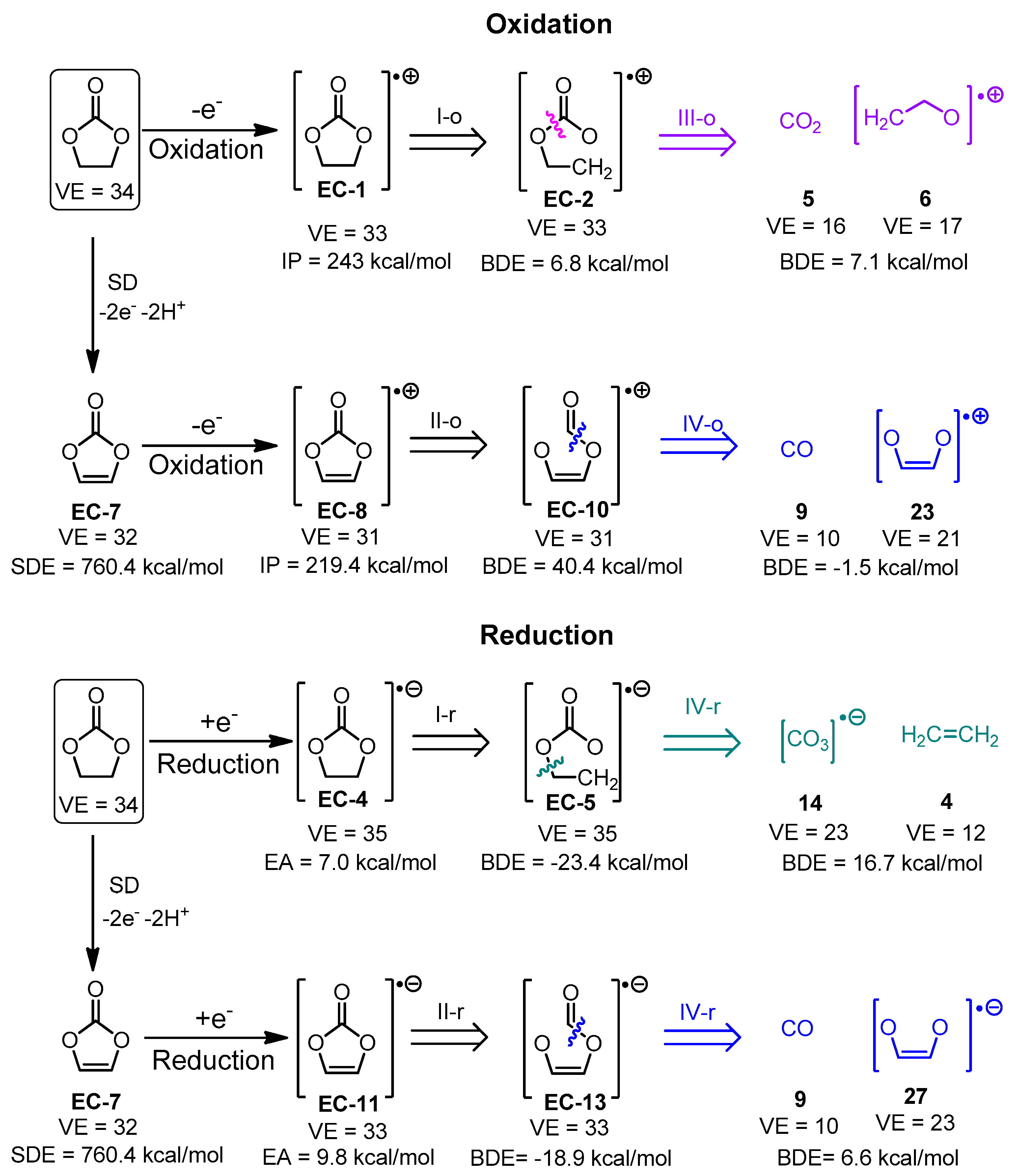
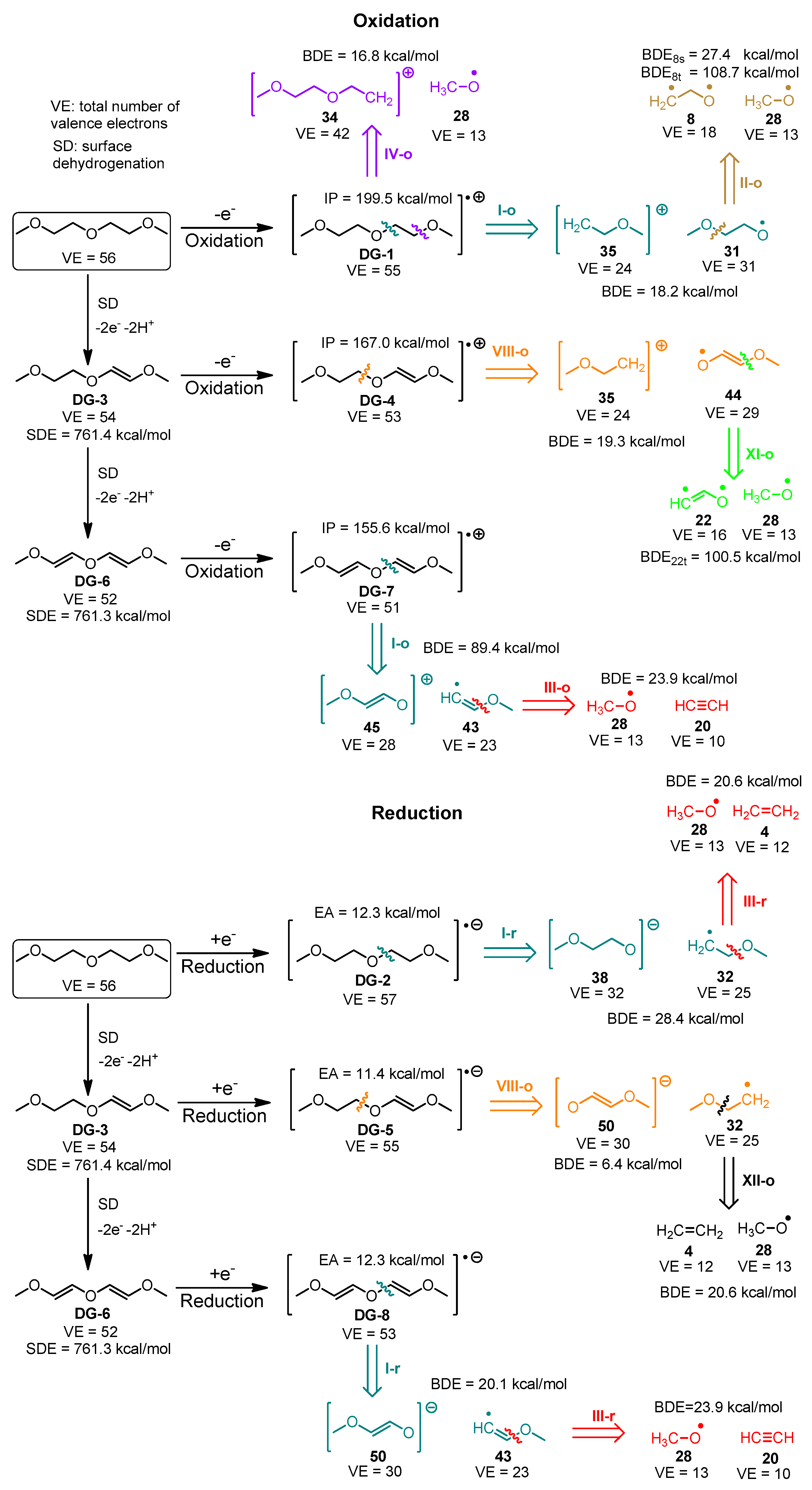
| Degradation Product | Algorithm Steps | Electrochemical Cell Configuration | Detection Experimental Conditions | Ref. |
|---|---|---|---|---|
| [CO2]•− | Figure S1/IV-o and IV-r Figure S2 IV-o and IV-r | - | EPR in ethylene carbonate reduced by irradiation with 2.5 MeV electron beam to 3 kGy for 1 min at 77 K | [43] |
| Ethylene oxide | Figure S1/III-r | Li/1 M LiPF6 in EC50:DMC50/ SFG6 (90 wt. %) and Super P carbon black (10 wt. %) | DSC of lithiated electrode material combined GC/MS study of the compounds corresponding to each DSC peak | [46,47] |
| CO and CO2 | Figure S1/III-o, III-r, IV-o, IV-r, V-o, V-r; Figure S2/III-o, III-r, IV-o, IV-r, V-o, V-r | Li/1 M LiPF6 in EC50:DMC50/ SFG6 (90 wt. %) and Super P carbon black (10 wt. %) | DSC combined GC/MS study of the compounds corresponding to each DSC peak | [46] |
| CO and CO2 | Figure S1/III-o, III-r, IV-o, IV-r, V-o, V-r; Figure S2/III-o, III-r, IV-o, IV-r, V-o, V-r | NCM622-Li, NCM811-Li and NCM111-Li cells | In situ differential mass spectroscopy techniques | [48] |
| Ethene | Figure S1/I-o and I-r | Li/1.5 M LiPF6 in EC/NMC622 and graphite/1.5 M LiPF6 in EC/NMC62 | Online mass spectroscopy experiments (OLMS) | [49] |
| Total gas evolution | Figures S1 and S2—all paths leading to gaseous products | Na/in 1 M NaPF6 in EC50:DMC50 /hard C | Continuous measurements of the pressure change invoked by gas evolution | [45] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borislavov, L.; Tadjer, A.; Stoyanova, R. Graph-Theory Algorithm for Prediction of Electrolyte Degradation Reactions in Lithium- and Sodium-Ion Batteries. Materials 2025, 18, 832. https://doi.org/10.3390/ma18040832
Borislavov L, Tadjer A, Stoyanova R. Graph-Theory Algorithm for Prediction of Electrolyte Degradation Reactions in Lithium- and Sodium-Ion Batteries. Materials. 2025; 18(4):832. https://doi.org/10.3390/ma18040832
Chicago/Turabian StyleBorislavov, Lyuben, Alia Tadjer, and Radostina Stoyanova. 2025. "Graph-Theory Algorithm for Prediction of Electrolyte Degradation Reactions in Lithium- and Sodium-Ion Batteries" Materials 18, no. 4: 832. https://doi.org/10.3390/ma18040832
APA StyleBorislavov, L., Tadjer, A., & Stoyanova, R. (2025). Graph-Theory Algorithm for Prediction of Electrolyte Degradation Reactions in Lithium- and Sodium-Ion Batteries. Materials, 18(4), 832. https://doi.org/10.3390/ma18040832








