Assessment of Externally Prestressed Beams with FRP Rebars Considering Bond–Slip Effects †
Abstract
1. Introduction
2. FEM and Verification
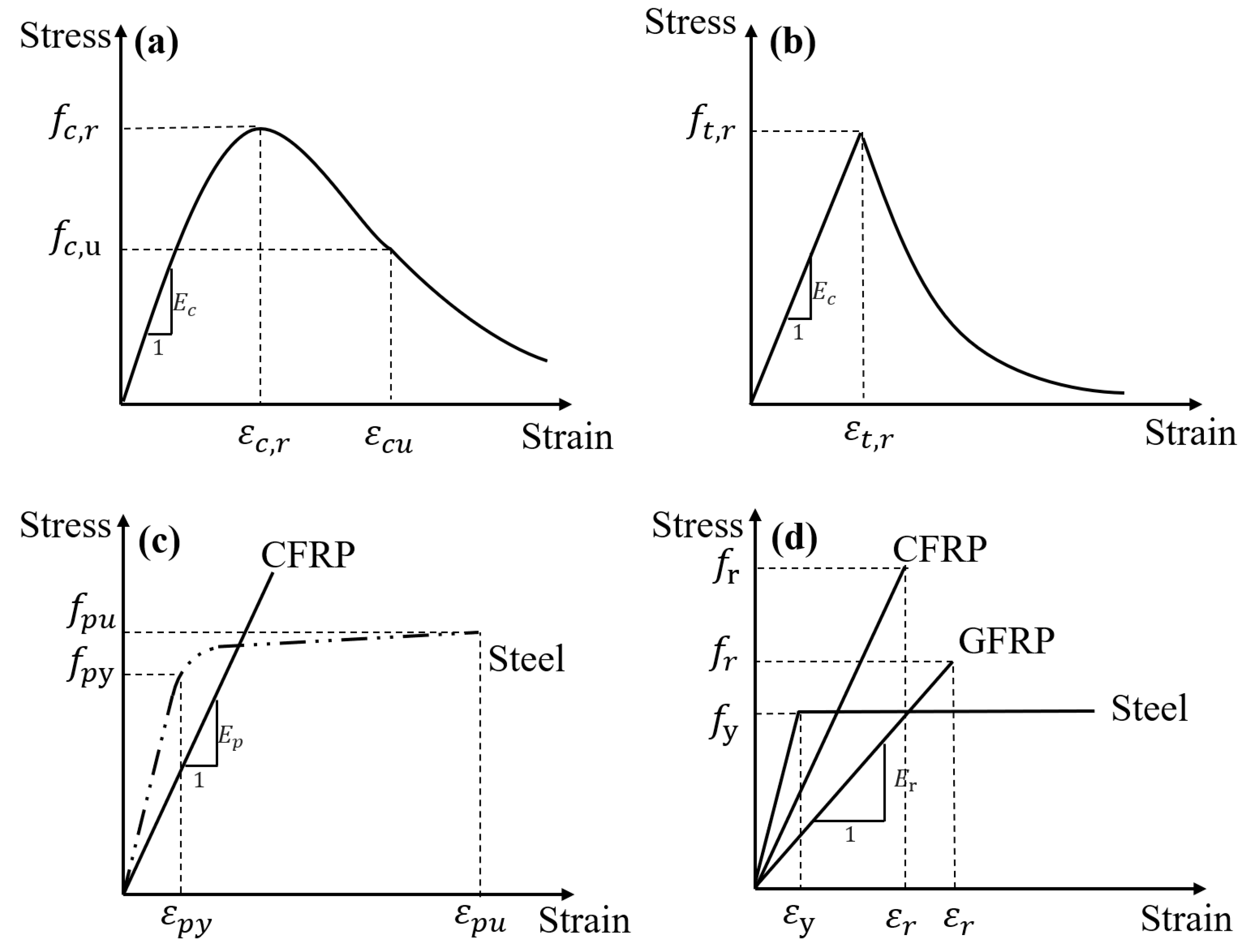
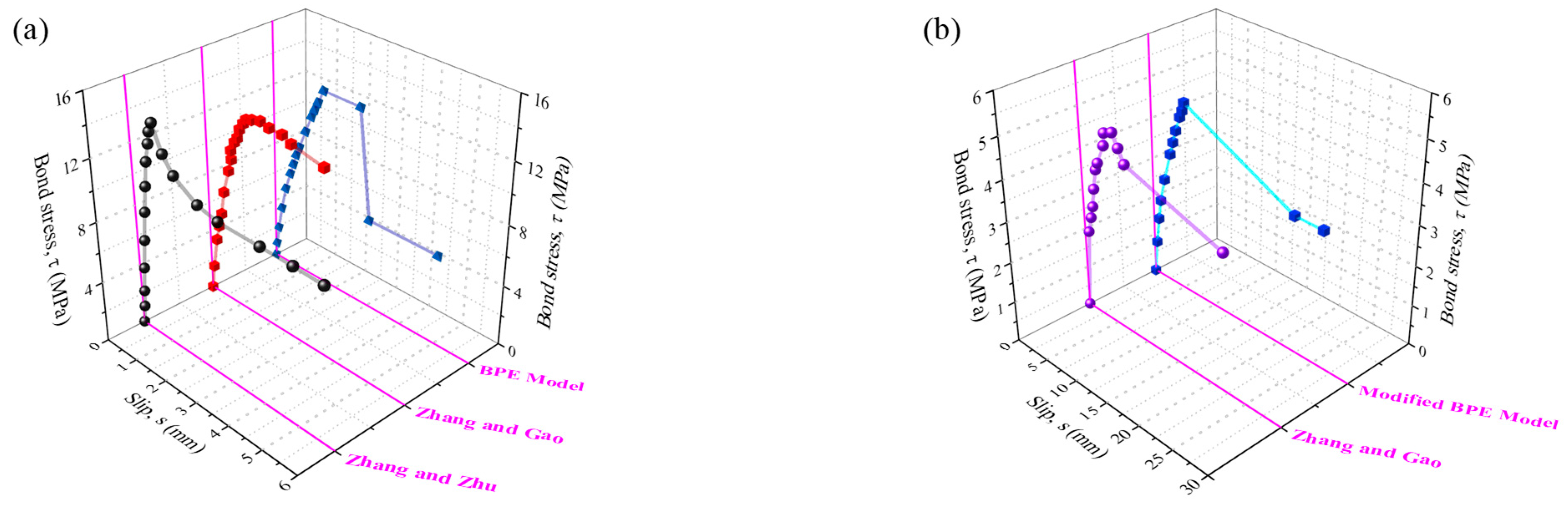
2.1. Material Property and Bond Stress–Slip
2.2. Bond Stress–Slip Model Validation
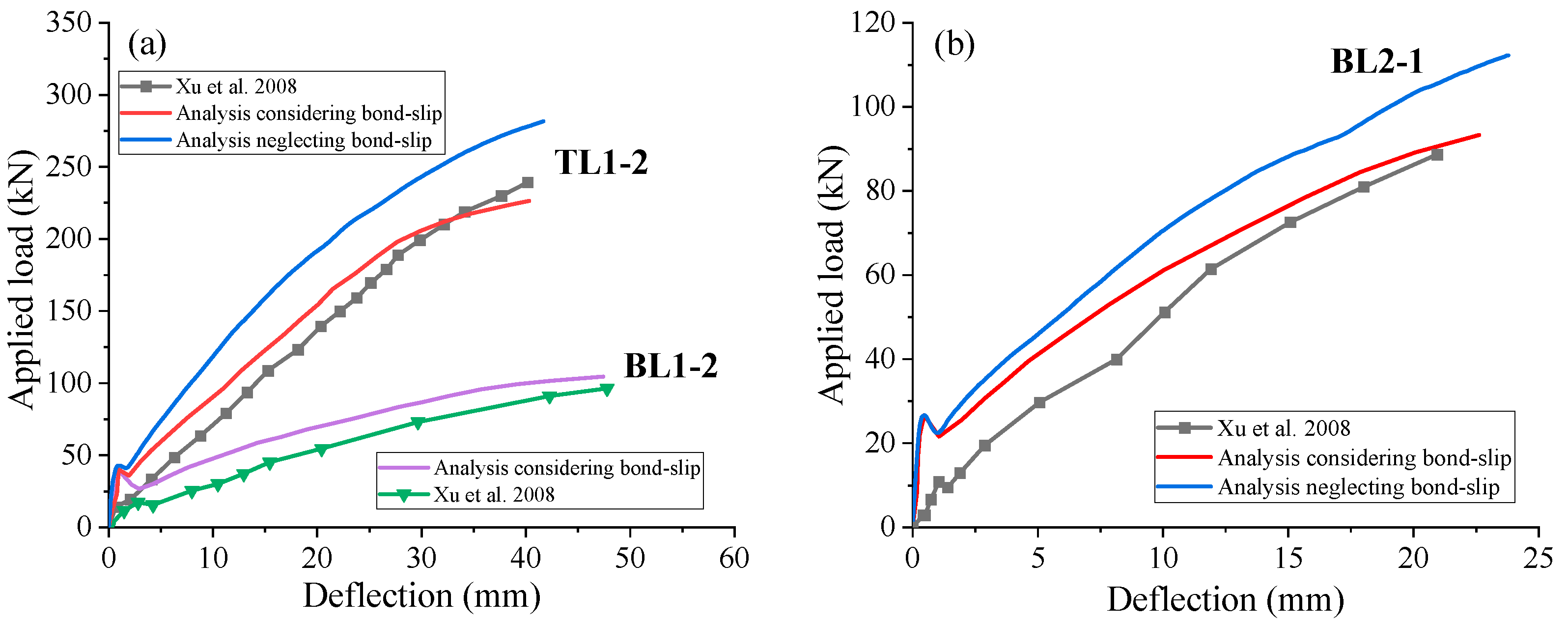
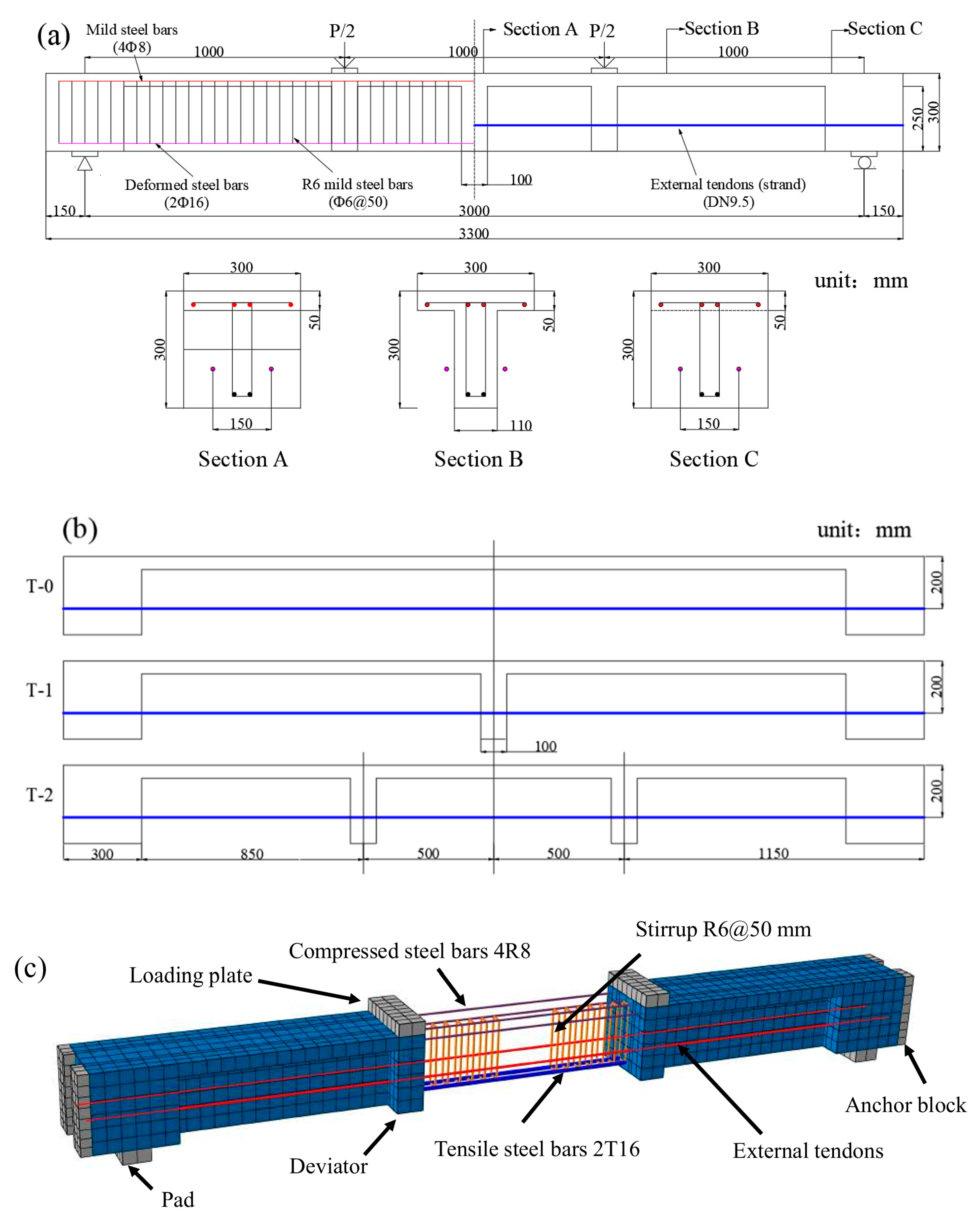
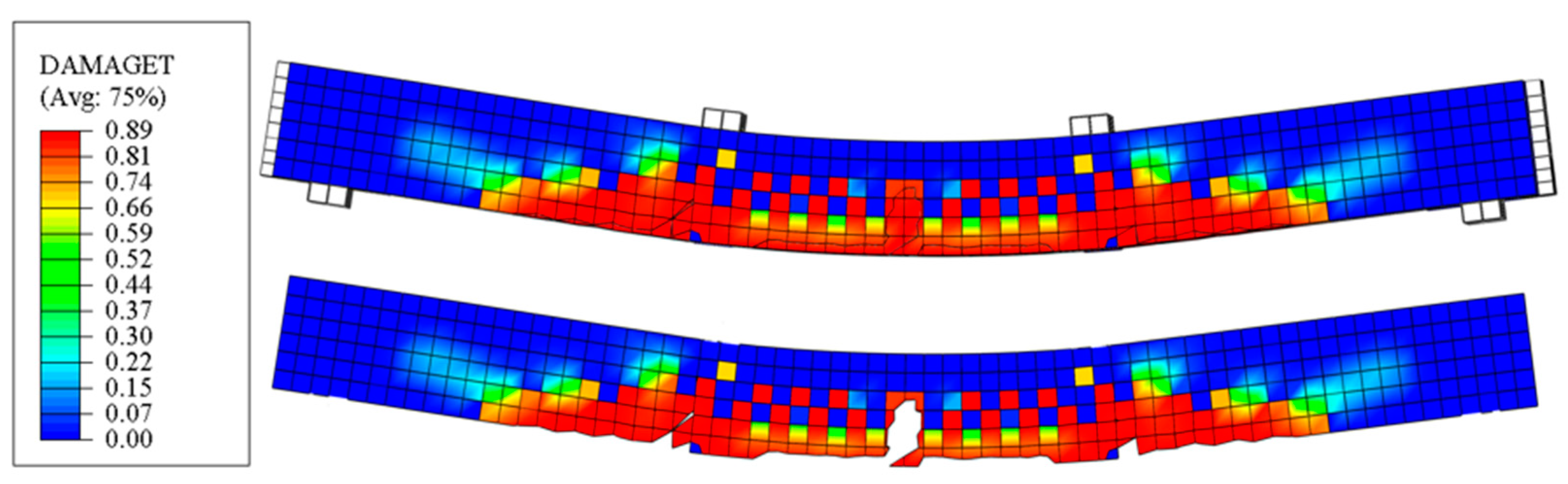
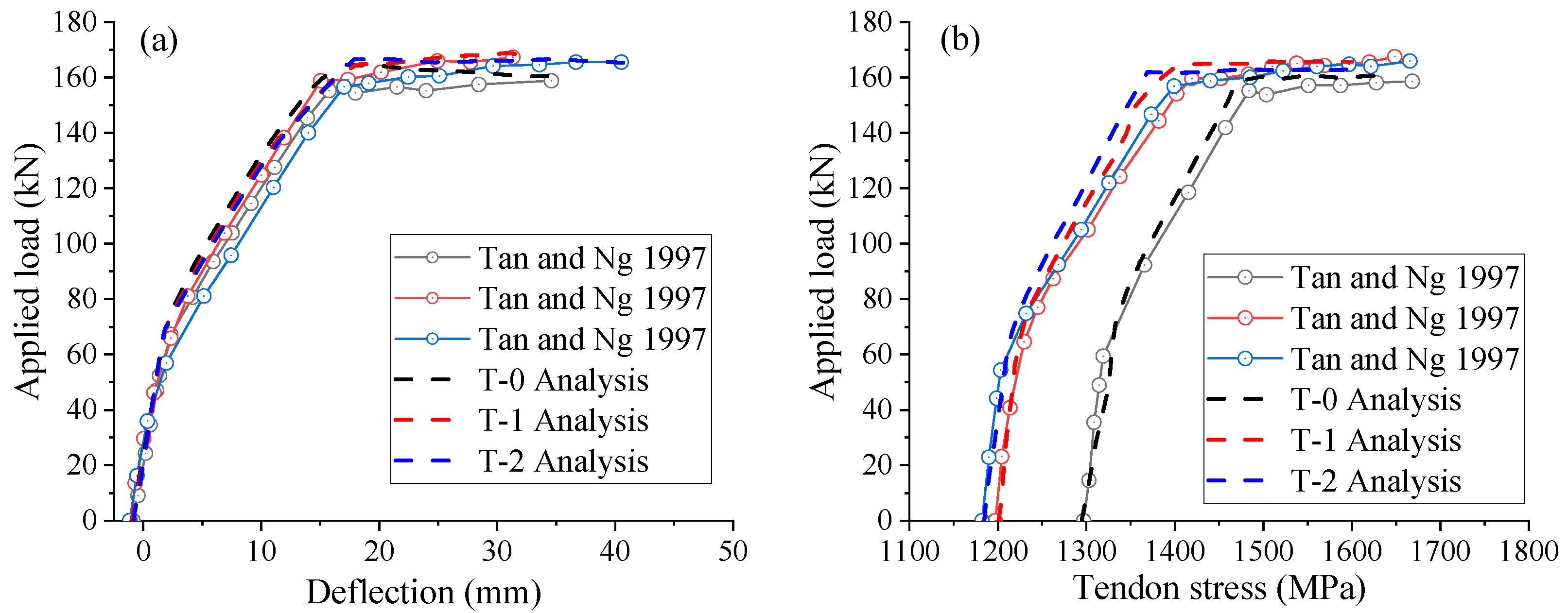
2.3. Verification with Experimental Results of EPC Beams
3. FEM Assessment
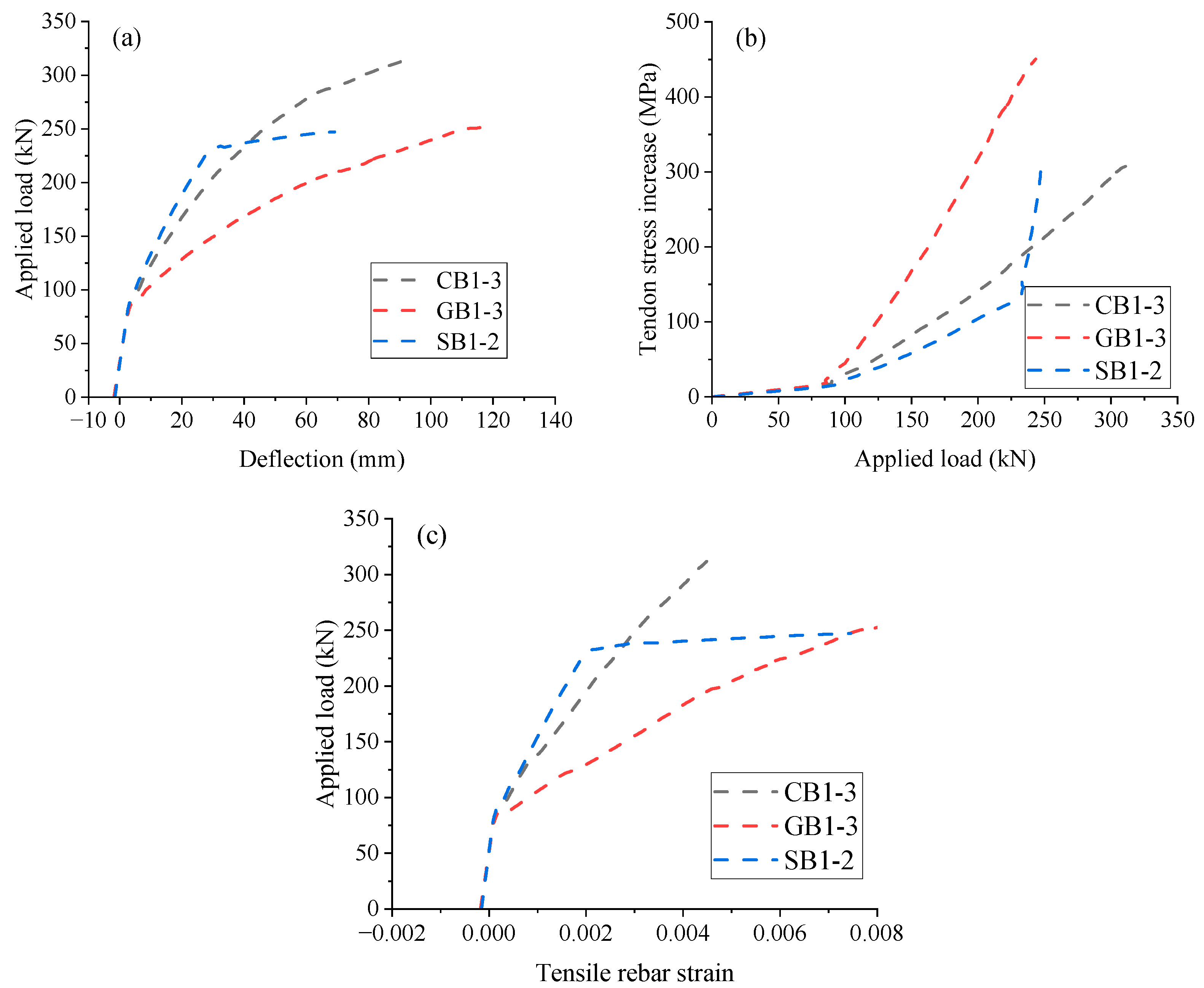
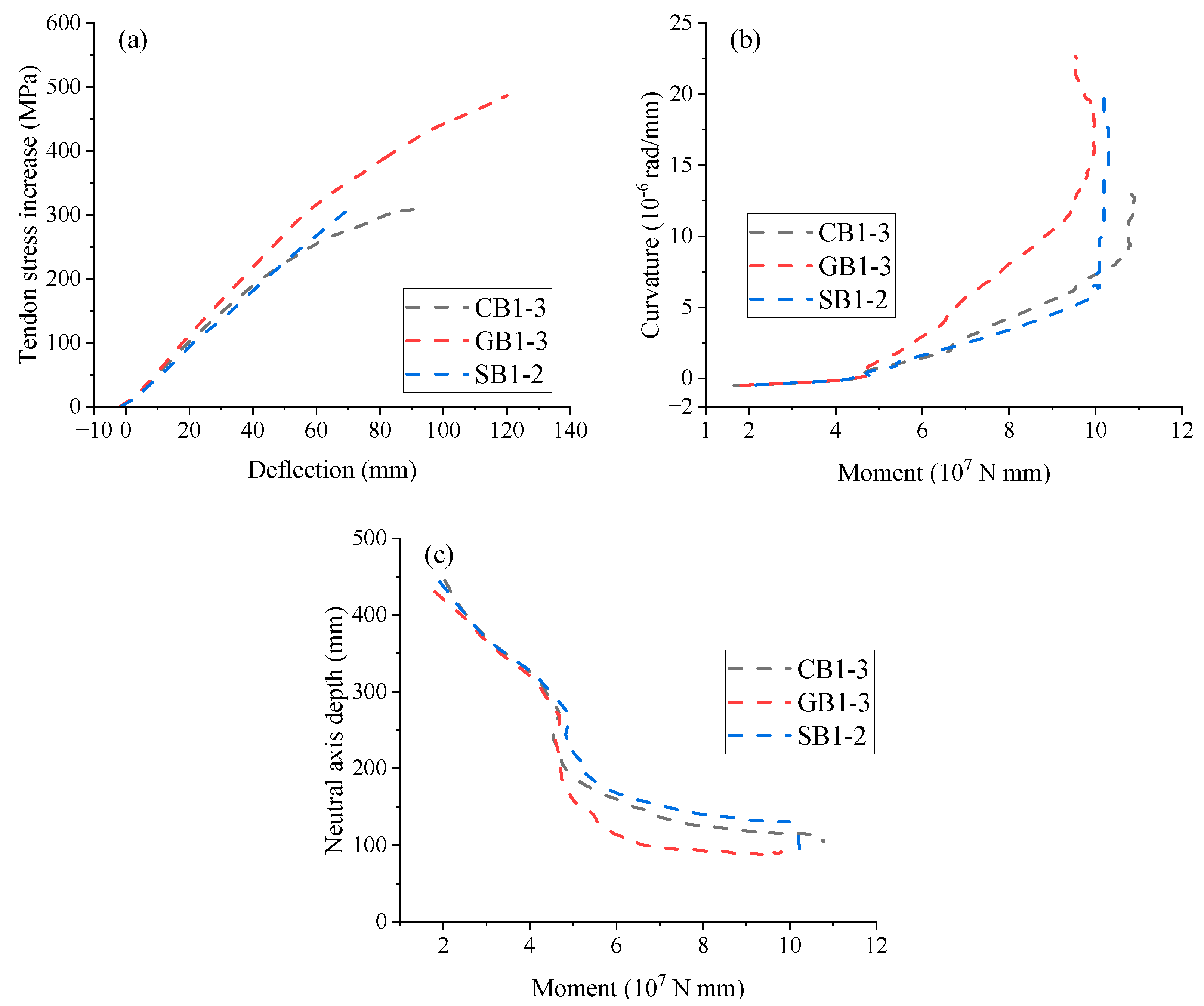
3.1. Effect of Rebar Type
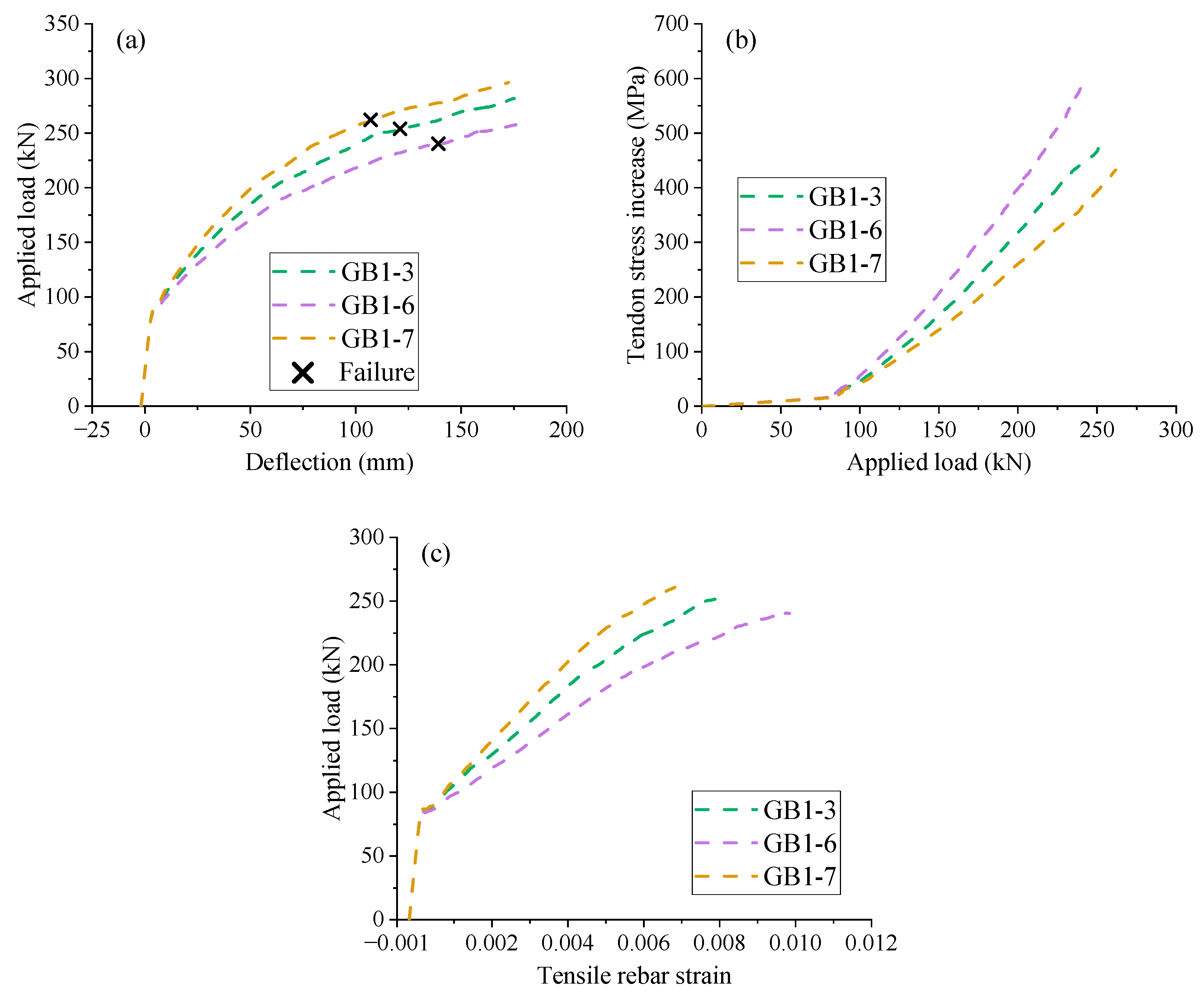
3.2. Effect of GFRP Modulus of Elasticity
3.3. Effect of Concrete Grade
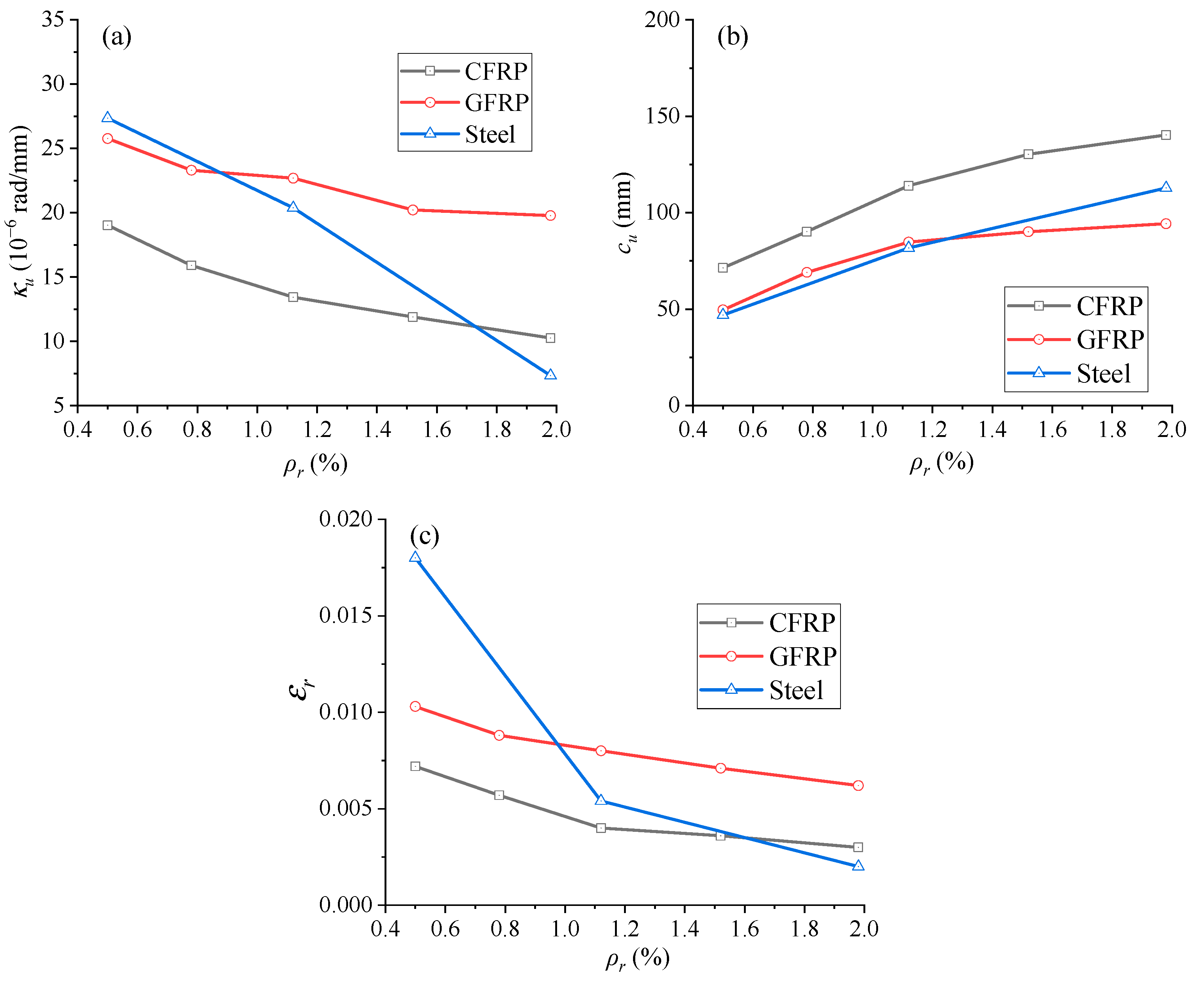
3.4. Effect of Reinforcement Ratio
4. Assessment of Typical Models for Predicting the Ultimate Tendon Stress
4.1. Typical Models
4.2. Comparative Analysis
4.3. Applicability to Real-World Engineering Structures
5. Conclusions
- A high-fidelity 3D FEM for EPC beams with FRP rebars is developed. The interaction between FRP rebars and concrete is considered by implementing a self-designed program that links FRP rebar nodes to concrete and incorporates appropriate bond–slip relationships. The model effectively captures the slip behavior of the FRP rebars. Its reliability is validated by comparing simulation outcomes with experimental data.
- There is a specific phenomenon of stress degradation of FRP rebars due to the bond–slip effect. This effect reduces the structural stiffness and load-carrying capacity and may lead to interface failure due to stress concentration. Thus, the bond–slip effect is essential for the accurate simulation and design of EPC beams with FRP rebars.
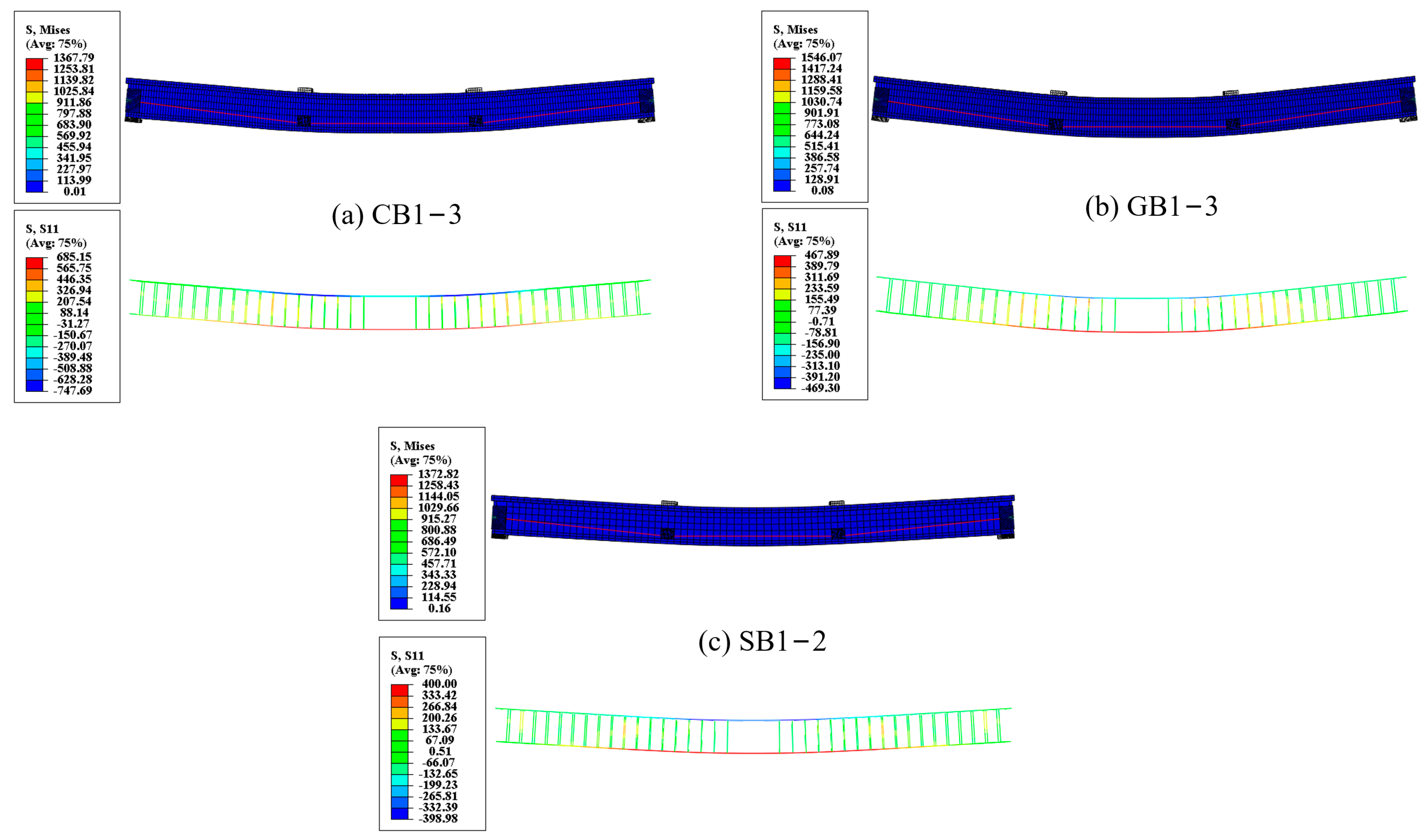
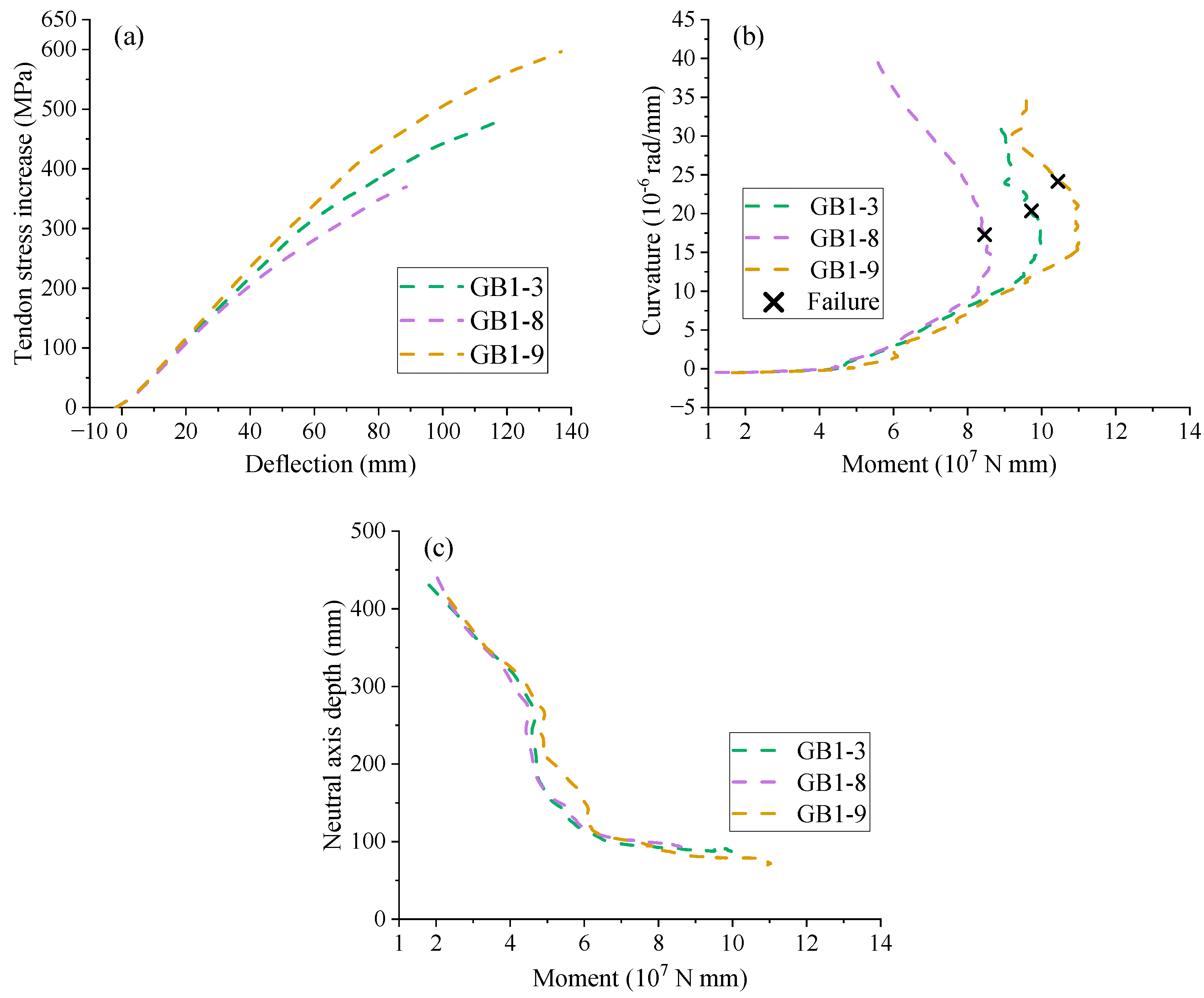
- As ρr in EPC beams with CFRP rebars increases, Δu, Δσp, εr, and κu tend to decrease, while Pu and cu tend to increase. Within ρr studied, EPC beams with CFRP rebars exhibit greater Pu, Δu, cu, and Δσp compared to EPC beams with steel rebars. The difference in cu between EPC beams with CFRP and GFRP rebars gradually increases with increasing ρr. Additionally, enhancing concrete grade significantly improves structural stiffness and ultimate bearing capacity.
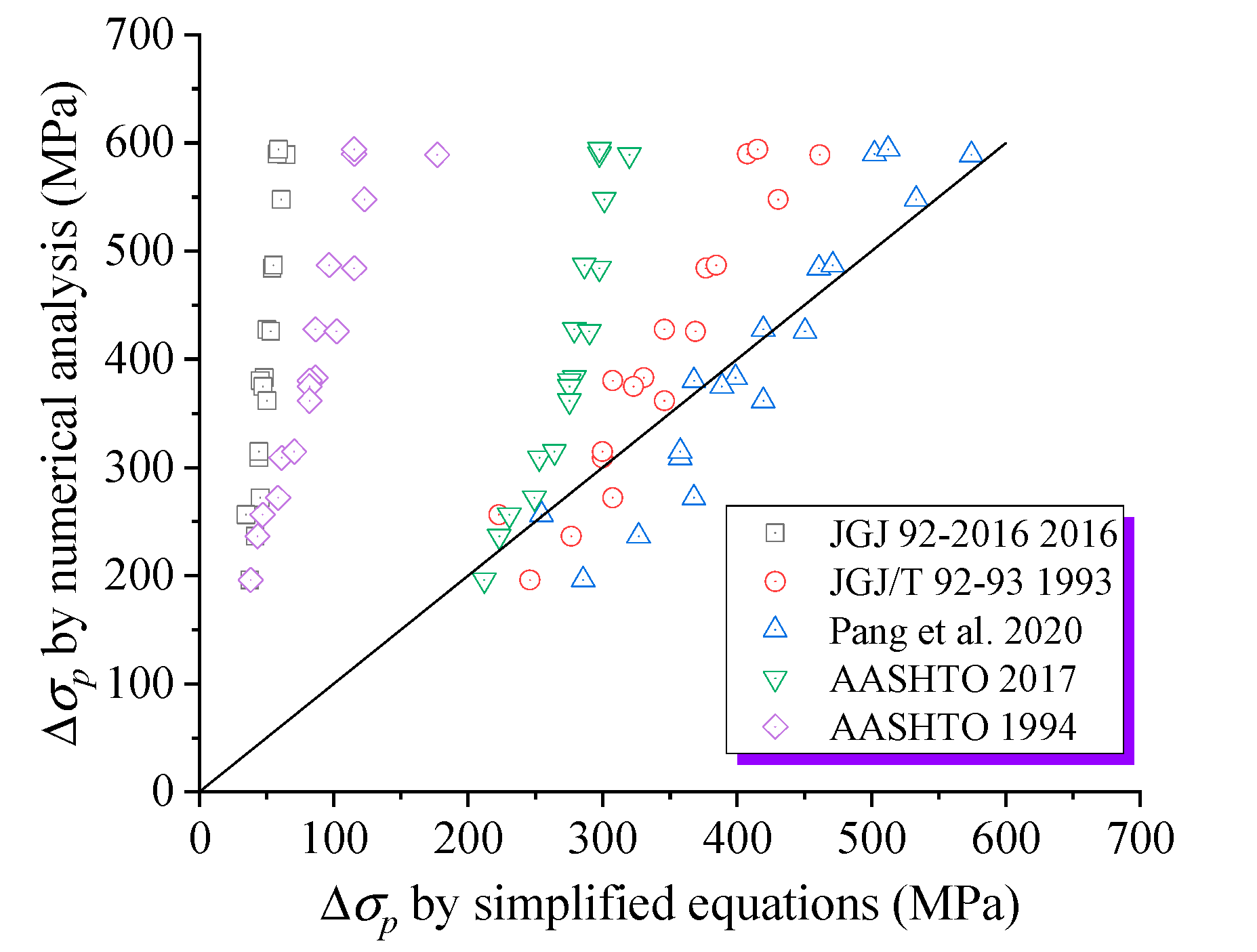
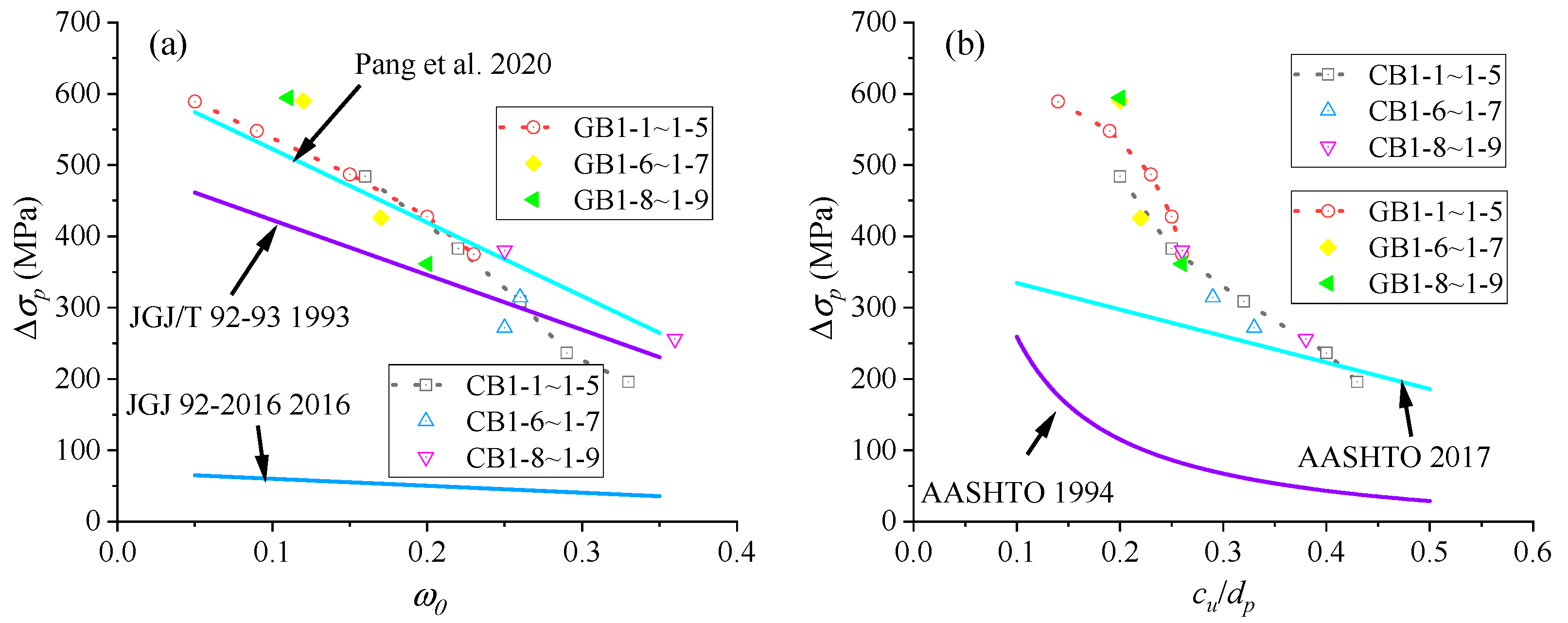
- JGJ 92-2016 and AASHTO-1994 yield the poorest results, being significantly over-conservative, while JGJ/T 92-93 demonstrates reasonable accuracy in predicting Δσp in EPC beams with FRP rebars, particularly when ω0 exceeds 0.2. AASHTO-2017 shows a relatively poor correlation with the numerical results. The Pang et al. model offers better accuracy in predicting the Δσp for EPC beams with FRP rebars than the aforementioned design codes, although it ignores the bond–slip interaction between FRP rebars and concrete.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Du, M.; Wang, D.; Wang, X.; Chen, H.; Gao, K.; Liu, S.; Fang, H. Numerical simulation of reinforcement design and bearing capacity for external prestressing deviator based on strut-and-tie model. In Proceedings of the 2022 International Conference on Cloud Computing, Big Data and Internet of Things (3CBIT), Wuhan, China, 22–23 October 2022; pp. 213–218. [Google Scholar]
- Qi, J.; Ma, Z.J.; Wang, J. Post-cracking shear behavior of concrete beams strengthened with externally prestressed tendons. Structures 2020, 23, 214–224. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, B.; Lopes, S.M.R.; Lopes, A.V.; Lou, T. A critical review of prestressed concrete structures with external FRP tendons. Structures 2025, 71, 108049. [Google Scholar] [CrossRef]
- Zucca, M.; Reccia, E.; Longarini, N.; Eremeyev, V.; Crespi, P. On the structural behaviour of existing RC bridges subjected to corrosion effects: Numerical insight. Eng. Fail. Anal. 2023, 152, 107500. [Google Scholar] [CrossRef]
- Fuhaid, A.F.A.; Niaz, A. Carbonation and corrosion problems in reinforced concrete structures. Buildings 2022, 12, 586. [Google Scholar] [CrossRef]
- Chen, A.; Alateeq, A. Performance of FRP-confined reinforced concrete beams integrated with solar cells. Int. J. Civ. Eng. 2023, 21, 491–506. [Google Scholar] [CrossRef]
- Al-Thairy, H. A simplified method for steady state and transient state thermal analysis of hybrid steel and FRP RC beams at fire. Case Stud. Constr. Mater. 2020, 13, e00465. [Google Scholar] [CrossRef]
- Lou, T.; Shi, S.; Lopes, S.M.R.; Chen, B. Rational prediction of moment redistribution in continuous concrete beams reinforced with FRP bars. Eng. Struct. 2024, 303, 117515. [Google Scholar] [CrossRef]
- ACI Committee 440. Guide for The Design and Construction of Structural Reinforced with Fiber Concrete Reinforced Polymer Bars. In ACI440.1R; ACI: Farmington Hills, MI, USA, 2015. [Google Scholar]
- Shi, J.; Wang, X.; Wu, Z.; Wei, X.; Ma, X. Long-term mechanical behaviors of uncracked concrete beams prestressed with external basalt fiber-reinforced polymer tendons. Eng. Struct. 2022, 262, 114309. [Google Scholar] [CrossRef]
- Abdallah, M.; Al-Mahmoud, F.; Boissiere, R.; Khelil, A.; Mercier, J. Experimental study on strengthening of RC beams with Side Near Surface Mounted technique-CFRP bars. Compos. Struct. 2020, 234, 111716. [Google Scholar] [CrossRef]
- Bennitz, A.; Schmidt, J.W.; Nilimaa, J.; Taljsten, B.; Goltermann, P.; Ravn, D.L. Reinforced concrete T-beams externally prestressed with unbonded carbon fiber-reinforced polymer tendons. ACI Struct. J. 2012, 109, 521. [Google Scholar]
- Mohamed, A.M.; Mahmoud, K.; El-Salakawy, E.F. Behavior of simply supported and continuous concrete deep beams reinforced with GFRP bars. J. Compos. Constr. 2020, 24, 04020032. [Google Scholar] [CrossRef]
- Xue, W.; Tan, Y.; Peng, F. Experimental study on damaged prestressed concrete beams using external post-tensioned tendons. ACI Struct. J. 2020, 117, 159–168. [Google Scholar] [CrossRef]
- Lou, T.; Karavasilis, T.L. Numerical evaluation of prestressed steel-concrete composite girders with external FRP or steel tendons. J. Constr. Steel Res. 2019, 162, 105698. [Google Scholar] [CrossRef]
- Grace, N.F.; Abdel-Sayed, G. Behavior of externally draped CFRP tendons in prestressed concrete bridges. PCI J. 1998, 43, 88–101. [Google Scholar] [CrossRef]
- Yu, T.; Tian, S.; Zhao, Y. Experimental and theoretical investigation of bending in concrete beams strengthened with external prestressing CFRP tendons. Open Constr. Build. Technol. J. 2016, 10, 492–510. [Google Scholar]
- Ghallab, A.; Beeby, A.W. Factors affecting the external prestressing stress in externally strengthened prestressed concrete beams. Cem. Concr. Compos. 2005, 27, 945–957. [Google Scholar] [CrossRef]
- Ghallab, A. Calculating ultimate tendon stress in externally prestressed continuous concrete beams using simplified formulas. Eng. Struct. 2013, 46, 417–430. [Google Scholar] [CrossRef]
- Kantaros, A.; Soulis, E.; Ganetsos, T.; Petrescu, F.I.T. Applying a combination of cutting-edge industry 4.0 processes towards fabricating a customized component. Processes 2023, 11, 1385. [Google Scholar] [CrossRef]
- Duan, N.; Zhang, J.; Cheng, J. Simulation research on continuous concrete beams reinforced with external prestressed CFRP tendons. Materials 2022, 15, 5697. [Google Scholar] [CrossRef] [PubMed]
- Tran, D.T.; Pham, T.M.; Hao, H.; Chen, W. Numerical study on bending response of precast segmental concrete beams externally prestressed with FRP tendons. Eng. Struct. 2021, 241, 112423. [Google Scholar] [CrossRef]
- Pang, M.; Li, Z.; Lou, T. Numerical study of using FRP and steel rebars in simply supported prestressed concrete beams with external FRP tendons. Polymers 2020, 12, 2773. [Google Scholar] [CrossRef] [PubMed]
- Lou, T.; Li, Z.; Pang, M. Behavior of externally prestressed continuous beams with FRP/steel rebars under symmetrical/unsymmetrical loading: Numerical study. Case Stud. Constr. Mater. 2022, 17, e01196. [Google Scholar] [CrossRef]
- Biscaia, H.C.; Carmo, N. Bond assessment between rebars embedded into a parent material using a single-function bond-slip model. Constr. Build. Mater. 2023, 397, 132396. [Google Scholar] [CrossRef]
- Kim, S.; Kim, J.; Park, C. Bond properties of glass-fiber-reinforced polymer hybrid rebar in reinforced concrete with respect to bond length. Appl. Sci. 2024, 14, 4576. [Google Scholar] [CrossRef]
- Rahimi, M.; Davoodi, M.R.; Nematzadeh, M.; Yousefpour, H.; Azarbera, M.; Fattahi, Z. A comparative study between beam and pull-out tests on bond behavior of ribbed GFRP bar in concrete conforming to RILEM standards. Arch. Civ. Mech. Eng. 2024, 25, 37. [Google Scholar] [CrossRef]
- Xue, W.; Zheng, Q.; Yang, Y.; Fang, Z. Bond behavior of sand-coated deformed glass fiber reinforced polymer rebars. J. Reinf. Plast. Compos. 2014, 33, 895–910. [Google Scholar] [CrossRef]
- Fahmy, M.F.M.; Ahmed, S.A.S.; Wu, Z. Bar surface treatment effect on the bond-slip behavior and mechanism of basalt FRP bars embedded in concrete. Constr. Build. Mater. 2021, 289, 122844. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, Y. Evaluation of bond stress-slip models for FRP reinforcing bars in concrete. Compos. Struct. 2014, 107, 131–141. [Google Scholar] [CrossRef]
- Eligehausen, R.; Popov, E.P.; Bertero, V.V. Local Bond Stress-Slip Relationships of Deformed Bars Under Generalized Excitations; Rep No.83, EERC; University of California: Berkeley, CA, USA, 1983. [Google Scholar]
- Cosenza, E.; Manfredi, G.; Realfonzo, R. Bond characteristics and anchorage length of FRP rebars. In Proceedings of the 2nd International Conference on Advanced Composite Materials in Bridges and Structures (ACMBS-II), Montréal, QC, Canada, 11–14 August 1996; El-Badry, M., Ed.; pp. 909–916. [Google Scholar]
- Gao, D.; Zhu, H.; Xie, J. The constitutive models for bond slip relation between FRP rebars and concrete. Ind. Constr. 2003, 33, 41–43. (In Chinese) [Google Scholar]
- GB50010-2010; Code for Design of Concrete Structure. The Ministry of Construction of the People’s Republic of China: Beijing, China, 2010.
- Menegotto, M.; Pinto, P.E. Method of analysis for cyclically loaded reinforced concrete plane frames. In Proceedings of the IABSE Preliminary Report for Symposium on Resistance and Ultimate Deformability of Structures Acted on Well-Defined Repeated Loads, Lisbon, Portugal, 13–14 September 1973; pp. 15–22. [Google Scholar]
- Zhang, H.; Zhu, F. Study on the anchorage length of FRP bars with bond-slip constitutive relationship. Sichuan Build. Sci. 2007, 33, 43–46. (In Chinese) [Google Scholar]
- Zhang, Y.; Gao, X. Experimental study on the bonding performance between FRP bars and concrete. Urban Roads Bridges Flood Control 2012, 148–151. (In Chinese) [Google Scholar]
- Xu, X.; Ji, T.; Zheng, Y. Test and design method on flexural resistance performance of concrete beam with FRP bar. Build. Struct. 2008, 38, 45–48. (In Chinese) [Google Scholar]
- ABAQUS/Standard User’s Manual, Version 2022; Dassault Systèmes Simulia Corp: Johnston, RI, USA, 2022.
- Tan, K.H.; Ng, C.K. Effects of deviators and tendon configuration on behavior of externally prestressed beams. ACI Struct. J. 1997, 94, 13–22. [Google Scholar]
- Li, Z.; Shi, S.; Lou, T. 3D finite element modeling of externally prestressed concrete beams. In Proceedings of the The 2023 World Congress on Advances in Structural Engineering and Mechanics (ASEM23) GECE, Seoul, Korea, 16–18 August 2023. [Google Scholar]
- Xiao, X.; Gu, X.; Zhang, X. Combination of thermoacoustic heat dissipation with oscillating convection: A novel cooling method. Int. J. Heat Mass Transf. 2020, 160, 120177. [Google Scholar] [CrossRef]
- JGJ 92-2016; Technical Specification for Concrete Structures Prestressed with Unbonded Tendons. China Architecture and Building Press: Beijing, China, 2016.
- JGJ/T 92-93; Technical Specification for Concrete Structures Prestressed with Unbonded Tendons. China Planning Press: Beijing, China, 1993.
- AASHTO. LRFD Bridge Design Specifications; American Association of State Highway and Transportation Officials: Washington, DC, USA, 1994. [Google Scholar]
- AASHTO. LRFD Bridge Design Specifications, 8th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2017. [Google Scholar]
- Roberts-Wollmann, C.L.; Kreger, M.E.; Rogowsky, D.M.; Breen, J.E. Stresses in external tendons at ultimate. ACI Struct. J. 2005, 102, 206–213. [Google Scholar]



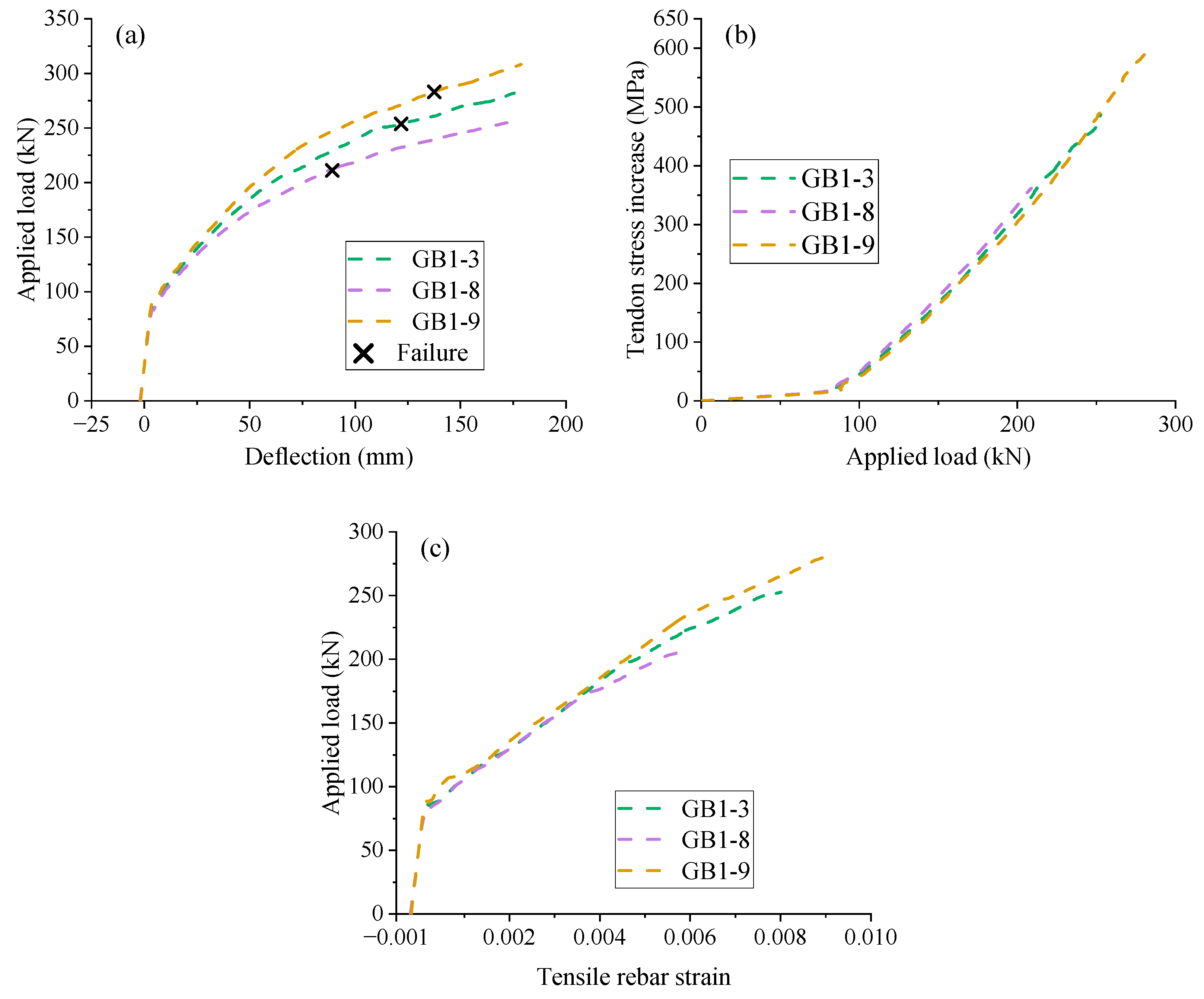

| Beam | Compressive Steel | Stirrup | Concrete | ||||
|---|---|---|---|---|---|---|---|
| D1 (mm) | Es1 (GPa) | fy1 (MPa) | D2 (mm) | Es2 (GPa) | fy2 (MPa) | fcu (MPa) | |
| BL1-2 (P-GFRP) | 14 | 200 | 380 | 8 | 210 | 308 | 31.5 |
| TL1-2 (R-CFRP) | 16 | 200 | 380 | 12 | 210 | 308 | 31.5 |
| BL2-1 (R-GFRP) | 12 | 200 | 380 | 10 | 210 | 308 | 31.5 |
| Beam | Test [38] | Analysis Considering Bond–Slip | Analysis Neglecting Bond–Slip | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| UL (kN) | UD (mm) | UL (kN) | Error (%) | UD (mm) | Error (%) | UL (kN) | Error (%) | UD (mm) | Error (%) | |
| TL1-2 | 239.22 | 40.17 | 226.50 | −5.32 | 40.33 | 0.40 | 281.73 | 17.77 | 41.69 | 3.78 |
| BL1-2 | 96.39 | 47.78 | 104.50 | 8.41 | 47.43 | −0.73 | - | - | - | - |
| BL2-1 | 88.66 | 20.94 | 93.31 | 5.24 | 22.61 | 7.98 | 112.27 | 23.61 | 23.78 | 13.56 |
| Beam | Steel Rebars | External Tendons | Concrete | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| As (mm2) | fy (MPa) | Es (GPa) | (mm2) | (MPa) | (GPa) | Ap (mm2) | Ep (GPa) | fpu (MPa) | σpe (MPa) | fc,r (MPa) | |
| T-0 | 402 | 530 | 210 | 201 | 338 | 180 | 110.2 | 193 | 1900 | 1297 | 34.6 |
| T-1 | 402 | 530 | 210 | 201 | 338 | 180 | 110.2 | 193 | 1900 | 1197 | 34.2 |
| T-2 | 402 | 530 | 210 | 201 | 338 | 180 | 110.2 | 193 | 1900 | 1182 | 28.7 |
| Beam | Ultimate Deflection (mm) | Ultimate Tendon Stress (MPa) | ||||
|---|---|---|---|---|---|---|
| Test | Numerical | Error (%) | Test | Numerical | Error (%) | |
| T-0 | 34.62 | 35.69 | 3.09 | 1668.32 | 1628.34 | −2.40 |
| T-1 | 31.32 | 32.87 | 4.95 | 1648.43 | 1600.18 | −2.93 |
| T-2 | 40.51 | 41.73 | 3.01 | 1665.62 | 1611.17 | −3.27 |
| Contents | Beam | Tensile Rebars | Compressive Rebars | Stirrup (CFRP) | Tendons (CFRP) | Concrete | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Type | Et (GPa) | Dt (mm) | ρr (%) | Type | En (GPa) | Dc (mm) | ρc,r (%) | Es (GPa) | Ds (mm) | Ep (GPa) | Dp (mm) | σpe (MPa) | fcu (MPa) | ||
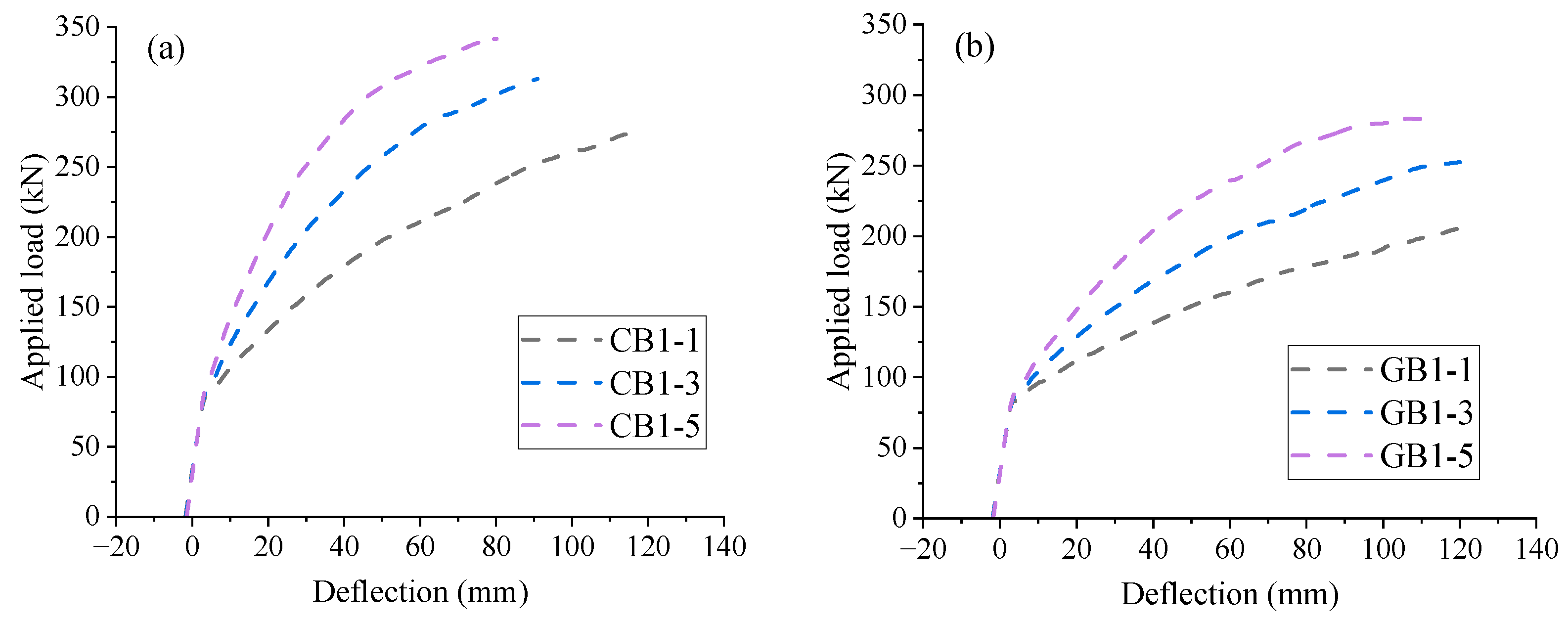
| Group A | CB1-1 | CFRP | 145 | 16 | 0.50 | CFRP | 145 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 40 |
| CB1-2 | CFRP | 145 | 20 | 0.78 | CFRP | 145 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 40 | |
| CB1-3 | CFRP | 145 | 24 | 1.12 | CFRP | 145 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 40 | |
| CB1-4 | CFRP | 145 | 28 | 1.52 | CFRP | 145 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 40 | |
| CB1-5 | CFRP | 145 | 32 | 1.98 | CFRP | 145 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 40 | |
| CB1-6 | CFRP | 130 | 24 | 1.12 | CFRP | 145 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 40 | |
| CB1-7 | CFRP | 160 | 24 | 1.12 | CFRP | 145 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 40 | |
| CB1-8 | CFRP | 145 | 24 | 1.12 | CFRP | 145 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 30 | |
| CB1-9 | CFRP | 145 | 24 | 1.12 | CFRP | 145 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 50 | |
| Group B | GB1-1 | GFRP | 55 | 16 | 0.50 | GFRP | 55 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 40 |
| GB1-2 | GFRP | 55 | 20 | 0.78 | GFRP | 55 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 40 | |
| GB1-3 | GFRP | 55 | 24 | 1.12 | GFRP | 55 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 40 | |
| GB1-4 | GFRP | 55 | 28 | 1.52 | GFRP | 55 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 40 | |
| GB1-5 | GFRP | 55 | 32 | 1.98 | GFRP | 55 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 40 | |
| GB1-6 | GFRP | 40 | 24 | 1.12 | GFRP | 55 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 40 | |
| GB1-7 | GFRP | 70 | 24 | 1.12 | GFRP | 55 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 40 | |
| GB1-8 | GFRP | 55 | 24 | 1.12 | GFRP | 55 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 30 | |
| GB1-9 | GFRP | 55 | 24 | 1.12 | GFRP | 55 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 50 | |
| Group C | SB1-1 | Steel | 200 | 16 | 0.50 | Steel | 200 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 40 |
| SB1-2 | Steel | 200 | 24 | 1.12 | Steel | 200 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 40 | |
| SB1-3 | Steel | 200 | 32 | 1.98 | Steel | 200 | 10 | 0.33 | 147 | 8 | 160 | 12 | 1060 | 40 | |
| Group | Beam | Ultimate Behavior | |||||
|---|---|---|---|---|---|---|---|
| Deflection (mm) | Load (kN) | Tendon Stress Increase (MPa) | Curvature (10−6 rad/mm) | Neutral Axis Depth (mm) | Tensile Rebar Strain | ||
| A | CB1-1 | 115.99 | 274.57 | 484.19 | 19.03 | 71.41 | 0.0072 |
| CB1-2 | 101.42 | 297.12 | 382.93 | 15.91 | 90.22 | 0.0057 | |
| CB1-3 | 90.91 | 313.06 | 308.80 | 13.44 | 114.01 | 0.0040 | |
| CB1-4 | 85.07 | 324.03 | 236.42 | 11.90 | 130.32 | 0.0036 | |
| CB1-5 | 73.41 | 336.92 | 195.93 | 10.26 | 140.27 | 0.0030 | |
| CB1-6 | 100.94 | 311.26 | 314.54 | 14.4 | 102.83 | 0.0051 | |
| CB1-7 | 73.76 | 301.64 | 271.91 | 12.38 | 118.70 | 0.0036 | |
| CB1-8 | 75.47 | 274.77 | 256.28 | 9.92 | 137.71 | 0.0034 | |
| CB1-9 | 120.92 | 367.70 | 380.24 | 15.88 | 93.61 | 0.0045 | |
| B | GB1-1 | 120.95 | 206.51 | 588.98 | 25.76 | 49.62 | 0.0103 |
| GB1-2 | 119.69 | 229.49 | 547.89 | 23.30 | 69.10 | 0.0088 | |
| GB1-3 | 120.01 | 252.65 | 486.93 | 22.69 | 84.79 | 0.0080 | |
| GB1-4 | 116.59 | 273.08 | 427.62 | 20.21 | 90.16 | 0.0071 | |
| GB1-5 | 114.59 | 285.76 | 374.89 | 19.78 | 94.30 | 0.0062 | |
| GB1-6 | 140.78 | 240.32 | 589.85 | 17.57 | 72.89 | 0.0098 | |
| GB1-7 | 107.71 | 261.78 | 425.86 | 15.51 | 80.46 | 0.0069 | |
| GB1-8 | 84.96 | 206.29 | 361.53 | 17.41 | 94.02 | 0.0060 | |
| GB1-9 | 135.86 | 282.96 | 594.26 | 24.12 | 72.59 | 0.0091 | |
| C | SB1-1 | 79.97 | 166.62 | 166.74 | 27.35 | 46.95 | 0.0180 |
| SB1-2 | 69.08 | 248.21 | 194.85 | 20.37 | 81.79 | 0.0054 | |
| SB1-3 | 69.67 | 323.04 | 117.80 | 7.34 | 112.84 | 0.0020 | |
| RaberType | Beam | ρr (%) | ω0 | cu/dp | Δσp (MPa) | (Δσp)Equation/(Δσp)Numerical | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Num | JGJ16 | JGJ92 | Pang | AO17 | AO94 | JGJ16 | JGJ92 | Pang | AO17 | AO94 | |||||
| CFRP | CB1-1 | 0.5 | 0.16 | 0.22 | 484.19 | 54.06 | 376.80 | 460.88 | 297.60 | 115.20 | 0.11 | 0.78 | 0.95 | 0.61 | 0.24 |
| CB1-2 | 0.78 | 0.22 | 0.25 | 382.93 | 48.23 | 330.60 | 398.96 | 279.00 | 86.40 | 0.13 | 0.86 | 1.04 | 0.73 | 0.23 | |
| CB1-3 | 1.12 | 0.26 | 0.32 | 308.80 | 44.34 | 299.80 | 357.68 | 252.96 | 61.20 | 0.14 | 0.97 | 1.16 | 0.82 | 0.20 | |
| CB1-4 | 1.52 | 0.29 | 0.4 | 236.42 | 41.43 | 276.70 | 326.72 | 223.20 | 43.20 | 0.18 | 1.17 | 1.38 | 0.94 | 0.18 | |
| CB1-5 | 1.98 | 0.33 | 0.43 | 195.93 | 37.54 | 245.90 | 285.44 | 212.04 | 38.17 | 0.19 | 1.26 | 1.46 | 1.08 | 0.19 | |
| CB1-6 | 1.12 | 0.26 | 0.29 | 314.54 | 44.34 | 299.80 | 357.68 | 264.12 | 70.51 | 0.14 | 0.95 | 1.14 | 0.84 | 0.22 | |
| CB1-7 | 1.12 | 0.25 | 0.33 | 271.91 | 45.31 | 307.50 | 368.00 | 249.24 | 58.47 | 0.17 | 1.13 | 1.35 | 0.92 | 0.22 | |
| CB1-8 | 1.12 | 0.36 | 0.38 | 256.28 | 34.63 | 222.80 | 254.48 | 230.64 | 46.99 | 0.14 | 0.87 | 0.99 | 0.90 | 0.18 | |
| CB1-9 | 1.12 | 0.25 | 0.26 | 380.24 | 45.31 | 307.50 | 368.00 | 275.28 | 81.97 | 0.12 | 0.81 | 0.97 | 0.72 | 0.22 | |
| GFRP | GB1-1 | 0.5 | 0.05 | 0.14 | 588.98 | 64.74 | 461.50 | 574.40 | 319.92 | 176.91 | 0.11 | 0.78 | 0.98 | 0.54 | 0.30 |
| GB1-2 | 0.78 | 0.09 | 0.19 | 547.89 | 60.85 | 430.70 | 533.12 | 301.32 | 122.78 | 0.11 | 0.79 | 0.97 | 0.55 | 0.22 | |
| GB1-3 | 1.12 | 0.15 | 0.23 | 486.93 | 55.03 | 384.50 | 471.20 | 286.44 | 96.42 | 0.11 | 0.79 | 0.97 | 0.59 | 0.20 | |
| GB1-4 | 1.52 | 0.2 | 0.25 | 427.62 | 50.17 | 346.00 | 419.60 | 279.00 | 86.40 | 0.12 | 0.81 | 0.98 | 0.65 | 0.20 | |
| GB1-5 | 1.98 | 0.23 | 0.26 | 374.89 | 47.26 | 322.90 | 388.64 | 275.28 | 81.97 | 0.13 | 0.86 | 1.04 | 0.73 | 0.22 | |
| GB1-6 | 1.12 | 0.12 | 0.20 | 589.85 | 57.94 | 407.60 | 502.16 | 297.60 | 115.20 | 0.10 | 0.69 | 0.85 | 0.50 | 0.20 | |
| GB1-7 | 1.12 | 0.17 | 0.22 | 425.86 | 53.08 | 369.10 | 450.56 | 290.16 | 102.11 | 0.12 | 0.87 | 1.06 | 0.68 | 0.24 | |
| GB1-8 | 1.12 | 0.20 | 0.26 | 361.53 | 50.17 | 346.00 | 419.60 | 275.28 | 81.97 | 0.14 | 0.96 | 1.16 | 0.76 | 0.23 | |
| GB1-9 | 1.12 | 0.11 | 0.20 | 594.26 | 58.91 | 415.30 | 512.48 | 297.60 | 115.20 | 0.10 | 0.70 | 0.86 | 0.50 | 0.19 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Chen, B.; Wang, X.; Lou, T. Assessment of Externally Prestressed Beams with FRP Rebars Considering Bond–Slip Effects. Materials 2025, 18, 787. https://doi.org/10.3390/ma18040787
Li Z, Chen B, Wang X, Lou T. Assessment of Externally Prestressed Beams with FRP Rebars Considering Bond–Slip Effects. Materials. 2025; 18(4):787. https://doi.org/10.3390/ma18040787
Chicago/Turabian StyleLi, Zhangxiang, Bo Chen, Xueliang Wang, and Tiejiong Lou. 2025. "Assessment of Externally Prestressed Beams with FRP Rebars Considering Bond–Slip Effects" Materials 18, no. 4: 787. https://doi.org/10.3390/ma18040787
APA StyleLi, Z., Chen, B., Wang, X., & Lou, T. (2025). Assessment of Externally Prestressed Beams with FRP Rebars Considering Bond–Slip Effects. Materials, 18(4), 787. https://doi.org/10.3390/ma18040787