Terahertz Metamaterial Absorber and Equivalent Circuit Model for Refractive Index Sensing
Abstract
1. Introduction
2. Design and Simulation
3. Results and Discussion
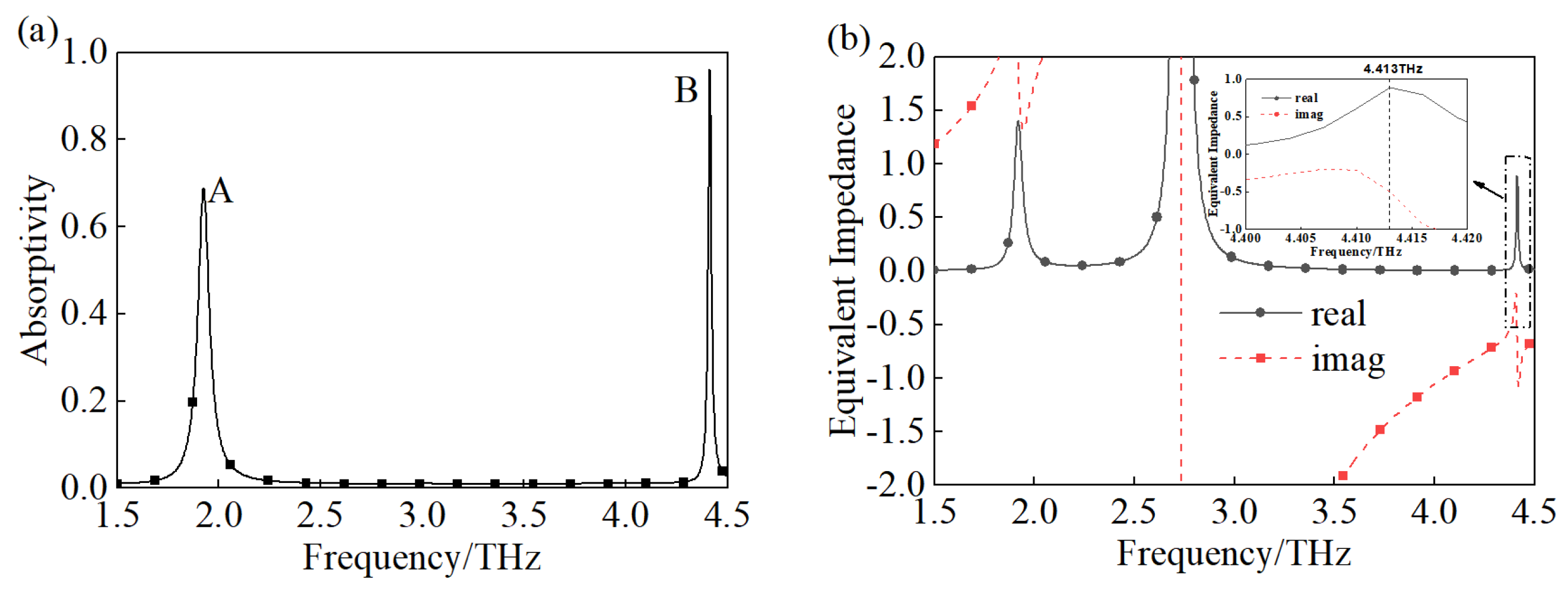
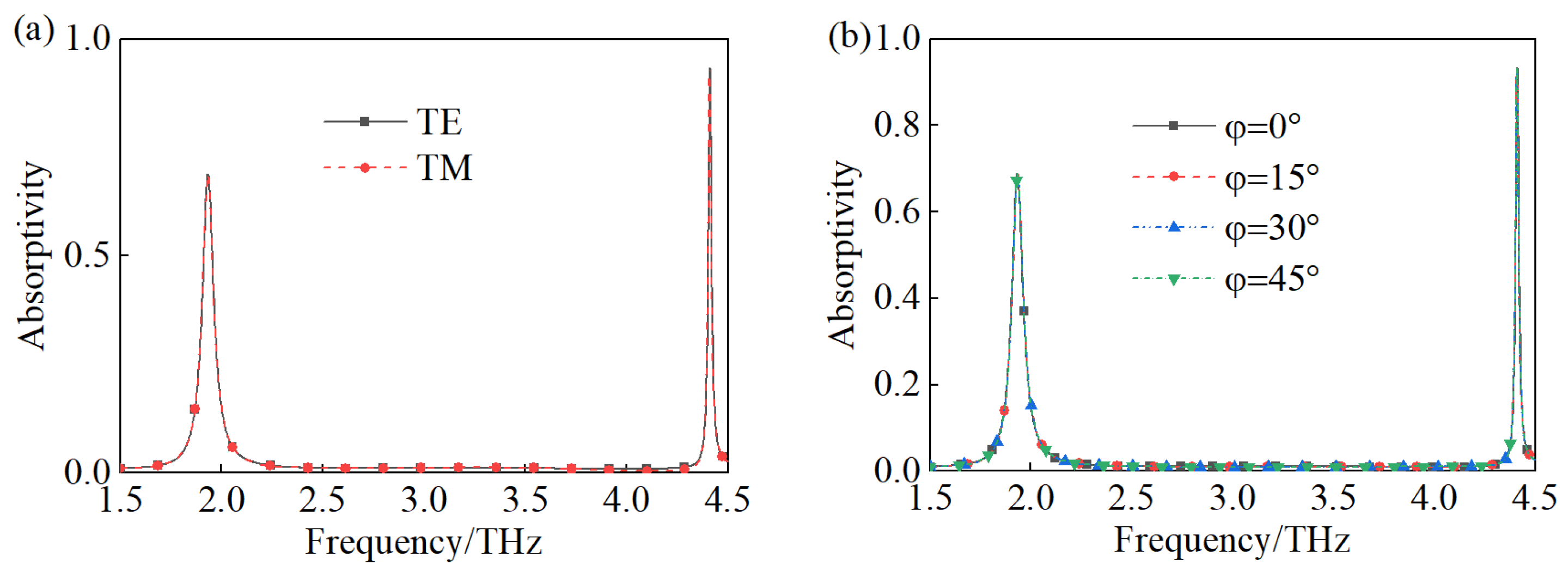
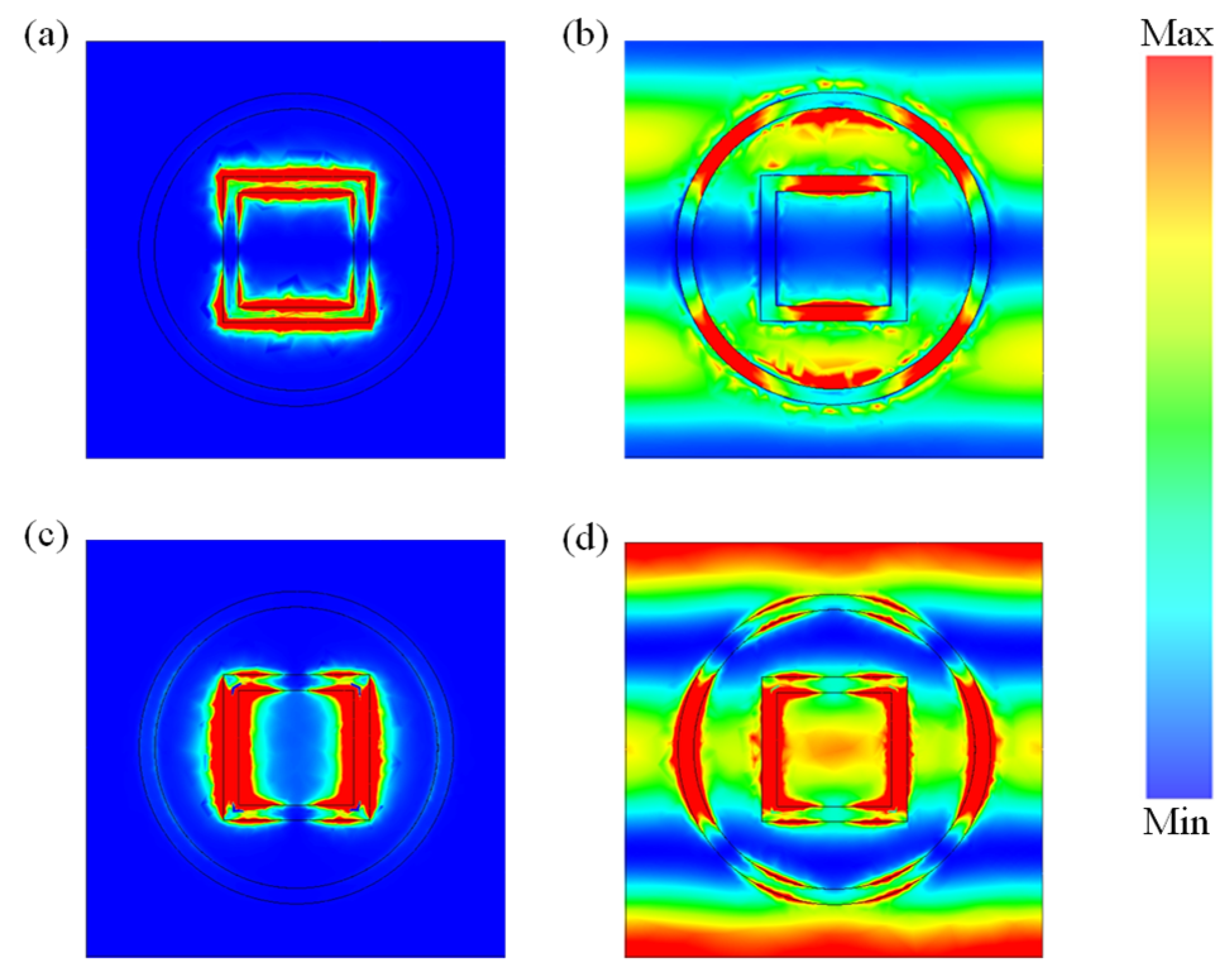
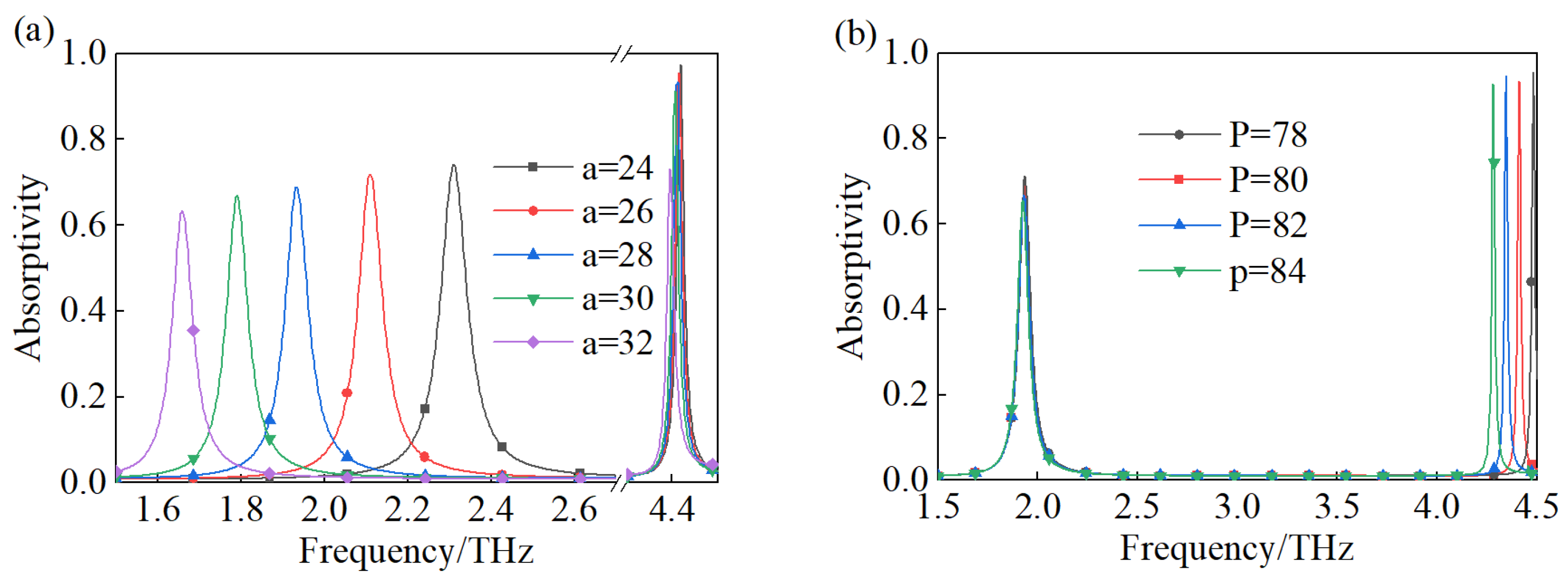
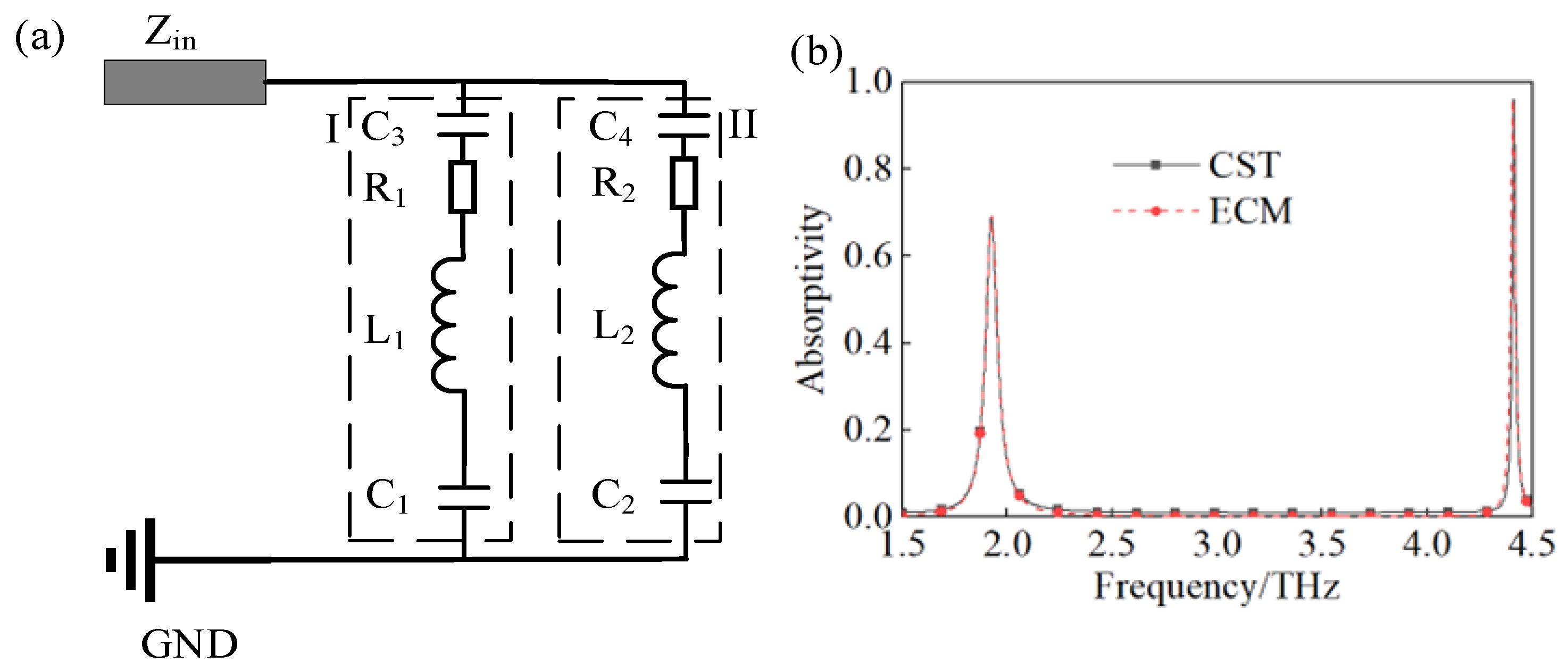
3.1. Narrow-Band Terahertz Metamaterial Absorber
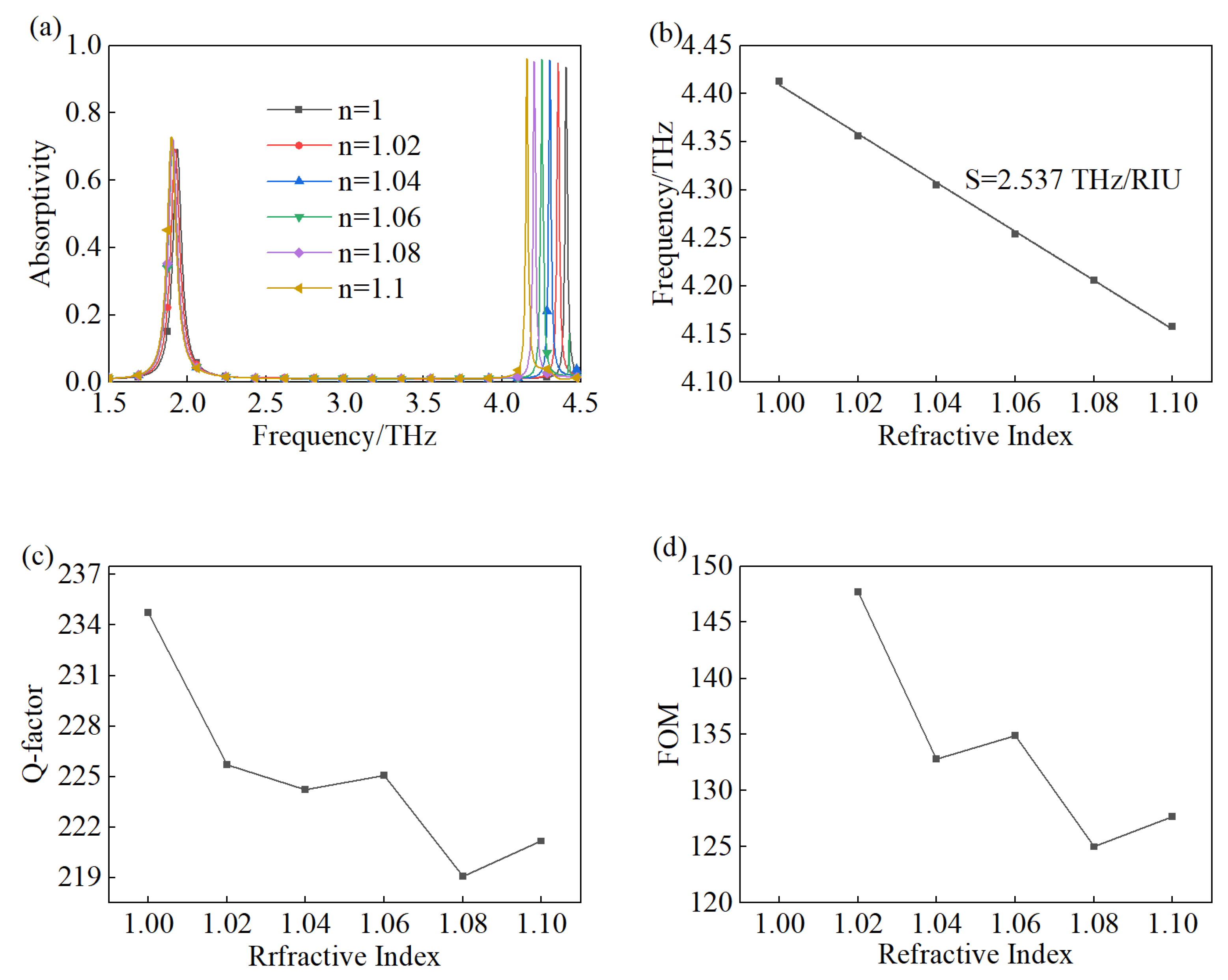
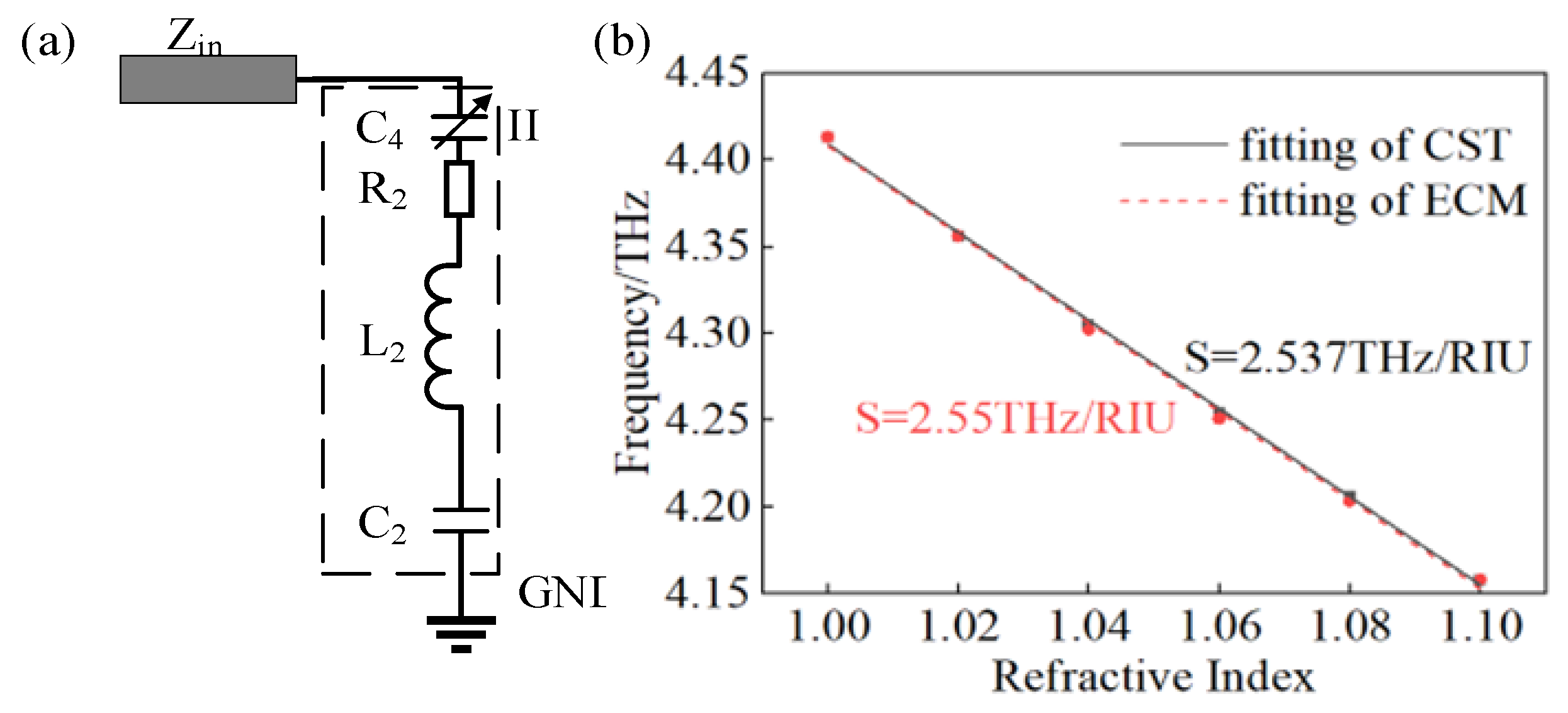
3.2. Refractive Index Sensing
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TMA | Terahertz Metamaterial Absorber |
| RIU | Refractive Index Unit |
| RLC | Resistor–Inductor–Capacitor |
| ECM | Equivalent Circuit Model |
| FOM | Figure of Merit |
| CST | Computer Simulation Technology |
References
- Pendry, J.B.; Holden, A.J.; Stewart, W.J.; Youngs, I. Extremely Low Frequency Plasmons in Metallic Mesostructures. Phys. Rev. Lett. 1996, 76, 4773–4776. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J. Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory Tech. 1999, 47, 2075–2084. [Google Scholar] [CrossRef]
- Shelby, R.A.; Smith, D.R.; Schultz, S. Experimental Verification of a Negative Index of Refraction. Science 2001, 292, 77–79. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Xie, Z.T.; Sha, Y.; Fu, H.; Li, Q. Epsilon-near-zero photonics: Infinite potentials. Photon Res. 2021, 9, 1616–1644. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect metamaterial absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef]
- Zhou, P.; Wang, L.; Zhang, G.; Jiang, J.; Chen, H.; Zhou, Y.; Liang, D.; Deng, L. A Stretchable Metamaterial Absorber with Deformation Compensation Design at Microwave Frequencies. IEEE Trans. Antennas Propag. 2018, 67, 291–297. [Google Scholar] [CrossRef]
- Han, W.; Park, Q.-H. Broadband absorber with dispersive metamaterials. Nanophotonics 2023, 12, 2443–2449. [Google Scholar] [CrossRef]
- Wang, G.-Z.; Wang, B.-X. Five-Band Terahertz Metamaterial Absorber Based on a Four-Gap Comb Resonator. J. Light. Technol. 2015, 33, 5151–5156. [Google Scholar] [CrossRef]
- Song, S.; Ma, X.; Pu, M.; Li, X.; Guo, Y.; Gao, P.; Luo, X. Tailoring active color rendering and multiband photodetection in a vanadium-dioxide-based metamaterial absorber. Photon Res. 2018, 6, 492–497. [Google Scholar] [CrossRef]
- Li, H.-J.; Chen, B.; Zhai, X.; Xu, L.; Wang, L.-L. Tunable Ultra-Multispectral Metamaterial Perfect Absorbers Based on Out-of-Plane Metal-Insulator-Graphene Heterostructures. J. Light. Technol. 2020, 38, 1858–1864. [Google Scholar] [CrossRef]
- Zhou, Y.; Qin, Z.; Liang, Z.; Meng, D.; Xu, H.; Smith, D.R.; Liu, Y. Ultra-broadband metamaterial absorbers from long to very long infrared regime. Light. Sci. Appl. 2021, 10, 138. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Xiao, F.; Rukhlenko, I.D.; Geng, J.; Liang, X.; Premaratne, M.; Jin, R. Wideband visible-light absorption in an ultrathin silicon nanostructure. Opt. Express 2017, 25, 5781–5786. [Google Scholar] [CrossRef]
- Liang, J.; Song, X.; Li, J.; Lan, K.; Li, P. A visible-near infrared wavelength-tunable metamaterial absorber based on the structure of Au triangle arrays embedded in VO2 thin film. J. Alloys Compd. 2017, 708, 999–1007. [Google Scholar] [CrossRef]
- Hoque, A.; Islam, M.T.; Almutairi, A.F.; Faruque, M.R.I. Design of Split Hexagonal Patch Array Shaped Nano-metaabsorber with Ultra-wideband Absorption for Visible and UV Spectrum Application. Nanoscale Res. Lett. 2019, 14, 393. [Google Scholar] [CrossRef] [PubMed]
- Hedayati, M.K.; Zillohu, A.U.; Strunskus, T.; Faupel, F.; Elbahri, M. Plasmonic tunable metamaterial absorber as ultraviolet protection film. Appl. Phys. Lett. 2014, 104, 041103. [Google Scholar] [CrossRef]
- Li, M.; Muneer, B.; Yi, Z.; Zhu, Q. A Broadband Compatible Multispectral Metamaterial Absorber for Visible, Near-Infrared, and Microwave Bands. Adv. Opt. Mater. 2018, 6, 1701238. [Google Scholar] [CrossRef]
- Ustunsoy, M.P.; Sabah, C. Dual-band high-frequency metamaterial absorber based on patch resonator for solar cell ap-plications and its enhancement with graphene layers. J. Alloys Compd. 2016, 687, 514–520. [Google Scholar] [CrossRef]
- Chakradhary, V.K.; Baskey, H.B.; Roshan, R.; Pathik, A.; Akhtar, M.J. Design of Frequency Selective Surface-Based Hybrid Nanocomposite Absorber for Stealth Applications. IEEE Trans. Microw. Theory Tech. 2018, 66, 4737–4744. [Google Scholar] [CrossRef]
- Shi, M.; Xu, C.; Yang, Z.; Liang, J.; Wang, L.; Tan, S.; Xu, G. Achieving good infrared-radar compatible stealth property on metamaterial-based absorber by controlling the floating rate of Al type infrared coating. J. Alloys Compd. 2018, 764, 314–322. [Google Scholar] [CrossRef]
- Shrekenhamer, D.; Xu, W.; Venkatesh, S.; Schurig, D.; Sonkusale, S.; Padilla, W.J. Experimental Realization of a Metamaterial Detector Focal Plane Array. Phys. Rev. Lett. 2012, 109, 177401. [Google Scholar] [CrossRef]
- Tantiwanichapan, K.; Durmaz, H. Improvement of Response Time and Heat-Transfer Capacity of Metamaterial Absorber for Terahertz Detector Applications. IEEE Sens. J. 2023, 23, 4700–4706. [Google Scholar] [CrossRef]
- Wang, W.; Chen, Y.; Yang, S.; Cao, Q.; Li, H.; Zheng, X.; Wang, Y. Wireless inter/intra-chip communication using an innovative PCB channel bounded by a metamaterial absorber. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1634–1637. [Google Scholar] [CrossRef]
- Liu, X.; Starr, T.; Starr, A.F.; Padilla, W.J. Infrared spatial and frequency selective metamaterial with near-unity absorbance. Phys. Rev. Lett. 2010, 104, 207403. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Tyler, T.; Starr, T.; Starr, A.F.; Jokerst, N.M.; Padilla, W.J. Taming the Blackbody with Infrared Metamaterials as Selective Thermal Emitters. Phys. Rev. Lett. 2011, 107, 045901. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Chang, J.-Y.; Yang, Y.; Wang, L. Performance analysis of solar thermophotovoltaic conversion enhanced by selective metamaterial absorbers and emitters. Int. J. Heat Mass Transf. 2016, 98, 788–798. [Google Scholar] [CrossRef]
- Liu, N.; Mesch, M.; Weiss, T.; Hentschel, M.; Giessen, H. Infrared Perfect Absorber and Its Application as Plasmonic Sensor. Nano Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef]
- Alves, F.; Grbovic, D.; Kearney, B.; Karunasiri, G. Microelectromechanical systems bimaterial terahertz sensor with integrated metamaterial absorber. Opt. Lett. 2012, 37, 1886–1888. [Google Scholar] [CrossRef]
- Xu, X.; Xu, R.; Lin, Y.S. A voltage-controllable VO2based metamaterial perfect absorber for CO2gas sensing application. Nanoscale 2022, 14, 2722–2728. [Google Scholar] [CrossRef]
- Linyang, G.; Xiaohui, M.; Zhaoqing, C.; Chunlin, X.; Jun, L.; Ran, Z. Tunable a temperature-dependent GST-based metamaterial absorber for switching and sensing applications. J. Mater. Res. Technol. 2021, 14, 772–779. [Google Scholar] [CrossRef]
- Molaei, A.; Juesas, J.H.; Blackwell, W.J.; Martinez-Lorenzo, J.A. Interferometric Sounding Using a Metamaterial-Based Compressive Reflector Antenna. IEEE Trans. Antennas Propag. 2018, 66, 2188–2198. [Google Scholar] [CrossRef]
- Ling, K.; Yoo, M.; Lim, S. Frequency Tunable Metamaterial Absorber Using Hygroscopicity of Nature Cork. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 1598–1601. [Google Scholar] [CrossRef]
- Nie, P.; Zhu, D.; Cui, Z.; Qu, F.; Lin, L.; Wang, Y. Sensitive detection of chlorpyrifos pesticide using an all-dielectric broadband terahertz metamaterial absorber. Sens. Actuators B Chem. 2019, 307, 127642. [Google Scholar] [CrossRef]
- Jeong, H.; Cui, Y.; Tentzeris, M.M.; Lim, S. Hybrid (3D and inkjet) printed electromagnetic pressure sensor using metamaterial absorber. Addit. Manuf. 2020, 35, 101405. [Google Scholar] [CrossRef]
- Hakim, M.L.; Alam, T.; Almutairi, A.F.; Mansor, M.F.; Islam, M.T. Polarization insensitivity characterization of dual-band perfect metamaterial absorber for K band sensing applications. Sci. Rep. 2021, 11, 17829. [Google Scholar] [CrossRef]
- Bhattarai, K.; Ku, Z.; Silva, S.; Jeon, J.; Kim, J.O.; Lee, S.J.; Urbas, A.; Zhou, J. A Large-Area, Mushroom-Capped Plasmonic Perfect Absorber: Refractive Index Sensing and Fabry-Perot Cavity Mechanism. Adv. Opt. Mater. 2015, 3, 1779–1786. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, Z.; Yu, H.; Yang, L.; Gou, P.; Cao, J.; Zou, Y.; Qian, J.; Shi, T.; Ren, Q.; et al. Design of triple-band metamaterial absorbers with refractive index sensitivity at infrared frequencies. Opt. Express 2016, 24, 25742–25751. [Google Scholar] [CrossRef]
- Singh, H.; Gupta, A.; Kaler, R.S.; Singh, S.; Gill, A.S. Designing and Analysis of Ultrathin Metamaterial Absorber for W Band Biomedical Sensing Application. IEEE Sensors J. 2022, 22, 10524–10531. [Google Scholar] [CrossRef]
- Cong, L.; Tan, S.; Yahiaoui, R.; Yan, F.; Zhang, W.; Singh, R. Experimental demonstration of ultrasensitive sensing with terahertz metamaterial absorbers: A comparison with the metasurfaces. Appl. Phys. Lett. 2015, 106, 031107. [Google Scholar] [CrossRef]
- Hu, X.; Xu, G.; Wen, L.; Wang, H.; Zhao, Y.; Zhang, Y.; Cumming, D.R.S.; Chen, Q. Metamaterial absorber integrated microfluidic terahertz sensors. Laser Photon Rev. 2016, 10, 962–969. [Google Scholar] [CrossRef]
- Zhou, H.; Yang, C.; Hu, D.; Li, D.; Hui, X.; Zhang, F.; Chen, M.; Mu, X. Terahertz biosensing based on bi-layer metamaterial absorbers toward ultra-high sensitivity and simple fabrication. Appl. Phys. Lett. 2019, 115, 143507. [Google Scholar] [CrossRef]
- Wang, B.-X.; He, Y.; Lou, P.; Xing, W. Design of a dual-band terahertz metamaterial absorber using two identical square patches for sensing application. Nanoscale Adv. 2020, 2, 763–769. [Google Scholar] [CrossRef] [PubMed]
- Mohanty, A.; Acharya, O.P.; Appasani, B.; Mohapatra, S.K.; Khan, M.S. Design of a Novel Terahertz Metamaterial Absorber for Sensing Applications. IEEE Sens. J. 2021, 21, 22688–22694. [Google Scholar] [CrossRef]
- Du, X.; Yan, F.; Wang, W.; Zhang, L.; Bai, Z.; Zhou, H.; Hou, Y. Thermally-stable graphene metamaterial absorber with excellent tunability for high-performance refractive index sensing in the terahertz band. Opt. Laser Technol. 2021, 144, 107409. [Google Scholar] [CrossRef]
- Chen, Y.S.; Cheng, Y.Y.; Meng, D.; You, K.W.; Liu, Y.; Wu, Y.C.; Liu, J. Terahertz refractive index sensor based on tunable patterned graphene absorber. Diam. Relat. Mater. 2023, 131, 109537. [Google Scholar] [CrossRef]
- Zhu, J.; Wu, C. Detection of amino acid with metamaterial perfect absorbers in the terahertz band. Measurement 2022, 192, 110738. [Google Scholar] [CrossRef]
- Chen, T.; Jiang, W.; Yin, X. Dual-band ultrasensitive terahertz sensor based on tunable graphene metamaterial absorber. Superlattices Microstruct. 2021, 154, 106898. [Google Scholar] [CrossRef]
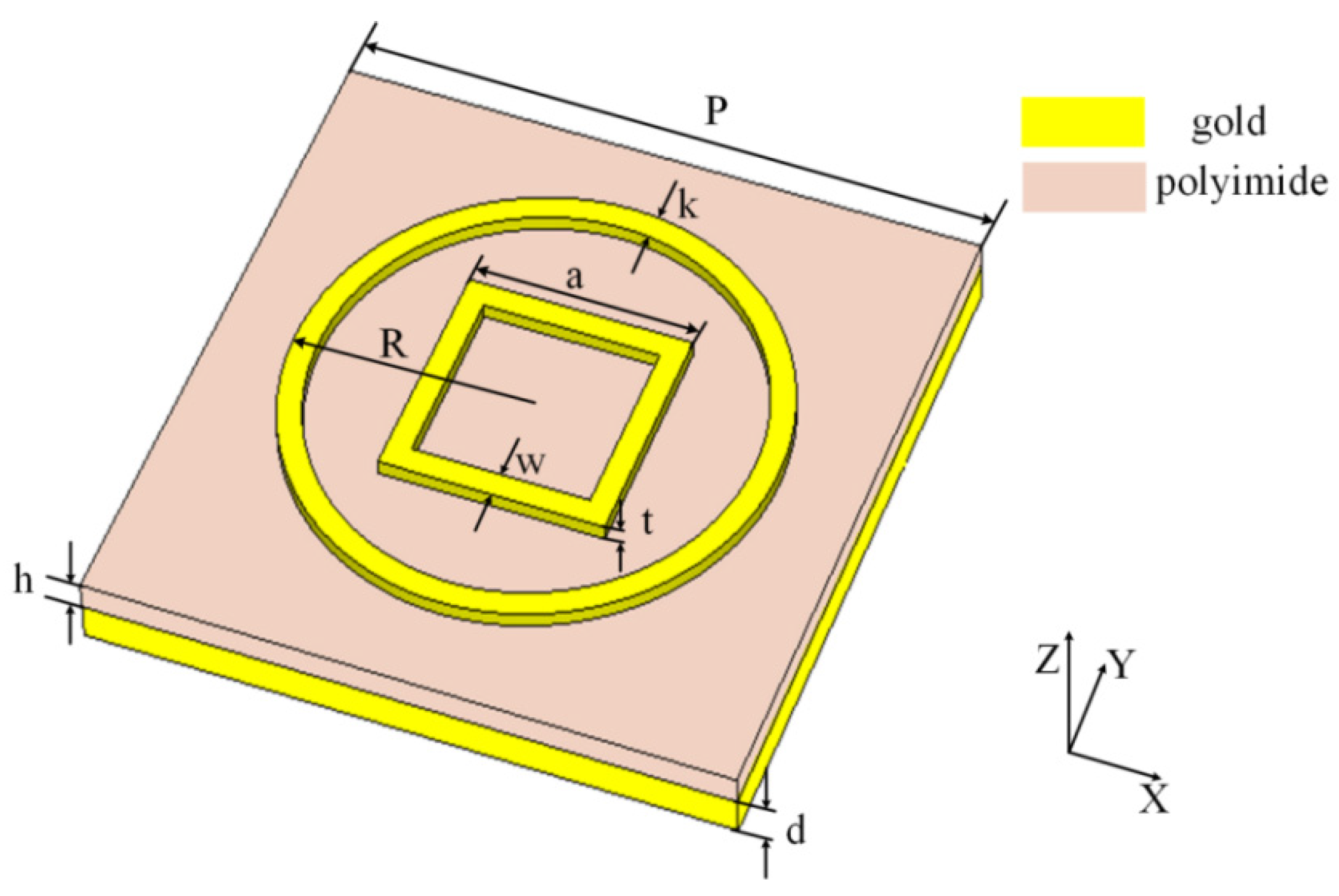
| Parameter | Size (μm) | Parameter | Size (μm) |
|---|---|---|---|
| p | 80 | w | 6 |
| t | 0.2 | a | 28 |
| h | 3 | R | 30 |
| k | 3 | d | 3 |
| Reference | Sensitivity (THz/RIU) | Q-Factor | FOM (RIU−1) | Resonate Frequency (THz) |
|---|---|---|---|---|
| [42] | 1.6 | 225 | 80 | 4.5 |
| [43] | 1.563 | 100.5 | - | 1.628 |
| 1.9 | 268.4 | 1.959 | ||
| [44] | 2 | - | 75 | 3.94 |
| 3 | 50 | 8.28 | ||
| [45] | 1.1 | - | - | 5.9 |
| 1.5 | 8.1 | |||
| [46] | 1.15 | 97.88 | 34.99 | 3.74 |
| 2.475 | 216.29 | 76.89 | 7.73 | |
| This paper | 2.537 | 234.73 | 147.67 | 4.413 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Z.; Li, P.; Zhang, C.; Li, S.; Chen, R.; Zhou, Z.; Huang, X. Terahertz Metamaterial Absorber and Equivalent Circuit Model for Refractive Index Sensing. Materials 2025, 18, 765. https://doi.org/10.3390/ma18040765
Lu Z, Li P, Zhang C, Li S, Chen R, Zhou Z, Huang X. Terahertz Metamaterial Absorber and Equivalent Circuit Model for Refractive Index Sensing. Materials. 2025; 18(4):765. https://doi.org/10.3390/ma18040765
Chicago/Turabian StyleLu, Zhengxiong, Peixuan Li, Chuanwei Zhang, Shuaitian Li, Ruibo Chen, Ziliang Zhou, and Xiaojun Huang. 2025. "Terahertz Metamaterial Absorber and Equivalent Circuit Model for Refractive Index Sensing" Materials 18, no. 4: 765. https://doi.org/10.3390/ma18040765
APA StyleLu, Z., Li, P., Zhang, C., Li, S., Chen, R., Zhou, Z., & Huang, X. (2025). Terahertz Metamaterial Absorber and Equivalent Circuit Model for Refractive Index Sensing. Materials, 18(4), 765. https://doi.org/10.3390/ma18040765






