The Effect of A-Cation and X-Anion Substitutions on the Electronic and Structural Properties of A2ZrX6 ‘Defect’ Perovskite Materials: A Theoretical Density Functional Theory Study
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
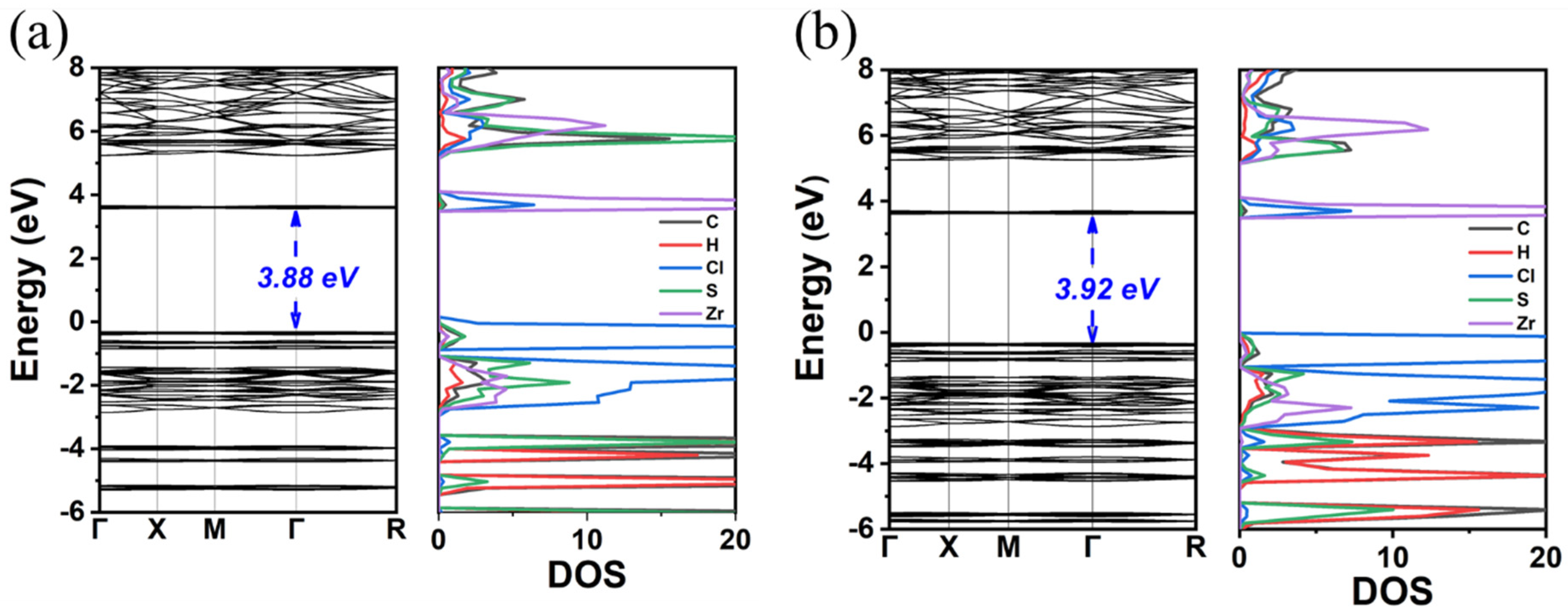
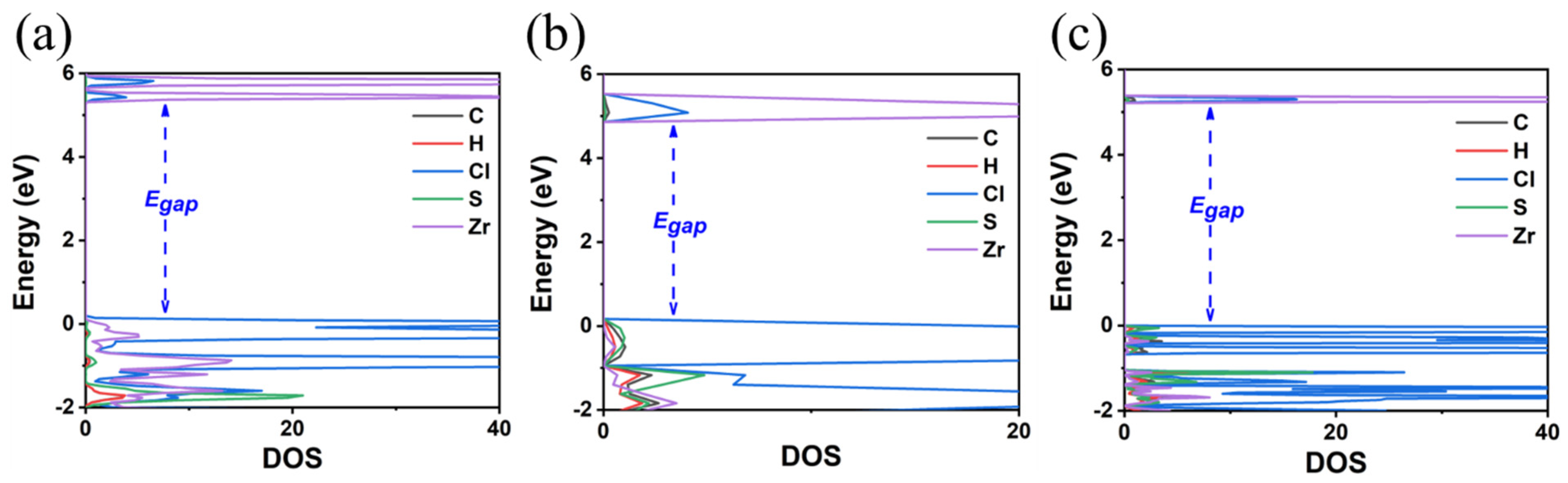
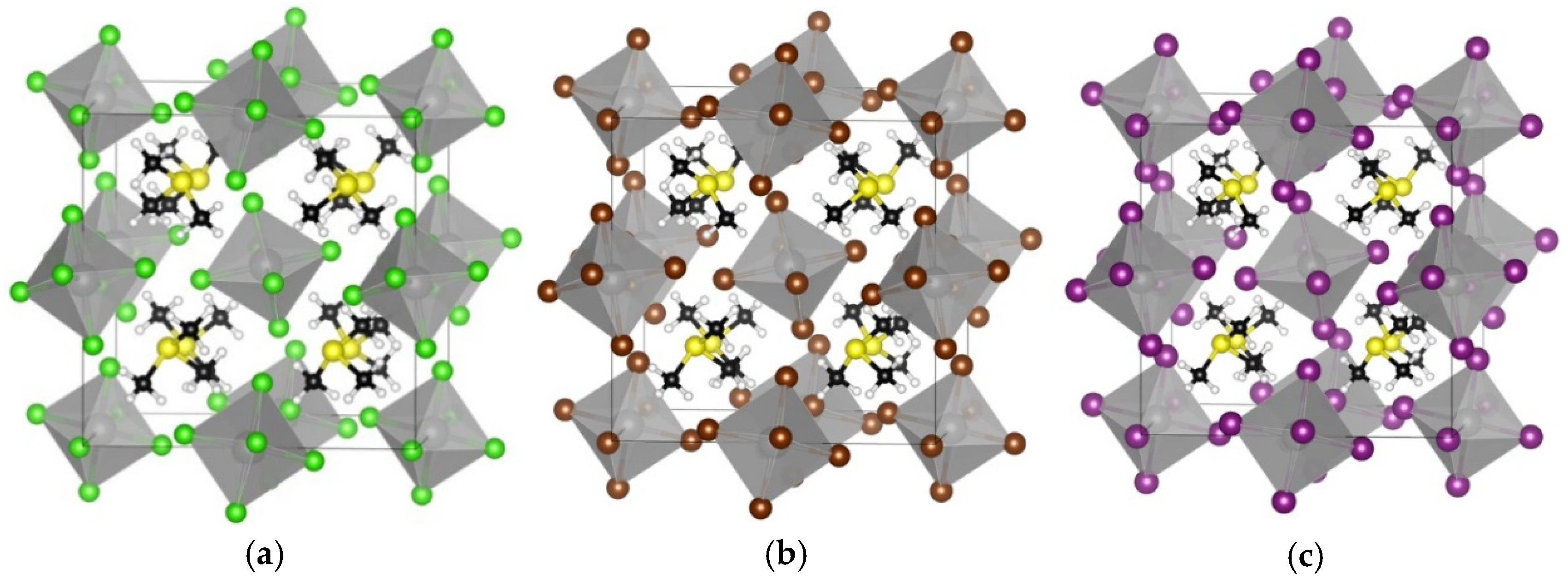
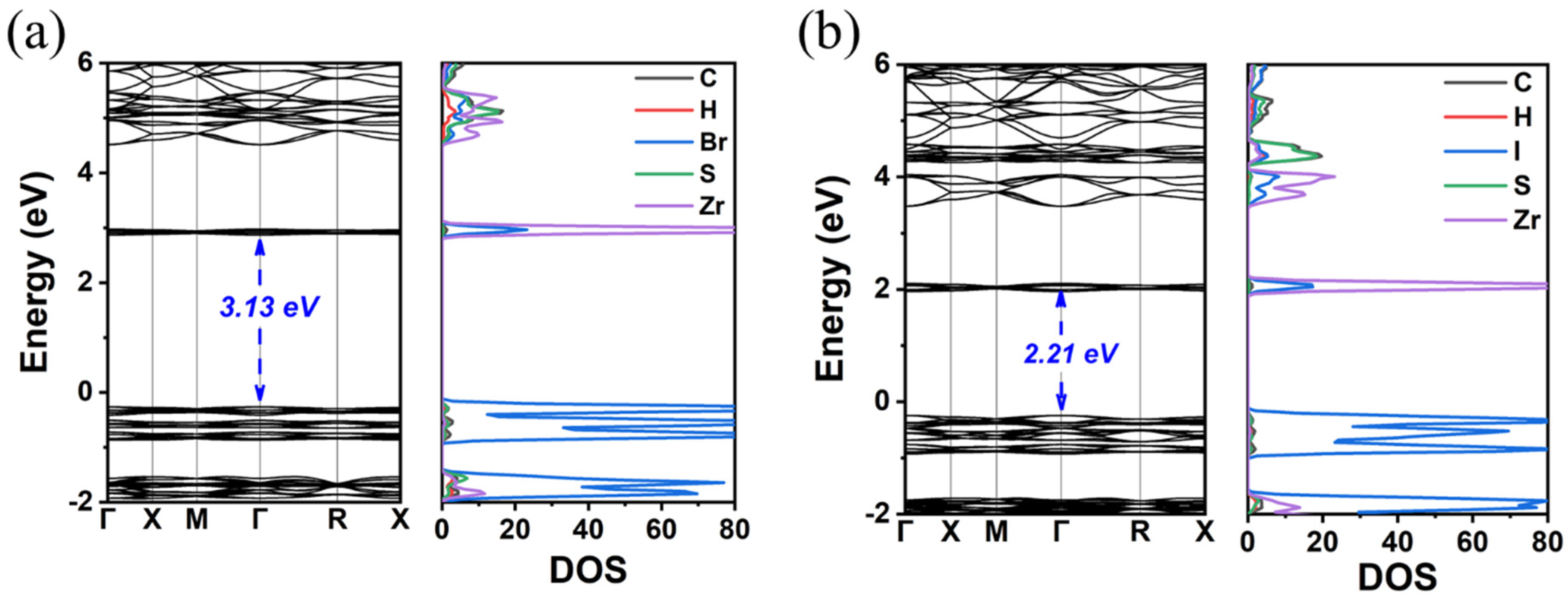
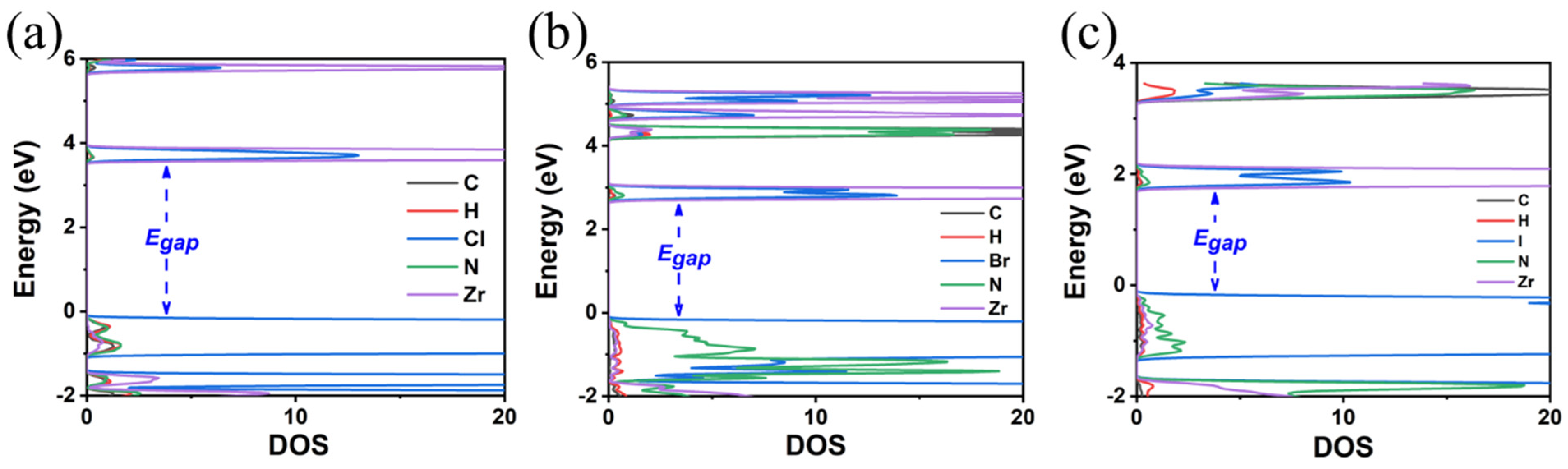
3.1. TMS2ZrX6 (X = Cl, Br, I)
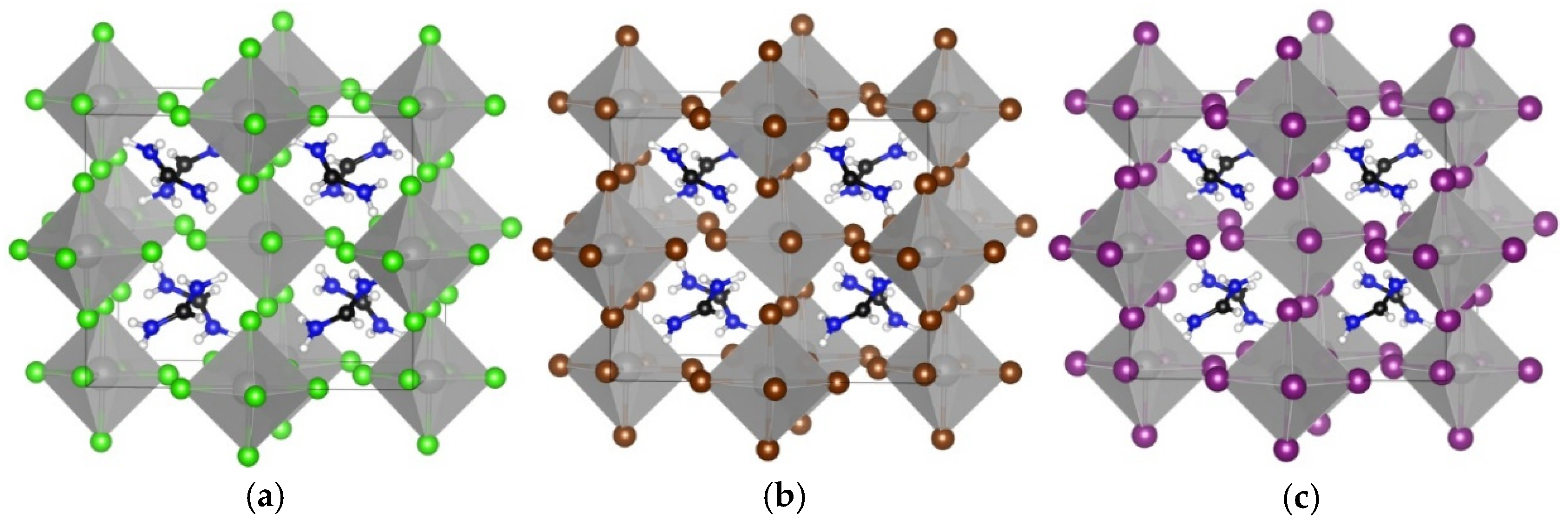
3.2. MA2ZrX6 (X = Cl, Br, I)
3.3. FA2ZrX6 (X = Cl, Br, I)
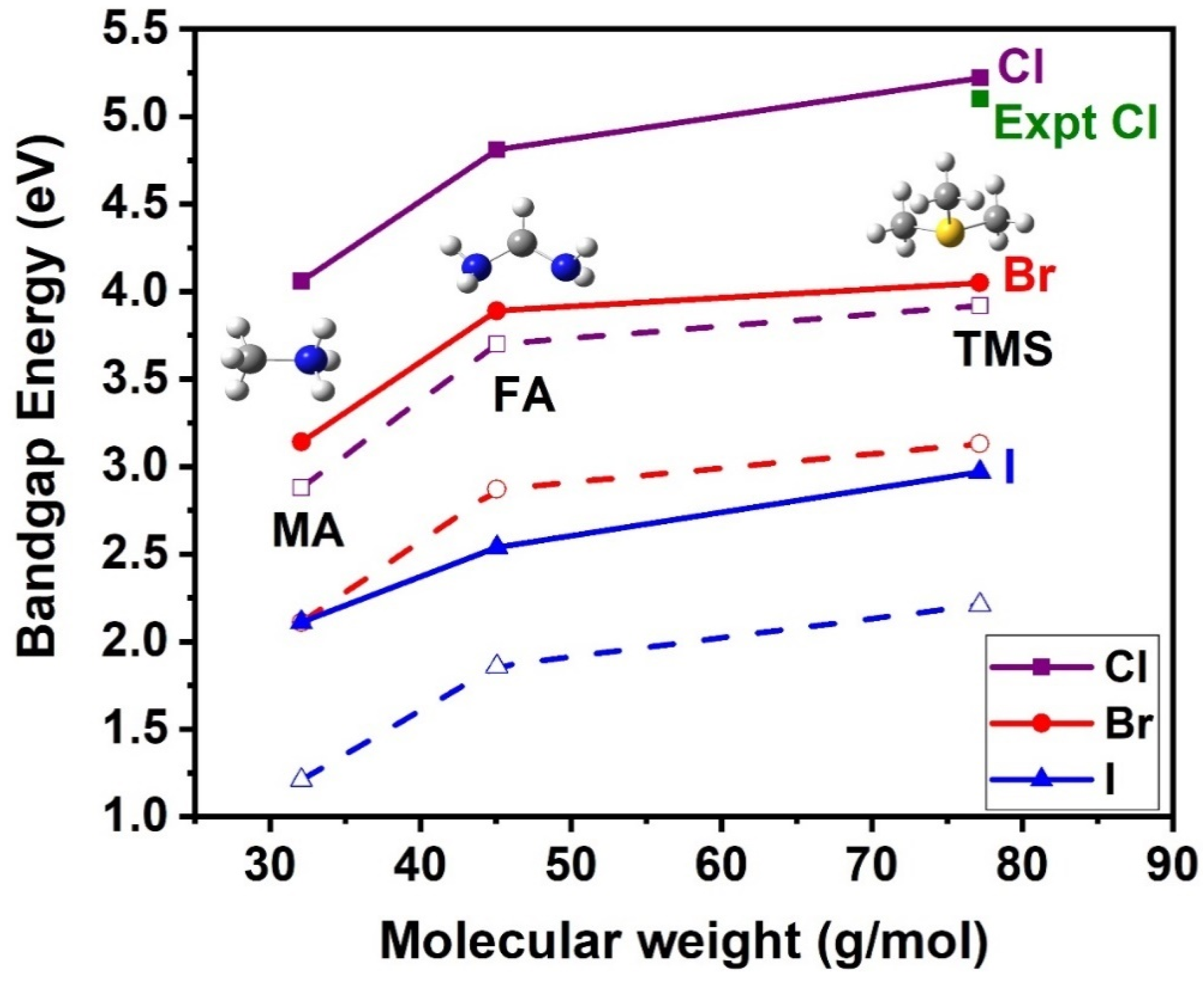
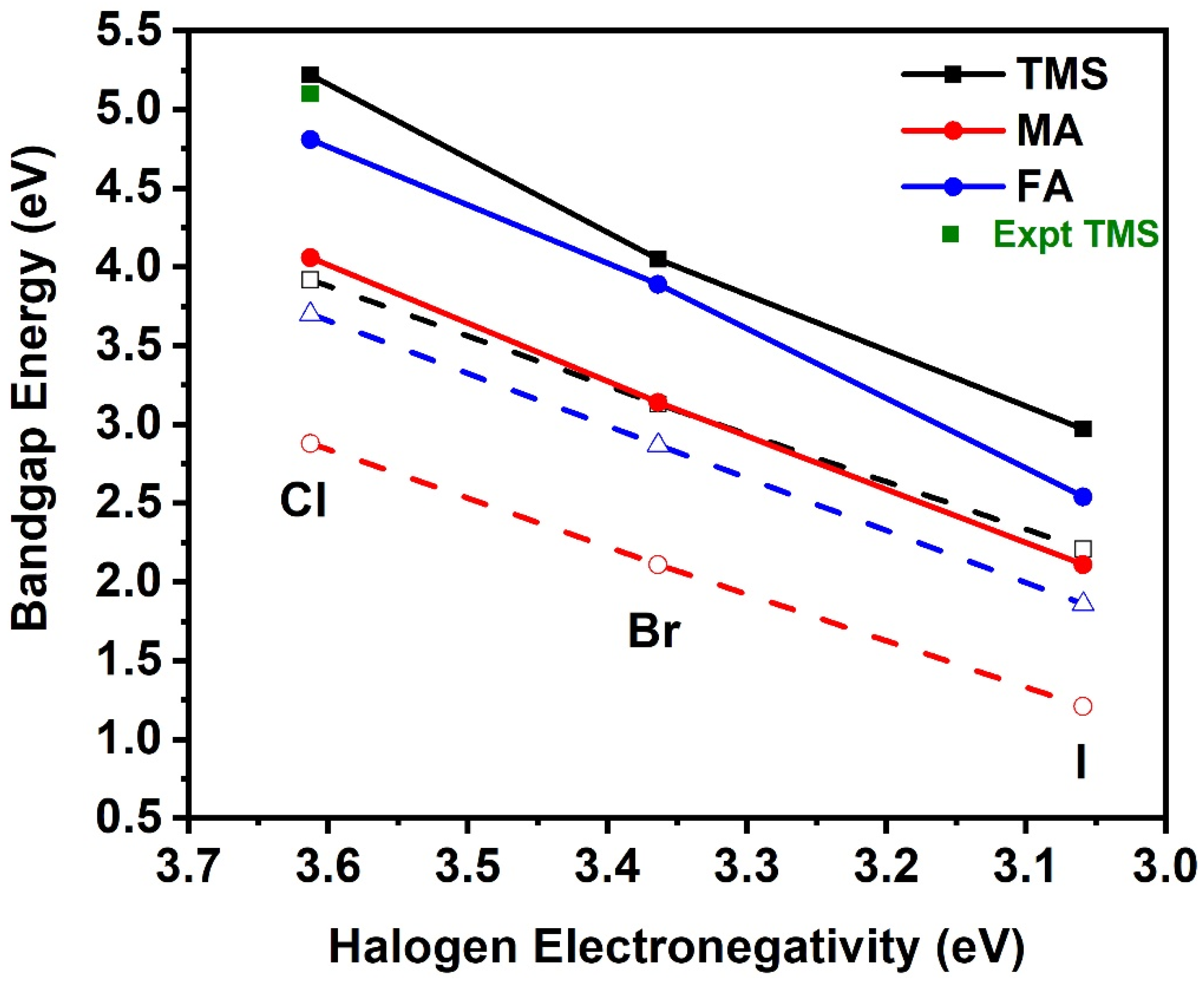
4. Trends
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mitzi, D.B. Synthesis, Structure, and Properties of Organic-Inorganic Perovskites and Related Materials. Prog. Inorg. Chem. 2007, 48, 1–121. [Google Scholar]
- Mitzi, D.B. Introduction: Perovskites. Chem. Rev. 2019, 119, 3033–3035. [Google Scholar] [CrossRef]
- Arya, S.; Mahajan, P.; Gupta, R.; Srivastava, R.; Tailor, N.K.; Satapathi, S.; Sumathi, R.R.; Datt, R.; Gupta, V. A comprehensive review on synthesis and applications of single crystal perovskite halides. Prog. Solid State Chem. 2020, 60, 100286. [Google Scholar] [CrossRef]
- Sharif, R.; Khalid, A.; Ahmad, S.W.; Rehman, A.; Qutab, H.G.; Akhtar, H.H.; Mahmood, K.; Afzal, S.; Saleem, F. A comprehensive review of the current progress and material advances in perovskite solar cells. Nanoscale Adv. 2023, 5, 3803–3833. [Google Scholar] [CrossRef] [PubMed]
- Cui, J.; Liu, Y.; Deng, Y.; Lin, C.; Fang, Z.; Xiang, C.; Bai, P.; Du, K.; Zuo, X.; Wen, K.; et al. Efficient Light-Emitting Diodes Based on Oriented Perovskite Nanoplatelets. Sci. Adv. 2021, 7, eabg8458. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Meng, W.; Luo, G.; Xu, G.; Peng, M.; Xu, B.; Nie, S.; Deng, Z. RGB tri-luminescence in organic–inorganic zirconium halide perovskites. Chem. Sci. 2024, 15, 2954. [Google Scholar] [CrossRef]
- Stranks, S.D.; Snaith, H.J. Metal-Halide Perovskites for Photovoltaic and Light-Emitting Devices. Nat. Nanotechnol. 2015, 10, 391–402. [Google Scholar] [CrossRef]
- Xing, G.; Mathews, N.; Sun, S.; Lim, S.S.; Lam, Y.M.; Gratzel, M.; Mhaisalkar, S.; Sum, T.C. Long-Range Balanced Electron- and Hole-Transport Lengths in Organic-Inorganic CH3NH3PbI3. Science 2013, 342, 344–347. [Google Scholar] [CrossRef]
- Waser, R.; Dittmann, R.; Staikov, G.; Szot, K. Redox-Based Resistive Switching Memories-Nanoionic Mechanisms, Prospects, and Challenges. Adv. Mater. 2009, 21, 2632–2663. [Google Scholar] [CrossRef] [PubMed]
- Reyren, N.; Thiel, S.; Caviglia, A.; Kourkoutis, L.F.; Hammerl, G.; Richter, C.; Schneider, C.W.; Kopp, T.; Ruetschi, A.-S.; Jaccard, D.; et al. Superconducting Interfaces Between Insulating Oxides. Science 2007, 317, 1196–1199. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Liang, Y.; Huang, H.; Liu, X.; Li, Q.; Chen, L.; Xu, D. Stable and Highly Efficient Photocatalysis with Lead-Free Double-Perovskite of Cs2AgBiBr6. Angew. Chem. Int. Ed. 2019, 58, 7263–7267. [Google Scholar] [CrossRef] [PubMed]
- Cucco, B.; Katan, C.; Even, J.; Kepenekian, M.; Volonakis, G. Fine Structure of Excitons in Vacancy-Ordered Halide Double Perovskites. ACS Mater. Lett. 2023, 5, 52–59. [Google Scholar] [CrossRef]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal halide perovskites as visible-light spensitizer for photovoltaic cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef]
- Kim, H.S.; Lee, C.R.; Im, J.H.; Lee, K.B.; Moehl, T.; Machioro, A.; Moon, S.J.; Baker, R.H.; Yum, J.H.; Moser, J.E.; et al. Lead iodide perovskite sensitized all-solid-state submicron thin film mesoscopic solar cell with efficiency exceeding 9%. Sci. Rep. 2012, 2, 591. [Google Scholar] [CrossRef]
- Jeon, N.J.; Noh, J.H.; Yang, W.S.; Kim, Y.C.; Ryu, S.; Seo, J.; Seok, S.I.I. Compositional engineering of perovskite materials for high-performance solar cells. Nature 2015, 517, 476–480. [Google Scholar] [CrossRef] [PubMed]
- Kaltzoglou, A.; Stoumpos, C.C.; Kontos, A.G.; Manolis, G.K.; Papadopoulos, K.; Papadokostaki, K.G.; Psycharis, V.; Tang, C.C.; Jung, Y.-K.; Walsh, A.; et al. Trimethylsulfonium lead triiodide: An air-stable hybrid halide perovskite. Inorg. Chem. 2017, 56, 6302. [Google Scholar] [CrossRef]
- Abfalterer, A.; Shamsi, J.; Kubicki, D.J.; Savory, C.N.; Xiao, J.; Divitini, G.; Li, W.; Macpherson, S.; Gałkowski, K.; MacManus-Driscoll, J.L. Colloidal Synthesis and Optical Properties of Perovskite-Inspired Cesium Zirconium Halide Nanocrystals. ACS Mater. Lett. 2020, 2, 1644–1652. [Google Scholar] [CrossRef]
- Dai, G.; Ma, Z.; Qiu, Y.; Li, Z.; Fu, X.; Jiang, H.; Ma, Z. Excitation-Dependent Luminescence of 0D ((CH3)4N)2ZrCl6 across the Full Visible Region. J. Phys. Chem. Lett. 2022, 13, 7553–7560. [Google Scholar] [CrossRef]
- Lin, J.-W.; Lu, X.; Liu, Z.; Lin, Y.-P.; Yang, J.; Ge, Y.; Zhou, C.; Wang, X.; Li, J.-R.; Du, K.-Z.; et al. Optical Property Regulation through Host–Guest Interaction in a Zero-Dimensional Zr Chloride. Chem. Mater. 2024, 36, 4600–4606. [Google Scholar] [CrossRef]
- Tagiara, N.S.; Psycharis, V.; Kaltzoglou, A. Synthesis, crystal structure and luminescence of [(CH3)3S]2ZrCl6. J. Coord. Chem. 2024, 77, 286–294. [Google Scholar] [CrossRef]
- Patterson, H.H.; Nims, J.L.; Valencia, C.M. Sharp-Line Luminescence of the Hexabromorhenate (IV) Ion in Single Crystal of Cesium Hexabromozirconate (IV) at 20 °K. J. of Molec. Spectr. 1972, 42, 567–574. [Google Scholar] [CrossRef]
- Sinram, D.; Brendel, C.; Krebs, B. Hexa-iodoanions of Titanium, Zirconium, Hafnium, Palladium and Platinum: Preparation, Properties and Crystal Structures of the Caesium Salts. Inorg. Chim. Acta 1982, 64, L131–L132. [Google Scholar] [CrossRef]
- Schroder, D.K. Semiconductor Material and Device Characterization; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Wide Bandgap Semiconductors: Fundamental Properties and Modern Photonic and Electronic Devices; Takahashi, K., Yoshikawa, A., Sandhu, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Kresse, G.; Furthmuller, J. Efficiency of ab-initio total energy calculations for metal and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B. 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Blochl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Perdew, P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Becke, A.D.; Johnson, E.R. A simple effective potential for exchange. J. Chem. Phys. 2006, 124, 221101. [Google Scholar] [CrossRef]
- Tran, F.; Blaha, P. Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential. Phys. Rev. Lett. 2009, 102, 226401. [Google Scholar] [CrossRef]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef] [PubMed]
- Schimka, L.; Harl, J.; Krese, G. Improved hybrid functional for solids: The HSEsol functional. J. Chem. Phys. 2011, 134, 024116. [Google Scholar] [CrossRef] [PubMed]
- Glazer, A.M. The Classification of Tilted Octahedra in Perovskites. Acta Cryst. 1972, B28, 3384. [Google Scholar] [CrossRef]
- Maughan, A.E.; Ganose, A.M.; Almaker, M.A.; Scanlon, D.O.; Neilson, J.R. Tolerance Factor and Cooperative Tilting Effects in Vacancy-Ordered Double Perovskite Halides. Chem. Mater. 2018, 30, 3909–3919. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Elsenety, M.M.; Kaltzoglou, A.; Antoniadou, M.; Koutselas, I.; Kontos, A.G.; Falaras, P. Synthesis, characterization and use of highly stable trimethyl sulfonium tin(IV) halide defect perovskites in dye sensitized solar cells. Polyhedron 2018, 150, 83–91. [Google Scholar] [CrossRef]
- Manser, J.S.; Christians, J.A.; Kama, P.V. Intriguing Optoelectronic Properties of Metal Halide Perovskites. Chem. Rev. 2016, 116, 12956–13008. [Google Scholar] [CrossRef]
- Kieslich, G.; Sun, S.; Cheetham, A.K. Solid-state principles applied to organic–inorganic perovskites: New tricks for an old dog. Chem. Sci. 2014, 5, 4712–4715. [Google Scholar] [CrossRef]
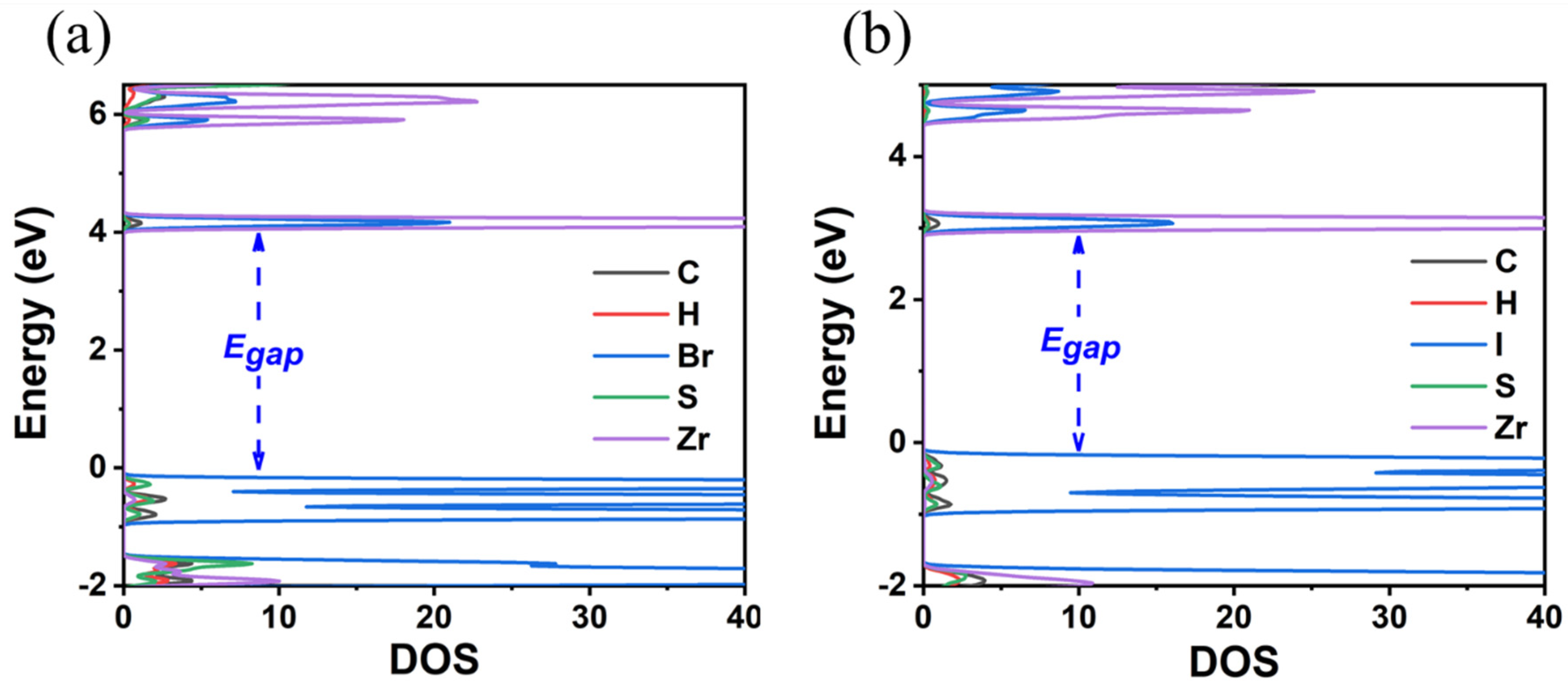
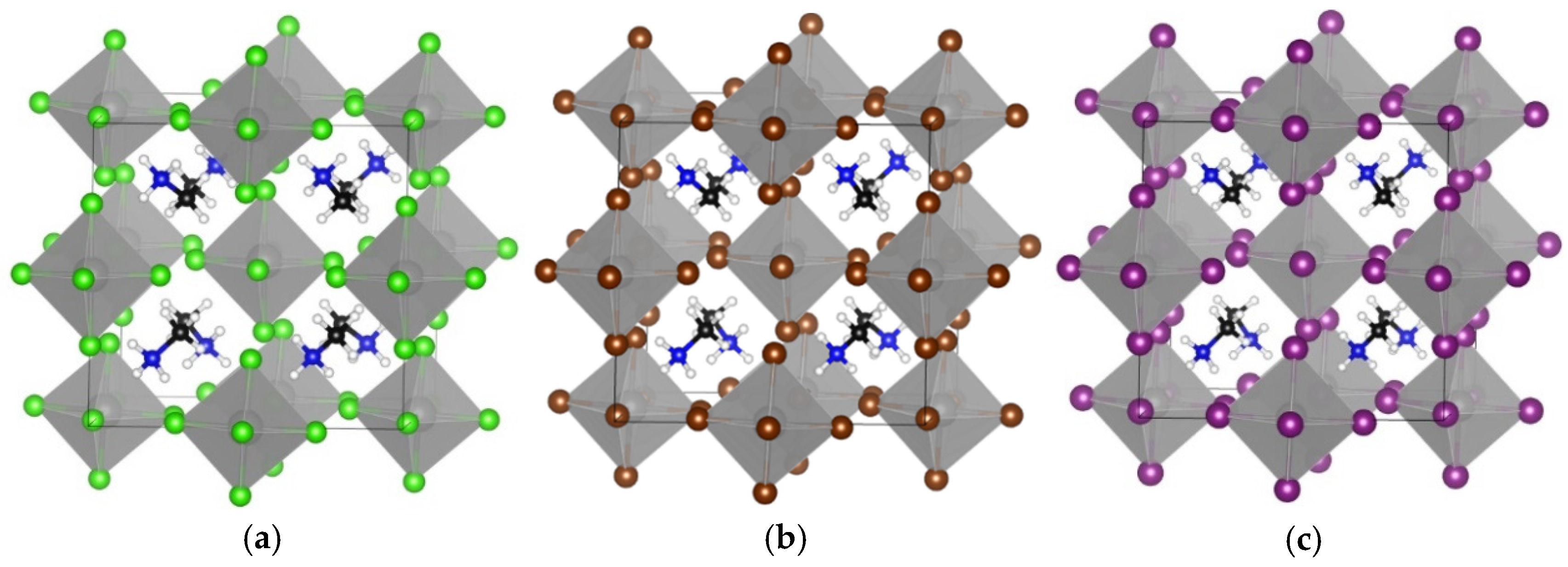
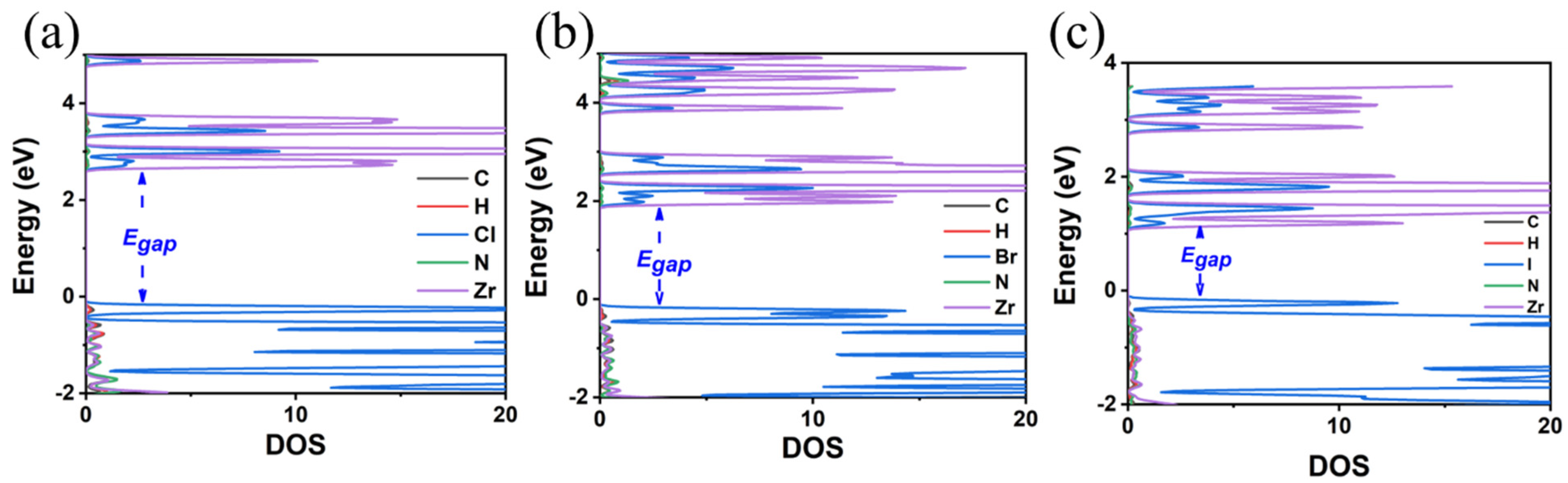
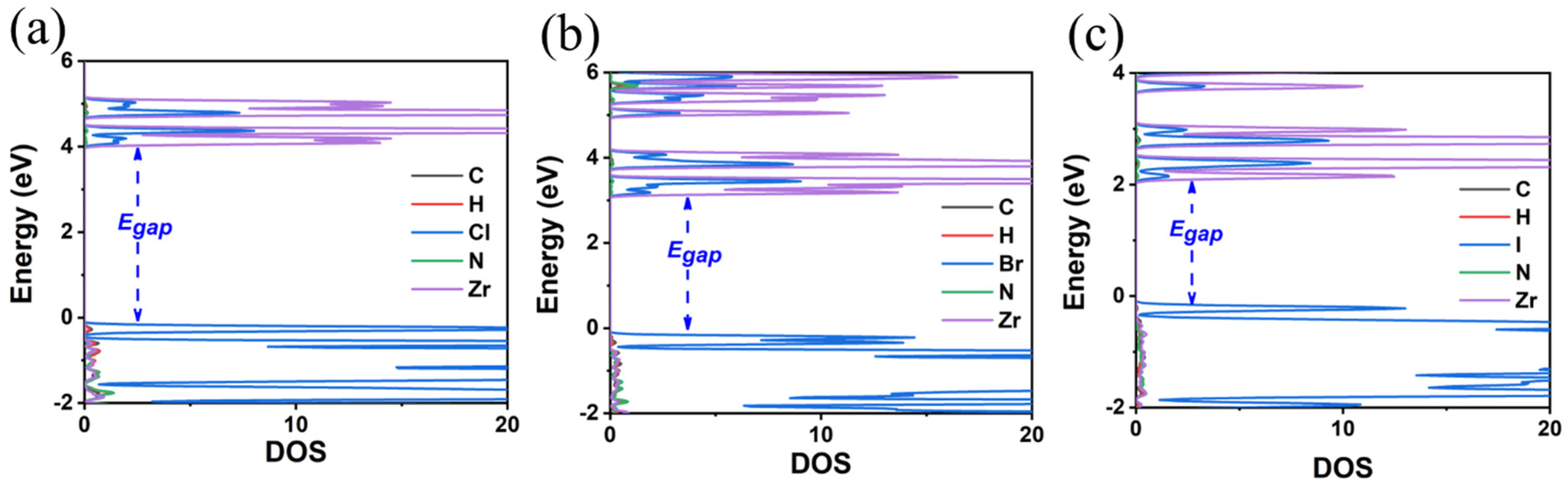

| Functional | Egap |
|---|---|
| GGA-PBE | 3.92 |
| MBJ | 5.23 |
| HSEsol | 4.69 |
| HSE06 | 5.22 |
| Experimental a | 5.1 |
| Compound | Egap (GGA-PBE) | Egap (HSE06) | Egap Expt | Crystal System | Lattice Constants | d* | d** |
|---|---|---|---|---|---|---|---|
| TMS2ZrCl6 | 3.92 | 5.22 | 5.1 a | cubic | 12.65 | 3.51 | 4.90 |
| TMS2ZrBr6 | 3.13 | 4.05 | - | cubic | 12.86 | 3.73 | 4.78 |
| TMS2ZrI6 | 2.21 | 2.97 | - | cubic | 13.49 | 4.06 | 4.87 |
| Compound | Egap (GGA-PBE) | Egap (HSE06) | Crystal System | Lattice Constants | ||||
|---|---|---|---|---|---|---|---|---|
| a | b | c | d* | d** | ||||
| MA2ZrCl6 | 2.88 | 4.06 | triclinic | 11.26 | 10.84 | 11.18 | 3.40 | 4.13 |
| MA2ZrBr6 | 2.11 | 3.14 | triclinic | 11.64 | 11.23 | 11.59 | 3.63 | 4.21 |
| MA2ZrI6 | 1.21 | 2.11 | triclinic | 12.30 | 11.92 | 12.28 | 3.98 | 4.39 |
| Compound | Egap (GGA-PBE) | Egap (HSE06) | Crystal System | Lattice Constants | d* | d** | ||
|---|---|---|---|---|---|---|---|---|
| a | b | c | ||||||
| FA2ZrCl6 | 3.70 | 4.81 | triclinic | 11.94 | 9.94 | 11.49 | 3.47 | 4.18 |
| FA2ZrBr6 | 2.87 | 3.89 | triclinic | 12.40 | 10.23 | 11.98 | 3.70 | 4.12 |
| FA2ZrI6 | 1.86 | 2.54 | triclinic | 13.04 | 10.80 | 12.69 | 4.02 | 4.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolokytha, C.; Lathiotakis, N.N.; Kaltzoglou, A.; Petsalakis, I.D.; Tzeli, D. The Effect of A-Cation and X-Anion Substitutions on the Electronic and Structural Properties of A2ZrX6 ‘Defect’ Perovskite Materials: A Theoretical Density Functional Theory Study. Materials 2025, 18, 726. https://doi.org/10.3390/ma18030726
Kolokytha C, Lathiotakis NN, Kaltzoglou A, Petsalakis ID, Tzeli D. The Effect of A-Cation and X-Anion Substitutions on the Electronic and Structural Properties of A2ZrX6 ‘Defect’ Perovskite Materials: A Theoretical Density Functional Theory Study. Materials. 2025; 18(3):726. https://doi.org/10.3390/ma18030726
Chicago/Turabian StyleKolokytha, Christina, Nektarios N. Lathiotakis, Andreas Kaltzoglou, Ioannis D. Petsalakis, and Demeter Tzeli. 2025. "The Effect of A-Cation and X-Anion Substitutions on the Electronic and Structural Properties of A2ZrX6 ‘Defect’ Perovskite Materials: A Theoretical Density Functional Theory Study" Materials 18, no. 3: 726. https://doi.org/10.3390/ma18030726
APA StyleKolokytha, C., Lathiotakis, N. N., Kaltzoglou, A., Petsalakis, I. D., & Tzeli, D. (2025). The Effect of A-Cation and X-Anion Substitutions on the Electronic and Structural Properties of A2ZrX6 ‘Defect’ Perovskite Materials: A Theoretical Density Functional Theory Study. Materials, 18(3), 726. https://doi.org/10.3390/ma18030726









