First-Principles Understanding of Mono- and Dual-Emissions in AZnOS:Bi3+ (A = Ba, Ca) Phosphors
Highlights
- The electronic and optical properties of Bi-doped CaZnOS and BaZnOS were calculated;
- Different oxidation states of Bi were considered;
- Different antisite (cation and anion) defects were modeled;
- The energies of all defect formations were calculated.
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
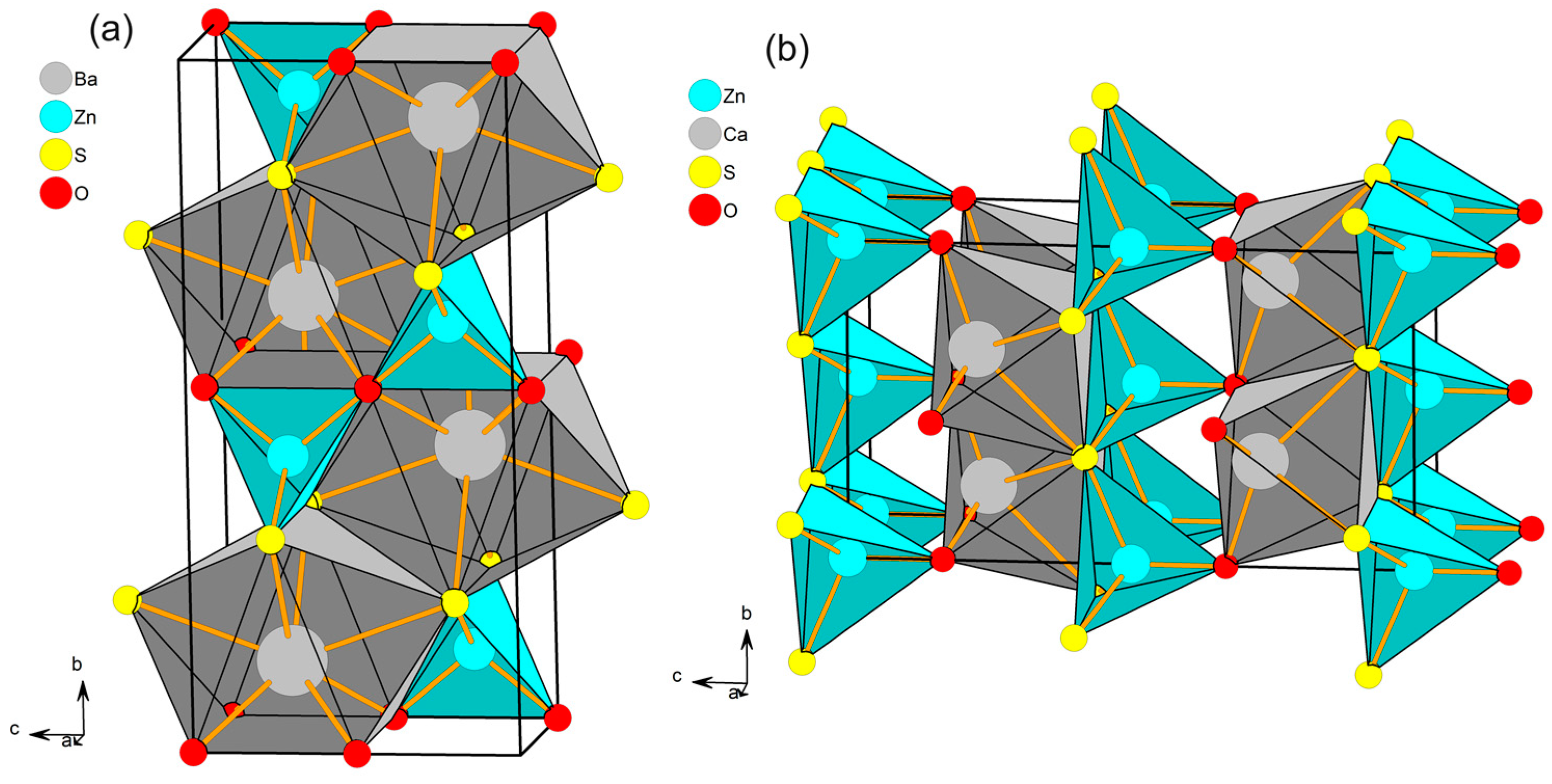
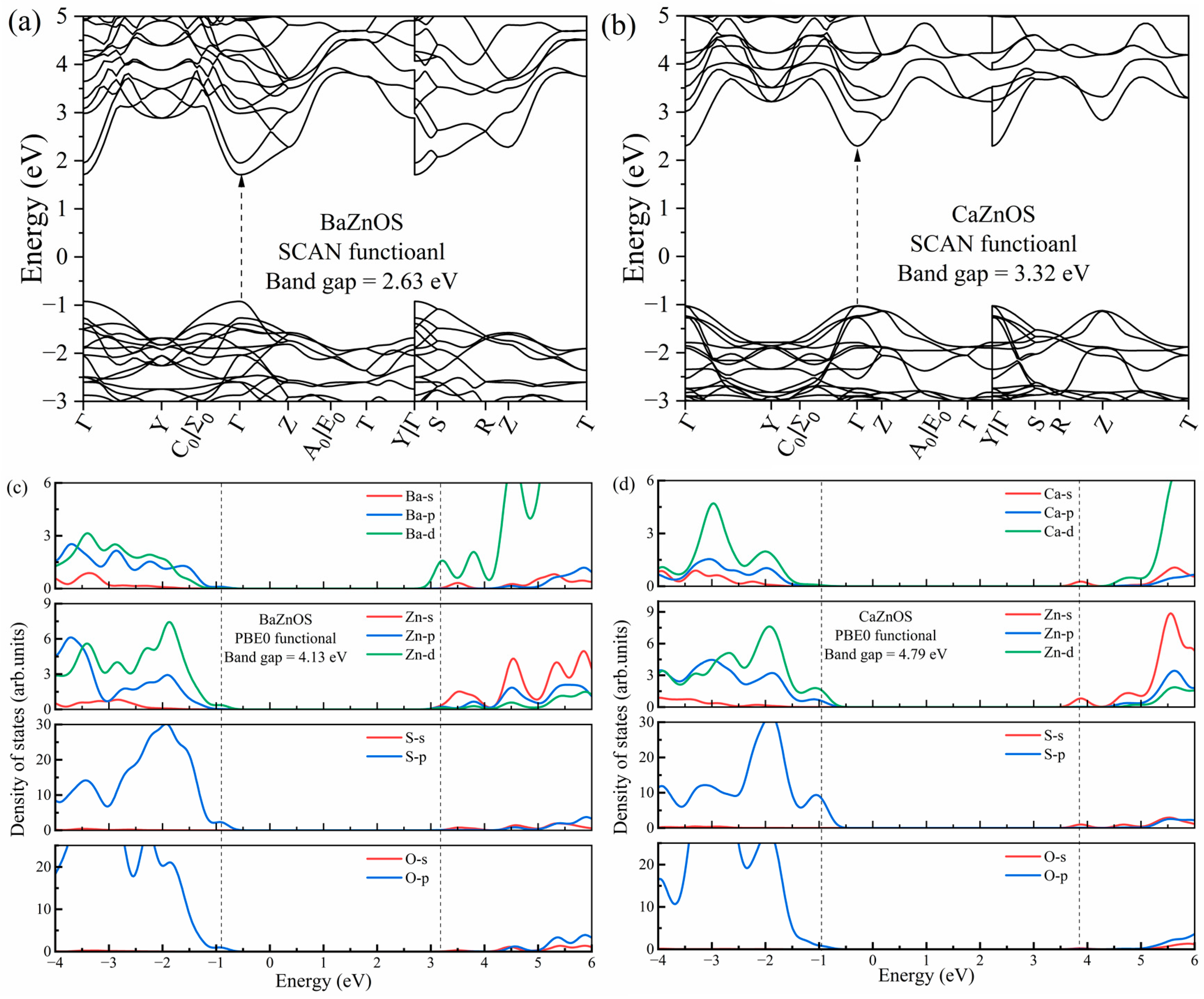
3.1. Geometric and Electronic Structures of Hosts
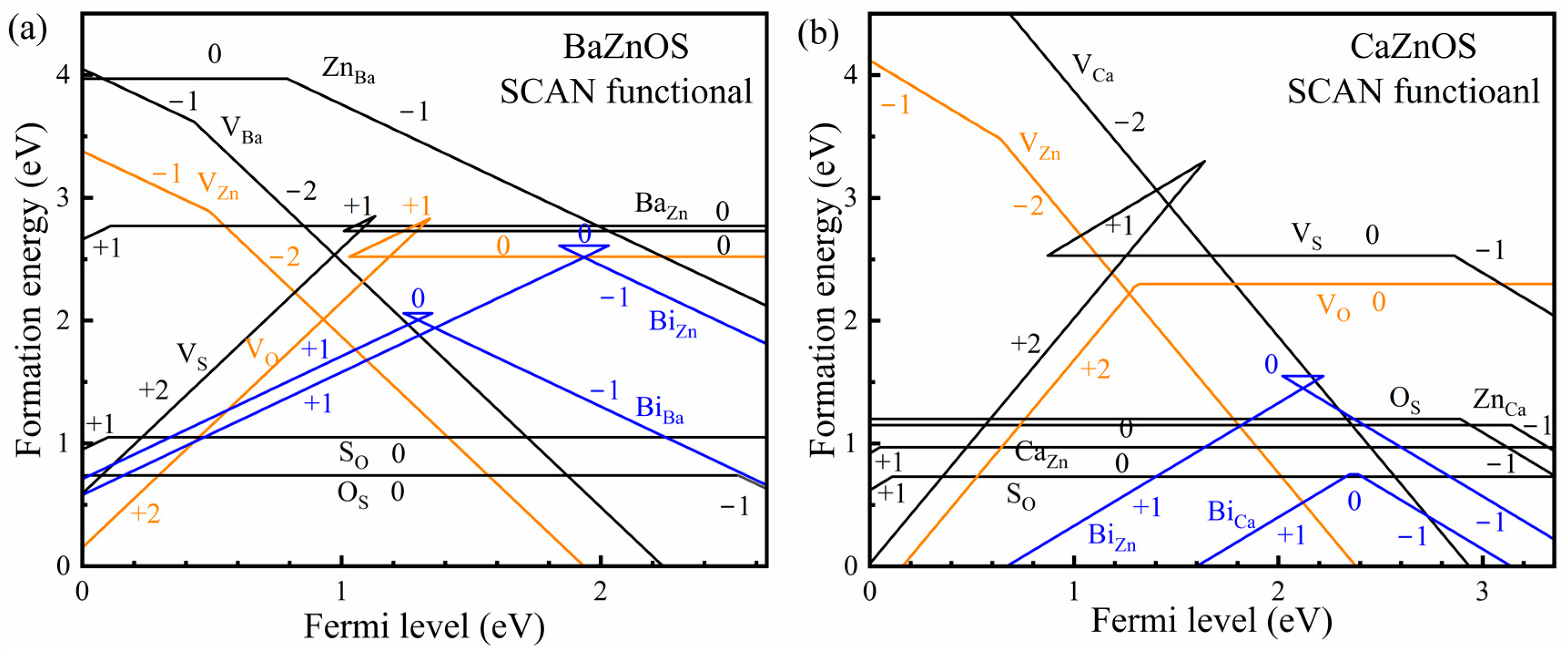
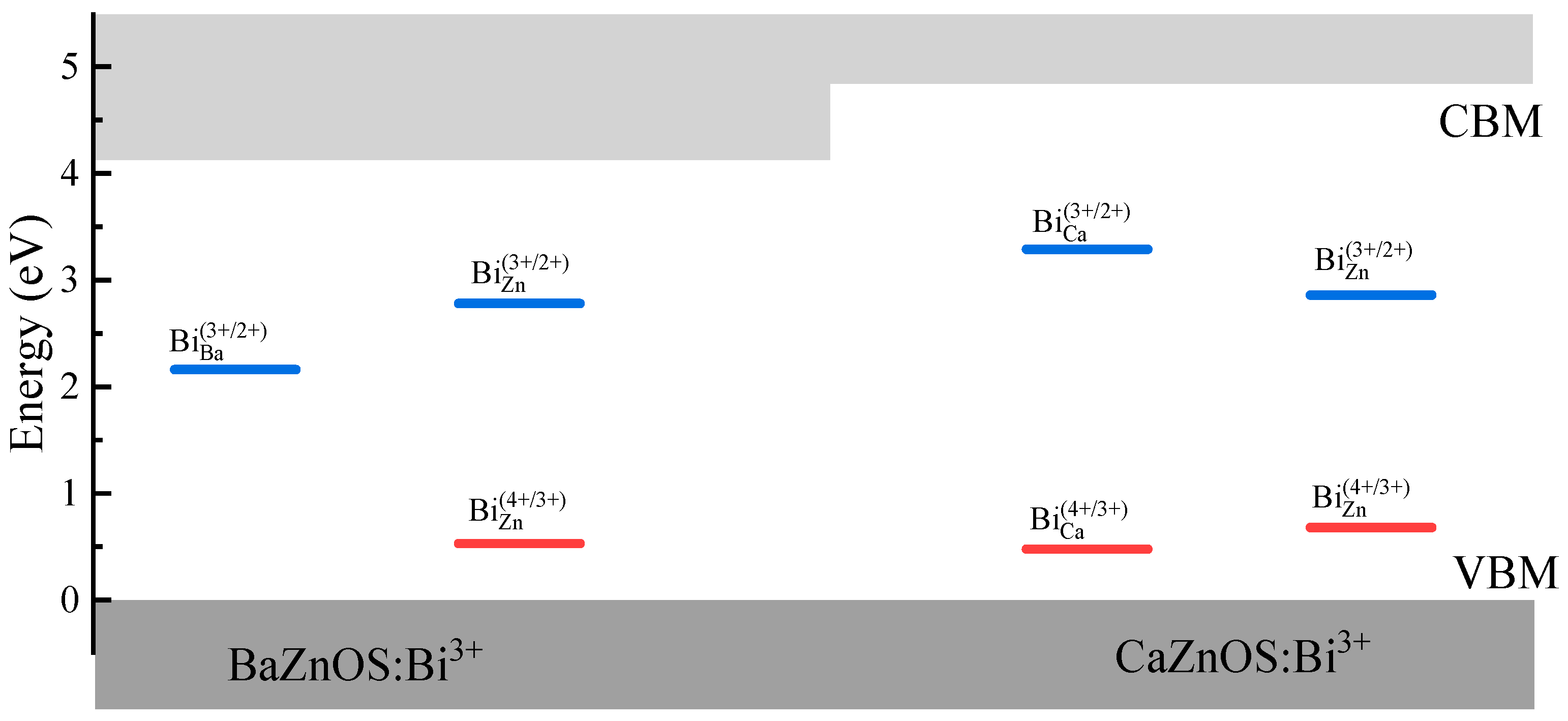
3.2. Formation of the Intrinsic Defects and Bi Dopants
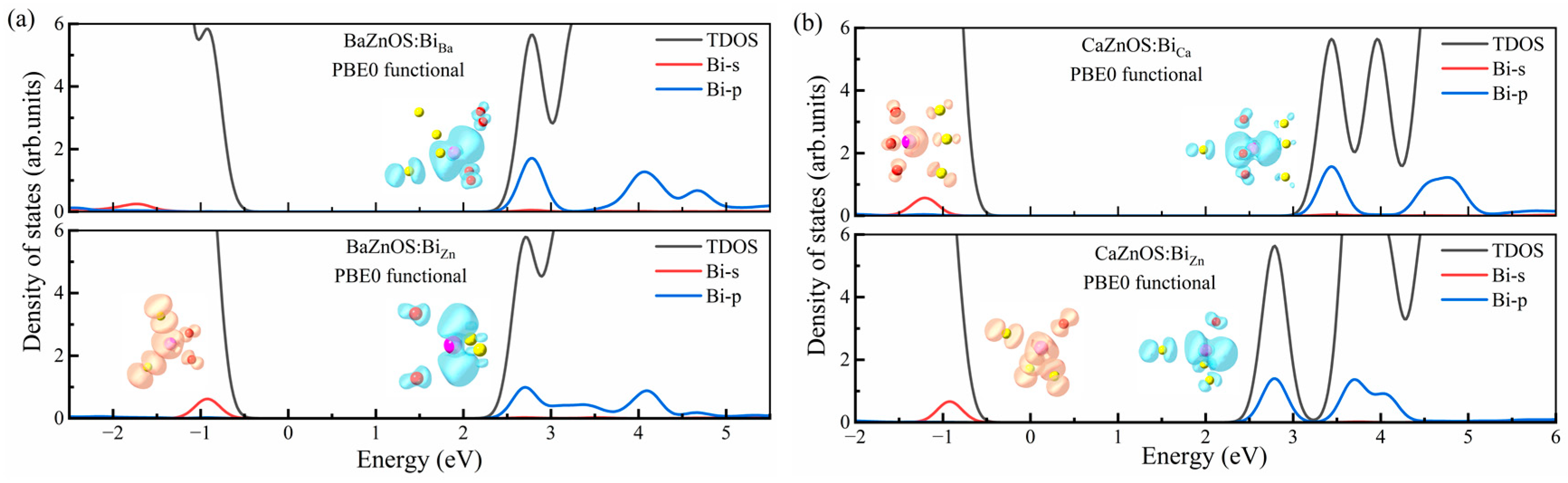
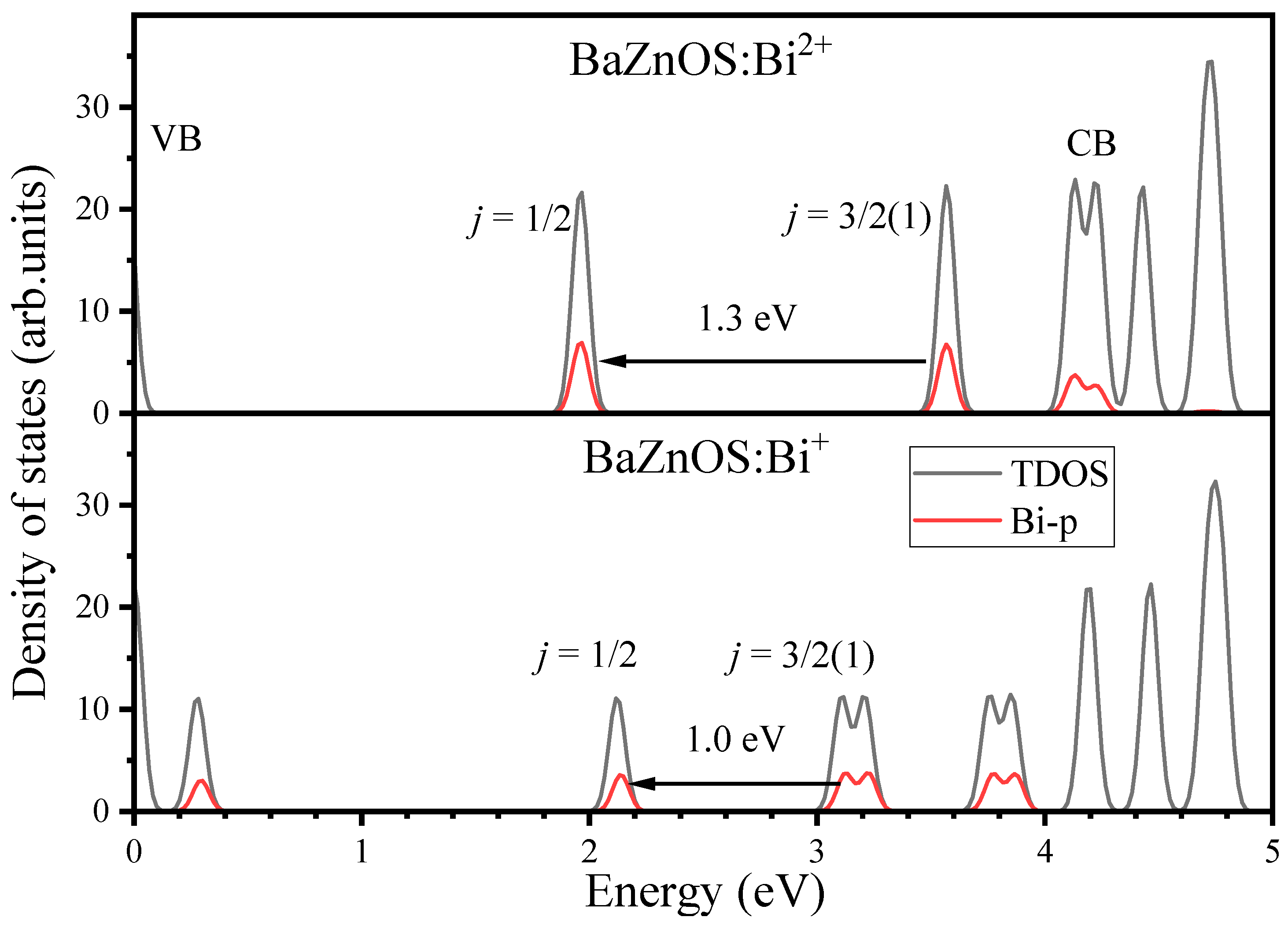
3.3. Electronic Properties of Bi3+ Dopants
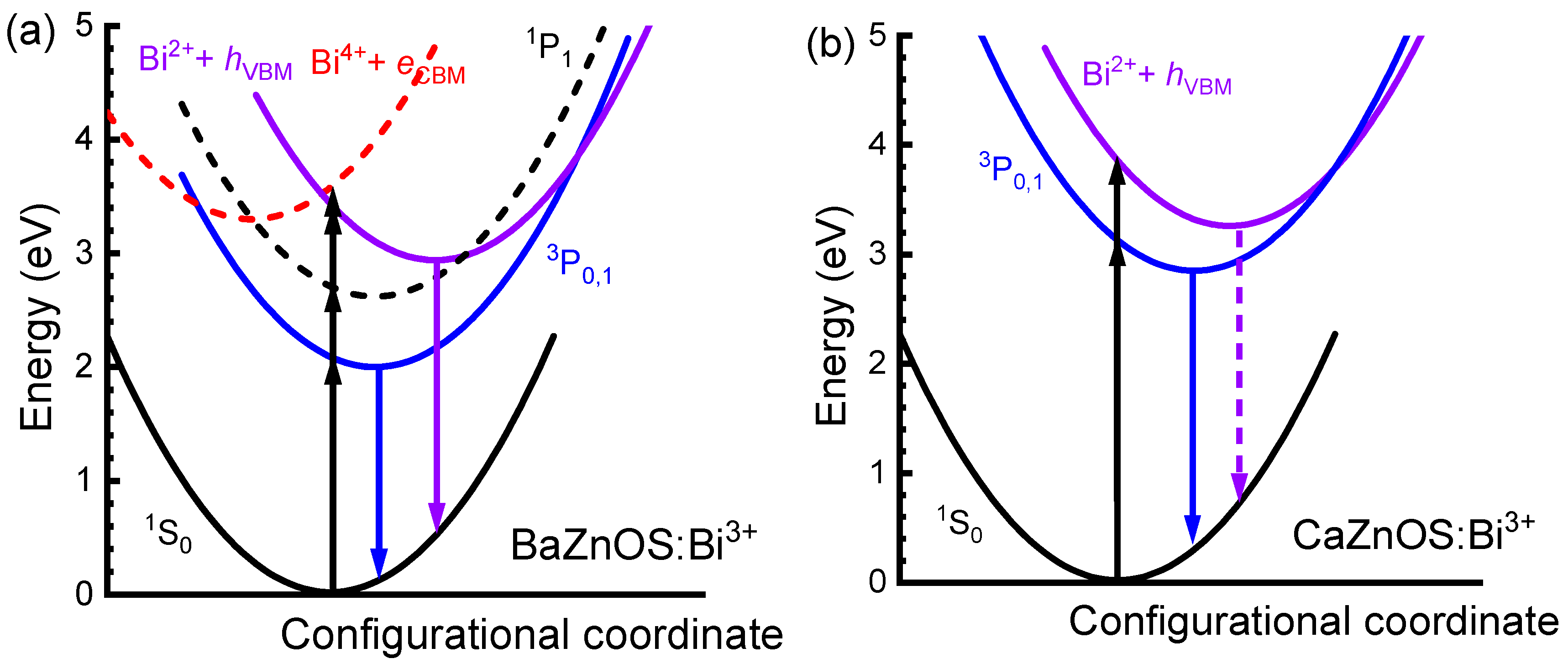
3.4. Excitation and Luminescence of Bi3+ Dopants
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khan, S.; Choi, H.; Lee, S.Y.; Lee, K.-R.; Ntwaeaborwa, O.M.; Kim, S.; Cho, S.-H. Unexpected Roles of Interstitially Doped Lithium in Blue and Green Light Emitting Y2O3:Bi3+: A Combined Experimental and Computational Study. Inorg. Chem. 2017, 56, 12139–12147. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, Y.; Li, B.; Han, L.; Xu, Y. Trap depth engineering in MgGa2O4:Bi3+ for muticolor dynamic anti-counterfeiting; encryption and optical temperature sensing applications. Chem. Eng. J. 2022, 437, 135389. [Google Scholar] [CrossRef]
- Peng, S.; Liu, L.; Wang, L.; Rong, R.; Song, L.; You, W.; Shi, J.; Zhang, Y. A novel self-activated ultraviolet persistent luminescence material and its anti-counterfeiting application based on intensity and time resolution from persistent luminescence. J. Rare Earths 2022, 40, 1417–1423. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, J.; Tong, Y.; Zhang, W.; Peng, X.; Guo, H.; Huang, D. Y4GeO8:Er3+,Yb3+ up-conversion phosphors for optical temperature sensor based on FIR technique. J. Rare Earths 2021, 39, 1512–1519. [Google Scholar] [CrossRef]
- Xu, Y.; Li, G.; Guan, X.; Wei, Y.; Zhang, M. Synthesis, crystal structure and photoluminescence properties of novel double perovskite La2CaSnO6:Eu3+ red-emitting phosphors. J. Rare Earths 2022, 40, 1682–1690. [Google Scholar] [CrossRef]
- Gao, Z.H.; Fu, F.Y.; Niu, L.L.; Jin, M.; Wang, X.H. Emission-tunable Ba2Y1−xScxNbO6:Bi3+ (0 ≤ x ≤ 1.0) phosphors for white LEDs. J. Rare Earths 2022, 40, 1819–1826. [Google Scholar] [CrossRef]
- Jin, M.; Zheng, W.; Gong, Z.; Huang, P.; Li, R.; Xu, J.; Cheng, X.; Zhang, W.; Chen, X. Unraveling the triplet excited-state dynamics of Bi3+ in vacancy ordered double perovskite Cs2SnCl6 nanocrystals. Nano Res. 2022, 15, 6422–6429. [Google Scholar] [CrossRef]
- Lou, B.; Wen, J.; Ning, L.X.; Yin, M.; Ma, C.-G.; Duan, C.-K. Understanding the defect levels and photoluminescence in a series of bismuth-doped perovskite oxides: First-principles study. Phys. Rev. B 2021, 104, 115101. [Google Scholar] [CrossRef]
- Lyu, T.; Dorenbos, P.; Li, C.; Li, S.; Xu, J.; Wei, Z. Unraveling electron liberation from Bi2+ for designing Bi3+-based afterglow phosphor for anti-counterfeiting and flexible X-ray imaging. Chem. Eng. J. 2022, 435, 135038. [Google Scholar] [CrossRef]
- Pan, D.; Yang, Y.; Yang, X.; Xu, T.; Cui, Y.; Sun, X.; Feng, H.; Liu, L.; Shen, Y.; Zhao, J.; et al. The effect of site occupation and valence state of Bi on the luminescence properties of Bi-activated oxysulfide MZnOS (M = Ca, Ba) with layer structure. J. Alloys Compd. 2018, 742, 1037–1045. [Google Scholar] [CrossRef]
- Li, X.; Zheng, Y.; Ma, R.; Huang, Z.; Wang, C.; Zhu, M.; Jiang, F.; Du, Y.; Chen, X.; Huang, B.; et al. Broadband multimodal emission in Sb-doped CaZnOS-layered semiconductors. Sci. China Mater. 2021, 65, 1329. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Q.; Yang, X.; Yang, W.; An, R.; Li, T.; Zhou, Y.; Zhang, H.; Zhao, J.; Zhang, Z. Color manipulation of Bi3+-activated CaZnOS under stress with ultra-high efficiency and low threshold for anticounterfeiting applications. J. Mater. Chem. C 2020, 8, 3308–3315. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, X.; Yuan, J.; Li, T.; Fan, Y.; Wang, L.; Deng, Z.; Li, Q.; Wan, D.; Zhao, J.; et al. Time-resolved bright red to cyan color tunable mechanoluminescence from CaZnOS:Bi3+,Mn2+ for anti-counterfeiting device and stress sensor. Adv. Opt. Mater. 2021, 9, 2100668. [Google Scholar] [CrossRef]
- Yuan, J.; Yang, Y.; Yang, X.; Fan, Y.; Li, T.; Huang, M.; Zhang, F.; Li, Q.; Zhao, J.; Zhang, Z. Regulating the trap distribution to achieve high-contrast mechanoluminescence with an extended saturation threshold through co-doping Nd3+ into CaZnOS:Bi3+,Li+. J. Mater. Chem. C 2021, 9, 7689–7696. [Google Scholar] [CrossRef]
- Liu, M.Z.; Duan, C.K.; Tanner, P.A.; Ma, C.G.; Wei, X.T.; Yin, M. Understanding photoluminescence of Cs2ZrCl6 doped with post-transition-metal ions using first-principles calculations. Phys. Rev. B 2022, 105, 195137. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Feng, A.; Zhang, S.L.; Zhang, W.B.; Yang, W. Mechanical properties of layered oxysulfide CaZnOS from first principle calculations. J. Alloys Compd. 2016, 670, 41–47. [Google Scholar] [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for Ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Paier, J.; Hirschl, R.; Marsman, M.; Kresse, G. The Perdew–Burke–Ernzerhof exchange-correlation functional applied to the G2-1 test set using a plane-wave basis set. J. Chem. Phys. 2005, 122, 234102. [Google Scholar] [CrossRef] [PubMed]
- Freysoldt, C.; Grabowski, B.; Hickel, T.; Neugebauer, J.; Kresse, G.; Janotti, A.; Van Dewalle, C.G. First-Principles Calculations for Point Defects in Solids. Rev. Mod. Phys. 2014, 86, 253. [Google Scholar] [CrossRef]
- Durrant, T.R.; Murphy, S.T.; Watkins, M.B.; Shluger, A.L. Relation between image charge and potential alignment corrections for charged defects in periodic boundary conditions. J. Chem. Phys. 2018, 149, 024103. [Google Scholar] [CrossRef]
- Liu, M.Z.; Duan, C.K.; Hao, R.J.; Yin, M. Luminescence Mechanism of ns2 Ions in Cs2(Sn/Hf)Cl6 Revealed by First-Principles Calculations. J. Phys. Chem. C 2023, 127, 3742–3749. [Google Scholar]
- Lou, B.; Wen, J.; Cai, J.; Yeung, Y.-Y.; Yin, M.; Duan, C.-K. First-Principles Study of Bi3+-Related Luminescence and Traps in the Perovskites CaMO3 (M = Zr, Sn, Ti). Phys. Rev. B 2021, 103, 075109. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.Z.; Chen, B.; Zhang, X.; Suo, H.; Zheng, W.L.; Shen, J.D.; Li, Y.Y.; Wang, F. Doubly Doped BaZnOS Microcrystals for Multicolor Luminescence Switching. Adv. Opt. Mater. 2022, 10, 2102430. [Google Scholar] [CrossRef]
- Chen, Q.; Lou, B.; Jing, W.; Yin, M.; Yeung, Y.-Y.; Su, L.; Duan, C.-K. First Principles Study on Low Valence States Photoluminescence in Bi-doped M2B5O9Cl Crystals. J. Alloys Compd. 2021, 863, 158704. [Google Scholar] [CrossRef]
| 3P0,1 | MMCT | CT | ||
|---|---|---|---|---|
| CaZnOS:BiCa | Excitation | 3.23 | / | 3.95 |
| Emission | 2.58 | / | 2.57 | |
| CaZnOS:BiZn | Excitation | 2.31 | 4.29 | 3.54 |
| Emission | 1.56 | 3.57 | 2.18 | |
| BaZnOS:BiBa | Excitation | / | / | 3.68 |
| Emission | / | / | 1.54 | |
| BaZnOS:BiZn | Excitation | 2.29 | 3.67 | 3.60 |
| Emission | 1.74 | 2.99 | 2.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kougong, Q.; Lou, B.; Brik, M.G. First-Principles Understanding of Mono- and Dual-Emissions in AZnOS:Bi3+ (A = Ba, Ca) Phosphors. Materials 2025, 18, 657. https://doi.org/10.3390/ma18030657
Kougong Q, Lou B, Brik MG. First-Principles Understanding of Mono- and Dual-Emissions in AZnOS:Bi3+ (A = Ba, Ca) Phosphors. Materials. 2025; 18(3):657. https://doi.org/10.3390/ma18030657
Chicago/Turabian StyleKougong, Quanzhi, Bibo Lou, and Mikhail G. Brik. 2025. "First-Principles Understanding of Mono- and Dual-Emissions in AZnOS:Bi3+ (A = Ba, Ca) Phosphors" Materials 18, no. 3: 657. https://doi.org/10.3390/ma18030657
APA StyleKougong, Q., Lou, B., & Brik, M. G. (2025). First-Principles Understanding of Mono- and Dual-Emissions in AZnOS:Bi3+ (A = Ba, Ca) Phosphors. Materials, 18(3), 657. https://doi.org/10.3390/ma18030657






