Behaviour of Knitted Materials in a Vibrating Environment
Abstract
1. Introduction
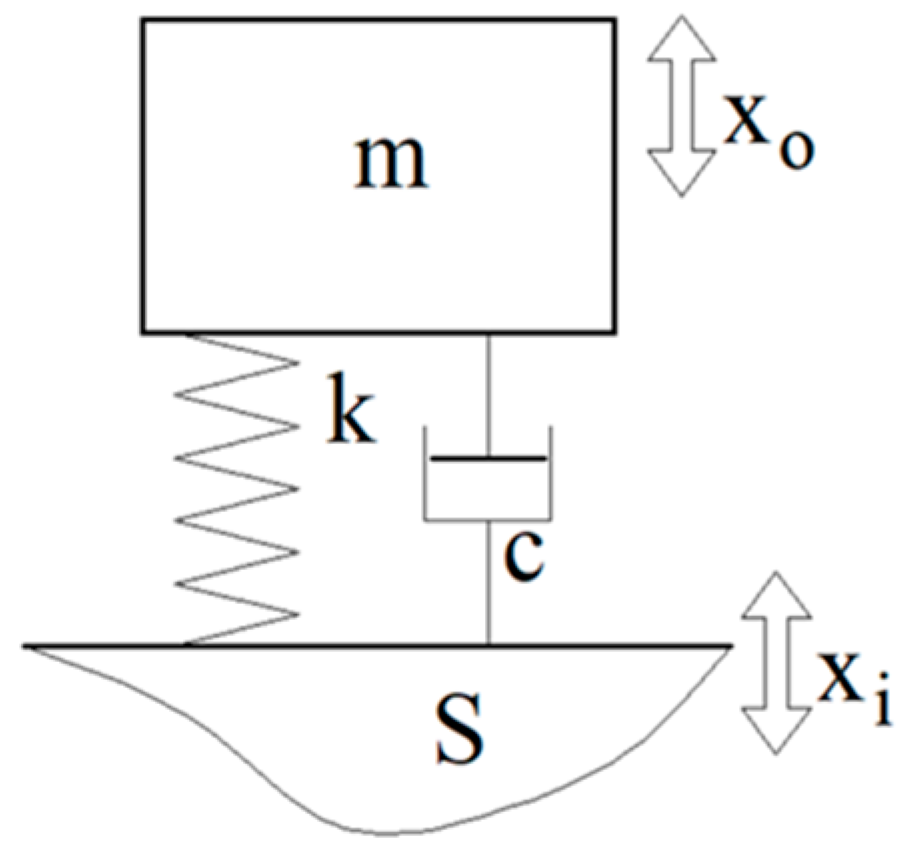
2. Natural Frequencies and Vibration Transmissibility of Knitted Materials
2.1. Vibration Parameters
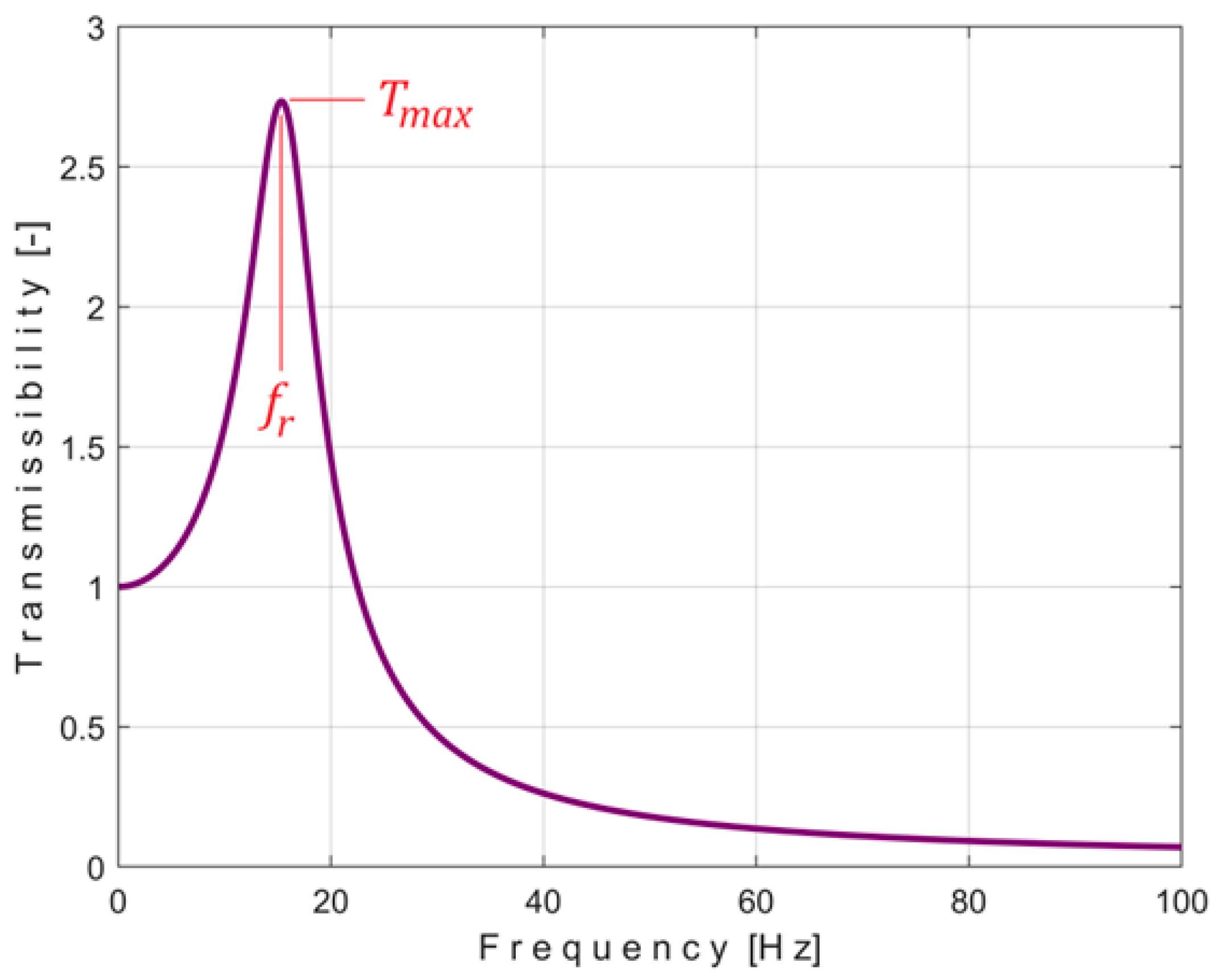
2.2. Vibration Transmissibility
- -
- The natural undamped angular frequency: p = √(k/m);
- -
- The damping ratio: ξ = c/2mp;
- -
- The relative angular frequency: η = ω/p.
3. Materials and Methods
3.1. Knitted Materials
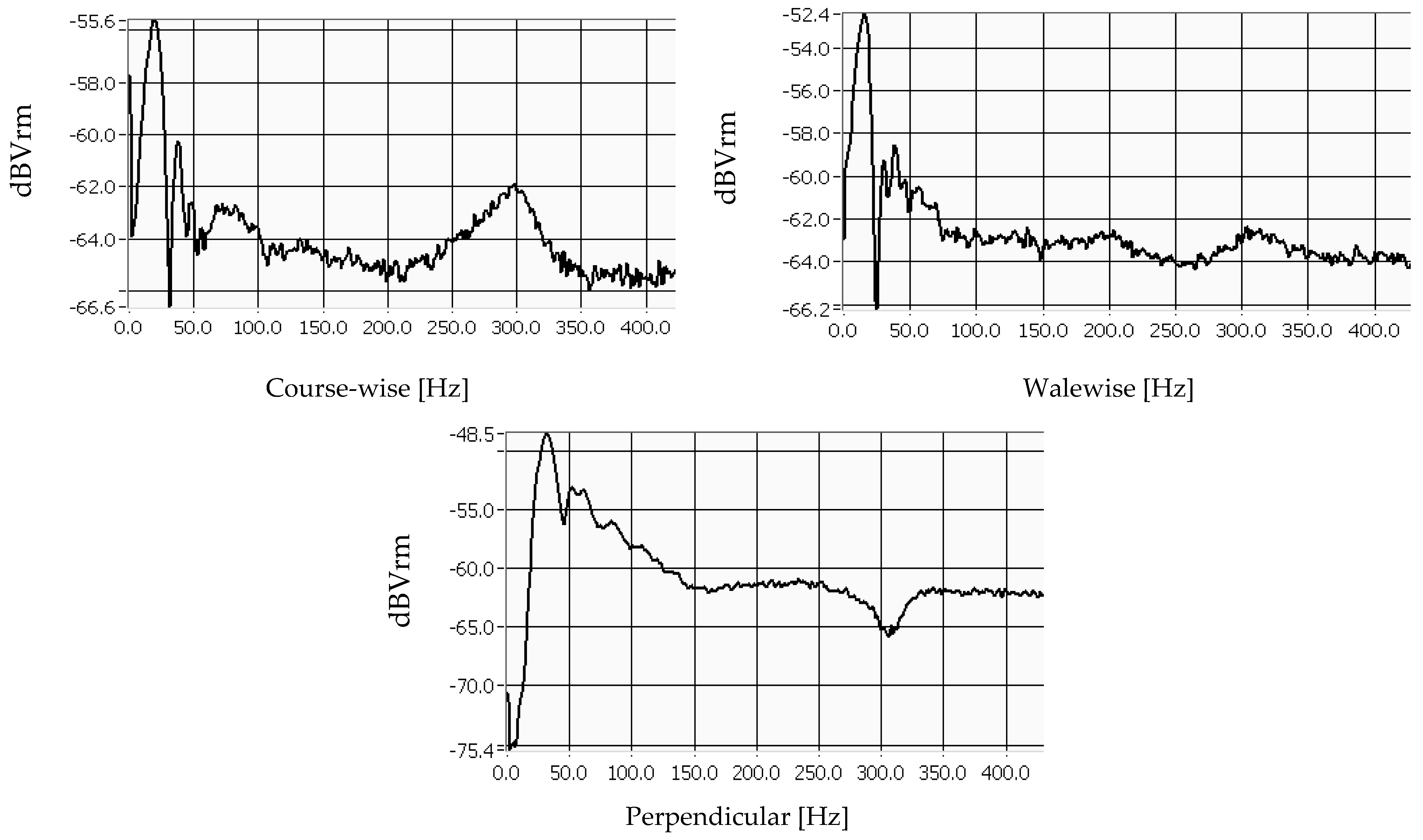
3.2. Measurement of the Natural Frequencies of the Materials
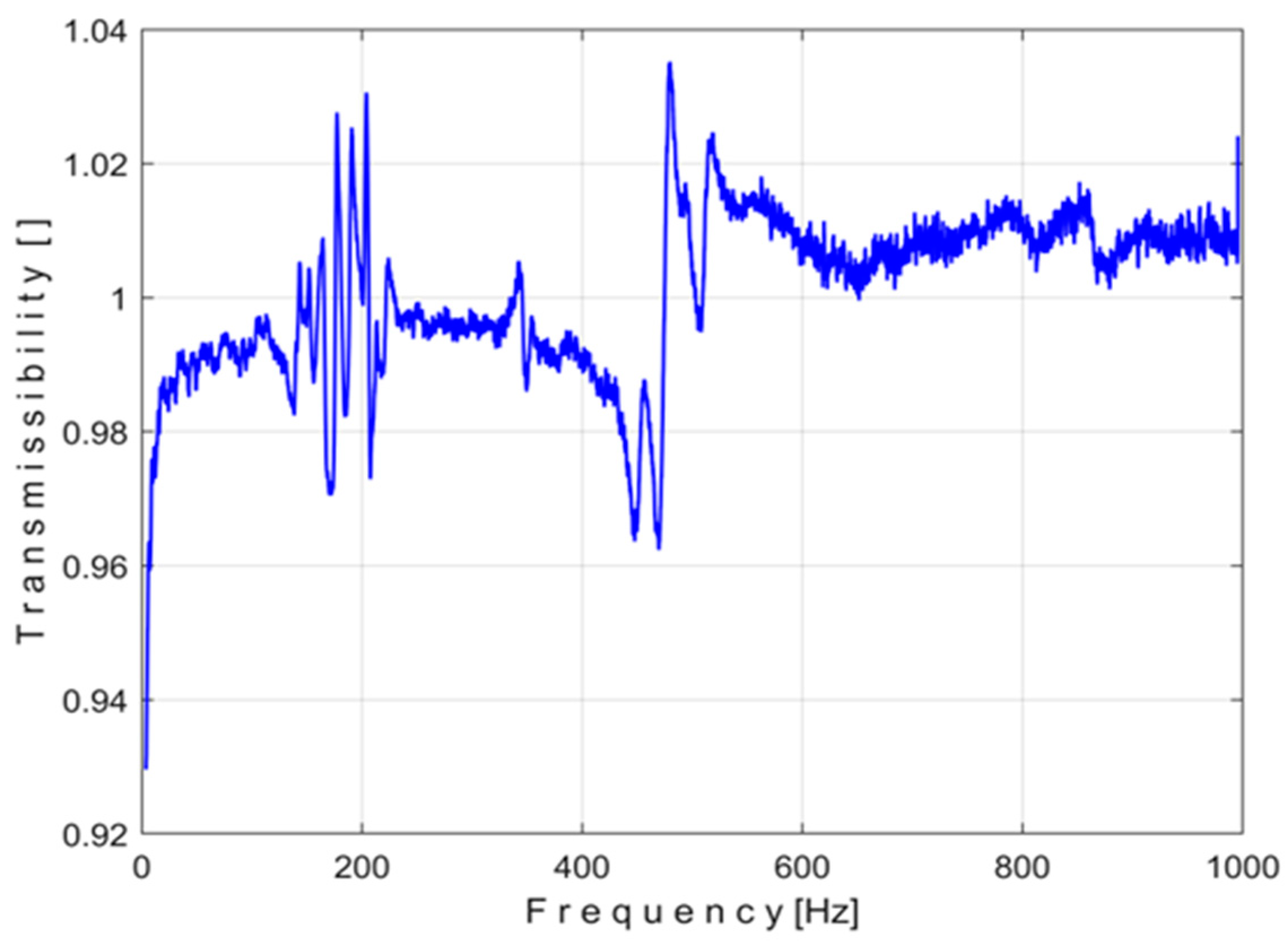
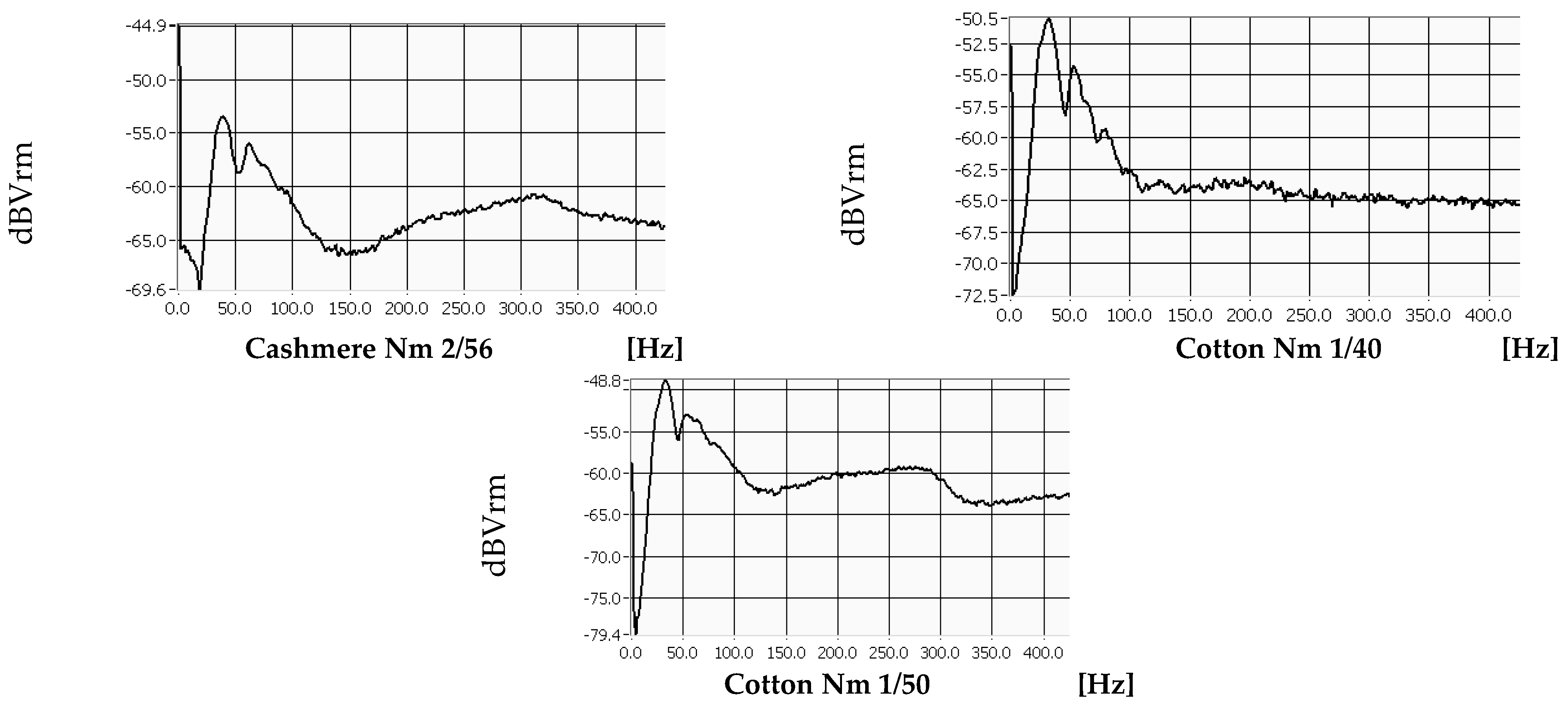
3.3. Measurement of the Vibration Transmissibility
4. Results and Discussion
4.1. Knitted Fabric’s Natural Frequencies
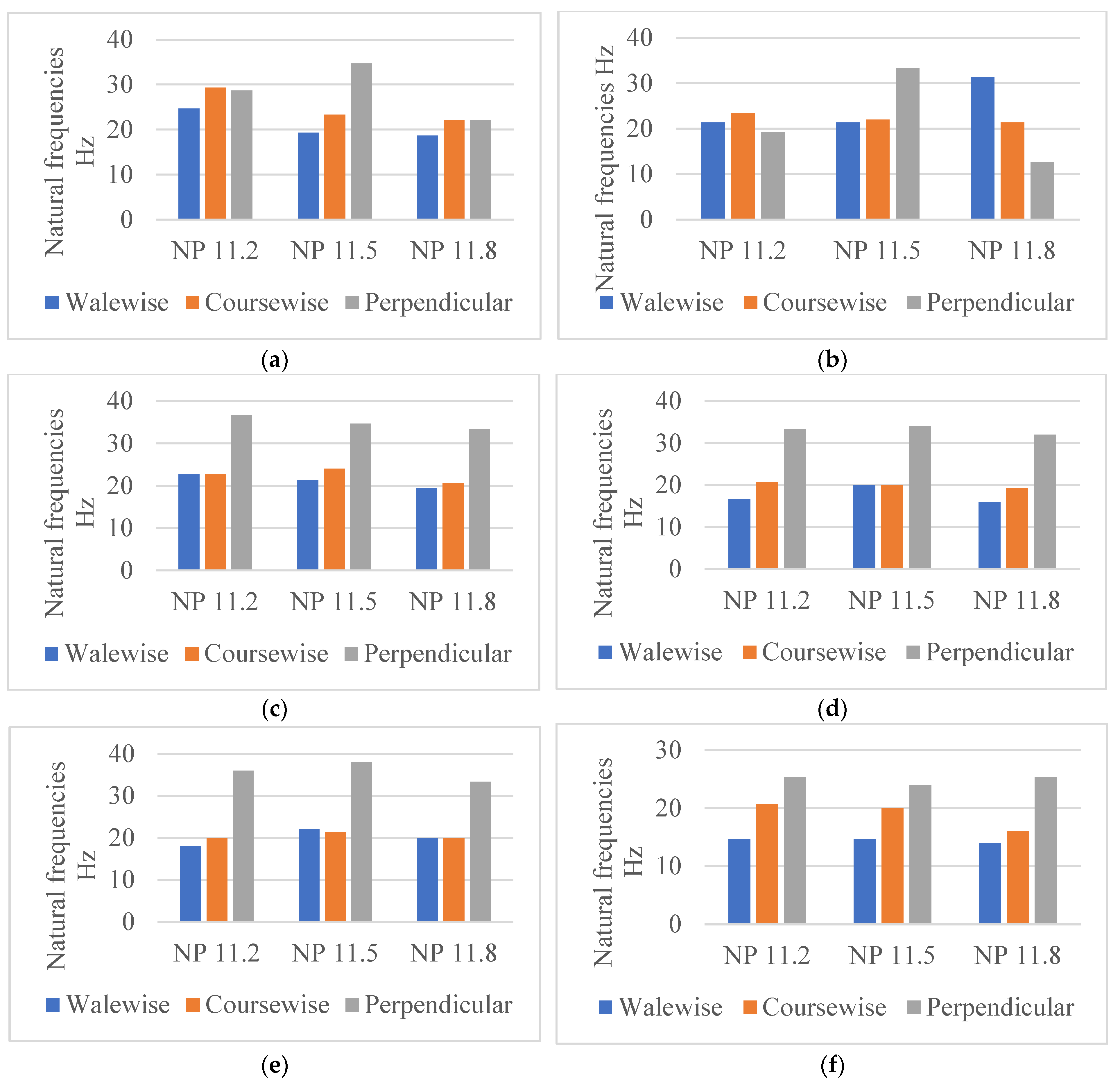
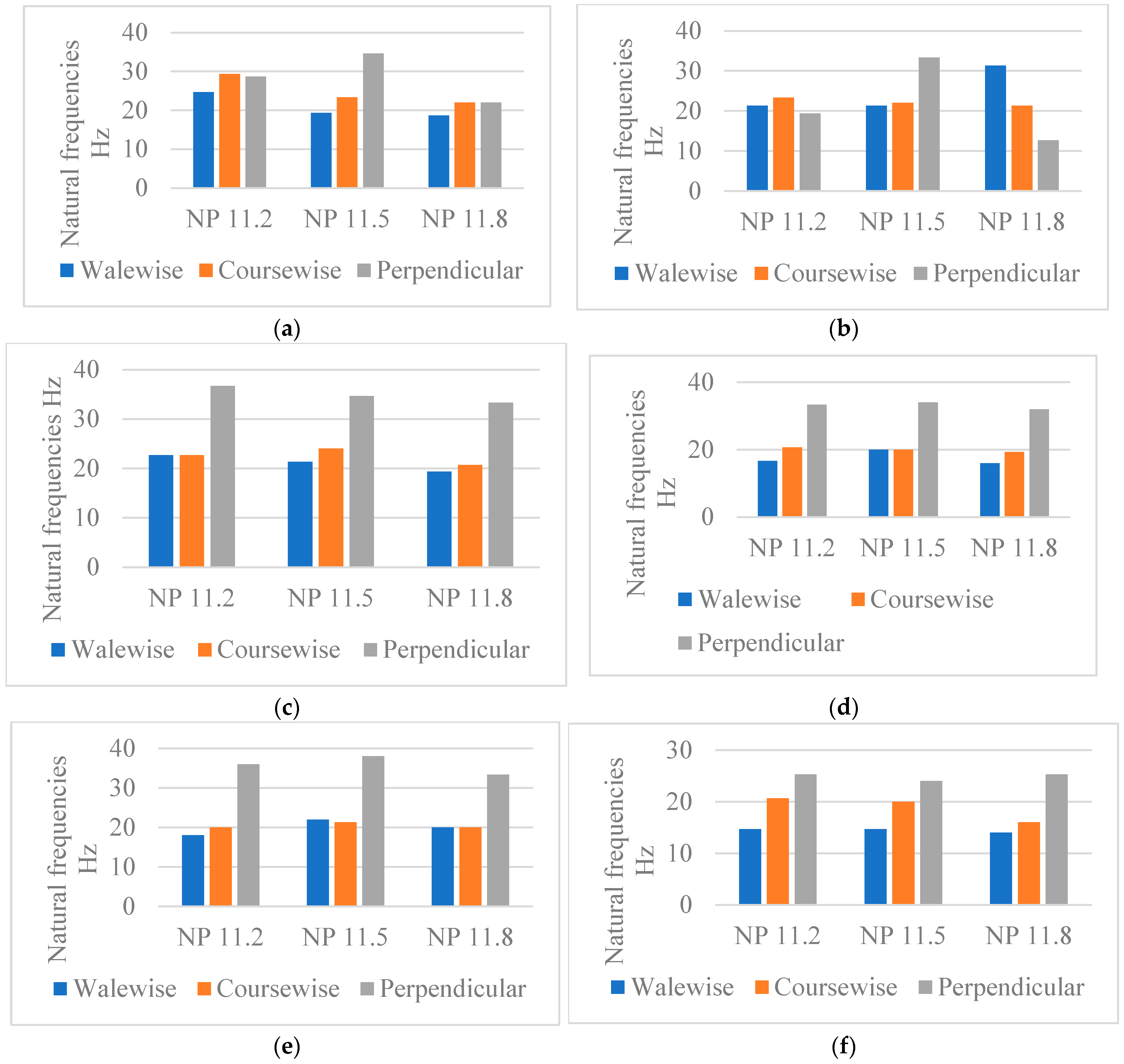
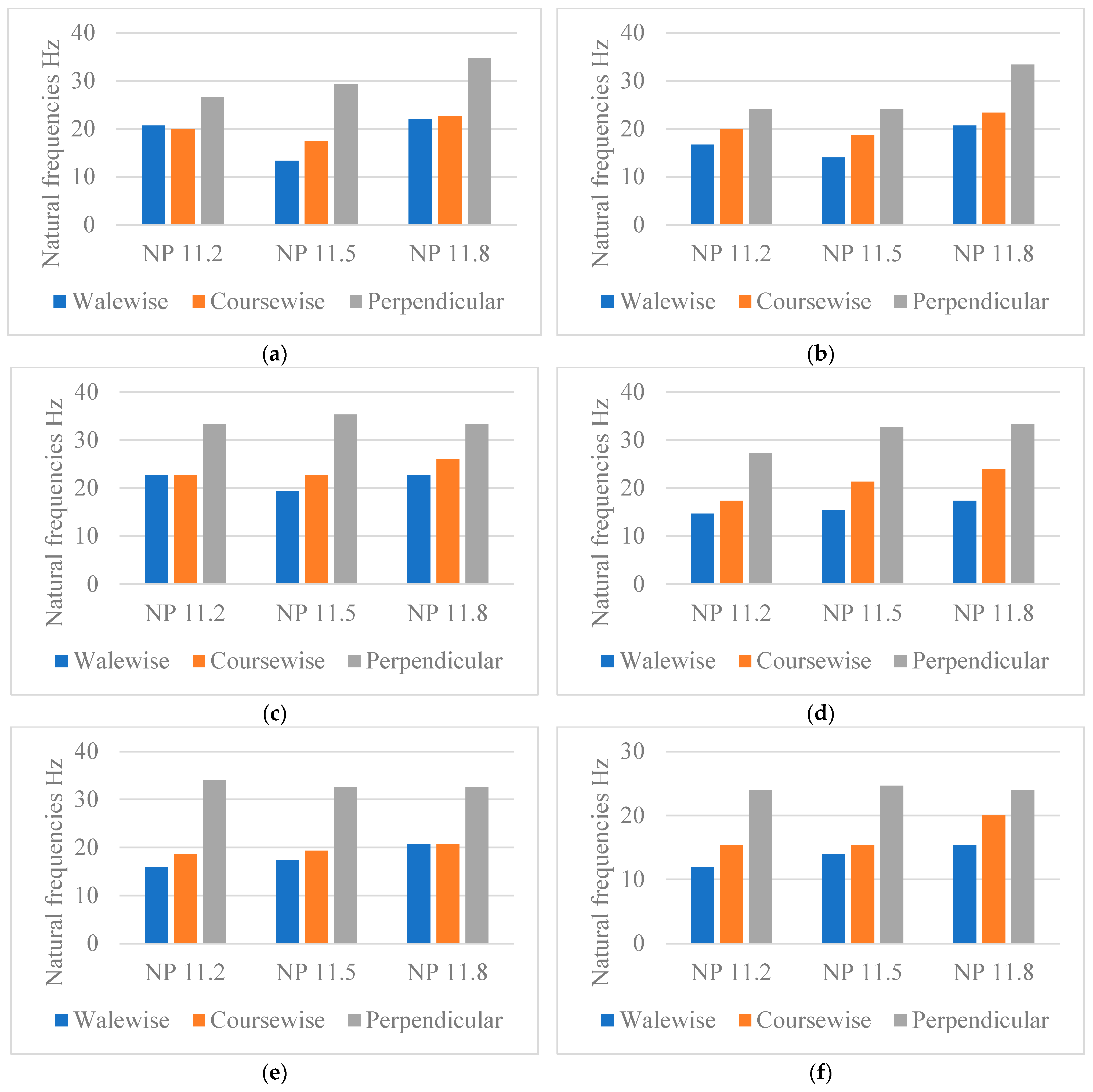
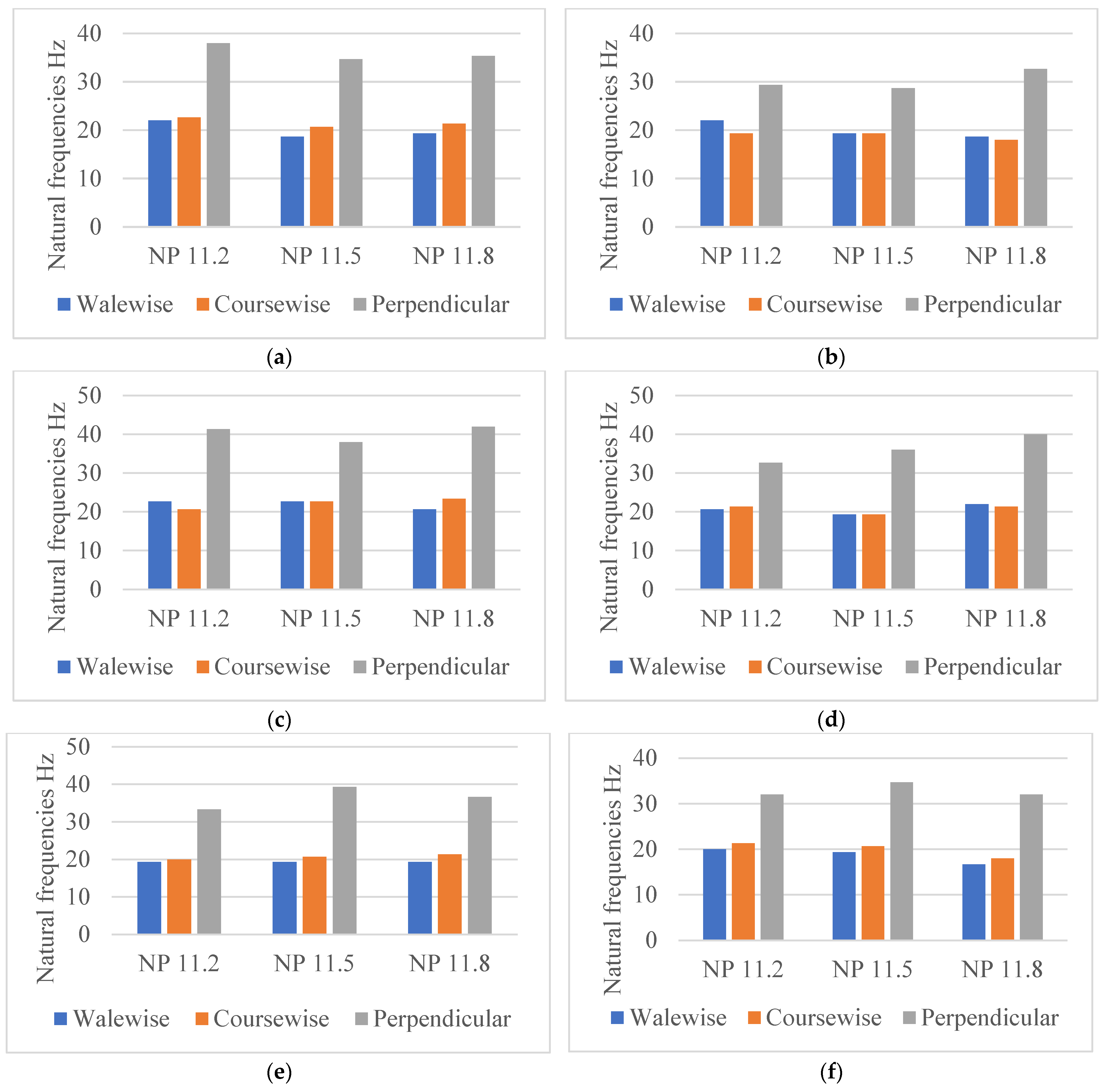
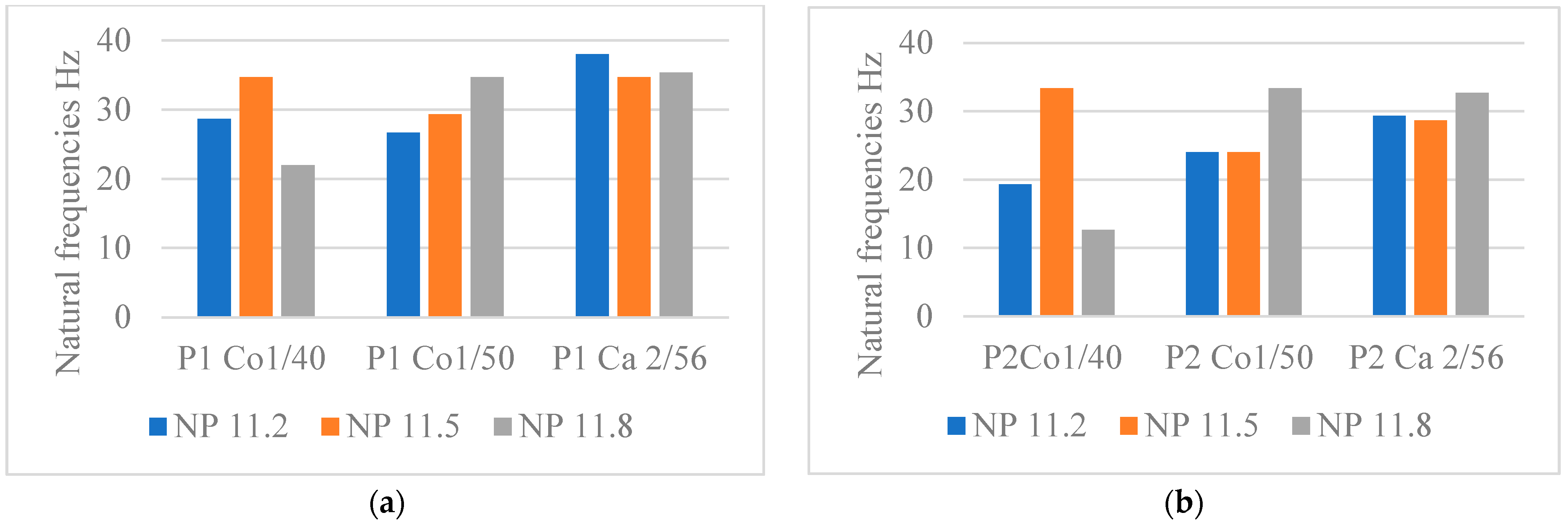
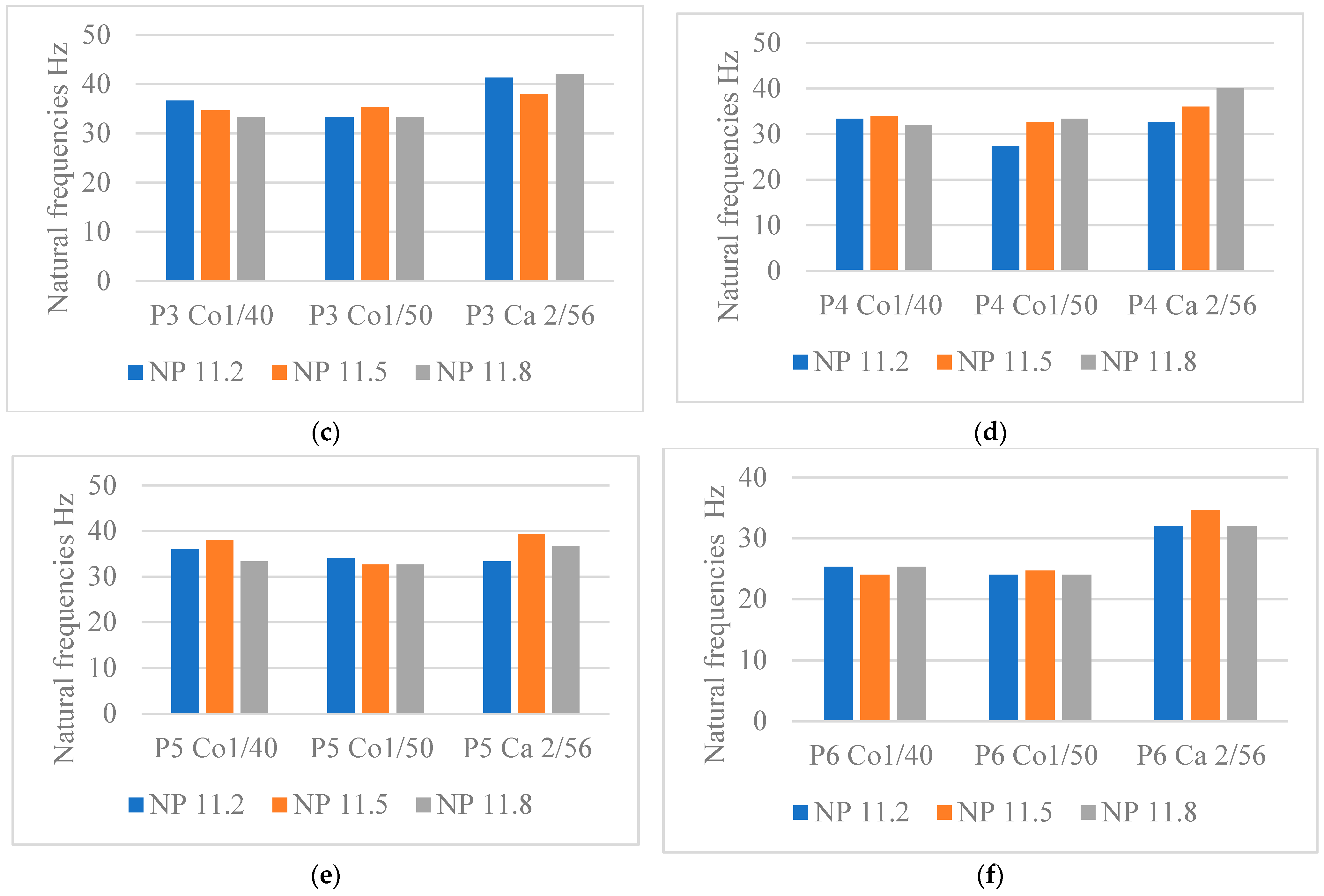
4.1.1. Influence of the Test Direction on the Natural Frequencies of the Fabrics
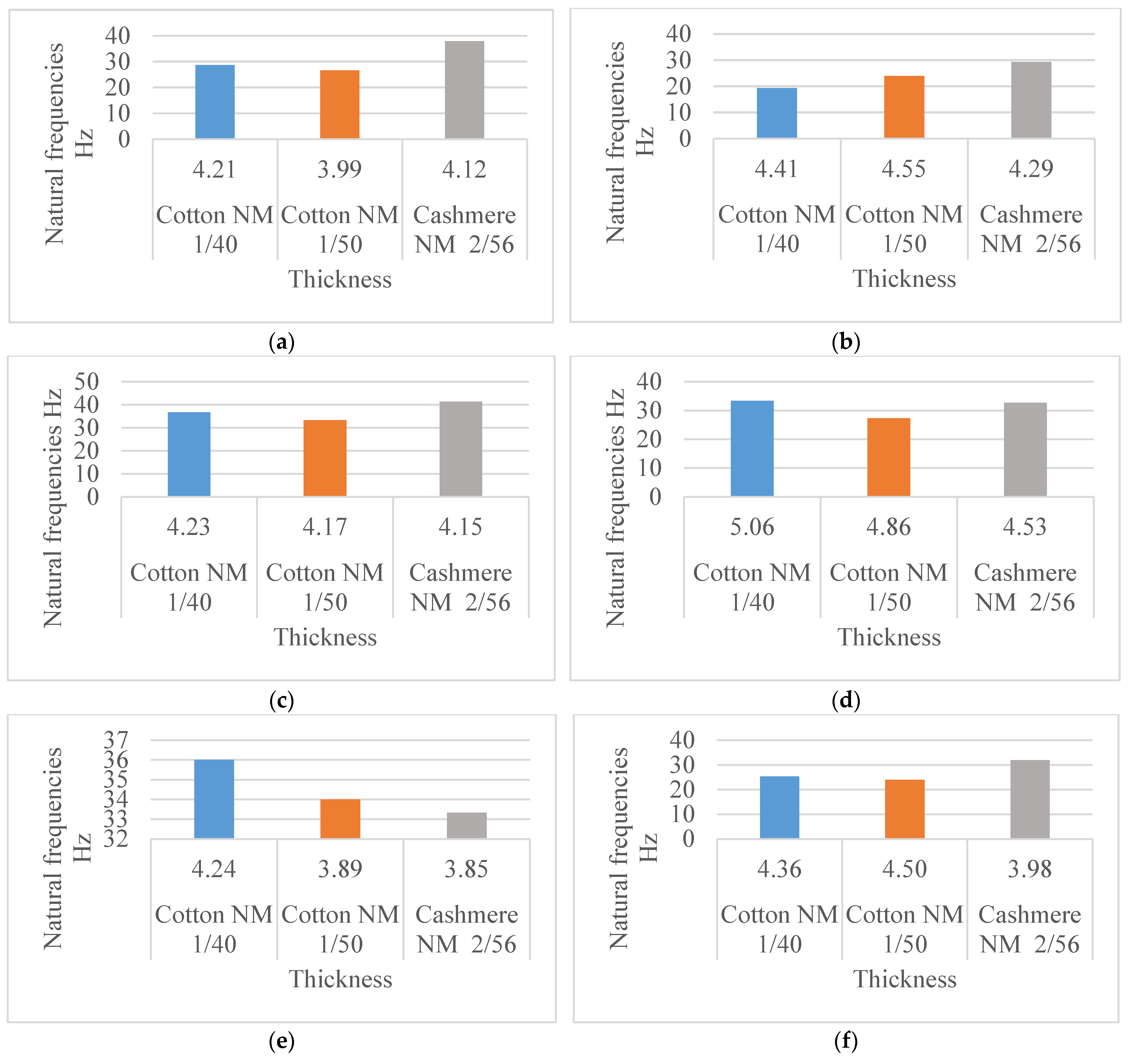
4.1.2. Influence of the Fabric’s Thickness on the Natural Frequencies
4.1.3. Influence of the Fabric’s Stitch Density on the Natural Frequencies
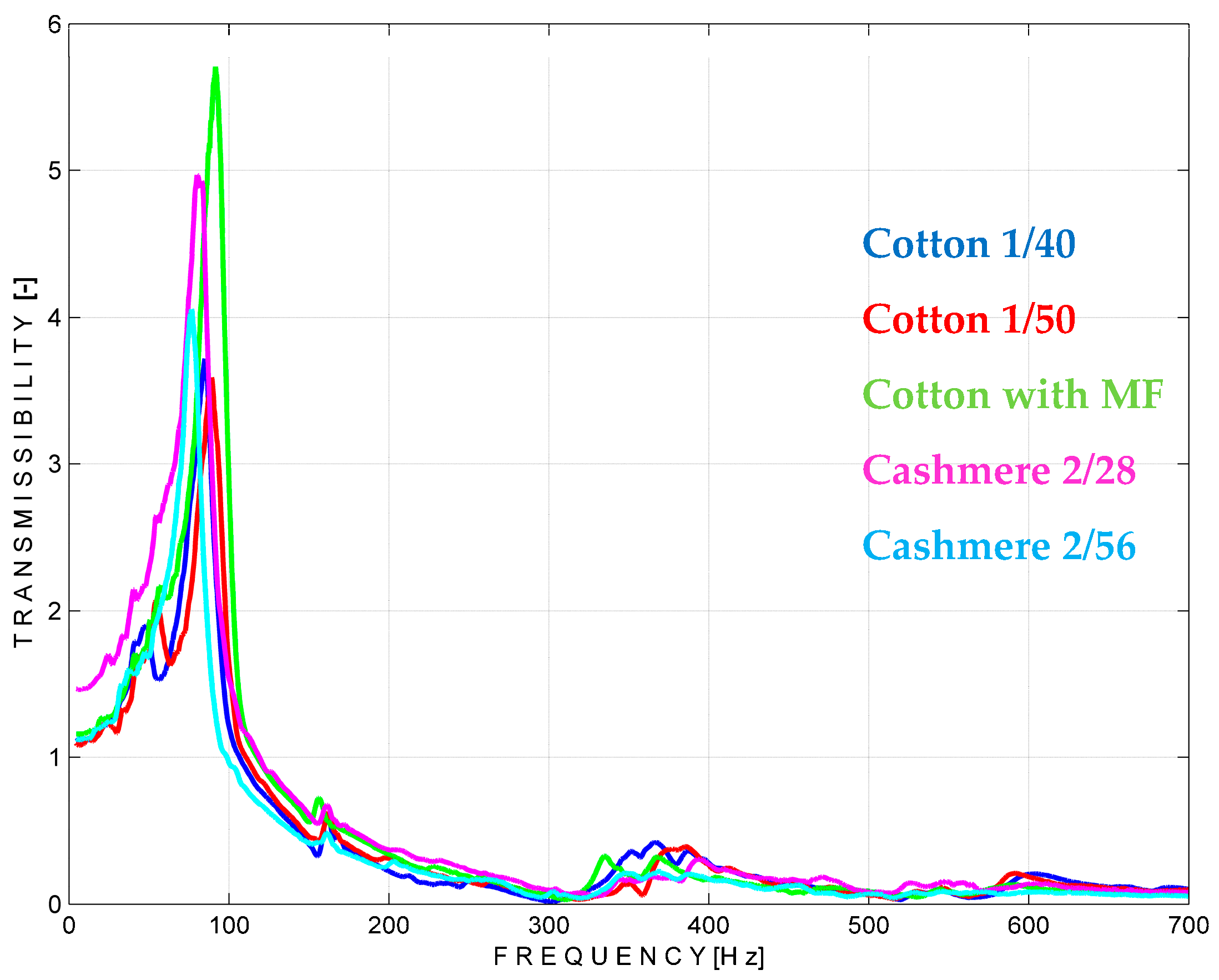
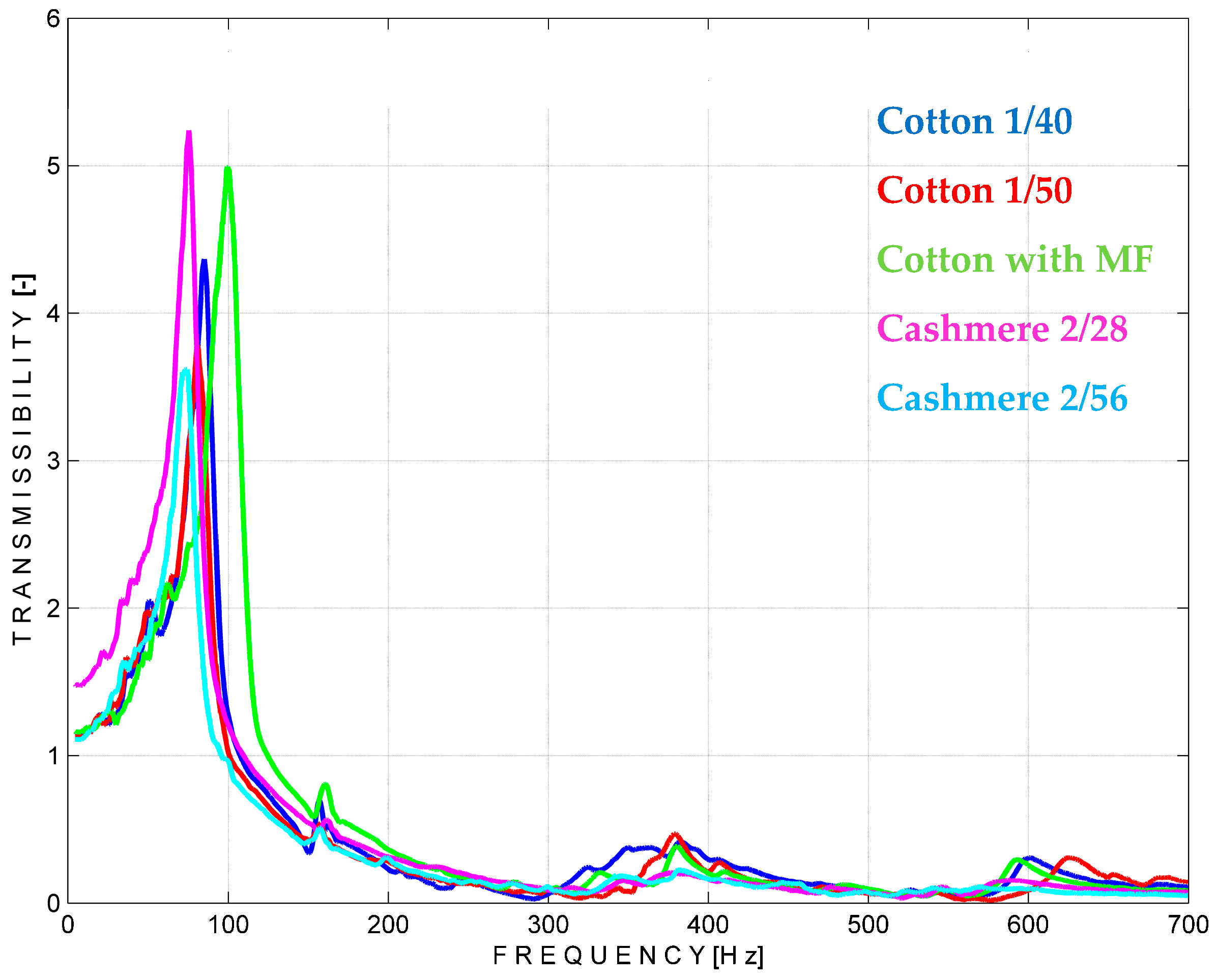
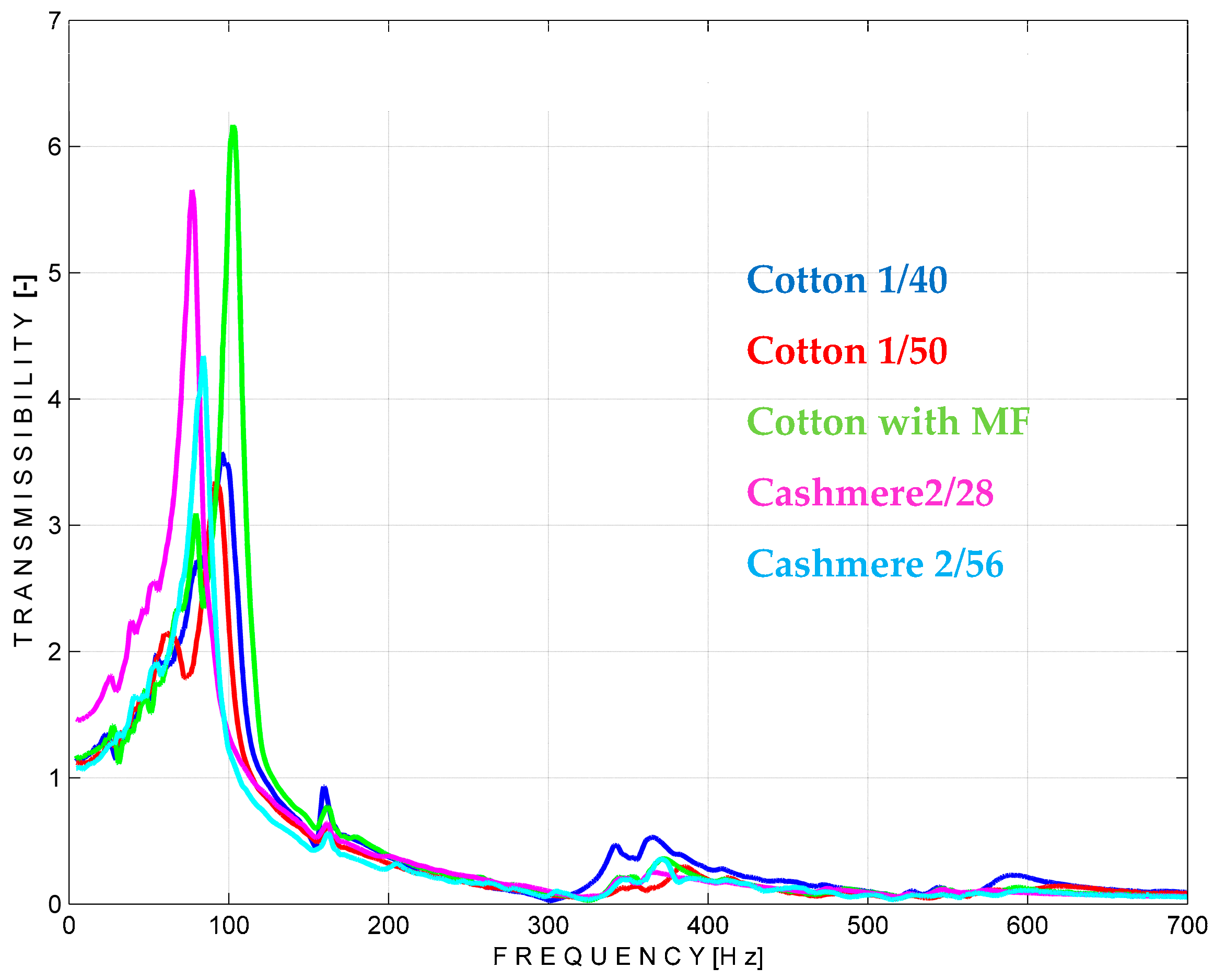
4.1.4. The Influence of the Yarn Type and Count on the Natural Frequencies
- -
- Firstly, it is the characteristics of each of these yarns, such as the count of the yarn and the twisting process, that make up the difference between cashmere and cotton, with the section of cashmere yarn being larger due to the twisting process, unlike cotton yarns where the two yarns are fed into the yarn feeder parallel to each other;
- -
- Secondly, the distribution of the connecting yarn in these programs plays a factor, which influences the distances between the two outer layers depending on the NP.
4.2. Knitted Fabric’s Vibration’s Transmissibility
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Raynaud, M. De l’Asphyxie Locale Et de la Gangrène Symétrique des Extrémités; Imprimeur de la Faculté de Médicine: Paris, France, 1862. [Google Scholar]
- Mansfield, J.N. Human Respons to Vibration; Taylor & Francis e-Library: New York, NY, USA; Washington, DC, USA, 2005. [Google Scholar]
- Almagirby, A. Understanding Vibration Transmitted to the Human Finger. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 2016. [Google Scholar]
- Canadian Center for Occupational Health and Safety. Vibration- Health Effects. Available online: https://www.ccohs.ca/oshanswers/phys_agents/vibration/vibration_effects.html (accessed on 30 November 2024).
- Health and Safety Executive. Construction Physical Ill Health Risks: Vibration. Available online: https://www.hse.gov.uk/construction/healthrisks/physical-ill-health-risks/vibration.htm (accessed on 14 January 2025).
- European Parliament and of the Council. Directive 2002/44/EC of the European Parliament and of the Council of 25 June 2002 on the Minimum Health and Safety Requirements Regarding the Exposure of Workers to the Risks Arising from Physical Agents (Vibration). Available online: https://eur-lex.europa.eu/ (accessed on 20 October 2024).
- Eurofound. Sixth European Working Conditions Survey—Overview Report (2017 Update); Publications Office of the European Union: Luxembourg. Available online: https://www.eurofound.europa.eu/en/publications/2016/sixth-european-working-conditions-survey-overview-report (accessed on 30 September 2024).
- Memmi, N.J.; Maâtoug, N.; Chemkhi, N.; Faouzi, S. Evaluation of psychological occupational health constraints according to the Karasek model among female sewing machine operators in Tunisia. Ind. Textila 2024, 75, 137–141. [Google Scholar] [CrossRef]
- Rades, M. Vibratii Mecanice; Printech: Bucharest, Romania, 2008. [Google Scholar]
- Evich, K.O.; Olegovna, S.M. Glove for Protection Hands from Vibration. Russia Patent No. RU244337, 3 February 2011. [Google Scholar]
- McDowell, T.W.; Dong, R.G.; Welcome, D.E.; Xu, X.S.; Warren, C. Vibration-reducing gloves: Transmissibility at the palm of the hand in three orthogonal directions. Ergonomics 2013, 56, 1823–1840. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, C. High Performance Textiles and Their Applications; Woodhead Publishing: Sawston, UK, 2014. [Google Scholar]
- Anti-Vibration Glove Reviews-Worth Every Penny. Chainsaw Journal. Available online: https://www.chainsawjournal.com/ (accessed on 30 November 2024).
- Sum, N.W. Development of Anti-Vibration Glove with Weft Knitted Spacer Fabric. Bachelor’s Thesis, The Hong Kong Polytechnic University, Hong Kong, China, 2013. [Google Scholar]
- Blaga, M.; Seghedin, N.E.; Ciobanu, A.R. Warp knitted fabrics behaviour under dynamic testing. Ind. Textila 2013, 64, 334–341. [Google Scholar]
- Blaga, M.; Seghedin, N. Knitted spacer fabrics behaviour at vibrations. J. Fash. Technol. Text. Eng. 2017, 3, 602–608. [Google Scholar] [CrossRef][Green Version]
- Chen, C.; Chen, J.; Sun, F.; Yang, H.; Du, Z. Analysis of the damping property of warp-knitted spacer fabrics under damped free vibration. Text. Res. J. 2018, 88, 790–799. [Google Scholar] [CrossRef]
- Annie, Y.; Sukigara, S.; Masuda, A. Investigation of Vibration Isolation Behaviour of Spacer Fabrics with Elastic Inlay. J. Text. Eng. 2020, 66, 65–69. [Google Scholar] [CrossRef]
- Frydrysiak, M.; Pawliczak, Z. Vibro-insulation properties for spacer knitted fabric as a comparative study. J. Ind. Text. 2021, 51, 806–820. [Google Scholar] [CrossRef]
- Frydrysiak, M.; Pawliczak, Z. Design and Testing of 3D Textile Materials with VibroInsulating Properties, Applicable in the Construction of Vibroisolating Seats for Machine and Device Operators. Fibres Text. East. Eur. 2024, 32, 57–68. [Google Scholar] [CrossRef]
- Tatsuno, J.; Maeda, S. Effect of Whole-Body Vibration Exposure in Vehicles on Static Standing Balance after Riding. Vibration 2023, 6, 343–358. [Google Scholar] [CrossRef]
- Wei, C. Vibration-Absorbing Mitten. China Patent No. CN206565350, 13 December 2016. [Google Scholar]
- Palicska, K.L.; Augusztinovicz, F.; Szemeredy, A.; Szucs, L. Development and test of new kinds of anti-vibration. In Proceedings of the World Textile AUTEX, Gent, Belgium, 11–15 June 2019. [Google Scholar]
- Blaga, M.; Harpa, R.; Seghedin, N.E.; Marmarali, A.; Ertekin, G. Evaluation of the knitted fabrics stiffness through dynamic testing. IOP Conf. Series. Mater. Sci. Eng. 2018, 459, 012033. [Google Scholar] [CrossRef]
- Chen, F.; Wang, J.; Gao, S.; Ning, X.; Yan, P.; Tian, M. An experimental study on the vibration behavior and the physical properties of weft-knitted spacer fabrics manufactured using flat knitting technology. Text. Res. J. 2023, 93, 615–631. [Google Scholar] [CrossRef]
- Yu, A.; Sukigara, S.; Masuda, A. Vibration Isolation Properties of Novel Spacer Fabric with Silicone Inlay. Polymers 2023, 15, 1089. [Google Scholar] [CrossRef] [PubMed]
- Taghvaie, M.; Payvandy, P.; Jalili, M.M. Introduction and Optimization of a Novel Nonlinear Model for the Free Vibration of Warp-knitted Spacer Fabrics. Fibers Polym 2020, 21, 1849–1856. [Google Scholar] [CrossRef]
- Chen, F.; Hu, H. Nonlinear vibration of knitted spacer fabric under harmonic excitation. J. Eng. Fibers Fabr. 2020, 15, 1558925020983561. [Google Scholar] [CrossRef]
- Hewitt, S.; Dong, R.; McDowell, T.; Welcome, D. The Efficacy of Anti-vibration Gloves. Acoust. Aust. 2016, 44, 121–127. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Gerhard, K.; Joel, B.; Romain, B. Vibration Protection Glove. France Patent No. WO2020094966, 5 November 2019. [Google Scholar]
- INCD. Alexandru Darabont. In Ghid de Securitate si Sanatate in Munca Privind Vibratiile Mecanice; INCDPM: Bucharest, Romania, 2013. [Google Scholar]
- Chen, F. A study of Vibration Behavior of Weft-Knitted Spacer Fabrics. Ph.D. Thesis, Hong Kong Polytechnic University, Hong Kong, China, 2015. [Google Scholar]
- Ok, K.J. Glove for Absorbing Vibration, Having Vibration Isolation Structure Contained Within. Korea Patent No. KR100487752, 28 May 2003. [Google Scholar]
- Liu, Y.; Hu, H. Vibration Isolation Performance of Warp-knitted Spacer Fabrics. In Fiber Society Spring Conference; Curran Associates, Inc.: Hong Kong, China, 2011; pp. 63–64. [Google Scholar]
- Liu, Y.; Hu, H. An Experimental Study of Compression Behavior of Warp-knitted Spacer Fabric. J. Eng. Fibers Fabr. 2014, 9, 61–69. Available online: http://www.jeffjournal.org (accessed on 31 August 2024).
- Liu, Y.; Hu, H. Vibration isolation behaviour of 3D polymeric knitted spacer fabrics under harmonic vibration testing conditions. Polym. Test. 2015, 47, 120–129. [Google Scholar] [CrossRef]
- Blaga, M.; Seghedin, N.E.; Grosu, C. Measuring the natural frequencies of knitted materials for protection. Ind. Textila 2022, 3, 89–95. [Google Scholar] [CrossRef]
- Emadi, M.; Payvandy, P.; Tavanaie, M.A.; Jalili, M.M. Measurement of vibration in polyester filament yarns to detect their apparent properties. J. Text. Inst. 2021, 113, 1270–1280. [Google Scholar] [CrossRef]
- Rahemtulla, Z.; Hughes-Riley, T.; Dias, T. Vibration-Sensing Electronic Yarns for the Monitoring of Hand Transmitted Vibrations. Sensors 2021, 21, 2780. [Google Scholar] [CrossRef]
- Wang, H.; Cao, H.; Yang, L. Machine Learning-Driven Multidomain Nanomaterial Design: From Bibliometric Analysis to Applications. ACS Appl. Nano Mater. 2024, 7, 26579–26600. [Google Scholar] [CrossRef]
- Yang, L.; Wang, H.; Leng, D.; Fang, S.; Yang, Y.; Du, Y. Machine learning applications in nanomaterials: Recent advances and future perspectives. Chem. Eng. J. 2024, 500, 156687. [Google Scholar] [CrossRef]
- TS 251; Woven Fabrics—Determination of Unit Length and Unit Area Mass. Turkish Standards Institution: Ankara, Turkey, 1991.
- TS 7128 EN ISO 5084; Textiles-Determination of Thickness of Textiles and Textile Products. Turkish Standards Institution: Ankara, Turkey, 1998.
- Yang, L.; Wang, H. High-performance electrically responsive artificial muscle materials for soft robot actuation. Acta Biomater. 2024, 185, 24–40. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Yang, L.; Yang, Y.; Zhang, D.; Tian, A. Highly flexible, large-deformation ionic polymer metal composites for artificial muscles: Fabrication, properties, applications, and prospects. Chem. Eng. J. 2023, 469, 143976. [Google Scholar] [CrossRef]
- Song, X.; Sassi, A.; Seaman, K.; Lin, C.-Y.; You, L. Vibration Therapy for Cancer-Related Bone Diseases. Vibration 2023, 6, 449–465. [Google Scholar] [CrossRef]



| Yarns | Yarn Count and Diameter | Number of Yarns per Feeder | Characteristics |
|---|---|---|---|
| Cotton | Nm 1/40 | 2 | High breathability; good moisture-wicking properties; very susceptible to pilling; very comfortable; hypoallergenic; odour-free; easy care. |
| Nm 1/50 | 2 | ||
| Cashmere | Nm 2/56 | 1 | High breathability; good moisture wicking; high tendency to pilling; soft feel on the skin; good protection against low temperatures. |
| Polyester | Ø 0.08 mm | 2 | Strong and elastic; can be blended with other fibres; high moisture-wicking capacity; high flame resistance; hydrophobic. |
| Knitted Patterns | Knitted Sections | Structure Description | Fabric Appearance |
|---|---|---|---|
| P1 |  | Two single jersey layers joined by a single row of connecting yarn working with all needles. |  |
| P2 | 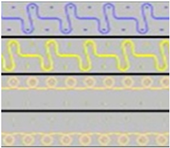 | Two single jersey layers joined by two rows of connecting yarns, 1:1 successively knitted. |  |
| P3 | 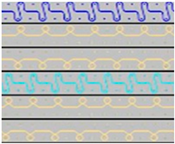 | Four single jersey rows, 1:1 successively knitted, connected by two rows of connecting yarns, 1:1 successively knitted. |  |
| P4 | 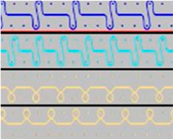 | Two 1:1 single jersey rows are joined by two rows of connecting yarns, 1:1 needles are working, respectively, and 1:2 needles are working. |  |
| P5 | 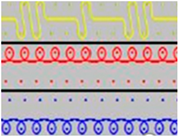 | Two single jersey layers are connected together by a single row of connecting yarns, working with 2:2 needles selection. |  |
| P6 | 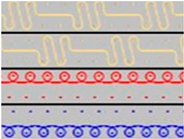 | Two single jersey layers are connected together by two rows of connecting yarns, working with 2:2 needles selection. |  |
| Parameters | Measuring Device |
|---|---|
| Mass per unit area | Scale |
| Thickness | SDL Atlas M 034A digital thickness gauge |
| Specific Vibration Parameters | Cashmere 2/56 | Cotton 1/40 | Cotton 1/50 |
|---|---|---|---|
| Damping constant c [N·s/m] | 73.7128 | 89.5588 | 97.4675 |
| Specific damping cs [N·s/m/cm2] | 0.6203 | 0.7537 | 0.8202 |
| Stiffness of the material k [N/m] | 139,601.5822 | 172,334.259 | 189,992.2025 |
| Specific stiffness ks [N/m/cm2] | 1174.8711 | 1450.3456 | 1598.9529 |
| Specific Vibration Parameters | Cashmere 2/56 | Cotton 1/40 | Cotton 1/50 |
|---|---|---|---|
| Damping constant c [N·s/m] | 79.856 | 76.1949 | 83.5349 |
| Specific damping cs [N·s/m/cm2] | 0.672 | 0.6412 | 0.703 |
| Stiffness of the material k [N/m] | 129,456.085 | 173,772.866 | 155,537.3860 |
| Specific stiffness ks [N/m/cm2] | 1089.4877 | 1462.4528 | 1308.9850 |
| Specific Vibration Parameters | Cashmere Nm 2/56 | Cotton Nm 1/40 | Cotton Nm 1/50 |
|---|---|---|---|
| Damping constant c [N·s/m] | 75.3829 | 104.8067 | 107.8516 |
| Specific damping cs [N·s/m/cm2] | 0.6344 | 0.882 | 0.9076 |
| Stiffness of the material k [N/m] | 168,054.3158 | 218,093.623 | 200,690.3161 |
| Specific stiffness ks [N/m/cm2] | 1414.3261 | 1835.4512 | 1688.9870 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blaga, M.; Seghedin, N.E.; Horodincă, M.; Grosu, C.; Gaaloul, H.; Babay, A.; Dhouib, S.; Azouz, B. Behaviour of Knitted Materials in a Vibrating Environment. Materials 2025, 18, 479. https://doi.org/10.3390/ma18030479
Blaga M, Seghedin NE, Horodincă M, Grosu C, Gaaloul H, Babay A, Dhouib S, Azouz B. Behaviour of Knitted Materials in a Vibrating Environment. Materials. 2025; 18(3):479. https://doi.org/10.3390/ma18030479
Chicago/Turabian StyleBlaga, Mirela, Neculai Eugen Seghedin, Mihăiță Horodincă, Cristina Grosu, Hassen Gaaloul, Amel Babay, Soufien Dhouib, and Bechir Azouz. 2025. "Behaviour of Knitted Materials in a Vibrating Environment" Materials 18, no. 3: 479. https://doi.org/10.3390/ma18030479
APA StyleBlaga, M., Seghedin, N. E., Horodincă, M., Grosu, C., Gaaloul, H., Babay, A., Dhouib, S., & Azouz, B. (2025). Behaviour of Knitted Materials in a Vibrating Environment. Materials, 18(3), 479. https://doi.org/10.3390/ma18030479







