On Numerical and Analytical Investigation of the Effectiveness of Strengthening of Steel Columns—Case Study
Abstract
1. Introduction
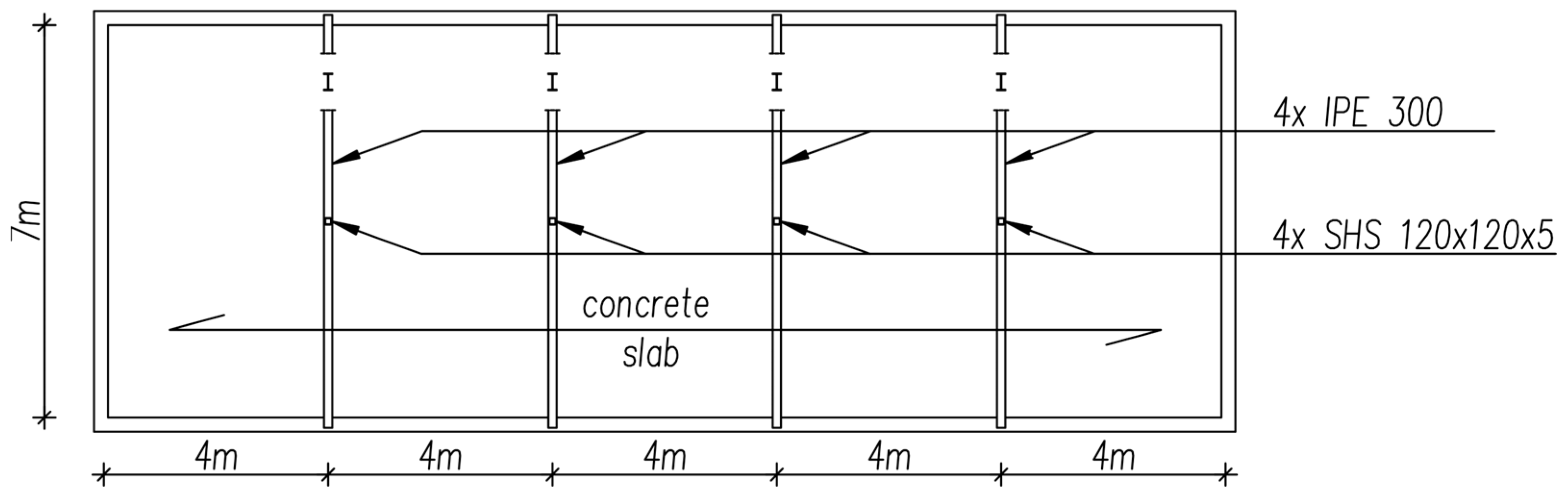
2. The Subject of the Analyses
2.1. The Column in Its Existing Condition
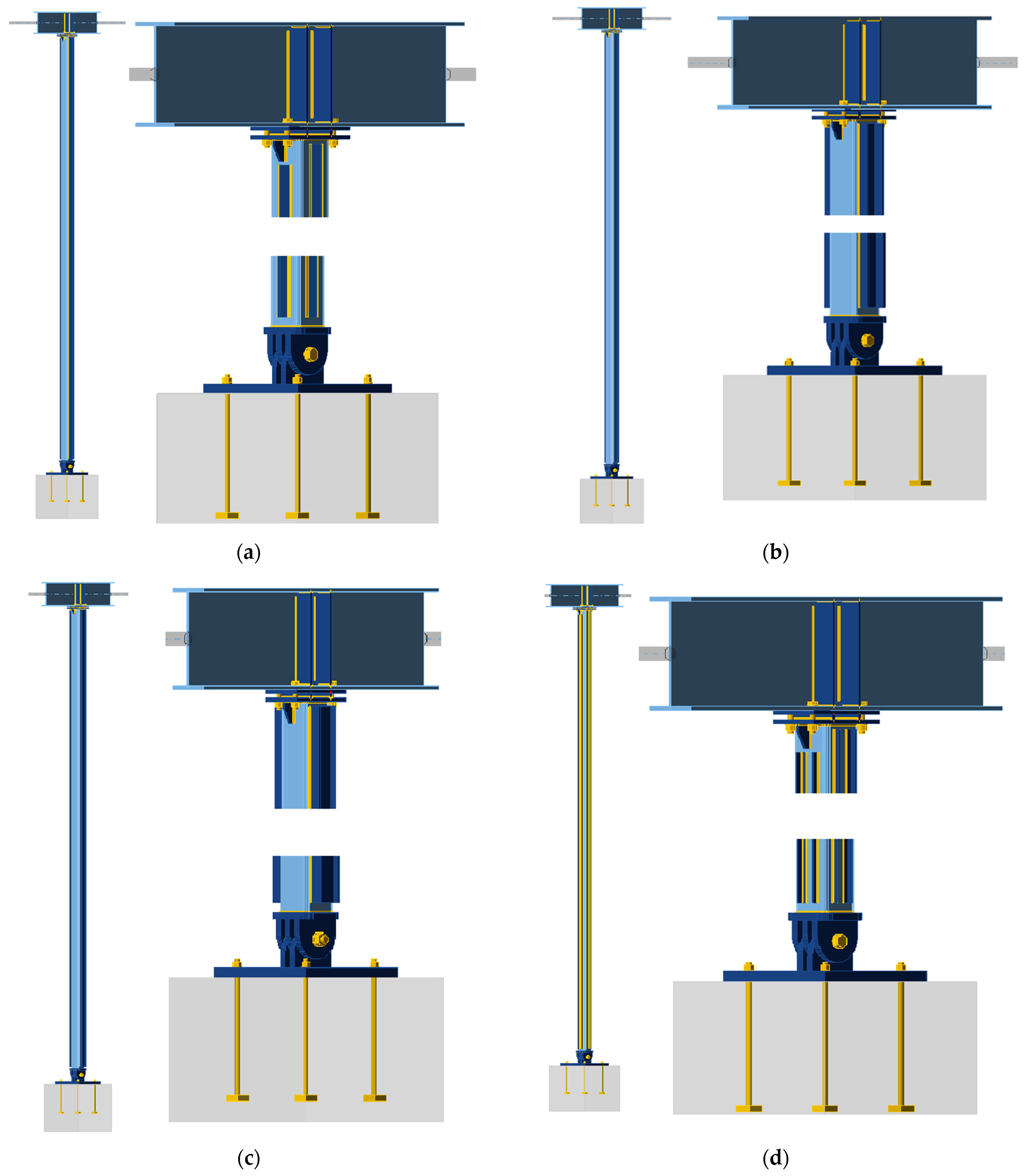
2.2. Reinforcement Options
- (A)
- four L-sections L 30 × 30 × 5;
- (B)
- two C-sections CE80;
- (C)
- two I-sections IPE80;
- (D)
- eight L-sections 20 × 20 × 3.
3. CBFEM Analysis
3.1. Main Assumptions of Analyses
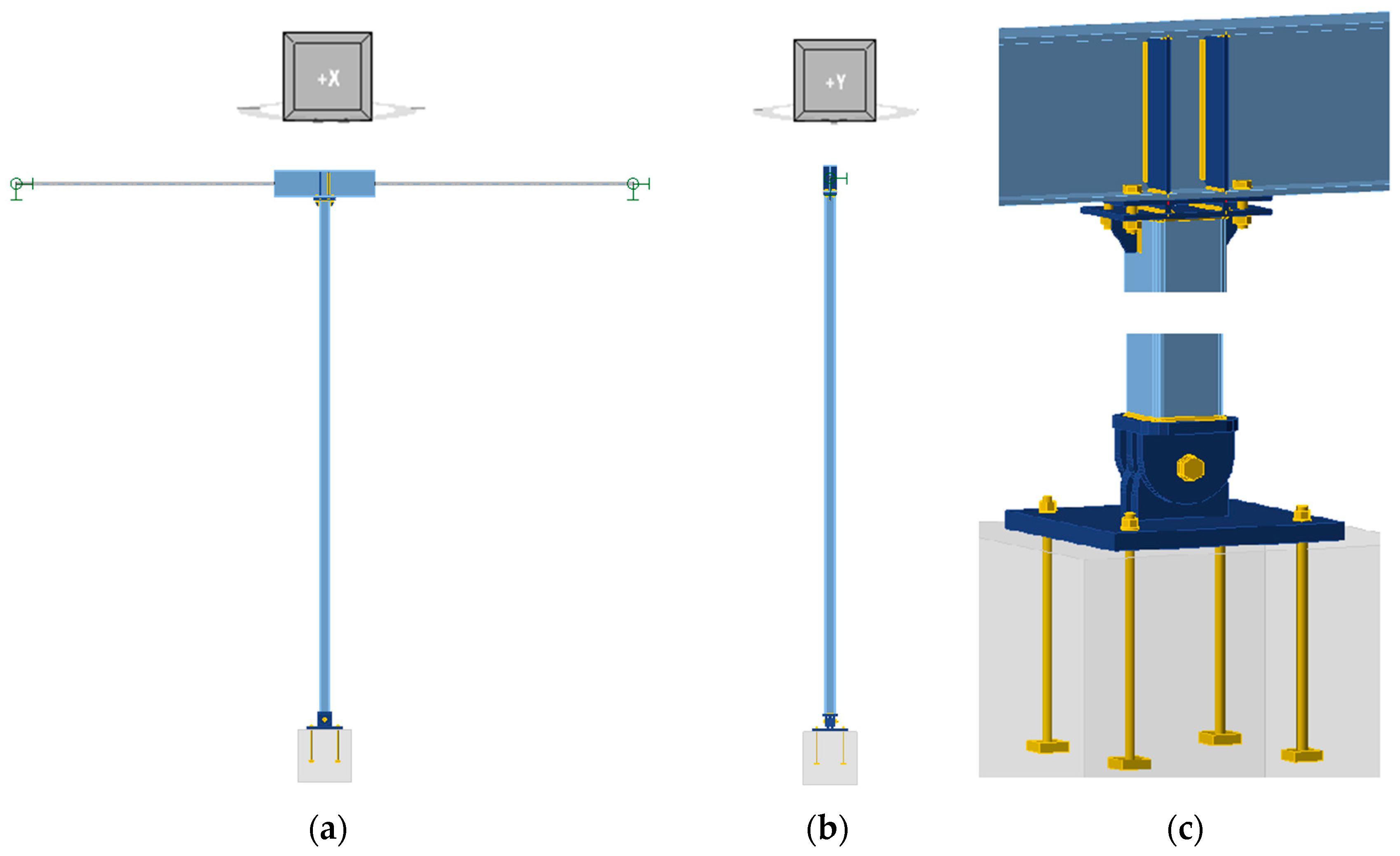
- preload, which is the case corresponding to the column at the time the strengthening was performed. The compressive force acting on the column during the reinforcement installation work, equal to 150 kN, was introduced as the load on the column in this variant. At this stage of the analysis, IdeaStatiCa Member neglects the effect of the stiffeners—an unreinforced column is analysed.
- target design load, i.e., the case corresponding to a reinforced column under the target design load (compression force of 250 kN). At this stage, the effect of the stiffening elements on the stiffness of the system and on the stress distribution is considered.
- nominal value of yield strength
- modulus of elasticity
- Poisson’s ratio
3.2. Calculation Models
3.2.1. Unreinforced Column Model
3.2.2. Reinforced Column Models
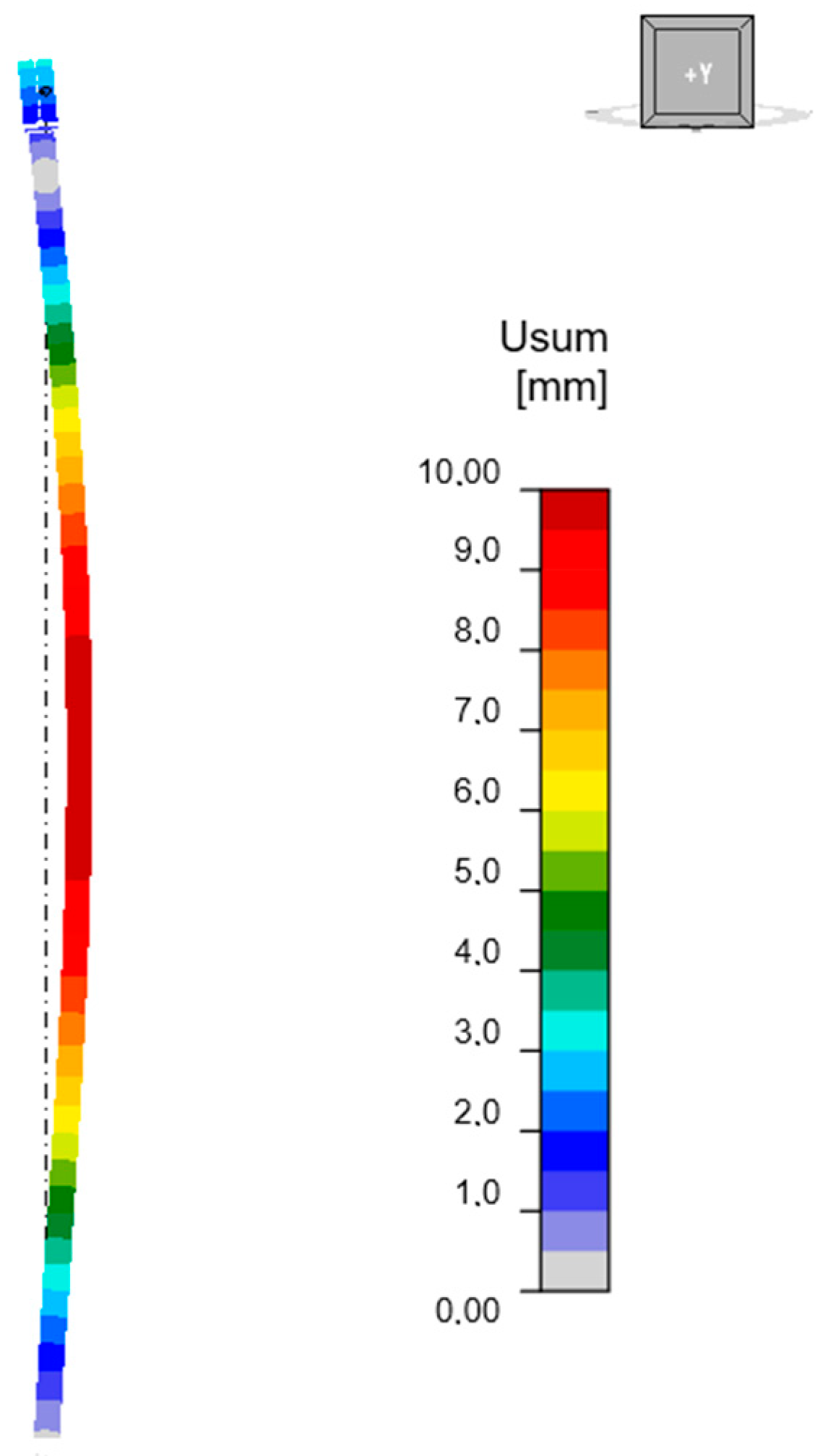
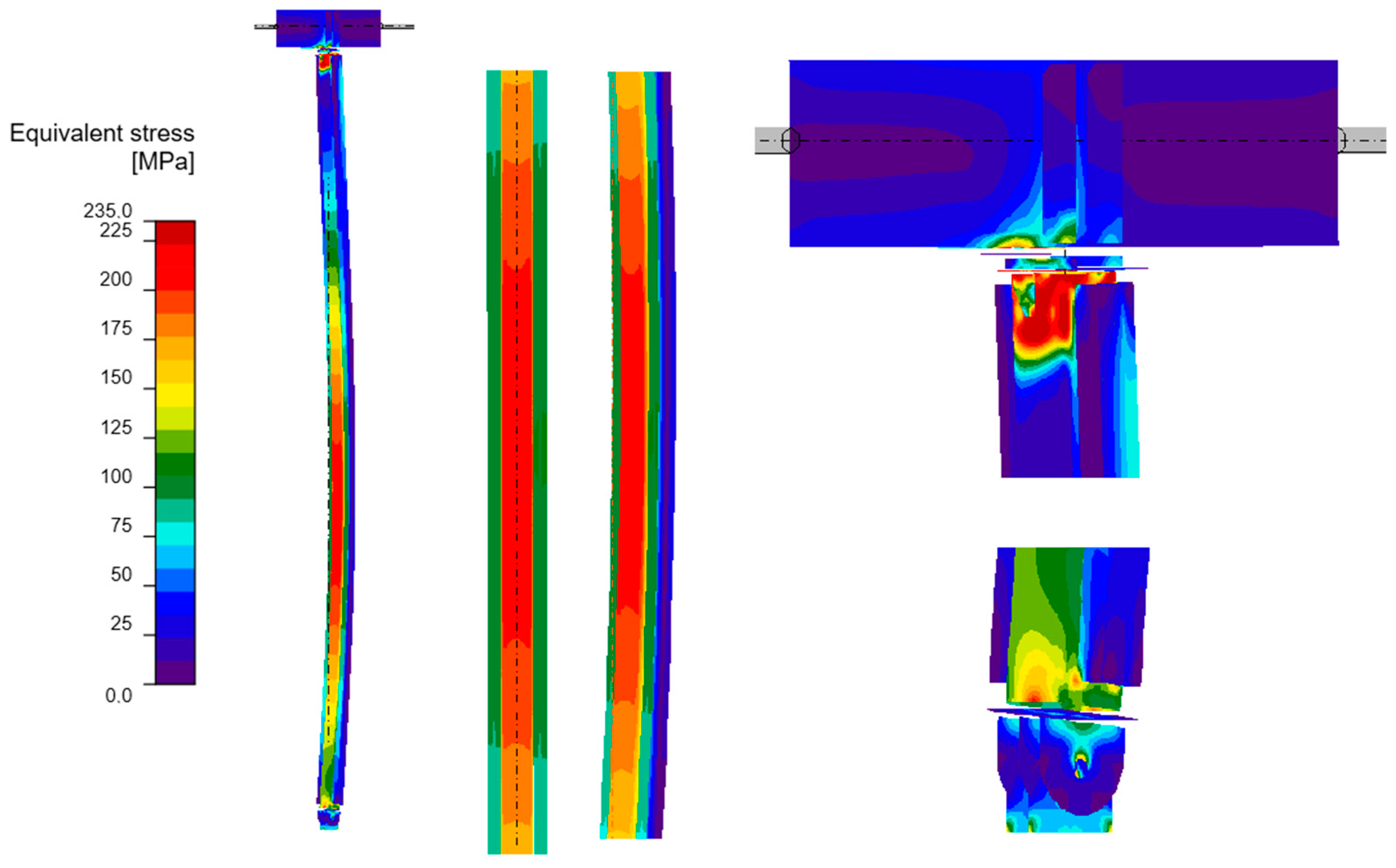
3.3. Results of Analysis for Unreinforced Column
3.3.1. LBA
3.3.2. GMNIA Analysis
3.4. Results of Analyses for Different Reinforcement Options
3.4.1. LBA
3.4.2. GMNIA Analysis
4. Analytical Approach
4.1. Resistance of an Unreinforced Axially Compressed Member
4.2. Resistance of the Reinforced Axially Compressed Member
- the buckling resistance of a reinforced compressed member under assumption that it buckles as one member:
- the buckling resistance of a reinforced compressed member when initial member and additional parts buckle independentlywhere and where are the buckling reduction factors for the primary member and added members, respectively. If due to strengthening of the member the boundary conditions are changed, new conditions should be included in computations.
4.3. Evaluation of Effectiveness of Selected Reinforcement Variants
5. Comparison of Results
6. Discussion
7. Conclusions
- It is asserted that all variants analysed will ensure the safe transfer of increased loads. With regard to load-bearing capacity, variant A is demonstrably superior when a comparison is made between the results obtained from both methods. Nonetheless, prior to determining a definitive solution, it is imperative to consider the expenses associated with workmanship and welding stresses, which have the potential to influence the load-bearing capacity of the element.
- The reinforcement efficiency of elements in compression is a complex function, depending on both the increase in cross-sectional area and the increase in moment of inertia. It is imperative that the reinforcement elements are positioned in as symmetrical manner as possible with respect to the centre of gravity of the cross-section, thereby facilitating optimised stress distribution.
- It is evident that both the analytical and geometrical imperfection methods possess a range of advantages and limitations. The geometrical imperfection method necessitates the acquisition of licensed software and the attainment of proficiency in its utilisation. However, it should be noted that this approach enables the finite stiffness of the nodes to be incorporated into the analysis in an automatic manner. Furthermore, it facilitates the identification of local stress concentrations, thereby providing a response of the structure to a given load that is proximate to the actual response. Conversely, the analytical method is characterised by its expeditiousness and accessibility, both in terms of implementation and interpretation. The tool is to be regarded as a highly effective instrument for preliminary comparative assessment. However, given the necessity of incorporating the rigidity of nodes and the intricacies of stress states, undertaking analytical method necessitates complex calculations. The assumption of the buckling length and plane is of crucial importance.
- It is not possible to provide a definitive answer to the question of which method (analytical or imperfection) exhibits a greater degree of conservatism. The result of the analysis is contingent on the designer’s assumptions and the modelling strategy adopted for the structure. The accuracy of the results obtained by means of the geometrical imperfection method is directly proportional to the precision of the joint modelling, the correctness of the implementation of geometric imperfections, and the density and quality of the finite element mesh. The cornerstone of the analytical method is the accurate evaluation of the boundary conditions and the precise determination of the buckling length and buckling plane of the element.
- It is recommended that a hybrid approach be employed in the case of structures exhibiting significant slenderness and complex static schemes, whereby both methods are applied simultaneously. The analytical method has been demonstrated to be a successful approach for the preliminary selection and comparison of the effectiveness of different structural solutions. Subsequently, the selected variants should be analysed in detail using the geometrical imperfection method. This will allow the ultimate load capacity to be estimated and the actual response of the structure to applied loads to be observed.
- The application of the analytical method in the analysis of reinforced structures is contingent upon the introduction of a new European standard. The new standard should be dedicated solely to the analysis of reinforced steel structures and should contain detailed guidelines and analytical formulae for various reinforcement scenarios.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zamorowski, J.; Gremza, G. Global analysis and element analysis of reinforced steel bar structures. In Repairs and Reinforcement of Building Structures. Metal Structures, Industrial Floors, Lightweight Housing, Scaffolding. Volume I: Provisions, Analyses and Evaluations of Reinforced Steel Constructions; Zamorowski, J., Ed.; Scientific Publishing House of the University of Bielsko-Biala: Bielsko Biała, Poland, 2025; pp. 341–382. (In Polish) [Google Scholar]
- Chen, J.; Zhou, L.; Liu, Y.; Wang, Y. A Safety Risk Analysis of a Steel-Structure Building Using an Improved Controlled Interval and Memory Model. Buildings 2024, 14, 1553. [Google Scholar] [CrossRef]
- Khan, K.; Chen, Z.; Liu, J.; Javed, K. State-of-the-Art on Technological Developments and Adaptability of Prefabricated Industrial Steel Buildings. Appl. Sci. 2023, 13, 685. [Google Scholar] [CrossRef]
- Gajdzik, B.; Wolniak, R.; Sączewska-Piotrowska, A.; Grebski, W.W. Polish Steel Production Under Conditions of Decarbonization-Steel Volume Forecasts Using Time Series and Multiple Linear Regression. Energies 2025, 18, 1627. [Google Scholar] [CrossRef]
- Recommendations for Reuse of Steel Products—Volume 1: Reusing Existing Steel Products and Buildings, 2nd ed.; ECCS—European Committee for Constructional: Brussels, Belgium, 2025.
- Masłowski, E.; Spiżewska, D. Wzmacnianie Konstrukcji Budowlanych, 3rd ed.; Arkady: Warsaw, Poland, 2000; pp. 177–224. [Google Scholar]
- Zeng, C.; Cai, T.; Chen, Z.; Chen, Z.; Su, N. Enhancing the wind-resistant capacity of transmission towers with buckling-restrained angle-steel-members (BRR-ASMs). J. Constr. Steel Res. 2025, 228, 109434. [Google Scholar] [CrossRef]
- Szafran, J.; Juszczyk-Andraszyk, K.; Kaszubska, P. Effectiveness Analysis of the Non-Standard Reinforcement of Lattice Tower Legs Using the Component-Based Finite Element Method. Materials 2025, 18, 1242. [Google Scholar] [CrossRef]
- Szafran, J.; Juszczyk-Andraszyk, K.; Kaszubska, P. Analysis of the lattice tower bracings reinforcement by their extension to closely spaced built-up members. Build. Mater. 2025, 630, 9–16. [Google Scholar] [CrossRef]
- Gocál, J.; Odrobiňák, J. On the Influence of Corrosion on the Load-Carrying Capacity of Old Riveted Bridges. Materials 2020, 13, 717. [Google Scholar] [CrossRef] [PubMed]
- Tall, L. The Reinforcement of Steel Columns. Eng. J. 1989, 26, 33–37. [Google Scholar] [CrossRef]
- Wang, S.; Su, Q.; Jiang, X.; Ghafoori, E. Stability of steel columns with bolted strengthening under preload: Experimental study. J. Constr. Steel Res. 2022, 190, 107119. [Google Scholar] [CrossRef]
- Harries, K.A.; Peck, A.J.; Abraham, E.J. Enhancing stability of structural steel sections using FRP. Thin-Walled Struct. 2009, 47, 1092–1101. [Google Scholar] [CrossRef]
- Kowal, M.; Pietras, D. Carbon Fibre Reinforced Polymer Fatigue Strengthening of Old Steel Material. Adv. Sci. Technil. Res. J. 2023, 17, 197–209. [Google Scholar] [CrossRef]
- Delzendeh Moghadam, M.; Fathi, A.; Chaallal, O. Retrofitting of Steel Structures with CFRP: Literature Review and Research Needs. Appl. Sci. 2024, 14, 5958. [Google Scholar] [CrossRef]
- Yang, Z.; Xu, C. Research on Compression Behavior of Square Thin-Walled CFST Columns with Steel-Bar Stiffeners. Appl. Sci. 2018, 8, 1602. [Google Scholar] [CrossRef]
- Cavalheiro, F.N.; Cabaleiro, M.; Conde, B.; Cruz, Y. Elastic Structural Assessment of Clamp-Based Steel Beam-to-Column Connections for Reusable Steel Systems. Appl. Sci. 2025, 15, 5398. [Google Scholar] [CrossRef]
- Yun, X.; Gardner, L.; Boissonnade, N. Ultimate capacity of I-sections under combined loading—Part 1: Experiments and FE model validation. J. Constr. Steel Res. 2018, 147, 408–421. [Google Scholar] [CrossRef]
- Kucukler, M.; Gardner, L.; Macorin, L. Flexural-torsional buckling assessment of steel beam-columns through a stiffness reduction method. Eng. Struct. 2015, 101, 662–676. [Google Scholar] [CrossRef][Green Version]
- Ju, H.; Jiang, W.; Hu, X.; Zhang, K.; Guo, Y.; Yang, J.; Hao, K. A Study on the Seismic Performance of Steel H-Column and T-Beam-Bolted Joints. Appl. Sci. 2025, 15, 4643. [Google Scholar] [CrossRef]
- Nawar, M.T.; El-Zohairy, A.; Arafa, I.T. Finite Element Modeling and Analysis of Perforated Steel Members under Blast Loading. Modelling 2023, 4, 628–649. [Google Scholar] [CrossRef]
- Prokop, J.; Vičan, J.; Jošt, J. Numerical Analysis of the Beam-Column Resistance Compared to Methods by European Standards. Appl. Sci. 2021, 11, 3269. [Google Scholar] [CrossRef]
- Chen, X.; Xia, J.; Xu, B.; Ma, R. Mechanical Performance of Built-Up Columns Composed of Four Cold-Formed Square Steel Tubes. Appl. Sci. 2019, 9, 1204. [Google Scholar] [CrossRef]
- Slack, H.; Walport, F.; Chan, H.U.; Wadee, A.; Gardner, L. A consistent approach to the definition of initial geometric imperfections for in-plane stability design of steel moment frames. Structures 2024, 65, 106596. [Google Scholar] [CrossRef]
- Quan, C.; Walport, F.; Gardner, L.; Quan, C.; Walport, F.; Gardner, L. Equivalent geometric imperfections for the design of steel and stainless steel beam-columns by GMNIA. J. Constr. Steel Res. 2024, 215, 108502. [Google Scholar] [CrossRef]
- EN 1993-1-1:2005; Eurocode 3: Design of Steel Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2005.
- EN 1999-1-1, 2007 + A1 + A2; Eurocode 9, Design of Aluminium Structures, Part 1-1, General Structural Rules. European Committee for Standardization: Brussels, Belgium, 2009.
- AISI-S100-12; North American Specification for the Design of Cold-Formed Steel Structural Members. American Iron and Steel Institute: Washington, DC, USA, 2012.
- Wald, F.; Sabatka, L.; Bajer, M.; Kožich, M.; Vild, M.; Golubiatnikov, K.; Kabeláč, J.; Kuříková, M. Component-Based Finite Element Design of Steel Connections, 9th ed.; Czech Technical University: Prague, Czech Republic, 2021. [Google Scholar]
- Denavit, M.D.; Nassiri, A.; Vild, M.; Wald, F.; Sezen, H. Steel Connection Design by Inelastic Analysis, 1st ed.; John Wiley & Sons, Incorporated: Newark, NJ, USA, 2024. [Google Scholar]
- IDEA StatiCa. IDEA StatiCa Member-Member Stability Theoretical Background. Available online: https://www.ideastatica.com/support-center/idea-statica-member-theoretical-background (accessed on 10 November 2025).
- Dvorkin, E.N.; Bathe, J.-K. A continuum mechanics based four-node shell element for general non-linear analysis. Eng. Comput. 1984, 1, 77–88. [Google Scholar] [CrossRef]
- Mindlin, R.D. Influence of Rotary Inertia and Shear on Flexural Motions of Isotropic, Elastic Plates. J. Appl. Mech. 1951, 18, 31–38. [Google Scholar] [CrossRef]
- Ibrahimbegovic, A.; Taylor, R.L.; Wilson, E.L. A robust quadrilateral membrane finite element with drilling degrees of freedom. Int. J. Numer. Methods Eng. 1990, 30, 445–457. [Google Scholar] [CrossRef]
- EN 1993-1-5:2006; Eurocode 3: Design of Steel Structures-Part 1-5: General Rules-Plated Structural Elements. European Committee for Standardization: Brussels, Belgium, 2006.
- Bródka, J.; Broniewicz, M. Design of Steel Structures According to Eurocode 3-1-1 with Calculation Examples; Wydawnictwa Politechniki Białostockiej: Białystok, Poland, 2001; pp. 415–488. [Google Scholar]
- Rykaluk, K. Zagadnienia Stabilczności Konstrukcji Metalowych, 1st ed.; Dolnośląskie Wydawnictwo Edukacyjne: Wrocław, Poland, 2012. [Google Scholar]
- Timoshenko, S. Strength of Materials. Part I: Elementary Theory and Problems, 2nd ed.; Lancaster Press: New York, NY, USA, 1940. [Google Scholar]
- Kulak, G.L.; Grondin, G.Y. Limit States Design in Structural Steel, 9th ed.; Canadian Institute of Steel Construction: Markham, ON, Canada, 2011. [Google Scholar]
- Lam, D.; Ang, T.-C.; Chiew, S.-P. Structural Steelwork. Design to Limit State Theory, 4th ed.; Elsevier: Oxford, UK, 2014. [Google Scholar]




| Force | Notation | Value |
|---|---|---|
| Initial axial force | 150 kN | |
| Additional axial force after reinforcement | 100 kN |
| Parameters of the Cross-Section | ||||
|---|---|---|---|---|
| No. | Geometry | A [cm2] | I(z) [cm4] | I(y) [cm4] |
| 0 |  | 22.70 | 498.00 | 498.00 |
| A |  | 33.81 | 784.47 | 784.47 |
| B |  | 40.66 | 676.80 | 1483.31 |
| C | 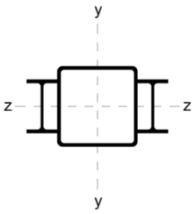 | 37.99 | 658.28 | 1568.09 |
| D | 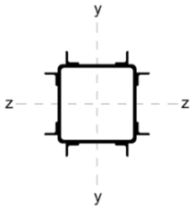 | 31.68 | 774.16 | 774.16 |
| Model A | Model B | Model C | Model D | |
|---|---|---|---|---|
| Form of buckling |  |  |  |  |
| Direction of buckling | Buckling in the X direction of the model’s global coordinate system | Buckling in the Y direction of the model’s global coordinate system | Buckling in the Y direction of the model’s global coordinate system | Buckling in the X direction of the model’s global coordinate system |
| Model | [-] | [kN] |
|---|---|---|
| A | 2.42 | 605.0 |
| B | 2.60 | 650.0 |
| C | 2.55 | 637.5 |
| D | 2.27 | 567.5 |
| Model | Maximum Stresses [MPa] |
|---|---|
| A | 227.7 |
| B | 236.7 |
| C | 236.9 |
| D | 235.0 |
| Parameter | Notation | Value |
|---|---|---|
| A | cross-sectional area | 22.70 cm2 |
| fy | yield strength of steel | 235 MPa |
| γM1 | safety factor | 1.0 |
| χ | reduction factor | |
| ϕ | parameter | |
| α | imperfection factor of the buckling curve a | 0.21 |
| relative slenderness | ||
| Euler buckling critical force | ||
| buckling length coefficient | 1.0 | |
| modulus of elasticity | 210 GPa | |
| I | moment of inertia of a cross-section | 498 cm4 |
| L | length of the analysed element | 6.0 m |
| Cross-Section | [kN] | [-] | α [-] | [-] | [-] | [kN] | [-] |
|---|---|---|---|---|---|---|---|
| SHS 120×120×5 | 286.71 | 1.364 | 0.21 | 1.553 | 0.436 | 232.55 | 1.075 |
| Parameter | Notation | Value |
|---|---|---|
| A | cross-sectional area | individual for each reinforcement method (Table 2) |
| fy | yield strength of steel | 235 MPa |
| γM1 | safety factor | 1.0 |
| χ | reduction factor | |
| ϕ | parameter | |
| α | imperfection factor of the buckling curve c | 0.49 |
| relative slenderness | ||
| Euler buckling critical force | ||
| buckling length coefficient | 1.0 | |
| modulus of elasticity | 210 GPa | |
| I | moment of inertia of a cross-section | individual for each reinforcement method (Table 2) |
| L | length of the analysed element | 6.0 m |
| Reinforcement | Axis | [kN] | [-] | [-] | * [-] | [kN] |
|---|---|---|---|---|---|---|
| A | y | 451.64 | 1.326 | 1.656 | 0.378 | 300.24 |
| z | 451.64 | 1.326 | 1.656 | 0.378 | ||
| B | y | 853.98 | 1.058 | 1.270 | 0.507 | 281.00 |
| z | 389.65 | 1.566 | 2.061 | 0.294 | ||
| C | y | 902.79 | 0.994 | 1.189 | 0.543 | 270.96 |
| z | 378.99 | 1.535 | 2.005 | 0.305 | ||
| D | y | 445.71 | 1.293 | 1.603 | 0.329 | 291.88 |
| z | 445.71 | 1.293 | 1.603 | 0.329 |
| Reinforcement Variant | Cross-Sectional Area Increment [%] | Moment of Inertia Increment [%] | Bearing Capacity Condition (Equation (3)) [-] | Bearing Capacity Increment [%] |
|---|---|---|---|---|
| A | 48.94 | 57.52 | 0.927 | 29.11 |
| B | 79.12 | 35.90 | 0.964 | 20.83 |
| C | 67.36 | 32.18 | 0.984 | 16.52 |
| D | 39.56 | 55.45 | 0.944 | 25.51 |
| Model | Moment of Inertia Corresponding to the Decisive Form of Buckling | Critical Force from Numerical Analyses Numerical Analysis Ncr,FEM | Euler Elastic Critical Force from Analytical Calculations Ncr,Euler | Ncr,FEM/Ncr,Euler |
|---|---|---|---|---|
| [cm4] | [kN] | [kN] | [-] | |
| 0 | 498.00 | 425.0 | 286.71 | 1.48 |
| A | 784.47 | 605.0 | 451.64 | 1.34 |
| B | 676.80 | 650.0 | 389.65 | 1.67 |
| C | 658.28 | 637.5 | 378.99 | 1.68 |
| D | 774.16 | 567.5 | 445.71 | 1.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szafran, J.; Świątkiewicz, P.; Kaszubska, P. On Numerical and Analytical Investigation of the Effectiveness of Strengthening of Steel Columns—Case Study. Materials 2025, 18, 5667. https://doi.org/10.3390/ma18245667
Szafran J, Świątkiewicz P, Kaszubska P. On Numerical and Analytical Investigation of the Effectiveness of Strengthening of Steel Columns—Case Study. Materials. 2025; 18(24):5667. https://doi.org/10.3390/ma18245667
Chicago/Turabian StyleSzafran, Jacek, Paulina Świątkiewicz, and Paulina Kaszubska. 2025. "On Numerical and Analytical Investigation of the Effectiveness of Strengthening of Steel Columns—Case Study" Materials 18, no. 24: 5667. https://doi.org/10.3390/ma18245667
APA StyleSzafran, J., Świątkiewicz, P., & Kaszubska, P. (2025). On Numerical and Analytical Investigation of the Effectiveness of Strengthening of Steel Columns—Case Study. Materials, 18(24), 5667. https://doi.org/10.3390/ma18245667







