The Modern Numerical and Experimental Methods for the Sound Absorbing Characteristics of Dissipative Sound Absorbing Materials: A Review
Abstract
1. Introduction
- To systematically catalog and critically evaluate the full spectrum of modern methods for characterizing SAC, encompassing in situ and laboratory experimental techniques, empirical, theoretical, and computational numerical models, and the emerging paradigm of machine learning.
- To elucidate the interconnections, advantages, and limitations of each method, thereby constructing a coherent methodological framework.
- To provide a comparative analysis that guides method selection based on accuracy, complexity, cost, and application context.
2. Experimental Methods for SAC
2.1. In Situ Measurement Methods
2.1.1. Pulse Reflection Method
2.1.2. Two-Microphone Method
2.1.3. p-u Probe Method
2.1.4. Spatial Fourier Transform Method
2.2. Laboratory Measurement Methods
2.2.1. Impedance Tube Method
Standing Wave Ratio Method
Transfer Function Method
The p-u Probe Method in an Impedance Tube
2.2.2. Reverberation Room Method
2.3. Other Measurement Methods
3. Numerical Calculation Methods for SAC
3.1. Empirical Models
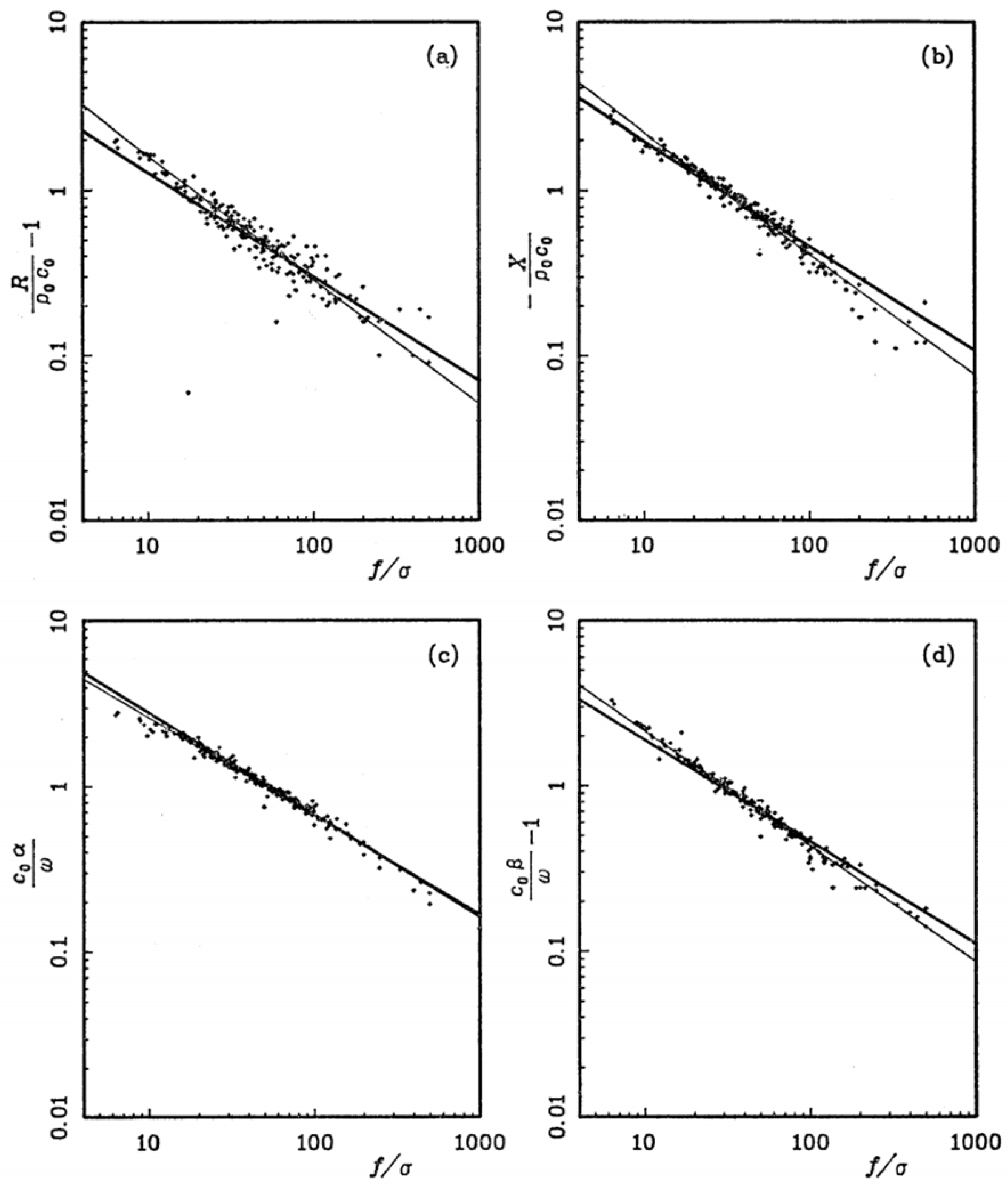
3.1.1. Delany and Bazley Empirical Model
3.1.2. Miki Empirical Model
3.1.3. Komatsu Empirical Model
3.2. Theoretical Model
3.2.1. Johnson-Champoux-Allard Theoretical Model
3.2.2. Extension of the Johnson-Champoux-Allard Model
3.3. Numerical Simulation Methods
3.3.1. Representative Unit Cell Estimation
3.3.2. Computational Fluid Dynamics Simulation Calculation
3.4. Methods for Calculating Flow Resistivity
3.4.1. Empirical Models for Calculating Flow Resistivity
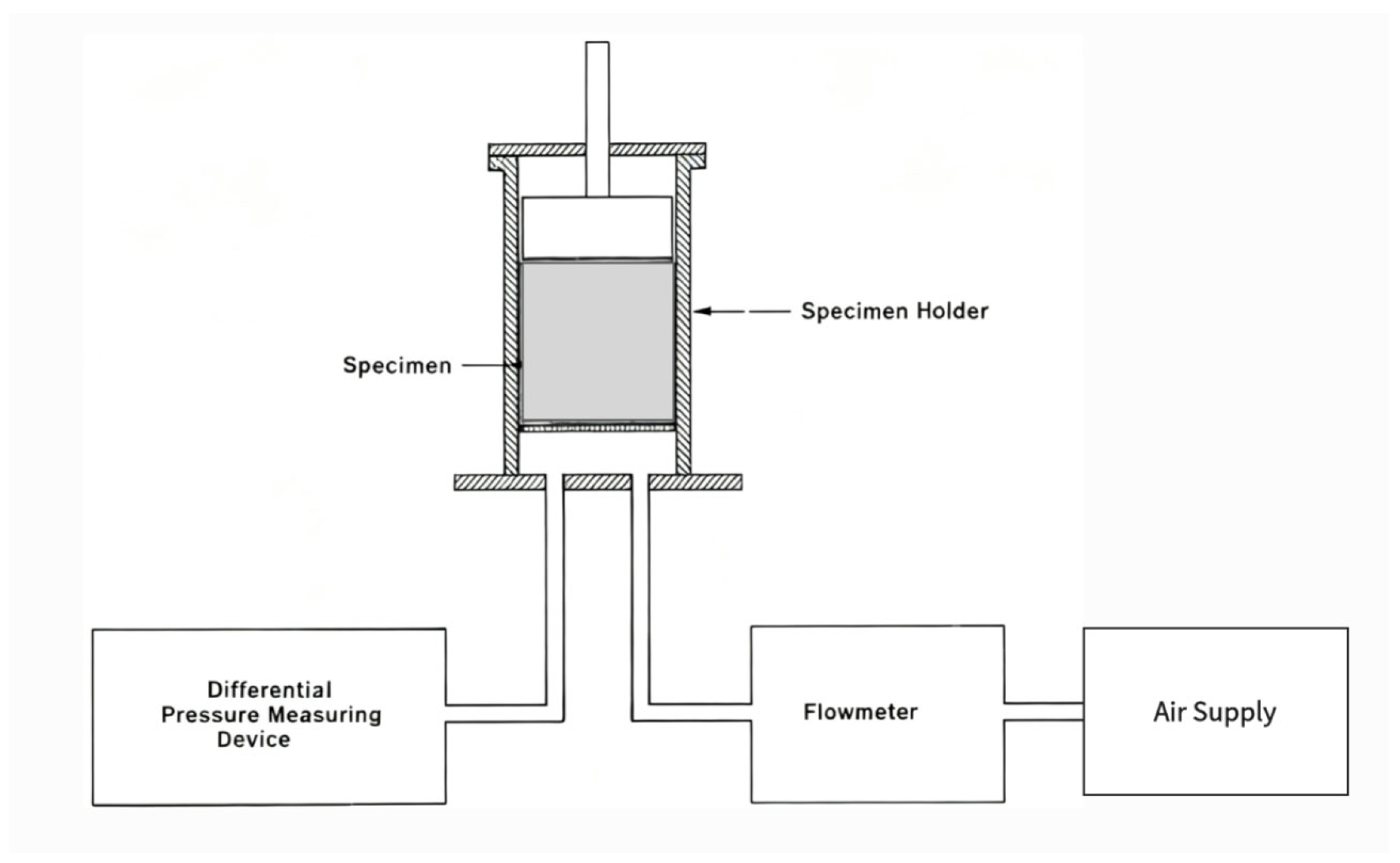
3.4.2. Experiment Method
4. Machine Learning Methods for SAC
4.1. Generalized Neural Regression Network
4.2. Radial Basis Function Neural Network
4.3. Artificial Neural Network
4.4. Multiple Regression
5. Comparative Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SAC | Sound Absorption Coefficient |
| DB | Delany-Bazley |
| JCA | Johnson-Champoux-Allard |
| JCAL | Johnson-Champoux-Allard-Lafarge |
| GRNN | Generalized Regression Neural Network |
| RBFNN | Radial Basis Function Neural Network |
| ANN | Artificial Neural Network |
| ML | Machine Learning |
| RUC | Representative Unit Cell |
| CFD | Computational Fluid Dynamics |
| μCT | Micro-Computed Tomography |
| CT | Computed Tomography |
| TMM | Transfer Matrix Method |
| IDNN | Integrated Deep Neural Network |
| CNN | Convolutional Neural Network |
| PAM | Parallel Acoustic Material |
| ASTM | American Society for Testing and Materials |
| ISO | International Organization for Standardization |
References
- Karami, F.; Shokri Rad, M.; Karimipour, I. Review on attenuation methods of low-frequency noise in passive silencers. J. Low Freq. Noise Vib. Act. Control. 2024, 43, 1679–1695. [Google Scholar] [CrossRef]
- Yu, X.; Cheng, L.; You, X. Hybrid silencers with micro-perforated panels and internal partitions. J. Acoust. Soc. Am. 2015, 137, 951–962. [Google Scholar] [CrossRef] [PubMed]
- Wentzel, R.; VanBuskirk, J. A Dissipative Approach to Vehicle Sound Abatement; SAE Technical Paper 1999-01-1668; SAE International: Warrendale, PA, USA, 1999. [Google Scholar] [CrossRef]
- Sharma, S.S.; Yadav, S.; Joshi, A.; Goyal, A.; Khatri, R. Application of metallic foam in vehicle structure: A review. Mater. Today Proc. 2022, 63, 347–353. [Google Scholar] [CrossRef]
- Otaru, A.J.; Odumu, O.E.; Manko, Z.; Isah, A.G.; Isa, R.O.; Corfield, M.R. The impact of microcellular structures on the sound absorption spectra for automotive exhaust performance mufflers. Appl. Acoust. 2022, 187, 108508. [Google Scholar] [CrossRef]
- Krasnov, A. Contribution of side surfaces to the effectiveness of automotive sound-absorbing materials. Transp. Res. Procedia 2023, 68, 511–515. [Google Scholar] [CrossRef]
- Yuvaraj, L.; Prashanth, K.P.; Venkatesha, B.K.; Sanman, S.; Venkatesh, N. Investigation of light weight closed cell metallic foam for noise reduction in automobile application. Mater. Today Proc. 2022, 54, 359–365. [Google Scholar] [CrossRef]
- Wang, Z.T.; Zhang, R. Performance of foam aluminum and its production technology. Light Alloy Fabr. Technol. 2011, 39, 10–22. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, R. Intrinsic mechanism, preparation and application of noise reduction polymer-based composites for aviation noise: A mini-review. Compos. Part A Appl. Sci. Manuf. 2025, 199, 109246. [Google Scholar] [CrossRef]
- Badri, Y.; Dodd, G.; Cater, J.; Hall, A.; Schmid, G.; Emms, G.; Calius, E. Review of granular material damping and sound absorption for possible application in the sound insulation of lightweight floors. J. Build. Eng. 2024, 97, 110881. [Google Scholar] [CrossRef]
- Mehrzad, S.; Taban, E.; Soltani, P.; Samaei, S.E.; Khavanin, A. Sugarcane bagasse waste fibers as novel thermal insulation and sound-absorbing materials for application in sustainable buildings. Build. Environ. 2022, 211, 108753. [Google Scholar] [CrossRef]
- García-Moreno, F. Commercial Applications of Metal Foams: Their Properties and Production. Materials 2016, 9, 85. [Google Scholar] [CrossRef] [PubMed]
- Delany, M.E.; Bazley, E.N. Acoustical properties of fibrous absorbent materials. Appl. Acoust. 1970, 3, 105–116. [Google Scholar] [CrossRef]
- Miki, Y. Acoustical properties of porous materials—Generalizations of empirical models. J. Acoust. Soc. Jpn. (E) 1990, 11, 25–28. [Google Scholar] [CrossRef]
- Miki, Y. Acoustical properties of porous materials—Modifications of Delany-Bazley models. J. Acoust. Soc. Jpn. (E) 1990, 11, 19–24. [Google Scholar] [CrossRef]
- Komatsu, T. Improvement of the Delany–Bazley and Miki models for fibrous sound-absorbing materials. Acoust. Sci. Technol. 2008, 29, 121–129. [Google Scholar] [CrossRef]
- Champoux, Y.; Allard, J.F. Dynamic tortuosity and bulk modulus in air-saturated porous media. J. Appl. Phys. 1991, 70, 1975–1979. [Google Scholar] [CrossRef]
- Johnson, D.L.; Koplik, J.; Dashen, R. Theory of dynamic permeability and tortuosity in fluid-saturated porous media. J. Fluid Mech. 1987, 176, 379–402. [Google Scholar] [CrossRef]
- Bies, D.A.; Hansen, C.H. Flow resistance information for acoustical design. Appl. Acoust. 1980, 13, 357–391. [Google Scholar] [CrossRef]
- Sagartzazu, X.; Hervella-Nieto, L.; Pagalday, J.M. Review in Sound Absorbing Materials. Arch. Computat. Methods Eng. 2008, 15, 311–342. [Google Scholar] [CrossRef]
- Hirosawa, K.; Takashima, K.; Nakagawa, H. Comparison of three measurement techniques for the normal absorption coefficient of sound absorbing materials in the free field. J. Acoust. Soc. Am. 2009, 126, 3020–3027. [Google Scholar] [CrossRef]
- Oliva, D.; Hongisto, V. Sound absorption of porous materials—Accuracy of prediction methods. Appl. Acoust. 2013, 74, 1473–1479. [Google Scholar] [CrossRef]
- Dunne, R.; Desai, D.; Sadiku, R. A Review of the Factors that Influence Sound Absorption and the Available Empirical Models for Fibrous Materials. Acoust. Aust. 2017, 45, 453–469. [Google Scholar] [CrossRef]
- Egab, L.; Wang, X.; Fard, M. Acoustical characterisation of porous sound absorbing materials: A review. Int. J. Veh. Noise Vib. 2014, 10, 129–149. [Google Scholar] [CrossRef]
- Fang-rong, W. Discussion of two methods for sound absorption coefficient measurement. Noise Vib. Control 2009, 4, 164–167. Available online: https://api.semanticscholar.org/CorpusID:123737035 (accessed on 24 November 2025).
- Xie, R.; Wan, Y.; Gui, G. On-site sound absorption coefficient measuring system based on reflection method. China Meas. Test 2016, 42, 77–80. Available online: https://api.semanticscholar.org/CorpusID:117580890 (accessed on 24 November 2025).
- Chen, K.; Zeng, X. A study on the measurement of sound absorption coefficient at oblique incidence by the use of two-microphone technique. J. Appl. Acoust. 1999, 18, 28–32. [Google Scholar] [CrossRef]
- Wang, X. Measurement of Absorption Coefficient of Material in Situ. Audio Eng. 2007, 31, 11–13. [Google Scholar] [CrossRef]
- Zhang, Y.; Kuang, Z.; Wu, M.; Yang, J. Method for measuring material sound absorption coefficient based on sound field reproduction. J. Appl. Acoust. 2017, 36, 1–8. [Google Scholar] [CrossRef]
- Allard, J.F.; Champoux, Y. In Situ Two-Microphone Technique for the Measurement of the Acoustic Surface Impedance of Materials. Noise Control Eng. J. 1989, 32, 15–22. [Google Scholar] [CrossRef]
- Duval, A.; Rondeau, J.; Bischoff, L.; Dejaeger, L.; Morgenstern, C.; De Bree, H. In situ impedance and absorption coefficient measurements compared to poro-elastic simulation in free, diffuse or semi-statistical fields using microflown pu probes. Fortschr. Akust. 2006, 32, 515. [Google Scholar]
- Müller-Trapet, M.; Dietrich, P.; Aretz, M.; van Gemmeren, J.; Vorländer, M. On the in situ impedance measurement with pu-probes—Simulation of the measurement setup. J. Acoust. Soc. Am. 2013, 134, 1082–1089. [Google Scholar] [CrossRef]
- Lanoye, R.; Vermeir, G.; Lauriks, W.; Kruse, R.; Mellett, V. Measuring the free field acoustic impedance and absorption coefficient of sound absorbing materials with a combined particle velocity-pressure sensor. J. Acoust. Soc. Am. 2006, 119, 2826–2831. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, J.; Chen, Z.; Hou, H.; Bao, M.; Yang, J. In situ measurement of sound absorption coefficient using impulse sound and pressure-particle velocity probe. J. Appl. Acoust. 2023, 42, 1207–1214. [Google Scholar] [CrossRef]
- Opdam, R.; Hoen, S.; de Vries, D.; Vorlander, M. Measurement of angle-dependent reflection coefficients with a microphone array and spatial Fourier transform post-processing. In Proceedings of the International Congress on Acoustics, Montreal, QC, Canada, 2–7 June 2013. [Google Scholar]
- GB/T 18696.1-2004; Acoustics—Determination of Sound Absorption Coefficient and Impedance in Impedance Tubes—Part 1: Method Using Standing Wave Ratio. Standards Press of China: Beijing, China, 2004.
- Liu, P.S.; Qing, H.B.; Hou, H.L. Primary investigation on sound absorption performance of highly porous titanium foams. Mater. Des. 2015, 85, 275–281. [Google Scholar] [CrossRef]
- Cheng, W.; Duan, C.Y.; Liu, P.S.; Lu, M. Sound absorption performance of various nickel foam-base multi-layer structures in range of low frequency. Trans. Nonferrous Met. Soc. China 2017, 27, 1989–1995. [Google Scholar] [CrossRef]
- Tang, H.P.; Zhu, J.L.; Wang, J.Y.; Ge, Y.; Li, C.; Di, X.B. Sound absorbing properties of stainless steel fiber porous materials. Chin. J. Nonferrous Met. 2007, 17, 1943–1947. [Google Scholar] [CrossRef]
- Jia, C.; Li, L.; Liu, Y.; Fang, B.; Ding, H.; Song, J.; Liu, Y.; Xiang, K.; Lin, S.; Li, Z.; et al. Highly compressible and anisotropic lamellar ceramic sponges with superior thermal insulation and acoustic absorption performances. Nat. Commun. 2020, 11, 3732. [Google Scholar] [CrossRef]
- Yu, X.; Lu, Z.; Zhai, W. Enhancing the flow resistance and sound absorption of open-cell metallic foams by creating partially-open windows. Acta Mater. 2021, 206, 116666. [Google Scholar] [CrossRef]
- Liu, P.S.; Xu, X.B.; Cheng, W.; Chen, J.H. Sound absorption of several various nickel foam multilayer structures at aural frequencies sensitive for human ears. Trans. Nonferrous Met. Soc. China 2018, 28, 1334–1341. [Google Scholar] [CrossRef]
- ISO 10534-2:1998; Acoustics—Determination of Sound Absorption Coefficient and Impedance in Impedance Tubes—Part 2: Transfer-Function Method. International Organization for Standardization: Geneva, Switzerland, 1998.
- Gu, S.; Wang, P.F.; Wei, D.B.; Xie, J.G.; Li, H. Research on the relationship between void characteristic parameters and sound absorption coefficient of drainage asphalt pavement. Highway 2024, 11, 1–7. [Google Scholar]
- Wang, X.; Peng, F.; Chang, B. Sound absorption of porous metals at high sound pressure levels. J. Acoust. Soc. Am. 2009, 126, EL55–EL61. [Google Scholar] [CrossRef]
- Ao, Q.B.; Wang, J.Z.; Li, A.J.; Zhi, H.; Ma, J.; Tang, H.P. Sound absorption properties of fibrous porous metals. Rare Met. Mater. Eng. 2017, 46, 387–391. [Google Scholar]
- Huang, K.; Yang, D.; He, S.; He, D. Acoustic absorption properties of open-cell Al alloy foams with graded pore size. J. Phys. D Appl. Phys. 2011, 44, 365405. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Han, F. Air flow resistance and sound absorption behavior of open-celled aluminum foams with spherical cells. Procedia Mater. Sci. 2014, 4, 187–190. [Google Scholar] [CrossRef]
- Meng, H.; Ao, Q.; Ren, S.; Xin, F.; Tang, H.; Lu, T. Anisotropic acoustical properties of sintered fibrous metals. Compos. Sci. Technol. 2015, 107, 10–17. [Google Scholar] [CrossRef]
- Xu, Y.; Li, S.; Wang, C.L.; Luo, L.; Hou, H. Exploring sound absorption performance of stainless steel fiber porous materials. J. Northwestern Polytech. Univ. 2015, 33, 401–405. [Google Scholar] [CrossRef]
- Cops, M.J.; McDaniel, J.G.; Magliula, E.A.; Bamford, D.J.; Bilefnick, J. Measurement and analysis of sound absorption by a composite foam. Appl. Acoust. 2020, 160, 107138. [Google Scholar] [CrossRef]
- Lin, J.-H.; Lin, C.-M.; Huang, C.-C.; Lin, C.-C.; Hsieh, C.-T.; Liao, Y.-C. Evaluation of the manufacture of sound absorbent sandwich plank made of PET/TPU honeycomb grid/PU foam. J. Compos. Mater. 2011, 45, 1355–1362. [Google Scholar] [CrossRef]
- Liu, Y.; Jacobsen, F. Measurement of absorption with a p-u sound intensity probe in an impedance tube. J. Acoust. Soc. Am. 2005, 118, 2117–2120. [Google Scholar] [CrossRef]
- ISO 354:2003; Acoustics—Measurement of Sound Absorption in a Reverberation Room. International Organization for Standardization: Geneva, Switzerland, 2003.
- Zhang, W.; Tang, W. Analysis on the Error of Calculating the Sound Absorption Coefficient Using the Reverberation Chamber Method. Audio Eng. 2007, 31, 14–19. [Google Scholar] [CrossRef]
- Na, Y.; Lancaster, J.; Casali, J.; Cho, G. Sound Absorption Coefficients of Micro-fiber Fabrics by Reverberation Room Method. Text. Res. J. 2007, 77, 330–335. [Google Scholar] [CrossRef]
- Toyoda, E.; Sakamoto, S.; Tachibana, H. Effects of room shape and diffusing treatment on the measurement of sound absorption coefficient in a reverberation room. Acoust. Sci. Technol. 2004, 25, 255–266. [Google Scholar] [CrossRef]
- Lou, H.D.; Min, H.Q. Measurements of normal incidence sound absorption coefficient for non-standard sized samples in impedance tubes. Acta Acust. 2023, 48, 1012–1020. [Google Scholar] [CrossRef]
- Sun, F.; Chen, H.; Wu, J.; Feng, K. Sound absorbing characteristics of fibrous metal materials at high temperatures. Appl. Acoust. 2010, 71, 221–235. [Google Scholar] [CrossRef]
- Yin, Y. Research on Measurement of Absorption Coefficient of Underwater Acoustic Materials by Reverberation Method. Master’s Thesis, Harbin Engineering University, Harbin, China, 2024. [Google Scholar] [CrossRef]
- Sun, Y.; Hua, B. System error calculation and analysis of underwater sound absorption coefficient measurement experiment. Appl. Acoust. 2022, 186, 108489. [Google Scholar] [CrossRef]
- Chua, J.W.; Li, X.; Li, T.; Chua, B.W.; Yu, X.; Zhai, W. Customisable sound absorption properties of functionally graded metallic foams. J. Mater. Sci. Technol. 2022, 108, 196–207. [Google Scholar] [CrossRef]
- Caniato, M.; Cozzarini, L.; Schmid, C.; Gasparella, A. Acoustic and thermal characterization of a novel sustainable material incorporating recycled microplastic waste. Sustain. Mater. Technol. 2021, 28, e00274. [Google Scholar] [CrossRef]
- Abdi, D.D.; Monazzam, M.; Taban, E.; Putra, A.; Golbabaei, F.; Khadem, M. Sound absorption performance of natural fiber composite from chrome shave and coffee silver skin. Appl. Acoust. 2021, 182, 108264. [Google Scholar] [CrossRef]
- Lafarge, D.; Lemarinier, P.; Allard, J.F.; Tarnow, V. Dynamic compressibility of air in porous structures at audible frequencies. J. Acoust. Soc. Am. 1997, 102, 1995–2006. [Google Scholar] [CrossRef]
- Kino, N.; Ueno, T. Improvements to the Johnson–Allard model for rigid-framed fibrous materials. Appl. Acoust. 2007, 68, 1468–1484. [Google Scholar] [CrossRef]
- Horoshenkov, K.V.; Hurrell, A.; Groby, J.-P. A three-parameter analytical model for the acoustical properties of porous media. J. Acoust. Soc. Am. 2019, 145, 2512–2517. [Google Scholar] [CrossRef]
- Horoshenkov, K.V.; Groby, J.-P.; Dazel, O. Asymptotic limits of some models for sound propagation in porous media and the assignment of the pore characteristic lengths. J. Acoust. Soc. Am. 2016, 139, 2463–2474. [Google Scholar] [CrossRef] [PubMed]
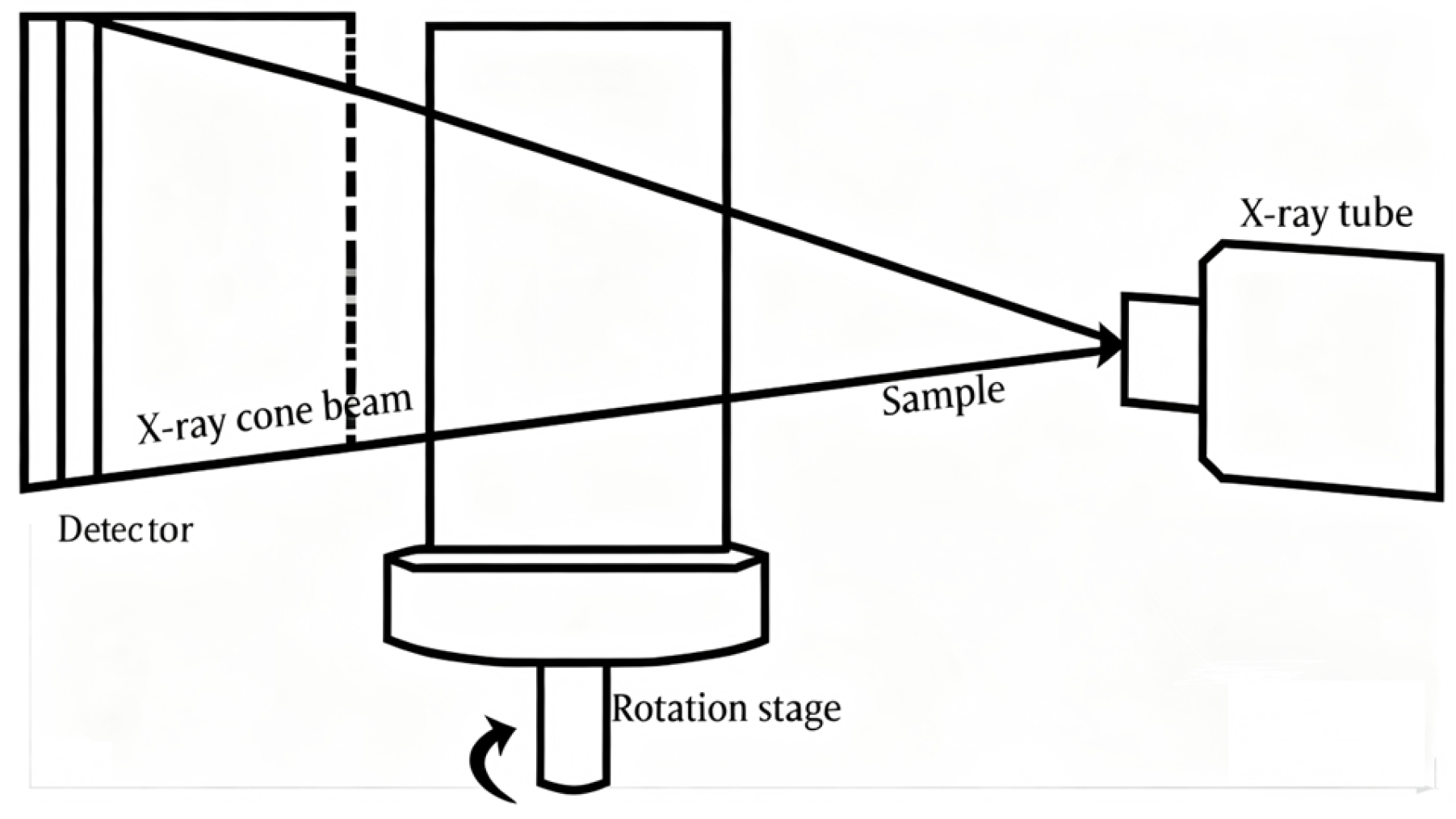
- Sakamoto, S.; Suzuki, K.; Toda, K.; Seino, S. Estimation of the Acoustic Properties of the Random Packing Structures of Granular Materials: Estimation of the Sound Absorption Coefficient Based on Micro-CT Scan Data. Materials 2023, 16, 337. [Google Scholar] [CrossRef] [PubMed]
- Meftah, R.; Van Stappen, J.; Berger, S.; Jacqus, G.; Laluet, J.-Y.; Guering, P.-H.; Van Hoorebeke, L.; Cnudde, V. X-ray Computed Tomography for Characterization of Expanded Polystyrene (EPS) Foam. Materials 2019, 12, 1944. [Google Scholar] [CrossRef] [PubMed]
- Zhai, W.; Yu, X.; Song, X.; Ang, L.Y.L.; Cui, F.; Lee, H.P.; Li, T. Microstructure-based experimental and numerical investigations on the sound absorption property of open-cell metallic foams manufactured by a template replication technique. Mater. Des. 2018, 137, 108–116. [Google Scholar] [CrossRef]
- Yu, X.; Zhai, W.; Song, X.; Cui, F. Numerical and experimental study on the acoustic performance of Ni-based superalloy open cell foam. Procedia Eng. 2017, 214, 4–8. [Google Scholar] [CrossRef]
- Soltani, P.; Norouzi, M. Prediction of the sound absorption behavior of nonwoven fabrics: Computational study and experimental validation. J. Sound Vib. 2020, 485, 115607. [Google Scholar] [CrossRef]
- Otaru, A.J. Enhancing the sound absorption performance of porous metals using tomography images. Appl. Acoust. 2019, 143, 183–189. [Google Scholar] [CrossRef]
- Ramis, J.; Alba, J.; del Rey, R.; Escuder, E.; Sanchis, V.J. New absorbent material acoustic based on kenaf’s fibre. Mater. Construcc. 2007, 60, 133–143. [Google Scholar] [CrossRef]
- Garai, M.; Pompoli, F. A simple empirical model of polyester fibre materials for acoustical applications. Appl. Acoust. 2005, 66, 1383–1398. [Google Scholar] [CrossRef]
- Hurrell, A.I.; Horoshenkov, K.V.; Pelegrinis, M.T. The accuracy of some models for the airflow resistivity of nonwoven materials. Appl. Acoust. 2018, 130, 230–237. [Google Scholar] [CrossRef]
- ISO 9053: 2018; Acoustics–Materials for Acoustical Applications–Determination of Airflow Resistance. International Standards Organization: Geneva, Switzerland, 2018.
- ASTM C522-03; Standard Test Method for Airflow Resistance of Acoustical Materials. ASTM International: West Conshohocken, PA, USA, 2016.
- Tang, X.; Yan, X. Airflow Resistance of Acoustical Fibrous Materials: Measurements, Calculations and Applications. J. Ind. Text. 2020, 49, 981–1010. [Google Scholar] [CrossRef]
- ISO 9237:2023; Textiles—Determination of the Permeability of Fabrics to Air. International Organization for Standardization: Geneva, Switzerland, 2023.
- Ingard, K.U.; Dear, T.A. Measurement of acoustic flow resistance. J. Sound Vib. 1985, 103, 567–572. [Google Scholar] [CrossRef]
- Dragonetti, R.; Iannello, C.; Romano, R.A. Measurement of the resistivity of porous materials with an alternating air-flow method. J. Acoust. Soc. Am. 2011, 129, 753–764. [Google Scholar] [CrossRef]
- Rey, R.d.; Alba, J.; Arenas, J.P.; Ramis, J. Technical notes: Evaluation of two alternative procedures for measuring airflow resistance of sound absorbing materials. Arch. Acoust. 2013, 38, 547–554. [Google Scholar] [CrossRef]
- Doutres, O.; Salissou, Y.; Atalla, N.; Panneton, R. Evaluation of the acoustic and non-acoustic properties of sound absorbing materials using a three-microphone impedance tube. Appl. Acoust. 2010, 71, 506–509. [Google Scholar] [CrossRef]
- Lomte, A.; Sharma, B.; Drouin, M.; Schaffarzick, D. Sound absorption and transmission loss properties of open-celled aluminum foams with stepwise relative density gradients. Appl. Acoust. 2022, 193, 108780. [Google Scholar] [CrossRef]
- Bianco, M.J.; Gerstoft, P.; Traer, J.; Ozanich, E.; Roch, M.A.; Gannot, S.; Deledalle, C.-A. Machine learning in acoustics: Theory and applications. J. Acoust. Soc. Am. 2019, 146, 3590–3628. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Zhang, J.; Hou, H.; Xu, Y. The prediction of sound absorption coefficient of film multi-cavity materials based on generalized regression neural network (GRNN). Appl. Acoust. 2024, 224, 110134. [Google Scholar] [CrossRef]
- Mi, H.; Guo, W.; Liang, L.; Ma, H.; Zhang, Z.; Gao, Y.; Li, L. Prediction of the Sound Absorption Coefficient of Three-Layer Aluminum Foam by Hybrid Neural Network Optimization Algorithm. Materials 2022, 15, 8608. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Bao, W.; Shi, L.; Zuo, B.; Gao, W. General regression neural network for prediction of sound absorption coefficients of sandwich structure nonwoven absorbers. Appl. Acoust. 2014, 76, 128–137. [Google Scholar] [CrossRef]
- Liang, L.; Mi, H.; Guo, W.; Zhang, Y.; Ma, H.; Zhang, Z.; Li, L. Estimation of sound absorption coefficient of composite structured aluminum foam by radial basis function neural network. Appl. Acoust. 2022, 185, 108414. [Google Scholar] [CrossRef]
- Zhang, J.; Yao, D.; Li, J. Enhanced sound insulation in double wall structures via MAMs: An RBF-based optimisation approach. Mater. Des. 2025, 254, 114058. [Google Scholar] [CrossRef]
- Jeon, J.H.; Yang, S.S.; Kang, Y.J. Estimation of sound absorption coefficient of layered fibrous material using artificial neural networks. Appl. Acoust. 2020, 169, 107476. [Google Scholar] [CrossRef]
- Ciaburro, G.; Iannace, G.; Passaro, J.; Bifulco, A.; Marano, A.D.; Guida, M.; Branda, F.; Marulo, F. Artificial neural network-based models for predicting the sound absorption coefficient of electrospun poly(vinyl pyrrolidone)/silica composite. Appl. Acoust. 2020, 169, 107472. [Google Scholar] [CrossRef]
- Lin, M.-D.; Tsai, K.-T.; Su, B.-S. Estimating the sound absorption coefficients of perforated wooden panels by using artificial neural networks. Appl. Acoust. 2009, 70, 31–40. [Google Scholar] [CrossRef]
- Gao, N.; Wang, M.; Liang, X.; Pan, G. On-demand prediction of low-frequency average sound absorption coefficient of underwater coating using machine learning. Results Eng. 2025, 25, 104163. [Google Scholar] [CrossRef]
- Otaru, A.J. Research of the numerical simulation and machine learning backpropagation networks analysis of the sound absorption properties of cellular soundproofing materials. Results Eng. 2023, 20, 101588. [Google Scholar] [CrossRef]
- Zhang, Z.; Ye, R.; Zhu, G.; Huang, X.; Qian, Y.; Yurchenko, D. Research on sound absorption performance prediction of microporous structures based on integrated learning. Mater. Today Commun. 2025, 46, 112866. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, H.; Wang, Y.; Zhao, H.; Yu, D.; Wen, J. Prediction of sound absorption coefficient for metaporous materials with convolutional neural networks. Appl. Acoust. 2022, 200, 109052. [Google Scholar] [CrossRef]
- Tang, X.; Kong, D.; Yan, X. Multiple regression analysis of a woven fabric sound absorber. Text. Res. J. 2018, 89, 855–866. [Google Scholar] [CrossRef]
- Iannace, G.; Ciaburro, G.; Trematerra, A. Modelling sound absorption properties of broom fibers using artificial neural networks. Appl. Acoust. 2020, 163, 107239. [Google Scholar] [CrossRef]
- Babacan, O. An Artificial Intelligence Approach to Evaluating the Sound Absorption Performance of Materials: A Systematic Review. Duzce Univ. J. Sci. Technol. 2025, 13, 718–734. [Google Scholar] [CrossRef]

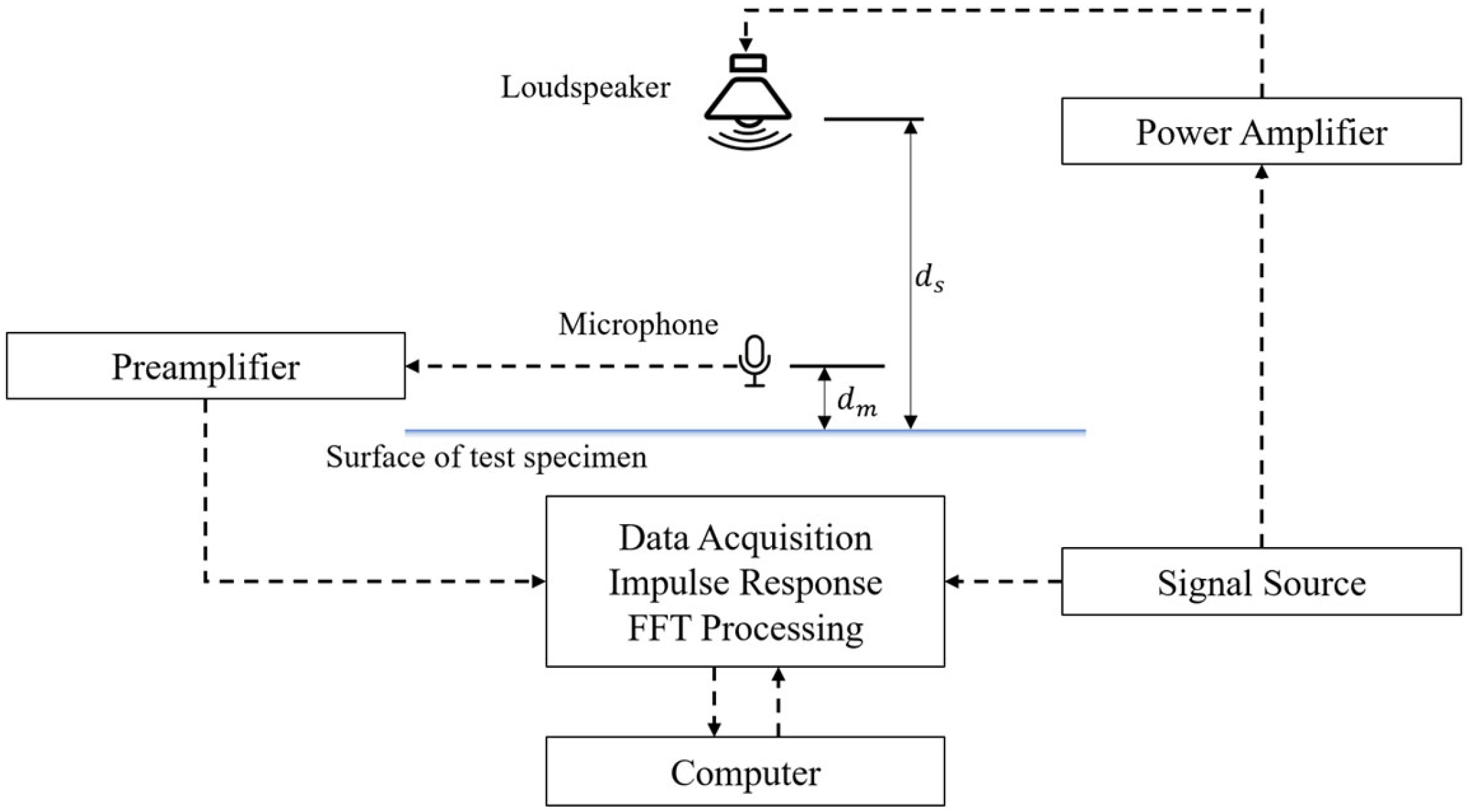

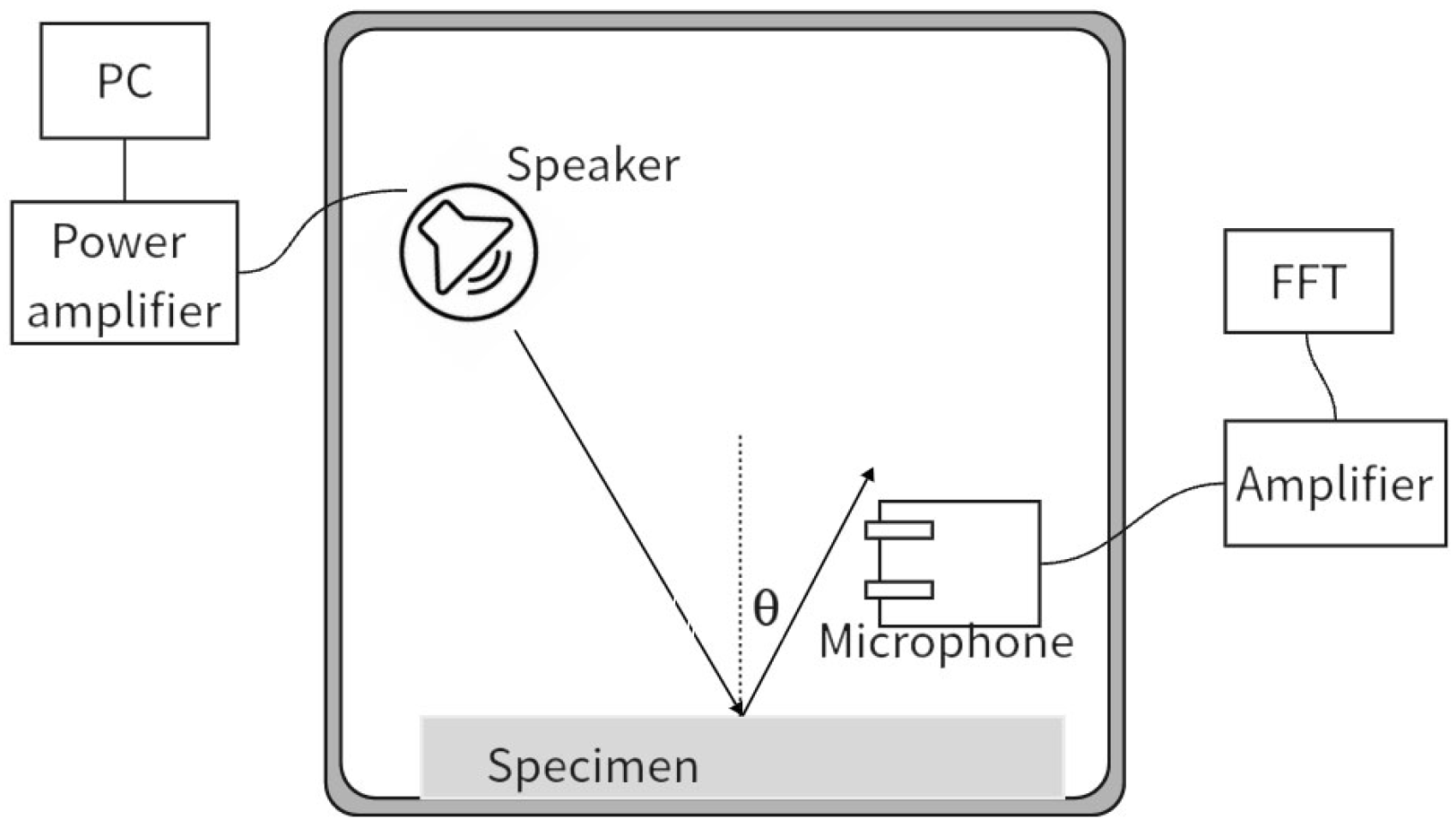

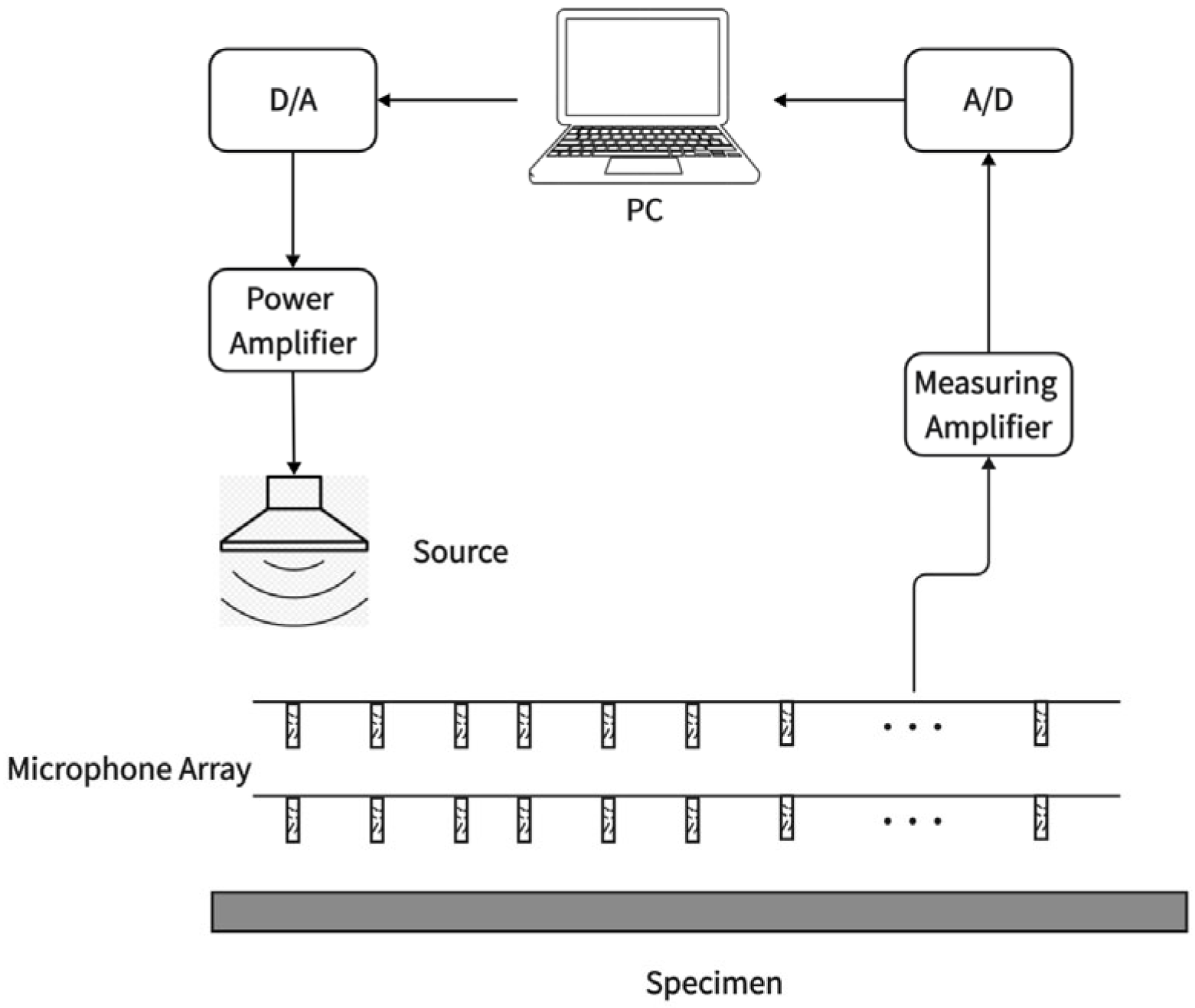
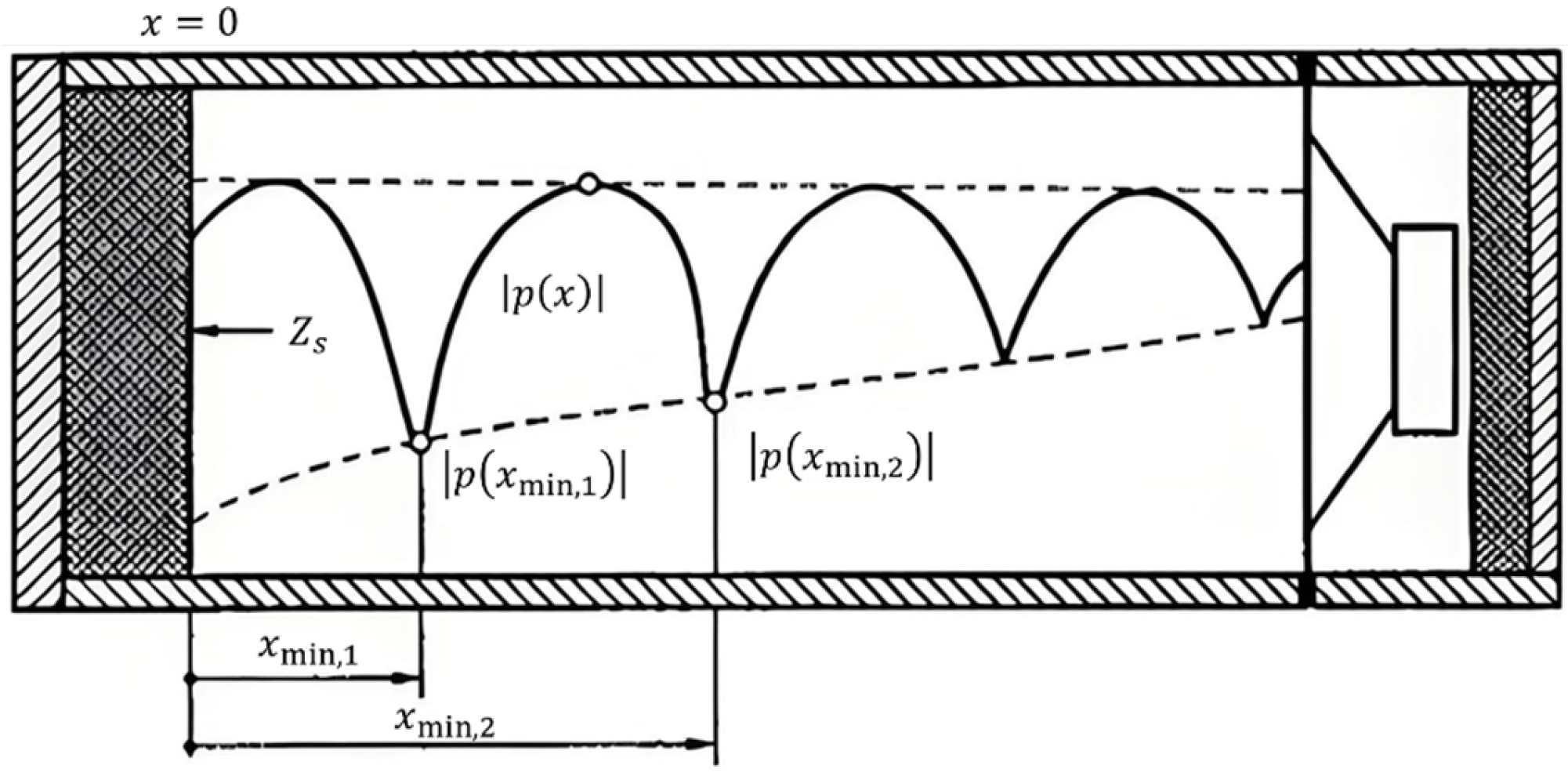
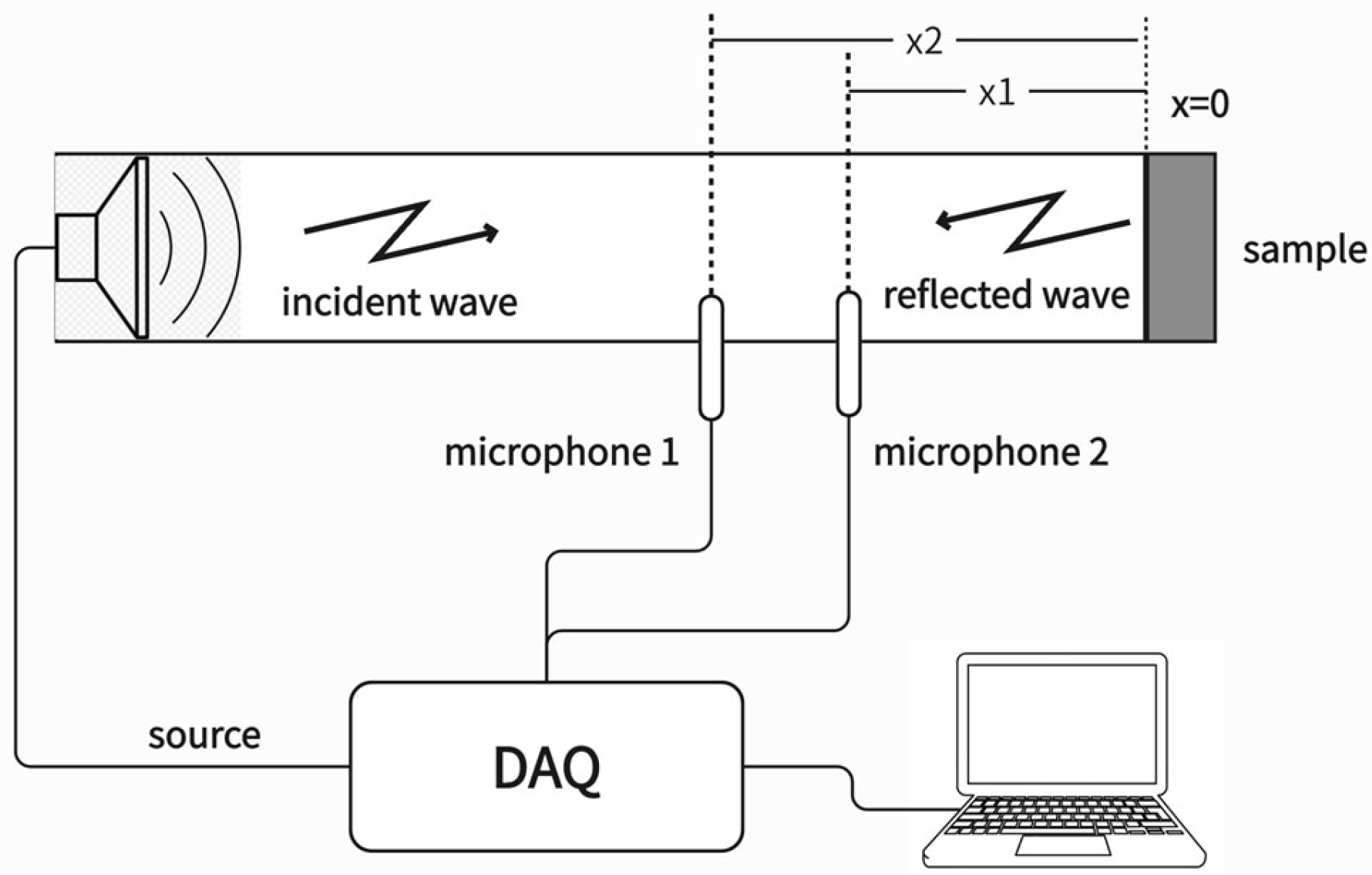


| Method Category | Method Name | Key Advantages | Limitations |
|---|---|---|---|
| In situ methods | Pulse reflection method | suitable for in situ measurement where sampling is impossible; efficient, flexible, and rapid measurement | model errors in the low-frequency range; susceptible to background noise and complex sound fields |
| Two-microphone method | suitable for oblique incidence SAC measurement; | must be performed under free-field conditions; limited by background noise | |
| p-u probe method | directly measures sound pressure and particle velocity; simplified setup compared to two-microphone method | requires high-precision calibration for probe | |
| Spatial Fourier transform method | non-contact measurement; obtains angle-dependent SAC in a single measurement | requires microphone array and complex processing; laboratory setup may not suit all in situ scenarios | |
| Laboratory methods | Impedance tube (standing wave ratio) | direct and classic method; relatively simple principle and setup | time-consuming point-by-point measurement; requires tube |
| Impedance tube (transfer function/two microphones) | fast and efficient broadband measurement; high accuracy and repeatability; international standard | requires tube and calibrated microphones; limited to normal incidence SAC; sample must fit tube cross-section | |
| Reverberation room method | measures random incidence SAC, closer to real applications; international standard for product rating | requires large, specialized, and expensive room; requires large sample size; sensitive to room diffusion and sample mounting | |
| Other methods | For non-standard samples | enables testing of samples smaller than the tube cross-section or special geometry | accuracy depends on PAM selection and sample geometry |
| High-temperature impedance tube | allows for SAC measurement under high temperatures | requires a customized and complex system | |
| Underwater reverberation method | adapts the reverberation principle for underwater use | weak sound field diffusion increases uncertainty |
| Model Name | Input Parameters | Validity Range | Limitations |
|---|---|---|---|
| DB empirical model | flow resistivity (σ) | 0.01 < f/σ < 1 | Inaccurate for extreme f/σ; limited to fibrous materials |
| Miki empirical model | flow resistivity (σ) | Extended f/σ range, better at low f/σ | Still empirical; less accurate for non-fibrous materials |
| Komatsu empirical model | flow resistivity (σ) | Improved for extreme f/σ | Complexity increases with logarithmic terms |
| JCA theoretical model | ϕ, σ, α∞, Λ, Λ′ | Broad frequency, various materials | Requires 5 microstructural parameters; weak at low frequencies |
| JCAL theoretical model (Lafarge et al.) | ϕ, σ, α∞, Λ, Λ′, k0′ | Improved thermal effects modeling | More parameters; complex calibration |
| Kino’s modified JCA model | ϕ, σ, α∞, Λ, Λ′, N1, N2 | 800 Hz~5 kHz, low-flow-resistivity materials | Requires correction factors from fitting |
| Horoshenkov’s modified JCA model | porosity (ϕ); median pore size (x−); standard deviation of pore diameter (σx). | Wide range; granular, fibrous, foam materials | Assumes log-normal pore distribution |
| Standard Name | Main Features | Application Scenarios |
|---|---|---|
| ISO 9053 Steady-State Flow Method | data direct principle; reference method; technically challenging. | laboratory calibration; material research and development. |
| ISO 9053 Alternating Flow Method | avoids low-flow measurement; high precision and repeatability; complex equipment. | high-precision measurement; quality control. |
| ASTM C522-03 | equivalent to ISO; industry standard. | industrial testing; North American projects. |
| ISO 10534-2 Acoustical Transfer Function Method [43] | indirect measurement; model-dependent; inversion calculation. | model parameterization; research and characterization. |
| ISO 9237 [81] | rapid and simple; derivation from air permeability; approximate estimation. | rapid screening; quality monitoring |
| Method Category | Empirical Models (DB, Miki, Komatsu) | Theoretical Models (JCA and Extensions) | Experimental Methods | Machine Learning |
|---|---|---|---|---|
| Core principle | Statistical regression based on extensive experimental data | Based on the physics of sound propagation in porous media (viscous and thermal effects) | Directly measuring the interaction between sound waves and materials. | Learning complex nonlinear mappings between material parameters and SAC from data. |
| Typical accuracy | Medium-Low (Significant errors at extreme f/σ values) | High (Excellent especially in mid-to-high frequencies) | Very high (The standard for validating other methods) | Variable (Data-dependent) |
| Complexity/Cost | Low (Simple formulas, fast computation) | Medium (Requires multiple microstructural parameters, difficult to obtain; complex model computation) | High (Requires specialized equipment and laboratory environment; time-consuming) | Medium (High upfront cost for data collection and model training; but fast prediction phase) |
| Key advantages | Requires only flow resistivity (σ), extremely simple and efficient; suitable for rapid estimation and preliminary design. | Clear physical meaning, high prediction accuracy, applicable to various materials. | Direct, reliable, most convincing results; standardized methods ensure comparability. | Capable of handling highly nonlinear problems; no need for explicit physical equations. |
| Key limitations | Applicability limited to the dataset used for model development; accuracy decreases with extreme parameters. | High cost of parameter acquisition; still weak in predicting low-frequency and nonlinear behavior. | Expensive equipment; sample size requirements; in situ measurements susceptible to environmental interference. | “Black-box” nature, lacks physical interpretability; heavily reliant on large volumes of high-quality training data; risk of overfitting. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Zhang, Z.; Zheng, X. The Modern Numerical and Experimental Methods for the Sound Absorbing Characteristics of Dissipative Sound Absorbing Materials: A Review. Materials 2025, 18, 5353. https://doi.org/10.3390/ma18235353
Liu R, Zhang Z, Zheng X. The Modern Numerical and Experimental Methods for the Sound Absorbing Characteristics of Dissipative Sound Absorbing Materials: A Review. Materials. 2025; 18(23):5353. https://doi.org/10.3390/ma18235353
Chicago/Turabian StyleLiu, Ruijun, Zhicheng Zhang, and Xu Zheng. 2025. "The Modern Numerical and Experimental Methods for the Sound Absorbing Characteristics of Dissipative Sound Absorbing Materials: A Review" Materials 18, no. 23: 5353. https://doi.org/10.3390/ma18235353
APA StyleLiu, R., Zhang, Z., & Zheng, X. (2025). The Modern Numerical and Experimental Methods for the Sound Absorbing Characteristics of Dissipative Sound Absorbing Materials: A Review. Materials, 18(23), 5353. https://doi.org/10.3390/ma18235353






