Experimental Investigation on the Bending Performance of Steel–Concrete Composite Beams After Creep
Abstract
1. Introduction
2. Materials and Methods
2.1. Explanation of Key Symbols
2.2. Specimen Design
2.2.1. Degree of Shear Connection (η)
2.2.2. Cross-Sectional Form of Steel Beams
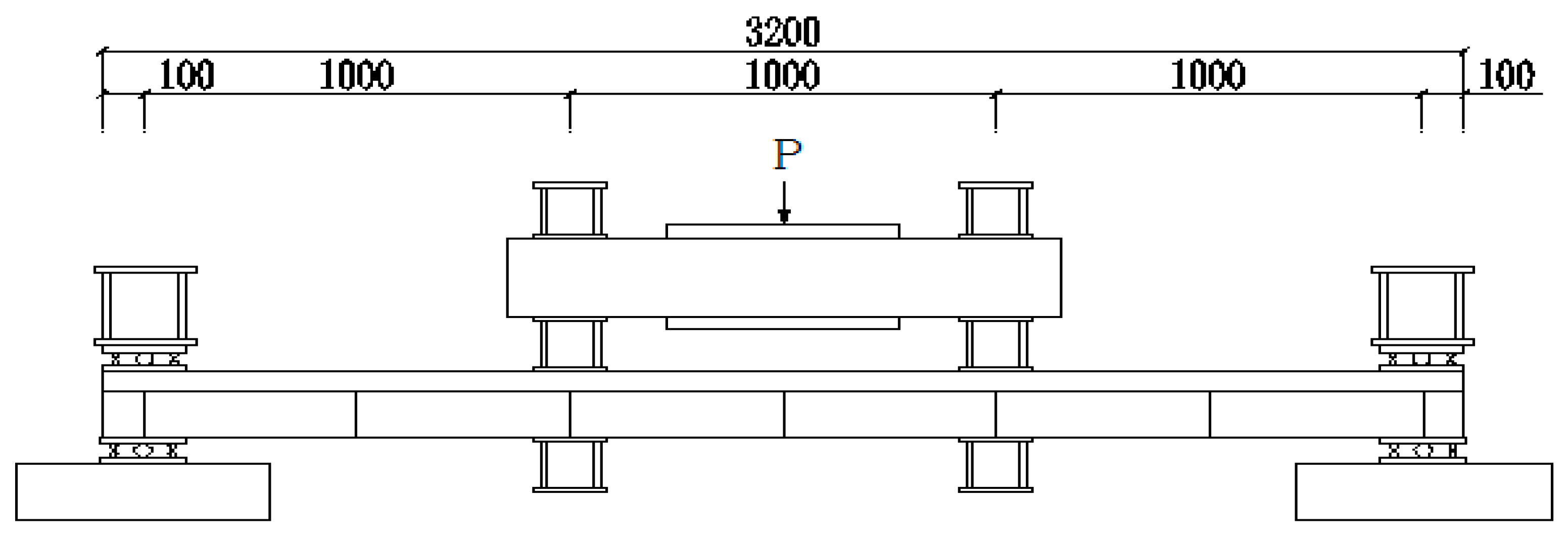
- Span Design: Span parameters were determined with reference to engineering examples of medium- and small-span composite beams (e.g., urban footbridges, floor beams in industrial plants). The design of a 3000 mm net span for simply supported beams and a 5000 mm total span (3 m + 2 m unequal span) for continuous beams not only adapts to the range limitations of the test loading equipment to ensure stable and controllable loading processes but also realistically simulates the actual stress state of composite beams under common spans in engineering, enhancing the engineering reference value of test results.
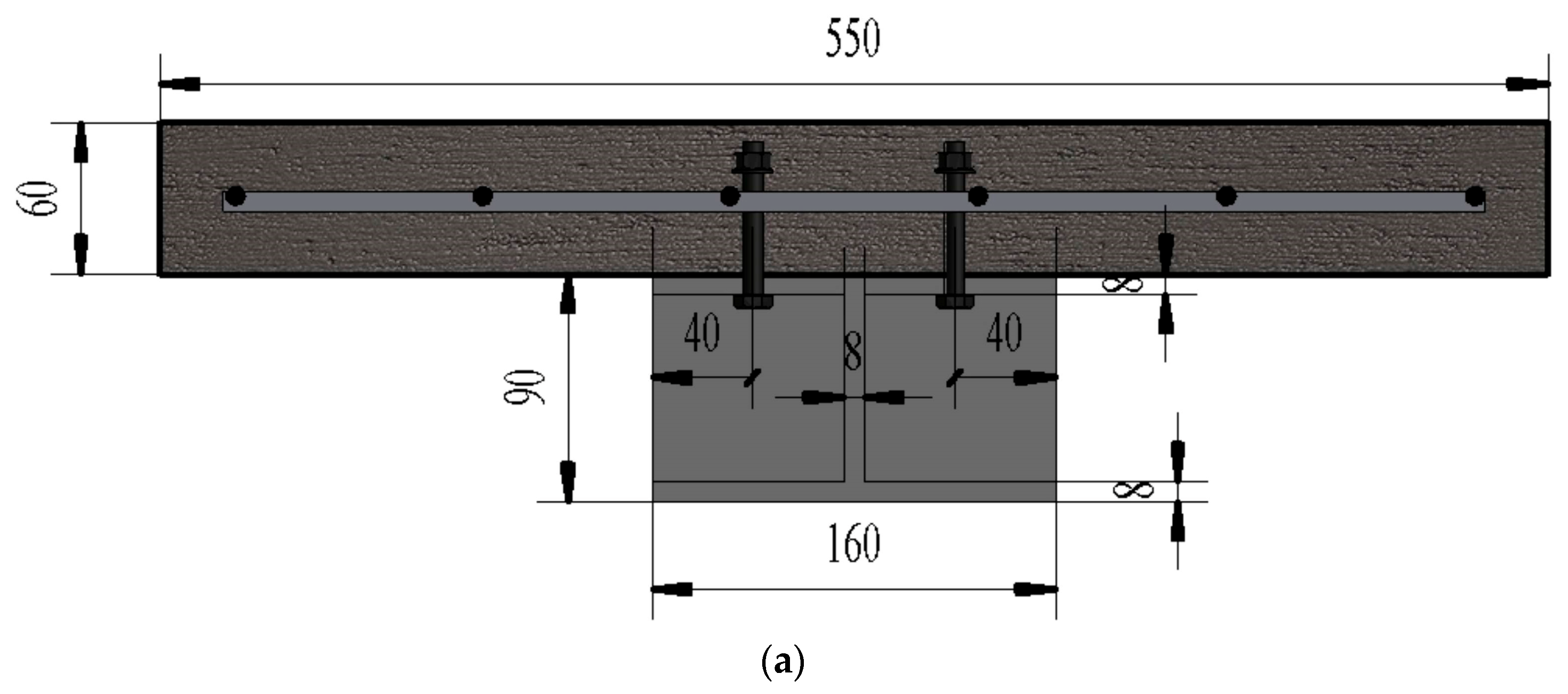
- Steel Beam Structure: The box-section steel beam had dimensions of 80 mm (height) × 260 mm (width), and the I-section steel beam had dimensions of 160 mm (height) × 100 mm (flange width). To improve the local stability of the steel beams and avoid premature local buckling of the steel beams during the test (which would affect result accuracy), 10 mm-thick diaphragms were installed every 500 mm along the length of the steel beams. Meanwhile, longitudinal stiffeners were added to the bottom of the box-section steel beams to further enhance their anti-buckling capacity.
- Concrete Slab and Reinforcement: The concrete slab was designed with a thickness of 60 mm and a width of 550 mm, with HRB335 grade Φ8@100 steel mesh embedded inside. This configuration conforms to the conventional engineering practice for reinforcing the tension zone of flexural members in composite beams-the steel mesh can effectively bear the tensile force in the tension zone of the concrete slab, preventing a sudden drop in bearing capacity after concrete cracking, while strengthening the collaborative working effect between the concrete slab and the steel beam to ensure they participate in force bearing together.
- Shear Connectors: Grade 4.6 studs with a diameter of 12.8 mm and a length of 45 mm were selected as shear connectors. In simply supported beams, three stud spacings (90 mm, 180 mm, and 270 mm) were set to simulate shear connection degrees of 0.57, 1.08, and 1.53, respectively; in continuous beams, two stud spacings (90 mm and 270 mm) were used to represent full shear connection and partial shear connection, respectively. Grade 4.6 studs are the mainstream type of shear connectors in engineering, and their diameter and length were determined based on the shear force transfer requirements of composite beams; the stud spacing was calculated according to the designed shear connection degree and verified against the requirements for construction accuracy and spacing deviation in the Code for Manufacture of Railway Steel Bridges (TB 10212-2009) [89] to ensure the fabrication quality of specimens meets engineering standards.
- The cross-sectional forms and reinforcement details of the beams are shown in Figure 2, and the specific parameters of all specimens are listed in Table 2, which can provide complete basic data support for subsequent creep tests, static loading tests, and result analysis. In addition, strict control was imposed on material quality and construction accuracy during specimen fabrication: all specimens were made of Grade II reinforcing steel and Q235 grade steel beams; commercial C40 concrete was used, with a measured compressive strength of 34.5 MPa; the entire fabrication process complied with the requirements of the Code for Manufacture of Railway Steel Bridges (TB 10212-2009) [89] to ensure all specimens meet quality standards and have good performance consistency, avoiding the impact of individual specimen differences on test result accuracy.
2.3. Experimental Procedures
2.3.1. Creep Test of Composite Beam Specimens
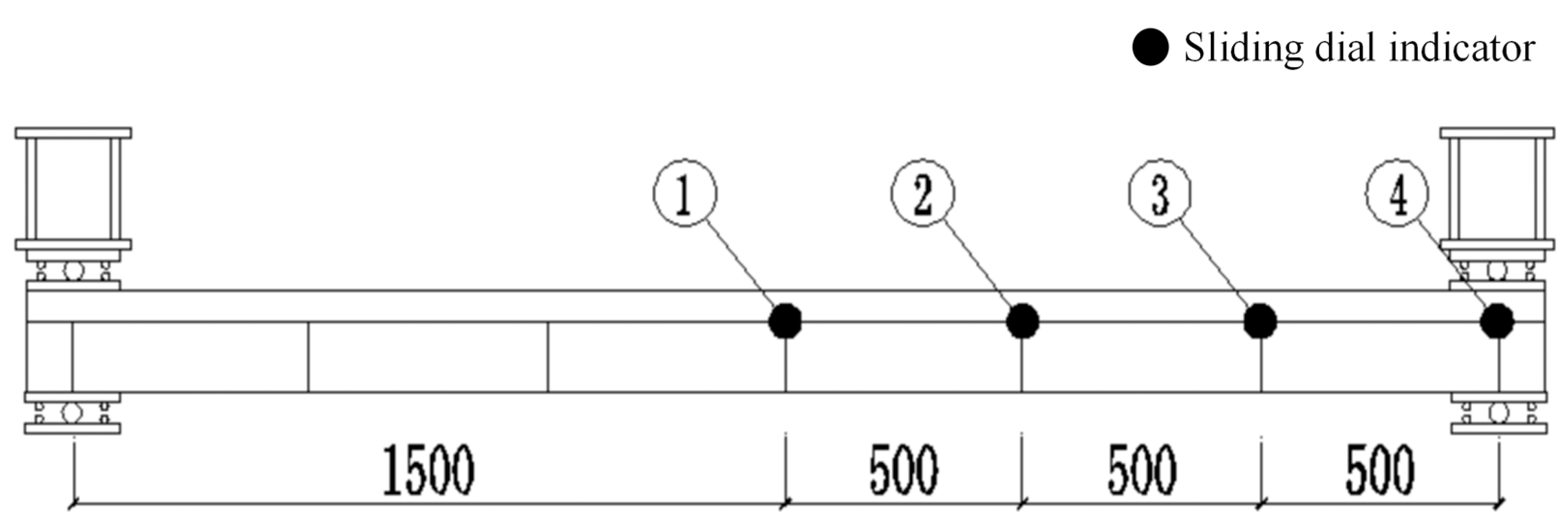
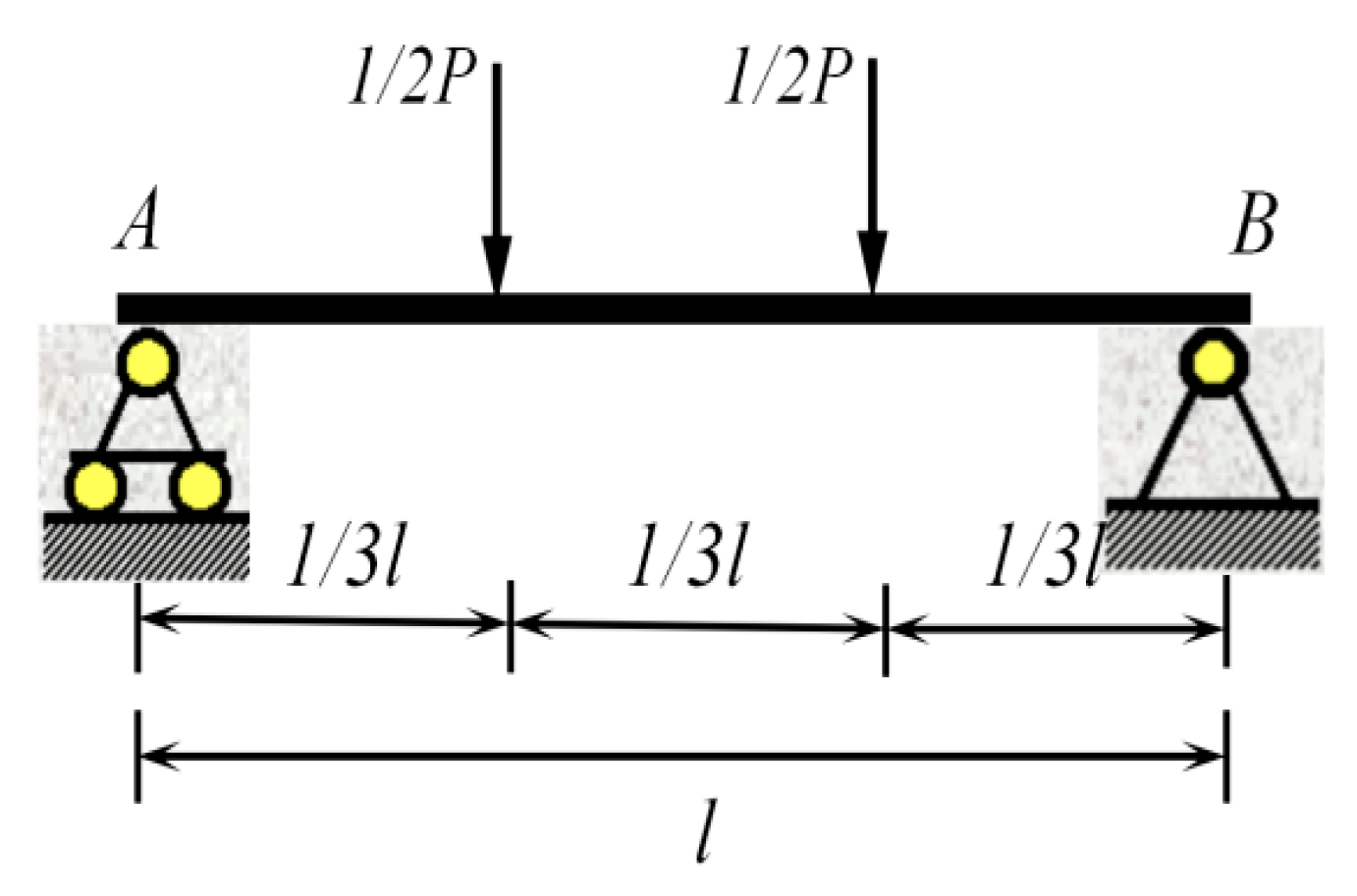
2.3.2. Static Test Loading Scheme
3. Results
3.1. Experimental Phenomena
3.2. Analysis of Experimental Results
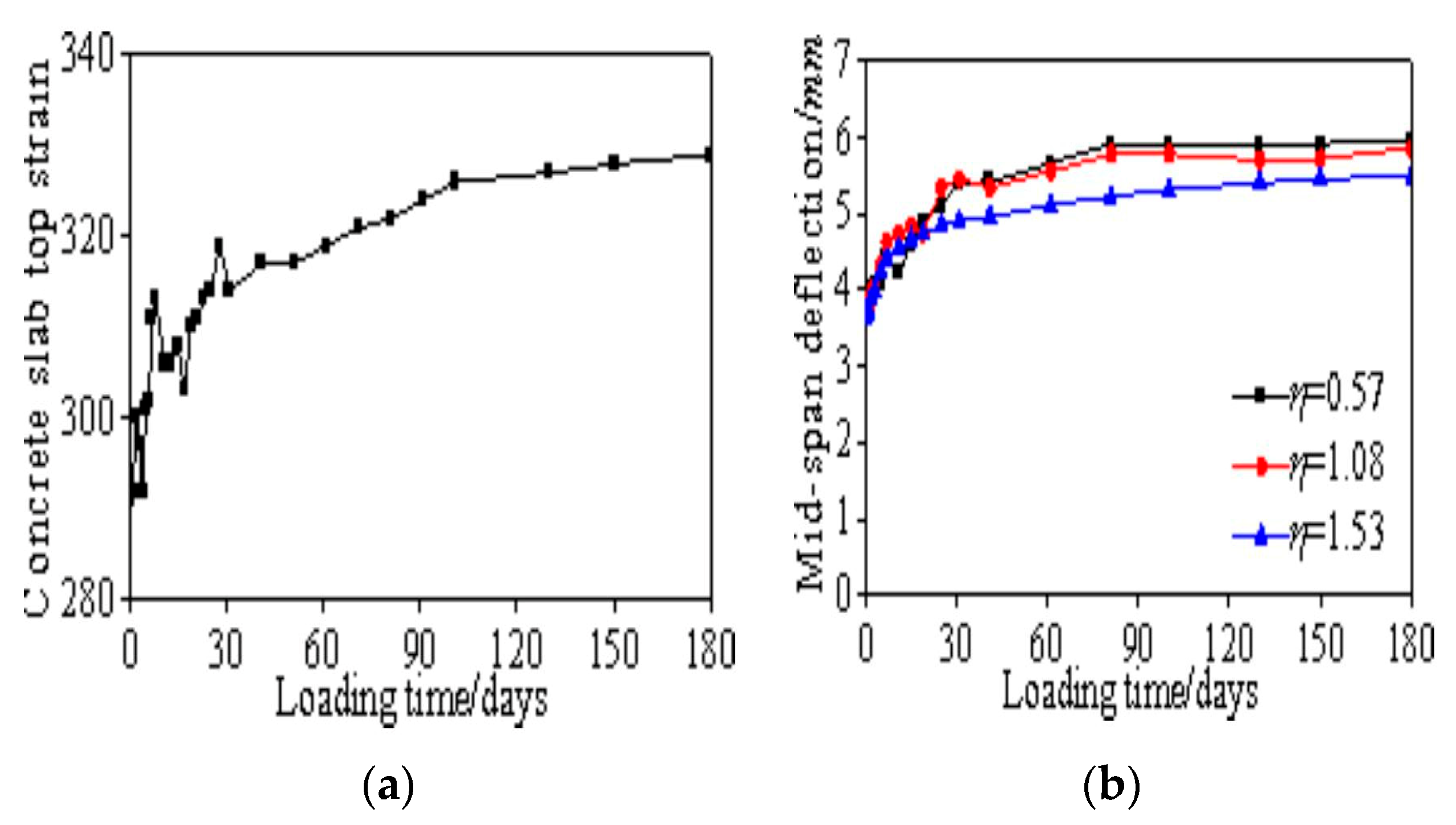
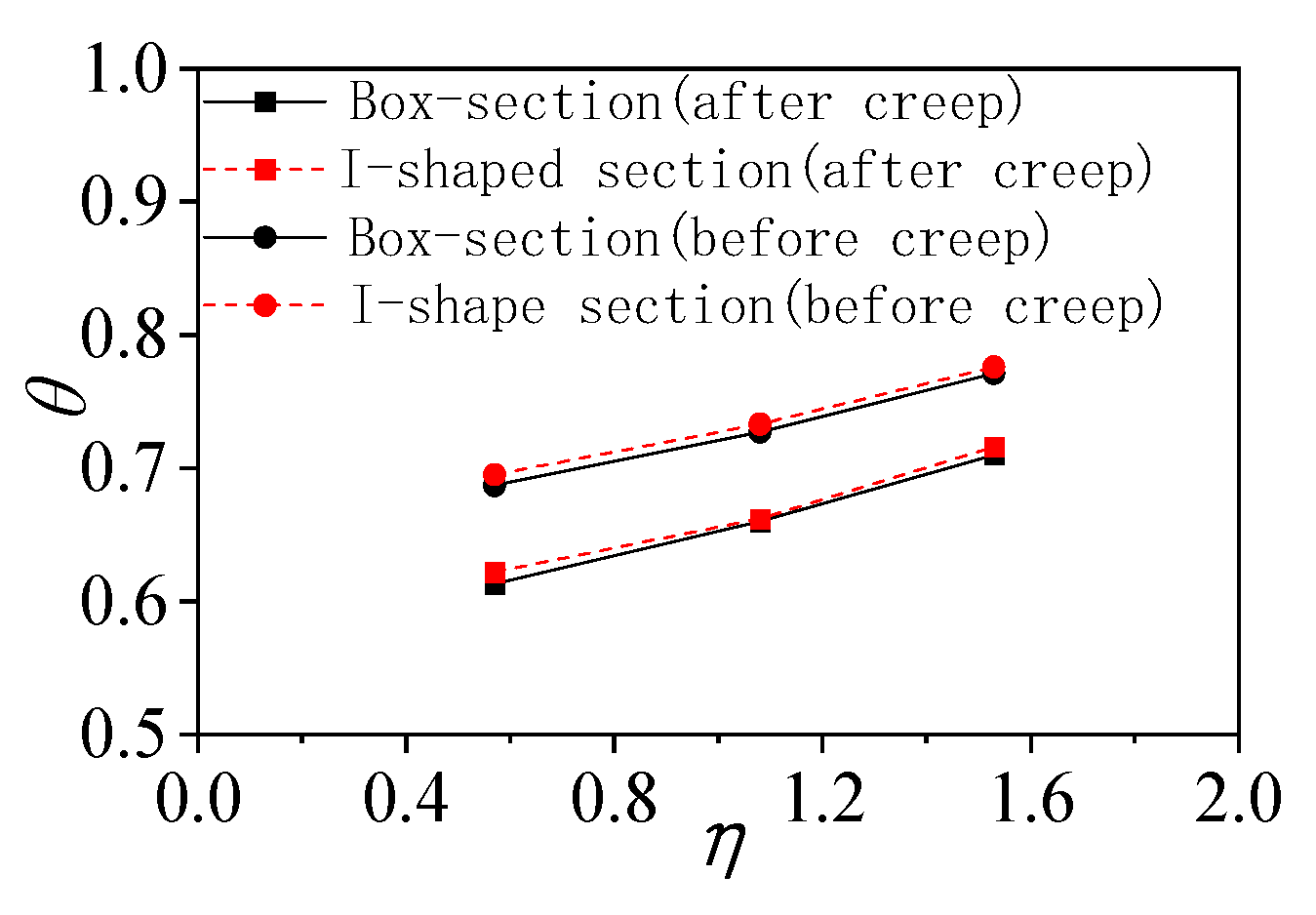
3.2.1. Stiffness Analysis
- Stiffness evolution analysis under creep effects
- 2.
- Correlation between stiffness calculation and deflection in negative moment regions
3.2.2. Load-Bearing Capacity Analysis
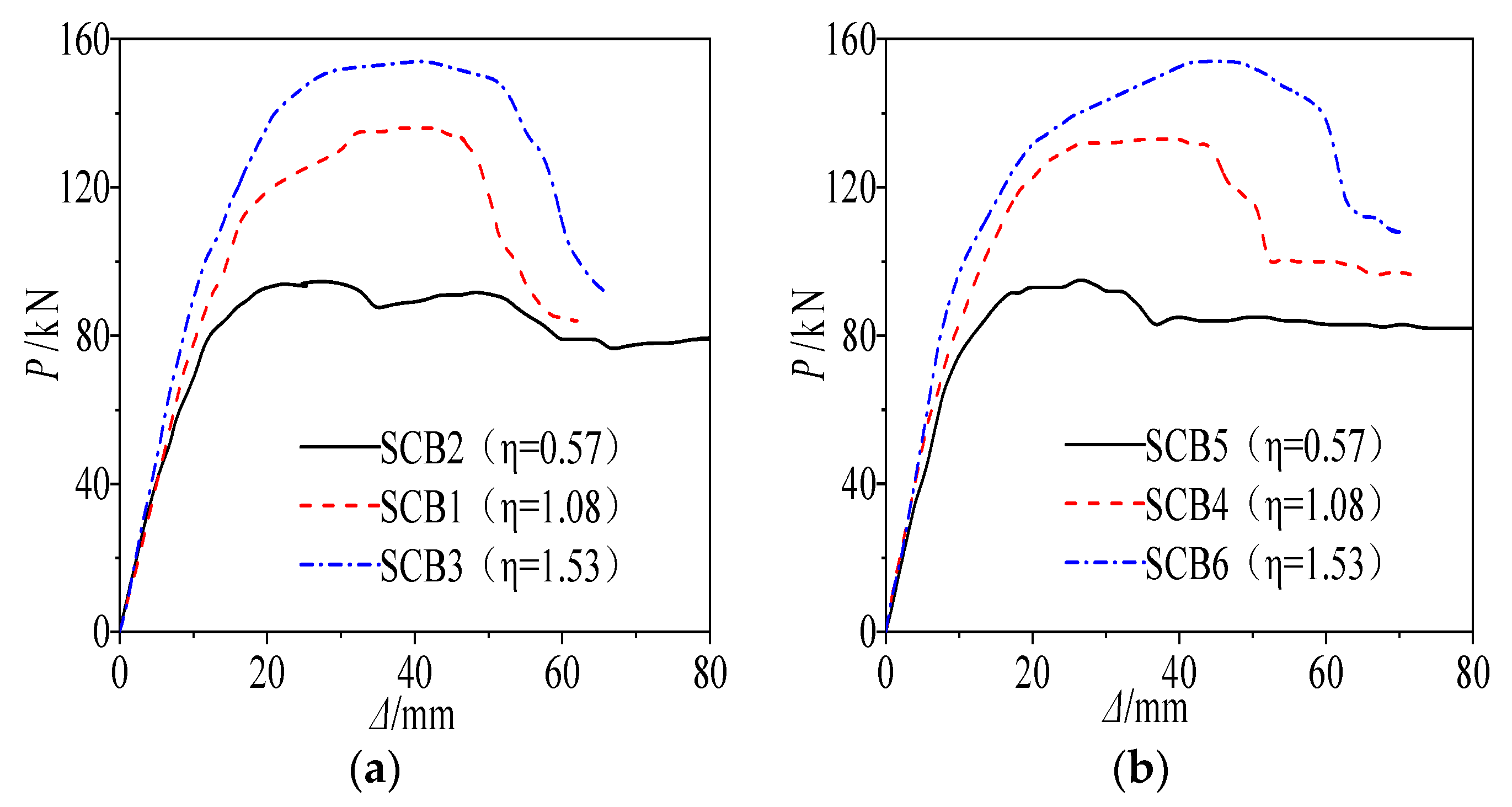
- Influence of shear connection degree
- 2.
- Effects of cross-sectional configuration
- 3.
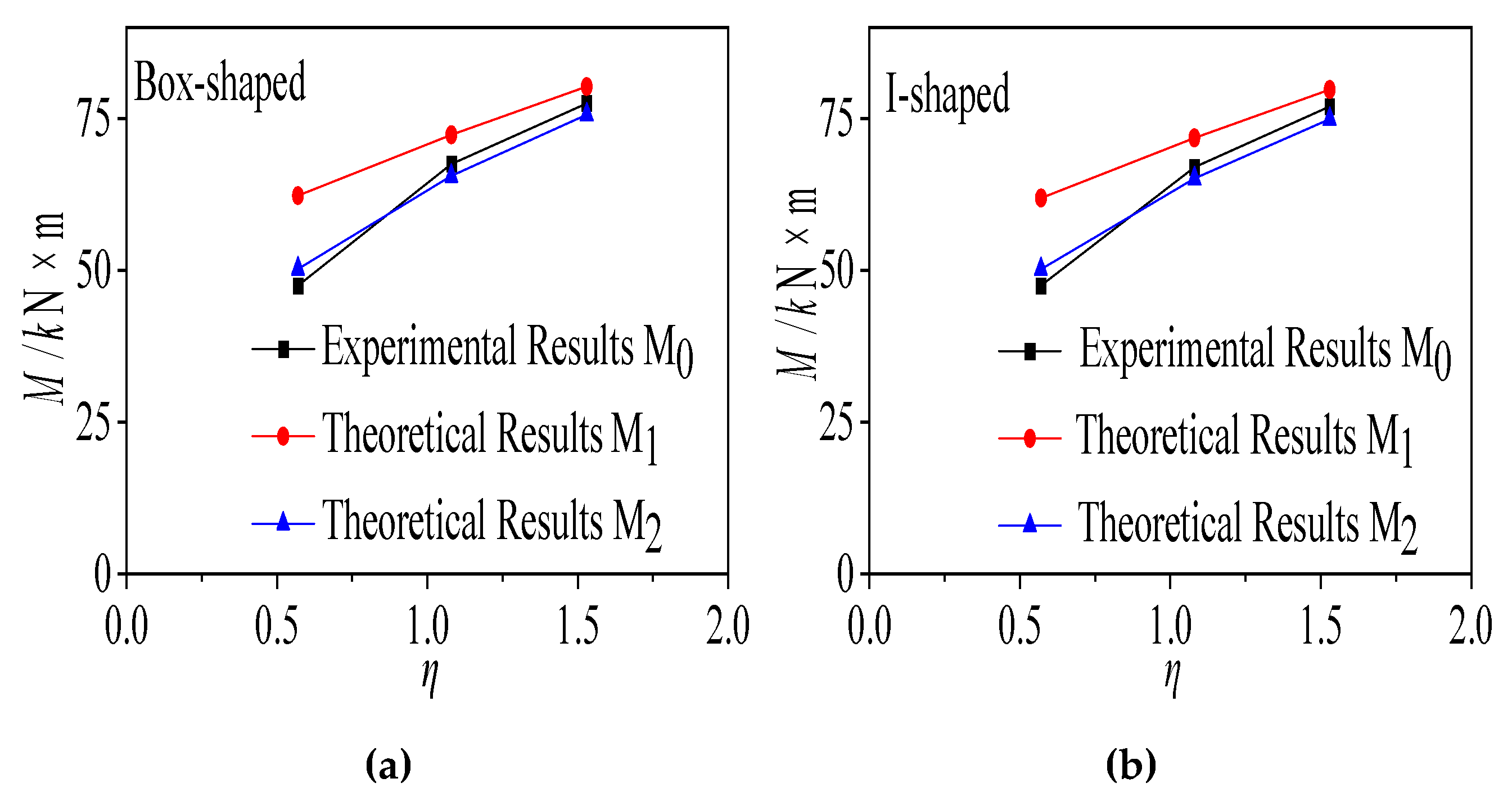
- Theoretical calculation results
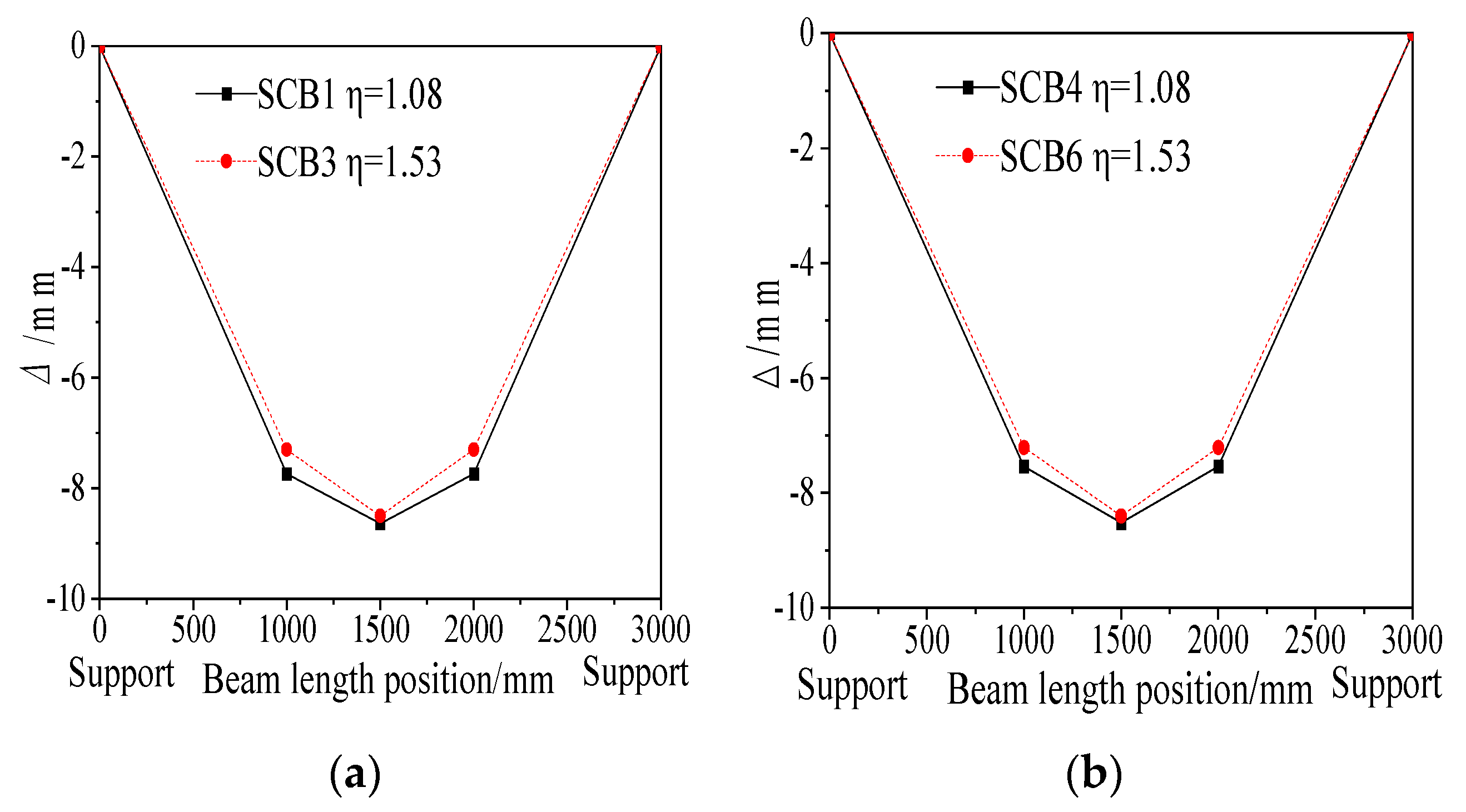
3.2.3. Deflection Curve Analysis
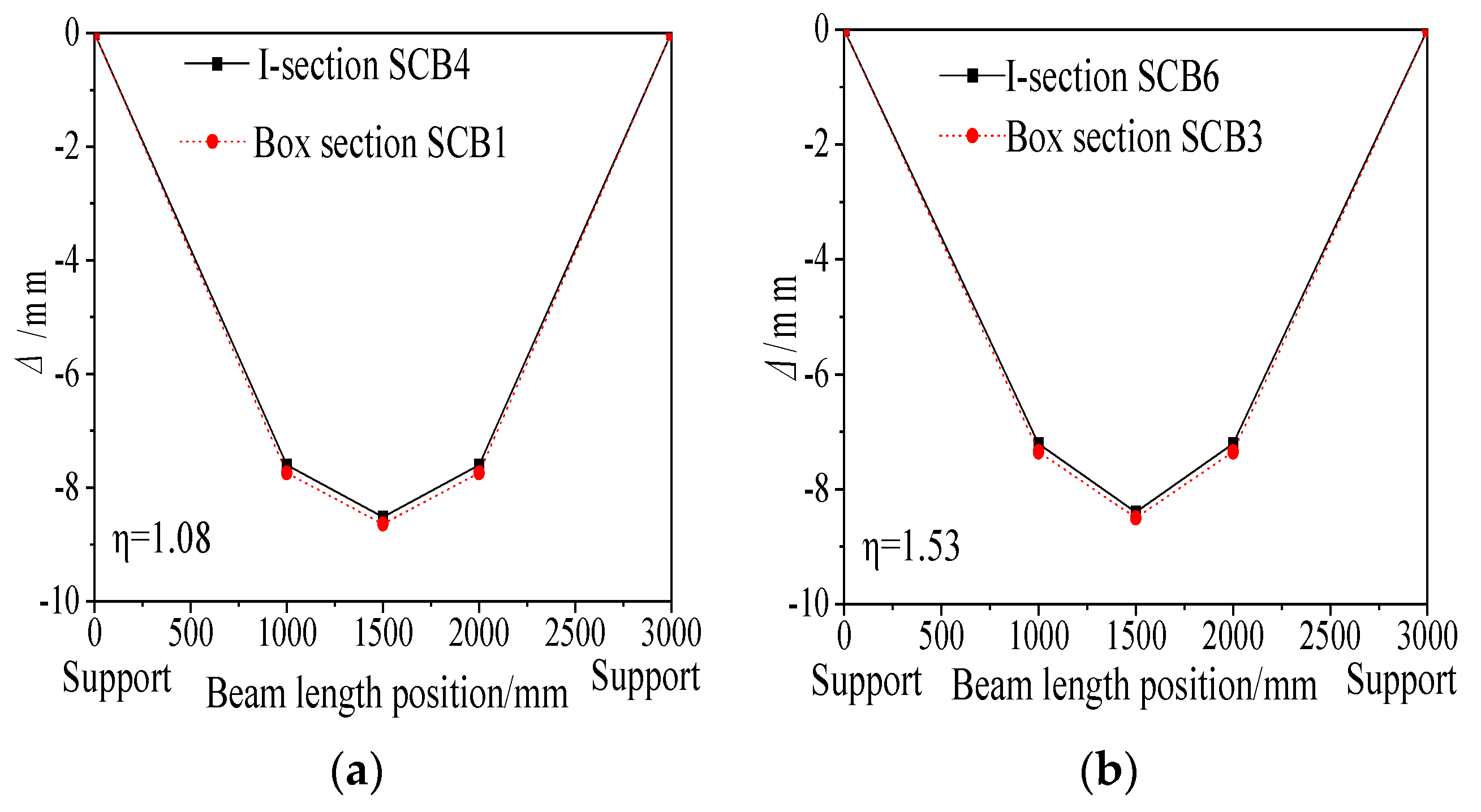
- Impact of shear connection degree
- 2.
- Influence of cross-sectional form
4. Discussion
4.1. Verification of Results and Comparative Analysis
- Theoretical Verification: The theoretical ultimate bending moment and stiffness of the specimens were calculated based on the Chinese “Code for Design of Steel Structures” (GB 50017-2017) [88] and the stiffness reduction method considering interface slip proposed by Nie Jianguo et al. [35]. The results show that for specimens subjected to creep, the theoretical ultimate bending moment calculated using the reduced concrete strength (M2) agrees well with the experimental values (M0) (Table 7), validating the effectiveness of this method.
- Inverse Analysis Verification: The post-creep elastic modulus (Ec) and compressive strength (fcu) of the concrete were determined by back-calculating from the measured load-deflection curves and stiffness, thereby quantifying the degree of material property degradation due to creep (Table 5).
4.2. Key Parameters and Failure Mechanisms
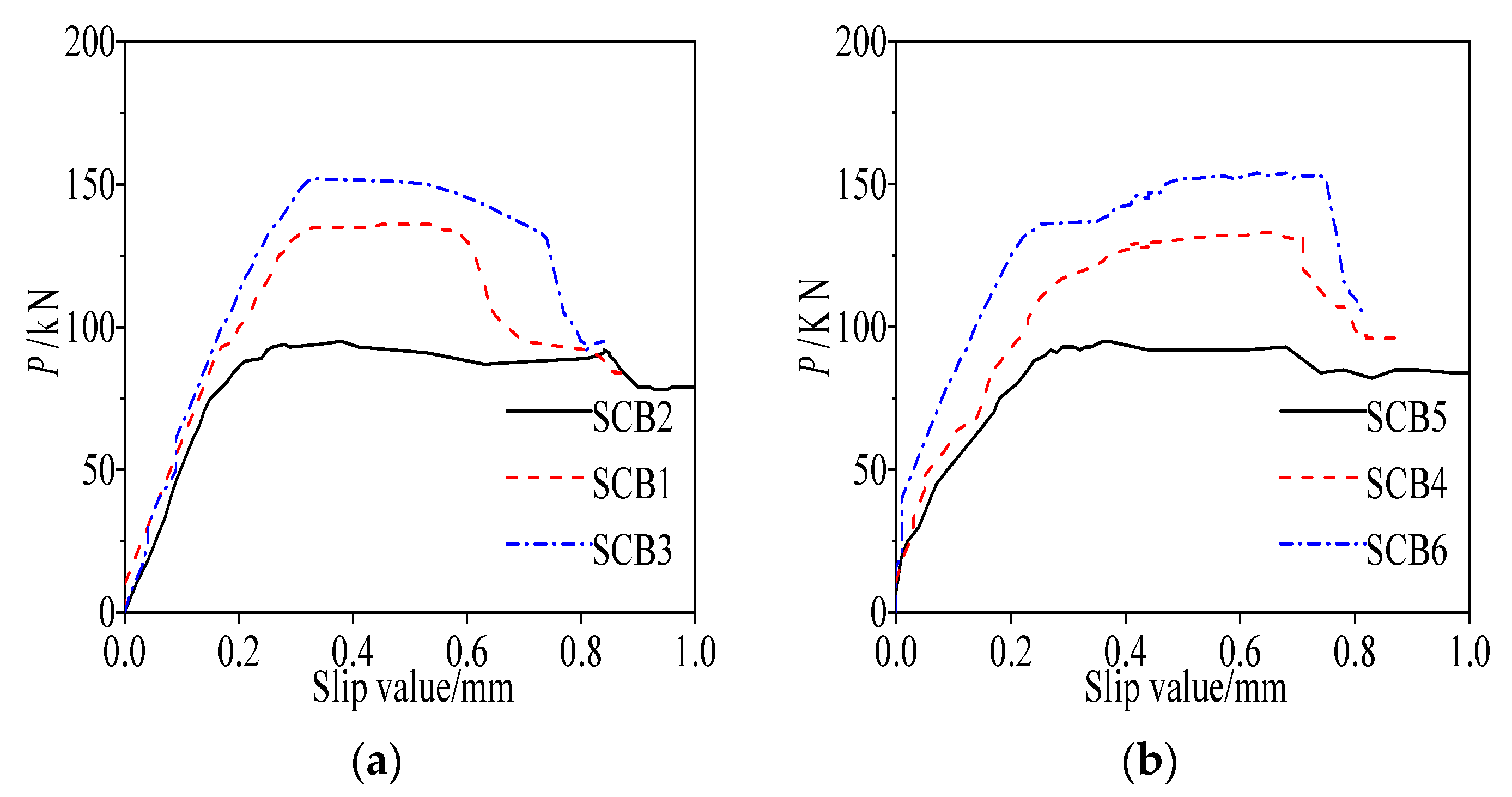
- Shear Connection Degree (η): This is the most critical parameter. It directly controls the composite action between steel and concrete, playing a decisive role in the beam’s stiffness, load-bearing capacity, and interface slip behavior. The load-bearing capacity of fully shear-connected (η = 1.53) specimens was over 60% higher than that of partially connected (η = 0.57) specimens and could significantly delay the onset of interface slip.
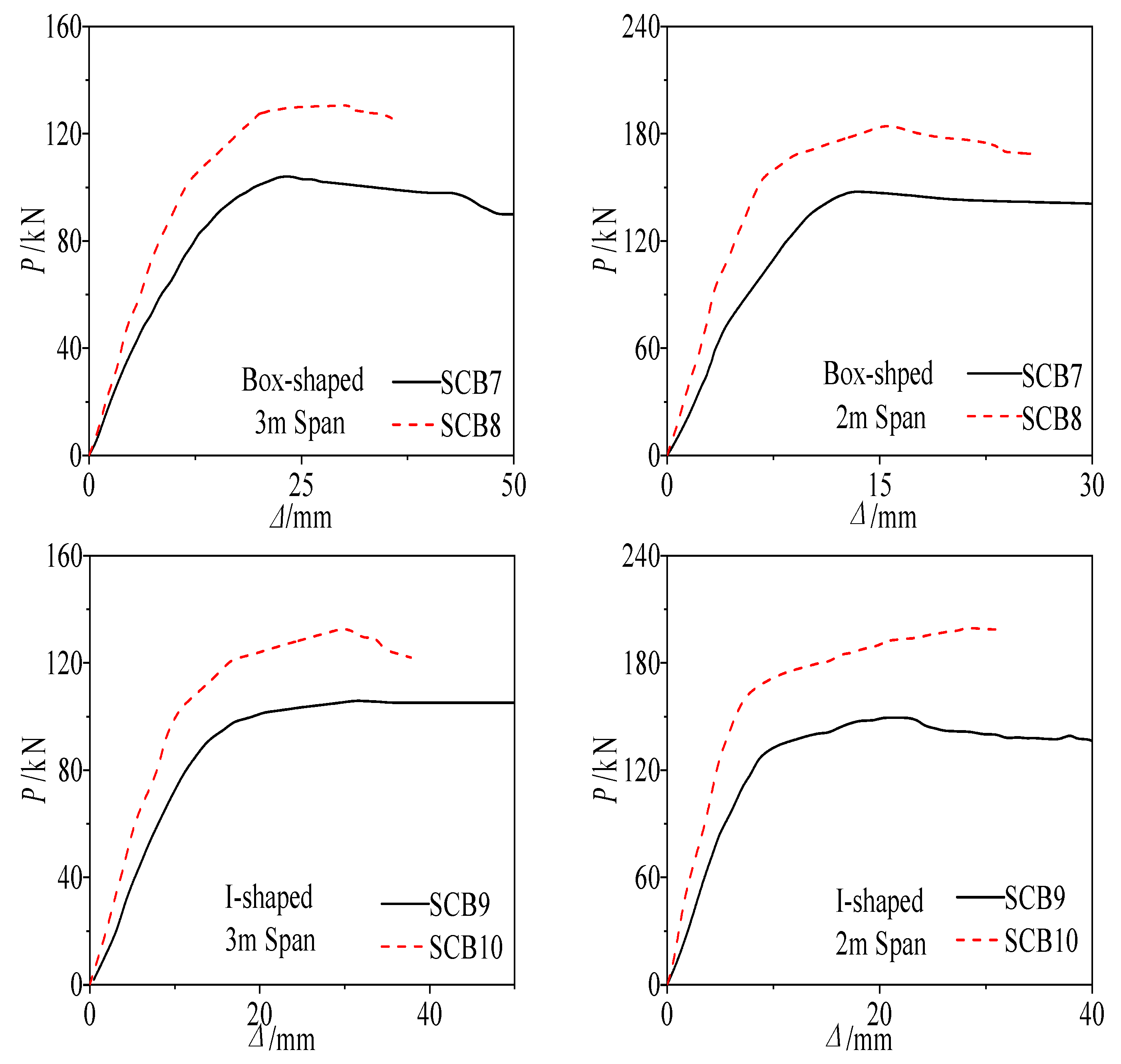
- Boundary Conditions: Through internal force redistribution, continuous beams exhibit better crack resistance in the negative moment region and higher mid-span load-bearing capacity than simply supported beams, with a plastic moment redistribution coefficient reaching up to 40%.
- Creep Effects: Concrete creep leads to significant internal force redistribution, an overall stiffness reduction (approximately 10%), and a substantial decrease in the concrete elastic modulus (40~60%). The extent of this degradation is inversely related to the shear connection degree.
- Cross-Sectional Form: Due to their better torsional restraint, box-sections exhibited 10~15% lower creep deflections than I-sections, but their influence on ultimate load-bearing capacity and stiffness was much smaller than that of the shear connection degree.
4.3. Experimental Errors and Data Analysis
- Material Variability: Natural fluctuations in concrete strength and minor variations in stud weld quality are inherent causes.
- Measurement and Installation Errors: Load eccentricity, support settlement, and strain gauge misalignment can all introduce errors.
- Theoretical Model Simplifications: The theoretical calculations did not fully simulate the nonlinear development of interface slip or the complex stress state in cracked concrete.
- The measured load-bearing capacity of the partially shear-connected specimen SCB7 was slightly lower than the theoretical value (approximately 93~95% of theoretical). This is likely because its interface slip occurred earlier, limiting the full development of composite action.
- The experimental data for the fully shear-connected specimen SCB8 agreed well with theoretical values, proving that full connection can effectively suppress detrimental slip.
- A general trend was that the measured deflections of all specimens in the elastic stage were smaller than the code-calculated values (Table 6). This suggests that current design codes may underestimate the actual stiffness of composite beams, as they do not fully account for the “tension stiffening effect” of cracked concrete.
4.4. New Insights into Basic Materials Science
- Coupling mechanism between shear connection degree and concrete creep: It is found that a high shear connection degree effectively suppresses the steel-concrete interfacial slip, reduces the stress concentration inside concrete, and thereby delays the degradation rate of its elastic modulus and strength. This reveals the intrinsic correlation between the degree of mechanical connection and the time-dependent degradation of composite component performance, providing an important supplement to the research on composite interfacial behavior.
- Residual stiffness mechanism of cracked concrete in negative moment regions: Experiments confirm that even after concrete cracking, it can still effectively participate in force transmission within a range of approximately 0.6 times the slab thickness and provide continuous stiffness contribution. This finding revises the traditional simplified assumption that “cracked concrete completely ceases to work” and improves the basic theory for stiffness calculation of composite materials.
- Quantitative law of creep-induced stiffness degradation in composite beams: This study quantifies for the first time that “the overall stiffness decreases by approximately 10% after 180 days of creep” and clarifies the quantitative relationship that “for every 0.5 increase in shear connection degree, the stiffness degradation rate can be reduced by 8–10%”. This provides key experimental data support for the development of more accurate long-term performance prediction models for composite materials.
4.5. Novel Achievements in Engineering Applications
- Optimized design criteria for shear connection degree: For projects with strict requirements on long-term deflection control (e.g., bridges, long-span floor systems), an ultra-full shear connection design with a shear connection degree of 1.53 is recommended. This measure can reduce creep-induced deflection by 15–20% and increase the strength retention rate to over 55%. For cost-sensitive projects, a full shear connection design with a shear connection degree of 1.08 can be adopted to balance performance and economy.
- Guidelines for cross-sectional form selection: Box sections are suitable for scenarios with strict restrictions on creep-induced deflection (e.g., floors of precision industrial plants), while I-sections can be used in scenarios with relatively relaxed deflection requirements (e.g., secondary beams of industrial plants). Given that the difference in ultimate bearing capacity between the two is only 0.65%, engineers can make selections based on specific deformation control requirements.
4.6. Research Summary and Outlook
5. Conclusions
- Increased shear connection degrees (1.53) led to a 15~20% reduction in creep-induced deflections compared to partial connections (0.57), indicating enhanced composite action under long-term loading. Full shear connections delayed interfacial slip initiation to approximately 30% of load capacity and maintained strain continuity up to 0.6 times the ultimate load. In contrast, partial connections showed early slip-induced strain discontinuities.
- Box sections demonstrated 10~15% lower creep deflections than I-sections under identical loading, due to their superior torsional restraint on concrete slab deformation. When shear connection degrees were equivalent, both cross-sectional forms exhibited comparable patterns of creep-induced stiffness reduction (40~60%), suggesting that cross-sectional form plays a secondary role in creep resistance.
- Continuous beams exhibited a 25% higher cracking load in negative moment regions and a 1.5-fold increase in mid-span moments compared to simply supported beams, due to creep-induced moment redistribution. The plastic moment redistribution coefficient reached 40%, aligning with Eurocode recommendations and highlighting creep’s significant role in internal force redistribution.
- Post-creep concrete showed a 40~60% reduction in elastic modulus, with the degradation extent inversely related to the shear connection degree. The improved stiffness reduction method effectively quantified residual performance, revealing that fully connected specimens retained 55~61% of their strength, compared to 43~49% for partially connected specimens.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Strain Distribution
- Strain distribution patterns at mid-span cross-sections
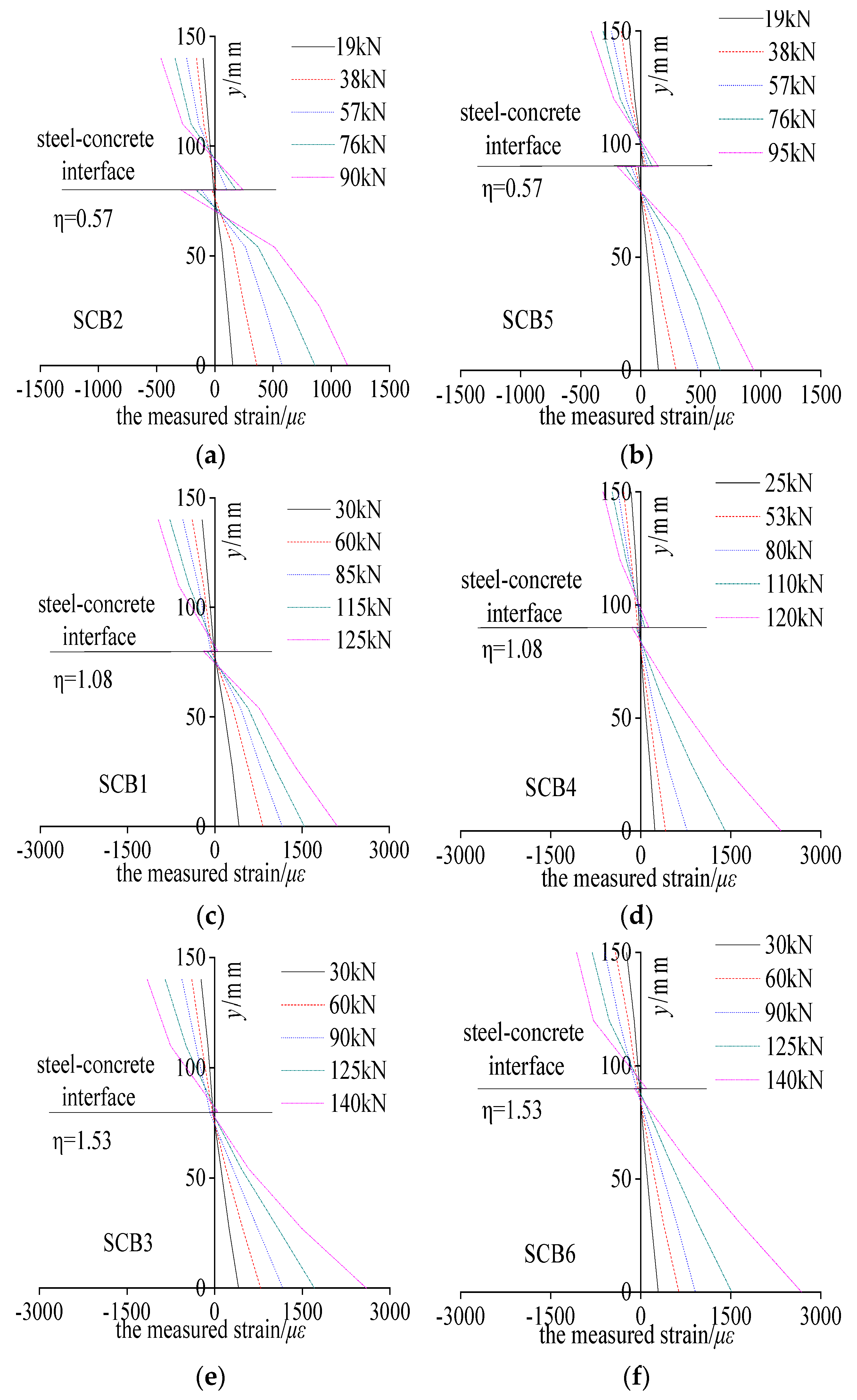
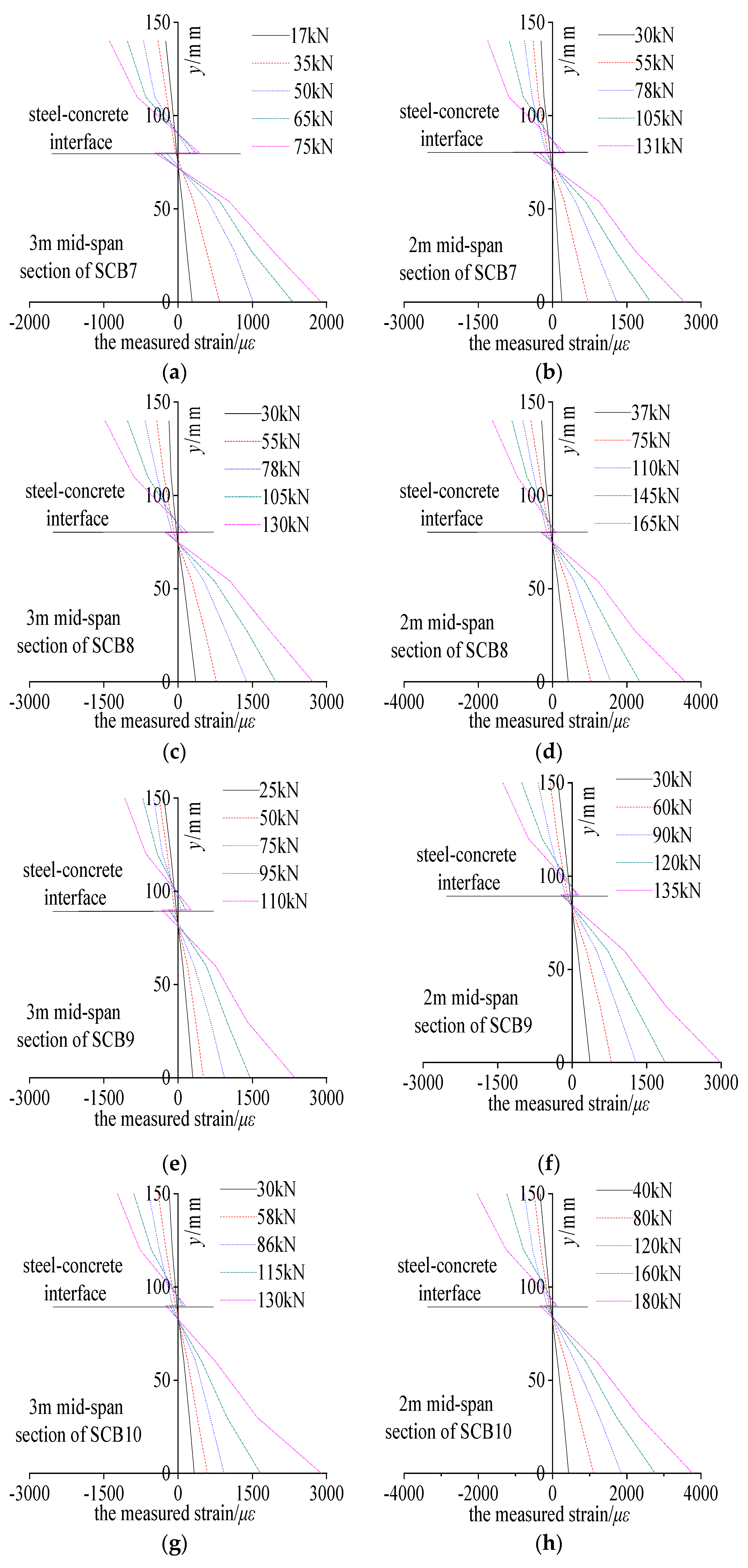
- 2.
- Strain development characteristics in steel beam bottom flanges at mid-span

- 3.
- Strain distribution features at intermediate support sections

Appendix B
Interfacial Slip Behavior
| Shear Connection Degree η | Box-Section Specimen | Slip Value at Position ③ (mm) | Section Specimen | Slip Value at Position ③ (mm) |
|---|---|---|---|---|
| 1.08 | SCB1 | 0.21 | SCB4 | 0.24 |
| 0.57 | SCB2 | 0.28 | SCB5 | 0.31 |
| 1.53 | SCB3 | 0.14 | SCB6 | 0.20 |
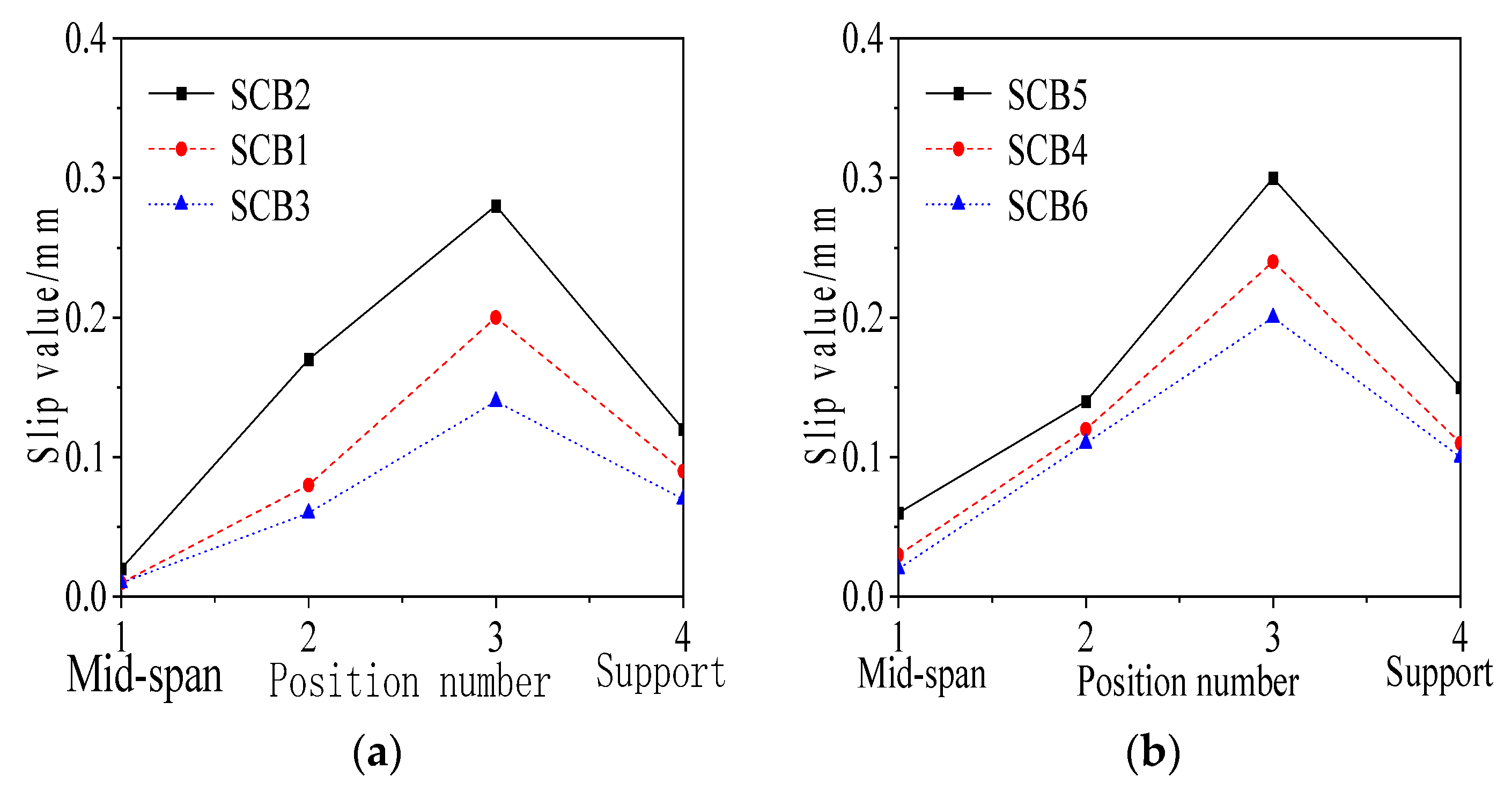
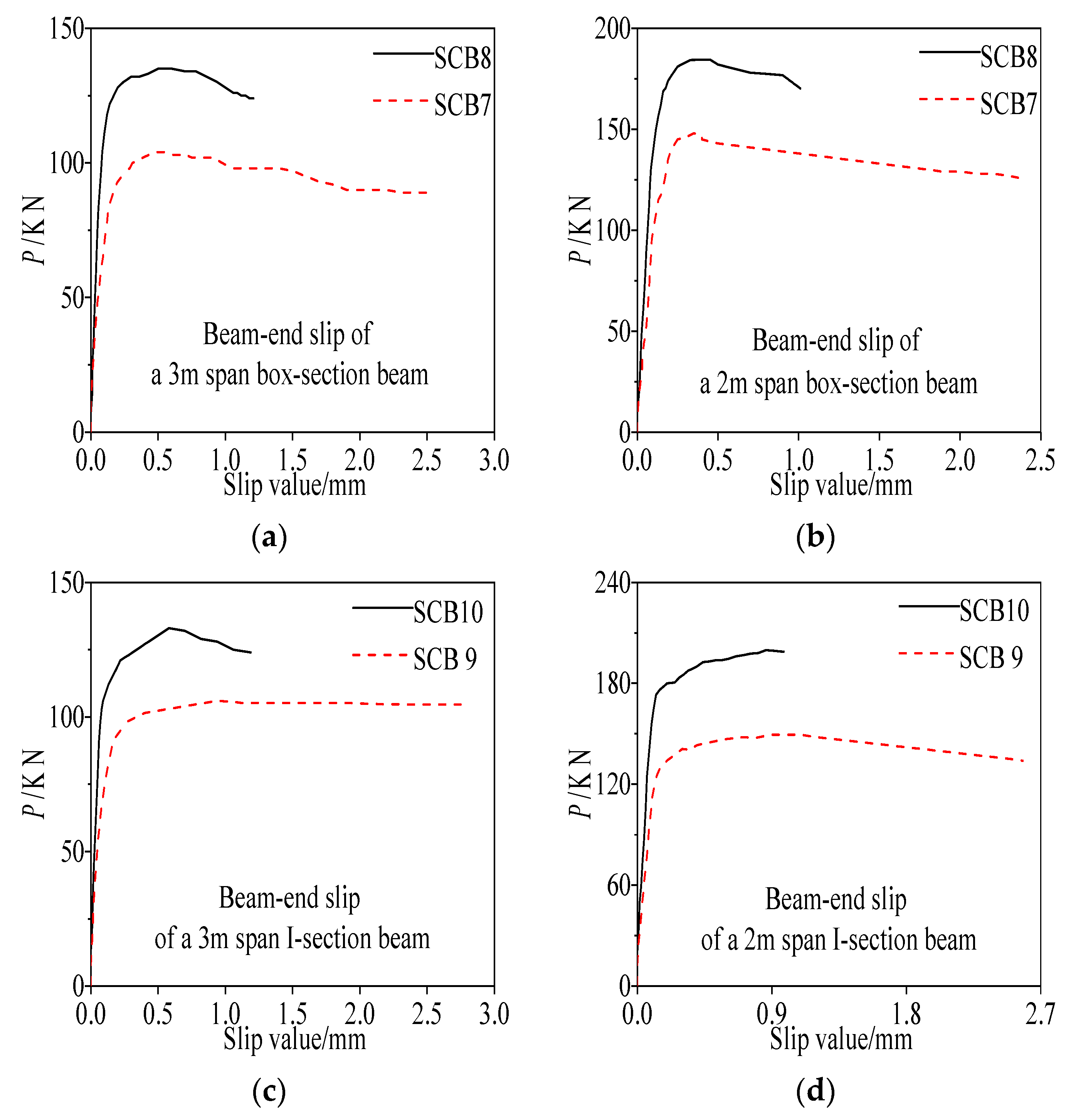
| Steel Beam Section Form | Specimen | Maximum Beam-End Slip of a 3 m Span Beam (mm) | Maximum Beam-End Slip of a 2 m Span Beam (mm) |
|---|---|---|---|
| Box section | SCB7 | 2.55 | 2.36 |
| SCB8 | 1.21 | 1.01 | |
| I section | SCB9 | 2.75 | 2.58 |
| SCB10 | 1.19 | 0.98 |
References
- Nie, J.; Fan, J.; Cai, C.S. Experimental study of partially shear-connected composite beams with profiled sheeting. Eng. Struct. 2008, 30, 1–12. [Google Scholar] [CrossRef]
- Tesser, L.; Scotta, R. Flexural and shear capacity of composite steel truss and concrete beams with inferior precast concrete base. Eng. Struct. 2013, 49, 135–145. [Google Scholar] [CrossRef]
- Gao, S.; Bai, Q.; Guo, L.; Kang, S.-B.; Derlatka, A.; Deng, S. Study on flexural behavior of spliced shallow composite beams with different shear connectors. Eng. Struct. 2022, 253, 113816. [Google Scholar] [CrossRef]
- Banaeipour, A.; Al Sarfin, A.; Thomas, R.J.; Maguire, M.; Sorensen, A.D. Laboratory and field evaluation of commercially available rapid-repair materials for concrete bridge deck repair. J. Perform. Constr. Facil. 2022, 36, 04022031. [Google Scholar] [CrossRef]
- Hossain-Zada, M.K.; Kolagar, S.; Fakoor, M.; Vahedi, A.; Nematzadeh, M.; Tabari, M. Post-heating flexural behavior of reinforced concrete beam with lap-spliced bar and feasibility of improving flexural performance by adding hybrid fibers. Structures 2023, 55, 965–982. [Google Scholar] [CrossRef]
- Kaviani, R.; Naghashnejad, M.; Shabgard, H. Migration and heat transfer modeling of a neutrally buoyant melting particle in Poiseuille flow. Phys. Fluids 2023, 35, 063327. [Google Scholar] [CrossRef]
- Anbari, M.; Oztürk, E.A.; Ates, H. Urban design and upgrading traffic and urban street safety from the perspective of urban users (case study: Tunalı HilmiAnkara Residential Commercial Street). J. Int. Soc. Res. 2020, 13, 506–515. [Google Scholar] [CrossRef]
- Nejad, F.M.; Asadi, M.; Hamedi, G.H.; Esmaeeli, M.R. Using hydrophobic coating on aggregate surfaces to reduce moisture damage in asphalt mixture. J. Mater. Civ. Eng. 2018, 30, 04018238. [Google Scholar] [CrossRef]
- Hamedi, G.H.; Asadi, M.; Nejad, F.M.; Esmaeeli, M.R. Applying asphalt binder modifier in reducing moisture-induced damage of asphalt mixtures. Eur. J. Environ. Civ. Eng. 2021, 25, 2039–2056. [Google Scholar] [CrossRef]
- Iravani, S.N.N.; Ahd, P.D.R.S. Investigation of retrofitting reinforced concrete structures in near-fault regions. Turk. J. Comput. Math. Educ. (TURCOMAT) 2021, 12, 7729–7738. [Google Scholar]
- Khorshidi, M.; Ameri, M.; Goli, A. Cracking performance evaluation and modelling of RAP mixtures containing different recycled materials using deep neural network model. Road Mater. Pavement Des. 2024, 25, 716–735. [Google Scholar] [CrossRef]
- Memarzadeh, A.; Shahmansouri, A.; Nematzadeh, M.; Gholampour, A. A review on fire resistance of steel-concrete composite slim-floor beams. Steel Compos. Struct. Int. J. 2021, 40, 13–32. [Google Scholar] [CrossRef]
- Qin, Y.; Xiong, C.; Zhu, X.; Yin, J.; Zhang, Y.; Fan, Z.; Zou, Y.; Huang, Z. Failure mechanism and impact resistance of a novel all-composite double-corrugated sandwich plate under low-velocity impact. Case Stud. Constr. Mater. 2024, 20, e02724. [Google Scholar] [CrossRef]
- Xu, C.; Su, Q.; Wu, C.; Sugiura, K. Experimental study on double composite action in the negative flexural region of two-span continuous composite box girder. J. Constr. Steel Res. 2011, 67, 1636–1648. [Google Scholar] [CrossRef]
- Memarzadeh, A.; Nematzadeh, M.; Jafarzadeh, H. Experimental study on elastic modulus of steel stub columns encased in RC containing steel fibers. J. Struct. Constr. Eng. 2022, 8, 325–343. [Google Scholar]
- Behseresht, S.; Mehdizadeh, M. Mode I&II SIFs for semi-elliptical crack in a cylinder wrapped with a composite layer. In Proceedings of the 28th Annual International Conference of Iranian Society of Mechanical Engineers-ISME2020, Tehran, Iran, 27–29 May 2020. [Google Scholar]
- Zadeh, S.S.; Joushideh, N.; Bahrami, B.; Niyafard, S. A review on concrete recycling. World J. Adv. Res. Rev. 2023, 19, 784–793. [Google Scholar] [CrossRef]
- Akbarzadeh, M.R.; Ghafourian, H.; Anvari, A.; Pourhanasa, R.; Nehdi, M.L. Estimating compressive strength of concrete using neural electromagnetic field optimization. Materials 2023, 16, 4200. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.Z.; Shi, Y.J.; Wang, Y.Q.; Zhang, R.H. Nonlinear finite element analysis on bending capacity of composite slim beam with deep decking. In Fourth International Conference on Advances in Steel Structures; Shen, Z.Y., Li, G.Q., Chan, S.L., Eds.; Elsevier Science Ltd.: Oxford, UK, 2005; pp. 1445–1450. [Google Scholar] [CrossRef]
- Wang, G.-M.; Zhu, L.; Ji, X.-L.; Ji, W.-Y. Finite Beam Element for Curved Steel–Concrete Composite Box Beams Considering Time-Dependent Effect. Materials 2020, 13, 3253. [Google Scholar] [CrossRef]
- Wang, G.-M.; Zhu, L.; Zhou, G.-P.; Han, B.; Ji, W.-Y. Experimental Research of the Time-Dependent Effects of Steel–Concrete Composite Girder Bridges during Construction and Operation Periods. Materials 2020, 13, 2123. [Google Scholar] [CrossRef] [PubMed]
- Shi, H.; Wei, X.; Fang, H.; Yang, C.; Tang, B. Shear behavior of multi-axial fiber reinforced composite sandwich structures with pultruded profile core. Case Stud. Constr. Mater. 2022, 17, e01652. [Google Scholar] [CrossRef]
- Dehghan, S. Comparison of Seismic Behavior Factors for Reinforced Concrete (RC) Special Moment Resisting Frames (SMRFs) in Iran in Low-, Mid-, and Highrise Buildings Based on Iranian Seismic Standard 2800 and ASCE. J. Econ. Adm. Sci. 2022, 5, 744–750. [Google Scholar]
- Banaeipour, A.; Tavakkolizadeh, M.; Akbar, M.; Hussain, Z.; Ostrowski, K.A.; Bahadori, A.; Spyrka, M. Effects of small deviations in fiber orientation on compressive characteristics of plain concrete cylinders confined with FRP laminates. Materials 2023, 16, 261. [Google Scholar] [CrossRef] [PubMed]
- Deix, K.; Huber, C.; Gogic, J. Efficiency of Alternative Reinforcement Methods for Wooden Ceilings and Their Ecological Aspects. Materials 2025, 18, 2032. [Google Scholar] [CrossRef]
- Lechman, M. Cross-Sectional Analysis of the Resistance of RC Members Subjected to Bending with/without Axial Force. Materials 2022, 15, 1957. [Google Scholar] [CrossRef] [PubMed]
- Mackay, H.M.; Gillespie, P.; Leluau, C. Report on the strength of steel I-beams haunched with concrete. Eng. J. Can. 1923, 6, 365–369. [Google Scholar]
- Viest, I.M. Investigation of stud shear connectors for composite concrete and steel T-beams. J. Am. Concr. Inst. 1956, 27, 875–891. [Google Scholar] [CrossRef]
- ThurliMann, B. Fatigue and static strength of stud sheer connectors. J. ACI 1959, 30, 1287–1302. [Google Scholar] [CrossRef]
- Chen, D. Research on the Effect of Slippage on the Load—Bearing Performance of High—Performance Encased Steel—Concrete Composite Continuous Beams. Master’s Thesis, Jiangsu University, Zhejiang, China, 2016. [Google Scholar]
- Johnson, R.P.; Greenwood, R.D.; Van Dalen, K. Stud Shear-Connectors in Hogging Moment Regions of Composite Beams. Struct. Eng. 1969, 47, 345–350. [Google Scholar]
- Highway Planning and Design Institute; Ministry of Communications (Eds.) Ministry Standard of the People’s Republic of China: Design Specifications for Highway Bridges and Culverts; China Communications Press: Beijing, China, 1975. [Google Scholar]
- JTJ 025-86; Design Specifications for Steel Structures and Timber Structures of Highway Bridges and Culverts. Ministry of Communications of the People’s Republic of China: Beijing, China, 1986.
- EN 1994-1-1—Eurocode 4; Design of Composite Steel and Concrete Structures. European Committee for Standardization (CEN): Brussels, Belgium, 2004.
- Nie, J.; Yu, Z. Reduced Stiffness Method for Deformation Calculation of Steel-Concrete Composite Beams Considering Slip Effects. China Civ. Eng. J. 1995, 6, 11–17. [Google Scholar]
- Nie, J. Calculation and Analysis of Long-Term Deformation of Steel-Concrete Composite Beams. Build. Struct. 1997, 1, 42–46. [Google Scholar]
- Nie, J.; Shen, J. Influence of Slip Effects on the Bending Strength of Steel-Concrete Composite Beams and Its Calculation. China Civ. Eng. J. 1997, 1, 31–36. [Google Scholar]
- Nie, J.; Wang, H.; Tan, Y.; Chen, G. Experimental Study on Steel-High Strength Concrete Composite Beams. J. Build. Struct. 2004, 25, 58–62. [Google Scholar]
- Nie, J.; Li, F.; Fan, J.; Kang, H. Double Reconfiguration of Long-Span Steel-Concrete Continuous Composite Box Girder Bridge. J. Tsinghua Univ. Sci. Technol. 2012, 52, 133–138. [Google Scholar]
- Nie, J.G.; Tao, M.X.; Wu, L.L.; Nie, X.; Li, F.; Lei, L. Advances of Research on Steel-concrete Composite Bridges. China Civ. Eng. J. 2012, 45, 110–122. [Google Scholar]
- Leonhardt, F.; Andrä, W.; Andrä, H.-P. Harre Neues, Verteihafes Verbundmitttel Fur Stahverbund Tragwerke Mit Hoher Dauerfestiigkeit. Beton-Und Stahlbetonbau 1987, 82, 325–331. [Google Scholar] [CrossRef]
- Rong, X.L.; Huang, Q. Experimental Analysis on Mechanical Properties of Corroded Stud Shear Connectors. J. Civ. Environ. Eng. 2012, 34, 15–20. [Google Scholar]
- Nie, J.G.; Qin, K.; Zhou, T.R.; Gao, C.X. Study on Rigidity of Prestressed Steel-concrete Composite Beams. Ind. Constr. 2003, 33, 6–8. [Google Scholar]
- Hou, Z.M.; Xia, H.; Zhang, Y.L. Analytical Solutions to Dynamic Characteristics of Simply-supported Steel-concrete Composite Beams. J. China Railw. Soc. 2014, 36, 100–105. [Google Scholar]
- Hou, Z.M.; Xia, H.; Zhang, Y.L. Dynamic Analysis on Simply-supported Steel-concrete Composite Beams under Moving Loads. J. China Railw. Soc. 2014, 36, 103–108. [Google Scholar]
- Wang, W.A.; Li, Q.; Zhao, C.H.; Zhuang, W.L.; Jiang, J.S.; Xie, B.Z. Dynamic Characteristics of Long-span Externally Prestressed Steel-concrete Composite Structure Bridges. J. Highway Transp. Res. Dev. 2013, 71, 59–65. [Google Scholar]
- Chen, Y.J.; Luo, Q.Z. Fundamental fnatural frequency of steel-concrete composite beams considering shear lag and slip effects. J. Yantai Univ. (Nat. Sci. Eng. Ed.) 2015, 69, 49–53. [Google Scholar]
- Yang, J.J. Analysis of creep stress in steel-concrete composite beams. J. Transp. Sci. Technol. 2014, 1–3. [Google Scholar]
- Wang, Y.H.; Nie, J.G.; Fan, J.S.; Yang, X.G. Torsion Effect in Piers of Curved Steel-concrete Composite Bridges Under Rare Earthquakes. Eng. Mech. 2014, 31, 42–50+56. [Google Scholar]
- Lu, Z.F.; Liu, M.Y.; Li, Q. Creep Effect Analysis of Steel-concrete Composite Bridge Considering Mutative Temperature and Relative Humidity. J. Cent. South Univ. (Sci. Technol.) 2015, 46, 2650–2657. [Google Scholar]
- Cai, J.J.; Tao, M.X.; Nie, J.G. Calculation of Prestress Loss of Externally Prestressed Composite Girder Bridges. Bridge Constr. 2011, 6, 67–70. [Google Scholar]
- He, Y. Durability study of prestressed concrete bridges: A case study of Wuhan Yangtze River Bridge Project. China Sci. Technol. J. Database (Ind. A) 2024, 10, 115–118. [Google Scholar]
- Li, Z.; Yan, S. Seismic test study on frame joint model of Taiyuan First Thermal Power Plant project. Ind. Constr. 1991, 1, 23–30+55. [Google Scholar]
- Nie, J.; Li, S.; Liu, R.; Mo, W. Large-span steel-concrete composite structure for crescent-shaped atrium of Shenzhen China Resources Center. J. Build. Struct. 2004, 6, 126–128. [Google Scholar]
- Hou, G. Structural design of Beijing LG Tower. In Proceedings of the 20th National Conference on High-Rise Building Structures, Hyderabad, India, 11–12 July 2025. [Google Scholar]
- McDonald, B.; Saraf, V.; Ross, B. A spectacular collapse: Koror-Babeldaob (Palau) balanced cantilever prestressed, post-tensioned bridge. Indian Concr. J. 2003, 77, 955–962. [Google Scholar]
- He, X. Stress Redistribution Study and Material Inelasticity and Prestress Loss Coupling Effect in Segmental Concrete Bridges. Preprints 2023, in press. [Google Scholar] [CrossRef]
- Hubler, M.H.; Bazant, Z.P.; Yu, Q. Pervasiveness of excessive segmental bridge deflections: Wake-up call for creep. ACI Struct. J. 2011, 108, 766–774. [Google Scholar] [CrossRef]
- Li, B.X.; Guan, A.J.; Zhou, M.K. Preparation and Performances of Self-Compacting Concrete Used in the Joint Section between Steel and Concrete Box Girders of Edong Yangtze River Highway Bridge. Adv. Mater. Res. 2010, 168, 334–340. [Google Scholar] [CrossRef]
- Yan, X.; Tong, L.; Li, H.; Huang, S.; Fu, Y.; Wang, W.; Pan, H. Effects of the excavation of deep foundation pits on adjacent approach bridges: A case study of Nanjing Yangtze River Bridge. J. Civ. Struct. Health Monit. 2025, 15, 1185–1205. [Google Scholar] [CrossRef]
- Tarantino, A.M.; Dezi, L. Creep Effects in Composite Beams with Flexible Shear Connectors. J. Struct. Eng. 1992, 118, 2063–2080. [Google Scholar] [CrossRef]
- Gilbert, R.I. Time-Dependent Analysis of Composite Steel-Concrete Sections. J. Struct. Eng. 1989, 115, 2687–2705. [Google Scholar] [CrossRef]
- Bradford, M.A.; Gilbert, R.I. Time-Dependent Behavior of Continuous Composite Beams at Service Loads. J. Struct. Eng. 1995, 121, 319–327. [Google Scholar] [CrossRef]
- Fan, L.; Du, G.; Liu, B. Creep Analysis of Steel-Concrete Composite Beams. J. Chongqing Jiaotong Univ. (Nat. Sci. Ed.) 1990, 9, 9–24. [Google Scholar]
- Fan, J.; Nie, J.; Li, Q.; Wang, H. Long-term behavior of composite beams under positive and negative bending. I: Experimental study. J. Struct. Eng. 2010, 136, 849–857. [Google Scholar] [CrossRef]
- Fan, J.; Nie, X.; Li, Q.; Li, Q. Long-term behavior of composite beams under positive and negative bending. II: Analytical study. J. Struct. Eng. 2010, 136, 858–865. [Google Scholar] [CrossRef]
- Li, F.; Wang, X.; Huang, H.; Wang, J. Influence of Shrinkage and Creep on Steel-Concrete Composite Beam Cable-Stayed Bridge. J. Highw. Transp. Res. Dev. 2013, 30, 54–60. [Google Scholar]
- Zhao, G.; Xiang, T.; Xu, T.; Zhan, Y. Stochastic Analysis of Shrinkage and Creep Effects in Steel-Concrete Composite Beams. Chin. J. Comput. Mech. 2014, 31, 67–71. [Google Scholar]
- Bazant, Z.P. Discussion: Algebraic Methods for Creep Analysis of Continuous Composite Beams. J. Struct. Eng. 1996, 122, 423–430. [Google Scholar] [CrossRef]
- Lin, G.; Wang, L.; Lu, Z.-R. Output-only modal analysis of the Humen Bridge from video measurement. J. Phys. Conf. Ser. 2022, 2184, 012043. [Google Scholar] [CrossRef]
- Zhou, Z. A Study on the Distribution of Vortex-Induced Forces on Bridge Main Beams and the Effects of Turbulence. Master’s Thesis, Hunan University, Changsha, China, 2020. [Google Scholar]
- Xu, B.; Li, J.; Luo, Z.; Wu, J.; Liu, Y.; Yang, H.; Pei, X. Analyzing the Spatiotemporal Vegetation Dynamics and Their Responses to Climate Change Along the Ya’an-Linzhi Section of the Sichuan-Tibet Railway. Remote Sens. 2022, 14, 3584. [Google Scholar] [CrossRef]
- Zhao, Y.; Shi, S.S.; Tian, S.M.; Li, G.; Tao, W.; Guo, W. Technical Difficulties and Countermeasure Suggestions in Tunnel Construction of Ya′an-Linzhi Section of Sichuan-Tibet Railway. Tunn. Constr. 2021, 41, 1079–1090. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, L.; Jiang, L.; Wang, K.; Zhang, G.; Feng, T.; Wang, D.; Song, Z.; Yi, X.; Wang, Z.; et al. Engineering Geological Environment and Main Engineering Geological Problems of Ya’an—Linzhi Section of the Sichuan—Tibet Railway. Adv. Eng. Sci. 2021, 53, 29–42. [Google Scholar]
- Fan, R.; Tian, A.; Li, Y.; Gu, Y.; Wei, Z. Research Progress on Machine Learning Prediction of Compressive Strength of Nano-Modified Concrete. Appl. Sci. 2025, 15, 4733. [Google Scholar] [CrossRef]
- Srinivasan, K.; Vivek, S.; Mujiburrahman, K. Investigation of Microstructural Properties of Nano-modified Concrete for Sustainable Environment. J. Environ. Nanotechnol. 2024, 13, 41–47. [Google Scholar] [CrossRef]
- Waki, T.; Ishii, K.; Kikuchi, M. Improved thermo-dynamic behavior of lead-rubber isolation bearings due to distributed lead-core configurations. J. Struct. Constr. Eng. 2019, 84, 1187–1197. [Google Scholar] [CrossRef]
- Zhelyazov, T. Modeling the Response of a Lead Core Rubber Bearing for Seismic Isolation. Adv. Transdiscipl. Eng. 2023, 43, 11–17. [Google Scholar]
- He, Y.; Li, J.; He, W.; Wu, Q.; Xiang, Y.; Yang, Y. Static Behavior of Post-Installed High-Strength Large-Bolt Shear Connector with Fabricated Hybrid Fiber-Reinforced Concrete/Ordinary Concrete Deck. Materials 2025, 18, 1091. [Google Scholar] [CrossRef]
- Zhao, K.; Wei, Y.; Yan, Z.; Li, Q.; Fang, X. Experimental and Analytical Study on the Short-Term Behavior of Locally Bonded Connections in Bamboo–UHPC Composite Beams. Materials 2025, 18, 1224. [Google Scholar] [CrossRef]
- Gautam, B.G.; Xiang, Y.; Liao, X.; Qiu, Z.; Guo, S. Experimental Investigation of a Slip in High-Performance Steel-Concrete Small Box Girder with Different Combinations of Group Studs. Materials 2019, 12, 2781. [Google Scholar] [CrossRef] [PubMed]
- Di, J.; Cao, L.; Han, J. Experimental Study on the Shear Behavior of GFRP–Concrete Composite Beam Connections. Materials 2020, 13, 1067. [Google Scholar] [CrossRef] [PubMed]
- Ni, X.; Anselme, A.O.; Wang, G.; Xing, Y.; Xu, R. Experimental Investigation of Shear Keys for Adjacent Precast Concrete Box Beam Bridges. Materials 2022, 15, 1459. [Google Scholar] [CrossRef]
- Alemayehu, R.W.; Bae, J.; Ju, Y.K.; Park, M.J. Bond Behavior of Concrete-Filled Steel Tube Mega Columns with Different Connectors. Materials 2022, 15, 2791. [Google Scholar] [CrossRef] [PubMed]
- Szewczyk, P. Experimental and Numerical Study of Steel–Concrete Composite Beams Strengthened under Load. Materials 2024, 17, 4510. [Google Scholar] [CrossRef]
- Li, S.; Luo, H.; Zhao, Y.; Zhou, X. Study on the Robust Bridge Deck Pavement System Based on Horseshoe-Shaped Shear Keys. Materials 2025, 18, 1095. [Google Scholar] [CrossRef]
- Hu, Y.; Wei, Y.; Chen, S.; Yan, Y.; Zhang, W. Experimental Study on Timber−Lightweight Concrete Composite Beams with Ductile Bolt Connectors. Materials 2021, 14, 2632. [Google Scholar] [CrossRef]
- GB 50017-2017; Code for Design of Steel Structures. China Planning Press: Beijing, China, 2003.
- TB 10212-2009; Code for Manufacture of Railway Steel Bridges. China Railway Publishing House: Beijing, China, 2009.
- Liu, J. Research on Seismic Energy Dissipation of Steel-Concrete Composite Beams Considering the Performance of Stud Connectors. Master’s Thesis, Central South University, Changsha, China, 2016. [Google Scholar]
- GB 50010-2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2010.
- Nan, H.; Wang, P.; Zhang, Q.; Meng, D.; Lei, Q. Study on the Mechanical Properties of Continuous Composite Beams under Coupled Slip and Creep. Materials 2023, 16, 4741. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Q.; Peng, X.; Xia, K.; Xu, B. A Review of Mechanical Performance Studies on Composite Concrete Beams and Slabs. Materials 2025, 18, 3259. [Google Scholar] [CrossRef] [PubMed]







| Symbol | Description | Unit |
|---|---|---|
| Degree of shear connection | - | |
| Actual number of shear connectors provided | piece | |
| Number of shear connectors required for full shear connection design | piece | |
| Axial compressive strength | MPa | |
| Cube Compressive Strength of Concrete | MPa | |
| Elastic modulus of concrete | MPa | |
| Elastic modulus of steel beam | MPa | |
| Elastic Modulus of Steel Beam | MPa | |
| Stress | MPa | |
| Strain | - | |
| Net span length of composite beam | mm | |
| Calculated span of composite beam | mm | |
| Degree of shear connection in positive moment region | - | |
| degree of shear connection in negative moment region | - | |
| Ultimate bending moment at intermediate support (continuous beam) | kN·m | |
| Ultimate bending moment at mid-span of 3 m span (continuous beam) | kN·m | |
| Ultimate bending moment at mid-span of 2 m span (continuous beam) | kN·m | |
| Ultimate bearing capacity at mid-span of 3 m span (continuous beam) | kN | |
| Ultimate bearing capacity at mid-span of 2 m span (continuous beam) | kN | |
| Load | kN | |
| Ultimate load | kN | |
| Deflection | mm | |
| Measured Deflection | mm | |
| Moment of Inertia | mm4 | |
| Measured Moment of Inertia | mm4 | |
| Transformed section moment of inertia of composite beam | mm4 | |
| Reduced stiffness | 106 N·mm2 | |
| Stiffness reduction coefficient | - | |
| Calculated stiffness value before creep | 106 N·mm2 | |
| Calculated stiffness of the composite beam | 106 N·mm2 | |
| Post-creep measured flexural stiffness | 106 N·mm2 | |
| Pre-creep calculated flexural stiffness | 106 N·mm2 | |
| Measured flexural stiffness of steel-concrete composite beam | 106 N·mm2 | |
| Transformed flexural stiffness of section considering creep | 106 N·mm2 | |
| Flexural stiffness calculated in accordance with Code for Design of Steel Structures (GB 50017-2017) [63] | 106 N·mm2 | |
| Flexural stiffness calculated with reference to provisions in Code for Design of Concrete Structures (GB50010-2010) [66] | 106 N·mm2 | |
| Flexural stiffness coefficient | - | |
| Post-creep stiffness coefficient | - | |
| Pre-creep stiffness coefficient | - | |
| Reduction factor of cubic compressive strength of concrete | - | |
| Measured deflection corresponding to 0.4 times the ultimate load | mm | |
| Theoretical deflection calculated with as the stiffness in the negative moment region | mm | |
| Theoretical deflection calculated with as the stiffness in the negative moment region | mm | |
| Thickness of concrete slab | mm |
| Supporting Method | Simply Supported Composite Beams | Continuous Composite Beams | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Specimen | SCB-1 | SCB-2 | SCB-3 | SCB-4 | SCB-5 | SCB-6 | SCB-7 | SCB-8 | SCB-9 | SCB-10 | |
| Steel Beam Section Form | Box-shaped cross-section | I-shaped cross-section | Box-shaped cross-section | I-shaped cross-section | |||||||
| Number of Studs | 34 | 18 | 48 | 34 | 18 | 48 | 34 | 80 | 34 | 80 | |
| Stud Spacing (mm) | 180 | 310 | 125 | 180 | 310 | 125 | 310 | 125 | 310 | 125 | |
| Shear Connection Degree | Positive Moment Region | 1.08 | 0.57 | 1.53 | 1.08 | 0.57 | 1.53 | 0.57 | 1.53 | 0.57 | 1.53 |
| Negative Moment Region | 0.85 | 1.68 | 0.85 | 1.68 | |||||||
| Span Length (mm) | 3000 | 5000 | |||||||||
| Concrete Slab Width (mm) | 550 | ||||||||||
| Concrete Slab Thickness (mm) | 60 | ||||||||||
| Number of Stirrups | 32Φ8@100 | 50Φ8@100 | |||||||||
| Number of Longitudinal Reinforcing Bars | 6Φ8@100 | 6Φ8@100 (Dense arrangement in the support zone) | |||||||||
| Steel Beam Section Form | Specimen | Shear Connection Degree | Calculated Value of Ultimate Bending Moment (kN.m) | Ultimate Bending Moment Ratio | ||||
|---|---|---|---|---|---|---|---|---|
| Midspan of 3 m Span M1 | Mid-Support M0 | Midspan of 2 m Span M2 | ||||||
| Box Section | SCB7 | 0.57 | 0.85 | 51.91 | −42.27 | 49.25 | 1.23 | 1.17 |
| SCB8 | 1.53 | 1.68 | 65.8 | −53.49 | 62.45 | 1.23 | 1.17 | |
| I-Section | SCB9 | 0.57 | 0.85 | 52.03 | −42.31 | 49.33 | 1.23 | 1.17 |
| SCB10 | 1.53 | 1.68 | 66.16 | −53.68 | 62.62 | 1.23 | 1.17 | |
| Steel Beam Section Form | Specimen | Calculated Value of Bearing Capacity (kN) | Bearing Capacity Ratio | |
|---|---|---|---|---|
| Midspan of 3 m Span P1 | Midspan of 2 m Span P2 | P1/P2 | ||
| Box Section | SCB7 | 109.92 | 159.93 | 0.69 |
| SCB8 | 139.35 | 202.78 | 0.69 | |
| I-Section | SCB9 | 110.17 | 160.22 | 0.69 |
| SCB10 | 140.05 | 203.46 | 0.69 | |
| Steel Beam Section Form | Specimen | Cracking Load in the Negative Moment Region (kN) | Cracking Load for the 3 m Span (kN) | Cracking Load for the 2 m Span (kN) | Average Crack Spacing (mm) | |
|---|---|---|---|---|---|---|
| 3 m Span | 2 m Span | |||||
| Box Section | SCB7 | 20 | 30 | 52 | 74 | 107 |
| SCB8 | 25 | 35 | 61 | 90 | 98 | |
| I-Section | SCB9 | 20 | 30 | 53 | 76 | 105 |
| SCB10 | 25 | 35 | 62 | 93 | 99 | |
| Specimen | η | ζ | EIp (106 N·mm2) | EIm (106 N·mm2) | θm |
| SCB1 | 1.08 | 0.375 | 2.584 | 2.342 | 0.660 |
| SCB2 | 0.57 | 0.455 | 2.442 | 2.176 | 0.613 |
| SCB3 | 1.53 | 0.297 | 2.738 | 2.519 | 0.710 |
| SCB4 | 1.08 | 0.363 | 2.612 | 2.371 | 0.662 |
| SCB5 | 0.57 | 0.439 | 2.475 | 2.228 | 0.622 |
| SCB6 | 1.53 | 0.288 | 2.764 | 2.565 | 0.716 |
| Specimen | EIc (106 N·mm2) | θc | Ec (MPa) | fcu (MPa) | Rfcu (%) |
| SCB1 | 2.584 | 0.727 | 25,394 | 19.1 | 55.36 |
| SCB2 | 2.442 | 0.687 | 24,331 | 16.8 | 48.70 |
| SCB3 | 2.738 | 0.771 | 26,293 | 21.2 | 61.45 |
| SCB4 | 2.612 | 0.734 | 25,080 | 18.4 | 53.33 |
| SCB5 | 2.475 | 0.695 | 23,481 | 15.1 | 43.77 |
| SCB6 | 2.764 | 0.776 | 25,962 | 20.4 | 59.13 |
| Specimen | 3 m Span Deflection (mm) | 2 m Span Deflection (mm) | 3 m Span Deflection (mm) | 2 m Span Deflection (mm) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCB7 | 0.875 | 1.851 | 2.094 | 5.29 | 5.38 | 5.31 | 3.41 | 3.5 | 3.43 | 1.017 | 1.004 | 1.026 | 1.006 |
| SCB8 | 1.75 | 2.041 | 2.313 | 4.75 | 4.82 | 4.77 | 2.69 | 2.74 | 2.7 | 1.015 | 1.004 | 1.019 | 1.004 |
| SCB9 | 0.875 | 1.926 | 2.162 | 5.07 | 5.18 | 5.1 | 3.14 | 3.2 | 3.15 | 1.022 | 1.006 | 1.019 | 1.003 |
| SCB10 | 1.75 | 2.119 | 2.381 | 4.57 | 4.65 | 4.59 | 2.48 | 2.53 | 2.49 | 1.018 | 1.004 | 1.020 | 1.004 |
| Specimen | Shear Connection Degree η | Measured Ultimate Moment | Theoretical Calculated Ultimate Moment | Ultimate Moment Reduction Factor | |
|---|---|---|---|---|---|
| SCB1 | 1.08 | 67.5 | 72.33 | 65.53 | 0.907 |
| SCB2 | 0.57 | 47.5 | 62.31 | 50.24 | 0.806 |
| SCB3 | 1.53 | 77.5 | 80.27 | 75.62 | 0.942 |
| SCB4 | 1.08 | 67 | 71.81 | 65.12 | 0.907 |
| SCB5 | 0.57 | 47.5 | 61.93 | 50.19 | 0.810 |
| SCB6 | 1.53 | 77 | 79.78 | 74.89 | 0.939 |
| Steel Beam Section Form | Specimen | Measured Ultimate Bearing Capacity (kN) | Ratio to Theoretical Bearing Capacity | ||
|---|---|---|---|---|---|
| 3 m Span | 2 m Span | 3 m Span | 2 m Span | ||
| Box-shaped cross-section | SCB7 | 104 | 148 | 0.95 | 0.93 |
| SCB8 | 131 | 185 | 0.94 | 0.91 | |
| I-shaped cross-section | SCB9 | 106 | 149 | 0.96 | 0.93 |
| SCB10 | 133 | 193 | 0.95 | 0.95 | |
| Author (Year) | Specimen Type | Core Variables | Key Post-Creep Indicators | Main Conclusions | This Study’s Advantages |
|---|---|---|---|---|---|
| Fan et al. (2010) [65,66] | Simply supported/cantilever steel-concrete composite beams | Positive/negative bending | 3-year deflection = 2.5× initial; negative moment cracking reduces stiffness | Creep/shrinkage increase deflection; cracking must be considered | Adds box/I-section comparison; quantifies shear connection’s creep inhibition |
| Gilbert & Bradford (1995) [63] | Two-span continuous steel-concrete composite beams | Shrinkage/creep | 340-day deflection increased; internal force redistribution driven by shrinkage | Shrinkage dominates creep-period force redistribution | Studies shear connection × section form coupling; provides clearer parameter rules |
| Nan et al. (2023) [92] | Two-span continuous steel-concrete composite beams | Slip-creep coupling | 728-day deflection +14%; steel beam moment +12% | Slip-creep coupling aggravates deflection; higher shear stiffness mitigates creep | Supplements simply supported/continuous comparison; clarifies negative moment cracking protection |
| Wang et al. (2025) [93] | UHPC/ECC/RC composite beams | Interface roughness, composite layer thickness | Flexural capacity +10–40%; interface bond strength enhanced | Optimizing interface/layer thickness improves creep-period load-bearing capacity | Focuses on classic steel-concrete system (vs. UHPC/ECC); longer test period (3-year data); parameters more engineering-oriented |
| This Study | Simply supported/continuous steel-concrete composite beams (box/I-section) | Shear connection, section form | Full shear connection reduces creep deflection by 15–20%; box-section < I-section by 10–15% | Shear connection is key to creep inhibition; negative moment reinforcement improves crack resistance | Multi-variable coupling tests; quantifies parameter weights; offers direct engineering design suggestions |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, F.; Dai, Y.; He, X.; Lyu, F.; Duan, L. Experimental Investigation on the Bending Performance of Steel–Concrete Composite Beams After Creep. Materials 2025, 18, 5332. https://doi.org/10.3390/ma18235332
Ding F, Dai Y, He X, Lyu F, Duan L. Experimental Investigation on the Bending Performance of Steel–Concrete Composite Beams After Creep. Materials. 2025; 18(23):5332. https://doi.org/10.3390/ma18235332
Chicago/Turabian StyleDing, Faxing, Yang Dai, Xiaolei He, Fei Lyu, and Linli Duan. 2025. "Experimental Investigation on the Bending Performance of Steel–Concrete Composite Beams After Creep" Materials 18, no. 23: 5332. https://doi.org/10.3390/ma18235332
APA StyleDing, F., Dai, Y., He, X., Lyu, F., & Duan, L. (2025). Experimental Investigation on the Bending Performance of Steel–Concrete Composite Beams After Creep. Materials, 18(23), 5332. https://doi.org/10.3390/ma18235332








