Effect of Low Corrosion Levels on the Bond Performance of Lap-Splices in Reinforced Concrete Beams
Abstract
1. Introduction
2. Materials and Methods
2.1. Test Specimens
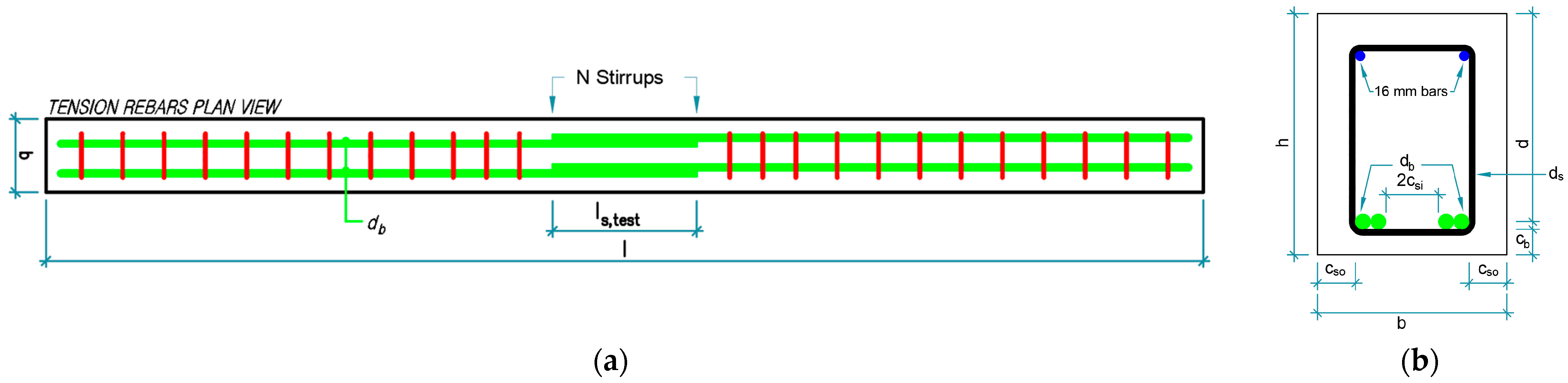
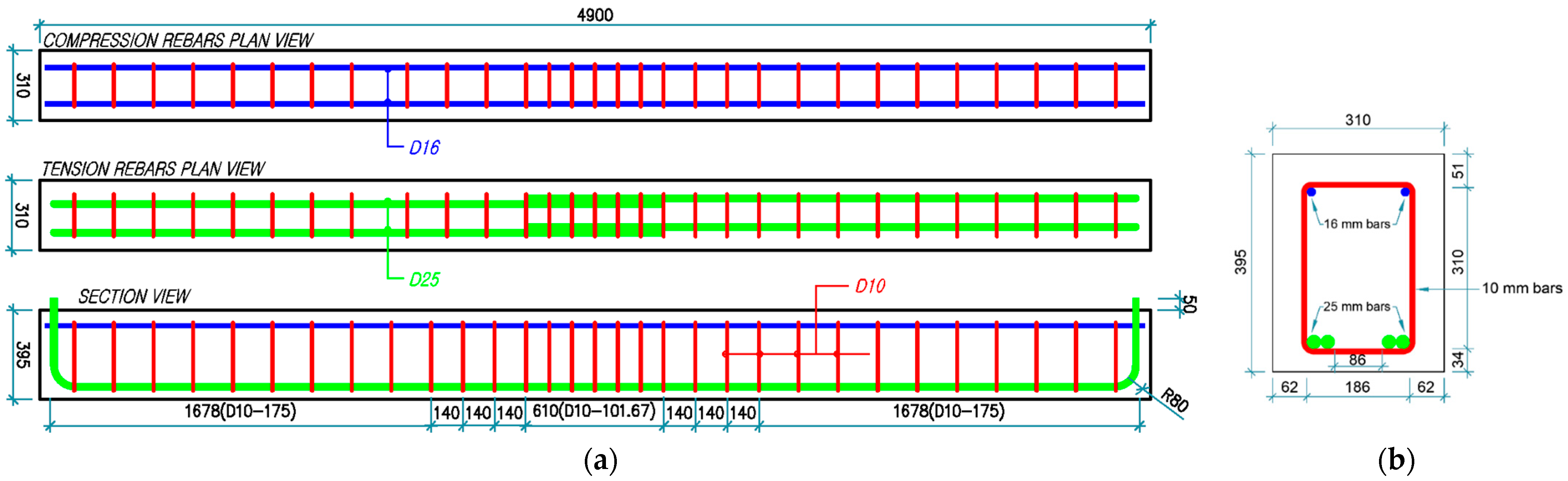
2.1.1. Specimen Fabrication and Configuration
2.1.2. Lap-Splice Length
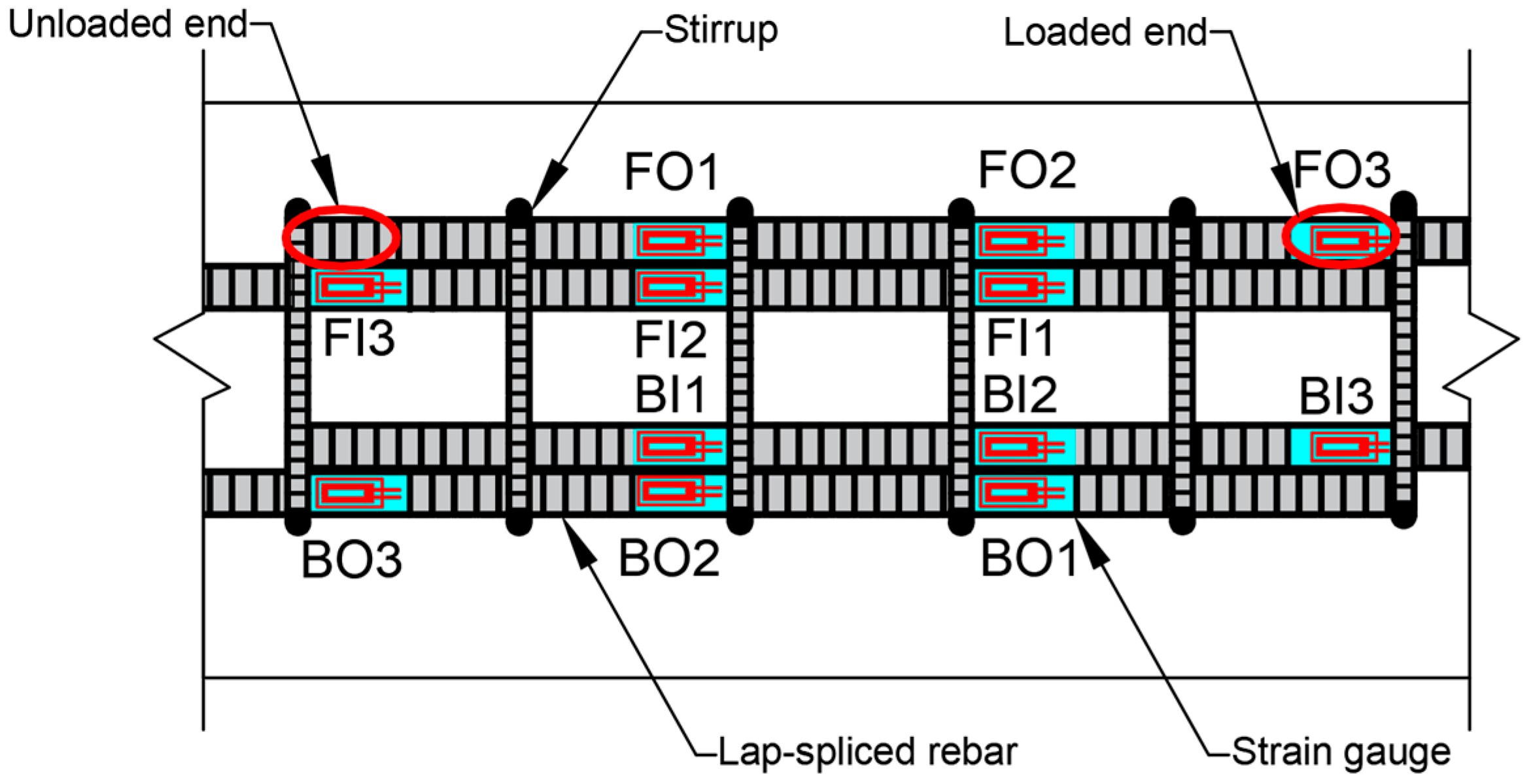
2.1.3. Location of the Strain Gauges
2.1.4. Rebar Ribs
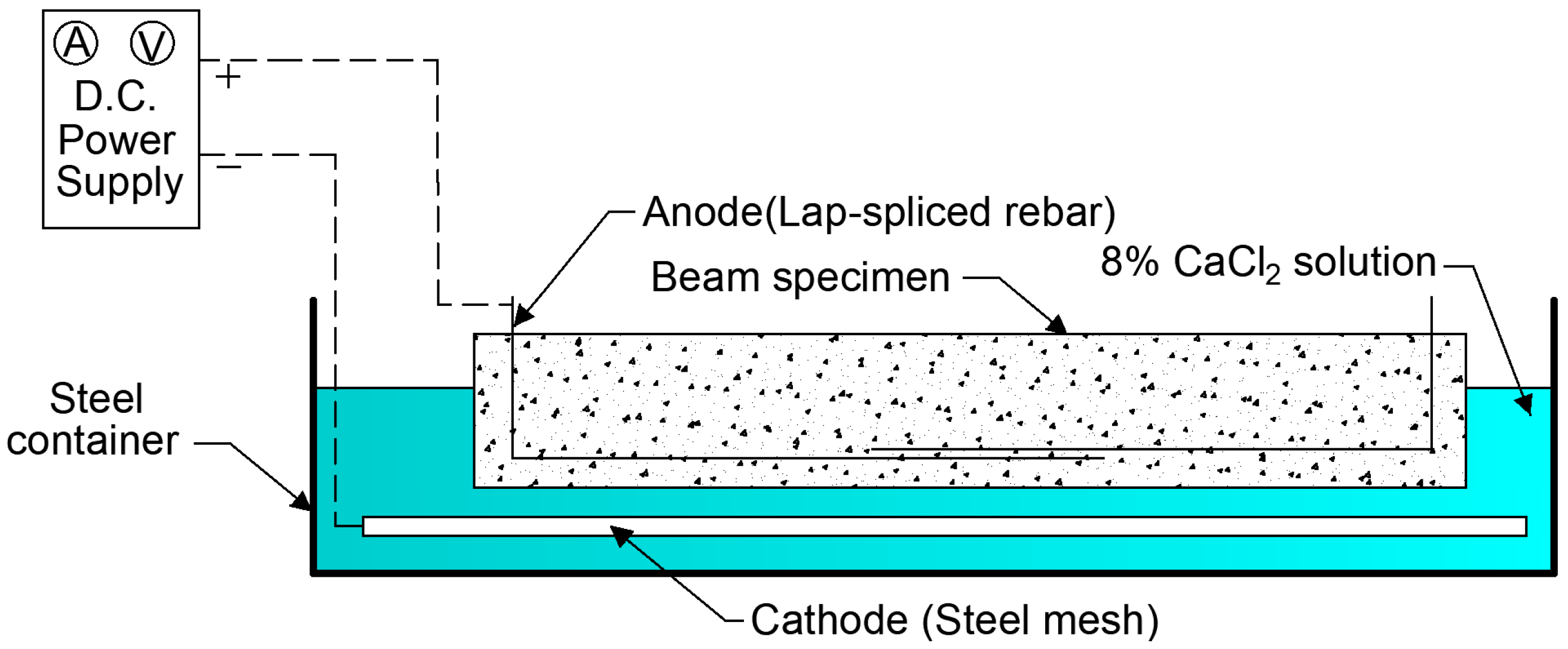
2.2. Electrochemical Corrosion
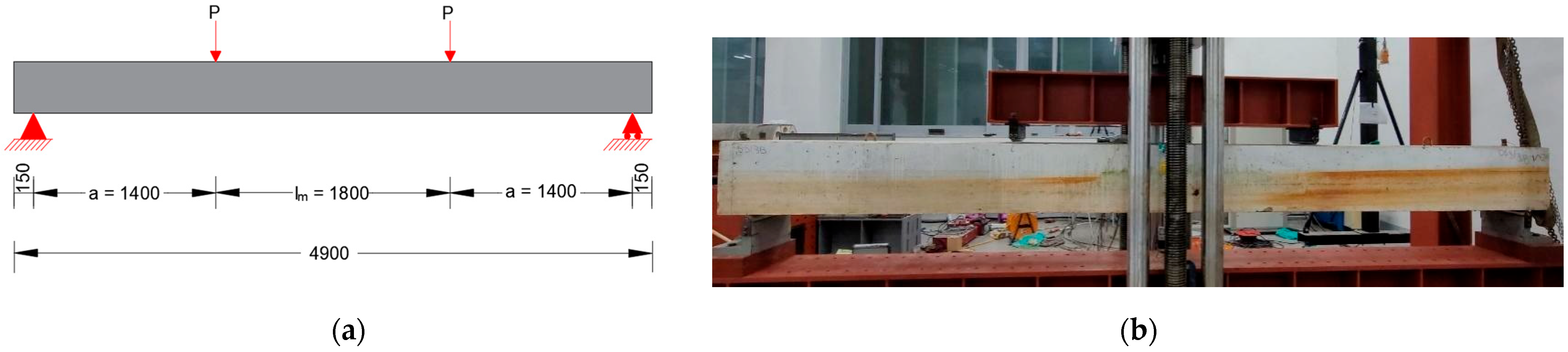
2.3. Test Setup
2.4. Corrosion Measurement
3. Results and Analysis
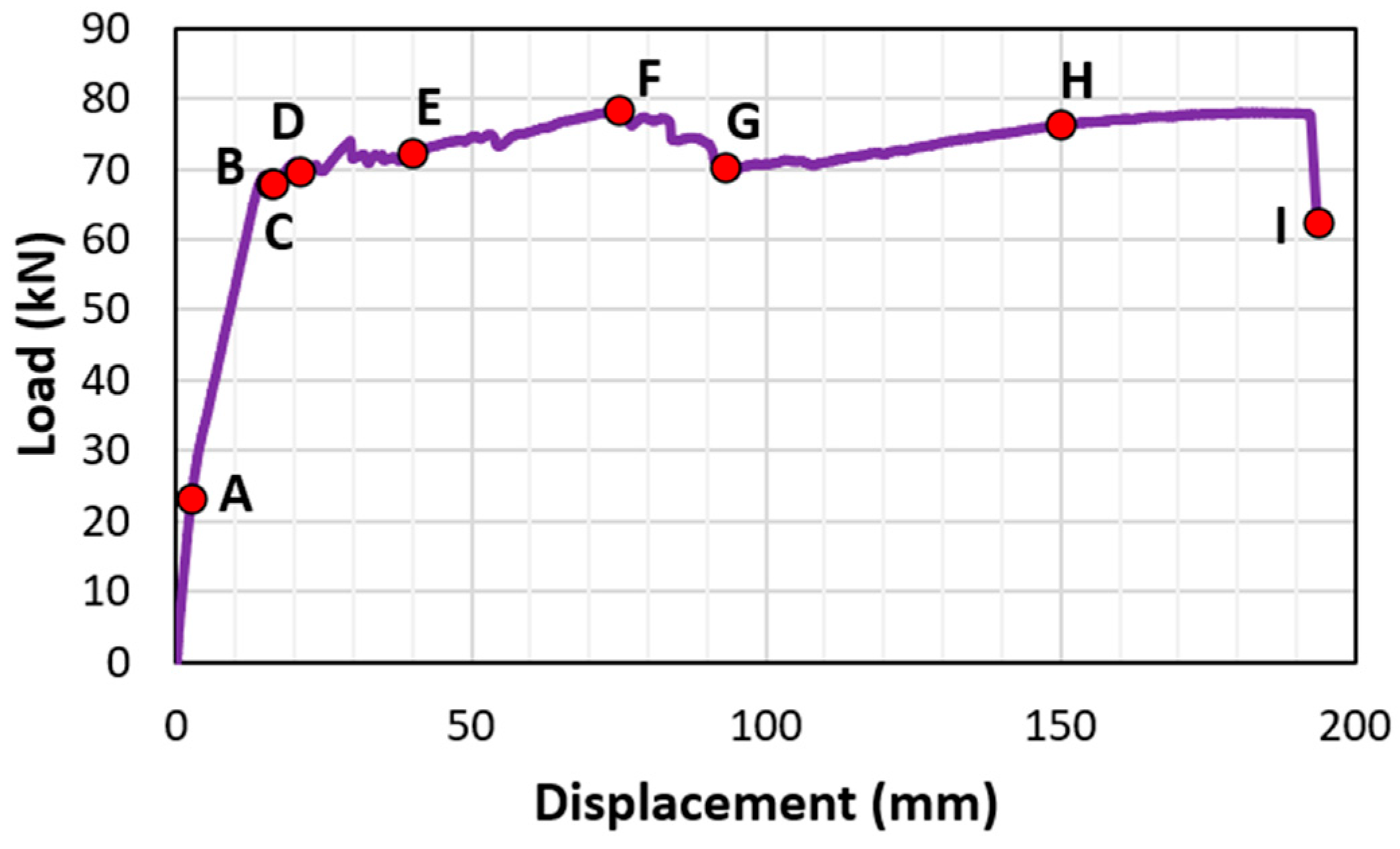
3.1. Failure Mode
3.2. Corrosion Level and Load-Carrying Capacity
3.3. Cracking Patterns According to the Failure Mode
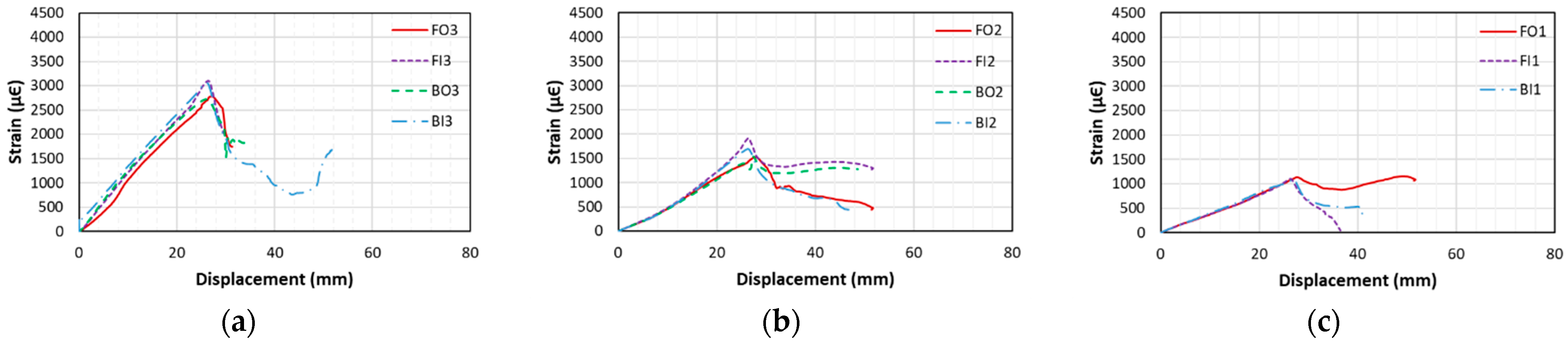
3.4. Strain in Lap-Spliced Rebars
3.4.1. Beams with Insufficient Lap-Splice Lengths
3.4.2. Beams with Sufficient Lap-Splice Lengths
3.5. Initial Stiffness and Ductility
3.6. Bond Strength and Stresses in Rebars with Insufficient Lap-Splice Lengths
3.6.1. Bond Strength
3.6.2. Verification of the Measured Stress with Theoretical Values
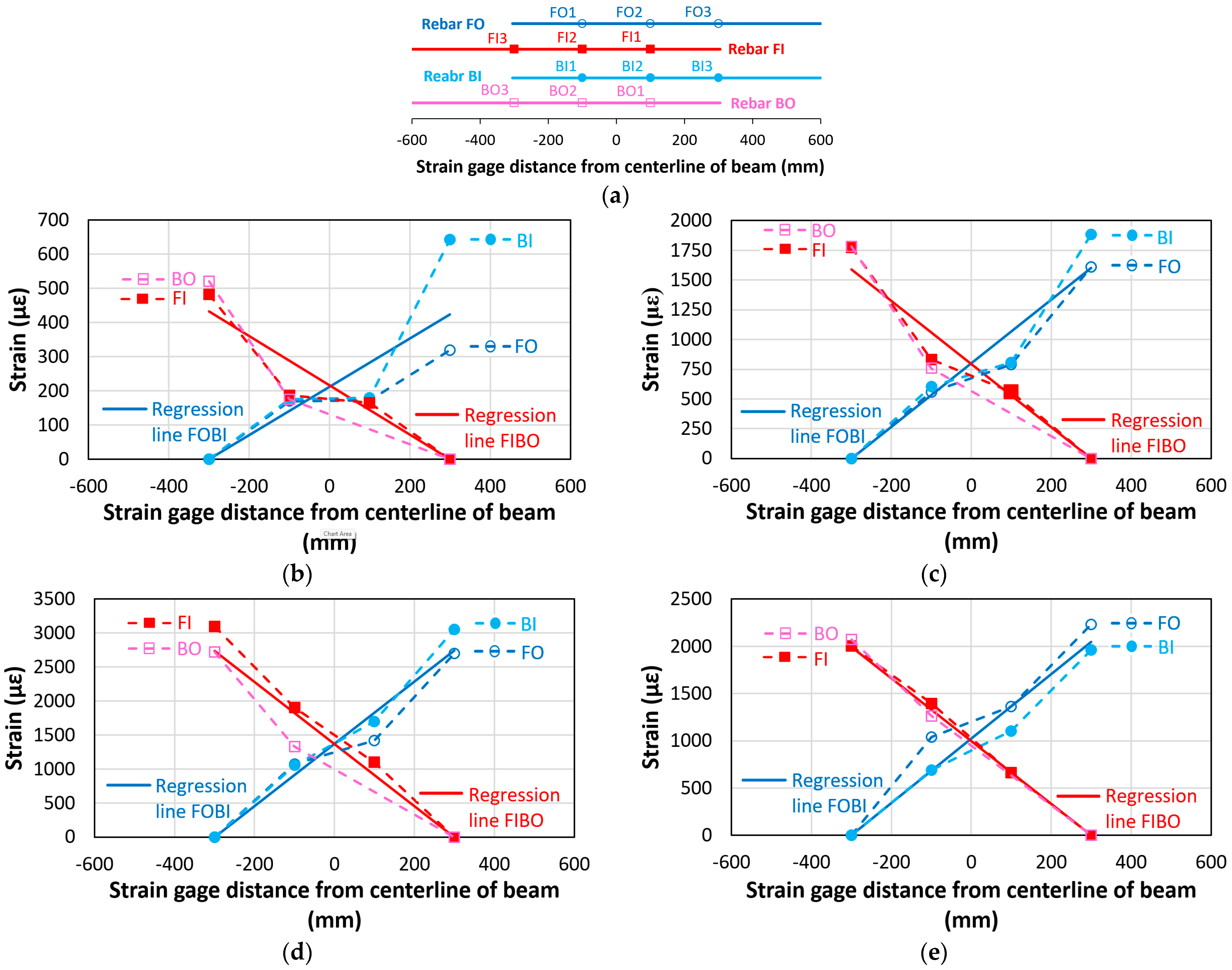
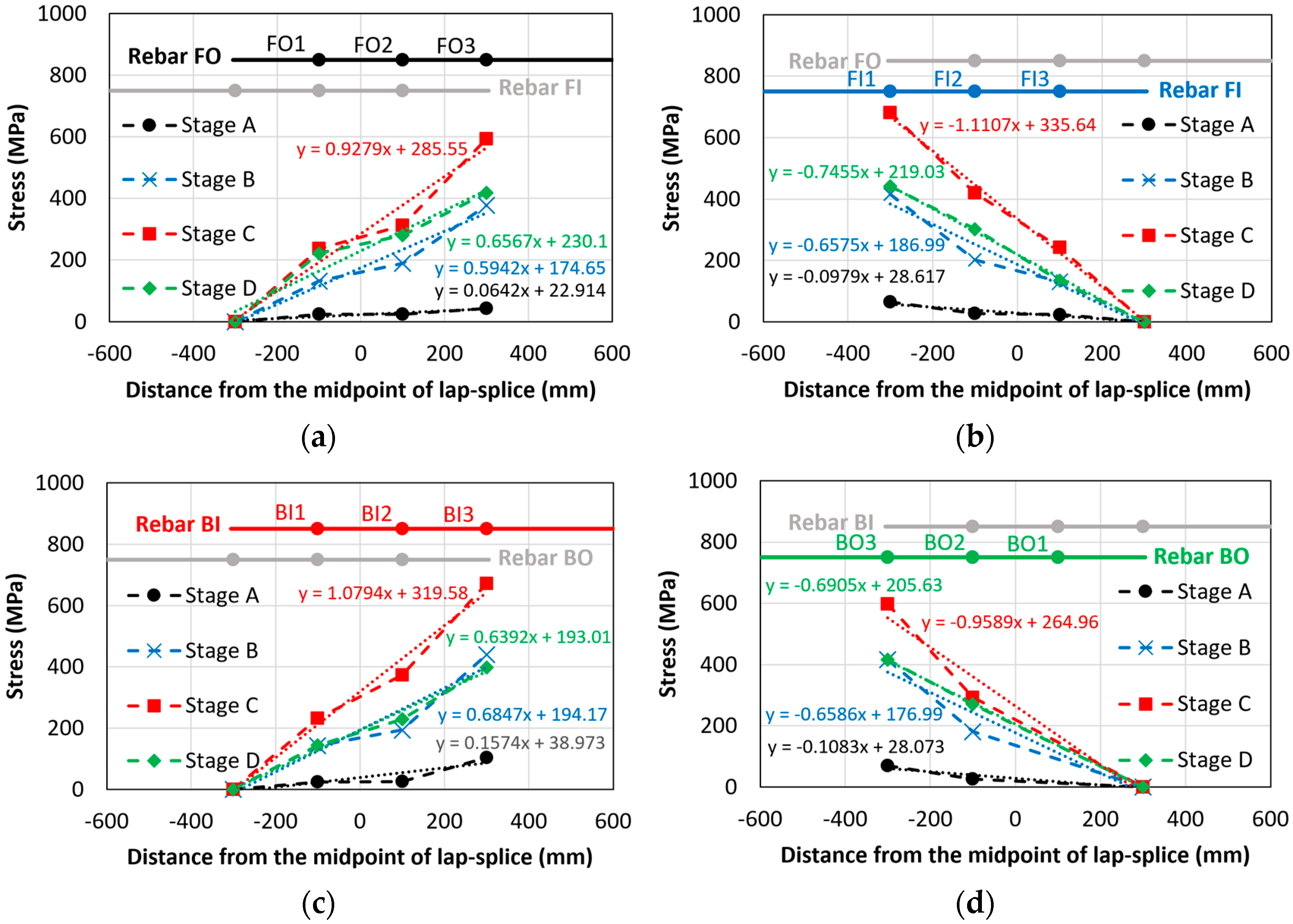
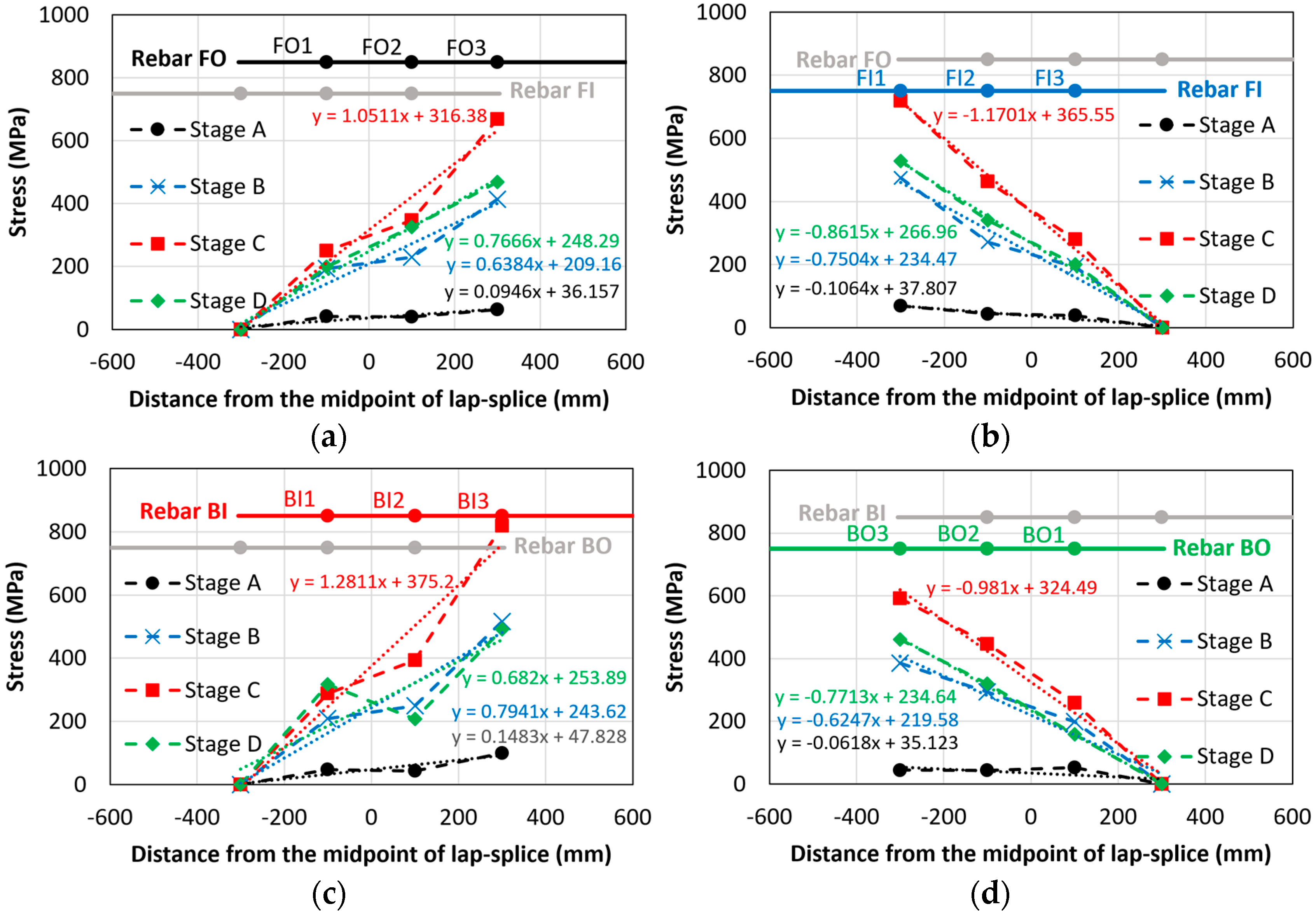
3.6.3. Stress Distribution in Rebars with Insufficient Lap-Splice Lengths
4. Conclusions
- All the corroded beams exhibited higher load-carrying capacities than their non-corroded counterparts. For brittle failure beams, the peak load increase was 8.64–27.68%. Conversely, the value was 0.13–5.77% for the ductile failure beams. These findings can be explained thus: low corrosion causes an increase in surface roughness of rebars and formation of expansive rust particles, which improve the frictional stress and mechanical interlock between rebar and surrounding concrete, thereby improving the bond strength and load-carrying capacity of beams.
- The stirrups, despite corrosion, provided sufficient confinement to tensile rebars and did not affect the bond performance of lap-splices.
- The improved bonding between rebar and surrounding concrete due to low corrosion levels increased the initial stiffnesses of the corroded beams more than those of the non-corroded beams. This indicated that the deflections of beams with lower corrosion levels would be less than those of non-corroded beams.
- Some corroded beams with sufficient lap-splice lengths exhibited decreased ductility index compared with the non-corroded beams of their respective groups. However, residual ductility still sufficiently satisfied the seismic-design requirements.
- Although most corroded beams with insufficient lap-splice lengths exhibited higher ductility indices than their corresponding non-corroded counterparts (with a few exceptions), these beams still suffered sudden (brittle) failures primarily because of the insufficient lap-splice length rather than the corrosion itself. Therefore, retrofitting should be provided for old RC piers with insufficient lap-splice lengths.
- Corroded beams with insufficient lap-splice lengths exhibited increased bond strengths of 13–43% compared with the predictions from existing empirical equations, such as those proposed by Orangun et al. [65], Darwin et al. [66], and Esfahani and Kianoush [67]. This variance indicated that these established equations only provided conservative predictions for the bond strengths of lap-splices at low corrosion levels.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Korean Ministry of Construction. Korean Road Bridge Standard Specification; Korean Ministry of Construction: Sejong, Republic of Korea, 1987.
- Korean Ministry of Construction and Transportation. Korean Highway Bridge Design Code; Korean Ministry of Construction and Transportation: Sejong, Republic of Korea, 2005.
- Sagoe-Crentsil, K.K.; Glasser, F.P. Steel in concrete: Part IA review of the electrochemical and thermodynamic aspects. Mag. Concr. Res. 1989, 41, 205–212. [Google Scholar] [CrossRef]
- Gulikers, J.J.W. Experimental investigations on macrocell corrosion in chloride-contaminated concrete. Heron 1996, 41, 107–123. [Google Scholar]
- López, W.; González, J.A. Influence of the degree of pore saturation on the resistivity of concrete and the corrosion rate of steel reinforcement. Cem. Concr. Res. 1993, 23, 368–376. [Google Scholar] [CrossRef]
- Glass, G.K.; Page, C.L.; Short, N.R. Factors affecting the corrosion rate of steel in carbonated mortars. Corros. Sci. 1991, 32, 1283–1294. [Google Scholar] [CrossRef]
- Gonzalez, J.A.; Lopez, W.; Rodriguez, P. Effects of moisture availability on corrosion kinetics of steel embedded in concrete. Corrosion 1993, 49, 1004–1010. [Google Scholar] [CrossRef]
- Arya, C.; Vassie, P.R.W. Influence of cathode-to-anode area ratio and separation distance on galvanic corrosion currents of steel in concrete containing chlorides. Cem. Concr. Res. 1995, 25, 989–998. [Google Scholar] [CrossRef]
- Alonso, C.; Andrade, C.; González, J.A. Relation between resistivity and corrosion rate of reinforcements in carbonated mortar made with several cement types. Cem. Concr. Res. 1988, 18, 687–698. [Google Scholar] [CrossRef]
- Almusallam, A.A.; Al-Gahtani, A.S.; Aziz, A.R. Effect of reinforcement corrosion on bond strength. Constr. Build. Mater. 1996, 10, 123–129. [Google Scholar] [CrossRef]
- Lundgren, K. Modelling the effect of corrosion on bond in reinforced concrete. Mag. Concr. Res. 2002, 54, 165–173. [Google Scholar] [CrossRef]
- Turan, A.I.; Ayaz, Y.; Yalciner, H.; Kumbasaroglu, A. An experimental evaluation on structural performance level of corroded reinforced concrete frames. Eng. Struct. 2025, 325, 119479. [Google Scholar] [CrossRef]
- Coronelli, D.; Gambarova, P. Structural assessment of corroded reinforced concrete beams: Modeling guidelines. J. Struct. Eng. 2004, 130, 1214–1224. [Google Scholar] [CrossRef]
- Azad, A.K.; Ahmad, S.; Azher, S.A. Residual strength of corrosion-damaged reinforced concrete beams. ACI Mater. J. 2007, 104, 40–47. [Google Scholar] [CrossRef]
- Tuutti, K. Corrosion of Steel in Concrete; Swedish Cement and Concrete Research Institute: Stockholm, Sweden, 1977; pp. 655–661. [Google Scholar]
- Pantazopoulou, S.J.; Papoulia, K.D. Modeling cover-cracking due to reinforcement Corrosion in RC structures. J. Eng. Mech. 2001, 127, 342–351. [Google Scholar] [CrossRef]
- Lee, H.-S.; Noguchi, T.; Tomosawa, F. Evaluation of the bond properties between concrete and reinforcement as a function of the degree of reinforcement corrosion. Cem. Concr. Res. 2002, 32, 1313–1318. [Google Scholar] [CrossRef]
- Lundgren, K. Bond between ribbed bars and concrete. Part 2: The effect of corrosion. Mag. Concr. Res. 2005, 57, 383–395. [Google Scholar] [CrossRef]
- Cairns, J.; Du, Y.; Law, D. Residual bond strength of corroded plain round bars. Mag. Concr. Res. 2006, 58, 221–231. [Google Scholar] [CrossRef]
- Wang, X.G.; Zhang, W.P.; Cui, W.; Wittmann, F.H. Bond strength of corroded steel bars in reinforced concrete structural elements strengthened with CFRP sheets. Cem. Concr. Compos. 2011, 33, 513–519. [Google Scholar] [CrossRef]
- Lin, H.; Zhao, Y. Effects of confinements on the bond strength between concrete and corroded steel bars. Constr. Build. Mater. 2016, 118, 127–138. [Google Scholar] [CrossRef]
- Law, D.W.; Tang, D.; Molyneaux, T.K.C.; Gravina, R. Impact of crack width on bond: Confined and unconfined rebar. Mater. Struct. 2011, 44, 1287–1296. [Google Scholar] [CrossRef]
- Tondolo, F. Bond behaviour with reinforcement corrosion. Constr. Build. Mater. 2015, 93, 926–932. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, X.; Wang, Z.; Huang, H.; Zhou, H. An experimental study on effect of steel corrosion on the bond–slip performance of reinforced concrete. In Proceedings of the 5th International Conference on the Durability of Concrete Structures, ICDCS, Shenzhen, China, 30 June–1 July 2016; Purdue University Press: West Lafayette, IN, USA, 2016; pp. 290–295. [Google Scholar]
- Ma, Y.; Guo, Z.; Wang, L.; Zhang, J. Experimental investigation of corrosion effect on bond behavior between reinforcing bar and concrete. Constr. Build. Mater. 2017, 152, 240–249. [Google Scholar] [CrossRef]
- Vassie, P. Reinforcement corrosion and the durability of concrete bridges. Corros. Prev. Control 1985, 32, 43–49. [Google Scholar] [CrossRef]
- Val, D.V.; Melchers, R.E. Reliability of deteriorating RC slab bridges. J. Struct. Eng. 1997, 123, 1638–1644. [Google Scholar] [CrossRef]
- Castel, A.; François, R.; Arliguie, G. Mechanical behaviour of corroded reinforced concrete beams—Part 1: Experimental study of corroded beams. Mat. Struct. 2000, 33, 539–544. [Google Scholar] [CrossRef]
- Vidal, T.; Castel, A.; François, R. Corrosion process and structural performance of a 17 year old reinforced concrete beam stored in chloride environment. Cem. Concr. Res. 2007, 37, 1551–1561. [Google Scholar] [CrossRef]
- Zhang, R.; Castel, A.; François, R. Serviceability limit state criteria based on steel–concrete bond loss for corroded reinforced concrete in chloride environment. Mater. Struct. 2009, 42, 1407–1421. [Google Scholar] [CrossRef]
- Andrade, C.; Mancini, G. Modelling of Corroding Concrete Structures; RILEM Bookseries; Springer: Dordrecht, The Netherlands, 2011; Volume 5, pp. 243–258. [Google Scholar] [CrossRef]
- Dang, V.H.; François, R. Influence of long-term corrosion in chloride environment on mechanical behaviour of RC beam. Eng. Struct. 2013, 48, 558–568. [Google Scholar] [CrossRef]
- Almusallam, A.A.; Al-Gahtani, A.S.; Aziz, A.R.; Dakhil, F.H.; Rasheeduzzafar. Effect of reinforcement corrosion on flexural behavior of concrete slabs. J. Mater. Civ. Eng. 1996, 8, 123–127. [Google Scholar] [CrossRef]
- Du, Y.G.; Clark, L.A.; Chan, A.H.C. Effect of corrosion on ductility of reinforcing bars. Mag. Concr. Res. 2005, 57, 407–419. [Google Scholar] [CrossRef]
- Torres-Acosta, A.A.; Navarro-Gutierrez, S.; Terán-Guillén, J. Residual flexure capacity of corroded reinforced concrete beams. Eng. Struct. 2007, 29, 1145–1152. [Google Scholar] [CrossRef]
- Rodriguez, J.; Ortega, L.; Casal, J. Load carrying capacity of concrete structures with corroded reinforcement. Constr. Build. Mater. 1997, 11, 239–248. [Google Scholar] [CrossRef]
- Yoon, S.; Wang, K.; Weiss, W.J.; Shah, S.P. Interaction between loading, corrosion, and serviceability of reinforced concrete. ACI Mater. J. 2000, 97, 637–644. [Google Scholar] [CrossRef]
- Otieno, M.; Beushausen, H.; Alexander, M. Prediction of corrosion rate in reinforced concrete structures—A critical review and preliminary results. Mater. Corros. 2012, 63, 777–790. [Google Scholar] [CrossRef]
- Chung, L.; Cho, S.H.; Jay Kim, J.H.; Yi, S.T. Correction factor suggestion for ACI development length provisions based on flexural testing of RC slabs with various levels of corroded reinforcing bars. Eng. Struct. 2004, 26, 1013–1026. [Google Scholar] [CrossRef]
- Banić, D.; Grandić, D.; Bjegović, D. Bond characteristics of corroding reinforcement in concrete beams. In Proceedings of the International Conference Held at the University of Dundee, Scotland, UK, 5–7 July 2005; Thomas Telford Publishing: London, UK, 2005; pp. 203–210. [Google Scholar]
- Mangat, P.S.; Elgarf, M.S. Bond characteristics of corroding reinforcement in concrete beams. Mat. Struct. 1999, 32, 89–97. [Google Scholar] [CrossRef]
- Xia, M.Y.; Guo, R.; Lin, Q.S.; Yu, Z.X. Prediction model for the bond behaviour of low-corrosion reinforced concrete considering corrosion time variability. Constr. Build. Mater. 2024, 444, 137891. [Google Scholar] [CrossRef]
- Yalciner, H.; Eren, O.; Sensoy, S. An experimental study on the bond strength between reinforcement bars and concrete as a function of concrete cover, strength and corrosion level. Cem. Concr. Res. 2012, 42, 643–655. [Google Scholar] [CrossRef]
- Zhang, W.P.; Chen, H.; Gu, X.L. Bond behaviour between corroded steel bars and concrete under different strain rates. Mag. Concr. Res. 2016, 68, 364–378. [Google Scholar] [CrossRef]
- Dai, J.; Kato, E.; Iwanami, M.; Yokota, H. Cracking and tension stiffening behavior of corroded RC members. Rep. Port Airpt. Res. Inst. 2008, 46, 3–24. [Google Scholar]
- Fang, C.; Lundgren, K.; Chen, L.; Zhu, C. Corrosion influence on bond in reinforced concrete. Cem. Concr. Res. 2004, 34, 2159–2167. [Google Scholar] [CrossRef]
- Aryanto, A.; Shinohara, Y. Bond behavior between steel and concrete in low level corrosion of reinforcing steel. In Proceedings of the 15th World Conference on Earthquake Engineering (15WCEE), Lisbon, Portugal, 24–28 September 2012; pp. 24–28. Available online: https://www.iitk.ac.in/nicee/wcee/article/WCEE2012_0369.pdf (accessed on 16 November 2025).
- Kim, H.R.; Choi, W.C.; Yoon, S.C.; Noguchi, T. Evaluation of bond properties of reinforced concrete with corroded reinforcement by uniaxial tension testing. Int. J. Concr. Struct. Mater. 2016, 10, 43–52. [Google Scholar] [CrossRef]
- Al-Hammoud, R.; Soudki, K.; Topper, T.H. Bond analysis of corroded reinforced concrete beams under monotonic and fatigue loads. Cem. Concr. Compos. 2010, 32, 194–203. [Google Scholar] [CrossRef]
- Sotoud, S.; Aboutaha, R.S. Flexural strength of corroded lap spliced RC bridge column section. In Proceedings of the Structures Congress 2014, Boston, MA, USA, 3–5 April 2014; American Society of Civil Engineers: Reston, VA, USA, 2014; pp. 303–312. [Google Scholar]
- Shihata, A. CFRP Strengthening of RC Beams with Corroded Lap Spliced Steel Bars. Master of Applied Science Thesis, University of Waterloo, Waterloo, ON, Canada, 2011. [Google Scholar]
- Pantazopoulou, S.J.; Petrou, M.F.; Spastri, V.; Archontas, N.; Christofides, C. The performance of corroded lap splices in reinforced concrete beams. Corros. Rev. 2019, 37, 31–44. [Google Scholar] [CrossRef]
- Moodi, Y.; Sohrabi, M.R.; Mousavi, S.R. Effects of stirrups in spliced region on the bond strength of corroded splices in reinforced concrete (RC) beams. Constr. Build. Mater. 2020, 230, 116873. [Google Scholar] [CrossRef]
- Gillani, A.S.M.; Lee, S.G.; Lee, S.H.; Lee, H.; Hong, K.J. Local behavior of lap-spliced deformed rebars in reinforced concrete beams. Materials 2021, 14, 7186. [Google Scholar] [CrossRef]
- ACI 318-19; Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2022.
- ACI 408R-03; Bond and Development of Straight Reinforcing Bars in Tension. American Concrete Institute: Farmington Hills, MI, USA, 2003; pp. 1–49.
- ASTM G1-03(2017); Standard Practice for Preparing, Cleaning, and Evaluating Corrosion Test Specimens. 1st ed, ASTM International: West Conshohocken, PA, USA, 2015.
- Tastani, S.P.; Pantazopoulou, S.J. Behavior of corroded bar anchorages. ACI Struct. J. 2007, 104, 756. [Google Scholar] [CrossRef]
- Jang, I.Y.; Park, H.G.; Kim, S.S.; Kim, J.H.; Kim, Y.G. On the ductility of high-strength concrete beams. Int. J. Concr. Struct. Mater. 2008, 2, 115–122. [Google Scholar] [CrossRef]
- Pam, H.J.; Kwan, A.K.H.; Islam, M.S. Flexural strength and ductility of reinforced normal- and high-strength concrete beams. Proc. Inst. Civ. Eng.—Struct. Build. 2001, 146, 381–389. [Google Scholar] [CrossRef]
- Ling, J.H.; Lim, Y.T.; Jusli, E. Methods to determine ductility of structural members: A review. J. Civ. Eng. Forum 2000, 9, 181–194. [Google Scholar] [CrossRef]
- Transportation Officials. Subcommittee on Bridges. AASHTO Guide Specifications for LRFD Seismic Bridge Design; AASHTO: Washington, DC, USA, 2011. [Google Scholar]
- Department of Transportation, State of California. Caltrans Seismic Design Criteria, Version 1.7; California Department of Transportation: Sacramento, CA, USA, 2013.
- Rakhshanimehr, M.; Esfahani, M.R.; Kianoush, M.R.; Mohammadzadeh, B.A.; Mousavi, S.R. Flexural ductility of reinforced concrete beams with lap-spliced bars. Can. J. Civ. Eng. 2014, 41, 594–604. [Google Scholar] [CrossRef]
- Ahmad, S.H.; Barker, R. Flexural behavior of reinforced high-strength lightweight concrete beams. ACI Struct. J. 1991, 88, 69–77. [Google Scholar] [CrossRef] [PubMed]
- Ashour, S.A. Effect of compressive strength and tensile reinforcement ratio on flexural behavior of high-strength concrete beams. Eng. Struct. 2000, 22, 413–423. [Google Scholar] [CrossRef]
- Orangun, J.; Jirsa, C.; Breen, J.O. The Strength of Anchor Bars: A Reevaluation of Test Data on Development Length and Splices; Center for Highway Research, University of Texas at Austin: Austin, TX, USA, 1975. [Google Scholar]
- Darwin, D.; Tholen, M.L.; Idun, E.K.; Zuo, J. Splice Strength of High Relative Rib Area Reinforcing Bars; University of Kansas Center for Research, Inc.: Lawrence, KS, USA, 1995. [Google Scholar]
- Esfahani, M.R.; Kianoush, M.R. Development/splice length of reinforcing bars. ACI Struct. J. 2005, 102, 22–30. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Lin, H. The Bond Behaviour Between Concrete and Corroded Reinforcement: State of the Art. In Proceedings of the International Conference on Durability of Concrete Structures, Rovinj, Croatia, 20–22 March 2019. [Google Scholar]














| Specimens | Notation | MPa | MPa | mm | mm | mm | mm | mm | mm | mm | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Group 1 | C27Y500S10 | 27.10 | 500 | 10 | 7 | 348.50 | 34 | 62 | 43 | 610 | 1014 |
| Group 2 | C27Y500S13 | 27.50 | 500 | 13 | 6 | 350.50 | 32 | 56 | 49 | 610 | 1006 |
| Group 3 | C27Y300S10 | 26.75 | 300 | 10 | 7 | 348.50 | 34 | 62 | 43 | 610 | 532 |
| Group 4 | C24Y300S13 | 23.45 | 300 | 13 | 6 | 350.50 | 32 | 56 | 49 | 610 | 569 |
| Failure Mode | Corroded Specimens | Non-Corroded Specimens | Difference (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Specimen | Rebar Type | % | % | kN | Specimen | kN | |||
| Bond (brittle) Failure | CC27Y500S10-1 | KSHS | 3.17 | 14.36 | 108.79 | NC27Y500S10-1 | 104.23 | 98.46 | 10.49 |
| CC27Y500S10-2 | 3.03 | 19.08 | 125.71 | NC27Y500S10-2 | 101.83 | 27.68 | |||
| CC27Y500S10-3 | 2.34 | 13.80 | 106.97 | NC27Y500S10-3 | 89.32 | 8.64 | |||
| CC27Y500S13-1 | TWPS | 1.01 | 10.31 | 112.76 | NC27Y500S13-1 | 91.62 | 95.71 | 17.81 | |
| CC27Y500S13-2 | 0.78 | 8.77 | 113.94 | NC27Y500S13-2 | 104.87 | 19.05 | |||
| CC27Y500S13-3 | 1.02 | 5.04 | 113.11 | NC27Y500S13-3 | 90.64 | 18.18 | |||
| Yielding (ductile) Failure | CC27Y300S10-1 | TWPS | 0.79 | 5.66 | 78.72 | NC27Y300S10-1 | 74.26 | 74.85 | 5.17 |
| CC27Y300S10-2 | 0.91 | 11.76 | 79.17 | NC27Y300S10-2 | 76.27 | 5.77 | |||
| CC27Y300S10-3 | 1.05 | 6.44 | 74.95 | NC27Y300S10-3 | 74.02 | 0.13 | |||
| CC24Y300S13-1 | KSHS | 3.26 | 11.46 | 81.67 | NC24Y300S13-1 | 76.47 | 77.09 | 5.94 | |
| CC24Y300S13-2 | 3.52 | 4.21 | 78.18 | NC24Y300S13-2 | 78.78 | 1.41 | |||
| CC24Y300S13-3 | 1.20 | 8.82 | 79.26 | NC24Y300S13-3 | 76.03 | 2.81 | |||
| Failure Mode | Specimen | kN/mm | Specimen | kN/mm | ||
|---|---|---|---|---|---|---|
| Bond (brittle) Failure | CC27Y500S10-1 | 4.66 | 1.20 | NC27Y500S10-1 | 3.46 | 1.14 |
| CC27Y500S10-2 | 4.14 | 1.21 | NC27Y500S10-2 | 3.32 | 1.17 | |
| CC27Y500S10-3 | 4.56 | 1.21 | NC27Y500S10-3 | 3.36 | 1.18 | |
| CC27Y500S13-1 | 4.52 | 1.26 | NC27Y500S13-1 | 3.61 | 1.20 | |
| CC27Y500S13-2 | 4.69 | 1.23 | NC27Y500S13-2 | 3.78 | 1.16 | |
| CC27Y500S13-3 | 4.77 | 1.22 | NC27Y500S13-3 | 3.77 | 1.35 | |
| Yielding (ductile) Failure | CC27Y300S10-1 | 4.86 | 10.70 | NC27Y300S10-1 | 3.55 | 13.50 |
| CC27Y300S10-2 | 4.96 | 5.72 | NC27Y300S10-2 | 3.63 | 11.01 | |
| CC27Y300S10-3 | - | - | NC27Y300S10-3 | 3.52 | 9.90 | |
| CC24Y300S13-1 | 5.46 | 6.72 | NC24Y300S13-1 | 3.90 | 9.57 | |
| CC24Y300S13-2 | 5.17 | 12.77 | NC24Y300S13-2 | 3.66 | 11.97 | |
| CC24Y300S13-3 | 5.22 | 6.35 | NC24Y300S13-3 | 3.53 | 11.73 |
| Specimen | kN | MPa | MPa | MPa | MPa | ||||
|---|---|---|---|---|---|---|---|---|---|
| C27Y500S10-1 | 108.79 | 27.10 | 0.009083 | 24,467.10 | 8.99 | 0.33 | 0.89 | 500.55 | 5.13 |
| C27Y500S10-2 | 125.71 | 27.10 | 0.009083 | 24,467.10 | 8.99 | 0.33 | 0.89 | 578.40 | 5.93 |
| C27Y500S10-3 | 106.97 | 27.10 | 0.009083 | 24,467.10 | 8.99 | 0.33 | 0.89 | 492.18 | 5.04 |
| C27Y500S13-1 | 112.76 | 27.50 | 0.009031 | 24,647.01 | 8.93 | 0.33 | 0.89 | 515.53 | 5.28 |
| C27Y500S13-2 | 113.94 | 27.50 | 0.009031 | 24,647.01 | 8.93 | 0.33 | 0.89 | 520.92 | 5.34 |
| C27Y500S13-3 | 113.11 | 27.50 | 0.009031 | 24,647.01 | 8.93 | 0.33 | 0.89 | 517.13 | 5.30 |
| Reference | Equation |
|---|---|
| Orangun et al. (1975) [67] | |
| Darwin et al. (1995) [68] | |
| Esfahani and Kianoush (2005) [69] |
| Specimen (Corroded) | Corrosion Level (%) | Bond Strength (MPa) | Specimen (Non-Corroded) | Bond Strength (MPa) | Bond Strength (Percentage Increase in Bond Strength of Corroded Lap-Splices) | |||
|---|---|---|---|---|---|---|---|---|
| Average Non-Corroded | Orangun et al. (1975) [67] | Darwin et al. (1995) [68] | Esfahani & Kianoush (2005) [69] | |||||
| CC27Y500S10-1 | 3.17 | 5.13 | NC27Y500S10-1 | 5.07 | 4.79(7.17) | 4.46(15.02) | 4.15(23.61) | 4.08(25.74) |
| CC27Y500S10-2 | 3.03 | 5.93 | NC27Y500S10-2 | 4.95 | 4.79(23.89) | 4.46(32.96) | 4.15(42.89) | 4.08(45.34) |
| CC27Y500S13-3 | 2.34 | 5.04 | NC27Y500S13-3 | 4.34 | 4.79(5.29) | 4.46(13.00) | 4.15(21.45) | 4.08(23.53) |
| CC27Y300S10-1 | 1.01 | 5.28 | NC27Y300S10-1 | 4.43 | 4.63(14.12) | 4.39(20.27) | 4.22(25.12) | 4.33(21.94) |
| CC24Y300S10-2 | 0.78 | 5.34 | NC24Y300S10-2 | 5.07 | 4.63(15.42) | 4.39(21.64) | 4.22(26.54) | 4.33(23.33) |
| CC24Y300S10-3 | 1.02 | 5.30 | NC24Y300S10-3 | 4.38 | 4.63(14.55) | 4.39(20.73) | 4.22(25.59) | 4.33(22.40) |
| Beam | Loading Stage | Slope of Corroded Rebar Stress | Slope of Non-Corroded Rebar Stress | ||||||
|---|---|---|---|---|---|---|---|---|---|
| FO | FI | BI | BO | FO | FI | BI | BO | ||
| C27Y500S10-1 | A | 0.0642 | −0.0979 | 0.2125 | −0.1776 | 0.0946 | −0.1064 | 0.1483 | −0.0618 * |
| B | 0.5942 | −0.6575 | 0.6444 | −0.6200 | 0.6384 | −0.7504 | 0.7941 | −0.6247 * | |
| C | 0.9279 | −1.1107 | 1.0794 | −0.9589 | 1.0511 | −1.1701 | 1.2811 | −0.981 * | |
| D | 0.6567 | −0.7455 | 0.3796 | −0.7507 | 0.7666 | −0.8615 | 0.682 | −0.7713 * | |
| C27Y500S13-1 | A | 0.0434 | −0.0397 | 0.0502 | −0.0409 | 0.0778 | −0.1592 | 0.0862 | −0.1863 |
| B | 0.7510 | −0.7008 | 0.7172 | −0.7741 | 0.6936 | −0.6417 | 0.6386 | −0.7496 | |
| C | 1.1629 | −1.079 | 0.9513 | −1.3474 | 1.0247 | −0.9011 | 0.9208 | −1.0840 | |
| D | 0.7555 | −0.5207 | 0.9957 | −1.0539 | 0.8068 | −1.0006 | 0.8194 | −0.7835 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gillani, A.S.M.; Yi, C.; Hong, K.-J. Effect of Low Corrosion Levels on the Bond Performance of Lap-Splices in Reinforced Concrete Beams. Materials 2025, 18, 5300. https://doi.org/10.3390/ma18235300
Gillani ASM, Yi C, Hong K-J. Effect of Low Corrosion Levels on the Bond Performance of Lap-Splices in Reinforced Concrete Beams. Materials. 2025; 18(23):5300. https://doi.org/10.3390/ma18235300
Chicago/Turabian StyleGillani, Agha Syed Muhammad, Chongku Yi, and Kee-Jeung Hong. 2025. "Effect of Low Corrosion Levels on the Bond Performance of Lap-Splices in Reinforced Concrete Beams" Materials 18, no. 23: 5300. https://doi.org/10.3390/ma18235300
APA StyleGillani, A. S. M., Yi, C., & Hong, K.-J. (2025). Effect of Low Corrosion Levels on the Bond Performance of Lap-Splices in Reinforced Concrete Beams. Materials, 18(23), 5300. https://doi.org/10.3390/ma18235300







