The MT-FEM Model for Predicting Young’s Modulus of Graphene Composites with Complex Morphologies
Abstract
1. Introduction
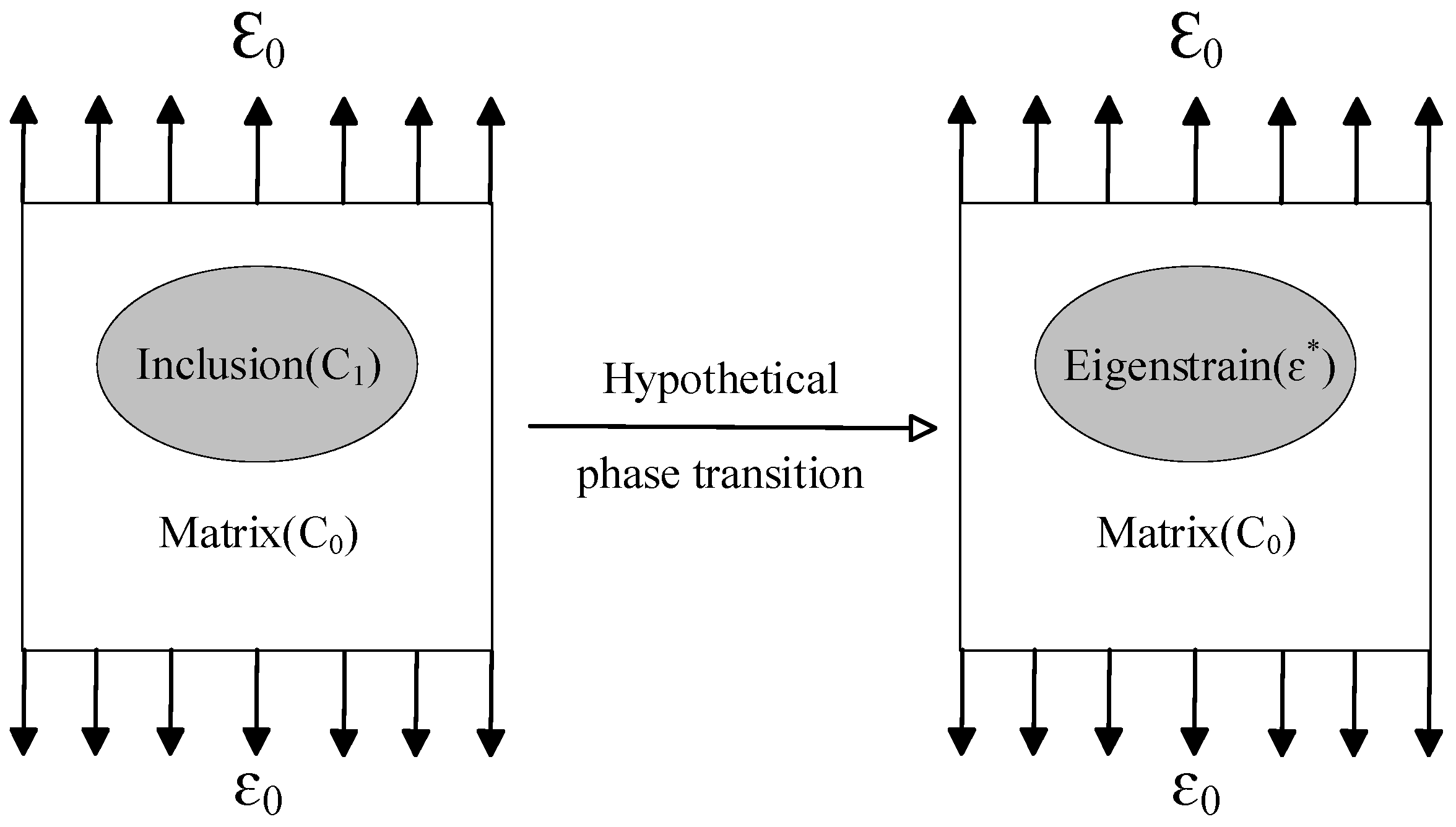
2. The Fundamental Theory
2.1. Mori-Tanaka Method
2.2. Common Forms of the Eshelby Tensor
2.2.1. Ellipsoidal (Where and Are Referred to as the Rotation Axes, with an Aspect Ratio of )
2.2.2. Spherica ()
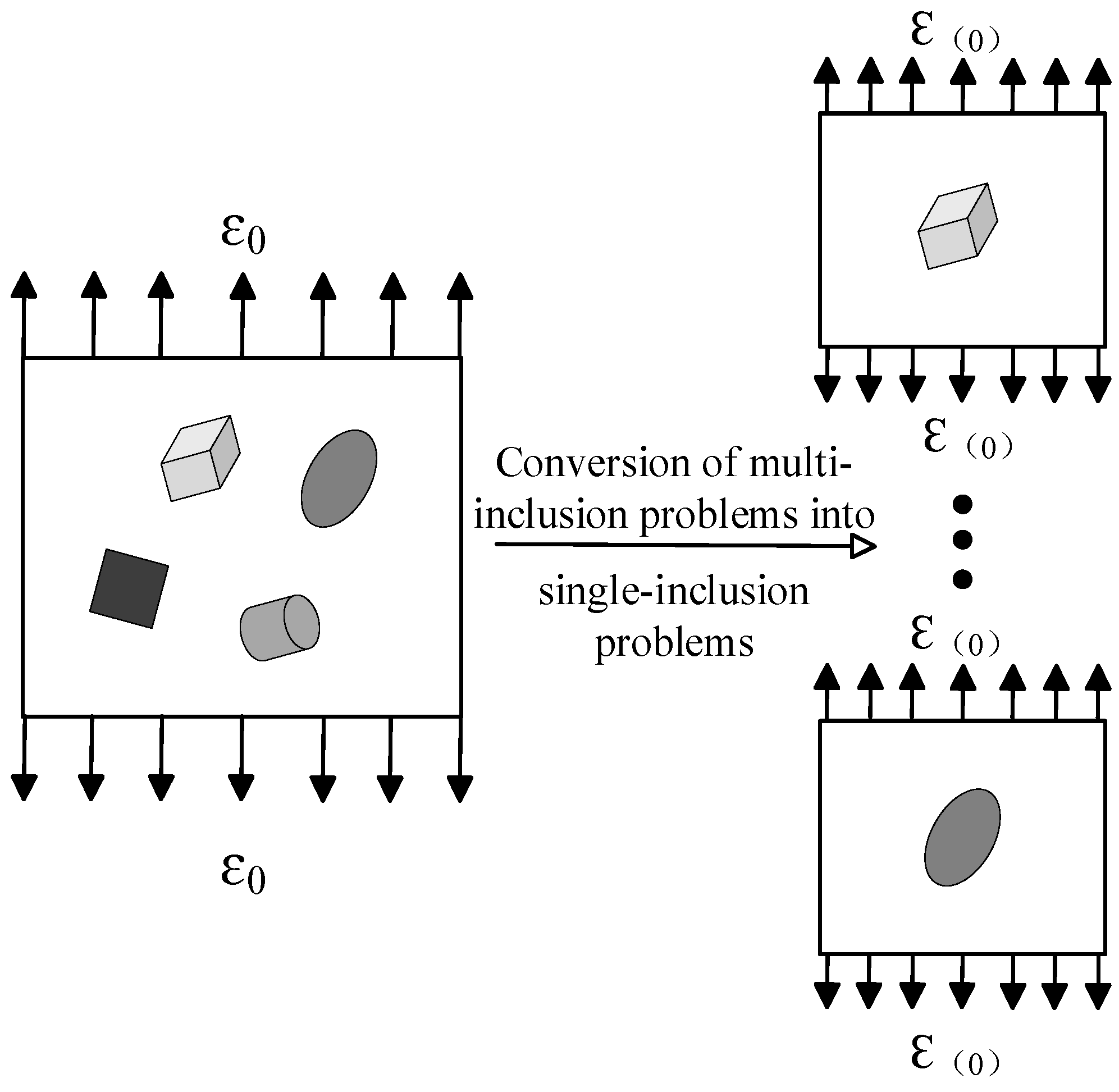
2.3. Numerical Method for Calculating Inclusion Strain Factors
2.3.1. Principle of Numerical Calculation
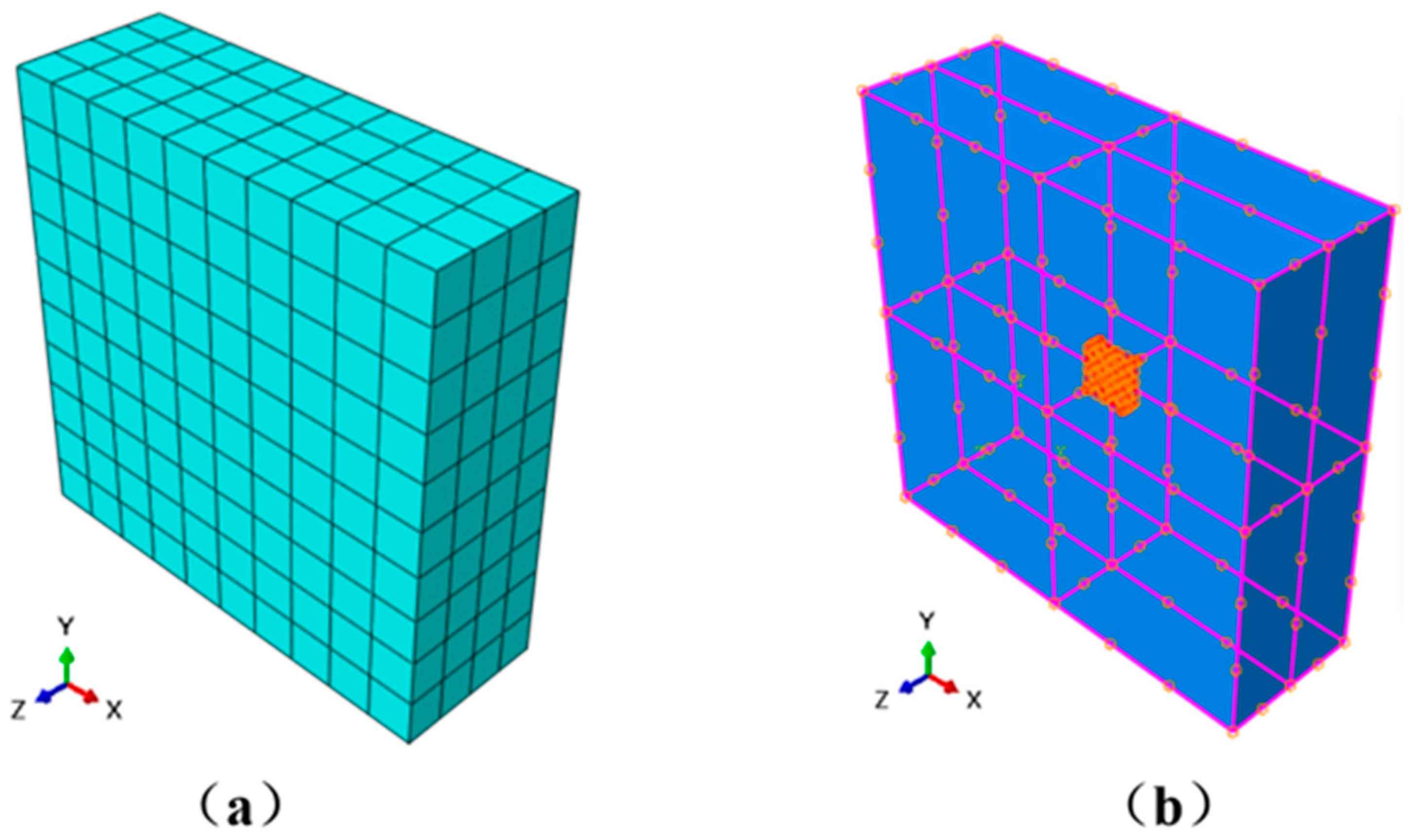
2.3.2. Establishment of the Finite Element Model
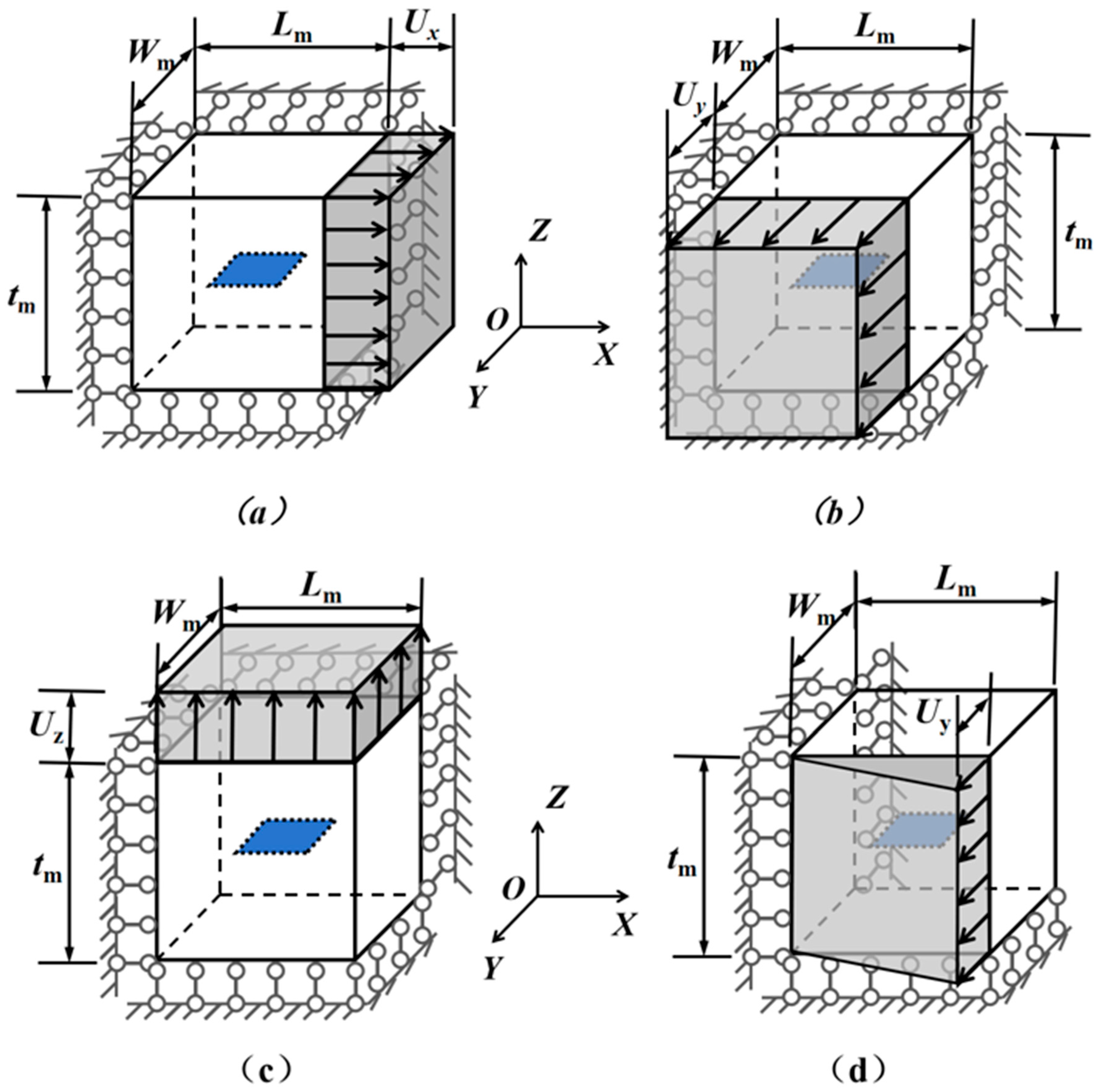
2.3.3. Application of Boundary Conditions
- (a)
- The boundary condition corresponding to is illustrated in Figure 5a. Displacement in the X-direction is constrained on the plane , while a small displacement is applied on the plane . In addition, displacements in the Y- and Z-directions are restricted on the planes and , respectively. All other surfaces remain unconstrained.
- (b)
- The boundary condition corresponding to is illustrated in Figure 5b. Displacement in the Y-direction is constrained on the plane , while a small displacement is applied on the plane . In addition, displacements in the X- and Z-directions are restricted on the planes and , respectively. All other surfaces remain unconstrained.
- (c)
- The boundary condition corresponding to is illustrated in Figure 5c. Displacement in the Z-direction is constrained on the plane , while a small displacement is applied on the plane . In addition, displacements in the X- and Y-directions are restricted on the planes and , respectively. All other surfaces remain unconstrained.
- (d)
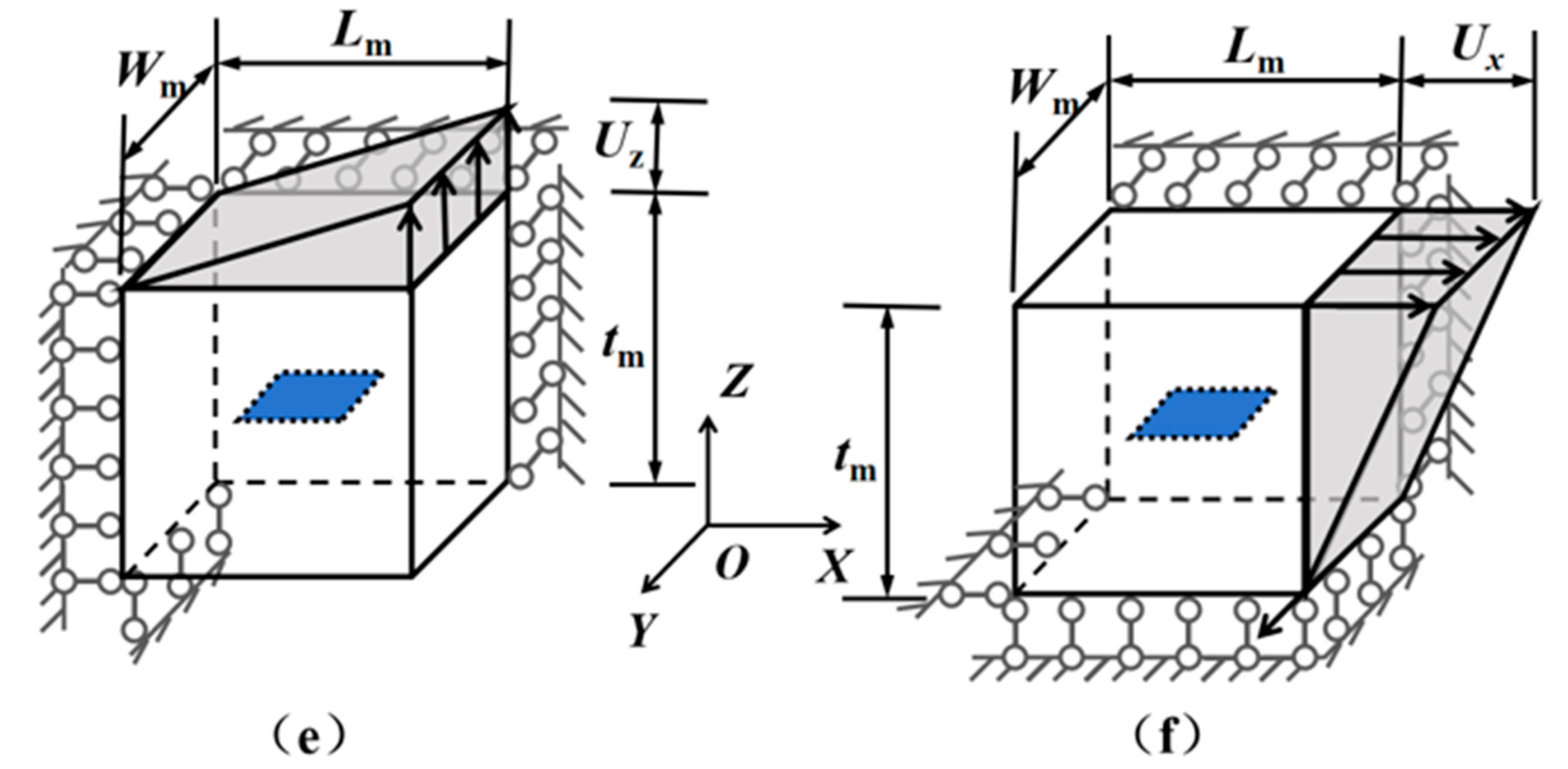
- The boundary condition corresponding to is illustrated in Figure 5d. Specifically, the X-direction displacement was fixed on the plane , and the Z-direction displacement was fixed on the plane . The Y-direction displacement was constrained along the model’s Z-axis, defined by the intersection line of planes and . A prescribed Y-direction displacement, , was applied at the intersection of the surfaces and . All other boundaries remained free of constraints.
- (e)
- The boundary condition corresponding to is illustrated in Figure 5e. Specifically, the X-direction displacement was fixed on the plane , and the Y-direction displacement was fixed on the plane . The Z-direction displacement was constrained along the model’s Y-axis, defined by the intersection line of planes and . A prescribed Z-direction displacement, , was applied at the intersection of the surfaces and . All other boundaries remained free of constraints.
- (f)
- The boundary condition corresponding to is illustrated in Figure 5f. Specifically, the Y-direction displacement was fixed on the plane , and the Z-direction displacement was fixed on the plane . The X-direction displacement was constrained along the model’s Y-axis, defined by the intersection line of planes and . A prescribed Z-direction displacement, , was applied at the intersection of the surfaces and . All other boundaries remained free of constraints.
3. Results and Discussion
3.1. Comparison Between the MT-FEM Method and the M-T Method
3.2. Comparison with Results from Other Studies
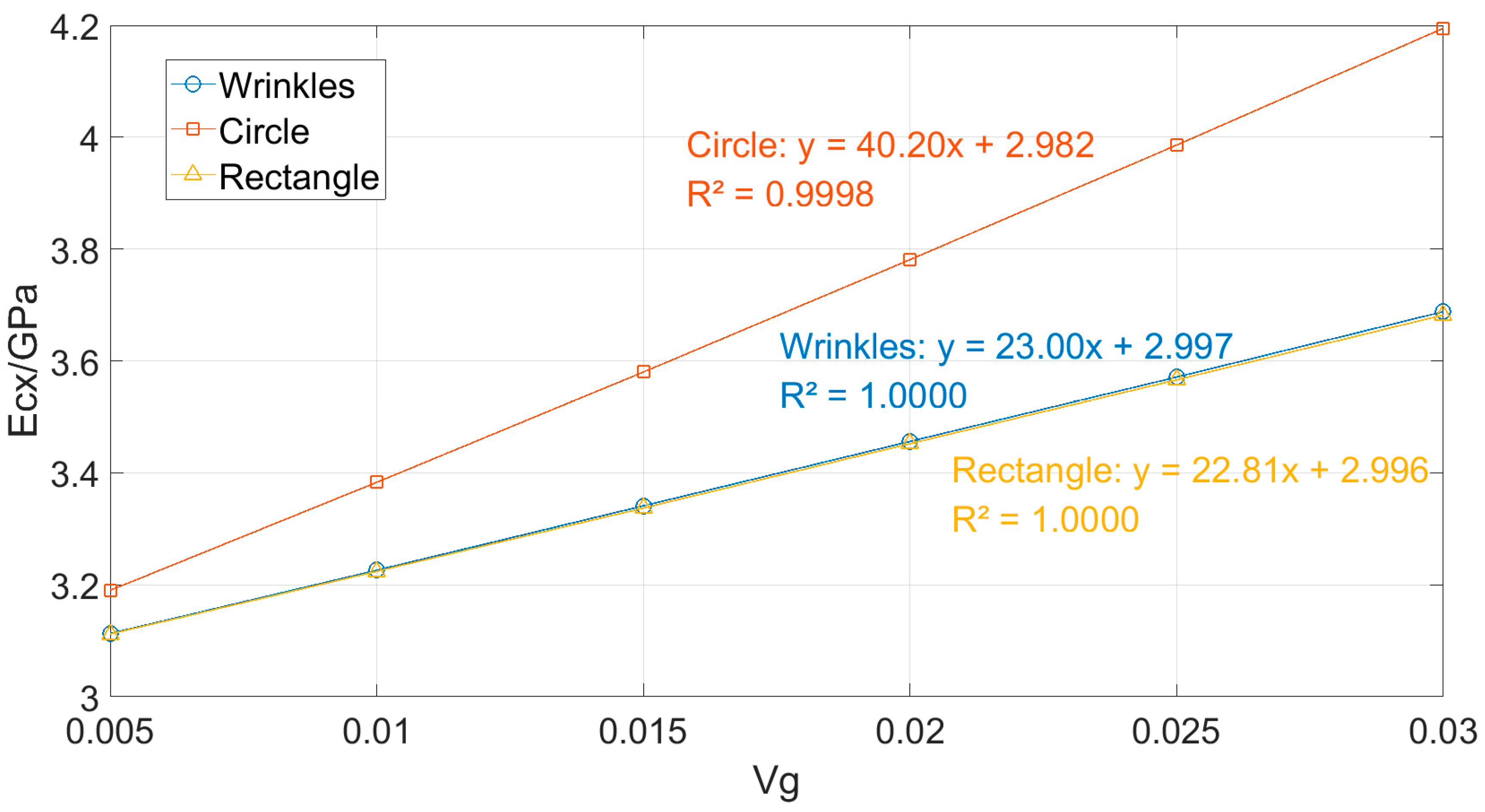
3.3. Influence of Graphene Shape on the Young’s Modulus of Composites
4. Conclusions
- (a)
- The MT-FEM method demonstrates consistent trends in modulus prediction with the conventional M-T approach, confirming their theoretical compatibility;
- (b)
- The deviations between MT-FEM predictions and experimental data from the literature are all within 5%, indicating high reliability;
- (c)
- A systematic comparison of three typical graphene morphologies reveals that the oblate shape provides the most significant reinforcement effect—at a volume fraction of 0.03, the composite modulus reaches 4.195 GPa, which is 13.75% and 13.93% higher than those reinforced by wrinkled (3.688 GPa) and rectangular (3.682 GPa) graphene, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen-Ying, W.; Zhuang-De, J.; Wei-Xuan, J.; Qi-Jing, L.; Feng, H. Research on the measurement of the single-layer thickness of graphene-like materials using high-resolution transmission electron microscopy. In Proceedings of the National Academic Exchange Conference on Measurement and Testing Technology, New Orleans, LA, USA, 7–9 May 2016. [Google Scholar]
- Wang, M.; Gustafsson, O.J.R.; Siddiqui, G.; Javed, I.; Kelly, H.G.; Blin, T.; Yin, H.; Kent, S.J.; Creek, D.J.; Kempe, K. Human plasma proteome association and cytotoxicity of nano-graphene oxide grafted with stealth polyethylene glycol and poly(2-ethyl-2-oxazoline). Nanoscale 2018, 10, 10863–10875. [Google Scholar] [CrossRef]
- Yi, J.; Choe, G.; Park, J.; Lee, J.Y. Graphene oxide-incorporated hydrogels for biomedical applications. Polym. J. 2020, 52, 823–837. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2009, 6, 11–19. [Google Scholar]
- Radmilović, V.V.; Carraro, C.; Uskoković, P.S.; Radmilović, V.R. Structure and properties of polymer nanocomposite films with carbon nanotubes and graphene. Polym. Compos. 2017, 38, E490–E497. [Google Scholar] [CrossRef]
- Akter, M.; Ozdemir, H.; Bilisik, K. Epoxy/Graphene Nanoplatelet (GNP) Nanocomposites: An Experimental Study on Tensile, Compressive, and Thermal Properties. Polymers 2024, 16, 1483. [Google Scholar] [CrossRef]
- Choudhury, N.D.; Saikia, P.; Saikia, M.; Kirtania, S.; Banerjee, S.; Kashyap, S. Evaluation of Elastic Properties of CNT/GNP/Epoxy Hybrid Nanocomposite for Different Weight Fractions of CNT and GNP. J. Inst. Eng. (India) Ser. D 2023, 105, 1575–1581. [Google Scholar] [CrossRef]
- Zulkefli, N.A.; Mustapha, R.; Jusoh, S.M.; Awang, M.; Ghazali, C.M.R.; Mustapha, S.N.H. The influence of different graphene nanoplatelets (GNPs) loadings on mechanical and thermal behavior of epoxidized palm oil–Epoxy resin nanocomposites. In Proceedings of the 3rd International Conference on Semiconductor Materials and Technology (3rd ICoSeMT 2023), Batu Ferringhi, Penang, Malaysia, 18–19 September 2023. [Google Scholar]
- Liu, Y.J.; Chen, X.L. Evaluations of the effective material properties of carbon nanotube-based composites using a nanoscale representative volume element. Mech. Mater. 2003, 35, 69–81. [Google Scholar] [CrossRef]
- Chen, X.L.; Liu, Y.J. Square representative volume elements for evaluating the effective material properties of carbon nanotube-based composites. Comput. Mater. Sci. 2004, 29, 1–11. [Google Scholar] [CrossRef]
- Joshi, P.; Upadhyay, S.H. Evaluation of elastic properties of multi walled carbon nanotube reinforced composite. Comput. Mater. Sci. 2014, 81, 332–338. [Google Scholar] [CrossRef]
- Ardeshana, B.A.; Jani, U.B.; Patel, A.M.; Joshi, A.Y. Investigating the elastic behavior of carbon nanocone reinforced nanocomposites. Mech. Eng. Sci. 2020, 203–210, 203–210. [Google Scholar] [CrossRef]
- Trivedi, S.; Sharma, S.C.; Harsha, S.P. Evaluations of young’s modulus of boron nitride nanotube reinforced nano-composites. Procedia Mater. Sci. 2014, 6, 1899–1905. [Google Scholar] [CrossRef]
- Affdl, J.C.H.; Kardos, J.L. The Halpin-Tsai Equations: A Review. Polym. Eng. Sci. 1976, 16, 344–352. [Google Scholar] [CrossRef]
- Fuchs, C.; Bhattacharyya, D.; Friedrich, K.; Fakirov, S. Application of Halpin–Tsai equation to microfibril reinforced polypropylene/poly(ethylene terephthalate) composites. Instrum. Sci. Technol. 2006, 13, 331–344. [Google Scholar] [CrossRef]
- Ramakrishna, S.; Lim, T.C.; Inai, R.; Fujihara, K. Modified Halpin-Tsai Equation for Clay-Reinforced Polymer Nanofiber. Mech. Adv. Mater. Struct. 2006, 13, 77–81. [Google Scholar] [CrossRef]
- Xue, Z.; Qian, J.; Zhao, Z. Mechanical Properties of Graphene/Polypropylene Composites. J. Liaoning Petrochem. Univ. 2025, 45, 27–32. [Google Scholar]
- Adhikari, J.; Kumar, R.; Jain, S.C. Using modified Halpin Tsai based approach for electromechanical analysis of functionally graded graphene reinforced piezoelectric tile. Int. J. Mech. Mater. Des. 2022, 19, 299–318. [Google Scholar] [CrossRef]
- Ali, G.; Stephan, S.; Clemens, H. A Review of Multiscale Computational Methods in Polymeric Materials. Polymers 2017, 9, 16. [Google Scholar] [CrossRef]
- Tandon, G.P.; Weng, G.J. The effect of aspect ratio of inclusions on the elastic properties of unidirectionally aligned composites. Polym. Compos. 1984, 5, 327–333. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Tandon, G.P.; Weng, G.J. Elastic moduli for a class of porous materials. Acta Mech. 1989, 76, 105–131. [Google Scholar] [CrossRef]
- Tandon, G.P.; Weng, G.J. A Theory of Particle-Reinforced Plasticity. J. Appl. Mech. 1988, 55, 126. [Google Scholar] [CrossRef]
- Li, J.; Weng, G.J. Effective creep behavior and complex moduli of fiber- and ribbon-reinforced polymer-matrix composites. Compos. Sci. Technol. 1994, 52, 615–629. [Google Scholar] [CrossRef]
- Li, J.; Weng, G.J. Anisotropic stress-strain relations and complex moduli of a viscoelastic composite with aligned spheroidal inclusions. Compos. Eng. 1994, 4, 1073–1097. [Google Scholar] [CrossRef]
- Li, J.; Weng, G.J. A secant-viscosity approach to the time-dependent creep of an elastic viscoplastic composite. J. Mech. Phys. Solids 1997, 45, 1069–1083. [Google Scholar] [CrossRef]
- Li, J.; Weng, G.J. Strain-Rate Sensitivity, Relaxation Behavior, and Complex Moduli of a Class of Isotropic Viscoelastic Composites. J. Eng. Mater. Technol. 1994, 116, 495–504. [Google Scholar] [CrossRef]
- Kuo, T.H.; Pan, H.H.; Weng, G.J. Micromechanics-Based Predictions on the Overall Stress-Strain Relations of Cement-Matrix Composites. J. Eng. Mech. 2008, 134, 1045–1052. [Google Scholar] [CrossRef]
- Weng, G.J. A homogenization scheme for the plastic properties of nanocrystalline materials. Rev. Adv. Mater. Sci. 2009, 19, 41–62. [Google Scholar]
- Li, J.; Weng, G.J. A micromechanical approach to the stress–strain relations, strain-rate sensitivity and activation volume of nanocrystalline materials. Int. J. Mech. Mater. Des. 2013, 9, 141–152. [Google Scholar] [CrossRef]
- Alian, A.R.; Kundalwal, S.I.; Meguid, S.A. Multiscale modeling of carbon nanotube epoxy composites. Polymer 2015, 70, 149–160. [Google Scholar] [CrossRef]
- Jia, H. Research on the Mechanical Properties of Particle-Reinforced Elastoplastic Matrix Composite Materials Based on the Mori-Tanaka Method. Master’s Thesis, Chongqing University, Chongqing, China, 2015. [Google Scholar]
- Qinghua, Q.; Qingsheng, Y. Macroscopic and Microscopic Theories of Multi-Field Coupling Behavior of Non-Uniform Materials; Higher Education Press: Beijing, China, 2006. [Google Scholar]
- Hang, Z.; Feng, C.; Shen, L.; Unluer, C.; Wang, S. Experimental and theoretical analysis on the thermomechanical properties of functionally graded graphene nanoplatelet reinforced cement composites. Cem. Concr. Compos. 2024, 153, 105740. [Google Scholar] [CrossRef]
- Zhinan, D.; Fengxiang, X.; Wei, G.; Lin, H.; Jianjun, S. Analysis of Open-Cell Panels of Short Fiber Composites Based on the Mori-Tanaka Method. Chin. Plast. 2020, 34, 8. [Google Scholar] [CrossRef]
- Chen, X.; Han, Y.; Ding, X.; Hou, D. Nanopatch Characterization and Multi-scale Calculation of the Elastic Modulus of Cement Paste. J. Shanghai Jiaotong Univ. 2022, 56, 56. [Google Scholar] [CrossRef]
- Mahmun, A.; Kirtania, S. Evaluation of elastic properties of graphene nanoplatelet/epoxy nanocomposites. Mater. Today Proc. 2021, 44, 1531–1535. [Google Scholar] [CrossRef]
- Odegard, G.M.; Clancy, T.C.; Gates, T.S. Modeling of the mechanical properties of nanoparticle/polymer composites. Polymer 2005, 46, 553–562. [Google Scholar] [CrossRef]
- Seidel, G.D.; Lagoudas, D.C. Micromechanical analysis of the effective elastic properties of carbon nanotube reinforced composites. Mech. Mater. 2006, 38, 884–907. [Google Scholar] [CrossRef]
- Dongkai, Z. Multiscale Simulation Analysis of Mechanical Properties of Carbon Nanotube Composite Materials. Master’s Thesis, Dalian University of Technology, Dalian, China, 2016. [Google Scholar]
- Hori, M.; Nemat-Nasser, S. Double-Inclusion Model and Overall Moduli of Multi-Phase Composites. J. Eng. Mater. Technol. 1993, 14, 189–206. [Google Scholar] [CrossRef]
- Li, J.Y. Magnetoelectroelastic multi-inclusion and inhomogeneity problems and their applications in composite materials. Int. J. Eng. Sci. 2000, 38, 1993–2011. [Google Scholar] [CrossRef]
- Shen, G.H.; Liu, B. Composite Materials Mechanic, 2nd ed.; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Qingsheng, Y.; Limin, T.; Haoran, C. Self-consistent finite element method: A new method of predicting effective properties of inclusion media. Finite Elem. Anal. Des. 1994, 17, 247–257. [Google Scholar] [CrossRef]
- Sun, Q.; Song, Z.; Li, Y. Mechanical property prediction of carbon nanotube reinforced epoxy resin composites based on the finite element method. Appl. Eng. Plast. 2021, 49, 55–60. [Google Scholar] [CrossRef]
- Cho, J.; Luo, J.J.; Daniel, I.M. Mechanical characterization of graphite/epoxy nanocomposites by multi-scale analysis. Compos. Sci. Technol. 2007, 67, 2399–2407. [Google Scholar] [CrossRef]
- Jianbin, Z. Research on Photothermal Conversion and Driving Behavior of Graphene/Polymer-Based Nanocomposites. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2022. [Google Scholar]
- Benveniste, Y. A new approach to the application of Mori-Tanaka’s theory in composite materials. Mech. Mater. 1987, 6, 147–157. [Google Scholar] [CrossRef]
- Yuli, C.; Yong, M.; Fei, P.; Shengtao, W. Progress in Multiscale Composite Material Mechanics Research. J. Solid Mech. 2018, 39, 68. [Google Scholar]
- Qingsheng, Y.; Xu, T. The step-by-step format with multiple intertwined issues. J. Compos. Mater. 2007, 24, 128–134. [Google Scholar] [CrossRef]
- Gljui, M.; Franulovi, M.; Lanc, D.; Božić, Ž. Application of digital image correlation in behavior modelling of AM CFRTP composites. Eng. Fail. Anal. 2022, 136, 106133. [Google Scholar] [CrossRef]
- Giannopoulos, G.I.; Kallivokas, I.G. Mechanical properties of graphene based nanocomposites incorporating a hybrid interphase. Finite Elem. Anal. Des. 2014, 90, 31–40. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, Q.; Chen, D.; Lu, P. Enhanced Mechanical Properties of Graphene-Based Poly(vinyl alcohol) Composites. Macromolecules 2010, 43, 2357–2363. [Google Scholar] [CrossRef]
- King, J.A.; Klimek, D.R.; Miskioglu, I.; Odegard, G.M. Mechanical properties of graphene nanoplatelet/epoxy composites. J. Compos. Mater. 2014, 49, 659–668. [Google Scholar] [CrossRef]

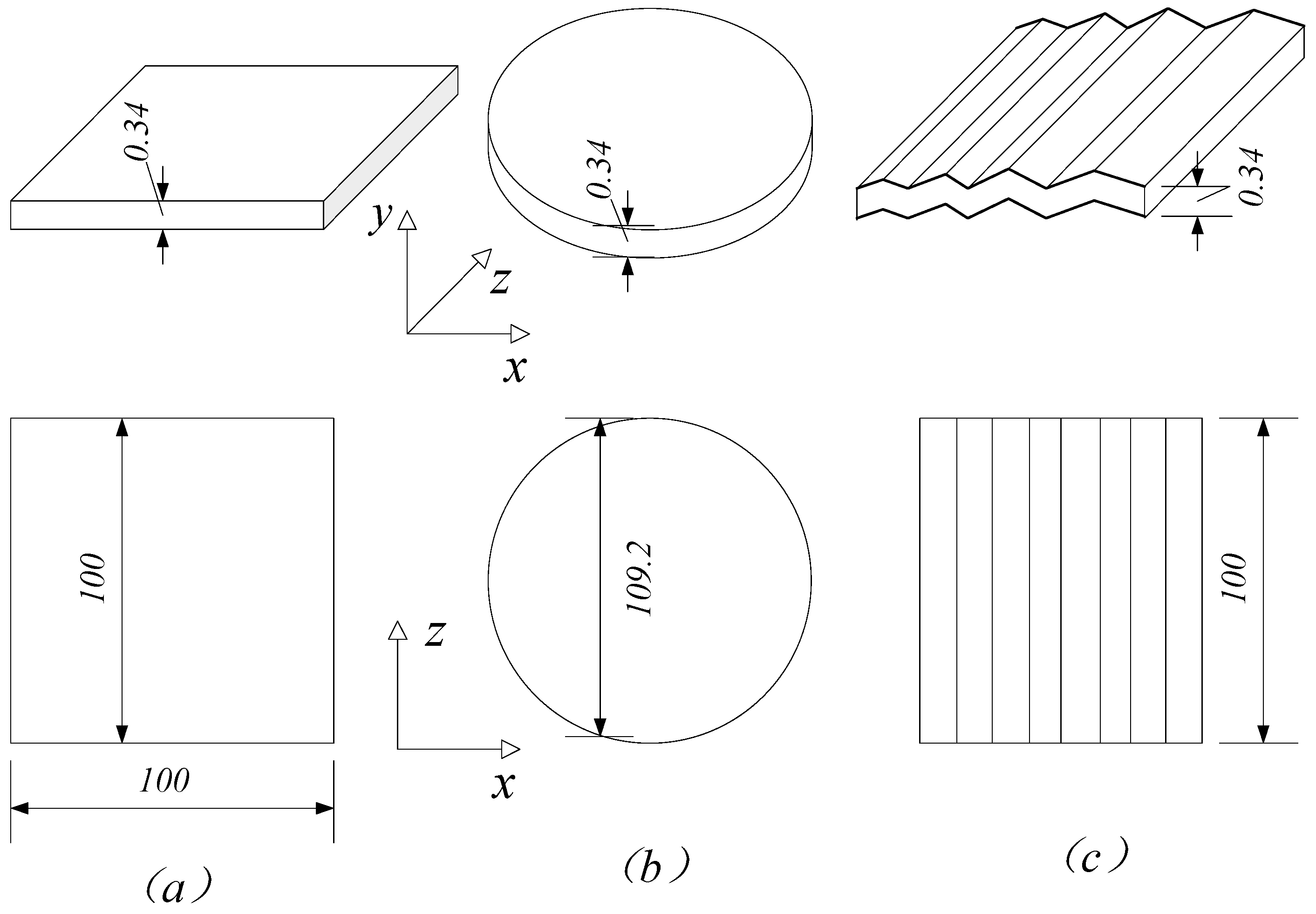
| No. | Far-Field Uniform Strain | Corresponding Matrix Element | Physical Meaning |
|---|---|---|---|
| 1 | The deformation response of the inclusion under far-field uniaxial tension (in the x-direction). | ||
| 2 | The deformation response of the inclusion under far-field uniaxial tension (in the y-direction). | ||
| 3 | The deformation response of the inclusion under far-field uniaxial tension (in the z-direction). | ||
| 4 | The deformation response of the inclusion under far-field shear in the xy-plane. | ||
| 5 | The deformation response of the inclusion under far-field shear in the yz-plane. | ||
| 6 | The deformation response of the inclusion under far-field shear in the xz-plane. |
| No. | Vg | Ellipsoidal Ecx [GPa] | Spherica Ecx [GPa] | ||||
|---|---|---|---|---|---|---|---|
| M-T (1) | MT-FEM (2) | M-T (3) | MT-FEM (4) | ||||
| 1 | 0.01 | 3.023 | 3.049 | 0.853 | 3.005 | 3.032 | 0.891 |
| 2 | 0.02 | 3.046 | 3.098 | 1.679 | 3.010 | 3.064 | 1.762 |
| 3 | 0.03 | 3.070 | 3.147 | 2.447 | 3.015 | 3.096 | 2.616 |
| 4 | 0.04 | 3.092 | 3.196 | 3.254 | 3.020 | 3.128 | 3.453 |
| 5 | 0.05 | 3.115 | 3.245 | 4.006 | 3.024 | 3.160 | 4.304 |
| No. | Vg (%) | Graphene Size | Em [GPa] | Eg [GPa] | Test Result (1) | Present Result (2) | Deviation (%) | |
|---|---|---|---|---|---|---|---|---|
| Lg = Wg (nm) | tg (nm) | |||||||
| 1 [52] | 0.3 | 1000 | 0.8 | 0.1 | 1000 | 0.2 | 0.201 | 0.5 |
| 2 [52] | 0.6 | 1000 | 0.8 | 0.1 | 1000 | 0.25 | 0.246 | −1.6 |
| 3 [52] | 1.8 | 1000 | 0.8 | 0.1 | 1000 | 1.04 | 1.029 | −1.1 |
| 4 [45] | 0.523 | 1000 | 200 | 3.27 | 1153 | 3.3 | 3.448 | 4.48 |
| 5 [45] | 0.523 | 1000 | 14.3 | 3.27 | 1153 | 3.65 | 3.559 | −2.49 |
| 6 [53] | 0.6 | 15,000 | 7 | 2.72 | 1000 | 2.8 | 2.75 | −1.78 |
| 7 [53] | 1.21 | 15,000 | 7 | 2.72 | 1000 | 2.94 | 2.895 | −1.53 |
| 8 [53] | 1.82 | 15,000 | 7 | 2.72 | 1000 | 3.03 | 2.984 | −1.52 |
| 9 [53] | 2.44 | 15,000 | 7 | 2.72 | 1000 | 3.11 | 3.073 | −1.19 |
| 10 [53] | 3.06 | 15,000 | 7 | 2.72 | 1000 | 3.24 | 3.163 | −2.38 |
| 11 [53] | 3.69 | 15,000 | 7 | 2.72 | 1000 | 3.35 | 3.255 | −2.84 |
| 12 [17] | 2 | 10,000 | 1.7 | 1.0182 | 1000 | 1.4800 | 1.452 | −1.89 |
| 13 [17] | 4 | 10,000 | 1.7 | 1.0182 | 1000 | 1.8034 | 1.868 | −1.58 |
| Wrinkle Profile |  | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| CP No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Coordinate | X | 0 | 12.498 | 24.996 | 37.494 | 49.992 | 62.490 | 74.988 | 87.487 | 99.985 |
| Y | 0 | 0.218 | 0 | 0.218 | 0 | 0.218 | 0 | 0.218 | 0 | |
| No. | Vg | Ecx [GPa] | Absolute Difference (GPa) | Relative Difference (%) | ||||
|---|---|---|---|---|---|---|---|---|
| Oblate (1) | Wrinkles (2) | Rectangle (3) | ||||||
| 1 | 0.005 | 3.19 | 3.113 | 3.112 | 0.077 | 0.078 | 2.47 | 2.51 |
| 2 | 0.01 | 3.383 | 3.226 | 3.224 | 0.157 | 0.159 | 4.87 | 4.93 |
| 3 | 0.015 | 3.58 | 3.341 | 3.337 | 0.239 | 0.243 | 7.15 | 7.28 |
| 4 | 0.02 | 3.781 | 3.456 | 3.452 | 0.325 | 0.329 | 9.40 | 9.53 |
| 5 | 0.025 | 3.986 | 3.571 | 3.566 | 0.415 | 0.42 | 11.62 | 11.78 |
| 6 | 0.03 | 4.195 | 3.688 | 3.682 | 0.507 | 0.513 | 13.75 | 13.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, X.; Hashim, H.B.; Huang, J.; Soo, E.Z.X.; Luo, L. The MT-FEM Model for Predicting Young’s Modulus of Graphene Composites with Complex Morphologies. Materials 2025, 18, 5225. https://doi.org/10.3390/ma18225225
Zhai X, Hashim HB, Huang J, Soo EZX, Luo L. The MT-FEM Model for Predicting Young’s Modulus of Graphene Composites with Complex Morphologies. Materials. 2025; 18(22):5225. https://doi.org/10.3390/ma18225225
Chicago/Turabian StyleZhai, Xiaoxia, Huzaifa Bin Hashim, Jun Huang, Eugene Zhen Xiang Soo, and Lina Luo. 2025. "The MT-FEM Model for Predicting Young’s Modulus of Graphene Composites with Complex Morphologies" Materials 18, no. 22: 5225. https://doi.org/10.3390/ma18225225
APA StyleZhai, X., Hashim, H. B., Huang, J., Soo, E. Z. X., & Luo, L. (2025). The MT-FEM Model for Predicting Young’s Modulus of Graphene Composites with Complex Morphologies. Materials, 18(22), 5225. https://doi.org/10.3390/ma18225225






