Energy Dynamics of Long-Wave Low-Amplitude Disturbances in an Anharmonic One-Dimensional Lattice
Abstract
1. Introduction
2. Energy Dynamics in Discrete System
2.1. Basic Equations
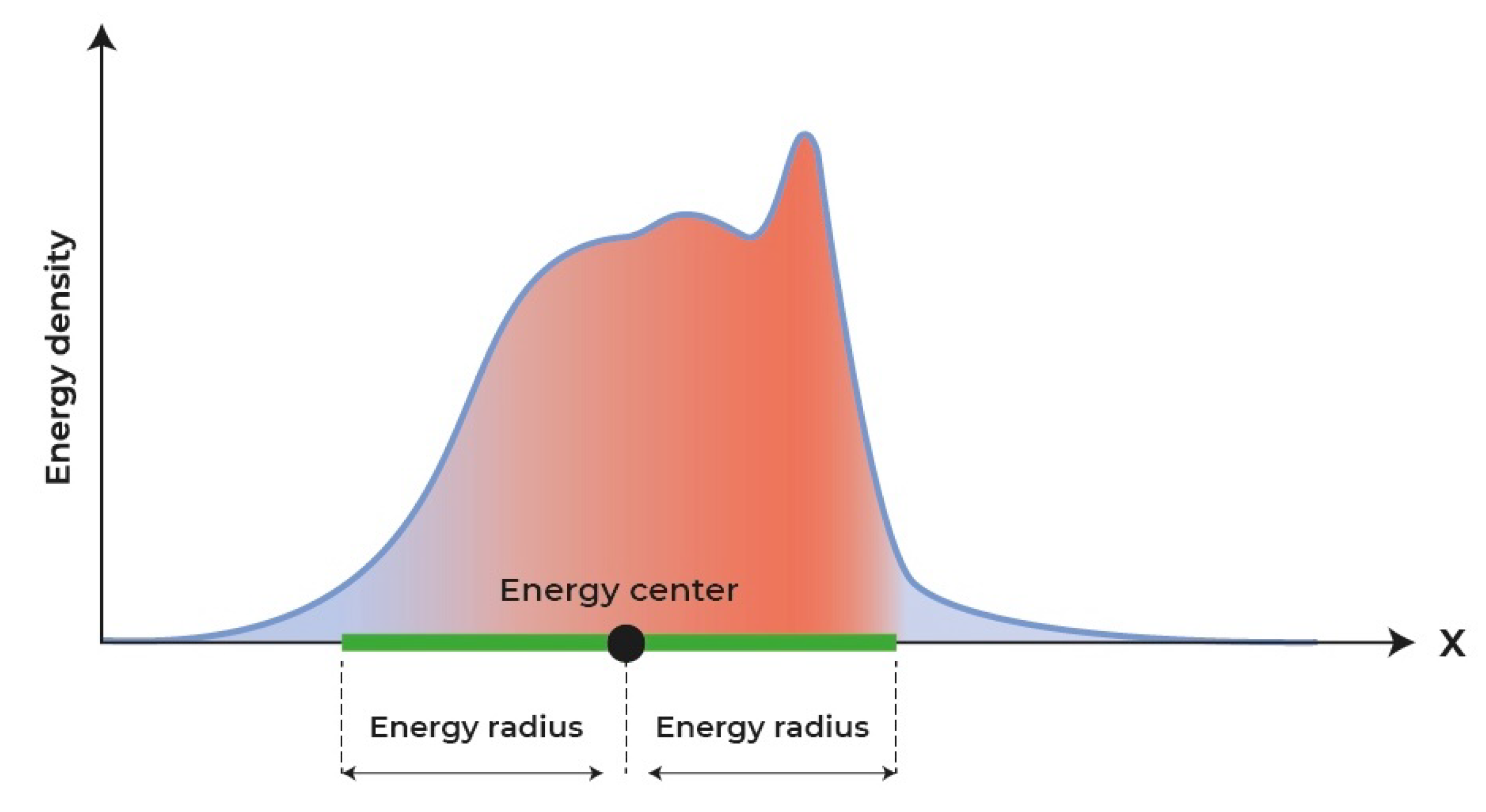
2.2. Energy Center
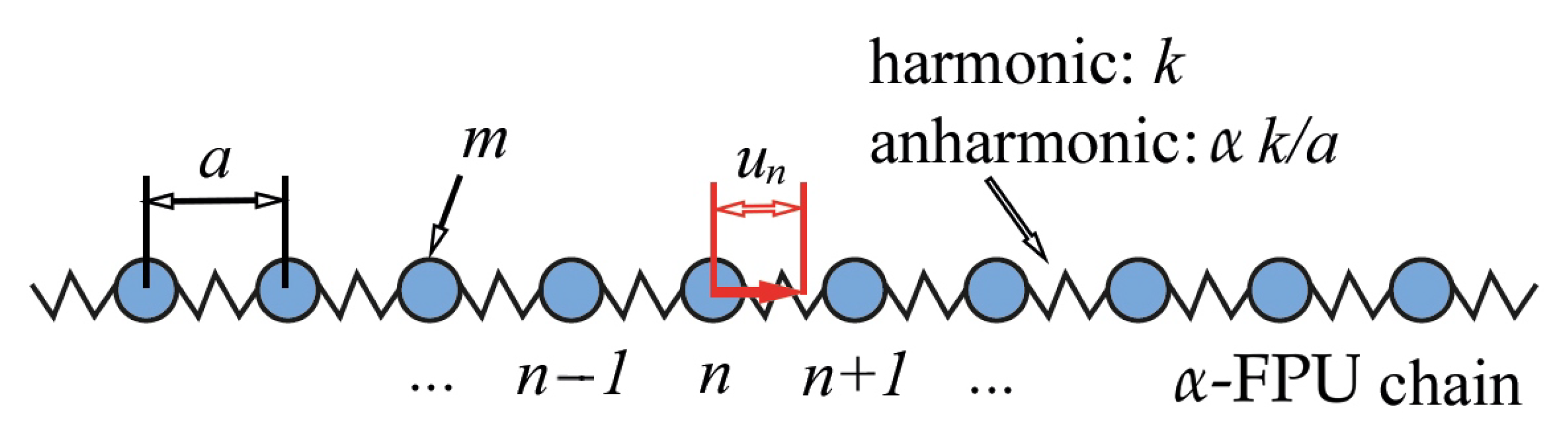
2.3. The -FPU Chain
3. Energy Dynamics in Continuum Limit
3.1. The Boussinesq Equation
3.2. The KdV Equation
3.3. The Reduced KdV Equations
4. Energy Dynamics Analysis of the KdV Equation
4.1. Energy Transfer
4.2. Energy Dispersion
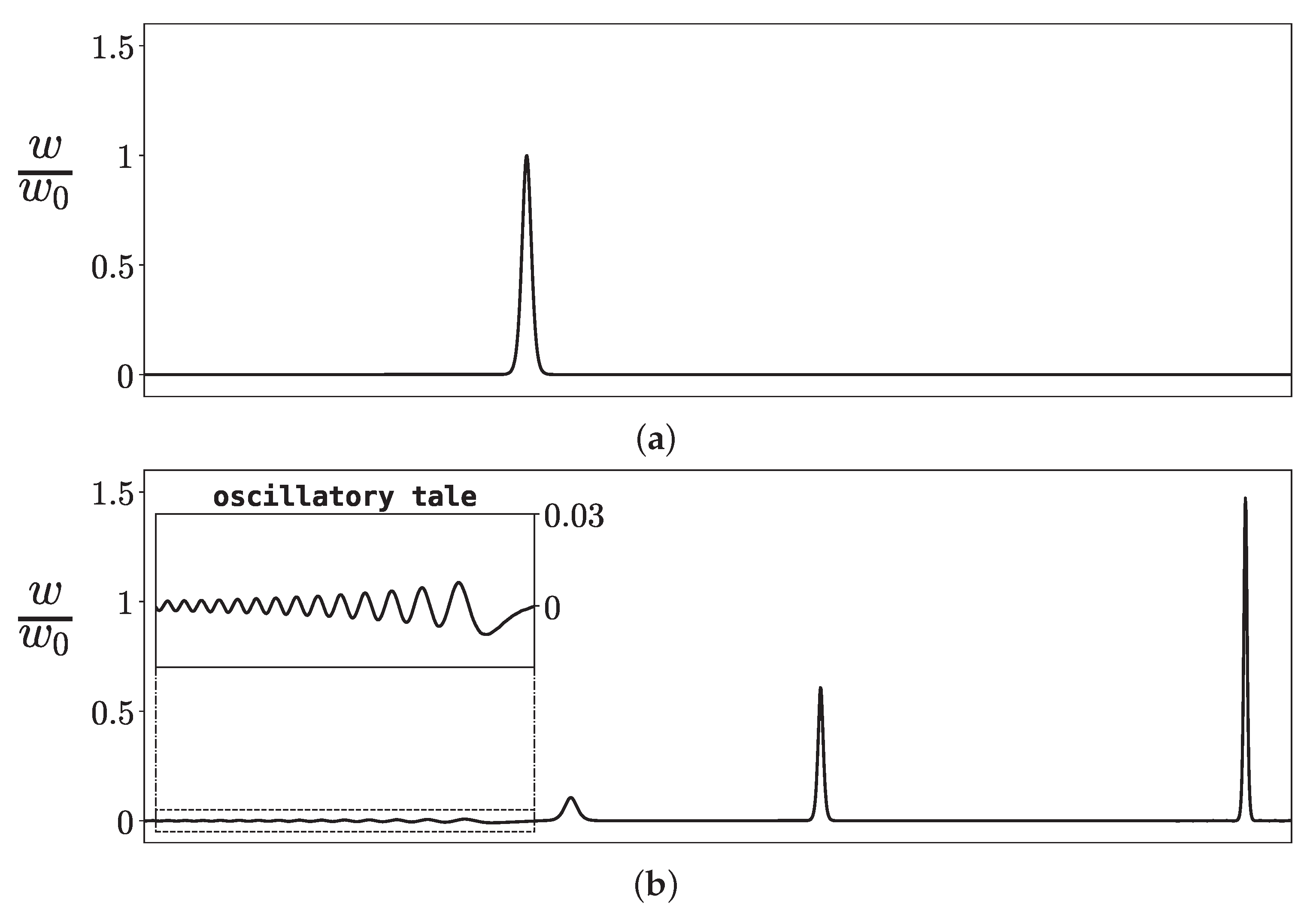
4.3. About the KdV Approximation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Transition from the α-FPU Chain to the Boussinesq Equation: Transformation of the Equations of Motion
Appendix B. Transition from the α-FPU Chain to the Boussinesq Equation: The Energy and the Energy Flux Densities
Appendix C. Transition from the Boussinesq Equation to the KdV Equation
Appendix D. Initial Disturbance in the Form of the Square of the Hyperbolic Secant in the KdV Equation
Appendix E. Conservation Laws and the First Two Energy Moments for the Linearized KdV Equation
References
- Achenbach, J.D. Wave Propagation in Elastic Solids; North Holland Series in Applied Mathematics and Mechanics; North-Holland Publishing Company: Amsterdam, The Netherlands; American Elsevier: New York, NY, USA, 1973; Volume 16. [Google Scholar]
- Whitham, G.B. Linear and Nonlinear Waves; John Wiley and Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Morozov, N.; Petrov, Y. Dynamics of Fracture; Foundations of Engineering Mechanics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Kaviany, M. Heat Transfer Physics, 2nd ed.; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar]
- Sheriff, R.E.; Geldart, L.P. Exploration Seismology, 2nd ed.; Cambridge University Press: New York, NY, USA, 1995. [Google Scholar]
- Spohn, H. Nonlinear Fluctuating Hydrodynamics for Anharmonic Chains. J. Stat. Phys. 2014, 154, 1191. [Google Scholar] [CrossRef]
- Gendelman, O.V.; Savin, A.V. Normal heat conductivity in chains capable of dissociation. Europhys. Lett. 2014, 106, 34004. [Google Scholar] [CrossRef]
- Lepri, S. (Ed.) Thermal Transport in Low Dimensions; Lecture Notes in Physics; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Mejía-Monasterio, C.; Politi, A.; Rondoni, L. Heat flux in one-dimensional systems. Phys. Rev. E 2019, 100, 032139. [Google Scholar] [CrossRef]
- Dhar, A.; Kundu, A.; Kundu, A. Anomalous Heat Transport in One Dimensional Systems: A Description Using Non-local Fractional-Type Diffusion Equation. Front. Phys. 2019, 7, 159. [Google Scholar] [CrossRef]
- Xu, X.; Chen, J.; Zhou, J.; Li, B. Thermal Conductivity of Polymers and Their Nanocomposites. Adv. Mater. 2018, 30, 1705544. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Liang, C.; Ma, T.; Guo, Y.; Kong, J.; Gu, J.; Chen, M.; Zhu, J. A review on thermally conductive polymeric composites: Classification, measurement, model and equations, mechanism and fabrication methods. Adv. Compos. Hybrid Mater. 2018, 1, 207–230. [Google Scholar] [CrossRef]
- Wei, X.; Wang, Z.; Tian, Z.; Luo, T. Thermal Transport in Polymers: A Review. J. Heat Transf. 2021, 143, 072101. [Google Scholar] [CrossRef]
- Cahill, D.G.; Ford, W.K.; Goodson, K.E.; Mahan, G.D.; Majumdar, A.; Maris, H.J.; Merlin, R.; Phillpot, S.R. Nanoscale thermal transport. J. Appl. Phys. 2003, 93, 793–818. [Google Scholar] [CrossRef]
- Gendelman, O.V.; Paul, J. Kapitza thermal resistance in linear and nonlinear chain models: Isotopic defect. arXiv 2021, arXiv:2102.02545. [Google Scholar] [CrossRef]
- Bonetto, F.; Lebowitz, J.L.; Rey-Bellet, L. Theorists. In Mathematical Physics 2000; World Scientific Publishing Co.: Singapore, 2000; pp. 128–150. [Google Scholar] [CrossRef]
- Dhar, A. Heat transport in low-dimensional systems. Adv. Phys. 2008, 57, 457–537. [Google Scholar] [CrossRef]
- Chen, G. Non-Fourier phonon heat conduction at the microscale and nanoscale. Nat. Rev. Phys. 2021, 3, 555–569. [Google Scholar] [CrossRef]
- Krivtsov, A.M. Heat transfer in infinite harmonic one-dimensional crystals. Dokl. Phys. 2015, 60, 407–411. [Google Scholar] [CrossRef]
- Krivtsov, A.M.; Kuzkin, V.A. Fast and slow thermal processes in harmonic scalar lattices. J. Phys. Condens. Matter 2017, 29, 505401. [Google Scholar]
- Krivtsov, A.M.; Murachev, A.S. Transition to thermal equilibrium in a crystal subjected to instantaneous deformation. J. Phys. Condens. Matter 2021, 33, 215403. [Google Scholar] [CrossRef] [PubMed]
- Kuzkin, V.A.; Krivtsov, A.M. Unsteady ballistic heat transport: Linking lattice dynamics and kinetic theory. Acta Mech. 2021, 232, 1983. [Google Scholar] [CrossRef]
- Sokolov, A.A.; Müller, W.H.; Porubov, A.V.; Gavrilov, S.N. Heat conduction in 1D harmonic crystal: Discrete and continuum approaches. Int. J. Heat Mass Transf. 2021, 176, 121442. [Google Scholar] [CrossRef]
- Shishkina, E.V.; Gavrilov, S.N.; Mochalova, Y.A. The anti-localization of non-stationary linear waves and its relation to the localization. The simplest illustrative problem. J. Sound Vib. 2023, 553, 117673. [Google Scholar] [CrossRef]
- Gavrilov, S.N.; Shishkina, E.V. Non-stationary elastic wave scattering and energy transport in a one-dimensional harmonic chain with an isotopic defect. Contin. Mech. Thermodyn. 2024, 36, 699–724. [Google Scholar] [CrossRef]
- Porubov, A.V.; Krivtsov, A.M. Dispersive propagation of localized waves in a mass-in-mass metamaterial lattice. Contin. Mech. Thermodyn. 2022, 34, 1475–1483. [Google Scholar] [CrossRef]
- Liazhkov, S.D.; Kuzkin, V.A. Unsteady two-temperature heat transport in mass-in-mass chains. Phys. Rev. E 2022, 105, 054145. [Google Scholar] [CrossRef]
- Gavrilov, S.N.; Krivtsov, A.M. Steady-state ballistic thermal transport associated with transversal motions in a damped graphene lattice subjected to a point heat source. Contin. Mech. Thermodyn. 2022, 34, 297–319. [Google Scholar] [CrossRef]
- Panchenko, A.Y.; Kuzkin, V.A.; Berinskii, I.E. Unsteady ballistic heat transport in two-dimensional harmonic graphene lattice. J. Phys. Condens. Matter 2022, 34, 165402. [Google Scholar] [CrossRef]
- Zhilin, P. Advanced Problems in Mechanics; Selection of Articles; IPME RAS: St. Petersburg, Russia, 2006; Volume 2. [Google Scholar]
- Kunin, I.A. Elastic Media with Microstructure. I. One-Dimensional Models; Springer Series in Solid-State Sciences; Springer: Berlin/Heidelberg, Germany, 1982; Volumes 1 and 2. [Google Scholar]
- Krivtsov, A.M. Dynamics of matter and energy. J. Appl. Math. Mech./Z. Angew. Math. Mech. 2023, 103, e202100496. [Google Scholar] [CrossRef]
- Baimova, J.A.; Bessonov, N.M.; Krivtsov, A.M. Motion of localized disturbances in scalar harmonic lattices. Phys. Rev. E 2023, 107, 065002. [Google Scholar] [CrossRef] [PubMed]
- Kuzkin, V.A. Acoustic transparency of the chain-chain interface. Phys. Rev. E 2023, 107, 065004. [Google Scholar] [CrossRef]
- Deen, W.M. Analysis of Transport Phenomena; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Guo, Y.; Wang, M. Phonon hydrodynamics and its applications in nanoscale heat transport. Phys. Rep. 2015, 595, 1. [Google Scholar] [CrossRef]
- Peierls, R. Zur kinetischen theorie der warmeleitung in kristallen. Ann. Phys. 1929, 3, 1055. [Google Scholar] [CrossRef]
- Kubo, R. The Boltzmann Equation in Solid State Physics. In The Boltzmann Equation; Cohen, E.G.D., Thirring, W., Eds.; Springer: Vienna, Austria, 1973; pp. 301–340. [Google Scholar]
- Minnich, A.J.; Chen, G.; Mansoor, S.; Yilbas, B.S. Quasiballistic heat transfer studied using the frequency-dependent Boltzmann transport equation. Phys. Rev. B 2011, 84, 235207. [Google Scholar] [CrossRef]
- Hua, C.; Minnich, A.J. Transport regimes in quasiballistic heat conduction. Phys. Rev. B 2014, 89, 094302. [Google Scholar] [CrossRef]
- Chen, G. Ballistic-diffusive heat conduction equations. Phys. Rev. Lett. 2001, 86, 2297. [Google Scholar] [CrossRef] [PubMed]
- Mahan, G.D.; Claro, F. Nonlocal theory of thermal conductivity. Phys. Rev. B 1988, 38, 1963. [Google Scholar] [CrossRef]
- Koh, Y.K.; Cahill, D.G.; Sun, B. Nonlocal theory for heat transport at high frequencies. Phys. Rev. B 2014, 90, 205412. [Google Scholar] [CrossRef]
- Ghosh, K.; Kusiak, A.; Battaglia, J.L. Phonon hydrodynamics in crystalline GeTe at low temperature. Phys. Rev. B 2020, 102, 094311. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, M. Phonon hydrodynamics for nanoscale heat transport at ordinary temperatures. Phys. Rev. B 2018, 97, 035421. [Google Scholar] [CrossRef]
- Xu, X.; Chen, J.; Li, B. Phonon thermal conduction in novel 2D materials. J. Phys. Condens. Matter 2016, 28, 483001. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Ouyang, Y.; Cheng, Y.; Chen, J.; Li, N.; Zhang, G. Size-dependent phononic thermal transport in low-dimensional nanomaterials. Phys. Rep. 2020, 860, 1–26. [Google Scholar] [CrossRef]
- Kiselev, A.P.; Plachenov, A.B.; Chamorro-Posada, P. Nonparaxial wave beams and packets with general astigmatism. Phys. Rev. A 2012, 85, 043835. [Google Scholar] [CrossRef]
- Malic, E.; Perea-Causin, R.; Rosati, R.; Erkensten, D.; Brem, S. Exciton transport in atomically thin semiconductors. Nat. Commun. 2023, 14, 3430. [Google Scholar] [CrossRef]
- Sneyd, A.J.; Fukui, T.; Paleček, D.; Prodhan, S.; Wagner, I.; Zhang, Y.; Sung, J.; Collins, S.M.; Slater, T.J.A.; Andaji-Garmaroudi, Z.; et al. Efficient energy transport in an organic semiconductor mediated by transient exciton delocalization. Sci. Adv. 2021, 7, eabh4232. [Google Scholar] [CrossRef]
- Fermi, E.; Pasta, J.; Ulam, S. Studies of Nonlinear Problems; Los Alamos Scientific Laborstory Report LA-1940; Los Alamos Scientific Laborstory: Los Alamos, NM, USA, 1955. [Google Scholar]
- Jones, J.E.; Chapman, S. On the determination of molecular fields from the variation of the viscosity of a gas with temperature. Proc. R. Soc. Lond. Ser. A 1924, 106, 441–462. [Google Scholar]
- Morse, P.M. Diatomic Molecules According to the Wave Mechanics. II. Vibrational Levels. Phys. Rev. 1929, 34, 57–64. [Google Scholar] [CrossRef]
- Bullough, R.K.; Caudrey, P.J. (Eds.) Solitons; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Newell, A.C. Solitons in Mathematics and Physics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1985. [Google Scholar]
- Scott, A. Nonlinear Science: Emergence and Dynamics of Coherent Structures, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003. [Google Scholar]
- Zabusky, N.J.; Kruskal, M.D. Interaction of “Solitons” in a Collisionless Plasma and the Recurrence of Initial States. Phys. Rev. Lett. 1965, 15, 240–243. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Segur, H. Solitons and the Inverse Scattering Transform; SIAM: Philadelphia, PA, USA, 1981. [Google Scholar]
- Boussinesq, J. Théorie générale des mouvements qui sont propagés dans un canal rectangulaire horizontal. Comptes Rendus Hebd. Séances Acad. Sci. 1871, 73, 256–260. [Google Scholar]
- Boussinesq, J. Théorie des ondes et des remous qui se propagent le long d’un canal rectangulaire horizontal, en communiquant au liquide contenu dans ce canal des vitesses sensiblement pareilles de la surface au fond. Comptes Rendus Hebd. Séances Acad. Sci. 1871, 73, 1210–1212. [Google Scholar]
- Boussinesq, J. Théorie des ondes et des remous qui se propagent le long d’un canal rectangulaire horizontal, en communiquant au liquide contenu dans ce canal des vitesses sensiblement pareilles de la surface au fond. J. Math. Pures Appl. 1872, 17, 55–108. [Google Scholar]
- Boussinesq, J. Essai sur la theorie des eaux courantes. In Mémoires Présentés par Divers Savants à l’Académie des Sciences de l’Institut National de France; Académie des Sciences: Paris, France, 1877; Volume 23, pp. 1–680. [Google Scholar]
- Miles, J.W. The Korteweg-de Vries equation: A historical essay. J. Fluid Mech. 1981, 106, 131–147. [Google Scholar] [CrossRef]
- Joseph Boussinesq’s Legacy in fluid mechanics. A century of fluid mechanics: 1870–1970. Comptes Rendus Mécanique 2017, 345, 427–445.
- d’Alembert, J.l.R. Recherches sur la courbe que forme une corde tendue mise en vibration. Histoire de l’Académie Royale des Sciences et Belles Lettres de Berlin 1747, 1750, 214–219. [Google Scholar]
- Korteweg, D.J.; de Vries, G. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Bogdanov, L.V.; Zakharov, V.E. The Boussinesq equation revisited. Phys. D Nonlinear Phenom. 2002, 165, 137–162. [Google Scholar] [CrossRef]
- Berezovski, A.; Engelbrecht, J.; Salupere, A.; Tamm, K.; Peets, T.; Berezovski, M. Dispersive waves in microstructured solids. Int. J. Solids Struct. 2013, 50, 1981–1990. [Google Scholar] [CrossRef]
- Lakshmanan, M.; Rajasekar, S. Basic Soliton Theory of KdV Equation. In Nonlinear Dynamics: Integrability, Chaos and Patterns; Springer: Berlin/Heidelberg, Germany, 2003; pp. 381–405. [Google Scholar]
- Gardner, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M. Method for Solving the Korteweg-deVries Equation. Phys. Rev. Lett. 1967, 19, 1095–1097. [Google Scholar] [CrossRef]
- Karpman, V. Chapter 4—Non-linear Waves in Weakly Dispersive Media. In Non-Linear Waves in Dispersive Media; International Series in Natural, Philosophy; Karpman, V.I., Ed.; Pergamon: Oxford, UK, 1975; Volume 71, pp. 53–105. [Google Scholar]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Haas, A.E.; Verschoyle, T. Introduction to Theoretical Physics; Number 1; Constable Limited: Wirral, UK, 1928. [Google Scholar]
- Friesecke, G.; Wattis, J.A.D. Existence theorem for solitary waves on lattices. Commun. Math. Phys. 1994, 161, 391–418. [Google Scholar] [CrossRef]
- Friesecke, G.; Pego, R.L. Solitary waves on FPU lattices: I. Qualitative properties, renormalization and continuum limit. Nonlinearity 1999, 12, 1601–1627. [Google Scholar] [CrossRef]
- Schneider, G.; Wayne, C.E. Counter-propagating waves on fluid surfaces and the continuum limit of the Fermi–Pasta–Ulam model. In Proceedings of the International Conference on Differential Equations, Berlin, Germany, 1–7 August 1999; World Science Publishing: River Edge, NY, USA, 2000; Volumes 1 and 2, pp. 390–404. [Google Scholar]
- Hong, Y.; Kwak, C.; Yang, C. On the Korteweg–de Vries Limit for the Fermi–Pasta–Ulam System. Arch. Ration. Mech. Anal. 2021, 240, 1091–1145. [Google Scholar] [CrossRef]
- Bambusi, D.; Ponno, A. On Metastability in FPU. Commun. Math. Phys. 2006, 264, 539–561. [Google Scholar] [CrossRef]
- Bambusi, D.; Carati, A.; Maiocchi, A.; Maspero, A. Some Analytic Results on the FPU Paradox. In Hamiltonian Partial Differential Equations and Applications; Guyenne, P., Nicholls, D., Sulem, C., Eds.; Springer: New York, NY, USA, 2015; pp. 235–254. [Google Scholar]
- Washimi, H.; Taniuti, T. Propagation of Ion-Acoustic Solitary Waves of Small Amplitude. Phys. Rev. Lett. 1966, 17, 996–998. [Google Scholar] [CrossRef]
- Wijngaarden, L.V. On the equations of motion for mixtures of liquid and gas bubbles. J. Fluid Mech. 1968, 33, 465–474. [Google Scholar] [CrossRef]
- Leibovich, S. Weakly non-linear waves in rotating fluids. J. Fluid Mech. 1970, 42, 803–822. [Google Scholar] [CrossRef]
- Tappert, F.D.; Varma, C.M. Asymptotic Theory of Self-Trapping of Heat Pulses in Solids. Phys. Rev. Lett. 1970, 25, 1108–1111. [Google Scholar] [CrossRef]
- Baholdin, I.B. Non-Dissipative Discontinuities in Continuum Mechanics; Physmathlit: Moscow, Russia, 2004. (In Russian) [Google Scholar]
- Shcherbinin, S.A. Dynamics of the Energy Center of a Long-Wave Low-Amplitude Disturbance in an Anharmonic One-Dimensional Lattice. Mech. Solids 2024, 59, 3235–3243. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shcherbinin, S.; Baimova, J.; Krivtsov, A. Energy Dynamics of Long-Wave Low-Amplitude Disturbances in an Anharmonic One-Dimensional Lattice. Materials 2025, 18, 5224. https://doi.org/10.3390/ma18225224
Shcherbinin S, Baimova J, Krivtsov A. Energy Dynamics of Long-Wave Low-Amplitude Disturbances in an Anharmonic One-Dimensional Lattice. Materials. 2025; 18(22):5224. https://doi.org/10.3390/ma18225224
Chicago/Turabian StyleShcherbinin, Stepan, Julia Baimova, and Anton Krivtsov. 2025. "Energy Dynamics of Long-Wave Low-Amplitude Disturbances in an Anharmonic One-Dimensional Lattice" Materials 18, no. 22: 5224. https://doi.org/10.3390/ma18225224
APA StyleShcherbinin, S., Baimova, J., & Krivtsov, A. (2025). Energy Dynamics of Long-Wave Low-Amplitude Disturbances in an Anharmonic One-Dimensional Lattice. Materials, 18(22), 5224. https://doi.org/10.3390/ma18225224





