Fast Thermal Resistance Distribution Analysis in High-Power VCSEL Array Module
Highlights
- Thermal resistance analysis can be used for a semiconductor laser module.
- Thermal resistance tests occur within extremely short times (25 s).
- Segmented thermal resistance distributions for the module are obtained.
- This study reveals a trustworthy and rapid thermal resistance analysis method for the VCSEL array module.
- This electrical transient measurement can identify the thermal resistance link of the module without any damage.
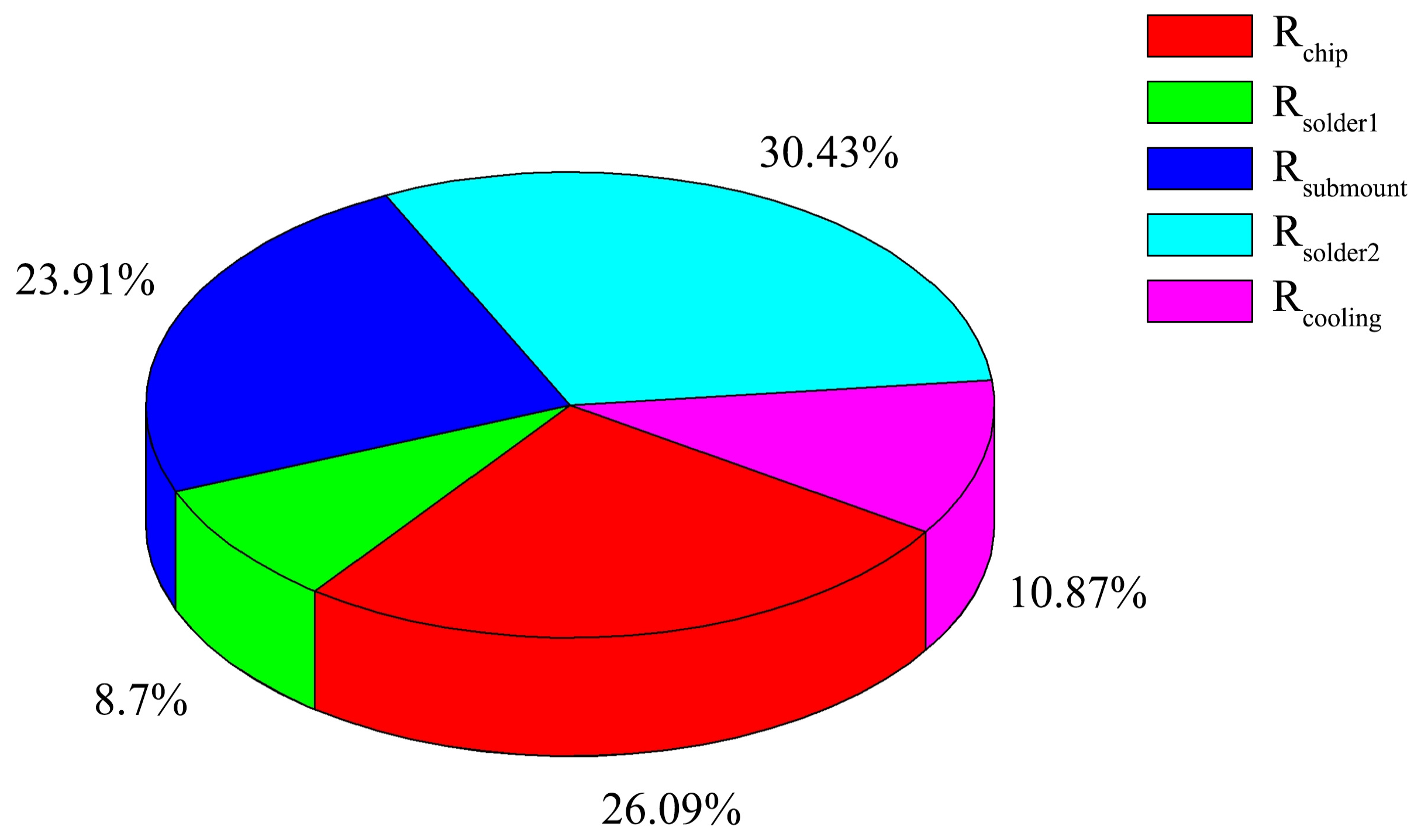
- Thermal resistances from Rsubmount and Rsolder2, which account for 54% of the total thermal resistance, have great potential for improvement.
Abstract
1. Introduction
2. Materials and Methods
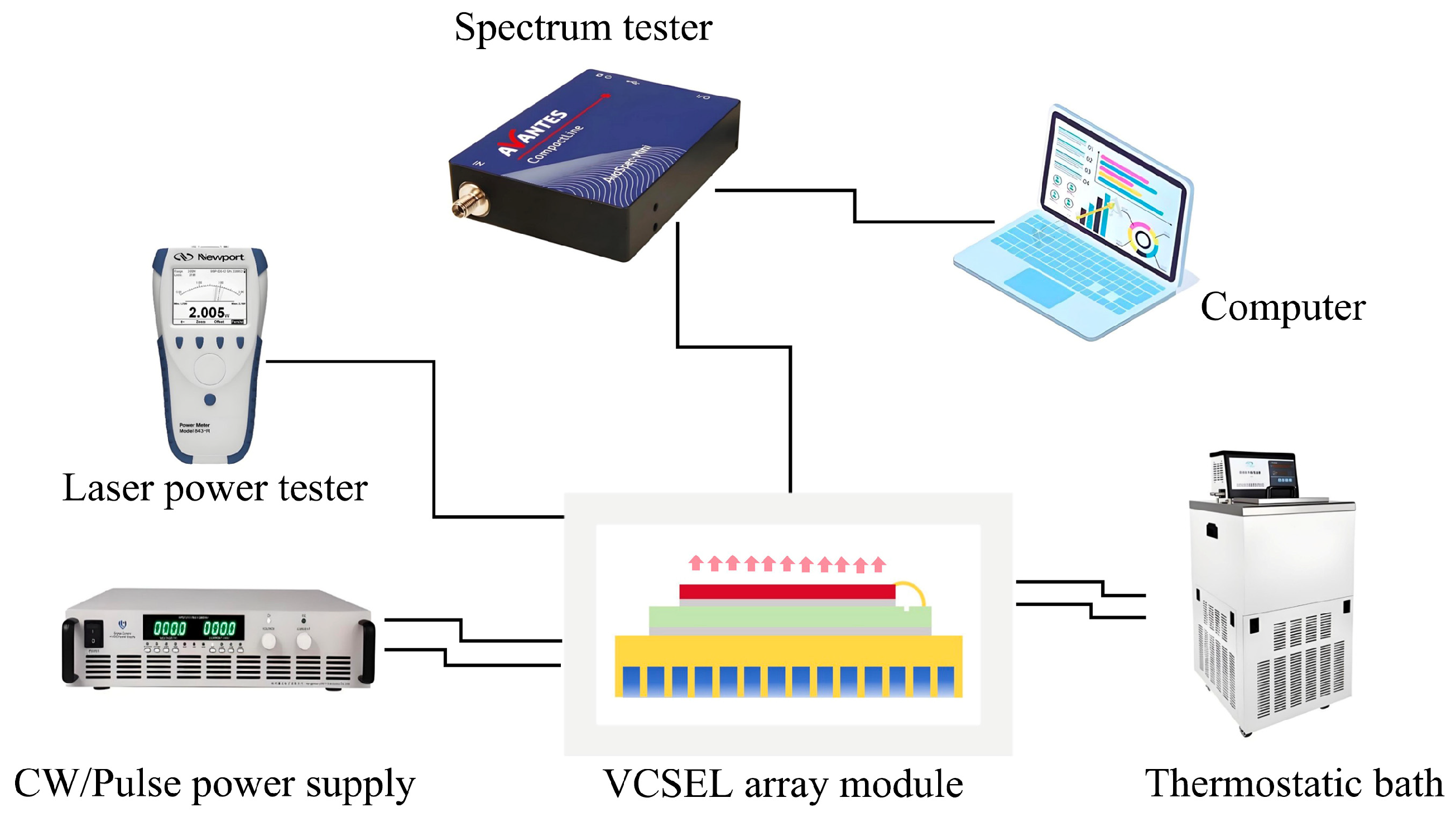
2.1. Materials’ Introduction
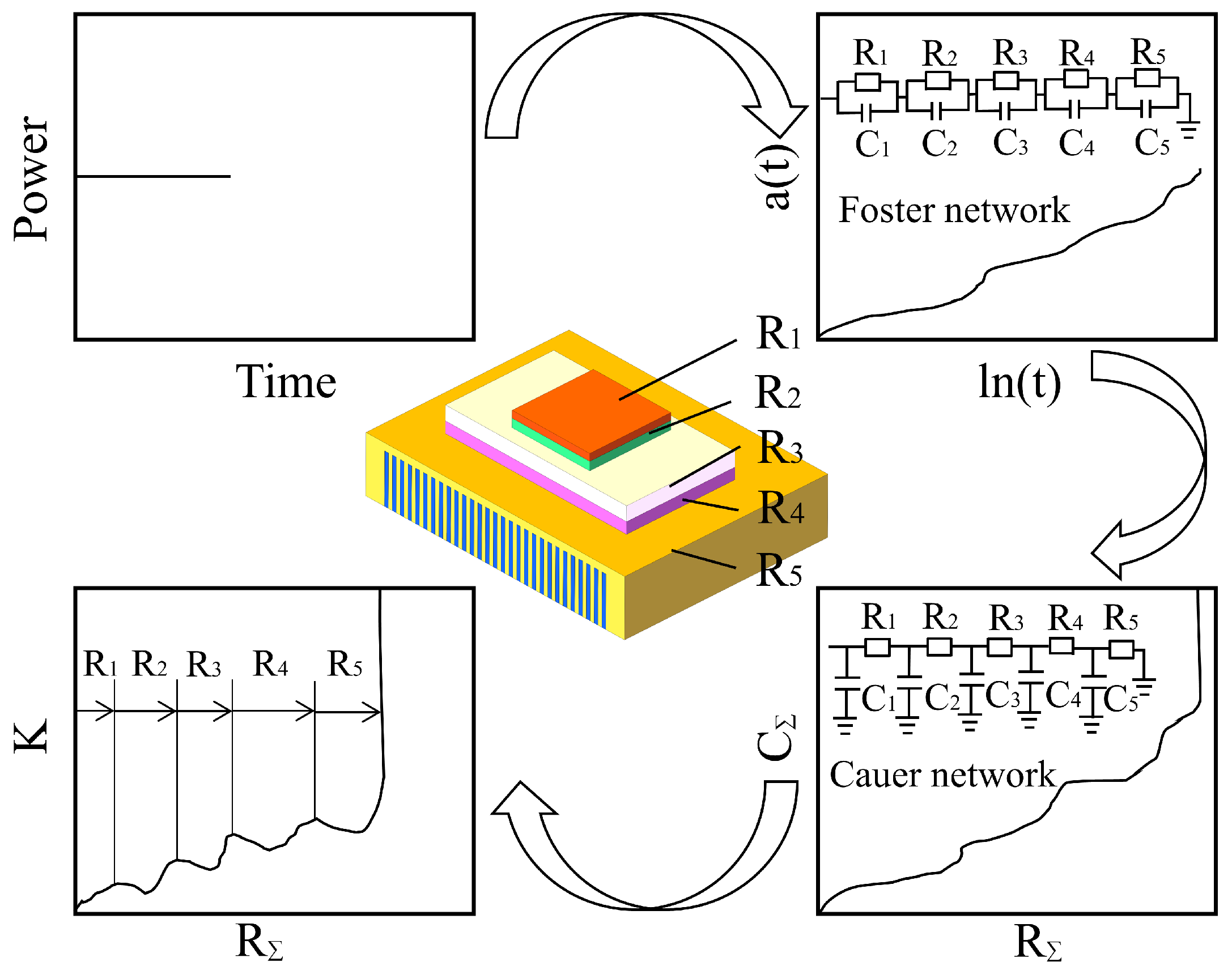
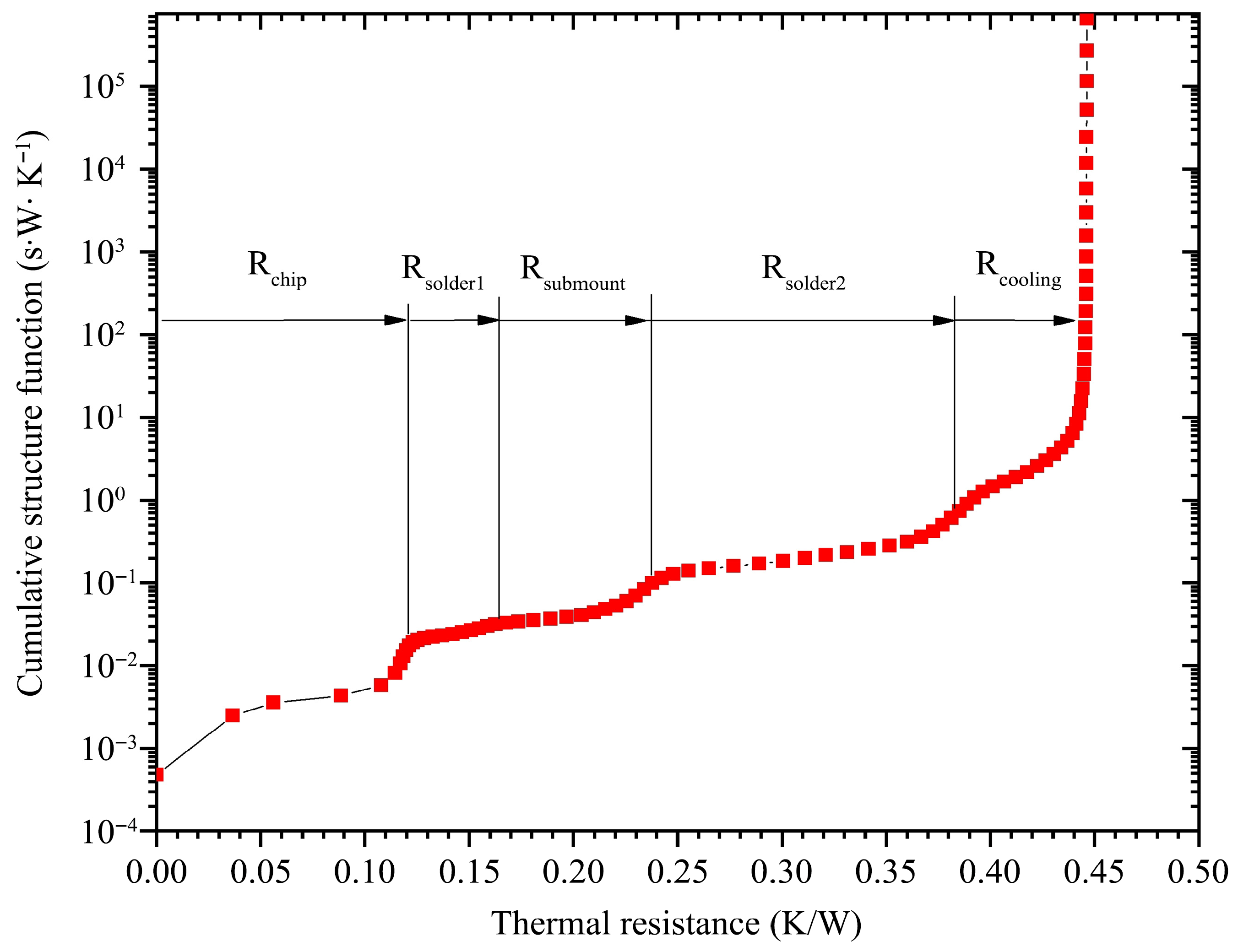
2.2. Structure Function Method
2.3. Spectroscopy Method
3. Results and Discussion
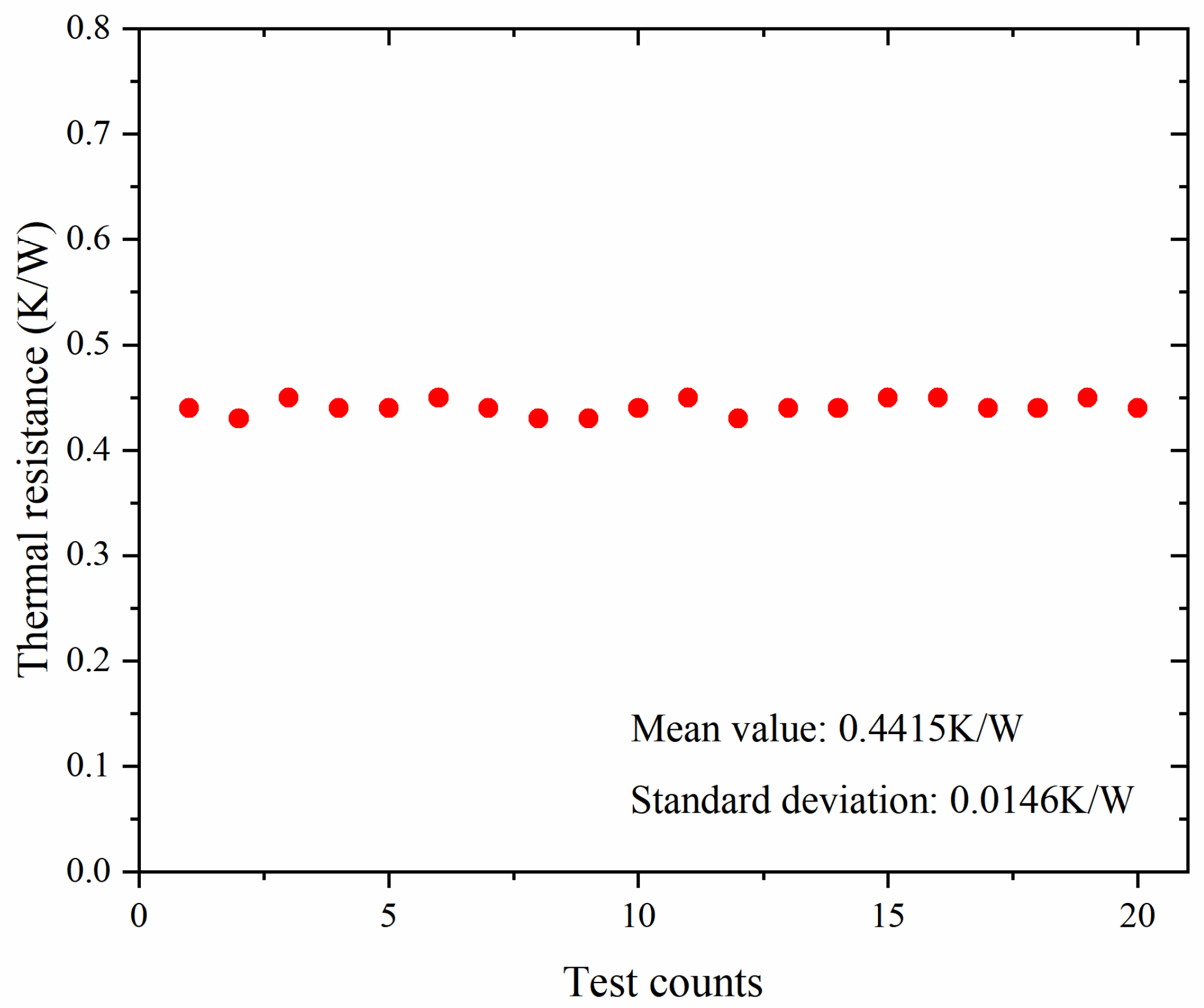
3.1. Thermal Resistance Analysis Using Structure Function Method
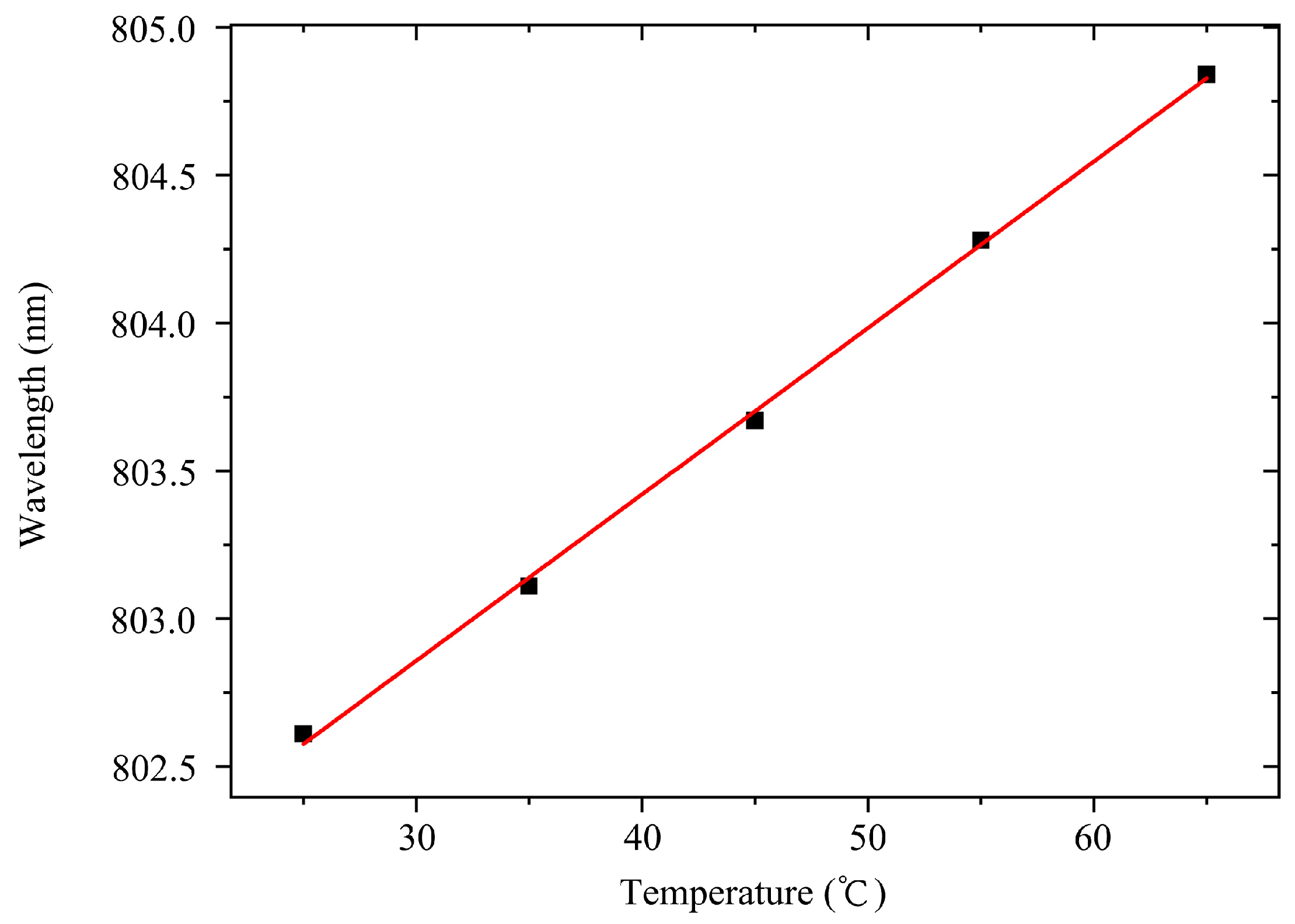
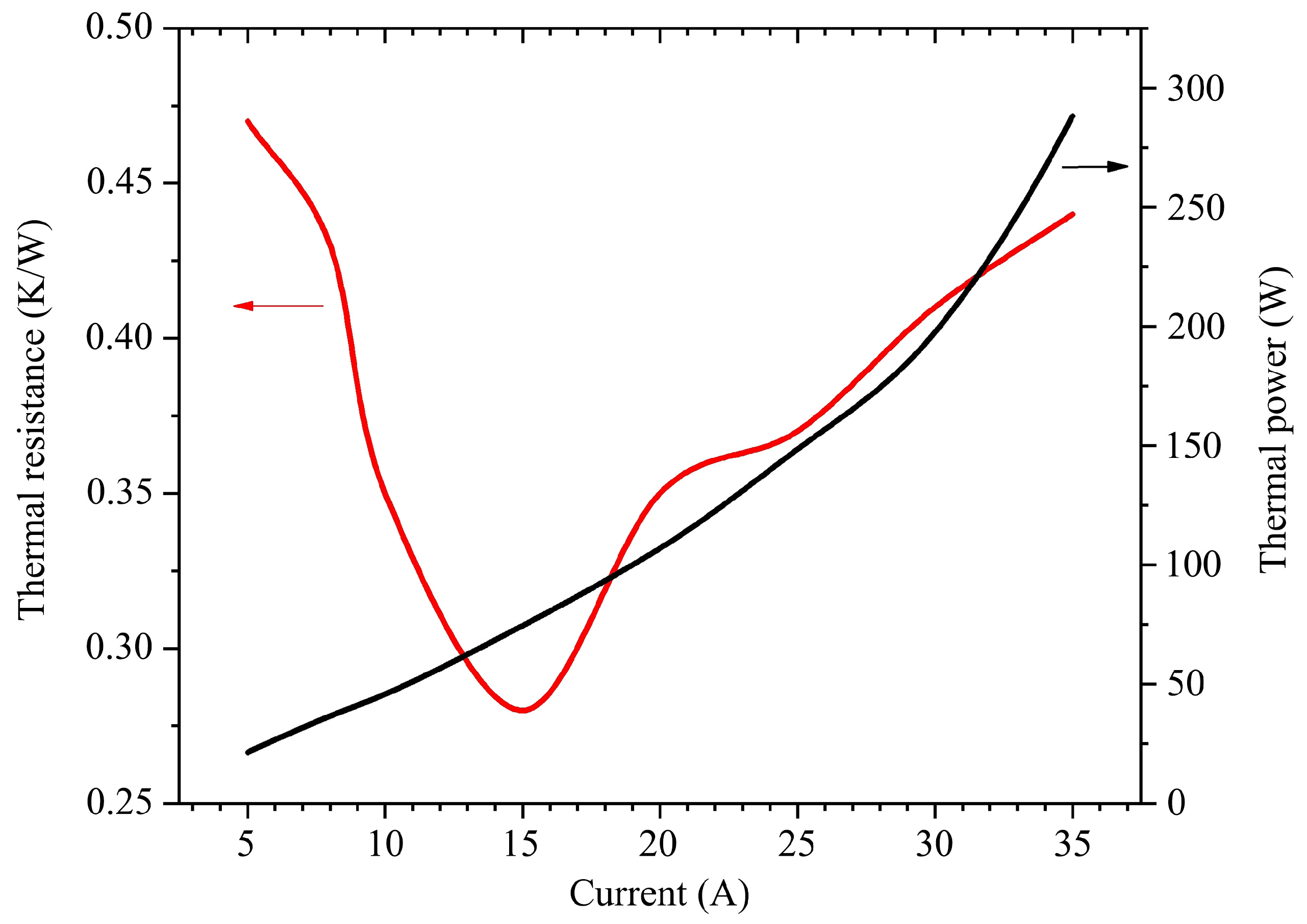
3.2. Thermal Resistance Analysis Using Spectroscopy Method
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, J.; Zhao, F.; Tang, Z.; Zhang, X.; Ren, A.; Wu, J. Advances in high-power vertical-cavity surface-emitting lasers. J. Phys. D Appl. Phys. 2024, 57, 353001. [Google Scholar] [CrossRef]
- Li, Y.; Li, C.; Wei, X.; Chen, L. High-power 786nm VCSEL-pumped Tm: YAG laser. In Proceedings of the Solid State Lasers XXXIV: Technology and Devices, San Francisco, CA, USA, 25–31 January 2025; SPIE: Bellingham, WA, USA, 2025; Volume 13341, pp. 254–260. [Google Scholar]
- Li, J.Y.; Yang, J.; Wang, H.; Li, X.P.; Guo, Y.D.; Gao, H.W.; Han, L.; Wang, X.J. Compact temperature-insensitive high-energy VCSEL side-pumped Nd: YAG laser with a VRM output coupler. Appl. Opt. 2025, 64, 1134–1138. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Li, C.; Wang, Z. Analysis of optical and thermal properties of 940-nm vertical-cavity surface-emitting lasers. Opt. Quantum Electron. 2022, 54, 438. [Google Scholar] [CrossRef]
- Filipchuk, A.; Nechay, K.; Ulkuniemi, R.; Talmila, S.; Uusimaa, P. Thermal management optimization in high-power 3D sensing VCSELs. In Proceedings of the Components and Packaging for Laser Systems VIII, San Francisco, CA, USA, 22 January–28 February 2022; SPIE: Bellingham, WA, USA, 2022; Volume 11982, pp. 84–89. [Google Scholar]
- Wang, J.; Yuan, C.; Li, Y.; Li, C.; Wang, Y.; Wei, X. Direct-to-chip immersion liquid cooling for high-power vertical-cavity surface-emitting laser (VCSEL). Appl. Therm. Eng. 2025, 269, 126137. [Google Scholar] [CrossRef]
- Yuan, C.; Li, Y.; Wang, Y.; Li, C.; Wei, X.; Chen, L. Thermal management of high-power vertical-cavity surface-emitting laser arrays. IEEE Trans. Electron Devices 2023, 70, 6421–6426. [Google Scholar] [CrossRef]
- Yan, G.X.; Hao, Y.Q.; Zhang, Q.B. Thermal characteristics of high-power vertical cavity surface emitting laser array. Acta Phys. Sin. 2024, 73. [Google Scholar] [CrossRef]
- Namvar, B.; Uusitalo, T.; Virtanen, H.; Guina, M.; Viheriälä, J. Improving p-doped DBRs operation at cryogenic temperatures: Investigating different mirror geometry. IEEE Photonics J. 2024, 16, 1502009. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, Y.; Lu, X.; Zhan, X.; Dai, Q.; Liu, J.; Li, Q.; Zhang, X.; Zhang, Y.; Sun, Q.; et al. Thermal resistance optimization of GaN-on-Si materials for RF HEMTs based on structure function method and static-pulsed I–V measurements. Appl. Phys. Lett. 2025, 126. [Google Scholar] [CrossRef]
- Guo, C.; Cui, S.; Tsai, W.; Liu, Y.; Ding, J.; Li, J.; Chen, Z.; Li, Y.; Pan, S.; Feng, S. Measuring double-sided thermal resistance of press-pack IGBT modules based on ratio of double-sided heat dissipation. IEEE Trans. Electron Devices 2023, 70, 1776–1781. [Google Scholar] [CrossRef]
- Górecki, P.; Górecki, K.; Kisiel, R.; Brzozowski, E.; Bar, J.; Guziewicz, M. Investigations of an influence of the assembling method of the die to the case on thermal parameters of IGBTs. IEEE Trans. Compon. Packag. Manuf. Technol. 2021, 11, 1988–1996. [Google Scholar] [CrossRef]
- An, T.; Zhou, R.; Qin, F.; Dai, Y.; Gong, Y.; Chen, P. Comparative study of the parameter acquisition methods for the cauer thermal network model of an IGBT module. Electronics 2023, 12, 1650. [Google Scholar] [CrossRef]
- EIA/JEDEC Standard, JESD51-1; Integrated Circuit Thermal Measurement Method-Electrical Test Method. Electronic Industries Association: Tokyo, Japan, 1995.
- Li, X.; Feng, S.; Feng, Z.; Pan, S.; Lv, Y.; Bai, K.; Lu, X.; Qin, J.; Zhang, Y. A thermal boundary resistance measurement method based on a designed chip with the heat source separated from the temperature sensor. Appl. Phys. Lett. 2023, 122, 073501. [Google Scholar] [CrossRef]
- Székely, V.; Van Bien, T. Fine structure of heat flow path in semiconductor devices: A measurement and identification method. Solid-State Electron. 1988, 31, 1363–1368. [Google Scholar] [CrossRef]
- Meng, X.; Zhang, M.; Duan, K.; Zheng, X.; Zhai, Y.; Feng, S.; Zhang, Y. Research on transient temperature rise measurement method for semiconductor devices based on photothermal reflection. IEEE Trans. Instrum. Meas. 2023, 72, 9000909. [Google Scholar] [CrossRef]
- Liu, G.; Li, X.; Wang, Y.; Huang, X.; Chang, G.; Luo, H. A method to derive the coupling thermal resistances at junction-to-case level in multichip power modules. IEEE Trans. Power Electron. 2022, 38, 1747–1756. [Google Scholar]
- Zhang, Y.; Zhang, Y.; Xu, Z.; Wang, Z.; Wong, H.; Lu, Z.; Caruso, A. A guideline for silicon carbide MOSFET thermal characterization based on source-drain voltage. In Proceedings of the 2023 IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 19–23 March 2023; IEEE: New York City, NY, USA, 2023; pp. 378–385. [Google Scholar]
- Kristensen, T.; Divinyi, A.; Bremer, J.; Nilsson, T.M.J.; Thorsell, M. Thermal transient measurements of GaN HEMT structures by electrical measurements. In Proceedings of the 2023 18th European Microwave Integrated Circuits Conference (EuMIC), Berlin, Germany, 18–19 September 2023; IEEE: New York City, NY, USA, 2023; pp. 293–296. [Google Scholar]
- He, L.; Du, W.; Li, Y.; He, Y.; Xie, P.; Zhou, K.; Zhang, L.; Hu, Y.; Yang, X.; Liu, S.; et al. Investigation of the gain match in high brightness 980 nm tapered diode laser. J. Lumin. 2023, 257, 119644. [Google Scholar] [CrossRef]
- Shakhovoy, R.; Puplauskis, M.; Sharoglazova, V.; Maksimova, E.; Hydyrova, S.; Kurochkin, V.; Duplinskiy, A. Wavelength-and time-division multiplexing via pump current variation of a pulsed semiconductor laser—A method of synchronization for quantum key distribution. IEEE J. Quantum Electron. 2023, 59, 8000110. [Google Scholar] [CrossRef]
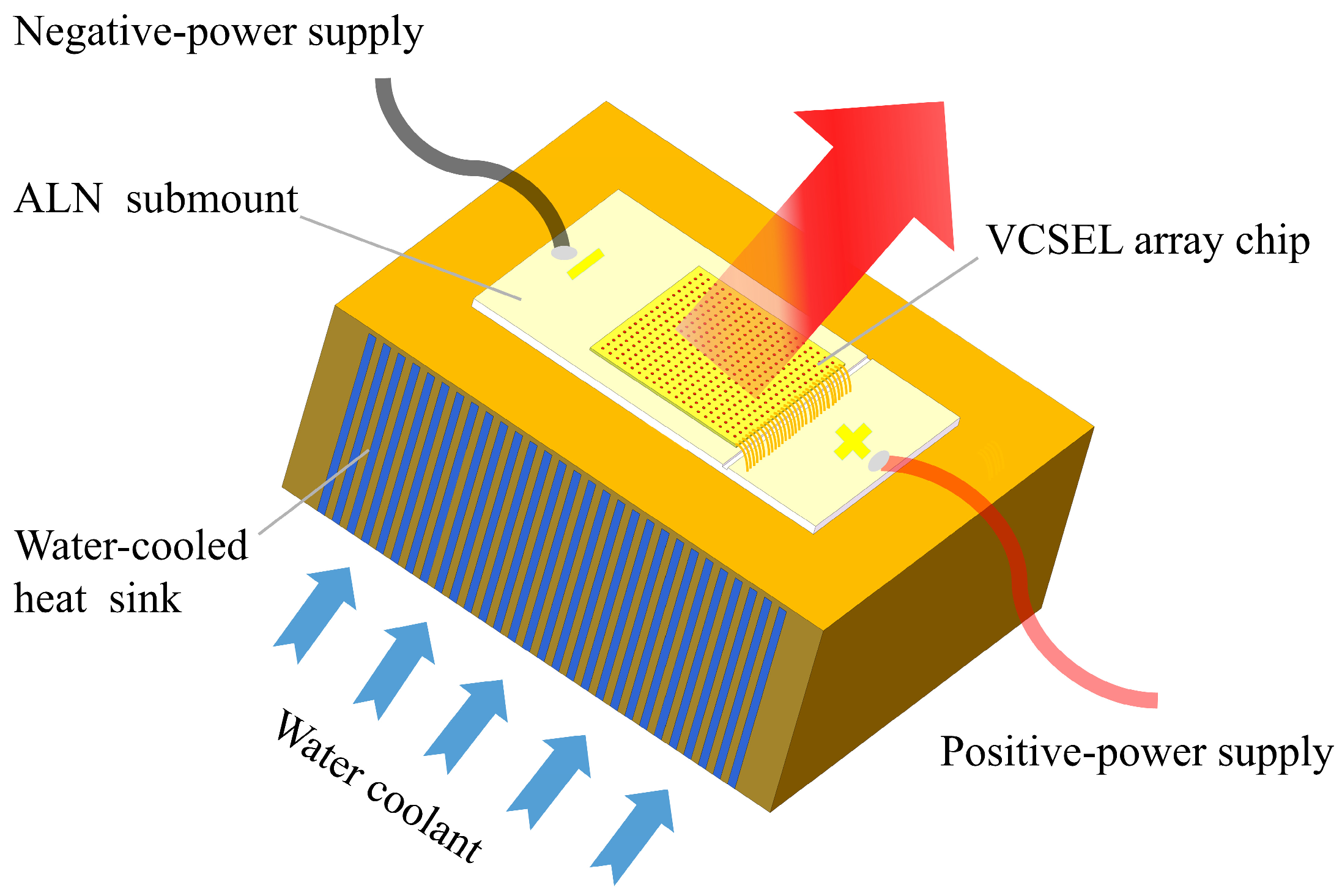
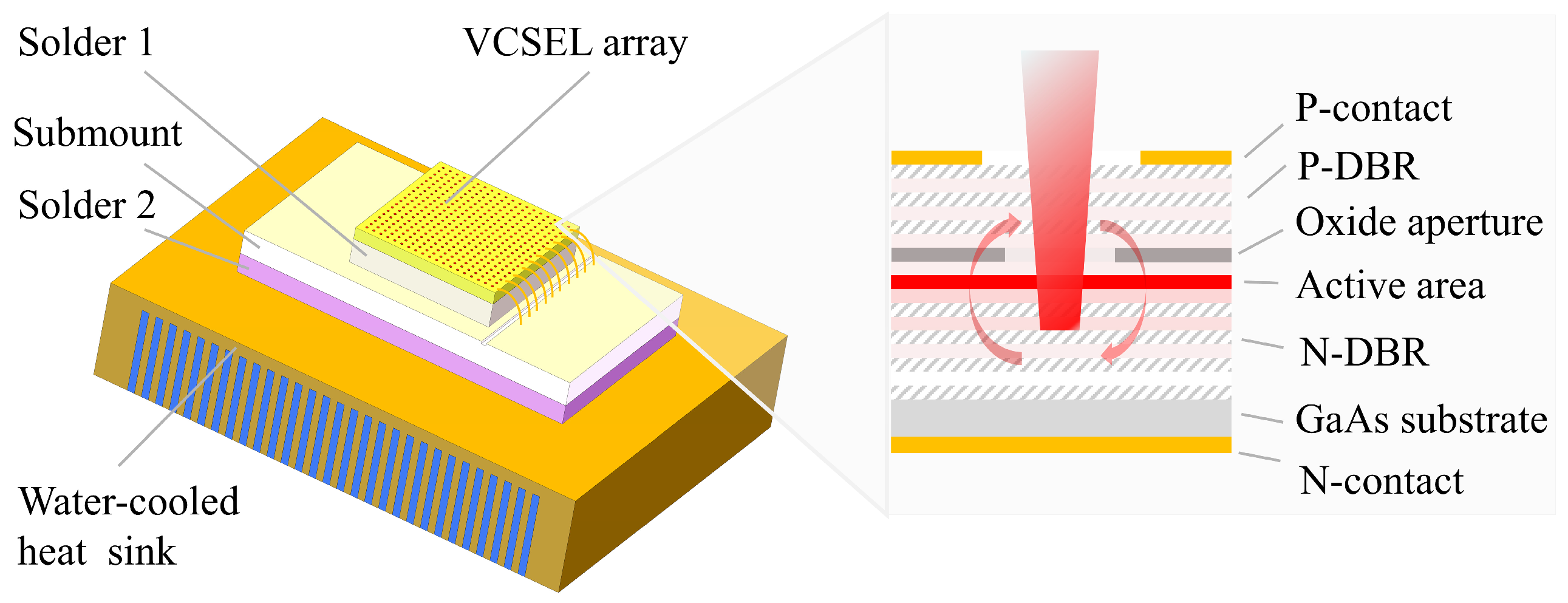
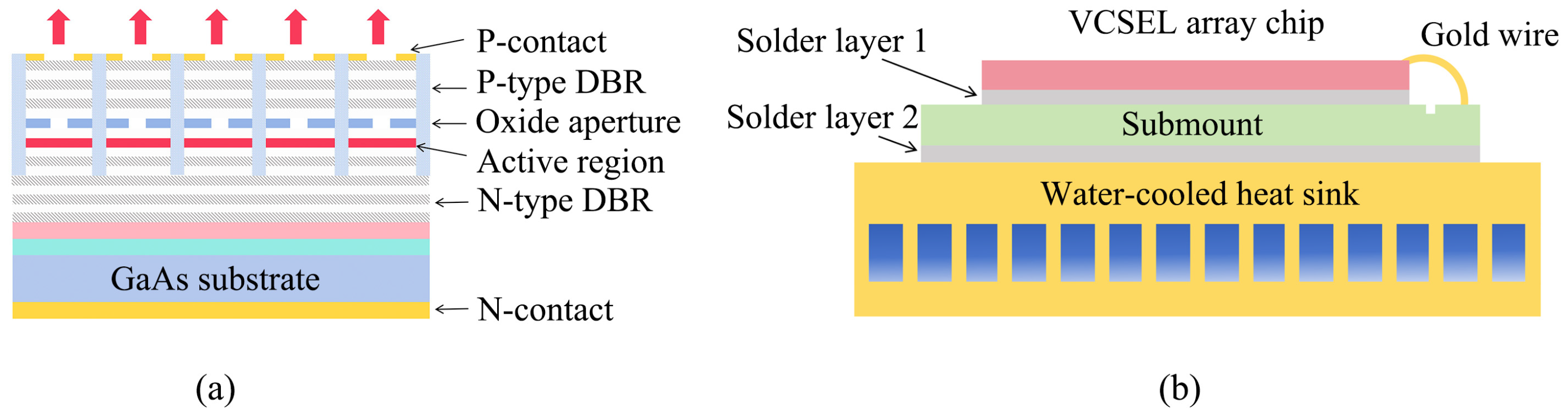

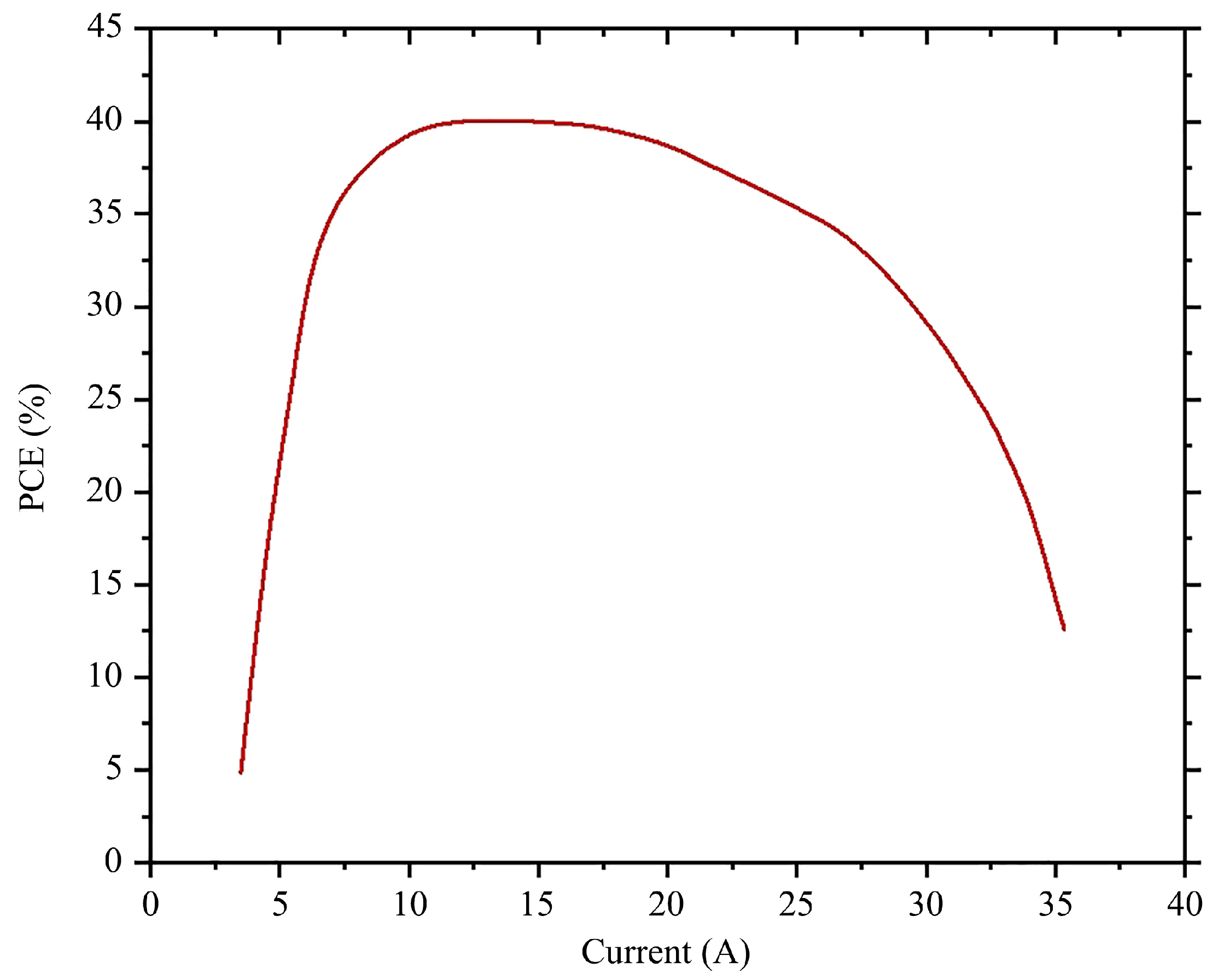




| Elements | VCSEL Array | Solder 1 | Submount | Solder 2 | |
|---|---|---|---|---|---|
| Parameters | |||||
| Main material | GaAs | Ag | ALN | Indium | |
| Thickness (μm) | 100 | 5 | 350 | 10 | |
| Area (mm2) | 36 | 36 | 112 | 112 | |
| Thermal conductivity (W/m·K) | 56 | 200 | 180 | 82 | |
| Current (A) | Voltage (V) | Laser Power (W) | Wavelength (nm) | Thermal Power (W) |
|---|---|---|---|---|
| 5 | 6.84 | 12.8 | 803.16 | 21.4 |
| 8 | 7.14 | 20.5 | 803.41 | 36.6 |
| 10 | 7.56 | 29.8 | 803.50 | 45.8 |
| 15 | 8.10 | 47.0 | 803.78 | 74.5 |
| 20 | 8.58 | 64.6 | 804.67 | 107.0 |
| 25 | 9.06 | 78.0 | 805.73 | 148.5 |
| 30 | 9.42 | 85.0 | 807.13 | 197.6 |
| 35 | 9.72 | 52.4 | 809.58 | 287.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Lan, T.; Wang, Z.; Ye, Z. Fast Thermal Resistance Distribution Analysis in High-Power VCSEL Array Module. Materials 2025, 18, 5210. https://doi.org/10.3390/ma18225210
Li D, Lan T, Wang Z, Ye Z. Fast Thermal Resistance Distribution Analysis in High-Power VCSEL Array Module. Materials. 2025; 18(22):5210. https://doi.org/10.3390/ma18225210
Chicago/Turabian StyleLi, Dezhen, Tian Lan, Zhiyong Wang, and Zhengyu Ye. 2025. "Fast Thermal Resistance Distribution Analysis in High-Power VCSEL Array Module" Materials 18, no. 22: 5210. https://doi.org/10.3390/ma18225210
APA StyleLi, D., Lan, T., Wang, Z., & Ye, Z. (2025). Fast Thermal Resistance Distribution Analysis in High-Power VCSEL Array Module. Materials, 18(22), 5210. https://doi.org/10.3390/ma18225210




