Geometry and Material Criteria for Low-Carbon Design of I/H-Beams in Sustainable Steel Structures Considering Both Mechanical Properties and Carbon Emissions
Abstract
1. Introduction
- The proposed CCR integrates both mechanical properties and carbon emissions and transforms the comprehensive performance into the geometry coefficient and material coefficient, which are mutually independent and allows for simpler performance optimization of components through the separate optimization of the two indices.
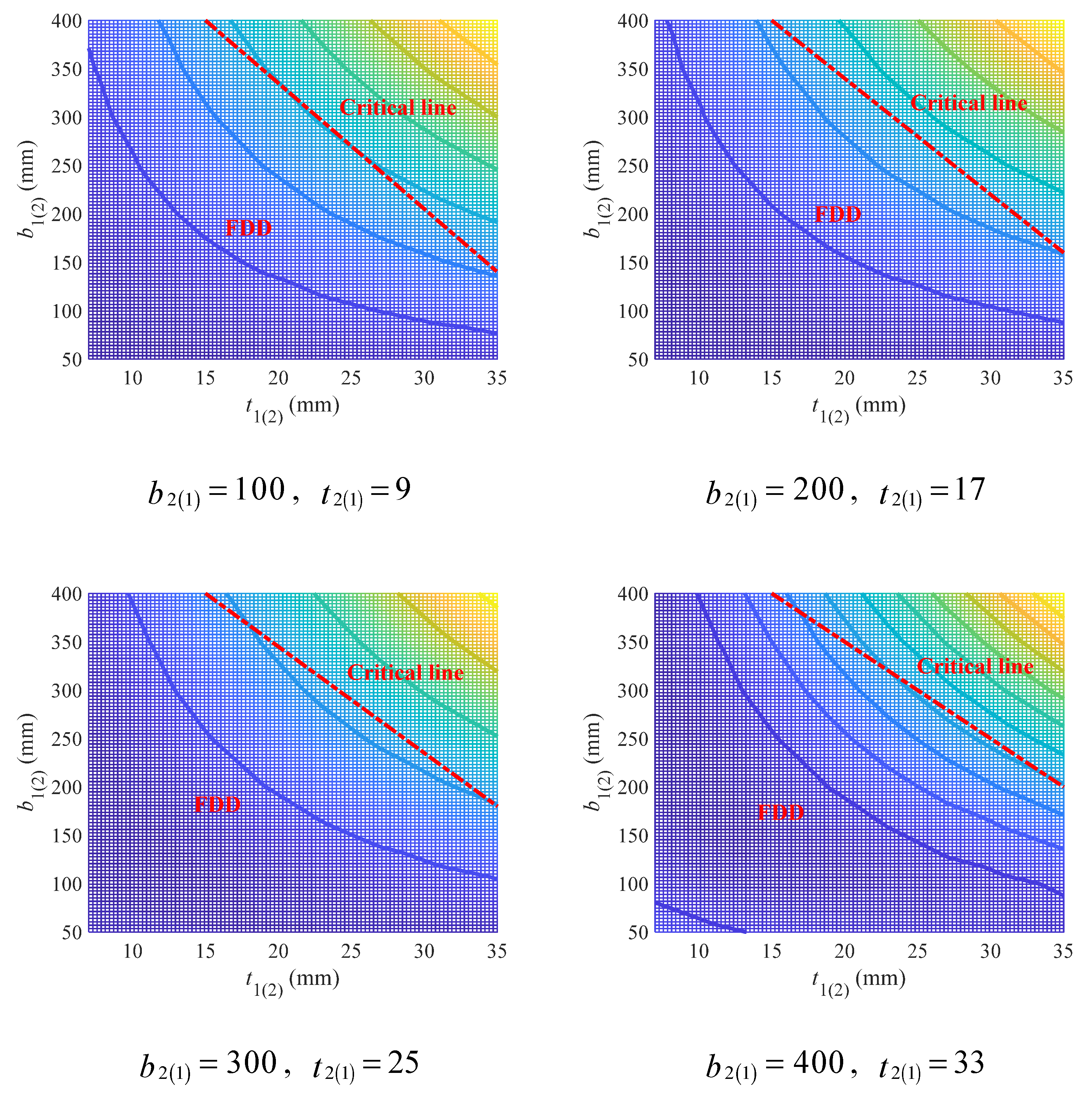
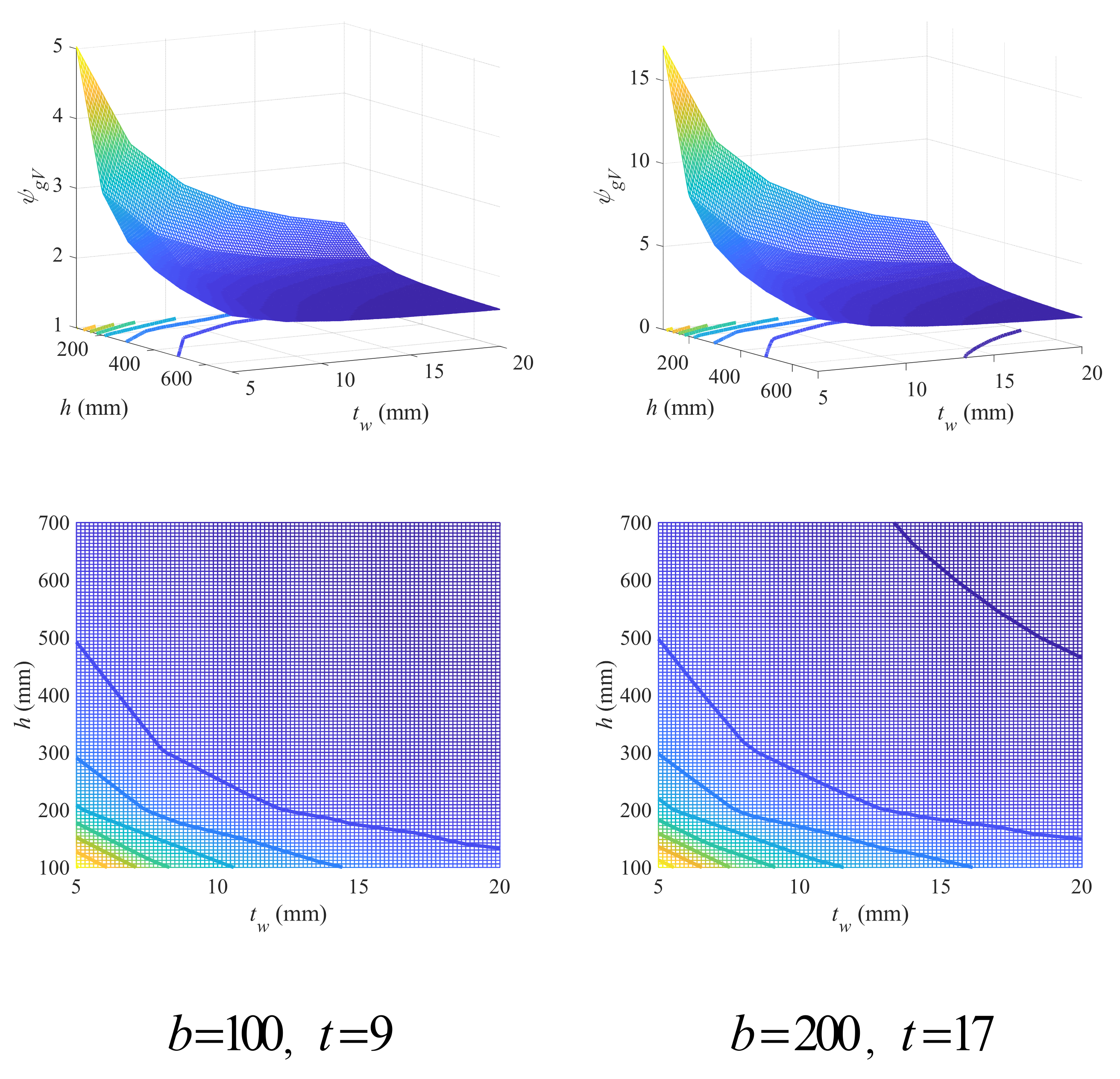
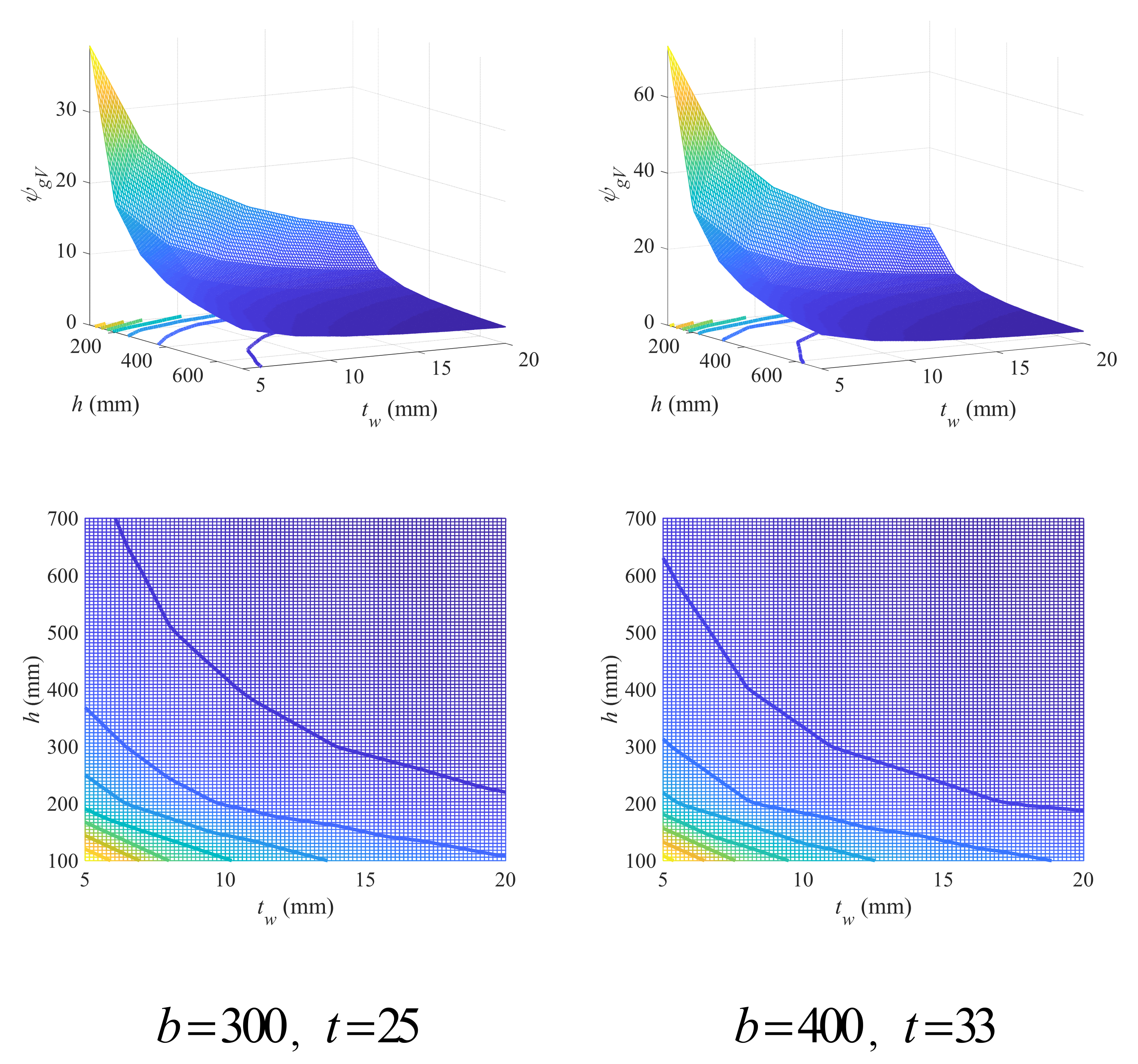
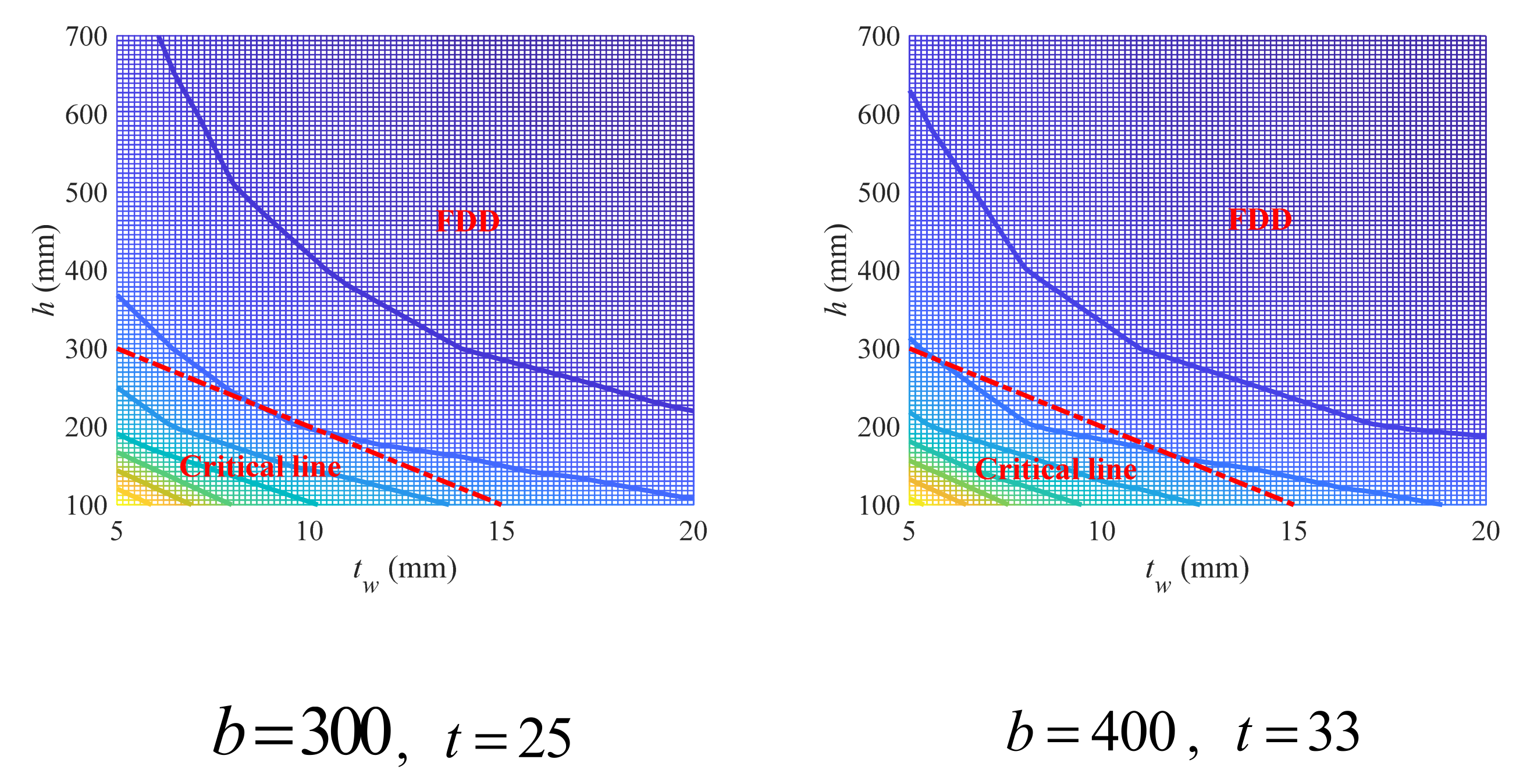
- The geometry coefficient was numerically investigated as an intermediate variable to establish the geometry criteria for the low-carbon design of I/H-beams, including the effect of different geometry variables as well as the feasible design domain (FDD) of I/H-beams under different load conditions. The FDD is a more generalized and universal analytical design recommendation that has nothing to do with predetermined design requirements and can be directly used as the constraints that are easier to resolve in the low-carbon optimization of I/H-beams.
- The material coefficient allows the life-cycle carbon emissions to be taken into account, which was analyzed to give the material criteria on material selection and beam fabrication regarding the low-carbon design of I/H-beams. When used as the constraints in optimization, there is no need to deal with the complex connections between the material coefficient and the FDD, thus making the optimization more efficient.
2. Methodology
2.1. Mechanical Properties
2.1.1. Flexural Capacity
Double-Symmetric Cross-Section
Single-Symmetric Cross-Section
- (a)
- If there is , then the relation of can be derived from Equation (12). That is, the cross-section has reduced to be double-symmetric with only four independent variables including the width () and thickness () of the flange, the height of the beam (), as well as the thickness of the web (), as previously discussed.
- (b)
- If there is , then the relation as Equation (13) can be derived. The cross-section is still single-symmetric, but the number of independent variables has reduced from 6 to 5, including the width () and thickness () of the upper flange, the width () and thickness () of the lower flange, as well as the height of the beam ().
2.1.2. Ultimate Shear Strength
2.2. Carbon Emissions
2.3. Comprehensive Index
3. Results and Discussion
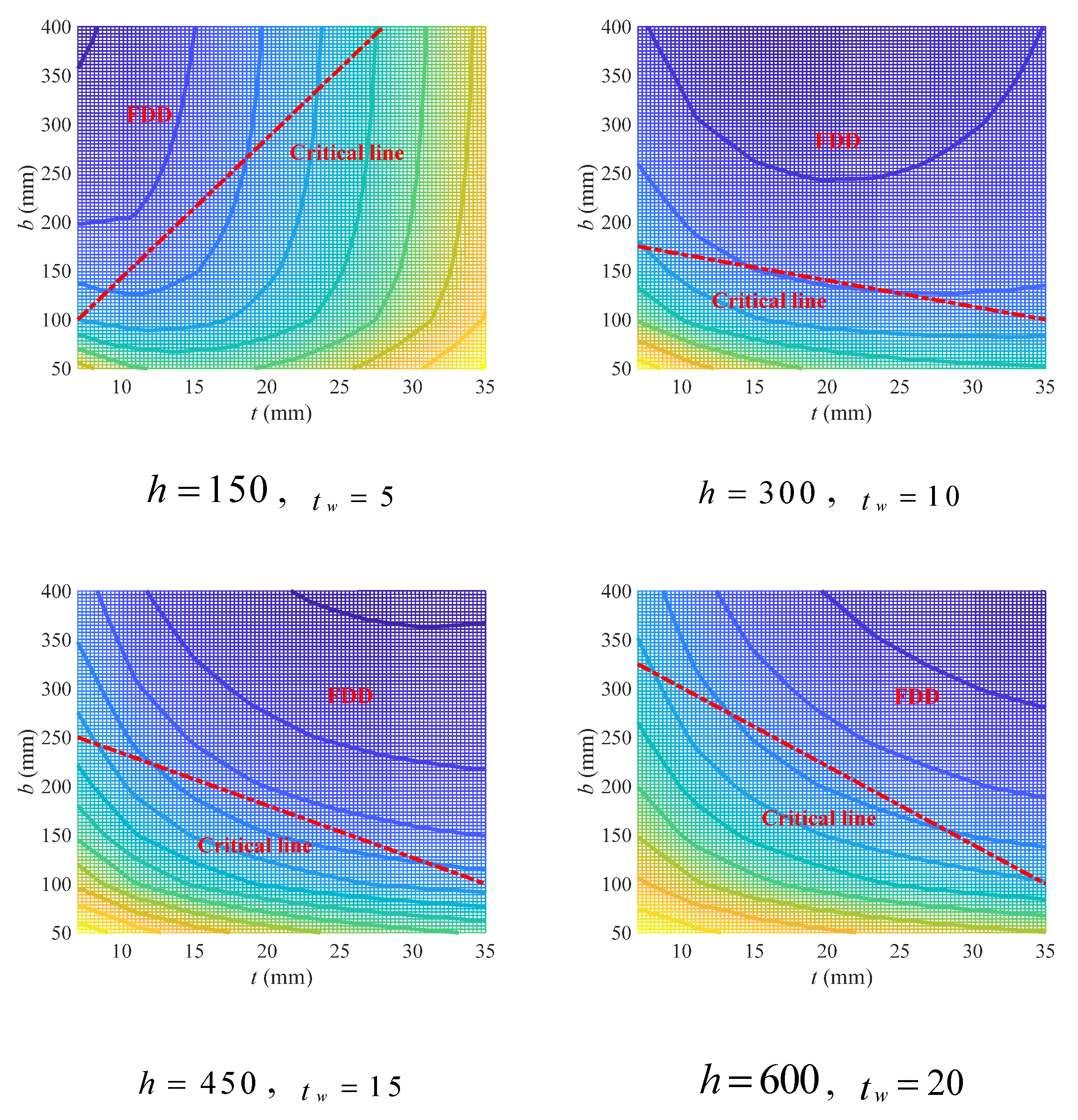
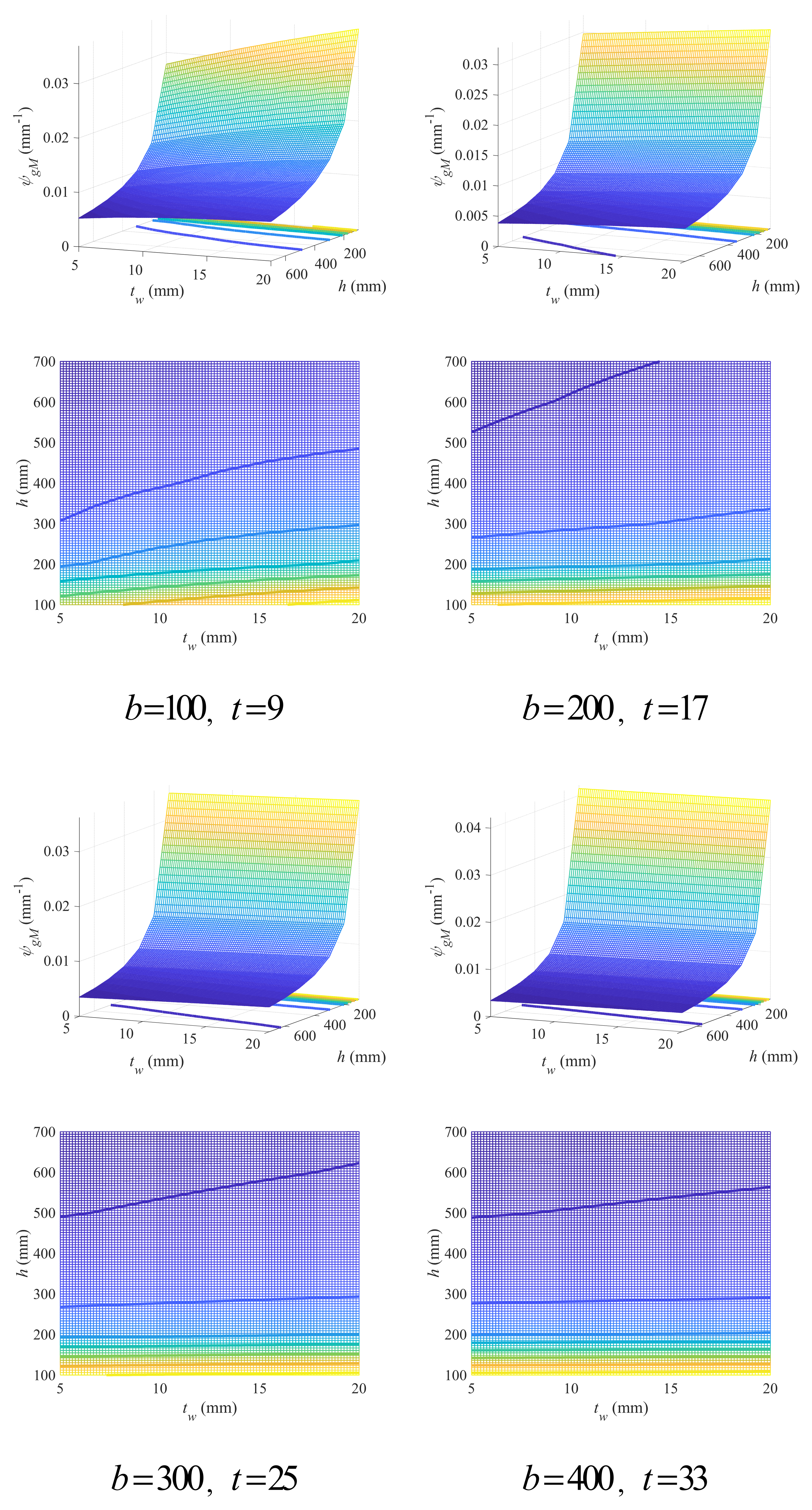
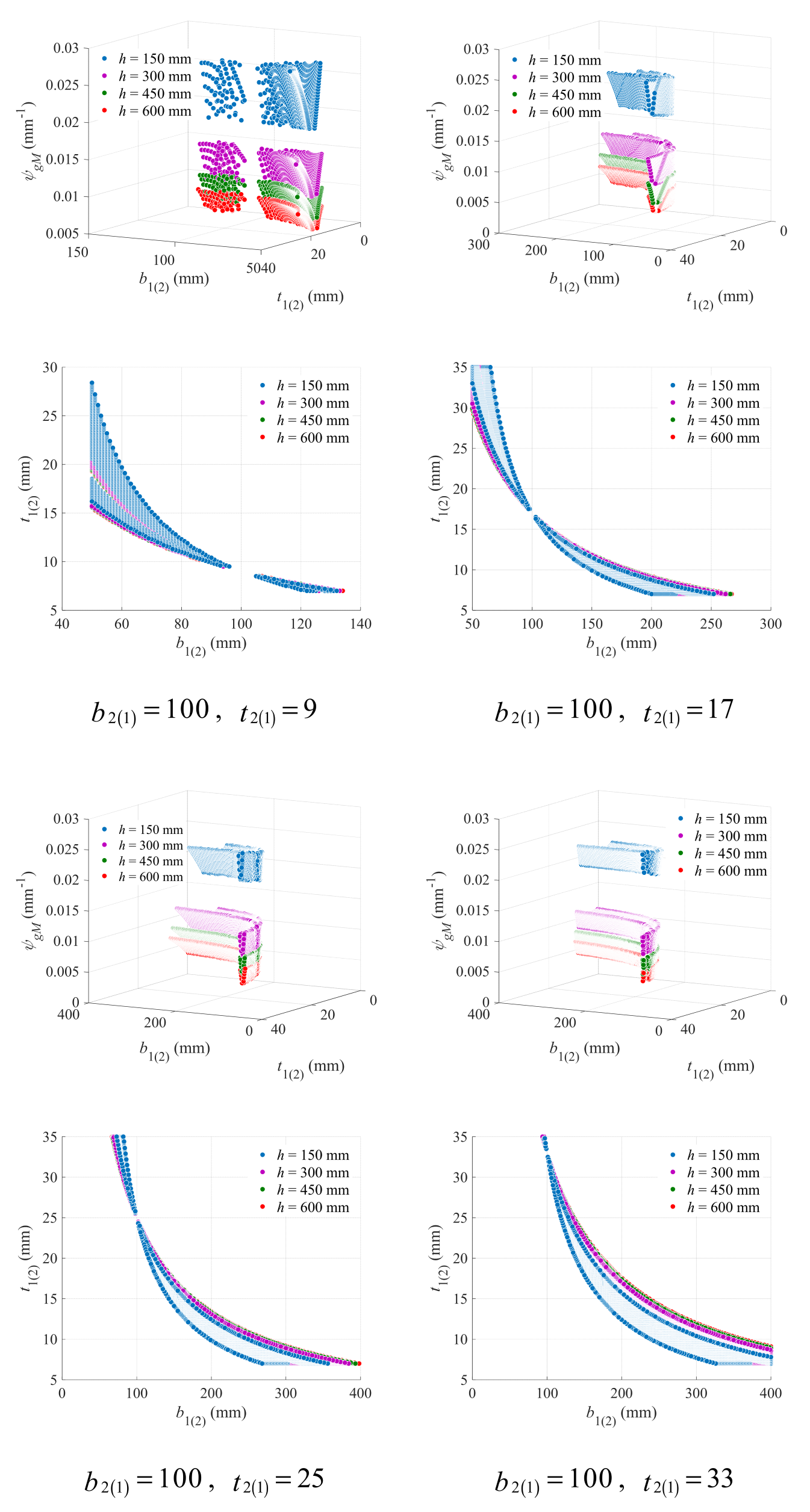
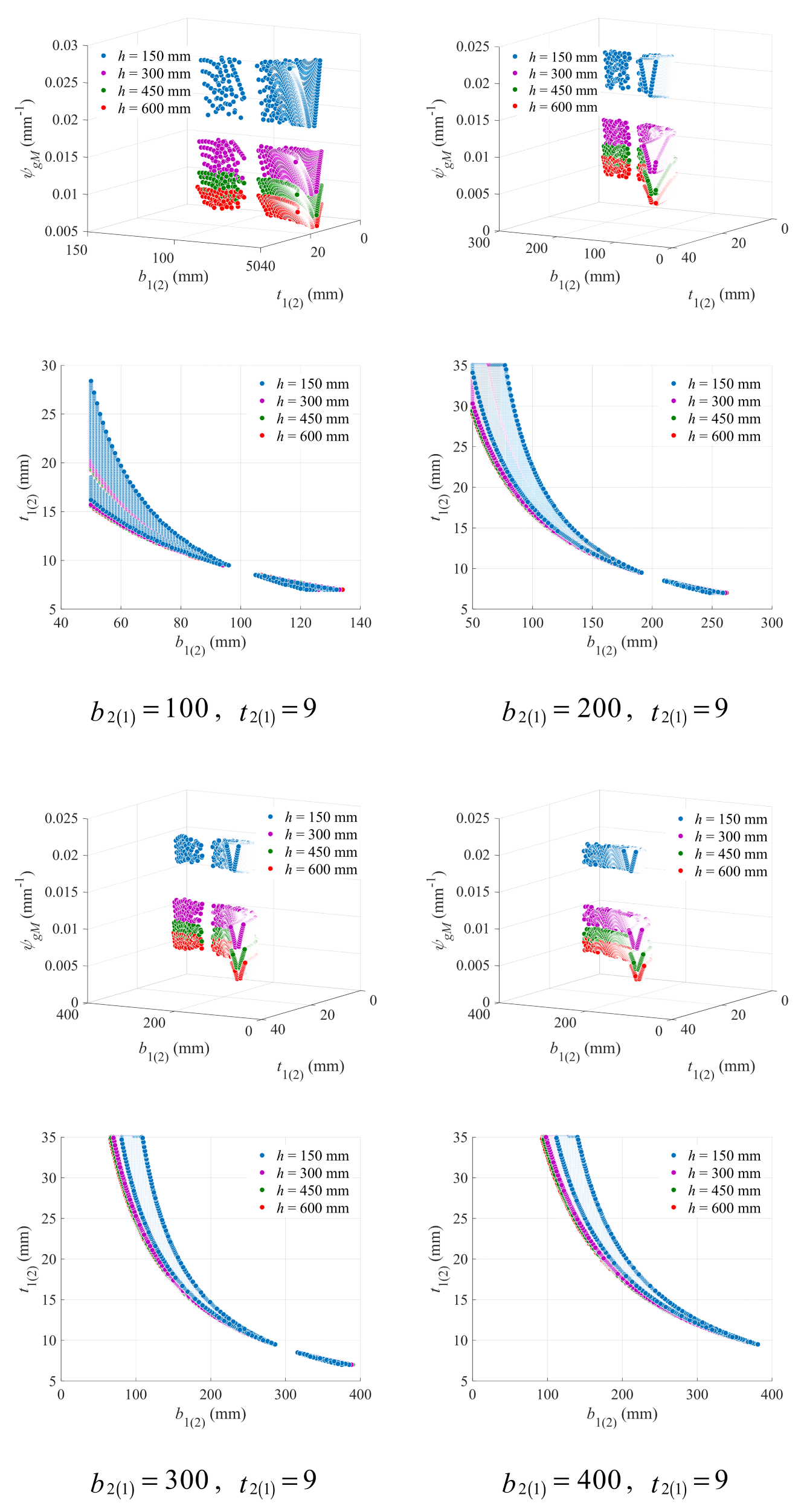
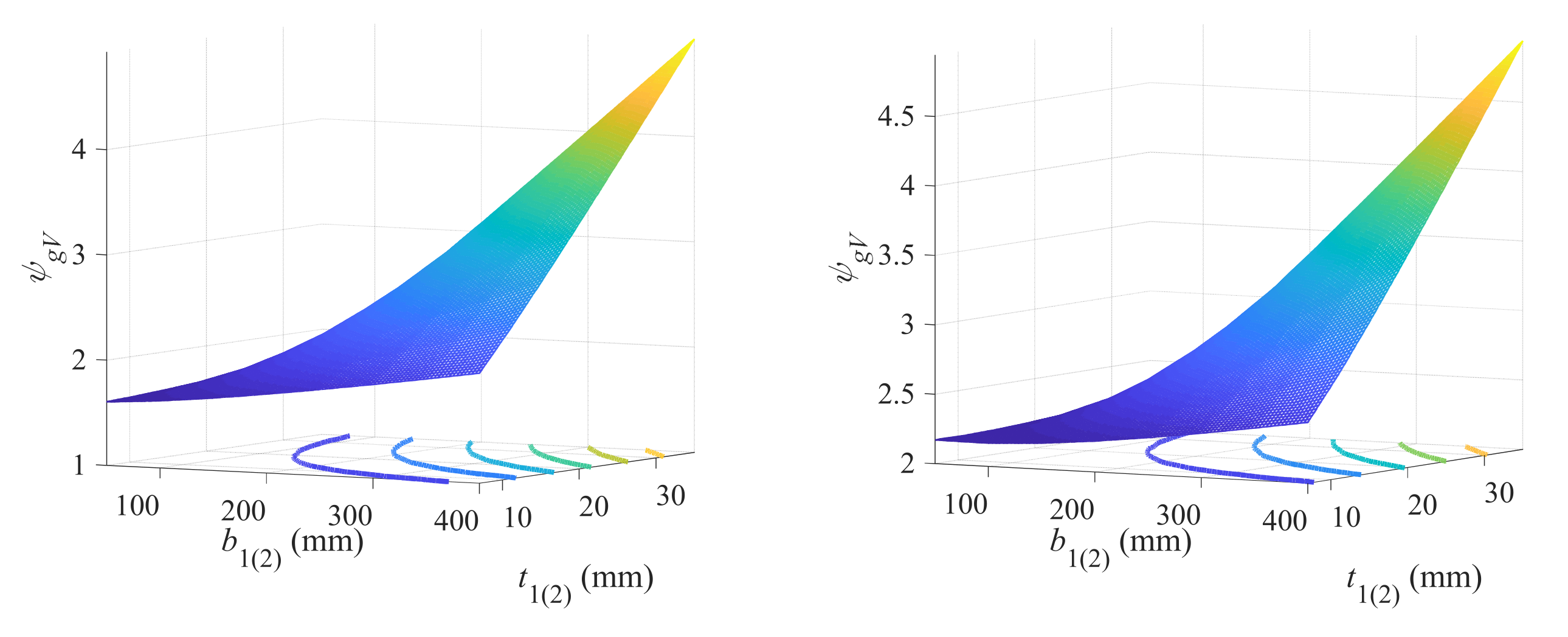
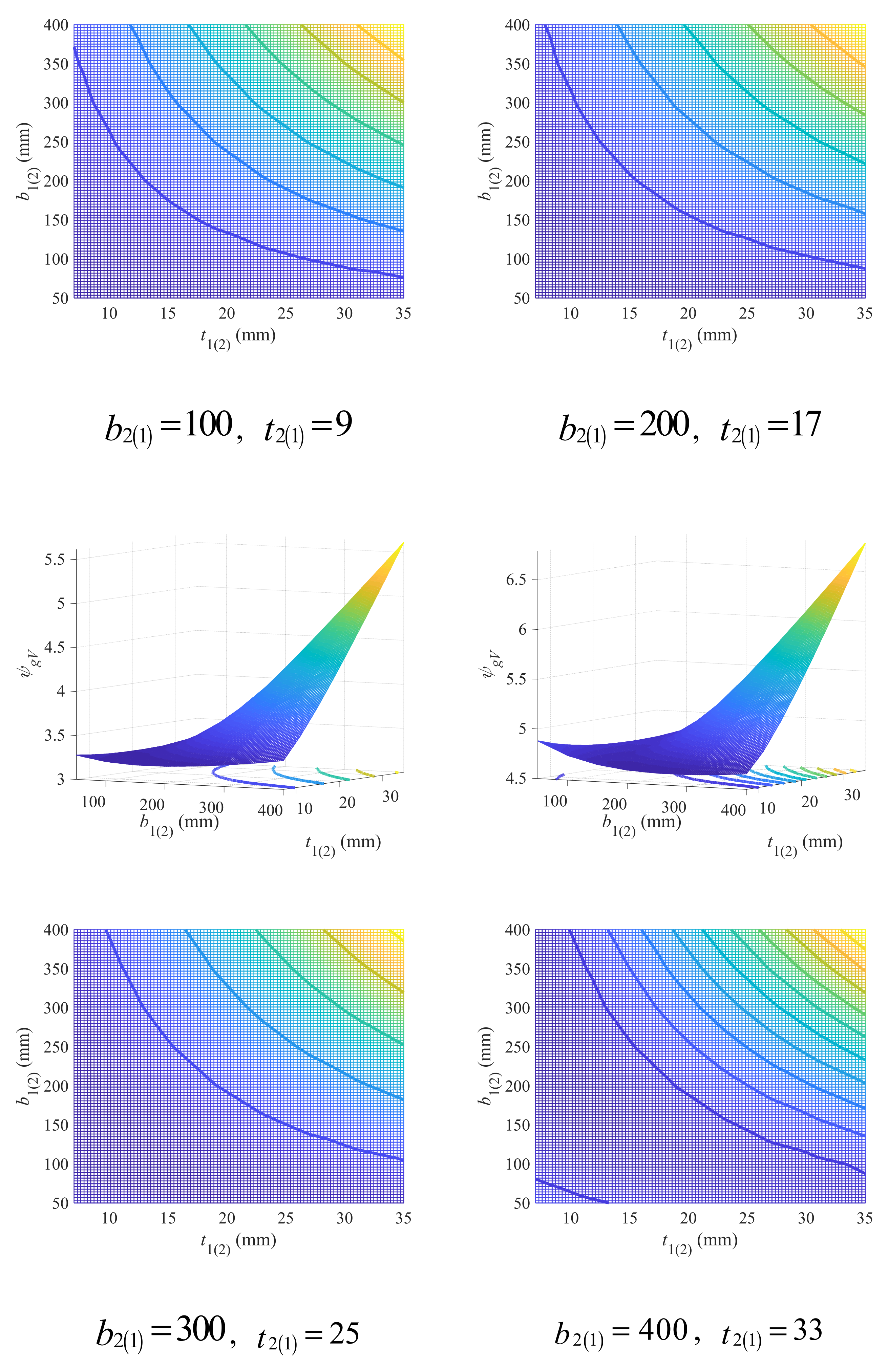
3.1. Geometry Criteria
3.1.1. Criteria Governed by Flexural Capacity
Double-Symmetric Cross-Section
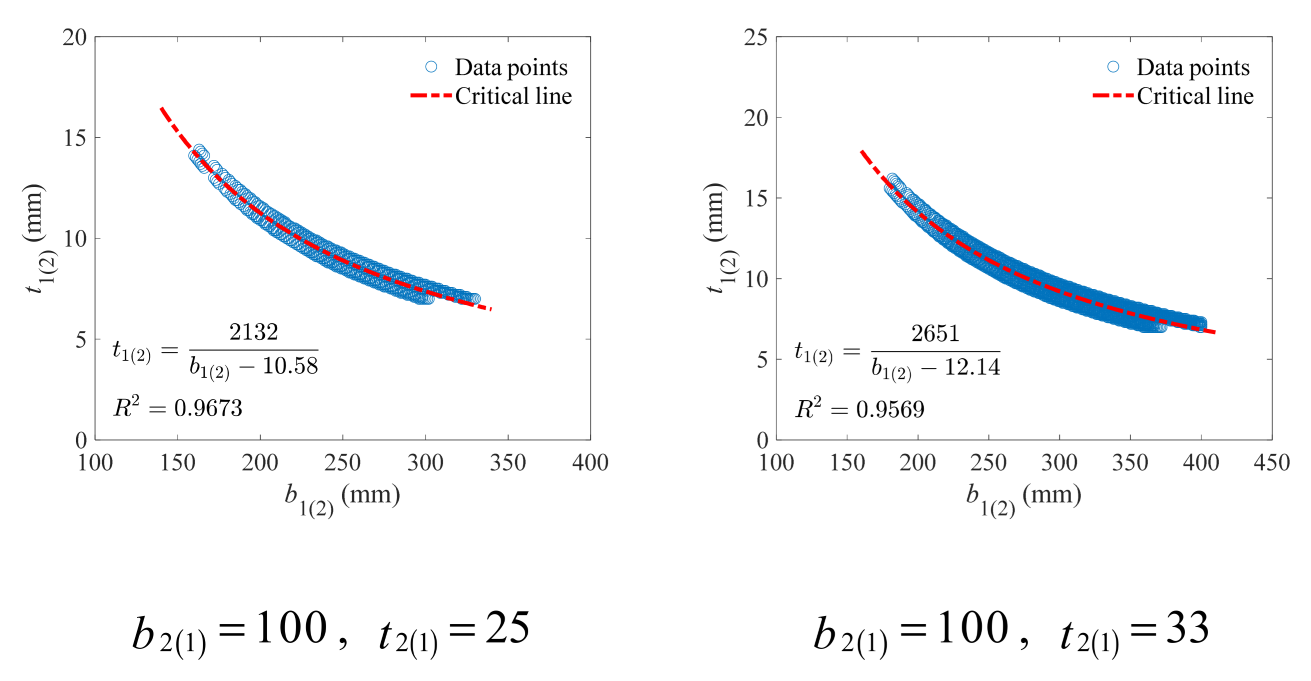
Single-Symmetric Cross-Section
3.1.2. Criteria Governed by Ultimate Shear Strength
3.2. Material Criteria
4. Conclusions
- (1)
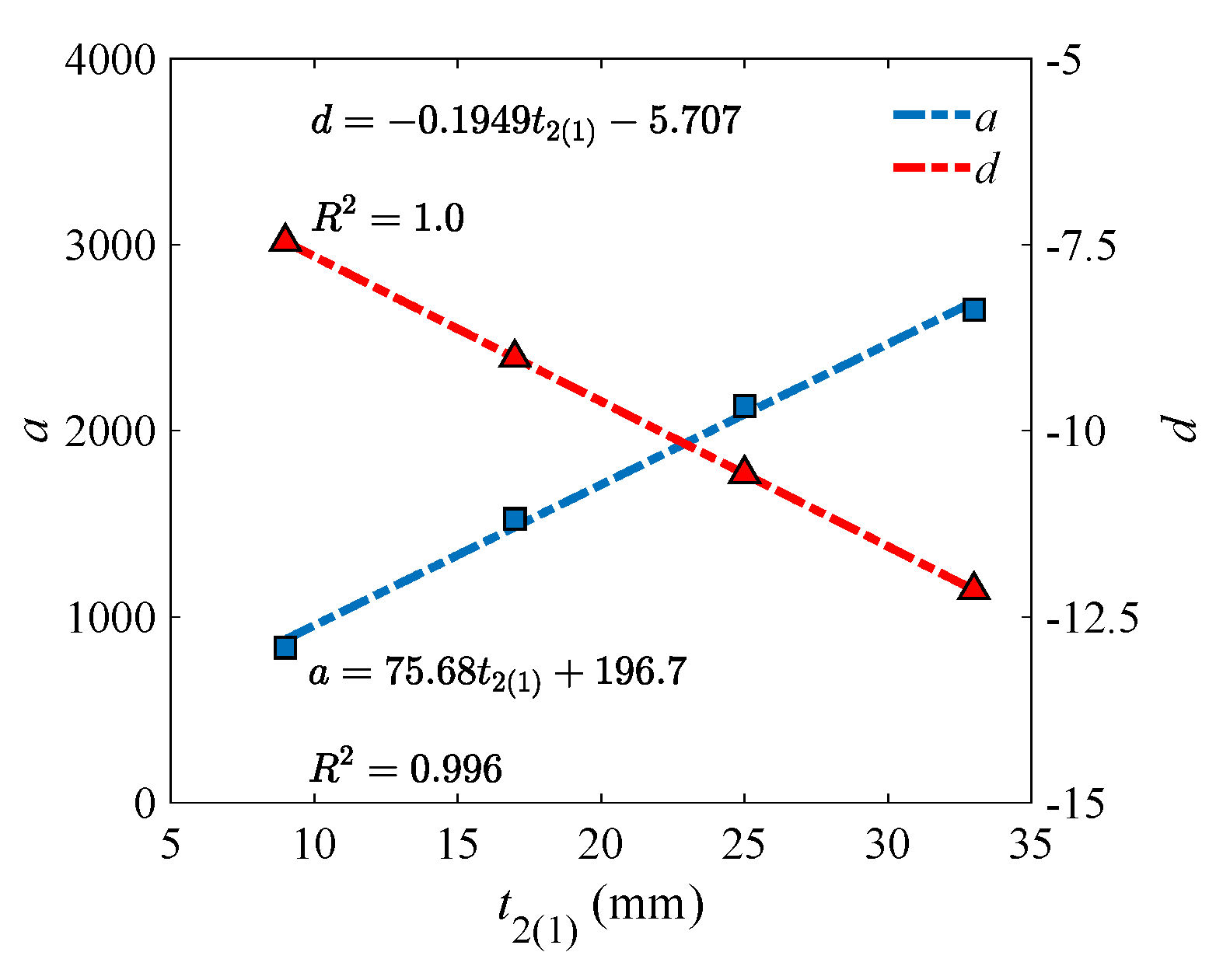
- For double-symmetric cross-sections bearing flexural loads, larger flange width and beam height are recommended, while the thickness of flange and web can form a coupling effect with other geometry variables and should be determined accordingly. The FDD for flange width and thickness depends heavily on beam height, which, together with that for beam height and web thickness, can be predicted through empirical linear design criteria with acceptable accuracy.
- (2)
- For single-symmetric cross-sections bearing flexural loads, increasing beam height as well as flange width and thickness are all conducive to the low-carbon design, but using large beam height is the most effective. The FDD for upper (lower) flange width and thickness falls on the neighborhood of the critical line, which is mainly affected by lower (upper) flange width and thickness, while the influence of beam height is not that significant. The critical line can be well described using a hyperbolic model, with all model parameters showing strong linear correlations with both lower (upper) flange width and thickness.
- (3)
- For cross-sections bearing shear loads, increasing beam height and web thickness is beneficial, while increasing the width or thickness of either upper or lower flange is not a good choice. The FDD for upper (lower) flange width and thickness is affected by the thickness of lower (upper) flange, but the width of lower (upper) flange was found to have no obvious impact. The FDD for beam height and web thickness is not sensitive to the variation in flange variables. Both the FDD for upper (lower) flange width and thickness and the one for beam height and web thickness can be predicted through empirical linear design criteria with relatively high accuracy.
- (4)
- For materials used in beams, steel with higher strength or that produced from recycled scrap using energy-saving technologies is suggested. Meanwhile, new prototyping techniques with lower energy and material loss are recommended for the beam fabrication process.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pan, W.; Zhang, Z. Benchmarking the sustainability of concrete and steel modular construction for buildings in urban development. Sustain. Cities Soc. 2023, 90, 104400. [Google Scholar] [CrossRef]
- Morsi, D.M.; Ismaeel, W.S.; Ehab, A.; Othman, A.A. BIM-based life cycle assessment for different structural system scenarios of a residential building. Ain Shams Eng. J. 2022, 13, 101802. [Google Scholar] [CrossRef]
- Larivière-Lajoie, R.; Blanchet, P.; Amor, B. Evaluating the importance of the embodied impacts of wall assemblies in the context of a low environmental impact energy mix. Build. Environ. 2022, 207, 108534. [Google Scholar] [CrossRef]
- Shang, W.-L.; Lv, Z. Low carbon technology for carbon neutrality in sustainable cities: A survey. Sustain. Cities Soc. 2023, 92, 104489. [Google Scholar] [CrossRef]
- He, J.; Yue, Q.; Li, Y.; Zhao, F.; Wang, H. Driving force analysis of carbon emissions in China’s building industry: 2000–2015. Sustain. Cities Soc. 2020, 60, 102268. [Google Scholar] [CrossRef]
- Xu, J.; Chang, F.; Bai, J.; Liu, C. Statistical analysis on the fracture behavior of rubberized steel fiber reinforced recycled aggregate concrete based on acoustic emission. J. Mater. Res. Technol. 2023, 24, 8997–9014. [Google Scholar] [CrossRef]
- Leslie, M. Construction Industry Innovation Takes Aim at Reducing Carbon Emissions. Engineering 2022, 19, 7–10. [Google Scholar] [CrossRef]
- Bai, J.; Zhang, S.; Liang, J.; Zhao, Y.; Li, W.; Diao, Y.; Shang, D. A systematic design method for green buildings based on the combined system of flexible solar cells and reactors on buildings. Build. Environ. 2022, 209, 108657. [Google Scholar] [CrossRef]
- Bai, J.; Chen, Z.; Zhang, S.; Liang, J. Building Form Optimization for Renewable Energy-Economic Utility of Flexible Solar Cells as Building Integrated Photovoltaics. Sustain. Cities Soc. 2025, 133, 106819. [Google Scholar] [CrossRef]
- Ferreira, F.P.V.; Tsavdaridis, K.D.; Martins, C.H.; De Nardin, S. Steel-concrete composite beams with precast hollow-core slabs: A sustainable solution. Sustainability 2021, 13, 4230. [Google Scholar] [CrossRef]
- Becker, I.; Anderson, F.; Phillips, A.R. Structural design of hybrid steel-timber buildings for lower production stage embodied carbon emissions. J. Build. Eng. 2023, 76, 107053. [Google Scholar] [CrossRef]
- Greene, J.M.; Hosanna, H.R.; Willson, B.; Quinn, J.C. Whole life embodied emissions and net-zero emissions potential for a mid-rise office building constructed with mass timber. Sustain. Mater. Technol. 2023, 35, e00528. [Google Scholar] [CrossRef]
- Karki, D.; Al-Hunaity, S.; Far, H.; Saleh, A. Composite connections between CFS beams and plywood panels for flooring systems: Testing and analysis. Structures 2022, 40, 771–785. [Google Scholar] [CrossRef]
- Navaratnam, S.; Small, D.W.; Gatheeshgar, P.; Poologanathan, K.; Thamboo, J.; Higgins, C.; Mendis, P. Development of cross laminated timber-cold-formed steel composite beam for floor system to sustainable modular building construction. Structures 2021, 32, 681–690. [Google Scholar] [CrossRef]
- Wu, C.; Duan, J.; Yang, Z.; Zhao, Z.; Xu, Y. A Novel Rectangular-Section Combined Beam of Welded Thin-Walled H-Shape Steel/Camphor Pine Wood: The Bending Performance Study. Sustainability 2023, 15, 7450. [Google Scholar] [CrossRef]
- Morris, F.; Allen, S.; Hawkins, W. On the embodied carbon of structural timber versus steel, and the influence of LCA methodology. Build. Environ. 2021, 206, 108285. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, J.; Wu, Y.; Xie, T.; Bo, L.; Li, Z. Life Cycle Assessment of Steel-Glued Laminated Bamboo (GluBam) Hybrid Truss in China. Energy Build. 2023, 294, 113218. [Google Scholar] [CrossRef]
- Mitra, S.; Bastani, A.; Das, S.; Lawn, D. Use of basalt fiber fabric for rehabilitation of steel beams with corroded compression flange. Compos. Struct. 2021, 255, 113014. [Google Scholar] [CrossRef]
- Chen, H.-M.; Wang, Y.; Zhou, K.; Lam, D.; Guo, W.; Li, L.; Ajayebi, A.; Hopkinson, P. Reclaiming structural steels from the end of service life composite structures for reuse–An assessment of the viability of different methods. Dev. Built Environ. 2022, 10, 100077. [Google Scholar] [CrossRef]
- Kim, S.; Kim, S.-A. Framework for designing sustainable structures through steel beam reuse. Sustainability 2020, 12, 9494. [Google Scholar] [CrossRef]
- Antwi-Afari, P.; Ng, S.T.; Chen, J.; Oluleye, B.I.; Antwi-Afari, M.F.; Ababio, B.K. Enhancing life cycle assessment for circular economy measurement of different case scenarios of modular steel slab. Build. Environ. 2023, 239, 110411. [Google Scholar] [CrossRef]
- Choi, I.; Kim, D.; Kim, J. Non-Iterative Optimal Design Method Based on LM Index for Steel Double-Beam Floor Systems Reinforced with Concrete Panels. Materials 2022, 15, 4538. [Google Scholar] [CrossRef] [PubMed]
- Choi, I.; Kim, J.; Kim, D. LCA-based investigation of environmental impacts for novel double-beam floor system subjected to high gravity loads. Sustainability 2020, 12, 9193. [Google Scholar] [CrossRef]
- Drewniok, M.P.; Campbell, J.; Orr, J. The Lightest Beam Method–A methodology to find ultimate steel savings and reduce embodied carbon in steel framed buildings. Structures 2020, 27, 687–701. [Google Scholar] [CrossRef]
- Es-Haghi, M.S.; Shishegaran, A.; Rabczuk, T. Evaluation of a novel Asymmetric Genetic Algorithm to optimize the structural design of 3D regular and irregular steel frames. Front. Struct. Civ. Eng. 2020, 14, 1110–1130. [Google Scholar] [CrossRef]
- Hayashi, K.; Ohsaki, M. Graph-based reinforcement learning for discrete cross-section optimization of planar steel frames. Adv. Eng. Inform. 2022, 51, 101512. [Google Scholar] [CrossRef]
- Wang, Z.; Tsavdaridis, K.D. Optimality criteria-based minimum-weight design method for modular building systems subjected to generalised stiffness constraints: A comparative study. Eng. Struct. 2022, 251, 113472. [Google Scholar] [CrossRef]
- Phan, D.T.; Mojtabaei, S.M.; Hajirasouliha, I.; Ye, J.; Lim, J.B. Coupled element and structural level optimisation framework for cold-formed steel frames. J. Constr. Steel Res. 2020, 168, 105867. [Google Scholar] [CrossRef]
- Aydın, Z. Size, layout and tendon profile optimization of prestressed steel trusses using Jaya algorithm. Structures 2022, 40, 284–294. [Google Scholar] [CrossRef]
- Cang, Y.; Yang, L.; Luo, Z.; Zhang, N. Prediction of embodied carbon emissions from residential buildings with different structural forms. Sustain. Cities Soc. 2020, 54, 101946. [Google Scholar] [CrossRef]
- Shi, L.; Qi, X.; Yang, Z.; Tao, L.; Li, Y.; Qiu, J.; Jiang, X. Comparative study of greenhouse gas emission calculations and the environmental impact in the life cycle assessment of buildings in China, Finland, and the United States. J. Build. Eng. 2023, 70, 106396. [Google Scholar] [CrossRef]
- Gatheeshgar, P.; Poologanathan, K.; Gunalan, S.; Tsavdaridis, K.D.; Nagaratnam, B.; Iacovidou, E. Optimised cold-formed steel beams in modular building applications. J. Build. Eng. 2020, 32, 101607. [Google Scholar] [CrossRef]
- Kanthasamy, E.; Hussain, J.; Thirunavukkarasu, K.; Poologanathan, K.; Roy, K.; Beulah Gnana Ananthi, G.; Suntharalingam, T. Flexural Behaviour of Built-Up Beams Made of Optimised Sections. Buildings 2022, 12, 1868. [Google Scholar] [CrossRef]
- Qadir, S.; Nguyen, V.B.; Hajirasouliha, I.; Cartwright, B.; English, M. Optimal design of cold roll formed steel channel sections under bending considering both geometry and cold work effects. Thin-Walled Struct. 2020, 157, 107020. [Google Scholar] [CrossRef]
- Thirunavukkarasu, K.; Kanthasamy, E.; Gatheeshgar, P.; Poologanathan, K.; Rajanayagam, H.; Suntharalingam, T.; Dissanayake, M. Sustainable performance of a modular building system made of built-up cold-formed steel beams. Buildings 2021, 11, 460. [Google Scholar] [CrossRef]
- Yuting, Z.; Yingkai, L.; Ruoqiang, F. A two-level optimization framework for new family of CFS sections. J. Constr. Steel Res. 2022, 197, 107460. [Google Scholar] [CrossRef]
- Jasion, P.; Pawlak, A.; Paczos, P. Buckling and post-buckling behaviour of selected cold-formed C-beams with atypical flanges. Eng. Struct. 2021, 244, 112693. [Google Scholar] [CrossRef]
- Parastesh, H.; Mojtabaei, S.M.; Taji, H.; Hajirasouliha, I.; Sabbagh, A.B. Constrained optimization of anti-symmetric cold-formed steel beam-column sections. Eng. Struct. 2021, 228, 111452. [Google Scholar] [CrossRef]
- Gatheeshgar, P.; Poologanathan, K.; Gunalan, S.; Shyha, I.; Tsavdaridis, K.D.; Corradi, M. Optimal design of cold-formed steel lipped channel beams: Combined bending, shear, and web crippling. Structures 2020, 28, 825–836. [Google Scholar] [CrossRef]
- Neves, M.; Basaglia, C.; Camotim, D. Stiffening optimisation of conventional cold-formed steel cross-sections based on a multi-objective Genetic Algorithm and using Generalised Beam Theory. Thin-Walled Struct. 2022, 179, 109713. [Google Scholar] [CrossRef]
- Fan, J.; Zhao, J.; Hua, L.; Zhang, D.; Chen, R.; Kang, Y. Seismic performance and analytical model of CFDST joint with endplates and long bolts. Structures 2022, 35, 483–499. [Google Scholar] [CrossRef]
- Alvarez-Fernandez, M.I.; Prendes-Gero, M.B.; Drouet, J.; Lopez-Gayarre, F.; Junco, J.R.-V. Application of genetic algorithms in the optimisation of steel rib supports. Tunn. Undergr. Space Technol. 2020, 103, 103462. [Google Scholar] [CrossRef]
- Whitworth, A.H.; Tsavdaridis, K.D. Genetic algorithm for embodied energy optimisation of steel-concrete composite beams. Sustainability 2020, 12, 3102. [Google Scholar] [CrossRef]
- Liang, H.; Roy, K.; Fang, Z.; Lim, J.B. A critical review on optimization of cold-formed steel members for better structural and thermal performances. Buildings 2022, 12, 34. [Google Scholar] [CrossRef]
- Tres Junior, F.L.; Yepes, V.; Medeiros, G.F.d.; Kripka, M. Multi-objective optimization applied to the design of sustainable pedestrian bridges. Int. J. Environ. Res. Public Health 2023, 20, 3190. [Google Scholar] [CrossRef] [PubMed]
- Gajewski, T.; Staszak, N.; Garbowski, T. Parametric optimization of thin-walled 3D beams with perforation based on homogenization and soft computing. Materials 2022, 15, 2520. [Google Scholar] [CrossRef] [PubMed]
- Guimarães, V.; Gilbert, B.; Talebian, N.; Wang, B. Shape optimisation of singly-symmetric cold-formed steel purlins. Thin-Walled Struct. 2021, 161, 107402. [Google Scholar] [CrossRef]
- Mojtabaei, S.M.; Becque, J.; Hajirasouliha, I. Structural size optimization of single and built-up cold-formed steel beam-column members. J. Struct. Eng. 2021, 147, 04021030. [Google Scholar] [CrossRef]
- Qadir, S.; Nguyen, V.; Hajirasouliha, I.; Ceranic, B.; Tracada, E.; English, M. Shape optimisation of cold roll formed sections considering effects of cold working. Thin-Walled Struct. 2022, 170, 108576. [Google Scholar] [CrossRef]
- Shimoda, M.; Liu, Y.; Ishikawa, K. Optimum shape design of thin-walled cross sections using a parameter-free optimization method. Thin-Walled Struct. 2020, 148, 106603. [Google Scholar] [CrossRef]
- Yin, L.; Deng, T.; Niu, Y.; Li, Z. Free-Form Shape Optimization of Advanced High-Strength Steel Members. Buildings 2022, 12, 2101. [Google Scholar] [CrossRef]
- Almatrafi, M.; Theofanous, M.; Dirar, S.; Bock, M. Structural response of cold-formed lipped Z purlins–Part 2 numerical modelling and optimisation of lip size. Thin-Walled Struct. 2021, 161, 107453. [Google Scholar] [CrossRef]
- Gao, F.; Yang, F.; Liang, H.; Zhu, H. Numerical study and strength model of concrete-filled high-strength tubular flange beam under mid-span load. Eng. Struct. 2021, 229, 111654. [Google Scholar] [CrossRef]
- Matloub, A.A.; Rizk, Y.S.; Fawzy, M.M.; Yousef, A.H. Innovative steel I-girder under bending having hollow tubular flanges. Ain Shams Eng. J. 2023, 14, 102146. [Google Scholar] [CrossRef]
- Ashby, M.F. Materials Selection in Mechanical Design, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2011; 646p. [Google Scholar]
- Shanley, F.R. Weight-Strength Analysis of Aircraft Structures, 2nd ed.; Dover Publications: Mineola, NY, USA, 1960. [Google Scholar]
- Wegst, U.G.; Ashby, M.F. The structural efficiency of orthotropic stalks, stems and tubes. J. Mater. Sci. 2007, 42, 9005–9014. [Google Scholar] [CrossRef]
- Ashby, M.F.; Bréchet, Y. Materials selection for a finite life time. Adv. Eng. Mater. 2002, 4, 335–341. [Google Scholar] [CrossRef]
- Wegst, U.G.; Ashby, M.F. Materials selection and design of products with low environmental impact. Adv. Eng. Mater. 2002, 4, 378–383. [Google Scholar] [CrossRef]
- Ashby, M.F. Materials and the Environment, 3rd ed.; Elsevier: Oxford, UK, 2021; 448p. [Google Scholar]
- Wegst, U.G.; Ashby, M.F. The mechanical efficiency of natural materials. Philos. Mag. 2004, 84, 2167–2186. [Google Scholar] [CrossRef]
- Sirisalee, P.; Ashby, M.F.; Parks, G.T.; John Clarkson, P. Multi-Criteria Material Selection of Monolithic and Multi-Materials in Engineering Design. Adv. Eng. Mater. 2006, 8, 48–56. [Google Scholar] [CrossRef]
- Sirisalee, P.; Ashby, M.F.; Parks, G.T.; Clarkson, P.J. Multi-criteria material selection in engineering design. Adv. Eng. Mater. 2004, 6, 84–92. [Google Scholar] [CrossRef]
- Ashby, M.; Brechet, Y.; Cebon, D.; Salvo, L. Selection strategies for materials and processes. Mater. Des. 2004, 25, 51–67. [Google Scholar] [CrossRef]
- Terreros-Bedoya, A.; Negrin, I.; Payá-Zaforteza, I.; Yepes, V. Hybrid steel girders: Review, advantages and new horizons in research and applications. J. Constr. Steel Res. 2023, 207, 107976. [Google Scholar] [CrossRef]
- Ding, Y. Principles of Steel Structures, 3rd ed.; Tianjin University Press: Tianjin, China, 2020. [Google Scholar]
- Huang, Z.; Zhou, H.; Tang, H.; Zhao, Y.; Lin, B. Carbon emissions of prefabricated steel structure components: A case study in China. J. Clean. Prod. 2023, 406, 137047. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, Q.; Wang, C.; Li, Z.; Geng, Y.; Hong, J.; Cheng, Y. Environmental sustainability challenges of China’s steel production: Impact-oriented water, carbon and fossil energy footprints assessment. Ecol. Indic. 2022, 136, 108660. [Google Scholar] [CrossRef]
- Kim, J.; Sovacool, B.K.; Bazilian, M.; Griffiths, S.; Lee, J.; Yang, M.; Lee, J. Decarbonizing the iron and steel industry: A systematic review of sociotechnical systems, technological innovations, and policy options. Energy Res. Soc. Sci. 2022, 89, 102565. [Google Scholar] [CrossRef]
- Liu, Y.; Cui, M.; Gao, X. Building up scrap steel bases for perfecting scrap steel industry chain in China: An evolutionary game perspective. Energy 2023, 278, 127742. [Google Scholar] [CrossRef]
- Wang, K.; Liu, S.; Liu, K.; Dan, M.; Ji, X.; Lu, Y.; Xing, Y. Tracking Carbon Flows in China’s Iron and Steel Industry. Environ. Sci. Technol. 2023, 57, 11510–11519. [Google Scholar] [CrossRef]
- Wang, X.; Yu, B.; An, R.; Sun, F.; Xu, S. An integrated analysis of China’s iron and steel industry towards carbon neutrality. Appl. Energy 2022, 322, 119453. [Google Scholar] [CrossRef]
- Duan, H.; Hou, C.; Yang, W.; Song, J. Towards lower CO2 emissions in iron and steel production: Life cycle energy demand-LEAP based multi-stage and multi-technique simulation. Sustain. Prod. Consum. 2022, 32, 270–281. [Google Scholar] [CrossRef]
- Teubler, J.; Weber, S.; Suski, P.; Peschke, I.; Liedtke, C. Critical evaluation of the material characteristics and environmental potential of laser beam melting processes for the additive manufacturing of metallic components. J. Clean. Prod. 2019, 237, 117775. [Google Scholar] [CrossRef]
- Bunaziv, I.; Ren, X.; Hagen, A.B.; Hovig, E.W.; Jevremovic, I.; Gulbrandsen-Dahl, S. Laser beam remelting of stainless steel plate for cladding and comparison with conventional CMT process. Int. J. Adv. Manuf. Technol. 2023, 127, 911–934. [Google Scholar] [CrossRef]
- Shah, I.H.; Hadjipantelis, N.; Walter, L.; Myers, R.J.; Gardner, L. Environmental life cycle assessment of wire arc additively manufactured steel structural components. J. Clean. Prod. 2023, 389, 136071. [Google Scholar] [CrossRef]
- Allwood, J.M.; Ashby, M.F.; Gutowski, T.G.; Worrell, E. Material efficiency: Providing material services with less material production. Phil. Trans. R. Soc. A 2013, 371, 20120496. [Google Scholar] [CrossRef]
- Bai, J.; Ge, C.; Liang, J.; Xu, J. Recycled Aggregate: A Solution to Sustainable Concrete. Materials 2025, 18, 2706. [Google Scholar] [CrossRef] [PubMed]
- Diao, Y.; Bai, J.; Huang, J.; Li, P.; Yang, C. Strength characteristics of biomimetic carbonate precipitation (BCP) treated mortar under cyclic loading. J. Build. Eng. 2023, 75, 107013. [Google Scholar] [CrossRef]
- Diao, Y.; Bai, J.; Huang, J.; Yang, C. A high-performance model for direct shear behavior of biomimetic carbonate precipitation treated mortar. Mater. Lett. 2023, 349, 134739. [Google Scholar] [CrossRef]
- Diao, Y.; Bai, J.; Sun, C.; Huang, J.; Yang, C.; Hu, Q. A simplified model for shear behavior of mortar using biomimetic carbonate precipitation. Materials 2023, 16, 5613. [Google Scholar] [CrossRef]
- Diao, Y.; Bai, J.; Zheng, G.; Hu, Q.; Li, P.; Liu, X.; Hu, W.; Huang, J. Development and optimization of biomimetic-chemically induced carbonate precipitation: A review of recent research. Biogeotechnics 2025, 3, 100110. [Google Scholar] [CrossRef]
- Diao, Y.; Hu, Q.; Li, P.; Zhu, D.; Wang, C.; Zhang, L.; Yan, Y.; Huang, J. Mechanical performance of biomimetic mineralized mortar modified by carboxymethyl chitosan for marine environments. J. Build. Eng. 2025, 101, 111876. [Google Scholar] [CrossRef]
- Diao, Y.; Wang, C.; Huang, J.; Zhang, L.; Hu, H.; Bai, J.; Yang, C. Feasibility study on desert sand solidification using biomimetic mineralization method: Mechanical properties and wind erosion resistance. Constr. Build. Mater. 2025, 463, 139995. [Google Scholar] [CrossRef]
- Liu, C.; Bai, J.; Zhang, S.; Yang, Z.; Luo, M. Applications and advances in TiO2 based photocatalytic building materials. J. Phys. Conf. Ser. 2021, 2011, 012049. [Google Scholar] [CrossRef]
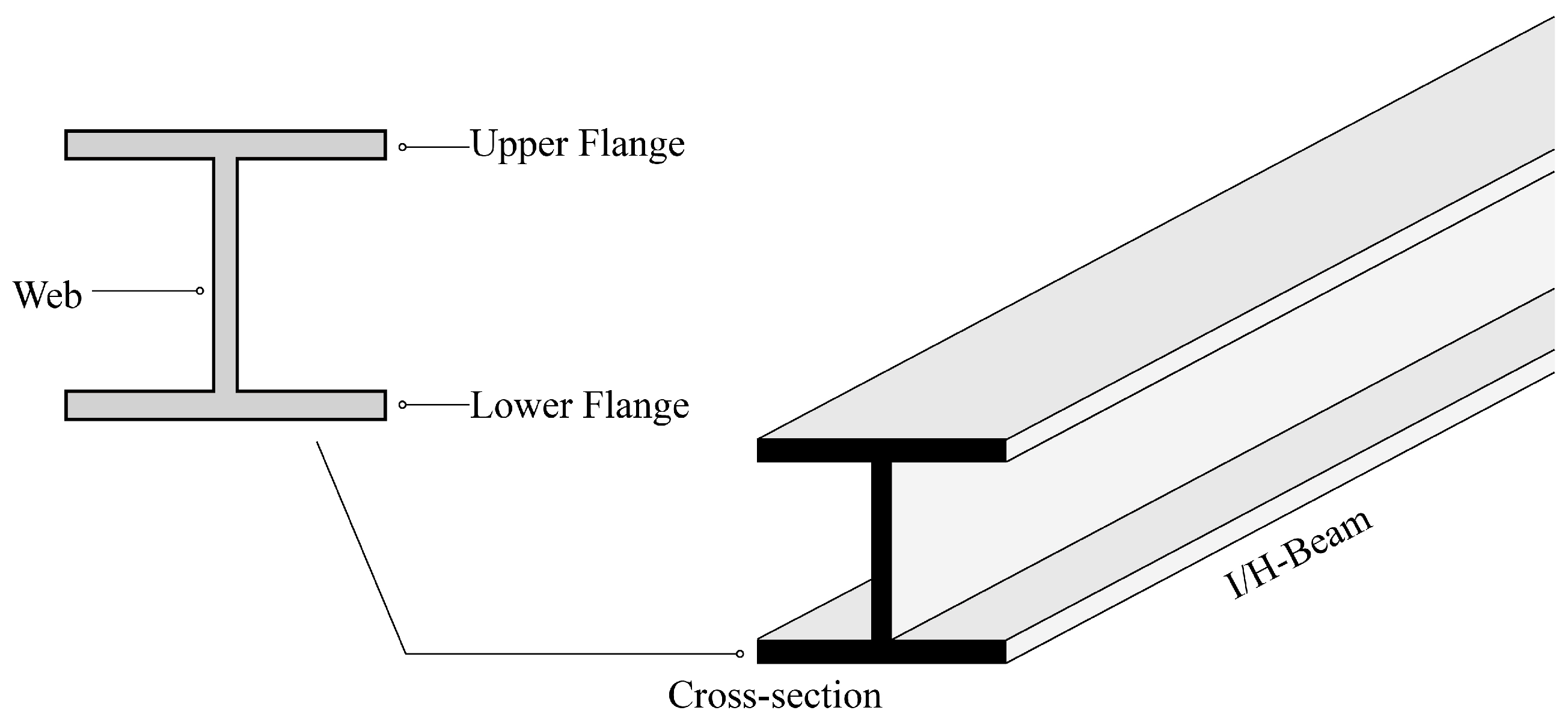
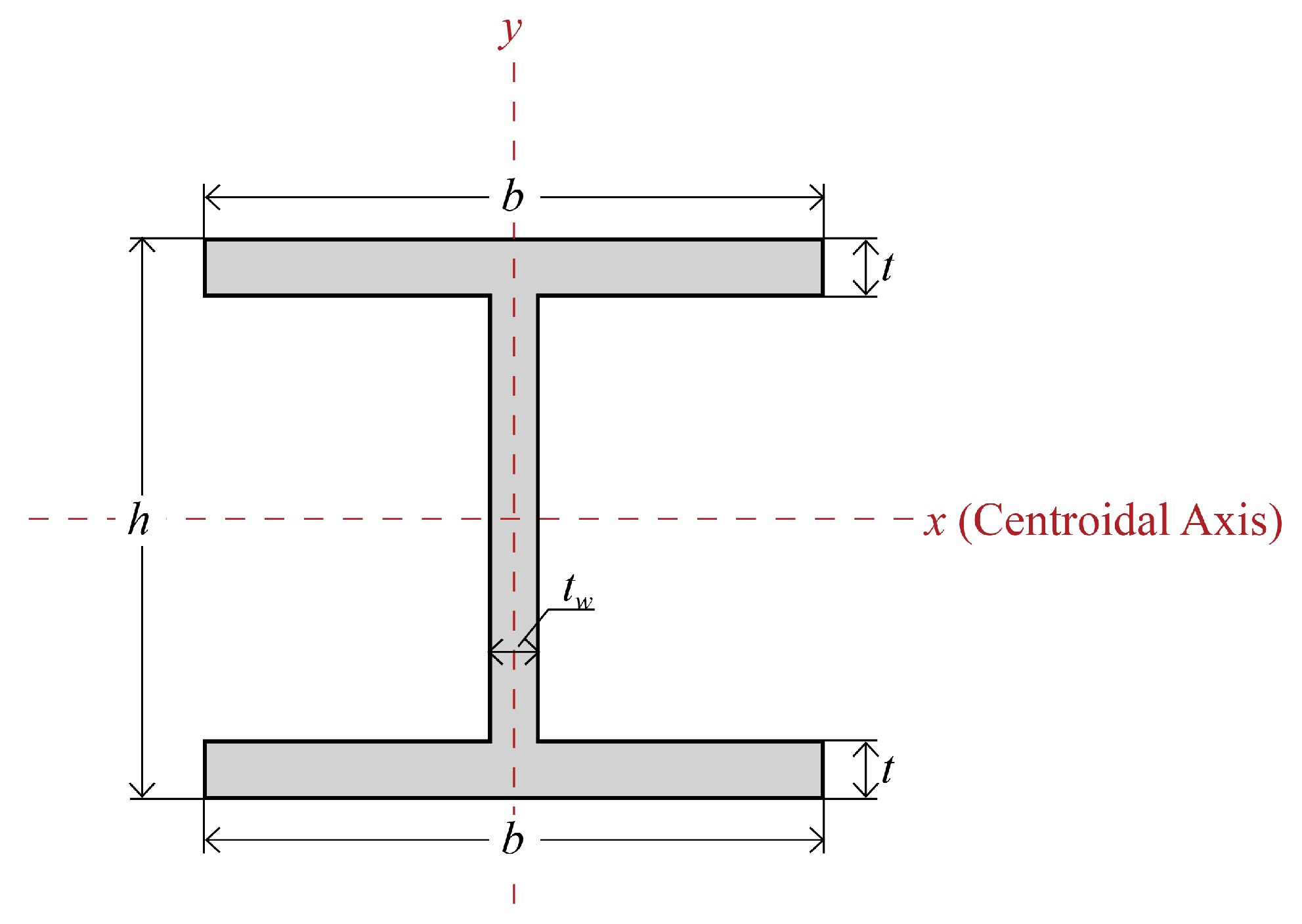
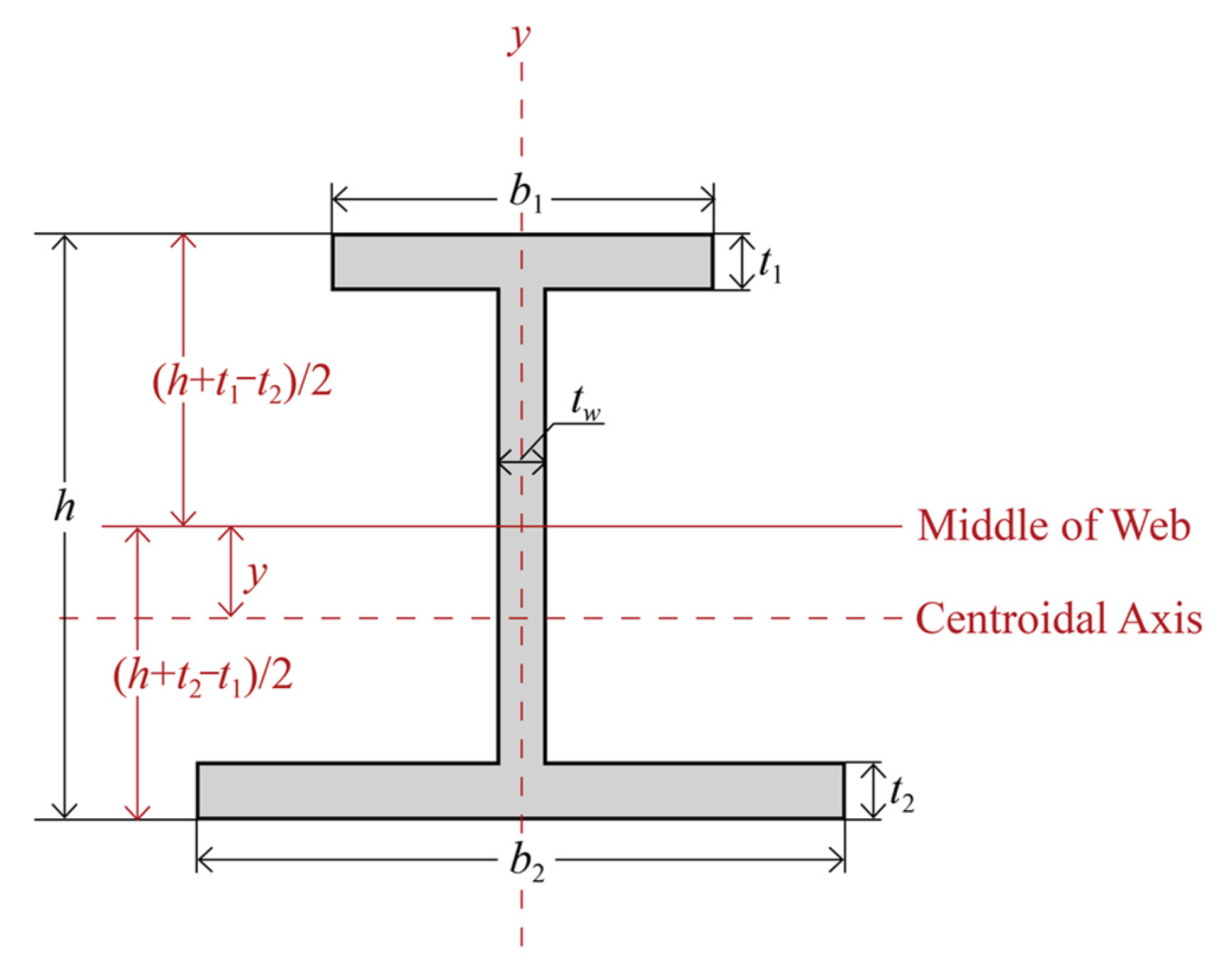
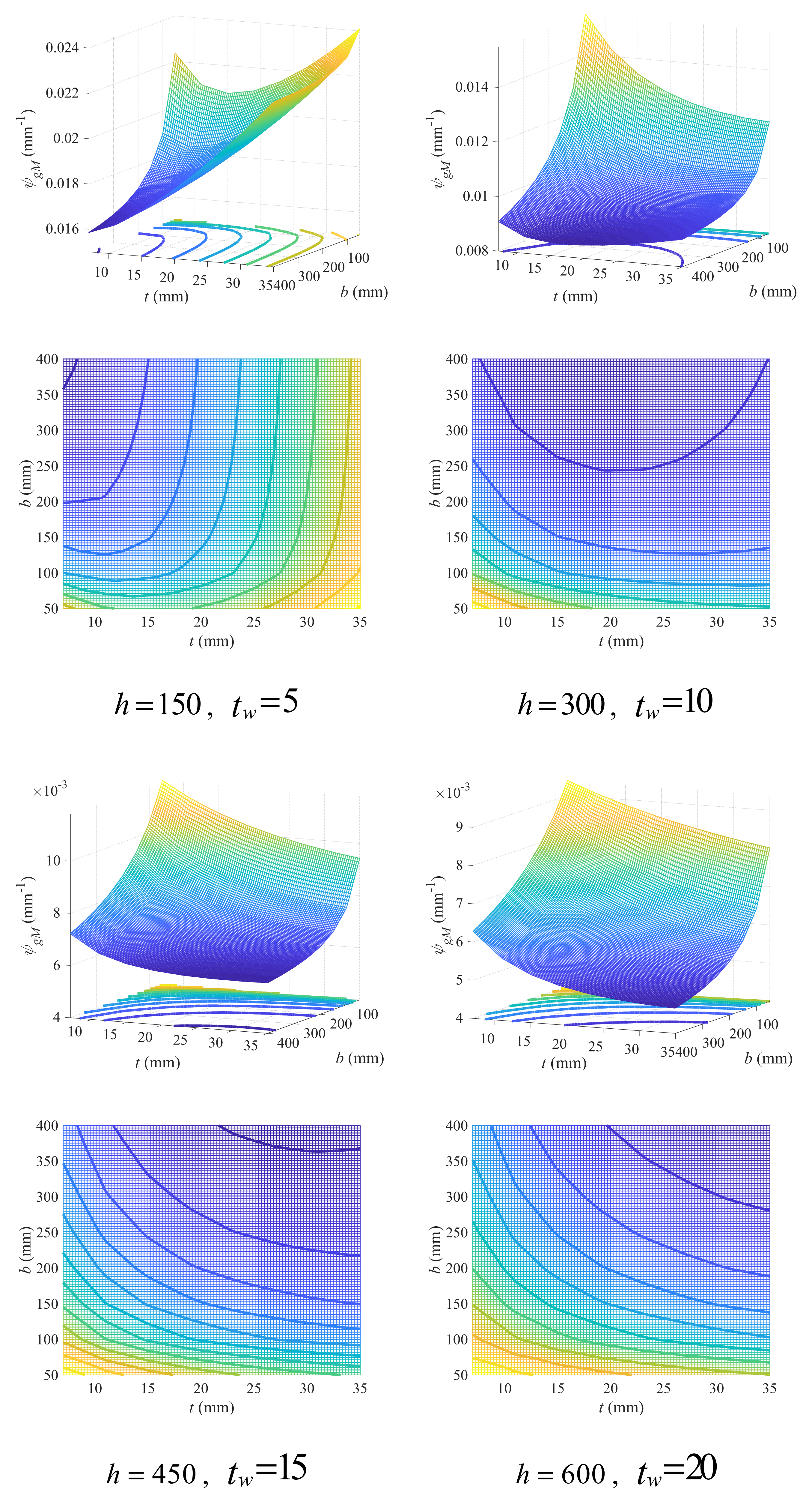





| Design Variables | Ranges |
|---|---|
| Flange width | 50~408 |
| Flange thickness | 7~35 |
| Beam height | 100~700 |
| Web thickness | 4.5~21 |
| Load | Feasible Design Domain |
|---|---|
| Flexural | Double-symmetric cross-section: Single-symmetric cross-section: |
| Shear |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, J.; Yang, K.; Chen, Z.; Liang, J.; Zhang, S.; Diao, Y. Geometry and Material Criteria for Low-Carbon Design of I/H-Beams in Sustainable Steel Structures Considering Both Mechanical Properties and Carbon Emissions. Materials 2025, 18, 4930. https://doi.org/10.3390/ma18214930
Bai J, Yang K, Chen Z, Liang J, Zhang S, Diao Y. Geometry and Material Criteria for Low-Carbon Design of I/H-Beams in Sustainable Steel Structures Considering Both Mechanical Properties and Carbon Emissions. Materials. 2025; 18(21):4930. https://doi.org/10.3390/ma18214930
Chicago/Turabian StyleBai, Jitao, Keyong Yang, Zhonghao Chen, Jiahe Liang, Simiao Zhang, and Yu Diao. 2025. "Geometry and Material Criteria for Low-Carbon Design of I/H-Beams in Sustainable Steel Structures Considering Both Mechanical Properties and Carbon Emissions" Materials 18, no. 21: 4930. https://doi.org/10.3390/ma18214930
APA StyleBai, J., Yang, K., Chen, Z., Liang, J., Zhang, S., & Diao, Y. (2025). Geometry and Material Criteria for Low-Carbon Design of I/H-Beams in Sustainable Steel Structures Considering Both Mechanical Properties and Carbon Emissions. Materials, 18(21), 4930. https://doi.org/10.3390/ma18214930







