Comparative Analysis of Thermophysical Properties of Functional Epoxy Matrix Composites Reinforced with Glass or Carbon Fibers in the Context of Heat Transfer Anisotropy
Abstract
1. Introduction
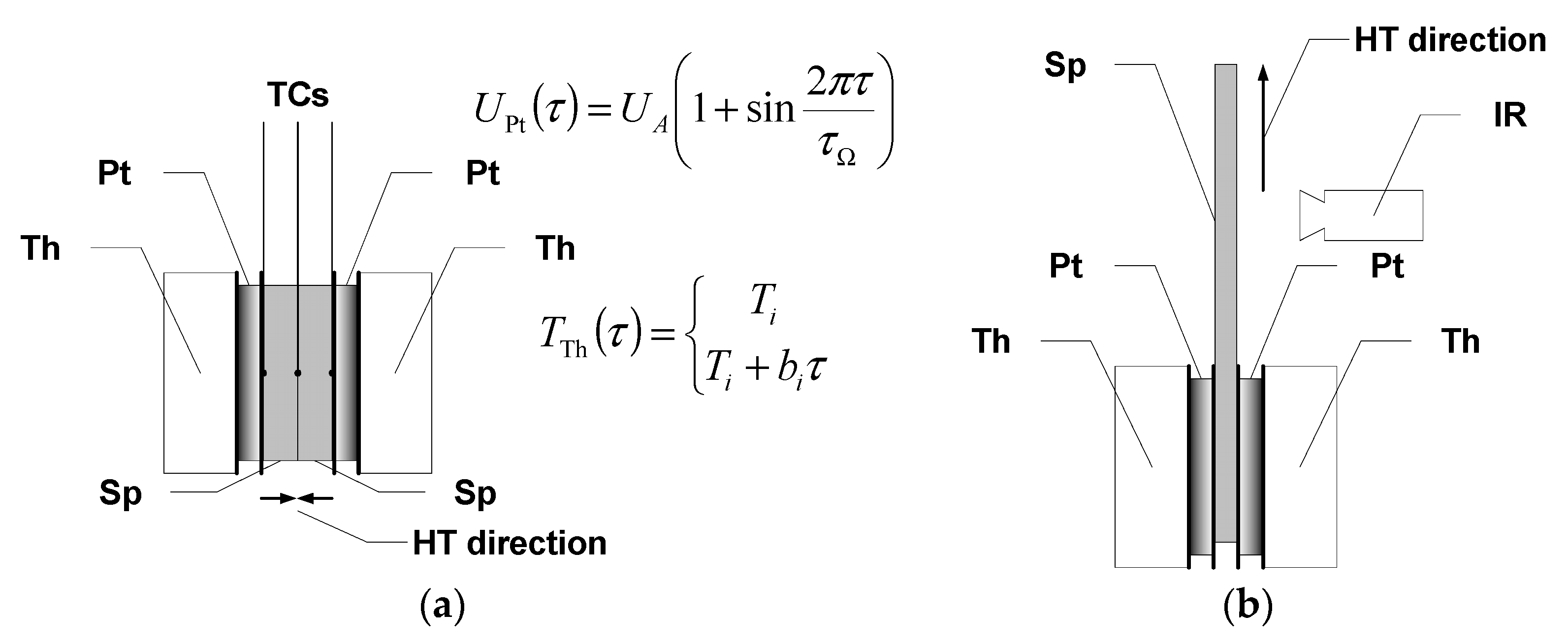
2. Materials and Methods
- -
- two glass-fiber reinforced polymer composites (3A Composites Mobility S.A., Mielec, Poland) with different thicknesses:
- ○
- with a thickness of 6.2–6.4 mm-designated GFRP A;
- ○
- with a thickness of 4.5–5.2 mm-designated GFRP B;
- -
- a carbon-fiber reinforced polymer composite (Rega Yacht sp. z o.o., Ropczyce, Poland) reinforced with carbon fabric layers (designated “CFRP”).
3. Results
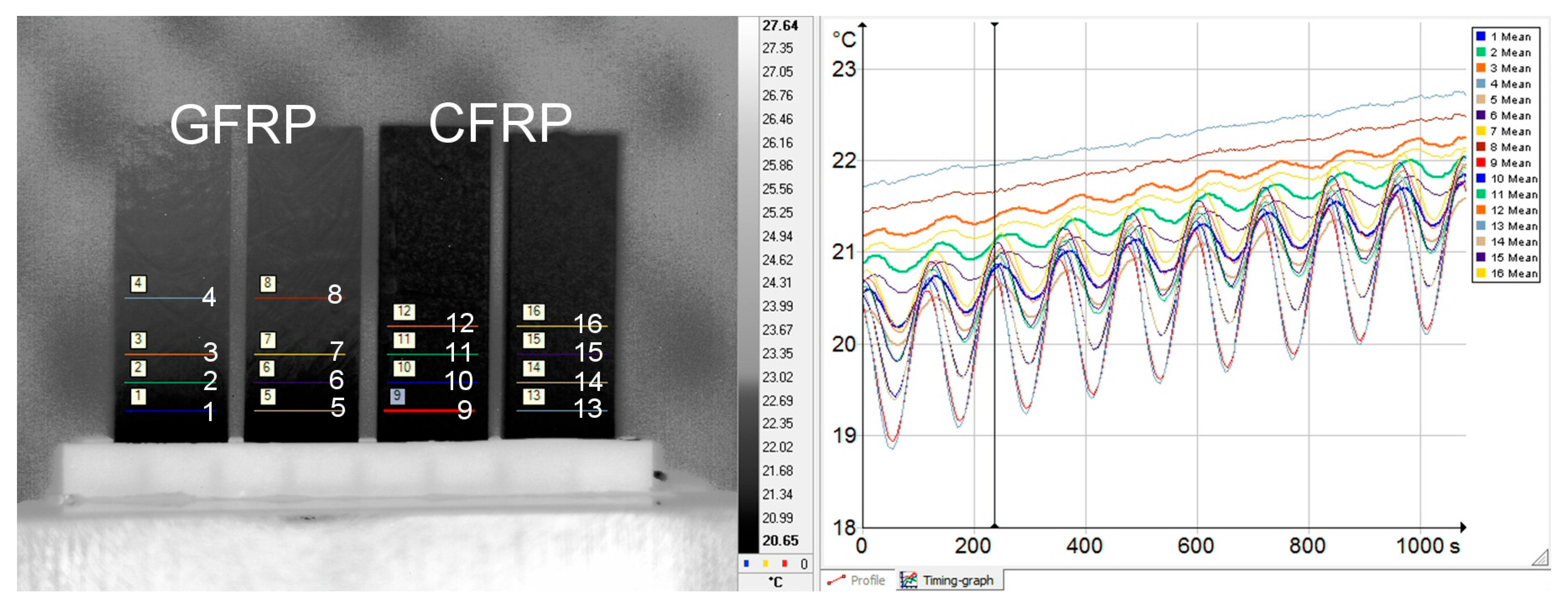
3.1. Macrostructure, Microstructure, and Effective Density
3.2. Thermophysical Properties
- Providing material data in terms of the thermodynamic (thermophysical) parameters studied for engineering calculations;
- Determination of thermal stability and determination of parameters of characteristic transformation of the matrix material of the studied composite structures.
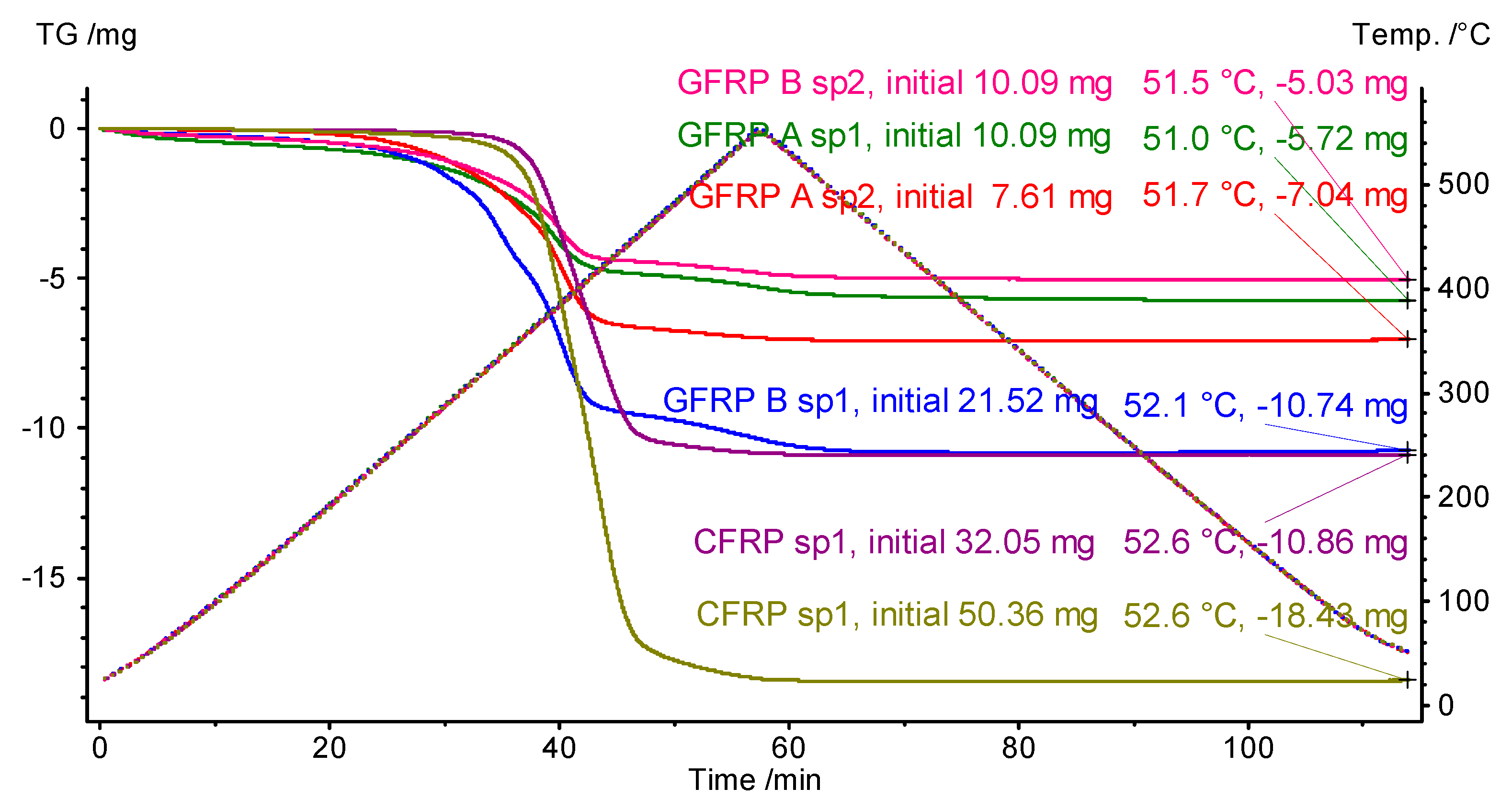
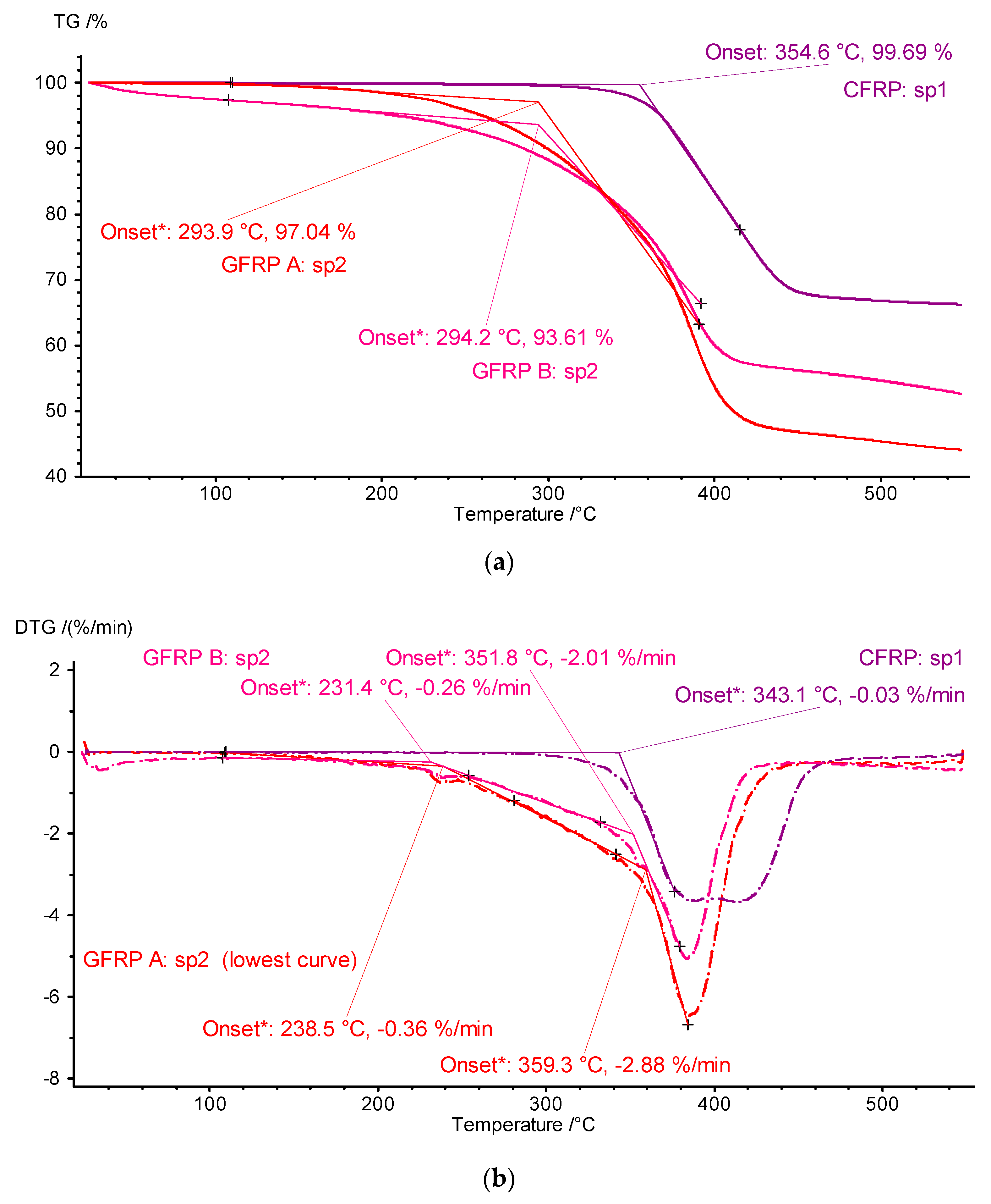
3.3. TG/DTG Thermogravimetric Studies
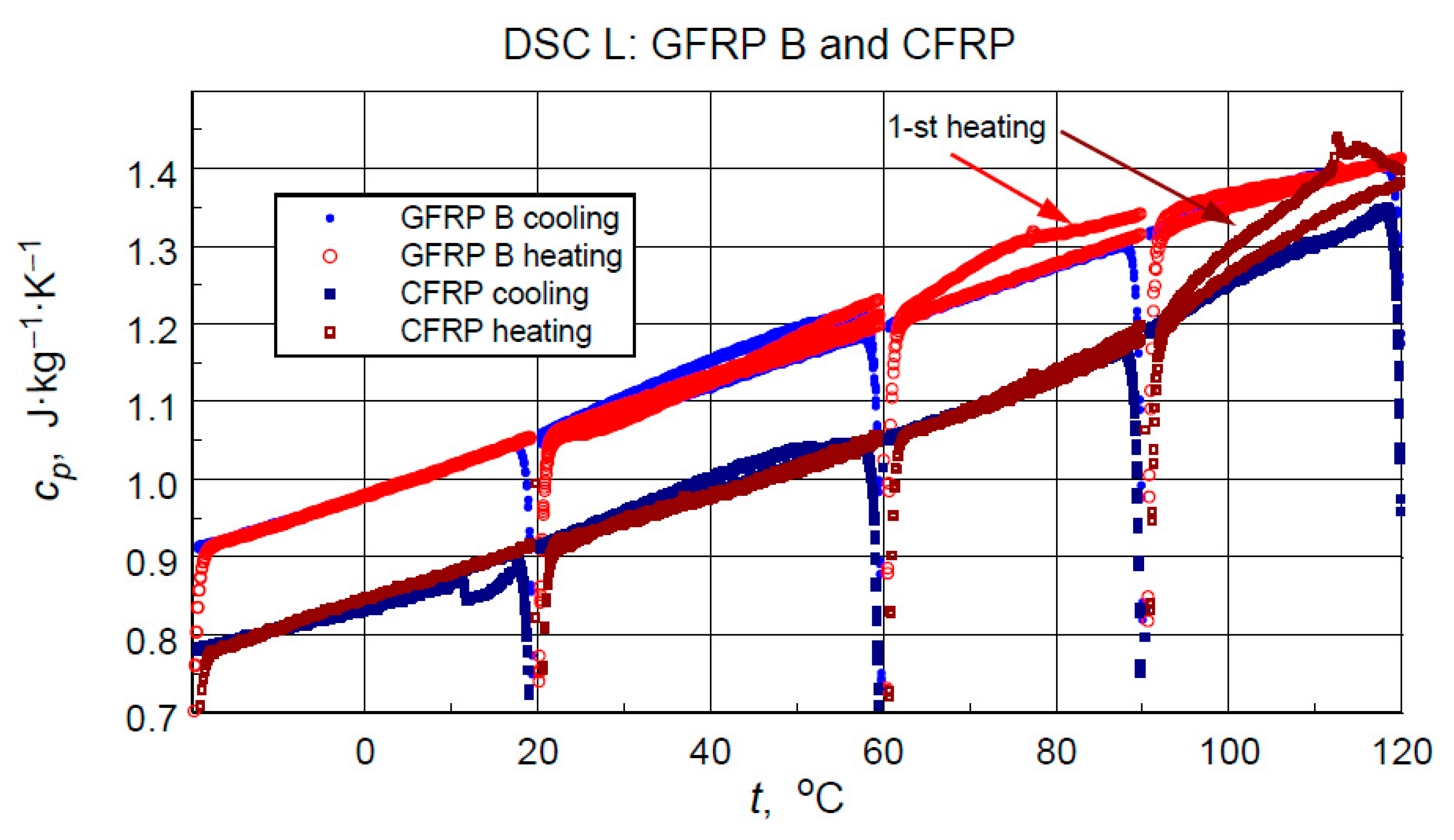
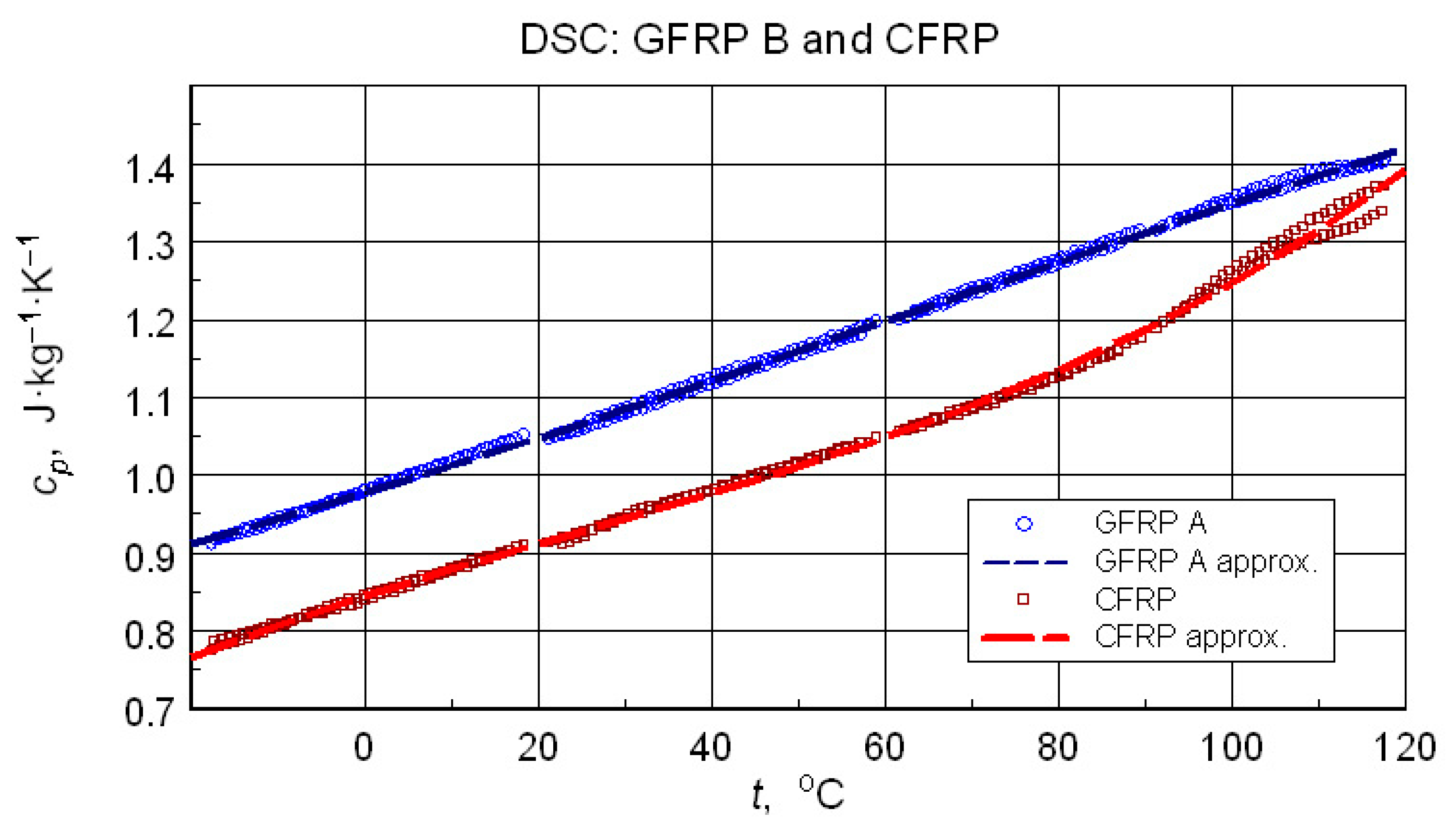
3.4. Microcalorimetric Studies
- i.
- As expected, the higher specific heat values of the glass-filled structure sample compared to the graphite structure. This is determined by the higher specific heat of glass than the specific heat of carbon [11] and the higher values of the mass share of graphite filling shown by thermogravimetric studies.
- ii.
- Stability and compatibility of thermal properties of the tested structures in the range of low-temperature excitation.
- iii.
- Possible minor effects of moisture or another volatile agent, for example, excess hardener release marked in the form of slightly higher specific heat values in the first heating cycles in the temperature range above 60 °C for glass composite and 90 °C for graphite composite. In addition to the above-mentioned effects, these phenomena may be caused by hardening effects or thermally induced irreversible structural changes.
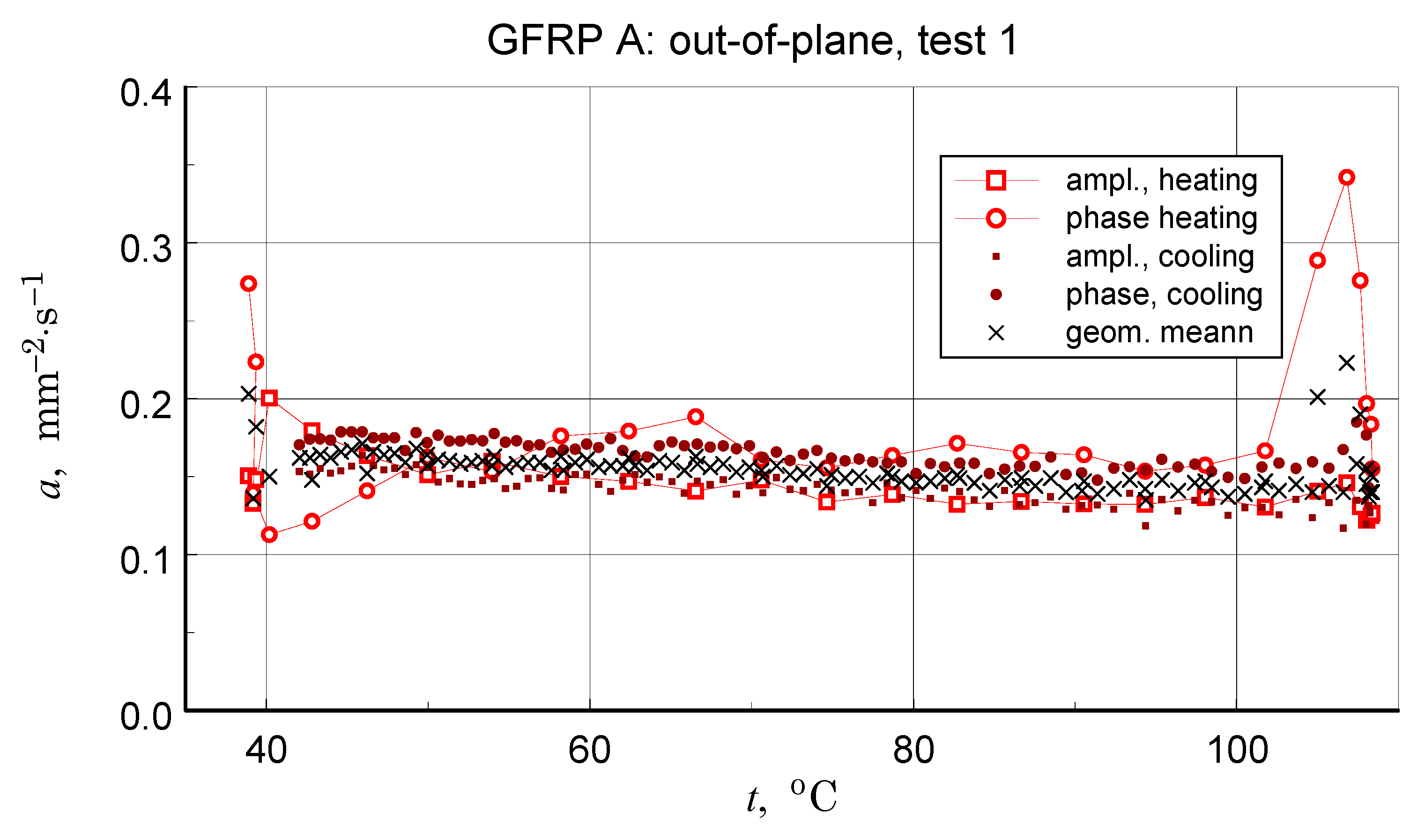
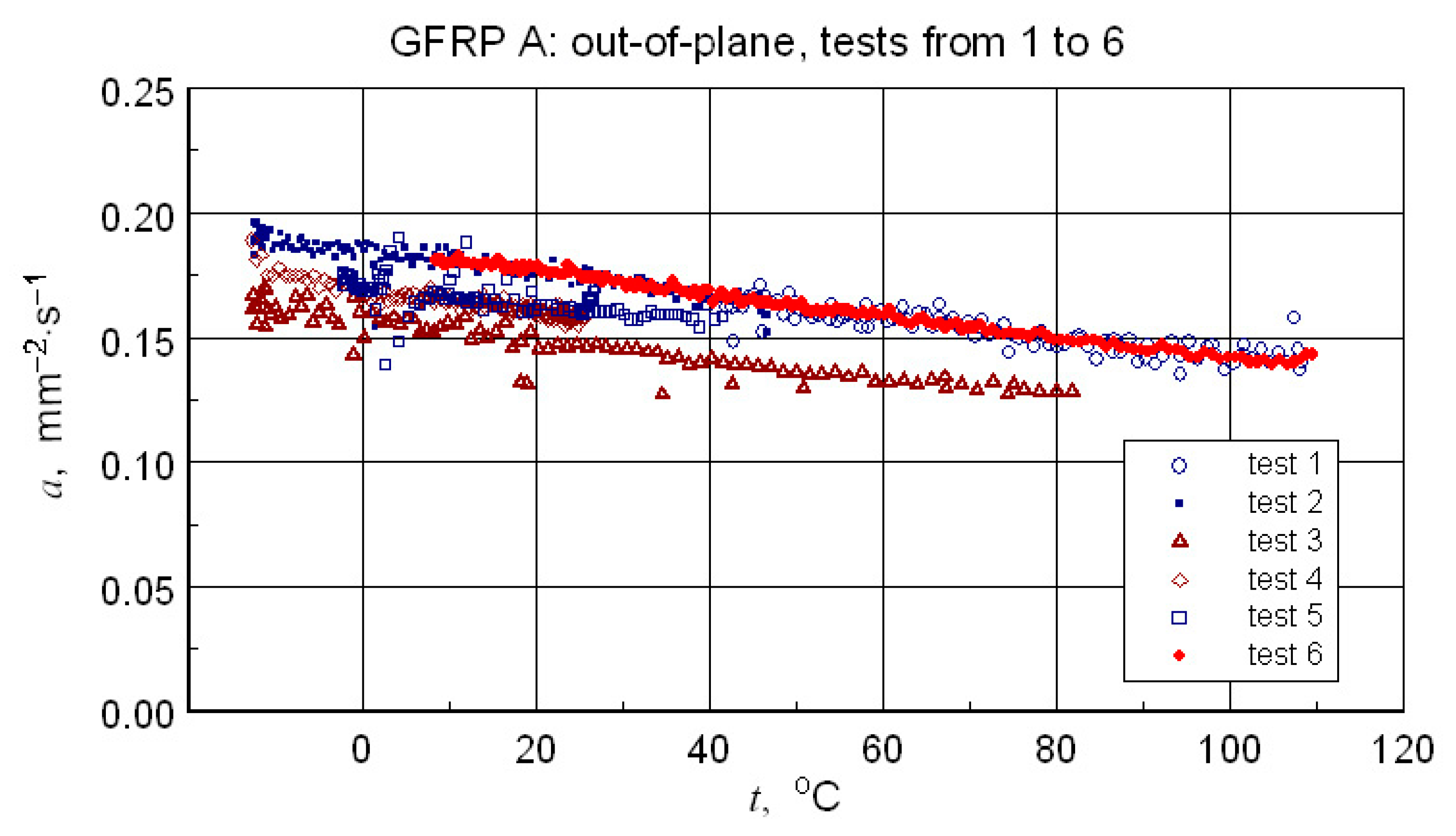
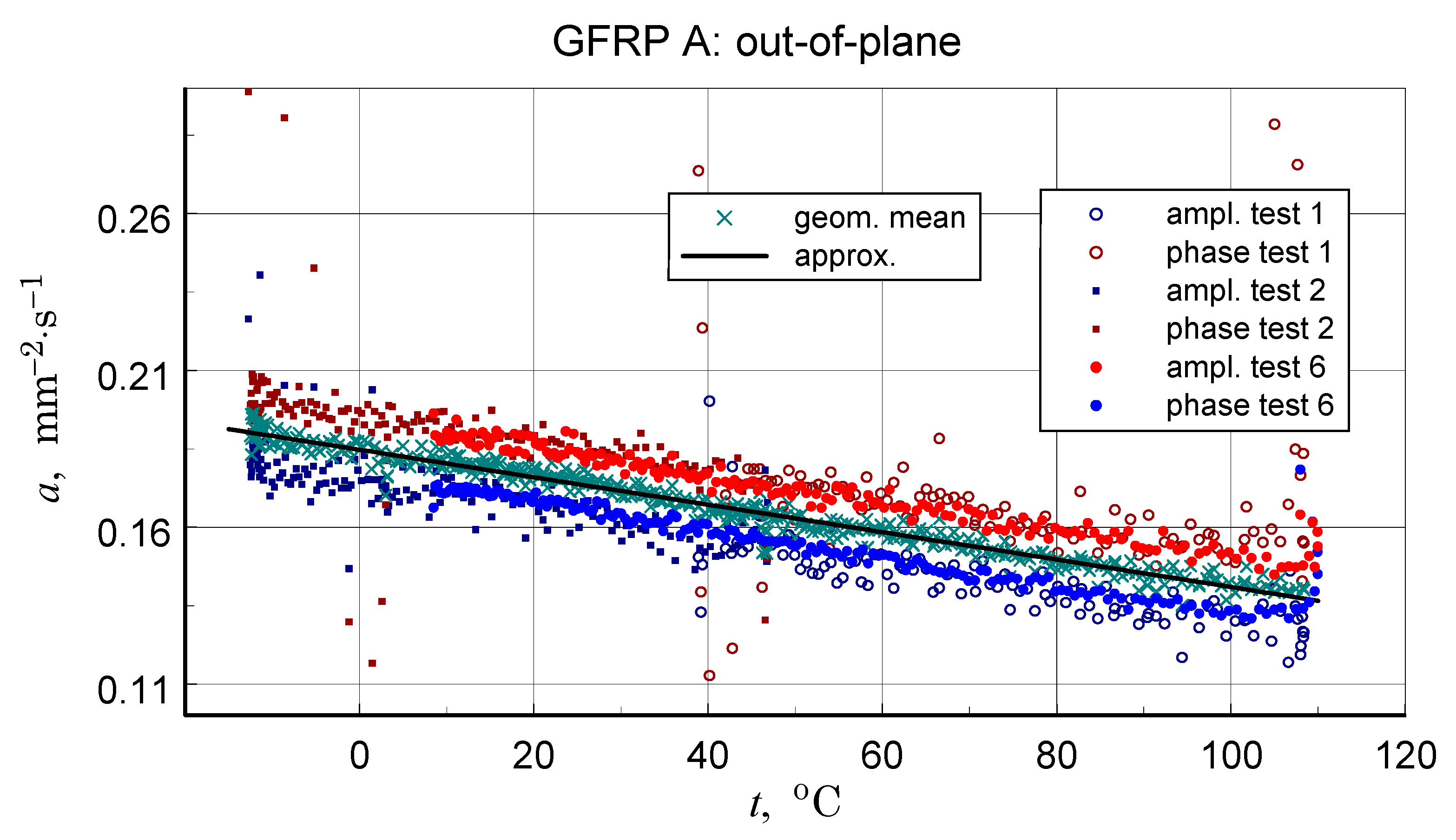
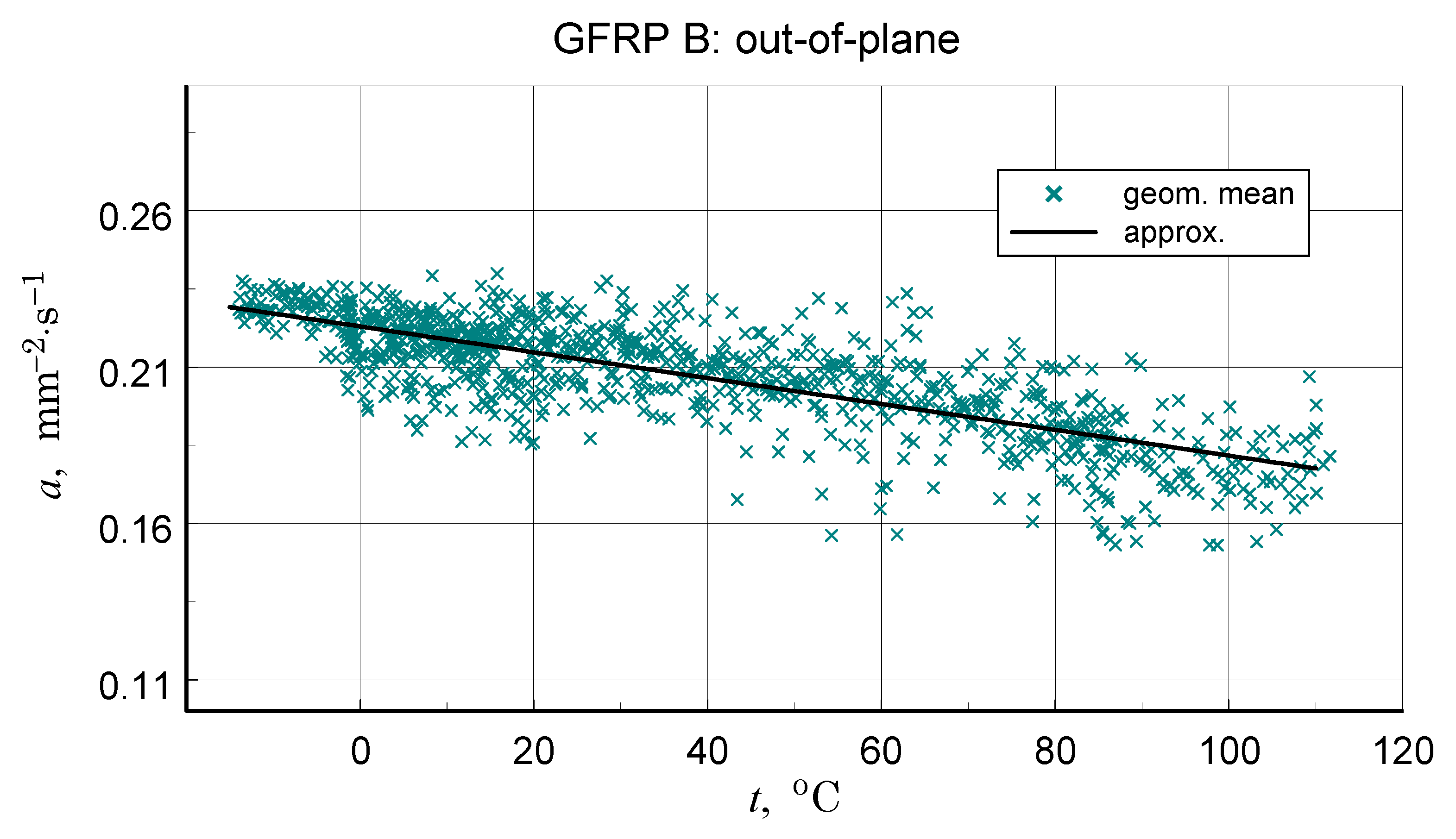
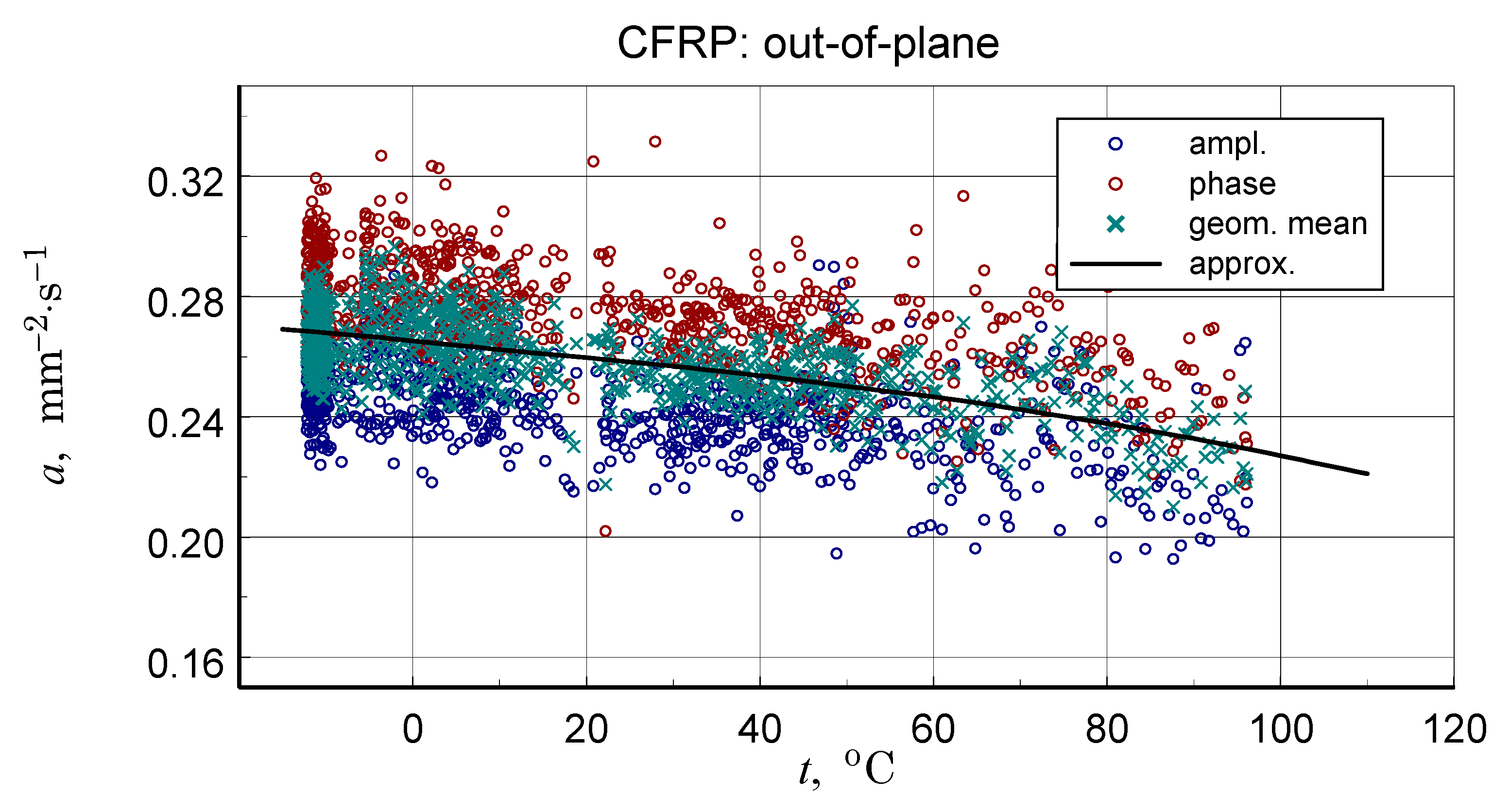
3.5. Thermal Diffusivity
3.6. Thermal Conductivity
4. Discussion
5. Conclusions
- Thermogravimetric analysis-thermogravimetric (TG) analysis revealed qualitative similarities in mass change profiles for the two glass reinforced composites (GFRP A and GFRP B), with similar conventional onset temperatures (ONSET) of approximately 294 °C. However, distinct differences in weight change and a significantly higher ONSET temperature (approximately 355 °C) for the CFRP composite compared to the glass composites. Given the differences in ONSET TG and ONSET DTG temperatures, the lower DTG values of 230 °C for the GFRP composites and 340 °C for the CFRP composite should be used as a basis for establishing limits for subsequent measurements and defining operational limits.
- Microcalorimetric analysis–(i) a glass transition in the CFRP composite, shifting from 95–110 °C (as-delivered) to 110–130 °C after heating to 280 °C; (ii) a strong likelihood of a similar glass transition in the glass-filled composite but with a difficult to determine transition temperature value, (iii) a slight decrease in specific heat for the CFRP composite after exposure to high temperatures.
- Diffusivity studies-the CFRP composite exhibited the highest transverse and longitudinal thermal diffusivity. While the longitudinal diffusivity was approximately twice the transverse diffusivity for the glass composites, this ratio was closer to 10:1 for the graphite composite, consistent with previous findings [22]. Moreover, for carbon fiber/epoxy resin, a similar relationship-exhibiting higher longitudinal thermal diffusivity than transverse diffusivity-had also been reported previously, e.g., in [21,28]. The study investigates the thermal anisotropy of reinforced carbon fiber/epoxy composites, revealing that the obtained anisotropy ratio was even higher than in our research, primarily due to the enhanced in-plane thermal conductivity achieved through the introduction of high thermal conductive coaxial PAN/PBO carbon fibers.
- The obtained results not only confirm the benefits of comprehensive testing but also illustrate the potential of using comparative analysis to cross-validate the obtained results. The measurement data from the studies of structures with imperfections provide an insight into the possible deviations of the effective property values from those obtained in the studies of well-defined structures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFRP | Carbon-fiber Reinforced Polymer |
| CTE | Coefficient of Thermal Expansion |
| DSC | Differential Scanning Calorimetry |
| GFRP | Glass-fiber Reinforced Polymer |
| LFA | Laser Flash Analysis |
| RT | Room Temperature |
| SEM | Scanning Electron Microscope |
| TG/DTG | Thermogravimetry/Differential Thermogravimetric |
References
- Peters, S.T. Handbook of Composites, 2nd ed.; Springer: New York, NY, USA, 1998. [Google Scholar]
- Luo, R. Friction performance of C/C composites prepared using a rapid directional diffused chemical vapor infiltration process. Carbon 2001, 39, 1278–1285. [Google Scholar]
- Luo, R.; Liu, T.; Li, J.; Zhang, H.; Chen, Z.; Tian, G. Thermophysical properties of carbon/carbon composites and physical mechanism of thermal expansion and thermal conductivity. Carbon 2004, 42, 2887–2895. [Google Scholar] [CrossRef]
- Siron, O.; Chollon, G.; Tsuda, H.; Yamauchi, H.; Maeda, K.; Kosaka, K. Microstructural and mechanical properties of filler-added coal-tar pitch-based C/C composites: The damage and fracture process in correlation with AE waveform parameters. Carbon 2000, 38, 1369–1389. [Google Scholar] [CrossRef]
- Barker, A.; Dutton, S.; Kelly, D. Composite Materials for Aircraft Structures; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2004. [Google Scholar]
- Panas, A.J. Comparative-Complementary Investigations of Thermophysical Properties—High Thermal Resolution Procedures in Practice. In Thermophysics; Faculty of Chemistry, Brno University of Technology: Brno, Czech Republic, 2010; pp. 218–235. [Google Scholar]
- Li, C.; Xian, G.; Li, H. Tension–tension fatigue performance of a large-diameter pultruded carbon/glass hybrid rod. Int. J. Fatigue 2019, 120, 141–149. [Google Scholar] [CrossRef]
- Yu, Y.; Pan, Y.; Zhou, R.; Miao, X. Effects of water and alkaline solution on durability of carbon–glass hybrid fiber reinforced polymer bars. Polymers 2021, 13, 3844. [Google Scholar] [CrossRef] [PubMed]
- Grimvall, G. Thermophysical Properties of Materials; Elsevier: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Kaviany, M. Heat Transfer Physics; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Rohsenow, W.M.; Hartnett, J.P.; Cho, Y.I. (Eds.) Handbook of Heat Transfer; McGraw-Hill: New York, NY, USA, 1998. [Google Scholar]
- Maglić, K.D.; Cezairliyan, A.; Peletsky, V.E. Compendium of Thermophysical Property Measurement Methods; Plenum Press: New York, NY, USA, 1984. [Google Scholar]
- Panas, A.J.; Panas, D. DSC investigation of binary iron-nickel alloys. High Temp. High Press. 2009, 38, 63–78. [Google Scholar]
- McNaughton, J.L.; Mortimer, C.T. Differential Scanning Calorimetry; IRS Physical Chemistry Series; Butterworths: London, UK; Perkin-Elmer Corporation: Norwalk, CT, USA, 1975; Volume 10. [Google Scholar]
- Cezairliyan, A. Specific Heat of Solids; Hemisphere Publishing Corporation: Washington, DC, USA, 1988. [Google Scholar]
- Wendlandt, W.T. Thermal Analysis, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1986. [Google Scholar]
- Ångström, A.J. Neue Methode, das Wärmeleitungsvermögen der Körper zubestimmen. Ann. Phys. Chem. 1861, 190, 114. [Google Scholar]
- Belling, J.M.; Unsworth, J. Modified Angström’s method for measurement of thermal diffusivity of materials with low conductivity. Rev. Sci. Instrum. 1987, 58, 997–1002. [Google Scholar] [CrossRef]
- Panas, A.J. IR support of thermophysical property investigation—Study of medical and advanced technology materials. In Infrared Thermography; InTech: Rijeka, Croatia, 2012. [Google Scholar]
- Min, S.; Blumm, J.; Lindemann, A. A new laser flash system for measurement of the thermophysical properties. Thermochim. Acta 2007, 455, 46–49. [Google Scholar] [CrossRef]
- Tranchard, P.; Samyn, F.; Duquesne, S.; Estèb, B.; Bourbigot, S. Modelling behaviour of a carbon epoxy composite exposed to fire: Part I—Characterisation of thermophysical properties. Materials 2017, 10, 494. [Google Scholar] [CrossRef] [PubMed]
- Panas, A.J.; Talkowski, M. Investigation on directional thermal diffusivity for graphite composite. J. KONES—Powertrain Transp. 2016, 23, 715–720. [Google Scholar] [CrossRef]
- Panas, A.J.; Białecki, M.; Dudziński, A.; Figur, K.; Krupińska, A.; Nowakowski, M.; Omen, Ł. Investigation of thermophysical and thermomechanical properties of aviation epoxy-glass composite. In Mechanika w Lotnictwie ML-XVIII; PTMTS: Warszawa, Poland, 2018; pp. 163–178. (In Polish) [Google Scholar]
- Panas, A.J.; Błaszczyk, J.; Dudziński, A.; Figur, K.; Foltyńska, A.; Krupińska, A.; Nowakowski, M. Investigation of temperature dependence on thermophysical and thermomechanical properties of the aircraft composite matrix. In Mechanika w Lotnictwie ML-XVII; Tom II; PTMTS: Warszawa, Poland, 2016; pp. 147–158. (In Polish) [Google Scholar]
- Kowaleczko, P.; Panas, A.J.; Nowakowski, M. Numerical analysis of a DMA epoxy-carbon composite study. Probl. Mechatron. Armament Aviat. Saf. Eng. 2018, 9, 101–112. [Google Scholar] [CrossRef]
- Bresson, G.; Ahmadi-Sénichault, A.; Caty, O.; Ayvazyan, V.; Gregori, M.L.; Costa, S.F.; Vignoles, G.L. Thermographic and tomographic methods for tridimensional characterization of thermal transfer in silica/phenolic composites. Compos. Part B Eng. 2016, 104, 71–79. [Google Scholar] [CrossRef]
- Weidenfeller, B.; Kirchberg, S. Thermal and mechanical properties of polypropylene-iron-diamond composites. Compos. Part B Eng. 2016, 92, 133–140. [Google Scholar] [CrossRef]
- Hao, M.; Hu, Z.; Huang, Y.; Qian, X.; Wen, Z.; Wang, X.; Liu, L.; Lu, F.; Zhang, Y. Enhanced both in-plane and through-thickness thermal conductivity of carbon fiber/epoxy composites by fabricating high thermal conductive coaxial PAN/PBO carbon fibers. Compos. Part B Eng. 2022, 229, 109468. [Google Scholar] [CrossRef]
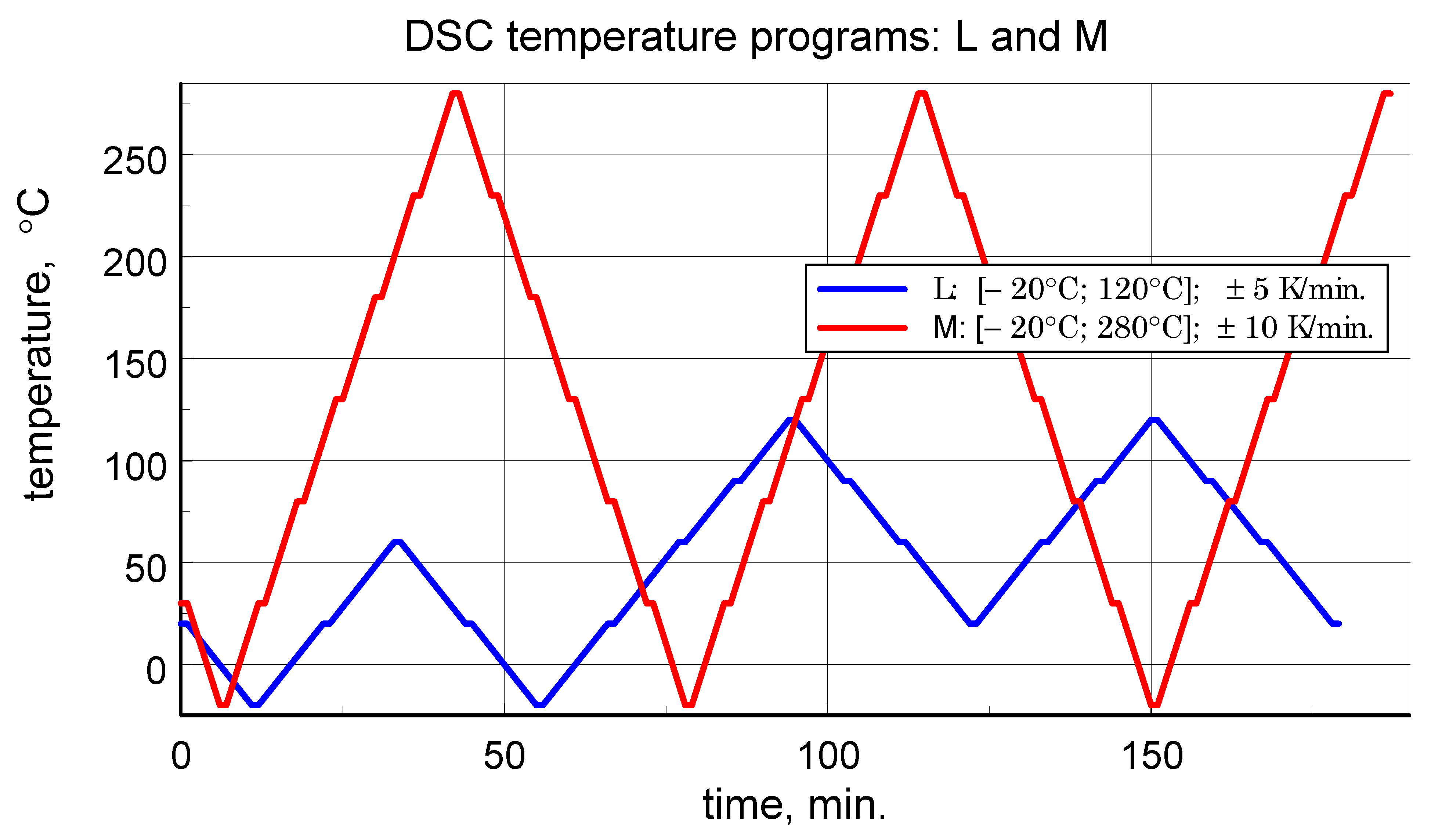








| Program | Temperature Range [tmin; tmax], °C | Rate of Temperature Change, K/min. | Number of Subintervals of the Range [tmin; tmax] | Number of Repetitions of Cycles |
|---|---|---|---|---|
| L | [−20; 120] | ±5 | 4 | 2 |
| M | [−20; 280] | ±10 | 6 | 2.5 |
| Type of Reinforcement | Filling | Indication | Porosity, % | Density (Effective), kg/m3 |
|---|---|---|---|---|
| glass | mat, layers | GFRP A | 33.0 | 1407 ± 3.4 |
| glass | mat, layers | GFRP B | 3.5 | 1677 ± 1.4 |
| graphite | fabric, layers | CFRP | 0.2 | 1484 ± 0.9 |
| Code | Volume Fraction of Reinforcement, % | Density of Reinforcement, kg/m3 | Density of Matrix, kg/m3 | Mass Fraction of Reinforcement, % |
|---|---|---|---|---|
| GFRP A | 56 ± 7 | 2.40 | 1.2 | 72 |
| GFRP B | 43 ± 6 | 2.40 | 1.2 | 60 |
| CFRP | 57 ± 4 | 1.94 | 1.2 | 68 |
| Structure | Sample Indication | mpost, mg | ∆m, mg | mkon, mg | Residue, % by Weight |
|---|---|---|---|---|---|
| GFRP A | specimen 1 | 7.61 | −5.03 | 2.58 | 33.90 |
| specimen 2 | 12.45 | −7.04 | 5.41 | 43.45 | |
| GFRP B | specimen 1 | 21.52 | −10.74 | 10.78 | 50.09 |
| specimen 2 | 10.09 | −5.03 | 5.06 | 50.15 | |
| CFRP | specimen 1 | 32.05 | −10.86 | 21.19 | 66.12 |
| specimen 2 | 50.36 | −18.43 | 31.93 | 63.40 |
| i | μi; n = 3 [See Equation (2)] | |
|---|---|---|
| GFRP B | CFRP | |
| 0 | 0.9770227 | 0.8444762 |
| 1 | 3.4229070 × 10−3 | 3.593296 × 10−3 |
| 2 | 5.8989400 × 10−6 | −1.490891 × 10−5 |
| 3 | −3.0474150 × 10−8 | 1.912467 × 10−7 |
| i | μi; n = 3 [See Equation (3)] | ||
|---|---|---|---|
| GFRP A | GFRP B | CFRP | |
| 0 | 0.1847094 | 0.2230017 | 0.2651952 |
| 1 | −4.376068 × 10−4 | −4.129915 × 10−4 | 2.678888 × 10−4 |
| 2 | n.a. | n.a. | −1.297996 × 10−7 |
| 3 | n.a. | n.a. | −9.988168 × 10−9 |
| ain-plane, mm2·s−1 | ||
|---|---|---|
| GFRP A | GFRP B | CFRP |
| 0.323 | 0.498 | 2.628 |
| GFRP A | GFRP B | CFRP | |
|---|---|---|---|
| kp,eff,in-plane, W·m−1·K−1 | 0.475 | 0.875 | 3.556 |
| keff,out-of-plane, W·m−1·K−1 | 0.259 | 0.378 | 1.234 |
| GFRP | CFRP | ||
|---|---|---|---|
| [23] | [22] | [21] | |
| ρ, kg·m−3 | 1769 | 1468 | 1575 |
| cp,eff, J·g−1·K−1 | 930 | 846 | 740 |
| aout-of-plane, mm2·s−1 | 0.19 | 0.36 | 0.17 |
| ain-plane, mm2·s−1 | 0.32 | 2.0 | 2.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panas, A.J.; Leciejewski, Z.; Sienkiewicz, J.; Nowakowski, M. Comparative Analysis of Thermophysical Properties of Functional Epoxy Matrix Composites Reinforced with Glass or Carbon Fibers in the Context of Heat Transfer Anisotropy. Materials 2025, 18, 4838. https://doi.org/10.3390/ma18214838
Panas AJ, Leciejewski Z, Sienkiewicz J, Nowakowski M. Comparative Analysis of Thermophysical Properties of Functional Epoxy Matrix Composites Reinforced with Glass or Carbon Fibers in the Context of Heat Transfer Anisotropy. Materials. 2025; 18(21):4838. https://doi.org/10.3390/ma18214838
Chicago/Turabian StylePanas, Andrzej J., Zbigniew Leciejewski, Judyta Sienkiewicz, and Mirosław Nowakowski. 2025. "Comparative Analysis of Thermophysical Properties of Functional Epoxy Matrix Composites Reinforced with Glass or Carbon Fibers in the Context of Heat Transfer Anisotropy" Materials 18, no. 21: 4838. https://doi.org/10.3390/ma18214838
APA StylePanas, A. J., Leciejewski, Z., Sienkiewicz, J., & Nowakowski, M. (2025). Comparative Analysis of Thermophysical Properties of Functional Epoxy Matrix Composites Reinforced with Glass or Carbon Fibers in the Context of Heat Transfer Anisotropy. Materials, 18(21), 4838. https://doi.org/10.3390/ma18214838






