Finite Element Analysis of Thermal–Mechanical Coupling and Process Parameter Optimization in Laser Etching of Al–Tedlar–Kevlar Composite Films
Abstract
1. Introduction
2. Model and Methods
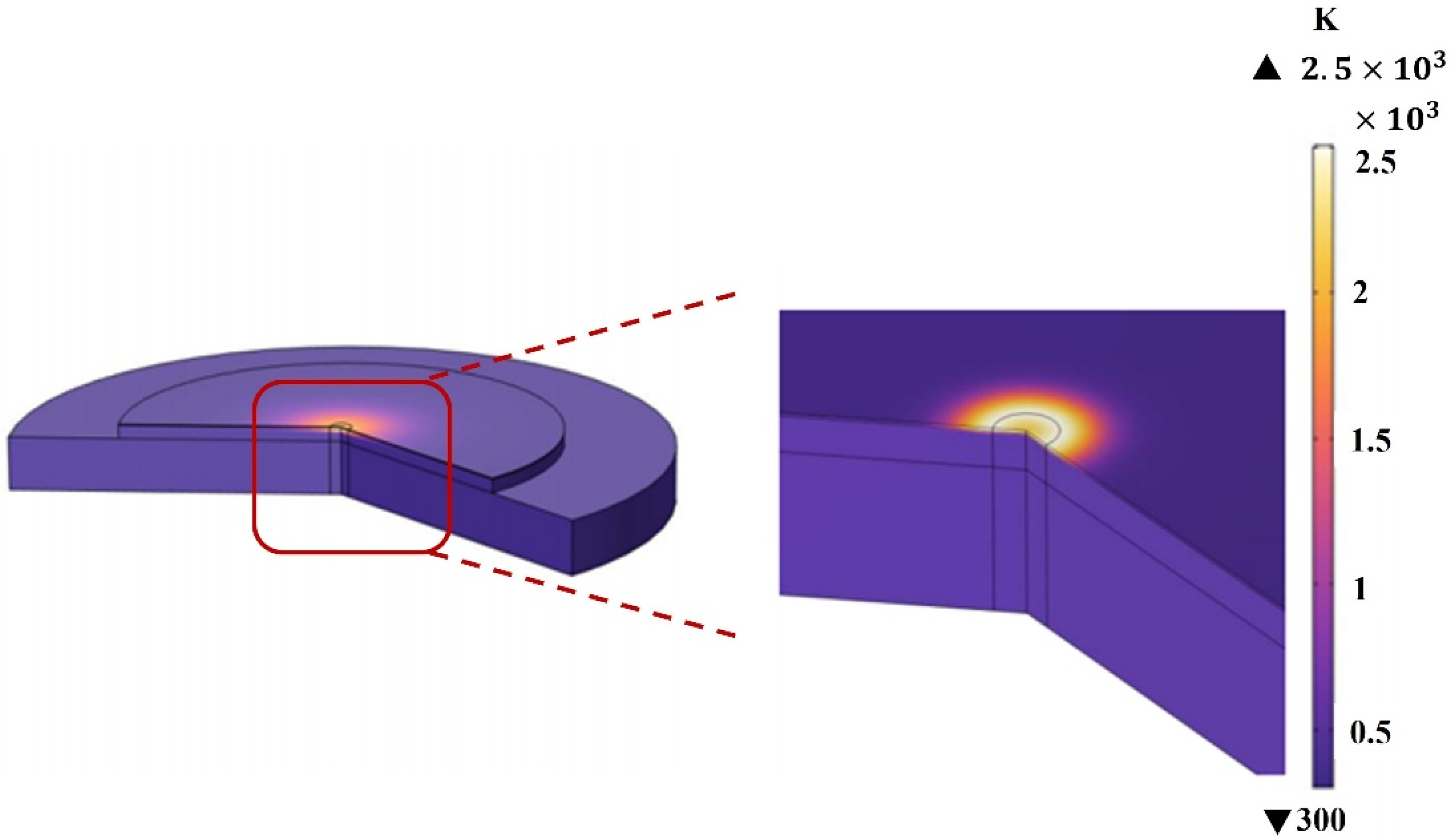
2.1. Physical Model and Geometric Modeling
2.2. Material Properties and Laser Heat Source Configuration
- σ = 16.986 μm, FWHM = 2.3548 × 16.986 = 40 μm
- σ = 19.11 μm, FWHM = 2.3548 × 16.986 = 45 μm
- σ = 21.233 μm, FWHM = 2.3548 × 21.233 = 50 μm
2.3. Multi-Physics Coupling and Boundary Conditions
2.4. Simulation Strategy
3. Results and Discussion
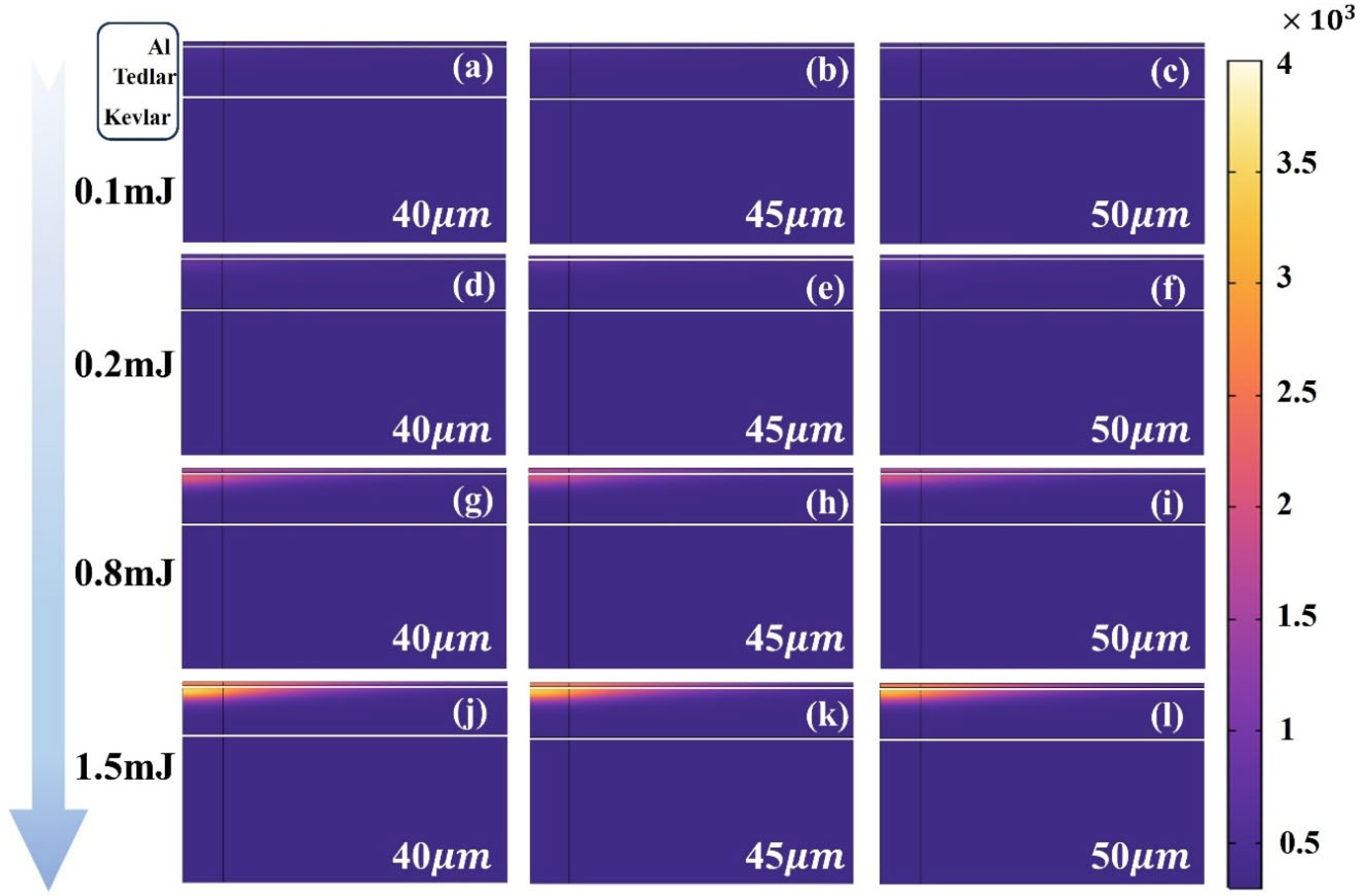
3.1. Impact of Laser Pulse Energy on Al–Tedlar–Kevlar Composite Film
3.2. Impact of Laser Repetition Frequency on Al–Tedlar–Kevlar Composite Film
3.3. Impact of Laser Pulse Width on Al–Tedlar–Kevlar Composite Film
3.4. Impact of Laser Parameters on Thermal Stress Behavior
3.5. Optimal Processing Parameters for Laser Etching
4. Conclusions
- Effect of Repetition Frequency: The laser repetition frequency significantly influences heat accumulation and stress evolution. An increase in frequency raises the heat input density and reduces the thermal diffusion interval, resulting in a sharp rise in localized temperature. Particularly when the frequency exceeds 20 kHz, distinct thermal stress concentration zones form within the material, increasing the risk of membrane cracking and interfacial delamination. Therefore, a balance must be achieved between processing efficiency and thermal stability.
- Effect of Pulse Energy: Pulse energy is a dominant factor determining the intensity of thermal excitation and the magnitude of stress. When the energy exceeds 0.8 mJ, the stress levels in the Tedlar layer approach its minimum tensile modulus (approximately 2.1 GPa), leading the material to likely enter the plastic deformation stage and potentially initiate micro-cracking. While higher energy can enhance etching efficiency, excessive energy input can severely compromise the structural integrity and service life of the membrane.
- Effect of Pulse Width: Pulse width significantly influences the thermo-mechanical response of the Al–Tedlar–Kevlar composite film. At fixed pulse energy, its effect on the temperature field is minimal, with a stable overall response. Under constant peak power, however, longer pulses increase per-pulse energy and extend thermal coupling, intensifying heat accumulation, temperature gradients, nonuniform expansion, and thermal stresses. Thus, in high–peak power laser processing, pulse width governs both thermal input and stress evolution, making it a critical parameter for optimization.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, F.D.; Ren, P.G.; Guo, Z.Z.; Wang, J.; Chen, Z.Y.; Zong, Z.; Hu, J.; Jin, Y.L.; Ren, F. Asymmetric multilayered MXene-AgNWs/cellulose nanofiber composite films with antibacterial properties for high-efficiency electromagnetic interference shielding. J. Mater. Sci. Technol. 2022, 129, 181–189. [Google Scholar] [CrossRef]
- Zhu, Z.; Lu, H.; Zhao, W.J.; Tuerxunjiang, A.; Chang, X.Q. Materials, performances and applications of electric heating films. Renew. Sustain. Energy Rev. 2023, 184, 113540. [Google Scholar] [CrossRef]
- Kwon, D.J.; Kwon, I.J.; Milam-Guerrero, J.; Yang, S.B.; Yeum, J.H.; Choi, H.H. Aramid nanofiber-reinforced multilayer electromagnetic-interference (EMI) shielding composites with high interfacial durability. Mater. Des. 2022, 215, 110452. [Google Scholar] [CrossRef]
- Xia, C.L.; Yu, J.; Shi, S.Q.; Qiu, Y.; Cai, L.P.; Wu, H.F.; Ren, H.; Nie, X.; Zhang, H.L. Natural fiber and aluminum sheet hybrid composites for high electromagnetic interference shielding performance. Compos. Part B-Eng. 2017, 114, 121–127. [Google Scholar] [CrossRef]
- Xue, L.L.; Xiong, S.S. Flexible metal foil/polymer sandwich composites for electromagnetic interference shielding with anti-wind-sand environment tolerance. J. Mater. Sci.-Mater. Electron. 2024, 35, 1685. [Google Scholar] [CrossRef]
- Ursache, S.; Cerbu, C.; Hadar, A. Characteristics of Carbon and Kevlar Fibres, Their Composites and Structural Applications in Civil Engineering-A Review. Polymers 2024, 16, 127. [Google Scholar] [CrossRef]
- Shang, K.; Wu, G.; Liu, X.; Yang, J.; Wang, R. Femtosecond Laser Etching of Aluminum Film on Tedlar Composite Surfaces. Chin. J. Lasers 2021, 48, 1002117. [Google Scholar] [CrossRef]
- Ehrhardt, M.; Lai, S.; Lorenz, P.; Zimmer, K. Guiding of LIPSS formation by excimer laser irradiation of pre-patterned polymer films for tailored hierarchical structures. Appl. Surf. Sci. 2020, 506, 144785. [Google Scholar] [CrossRef]
- Mezera, M.; van Drongelen, M.; Römer, G. Laser-Induced Periodic Surface Structures (LIPSS) on Polymers Processed with Picosecond Laser Pulses. J. Laser Micro Nanoeng. 2018, 13, 105–116. [Google Scholar]
- Ali, B.; Litvinyuk, I.V.; Rybachuk, M. Femtosecond laser micromachining of diamond: Current research status, applications and challenges. Carbon 2021, 179, 209–226. [Google Scholar] [CrossRef]
- Putz, B.; Völker, B.; Semprimoschnig, C.; Cordill, M.J. Influence of extreme thermal cycling on metal-polymer interfaces. Microelectron. Eng. 2017, 167, 17–22. [Google Scholar] [CrossRef]
- Emanuel, M.; Mahyari, P.; Maniscalco, M.; May, N.; Choi, H.; Bliznakov, T.; Moore, T.; Anaei, M.T.M.; Phoulady, A.; Blagojevic, A.; et al. Comprehensive Simulation of Laser Processing Systems: From Source to Surface Interaction. In Proceedings of the 19th Conference on Laser Based Micro and Nanoprocessing, San Francisco, CA, USA, 27–31 January 2025. [Google Scholar]
- Zhang, C.H.; Wang, F.; Zhang, C.S.; Bao, Y.L.; Wang, M.J.; Liu, D.; Wu, J.; Su, Z.M. Thermal-force coupling simulation of carbon fibre-reinforced poly-ether-ether-ketone thermoplastic composites during the laser-assisted automated tape placement process. Plast. Rubber Compos. 2024, 53, 181–189. [Google Scholar] [CrossRef]
- Bian, J.; Chen, F.; Yang, B.; Zhang, X.; Chen, J.; Zhuang, S.; Zhang, X.; Song, J. Laser-Induced Interfacial Spallation for Controllable and Versatile Delamination of Flexible Electronics. ACS Appl. Mater. Interfaces 2020, 12, 54230–54240. [Google Scholar] [CrossRef]
- Chakraborty, S.; Park, H.-Y.; Ahn, S.I. Copper Laser Patterning on a Flexible Substrate Using a Cost-Effective 3D Printer. Sci. Rep. 2022, 12, 21149. [Google Scholar] [CrossRef]
- Li, X.; Tang, R.; Li, D.; Luo, H.; Wang, T.; Zhang, J. Investigations of the Laser Ablation Mechanism of PMMA Microchannels Using Single-Pass and Multi-Pass Laser Scans. Polymers 2024, 16, 2361. [Google Scholar] [CrossRef]
- Said-Bacar, Z.; Leroy, Y.; Antoni, F.; Slaoui, A.; Fogarassy, E. Modeling of CW laser diode irradiation of amorphous silicon films. Appl. Surf. Sci. 2011, 257, 5127–5131. [Google Scholar] [CrossRef]
- von der Heide, C.; Seuthe, T.; Epple, M.; Nolte, S.; Chichkov, B.N. Methodology of Selective Metallic Thin Film Ablation from Susceptible Polymer Substrate Using Pulsed Femtosecond Laser. Appl. Phys. A 2020, 126, 89. [Google Scholar] [CrossRef]
- Kashihara, K.; Tomita, T.; Inoue, M.; Koshizaki, N. Simulation of Photothermal Synthesis Processes in Metal–Organic Framework Films under Laser Irradiation. ACS Appl. Nano Mater. 2021, 4, 1122–1130. [Google Scholar]
- Varlamov, P.; Marx, J.; Elgueta, Y.U.; Melnikov, I.; Temnov, V.V. Femtosecond Laser Ablation and Delamination of Functional Magnetic Multilayers at the Nanoscale. Nanomaterials 2024, 14, 1488. [Google Scholar] [CrossRef]
- Cengel, Y.A.; Turner, R.H.; Smith, R. Fundamentals of Thermal-Fluid Sciences; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Wang, H.-B. Introduction to Tedlar Poly(vinyl fluoride) Films; New Chemical Materials; DuPont: Wilmington, DE, USA, 1979; pp. 10–12. [Google Scholar]
- Chen, H.; Ginzburg, V.V.; Yang, J.; Yang, Y.; Liu, W.; Huang, Y.; Du, L.; Chen, B. Thermal Conductivity of Polymer-Based Composites: Fundamentals and Applications. Prog. Polym. Sci. 2016, 59, 41–85. [Google Scholar] [CrossRef]
- Joe, D.J.; Kim, S.; Park, J.H.; Park, D.Y.; Lee, H.E.; Im, T.H.; Choi, I.; Ruoff, R.S.; Lee, K.J. Laser-Material Interactions for Flexible Applications. Adv. Mater. 2017, 29, 1606586. [Google Scholar] [CrossRef]
- Self, S.A. Focusing of spherical Gaussian beams. Appl. Opt. 1983, 22, 658–661. [Google Scholar] [CrossRef] [PubMed]
- Vora, H.D.; Santhanakrishnan, S.; Harimkar, S.P.; Boetcher, S.K.S.; Dahotre, N.B. One-dimensional multipulse laser machining of structural alumina: Evolution of surface topography. Int. J. Adv. Manuf. Technol. 2013, 68, 69–83. [Google Scholar] [CrossRef]
- Kumar, K.K.; Samuel, G.L.; Shunmugam, M.S. Theoretical and experimental investigations of ultra-short pulse laser interaction on Ti6Al4V alloy. J. Mater. Process. Technol. 2019, 263, 266–275. [Google Scholar] [CrossRef]
- Varlamov, P.; Timofeev, V.; Andreev, A. Femtosecond Laser Ablation and Delamination of Thin Films on Substrates: Mechanisms and Dynamics. Nanomaterials 2024, 14, 1123. [Google Scholar]
- Ravi-Kumar, S. Laser Ablation of Polymers: A Review. Prog. Org. Coat. 2019, 135, 82–99. [Google Scholar]
- Nath, P.; Patel, R.S. Laser Processing of Polymer-Based Composites: A Review. Polymers 2020, 12, 2341. [Google Scholar]
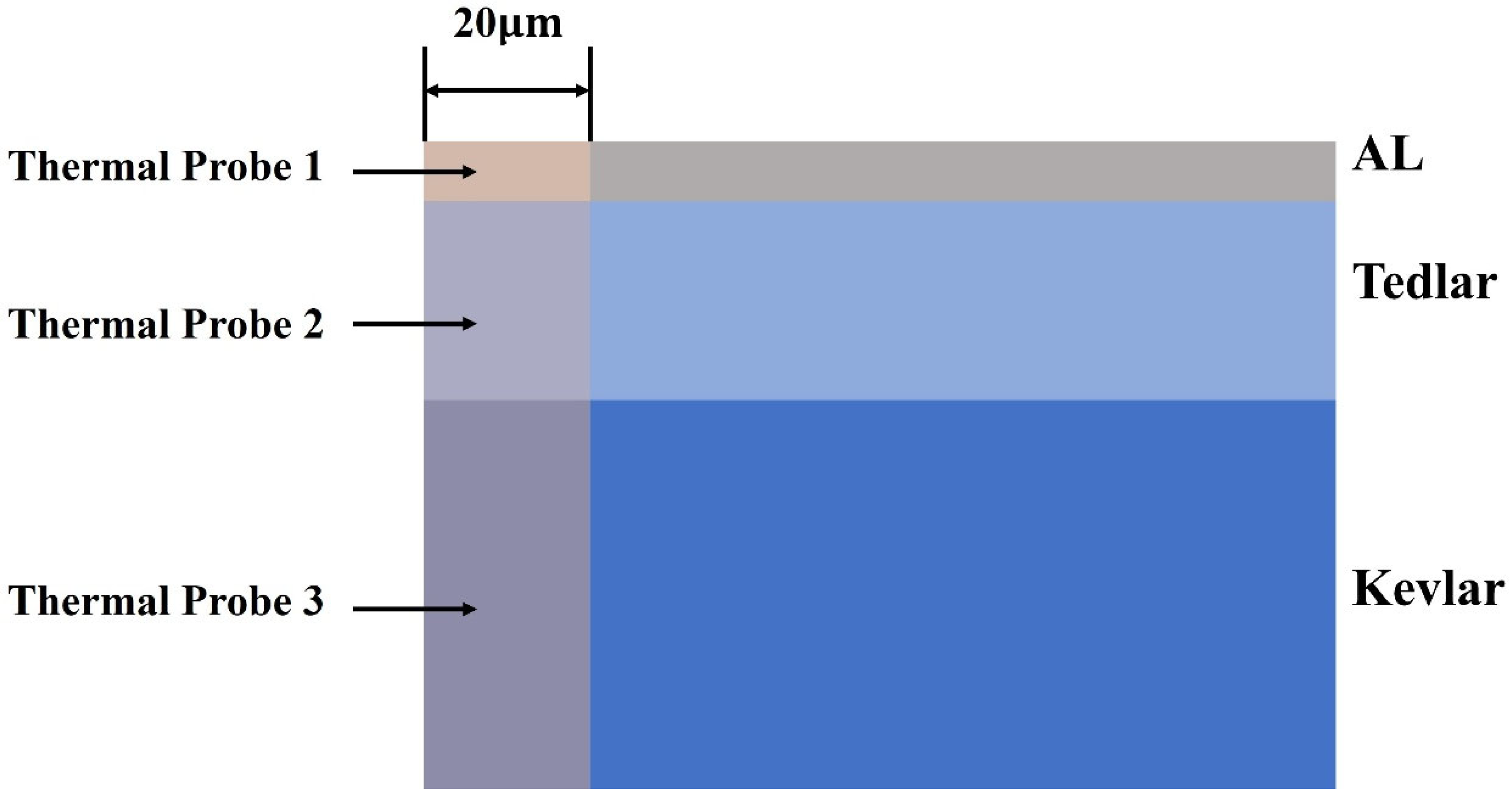










| Physical Parameters | Al | Tedlar | Kevlar |
|---|---|---|---|
| Specific heat (J/kg·K) | 900~1050 | 1010 | 1400~2500 |
| Density (kg/m3) | 2700 | 1500 | 1440 |
| Thermal conductivity (W/(m·K) | 235 | 0.206 | 1.7 |
| Real part of refractive index | 1.3763 | 1.46 | / |
| Imaginary part of refractive index | 10.245 | 10−6 | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Wang, R.; Hou, S.; Shang, K.; Gesang, D.; Wei, G. Finite Element Analysis of Thermal–Mechanical Coupling and Process Parameter Optimization in Laser Etching of Al–Tedlar–Kevlar Composite Films. Materials 2025, 18, 4839. https://doi.org/10.3390/ma18214839
Liu M, Wang R, Hou S, Shang K, Gesang D, Wei G. Finite Element Analysis of Thermal–Mechanical Coupling and Process Parameter Optimization in Laser Etching of Al–Tedlar–Kevlar Composite Films. Materials. 2025; 18(21):4839. https://doi.org/10.3390/ma18214839
Chicago/Turabian StyleLiu, Ming, Rui Wang, Shanglin Hou, Kaiwen Shang, Dunzhu Gesang, and Guang Wei. 2025. "Finite Element Analysis of Thermal–Mechanical Coupling and Process Parameter Optimization in Laser Etching of Al–Tedlar–Kevlar Composite Films" Materials 18, no. 21: 4839. https://doi.org/10.3390/ma18214839
APA StyleLiu, M., Wang, R., Hou, S., Shang, K., Gesang, D., & Wei, G. (2025). Finite Element Analysis of Thermal–Mechanical Coupling and Process Parameter Optimization in Laser Etching of Al–Tedlar–Kevlar Composite Films. Materials, 18(21), 4839. https://doi.org/10.3390/ma18214839





