Influence of Hydrogen-Based Direct Reduction Shaft Furnace Interior Structure on Shaft Furnace Performance
Abstract
1. Introduction
2. Methodology
2.1. Discrete Element Method
2.2. Simulated Setup
3. Results and Discussion
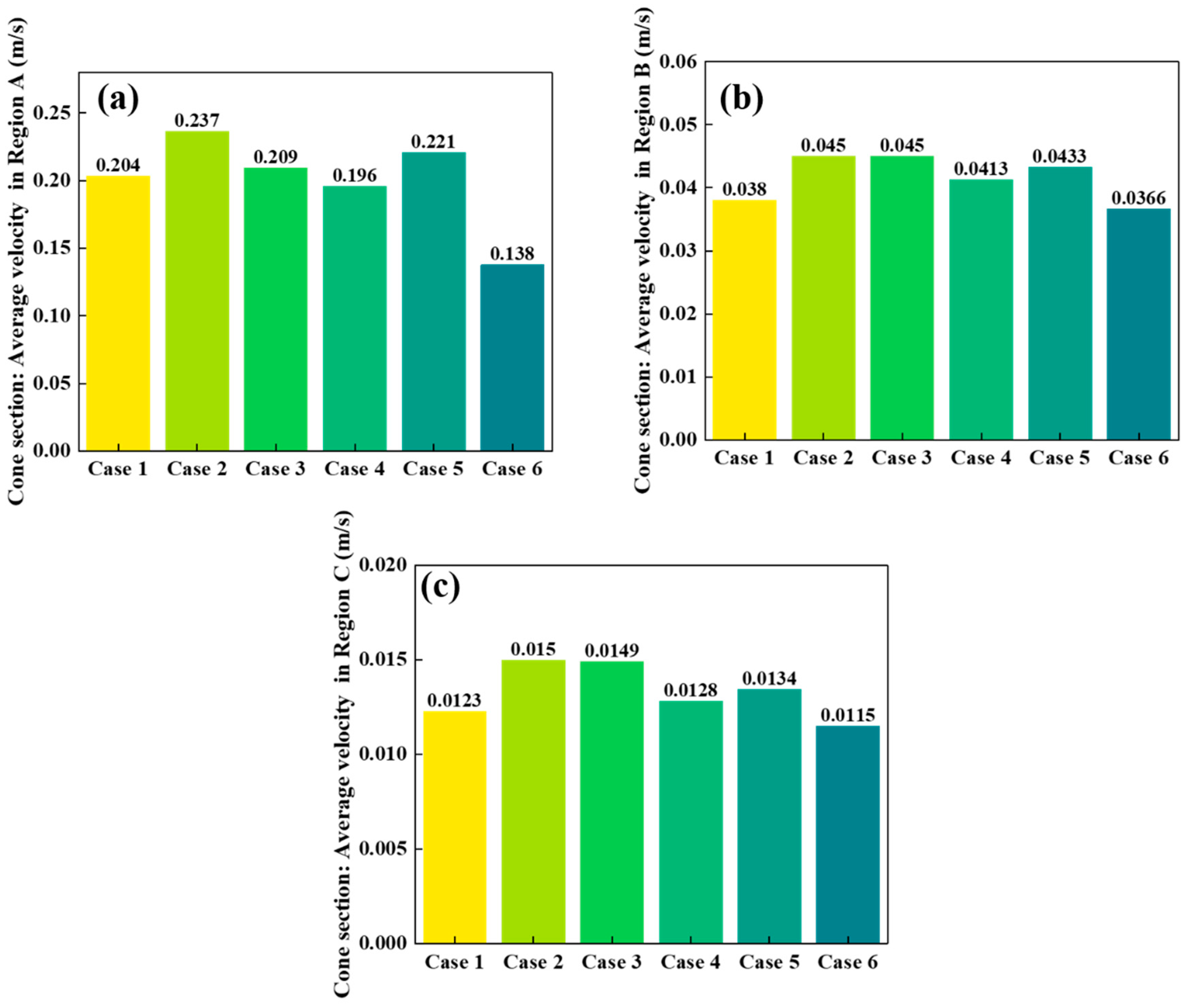
3.1. Analysis of the Effects on Particle Flow Velocity
3.2. Analysis of the Effects on Particle Flow Trajectories
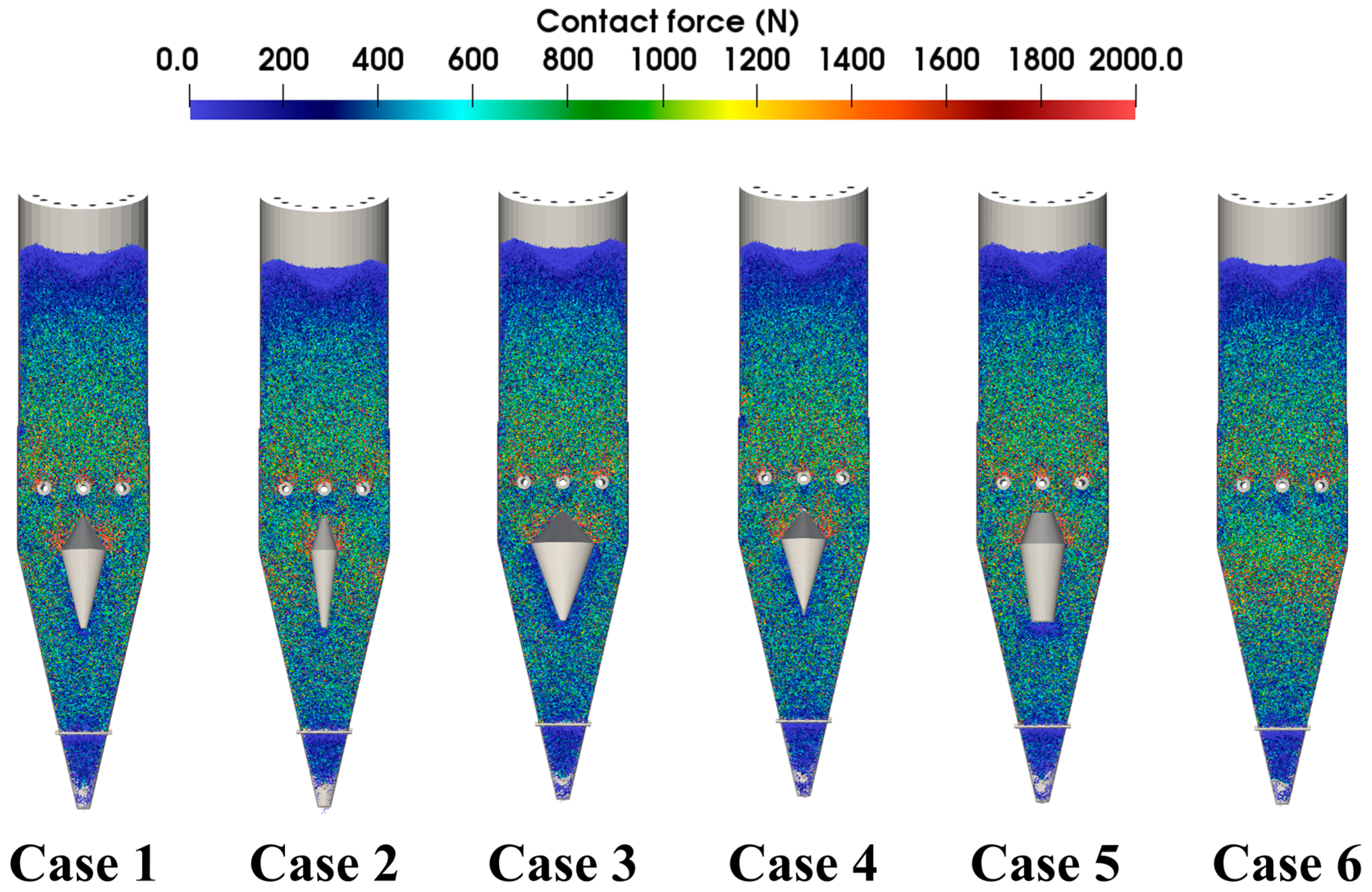
3.3. Analysis of the Effects on Particle Force Conditions
4. Conclusions
- (1)
- The results demonstrate that the introduction of a diverter device significantly improves the flow distribution of particles within the furnace. Specifically, the diverter device helps to mitigate the funnel flow phenomenon observed in the center of the furnace, improving the uniformity of particle descent and enhancing the overall flow behavior. The geometric parameters of the diverter device, such as its radial width and the top/bottom diameter, play a critical role in controlling particle velocity and promoting a more homogeneous flow.
- (2)
- In particular, Case 2, with a smaller central diameter, produced the most favorable dynamics, resulting in faster particle discharge and a more uniform descent compared to other cases. However, this configuration also exhibited relatively higher energy dissipation, implying a potential risk of pellet fragmentation. In contrast, larger distributor diameters (e.g., Case 3) reduced compressive force concentration and lowered average energy dissipation (8.28 J/kg), but with slightly reduced discharge efficiency. These findings highlight the trade-off between flow uniformity and particle integrity.
- (3)
- The results demonstrate that optimizing diverter geometry can provide practical guidance for improving flow behavior in hydrogen-based shaft furnaces, which is essential for stable operation and enhanced process performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Holappa, L. A General Vision for Reduction of Energy Consumption and CO2 Emissions from the Steel Industry. Metals 2020, 10, 1117. [Google Scholar] [CrossRef]
- Ariyama, T.; Takahashi, K.; Kawashiri, Y.; Nouchi, T. Diversification of the Ironmaking Process Toward the Long-Term Global Goal for Carbon Dioxide Mitigation. J. Sustain. Met. 2019, 5, 276–294. [Google Scholar] [CrossRef]
- Zhou, F.; Peng, D.; Li, K.; Conejo, A.N.; Liao, H.; Xiong, Z.; Li, D.; Zhang, J. Coke behavior with H2O in a hydrogen-enriched blast furnace: A review. Int. J. Miner. Metall. Mater. 2024, 31, 959–976. [Google Scholar] [CrossRef]
- Wang, M.; Li, Y.; Li, J.; Wang, Z. Green process innovation, green product innovation and its economic performance improvement paths: A survey and structural model. J. Environ. Manag. 2021, 297, 113282. [Google Scholar] [CrossRef]
- Weigel, M.; Fischedick, M.; Marzinkowski, J.; Winzer, P. Multicriteria analysis of primary steelmaking technologies. J. Clean. Prod. 2016, 112, 1064–1076. [Google Scholar] [CrossRef]
- Pei, M.; Petäjäniemi, M.; Regnell, A.; Wijk, O. Toward a fossil free future with HYBRIT: Development of iron and steelmaking technology in Sweden and Finland. Metals 2020, 10, 972. [Google Scholar] [CrossRef]
- Sohn, H.Y. Review of fluid-solid reaction analysis—Part 3: Complex fluid-solid reactions. Can. J. Chem. Eng. 2019, 97, 2326–2332. [Google Scholar] [CrossRef]
- Hamadeh, H.; Mirgaux, O.; Patisson, F. Detailed modeling of the direct reduction of iron ore in a shaft furnace. Materials 2018, 11, 1865. [Google Scholar] [CrossRef]
- Yu, Y.; Saxén, H. Experimental and DEM study of segregation of ternary size particles in a blast furnace top bunker model. Chem. Eng. Sci. 2010, 65, 5237–5250. [Google Scholar] [CrossRef]
- Shi, Y.; Zhu, D.; Pan, J.; Guo, Z.; Lu, S.; Xu, M. Improving hydrogen-rich gas-based shaft furnace direct reduction of fired hematite pellets by modifying basicity. Powder Technol. 2022, 408, 117782. [Google Scholar] [CrossRef]
- Shao, L.; Zhang, X.; Zhao, C.; Qu, Y.; Saxén, H.; Zou, Z. Computational analysis of hydrogen reduction of iron oxide pellets in a shaft furnace process. Renew. Energy 2021, 179, 1537–1547. [Google Scholar] [CrossRef]
- Bhattacharya, T.; McCarthy, J. Chute flow as a means of segregation characterization. Powder Technol. 2014, 256, 126–139. [Google Scholar] [CrossRef]
- Liao, H.; Zong, Y.; Li, K.; Bu, Y.; Bi, Z.; Jiang, C.; Liu, Z.; Zhang, J. Influence of lump ore ratio and shapes on the particle flow behavior inside the direct reduction shaft furnace by discrete element modeling model. Steel Res. Int. 2023, 94, 2200531. [Google Scholar] [CrossRef]
- Liao, H.; Zong, Y.; Li, K.; Bi, Z.; Jiang, C.; Liu, Z.; Zhang, J.; Zhang, C. Influence of Wall Angle of Direct Reduction Shaft Furnace on Particle Flow Pattern by DEM Modeling. Steel Res. Int. 2023, 94, 2300044. [Google Scholar] [CrossRef]
- Turkdogan, E.; Vinters, J. Gaseous reduction of iron oxides: Part I. Reduction of hematite in hydrogen. Met. Trans. 1971, 2, 3175–3188. [Google Scholar] [CrossRef]
- Zieliński, J.; Zglinicka, I.; Znak, L.; Kaszkur, Z. Reduction of Fe2O3 with hydrogen. Appl. Catal. A Gen. 2010, 381, 191–196. [Google Scholar] [CrossRef]
- Pineau, A.; Kanari, N.; Gaballah, I. Kinetics of reduction of iron oxides by H2: Part I: Low temperature reduction of hematite. Thermochim. Acta 2006, 447, 89–100. [Google Scholar] [CrossRef]
- Pineau, A.; Kanari, N.; Gaballah, I. Kinetics of reduction of iron oxides by H2: Part II. Low temperature reduction of magnetite. Thermochim. Acta 2007, 456, 75–88. [Google Scholar] [CrossRef]
- Zhao, Z.; Tang, J.; Chu, M.; Wang, X.; Zheng, A.; Wang, X.; Li, Y. Direct reduction swelling behavior of pellets in hydrogen-based shaft furnaces under typical atmospheres. Int. J. Miner. Met. Mater. 2022, 29, 1891–1900. [Google Scholar] [CrossRef]
- Lin, H.-Y.; Chen, Y.-W.; Li, C. The mechanism of reduction of iron oxide by hydrogen. Thermochim. Acta 2003, 400, 61–67. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Boechat, F.O.; de Carvalho, R.M.; Tavares, L.M. Simulation of mechanical degradation of iron ore pellets in a direct reduction furnace. KONA Powder Part. J. 2018, 35, 216–225. [Google Scholar] [CrossRef]
- Da Costa, A.R.; Wagner, D.; Patisson, F. Modelling a new, low CO2 emissions, hydrogen steelmaking process. J. Clean. Prod. 2013, 46, 27–35. [Google Scholar] [CrossRef]
- Kuang, S.; Li, Z.; Yu, A. Review on modeling and simulation of blast furnace. Steel Res. Int. 2018, 89, 1700071. [Google Scholar] [CrossRef]
- Zhou, H.; Wu, S.; Kou, M.; Luo, Z.; He, W.; Zou, Z.; Shen, Y. Discrete Particle Simulation of Solid Flow in a Large-Scale Reduction Shaft Furnace with Center Gas Supply Device. ISIJ Int. 2018, 58, 422–430. [Google Scholar] [CrossRef]
- Tian, X.; Zhou, H.; Xia, T.; Qin, Z.-T.; Guo, H.-D.; Sun, D.-W.; Kou, M.-Y.; Wu, S.-L. Influence of diversion cone structure on inner characteristic in hydrogen-enriched shaft furnace: A DEM study. J. Iron Steel Res. Int. 2025, 32, 1844–1855. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Zhu, H.P.; Yu, A.B.; Wright, B.; Zulli, P. Discrete particle simulation of gas–solid flow in a blast furnace. Comput. Chem. Eng. 2008, 32, 1760–1772. [Google Scholar] [CrossRef]
- Yu, Y.; Saxén, H. Flow of Pellet and Coke Particles in and from a Fixed Chute. Ind. Eng. Chem. Res. 2012, 51, 7383–7397. [Google Scholar] [CrossRef]
- Liao, H.; Zong, Y.; Li, K.; Bi, Z.; Jiang, C.; Zhang, J.; Ren, S. Effect of outlet characteristics and particle properties on the flow characteristics inside conical hoppers. Met. Res. Technol. 2022, 119, 524. [Google Scholar] [CrossRef]
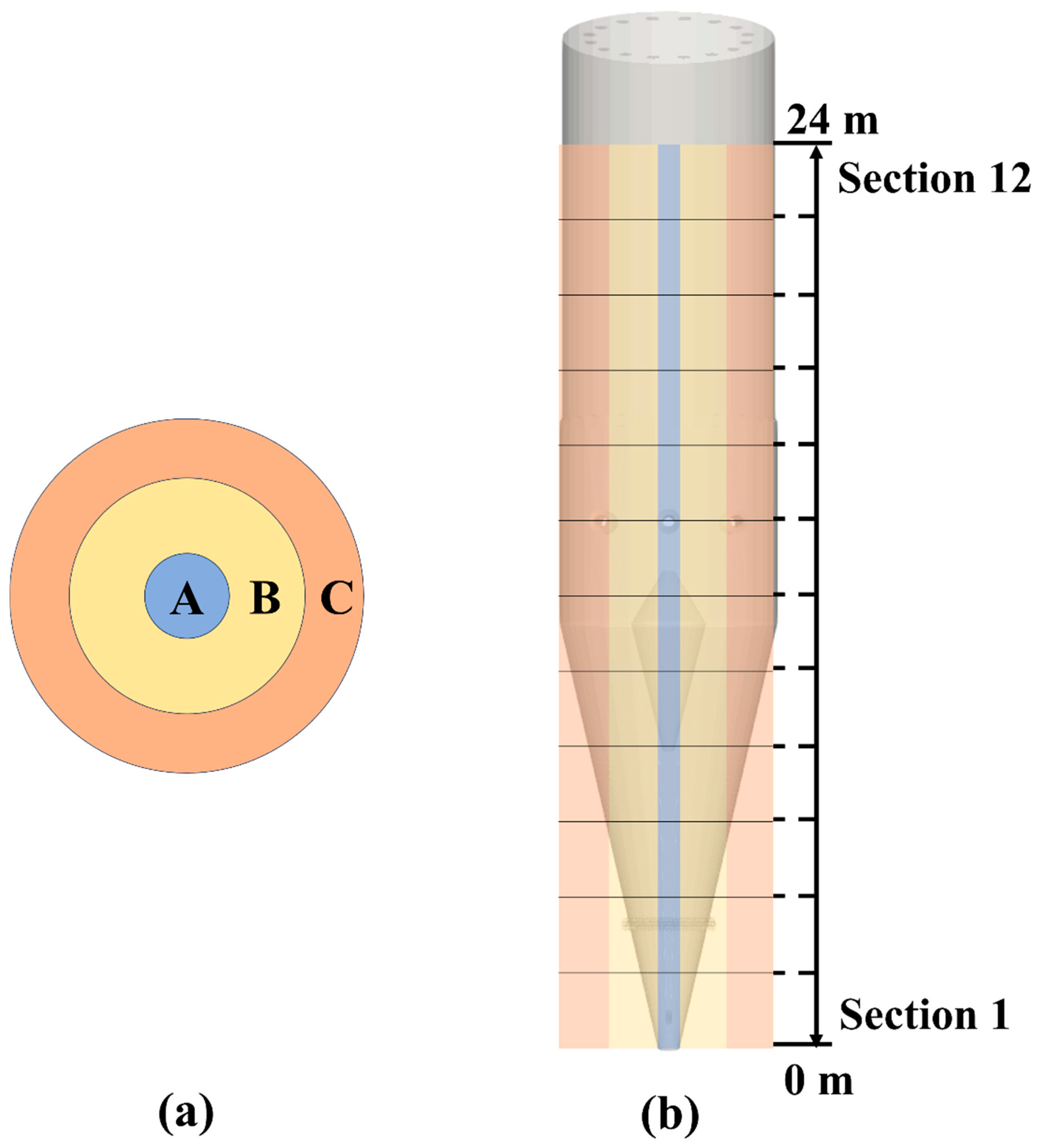








| Radial Width, mm | Longitudinal Height, mm | |
|---|---|---|
| Region A | 566 | 24,000 |
| Region B | 1276 | 24,000 |
| Region C | 1276 | 24,000 |
| Sections 1–12 | 5670 | 2000 |
| Parameters | Pellet | Wall | |
|---|---|---|---|
| Density, ρ (kg/m3) | 3425 | 7850 | |
| Young’s modulus, E (MPa) | 20 | 30 | |
| Poisson’s ratio, υ (-) | 0.25 | 0.3 | |
| Restitution coefficient, e (-) | Pellet | 0.4 | 0.35 |
| Static friction, μs (-) | Pellet | 0.5 | 0.4 |
| Rolling friction, μr (-) | Pellet | 0.2 | 0.4 |
| Time step, Δt | 1 × 10−5 |
| Detailed Description | |
|---|---|
| Case 1 | Baseline (central diameter 2000 mm; top/bottom diameter 300 mm) |
| Case 2 | Reduce the central diameter of the flow distributor to 1200 mm |
| Case 3 | Increase the central diameter of the flow distributor to 2800 mm |
| Case 4 | Reduce the top/bottom diameter of the flow distributor to 10 mm |
| Case 5 | Increase the top/bottom diameter of the flow distributor to 1000 mm |
| Case 6 | Remove the flow distributor |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, Q.; Liao, H.; Zhang, J.; Li, K. Influence of Hydrogen-Based Direct Reduction Shaft Furnace Interior Structure on Shaft Furnace Performance. Materials 2025, 18, 4794. https://doi.org/10.3390/ma18204794
Xue Q, Liao H, Zhang J, Li K. Influence of Hydrogen-Based Direct Reduction Shaft Furnace Interior Structure on Shaft Furnace Performance. Materials. 2025; 18(20):4794. https://doi.org/10.3390/ma18204794
Chicago/Turabian StyleXue, Qingbin, Haotian Liao, Jianliang Zhang, and Kejiang Li. 2025. "Influence of Hydrogen-Based Direct Reduction Shaft Furnace Interior Structure on Shaft Furnace Performance" Materials 18, no. 20: 4794. https://doi.org/10.3390/ma18204794
APA StyleXue, Q., Liao, H., Zhang, J., & Li, K. (2025). Influence of Hydrogen-Based Direct Reduction Shaft Furnace Interior Structure on Shaft Furnace Performance. Materials, 18(20), 4794. https://doi.org/10.3390/ma18204794







