Physical Zoo in Pb-Cu-P-S-O Apatite
Abstract
Highlights
- The formation of one-dimensional chain-like structures, through the co-doping of copper and an excess of non-metallic elements within the lead apatite framework, may be critical for achieving superconductivity.
- Doping of non-metallic elements in copper-doped lead apatite gives rise to a rich variety of physical phenomena within the system.
- The apatite family of materials holds significant potential as a key platform for advancing research on strongly correlated physics.
Abstract
1. Introduction
2. Experimental Approach
2.1. Synthesis
2.1.1. Synthesis (I–VI)
2.1.2. (Pb-Cu)10(, Synthesis (VII–X)
2.2. Characterization
3. Discussion
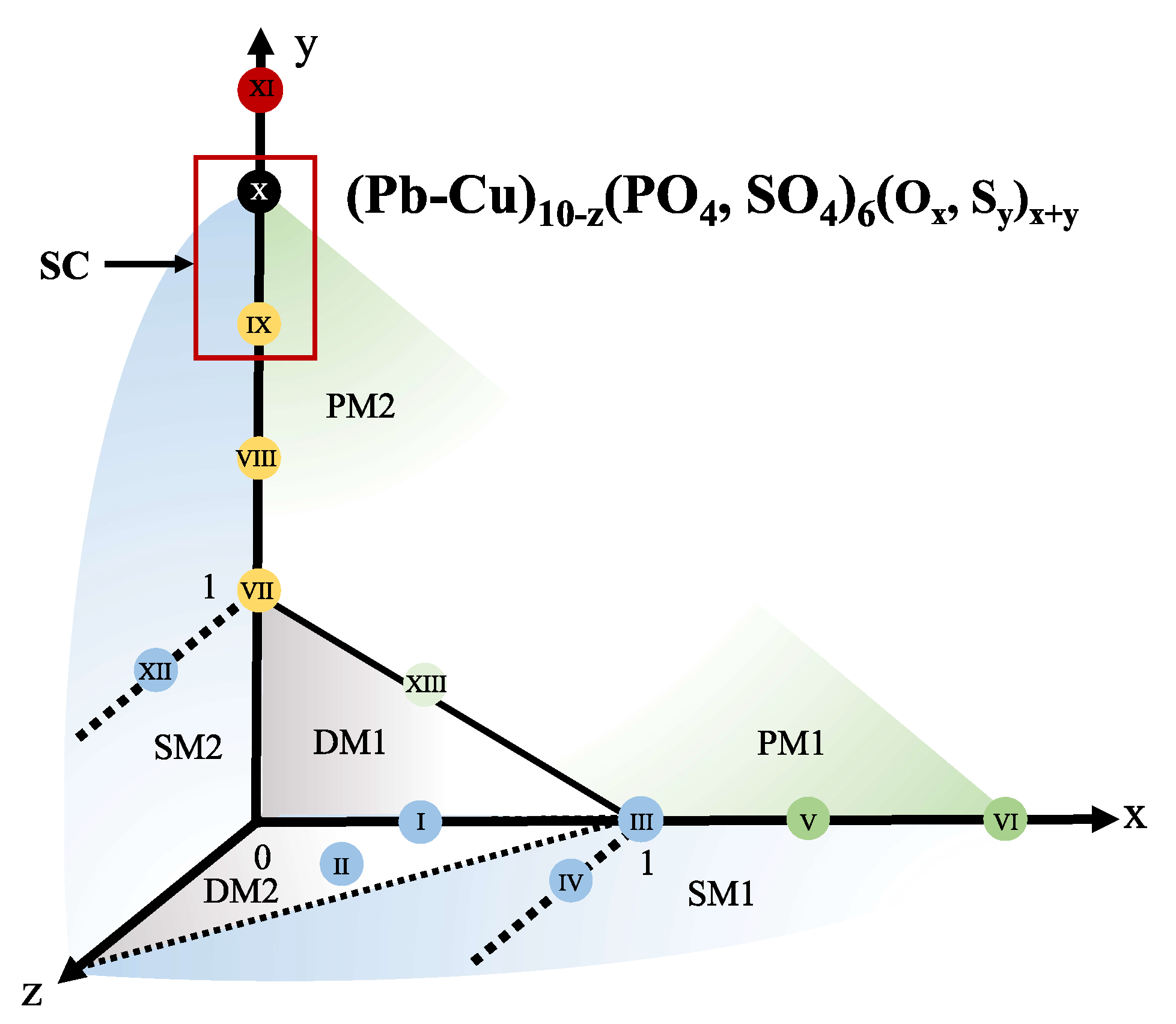
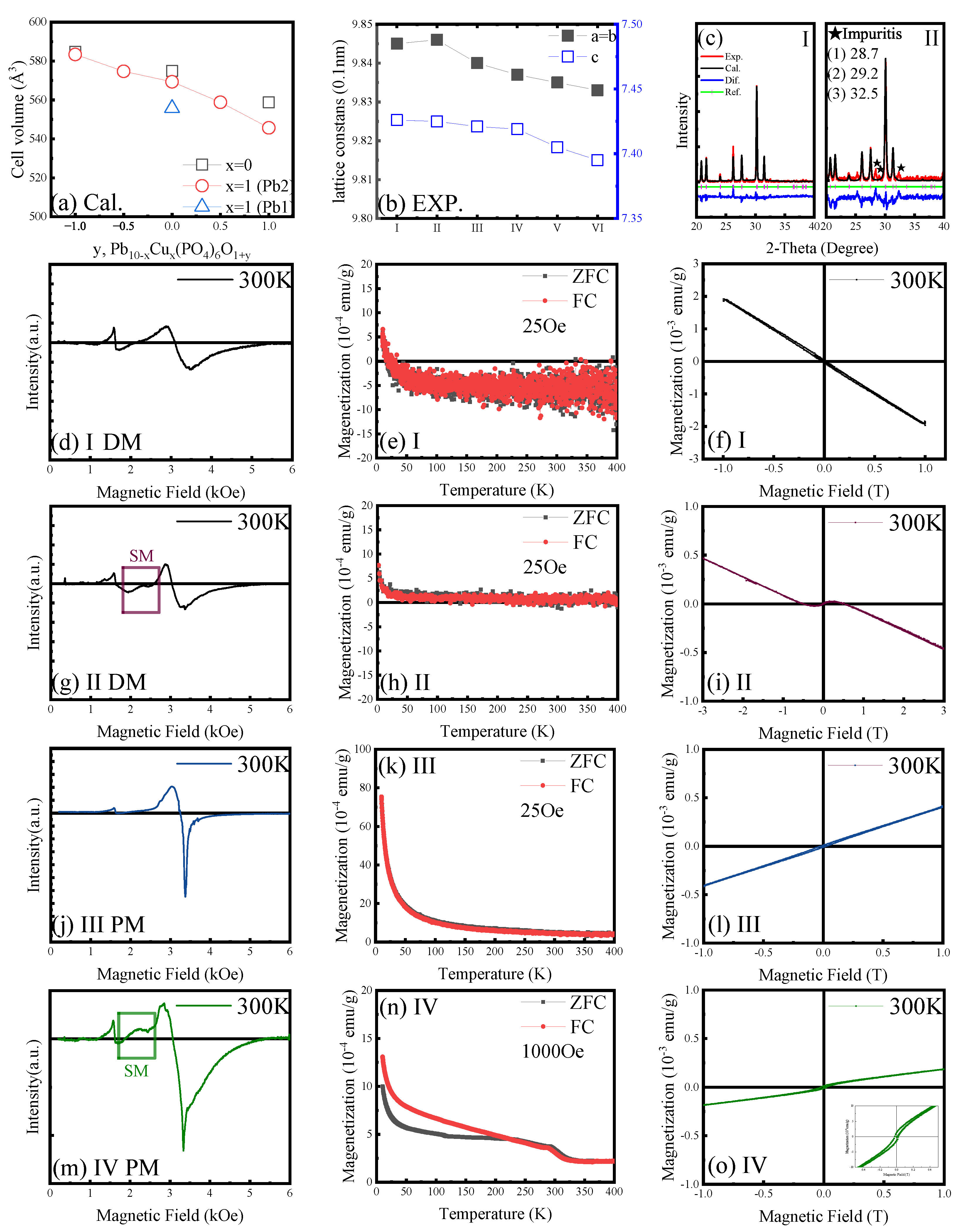
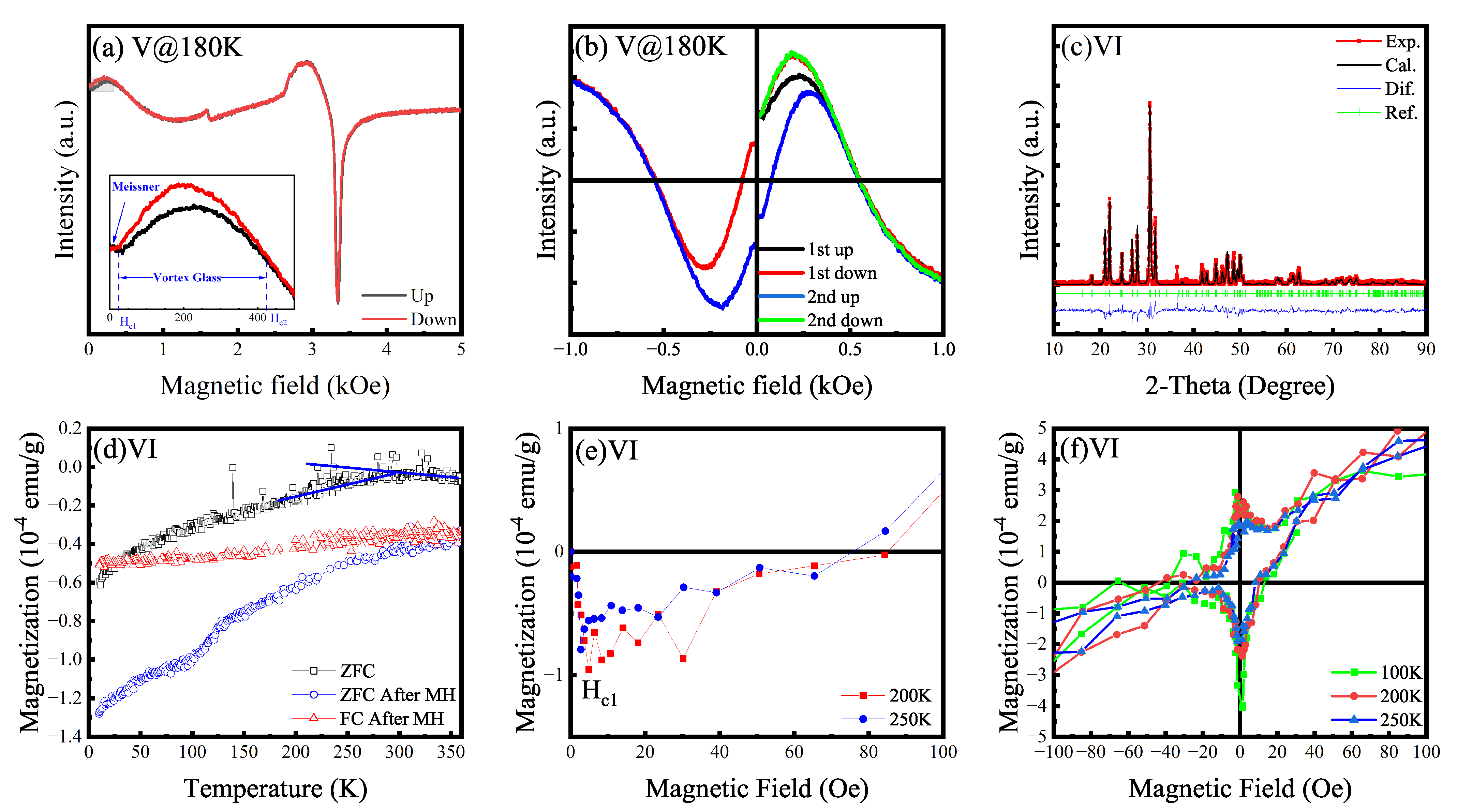
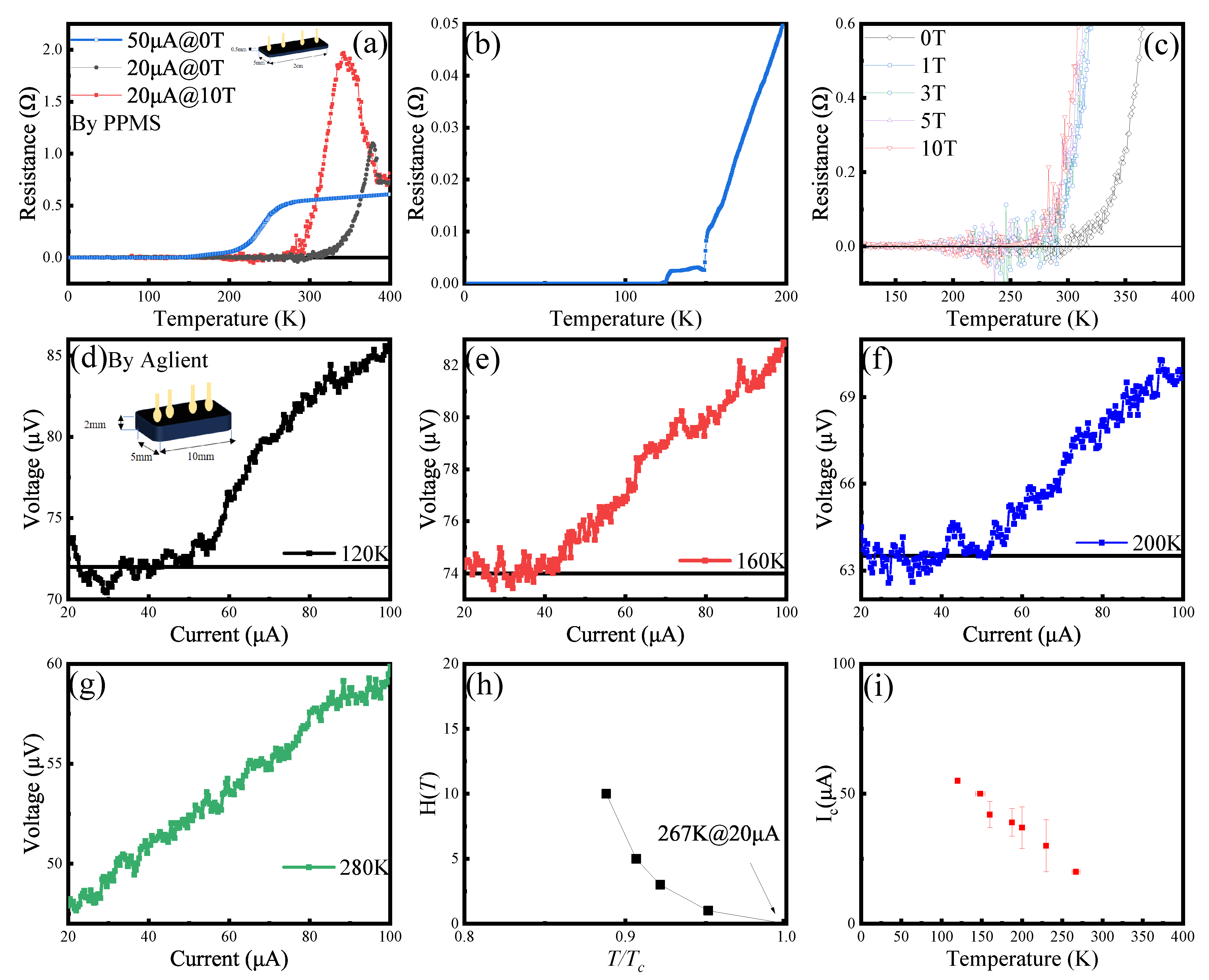
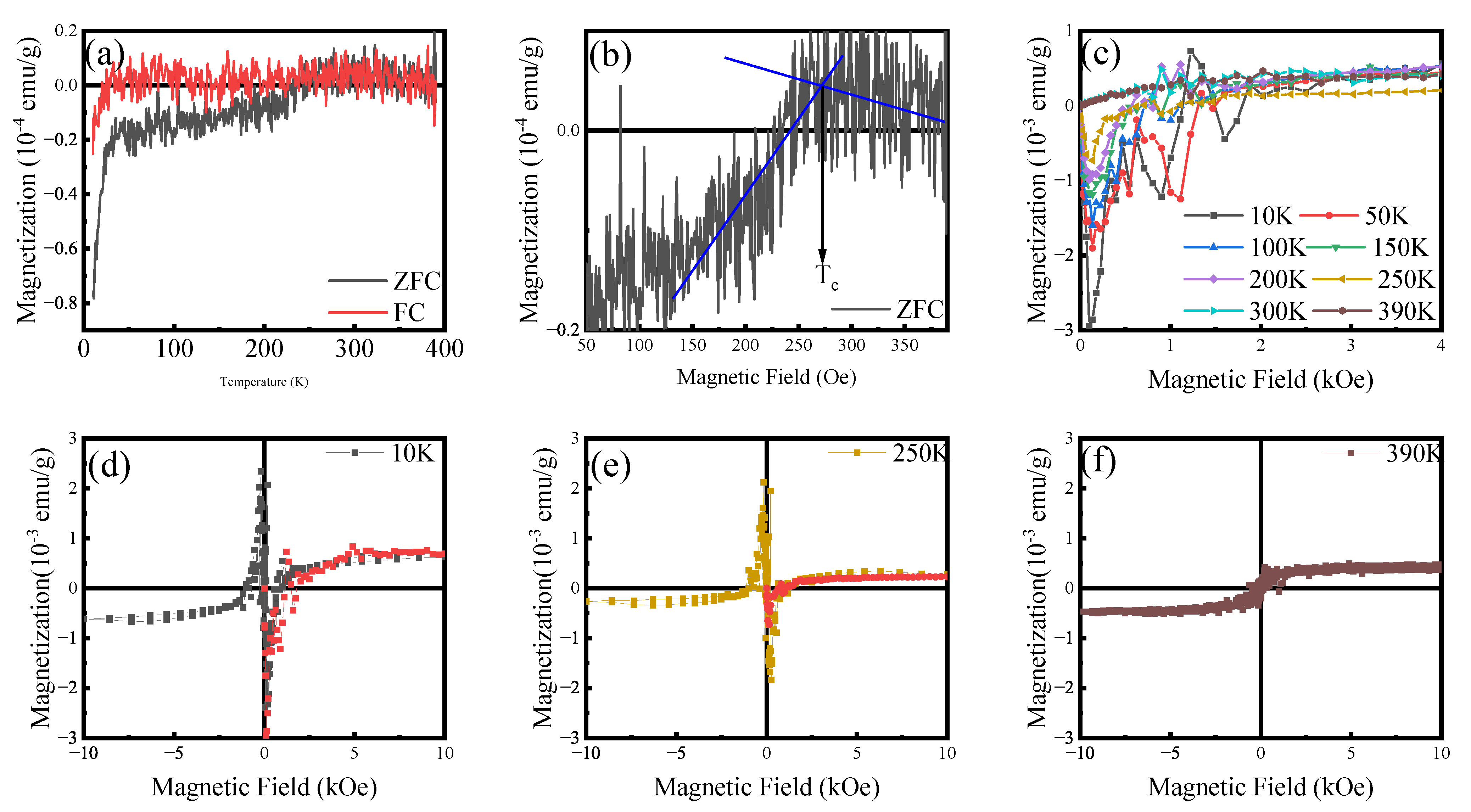
3.1. Complex Magnetism and Possible Meissner Effect (I to VI)
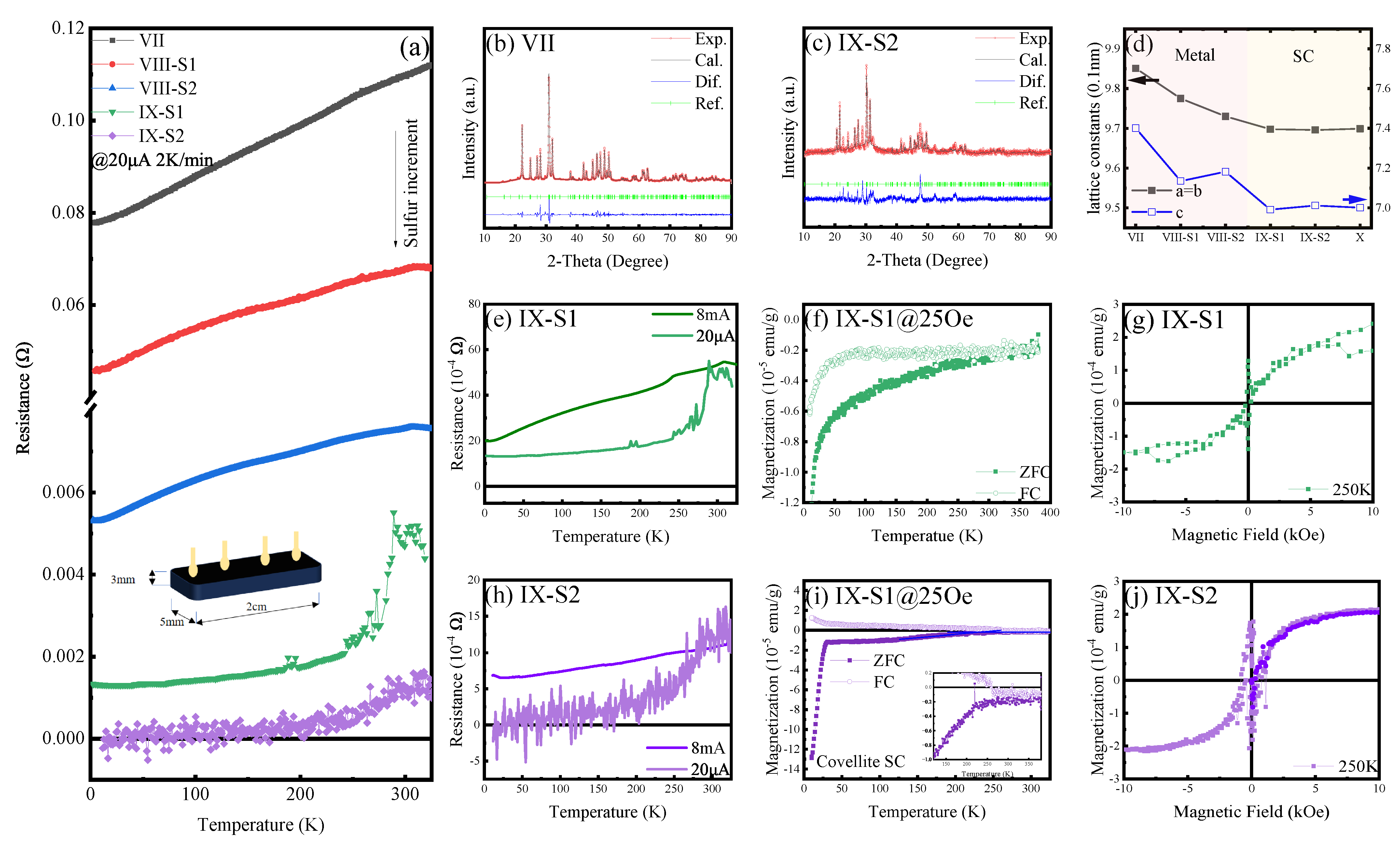
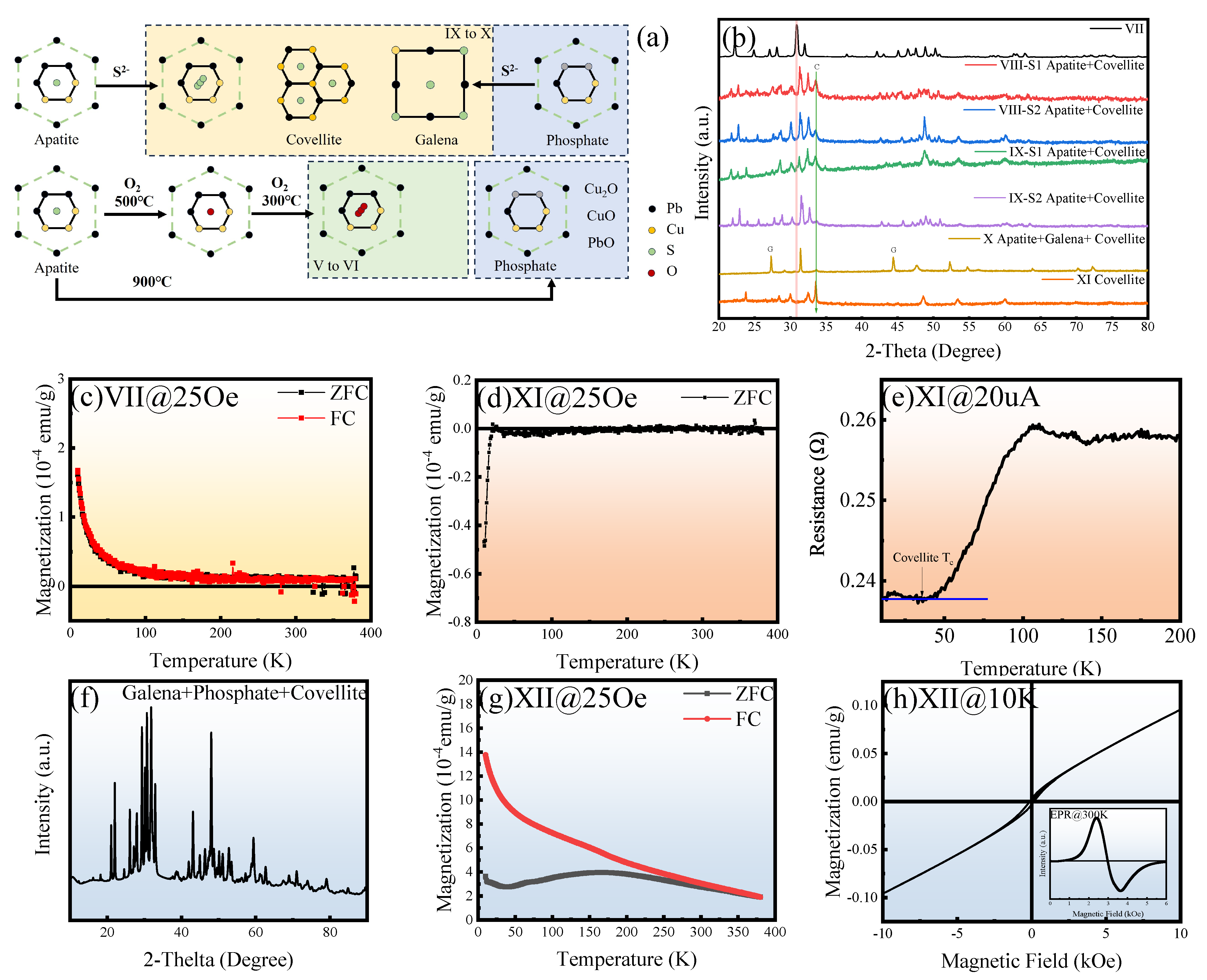
3.2. Properties of Sulfoapatite (VII to IX)
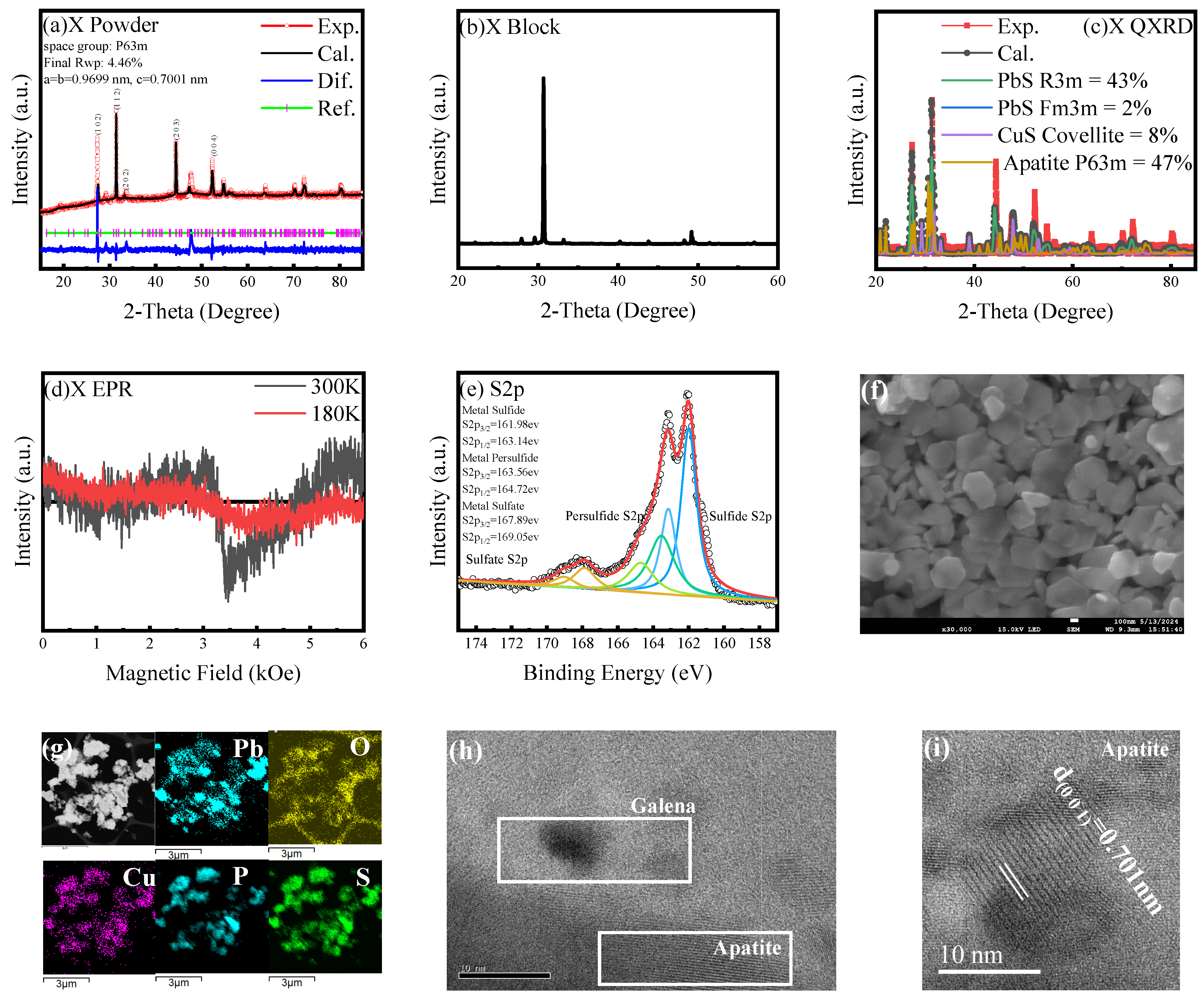
3.3. Signature of Superconductivity in Sample X
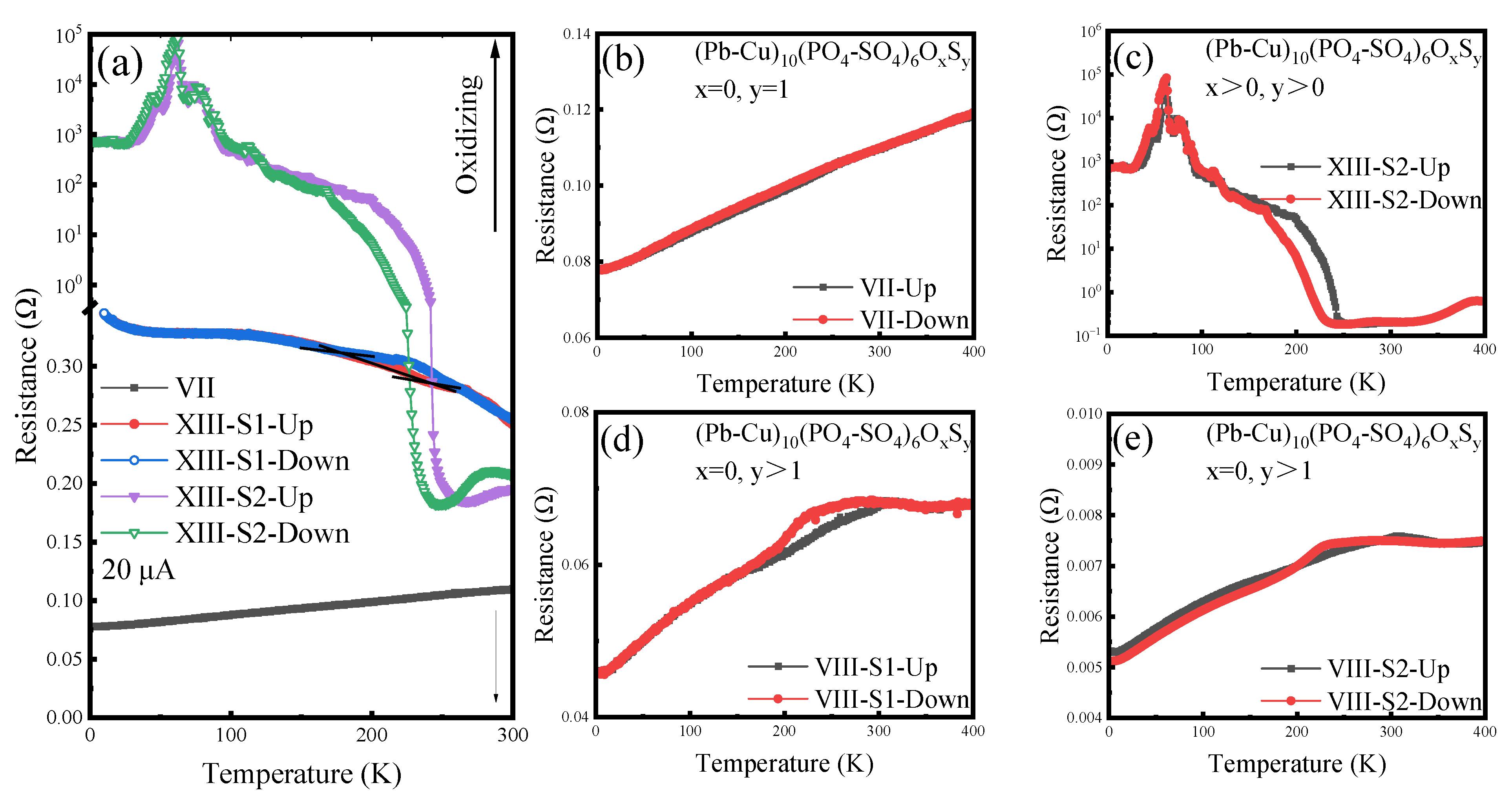
3.4. Distortion and Decomposition Process (XI to XIII)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Details of Syntheses and Challenges
Appendix A.1. Synthesis of Pb10−xCux(PO4)6O
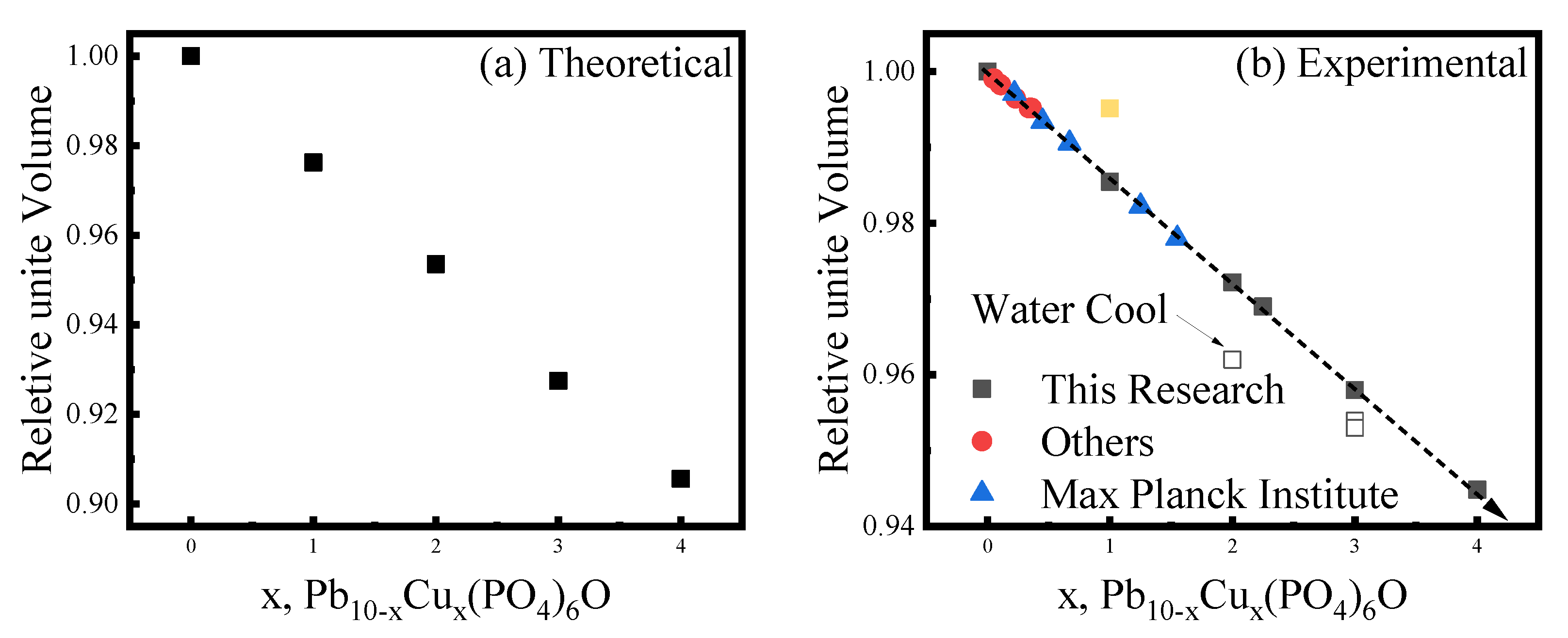
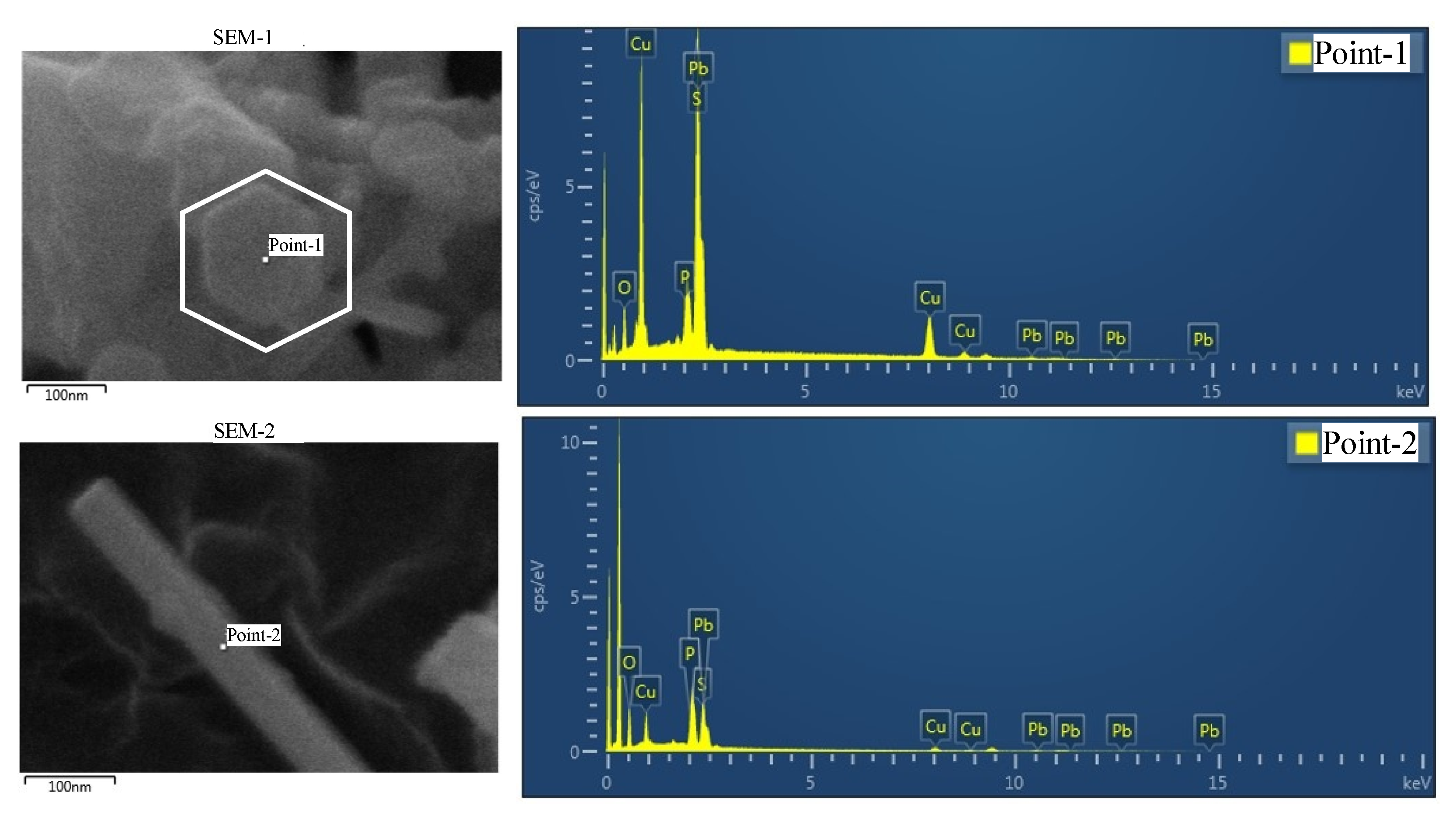
Appendix A.2. Synthesis of (Pb, Cu)10(PO4, SO4)6S1+x
- 1.
- It is imperative that the synthesis commences with copper(II) phosphate, , as the primary precursor. The introduction of copper in the form of copper sulfide (CuS) is to be avoided. This initial step is of fundamental importance. Lee likewise posits that copper(I) phosphide () is a critical starting material.
- 2.
- A stoichiometric excess of copper should be ensured during the synthesis. This promotes the formation of the desired composite of , lead(II) phosphate (), and lead(II) sulfide (PbS). Any resultant excess copper sulfide can be subsequently removed through mineral processing techniques.
- 3.
- A two-step synthesis protocol is mandatory. The initial step involves the formation of the apatite framework, which is then subjected to sulfur doping in the second step. A single-step approach is ineffective as it precludes the successful incorporation of dopants into the apatite structure, leading instead to a product mixture dominated by copper sulfides and lead phosphates.
- 4.
- The aging process holds significantly greater importance than the hydrothermal treatment. The temperature of the hydrothermal stage should not be excessively high. Close observation of the sample’s color evolution during the aging process is a critical indicator.
- 5.
- Achieving precise control over the copper doping concentration is challenging. Consequently, a high-throughput experimental approach is recommended to facilitate the screening of numerous samples and identify those with the desired properties.
Appendix A.3. Rapid Screening
Appendix A.4. Challenges in Repetitive Experiments

Appendix A.5. Challenges on the Uncertainty of Structures
| Apatite | Covellite | ||||||
|---|---|---|---|---|---|---|---|
| Pb | Cu | S | Cu | Pb | S | ||
| 9 | 1 | 6 | 0 | 2 | 0.95 | 0.05 | 1.16 |
| 8 | 2 | 5.5 | 0.5 | 2–3 | |||
| 7 | 3 | 5 | 1 | 2–4 | |||
| 6 | 4 | 4 | 2 | 3–4 | |||
Appendix B. Density Functional Theory Calculations
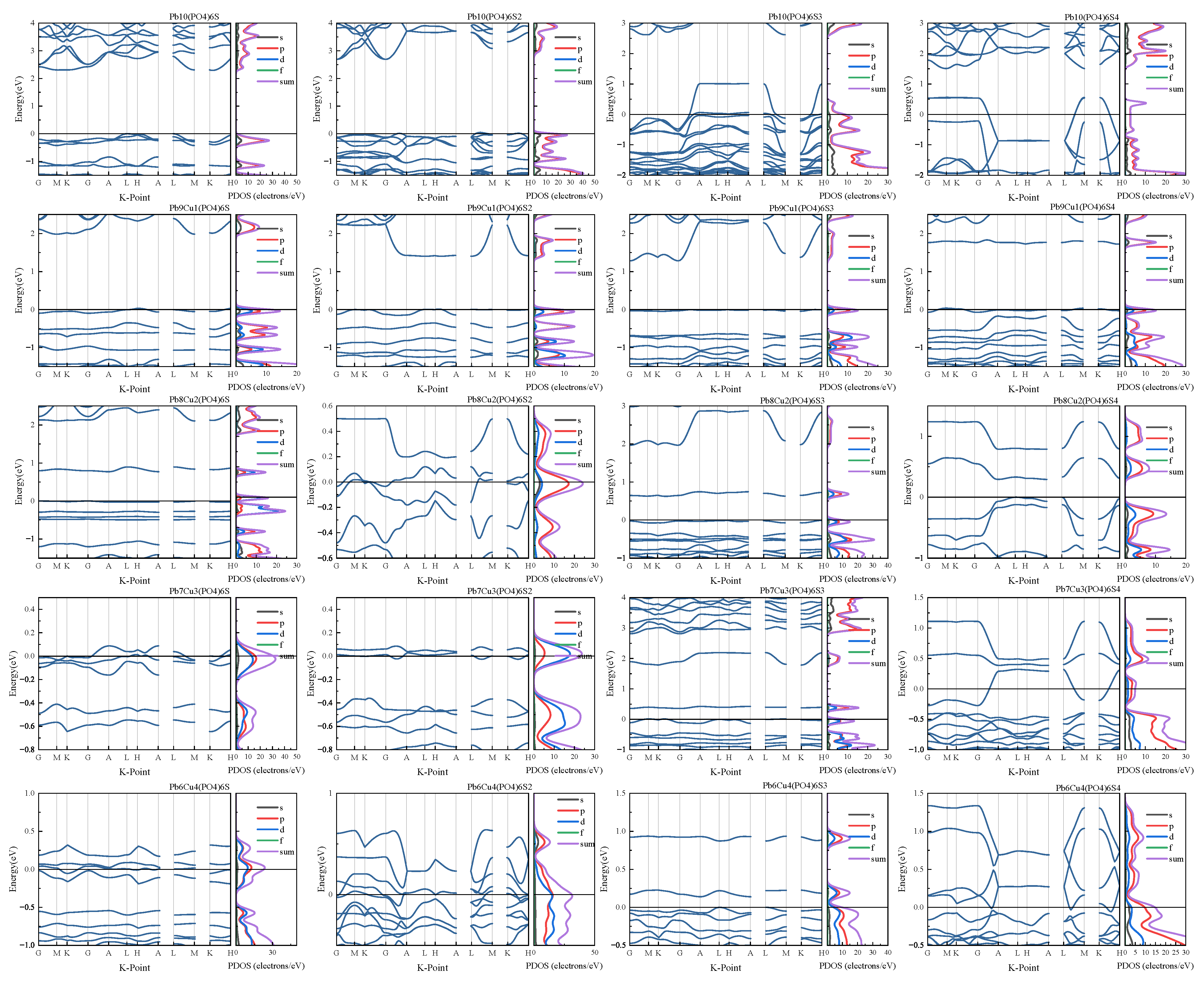
Appendix B.1. Electronic Structure of Variant Apatite
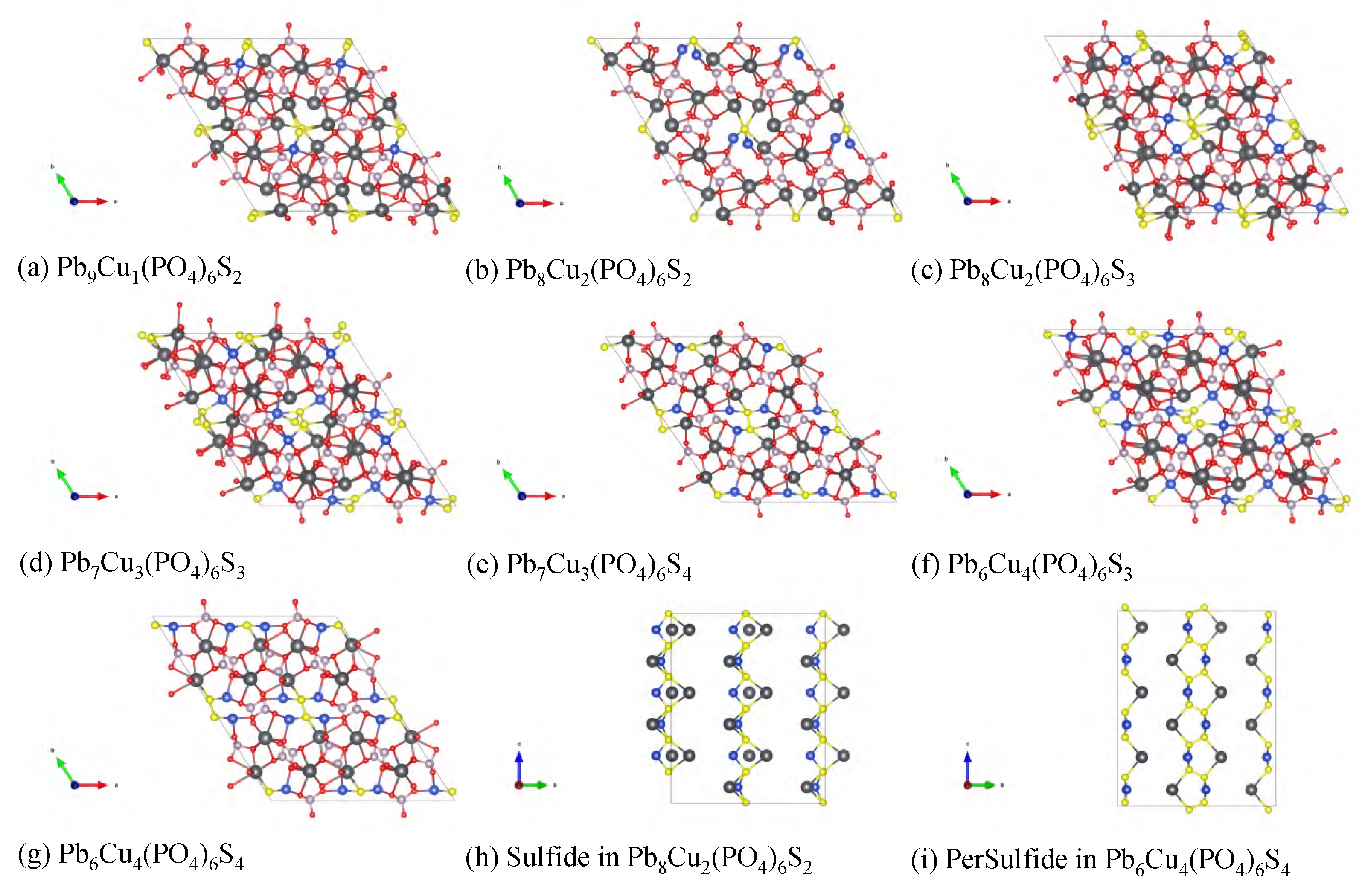

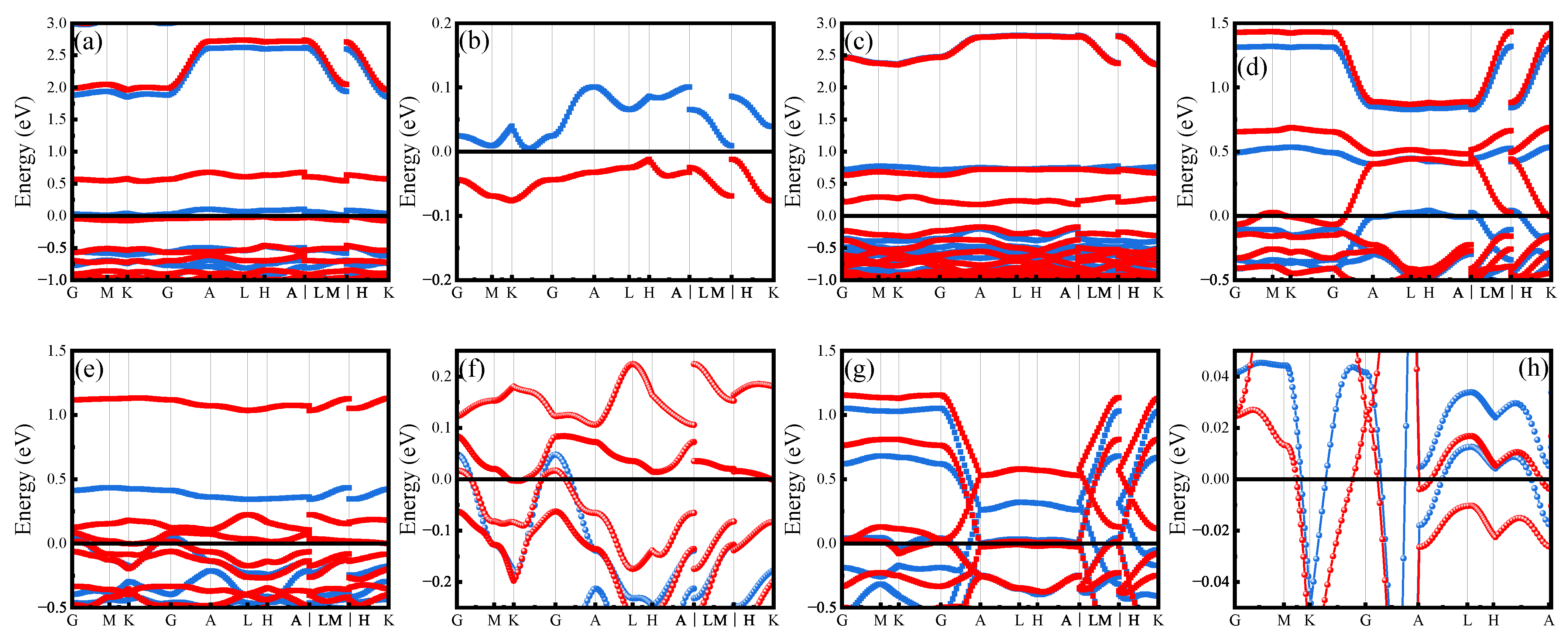
Appendix B.2. High-Throughput Screening of Apatite
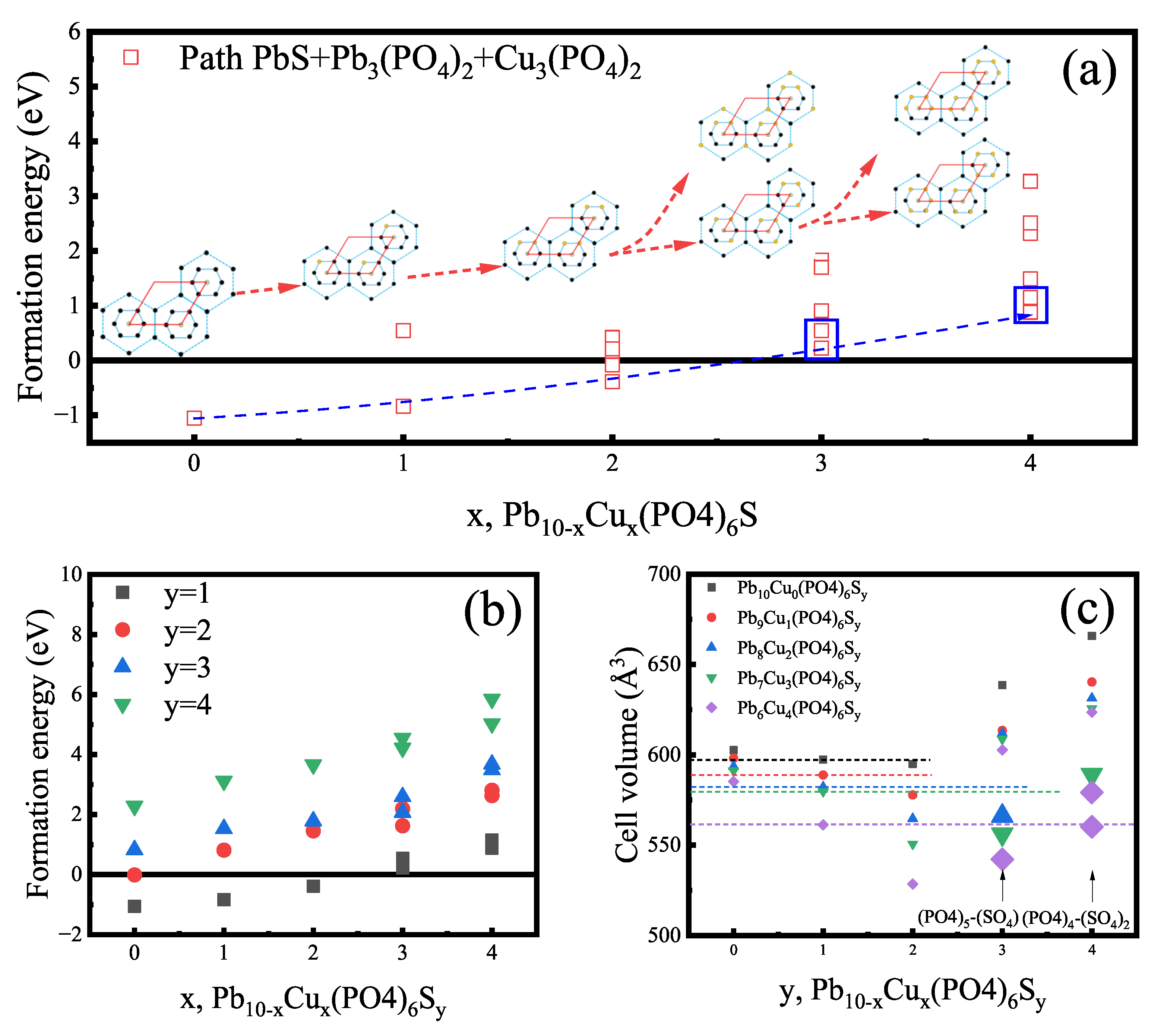
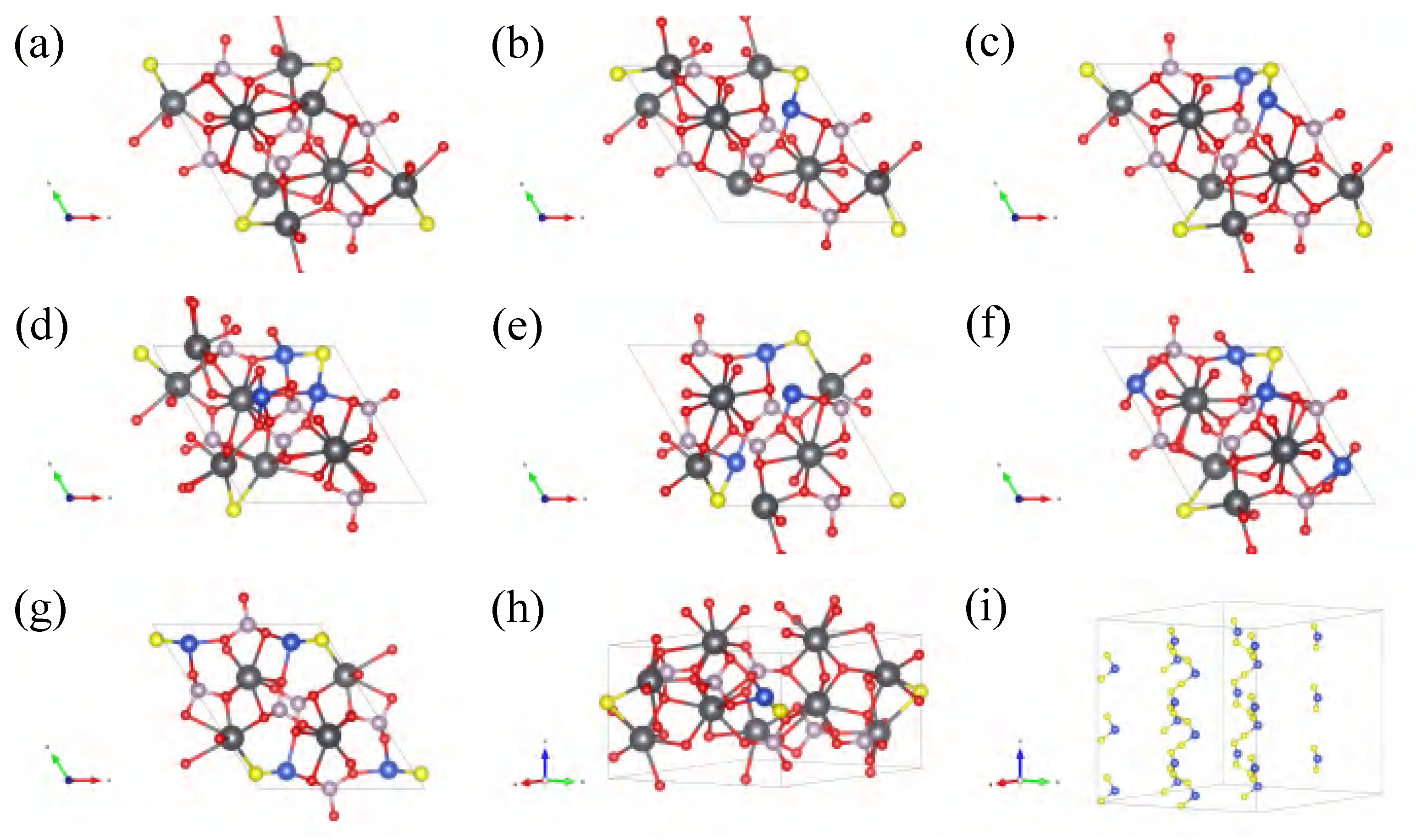
Appendix C. Detail in Lattice Parameters
| Order | a = b (Å) | c (Å) | Magnetic Pro. | Electrical Pro. | Impurities |
|---|---|---|---|---|---|
| I | 9.845 | 7.426 | DM | Insulator | |
| II | 9.846 | 7.425 | DM + SM | Insulator | |
| III | 9.84 | 7.421 | PM | Insulator | |
| IIII | 9.837 | 7.419 | PM + SM | Insulator | |
| V | 9.835 | 7.405 | PM | Insulator | |
| VI | 9.833 | 7.395 | PM + ME | Insulator | |
| VII | 9.851 | 7.401 | PM | Metallic | Covellite |
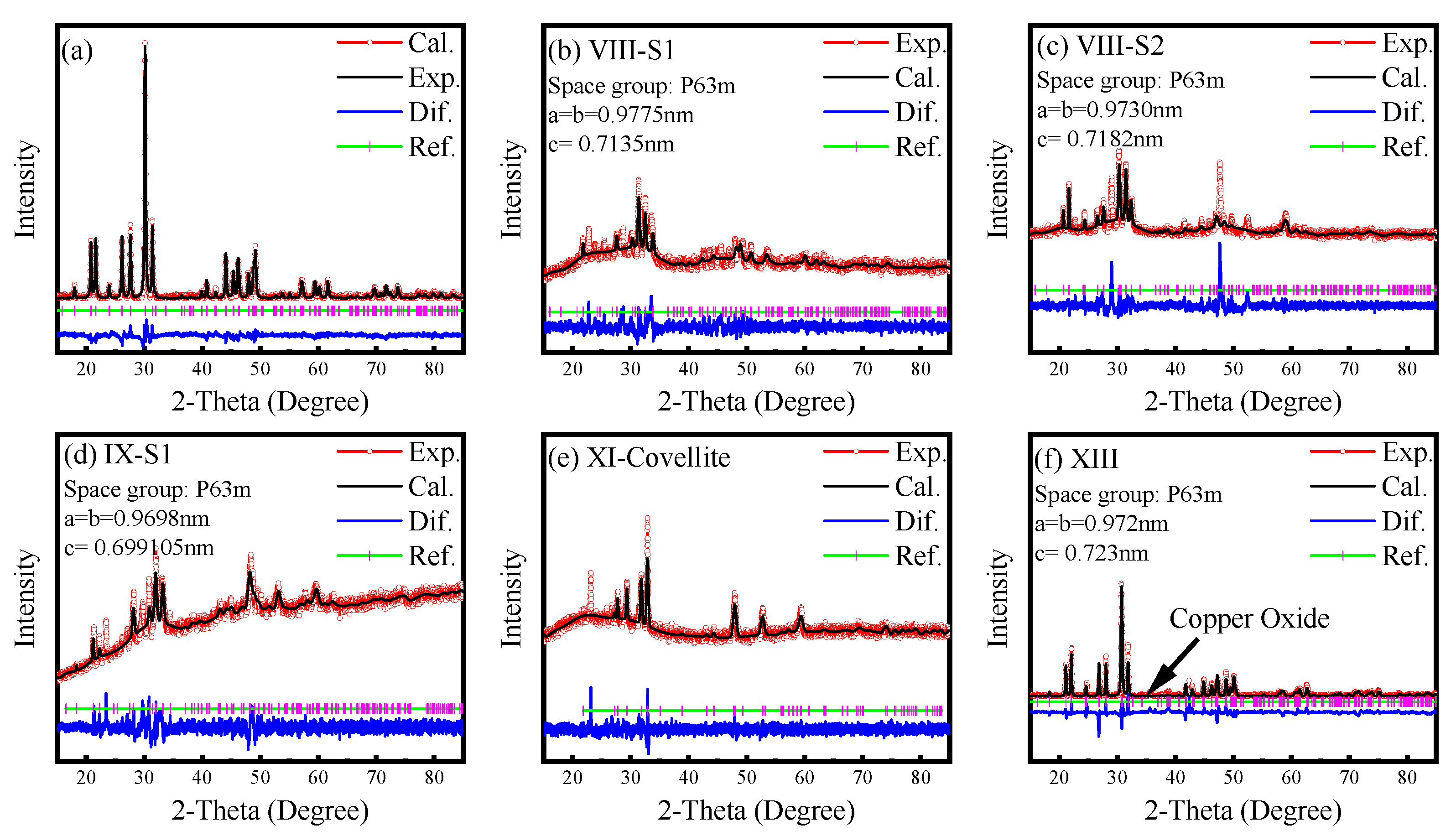
| VIII-S1 | 9.775 | 7.135 | - | Metallic | Covellite |
| VIII-S2 | 9.73 | 7.182 | - | Metallic | Covellite |
| IX-S1 | 9.698 | 6.991 | ME | Metallic | Covellite + Galena |
| IX-S2 | 9.696 | 7.012 | ME | Metallic | Covellite |
| X | 9.699 | 7.001 | ME | SC1 | Galena + Covellite |
| XI | Covellite | ME | SC2 | Galena | |
| XII | Phosphate | FM | Semiconductor | Covellite + galena | |
| XIII | 9.72 | 7.23 | MIT | Oxide | |
| XIII | 9.783 | 7.315 | PM | semiconcudtor | Oxide and sulfate |
| a (Å) | b (Å) | c (Å) | Space Group | ||
| X | 9.70 | 9.675 | 0.699 | P1 | |
| Lattice Type | |||||
| Triclinic | |||||
Appendix D. Detail in Test by Agilent

Appendix E. Detail in Secondary Processing
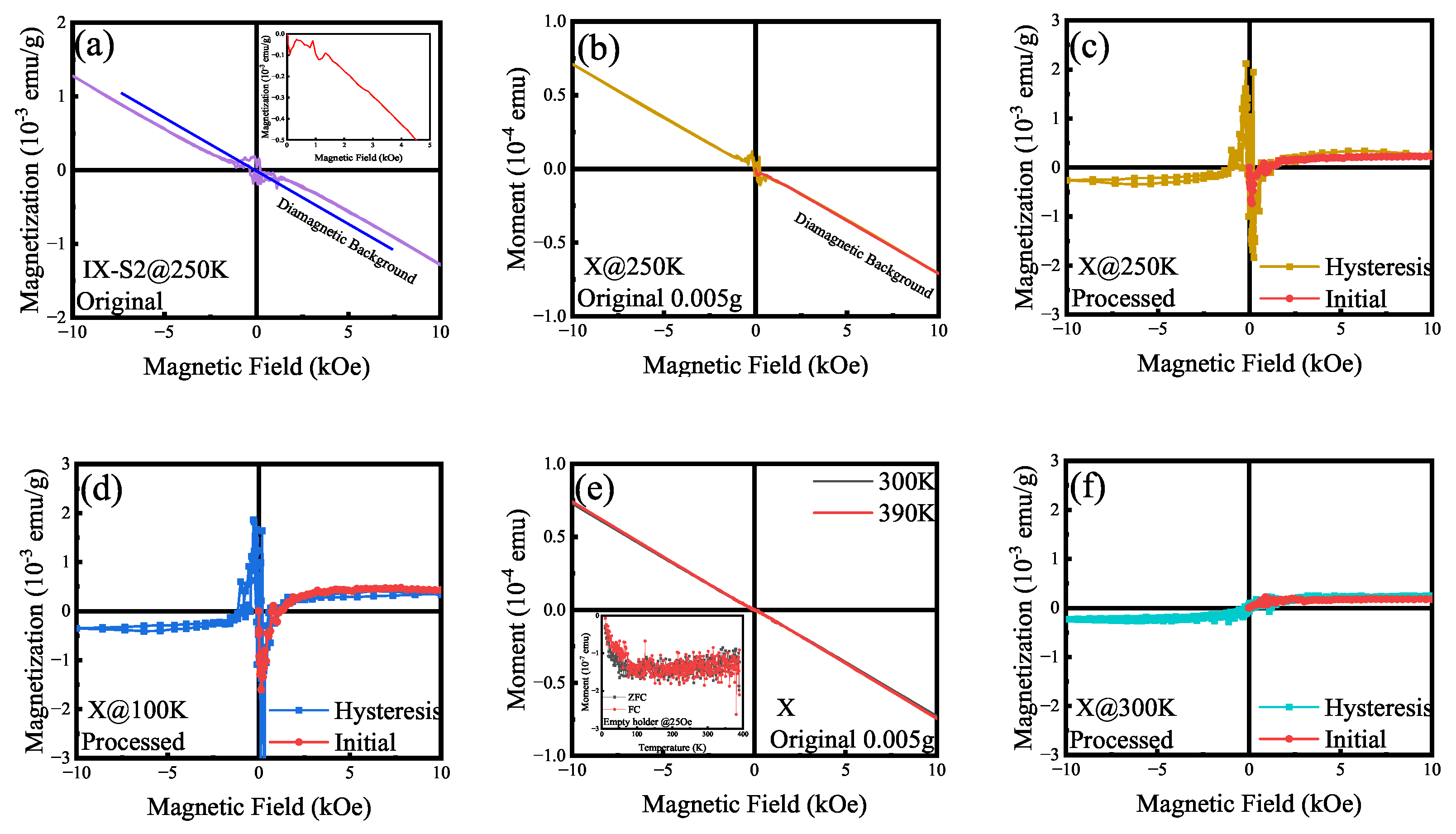
Appendix F. Authenticity of the Data

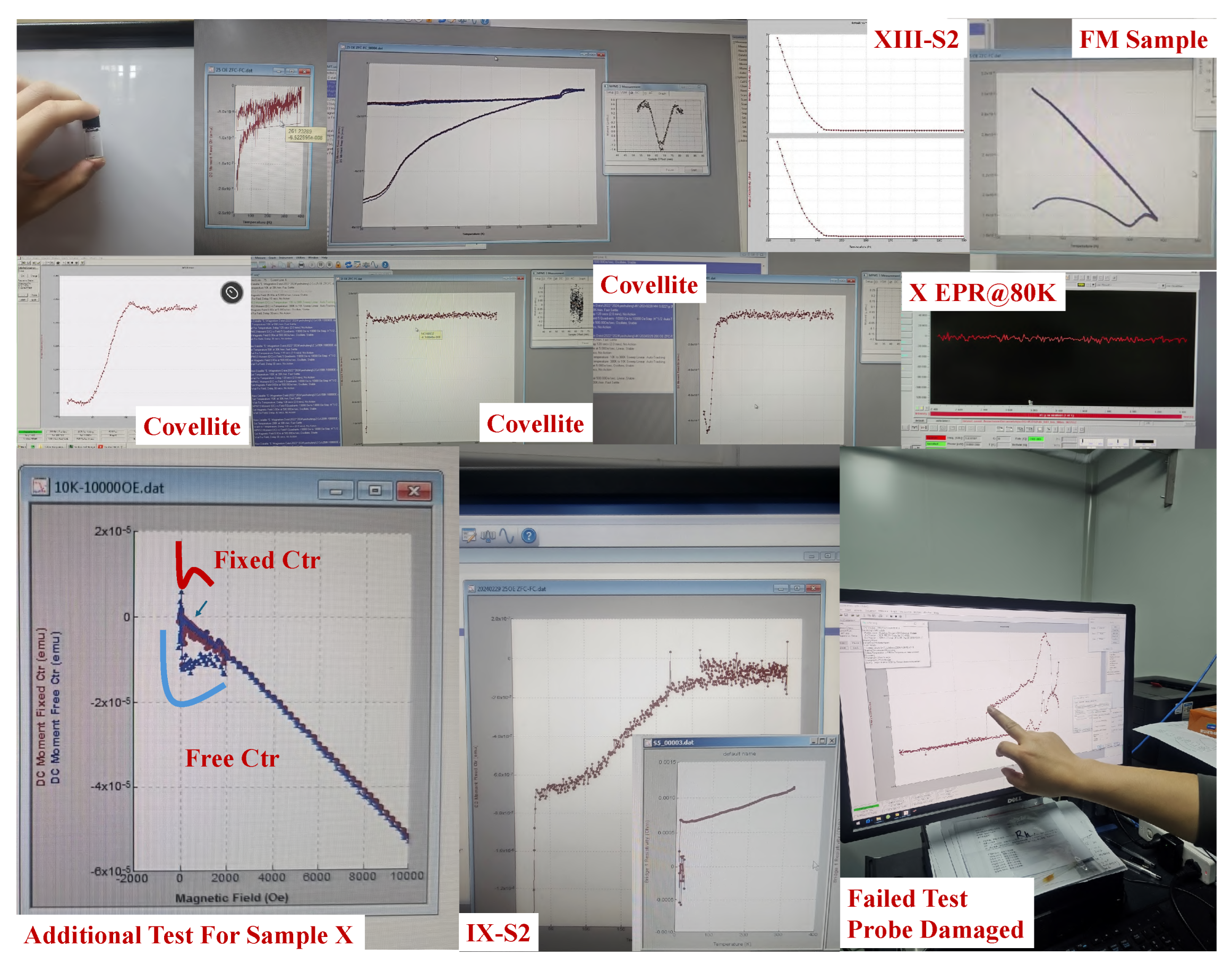

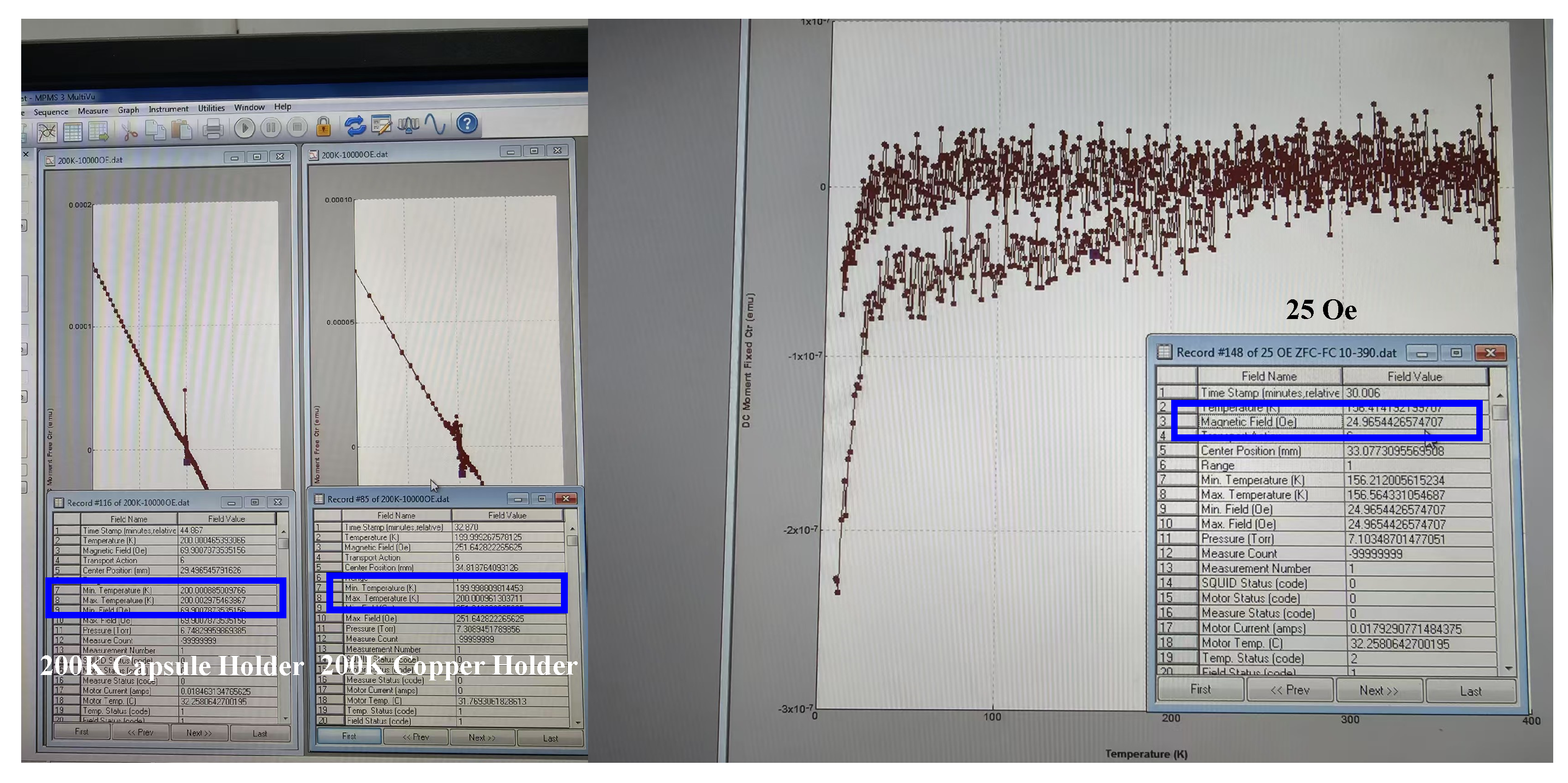
References
- Emery, V.J. Theory of high-Tc superconductivity in oxides. Phys. Rev. Lett. 1987, 58, 2794–2797. [Google Scholar] [CrossRef]
- Zhang, F.C.; Rice, T.M. Effective Hamiltonian for the superconducting Cu oxides. Phys. Rev. B 1988, 37, 3759–3761. [Google Scholar] [CrossRef]
- Shi, J.; Zhu, Y. Ionic-bond-driven atom-bridged room-temperature Cooper pairing in cuprates and nickelates: A theoretical framework supported by 32 experimental evidences. arXiv 2025, arXiv:2503.13104. [Google Scholar]
- Lee, S.; Kim, J.H.; Kwon, Y.W. The First Room-Temperature Ambient-Pressure Superconductor. arXiv 2023, arXiv:2307.12008. [Google Scholar]
- Wu, H.; Yang, L.; Xiao, B.; Chang, H. Successful growth and room temperature ambient-pressure magnetic levitation of LK-99. arXiv 2023, arXiv:2308.01516. [Google Scholar] [CrossRef]
- Krivovichev, S.V.; Engel, G. The Crystal Structure of Pb10(PO4)6O Revisited: The Evidence of Superstructure. Crystals 2023, 13, 1371. [Google Scholar] [CrossRef]
- Huang, Z.; Ni, X.; Huang, H.; Tu, Y.; Gu, Z.; Zeng, S. Exceptional metal–semiconductor–metal transition of lead apatites via oxygen defect tuning. Phys. Chem. Chem. Phys. 2024, 26, 3029–3035. [Google Scholar] [CrossRef]
- Mourachkine, A. Route to Room-Temperature Superconductivity from a Practical Point of View. arXiv 2007, arXiv:0704.2188. [Google Scholar] [CrossRef]
- Imaizumi, K.; Toyoura, K.; Nakamura, A.; Matsunaga, K. Strong correlation in 1D oxygen-ion conduction of apatite-type lanthanum silicate. J. Phys. Condens. Matter 2015, 27, 365601. [Google Scholar] [CrossRef]
- Kim, H.T. Analysis of the diverging effective mass in YaBa2Cu3O6+x for high-Tc mechanism and pairing symmetry. Int. J. Mod. Phys. B 2018, 32, 1840031. [Google Scholar] [CrossRef]
- Yang, W.; Pang, Z.; Ren, Z. One-step synthesis of Cu-doped Pb10(PO4)6Cl2 apatite: A wide-gap semiconductor. Inorg. Chem. Front. 2024, 11, 5858–5865. [Google Scholar] [CrossRef]
- Tao, K.; Chen, R.; Yang, L.; Gao, J.; Xue, D.; Jia, C. The 1/4 occupied O atoms induced ultraflat band and the one dimensional channels in the Pb10−xCux(PO4)6O4 (x = 0, 0.5) crystal. arXiv 2023, arXiv:2308.03218. [Google Scholar]
- Liu, L.; Ren, X.; Hu, J. Metallic states in Pb10(PO4)6O induced by the Cu/O-insertions and carrier doping. arXiv 2023, arXiv:2308.07345. [Google Scholar]
- Zhu, S.; Wu, W.; Li, Z.; Luo, J. First-order transition in LK-99 containing Cu2S. Matter 2023, 6, 4401–4407. [Google Scholar] [CrossRef]
- Sukhenko, I.V.; Karbivskyy, V.L. Reflecting on the LK-99 fervour: Insights and future prospects. J. Phys. Condens. Matter 2024, 37, 083002. [Google Scholar] [CrossRef]
- Baskaran, G. Broad Band Mott Localization is all you need for Hot Superconductivity: Atom Mott Insulator Theory for Cu-Pb Apatite. arXiv 2023, arXiv:2308.01307. [Google Scholar] [CrossRef]
- Qi, M.L.; He, K.; Huang, Z.N.; Shahbazian-Yassar, R.; Xiao, G.Y.; Lu, Y.P.; Shokuhfar, T. Hydroxyapatite fibers: A review of synthesis methods. JOM 2017, 69, 1354–1360. [Google Scholar] [CrossRef]
- Zhang, H.G.; Zhu, Q. Preparation of fluoride-substituted hydroxyapatite by a molten salt synthesis route. J. Mater. Sci. Mater. Med. 2006, 17, 691–695. [Google Scholar] [CrossRef]
- Wang, P.; Liu, X.; Ge, J.; Ji, C.; Ji, H.; Liu, Y.; Ai, Y.; Ma, G.; Qi, S.; Wang, J. Ferromagnetic and insulating behavior in both half magnetic levitation and non-levitation LK-99 like samples. Quantum Front. 2023, 2, 10. [Google Scholar] [CrossRef]
- Konecke, B.A.; Fiege, A.; Simon, A.C.; Linsler, S.; Holtz, F. An experimental calibration of a sulfur-in-apatite oxybarometer for mafic systems. Geochim. Cosmochim. Acta 2019, 265, 242–258. [Google Scholar] [CrossRef]
- Jung, S.H.; Han, S.H.; Lee, J.S.; Kim, Y.J. Synthesis and Phase Transformation of Ca10(PO4)6S Sulfoapatite by Solid-state Reaction with Sulfur Vapor. Synth. React. Inorg. Met.-Org. Nano-Met. Chem. 2008, 38, 303–306. [Google Scholar] [CrossRef]
- Parat, F.; Holtz, F. Sulfur partitioning between apatite and melt and effect of sulfur on apatite solubility at oxidizing conditions. Contrib. Mineral. Petrol. 2004, 147, 201–212. [Google Scholar] [CrossRef]
- Yazawa, A. Thermodynamic considerations of copper smelting. Can. Metall. Q. 1974, 13, 443–453. [Google Scholar] [CrossRef]
- Ding, Q.P.; Sun, Y.; Hou, Q.; Wei, W.; Zhou, X.; Wang, X.; Shi, Z.; Furukawa, Y. Microscopic Characterization of Pb10−xCux(PO4)6O by 31P and 63/65Cu NMR Measurements. J. Compos. Sci. 2025, 9, 377. [Google Scholar] [CrossRef]
- Jiang, Y.; Lee, S.B.; Herzog-Arbeitman, J.; Yu, J.; Feng, X.; Hu, H.; Călugăru, D.; Brodale, P.S.; Gormley, E.L.; Vergniory, M.G.; et al. Pb9Cu(PO4)6(OH)2: Phonon bands, localized flat-band magnetism, models, and chemical analysis. Phys. Rev. B 2023, 108, 235127. [Google Scholar] [CrossRef]
- Huo, M.; Liu, Z.; Sun, H.; Li, L.; Lui, H.; Huang, C.; Liang, F.; Shen, B.; Wang, M. Synthesis and properties of La1−xSrxNiO3 and La1-xSrxNiO2. Chin. Phys. B 2022, 31, 107401. [Google Scholar] [CrossRef]
- Sun, H.; Huo, M.; Hu, X.; Li, J.; Liu, Z.; Han, Y.; Tang, L.; Mao, Z.; Yang, P.; Wang, B.; et al. Signatures of superconductivity near 80 K in a nickelate under high pressure. Nature 2023, 621, 493–498. [Google Scholar] [CrossRef] [PubMed]
- Hou, Q.; Wei, W.; Zhou, X.; Wang, X.; Wang, T.; Sun, Y.; Shi, Z. Synthesis, transport and magnetic properties of Cu-doped apatite Pb10-Cu (PO4)6O. Matter 2023, 6, 4408–4418. [Google Scholar] [CrossRef]
- Kim, Y.; Konecke, B.; Fiege, A.; Simon, A.; Becker, U. An ab-initio study of the energetics and geometry of sulfide, sulfite, and sulfate incorporation into apatite: The thermodynamic basis for using this system as an oxybarometer. Am. Mineral. 2017, 102, 1646–1656. [Google Scholar] [CrossRef]
- Kim, Y.; Konecke, B.; Simon, A.; Fiege, A.; Becker, U. An ab-initio study on the thermodynamics of disulfide, sulfide, and bisulfide incorporation into apatite and the development of a more comprehensive temperature, pressure, pH, and composition-dependent model for ionic substitution in minerals. Am. Mineral. 2022, 107, 1995–2007. [Google Scholar] [CrossRef]
- Liao, T.; Sasaki, T.; Suehara, S.; Sun, Z. Position preference and diffusion path of an oxygen ion in apatite-type lanthanum silicate La9.33Si6O26: A density functional study. J. Mater. Chem. 2011, 21, 3234–3242. [Google Scholar] [CrossRef]
- Qiu, Z.; Wang, Q.; Fu, L.; Li, R.; Xu, T.l.; Wen, X.; Lewis, J.P. Dual-Anion Vacancies in Apatite Systems. ACS Appl. Electron. Mater. 2022, 4, 3655–3664. [Google Scholar] [CrossRef]
- Slater, P.; Sansom, J.; Tolchard, J. Development of apatite-type oxide ion conductors. Chem. Rec. 2004, 4, 373–384. [Google Scholar] [CrossRef] [PubMed]
- Tolchard, J.R.; Islam, M.S.; Slater, P.R. Defect chemistry and oxygen ion migration in the apatite-type materials La9.33Si6O26 and La8Sr2Si6O26. J. Mater. Chem. 2003, 13, 1956–1961. [Google Scholar] [CrossRef]
- Taitai, A.; Lacout, J. On the coupled introduction of Eu3+ and S2− ions into strontium apatites. J. Phys. Chem. Solids 1989, 50, 851–855. [Google Scholar] [CrossRef]
- Luo, C.; Shen, Z.; Li, X. Enhanced phytoextraction of Cu, Pb, Zn and Cd with EDTA and EDDS. Chemosphere 2005, 59, 1–11. [Google Scholar] [CrossRef]
- Morrison, J.L.; Kirkland, C.L.; Fiorentini, M.; Beresford, S.; Polito, P. An apatite to unravel petrogenic processes of the Nova-Bollinger Ni-Cu magmatic sulfide deposit, Western Australia. Precambrian Res. 2022, 369, 106524. [Google Scholar] [CrossRef]
- Wang, M.L.; Peng, Y.H.; Liao, J.H.; Yang, X.B.; Yao, Y.; Zhao, Y.J. Impact of sulfur doping on copper-substituted lead apatite. Phys. Rev. B 2024, 110, 104109. [Google Scholar] [CrossRef]
- Lacout, J.L.; Nadir, S. L’Apatite Sulfo-Vanadocalcique: Preparation, Comportement Thermique. Phosphorus Sulfur Silicon Relat. Elem. 1989, 46, 105–112. [Google Scholar] [CrossRef]
- Kim, S.W.; Wang, K.; Chen, S.; Conway, L.J.; Pascut, G.L.; Errea, I.; Pickard, C.J.; Monserrat, B. On the dynamical stability of copper-doped lead apatite. npj Comput. Mater. 2024, 10, 16. [Google Scholar] [CrossRef]
- Singh, R.J.; Sharma, P.K.; Singh, A.; Khan, S. EPR spectra of deoxygenated high Tc superconductors. Phys. C Supercond. 2001, 356, 285–296. [Google Scholar] [CrossRef]
- Shimizu, H.; Fujiwara, K.; Hatada, K. Magnetic and electronic properties of La2−xSrxCuO4 as studied by EPR of ER spin probes. Phys. C Supercond. 1997, 288, 190–198. [Google Scholar] [CrossRef]
- Miao, Y.; Tian, W.; Han, J.; Li, N.; Chen, D.; Xu, Q.; Lu, J. Oxygen vacancy-induced hydroxyl dipole reorientation in hydroxyapatite for enhanced piezocatalytic activity. Nano Energy 2022, 100, 107473. [Google Scholar] [CrossRef]
- Liu, J.; He, C.; Huang, W.; Zhen, Z.; Chen, G.; Luo, T.; Qiao, X.; Yao, Y.; Ma, D. Strange memory effect of low-field microwave absorption in copper-substituted lead apatite. arXiv 2023, arXiv:2312.10391. [Google Scholar]
- Li, P.; Jiang, K.; Hu, J. Paramagnetic contribution in superconductors with different-mass Cooper pairs. Phys. Rev. B 2024, 110, 094517. [Google Scholar] [CrossRef]
- Si, L.; Held, K. Electronic structure of the putative room-temperature superconductor. Phys. Rev. B 2023, 108, L121110. [Google Scholar] [CrossRef]
- Kwon, S.J.; Jung, D.Y. A novel hybrid of high-Tc cuprate and paramagnetic organic radical. Solid State Commun. 2004, 130, 287–291. [Google Scholar] [CrossRef]
- Hyunsoo, S. EPR Spectrum of the High-Temperature Superconductor YBa2Cu3O7−x Doped with Ytterbium. Bull. Korean Chem. Soc. 1989, 10, 23–26. [Google Scholar]
- Puphal, P.; Akbar, M.Y.P.; Hepting, M.; Goering, E.; Isobe, M.; Nugroho, A.A.; Keimer, B. Single crystal synthesis, structure, and magnetism of Pb10−xCux (PO4)6O. APL Mater. 2023, 11, 101128. [Google Scholar] [CrossRef]
- Kim, S.W.; Haule, K.; Pascut, G.L.; Monserrat, B. Non-Fermi liquid to charge-transfer Mott insulator in flat bands of copper-doped lead apatite. arXiv 2024, arXiv:2408.05277. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, Z.; Liu, H.; Zhong, J.; Qi, X. Defect engineering the electronic and optoelectronic properties of heterostructure of MoSSe/PbS (111). J. Phys. Condens. Matter 2023, 35, 365003. [Google Scholar] [CrossRef]
- Garifullin, I.A. EPR Study of Superconductors. J. Low Temp. Phys. 2014, 178, 243–271. [Google Scholar] [CrossRef]
- Konecke, B.A.; Fiege, A.; Simon, A.C.; Parat, F.; Stechern, A. Co-variability of S6+, S4+, and S2− in apatite as a function of oxidation state: Implications for a new oxybarometer. Am. Mineral. 2017, 102, 548–557. [Google Scholar] [CrossRef]
- Chowdhury, P.; Brounce, M.; Boyce, J.W.; McCubbin, F.M. The Oxidation State of Sulfur in Apatite of Martian Meteorite—Shergotty. J. Geophys. Res. Planets 2023, 128, e2022JE007634. [Google Scholar] [CrossRef]
- Piotrowski, A.; Kahlenberg, V.; Fischer, R.X. The Solid Solution Series of the Sulfate Apatite System Na6.45Ca3.55(SO4)6(FxCl1−x)1.55. J. Solid State Chem. 2002, 163, 398–405. [Google Scholar] [CrossRef]
- Deng, L.; Wang, B.; Halbert, C.; Schulze, D.J.; Gooch, M.; Bontke, T.; Kuo, T.W.; Shi, X.; Song, S.; Salke, N.; et al. Creation, stabilization, and investigation at ambient pressure of pressure-induced superconductivity in Bi0.5Sb1.5Te3. Proc. Natl. Acad. Sci. USA 2025, 122, e2423102122. [Google Scholar] [CrossRef]
- Jang, H.B.; Lim, J.S.; Yang, C.H. Film-thickness-driven superconductor to insulator transition in cuprate superconductors. Sci. Rep. 2020, 10, 3236. [Google Scholar] [CrossRef] [PubMed]
- Dos Santos, C.A.M.; Da Luz, M.S.; Yu, Y.K.; Neumeier, J.J.; Moreno, J.; White, B.D. Electrical transport in single-crystalline Li0.9Mo6O17: A two-band Luttinger liquid exhibiting Bose metal behavior. Phys. Rev. B—Condensed Matter Mater. Phys. 2008, 77, 193106. [Google Scholar] [CrossRef]
- Kremen, A.; Aviv, H.; Tischler, Y.R.; Sharoni, A. Evidence for Proximity Effect in Superconductor–Organic Semiconductor–Superconductor Stacked Devices. Appl. Sci. 2025, 15, 85. [Google Scholar] [CrossRef]
- Tagirov, L. Proximity effect and superconducting transition temperature in superconductor/ferromagnet sandwiches. Phys. C Supercond. 1998, 307, 145–163. [Google Scholar] [CrossRef]
- Raveau, B.; Sarkar, T. Superconducting-like behaviour of the layered Chalcogenides CuS and CuSe below 40 K. Solid State Sci. 2011, 13, 1874–1878. [Google Scholar] [CrossRef]
- Hanawa, M.; Muraoka, Y.; Tayama, T.; Sakakibara, T.; Yamaura, J.; Hiroi, Z. Superconductivity at 1 K in Cd2Re2O7. Phys. Rev. Lett. 2001, 87, 187001. [Google Scholar] [CrossRef]
- Abdel-Aziz, A.; Afifi, H.; Hager, I.; Aal, N.; Naqib, S. Unusual Enhancement of Normal and Superconducting State Properties of (100-x)YBa2Cu3O7-δ + xNi (x = 1, 2.5, 5, 7.5, 10, and 15 wt%) Composites with Low Level of Ni Additives. J. Supercond. Nov. Magn. 2020, 33, 661–674. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, X.; Zhao, X.; Li, J.; Herng, T.S.; Xu, H.; Lin, F.; Lyu, P.; Peng, X.; Yu, W.; et al. Imprinting ferromagnetism and superconductivity in single atomic layers of molecular superlattices. Adv. Mater. 2020, 32, 1907645. [Google Scholar] [CrossRef]
- Anoop, T.; Eloise, D.; Kalaivanan, N.; Guillaume, R.; Marcus, S.; Fanny, R.; Cyriaque, G.; Marc, D.; Thomas, W.E. Large Enhancement of Ferromagnetism under a Collective Strong Coupling of YBCO Nanoparticles. Nano Letters 2021, 21, 4365–4370. [Google Scholar] [CrossRef]
- Meng, X.; Kleinsasser, J.M.; Richards, J.P.; Tapster, S.R.; Jugo, P.J.; Simon, A.C.; Kontak, D.J.; Robb, L.; Bybee, G.M.; Marsh, J.H.; et al. Oxidized sulfur-rich arc magmas formed porphyry Cu deposits by 1.88 Ga. Nat. Commun. 2021, 12, 2189. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C.; Ou, Q.; Lv, P.; Huang, W.; Zou, Y. Biotite and apatite geochemistry of granites from the Caledonian Debao Sn-Cu deposit, South China: Implications for petrogenesis and mineralization. Ore Geol. Rev. 2025, 179, 106510. [Google Scholar] [CrossRef]
- Ogawa, K.; Tolborg, K.; Walsh, A. Models of oxygen occupancy in lead phosphate apatite Pb10(PO4)6O. ACS Energy Lett. 2023, 8, 3941–3944. [Google Scholar] [CrossRef]
- Xu, Y.; Sheng, Y.; Yang, Y.f. Mechanism of the insulator-to-metal transition and superconductivity in the spin liquid candidate NaYbSe2 under pressure. npj Quantum Mater. 2022, 7, 21. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, X.; Li, X.; Tang, W.; Li, X.; Wang, X.; Li, F.; Li, L.; Zhou, Q. Unveiling a Novel Insulator-to-Metal Transition in La2NiO4+δ: Challenging High-Temperature Superconductivity Claimed for Single-Layer Lanthanum Nickelates. Chin. Phys. Lett. 2024, 41, 097402. [Google Scholar] [CrossRef]
- Han, K.; Wang, H.; Wu, L.; Cao, Y.; Qi, D.C.; Li, C.; Huang, Z.; Li, X.; Renshaw Wang, X. Reversible modulation of metal–insulator transition in VO2 via chemically induced oxygen migration. Appl. Phys. Lett. 2021, 119, 133102. [Google Scholar] [CrossRef]
- Yang, C.; Liu, H.; Liu, Y.; Wang, J.; Qiu, D.; Wang, S.; Wang, Y.; He, Q.; Li, X.; Li, P.; et al. Signatures of a strange metal in a bosonic system. Nature 2022, 601, 205–210. [Google Scholar] [CrossRef]
- Krivovichev, S.V.; Burns, P.C. Crystal chemistry of lead oxide phosphates: Crystal structures of Pb4O(PO4)2, Pb8O5(PO4)2 and Pb10(PO4)6O. Z. Krist.—Cryst. Mater. 2003, 218, 357–365. [Google Scholar] [CrossRef]
- Ben Moussa, S.; Bachoua, H.; Brigui, N.; Badraoui, B. Synthesis, characterization and structural study of lead hydroxyapatite Pb10−xMx(PO4)6(OH)2 (M = Zn, Cu). J. Mater. Environ. Sci. 2016, 7, 4754–4766. [Google Scholar]
- Zhang, Y.; Liu, C.; Zhu, X.; Wen, H.H. Ferromagnetism and insulating behavior with a logarithmic temperature dependence of resistivity in Pb10−xCux(PO4)6O. Sci. China Physics, Mech. Astron. 2023, 67, 217413. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.; Im, S.; An, S.; Kwon, Y.W.; Auh, K.H. Consideration for the development of room-temperature ambient-pressure superconductor (LK-99). J. Korean Cryst. Growth Cryst. Technol. 2023, 33, 61–70. [Google Scholar]
- Wu, M.K.; Ashburn, J.R.; Torng, C.; Hor, P.H.; Meng, R.L.; Gao, L.; Huang, Z.J.; Wang, Y.; Chu, a. Superconductivity at 93 K in a new mixed-phase Y-Ba-Cu-O compound system at ambient pressure. Phys. Rev. Lett. 1987, 58, 908. [Google Scholar] [CrossRef]
- Hafner, J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. J. Comput. Chem. 2008, 29, 2044–2078. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Yu, T.; Li, J.; Wang, J.; Lai, J.; Sun, Y.; Chen, X.Q.; Liu, P. Symmetry breaking induced insulating electronic state in Pb9Cu(PO 4)6O. Phys. Rev. B 2023, 108, L161101. [Google Scholar] [CrossRef]
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43–50. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of superconductivity. Phys. Rev. 1957, 108, 1175. [Google Scholar] [CrossRef]
- Mathur, N.; Grosche, F.; Julian, S.; Walker, I.; Freye, D.; Haselwimmer, R.; Lonzarich, G. Magnetically mediated superconductivity in heavy fermion compounds. Nature 1998, 394, 39–43. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Krist.—Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Stampfl, C.; Van de Walle, C.G. Density-functional calculations for III-V nitrides using the local-density approximation and the generalized gradient approximation. Phys. Rev. B 1999, 59, 5521. [Google Scholar] [CrossRef]
- Pellegrini, C.; Sanna, A. Ab initio methods for superconductivity. Nat. Rev. Phys. 2024, 6, 509–523. [Google Scholar] [CrossRef]
- Choudhary, K.; Garrity, K. Designing high-TC superconductors with BCS-inspired screening, density functional theory, and deep-learning. npj Comput. Mater. 2022, 8, 244. [Google Scholar] [CrossRef]

| Target: | ||||||
|---|---|---|---|---|---|---|
| Order | Step 1 | Product 1 | Step 2 | Temp. (°C) | Chelating Agent | Atmosphere |
| I | H | A | R | 900 | EDTA | Air |
| II | H | A | R | 900 | EDTA | Air |
| III | H | A | R | 500 | — | Air |
| IV | H | A | R | 500 | — | Air |
| V | H | A | R | 500 | — | Air |
| VI | H | B | R | 500 | — | |
| Target: (Pb,Cu)10(, | ||||||
| Order | Step 1 | Product 1 | Step 2 | SIC (mol/L) | Period (h) | pH (@ 25 °C) |
| VII | H | C | — | — | — | 7–8 |
| VIII | H | C | H | 0.1 | 24 | 7–8 |
| IX | H | C | H | 0.2 | 24 | 7–8 |
| X | H | C | H | 0.2 | 24 | 7–8 |
| XI | H | C | H | 0.3 | 24 | 7–8 |
| Target: (Pb,Cu)10−z (, | ||||||
| Order | Step 1 | Product 1 | Step 2 | Temp. (°C) | Period (h) | Atmosphere |
| XII | H | D | — | — | — | — |
| XIII | H | C | R | 300 | 3 | Air |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wu, H.; Zhao, Y.; Tao, K.; Wu, Z.; Geng, Z.; Wang, T.; Ye, S.; Chen, N. Physical Zoo in Pb-Cu-P-S-O Apatite. Materials 2025, 18, 4728. https://doi.org/10.3390/ma18204728
Wang H, Wu H, Zhao Y, Tao K, Wu Z, Geng Z, Wang T, Ye S, Chen N. Physical Zoo in Pb-Cu-P-S-O Apatite. Materials. 2025; 18(20):4728. https://doi.org/10.3390/ma18204728
Chicago/Turabian StyleWang, Hongyang, Hao Wu, Yijing Zhao, Kun Tao, Zhixing Wu, Zhihui Geng, Tianbao Wang, Shufeng Ye, and Ning Chen. 2025. "Physical Zoo in Pb-Cu-P-S-O Apatite" Materials 18, no. 20: 4728. https://doi.org/10.3390/ma18204728
APA StyleWang, H., Wu, H., Zhao, Y., Tao, K., Wu, Z., Geng, Z., Wang, T., Ye, S., & Chen, N. (2025). Physical Zoo in Pb-Cu-P-S-O Apatite. Materials, 18(20), 4728. https://doi.org/10.3390/ma18204728








