Correlation Model of Damage Class and Deformation for Reinforced Concrete Beams Damaged by Earthquakes
Highlights
- This paper investigated the relationship between the damage to and deformation of RC beams, based on static loading tests on RC beam specimens with different shear strength margins, which showed effects on deformation capacity and the damage pattern of RC beams.
- Then, boundary values of ductility ratio to classify the damage class were presented for RC beams.
- Finally, correlation models of damage class and ductility ratio were proposed by applying the ultimate ductility ratio of 6 and 8 to represent the difference in the deformation capacity of RC beams.
Abstract
1. Introduction
2. Experiment Outline
2.1. Specimen Outline
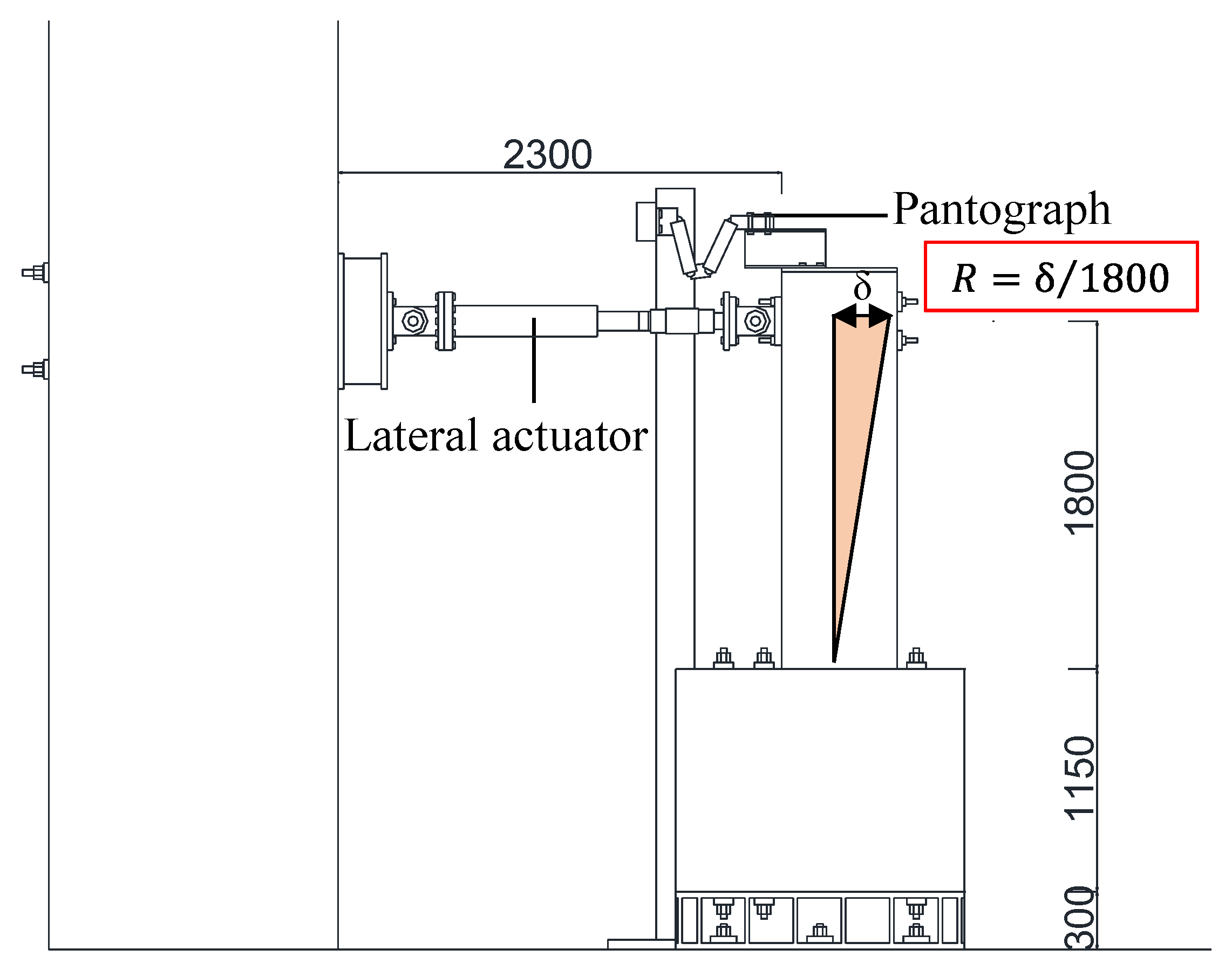
2.2. Loading Program and Instrumentation
3. Experimental Results
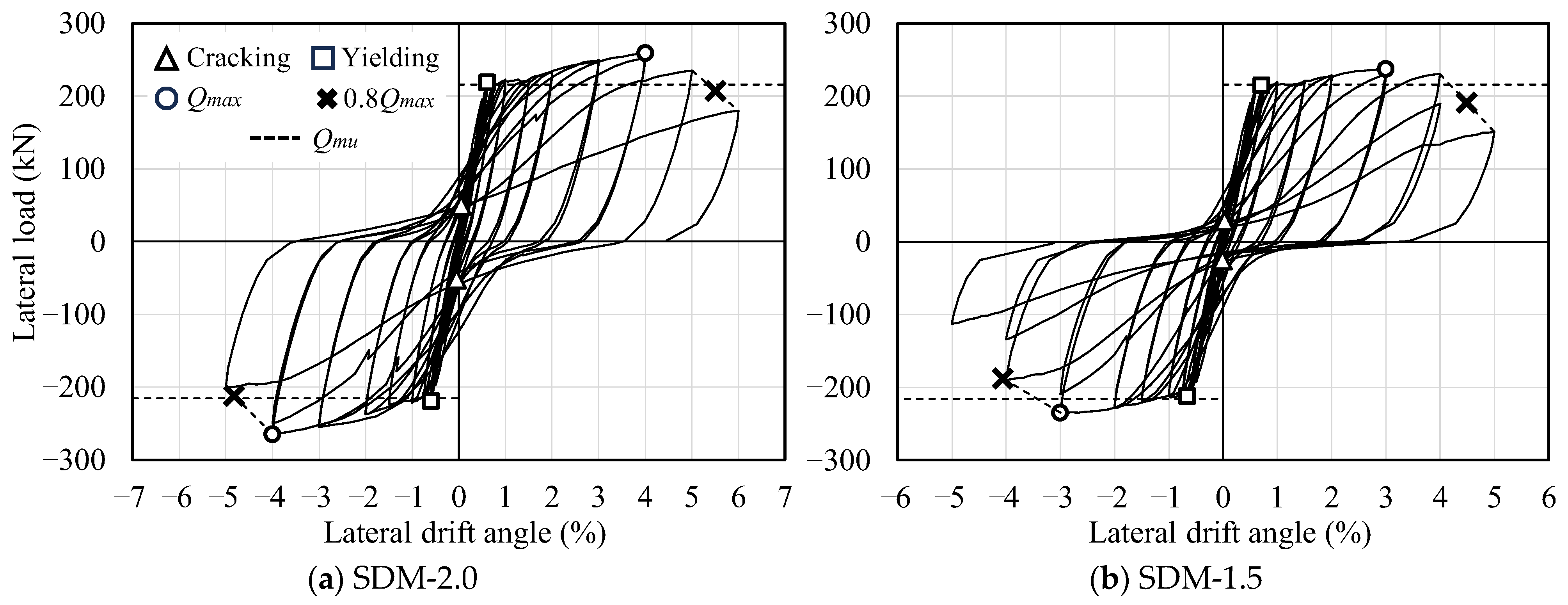
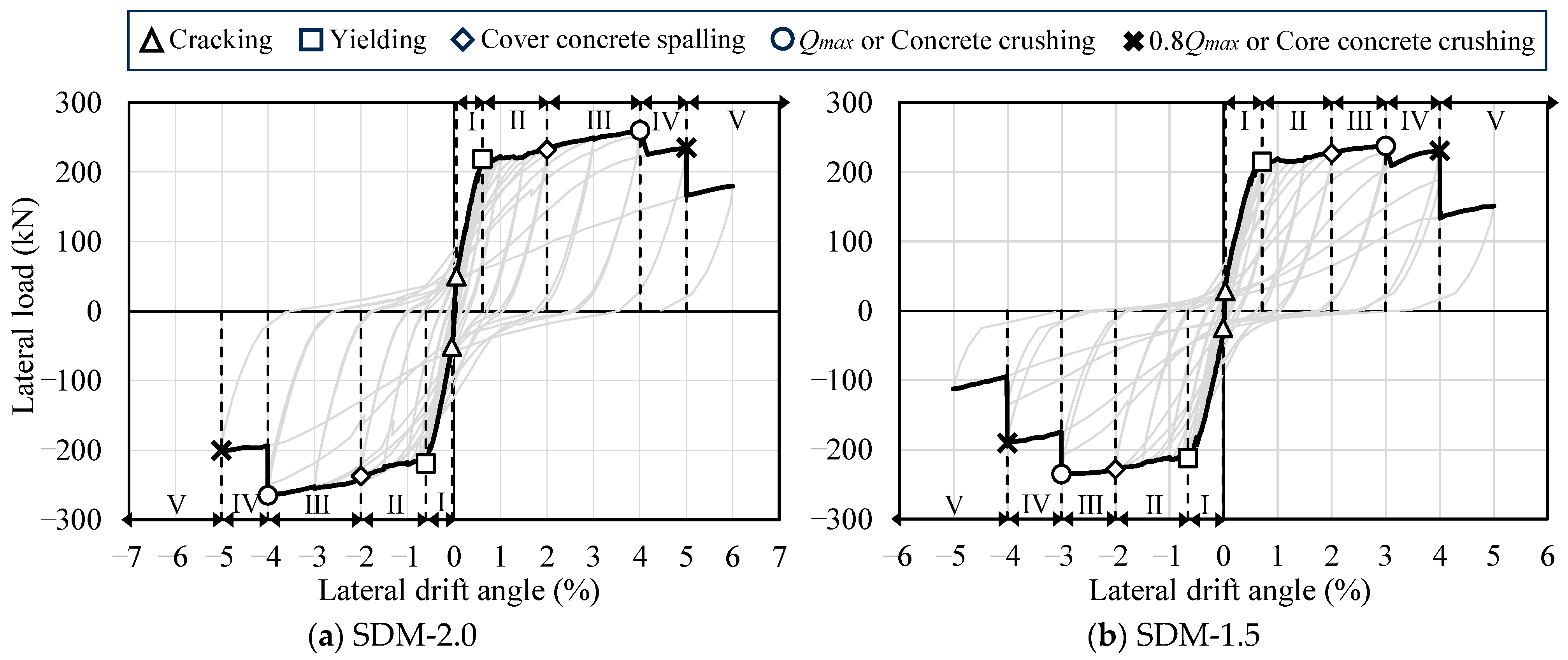
3.1. Load–Deformation Relationship
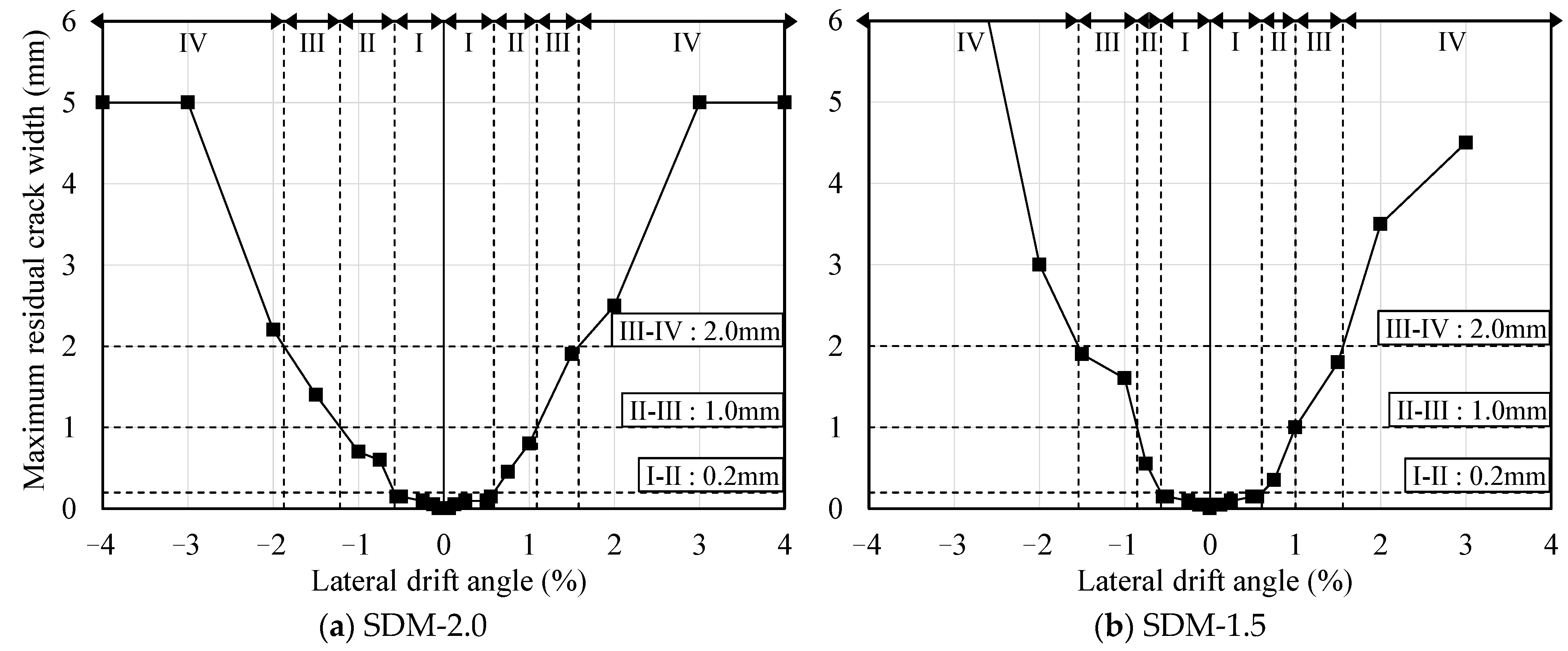
3.2. Failure Pattern
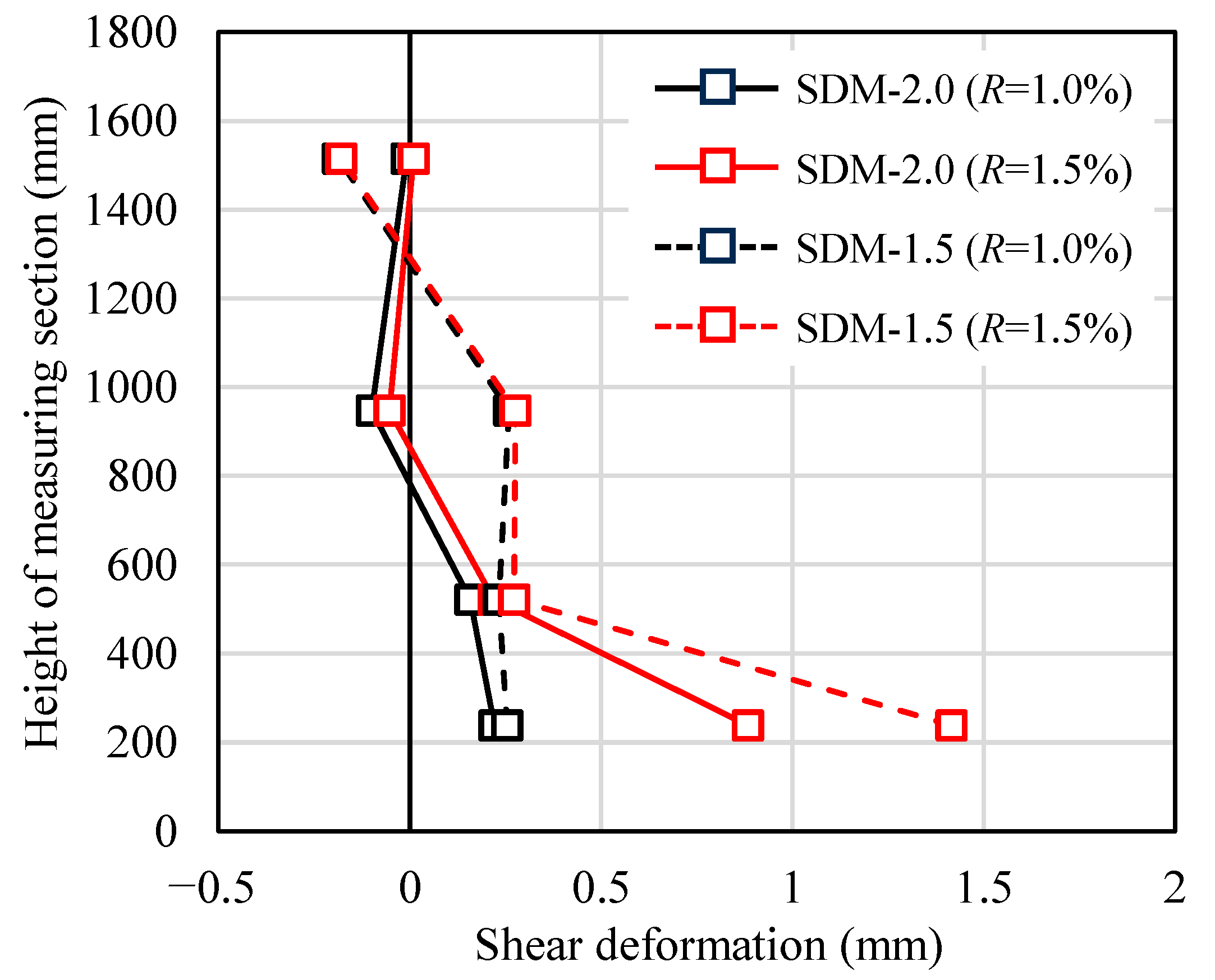
3.3. Distribution of Shear Deformation
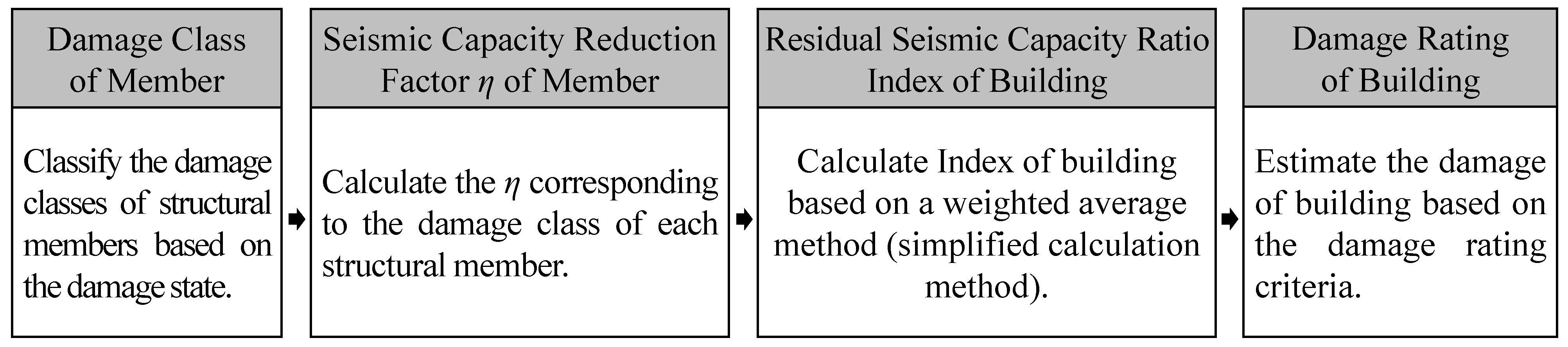
4. Evaluation of Damage Class and Seismic Capacity Reduction Factor η
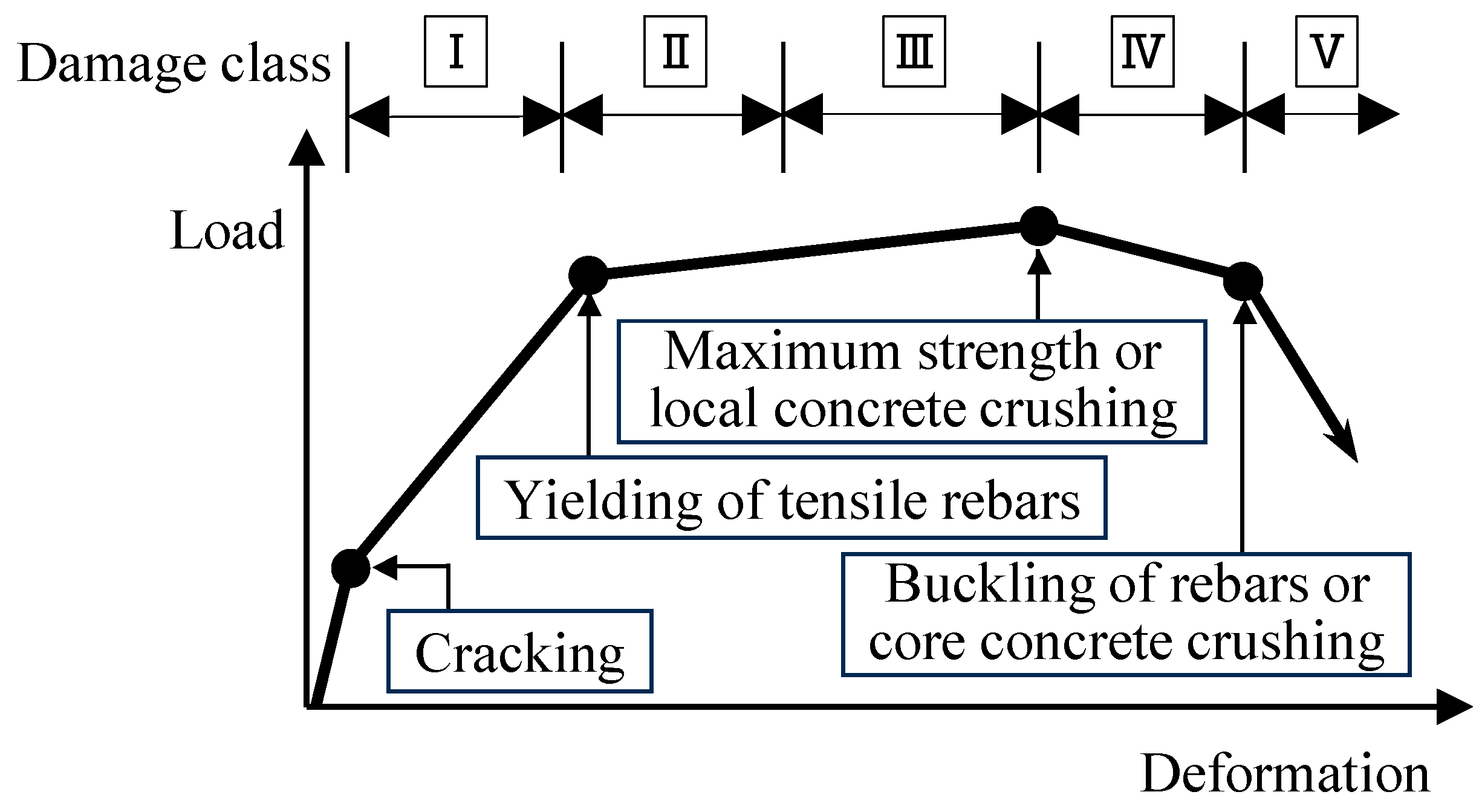
4.1. Definition for Damage Class
4.2. Damage Class
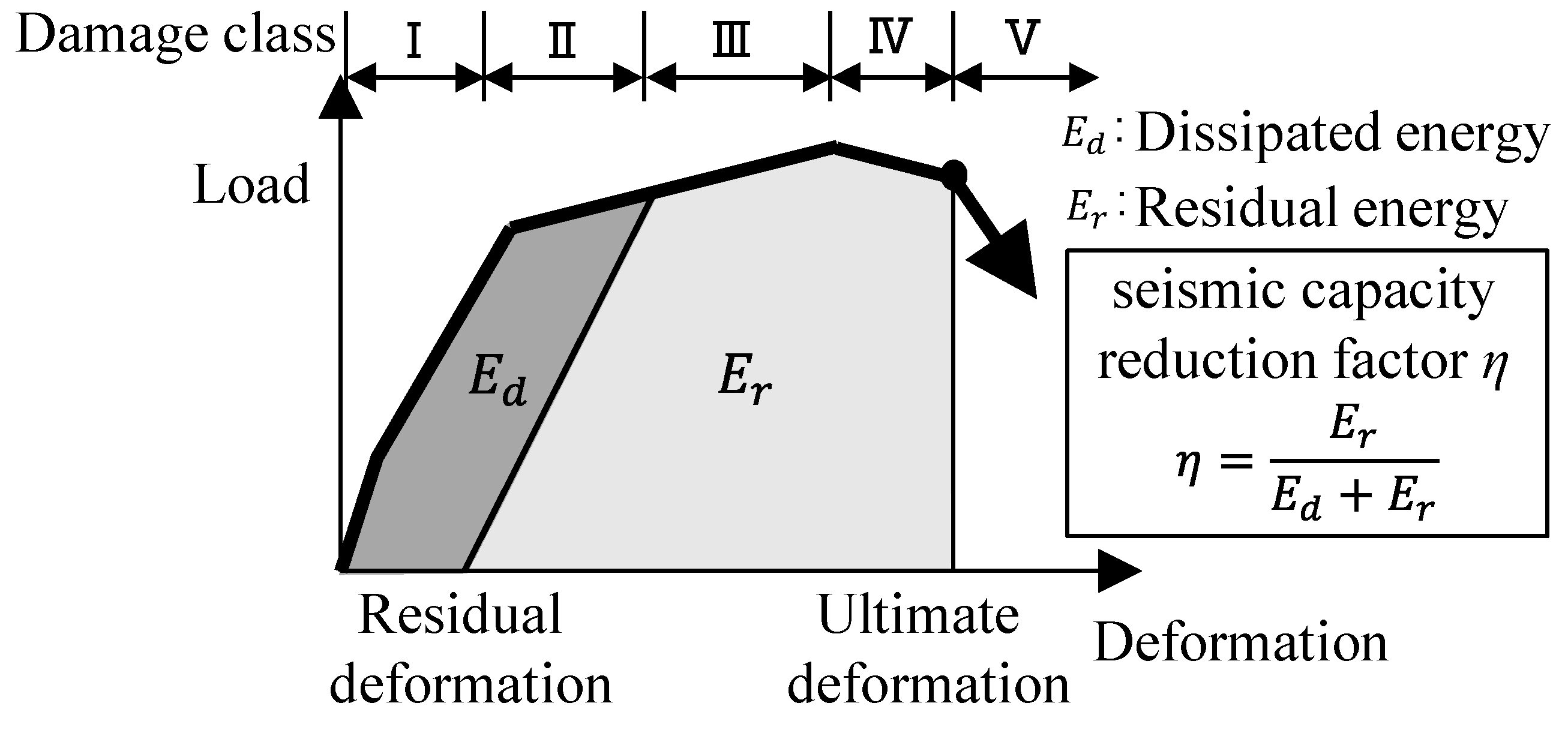
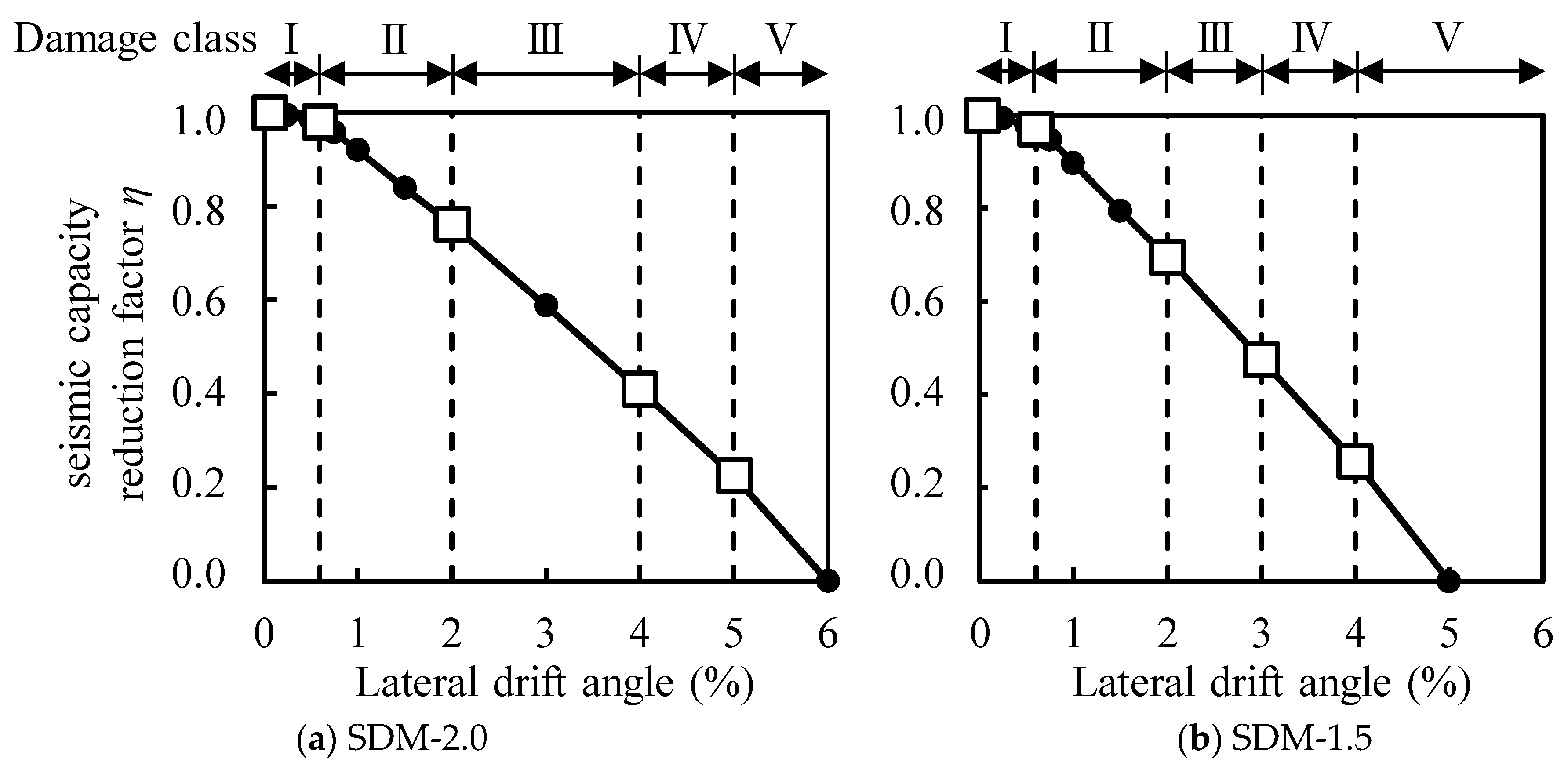
4.3. Seismic Capacity Reduction Factor η
5. Correlation Model of Damage Class and Deformation
6. Conclusions
- Based on the test results, the RC beam specimen with a smaller shear strength margin showed lower lateral load bearing capacity and deformation performance. In this specimen, the failure pattern was also different, for example, the tendency of shear failure was more remarkable, and shear deformation was more dominant.
- The damage classification of RC beam specimens was successfully performed based on the realignment concept, which comprehensively considers mechanical properties and damage development, such as the cracking and crushing of concrete, yielding of reinforcement, and deterioration of lateral load bearing capacity.
- The effect of the shear strength margin on the seismic capacity reduction factor η of RC beams was limited, whereas the specimen with a smaller shear strength margin exhibited lower ultimate deformation capacity.
- The boundary values of the seismic capacity reduction factor η to classify damage classes were similar for both specimens, and they were generally consistent with the specified values for ductile beams in the Japanese guidelines.
- The boundary values of the ductility ratio μ to classify damage classes in both specimens generally showed similar trends up to damage class III. However, after experiencing damage class III, the boundary values of the ductility ratio μ were lower in the specimen with a smaller shear strength margin.
- Correlation models of damage class and ductility ratio were proposed by applying ultimate ductility ratios of 6 and 8 to represent the difference in deformation capacity of RC beams, and the boundary values of the ductility ratio μ for classifying damage classes were also specified.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- The Japan Building Disaster Prevention Association (JBDPA). Guidelines for Post-Earthquake Damage Evaluation and Rehabilitation; JBDPA: Tokyo, Japan, 1991; (revised in 2001 and 2015). [Google Scholar]
- The Japan Building Disaster Prevention Association (JBDPA). Standard for Seismic Evaluation of Existing Reinforced Concrete Buildings; JBDPA: Tokyo, Japan, 1977; (revised in 1990, 2001 and 2017). [Google Scholar]
- Bunno, M.; Maeda, M.; Nagata, M. A study of the damage level estimation of RC buildings based on residual seismic capacity of members. Proc. Jpn. Concr. Inst. 2000, 22, 1447–1452. [Google Scholar]
- Maeda, M.; Bunno, M. Post-earthquake damage evaluation for RC buildings based on residual seismic capacity in structural members. In Proceedings of the US-Japan Workshop on Performance Based Seismic Design of Reinforced Concrete Building Structures, Seattle, WA, USA, 19–20 August 2001; pp. 19–20. [Google Scholar]
- Bunno, M.; Yukimura, N.; Maeda, M.; Kabeyazawa, T. Experimental study on behavior of reinforced concrete beams under axial restriction. Proc. Jpn. Concr. Inst. 1999, 21, 517–522. [Google Scholar]
- Bunno, M.; Nagayama, K.; Maeda, M. An evaluation of residual seismic capacity of reinforced concrete columns based on structural damage. Proc. Jpn. Concr. Inst. 2001, 23, 259–264. [Google Scholar]
- Ito, S.; Takahashi, K.; Maeda, M. Evaluation on residual seismic capacity of reinforced concrete columns and walls with shear failure. Proc. Jpn. Concr. Inst. 2013, 35, 859–864. [Google Scholar]
- Bao, S.; Matsukawa, K.; Maeda, M. Residual seismic capacity evaluation method for RC buildings with weak beam. In Proceedings of the 13th Japan Earthquake Engineering Symposium, Ibaraki, Japan, 17–20 November 2010; pp. 3255–3260. [Google Scholar]
- Miura, K.; Maeda, M.; Matsukawa, K.; Takahashi, K. Evaluation method of contribution factor of structural member for seismic capacity of single-story RC frames considering strength and energy dissipation (part 1). J. Struct. Constr. Eng. 2012, 77, 1283–1290. [Google Scholar]
- Quan, C.; Takahashi, N.; Choi, H.; Nakano, Y. Residual seismic capacity evaluation of overall weak-beam RC frame based on energy absorption capacity. J. Struct. Constr. Eng. 2013, 78, 1931–1938. [Google Scholar] [CrossRef][Green Version]
- Fujita, K.; Miura, K.; Tabata, Y.; Maeda, M.; Shegay, A.; Seki, M. Post-earthquake capacity evaluation of RC frame structures with multi-story flexural walls. J. Struct. Constr. Eng. 2021, 86, 1084–1094. [Google Scholar] [CrossRef]
- Architectural Institute of Japan (AIJ). Reconnaissance Report of the 1968 Tokachi-Oki Earthquake; AIJ: Tokyo, Japan, 1968. [Google Scholar]
- Architectural Institute of Japan (AIJ). Reconnaissance Report of the 1978 Miyagiken-Oki Earthquake; AIJ: Tokyo, Japan, 1978. [Google Scholar]
- Architectural Institute of Japan (AIJ). School Buildings Reconnaissance Report of the 1995 Kobe Earthquake; AIJ: Tokyo, Japan, 1995. [Google Scholar]
- Institute of Industrial Science of the University of Tokyo (IIS). Earthquake and Tsunami Reconnaissance Report of the 2011 Great East Japan Earthquake; Architectural Institute of Japan: Tokyo, Japan, 2012. [Google Scholar]
- Jung, M.; Maeda, M.; Tasai, A.; Nagata, M. Estimation of residual seismic performance for RC buildings damaged due to earthquake. J. Struct. Eng. 2002, 48B, 189–196. [Google Scholar]
- Architectural Institute of Japan (AIJ). Structural Design of Reinforced Concrete Buildings; AIJ: Tokyo, Japan, 1965; (revised in 2020). [Google Scholar]
- Architectural Institute of Japan (AIJ). AIJ Standard for Structural Calculation of Reinforced Concrete Structures; AIJ: Tokyo, Japan, 1971; (revised in 2024). [Google Scholar]
- Watanabe, H.; Korenaga, T.; Nakano, K.; Matsuzaki, Y. Experimental study on evaluation of ductility of reinforced concrete beams. J. Struct. Constr. Eng. 2002, 67, 161–168. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Uchino, S.; Sato, R.; Tajima, K.; Shirai, N. Effectiveness of steel brace reinforcement for a row-span RC frame with walls using round steel bars as main reinforcement. Proc. Jpn. Concr. Inst. 2015, 37, 841–846. [Google Scholar]
- Maeda, M.; Arizono, Y.; Yukimura, N. Experimental Study on Evaluation of Deformation in R/C Beams. Proc. Jpn. Concr. Inst. 1997, 19, 861–866. [Google Scholar]





| Specimen | Elastic Modulus | Compressive Strength | Tensile Strength |
|---|---|---|---|
| Specimen SDM-2.0 | 2.67 × 104 | 29.6 | 2.75 |
| Specimen SDM-1.5 | 2.66 × 104 | 31.4 | 3.06 |
| Rebar Specification | Elastic Modulus | Yield Strength | Tensile Strength |
|---|---|---|---|
| D25 (SD345) | 1.99 × 105 | 394.4 | 576.4 |
| D13 (SD345) | 1.95 × 105 | 399.3 | 554.6 |
| D10 (SD295) *a | 1.78 × 105 | 364.2 | 486.7 |
| Specimen | SDM-2.0 | SDM-1.5 |
|---|---|---|
| Cross-section | 360 mm × 600 mm | |
| Length | 1800 mm | |
| Longitudinal reinforcement | 8-D25 [SD345] | |
| Longitudinal tensile reinforcement ratio | 1.04% | |
| Transverse reinforcement | D13@150(3) [SD345] | D10@150(2) [SD295] |
| Transverse reinforcement ratio | 0.706% | 0.264% |
| Ultimate flexural strength Qmu | 218.6 kN | |
| Shear strength Qsu | 441.5 kN | 343.2 kN |
| Qsu/Qmu | 2.02 | 1.57 |
| Damage Class | Description of Damage |
|---|---|
| I | Visible narrow cracks on concrete surface (Crack width is less than 0.2 mm) |
| II | Visible clear cracks on concrete surface (Crack width is about 0.2–1.0 mm) |
| III | Local crush of concrete cover, remarkable wide cracks (Crack width is about 1.0–2.0 mm) |
| IV | Remarkable crush of concrete with exposed reinforcing bars, spalling of concrete cover (Crack width is more than 2.0 mm) |
| V | Buckling of reinforcing bars, cracks in core concrete, visible vertical and/or lateral deformation in columns and/or walls, visible settlement and/or leaning of the building |
| Damage Class | SDM-2.0 | SDM-1.5 | ||
|---|---|---|---|---|
| Positive Loading | Negative Loading | Positive Loading | Negative Loading | |
| 0 | ||||
| +0.06% | −0.05% | +0.03% | −0.01% | |
| I | ||||
| +0.59% | −0.58% | +0.60% | −0.58% | |
| II | ||||
| +2.0% | −2.0% | +2.0% | −2.0% | |
| III | ||||
| +4.0% | −4.0% | +3.0% | −3.0% | |
| IV | ||||
| +5.0% | −4.83% | +4.0% | −4.0% | |
| V | ||||
| Damage Class | SDM-2.0 | SDM-1.5 | Ductile Beam *b |
|---|---|---|---|
| I | 0.98 | 0.97 | 0.95 |
| II | 0.76 | 0.70 | 0.75 |
| III | 0.43 | 0.48 | 0.5 |
| IV | 0.22 | 0.25 | 0.2 |
| V | 0 | 0 | 0 |
| Damage Class | 0–I | I–II | II–III | III–IV | IV–V | |
|---|---|---|---|---|---|---|
| SDM-2.0 | Positive loading | 0.09 | 0.96 | 3.27 | 6.55 | 8.19 |
| Negative loading | 0.08 | 0.96 | 3.34 | 6.68 | 8.06 | |
| SDM-1.5 | Positive loading | 0.04 | 0.85 | 2.82 | 4.24 | 5.65 |
| Negative loading | 0.01 | 0.88 | 3.03 | 4.55 | 6.07 | |
| Damage Class | I–II | II–III | III–IV | IV–V | μu *c | |
|---|---|---|---|---|---|---|
| SDM-2.0 | Detailed | 0.96 | 3.27 | 6.55 | 8.06 | 8.06 |
| Simplified | 1.0 | 3.5 | 6.5 | 8.0 | 8.0 | |
| SDM-1.5 | Detailed | 0.85 | 2.82 | 4.24 | 5.65 | 5.65 |
| Simplified | 1.0 | 3.0 | 4.5 | 6.0 | 6.0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quan, C.; Choi, H.; Jin, K. Correlation Model of Damage Class and Deformation for Reinforced Concrete Beams Damaged by Earthquakes. Materials 2025, 18, 4638. https://doi.org/10.3390/ma18194638
Quan C, Choi H, Jin K. Correlation Model of Damage Class and Deformation for Reinforced Concrete Beams Damaged by Earthquakes. Materials. 2025; 18(19):4638. https://doi.org/10.3390/ma18194638
Chicago/Turabian StyleQuan, Chunri, Ho Choi, and Kiwoong Jin. 2025. "Correlation Model of Damage Class and Deformation for Reinforced Concrete Beams Damaged by Earthquakes" Materials 18, no. 19: 4638. https://doi.org/10.3390/ma18194638
APA StyleQuan, C., Choi, H., & Jin, K. (2025). Correlation Model of Damage Class and Deformation for Reinforced Concrete Beams Damaged by Earthquakes. Materials, 18(19), 4638. https://doi.org/10.3390/ma18194638






