Metallography of Quasicrystals in Al-Alloys
Abstract
1. Introduction
1.1. The Significance of Metallography
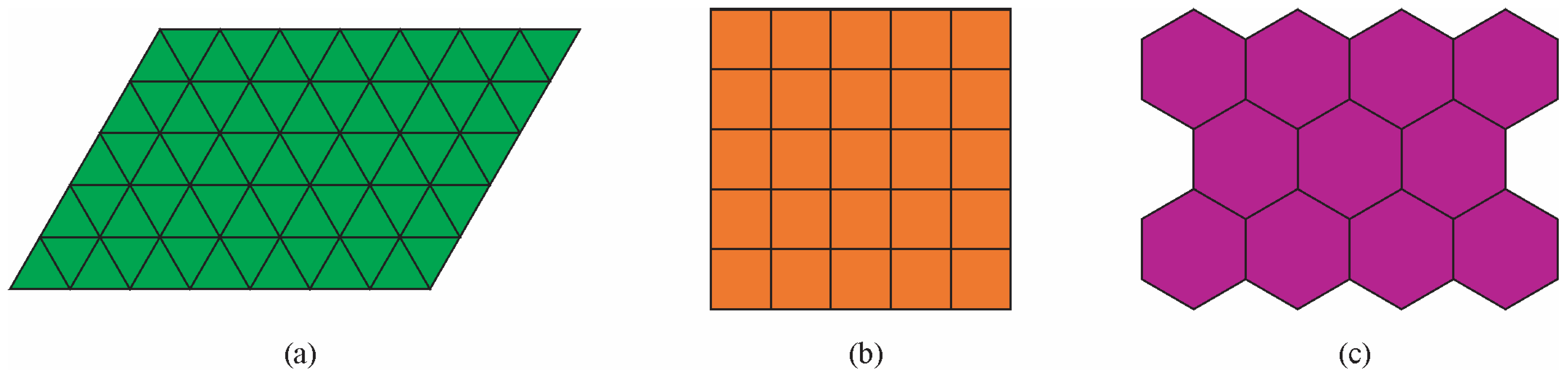
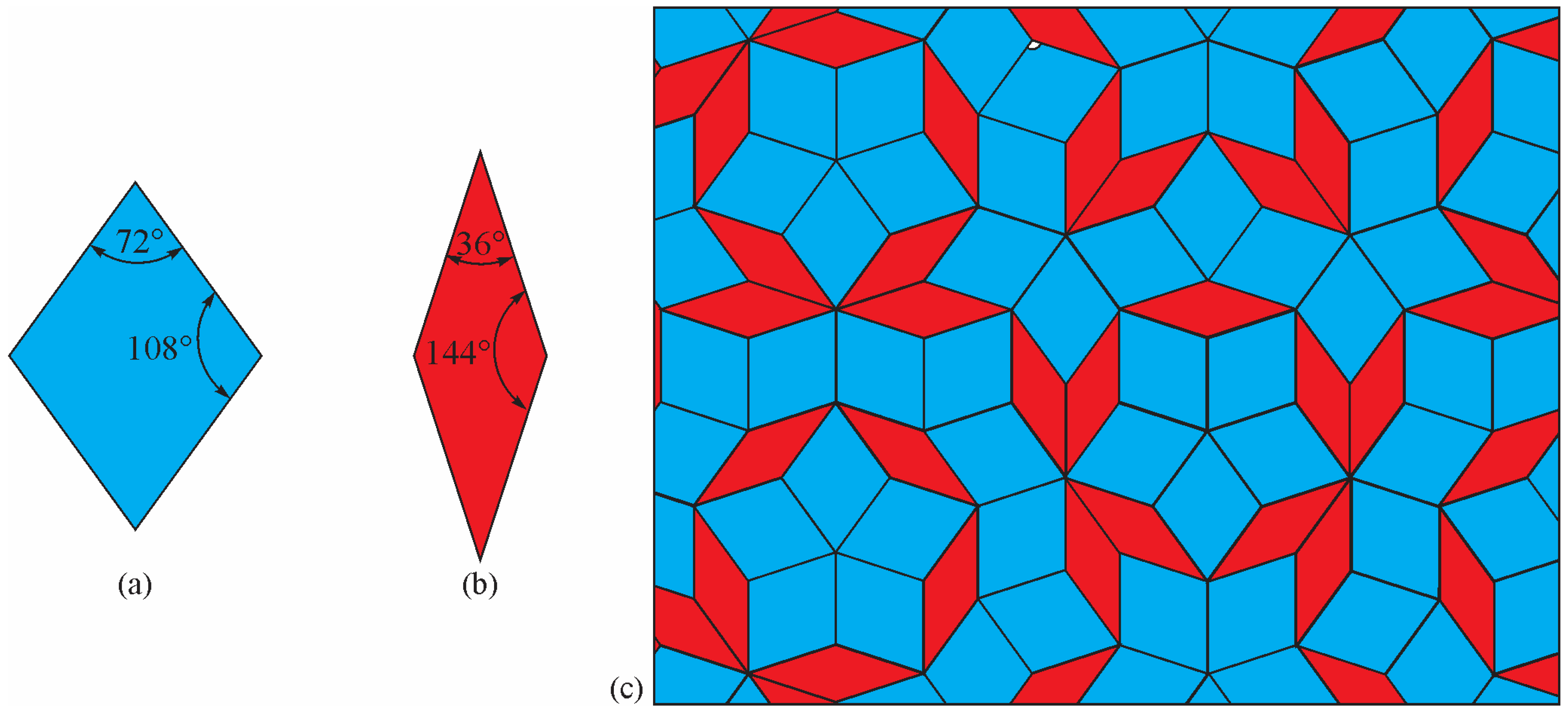
1.2. Quasicrystal Structure

1.3. Stability of Quasicrystals
1.4. Properties and Applications of Quasicrystals
1.5. The Aim of This Review
2. Light and Scanning Electron Microscopy of Polished and Lightly Etched Samples
2.1. Classical Metallographic Preparation of Aluminium Alloys
2.2. Quasicrystal in Melt-Spun Ribbons
2.3. Quasicrystals in As-Cast Samples
- Between the fivefold and threefold axes;
- Between the fivefold and twofold axes;
- Between the twofold and threefold axes;
- Within the stereographic triangle.
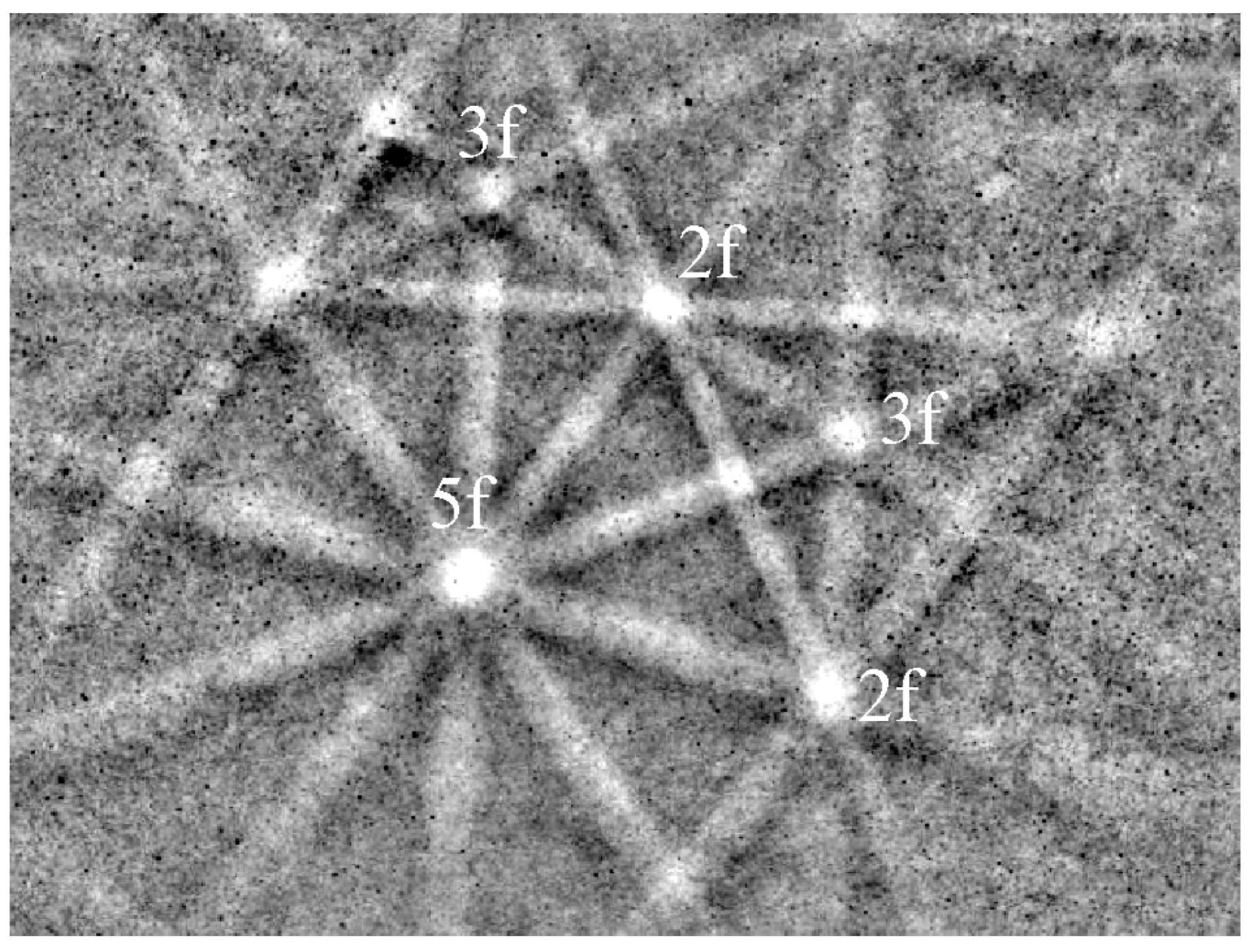
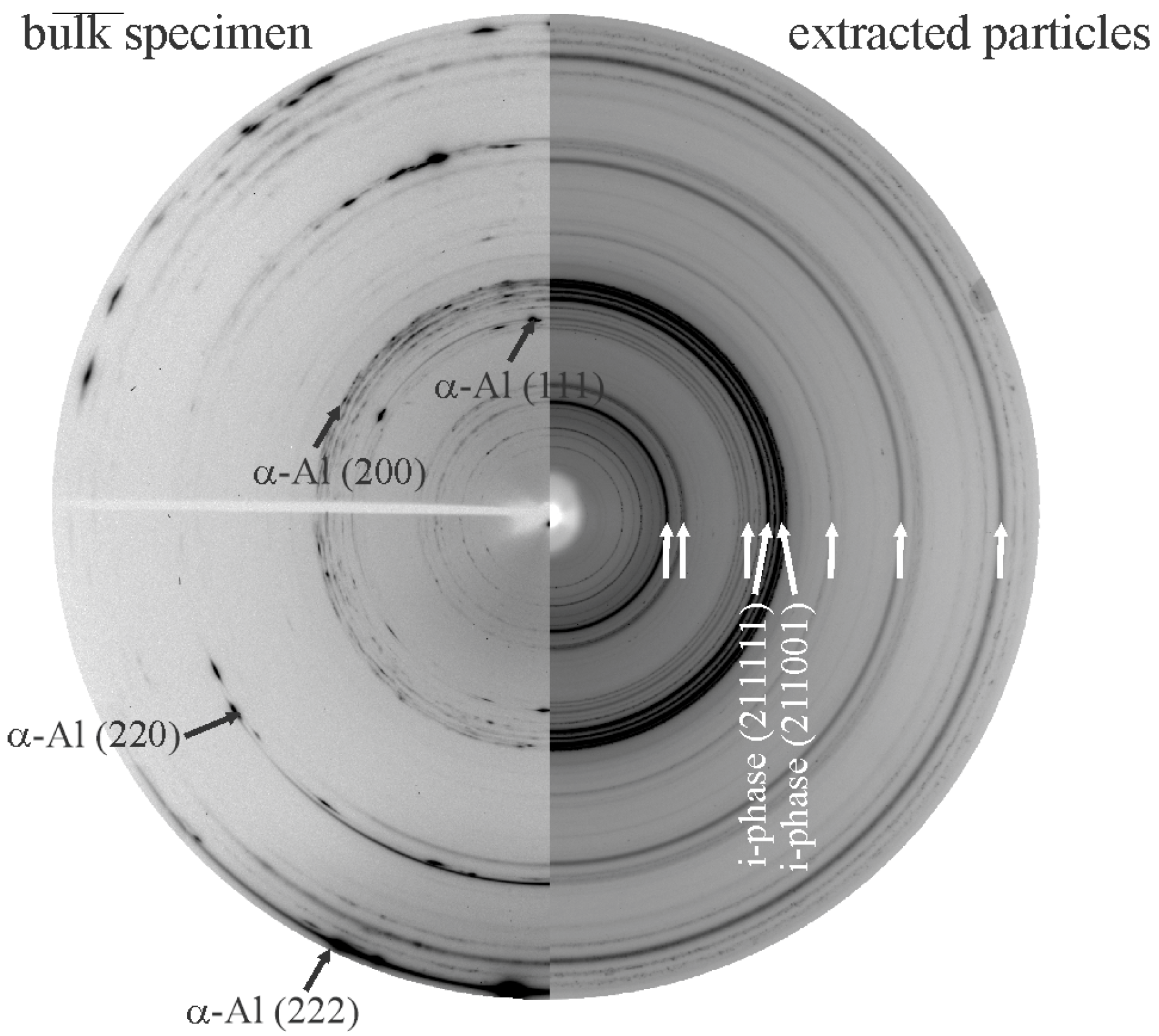
2.4. Identification of Quasicrystalline Precipitates in Al-Alloys
2.5. Alternative Methods for the Identification of Quasicrystalline Phases Using Metallography
3. Deep Etching and Particle Extraction
3.1. Deep Etching of Melt-Spun Ribbons
3.2. Deep Etching of Alloys with Polygonal and Dendritic Icosahedral Quasicrystals
3.3. Alternative Methods for Determining 3D Morphologies of Quasicrystals
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| QA | Quasicrystalline Approximant |
| EELS | Electron Energy Loss Spectroscopy |
| HAADF | High-Angle Annular Dark Field |
| TEM | Transmission Electron Microscopy |
| IQC | Icosahedral Quasicrystal |
| DQC | Decagonal Quasicrystal |
| STEM | Scanning TEM |
| EDS | Energy-Dispersive X-Ray Spectroscopy |
| WDS | Wavelength Dispersive X-Ray Spectroscopy |
| LM | Light Microscopy |
| SEM | Scanning Electron Microscopy |
| FIB | Focus Ion Beam |
| EBSD | Electron-BackScattered Diffraction |
| t-EBSD | transmission EBSD |
| HR SEM | High-Resolution SEM |
| XRD | X-ray Diffraction |
| APT | Atom-Probe Tomography |
| TKD | transmission Kikuchi diffraction |
| RE | rare-earth metal |
References
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951. [Google Scholar] [CrossRef]
- Levine, D.; Steinhardt, P.J. Quasicrystals—A new class of ordered structures. Phys. Rev. Lett. 1984, 53, 2477. [Google Scholar] [CrossRef]
- Chattopadhyay, K.; Ranganathan, S.; Subbanna, G.N.; Thangaraj, N. Electron microscopy of quasicrystals in rapidly solidified Al-14% Mn alloys. Scr. Metall. 1985, 19, 767–771. [Google Scholar] [CrossRef]
- Cahn, J.W. Quasicrystals. J. Res. Natl. Inst. Stand. Technol. 2001, 106, 975. [Google Scholar] [CrossRef]
- Yang, T.; Kong, Y.; Li, K.; Lu, Q.; Wang, Y.; Du, Y.; Schryvers, D. Quasicrystalline clusters transformed from C14-MgZn2 nanoprecipitates in Al alloys. Mater. Charact. 2023, 199, 112772. [Google Scholar] [CrossRef]
- Gokhale, A.B.; Banerjee, S. Sample Preparation For Metallography. In Characterization of Materials; Wiley Online Library: Hoboken, NJ, USA, 2002; p. 1. [Google Scholar]
- Zhang, L.; Wu, C. Preparation Method for Metallographic Specimen of Iron-Carbon and Silicon-aluminium Alloy. J. Phys. Conf. Ser. 2022, 2338, 012047. [Google Scholar] [CrossRef]
- Edyvean, R.H. Christofer, The metallurgical work of Henry Clifton Sorby and an annotated catalogue of his extant metallurgical specimens. Hist. Metall. 2022, 31, 54. [Google Scholar]
- Anderson, R.J. The metallography of aluminum. J. Frankl. Inst. 1919, 187, 1. [Google Scholar] [CrossRef]
- Exner, H.E. Metallography: Technique of metallurgical investigation or the science of describing metals? Prakt. Metallogr.-Pract. Metallogr. 1999, 36, 115. [Google Scholar] [CrossRef]
- McCall, J.L. Scanning Electron Microscopy for Microstructural Analysis. In Microstructural Analysis: Tools and Techniques; McCall, J.L., Mueller, W.M., Eds.; Springer: Boston, MA, USA, 1973; p. 93. [Google Scholar]
- Leonard, D.N.; Chandler, G.W.; Seraphin, S. Scanning Electron Microscopy. In Characterization of Materials; John Wiley & Sons: Hoboken, NJ, USA, 2012; p. 1. [Google Scholar]
- Hodoroaba, V.D.; Rades, S.; Salge, T.; Mielke, J.; Ortel, E.; Schmidt, R. Characterisation of nanoparticles by means of high-resolution SEM/EDS in transmission mode. IOP Conf. Ser. Mater. Sci. Eng. 2016, 109, 012006. [Google Scholar] [CrossRef]
- Steurer, W.; Deloudi, S. Crystallography of Quasicrystals, Concepts, Methods and Structures; Springer: Berlin/Heildelberg, Germany, 2009. [Google Scholar]
- Wang, H. Proving theorems by pattern recognition—II. Bell Syst. Tech. J. 1961, 40, 1. [Google Scholar] [CrossRef]
- Sharma, B.G. An introductory note on Quasicrystals. Recent Res. Sci. Technol. 2012, 4, 82–84. [Google Scholar]
- Pauling, L. So-called icosahedral and decagonal quasicrystals are twins of an 820-atom cubic crystal. Phys. Rev. Lett. 1987, 58, 365. [Google Scholar] [CrossRef] [PubMed]
- Bončina, T. Stabilisation and Identification of Quasicrystalline Phases in Al-Mn-Be Based Alloys; University of Ljubljana: Ljubljana, Slovenians, 2010. [Google Scholar]
- Penrose, R. The role of aesthetics in pure and applied mathematical research. Bull. Inst. Math. Appl. 1974, 10, 266. [Google Scholar]
- Elenius, M.; Zetterling, F.H.M.; Dzugutov, M.; Dzugutov, M.; Fredrickson, D.C.; Lidin, S. Structural model for octagonal quasicrystals derived from octagonal symmetry elements arising in beta-Mn crystallization of a simple monatomic liquid. Phys. Rev. B 2009, 79, 10. [Google Scholar] [CrossRef]
- Baipaywad, P.; Wi, J.-S.; Park, H.; Paik, T. Tailoring cubic and dodecagonal quasicrystalline mesophases of mesoporous organosilica nanoparticles and core/shell structure. Mater. Sci. Eng. C-Mater. Biol. Appl. 2019, 98, 666. [Google Scholar] [CrossRef]
- Krumeich, F.; Muller, E.; Wepf, R.A.; Conrad, M.; Reich, C.; Harbrecht, B.; Nesper, R. The structure of dodecagonal (Ta,V)(1.6)Te imaged by phase-contrast scanning transmission electron microscopy. J. Solid State Chem. 2012, 194, 106. [Google Scholar] [CrossRef]
- Ma, H.; You, L.; He, Z. Stable quaternary Al59Cr23Fe8Si10 decagonal quasicrystal. Mater. Charact. 2020, 166, 10424. [Google Scholar] [CrossRef]
- Mackay, A.L. Crystallography and the Penrose pattern. Phys. A Stat. Mech. Its Appl. 1982, 114, 609. [Google Scholar] [CrossRef]
- Boudard, M.; Deboissieu, M.; Janot, C.; Heger, G.; Beeli, C.; Nissen, H.U.; Vincent, H.; Ibberson, R.; Audier, M.; Dubois, J.M. Neutron and X-ray single-crystal study of the AlPdMn icosahedral phase. J. Phys.-Condes. Matter 1992, 4, 10149. [Google Scholar] [CrossRef]
- Mackay, A.L. A Dense Non-Crystallographic Packing of Equal Spheres. Acta Crystallogr. A-Found. Adv. 1962, 15, 916. [Google Scholar] [CrossRef]
- Sirindil, A.; Quiquandon, M.; Gratias, D. Mackay clusters and beyond in icosahedral quasicrystals seen from 6D space. Struct. Chem. 2017, 28, 123. [Google Scholar] [CrossRef]
- Bergman, G.; Waugh, J.L.T.; Pauling, L. The crystal structure of the metallic phase Mg32(Al, Zn)49. Acta Crystallogr. 1957, 10, 254. [Google Scholar] [CrossRef]
- Sun, W.; Lincoln, F.J.; Sugiyama, K.; Hiraga, K. Structure refinement of (Al, Zn)49Mg32-type phases by single-crystal X-ray diffraction. Mater. Sci. Eng. A 2000, 294–296, 327–330. [Google Scholar] [CrossRef]
- Guo, J.Q.; Abe, E.; Tsai, A.P. Stable icosahedral quasicrystals in binary Cd-Ca and Cd-Yb systems. Phys. Rev. B 2000, 62, R14605. [Google Scholar] [CrossRef]
- Loreto, L.; Farinato, R.; Catallo, S.; Janot, C.; Gerbasi, G.; Angelis, G.D. Polyhedral and chemical orders in icosahedral Al–Pd–Mn quasicrystals. Phys. B Condens. Matter 2003, 328, 193. [Google Scholar] [CrossRef]
- Lyonnard, S.; Coddens, G.; Calvayrac, Y.; Gratias, D. Atomic (phason) hopping in perfect icosahedral quasicrystals Al70.3Pd21.4Mn8.3 by time-of-flight quasielastic neutron scattering. Phys. Rev. B 1996, 53, 3150. [Google Scholar] [CrossRef]
- Lyonnard, S.; Coddens, G.; Hennion, B.; Calvayrac, Y. Dynamics of phason hopping in AlFeCu and AlMnPd quasicrystals. Phys. B 1997, 234, 28. [Google Scholar] [CrossRef]
- Hiraga, K.; Hirabayashi, M. Quenched phason strains in Al-Mn-Si icosahedral quasicrystal studied by high-resolution electron-microscopy. J. Electron Microsc. 1987, 36, 353. [Google Scholar]
- Kiani, M.; Samavat, F.; O’Connor, J. Phason mechanism for diffusion in quasicrystalline structures. Solid State Commun. 2020, 321, 14017. [Google Scholar] [CrossRef]
- Feuerbacher, M. Dislocations in icosahedral quasicrystals. Chem. Soc. Rev. 2012, 41, 6745. [Google Scholar] [CrossRef]
- Mompiou, F.; Caillard, D. Dislocations and mechanical properties of icosahedral quasicrystals. C. R. Phys. 2014, 15, 82. [Google Scholar] [CrossRef]
- Ramaswamy, S. The nature of dislocation-motion in quasicrystals. Bull. Mat. Sci. 1988, 10, 75. [Google Scholar] [CrossRef]
- Mehrer, H.; Galler, R. Vacancy-mediated diffusion in quasicrystalline alloys. J. Alloys Compd. 2002, 342, 296. [Google Scholar] [CrossRef]
- Cizek, J.; Vlcek, M.; Smola, B.; Stulikova, I.; Prochazka, I.; Kuzel, R.; Jager, A.; Lejcek, P. Vacancy-like defects associated with icosahedral phase in Mg-Y-Nd-Zr alloys modified by the addition of Zn. Scr. Mater. 2012, 66, 630. [Google Scholar] [CrossRef]
- Heggen, M.; Feuerbacher, M.; Schall, P.; Urban, K.; Wang, R. Antiphase domains in plastically deformed Zn-Mg-Dy single quasicrystals. Phys. Rev. B 2001, 64, 014202. [Google Scholar] [CrossRef][Green Version]
- Wang, R.H.; Feuerbacher, M.; Yang, W.G.; Urban, K. Stacking faults in high-temperature-deformed Al-Pd-Mn icosahedral quasicrystals. Philos. Mag. A-Phys. Condens. Matter Struct. Defect Mech. Prop. 1998, 78, 273. [Google Scholar] [CrossRef]
- Klein, H.; Feuerbacher, M. Structure of dislocations and stacking faults in the complex intermetallic ξ′-(Al-Pd-Mn) phase. Philos. Mag. 2003, 83, 4103. [Google Scholar] [CrossRef]
- Mikulla, R.; Stadler, J.; Krul, F.; Trebin, H.R.; Gumbsch, P. Crack propagation in quasicrystals. Phys. Rev. Lett. 1998, 81, 3163. [Google Scholar] [CrossRef]
- Trebin, H.R.; Mikulla, R.; Stadler, J.; Schaaf, G.; Gumbsch, P. Molecular dynamics simulations of crack propagation in quasicrystals. Comput. Phys. Commun. 1999, 122, 536. [Google Scholar] [CrossRef]
- Ronchetti, M.; Bertagnolli, M.; Jarić, M.V. Generation and Dynamics of Defects in Two-Dimensional Quasicrystals. In Geometry and Thermodynamics: Common Problems of Quasi-Crystals, Liquid Crystals, and Incommensurate Systems; Tolédano, J.C., Ed.; Springer: Boston, MA, USA, 1990; p. 141. [Google Scholar]
- Janot, C.; Loreto, L.; Farinato, R. Special defects in quasicrystals. Phys. Status Solidi B-Basic Res. 2000, 222, 121. [Google Scholar] [CrossRef]
- Bindi, L.; Steinhardt, P.J.; Yao, N.; Lu, P.J. Icosahedrite, Al63Cu24Fe13, the first natural quasicrystal. Am. Miner. 2011, 96, 928. [Google Scholar] [CrossRef]
- Bindi, L.; Yao, N.; Lin, C.; Hollister, L.S.; Andronicos, C.L.; Distler, V.V.; Eddy, M.P.; Kostin, A.; Kryachko, V.; MacPherson, G.J.; et al. Natural quasicrystal with decagonal symmetry. Sci. Rep. 2015, 5, 5. [Google Scholar] [CrossRef]
- Grushko, B.; Velikanova, T.Y. Stable and metastable quasicrystals in Al-based alloy systems with transition metals. J. Alloys Compd. 2004, 367, 58. [Google Scholar] [CrossRef]
- Hiraga, K.; Zhang, B.P.; Hirabayashi, M.; Inoue, A.; Masumoto, T. Highly ordered icosahedral quasicrystal of Al-Cu-Fe alloy studied by electron-diffraction and high-resolution electron-microscopy. Jpn. J. Appl. Phys. Part 2—Lett. 1988, 27, L951. [Google Scholar] [CrossRef]
- González, A.L.; Noguez, C.; Beránek, J.; Barnard, A.S. Size, Shape, Stability, and Color of Plasmonic Silver Nanoparticles. J. Phys. Chem. C 2014, 118, 9128. [Google Scholar] [CrossRef]
- Middya, A.R.; Ghosh, K. Quasicrystalline Phase of Silicon on Glass. MRS Online Proc. Libr. 2012, 1493, 24. [Google Scholar] [CrossRef]
- Franke, K.J.; Sharma, H.R.; Theis, W.; Gille, P.; Ebert, P.; Rieder, K.H. Quasicrystalline Epitaxial Single Element Monolayers on Icosahedral Al-Pd-Mn and Decagonal Al-Ni-Co Quasicrystal Surfaces. Phys. Rev. Lett. 2002, 89, 156104. [Google Scholar] [CrossRef]
- Fujita, E.; Liu, C.; Ishikawa, A.; Mato, T.; Kitahara, K.; Tamura, R.; Kimura, K.; Yoshida, R.; Katsura, Y. Comprehensive experimental datasets of quasicrystals and their approximants. Sci. Data 2024, 11, 1211. [Google Scholar] [CrossRef]
- Meisterernst, G.; Bauer, B.; Gille, P. Czochralski Growth of Decagonal AlCoNi Quasicrystals from Al-rich Solution. Acta Phys. Pol. A 2013, 124, 344. [Google Scholar] [CrossRef]
- Elser, V. Indexing problems in quasicrystal diffraction. Phys. Rev. B 1985, 32, 4892. [Google Scholar] [CrossRef]
- Singh, A.; Ranganathan, S. On the indexing and reciprocal space of icosahedral quasicrystal. J. Mater. Res. 1999, 14, 4182. [Google Scholar] [CrossRef]
- Zupanic, F.; Boncina, T.; Krizman, A.; Grogger, W.; Gspan, C.; Markoli, B.; Spaic, S. Quasicrystalline phase in melt-spun Al-Mn-Be ribbons. J. Alloys Compd. 2008, 452, 343. [Google Scholar] [CrossRef]
- Zupanič, F.; Gspan, C.; Burja, J.; Bončina, T. Quasicrystalline and L12 precipitates in a microalloyed Al-Mn-Cu alloy. Mater. Today Commun. 2020, 22, 100809. [Google Scholar] [CrossRef]
- Inoue, A.; Tsai, A.-P.; Masumoto, T. Stable decagonal and icosahedral quasicrystals. J. Non-Cryst. Solids 1990, 117–118, 824. [Google Scholar] [CrossRef]
- Tsai, A.P.; Inoue, A.; Masumoto, T. Preparation of a new Al-Cu-Fe quasicrystal with large grain sizes by rapid solidification. J. Mater. Sci. Lett. 1987, 6, 1403. [Google Scholar] [CrossRef]
- Guo, J.Q.; Tsai, A.P. Stable icosahedral quasicrystals in the Ag-In-Ca, Ag-In-Yb, Ag-In-Ca-Mg and Ag-In-Yb-Mg systems. Philos. Mag. Lett. 2002, 82, 349. [Google Scholar] [CrossRef]
- Abe, E.; Tsai, A.P. Structure of a metastable Al3Ni decagonal quasicrystal: Comparison with a highly perfect Al72Ni20Co8. J. Alloys Compd. 2002, 342, 96. [Google Scholar] [CrossRef]
- Guo, J.Q.; Abe, E.; Tsai, A.P. A new stable icosahedral quasicrystal in the Cd-Mg-Dy system. Philos. Mag. Lett. 2001, 81, 17. [Google Scholar] [CrossRef]
- Terauchi, M.; Ueda, H.; Tanaka, M.; Tsai, A.P.; Inoue, A.; Masumoto, T. Electron-energy-loss spectroscopy study of a stable decagonal quasicrystal Al70Ni20Rh10. Philos. Mag. B-Phys. Condens. Matter Stat. Mech. Electron. Opt. Magn. Prop. 1998, 77, 1625. [Google Scholar] [CrossRef]
- Tsai, A.P.; Inoue, A.; Masumoto, T. A stable decagonal quasicrystal in the Al-Cu-Co system. Mater. Trans. JIM 1989, 30, 300. [Google Scholar] [CrossRef][Green Version]
- Tsai, A.P.; Inoue, A.; Masumoto, T. Stable decagonal Al-Co-Ni and Al-Co-Cu quasicrystals. Mater. Trans. JIM 1989, 30, 463. [Google Scholar] [CrossRef]
- So, Y.-G.; Yoshikawa, T.; Saruhashi, F.; Edagawa, K.; Tamura, R. Formation of Icosahedral Quasicrystals and 1/1 Crystal Approximants in Al-Pd-RE (RE: Rare Earth Metals) Systems. Mater. Trans. 2011, 52, 2011. [Google Scholar] [CrossRef][Green Version]
- Naglič, I.; Samardžija, Z.; Delijić, K.; Kobe, S.; Dubois, J.-M.; Leskovar, B.; Markoli, B. Metastable quasicrystals in Al–Mn alloys containing copper, magnesium and silicon. J. Mater. Sci. 2017, 52, 13657. [Google Scholar] [CrossRef]
- Pedrazzini, S.; Galano, M.; Audebert, F.; Collins, D.M.; Hofmann, F.; Abbey, B.; Korsunsky, A.M.; Lieblich, M.; Garcia Escorial, A.; Smith, G.D.W. Strengthening mechanisms in an Al-Fe-Cr-Ti nano-quasicrystalline alloy and composites. Mater. Sci. Eng. A 2016, 672, 175. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, D.H.; Kuo, K.H. Quasicrystals, crystalline phases, and multiple twins in rapidly solidified Al-Cr alloys. Phys. Rev. B 1988, 37, 6220. [Google Scholar] [CrossRef]
- Swamy, V.T.; Ranganathan, S.; Chattopadhyay, K. Rapidly solidified Al-Cr alloys—Crystalline and quasicrystalline phases. J. Mater. Res. 1989, 4, 539. [Google Scholar] [CrossRef]
- He, G.; Shek, C.H.; Lai, J.K.L.; Bian, Z.; Hui, X.D.; Chen, G.L. Microstructure investigation of rapidly solidified Al-V-Fe alloys. J. Mater. Res. 2002, 17, 814. [Google Scholar] [CrossRef]
- Yuan, Y.; Hou, H.; Zhao, Y.H.; Yan, F.; Zhang, Y. Microstructure and mechanical properties of an aluminum alloy reinforced by Al-Ni-Co-Mn quasi-crystalline. Mater. Res. Express 2019, 6, 56529. [Google Scholar] [CrossRef]
- Mihalkovic, M.; Widom, M. Spontaneous formation of thermodynamically stable Al-Cu-Fe icosahedral quasicrystal from realistic atomistic simulations. Phys. Rev. Res. 2020, 2, 013196. [Google Scholar] [CrossRef]
- Tsai, A.P.; Yokoyama, Y.; Inoue, A.; Masumoto, T. Chemistry of Stable Quasi-Crystals. In Physics and Chemistry of Finite Systems: From Clusters to Crystals; Jena, P., Khanna, S.N., Rao, B.K., Eds.; Springer: Dordrecht, The Netherlands, 1992; p. 177. [Google Scholar]
- Zaitsev, A.I.; Zaitseva, N.E.; Shakhpazov, E.K.; Arutyunyan, N.A.; Dunaev, S.F. The conditions of formation and stability of quasi-crystalline phases in aluminum-manganese alloys. Russ. J. Phys. Chem. 2006, 80, 869. [Google Scholar] [CrossRef]
- Zaitsev, A.I.; Zaitseva, N.E.; Shimko, R.Y.; Arutyunyan, N.A.; Dunaev, S.F.; Kraposhin, V.S.; Lam, H.T. Thermodynamic properties of Al-Mn, Al-Cu, and Al-Fe-Cu melts and their relations to liquid and quasicrystal structure. J. Phys. Condens. Matter 2008, 20, 114121. [Google Scholar] [CrossRef] [PubMed]
- Inoue, A.; Kimura, H.M.; Sasamori, K.; Masumoto, T. Microstructure and novel properties of nanocrystalline and nanocrystalline alloys prepared in Al-based systems by rapid solidification. Sci. Rep. Res. Inst. Tohoku Univ. Ser. A-Phys. Chem. Metall. 1996, 42, 165. [Google Scholar]
- Nayak, S.S.; Murty, B.S.; Pabi, S.K. Structure of nanocomposites of Al-Fe alloys prepared by mechanical alloying and rapid solidification processing. Bull. Mater. Sci. 2008, 31, 449–454. [Google Scholar] [CrossRef]
- Novák, P.; Kubatík, T.; Vystrčil, J.; Hendrych, R.; Kříž, J.; Mlynár, J.; Vojtěch, D. Powder metallurgy preparation of Al–Cu–Fe quasicrystals using mechanical alloying and Spark Plasma Sintering. Intermetallics 2014, 52, 131. [Google Scholar] [CrossRef]
- Hosseini, S.; Novak, P. On the Formation of A1NiCo Nano-Quasicrystalline Phase during Mechanical Alloying through Electroless Ni-P Plating of Starting Particles. Materials 2019, 12, 2294. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Novak, P.; Vesely, M. Positive temperature dependence of compressive properties in an AlNiCo poly-quasicrystal fabricated by mechanical alloying and spark plasma sintering. Scr. Mater. 2020, 187, 169. [Google Scholar] [CrossRef]
- Michalcova, A.; Vojtech, D.; Schumacher, G.; Novak, P.; Plizingrova, E. Effect of iron and cerium additions on rapidly solidified Al-Tm-Ce alloys. Mater. Tehnol. 2013, 47, 757. [Google Scholar]
- Li, R.; Wang, Z.; Li, Z.; Khor, K.A.; Dong, Z. Dynamic Fracture Mechanism of Quasicrystal-Containing Al-Cr-Fe Consolidated Using Spark Plasma Sintering. Crystals 2018, 8, 385. [Google Scholar] [CrossRef]
- Shadangi, Y.; Sharma, S.; Shivam, V.; Basu, J.; Chattopadhyay, K.; Majumdar, B.; Mukhopadhyay, N.K. Fabrication of Al-Cu-Fe quasicrystal reinforced 6082 aluminium matrix nanocomposites through mechanical milling and spark plasma sintering. J. Alloys Compd. 2020, 828, 54258. [Google Scholar] [CrossRef]
- Li, R.T.; Dong, Z.L.; Khor, K.A. Al-Cr-Fe quasicrystals as novel reinforcements in Ti based composites consolidated using high pressure spark plasma sintering. Mater. Des. 2016, 102, 255. [Google Scholar] [CrossRef]
- Laplanche, G.; Gadaud, P.; Bonneville, J.; Joulain, A.; Gauthier-Brunet, V.; Dubois, S.; Jay, F. Spark plasma sintering synthesis and mechanical spectroscopy of the omega-Al0.7Cu0.2Fe0.1 phase. J. Mater. Sci. 2012, 47, 169. [Google Scholar] [CrossRef]
- Takagiwa, Y.; Kamimura, T.; Hosoi, S.; Okada, J.T.; Kimura, K. Thermoelectric properties of Al-Pd-Re quasicrystal sintered by Spark Plasma Sintering (SPS): Effect of improvement of microstructure. Z. Für Krist.-Cryst. Mater. 2009, 224, 79–83. [Google Scholar] [CrossRef]
- Fleury, E.; Lee, J.H.; Kim, S.H.; Kim, W.T.; Kim, J.S.; Kim, D.H. Spark plasma sintering of Al-Si-Cu-Fe quasi-crystalline powder. Metall. Mater. Trans. A-Phys. Metall. Mater. Sci. 2003, 34A, 841. [Google Scholar] [CrossRef]
- Li, C.F.; Carey, C.; Li, D.Q.; Caputo, M.; Bouch, R.; Hampikian, H. A study on spherical particles in Al65Cu20Fe15 alloy prepared by arc melting. Mater. Charact. 2018, 140, 162. [Google Scholar] [CrossRef]
- Iams, A.D.; Weaver, J.S.; Lane, B.M.; Giannuzzi, L.A.; Yi, F.; LaPlant, D.L.; Martin, J.H.; Zhang, F. Microstructural features and metastable phase formation in a high-strength aluminum alloy fabricated using additive manufacturing. J. Alloys Compd. 2025, 1025, 180281. [Google Scholar] [CrossRef]
- de Araujo, A.P.M.; Pauly, S.; Batalha, R.L.; Coury, F.G.; Kiminami, C.S.; Uhlenwinkel, V.; Gargarella, P. Additive manufacturing of a quasicrystal-forming Al95Fe2Cr2Ti1 alloy with remarkable high-temperature strength and ductility. Addit. Manuf. 2021, 41, 101960. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Xia, X.; Zou, L.; Yuan, T.; Liu, X.; Lai, D.; Deng, S.; Li, R. A novel Al-Cr-Sc-Zr alloy additively manufactured via laser directed energy deposition: Microstructure, phase analysis and mechanical properties. J. Mater. Process. Technol. 2023, 322, 118204. [Google Scholar] [CrossRef]
- Kairy, S.K.; Gharbi, O.; Nicklaus, J.; Jiang, D.; Hutchinson, C.R.; Birbilis, N. On the Characterization of a Hitherto Unreported Icosahedral Quasicrystal Phase in Additively Manufactured Aluminum Alloy AA7075. Metall. Mater. Trans. A-Phys. Metall. Mater. Sci. 2019, 50A, 529. [Google Scholar] [CrossRef]
- Stan-Głowińska, K.; Zięba, A.; Rogal, Ł. Characterization of quasicrystalline precipitates in artificially aged Al–Mg–Zn alloy with Ga addition. J. Mater. Res. Technol. 2022, 21, 1749. [Google Scholar] [CrossRef]
- Chen, Z.W.; Tang, M.J.; Zhao, K. Effect of rare earth samarium addition on the kinetics of precipitation in Al-Cu-Mn casting alloy. Int. J. Miner. Metall. Mater. 2014, 21, 155. [Google Scholar] [CrossRef]
- Mora, J.; Garcia, P.; Muelas, R.; Aguero, A. Hard Quasicrystalline Coatings Deposited by HVOF Thermal Spray to Reduce Ice Accretion in Aero-Structures Components. Coatings 2020, 10, 290. [Google Scholar] [CrossRef]
- Fu, Y.Q.; Peng, T.X.; Yang, D.M.; Sun, C.Q.; Chen, Y.Z.; Gao, Y. HVOF sprayed Al-Cu-Cr quasicrystalline coatings from coarse feedstock powders. Surf. Coat. Technol. 2014, 252, 29. [Google Scholar] [CrossRef]
- Lepeshev, A.; Sordelet, D.J.; Rozhkova, E.; Ushakov, A. Modification of Structure and Physico-Mechanical Properties of Al-Cu-Fe Quasicrystal Alloy at Plasma Spraying. J. Clust. Sci. 2011, 22, 289. [Google Scholar] [CrossRef]
- Fleury, E.; Kim, Y.C.; Kim, J.S.; Ahn, H.S.; Lee, S.M.; Kim, W.T.; Kim, D.H. Sliding friction and wear behavior of Al-Ni-Co-Si quasicrystalline coatings deposited by the high-velocity oxy-fuel spraying technique. J. Mater. Res. 2002, 17, 492. [Google Scholar] [CrossRef]
- Zupanič, F.; Macerl, M.; Haga, T.; Bončina, T. Microstructure and Indentation Properties of Single-Roll and Twin-Roll Casting of a Quasicrystal-Forming Al-Mn-Cu-Be Alloy. Metals 2022, 12, 187. [Google Scholar] [CrossRef]
- Wang, B.; Zhao, Y.-h.; Hou, H. Study on microstructure and mechanical properties of Mg-xY-6xZn by squeeze casting. Mater. Res. Express 2019, 6, 66574. [Google Scholar] [CrossRef]
- Koga, G.Y.; Branquinho e Silva, A.M.; Wolf, W.; Kiminami, C.S.; Bolfarini, C.; Botta, W.J. Microstructure and mechanical behavior of Al92Fe3Cr2X3 (X = Ce, Mn, Ti, and V) alloys processed by centrifugal force casting. J. Mater. Res. Technol-JMRT 2019, 8, 2092. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Q.; Dong, B.; Liu, Z. Microstructure and Thermal Stability of Icosahedral Quasicrystals in Suction Casting Al-6 at.%Mn(-2 at.%Be) Alloys. J. Mater. Eng. Perform. 2020, 29, 447. [Google Scholar] [CrossRef]
- Fleury, E.; Lee, S.M.; Choi, G.; Kim, W.T.; Kim, D.H. Comparison of Al-Cu-Fe quasicrystalline particle reinforced Al composites fabricated by conventional casting and extrusion. J. Mater. Sci. 2001, 36, 963. [Google Scholar] [CrossRef]
- Tamura, R.; Asao, T.; Takeuchi, S. Roles of Quasiperiodicity and Local Environment in the Electronic Transport of the Icosahedral Quasicrystals in Al-Pd-TM (TM = Fe, Ru, Os) Systems. Mater. Trans. 2001, 42, 928. [Google Scholar] [CrossRef][Green Version]
- Maniraj, M.; Rai, A.; Barman, S.R.; Krajci, M.; Schlagel, D.L.; Lograsso, T.A.; Horn, K. Unoccupied electronic states of icosahedral Al-Pd-Mn quasicrystals: Evidence of image potential resonance and pseudogap. Phys. Rev. B 2014, 90, 5. [Google Scholar] [CrossRef]
- Dolinsek, J.; Vrtnik, S.; Klanjsek, M.; Jaglicic, Z.; Smontara, A.; Smiljanic, I.; Bilusic, A.; Yokoyama, Y.; Inoue, A.; Landauro, C.V. Intrinsic electrical, magnetic, and thermal properties of single-crystalline Al64Cu23Fe13 icosahedral quasicrystal: Experiment and modeling. Phys. Rev. B 2007, 76, 054201. [Google Scholar] [CrossRef]
- Ivkov, J.; Stanic, D.; Popcevic, P.; Smontara, A.; Dolinsek, J.; Gille, P. Hall effect in the crystalline orthorombic o-Al13Co4 approximant to the decagonal quasicrystals. Mater. Tehnol. 2010, 44, 9. [Google Scholar]
- Matsuo, S.; Nakano, H.; Motomura, S.; Ishimasa, T. Ising spin orders conforming to local matching rule and long-range regularity of interactions in penrose lattice. J. Phys. Soc. Jpn. 2005, 74, 1036. [Google Scholar] [CrossRef]
- Shalaeva, E.V.; Prekul, A.F.; Shchegolikhina, N.I.; Medvedeva, N.I. Curie Temperature and Density of States at the Fermi Level for Al-Cu-Fe Phases: Beta-Solid State. Acta Phys. Pol. A 2014, 126, 572. [Google Scholar] [CrossRef]
- Hattori, Y.; Niikura, A.; Tsai, A.P.; Inoue, A.; Masumoto, T.; Fukamichi, K.; Arugakatori, H.; Goto, T. Spin-glass behavior of icosahedral Mg-Gd-Zn and Mg-Tb-Zn quasi-crystals. J. Phys.-Condes. Matter 1995, 7, 2313. [Google Scholar] [CrossRef]
- Takeuchi, T. Thermal conductivity of the Al-based quasicrystals and approximants. Z. Für Krist.-Cryst. Mater. 2009, 224, 35–38. [Google Scholar] [CrossRef]
- Takagiwa, Y.; Maeda, R.; Ohhashi, S.; Tsai, A.-P. Reduction of Thermal Conductivity for Icosahedral Al-Cu-Fe Quasicrystal through Heavy Element Substitution. Materials 2021, 14, 5238. [Google Scholar] [CrossRef]
- Dubois, J.M. Potential and marketed applications of quasicrystalline alloys at room temperature or above. Rend. Lincei.-Sci. Fis. Nat. 2023, 34, 689. [Google Scholar] [CrossRef]
- Yadav, T.P.; Mukhopadhyay, N.K. Quasicrystal: A low-frictional novel material. Curr. Opin. Chem. Eng. 2018, 19, 163. [Google Scholar] [CrossRef]
- Cyrot-Lackmann, F. Quasicrystals as potential candidates for thermoelectric materials. Mater. Sci. Eng. A 2000, 294–296, 611. [Google Scholar] [CrossRef]
- Takagiwa, Y.; Kimura, K.; Sawama, K.; Hiroto, T.; Nishio, K.; Tamura, R. Thermoelectric properties of Tsai-type Au-Al-RE (RE: Yb, Tm, Gd) quasicrystals and approximants. J. Alloys Compd. 2015, 652, 139. [Google Scholar] [CrossRef]
- Takeuchi, S.; Shinoda, K.; Edagawa, K. Dislocation migration and phason strain relaxation in a quasicrystal. Philos. Mag. A-Phys. Condens. Matter Struct. Defect Mech. Prop. 1999, 79, 317. [Google Scholar] [CrossRef]
- Zou, Y.; Kuczera, P.; Sologubenko, A.; Sumigawa, T.; Kitamura, T.; Steurer, W.; Spolenak, R. Superior room-temperature ductility of typically brittle quasicrystals at small sizes. Nat. Commun. 2016, 7, 7. [Google Scholar] [CrossRef] [PubMed]
- Feuerbacher, A.; Schall, P. Plastic behaviour of decagonal Al-Ni-Co single quasicrystals. Scr. Mater. 2003, 49, 25. [Google Scholar] [CrossRef]
- Heggen, M.; Feuerbacher, M.; Schall, P.; Klein, H.; Fisher, I.R.; Canfield, P.C.; Urban, K. Plasticity of icosahedral Zn-Mg-Dy single quasicrystals. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2000, 294, 781. [Google Scholar] [CrossRef]
- Ustinov, A.I.; Polishchuk, S.S.; Skorodzievskii, V.S.; Bliznuk, V.V. Effect of grain size on the damping capacity of quasicrystalline Al-Cu-Fe materials. Surf. Coat. Technol. 2008, 202, 5812. [Google Scholar] [CrossRef]
- Mukhopadhyay, N.K.; Ali, F.; Scudino, S.; Khoshkhoo, M.S.; Stoica, M.; Srivastava, V.C.; Uhlenwinkel, V.; Vaughan, G.; Suryanarayana, C.; Eckert, J. Inverse Hall Petch Like Mechanical Behaviour in Nanophase Al-Cu-Fe Quasicrystals: A New Phenomenon. Acta Phys. Pol. A 2014, 126, 543. [Google Scholar] [CrossRef]
- Boncina, T.; Albu, M.; Zupanic, F. Ageing of Al-Mn-Cu-Be Alloys for Stimulating Precipitation of Icosahedral Quasicrystals. Metals 2020, 10, 937. [Google Scholar] [CrossRef]
- Murty, B.S.; Hono, K. Al-Mg- and Fe-based nanocomposites by rapid solidification processing. Trans. Indian Inst. Met. 2005, 58, 769. [Google Scholar]
- Kenzari, S.; Weisbecker, P.; Curulla, M.; Geandier, G.; Fournee, V.; Dubois, J.M. Formation and properties of Al composites reinforced by quasicrystalline AlCuFeB particles. Philos. Mag. 2008, 88, 755. [Google Scholar] [CrossRef]
- Uflyand, I.E.; Drogan, E.G.; Burlakova, V.E.; Kydralieva, K.A.; Shershneva, I.N.; Dzhardimalieva, G.I. Testing the mechanical and tribological properties of new metal-polymer nanocomposite materials based on linear low-density polyethylene and Al65Cu22Fe13 quasicrystals. Polym. Test. 2019, 74, 178. [Google Scholar] [CrossRef]
- Inoue, A. Amorphous, nanoquasicrystalline and nanocrystalline alloys in Al-based systems. Prog. Mater. Sci. 1998, 43, 365. [Google Scholar] [CrossRef]
- Dubois, J.M.; Lifshitz, R. Quasicrystals: Diversity and complexity. Philos. Mag. 2011, 91, 2971. [Google Scholar] [CrossRef][Green Version]
- Dubois, J.M. Properties- and applications of quasicrystals and complex metallic alloys. Chem. Soc. Rev. 2012, 41, 6760. [Google Scholar] [CrossRef]
- Sekhar, J.A.; Mantri, A.S.; Saha, S.; Balamuralikrishnan, R.; Rao, P.R. Photonic, Low-Friction and Antimicrobial Applications for an Ancient Icosahedral/Quasicrystalline Nano-composite Bronze Alloy. Trans. Indian Inst. Met. 2019, 72, 2105. [Google Scholar] [CrossRef]
- Guo, Y.; Bataev, I.; Georgarakis, K.; Jorge, A.M.; Nogueira, R.P.; Pons, M.; Yavari, A.R. Ni- and Cu-free Ti-based metallic glasses with potential biomedical application. Intermetallics 2015, 63, 86. [Google Scholar] [CrossRef]
- Maciá Barber, E. Chemical Bonding and Physical Properties in Quasicrystals and Their Related Approximant Phases: Known Facts and Current Perspectives. Appl. Sci. 2019, 9, 2132. [Google Scholar] [CrossRef]
- VanCleve, J.E.; White, B.E.; Pohl, R.O. Elastic properties of quasicrystals. Phys. B Condens. Matter 1996, 219–220, 345. [Google Scholar] [CrossRef]
- Shaĭtura, D.S.; Enaleeva, A.A. Fabrication of quasicrystalline coatings: A review. Crystallogr. Rep. 2007, 52, 945. [Google Scholar] [CrossRef]
- Louzguine-Luzgin, D.V.; Inoue, A. Formation and Properties of Quasicrystals. Annu. Rev. Mater. Res. 2008, 38, 403. [Google Scholar] [CrossRef]
- Hippert, F.; Préjean, J.J. Magnetism in quasicrystals. Philos. Mag. 2008, 88, 2175. [Google Scholar] [CrossRef]
- Texier, M.; Joulain, A.; Bonneville, J.; Thilly, L.; Rabier, J. Al-Pd-Mn icosahedral quasicrystal: Deformation mechanisms in the brittle domain. Philos. Mag. 2007, 87, 1497. [Google Scholar] [CrossRef]
- Wollgarten, M.; Saka, H.; Inoue, A. Microstructural investigation of the brittle-to-ductile transition in Al-Pd-Mn quasicrystals. Philos. Mag. A-Phys. Condens. Matter Struct. Defect Mech. Prop. 1999, 79, 2195. [Google Scholar] [CrossRef]
- Vander Voort, G.F. Metallography Principles and Practice; McGraw-Hill: Columbus, OH, USA, 1984. [Google Scholar]
- Kraner, J.; Kevorkijan, V.; Godec, M.; Paulin, I. Metallographic methods for determining the quality of Aluminium alloys. Mater. Technol. 2021, 55, 541. [Google Scholar] [CrossRef]
- Spaić, S. Metalografska Analiza; Fakulteta za naravoslovje in tehnologijo, Oddelek za montanistiko: Ljubljana, Slovenia, 1993. [Google Scholar]
- Jin, Z.; Cai, C.; Hashimoto, T.; Yuan, Y.; Kang, D.; Hunter, J.; Zhou, X. Alkaline etching and desmutting of aluminium alloy: The behaviour of Mg2Si particles. J. Alloys Compd. 2020, 842, 155834. [Google Scholar] [CrossRef]
- Zhu, H. Etching Behavior of Aluminum Alloy Extrusions. JOM 2014, 66, 2222. [Google Scholar] [CrossRef]
- Zupanic, F. Extracting electron backscattering coefficients from backscattered electron micrographs. Mater. Charact. 2010, 61, 1335. [Google Scholar] [CrossRef]
- Vander Voort, G.F. (Ed.) Metallography and Microstructures; ASM Internationals: Science Park, OH, USA, 2004; Volume 9. [Google Scholar]
- Zhao, J.; Wang, B.; Liu, T.; Luo, L.; Wang, Y.; Zheng, X.; Wang, L.; Su, Y.; Guo, J.; Fu, H.; et al. Study of in situ formed quasicrystals in Al-Mn based alloys fabricated by SLM. J. Alloys Compd. 2022, 909, 164847. [Google Scholar] [CrossRef]
- Tiwari, S.; Kesharwani, R.; Jha, K.K.; Mishra, R.; Gope, P.C. Microstructural, texture, and crystallographic analysis of SiC particle incorporation in double-sided friction stir welding of dissimilar aluminium alloys. Mater. Today Commun. 2024, 40, 109543. [Google Scholar] [CrossRef]
- Gao, L.; Harada, Y.; Kumai, S. Microstructural characterization of aluminum alloys using Weck’s reagent, part I: Applications. Mater. Charact. 2015, 107, 426. [Google Scholar] [CrossRef]
- Gao, L.; Harada, Y.; Kumai, S. Microstructural characterization of aluminum alloys using Weck’s reagent, part II: Coloring mechanism. Mater. Charact. 2015, 107, 434. [Google Scholar] [CrossRef]
- Ma, C.; Zhao, Q.; Liu, X.; Li, Y.; Jiang, Q. Introducing high-density growth twins in aluminum alloys by laser surface remelting via templated nucleation of grains. J. Mater. Sci. Technol. 2025, 213, 315. [Google Scholar] [CrossRef]
- Zhao, Y.; He, W.; Zhao, F.; Song, C.; Zhang, W.; Song, D.; Tang, Y.; Sun, Z.; Yin, W.; Xue, Y.; et al. Insight into the Fe-rich phases strengthening mechanisms of non-heat-treatable Al-Mg-Mn-Fe-Cu alloys. J. Mater. Sci. Technol. 2025, 205, 232. [Google Scholar] [CrossRef]
- Möbius, J.; Lippmann, S.; Seyring, M. Vibratory polishing of multiphase CuZn30//CuZn80 diffusion pairs for electron backscatter diffraction (EBSD) characterization. Pract. Metallogr. 2023, 60, 363. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Wu, W.; Liu, Z.W.; Zeng, Y.; Ding, M.J.; Zhang, C.G. Application of Argon Ion Beam Cross Section Polishing in Material Microstructure Research. Key Eng. Mater. 2012, 492, 419. [Google Scholar] [CrossRef]
- Vandervoort, G.F. Imaging by Light Optical Microscopy. In Images Of Materials; Williams, D.B., Pelton, A.R., Gronsky, R., Hirsch, P.B., Eds.; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- DeVries, R.C.; Robertson, C. The microstructure of ballas (polycrystalline diamond) by electrostatic charging in the SEM. J. Mater. Sci. Lett. 1985, 4, 805. [Google Scholar] [CrossRef]
- Petersson, P.; Bergsåker, H.; Possnert, G.; Coad, J.P.; Koivuranta, S.; Likonen, J. Ion beam micro analysis of deposits at tokamak divertor surfaces. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2010, 268, 1838. [Google Scholar] [CrossRef]
- Remond, G.; Nockolds, C.; Phillips, M.; Roques-Carmes, C. Implications of Polishing Techniques in Quantitative X-Ray Microanalysis. J. Res. Natl. Inst. Stand. Technol. 2002, 107, 639. [Google Scholar] [CrossRef]
- Österreicher, J.A.; Kumar, M.; Schiffl, A.; Schwarz, S.; Hillebrand, D.; Bourret, G.R. Sample preparation methods for scanning electron microscopy of homogenized Al-Mg-Si billets: A comparative study. Mater. Charact. 2016, 122, 63. [Google Scholar] [CrossRef]
- Oz, T.; Karakose, E.; Keskin, M. Impact of beryllium additions on thermal and mechanical properties of conventionally solidified and melt-spun Al-4.5 wt.%Mn-x wt.%Be (x = 0, 1, 3, 5) alloys. Mater. Des. 2013, 50, 399. [Google Scholar] [CrossRef]
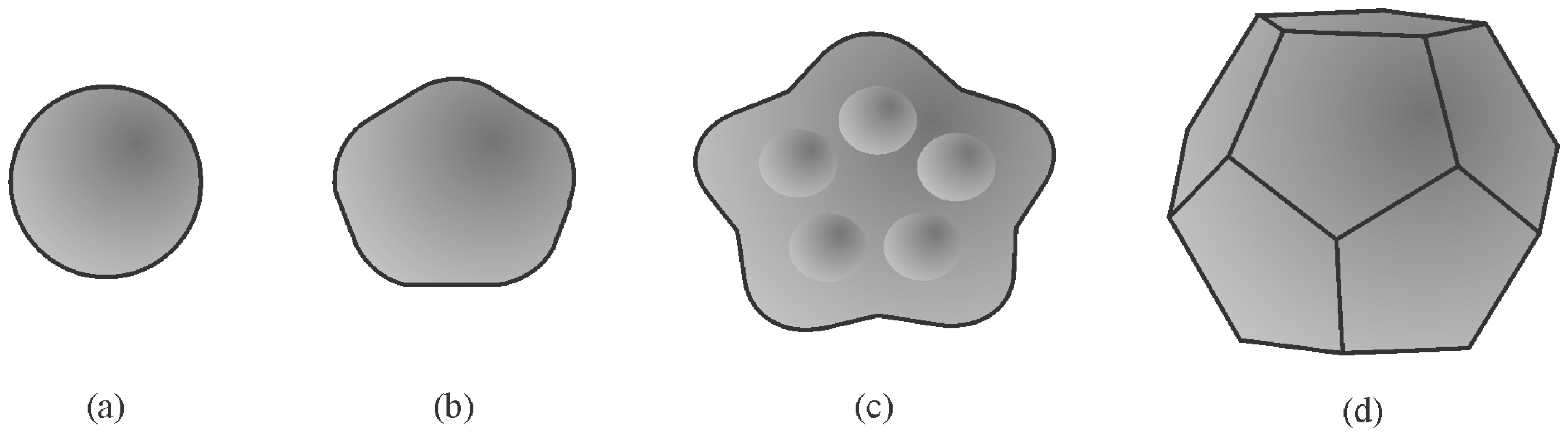
- Chattopadhyay, K.; Ravishankar, N.; Goswami, R. Shapes of quasicrystals. Prog. Cryst. Growth Charact. Mater. 1997, 34, 237. [Google Scholar] [CrossRef]
- Ingersent, K.; Steinhardt, P.J. Quasicrystals with dodecahedral equilibrium faceting. Phys. Rev. Lett. 1988, 60, 2444. [Google Scholar] [CrossRef] [PubMed]
- Thangaraj, N.; Subbanna, G.N.; Ranganathan, S.; Chattopadhyay, K. Electron-microscopy and diffraction of icosahedral and decagonal quasi-crystals in aluminum manganese alloys. J. Microsc.-Oxf. 1987, 146, 287. [Google Scholar] [CrossRef]
- Zhu, M.; Jian, Z.Y.; Liu, C.X.; Yang, G.C.; Zhou, Y.H. Characterization of the Icosahedral Quasicrystal in the Rapidly Solidified Mg-Al-Zn Ternary Alloy. Appl. Mech. Mater. 2011, 71–78, 822. [Google Scholar] [CrossRef]
- Michalcova, A.; Vojtech, D.; Schumacher, G.; Novak, P.; Klementova, M.; Serak, J.; Mudrova, M.; Valdaufova, J. Influence of cooling rate and cerium addition on rapidly solidified Al-TM alloys. Kov. Mater.-Met. Mater. 2010, 48, 1. [Google Scholar] [CrossRef]
- Ishimasa, T.; Nissen, H.U. Electron Microscopy and Image Contrast Calculation of Al-Mn Quasicrystal. Phys. Scr. 1986, 1986, 291. [Google Scholar] [CrossRef]
- Csanády, Á.; Wessicken, R.; Nissen, H.U.; Albert, B.; Griger, A.; Stefániay, V. Rapidly Quenched Al-5.3 at.% Mn Alloy Containing Quasicrystal Units. Mater. Sci. Forum 1987, 13–14, 559. [Google Scholar] [CrossRef]
- Chen, Z.; Hou, Y.; Xie, B.; Zhang, Q. Dendrite Morphology Evolution of Al6Mn Phase in Suction Casting Al-Mn Alloys. Materials 2020, 13, 2388. [Google Scholar] [CrossRef]
- Zupanic, F.; Boncina, T.; Sustarsic, B.; Anzel, I.; Markoli, B. Microstructure of Al-Mn-Be melt-spun ribbons. Mater. Charact. 2008, 59, 1245. [Google Scholar]
- Stan-Glowinska, K.; Rogal, L.; Goral, A.; Wierzbicka-Miernik, A.; Wojewoda-Budka, J.; Schell, N.; Litynska-Dobrzynska, L. Formation of a quasicrystalline phase in Al-Mn base alloys cast at intermediate cooling rates. J. Mater. Sci. 2017, 52, 7794. [Google Scholar] [CrossRef]
- Kim, K.B.; Xu, W.; Tomut, M.; Stoica, M.; Calin, M.; Yi, S.; Lee, W.H.; Eckert, J. Formation of icosahedral phase in an Al93Fe3Cr2Ti2 bulk alloy. J. Alloys Compd. 2007, 436, L1. [Google Scholar] [CrossRef]
- Kim, S.H.; Song, G.S.; Fleury, E.; Chattopadhyay, K.; Kim, W.T.; Kim, D.H. Icosahedral quasicrystalline and hexagonal approximant phases in the Al-Mn-Be alloy system. Philos. Mag. A-Phys. Condens. Matter Struct. Defect Mech. Prop. 2002, 82, 1495. [Google Scholar] [CrossRef]
- Boncina, T.; Markoli, B.; Zupanic, F. Characterization of cast Al86Mn3Be11 alloy. J. Microsc.-Oxf. 2009, 233, 364. [Google Scholar] [CrossRef]
- Chang, H.J.; Fleury, E.; Song, G.S.; Kim, W.T.; Kim, D.H. Formation of quasicrystalline phases in Al-rich Al-Mn-Be alloys. J. Non-Cryst. Solids 2004, 334, 12. [Google Scholar] [CrossRef]
- Ferreira, T.; Koga, G.Y.; Gargarella, P.; Kiminami, C.S.; Botta, W.J.; Bolfarini, C. New Al-alloys with dispersed stable quasicrystal approximant phases: Overcoming the barrier of conventional casting processing and microstructure design. J. Manuf. Process. 2023, 98, 196. [Google Scholar] [CrossRef]
- Schurack, F.; Eckert, J.; Schultz, L. Al-Mn-Ce quasicrystalline composites: Phase formation and mechanical properties. Philos. Mag. 2003, 83, 807. [Google Scholar] [CrossRef]
- Stan-Głowińska, K. Formation of Quasicrystalline Phases and Their Close Approximants in Cast Al-Mn Base Alloys Modified by Transition Metals. Crystals 2018, 8, 61. [Google Scholar] [CrossRef]
- Leskovar, B.; Samardzija, Z.; Koblar, M.; Naglic, I.; Markoli, B. Development of an Al-Mn-Si-Based Alloy with an Improved Quasicrystalline-Forming Ability. JOM 2020, 72, 1533. [Google Scholar] [CrossRef]
- Tahreen, N.; Zhang, D.F.; Pan, F.S.; Jiang, X.Q.; Li, C.; Li, D.Y.; Chen, D.L. Influence of yttrium content on phase formation and strain hardening behavior of Mg-Zn-Mn magnesium alloy. J. Alloys Compd. 2014, 615, 424. [Google Scholar] [CrossRef]
- Zupanic, F.; Boncina, T. Determination of shapes and preferred growth directions of icosahedral quasicrystals from the 2D-sections. J. Alloys Compd. 2016, 681, 532. [Google Scholar] [CrossRef]
- Beeli, C.; Nissen, H.U. Growth-morphology of icosahedral Al-Mn-Pd single quasi-crystals. Philos. Mag. B-Phys. Condens. Matter Stat. Mech. Electron. Opt. Magn. Prop. 1993, 68, 487. [Google Scholar]
- Nissen, H.U.; Wessicken, R.; Beeli, C.; Csanady, A. Al-Mn quasicrystal aggregates with icosahedral morphological symmetry. Philos. Mag. B-Phys. Condens. Matter Stat. Mech. Electron. Opt. Magn. Prop. 1988, 57, 587. [Google Scholar] [CrossRef]
- Zupanic, F.; Boncina, T.; Rozman, N.; Anzel, I.; Grogger, W.; Gspan, C.; Hofer, F.; Markoli, B. Development of an Al-Mn-Be-Cu alloy with improved quasicrystalline forming ability. Z. Kristall. 2008, 223, 735. [Google Scholar] [CrossRef]
- Rozman, N.; Boncina, T.; Zupanic, F. Analytical TEM of i-phase in an Al94Mn2Be2Cu2 alloy. Prakt. Metallogr.-Pract. Metallogr. 2010, 47, 388. [Google Scholar] [CrossRef]
- Boncina, T.; Markoli, B.; Anzel, I.; Zupanic, F. Phases in a quasicrystalline alloy Al(64,4)Cu(23,5)Fe13,1. Mater. Tehnol. 2007, 41, 271. [Google Scholar]
- Zupanič, F.; Bončina, T.; Rozman, N.; Markoli, B. Morphologies of icosahedral quasicrystals in Al-Mn-Be-(Cu) alloys. In Quasicrystals: Types, Systems, and Techniques; Nova Science Publisher, Inc.: New York, NY, USA, 2011; p. 195. [Google Scholar]
- Hansen, V.; Gjønnes, J. Quasicrystals in an aluminium alloy matrix and the transformation to α–AlMnSi via intermediate stages. Philos. Mag. A 1996, 73, 1147. [Google Scholar] [CrossRef]
- Li, Y.J.; Arnberg, L. Quantitative study on the precipitation behavior of dispersoids in DC-cast AA3003 alloy during heating and homogenization. Acta Mater. 2003, 51, 3415. [Google Scholar] [CrossRef]
- Mochugovskiy, A.; Tabachkova, N.; Mikhaylovskaya, A. Annealing induced precipitation of nanoscale icosahedral quasicrystals in aluminum based alloy. Mater. Lett. 2019, 247, 200. [Google Scholar] [CrossRef]
- Mochugovskiy, A.G.; Tabachkova, N.Y.; Ghayoumabadi, M.E.; Cheverikin, V.V.; Mikhaylovskaya, A.V. Joint effect of quasicrystalline icosahedral and L12-strucutred phases precipitation on the grain structure and mechanical properties of aluminum-based alloys. J. Mater. Sci. Technol. 2021, 87, 196. [Google Scholar]
- Mochugovskiy, A.G.; Tabachkova, N.Y.; Mikhaylovskaya, A.V. Nanodispersoids of the quasicrystalline I-phase in Mn- and Mg-bearing aluminum-based alloys. Mater. Lett. 2021, 284, 128945. [Google Scholar]
- Zhan, S.; Xiang, X.M.; Lai, Y.X.; Hu, X.J.; He, Z.B.; Chen, J.H. Nucleation and growth of quasicrystal-related precipitates within the Al-matrix of AlEr(Fe) alloys. Mater. Today Nano 2024, 28, 100522. [Google Scholar] [CrossRef]
- Yoshimura, R.; Konno, T.J.; Abe, E.; Hiraga, K. Transmission electron microscopy study of the evolution of precipitates in aged Al–Li–Cu alloys: The θ′ and T1 phases. Acta Mater. 2003, 51, 4251. [Google Scholar] [CrossRef]
- Lv, P.; Wang, R.; Peng, C.; Cai, Z.; Feng, Y.; Peng, X. The evolution of precipitates and mechanical properties in rapidly solidified 2195 Al–Cu–Li alloy during thermal exposure. J. Mater. Res. Technol. 2023, 27, 6159. [Google Scholar] [CrossRef]
- Gorlov, L.E.; Mosleh, A.O.; Ryzhakova, O.M.; Glavatskikh, M.V.; Barkov, R.Y.; Pozdniakov, A.V. High hardening effect and formation of three types precipitates in the Al-0.3Zr-0.3Gd(Yb) with Fe and Si impurities. J. Alloys Compd. 2025, 1021, 179724. [Google Scholar] [CrossRef]
- Boncina, T.; Zupanic, F. In situ TEM study of precipitation in a quasicrystal-strengthened AL-alloy. Arch. Metall. Mater. 2017, 62, 5. [Google Scholar] [CrossRef][Green Version]
- Zupanic, F.; Wang, D.; Gspan, C.; Boncina, T. Precipitates in a quasicrystal-strengthened Al-Mn-Be-Cu alloy. Mater. Charact. 2015, 106, 93. [Google Scholar][Green Version]
- Stan-Głowińska, K.; Zięba, A.; Chulist, R.; Czaja, P.; Shell, N.; Rogal, Ł. Formation of crystalline and quasicrystalline phases in as-cast and aged Al-Mg-Zn and Al-Mg-Zn-Ga alloys. J. Alloys Compd. 2025, 1016, 178948. [Google Scholar][Green Version]
- Zhang, X.D.; Bi, Y.J.; Loretto, M.H. Structure and stability of the precipitates in melt spun ternary Al-transition-metal alloys. Acta Metall. Et Mater. 1993, 41, 849. [Google Scholar] [CrossRef]
- Singh, A.; Tsai, A.P.; Nakamura, M.; Watanabe, M.; Kato, A. Nanoprecipitates of icosahedral phase in quasicrystal-strengthened Mg-Zn-Y alloys. Philos. Mag. Lett. 2003, 83, 543. [Google Scholar] [CrossRef]
- Ohhashi, S.; Saitoh, K.; Kato, A.; Tsai, A.-P. HAADF-STEM observation of unique quasicrystalline precipitates from solid solution in Mg-Cd-Yb system. Mater. Charact. 2021, 172, 10705. [Google Scholar] [CrossRef]
- Nilsson, J.O.; Stigenberg, A.H.; Liu, P. Isothermal formation of quasi-crystalline precipitates and their effect on strength in a 12Cr-9Ni-4Mo maraging stainless-steel. Metall. Mater. Trans. A-Phys. Metall. Mater. Sci. 1994, 25, 2225. [Google Scholar] [CrossRef]
- Lu, L.; Xiong, D.X.; Wang, J.B.; Zhao, D.S.; Sun, Y.F. Varied linear phason strain and its induced domain structure in quasicrystalline precipitates of Zr-Al-Ni-Cu-Nb bulk metallic glass matrix composites. J. Mater. Res. 2012, 27, 3041. [Google Scholar] [CrossRef]
- Kuhn, U.; Eckert, J.; Schultz, L. Annealing-induced phase transitions in a Zr-Ti-Nb-Cu-Ni-Albulkmetallic glass matrix composite containing quasicrystalline precipitates. Int. J. Mater. Res. 2006, 97, 996. [Google Scholar]
- Bončina, T.; Zupanič, F. Metallographic Techniques for analysing nanoparticles in high-strength Al-Mn-Cu-X based alloys. In Proceedings of the Aluminium Two Thousand—ICEB: 12th Aluminium Two Thousand World Congress—7th ICEB International Congress, Bologna, Italy, 19–23 September 2023; Interall: Bologna, Italy, 2023. [Google Scholar]
- Hanke, L.D.; Schenk, K.H.; Scholz, D.R. Broad Beam Ion Milling for Microstructure Characterization. Mater. Perform. Charact. 2016, 5, 767. [Google Scholar] [CrossRef]
- Barienti, K.; Kahra, C.; Herbst, S.; Nürnberger, F.; Maier, H.J. Ion Beam Processing for Sample Preparation of Hybrid Materials with Strongly Differing Mechanical Properties. Metallogr. Microstruct. Anal. 2020, 9, 54. [Google Scholar] [CrossRef]
- Hanke, L.D.; Scholz, D. Microstructure Enhancement Using Ion Beam Milling. Microsc. Microanal. 2015, 21, 597. [Google Scholar] [CrossRef]
- Naresh-Kumar, G.; Trager-Cowan, C.; Mingard, K.P. Electron Channelling Contrast Imaging in a Low Voltage Scanning Electron Microscope. Microsc. Microanal. 2019, 25, 504. [Google Scholar] [CrossRef]
- Shindo, D.; Hiraga, K.; Williams, T.; Hirabayashi, M.; Inoue, A.; Masumoto, T. Electron channeling effect in an Al-Fe-Cu quasicrystal. Jpn. J. Appl. Phys. Part 2—Lett. 1989, 28, L688. [Google Scholar] [CrossRef]
- Winkelmann, A.; Cios, G.; Tokarski, T.; Nolze, G.; Hielscher, R.; Koziel, T. EBSD orientation analysis based on experimental Kikuchi reference patterns. Acta Mater. 2020, 188, 376. [Google Scholar] [CrossRef]
- Labib, F.; Ohhashi, S.; Tsai, A.P. Formation and crystallographic orientation study of quasicrystal, 2/1 and 1/1 approximants in Cd-Mg-Y system using electron backscatter diffraction (EBSD). Philos. Mag. 2019, 99, 1528. [Google Scholar]
- Tanaka, R.; Ohhashi, S.; Fujita, N.; Demura, M.; Yamamoto, A.; Kato, A.; Tsai, A.P. Application of electron backscatter diffraction (EBSD) to quasicrystal-containing microstructures in the Mg-Cd-Yb system. Acta Mater. 2016, 119, 193. [Google Scholar] [CrossRef]
- Naglič, I.; Leskovar, B.; Samardžija, Z.; Markoli, B. Influence of Ga on the formation of phases in cast Al–Mn-based alloys. Intermetallics 2021, 136, 107263. [Google Scholar]
- Pinard, P.; Hovington, P.; Lagacé, M.; Gauvin, R. Development of Tools to Increase the Spatial Resolution of EBSD Maps. Microsc. Microanal. 2009, 15, 422. [Google Scholar] [CrossRef][Green Version]
- Brodusch, N.; Demers, H.; Trudeau, M.; Gauvin, R. Acquisition parameters optimization of a transmission electron forward scatter diffraction system in a cold-field emission scanning electron microscope for nanomaterials characterization. Scanning 2013, 35, 375. [Google Scholar] [CrossRef]
- Brodusch, N.; Demers, H.; Gauvin, R. Nanometres-resolution Kikuchi patterns from materials science specimens with transmission electron forward scatter diffraction in the scanning electron microscope. J. Microsc. 2013, 250, 1. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Xu, J.; Zhang, Y.; Wang, Y.; Zhang, J.; Yu, B.; Zeng, Y.; Miao, H. Spatial Resolutions of On-Axis and Off-Axis Transmission Kikuchi Diffraction Methods. Appl. Sci. 2019, 9, 4478. [Google Scholar] [CrossRef]
- Babinsky, K.; De Kloe, R.; Clemens, H.; Primig, S. A novel approach for site-specific atom probe specimen preparation by focused ion beam and transmission electron backscatter diffraction. Ultramicroscopy 2014, 144, 9. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.W.; Sun, C.; Gauvin, R.; Wu, W.; Zeng, Y.; Demers, H. High Spatial Resolution EDS Mapping of Nanoparticles at Low Accelerating Voltage. J. Test. Eval. 2016, 44, 2285. [Google Scholar]
- Farkoosh, A.R.; Dunand, D.C.; Seidman, D.N. Enhanced age-hardening response and creep resistance of an Al-0.5Mn-0.3Si (at.%) alloy by Sn inoculation. Acta Mater. 2022, 240, 118344. [Google Scholar] [CrossRef]
- Shao, X.H.; Yang, H.J.; Jin, Q.Q.; Song, Y.Y.; Wang, J.; Zhang, B.; Ma, X.L. Nanoscale precipitates with quasicrystal domains enhanced strength-ductility synergy in a Mg–6Zn–4Al–1Sn–0.5Mn alloy. Mater. Sci. Eng. A 2022, 848, 143425. [Google Scholar] [CrossRef]
- Kang, H.-J.; Hu, Z.-L.; Gao, X.-X.; Chen, Z.-N.; Lu, Y.-P.; Jie, J.-C.; Guo, J.-J. 3D Morphology and Formation Process of the Icosahedral Quasicrystalline Phase in Rapidly Solidified Al–Mn Alloy. Acta Metall. Sin. (Engl. Lett.) 2016, 29, 28. [Google Scholar] [CrossRef][Green Version]
- Boncina, T. Shapes of the icosahedral quasicrystalline phase in melt-spun ribbons. Metalurgija 2013, 52, 65. [Google Scholar][Green Version]
- Gupta, A.K.; Marois, P.H.; Lloyd, D.J. Review of the techniques for the extraction of second-phase particles from aluminum alloys. Mater. Charact. 1996, 37, 61. [Google Scholar] [CrossRef]
- Milenkovic, S.; Dalbert, V.; Marinkovic, R.; Hassel, A.W. Selective matrix dissolution in an Al–Si eutectic. Corros. Sci. 2009, 51, 1490. [Google Scholar] [CrossRef]
- Guzowski, M.M.; Sigworth, G.K.; Sentner, D.A. The role of boron in the grain Refinement of Aluminum with Titanium. Metall. Trans. A 1987, 18, 603. [Google Scholar] [CrossRef]
- Durinikova, E.; Tillová, E.; Chalupová, M.; Hurtalová, L. Use of unconventional methods of etching in the analysis of intermetallic phases in secondary aluminium alloy. MTM Int. Vurtual J. 2012, 9, 7–10. [Google Scholar]
- Davis, J.R. Corrosion of Aluminium and Aluminium Alloys; Butterworth-Heinemann Ltd.: Oxford, UK, 1995. [Google Scholar]
- Boncina, T.; Markoli, B.; Anzel, I.; Zupanic, F. Metallographic techniques for the characterization of quasicrystalline phases in aluminium alloys. Z. Kristall. 2008, 223, 747. [Google Scholar] [CrossRef]
- Kang, H.; Wang, T.; Lu, Y.; Jie, J.; Li, X.; Su, Y.; Guo, J. Controllable 3D morphology and growth mechanism of quasicrystalline phase in directionally solidified Al–Mn–Be alloy. J. Mater. Res. 2014, 29, 2547. [Google Scholar] [CrossRef]
- Wang, D.; Peng, L.; Gourlay, C.M. Al-Mn-based decagonal quasicrystal in AZ magnesium alloys and its nucleation on Al8Mn5 during solidification. Scr. Mater. 2024, 241, 115886. [Google Scholar] [CrossRef]
- Bončina, T.; Zupanič, F. Methods of Deep etching and particle extracting for controlling of aluminium alloys. Mater. Today Proc. 2019, 10, 248. [Google Scholar] [CrossRef]
- Bončina, T.; Zupanič, F.; Markoli, B. Procedure of Dynamic Deep Etching and Particle Extraction from Aluminium Alloys. EP2458033A1, 12 September 2013. [Google Scholar]
- Matsuo, Y.; Yamamoto, K.; Ishii, Y. Investigation of phason strains in decagonal Al-Pd-Mn single quasicrystals by means of x-ray diffraction. J. Phys.-Condes. Matter 1998, 10, 983. [Google Scholar] [CrossRef]
- Kral, M.V.; Mangan, M.A.; Spanos, G.; Rosenberg, R.O. Three-dimensional analysis of microstructures. Mater. Charact. 2000, 45, 17. [Google Scholar] [CrossRef]
- Mura, F.; Cognigni, F.; Ferroni, M.; Morandi, V.; Rossi, M. Advances in Focused Ion Beam Tomography for Three-Dimensional Characterization in Materials Science. Materials 2023, 16, 5808. [Google Scholar] [CrossRef] [PubMed]
- Lasagni, F.; Lasagni, A.; Marks, E.; Holzapfel, C.; Mücklich, F.; Degischer, H.P. Three-dimensional characterization of ‘as-cast’ and solution-treated AlSi12(Sr) alloys by high-resolution FIB tomography. Acta Mater. 2007, 55, 3875. [Google Scholar] [CrossRef]
- Singh, S.S.; Loza, J.J.; Merkle, A.P.; Chawla, N. Three dimensional microstructural characterization of nanoscale precipitates in AA7075-T651 by focused ion beam (FIB) tomography. Mater. Charact. 2016, 118, 102. [Google Scholar] [CrossRef]
- Hu, Y.; She, Y.; Wu, S.; Kan, Q.; Yu, H.; Kang, G. Critical physics-informed fatigue life prediction of laser 3D printed AlSi10Mg alloys with mass internal defects. Int. J. Mech. Sci. 2024, 284, 109730. [Google Scholar] [CrossRef]
- Matsuyama, S.; Yasuda, S.; Yamada, J.; Okada, H.; Kohmura, Y.; Yabashi, M.; Ishikawa, T.; Yamauchi, K. 50-nm-resolution full-field X-ray microscope without chromatic aberration using total-reflection imaging mirrors. Sci. Rep. 2017, 7, 46358. [Google Scholar] [CrossRef]
- Kleibert, A.; Vaz, C.A.F.; Erni, R. Correlative transmission electron and soft x-ray microscopy for bridging length scales and functional properties in nanoscience and materials research. Nano Today 2025, 63, 102732. [Google Scholar] [CrossRef]























| Alloy System | Quasicrystal Type |
|---|---|
| Al86Mn14 | icosahedral |
| Al4Mn | decagonal |
| Al70Mn10Pd20 | icosahedral |
| Al70Mn15Pd15 | decagonal |
| Al3Mn82Si15 | octagonal |
| Al65Cu25Fe5V5 | dodecagonal |
| Al55Si25Mn20 | icosahedral |
| Al63Cu25Fe12 | icosahedral |
| Al54Pd30Yb16 | icosahedral |
| Al70Ni20Rh10 | icosahedral |
| Al6Li3Au | icosahedral |
| Al70Pd20Tc10 | icosahedral |
| Al73Pd18Re9 | icosahedral |
| Al92Fe3Cr2Ti3 | icosahedral |
| Property | Typical Characteristics | Reference |
|---|---|---|
| Electrical conductivity | Extremely low: ~10−3 to 10−5 Ω−1·cm−1 (semiconductor-like) | [136] |
| Thermal conductivity | 1–2 W·m−1·K−1—low due to phonon scattering | [119] |
| Elastic moduli | Young’s modulus: 60–140 GPa | [137] |
| Hardness | Vickers hardness: 5–9 GPa | [138] |
| Friction coefficient | Extremely low: ~0.05 | |
| Thermoelectric power (Seebeck coefficient) | Up to 200–400 µV/K | [119] |
| Internal friction | Low at T < 4 K; resembles amorphous solids | [137] |
| Corrosion and oxidation resistance | High, similar to stainless steel | [139] |
| Magnetic properties | Low concentrations of magnetic atoms (e.g., Mn, rare-earth elements) and spin-glass behaviour are due to the random distribution of localised moments Competing Kondo and RKKY interactions without long-range magnetic order. Unusual antiferromagnetic correlations influenced by aperiodicity | [140] |
| Fracture behaviour | brittle | [141,142] |
| Etchant | Etching Conditions | Reference |
|---|---|---|
| Keller’s reagent (1 mL of HF, 1.5 mL of HCl, 2.5 mL of HNO3, 95 mL of distilled water) | Room temperature, 10–20 s | [150,151] |
| Kroll’s reagent (10 mL of HNO3, 5 mL of HF, 85 mL of H2O) | Room temperature, 5–15 s | [82] |
| NaOH, 0.83 mol/L | Room temperature | [70] |
| Weck’s reagent 4 g of KMnO4, 1 g of NaOH, and 100 mL of distilled water for colour etching | Room temperature, 15–30 s | [152,153] |
| Barker’s reagent (5 mL HBF4 (40%) in 200 mL of distilled water) | Electrolytic etching, 20–30 V, direct current, 30 s, room temperature | [154,155] |
| Chemical Extraction Method | Alloy | Characteristics | Reference |
|---|---|---|---|
| 250 mL methyl alcohol solution with 2 wt.% KI, electrolytic etching, 2–5 V, 0.1–0.3 A | Al6Mn (14.3 at.% Mn) and Al17Mn (5.6 at.% Mn) | Preservation of quasicrystalline particles | [185] |
| Slightly acidic medium | Al-5,3 at.% Mn | Preservation of Al6Mn and Al4Mn, but dissolved IQC | [170] |
| perchloric acid (HClO4) and 20% methanol, electropolishing at −20 °C | Al6Mn (14.3 at.% Mn) and Al17Mn (5.6 at.% Mn) | Complete dissolution of IQC | [185] |
| NaOH aqueous solution (undefined composition) | Al–6Mn–2.5Be | Preservation of primary IQC-particles | [234] |
| 5% aqueous solution of NaOH for 30 s | Al-Mn-Be-Cu alloy | Dissolution of IQC | [201] |
| electro-etched in a 250 mL methyl alcohol solution with 2 wt.% % KI; 10 V, 25 °C, 0.1 A/cm2 | Melt-spun Al-Mn | 3D morphology of IQC was preserved | [226] |
| 10% nitric acid in ethanol for 5–10 min. They could dissolve the magnesium-rich matrix to | AZ magnesium alloy | Preservation of Al-Mn-based decagonal quasicrystals and some other crystalline phases | [235] |
| 5% nitric acid solution in 95% ethanol | Mg-Al-Zn alloys | Preservation of IQC | [167] |
| 2.5 mL HCl, 5 mL HNO3, and 1 mL HF | Al-Mn-Be and Al-Mn-Be-Cu alloys | Strong attack on the intermetallic phases | [236] |
| 5 mL HNO3, 2,5 mL HCl, and 70 mL alcohol for 30 s | Al-Mn-Be and Al-Mn-Be-Cu alloys | Complete dissolution of IQC | [236] |
| 10 g of iodine and 25 g of tartaric acid in 250 mL of methanol | Al-Ti-B | Preservation of TiB2 and Al3Ti | [230] |
| Variable contents of iodine and tartaric acid in methanol | Al-Mn-Be and Al-Mn-Be-Cu alloys | Preservation of IQC and other intermetallic phases | [237] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bončina, T.; Zupanič, F. Metallography of Quasicrystals in Al-Alloys. Materials 2025, 18, 4575. https://doi.org/10.3390/ma18194575
Bončina T, Zupanič F. Metallography of Quasicrystals in Al-Alloys. Materials. 2025; 18(19):4575. https://doi.org/10.3390/ma18194575
Chicago/Turabian StyleBončina, Tonica, and Franc Zupanič. 2025. "Metallography of Quasicrystals in Al-Alloys" Materials 18, no. 19: 4575. https://doi.org/10.3390/ma18194575
APA StyleBončina, T., & Zupanič, F. (2025). Metallography of Quasicrystals in Al-Alloys. Materials, 18(19), 4575. https://doi.org/10.3390/ma18194575








