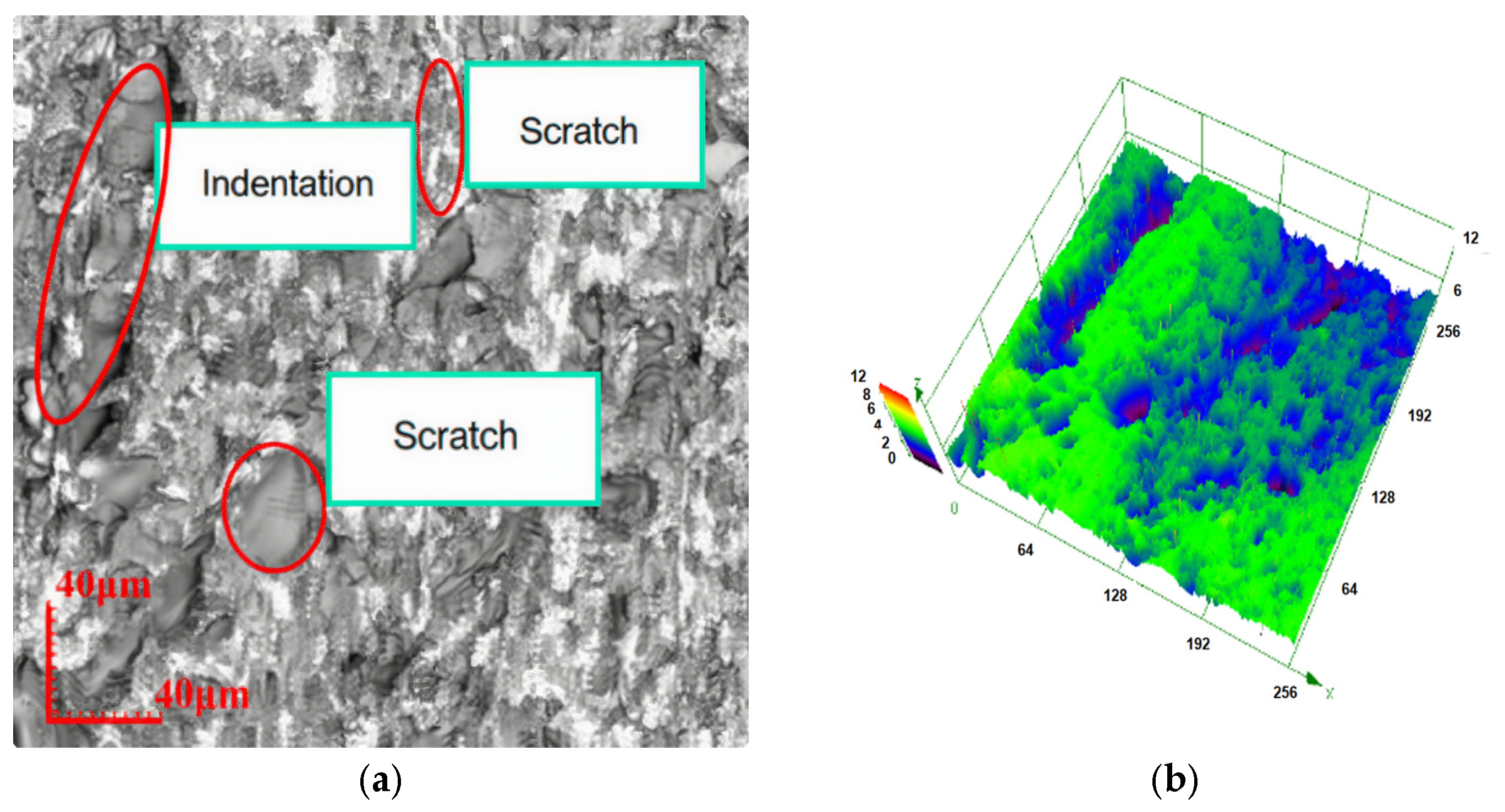
Figure 1.
Subsurface damage structure diagram.
Figure 1.
Subsurface damage structure diagram.
Figure 2.
Grinding schematic diagram.
Figure 2.
Grinding schematic diagram.
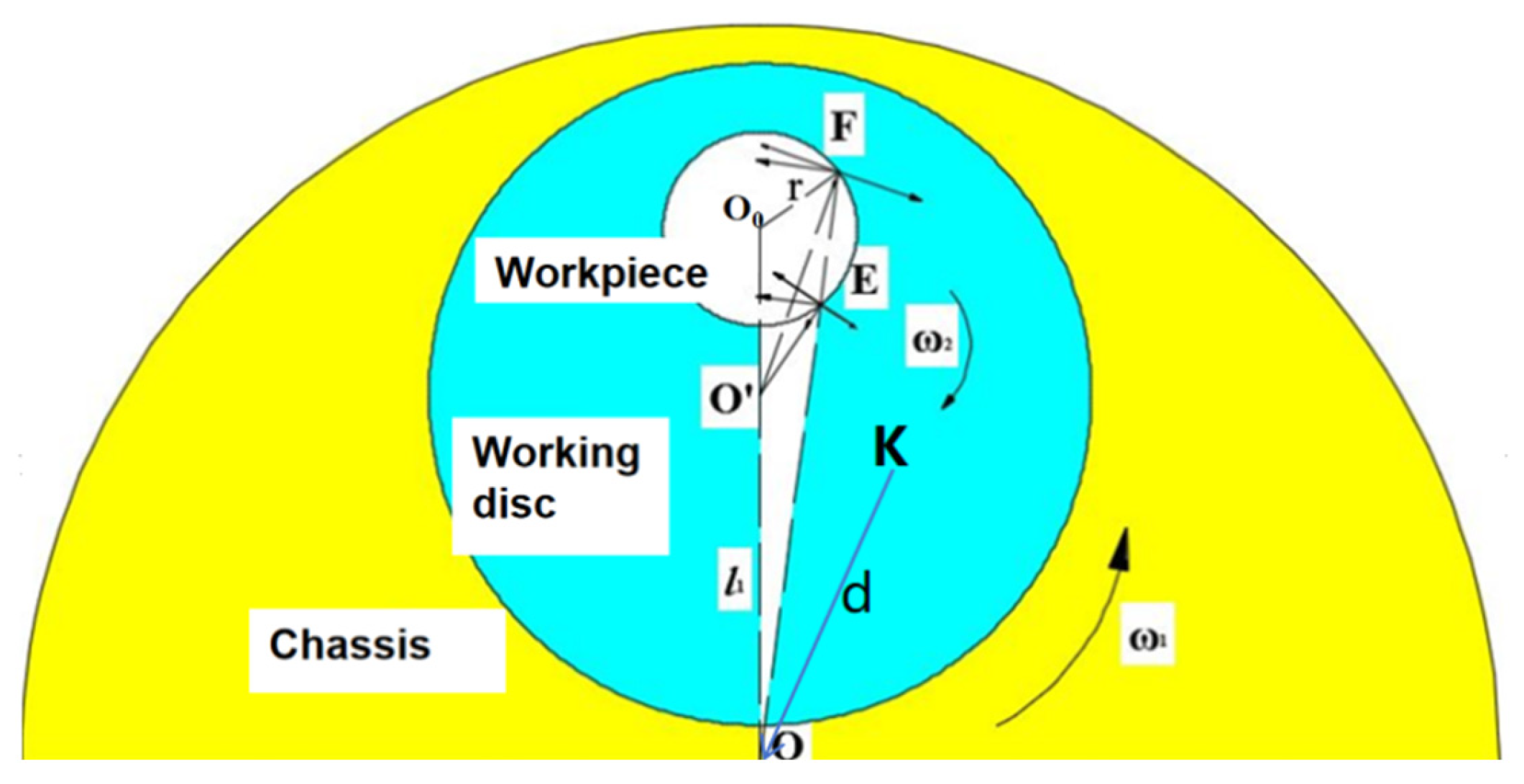
Figure 3.
Geometric representation of the workpiece disc.
Figure 3.
Geometric representation of the workpiece disc.
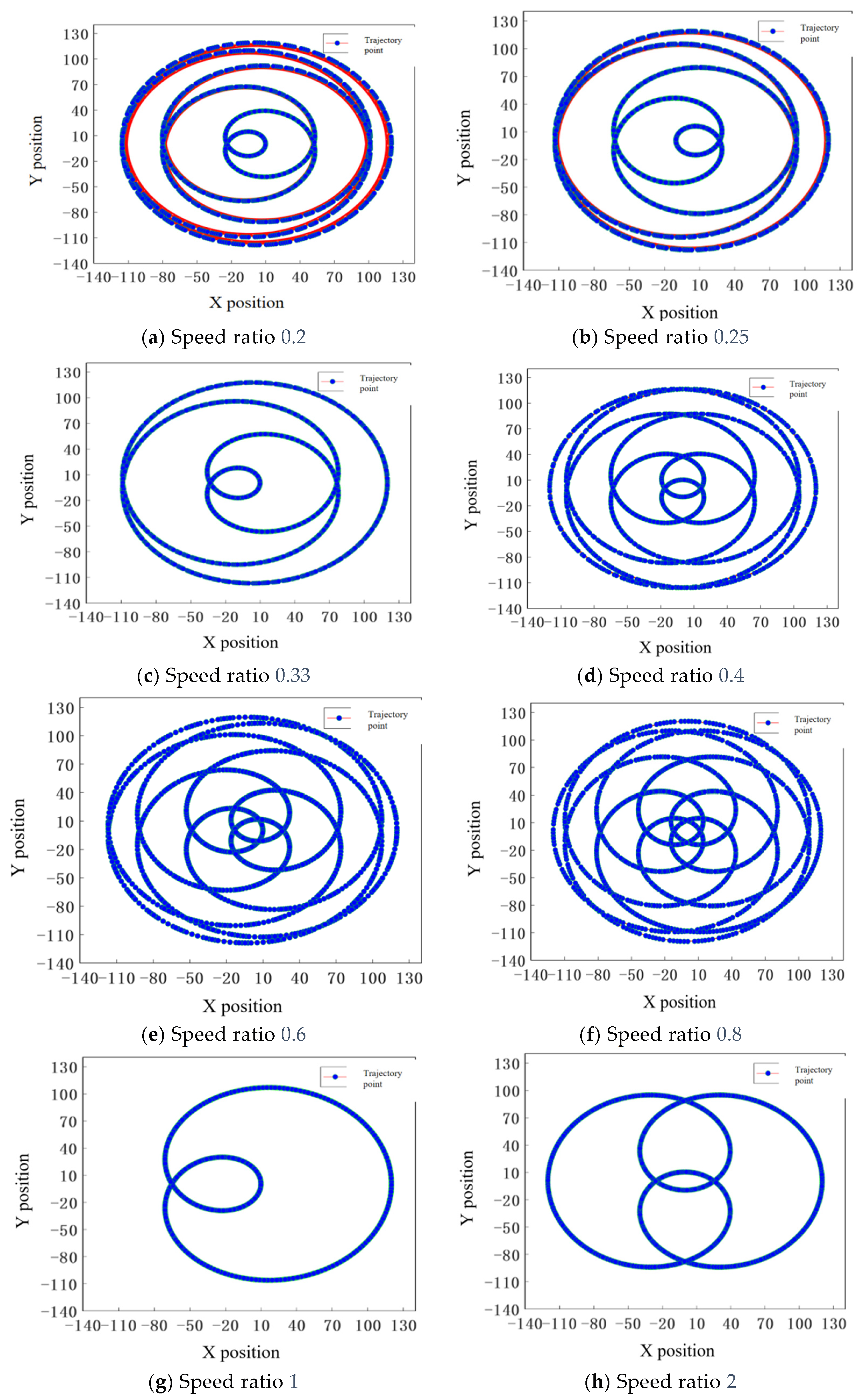
Figure 4.
Trajectory diagram of point K at different speed ratios.
Figure 4.
Trajectory diagram of point K at different speed ratios.
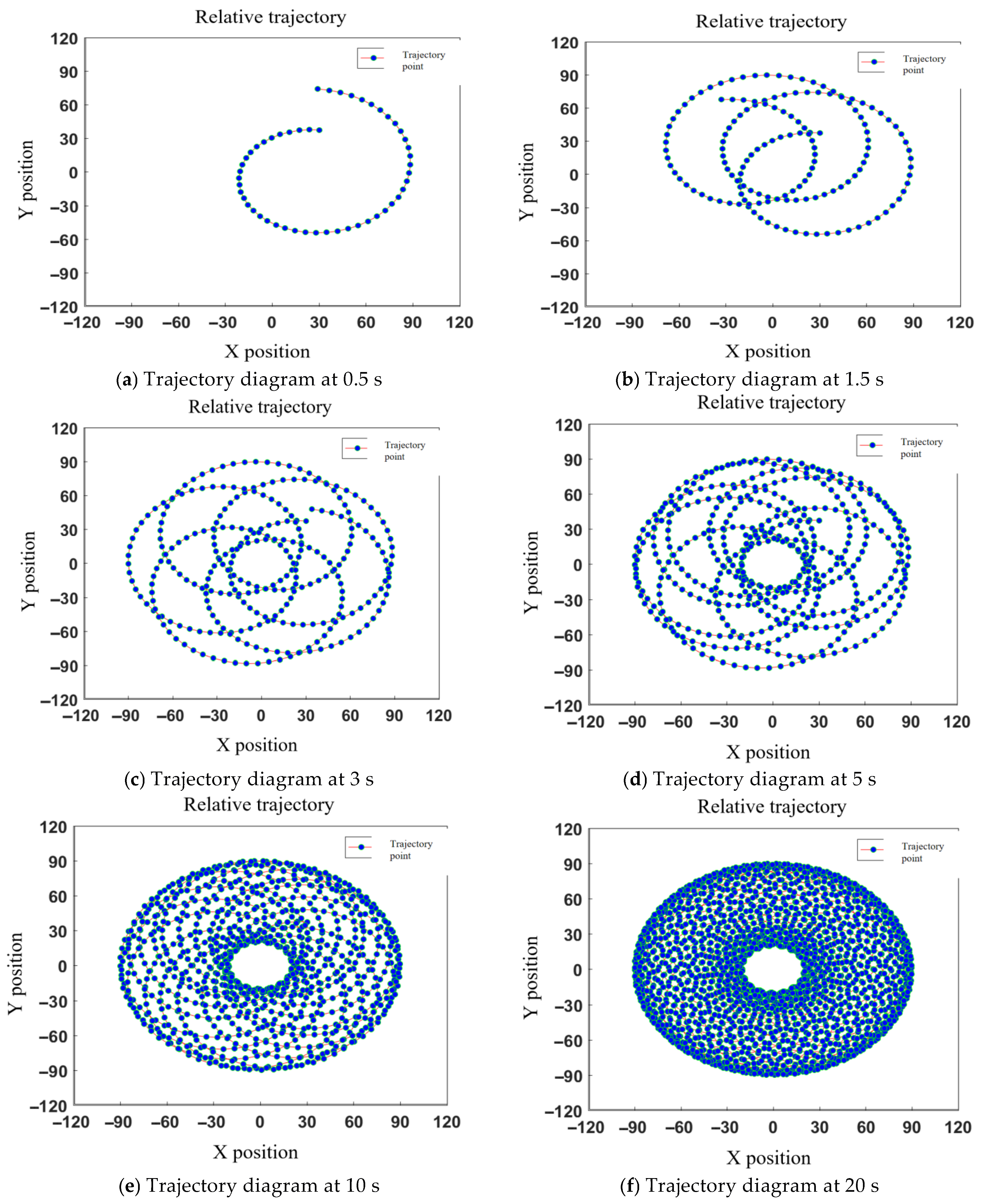
Figure 5.
Relative trajectory diagram of point K at different moments.
Figure 5.
Relative trajectory diagram of point K at different moments.
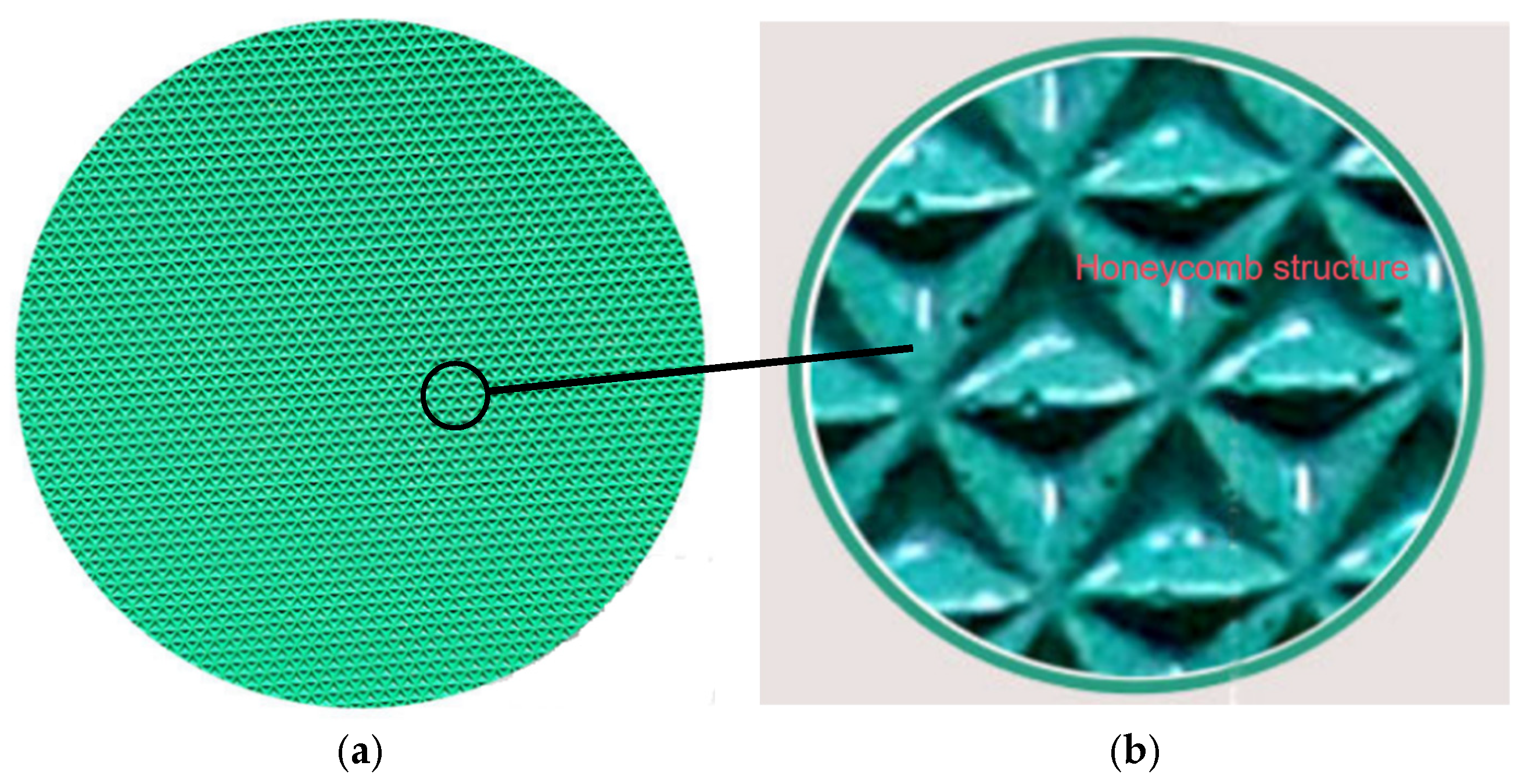
Figure 6.
(a) Schematic diagram of the grinding disc. (b) Partial view of the grinding disc.
Figure 6.
(a) Schematic diagram of the grinding disc. (b) Partial view of the grinding disc.
Figure 7.
Surface topographies for different abrasive grain sizes. (a) Two-dimensional surface after grinding with 28 μm grinding disc. (b) Three-dimensional surface after grinding with 28 μm grinding disc. (c) Two-dimensional surface after grinding with 20 μm grinding disc. (d) Three-dimensional surface after grinding with 20 μm grinding disc. (e) Two-dimensional surface after grinding with 14 μm grinding disc. (f) Three-dimensional surface after grinding with 14 μm grinding disc. (g) Two-dimensional surface after grinding with 10 μm grinding disc. (h) Three-dimensional surface after grinding with 10 μm grinding disc.
Figure 7.
Surface topographies for different abrasive grain sizes. (a) Two-dimensional surface after grinding with 28 μm grinding disc. (b) Three-dimensional surface after grinding with 28 μm grinding disc. (c) Two-dimensional surface after grinding with 20 μm grinding disc. (d) Three-dimensional surface after grinding with 20 μm grinding disc. (e) Two-dimensional surface after grinding with 14 μm grinding disc. (f) Three-dimensional surface after grinding with 14 μm grinding disc. (g) Two-dimensional surface after grinding with 10 μm grinding disc. (h) Three-dimensional surface after grinding with 10 μm grinding disc.
Figure 8.
Relationship between abrasive grain size and workpiece removal.
Figure 8.
Relationship between abrasive grain size and workpiece removal.
Figure 9.
Surface topography at different grinding pressures. (a) Two-dimensional surface at 13.61 10−3 MPa. (b) Three-dimensional surface at 13.61 10−3 MPa. (c) Two-dimensional surface at 10.42 10−3 MPa. (d) Three-dimensional surface at 10.42 10−3 MPa. (e) Two-dimensional surface at 7.24 10−3 MPa. (f) Three-dimensional surface at 7.24 10−3 MPa. (g) Two-dimensional surface at 4.05 10−3 MPa. (h) Three-dimensional surface at 4.05 10−3 MPa.
Figure 9.
Surface topography at different grinding pressures. (a) Two-dimensional surface at 13.61 10−3 MPa. (b) Three-dimensional surface at 13.61 10−3 MPa. (c) Two-dimensional surface at 10.42 10−3 MPa. (d) Three-dimensional surface at 10.42 10−3 MPa. (e) Two-dimensional surface at 7.24 10−3 MPa. (f) Three-dimensional surface at 7.24 10−3 MPa. (g) Two-dimensional surface at 4.05 10−3 MPa. (h) Three-dimensional surface at 4.05 10−3 MPa.
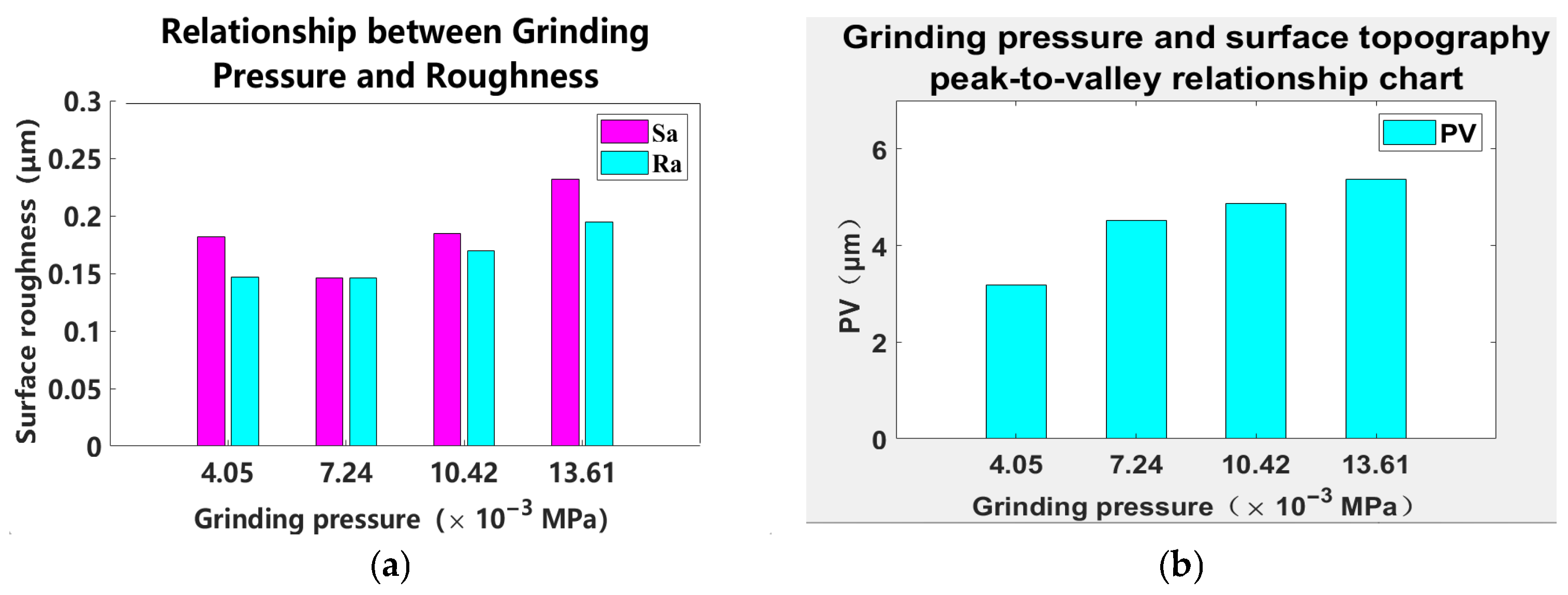
Figure 10.
Relationship between grinding pressure and surface quality. (a) Relationship between grinding pressure and roughness. (b) Relationship between grinding pressure and surface PV.
Figure 10.
Relationship between grinding pressure and surface quality. (a) Relationship between grinding pressure and roughness. (b) Relationship between grinding pressure and surface PV.
Figure 11.
Relationship between grinding pressure and workpiece removal. (a) Grinding pressure and removal amount. (b) Grinding pressure and removal rate.
Figure 11.
Relationship between grinding pressure and workpiece removal. (a) Grinding pressure and removal amount. (b) Grinding pressure and removal rate.
Figure 12.
Comparison of abrasive grain size and grinding pressure effects.
Figure 12.
Comparison of abrasive grain size and grinding pressure effects.
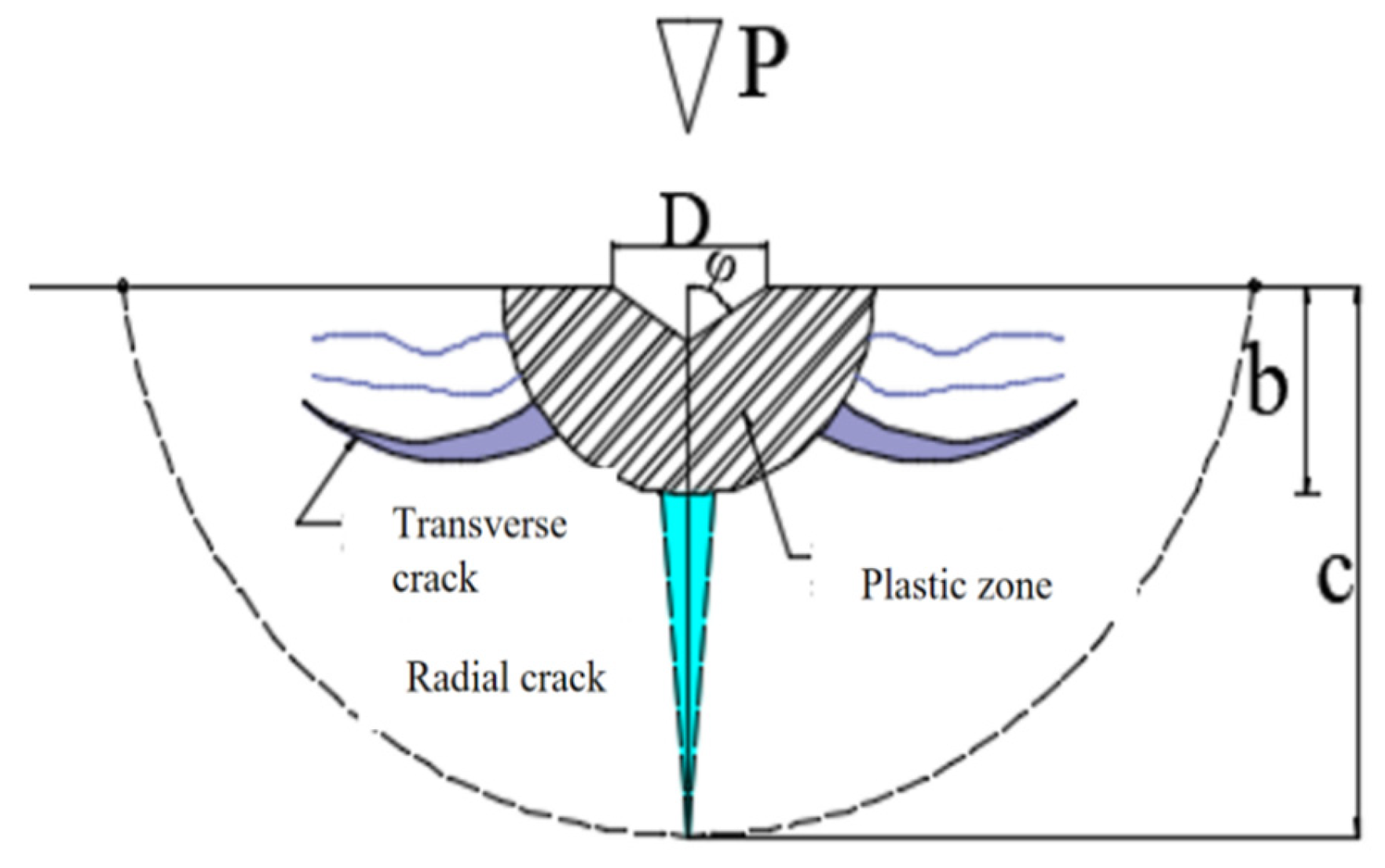
Figure 13.
Sharp indenter model.
Figure 13.
Sharp indenter model.
Figure 14.
Indenter penetration area.
Figure 14.
Indenter penetration area.
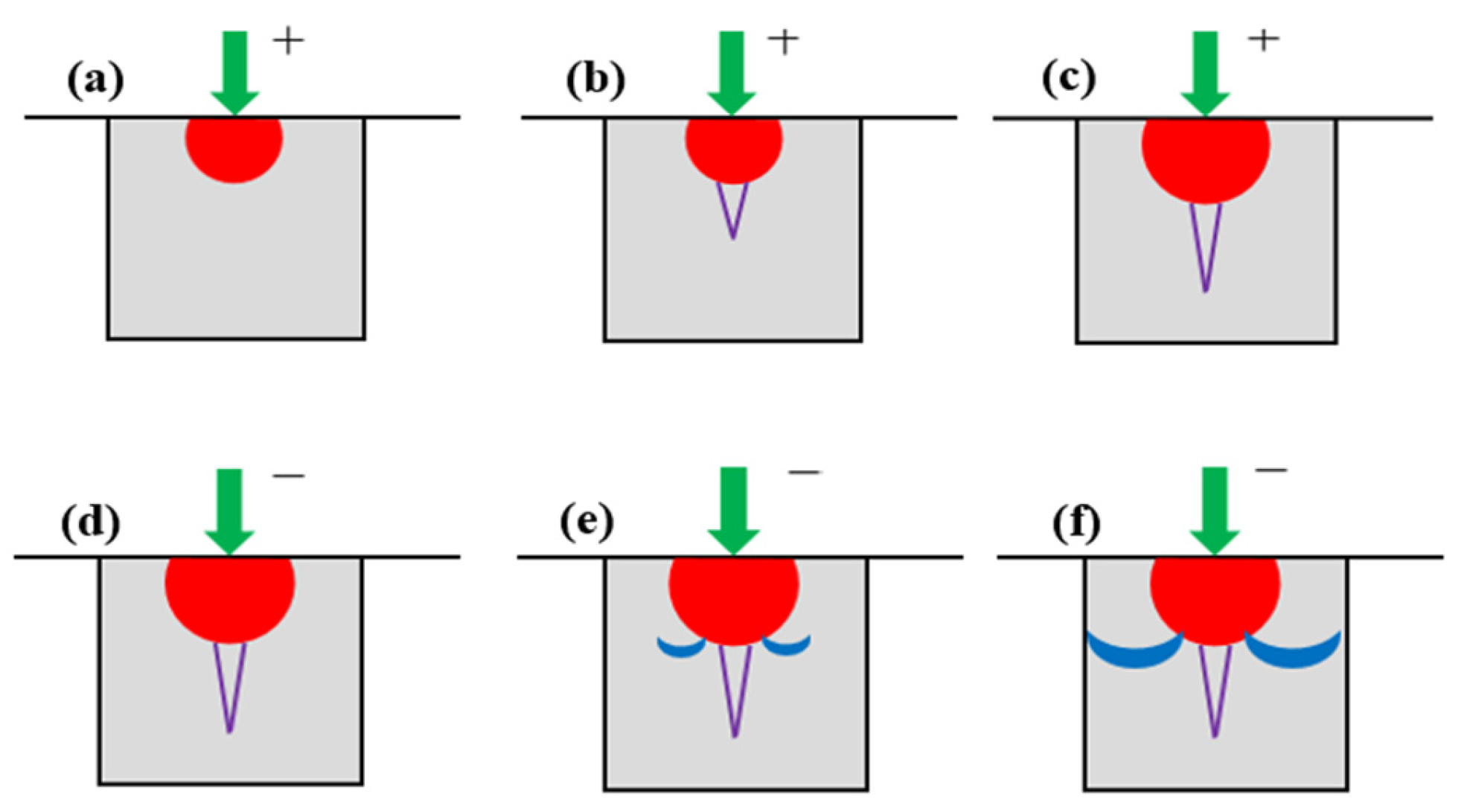
Figure 15.
Schematic of Crack Development Under the Action of a Sharp Indenter. (a) When the sharp indenter presses into the glass surface, plastic and irreversible deformation occurs in the contact area, accompanied by microcracks. (b) Damage propagates within the irreversible deformation zone, resulting in the generation of radial cracks. (c) Radial cracks extend further downward. (d) When the indenter begins to retract, the propagation of radial cracks below this deformation zone ceases and begins to close. (e) After the indenter is fully withdrawn, residual stresses cause radial cracks to extend and generate transverse cracks in the lower part of the deformation zone. (f) After the indenter completely separates from the glass surface, the propagation of cracks ceases.
Figure 15.
Schematic of Crack Development Under the Action of a Sharp Indenter. (a) When the sharp indenter presses into the glass surface, plastic and irreversible deformation occurs in the contact area, accompanied by microcracks. (b) Damage propagates within the irreversible deformation zone, resulting in the generation of radial cracks. (c) Radial cracks extend further downward. (d) When the indenter begins to retract, the propagation of radial cracks below this deformation zone ceases and begins to close. (e) After the indenter is fully withdrawn, residual stresses cause radial cracks to extend and generate transverse cracks in the lower part of the deformation zone. (f) After the indenter completely separates from the glass surface, the propagation of cracks ceases.
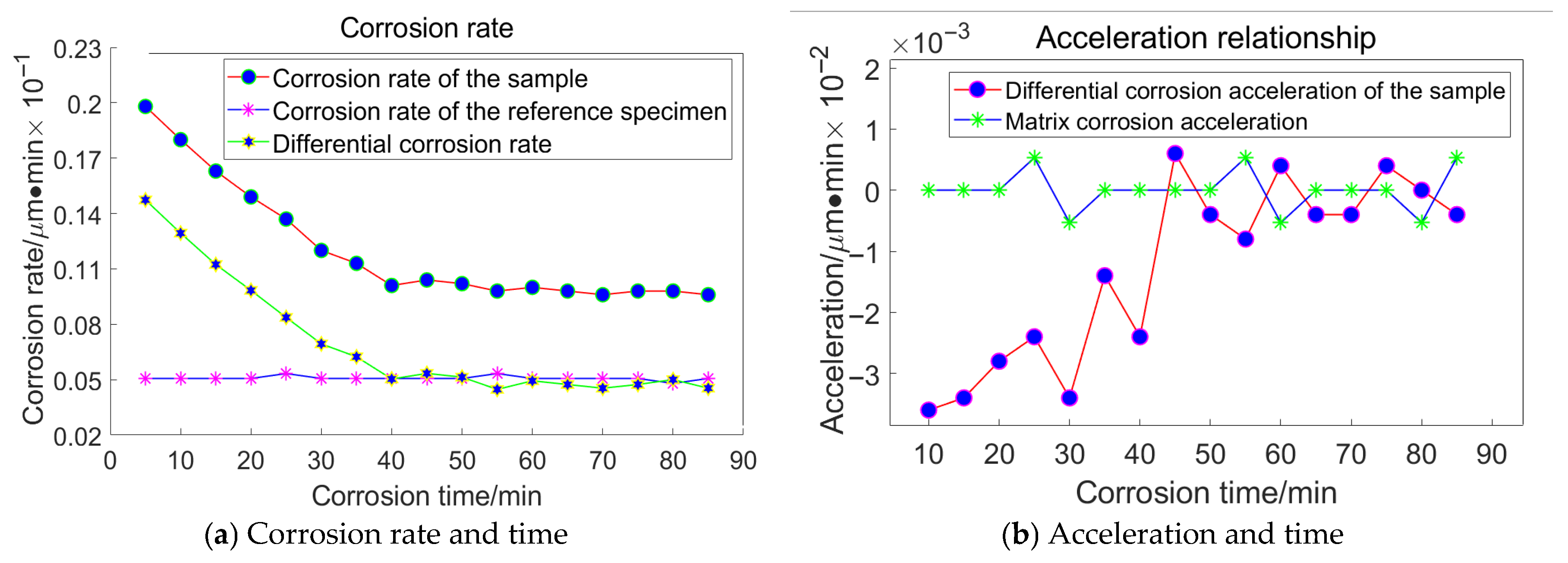
Figure 16.
Relationship between Corrosion Duration and the Quantity of Workpiece Material Removed Utilizing 23 μm Abrasive Grains.
Figure 16.
Relationship between Corrosion Duration and the Quantity of Workpiece Material Removed Utilizing 23 μm Abrasive Grains.
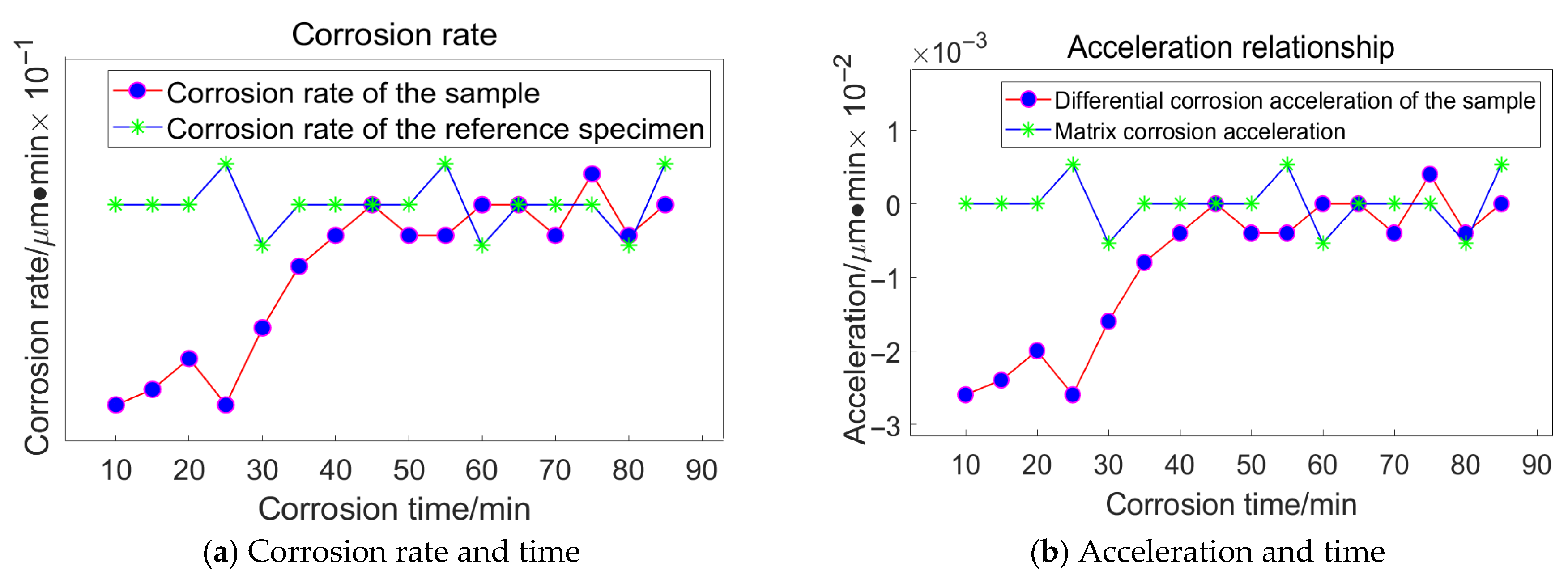
Figure 17.
Relationship between Corrosion Duration and the Quantity of Workpiece Material Removed Utilizing 18 μm Abrasive Grains.
Figure 17.
Relationship between Corrosion Duration and the Quantity of Workpiece Material Removed Utilizing 18 μm Abrasive Grains.
Figure 18.
Relationship between Corrosion Duration and the Quantity of Workpiece Material Removed Utilizing 13 μm Abrasive Grains.
Figure 18.
Relationship between Corrosion Duration and the Quantity of Workpiece Material Removed Utilizing 13 μm Abrasive Grains.
Figure 19.
Relationship between Corrosion Duration and the Quantity of Workpiece Material Removed Utilizing 6.5 μm Abrasive Grains.
Figure 19.
Relationship between Corrosion Duration and the Quantity of Workpiece Material Removed Utilizing 6.5 μm Abrasive Grains.
Figure 20.
Corrosion time and removal relationship.
Figure 20.
Corrosion time and removal relationship.
Figure 21.
Corrosion time and removal relationship.
Figure 21.
Corrosion time and removal relationship.
Figure 22.
Corrosion time and removal relationship.
Figure 22.
Corrosion time and removal relationship.
Figure 23.
Corrosion time and removal relationship.
Figure 23.
Corrosion time and removal relationship.
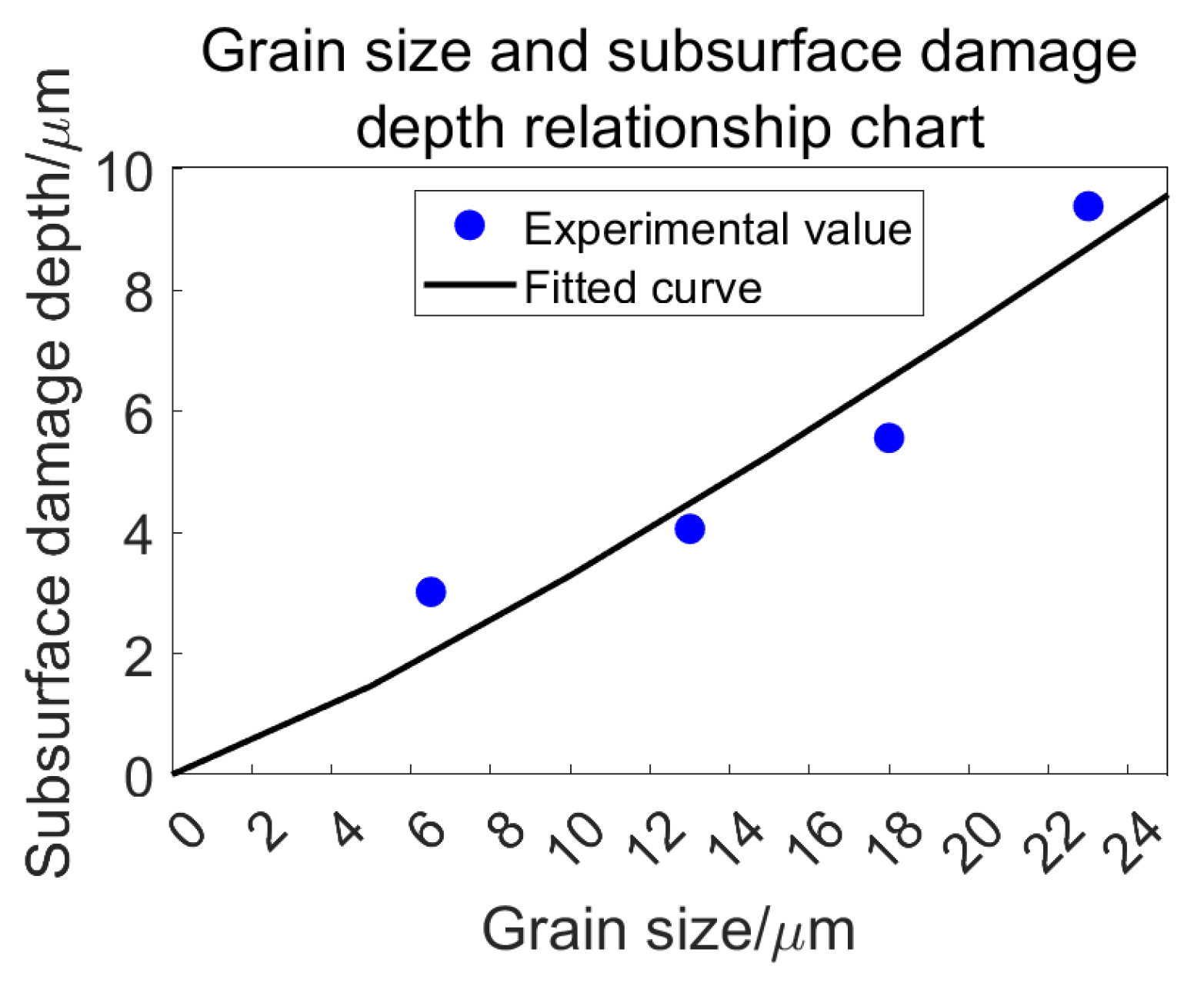
Figure 24.
Relationship between abrasive grain size and subsurface damage depth.
Figure 24.
Relationship between abrasive grain size and subsurface damage depth.
Figure 25.
The positional relationship between the abrasive particle, the grinding disc, and the workpiece.
Figure 25.
The positional relationship between the abrasive particle, the grinding disc, and the workpiece.
Figure 26.
Relationship between abrasive grain size and subsurface damage depth.
Figure 26.
Relationship between abrasive grain size and subsurface damage depth.
Figure 27.
Variation in subsurface damage depth with grinding pressure.
Figure 27.
Variation in subsurface damage depth with grinding pressure.
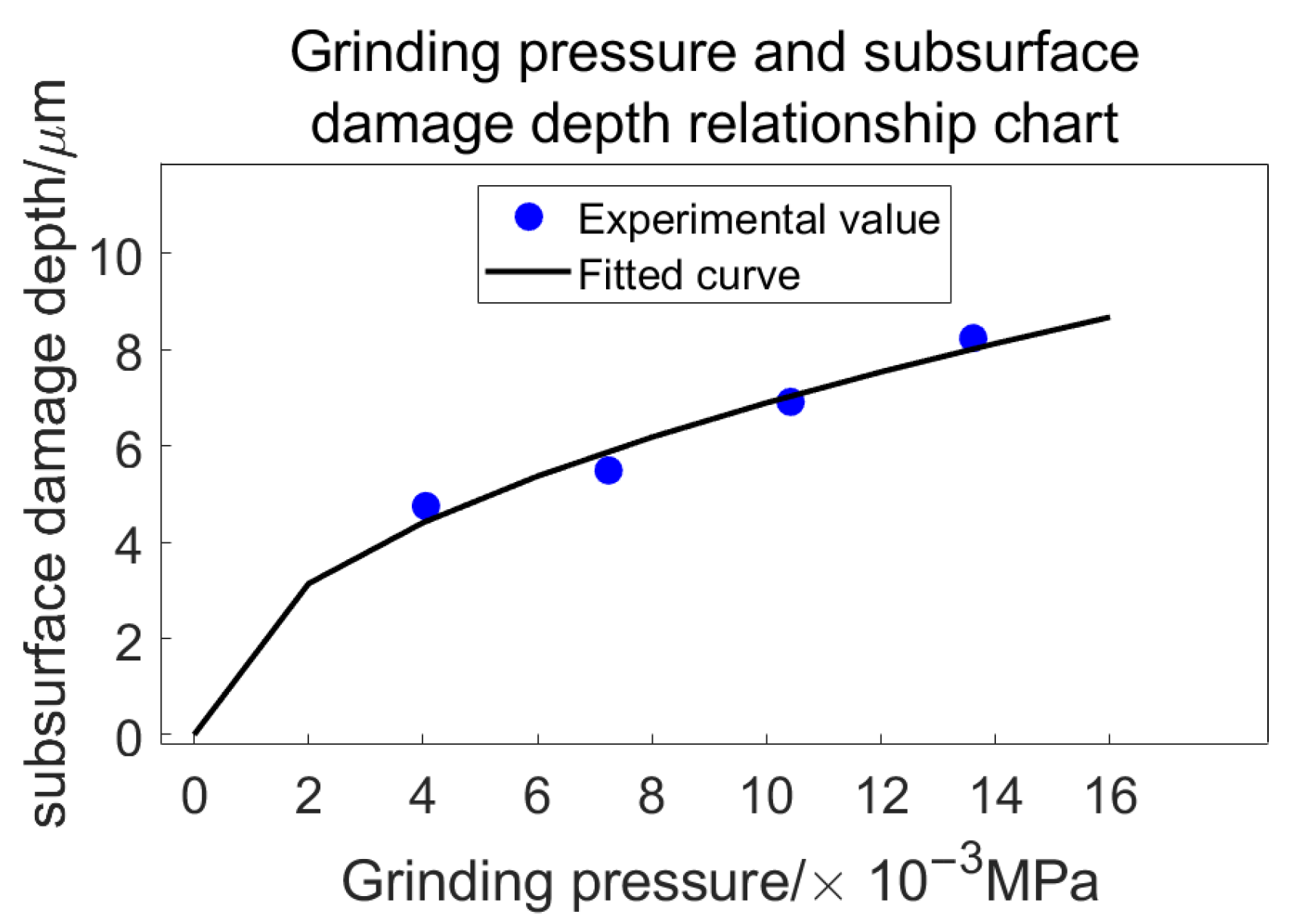
Figure 28.
Relationship between grinding pressure and subsurface damage depth.
Figure 28.
Relationship between grinding pressure and subsurface damage depth.
Figure 29.
Relationship between roughness and subsurface damage depth. (a) Relationship between abrasive particle size roughness and subsurface damage depth. (b) Relationship between grinding pressure roughness and subsurface damage depth.
Figure 29.
Relationship between roughness and subsurface damage depth. (a) Relationship between abrasive particle size roughness and subsurface damage depth. (b) Relationship between grinding pressure roughness and subsurface damage depth.
Table 1.
Grinding experimental parameters.
Table 1.
Grinding experimental parameters.
| Index | Parameter |
|---|
| Base Speed/r·min−1 | 150 |
| Workpiece Disc Speed/r·min−1 | 100 |
| Pressure/N | 3 |
| Eccentricity/mm | 55 |
Table 2.
Relationship between abrasive grain size and material removal.
Table 2.
Relationship between abrasive grain size and material removal.
| | Grain Size | 28 μm | 20 μm | 14 μm | 10 μm |
|---|
| Removal | |
|---|
| Removal Amount/g | 54.4 | 18.1 | 15.6 | 13.9 |
| Removal Rate/μm·min−1 | 4.5687 | 1.5249 | 1.3113 | 1.1689 |
Table 3.
Pressure parameter settings.
Table 3.
Pressure parameter settings.
Sample
Parameter | 1 | 2 | 3 | 4 |
|---|
| Pressure/10−3 MPa | 4.0500 | 7.2400 | 10.4200 | 13.6100 |
Table 4.
Relationship between pressure and surface quality.
Table 4.
Relationship between pressure and surface quality.
| | Pressure/10−3 MPa | 13.61 | 10.42 | 7.24 | 4.05 |
|---|
| Index | |
|---|
| Ra/μm | 0.2320 | 0.1850 | 0.1460 | 0.1820 |
| Sa/μm | 0.1970 | 0.1700 | 0.1460 | 0.1470 |
| PV/μm | 5.3740 | 4.8710 | 4.5240 | 3.1870 |
Table 5.
Relationship between grinding pressure and removal amount.
Table 5.
Relationship between grinding pressure and removal amount.
| | Pressure/10−3 MPa | 13.61 | 10.42 | 7.24 | 4.05 |
|---|
| Removal | |
|---|
| Removal Amount/g | 0.0347 | 0.0295 | 0.0204 | 0.0248 |
| Removal Rate/μm·min−1 | 2.9726 | 2.5217 | 1.7325 | 2.1241 |
Table 6.
Process Parameter Table.
Table 6.
Process Parameter Table.
| | Technology | 1 | 2 | 3 | 4 |
|---|
| Types of Variables | |
|---|
| Abrasive Grain Size/μm | 10 | 14 | 20 | 28 |
| Grinding Pressure/10−3 MPa | 4.0500 | 7.2400 | 10.4200 | 13.6100 |
Table 7.
Process parameter table.
Table 7.
Process parameter table.
| | Technology | 1 | 2 | 3 | 4 |
|---|
| Index | |
|---|
| Grinding disc speed (r/min) | 200 | 150 | 120 | 100 |
| Workpiece disc speed (r/min) | 100 | 100 | 80 | 60 |
| Pressure (N) | 3 | 2 | 1 | 0.8 |
| Particle size (μm) | 8.0000 | 4.0000 | 2.0000 | 0.0500 |
| Time (min) | 10 | 20 | 40 | 60 |
Table 8.
Relationship between abrasive grain size and subsurface damage depth.
Table 8.
Relationship between abrasive grain size and subsurface damage depth.
| Grain Size/μm | 23 | 18 | 13 | 6.5 |
|---|
| Damage depth/μm | 9.3917 | 8.0639 | 6.4598 | 3.0180 |
Table 9.
Relationship between grinding pressure and subsurface damage depth.
Table 9.
Relationship between grinding pressure and subsurface damage depth.
| Grinding Pressure/10−3 MPa | 13.61 | 10.42 | 7.24 | 4.05 |
|---|
| Damage depth/μm/ | 8.2375 | 6.915 | 5.4932 | 4.7523 |