Tribological Aspects of Slide Friction Diamond Burnishing Process
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
4. Measurement Results
4.1. Examination of 3D Surface Roughness Parameters
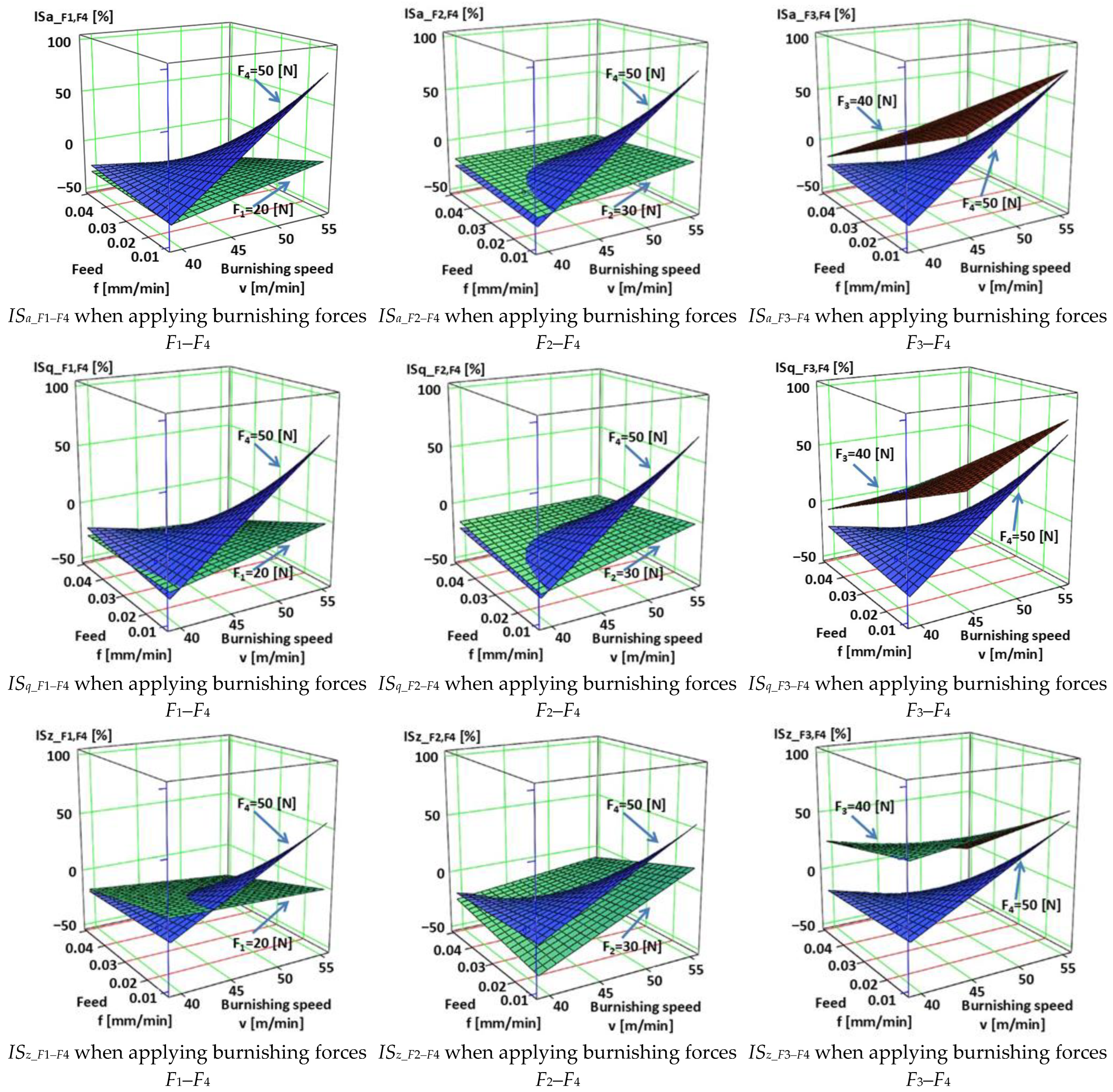
4.2. Full Factorial Experiment Design Analysis of Functional Volume Area Roughness Parameters
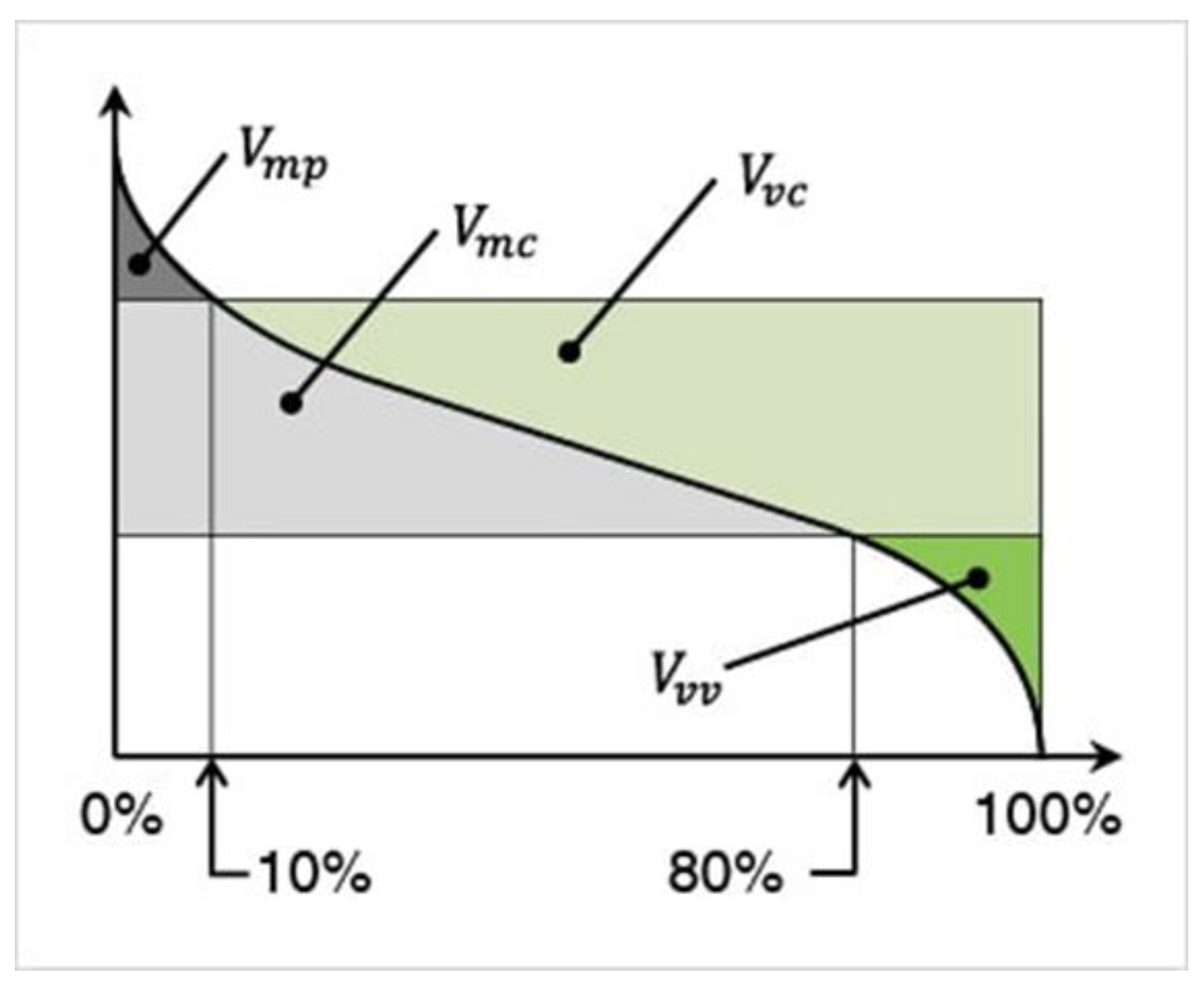
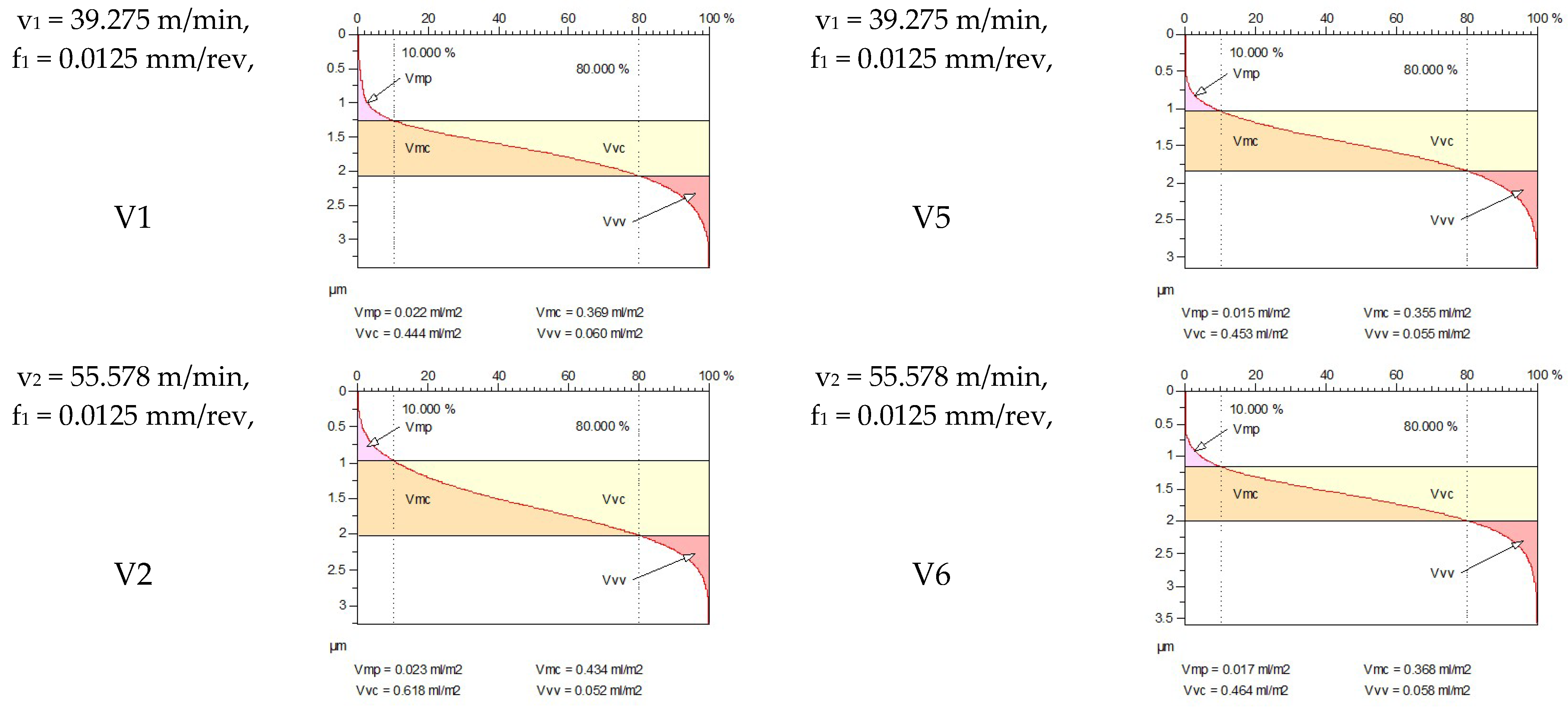
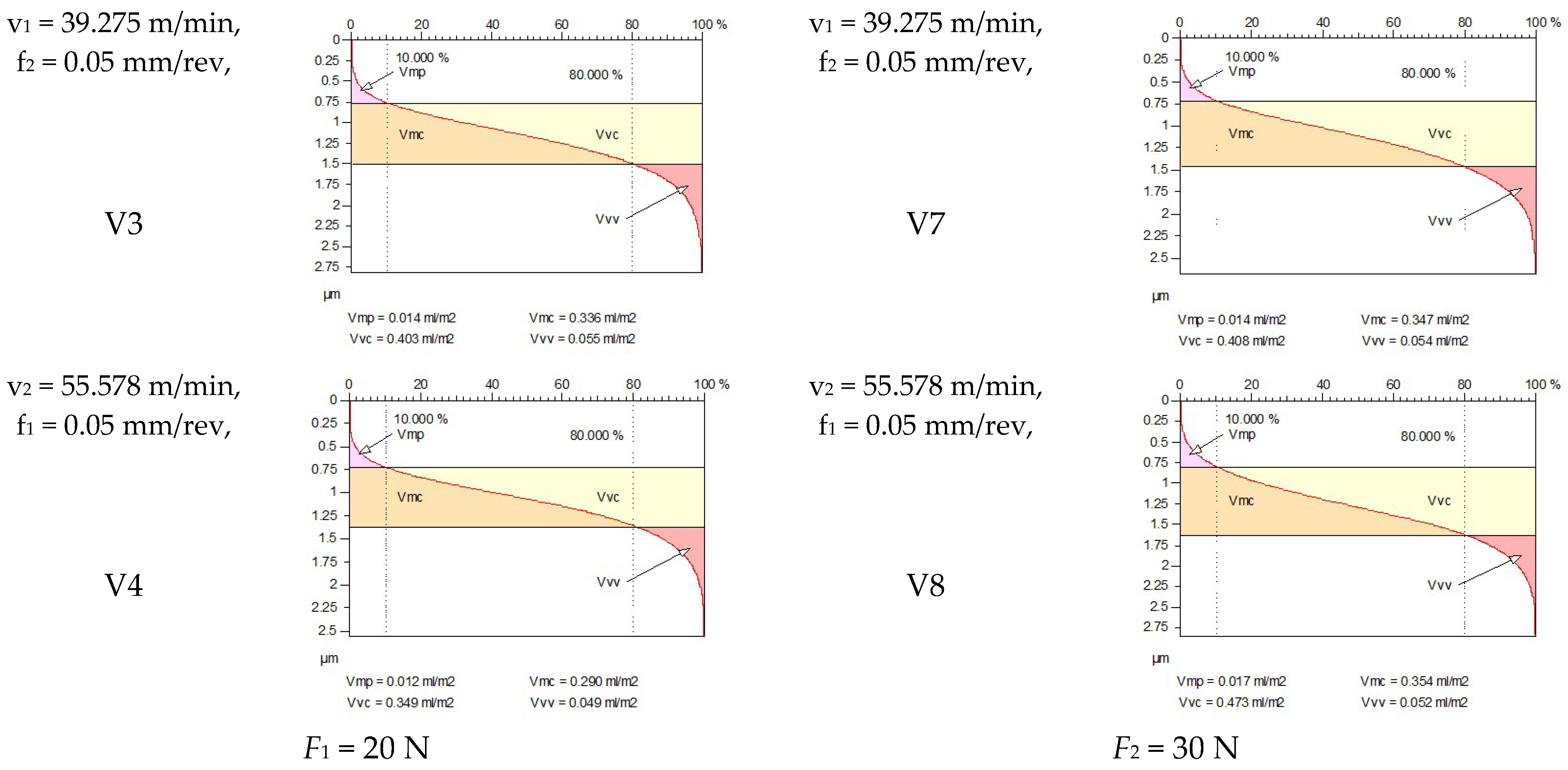
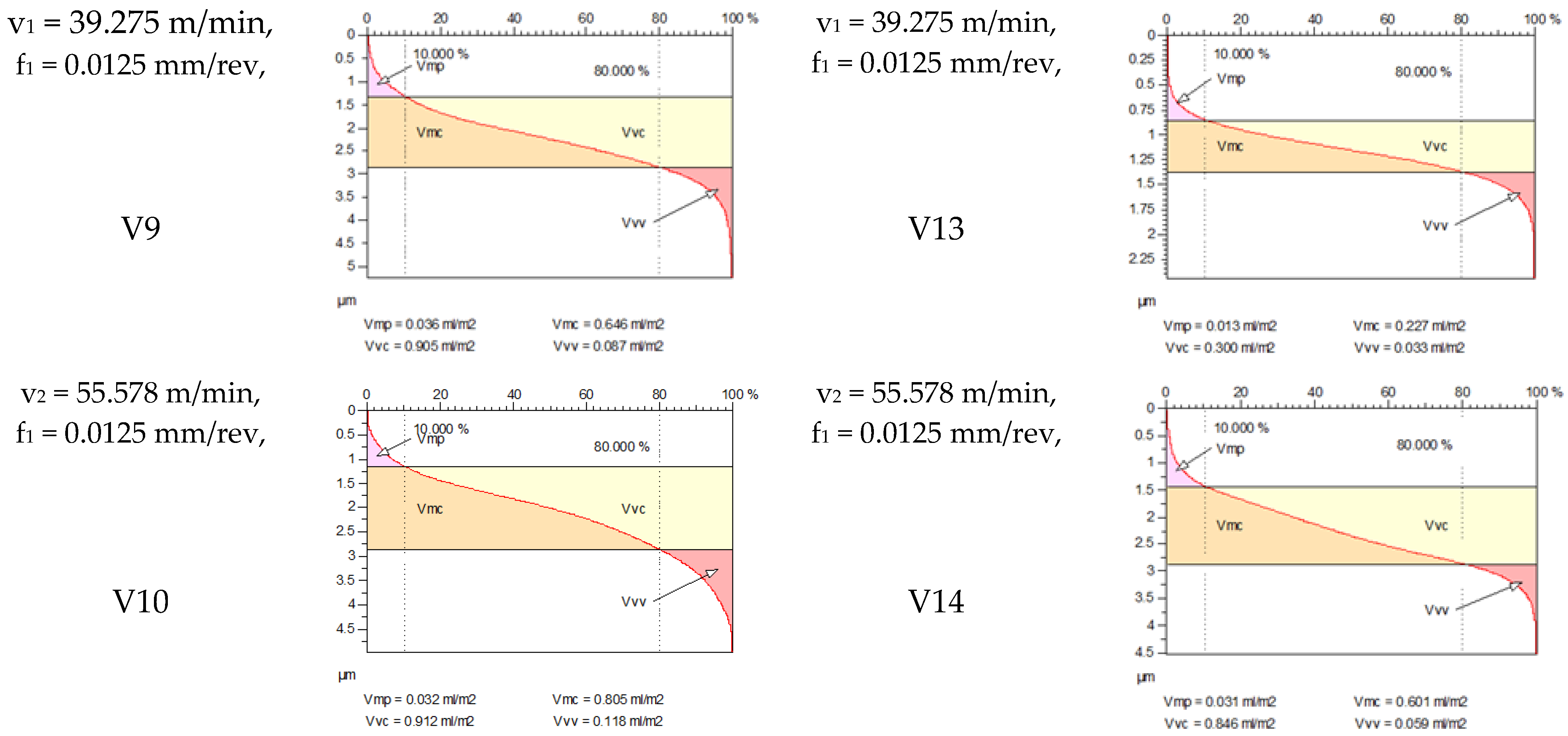
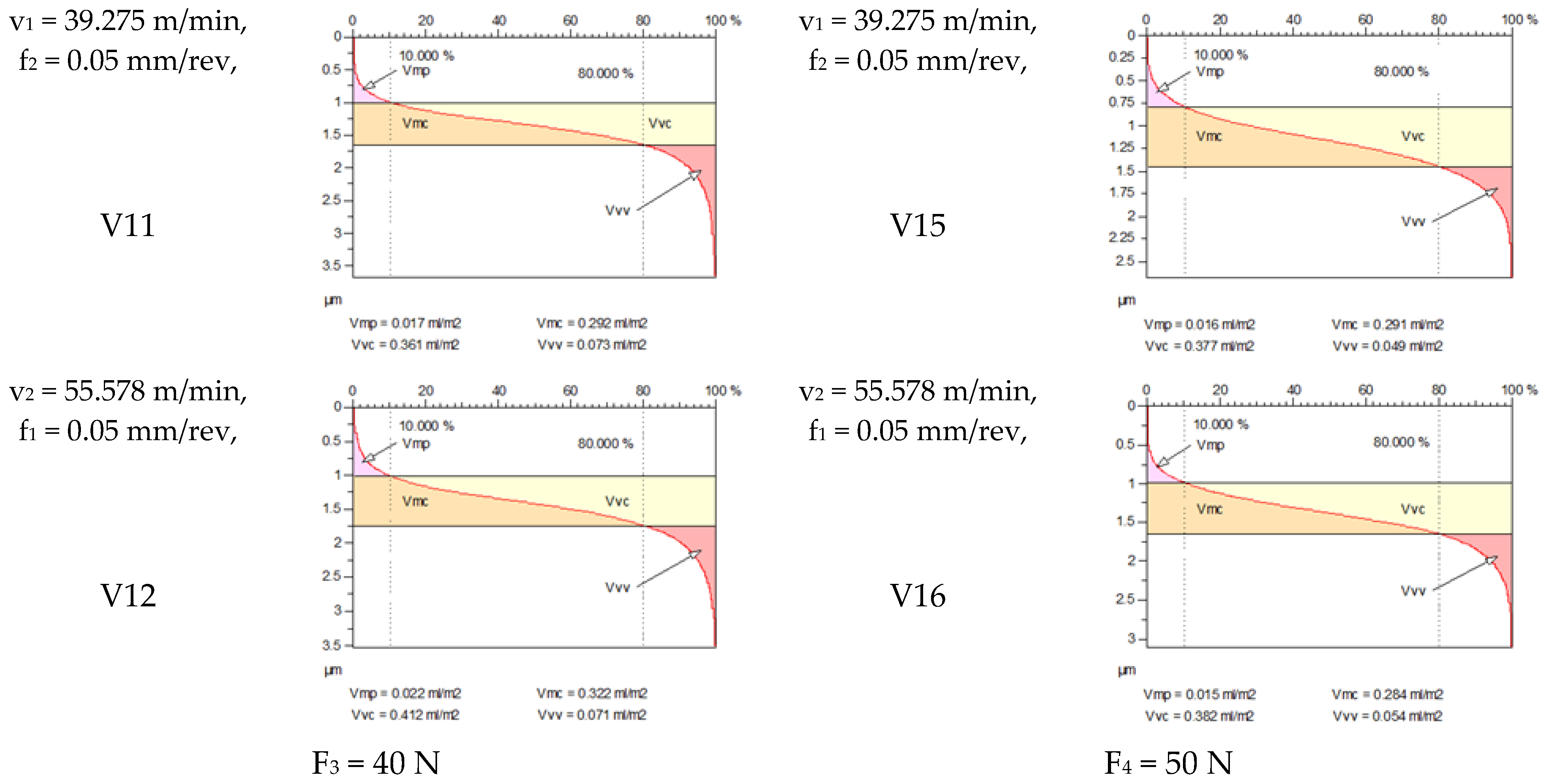
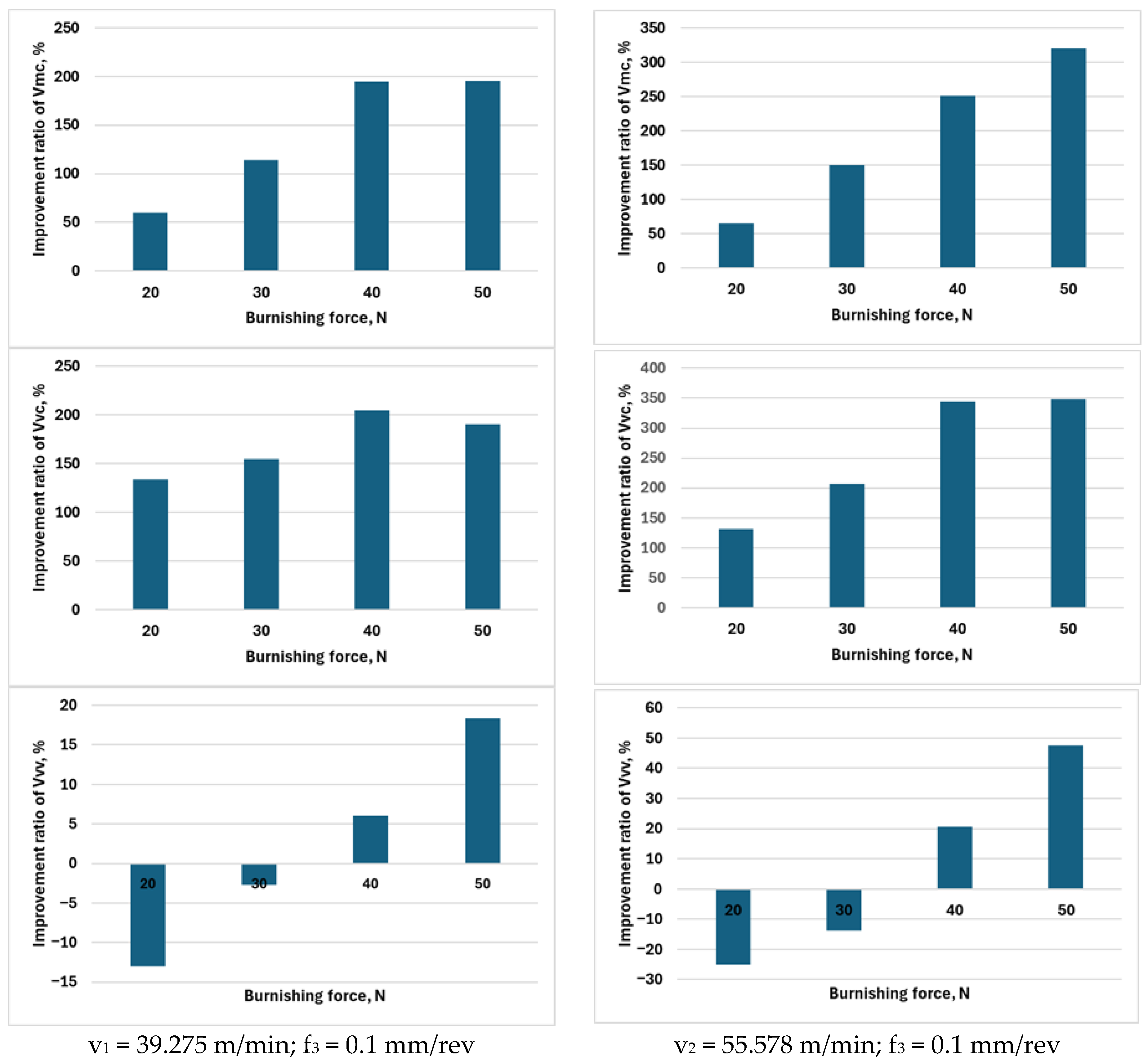
4.3. Examination of Functional Volume Area Roughness Parameters When Workpiece Feed Is Constant
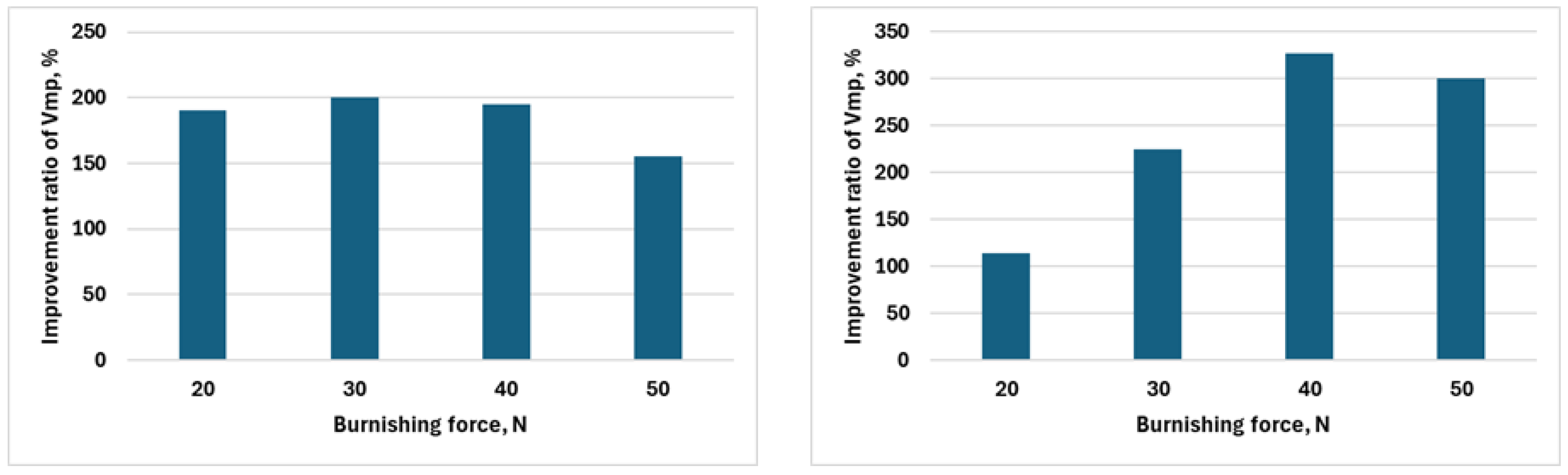
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Measurement Data and Improvement
| Techn. Parameters | Surface Roughness Parameters Before Burnishing | Surface Roughness Parameters After Burnishing | Improvements | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Speed | Feed | Force | ||||||||||
| v, m/min | f, mm/rev | F, N | Sa’, µm | Sq’, µm | Sz’, µm | Sa, µm | Sq, µm | Sz, µm | ISa [%] | ISq [%] | ISz [%] | |
| V1 | 39.275 | 0.0125 | 20 | 0.490 | 0.585 | 3.277 | 0.331 | 0.428 | 3.414 | −32.449 | −26.838 | 4.181 |
| V2 | 55.578 | 0.0125 | 20 | 0.402 | 0.493 | 3.278 | 0.386 | 0.486 | 3.265 | −3.980 | −1.420 | −0.397 |
| V3 | 39.275 | 0.0500 | 20 | 0.435 | 0.535 | 3.400 | 0.298 | 0.380 | 2.817 | −31.494 | −28.972 | −17.147 |
| V4 | 55.578 | 0.0500 | 20 | 0.446 | 0.557 | 3.603 | 0.258 | 0.330 | 2.556 | −42.152 | −40.754 | −29.059 |
| V5 | 39.275 | 0.0125 | 30 | 0.419 | 0.563 | 5.153 | 0.315 | 0.400 | 3.144 | −24.821 | −28.952 | −38.987 |
| V6 | 55.578 | 0.0125 | 30 | 0.343 | 0.428 | 3.019 | 0.329 | 0.421 | 3.588 | −4.082 | −1.636 | 18.847 |
| V7 | 39.275 | 0.0500 | 30 | 0.369 | 0.457 | 3.542 | 0.302 | 0.382 | 2.678 | −18.157 | −16.411 | −24.393 |
| V8 | 55.578 | 0.0500 | 30 | 0.386 | 0.478 | 3.149 | 0.318 | 0.402 | 2.849 | −17.617 | −15.900 | −9.527 |
| V9 | 39.275 | 0.0125 | 40 | 0.392 | 0.499 | 3.588 | 0.578 | 0.741 | 5.242 | 47.449 | 48.497 | 46.098 |
| V10 | 55.578 | 0.0125 | 40 | 0.379 | 0.466 | 3.060 | 0.682 | 0.852 | 4.988 | 79.947 | 82.833 | 63.007 |
| V11 | 39.275 | 0.0500 | 40 | 0.348 | 0.435 | 2.936 | 0.289 | 0.405 | 3.668 | −16.954 | −6.897 | 24.932 |
| V12 | 55.578 | 0.0500 | 40 | 0.384 | 0.492 | 3.669 | 0.310 | 0.425 | 3.526 | −19.271 | −13.618 | −3.898 |
| V13 | 39.275 | 0.0125 | 50 | 0.305 | 0.385 | 2.868 | 0.204 | 0.261 | 2.447 | −33.115 | −32.208 | −14.679 |
| V14 | 55.578 | 0.0125 | 50 | 0.305 | 0.388 | 2.923 | 0.547 | 0.663 | 4.521 | 79.344 | 70.876 | 54.670 |
| V15 | 39.275 | 0.0500 | 50 | 0.351 | 0.439 | 3.304 | 0.263 | 0.341 | 2.680 | −25.071 | −22.323 | −18.886 |
| V16 | 55.578 | 0.0500 | 50 | 0.480 | 0.730 | 6.568 | 0.267 | 0.353 | 3.115 | −44.375 | −51.644 | −52.573 |
| Before Burnishing, [ml/m2] | After Burnishing, [ml/m2] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| v, m/min | f, mm/rev | F, N | Vmc’ [ml/m2] | Vvc’, [ml/m2] | Vmc, [ml/m2] | Vvc, [ml/m2] | DVmc [ml/m2] | DVvc [ml/m2] | DVmc/DVvc | |
| V1 | 39.275 | 0.0125 | 20 | 0.586 | 0.722 | 0.369 | 0.444 | −0.217 | −0.278 | 0.781 |
| V2 | 55.578 | 0.0125 | 20 | 0.471 | 0.586 | 0.434 | 0.618 | −0.037 | 0.032 | −1.156 |
| V3 | 39.275 | 0.0500 | 20 | 0.500 | 0.646 | 0.336 | 0.403 | −0.164 | −0.243 | 0.675 |
| V4 | 55.578 | 0.0500 | 20 | 0.513 | 0.670 | 0.290 | 0.349 | −0.223 | −0.321 | 0.695 |
| V5 | 39.275 | 0.0125 | 30 | 0.448 | 0.620 | 0.365 | 0.453 | −0.083 | −0.167 | 0.497 |
| V6 | 55.578 | 0.0125 | 30 | 0.392 | 0.521 | 0.368 | 0.464 | −0.024 | −0.057 | 0.421 |
| V7 | 39.275 | 0.0500 | 30 | 0.427 | 0.566 | 0.347 | 0.408 | −0.080 | −0.158 | 0.506 |
| V8 | 55.578 | 0.0500 | 30 | 0.439 | 0.611 | 0.354 | 0.473 | −0.085 | −0.138 | 0.616 |
| V9 | 39.275 | 0.0125 | 40 | 0.441 | 0.545 | 0.646 | 0.905 | 0.205 | 0.360 | 0.569 |
| V10 | 55.578 | 0.0125 | 40 | 0.440 | 0.588 | 0.805 | 0.912 | 0.365 | 0.324 | 1.127 |
| V11 | 39.275 | 0.0500 | 40 | 0.393 | 0.537 | 0.292 | 0.361 | −0.101 | −0.176 | 0.574 |
| V12 | 55.578 | 0.0500 | 40 | 0.422 | 0.593 | 0.322 | 0.412 | −0.100 | −0.181 | 0.552 |
| V13 | 39.275 | 0.0125 | 50 | 0.342 | 0.454 | 0.227 | 0.300 | −0.115 | −0.154 | 0.747 |
| V14 | 55.578 | 0.0125 | 50 | 0.341 | 0.453 | 0.601 | 0.846 | 0.260 | 0.393 | 0.662 |
| V15 | 39.275 | 0.0500 | 50 | 0.396 | 0.539 | 0.291 | 0.377 | −0.105 | −0.162 | 0.648 |
| V16 | 55.578 | 0.0500 | 50 | 0.451 | 0.633 | 0.284 | 0.382 | −0.167 | −0.251 | 0.665 |
| Before Burnishing [mL/m2] | After Burnishing [mL/m2] | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| v, m/min | f, mm/rev | F, N | Vmp, [ml/m2] | Vmc, [ml/m2] | Vvc, [ml/m2] | Vvv, [ml/m2] | Vmp, [ml/m2] | Vmc, [ml/m2] | Vvc, [ml/m2] | Vvv, [ml/m2] | |
| F1 | 39.275 | 0.1 | 20 | 0.058 | 1.365 | 1.836 | 0.134 | 0.020 | 0.852 | 0.786 | 0.154 |
| F2 | 39.275 | 0.1 | 30 | 0.051 | 1.359 | 1.745 | 0.142 | 0.017 | 0.636 | 0.686 | 0.146 |
| F3 | 39.275 | 0.1 | 40 | 0.059 | 1.341 | 1.747 | 0.123 | 0.020 | 0.455 | 0.573 | 0.116 |
| F4 | 39.275 | 0.1 | 50 | 0.051 | 1.247 | 1.657 | 0.116 | 0.020 | 0.422 | 0.570 | 0.098 |
| F5 | 55.578 | 0.1 | 20 | 0.047 | 1.266 | 1.776 | 0.110 | 0.022 | 0.767 | 0.766 | 0.147 |
| F6 | 55.578 | 0.1 | 30 | 0.065 | 1.401 | 1.855 | 0.120 | 0.020 | 0.560 | 0.604 | 0.139 |
| F7 | 55.578 | 0.1 | 40 | 0.064 | 1.308 | 1.860 | 0.135 | 0.015 | 0.372 | 0.418 | 0.112 |
| F8 | 55.578 | 0.1 | 50 | 0.064 | 1.274 | 1.736 | 0.115 | 0.016 | 0.303 | 0.387 | 0.078 |
Appendix B
| Source | df | Mean Square | F | Sig | Partial Eta Squared |
|---|---|---|---|---|---|
| Corrected Model | 5 | 2751.96 | 2.772 | 0.08 | 0.581 |
| Intercept | 1 | 712.863 | 0.718 | 0.417 | 0.067 |
| v m/min | 1 | 1648.888 | 1.661 | 0.227 | 0.142 |
| f mm/rev | 1 | 6536.076 | 6.583 | 0.028 | 0.397 |
| F N | 3 | 1858.279 | 1.872 | 0.198 | 0.360 |
| Error | 10 | 992.907 | |||
| Total | 16 | ||||
| Corrected Total | 15 |
| Source | df | Mean Square | F | Sig | Partial Eta Squared |
|---|---|---|---|---|---|
| Corrected Model | 5 | 2701.375 | 2.906 | 0.071 | 0.592 |
| Intercept | 1 | 455.470 | 0.490 | 0.500 | 0.047 |
| v m/min | 1 | 1275.222 | 1.372 | 0.269 | 0.121 |
| f mm/rev | 1 | 5916.340 | 6.365 | 0.030 | 0.389 |
| F N | 3 | 2105.104 | 2.265 | 0.143 | 0.405 |
| Error | 10 | 929.571 | |||
| Total | 16 | ||||
| Corrected Total | 15 |
| Source | df | Mean Square | F | Sig | Partial Eta Squared |
|---|---|---|---|---|---|
| Corrected Model | 5 | 2079 | 3.259 | 0.053 | 0.620 |
| Intercept | 1 | 0.299 | 0 | 0.983 | 0 |
| v m/min | 1 | 399.5 | 0.626 | 0.447 | 0.059 |
| f mm/rev | 1 | 4333 | 6.792 | 0.026 | 0.404 |
| F N | 3 | 1887 | 2.958 | 0.084 | 0.470 |
| Error | 10 | 637.9 | |||
| Total | 16 | ||||
| Corrected Total | 15 |
| Dependent Variable: Sa’ | Dependent Variable: Sa | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Source | df | Mean Square | F | Sig | Source | df | Mean Square | F | Sig |
| Corrected Model | 5 | 0.004 | 1.325 | 0.329 | Corrected Model | 5 | 0.118 | 5.661 | 0.01 |
| Intercept | 1 | 2.429 | 901.136 | 0 | Intercept | 1 | 23.015 | 1100.347 | 0 |
| v m/min | 1 | 1.60 × 10−5 | 0.006 | 0.940 | v m/min | 1 | 0.033 | 1.581 | 0.237 |
| f mm/rev | 1 | 0.002 | 0.624 | 0.448 | f mm/rev | 1 | 0.206 | 9.828 | 0.011 |
| F N | 3 | 0.005 | 1.998 | 0.178 | F N | 3 | 0.118 | 5.633 | 0.016 |
| Error | 10 | 0.003 | Error | 10 | 0.021 | ||||
| Total | 16 | Total | 16 | ||||||
| Corrected Total | 15 | Corrected Total | 15 | ||||||
| R Squared = 0.398 (Adjusted R Squared = 0.098) | R Squared = 0.739 (Adjusted R Squared = 0.608) | ||||||||
| Dependent Variable: Sq’ | Dependent Variable: Sq | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Source | df | Mean Square | F | Sig | Source | df | Mean Square | F | Sig |
| Corrected Model | 5 | 0.004 | 0.425 | 0.821 | Corrected Model | 5 | 0.048 | 3.352 | 0.049 |
| Intercept | 1 | 3.930 | 430.220 | 0 | Intercept | 1 | 3.303 | 231.201 | 0 |
| v m/min | 1 | 0.001 | 0.123 | 0.733 | v m/min | 1 | 0.022 | 1.543 | 0.242 |
| f mm/rev | 1 | 0.006 | 0.683 | 0.428 | f mm/rev | 1 | 0.095 | 6.661 | 0.027 |
| F N | 3 | 0.004 | 0.439 | 0.730 | F N | 3 | 0.041 | 2.852 | 0.091 |
| Error | 10 | 0.009 | Error | 10 | 0.014 | ||||
| Total | 16 | Total | 16 | ||||||
| Corrected Total | 15 | Corrected Total | 15 | ||||||
| R Squared = 0.175 (Adjusted R Squared = −0.237) | R Squared = 0.626 (Adjusted R Squared = 0.439) | ||||||||
| Dependent Variable: Sz’ | Dependent Variable: Sz | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Source | df | Mean Square | F | Sig | Source | df | Mean Square | F | Sig |
| Corrected Model | 5 | 0.322 | 0.263 | 0.923 | Corrected Model | 5 | 1.607 | 5.898 | 0.009 |
| Intercept | 1 | 205.471 | 168.153 | 0 | Intercept | 1 | 185.627 | 681.065 | 0 |
| v m/min | 1 | 0.09 | 0.074 | 0.791 | v m/min | 1 | 0.336 | 1.232 | 0.293 |
| f mm/rev | 1 | 0.564 | 0.462 | 0.512 | f mm/rev | 1 | 2.822 | 10.355 | 0.009 |
| F N | 3 | 0.318 | 0.260 | 0.852 | F N | 3 | 1.626 | 5.967 | 0.013 |
| Error | 10 | 1.222 | Error | 10 | 0.273 | ||||
| Total | 16 | Total | 16 | ||||||
| Corrected Total | 15 | Corrected Total | 15 | ||||||
| R Squared = 0.116 (Adjusted R Squared = −0.325) | R Squared = 0.747 (Adjusted R Squared = 0.620) | ||||||||
References
- Kovács, G. Combination of Lean Value-Oriented Conception and Facility Layout Design for Even More Significant Efficiency Improvement and Cost Reduction. Int. J. Product. Res. 2020, 58, 2916–2936. [Google Scholar] [CrossRef]
- Afraa, K.; Sztankovics, I.; Felhő, C. Preliminary Experimental Comparison of Plunge Milling and Face Milling: Influences of Cutting Parameters on Cutting Force and Surface Roughness. ENG 2025, 6, 128. [Google Scholar] [CrossRef]
- Kundrák, J.; Felhő, C.; Nagy, A. Analysis and Prediction of Roughness of Face Milled Surfaces using CAD Model. Manuf. Technol. 2022, 22, 558–572. [Google Scholar] [CrossRef]
- Meng, Y.; Xu, J.; Ma, L.; Jin, Z.; Prakash, B.; Ma, T.; Wang, W. A Review of Advances in Tribology in 2020–2021. Friction 2022, 10, 1443–1595. [Google Scholar] [CrossRef]
- Tesfom, K.F.; Felho, C. Examining the Impact of Slide Burnishing Parameters on the 3D Surface Features Of Medium Carbon Steel. J. Prod. Eng. 2024, 27, 30–35. [Google Scholar] [CrossRef]
- Ferencsik, V. Analytical Analysis of the Theoretical Surface Roughness in the Case of Burnishing of Cylindrical Workpiece. Cut. Tool. Technol. Syst. 2023, 99, 101–109. [Google Scholar] [CrossRef]
- Dix, M.; Posdzich, M. Force-controlled Burnishing Process for High Surface Integrity on Additive Manufactured Parts. Procedia CIRP 2022, 108, 642–647. [Google Scholar] [CrossRef]
- Varga, G.; Smolnicki, S.; Babič, M.; Caesarendra, W. Energy Efficiency Analysis When Grinding and Diamond Burnishing of Components. In Towards Industry 5.0: Selected Papers from ISPR2022; Güneş, G.M., Durakbasa, N.M., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 378–396. [Google Scholar] [CrossRef]
- Maximov, J.; Duncheva, G. The Correlation between Surface Integrity and Operating Behaviour of Slide Burnished Components—A Review and Prospects. Appl. Sci. 2023, 13, 3313. [Google Scholar] [CrossRef]
- Maximov, J.; Duncheva, G. Effects of Cryogenic- and Cool-Assisted Burnishing on the Surface Integrity and Operating Behavior of Metal Components: A Review and Perspectives. Machines 2024, 12, 312. [Google Scholar] [CrossRef]
- Maximov, J.; Duncheva, G. Effects of Diamond Burnishing on Surface Integrity, Fatigue, Wear, and Corrosion of Metal Components—Review and Perspectives. Int. J. Adv. Manuf. Technol. 2025, 139, 4233–4267. [Google Scholar] [CrossRef]
- Korzynski, M.; Dudek, K.; Korzynska, K. Effect of Slide Diamond Burnishing on the Surface Layer of Valve Stems and the Durability of the Stem-Graphite Seal Friction Pair. Appl. Sci. 2023, 13, 6392. [Google Scholar] [CrossRef]
- Sedlacek, M.; Gregorcic, P.; Podgornik, B. Use of the Roughness Parameters Ssk and Sku to Control Friction—A Method for Designing Surface Texturing. Tribol. Trans. 2017, 60, 260–266. [Google Scholar] [CrossRef]
- Shuster, M.; Seasons, R.; Burke, D. Laboratory Simulation to Select Oil Seal and Surface Treatment. Wear 1999, 225–229 Pt 2, 954–961. [Google Scholar] [CrossRef]
- Prajapati, D.K.; Tiwari, M. The Correlation Between Friction Coefficient and Areal Topography Parameters for AISI 304 Steel Sliding Against AISI 52100 Steel. Friction 2021, 9, 41–60. [Google Scholar] [CrossRef]
- Sedlaček, M.; Podgornik, B.; Vižintin, J. Correlation Between Standard Roughness Parameters Skewness and Kurtosis and Tribological Behaviour of Contact Surfaces. Tribol. Int. 2012, 48, 102–112. [Google Scholar] [CrossRef]
- Reddy, M.V.K.; Kuriachen, B.; Joshy, J.; Joy, M.L. Influence of Areal Surface Parameters on The Tribological Behavior of Ti6Al4V Under Lubricated Condition. Tribol. Int. 2023, 179, 108147. [Google Scholar] [CrossRef]
- Shi, R.; Wang, B.; Yan, Z.; Wang, Z.; Dong, L. Effect of Surface Topography Parameters on Friction and Wear of Random Rough Surface. Materials 2019, 12, 2762. [Google Scholar] [CrossRef]
- Lavrys, S.; Pohrelyuk, I.; Padgurskas, J.; Shliakhetka, K. Improving Wear Resistance of Highly Porous Titanium by Surface Engineering Methods. Coatings 2023, 13, 1714. [Google Scholar] [CrossRef]
- Dzierwa, A.; Stelmakh, N.; Tikanashvili, N. Application of Taguchi Technique to Study Tribological Properties of Roller-Burnished 36CrNiMo4 Steel. Lubricants 2023, 11, 227. [Google Scholar] [CrossRef]
- Swirad, S. Influence of Ball Burnishing on Lubricated Fretting of the Titanium Alloy Ti6Al4V. Lubricants 2023, 11, 341. [Google Scholar] [CrossRef]
- Grudzien, J.; Grochała, D.; Grzejda, R.; Kochmanski, P. Testing the Effectiveness of Hybrid Milling and Surface Burnishing in Improving the Wear Resistance of Machine Parts Made of Structural Steel. Lubricants 2024, 12, 458. [Google Scholar] [CrossRef]
- Dzierwa, A.; Markopoulos, A.P. Influence of Ball-Burnishing Process on Surface Topography Parameters and Tribological Properties of Hardened Steel. Machines 2019, 7, 11. [Google Scholar] [CrossRef]
- Varga, G.; Dezső, G.; Szigeti, F. Surface Roughness Improvement by Sliding Friction Burnishing of Parts Produced by Selective Laser Melting of Ti6Al4V Titanium Alloy. Machines 2022, 10, 400. [Google Scholar] [CrossRef]
- Swirad, S.; Pawlus, P. The Effect of Ball Burnishing on Tribological Performance of 42CrMo4 Steel under Dry Sliding Conditions. Materials 2020, 13, 2127. [Google Scholar] [CrossRef] [PubMed]
- Swirad, S.; Pawlus, P. The Influence of Ball Burnishing on Friction in Lubricated Sliding. Materials 2020, 13, 5027. [Google Scholar] [CrossRef]
- Swirad, S.; Pawlus, P. The Effect of Ball Burnishing on Dry Fretting. Materials 2021, 14, 7073. [Google Scholar] [CrossRef] [PubMed]
- Swirad, S.; Pawlus, P. Effect of Ball Burnishing on Fretting at Elevated Temperatures. Materials 2024, 17, 5960. [Google Scholar] [CrossRef] [PubMed]
- Torres, A.; Cuadrado, N.; Llumà, J.; Vilaseca, M.; Travieso-Rodriguez, J.A. Influence of the Stainless-Steel Microstructure on Tribological Behavior and Surface Integrity after Ball Burnishing. Materials 2022, 15, 8829. [Google Scholar] [CrossRef]
- Velázquez-Corral, E.; Wagner, V.; Jerez-Mesa, R.; Liuma, J.; Travieso-Rodriguez, J.A.; Dessein, G. Analysis of Ultrasonic Vibration-Assisted Ball Burnishing Process on the Tribological Behavior of AISI 316L Cylindrical Specimens. Materials 2023, 16, 5595. [Google Scholar] [CrossRef]
- Kuznetsov, V.; Tatarintsev, I.; Voropaev, V.; Skorobogatov, A. Surface Nanocrystallization and Improvement of the Mechanical and Tribological Properties of AISI 304 Steel Using Multi-Pass Nanostructuring Burnishing. Materials 2024, 17, 5656. [Google Scholar] [CrossRef]
- Bednarski, P.; Biało, D.; Brostow, W.; Czechowski, K.; Polowski, W.; Rusek, P.; Tobola, D. Improvement of Tribological Properties of Matrix Composites by Means of Slide Burnishing. Mater. Sci. 2013, 19, 367–372. [Google Scholar] [CrossRef]
- Tomov, M.; Gecevska, V.; Vasileska, E. Modelling of Multiple Surface Roughness Parameters During Hard Turning: A Comparative Study Between the Kinematical-Geometrical Copying Approach and the Design of Experiments Method (DOE). Adv. Prod. Eng. Manag. 2022, 17, 75–88. [Google Scholar] [CrossRef]
- Nagy, A.; Kundrák, J. Roughness of Face-Milled Surface Topography in Directions Relative to the Feed Movement. Manuf. Techn. 2024, 24, 2. [Google Scholar] [CrossRef]
- Molnár, V.; Sztankovics, I. Analysis of Roughness Parameters Determining Tribological Properties in Hard Turned Surfaces. Hung. J. Ind. Chem. 2021, 49, 77–84. [Google Scholar] [CrossRef]
- Skoczylas, A.; Kłonica, M. Selected Properties of the Surface Layer of C45 Steel Samples after Slide Burnishing. Materials 2023, 16, 6513. [Google Scholar] [CrossRef]
- Kubatova, D.; Melichar, M. Roughness Evaluation Using Abbott-Firestone Curve Parameters. In Proceedings of the 30th DAAAM International Symposium, Zadar, Croatia, 23–26 October 2019; Katalinic, B., Ed.; DAAAM International: Vienna, Austria, 2019; pp. 0467–0475, ISBN 978-3-902734-22-8, ISSN 1726-9679. [Google Scholar] [CrossRef]
- Maximov, J.T.; Anchev, A.P.; Duncheva, G.V. Modeling of the Friction in the Tool Workpiece System in Diamond Burnishing Process. Coupled Syst. Mech. 2015, 4, 279–295. [Google Scholar] [CrossRef]
- Varga, G. Effect of burnishing technological parameters on the surface roughness and hardness of stainless-steel test pieces (A vasalástechnológiai paraméterek hatása a rozsdamentes acél próbadarabok felületi érdességére és keménységére). Mul-Tidiszcipl. Tudományok Miskolci Egy. Közleménye 2022, 12, 151–163. (In Hungarian) [Google Scholar]
- European Steel and Alloy Grades/Numbers SteelNumber. X5CrNi18-10 (1.4301). Available online: https://steelnumber.com/en/steel_composition_eu.php?name_id=100 (accessed on 9 September 2025).
- AltiSurf©520. Assuring Fast & Precise Optical Measurements. Available online: https://www.imeco-th.cz/files/tinymce/AltiSurf%E2%84%A2%20520.pdf (accessed on 13 July 2025).
- ISO 21920-2:2021; Geometrical Product Specifications (GPS)—Surface Texture: Profile Part 2: Terms, Definitions and Surface Texture Parameters. ISO: Geneva, Switzerland, 2021.
- ISO 25178-2:2021; Geometrical Product Specifications (GPS)—Surface Texture: Areal. Part 2: Terms, Definitions and Surface Texture Parameters. ISO: Geneva, Switzerland, 2021.
- Hisam, M.W.; Dar, A.A.; Elrasheed, M.O.; Khan, M.S.; Gera, R.; Azad, I. The Versatility of the Taguchi Method: Optimizing Experiments Across Diverse Disciplines. J. Stat. Theory Appl. 2024, 23, 365–389. [Google Scholar] [CrossRef]


| C % | Si % | Mn % | P % | S % | Cr % | Ni % | N % |
|---|---|---|---|---|---|---|---|
| ≤0.07 | ≤1.00 | ≤2.00 | ≤0.045 | ≤0.015 | 17.5–19.5 | 8.00–10.5 | ≤0.11 |
| Hardness HB 30 | 0.2% Yield Strength, Rp | Tensile Strength, Rm | Elongation A5 | Modulus of Elasticity |
|---|---|---|---|---|
| HB | N/mm2 | N/mm2 | % | kN/mm2 |
| ≤215 | ≥190 | 500–700 | ≥45/35 | 200 |
| No. | Burnishing Parameters | ||||
|---|---|---|---|---|---|
| n | v | f | F | ||
| [1/min] | [m/min] | [mm/rev] | [N] | ||
| V1 | 1_1 | 265 | 39.275 | 0.0125 | 20 |
| V2 | 1_2 | 375 | 55.578 | 0.0125 | 20 |
| V3 | 1_3 | 265 | 39.275 | 0.0500 | 20 |
| V4 | 1_4 | 375 | 55.578 | 0.0500 | 20 |
| V5 | 2_1 | 265 | 39.275 | 0.0125 | 30 |
| V6 | 2_2 | 375 | 55.578 | 0.0125 | 30 |
| V7 | 2_3 | 265 | 39.275 | 0.0500 | 30 |
| V8 | 2_4 | 375 | 55.578 | 0.0500 | 30 |
| V9 | 3_1 | 265 | 39.275 | 0.0125 | 40 |
| V10 | 3_2 | 375 | 55.578 | 0.0125 | 40 |
| V11 | 3_3 | 265 | 39.275 | 0.0500 | 40 |
| V12 | 3_4 | 375 | 55.578 | 0.0500 | 40 |
| V13 | 4_1 | 375 | 39.275 | 0.0125 | 50 |
| V14 | 4_2 | 375 | 55.578 | 0.0125 | 50 |
| V15 | 4_3 | 265 | 39.275 | 0.0500 | 50 |
| V16 | 4_4 | 375 | 55.578 | 0.0500 | 50 |
| F1 | 7_1 | 265 | 39.275 | 0.1000 | 20 |
| F2 | 7_2 | 375 | 55.578 | 0.1000 | 30 |
| F3 | 7_3 | 265 | 39.275 | 0.1000 | 40 |
| F4 | 7_4 | 375 | 55.578 | 0.1000 | 50 |
| F5 | 8_1 | 265 | 39.275 | 0.1000 | 20 |
| F6 | 8_2 | 375 | 55.578 | 0.1000 | 30 |
| F7 | 8_3 | 265 | 39.275 | 0.1000 | 40 |
| F8 | 8_4 | 375 | 55.578 | 0.1000 | 50 |
| Before Burnishing | After Burnishing |
|---|---|
| V1 | v1 = 39.275 m/min, f1 = 0.0125 mm/rev, F1 = 20 N |
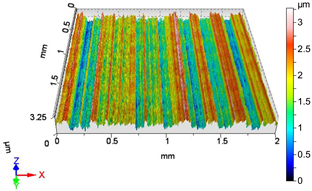 | 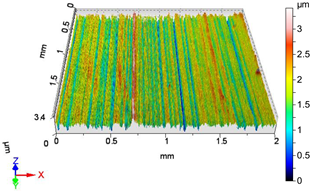 |
| Sa = 0.490 µm, Sq = 0.585 µm, Sz = 3.277 µm, Sp = 1.588 µm, Sv = 1.689 µm, Ssk = −0.037, Sku = 2.269 | Sa = 0.331 µm, Sq = 0.428 µm, Sz = 3.414 µm, Sp = 1.736 µm, Sv = 1.678 µm, Ssk = −0.264, Sku = 3.737 |
| V2 | v2 = 55.578 m/min, f1 = 0.0125 mm/rev, F1 = 20 N |
 |  |
| Sa = 0.402 µm, Sq = 0.493 µm, Sz = 3.278 µm, Sp = 1.567 µm, Sv = 1.711 µm, Ssk = −0.137, Sku = 2.652 | Sa = 0.386 µm, Sq = 0.486 µm, Sz = 3.265 µm, Sp = 1.611 µm, Sv = 1.654 µm, Ssk = 0.111, Sku = 2.928 |
| V3 | v1 = 39.275 m/min, f2 = 0.05 mm/rev, F1 = 20 N |
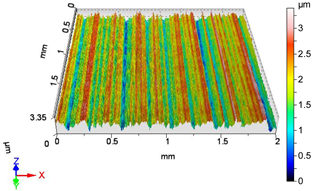 | 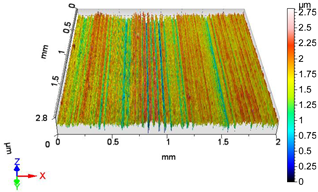 |
| Sa = 0.435 µm, Sq = 0.535 µm, Sz = 3.400 µm, Sp = 1.560 µm, Sv = 1.839 µm, Ssk = −0.150, Sku = 2.638 | Sa = 0.298 µm, Sq = 0.380 µm, Sz = 2.817 µm, Sp = 1.198 µm, Sv = 1.619 µm, Ssk = −0.606, Sku = 3.634 |
| V4 | v2 = 55.578 m/min, f2 = 0.05 mm/rev, F1 = 20 N |
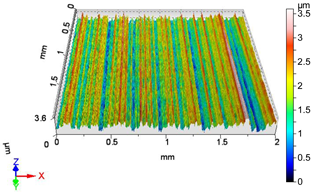 |  |
| Sa = 0.446 µm, Sq = 0.557 µm, Sz = 3.603 µm, Sp = 1.835 µm, Sv = 1.768 µm, Ssk = 0.062, Sku = 2.934 | Sa = 0.258 µm, Sq = 0.330 µm, Sz = 2.556 µm, Sp = 1.101 µm, Sv = 1.455 µm, Ssk = −0.598,Sku = 3.612 |
| V5 | v1 = 39.275 m/min, f1 = 0.0125 mm/rev, F2 = 30 N |
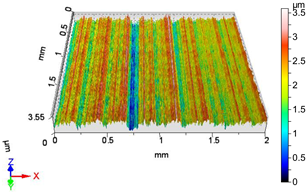 | 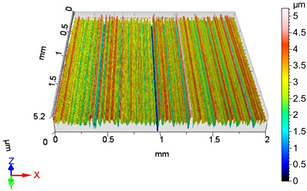 |
| Sa = 0.419 µm, Sq = 0.563 µm, Sz = 5.153 µm, Sp = 3.222 µm, Sv = 1.931 µm, Ssk = 0.958, Sku = 6.610 | Sa = 0.315 µm, Sq = 0.400 µm, Sz = 3.144 µm, Sp = 1.520 µm, Sv = 1.625 µm, Ssk = −0.377, Sku = 3.223 |
| V6 | v2 = 55.578 m/min, f1 = 0.0125 mm/rev, F2 = 30 N |
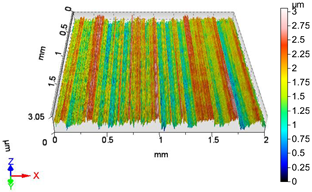 | 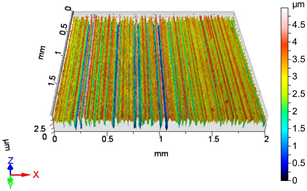 |
| Sa = 0.343 µm, Sq = 0.428 µm, Sz = 3.019 µm, Sp = 1.308 µm, Sv = 1.710 µm, Ssk = −0.127, Sku = 2.943 | Sa = 0.329 µm, Sq = 0.421 µm, Sz = 3.588 µm, Sp = 1.660 µm, Sv = 1.928 µm, Ssk = −0.474, Sku = 3.620 |
| V7 | v1 = 39.275 m/min, f2 = 0.05 mm/rev, F2 = 30 N |
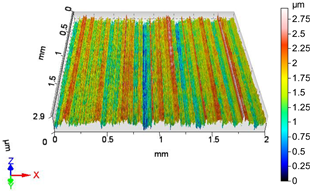 | 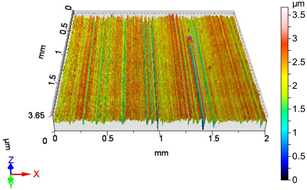 |
| Sa = 0.369 µm, Sq = 0.457 µm, Sz = 3.542 µm, Sp = 1.719 µm, Sv = 1.823 µm, Ssk = −0.059, Sku = 2.739 | Sa = 0.302 µm, Sq = 0.382 µm, Sz = 2.678 µm, Sp = 1.153 µm, Sv = 1.525 µm, Ssk = −0.554, Sku = 3.379 |
| V8 | v2 = 55.578 m/min, f2 = 0.05 mm/rev, F2 = 30 N |
 | 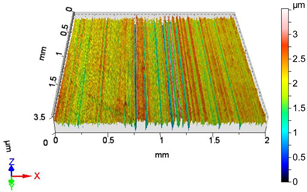 |
| Sa = 0.386 µm, Sq = 0.478 µm, Sz = 3.149 µm, Sp = 1.582 µm, Sv = 1.567 µm, Ssk = 0.210, Sku = 2.802 | Sa = 0.318 µm, Sq = 0.402 µm, Sz = 2.849 µm, Sp = 1.298 µm, Sv = 1.551 µm, Ssk = −0.206, Sku = 3.078 |
| V9 | v1 = 39.275 m/min, f1 = 0.0125 mm/rev, F3 = 40 N |
 | 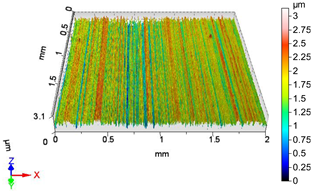 |
| Sa = 0.366 µm, Sq = 0.454 µm, Sz = 3.382 µm, Sp = 1.520 µm, Sv = 1.862 µm, Ssk = −0.082, Sku = 2.803 | Sa = 0.578 µm, Sq = 0.741 µm, Sz = 5.242 µm, Sp = 2.255 µm, Sv = 2.987 µm, Ssk = −0.116, Sku = 3.503 |
| V10 | v2 = 55.578 m/min, f1 = 0.0125 mm/rev, F3 = 40 N |
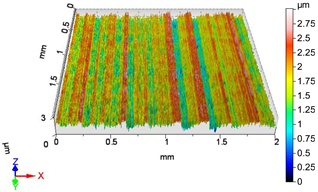 |  |
| Sa = 0.379 µm, Sq = 0.466 µm, Sz = 3.060 µm, Sp = 1.391 µm, Sv = 1.669 µm, Ssk = 0.022, Sku = 2.609 | Sa = 0.682 µm, Sq = 0.852 µm, Sz = 4.988 µm, Sp = 2.135 µm, Sv = 2.853 µm, Ssk = −0.495, Sku = 2.959 |
| V11 | v1 = 39.275 m/min, f2 = 0.05 mm/rev, F3 = 40 N |
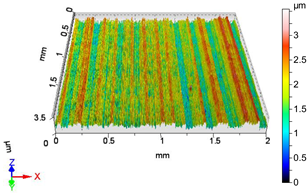 | 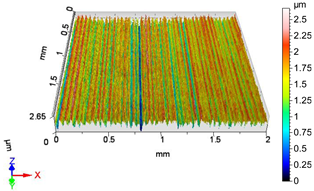 |
| Sa = 0.348 µm, Sq = 0.435 µm, Sz = 2.936 µm, Sp = 1.394 µm, Sv = 1.542 µm, Ssk = 0.012, Sku = 2.904 | Sa = 0.289 µm, Sq = 0.405 µm, Sz = 3.668 µm, Sp = 1.405 µm, Sv = 2.263 µm, Ssk = −1.275, Sku = 7.012 |
| V12 | v2 = 55.578 m/min, f2 = 0.05 mm/rev, F3 = 40 N |
 | 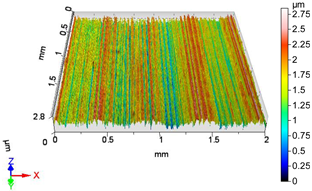 |
| Sa = 0.384 µm, Sq = 0.492 µm, Sz = 3.669 µm, Sp = 1.732 µm, Sv = 1.937 µm, Ssk = −0.069, Sku = 3.147 | Sa = 0.310 µm, Sq = 0.425 µm, Sz = 3.526 µm, Sp = 1.457 µm, Sv = 2.069 µm, Ssk = −0.737, Sku = 5.044 |
| V13 | v1 = 39.275 m/min, f1 = 0.0125 mm/rev, F4 = 50 N |
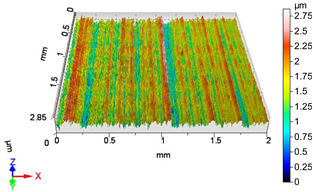 | 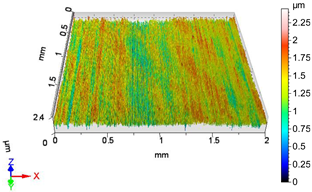 |
| Sa = 0.305 µm, Sq = 0.385 µm, Sz = 2.868 µm, Sp = 1.313 µm, Sv = 1.555 µm, Ssk = −0.084, Sku = 3.148 | Sa = 0.204 µm, Sq = 0.261 µm, Sz = 2.447 µm, Sp = 1.160 µm, Sv = 1.286 µm, Ssk = −0.163, Sku = 3.508 |
| V14 | v2 = 55.578 m/min, f1 = 0.0125 mm/rev, F4 = 50 N |
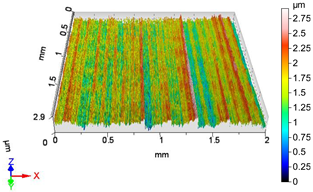 |  |
| Sa = 0.305 µm, Sq = 0.388 µm, Sz = 2.923 µm, Sp = 1.358 µm, Sv = 1.565 µm, Ssk = −0.021, Sku = 3.290 | Sa = 0.547 µm, Sq = 0.663 µm, Sz = 4.521 µm, Sp = 2.285 µm, Sv = 2.236 µm, Ssk = 0.238, Sku = 2.722 |
| V15 | v1 = 39.275 m/min, f2 = 0.05 mm/rev, F4 = 50 N |
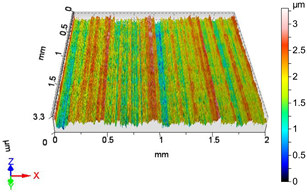 | 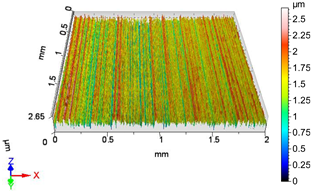 |
| Sa = 0.351 µm, Sq = 0.439 µm, Sz = 3.304 µm, Sp = 1.493 µm, Sv = 1.812 µm, Ssk = −0.027, Sku = 2.915 | Sa = 0.263 µm, Sq = 0.341 µm, Sz = 2.680 µm, Sp = 1.188 µm, Sv = 1.491 µm, Ssk = −0.387, Sku = 3.611 |
| V16 | v2 = 55.578 m/min, f2 = 0.05 mm/rev, F4 = 50 N |
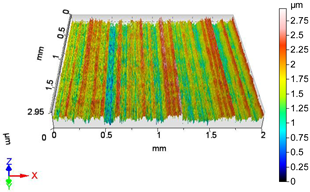 | 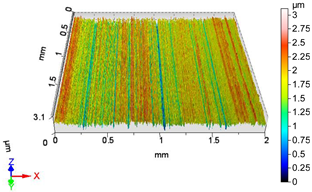 |
| Sa = 0.337 µm, Sq = 0.419 µm, Sz = 2.957 µm, Sp = 1.338 µm, Sv = 1.691 µm, Ssk = -0.019, Sku = 2.777 | Sa = 0.267 µm, Sq = 0.353 µm, Sz = 3.115 µm, Sp = 1.401 µm, Sv = 1.714 µm, Ssk = −0.533, Sku = 4.120 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varga, G.; Markopoulos, A.P. Tribological Aspects of Slide Friction Diamond Burnishing Process. Materials 2025, 18, 4500. https://doi.org/10.3390/ma18194500
Varga G, Markopoulos AP. Tribological Aspects of Slide Friction Diamond Burnishing Process. Materials. 2025; 18(19):4500. https://doi.org/10.3390/ma18194500
Chicago/Turabian StyleVarga, Gyula, and Angelos P. Markopoulos. 2025. "Tribological Aspects of Slide Friction Diamond Burnishing Process" Materials 18, no. 19: 4500. https://doi.org/10.3390/ma18194500
APA StyleVarga, G., & Markopoulos, A. P. (2025). Tribological Aspects of Slide Friction Diamond Burnishing Process. Materials, 18(19), 4500. https://doi.org/10.3390/ma18194500







