Next Article in Journal
Compositional Effects on the Performance of High-Permeability Emulsified Asphalt for Prime Coat Applications
Previous Article in Journal
Data-Driven Optimization and Mechanical Assessment of Perovskite Solar Cells via Stacking Ensemble and SHAP Interpretability
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Materials
Volume 18
Issue 18
10.3390/ma18184428
materials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Positron Annihilation Studies of Hydrostatically Extruded AA1050 Aluminum

by
Ewa Dryzek
1,*,
Mirosław Wróbel
2,
Maciej Sarnek
3 and
Jacek Skiba
4
1
Institute of Nuclear Physics, Polish Academy of Sciences, PL-31342 Kraków, Poland
2
Faculty of Metals Engineering and Industrial Computer Science, AGH University of Krakow, Mickiewicza 30 Ave., 30-059 Kraków, Poland
3
Institute of Quality Sciences and Product Management, Cracow University of Economics, Rakowicka 27 Str., 31-510 Kraków, Poland
4
Institute of High Pressure Physics Polish Academy of Sciences (Unipress), ul. Sokołowska 29, 01-142 Warszawa, Poland
*
Author to whom correspondence should be addressed.
Materials 2025, 18(18), 4428; https://doi.org/10.3390/ma18184428
Submission received: 24 July 2025 / Revised: 5 September 2025 / Accepted: 16 September 2025 / Published: 22 September 2025
(This article belongs to the Section Metals and Alloys)
Browse Figures
Versions Notes

Abstract

AA1050 aluminum was hydrostatically extruded at room temperature to true strains of 0.9 and 3.2, and at cryogenic temperature to a true strain of 0.9. As a result of the extrusion process, the yield strength (YS) increased by 130–160% to 120–130 MPa, and the ultimate tensile strength (UTS) rose by 64–81% to 125–140 MPa. The hardness reached 46–49 HV. YS and UTS values correspond to mechanical properties typical of the H6 or H8 temper designations, with unusually high elongation at break ranging from 15% to 16.4%. Differences in lattice parameters, crystallite size, and lattice strain between samples deformed under various conditions—as well as those annealed after deformation—were within the margin of measurement uncertainty. This indicated that differences in defect density between the samples were relatively small, due to dynamic recovery occurring during extrusion. However, positron annihilation spectroscopy demonstrated that the cryo-cooled material extruded at a true strain of 0.9, as well as the one extruded at RT at a true strain of 3.2, exhibited significantly higher mean lattice defect concentrations compared to the sample extruded at RT at a true strain of 0.9. The predominant defects detected were vacancies associated with dislocations. The extrusion parameters also significantly affected the crystallographic texture. In particular, they altered the relative proportions of the <111> and <100> components in the axial texture, with the <100> component becoming dominant in cryogenically extruded samples. This trend was further intensified during recrystallization, which enhanced the <100> component even more. Recrystallization of the deformed materials occurred in the temperature range of 520–570 K. The activation energy for grain boundary migration during recrystallization was estimated to be approximately 1.5 eV.

1. Introduction

The global aluminum extruded products market size was estimated to be worth USD 91 billion in 2024, with an estimated compound annual growth rate (CAGR) of 8.4% during 2025–2030 [1]. However, the share of the Al alloys from the 1xxx family (i.e., commercially pure aluminum with purity over 99 wt.%), which includes AA 1050 alloy, is relatively small because of their softness. For this reason, such alloys are seldom used for structural applications. However, their low density combined with excellent corrosion resistance and workability, high electrical and thermal conductivity, and highest weldability among aluminum alloys predisposes them to applications in electrotechnics, electronics, packaging, and kitchenware. Long products of these alloys (such as bars, wires, and profiles) are often shaped by a high-temperature extrusion (about 450–550 °C [2]) to reduce work hardening and to improve productivity and surface finish. This temperature corresponds to a homologous temperature of 0.77–0.78 and is higher than the pure metal homologous temperature of the recrystallization (typically about 0.4). Recrystallization as a diffusion-driven process depends on temperature and time. It can be limited to some extent by quenching the product with water after it has passed through the die. The reduction ratio and the exit speed up to 100 and up to 75 mm/s, respectively, are not uncommon (but less common when extruding profiles [3]) and depend on each other as well as on the available pressure and extrusion temperature. Therefore, an economically acceptable way to eliminate recovery and recrystallization is virtually impossible while maintaining high efficiency, i.e., maximizing the deformation rate. The operating window of extrusion parameters must be carefully selected from the limit diagrams, such as those described in Ref. [4] (Sections 4.13 and 5.2.1 and in Figure 5.23). In particular, heterogeneity in the flow rate and stress distribution over the extrusion product cross-section resulting from friction against the die causes product discontinuities and cracking, e.g., crow’s feet and fir-tree cracking, which can be formed at too high deformation rates.
The increase in the deformation temperature usually improves metal plasticity but also intensifies recovery and recrystallization processes. These processes should be minimized to ensure significant strain hardening and thus eliminate important disadvantages of the aluminum alloys from the 1xxx family. Therefore, forming should take place at most at room temperature (RT), which is possible at relatively low deformation rates. At economically acceptable deformation rates, it is also possible to reduce the heterogeneity of the extruded material flow rate and stress distribution over its cross-section, consequently preventing product discontinuity by appropriate die geometry and minimizing friction by lubrication. Near-perfect lubrication can be provided by the hydrostatic extrusion (HE) process, in which the billet is surrounded by pressurized liquid, i.e., there is no friction between the container walls and billet and friction of the die can be largely reduced by a film of pressurized lubricant between the extrusion product and die (when designing presses, it is assumed that the working liquid does not surround the die orifice). In such conditions, the shear stress on the die face is small and can be neglected, as was assumed by Pugh and Ashcroft [5]. Thus, the billet extrusion occurs under hydrostatic conditions formulated by Sachs et al. [6]
To the best of our knowledge, the HE process was first patented by James Robertson between 1891 and 1899 (a series of British and US patents [7,8,9,10,11,12,13,14,15]), but Kronberger [16] attributed its first implementation into practice to Percy Williams Bridgman, who was awarded the Nobel Prize in 1946 for his studies of materials at high temperatures and pressures. Indeed, in 1951, he received a US patent for this method and apparatus [17]. Since then, HE technology has been intensively researched in the USA, Europe, and Japan (a short overview of older studies can be found elsewhere, e.g., [4,18]). The improvement continued, and new patents related to this technology appeared, e.g., [19,20,21,22]. Any product suitable for extrusion by conventional technology can be extruded by HE, but the extrusion ratio and exit rate can reach the value of 10,000:1 [23] and 2.5 m/s [24], respectively. Hydrostatically extruded aluminum has been reported to have better mechanical properties than its cold-drawn counterparts [25]. A significant increase in the strength of HE aluminum was confirmed by, among others, Herø and Mikkelsen [26] and Lee et al. [27], and related to the subgrain refinement [28]. Hydrostatic extrusion results in a more uniform strain distribution across the cross-section and a more homogenous microstructure of the product. Hydrostatic compressive stresses increase ductility, allowing for greater deformation without failure, lowering the deformation temperature, and refining microstructure as was reported for aluminum [29,30]. Therefore, the product properties, such as increased strength, fatigue resistance, and corrosion resistance, are superior to those achieved through conventional plastic working methods, such as rolling, drawing, or hot extrusion [30,31,32,33,34,35,36,37].
The current work aims to investigate the effect of the HE temperature and strain rate on the mechanical properties, thermal stability, and recrystallization of the AA 1050 alloy. Its novelty lies in the combination of X-ray diffraction and positron annihilation techniques used in this type of material research. In particular, positron annihilation spectroscopy is known as a valuable non-destructive tool for studies of changes in the microstructure of metals and alloys due to its exceptional sensitivity to open-volume defects of the crystal lattice, such as vacancies, vacancy clusters, voids, and dislocations [38,39]. The presence of defects alters the annihilation characteristics, allowing for their identification and tracking of changes in their concentration. Unlike transmission electron microscopy (TEM) techniques, where significant recovery must be taken into account when preparing and observing pure aluminum samples, the methods we use enable the examination of bulk samples for which such effects can be negligible.

2. Materials and Methods

Commercial aluminum of 99.5% purity (AA1050) in the form of rods was deformed by the single-step HE according to the specifications in Table 1. Before extrusion, the billets were annealed at 623 K for 1 h to alleviate the effects of previous mechanical processing and to produce homogeneous coarse grains of ca. 30 μm. The billet extruded at low temperature (referred to as cryo-cooled) was immersed in a liquid nitrogen (LN) bath for 1 h immediately before extrusion. The time between removing the billet from the LN container and starting its extrusion did not exceed 15 s. Room temperature oil and propylene glycol overcooled to −30 °C were used as the pressure-transmitting medium for the RT and low temperature HE, respectively. The HE processing parameters were selected to ensure that the extrusion temperatures of the samples differed, despite having a similar reduction ratio (R) of approximately 2.5. Sample Al-2.5 was extruded at RT, and sample Al-2.5C was cryo-cooled before HE. The third sample (labeled Al-25) was extruded at RT at a reduction ratio ten times higher, i.e., 25.3.
One-step HE was performed at the Institute of High Pressure Physics (Unipress), Warsaw, Poland. The extrusion die with an opening angle 2α of 45° was used. Before starting the extrusion process, the die opening was closed with a charge cone that matched the die opening and apex angle. After loading the billet into the chamber, it was flooded with a high pressure medium, which was then compressed with a movable piston on one side, closing the working chamber. The pressure medium surrounded the entire not-encapsulated billet; thus, it did not come into contact with the chamber walls. The pressure of the pressure-transmitting medium was gradually increased to the critical value at which extrusion started. The samples were not cooled after exit. The product surface temperature was contact-measured using a Pt-PtRh thermocouple (Simex Ltd., Gdańsk, Poland) immediately after extrusion. It was equal to 262 K, 332 K, and 361 K for Al-2.5C, Al-2.5, and Al-25, respectively. The increase in the sample temperature due to almost adiabatic deformation was therefore ca. 37 K and 66 K for Al-2.5 and Al-25 material, respectively. Determining the temperature increase in sample Al-2.5C was not possible because its exact temperature before the start of the HE process was not known precisely.
Mechanical properties were determined by the tensile tests and Vickers hardness measurements (under a load of 0.2 kgf) performed following the recommendations of the relevant standards, i.e., [40,41,42,43]. The result of the tensile tests was considered correct if the crack occurred in the middle of the gage length measured by an extensometer. Hardness measurements were performed on the billets and the extruded rods’ cross-section.
Samples used for hardness, XRD, and for the positron annihilation measurements were ground using SiC papers (grids from 500 to 1200) and deeply etched in a Keller’s solution to remove a subsurface layer deformed by cutting and grinding.
The annealing regimes of the samples were as follows. For the positron annihilation measurements, the isochronal annealing from room RT up to 630 K with a step of 20 K in a nitrogen atmosphere was performed (20 min each step). After each annealing step, the positron annihilation spectroscopy measurements were carried out at RT. For X-ray measurements, the samples were annealed at 590 K for one hour. The positron annihilation and X-ray diffraction (XRD) measurements were done for both the as-deformed material and the material annealed after deformation. The reference sample was annealed at 773 K in a vacuum (~10−4 Pa) for 1 h and then slowly cooled inside the furnace.
A Panalytical Empyrean diffractometer (Malvern Panalytical, Almelo, The Netherlands) was used for the X-ray measurements. Ni-filtered Cu radiation (the filter thickness was 0.02 mm) was applied. A parallel Goebel mirror (length 55.3 mm, acceptance angle 0.8°) and Soller slit (length 0.04 rad) collimated the incident beam. The same type of Soller slit, together with the parallel plate collimator (opening 0.18°), was placed in front of the PIXcel 3D detector (Malvern Panalytical, Almelo, The Netherlands). X-ray patterns were recorded from the symmetric diffraction data (2 theta in the range of 20–150°, step 0.02°). The trial and error (TREOR) methodology developed by Werner et al. [44] and the Dicevol procedure developed by Boultif and Louër [45] were applied to determine the crystal structure and the lattice parameters. The methodology of Williamson and Hall [46] was used to determine the crystalline size and lattice strain. Calculations were performed using software HighScore Plus v.3.05 (Malvern Panalytical, Almelo, The Netherlands). Our previous study demonstrated that these parameters are sensitive to the recovery of deformed metal, and the crystallographic texture is more sensitive to recrystallization [47,48,49,50].
The crystallographic texture was calculated from the incomplete pole figures 111, 200, 220, and 311 measured on an equiangular measurement grid using the Schulz reflection methodology [51]. The range of the azimuthal angle (α) and the polar angle (β) were 0–80° and 0–360°, respectively. The angle step was Δα = Δβ = 5°. The orientation distribution function (ODF) and complete pole figures were calculated from the incomplete pole figures for the α angle range of 0–60° using the discrete Arbitrarily Defined Cell (ADC) methodology [52] implemented in the LaboTex software v. 3.0 by LaboSoft [53]. According to Caleyo et al., this methodology reproduces the texture well throughout its entire sharpness range [54]. Lack of sample symmetry and the cubic crystal symmetry confirmed by XRD measurements (space group Fm-3m/No. 225 and Laue class Oh) were confirmed and assumed in these calculations.
The variable energy positron (VEP) beam was used [55] to determine the positron diffusion length in the material studied. The positrons emitted from the 22Na source of 30 mCi activity were moderated using frozen neon, accelerated to an appropriate energy in the range of 50 eV to 30 keV, and formed into a monoenergetic beam of 5 mm diameter, guided to the sample. The beam intensity was 106 e+/s. Annihilation quanta (511 keV) were registered by the Doppler broadening of the annihilation line spectrometer (Ametek Ortec, Oakridge, TN, USA) with the HpGe (1.2 keV FWHM energy resolution, interpolated at 511 keV). Based on the annihilation spectra, two commonly used parameters, S and Wr, were determined. The S parameter is defined as the ratio of the area under the fixed central part of the annihilation line to the area under the whole annihilation line. It is sensitive to the annihilation of positrons with low-momentum electrons present in open volume defects. The Wr parameter is calculated as the ratio of the area under the fixed wing region of the annihilation line to the area under the whole annihilation line. It is influenced by the annihilation with high-momentum electrons, i.e., the core ones, and is sensitive to the chemical environment at the annihilation site.
For positron annihilation lifetime spectroscopy (PALS) measurements, the digital spectrometer manufactured by TechnoAP (Hitachinaka, Japan) with BaF2 scintillators connected to the H3378-50 photomultipliers (Hamamatsu Photonics, Iwata City, Japan) was employed. The time resolution of the spectrometer was about 210 ps (full width at half maximum). The positron source, consisting of a 22Na isotope with an activity of 40 μCi, enveloped in a 7 μm thick Kapton foil, was used in the measurements. The analysis of the spectra containing at least 106 counts was performed by applying the LT code, subtracting background, and taking into account source contribution [56].

3. Results and Discussion

The selected HE process parameters, the properties of the initial material, and the extruded material are summarized in Table 1. The noted increase of 131–159% in YS, 64–81% increase in UTS, and 1.5 times greater hardness due to extrusion are not surprising. It is important that these increases were accompanied by an elongation at break of 15–16% Thus, YS and UTS reach the level typical of H6 or H8, treatments for which the elongation at break is only 6–7% and the hardness is no higher than 44 HV [57]. The improvement in mechanical properties is therefore significant. However, the differences in the HE process parameters for RT extrusion have a relatively weak impact on the mechanical properties of the product. This can be attributed to the relatively low sensitivity of the mechanical properties of technically pure Al to the strain rate in the range used in this work [58,59]. The extrusion temperature appears to exert a more substantial influence on the resultant material properties. For the cryo-cooled sample with true strain of 0.9, the YS and UTS are about 10% higher, and the elongation at break is about 8% lower than for the samples extruded at RT.

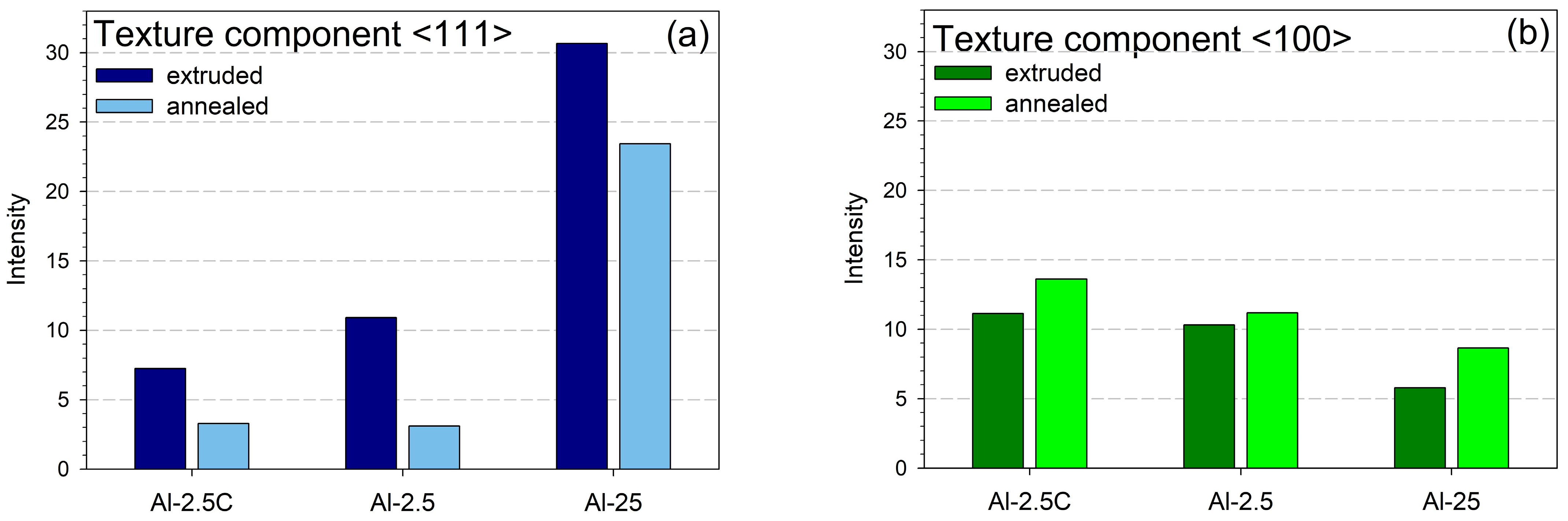
3.1. X-Ray Diffraction

The lattice parameters, crystallite size, and lattice strain of the samples deformed under different conditions, as well as samples annealed after deformation, are shown in Table 2. The differences between the samples practically fall within the measurement uncertainty, which can be related to comparatively small differences in the defect density due to dynamic recovery during extrusion as a result of the deformation temperature. Indeed, the homologous deformation temperature of HE is close to 0.3–0.4, i.e., it falls into the range typical for pure metals recrystallization. Moreover, the relatively high deformation rate of HE results in intensive dynamic recovery, which seems to be responsible for the relatively low difference in the mechanical properties and the microstructure parameters collected in Table 1 and Table 2. The results for the samples annealed at 590 K for 1 h indicate the stability of the lattice parameters, crystallite size, and lattice strain (Table 2). A tendency for a decrease in the lattice parameter due to annealing could be associated with static recovery and/or recrystallization. However, the differences between the samples before and after annealing seem to be very small.
Both the deformed and post-deformation annealed samples exhibited distinct axial textures typical of axisymmetric deformation, e.g., extrusion or drawing of face-centered cubic (fcc) metals. Particularly, good axial symmetry was visible in the deformed state. The relative contributions of the main components of the texture, i.e., <111> and <100>, depend on the extrusion conditions (Figure 1). For the most strongly deformed material, Al-25, the <111> component dominates over the <100> one, which is typical for highly deformed fcc metals with a high stacking fault energy (SFE), such as aluminum. The deformation textures of the remaining, much less deformed materials are more similar to those obtained for metals with lower SFE, strongly deformed in classical uniaxial deformation processes. For the Al-2.5 sample, the contributions of components <111> and <100> are nearly equal. For the Al-2.5C sample, the contribution of component <100> is greater than that of the <111> one. The samples Al-2.5 and Al-2.5C differ mainly in the deformation temperature.
Similar texture effects were previously registered for classical uniaxial deformation and related to the SFE value of fcc metals. A relationship between the relative intensity of the <100> and <111> components and the SFE in fcc metals was proposed by English et al. [60]. From Figure 2 in Ref. [60], one can conclude that an increase in the <100> component contribution in the texture of pure metal with fcc structure can be related to a decrease in SFE. However, large uncertainties in the temperature dependence of the SFE were noticed already by Hirth and Lothe [61]. Both increasing and decreasing tendencies of the SFE dependence on temperature could be found among the results of theoretical calculations [62,63,64,65,66,67]. For aluminum, a decreasing trend of the SFE with increasing temperature was reported in Refs. [68,69,70,71] However, between cryogenic temperature and RT, the effect is rather small. Nevertheless, the implementation of TEM or X-ray diffraction techniques for the SFE measurement poses serious challenges, especially for pure, low-melting-point metals with high SFE, such as aluminum. The use of TEM is easier for low SFE metals. In this case, an increase in SFE with increasing temperature was reported [65,66,72]. The same tendency was observed in X-ray diffraction measurements [73,74,75] and seems to also apply to the current results. However, the difference in the strain rate, which is higher for the cryo-extruded sample, also has some influence on SFE, and presumably this effect is stronger. Indeed, Hu et al. previously reported that an increase in the contribution of the <100> texture component can be related to a decrease in the deformation temperature and an increase in the strain rate (see Table 2 in Ref. [76]). There is experimental evidence that high strain rates and nanocrystalline microstructure may favor mechanical twinning in pure aluminum, e.g., Refs. [77,78], respectively, although this deformation process is typical for low SFE metals with fcc structure. Thus, it can be concluded that the texture effect observed for the cryo-cooled material can be related more to a high strain rate and a refined microstructure typical for hydrostatic extrusion processing at cryogenic temperatures. An increase in the intensity of the <100> texture component, as illustrated in Figure 1, combined with a decrease in the intensity of the <111> component due to annealing, can be related to recrystallization.
Our previous studies have shown that positron annihilation techniques are highly sensitive tools for studying recovery and recrystallization processes [47,50]. Thus, this technique was used to study the course of recrystallization in detail (Section 3.2).

3.2. The Positron Annihilation Studies

3.2.1. Extruded Material

The VEP beam application allowed us to obtain the values of positron diffusion length, which, together with positron lifetime results, may provide information on the defect types and densities [79]. The analysis of the VEP measurement results requires knowledge of the positron implantation profile. This profile for monoenergetic positrons entering a semi-infinite material can be described using the Gaussian derivative, which can be expressed as the Makhovian function [80].
Figure 2 shows the dependencies of the S parameter on the positron implantation energy (bottom axis) and the mean implantation depth (top axis) for the extruded samples and the well-annealed reference one. The mean implantation depth z ¯ was calculated using the formula [81]:
z ¯ = A E n ρ ,
where E is the positron energy in keV, and A and n are the Makhovian function parameters.
Materials 18 04428 g002
Figure 2. The dependencies of the S parameter on the incident positron energy for the extruded aluminum samples and the reference sample. Solid black lines represent the best fit using the VEPFIT code [82].
Figure 2. The dependencies of the S parameter on the incident positron energy for the extruded aluminum samples and the reference sample. Solid black lines represent the best fit using the VEPFIT code [82].
Materials 18 04428 g002
The initial increase in the S parameter at the surface visible for all samples is caused by a thin surface oxide layer and an interface between this layer and the bulk metal [83,84]. For the positron energy higher than 0.1 keV, the S parameter decreases and finally reaches a constant value distinctive for each sample. Solid lines represent the best fits obtained using the VEPFIT code [82] with parameters A = 2.53 µg cm−2 keV−n, n = 1.748, ρ = 2.70 g/cm3 taken for aluminum from Ref. [85]. The thickness of the oxide layer obtained from VEPFIT was a few nanometers for all the studied samples. The values of the positron diffusion length and the S parameter for the bulk of the extruded aluminum samples and the reference one, Sbulk, are given in Table 3. The positron diffusion length for the reference sample, found to be close to 100 nm, is lower than the 150 nm estimated in the literature, e.g., Ref. [83]. This can be related to the lower purity of the commercial AA1050 aluminum samples or the presence of residual lattice defects. Nevertheless, a reduction in the positron diffusion length (L+) is observed in all extruded samples compared to the reference material. This reduction is relatively small for sample Al-2.5, while significantly larger for samples Al-2.5C and Al-25. Similarly, the increase in the bulk value of the S-parameter (Sbulk) for Al-2.5 is much smaller than that for Al-2.5C and Al-25. These results indicate that the concentration of lattice defects introduced during RT extrusion with the reduction ratio (R) of 2.5 is lower than that produced by the extrusion of a cryo-cooled sample at a similar R or room temperature HE at R = 25. This further confirms the superior sensitivity of the positron annihilation technique compared to X-ray diffraction.
The mutual dependence of the Wr and S parameters is shown in Figure 3. The so-called S-Wr plot can reveal information about the changes in the types of lattice defects in the sample. When only two positron states with a variable relative input contribute to annihilation, the S-Wr dependence is proportional, and the plot shows a straight-line segment. The endpoints of this segment correspond to the lattice defects or phases exhibiting specific values of the S and Wr parameters. It is visible in Figure 3 that the points originating from positron annihilation on the surface, in the oxide layer, or at the interface deviate from the straight line along which the majority of the experimental points are roughly arranged. The upper left end of this line corresponds to positron annihilation in the bulk of the reference sample. The lower right end corresponds to positron annihilation in the bulk of the Al-2.5C sample with the highest concentration of lattice defects. Therefore, it can be assumed that the lattice defects induced by HE are similar for the three samples studied, differing only in concentration, which is the highest for the Al-2.5C sample and the lowest for the Al-2.5 one.
Two lifetime components can be resolved in the PALS spectra obtained for the extruded samples, i.e., τ 1 and τ 2 . Their values and intensity of the second component, I2, are gathered in Table 4 ( I 1 + I 2 = 1 ). The mean positron lifetime, τ ¯ , calculated as follows:
τ ¯ = I 1 τ 1 + I 2 τ 2
is also given in Table 4. The mean positron lifetime is a robust parameter that does not depend on the spectrum deconvolution procedure and allows for a more reliable assessment of the extent of changes in the lattice defect type and concentration connected to the changes in the microstructure.
The mean positron lifetime changes from 190 to 203 ps (Table 4). For the sample Al-2.5, it is lower than for the other two samples, which reflects the behavior of Sbulk obtained in the VEP beam measurements. This suggests a lower average density of crystal lattice defects, taking into account that these defects are similar in all samples. The longer lifetime, τ 2 , in the range 247–251 ps, comes from the annihilation of positrons trapped in defects. The shorter lifetime, τ 1 , has values close to 130 ps, which are much lower than the so-called bulk positron lifetime obtained for well annealed Al, i.e., 162 ps. It is well explained in accordance with the two-state positron trapping model or a positron diffusion trapping model [86,87]. In the case of a dislocation cell structure or small grains, if the cells/grains are small enough, positrons can diffuse to the cell walls/grain boundaries and be trapped in defects in those regions. Inside the cells/grains, positrons can annihilate from a free state in the undisturbed crystal lattice, where their lifetime is shorter, or become trapped in defects, if such are present inside cells/grains, contributing to the longer component. Then, the shorter lifetime component originates from positron annihilation in areas of low lattice defect concentration. Its presence indicates that, despite relatively high deformation, regions with a low concentration of the lattice defects remain.
It is known that the distribution of lattice defects induced by deformation is not homogeneous, resulting in a cellular dislocation substructure with low dislocation density in cell interiors and high dislocation density in cell walls and subgrain boundaries. The cell size decreases with deformation [88]. Dynamic recovery favors such a type of microstructure, which is more pronounced for deformation at relatively high homologous temperatures. This is consistent with the results of the TEM study of HE aluminum of commercial purity, performed by Pachla et al. [29]. Those authors demonstrated that the product extruded to a true strain of nearly 1, which is only slightly higher than that of the Al-2.5 and Al-2.5C samples, exhibited a microstructure consisting of subgrains within the micrometer-sized primary grains. The subgrain size of approximately 900 nm is typical for both cryo-cooled and RT extruded products in this case. Thus, the microstructure of both products (i.e., Al-2.5 and Al-2.5C) should be similar despite significantly different deformation temperatures. For the RT extruded material with a strain close to 3, Pachla et al. reported smaller subgrains (i.e., 600 nm). It should be noted, however, that the samples investigated by Pachla et al. were additionally cooled with water to limit static recovery after they left the die [29]. Therefore, the subgrain sizes of the samples investigated in the present paper may be slightly larger. Nevertheless, the currently studied samples do not differ significantly in terms of the hardness and yield strength from those quenched and studied in previous research [29]. Therefore, we do not expect a significant difference in the subgrain size of the material in the current study. Indeed, Styczyński et al. showed that the water cooling after extrusion did not affect the grain size, and the deformation-induced microstructure effect was limited mainly to a change in relative dislocation density inside the grains [89]. The positron lifetime in aluminum lattice defects has been extensively studied both experimentally and theoretically. Fluss et al. reported a positron lifetime of 244 ps for monovacancies in polycrystalline aluminum at 350 °C [90]. Theoretical calculations performed for Al by Häkkinen et al. indicated a positron lifetime of 252 ps for bulk monovacancies [91]. For divacancies, the theoretically calculated positron lifetime is larger and equal to 273 ps [92]. The positron lifetime for vacancies associated with dislocations, which have lower symmetry than thermally generated monovacancies, was experimentally determined to be equal to 220 ps for the Al single crystal [93,94]. Theoretical calculations gave the values of 224–225 ps [95]. However, Čížek et al. attributed a higher positron lifetime value of 243 ps to positrons trapped at vacancies associated with dislocations in high-purity polycrystalline aluminum rolled at 77 K [87].
The results obtained by us for the extruded samples are close to those obtained by Su et al. [87] and Cao et al. [96] for commercially pure Al grade AA1050 processed by equal-channel angular pressing (ECAP) at room and cryogenic temperatures, for which τ 2 was in the range of 220–251 ps and about 241 ps, respectively. In addition to positron annihilation in vacancies associated with dislocations, Su et al. also considered the contribution to τ 2 from positron annihilation in bulk monovacancies and divacancies to explain the longest lifetimes [87].
The highest mean positron lifetime and the shortest positron diffusion length obtained for the Al-2.5C sample indicate the highest average defect density. The clear difference between the Al-2.5C sample and Al-2.5 one is particularly noticeable, even though, according to Pachla et al., the difference in structure and grain size between cryo-cooled and RT extrusion at low strains is small due to comparable adiabatic effects [29]. The higher average defect density in the Al-2.5C sample may be related not only to the higher density of dislocations near the subgrain boundaries, but also to their presence in the subgrain interior.
As reported by Pachla et al., due to recovery, the material extruded at RT at higher strains exhibits grains with a dislocation-free interior and a higher density of dislocations at grain boundaries [29]. The mean positron lifetime and positron diffusion length for the samples Al-2.5C and Al-25 have similar values despite the differences in microstructure and grain size. However, a slightly higher average defect density is still found in the cryo-cooled sample extruded at a much lower true strain. Therefore, it can be concluded that microstructure refinement has a significant contribution to the strain hardening of hydroextruded aluminum. The difference in subgrain size between 600 and 900 nm explains the higher yield strength of the Al-25 sample than the Al-2.5 one [97]. The highest value of the cooled sample Al2.5C can be related to the higher dislocation density inside the subgrains, and therefore to increased dislocation hardening.

3.2.2. Isochronal Annealing of the Extrusion Products

Figure 4 shows the dependencies of two positron lifetime components and the intensity of the longer of them, I2, on the annealing temperature. In all cases, it can be seen that the values of τ 1 , τ 2 , and I2 do not change significantly up to a temperature of about 500 K. A steady, slight decrease in I2, indicating a slight reduction in defect concentration, precedes its rapid decline to virtually zero. This slight decrease can be attributed to static recovery of the material. In the case of the Al-2.5 sample, a clear but gradual decrease in I2, ending with the disappearance of this component, occurs in the temperature range of 530–590 K. This decrease in I2 is accompanied by an increase in τ1, which finally reaches the bulk value. For samples Al-2.5C and Al-25, I2 drops virtually to zero at temperatures of 530 and 550 K, respectively. Such behavior indicates that the recrystallization of the Al-2.5 sample occurs within the temperature range of 530–590 K, while for the remaining samples, it ends at temperatures of approximately 530 and 550 K. This relatively low difference corresponds to the variations in the deformed material microstructure, texture, and properties. As expected, the recrystallization temperature of the less deformed sample Al-2.5 is slightly higher than that of the other two.
The temperature dependencies of the mean positron lifetime τ ¯ and the S parameter are shown in Figure 5 and Figure 6, respectively. For the samples Al-2.5C and Al-25 the slight decrease in τ ¯ and the S-parameter caused by static recovery starts above 400–430 K, which agrees with observations of Pachla at all. [29]. It is least visible at about 450 K for the sample 2.5Al with the lowest initial defect concentration. The drop in the mean positron lifetime τ ¯ starting at 450–470 K for the Al-2.5C and Al-25 samples and at 490–510 K for the Al-2.5 sample indicate the beginning of recrystallization, which ends earliest in the case of the Al-2.5C sample. This is visible both in the course of the τ ¯ and S parameters (Figure 5 and Figure 6). Additionally, the range of changes in both parameters τ ¯ and S), which can be associated with the extent of recrystallization, is smallest for Al-2.5C and largest for Al-2.5.
The temperature dependencies of the S-parameter or τ ¯ resulting from recrystallization can be used in the diffusion trapping model to determine the activation energy of the grain boundaries migration during recrystallization [98]. The model assumes positron annihilation in the defect-free interior of the new grains. Positrons can also diffuse to the grain boundaries, where they become trapped at crystal lattice defects and then annihilate. The model takes into account grain growth kinetics induced by temperature. Thus, the increase in temperature causes grain boundary migration, which leads to an increase in the grain size reflected in the decreasing S-parameter or τ ¯ values. However, the positron diffusion length of approximately 0.1 μm allows tracing for only the initial stage of recrystallization when the grain radii reach several micrometers. For larger, well-annealed grains, positron trapping and annihilation at grain boundary regions can be neglected. The solid curves in Figure 5 and Figure 6 are the results of fitting the model describing the grain boundary migration to the experimental points for the studied samples. The values of activation energy of the grain boundary migration, obtained for these two relationships, were used to calculate a weighted average taking into account their uncertainties. The results are gathered in Table 5. The obtained values are close to 1.5 eV and vary little from sample to sample. They are higher than 0.63 ± 0.1 eV determined for high-purity aluminum subjected to a rapid solidification process [99]. They are also larger than the activation energy for grain boundary diffusion in aluminum, which is 0.87 eV, as measured by TEM [88]. However, alloying elements in aluminum raise the activation energy for grain boundary migration. For example, 1 wt.% of Au increases it to 1.73 ± 0.40 eV [99]. Therefore, values near 1.5 eV may result from about 0.5% impurities (mainly Fe and Si) in the studied grade AA1050. Although the uncertainties in the energy values obtained from the fitting procedure are comparable to the differences between the samples, a pattern can be observed. Thus, the smallest activation energy of the grain boundary migration for cryo-cooled Al-2.5C coincides with this sample’s slightly lower recrystallization temperature. In turn, the highest energy is shown by the least deformed Al-2.5 sample.

4. Conclusions

  • Distinct axial textures were found both for the hydrostatically extruded and post-deformation annealed samples of aluminum grade AA1050. The relative contributions of the main components of the axial texture, i.e., <111> and <100>, depend on the HE conditions. An increase in the contribution of the <100> texture component for the cryo-cooled material can be related to the effect of the low temperature and high stress rate of deformation. Recrystallization causes an increase in the intensity of the <100> texture component, combined with a decrease in the intensity of the <111> one.
  • Shortening in the positron diffusion path, more significant for the cryo-cooled material at the true strain of 0.9 and that extruded at RT at the strain of 3.2, resulted from increased density of the lattice defects. This was also reflected in the bulk values of the S parameter and the mean positron lifetime.
  • Vacancies associated with dislocations are the main positron-trapping defects revealed by PALS. However, the contribution of monovacancies or even divacancies cannot be excluded.
  • The cryo-cooled material extruded at a true strain of 0.9, as well as the one extruded at RT at a true strain of 3.2, exhibited significantly higher mean lattice defect concentrations and considerably lower recrystallization temperatures compared to the sample extruded at RT at a true strain of 0.9, which had a less defective crystal structure.
  • The activation energy for grain boundary migration during the recrystallization of hydrostatically extruded AA1050 aluminum, as determined from the positron diffusion trapping model, is approximately 1.5 eV and showed only a slight dependence on the extrusion temperature and true strain.

Author Contributions

Conceptualization, E.D. and M.S.; Methodology, E.D., M.W. and J.S.; Investigation, E.D., M.W., M.S. and J.S.; Writing—original draft, E.D. and M.W.; Writing—review & editing, E.D., M.W., M.S. and J.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on request from the corresponding author due to technical/time limitations.

Acknowledgments

The paper is dedicated to the memory of Wacław Pachla, a scientist of Unipress, Poland, our friend and expert in hydrostatic extrusion. M.W. would like to thank for financial support under the AGH contract no. 16.16.110.663/1.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
PALSPositron Annihilation Lifetime Spectroscopy
DBDoppler Broadening
CAGRCompound Annual Growth Rate
HEHydrostatic Extrusion
TEMTransmission Electron Microscopy
RTRoom Temperature
XRDX-ray Diffraction
TREORTrial and Error
ODFOrientation Distribution Function
ADCArbitrarily Defined Cell
VEPVariable Energy Positron
YSYield Strength
UTSUltimate Tensile Strength
ETExtrusion Temperature
EPExtrusion Pressure
RCross-Section Area Reduction Ratio
TSTrue Strain
MESMean Extrusion Speed
fccFace Centered Cubic
SFEStacking Fault Energy
ECAPEqual-Channel Angular Pressing

References

  1. Aluminum Extrusion Market (2025–2030). Grant View Research Report ID: GVR-3-68038-700-1. Available online: https://www.grandviewresearch.com/industry-analysis/aluminum-extrusion-market (accessed on 15 September 2025).
  2. Sheppard, T. Extrusion of Aluminium Alloys, 1st ed.; Springer: New York, NY, USA, 1999. [Google Scholar]
  3. Dančenko, V.N.; Milenin, A.A.; Golovko, A.N. Proizvodstvo Profilej iz Aljuminievyh Splavov, 1st ed.; Sistemnye Tehnologii: Dnepropetrovsk, Ukraine, 2002. [Google Scholar]
  4. Meyer, G.E.; Simonen, F.A.; Gerdeen, J.C.; Fiorentino, R.J.; Sabroff, A.M. Design of a Production hydrostatic Extrusion Press; Technical Report AFML-TR-68-52; Battelle Columbus Memorial Institute Laboratories: Columbus, OH, USA, 1968; Available online: https://apps.dtic.mil/sti/tr/pdf/AD0855302.pdf (accessed on 1 July 2024).
  5. Pugh, H.L.; Ashcroft, K. The Hydrostatic or Ramless Extrusion of Metals by Fluid Pressure; NEL Report No. 32; National Engineering Laboratory: Glasgow, Scotland, 1962. [Google Scholar]
  6. Sachs, G.; Eisbein, W.; Kuntze, W.; Linicus, W. Kraftbedarf und Fließvorgänge beim Stangenpressen. In Spanlose Formung der Metalle. Mitteilungen der Deutschen Materialprüfugsanstalten; Springer: Berlin/Heidelberg, Germany, 1931; Volume 16, pp. 67–96. [Google Scholar] [CrossRef]
  7. Robertson, J. Improvements in or Appertaining to the Manufacture of Compressing, Shaping, and Drawing of Metal Tubes, Tubular, Hollow, and Solid Articles, and in Means and Apparatus Therefor. British Patent No. 11436, 6 July 1891. [Google Scholar]
  8. Robertson, J. Method of an Apparatus for Forming Metal Articles. British Patent No. 19356, 14 October 1893. [Google Scholar]
  9. Robertson, J. Shaping Metal Tubes. US481060, 16 August 1892. [Google Scholar]
  10. Robertson, J. Method of and Apparatus for Shaping and Drawing Metal Tubes. US493946, 21 March 1893. [Google Scholar]
  11. Robertson, J. Method of and Apparatus for Forming Metal Articles. US524504, 14 August 1894. [Google Scholar]
  12. Robertson, J. Apparatus for Forming Metal Articles. US524505, 14 August 1894. [Google Scholar]
  13. Robertson, J. Apparatus for the Manufacture of Metal Tubes, Rods &c. US524506, 14 August 1894. [Google Scholar]
  14. Robertson, J. Method of Forming Metal Articles. US524508, 14 August 1894. [Google Scholar]
  15. Robertson, J. Apparatus for Shaping, Drawing, Solidifying and Squirting Metals. US629610, 25 July 1899. [Google Scholar]
  16. Kronberger, H. Review Lecture. Hydrostatic Extrusion. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1969, 311, 331–347. Available online: http://www.jstor.org/stable/2416236 (accessed on 1 July 2024).
  17. Bridgman, P.J. Method and Apparatus for Cold Drawing. US2558035, 26 June 1951. [Google Scholar]
  18. Inoue, N. Introduction. In Hydrostatic Extrusion, Theory and Application; Inoue, N., Nishihara, M., Eds.; Springer: Dordrecht, The Netherlands, 1985. [Google Scholar] [CrossRef]
  19. Vladislav, I.E.; Livenko, N.D. Method and Means for Shaping Parts by Hydraulic Extrusion. US4011744A, 15 March 1977. [Google Scholar]
  20. Cerovsky, F. Hydraulic Extrusion Tool with Integrated Induction Device. US11141766B2, 12 October 2021. [Google Scholar]
  21. Poggenpohl, K. Hydraulic Extrusion Press and Method for Operating a Hydraulic Extrusion Press. WO 2013/167111A1, 2 April 2015. [Google Scholar]
  22. Poggenpohl, K. Presse à Filer Hydraulique et Procédé de Fonctionnement d’Une Presse à Filer Hydraulique. US11407192B2, 9 August 2022. [Google Scholar]
  23. Alexander, J.M. Hydrostatic extrusion, the state of the art. In Proceedings of the Fourteenth International Machine Tool Design and Research Conference, Manchester, UK, 12–14 September 1973; Koenigsberger, F., Tobias, S.A., Eds.; Palgrave: London, UK, 1974. [Google Scholar] [CrossRef]
  24. Moodij, E. Friction Phenomena in Hydrostatic Extrusion of Magnesium. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2014. [Google Scholar]
  25. Hettwer, P.F.; Uy, J.C.; McCann, D.R. Aluminum wire by cold hydrostatic extrusion. J. Basic Eng. 1969, 91, 822–829. [Google Scholar] [CrossRef]
  26. Herø, H.; Mikkelsen, J.A. Some mechanical and structural properties of hydrostatically extruded aluminum and aluminum alloys. J. Inst. Metals 1969, 97, 18–22. [Google Scholar]
  27. Lee, E.H.; Mallett, R.L.; McMeeking, R.M.; Sherby, O.J.; Shyne, J.C.; Whalen, R.T. Hydrostatic Extrusion; Final Rep.; Department of Materials Science and Engineering of Stanford University: Stanford, CA, USA, 1978; Available online: https://apps.dtic.mil/sti/tr/pdf/ADA052056.pdf (accessed on 1 July 2024).
  28. Kalish, D.; LeFevre, B.G. Subgrain strengthening of aluminum conductor wires. Metall. Trans. A 1975, 6, 1319–1324. [Google Scholar] [CrossRef]
  29. Pachla, W.; Kulczyk, M.; Smalc-Koziorowska, J.; Wróblewska, M.; Skiba, J.; Przybysz, S.; Przybysz, M. Mechanical properties and microstructure of ultrafine grained commercial purity aluminium prepared by cryo-hydrostatic extrusion. Mater. Sci. Eng. A 2017, 695, 178–192. [Google Scholar] [CrossRef]
  30. Richert, M.W.; Leszczyńska-Madej, B.; Pachla, W.; Skiba, J. The microstructure and properties of hydrostatically extruded polycrystalline aluminium Al99.5. Arch. Metal. Mater. 2012, 57, 911–917. [Google Scholar] [CrossRef]
  31. Pachla, W.; Kulczyk, M.; Świderska-Środa, A.; Lewandowska, M.; Garbacz, H.; Mazur, A.; Kurzydłowski, K.J. Nanostructuring of metals by hydrostatic extrusion. In Proceedings of 9th International Conference on Metal Forming ESAFORM 2006, Glasgow, UK, 26–28 April 2006; Juster, N., Rosochowski, A., Eds.; Publ. House Akapi: Kraków, Poland, 2006; pp. 535–538. [Google Scholar]
  32. Kulczyk, M.; Skiba, J.; Pachla, W. Microstructure and mechanical properties of AA5483 treated by a combination of ECAP and hydrostatic extrusion. Arch. Metal. Mater. 2014, 59, 163–166. [Google Scholar] [CrossRef]
  33. Towarek, A.; Jurczak, W.; Zdunek, J.; Kulczyk, M.; Mizera, J. Influence of Hydrostatic Extrusion on the Mechanical Properties of the Model Al-Mg Alloys. J. Mater. Eng. Perform. 2021, 30, 3502–3509. [Google Scholar] [CrossRef]
  34. Brynk, T.; Pakieła, Z.; Kulczyk, M.; Kurzydłowski, K.J. Fatigue crack growth rate in ultrafine-grained Al 5483 and 7475 alloys processed by hydro-extrusion. Mech. Mater. 2013, 67, 46–52. [Google Scholar] [CrossRef]
  35. Orłowska, M.; Ura-Bińczyk, E.; Śnieżek, L.; Skudniewski, P.; Kulczyk, M.; Adamczyk-Cieślak, B.; Mizera, J. Increasing the Mechanical Strength and Corrosion Resistance of Aluminum Alloy 7075 via Hydrostatic Extrusion and Aging. Materials 2022, 15, 4577. [Google Scholar] [CrossRef]
  36. Skiba, J.; Kossakowska, J.; Kulczyk, M.; Pachla, W.; Przybysz, S.; Smalc-Koziorowska, J.; Przybysz, M. The impact of severe plastic deformations obtained by hydrostatic extrusion on the machinability of ultrafine-grained AA5083 alloy. J. Manuf. Process. 2020, 58, 1232–1240. [Google Scholar] [CrossRef]
  37. Kulczyk, M.; Skiba, J.; Pachla, W.; Smalc-Koziorowska, J.; Przybysz, S.; Przybysz, M. The effect of high-pressure plastic forming on the structure and strength of AA5083 and AA5754 alloys intended for fasteners. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 903–911. [Google Scholar] [CrossRef]
  38. Selim, F.A. Positron Annihilation Spectroscopy Applied to Materials Science and Engineering. Solid State Phenom. 2025, 372, 99–114. [Google Scholar] [CrossRef]
  39. Čížek, J. Characterization of lattice defects in metallic materials by positron annihilation spectroscopy: A review. J. Mater. Sci. Technol. 2018, 34, 577–598. [Google Scholar] [CrossRef]
  40. ISO-6892-1:2019; Metallic Materials—Tensile Testing. Part 1: Method of Test at Room Temperature. ISO: Geneva, Switzerland, 2019.
  41. ASTM E8/E8M-22; Standard Test Methods for Tension Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2024.
  42. ISO 6507-1:2023; Metallic Materials-Vickers Hardness Test—Part 1: Test Method. ISO: Geneva, Switzerland, 2023.
  43. ASTM E384-22; Standard Test Method for Microindentation Hardness of Materials. ASTM International: West Conshohocken, PA, USA, 2023.
  44. Werner, P.E.; Eriksson, L.; Westdahl, M. TREOR, a semi-exhaustive trial-and-error powder indexing program for all symmetries. J. Appl. Cryst. 1985, 18, 367–370. [Google Scholar] [CrossRef]
  45. Boultif, A.; Louër, D. Powder pattern indexing with the dichotomy method. J. Appl. Cryst. 2004, 37, 724–731. [Google Scholar] [CrossRef]
  46. Williamson, G.K.; Hall, W.H. X-ray line broadening from filed aluminium and wolfram. Acta Met. 1953, 1, 22–31. [Google Scholar] [CrossRef]
  47. Dryzek, J.; Wróbel, M.; Dryzek, E. Recrystallization in severely deformed Ag, Au, and Fe studied by positron-annihilation and XRD methods. Phys. Status Solidi B 2016, 253, 2031–2042. [Google Scholar] [CrossRef]
  48. Dryzek, J.; Wróbel, M. Observation of the recrystallization process in pure Nb and Zr using positron lifetime spectroscopy and XRD techniques. Phys. Status Solidi B 2018, 255, 1800051. [Google Scholar] [CrossRef]
  49. Dryzek, J.; Wróbel, M. Recovery and recrystallization in molybdenum studied by positron annihilation and X-ray methods. Int. J. Refract. Met. Hard Mater. 2021, 97, 105514. [Google Scholar] [CrossRef]
  50. Dryzek, J.; Wróbel, M.; Czeppe, T. Recovery and recrystallization in vanadium foil studied by positron annihilation and X-ray methods. Int. J. Refract. Met. Hard Mater. 2022, 103, 105759. [Google Scholar] [CrossRef]
  51. Schulz, L.G. A direct method of determining preferred orientation of a flat reflection sample using a Geiger counter X-ray spectrometer. J. Appl. Phys. 1949, 20, 1030–1033. [Google Scholar] [CrossRef]
  52. Pawlik, K. Determination of the orientation distribution function from pole figures in arbitrarily defined cells. Phys. Status Solidi B 1986, 134, 477–483. [Google Scholar] [CrossRef]
  53. LaboTex, the Texture Analysis Software for Windows. Available online: http://www.labosoft.com.pl/ (accessed on 16 September 2024).
  54. Caleyo, F.; Baudin, T.; Mathon, M.H.; Penelle, R. Comparison of several methods for the reproduction of the orientation distribution function from pole figures in medium to strong textured materials. Eur. Phys. J. Appl. Phys. 2001, 15, 85–96. [Google Scholar] [CrossRef]
  55. Horodek, P.; Kobets, A.G.; Meshkov, I.N.; Sidorin, A.A.; Orlov, O.S. Slow positron beam at the JINR, Dubna. Nukleonika 2015, 60, 725–728. [Google Scholar] [CrossRef]
  56. Kansy, J. Microcomputer program for analysis of positron annihilation lifetime spectra. Nucl. Instrum. Methods Phys. Res. A 1996, 374, 235–244. [Google Scholar] [CrossRef]
  57. Aluminium: Specifications, Properties, Classifications and Classes. Available online: https://www.azom.com/article.aspx?ArticleID=2863 (accessed on 10 January 2024).
  58. Sun, P.L.; Cerreta, E.K.; Gray III, G.T.; Bingert, J.F. The effect of grain size, strain rate, and temperature on the mechanical behavior of commercial purity aluminum. Metall. Mater. Trans. A 2006, 37, 2984–2994. [Google Scholar] [CrossRef]
  59. Takata, N.; Okitsu, Y.; Tsuji, N. Dynamic deformation behavior of ultrafine grained aluminum produced by ARB and subsequent annealing. J. Mater. Sci. 2008, 43, 7385–7390. [Google Scholar] [CrossRef]
  60. English, A.T.; Chin, G.Y. On the variation of wire texture with stacking fault energy in f.c.c. metals and alloys. Acta Metall. 1965, 13, 1013–1016. [Google Scholar] [CrossRef]
  61. Hirth, J.P.; Lothe, J. Theory of Dislocations; John Wiley & Sons, Inc.: Malabar, FL, USA, 1982. [Google Scholar]
  62. Curtze, S.; Kuokkala, V.T.; Oikari, A.; Talonen, J.; Hänninen, H. Thermodynamic modeling of the stacking fault energy of austenitic steels. Acta Mater. 2011, 59, 1068–1076. [Google Scholar] [CrossRef]
  63. Yamanaka, K.; Mori, M.; Kurosu, S.; Matsumoto, H.; Chiba, A. Ultrafine grain refinement of biomedical Co–29Cr–6Mo alloy during conventional hot-compression. Metall. Mater. Trans. A 2009, 40, 1980–1994. [Google Scholar] [CrossRef]
  64. Lee, B.S.; Koizumi, Y.; Matsumoto, H.; Chiba, A. Collective behavior of strain-induced martensitic transformation (SIMT) in biomedical Co–Cr–Mo–N alloy polycrystal: An ex-situ electron backscattering diffraction study. Mater. Sci. Eng. A 2014, 611, 263–273. [Google Scholar] [CrossRef]
  65. Rémy, L.; Pineau, A. Temperature dependence of stacking fault energy in close-packed metals and alloys. Mater. Sci. Eng. 1978, 36, 47–63. [Google Scholar] [CrossRef]
  66. Ericsson, T. The temperature and concentration dependence of the stacking fault energy in the Co-Ni system. Acta Metall. 1966, 14, 853–865. [Google Scholar] [CrossRef]
  67. Dryzek, E.; Wróbel, M.; Rogal, Ł.; Sarnek, M. Effect of rolling temperature on martensitic transformation and strain hardening of Fe–21.2Mn–0.68C Steel. Metall. Mater. Trans. A 2024, 55, 839–853. [Google Scholar] [CrossRef]
  68. Bhogra, M.; Ramamurty, U.; Waghmare, U.V. Temperature-dependent stability of stacking faults in Al, Cu, and Ni: First-principles analysis. J. Phys. Condens. Matter 2014, 26, 385402. [Google Scholar] [CrossRef]
  69. Liu, L.H.; Chen, J.H.; Fan, T.W.; Liu, Z.R.; Zhang, Y.; Yuan, D.W. The possibilities to lower the stacking fault energies of aluminum materials investigated by first-principles energy calculations. Comput. Mater. Sci. 2015, 108, 136–146. [Google Scholar] [CrossRef]
  70. Zhang, X.; Grabowski, B.; Körmann, F.; Ruban, A.V.; Gong, Y.; Reed, R.C.; Hickel, T.; Neugebauer, J. Temperature dependence of the stacking-fault Gibbs energy for Al, Cu, and Ni. Phys. Rev. B 2018, 98, 224106. [Google Scholar] [CrossRef]
  71. Liu, L.L.; Wang, R.; Wu, X.Z.; Gan, L.Y.; Wei, Q.Y. Temperature effects on the generalized planar fault energies and twinnabilities of Al, Ni, and Cu: First principles calculations. Comput. Mater. Sci. 2014, 88, 124–130. [Google Scholar] [CrossRef]
  72. Tisone, T.C. The concentration and temperature dependence of the stacking fault energy in face-centered cubic Co-Fe alloys. Acta Metall. 1973, 21, 229–236. [Google Scholar] [CrossRef]
  73. Walter, M.; Mujica Roncery, L.; Weber, S.; Leich, L.; Theisen, W. XRD measurement of stacking fault energy of Cr–Ni austenitic steels: Influence of temperature and alloying elements. J. Mater. Sci. 2020, 55, 13424–13437. [Google Scholar] [CrossRef]
  74. Pontini, A.E.; Hermida, J.D. X-ray diffraction measurement of the stacking fault energy reduction induced by hydrogen in an AISI 304 steel. Scr. Mater. 1997, 37, 1831–1837. [Google Scholar] [CrossRef]
  75. Fu, W.; Zheng, W.; Huang, Y.; Guo, F.; Jiang, S.; Xue, P.; Ren, Y.; Fan, H.; Ning, Z.; Sun, J. Cryogenic mechanical behaviors of CrMnFeCoNi high-entropy alloy. Mater. Sci. Eng. A 2020, 789, 139579. [Google Scholar] [CrossRef]
  76. Hu, H. Textures of materials. Texture Stress Microstruct. 1979, 1, 233–258. [Google Scholar] [CrossRef]
  77. Zhao, F.; Zhu, Y.; Xie, J. Deformation twinning in pure aluminum under ultrahigh strain rate: Dependence of strain rate and crystallographic orientation. Mater. Lett. 2021, 285, 129181. [Google Scholar] [CrossRef]
  78. Chen, M.; Ma, E.; Hemker, K.J.; Shehg, H.; Wang, Y.; Cheng, X. Deformation Twinning in Nanocrystalline Aluminum. Science 2003, 300, 1275–1277. [Google Scholar] [CrossRef]
  79. Krause-Rehberg, R.; Bondarenko, V.; Thiele, E.; Klemm, R.; Schell, N. Determination of absolute defect concentrations for saturated positron trapping-deformed polycrystalline Ni as a case study. Nucl. Instr. Meth. Phys. Res. B 2005, 240, 719–725. [Google Scholar] [CrossRef]
  80. Hansen, H.E.; Ingerslev-Jensen, U. Penetration of fast electrons and positrons. J. Phys. D Appl. Phys. 1983, 16, 1353–1370. [Google Scholar] [CrossRef]
  81. Valkealahti, S.; Nieminen, R.M. Monte-Carlo calculations of keV electron and positron slowing down in solids. Appl. Phys. A 1983, 32, 95–106. [Google Scholar] [CrossRef]
  82. Van Veen, A.; Schut, H.; Clement, M.; De Nijs, J.M.M.; Kruseman, A.; Ijpma, M.R. VEPFIT applied to depth profiling problems. Appl. Surf. Sci. 1995, 85, 216–224. [Google Scholar] [CrossRef]
  83. Hebert, K.R.; Gessmann, T.; Lynn, K.G.; Asoka-Kumar, P. Positron annihilation spectroscopy study of interfacial defects formed by anodic oxidation of aluminum. J. Electrochem. Soc. 2004, 151, B22. [Google Scholar] [CrossRef]
  84. Wu, Y.C.; Zhai, T.; Coleman, P.G. A positron annihilation study of corrosion of aluminum and aluminum alloy by NaOH. Metall. Mater. Trans. A 2012, 43, 2823–2831. [Google Scholar] [CrossRef]
  85. Dryzek, J.; Horodek, P. GEANT4 simulation of slow positron beam implantation profiles. Nucl. Instr. Methods Phys. Res. B 2008, 266, 4000–4009. [Google Scholar] [CrossRef]
  86. Bergersen, B.; Stott, M.J. The effect of vacancy formation on the temperature dependence of the positron lifetime. Solid State Commun. 1969, 7, 1203–1205. [Google Scholar] [CrossRef]
  87. Su, L.H.; Lu, C.; He, L.Z.; Zhang, L.C.; Guagliardo, P.; Tieu, A.K.; Samarin, S.N.; Williams, J.F.; Li, H.J. Study of vacancy-type defects by positron annihilation in ultrafine-grained aluminum severely deformed at room and cryogenic temperatures. Acta Mater. 2012, 60, 4218–4228. [Google Scholar] [CrossRef]
  88. Humphreys, F.J.; Hatherly, M. Recrystallization and Related Annealing Phenomena, 2nd ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2004. [Google Scholar]
  89. Styczyński, L.; Pachla, W.; Wojciechowski, S. Thermal-softening processes in polycrystalline aluminium during hydrostatic extrusion. Met. Sci. 1982, 16, 525–528. [Google Scholar] [CrossRef]
  90. Fluss, M.J.; Smedskjaer, L.C.; Chason, M.K.; Legnini, D.G.; Siegel, R.W. Measurements of the vacancy formation enthalpy in aluminum using positron annihilation spectroscopy. Phys. Rev. B 1978, 17, 3444. [Google Scholar] [CrossRef]
  91. Häkkinen, H.; Mäkinen, S.; Manninen, M. Edge dislocations in fcc metals: Microscopic calculations of core structure and positron states in Al and Cu. Phys. Rev. B 1990, 41, 12441. [Google Scholar] [CrossRef]
  92. Puska, M.J.; Nieminen, R.M. Defect spectroscopy with positrons: A general calculational method. J. Phys. F Met. Phys. 1983, 13, 333–346. [Google Scholar] [CrossRef]
  93. Petersen, K.; Repin, I.A.; Trumpy, G. Positron lifetime analysis of dislocations arising from tensile strain. J. Phys. Condens. Matter. 1996, 8, 2815. [Google Scholar] [CrossRef]
  94. Hidalgo, C.; González-Doncel, G.; Linderoth, S.; San Juan, J. Structure of dislocations in Al and Fe as studied by positron-annihilation spectroscopy. Phys. Rev. B 1992, 45, 7017. [Google Scholar] [CrossRef]
  95. Čížek, J.; Procházka, I.; Kmječ, T.; Vostrý, P. Using of modified trapping model in positron lifetime study of cold-worked aluminium. Phys. Status Solidi A 2000, 180, 439–458. [Google Scholar] [CrossRef]
  96. Cao, Y.; He, L.; Cao, X.; Zhang, P.; Wang, B.; Zhou, Y.; Wang, P.; Cui, J. The relationship of dislocation and vacancy cluster with yield strength in magnetic annealed UFG 1050 aluminum alloy. Mater. Sci. Eng. A 2017, 679, 417–421. [Google Scholar] [CrossRef]
  97. Dangwal, S.; Edalati, K.; Valiev, R.Z.; Langdon, T.G. Breaks in the Hall–Petch Relationship after Severe Plastic Deformation of Magnesium, Aluminum, Copper, and Iron. Crystals 2023, 13, 413. [Google Scholar] [CrossRef]
  98. Dryzek, J. Positron annihilation studies of recrystallization in the subsurface zone induced by friction in magnesium-effect of the inhomogeneity on measured positron annihilation characteristics. Appl. Phys. A 2014, 114, 465–475. [Google Scholar] [CrossRef]
  99. Dryzek, J.; Siemek, K.; Ziewiec, K.; Schut, H. Positron annihilation and tribological studies of nano-embedded Al alloys. Bull. Mater. Sci. 2015, 38, 1141–1148. [Google Scholar] [CrossRef]
Materials 18 04428 g001
Figure 1. Intensity of the components of the axial textures: (a) <111>; (b) <100>.
Figure 1. Intensity of the components of the axial textures: (a) <111>; (b) <100>.
Materials 18 04428 g001
Materials 18 04428 g003
Figure 3. The dependencies of the S parameter as a function of the Wr parameter for the extruded aluminum samples and the reference sample.
Figure 3. The dependencies of the S parameter as a function of the Wr parameter for the extruded aluminum samples and the reference sample.
Materials 18 04428 g003
Materials 18 04428 g004
Figure 4. Dependencies of the positron lifetimes τ 1 , τ 2 and intensity of the long lifetime I2 on the annealing temperature: (a) Al-2.5; (b) Al-2.5C; (c) Al-25.
Figure 4. Dependencies of the positron lifetimes τ 1 , τ 2 and intensity of the long lifetime I2 on the annealing temperature: (a) Al-2.5; (b) Al-2.5C; (c) Al-25.
Materials 18 04428 g004
Materials 18 04428 g005
Figure 5. The mean lifetime vs. temperature annealing for AA1050 aluminum samples.
Figure 5. The mean lifetime vs. temperature annealing for AA1050 aluminum samples.
Materials 18 04428 g005
Materials 18 04428 g006
Figure 6. The S parameter vs. the annealing temperature.
Figure 6. The S parameter vs. the annealing temperature.
Materials 18 04428 g006
Table 1. Specification and parameters for AA1050 samples of the HE process.
Table 1. Specification and parameters for AA1050 samples of the HE process.
SampleETEP [MPa]R = A0/AfTS
lnR		MES
[1/s]		Hardness HV0.2UTS Rm [MPa]YS R0.2 [MPa]Elongation at Break ε [%]
initial-----29765136
Al-2.5room2172.490.911.374612511815.7
Al-2.5Ccryo-cooled1752.510.922.024713813214.6
Al-25room18025.33.235.554912912116.4
ET—Extrusion temperature, EP—Extrusion pressure, R—Reduction ratio (A0—the cross-section surface area of the billet, Af—the cross-section surface area of the extruded product), TS—True strain, MES—Mean extrusion speed (value independent of the geometry of the system), UTS—Ultimate tensile strength, YS—Yield strength.
Table 2. XRD measurement results.
Table 2. XRD measurement results.
SampleAl-2.5CAl-2.5Al-25
ExtrudedAnnealedExtrudedAnnealedExtrudedAnnealed
Lattice parameter [Å]4.0504(2)4.0499(4)4.0504(2)4.0502(2)4.0510(3)4.0503(2)
Crystallite size [Å]371(36)479(118)382(28)381(51)381(61)332(21)
Lattice strain [%]−0.04(2)−0.06(4)−0.04(1)−0.06(2)−0.06(3)−0.08(1)
Table 3. The values of the positron diffusion length L+ and Sbulk parameter for the extruded aluminum samples obtained from VEPFIT (solid lines in Figure 2).
Table 3. The values of the positron diffusion length L+ and Sbulk parameter for the extruded aluminum samples obtained from VEPFIT (solid lines in Figure 2).
SampleL+ [nm]Sbulk
reference97(8)0.4964(3)
Al-2.578(10)0.5010(3)
Al-2.5C16(5)0.5124(2)
Al-2522(2)0.5092(2)
Table 4. Positron lifetimes and intensities.
Table 4. Positron lifetimes and intensities.
Sample τ 1 [ps] τ 2 [ps] I 2 [%] τ ¯ [ps]
Al-2.5125 ± 2247 ± 253 ± 1190
Al-2.5C131 ± 3251 ± 360 ± 2203
Al-25133 ± 2249 ± 258 ± 1200
Table 5. The activation energy of the grain boundary migration, Q, was obtained from the diffusion trapping model [98].
Table 5. The activation energy of the grain boundary migration, Q, was obtained from the diffusion trapping model [98].
SampleQ [eV]
Al-2.51.51 ± 0.21
Al-2.5C1.45 ± 0.36
Al-251.50 ± 0.25
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Dryzek, E.; Wróbel, M.; Sarnek, M.; Skiba, J. Positron Annihilation Studies of Hydrostatically Extruded AA1050 Aluminum. Materials 2025, 18, 4428. https://doi.org/10.3390/ma18184428

AMA Style

Dryzek E, Wróbel M, Sarnek M, Skiba J. Positron Annihilation Studies of Hydrostatically Extruded AA1050 Aluminum. Materials. 2025; 18(18):4428. https://doi.org/10.3390/ma18184428

Chicago/Turabian Style

Dryzek, Ewa, Mirosław Wróbel, Maciej Sarnek, and Jacek Skiba. 2025. "Positron Annihilation Studies of Hydrostatically Extruded AA1050 Aluminum" Materials 18, no. 18: 4428. https://doi.org/10.3390/ma18184428

APA Style

Dryzek, E., Wróbel, M., Sarnek, M., & Skiba, J. (2025). Positron Annihilation Studies of Hydrostatically Extruded AA1050 Aluminum. Materials, 18(18), 4428. https://doi.org/10.3390/ma18184428

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop