Integrating Microstructures and Dual Constitutive Models in Instrumented Indentation Technique for Mechanical Properties Evaluation of Metallic Materials
Abstract
1. Introduction
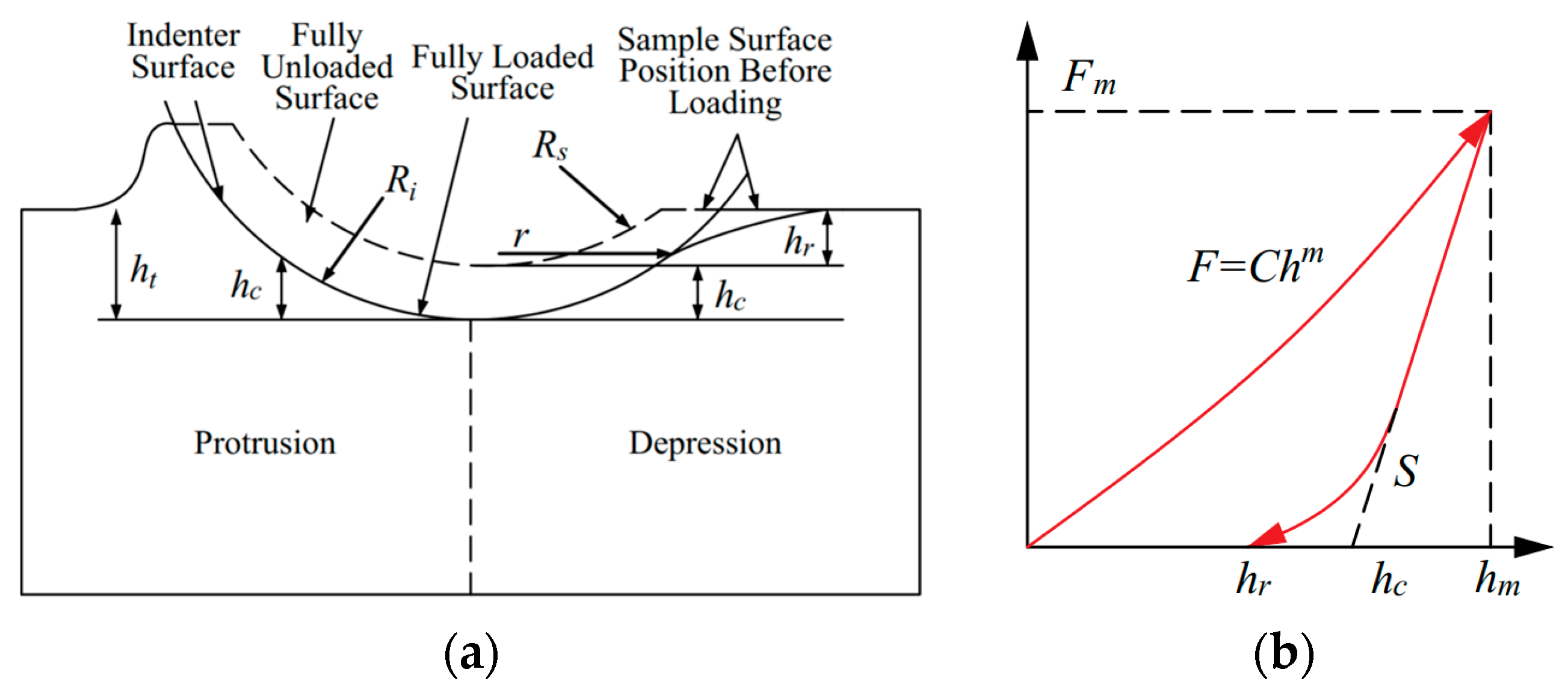
2. Methodology
3. Finite Element Model
4. Experimental Procedure
4.1. Microstructure Inspection
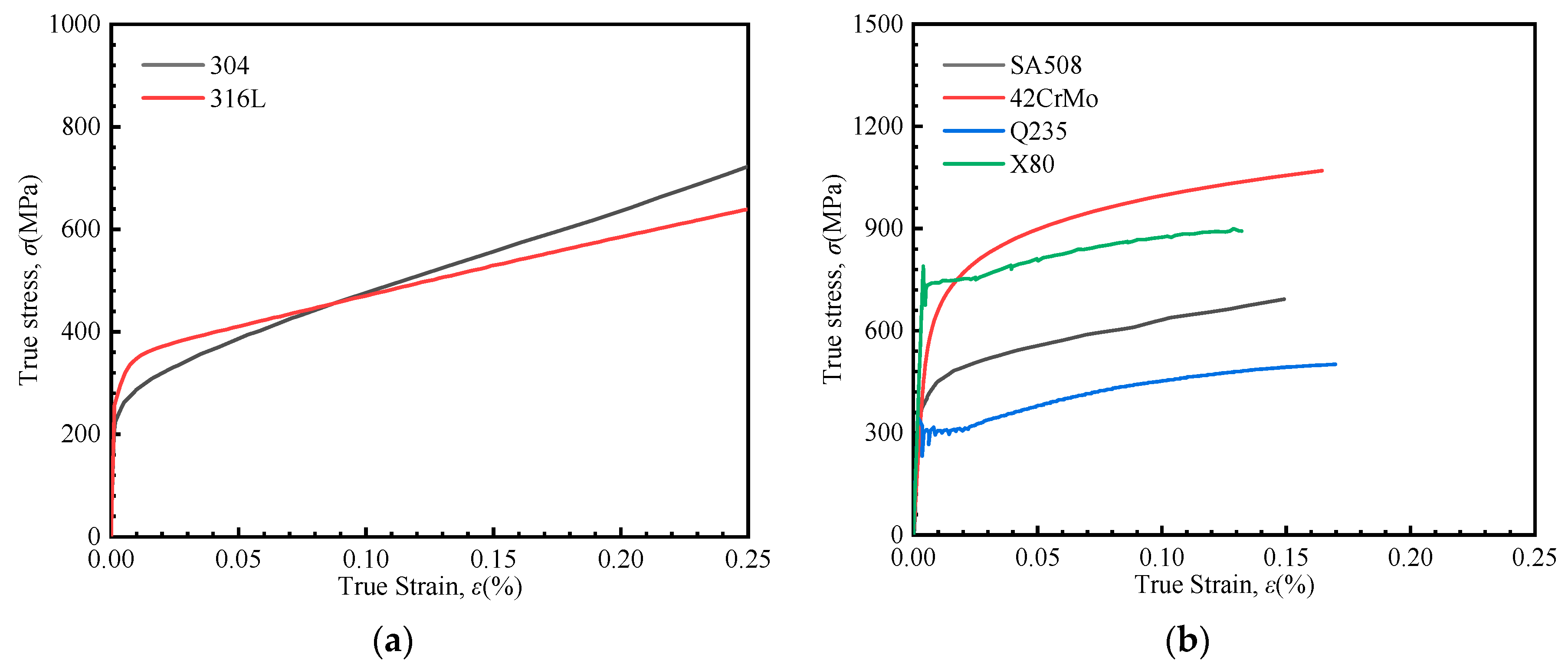
4.2. Uniaxial Tensile Test
4.3. Indentation Test
5. Results and Discussion
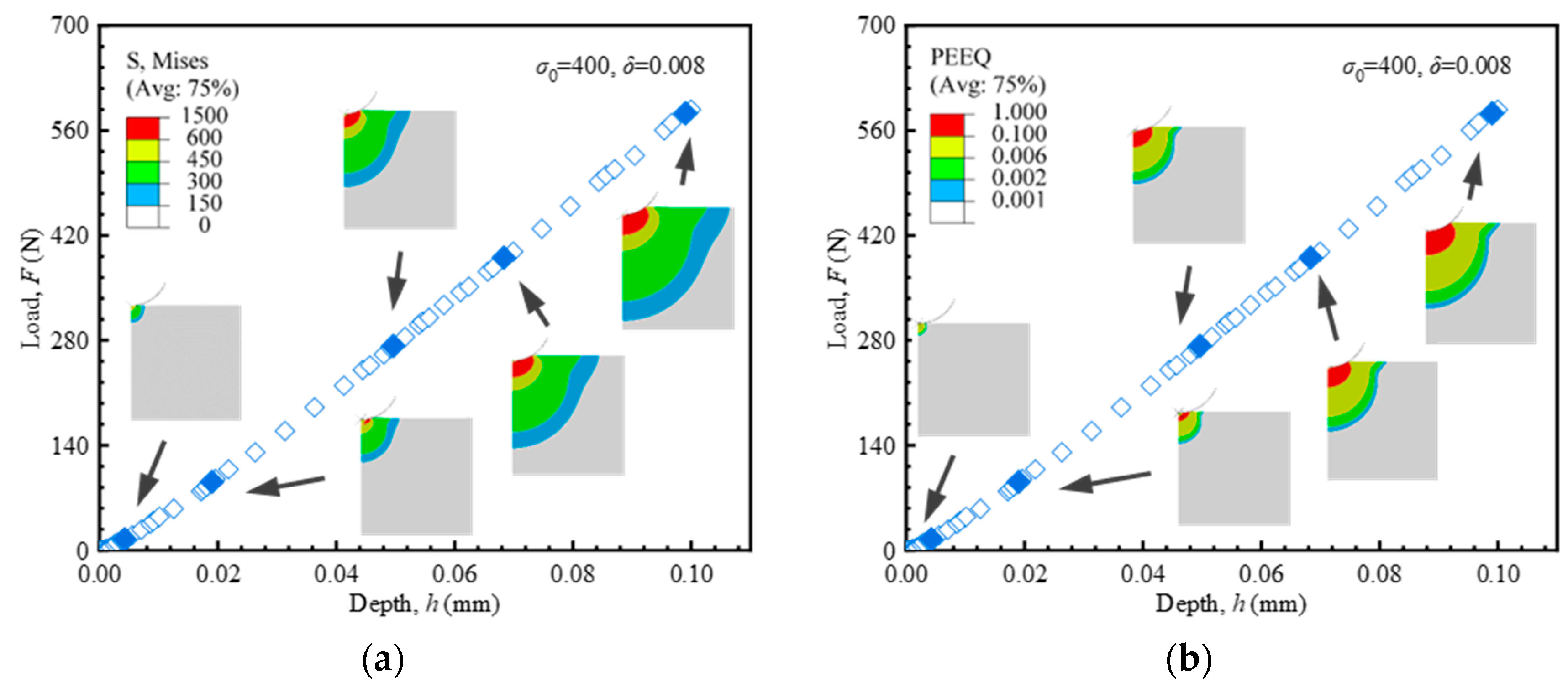
5.1. Influence of Plastic Parameters on Indentation Responses
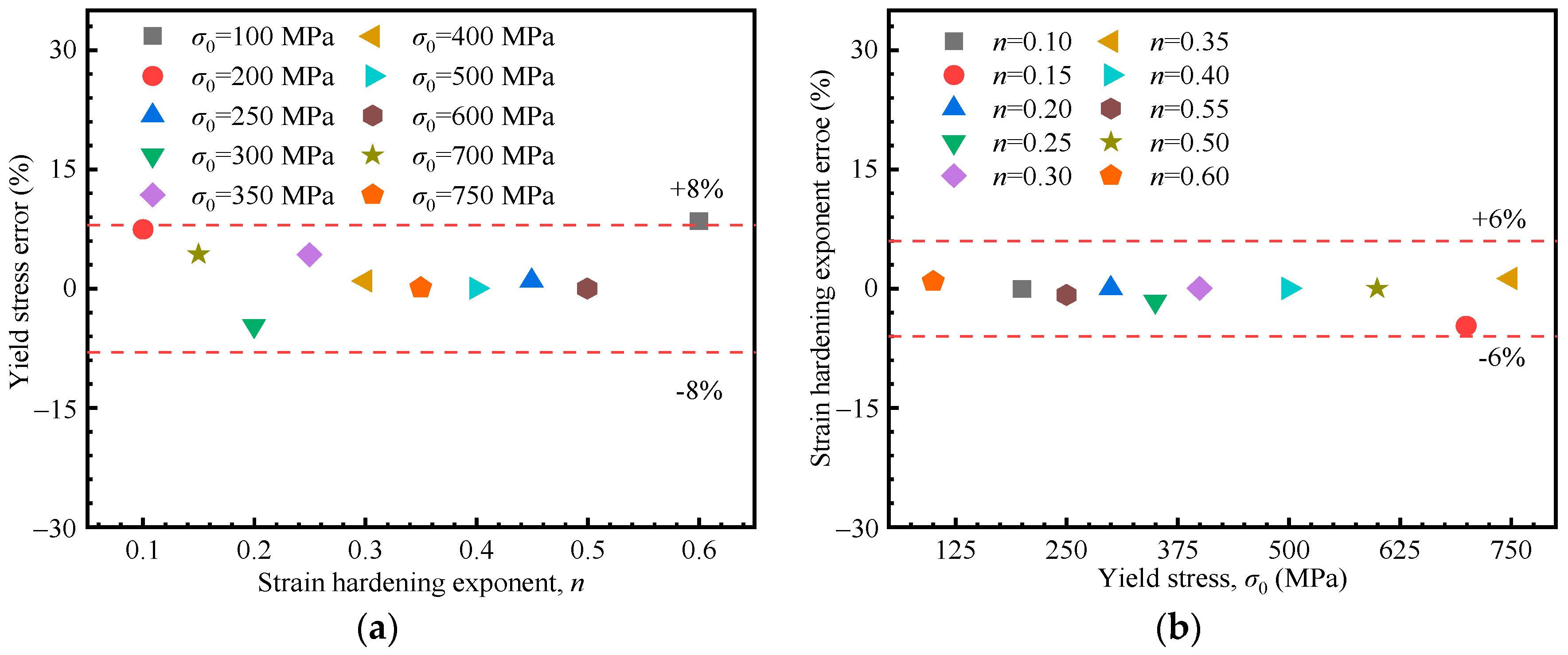
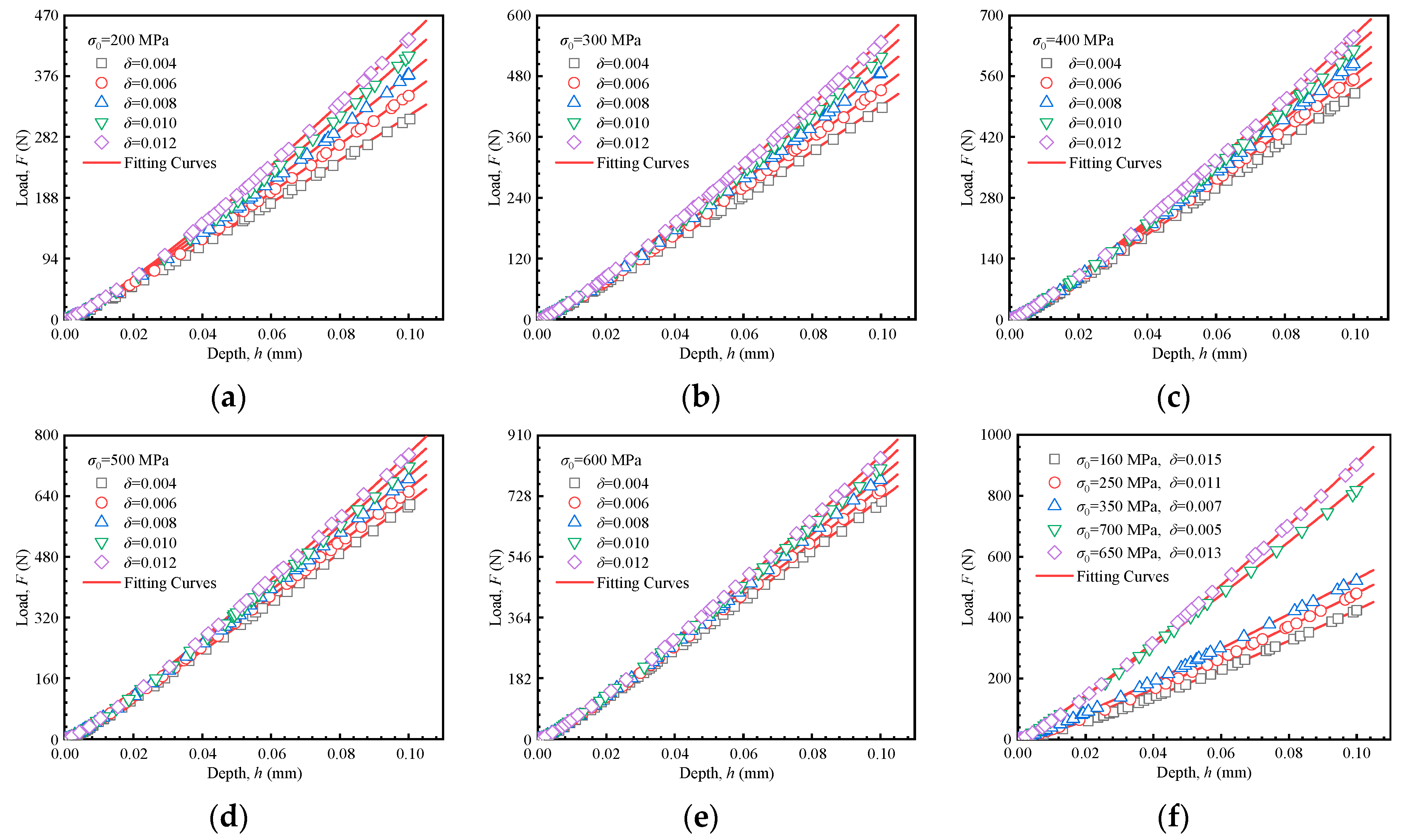
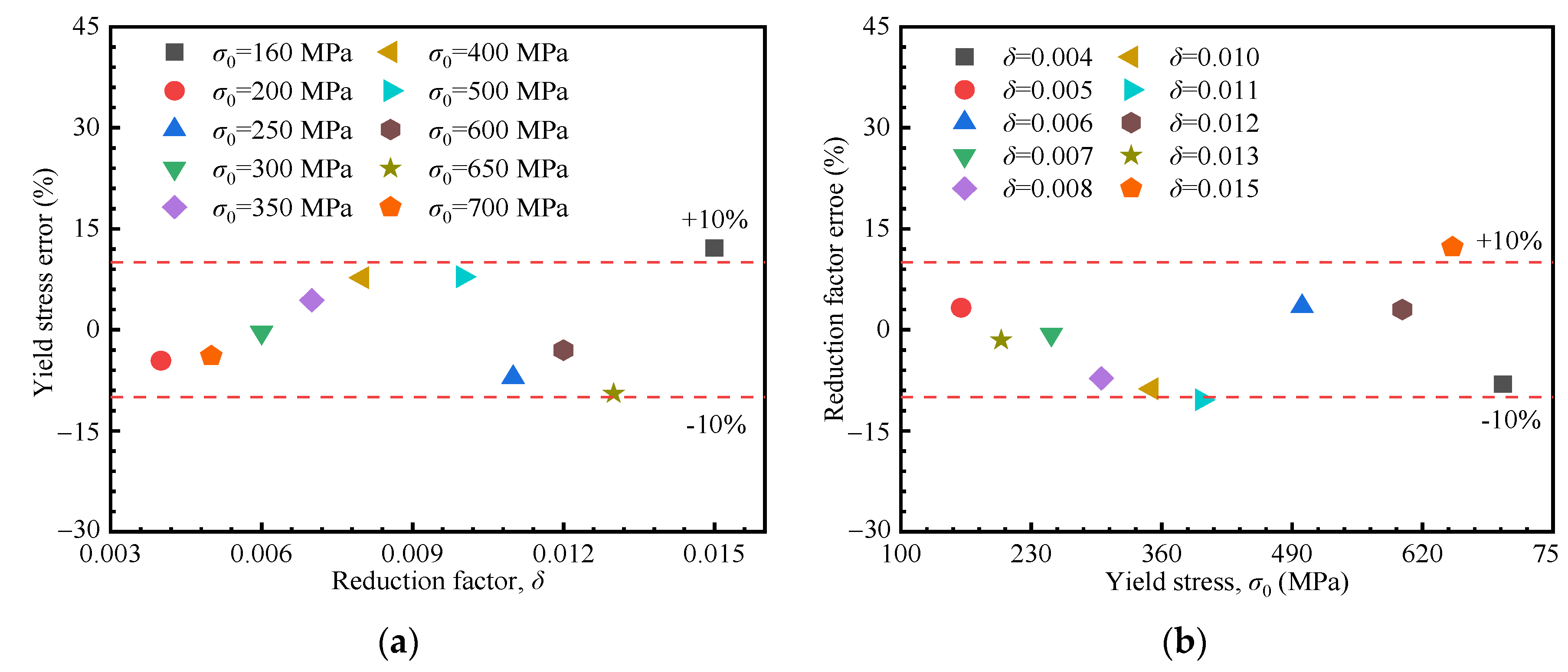
5.2. Establishment of Mechanical Properties Acquisition Method Based on the Hollomon Model
5.3. Establishment of Mechanical Properties Acquisition Method Based on Linear Hardening Model
5.4. Microstructure and Uniaxial Stress–Strain Curve
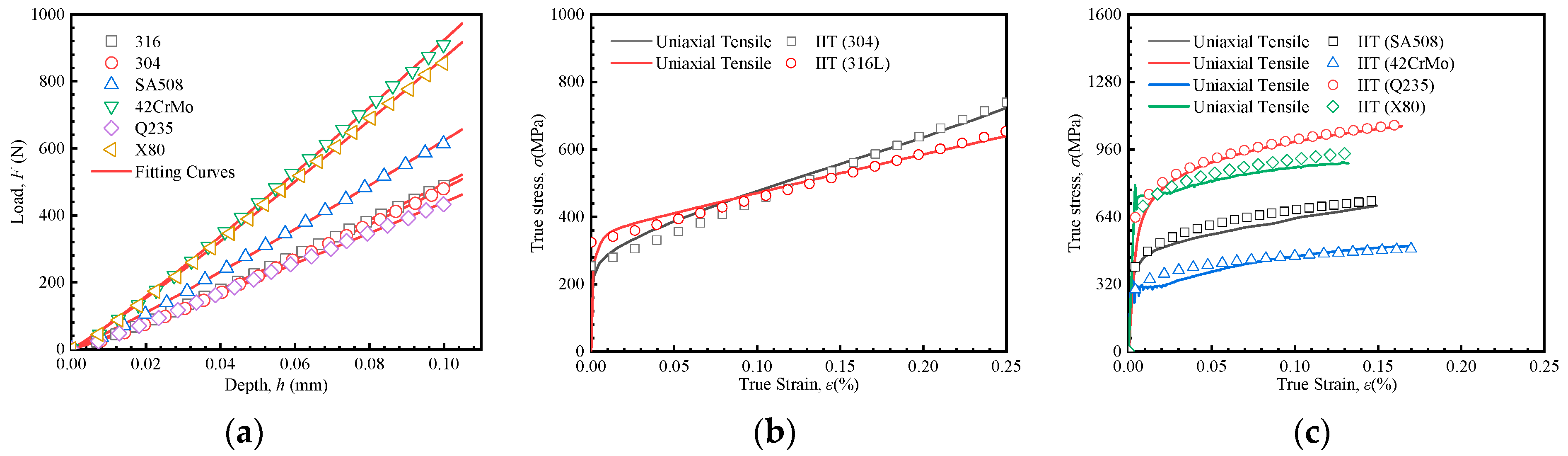
5.5. Experimental Verification
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Singh, M.P.; Shukla, D.K.; Kumar, R.; Arora, K.S. The structural integrity of high-strength welded pipeline steels: A review. Int. J. Struct. Integr. 2021, 12, 470–496. [Google Scholar] [CrossRef]
- Turcot, G.; Paquet, D.; Lévesque, M.; Turenne, S. A novel inverse methodology for the extraction of bulk elasto-plastic tensile properties of metals using spherical instrumented indentation. Int. J. Solids Struct. 2022, 236, 111317. [Google Scholar] [CrossRef]
- Kim, J.J.; Pham, T.H.; Kim, S.E. Instrumented indentation testing and FE analysis for investigation of mechanical properties in structural steel weld zone. Int. J. Mech. Sci. 2015, 103, 265–274. [Google Scholar] [CrossRef]
- Liu, H.; Song, J.; Wang, H.; Du, Y.; Yang, K.; Liu, Y.; Wang, Q.; Chen, Q. Heterogeneous microstructure and associated mechanical properties of thick electron beam welded Ti-5Al-2Sn-2Zr-4Mo-4Cr alloy joint. Mater. Sci. Eng. A 2021, 825, 141850. [Google Scholar] [CrossRef]
- Das, G.; Ghosh, S.; Ghosh, S. Structure–property correlation of EN steel and evaluation of mechanical properties through BIT. NDT E Int. 2006, 39, 155–161. [Google Scholar] [CrossRef]
- Wang, K.; Liao, T.; Xu, J.; Yang, J.; Wang, P.; Chen, R.; Qian, Y.; Kan, Q.; Li, L. Identification of elastoplastic properties of materials with gradient residual stresses using a co-simulation method and nanoindentation experiments. NDT E Int. 2023, 139, 102940. [Google Scholar] [CrossRef]
- Peng, W.; Jiang, W.; Gu, W.; Li, J.; Xu, T.; Guo, G.; Zhao, X.; Hu, X. Indentation energy method for evaluating the effect of local PWHT on pressure vessels. Int. J. Mech. Sci. 2025, 297–298, 110356. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Tabor, D. A simple theory of static and dynamic hardness. Proc. R. Soc. Lond. A 1948, 192, 247–274. [Google Scholar]
- Beghini, M.; Bertini, L.; Fontanari, V. Evaluation of the stress-strain curve of metallic materials by spherical indentation. Int. J. Solids Struct. 2006, 43, 2441–2459. [Google Scholar] [CrossRef]
- Hill, R.; Lee, E.H.; Tupper, S.J. The theory of wedge indentation of ductile materials. Proc. R. Soc. Lond. A 1947, 188, 273–289. [Google Scholar]
- Johnson, K.L. The correlation of indentation experiments. J. Mech. Phys. Solids 1970, 18, 115–126. [Google Scholar] [CrossRef]
- Park, Y.J.; Pharr, G.M. Nanoindentation with spherical indenters: Finite element studies of deformation in the elastic-plastic transition regime. Thin Solid Film. 2004, 447–448, 246–250. [Google Scholar] [CrossRef]
- Chen, H.; Cai, L.X. Theoretical model for predicting uniaxial stress-strain relation by dual conical indentation based on equivalent energy principle. Acta Mater. 2016, 121, 181–189. [Google Scholar] [CrossRef]
- Xue, H.; He, J.; Zhang, J.; Xue, Y. Approach for obtaining material mechanical properties in local region of structure based on accurate analysis of micro-indentation test. China Mech. Eng. 2021, 34, 130. [Google Scholar] [CrossRef]
- Peng, J. Experimental verification of five spherical indentation-based methods in determining plastic properties of metals. Rare Metal. Mat. Eng. 2012, 41, 2. [Google Scholar]
- Haggag, F.M.; Byun, T.S.; Hong, J.H.; Miraglia, P.Q.; Murty, K.L. Indentation-energy-to-fracture (IEF) parameter for characterization of DBTT in carbon steels using nondestructive automated ball indentation (ABI) technique. Scr. Mater. 1998, 38, 645–651. [Google Scholar] [CrossRef]
- Hu, Z.; Lynne, K.; Delfanian, F. Characterization of materials’ elasticity and yield strength through micro-/nano-indentation testing with a cylindrical flat-tip indenter. J. Mater. Res. 2015, 30, 578–591. [Google Scholar] [CrossRef]
- Hu, Z.; Lynne, K.J.; Markondapatnaikuni, S.P.; Delfanian, F. Material elastic-plastic property characterization by nanoindentation testing coupled with computer modeling. Mater. Sci. Eng. A 2013, 587, 268–282. [Google Scholar] [CrossRef]
- Zhang, Y.; Xue, H.; Wang, S.; Yang, C.; Wang, Z. Study on correlation and scaling protocol between indentation stress-strain and uniaxial stress-strain. Structures 2024, 59, 105684. [Google Scholar] [CrossRef]
- Subroto, T.; Miroux, A.; Eskin, D.G.; Katgerman, L. Tensile mechanical properties, constitutive parameters and fracture characteristics of an as-cast AA7050 alloy in the near-solidus temperature regime. Mater. Sci. Eng. A 2017, 679, 28–35. [Google Scholar] [CrossRef]
- Samuel, K.G. Limitations of Hollomon and Ludwigson stress–strain relations in assessing the strain hardening parameters. J. Phys. D Appl. Phys. 2005, 39, 203. [Google Scholar] [CrossRef]
- Zhang, Y.; Xue, H.; Zhang, S.; Wang, S.; Sun, Y.; Zhang, Y.; Yang, Y. Interaction of mechanical heterogeneity and residual stress on mechanical field at crack tips in DMWJs. Sci. Technol. Nucl. Ins. 2022, 2022, 7462200. [Google Scholar] [CrossRef]
- Pharr, G.M.; Oliver, W.C.; Brotzen, F.R. On the generality of the relationship among contact stiffness, contact area, and elastic modulus during indentation. J. Mater. Res. 1992, 7, 613–617. [Google Scholar] [CrossRef]
- Sneddon, I.N. The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 1965, 3, 47–57. [Google Scholar] [CrossRef]
- Chen, G.Y.; Zhang, X.C.; Zhong, J.R.; Shi, J.; Wang, Q.Q.; Guan, K.S. New inverse method for determining uniaxial flow properties by spherical indentation test. China Mech. Eng. 2021, 34, 156–164. [Google Scholar] [CrossRef]
- Huang, L.Y.; Guan, K.S.; Xu, T.; Zhang, J.M.; Wang, Q.Q. Investigation of the mechanical properties of steel using instrumented indentation test with simulated annealing particle swarm optimization. Theor. Appl. Fract. Mech. 2019, 102, 116–121. [Google Scholar] [CrossRef]
- Peng, W.; Jiang, W.; Sun, G.; Yang, B.X.; Shao, S.; Tu, T. Biaxial residual stress measurement by indentation energy difference method: Theoretical and experimental study. Int. J. Press. Vessels Pip. 2022, 195, 104573. [Google Scholar] [CrossRef]
- Hertelé, S.; Waele, W.D.; Denys, R. A generic stress–strain model for metallic materials with two-stage strain hardening behaviour. Int. J. Non Linear Mech. 2011, 46, 519–531. [Google Scholar] [CrossRef]
- Hradil, P.; Talja, A.; Real, E.; Mirambell, E.; Rossi, B. Generalized multi-stage mechanical model for non-linear metallic materials. Thin-Walled Struct. 2013, 63, 63–69. [Google Scholar] [CrossRef]
- Rasmussen, K.J.R. Full-range stress–strain curves for stainless steel alloys. J. Constr. Steel Res. 2003, 59, 47–61. [Google Scholar] [CrossRef]
- Chen, J.; Young, B. Stress-strain curves for stainless steel at elevated temperatures. Eng. Struct. 2006, 28, 229–239. [Google Scholar] [CrossRef]
- Chen, G.Y.; Zhong, J.R.; Zhang, X.C.; Guan, K.S.; Wang, Q.Q.; Shi, J. Estimation of tensile strengths of metals using spherical indentation test and database. Int. J. Press. Vessels Pip. 2021, 189, 104284. [Google Scholar] [CrossRef]
- GB/T 37782-2019; Metallic Materials—Indentation Test—Determination of Strength, Hardness and Stress-Strain Curve. Standardization Administration of China: Beijing, China, 2019.
- Mohan, S.; Millan-Espitia, N.; Yao, M.; Steenberge, N.V.; Kalidindi, S.R. Critical evaluation of spherical indentation stress-strain protocols for the estimation of the yield strengths of steels. Exp. Mech. 2021, 61, 641–652. [Google Scholar] [CrossRef]
- Zhao, M.; Ogasawara, N.; Chiba, N.; Chen, X. A new approach to measure the elastic–plastic properties of bulk materials using spherical indentation. Acta Mater. 2006, 54, 23–32. [Google Scholar] [CrossRef]
- EN 10088-2:2014; Stainless Steels—Part 2: Technical Delivery Conditions for Sheet/Plate and Strip of Corrosion Resisting Steels for General Purposes. European Committee for Standardization: Brussels, Belgium, 2014.
- GB/T 24511-2009; Stainless Steel Plate, Sheet and Strip for Pressure Equipments. Standardization Administration of China: Beijing, China, 2009.
- ISO 6892-1:2019; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. International Organization for Standardization: Geneva, Switzerland, 2019.
- Sreepriya, T.; Mythili, R.; Reddy, G.V.P. Correlation between microstructure and nanomechanical properties of 9Cr–1Mo ferritic martensitic steel through instrumented indentation technique. Mater. Sci. Eng. A 2022, 840, 142985. [Google Scholar] [CrossRef]
- Kim, J.; Choi, S.; Lee, J.; Ahn, H.; Kim, Y.; Choi, M.; Kwon, D. An indentation method for evaluation of residual stress: Estimation of stress-free indentation curve using stress-independent indentation parameter. J. Mater. Res. 2019, 34, 1103–1111. [Google Scholar] [CrossRef]
- Peng, W.; Jiang, W.; Yang, B.; Sun, G.; Shao, X. An indentation method for measuring welding residual stress: Estimation of stress-free indentation curve using BP neural network prediction model. Int. J. Press. Vessels Pip. 2023, 206, 105070. [Google Scholar] [CrossRef]
- Wu, S.; Xu, T.; Song, M.; Guan, K. Mechanical properties characterisation of welded joint of austenitic stainless steel using instrumented indentation technique. Mater. High. Temp. 2016, 33, 270–275. [Google Scholar] [CrossRef]
- Sun, G.; Xu, F.; Li, G.; Huang, X.; Li, Q. Determination of mechanical properties of the weld line by combining micro-indentation with inverse modeling. Comput. Mater. Sci. 2014, 85, 347–362. [Google Scholar] [CrossRef]
- Pamnani, R.; Karthik, V.; Jayakumar, T.; Vasudevan, M.; Sakthivel, T. Evaluation of mechanical properties across micro alloyed HSLA steel weld joints using Automated Ball Indentation. Mater. Sci. Eng. A 2016, 651, 214–223. [Google Scholar] [CrossRef]










| Yield Stress σ0 (MPa) | Strain Hardening Exponent n or Reduction Coefficient δ | |||||
|---|---|---|---|---|---|---|
| Hollomon | 200 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
| 300 | ||||||
| 400 | ||||||
| 500 | ||||||
| 600 | ||||||
| Linear hardening | 200 | 0.004 | 0.006 | 0.008 | 0.010 | 0.012 |
| 300 | ||||||
| 400 | ||||||
| 500 | ||||||
| 600 | ||||||
| C | Si | Mn | P | S | Cr | Ni | Mo | Cu | Al | Nb + V + Ti | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 304 | 0.03 | 0.75 | 2.00 | 0.03 | 0.02 | 16.7 | 12.01 | 2.12 | — | — | — |
| 316L | 0.08 | 0.75 | 2.00 | 0.045 | 0.02 | ≈19 | ≈10 | — | — | — | — |
| SA508 | 0.226 | 0.194 | 1.375 | 0.007 | 0.001 | — | — | — | 0.02 | 0.008 | — |
| 42CrMo | 0.41 | 0.24 | 0.66 | 0.09 | 0.05 | 1.01 | 0.01 | 0.18 | — | — | — |
| Q235 | 0.14 | 0.19 | 0.34 | 0.03 | 0.034 | — | — | — | — | — | — |
| X80 | 0.047 | 0.26 | 1.70 | 0.01 | 0.001 | 0.24 | 0.12 | 0.10 | 0.03 | 0.03 | 0.062 |
| Yield Stress σ0 (MPa) | aH | bH | dH | eH | fH |
|---|---|---|---|---|---|
| 200 | 112,878.245 | −16,291.832 | 4258.866 | 0.585 | 0.976 |
| 300 | 117,946.322 | −10,037.172 | 5162.260 | 0.579 | 0.988 |
| 400 | 117,779.420 | −2563.466 | 5871.541 | 0.578 | 0.997 |
| 500 | 123,780.779 | −119.329 | 7162.056 | 0.563 | 1.009 |
| 600 | 122,757.020 | 5428.674 | 8150.501 | 0.552 | 1.021 |
| Yield Stress σ0 (MPa) | aL | bL | dL | eL | fL |
|---|---|---|---|---|---|
| 200 | 346,679.047 | 2554.473 | −653.571 | 21.817 | 1.018 |
| 300 | 366,803.929 | 3680.230 | −751.964 | 22.365 | 1.003 |
| 400 | 363,242.973 | 4905.715 | −476.250 | 16.234 | 1.022 |
| 500 | 367,683.995 | 6057.947 | −305.179 | 12.586 | 1.034 |
| 600 | 402,339.115 | 6943.546 | −323.036 | 13.457 | 1.026 |
| Response Parameters | C | m |
|---|---|---|
| SS316L | 6417.500 | 1.114 |
| SS304 | 6742.122 | 1.148 |
| SA508 | 7574.917 | 1.085 |
| 42CrMo | 11,609.890 | 1.100 |
| Q235 | 5040.309 | 1.061 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, B.; Zhang, Y.; Wang, S.; Zhang, S.; Xue, H. Integrating Microstructures and Dual Constitutive Models in Instrumented Indentation Technique for Mechanical Properties Evaluation of Metallic Materials. Materials 2025, 18, 4159. https://doi.org/10.3390/ma18174159
Zhang Y, Wang B, Zhang Y, Wang S, Zhang S, Xue H. Integrating Microstructures and Dual Constitutive Models in Instrumented Indentation Technique for Mechanical Properties Evaluation of Metallic Materials. Materials. 2025; 18(17):4159. https://doi.org/10.3390/ma18174159
Chicago/Turabian StyleZhang, Yubiao, Bin Wang, Yonggang Zhang, Shuai Wang, Shun Zhang, and He Xue. 2025. "Integrating Microstructures and Dual Constitutive Models in Instrumented Indentation Technique for Mechanical Properties Evaluation of Metallic Materials" Materials 18, no. 17: 4159. https://doi.org/10.3390/ma18174159
APA StyleZhang, Y., Wang, B., Zhang, Y., Wang, S., Zhang, S., & Xue, H. (2025). Integrating Microstructures and Dual Constitutive Models in Instrumented Indentation Technique for Mechanical Properties Evaluation of Metallic Materials. Materials, 18(17), 4159. https://doi.org/10.3390/ma18174159







