Multi-Algorithm Ensemble Learning Framework for Predicting the Solder Joint Reliability of Wafer-Level Packaging
Abstract
1. Introduction
2. Fundamental Theory
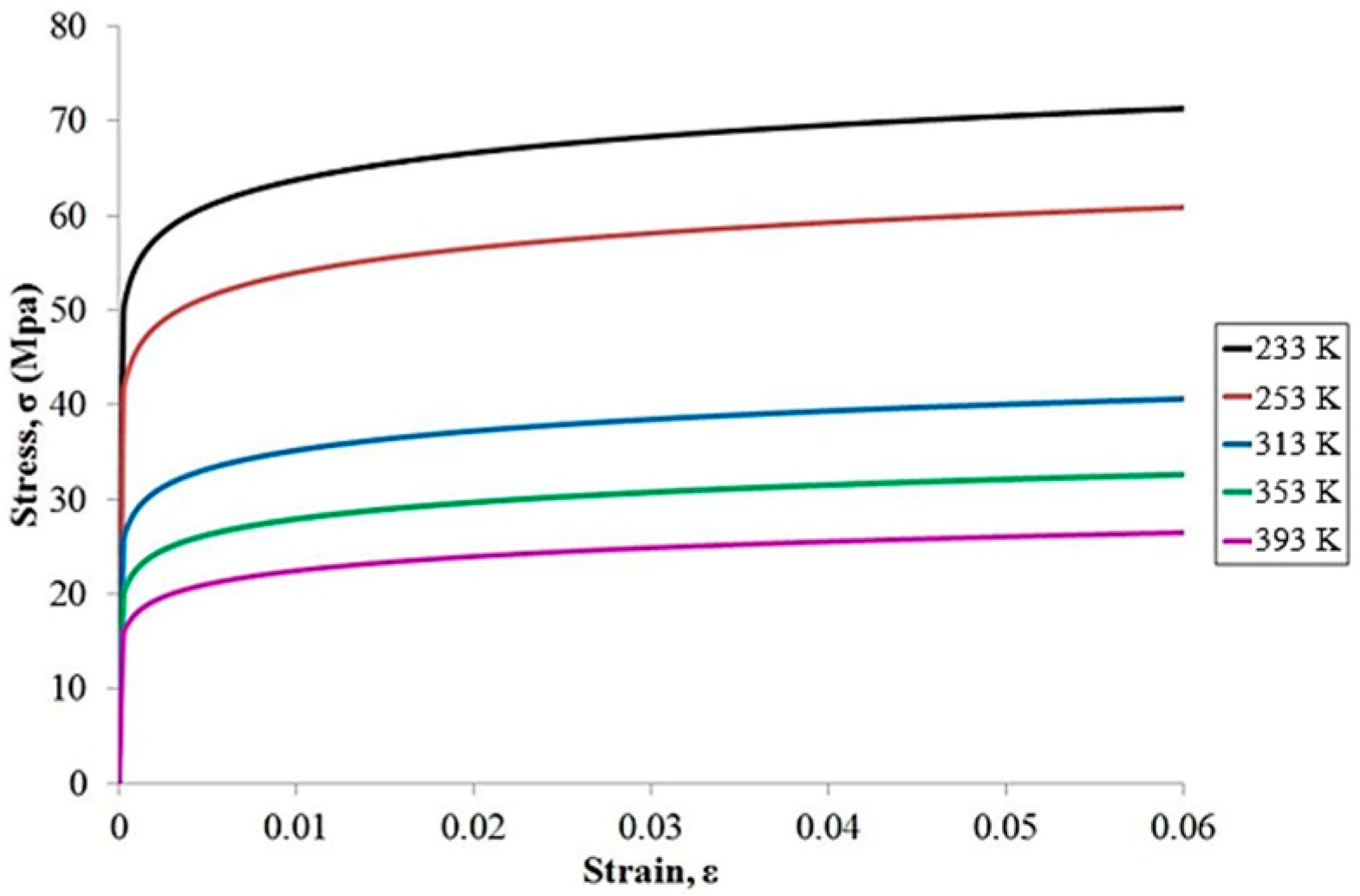
2.1. Coffin–Manson Model
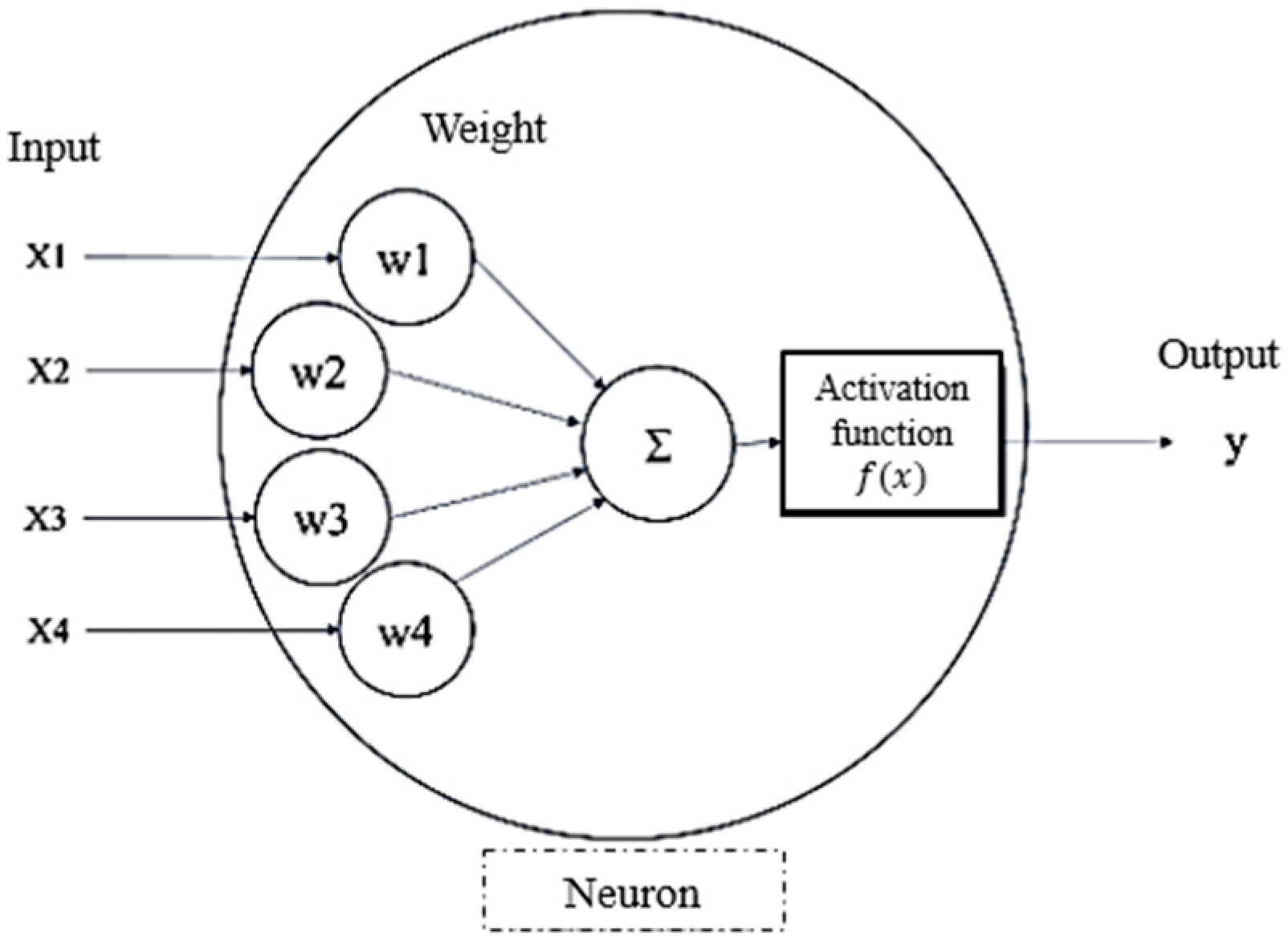
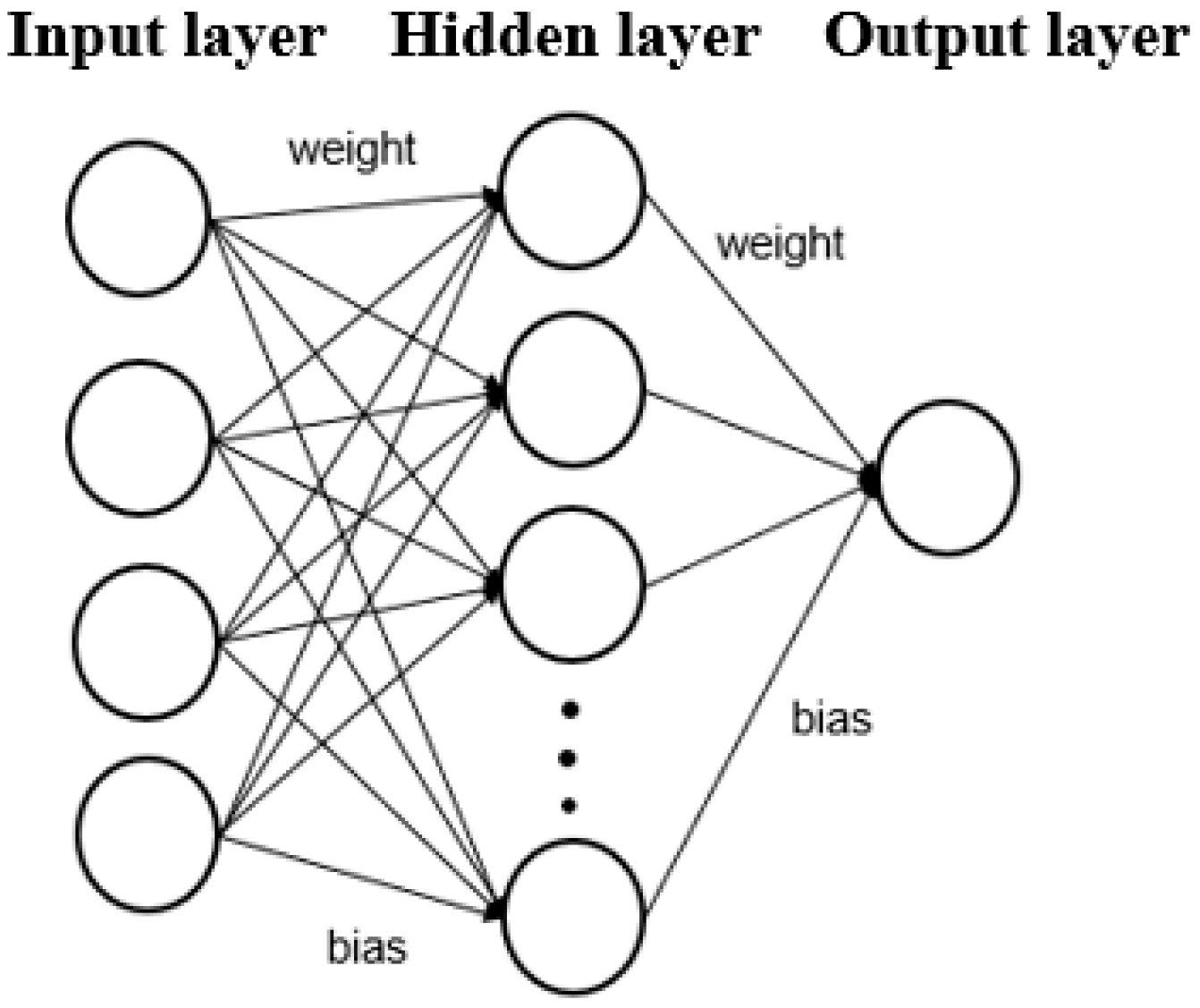
2.2. Artificial Neural Network (ANN)
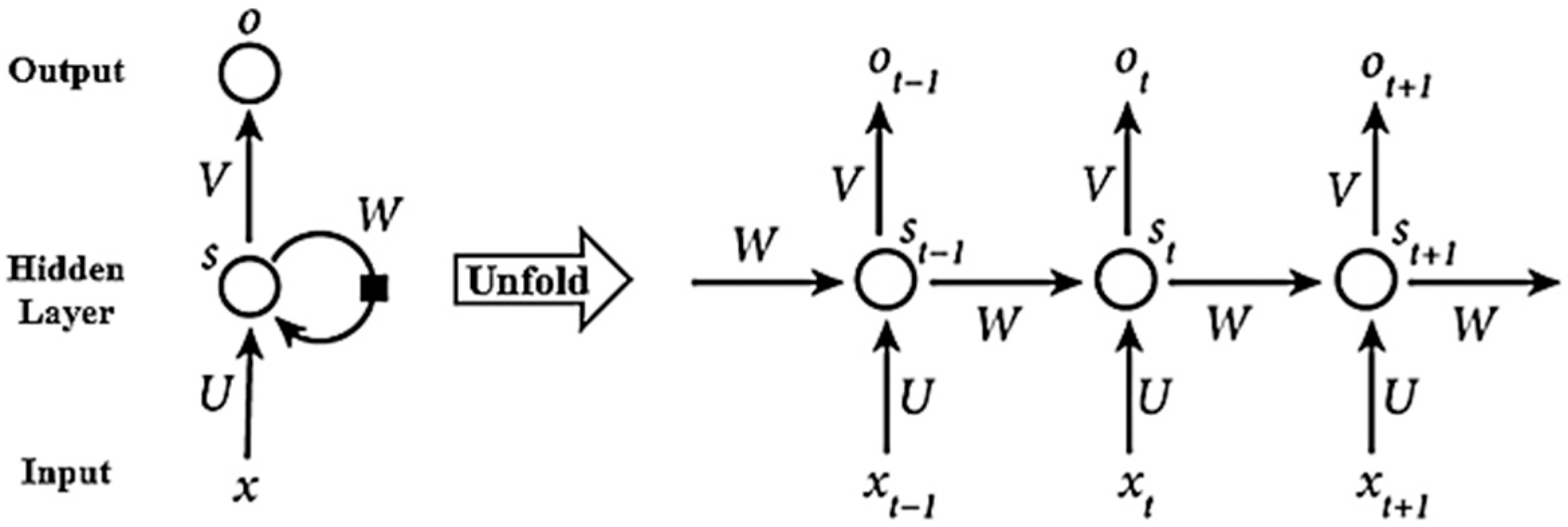
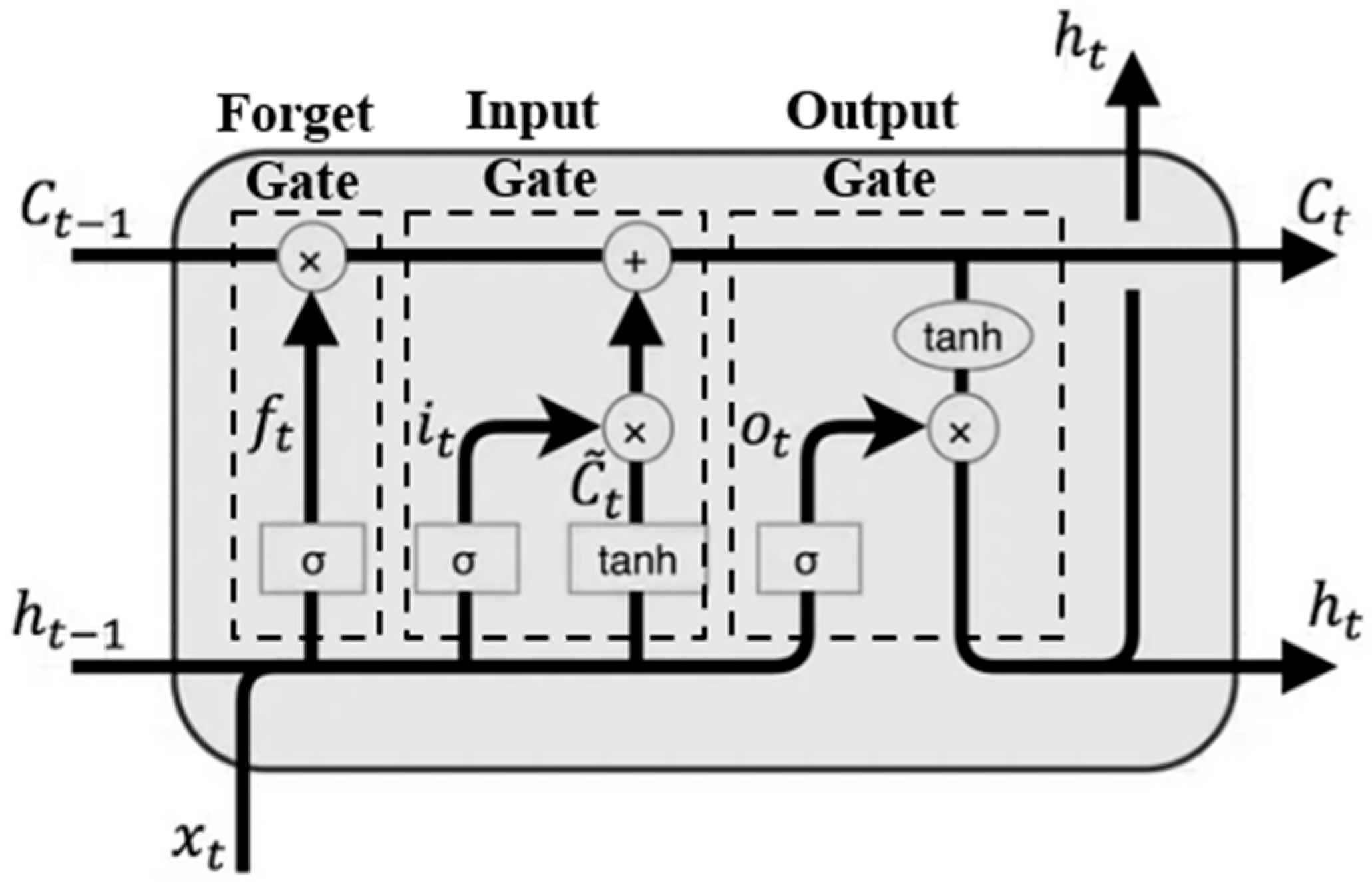
2.3. Recurrent Neural Network (RNN)
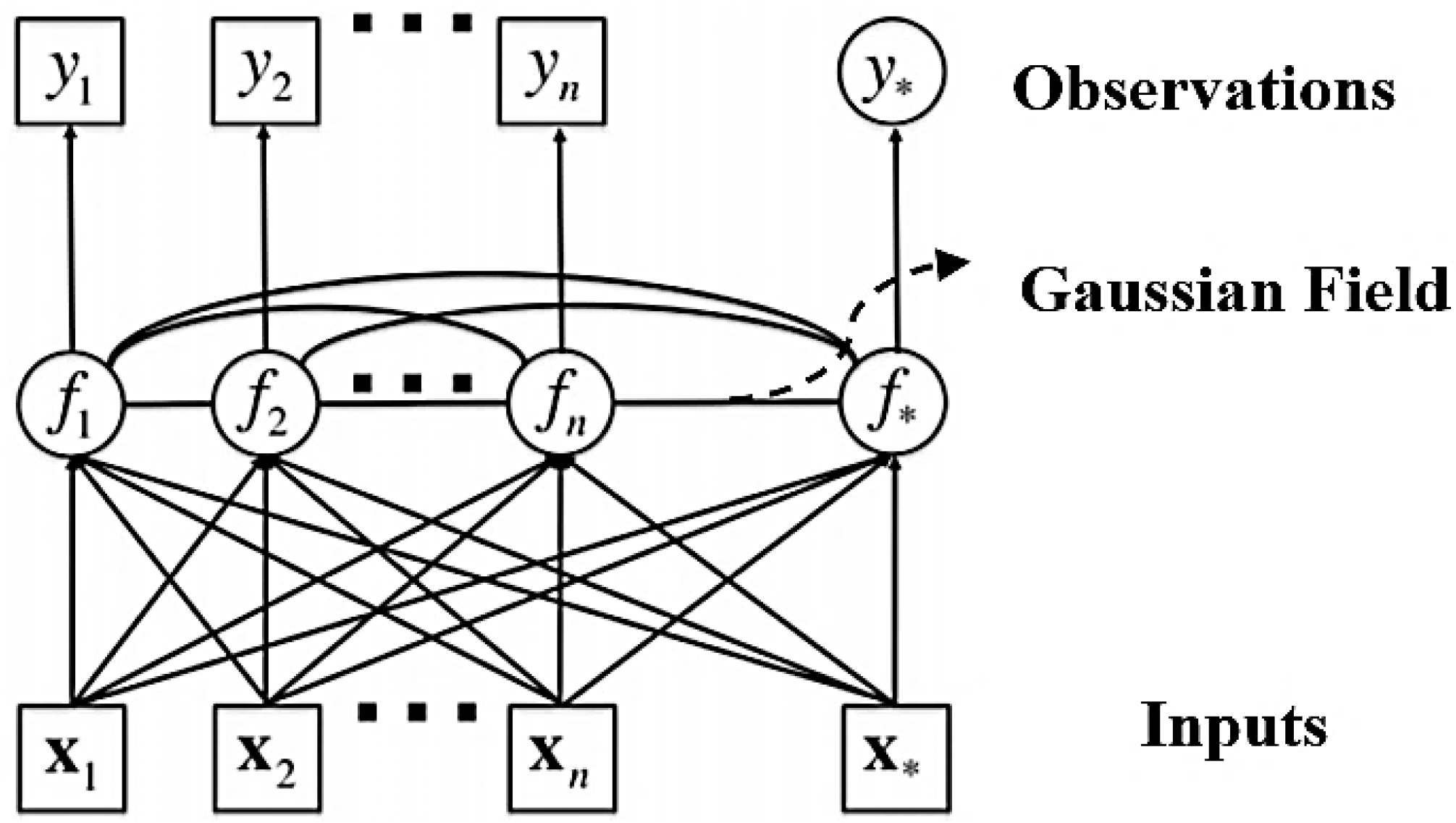
2.4. Gaussian Process Regression (GPR)
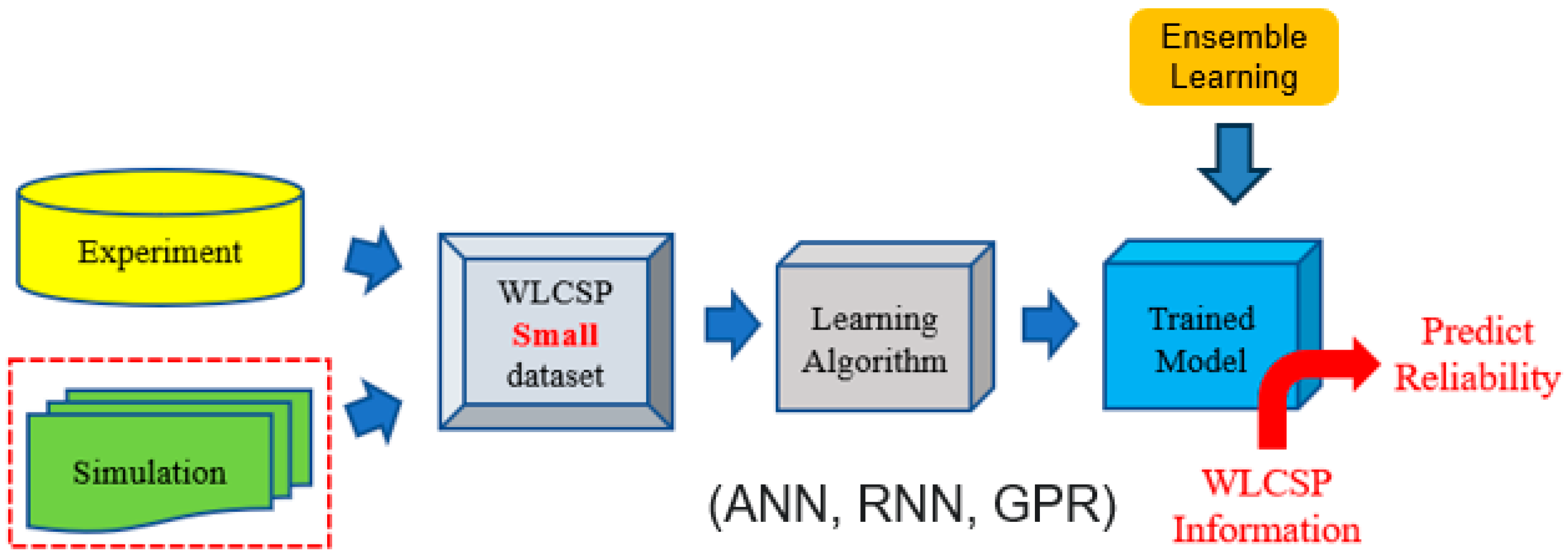
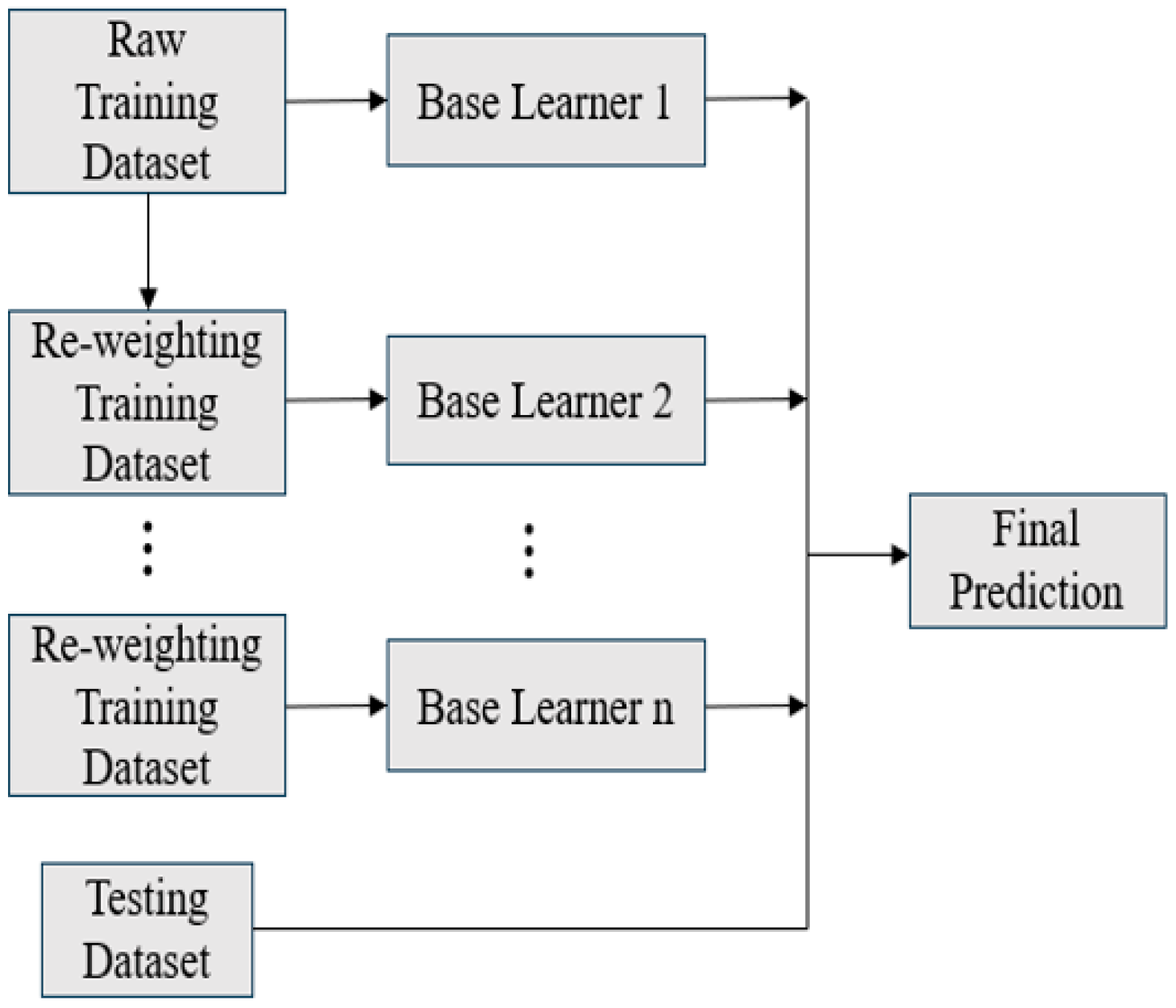
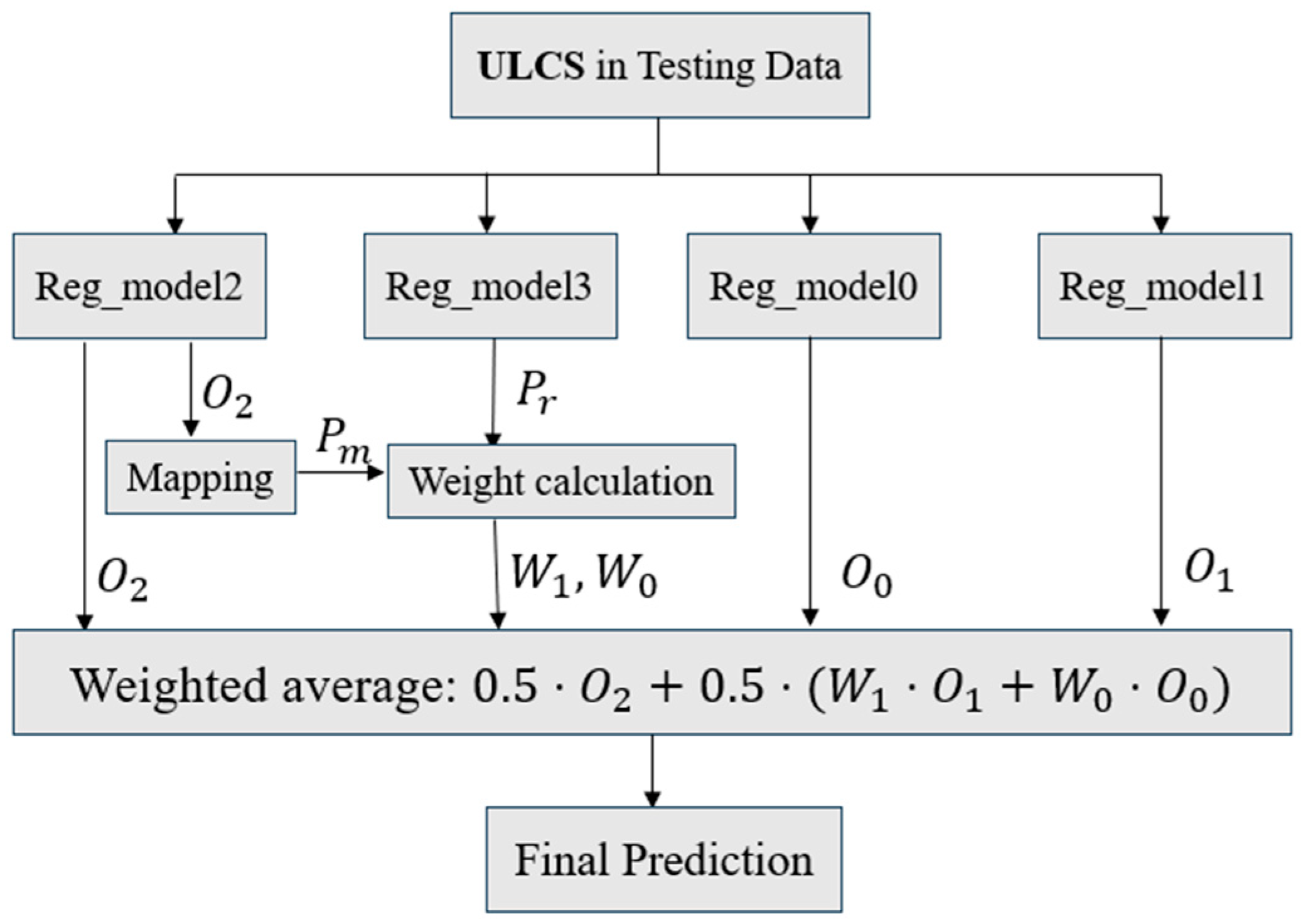
2.5. Ensemble Learning
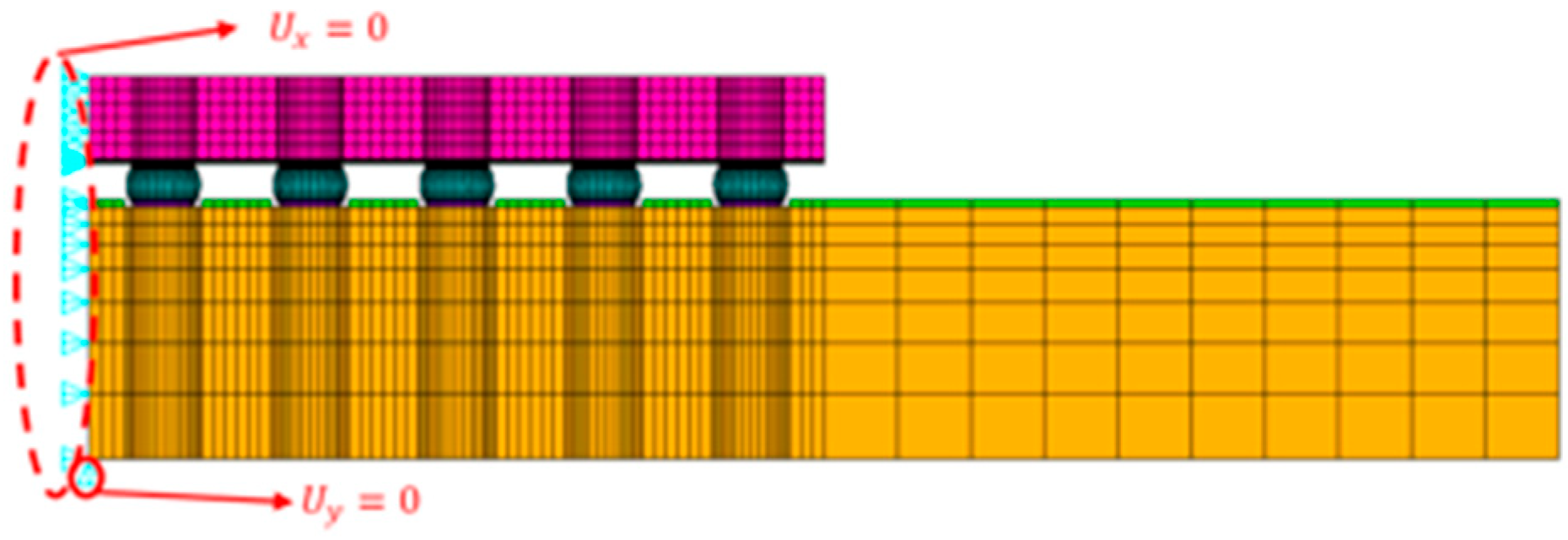
3. FEA Validation of WLCSP
4. Data Sampling and Model Training
4.1. Data Sampling
4.2. Prediction Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Z.; Zhang, J.; Wang, S.; Wong, C.-P. Challenges and prospects for advanced packaging. Fundam. Res. 2024, 4, 1455–1458. [Google Scholar] [CrossRef]
- Ismail, N.; Yusoff, W.Y.W.; Amat, A.; Manaf, N.A.A.; Ahmad, N. A review of extreme condition effects on solder joint reliability: Understanding failure mechanisms. Def. Technol. 2024, 41, 134–158. [Google Scholar] [CrossRef]
- Bender, E.; Bernstein, J.B.; Boning, D.S. Modern trends in microelectronics packaging reliability testing. Micromachines 2024, 15, 398. [Google Scholar] [CrossRef]
- Liu, C.-M.; Lee, C.-C.; Chiang, K.-N. Enhancing the reliability of wafer level packaging by using solder joints layout design. IEEE Trans. Compon. Packag. Technol. 2006, 29, 877–885. [Google Scholar] [CrossRef]
- Wu, P.L.; Wang, P.H.; Chiang, K.N. Empirical Solutions and Reliability Assessment of Thermal Induced Creep Failure for Wafer Level Packaging. IEEE Trans. Device Mater. Reliab. 2019, 19, 126–132. [Google Scholar] [CrossRef]
- Su, Q.; Yuan, C.; Chiang, K.-N. A small database with an adaptive data selection method for solder joint fatigue life prediction in advanced packaging. Materials 2024, 17, 4091. [Google Scholar] [CrossRef]
- Panigrahy, S.K.; Tseng, Y.-C.; Lai, B.-R.; Chiang, K.-N. An overview of AI-Assisted design-on-Simulation technology for reliability life prediction of advanced packaging. Materials 2021, 14, 5342. [Google Scholar] [CrossRef] [PubMed]
- Wei, X.; Hamasha, S.D.; Alahmer, A.; Belhadi, M.E.A. Assessing the SAC305 solder joint fatigue in ball grid array assembly using strain-controlled and stress-controlled approaches. J. Electron. Packag. 2023, 145, 031005. [Google Scholar] [CrossRef]
- Dubey, S.R.; Singh, S.K.; Chaudhuri, B.B. Activation functions in deep learning: A comprehensive survey and benchmark. Neurocomputing 2022, 503, 92–108. [Google Scholar] [CrossRef]
- Ye, J.C. Artificial Neural Networks and Backpropagation. In Geometry of Deep Learning; Springer: Singapore, 2021; Volume 37, pp. 91–112. [Google Scholar]
- Mannel, F.; Aggrawal, H.O.; Modersitzki, J. A structured L-BFGS method and its application to inverse problems. Inverse Probl. 2024, 40, 045022. [Google Scholar] [CrossRef]
- Zargar, S. Introduction to Sequence Learning Models: RNN, LSTM, GRU; Department of Mechanical and Aerospace Engineering, North Carolina State University: Raleigh, NC, USA, 2021. [Google Scholar]
- Meng, Q.; Xiao, M.; Yan, S.; Wang, Y.; Lin, Z.; Luo, Z.-Q. Towards memory-and time-efficient backpropagation for training spiking neural networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 6166–6176. [Google Scholar]
- Wang, J. An intuitive tutorial to Gaussian process regression. Comput. Sci. Eng. 2023, 25, 4–11. [Google Scholar] [CrossRef]
- Lotfi, S.; Izmailov, P.; Benton, G.; Goldblum, M.; Wilson, A.G. Bayesian model selection, the marginal likelihood, and generalization. In Proceedings of the 39th International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; pp. 14223–14247, PMLR: 162:14223-14247. [Google Scholar]
- Dong, X.; Yu, Z.; Cao, W.; Shi, Y.; Ma, Q. A survey on ensemble learning. Front. Comput. Sci. 2020, 14, 241–258. [Google Scholar] [CrossRef]
- Hsieh, M.-C.; Tzeng, S.-L. Solder joint fatigue life prediction in large size and low cost wafer-level chip scale packages. In Proceedings of the 2014 15th International Conference on Electronic Packaging Technology, Chengdu, China, 12–15 August 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 496–501. [Google Scholar]
- Hsieh, M.-C. Modeling correlation for solder joint fatigue life estimation in wafer-level chip scale packages. In Proceedings of the 2015 10th International Microsystems, Packaging, Assembly and Circuits Technology Conference (IMPACT), Taipei, Taiwan, 21–23 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 65–68. [Google Scholar]
- Januddi, M.A.F.M.S.; Harun, M.N. A study of micro-scale solder bump geometric shapes using minimizing energy approach for different solder materials. Ain Shams Eng. J. 2022, 13, 101769. [Google Scholar] [CrossRef]
- Motalab, M.; Cai, Z.; Suhling, J.C.; Lall, P. Determination of Anand constants for SAC solders using stress-strain or creep data. In Proceedings of the 13th InterSociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, San Diego, CA, USA, 30 May–1 June 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 910–922. [Google Scholar]
- Hai, L.; Wang, Y.; Ban, H.; Li, G.; Du, X. A simplified prediction method on Chaboche isotropic/kinematic hardening model parameters of structural steels. J. Build. Eng. 2023, 68, 106151. [Google Scholar] [CrossRef]
- Dhal, P.; Azad, C. A comprehensive survey on feature selection in the various fields of machine learning. Appl. Intell. 2022, 52, 4543–4581. [Google Scholar] [CrossRef]
- Fan, X.; Varia, B.; Han, Q. Design and optimization of thermo-mechanical reliability in wafer level packaging. Microelectron. Reliab. 2010, 50, 536–546. [Google Scholar] [CrossRef]
- Ladani, L.J. Numerical analysis of thermo-mechanical reliability of through silicon vias (TSVs) and solder interconnects in 3-dimensional integrated circuits. Microelectron. Eng. 2010, 87, 208–215. [Google Scholar] [CrossRef]
- Praful, P.; Bailey, C. Warpage in wafer-level packaging: A review of causes, modelling, and mitigation strategies. Front. Electron. 2025, 5, 1515860. [Google Scholar] [CrossRef]
- Fuhg, J.N.; Fau, A.; Nackenhorst, U. State-of-the-art and comparative review of adaptive sampling methods for kriging. Arch. Comput. Methods Eng. 2021, 28, 2689–2747. [Google Scholar] [CrossRef]
- Su, Q.; Yuan, C.; Chiang, K. Utilizing Ensemble Learning on Small Database for Predicting the Reliability Life of Wafer-Level Packaging. In Proceedings of the 2024 IEEE 26th Electronics Packaging Technology Conference (EPTC), Singapore, 3–6 December 2024; IEEE: Piscataway, NJ, USA, 2025; pp. 1248–1252. [Google Scholar]
- Ogunsanya, M.; Isichei, J.; Desai, S. Grid search hyperparameter tuning in additive manufacturing processes. Manuf. Lett. 2023, 35, 1031–1042. [Google Scholar] [CrossRef]
- Sharma, V. A study on data scaling methods for machine learning. Int. J. Glob. Acad. Sci. Res. 2022, 1, 31–42. [Google Scholar] [CrossRef]
- Jayaram, V.; Gupte, O.; Smet, V. Modeling and design for system-level reliability and warpage mitigation of large 2.5 D glass BGA packages. In Proceedings of the 2022 IEEE 72nd Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 31 May–3 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1060–1067. [Google Scholar]



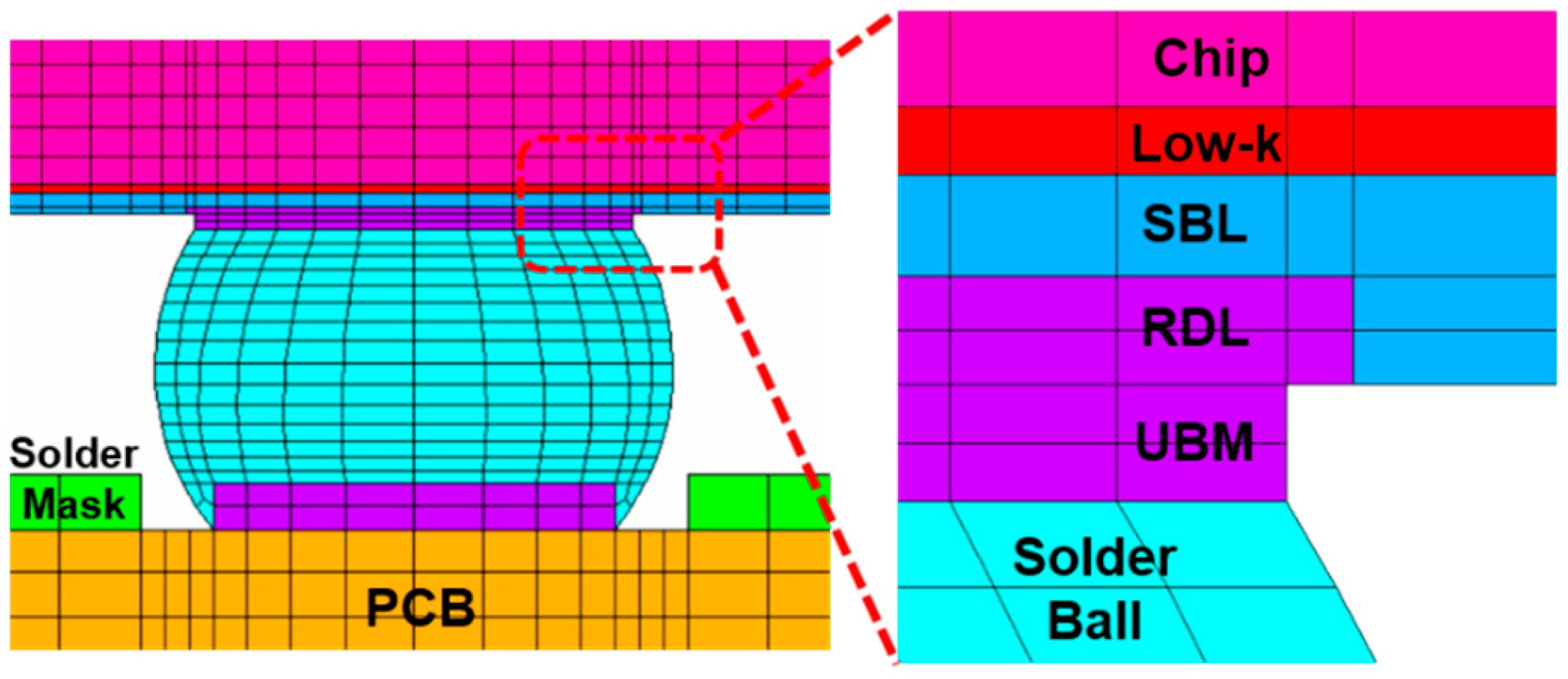
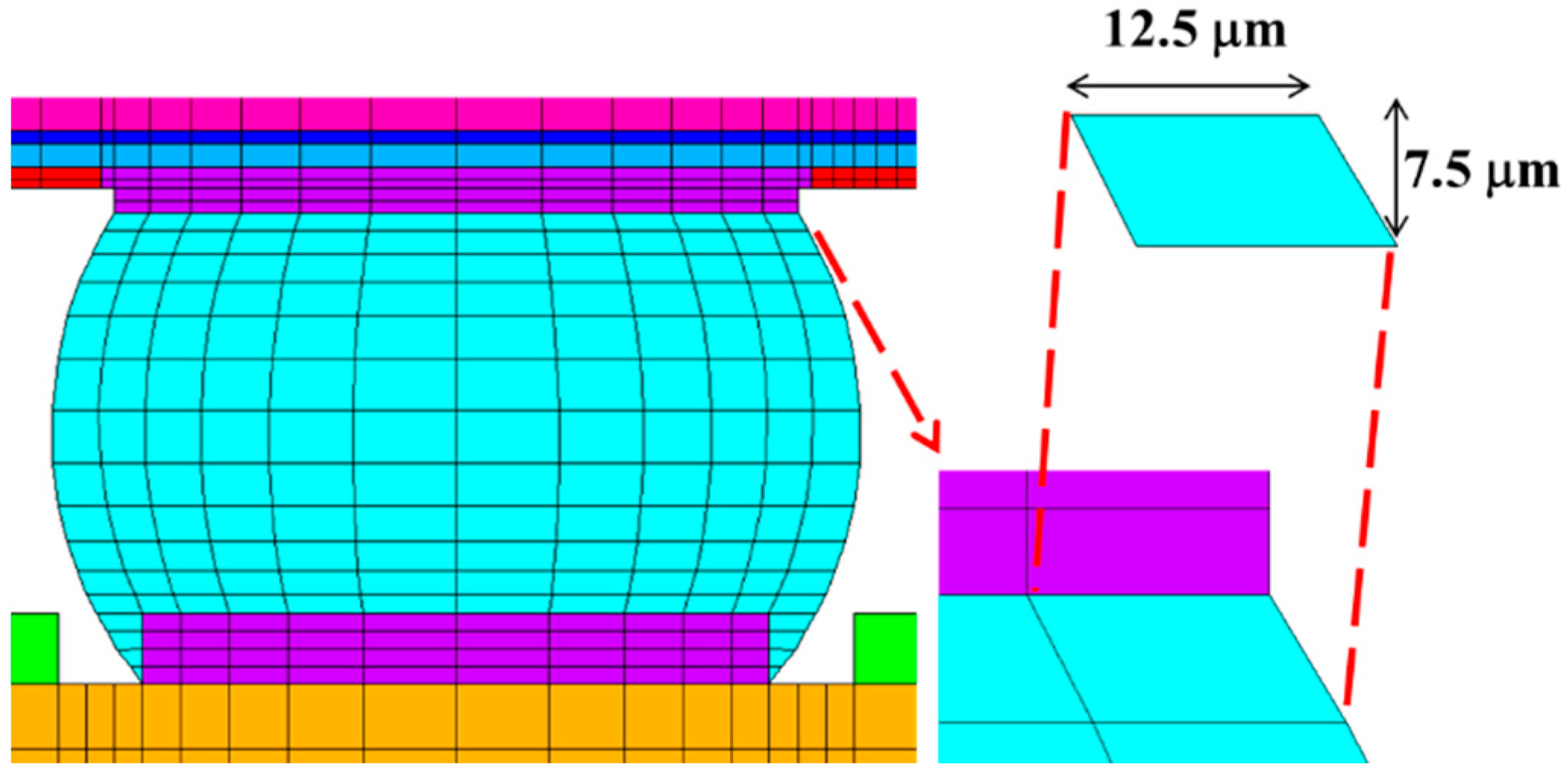



| Material | Young’s Modulus (GPa) | Poisson’s Ratio | CTE (ppm/°C) |
|---|---|---|---|
| Silicon chip | 150 | 0.28 | 2.62 |
| Low-k | 10 | 0.16 | 5 |
| SBL | 2 | 0.33 | 55 |
| Cu | 68.9 | 0.34 | 16.7 |
| Solder ball | 38.7−0.176T | 0.35 | 25 |
| Solder mask | 6.87 | 0.35 | 19 |
| PCB | 18.2 | 0.19 | 16 |
| T(K) | (GPa) | ||
|---|---|---|---|
| 233 | 47.64 | 8894.8 | 639.2 |
| 253 | 38.87 | 8573.3 | 660.0 |
| 313 | 24.06 | 6011.4 | 625.2 |
| 353 | 18.12 | 5804.2 | 697.7 |
| 395 | 14.31 | 4804.6 | 699.9 |
| TV | MTTF (Cycle) | Simulation (Cycle) | Difference (Cycle) | Difference (%) |
|---|---|---|---|---|
| 1 | 318 | 313 | 5 | 1.6% |
| 2 | 1013 | 982 | 31 | 3.1% |
| 3 | 587 | 587 | 0 | 0.0% |
| 4 | 876 | 804 | 72 | 8.2% |
| 5 | 904 | 885 | 19 | 2.1% |
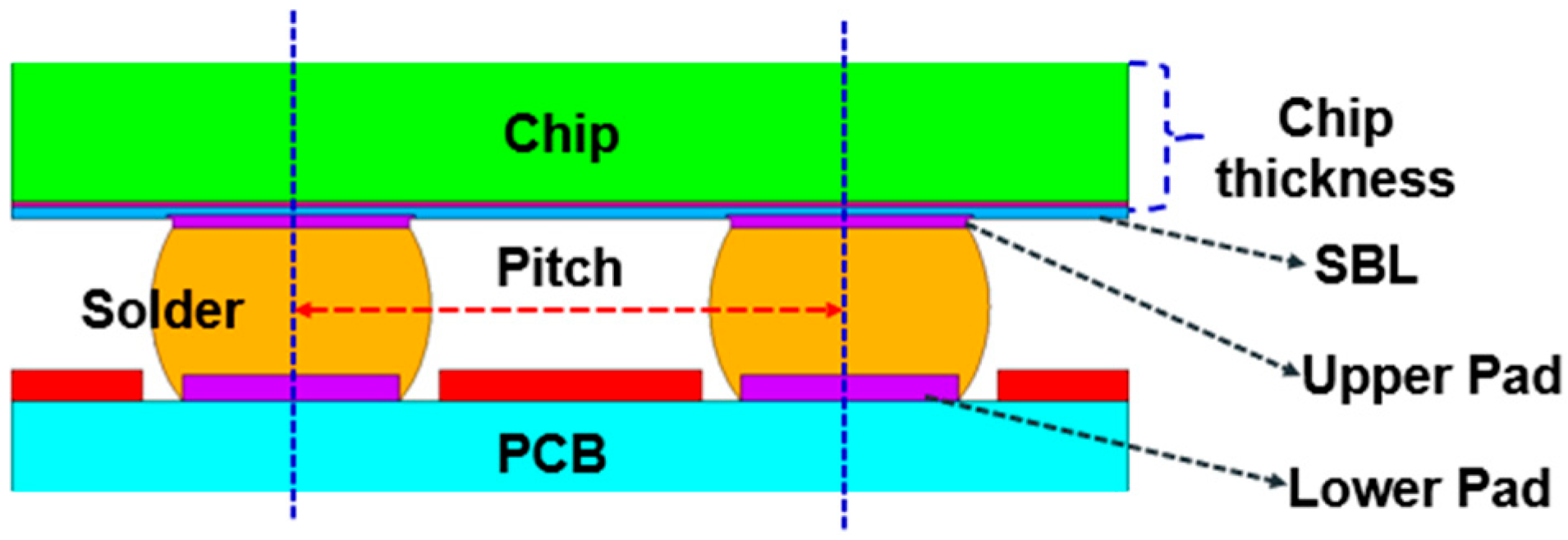
| Influence Factors | |
|---|---|
| Chip Thickness | Chip Size |
| Upper Pad Thickness | Upper Pad Diameter |
| Lower Pad Thickness | Lower Pad Diameter |
| SBL Thickness | PCB Thickness |
| Solder Diameter | Pitch |
| Features | Feature Values |
| Upper Pad Dia. (Unit: mm) | 0.18~0.24 |
| Lower Pad Dia. (Unit: mm) | 0.18~0.24 |
| Chip Thickness (Unit: mm) | 0.15~0.45 |
| SBL Thickness (Unit: μm) | 5~32.5 |
| Item | Step 1 | Step 2 | Step 3 |
|---|---|---|---|
| Training data | 144 | 144 + 14 | 432 |
| Testing data | 144 | 144 + 144 | —— |
| Optimal criteria | Test difference | Test difference | CV score |
| Hyperparameter | Setting |
|---|---|
| Activation function | ReLU |
| Solver | L-BFGS/Adam |
| Learning rate | Adaptive |
| Initial learning rate | 0.001 |
| Hidden layers | 3 |
| Neuron number | Grid search |
| Max_iter | 5000 |
| Loss function | MSE |
| Hyperparameter | Setting |
|---|---|
| Activation function | ReLU |
| Directions | Single |
| Unit | LSTM/Simple RNN |
| Learning rate | Adaptive |
| Initial learning rate | 0.001 |
| Hidden layers | 3 |
| Neuron number | 100/200 |
| Epochs | 2000 |
| Loss function | MAPE |
| Hyperparameter | Setting |
|---|---|
| Kernel function | Matérn/RBF |
| Alpha | Grid search (1 × 10−10~1) |
| Optimizer | fmin_l_bfgs_b |
| N_restarts | Grid search (0~20) |
| Item | ANN-1 | ANN-2 | ANN-3 | ANN-4 | ANN-5 |
|---|---|---|---|---|---|
| Training data | 144 | 158 | 432 | 432 | 432 |
| Feature | ULCS | ULCS | ULCS | ULCS | Reliability (3) |
| Solver | L-BFGS | L-BFGS | Adam | L-BFGS | L-BFGS |
| Neuron number | 88-112-96 | 104-72-76 | 112-112-52 | 88-64-60 | 56-96-44 |
| Maximum training difference | 0 (0) | 0 (0) | 61 660/721 (9.2%) | 6 1327/1333 (0.5%) | 31 903/872 (3.4%) |
| Average training difference | 0 (0) | 0 (0) | 8.3 (0.8%) | 0.7 (0.1%) | 4.8 (0.5%) |
| Maximum testing difference | 71 1396/1467 (5.1%) | 66 1311/1377 (5.0%) | —— | —— | —— |
| Average testing difference | 9.7 (1.0%) | 9.0 (0.9%) | —— | —— | —— |
| Item | RNN-1 | RNN-2 | RNN-3 | RNN-4 | RNN-5 |
|---|---|---|---|---|---|
| Training data | 144 | 158 | 432 | 432 | 432 |
| Feature | ULCS | ULCS | ULCS | ULCS | Reliability (3) |
| Unit | LSTM | LSTM | Simple RNN | LSTM | LSTM |
| Neuron number | 100 | 200 | 100 | 200 | 200 |
| Maximum training difference | 53 1319/1266 (4.0%) | 29 1145/1174 (2.5%) | 47 1690/1643 (2.8%) | 16 1470/1486 (1.1%) | 24 1230/1254 (2.0%) |
| Average training difference | 6.1 (0.6%) | 5.7 (0.6%) | 6.2 (0.6%) | 3.9 (0.4%) | 5.0 (0.5%) |
| Maximum testing difference | 85 828/743 (10.3%) | 64 927/991 (6.9%) | —— | —— | —— |
| Average testing difference | 15.7 (1.7%) | 13.3 (1.4%) | —— | —— | —— |
| Item | GPR-1 | GPR-2 | GPR-3 | GPR-4 | GPR-5 |
|---|---|---|---|---|---|
| Training data | 144 | 158 | 432 | 432 | 432 |
| Feature | ULCS | ULCS | ULCS | ULCS | Reliability (3) |
| Kernel | Matérn | Matérn | RBF | Matérn | Matérn |
| Alpha | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 |
| N_restarts | 11 | 13 | 12 | 19 | 15 |
| Maximum training difference | 23 1690/1667 (1.4%) | 20 1319/1299 (1.5%) | 50 1690/1640 (3.0%) | 21 1225/1204 (1.7%) | 53 1321/1268 (4.0%) |
| Average training difference | 4.2 (0.4%) | 4.2 (0.4%) | 8.7 (0.8%) | 3.0 (0.3%) | 7.4 (0.7%) |
| Maximum testing difference | 63 609/672 (10.3%) | 67 1321/1254 (5.1%) | —— | —— | —— |
| Average testing difference | 14.0 (1.4%) | 9.7 (1.0%) | —— | —— | —— |
| Item | Maximum Testing Difference | Average Testing Difference |
|---|---|---|
| ANN-1 | 102 (1141/1039/8.9%) | 13.9 (1.4%) |
| ANN-2 | 85 (1595/1680/5.3%) | 11.6 (1.1%) |
| ANN-3 | 104 (1595/1699/6.5%) | 9.0 (0.9%) |
| ANN-4 | 86 (689/775/12.5%) | 11.9 (1.2%) |
| ANN-5 | 78 (1595/1673/4.9%) | 9.0 (0.9%) |
| RNN-1 | 118 (1237/1355/9.5%) | 13.8 (1.4%) |
| RNN-2 | 140 (672/812/20.8%) | 14.6 (1.5%) |
| RNN-3 | 94 (864/770/10.9%) | 10.7 (1.0%) |
| RNN-4 | 114 (921/807/12.4%) | 8.3 (0.8%) |
| RNN-5 | 114 (664/778/17.2%) | 9.8 (1.0%) |
| GPR-1 | 124 (1340/1216/9.3%) | 15.2 (1.5%) |
| GPR-2 | 86 (1432/1346/6.0%) | 12.8 (1.3%) |
| GPR-3 | 83 (1340/1257/6.2%) | 12.7 (1.2%) |
| GPR-4 | 80 (1340/1260/6.0%) | 9.8 (0.9%) |
| GPR-5 | 82 (1585/1503/5.2%) | 11.6 (1.1%) |
| Ensemble | Maximum Testing Difference | Average Testing Difference |
|---|---|---|
| ANN | 66 (1595/1661/4.1%) | 8.1 (0.8%) |
| RNN | 82 (921/839/8.9%) | 8.0 (0.8%) |
| GPR | 69 (1097/1028/6.3%) | 11.3 (1.0%) |
| ANN + RNN | 63 (921/858/6.8%) | 7.0 (0.7%) |
| ANN + GPR | 70 (1097/1027/6.4%) | 8.7 (0.9%) |
| RNN + GPR | 77 (1340/1263/5.7%) | 8.8 (0.9%) |
| ALL | 67 (1142/1075/5.9%) | 7.9 (0.8%) |
| Ensemble Framework | Maximum Testing Difference | Average Testing Difference |
|---|---|---|
| 1 (ANN) | 66 (1595/1661/4.1%) | 8.1 (0.8%) |
| 2 (ANN) | 62 (1595/1657/3.9%) | 7.5 (0.8%) |
| 1 + 2 (ANN) | 64 (1595/1659/4.0%) | 6.5 (0.6%) |
| Method | Prediction (Cycles) | Difference from Experiment (Cycles) |
|---|---|---|
| Experiment | 1013 | - |
| Simulation | 982 | 31 (3.1%) |
| Machine Learning | 1029 | 16 (1.6%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Q.; Chiang, K.-N. Multi-Algorithm Ensemble Learning Framework for Predicting the Solder Joint Reliability of Wafer-Level Packaging. Materials 2025, 18, 4074. https://doi.org/10.3390/ma18174074
Su Q, Chiang K-N. Multi-Algorithm Ensemble Learning Framework for Predicting the Solder Joint Reliability of Wafer-Level Packaging. Materials. 2025; 18(17):4074. https://doi.org/10.3390/ma18174074
Chicago/Turabian StyleSu, Qinghua, and Kuo-Ning Chiang. 2025. "Multi-Algorithm Ensemble Learning Framework for Predicting the Solder Joint Reliability of Wafer-Level Packaging" Materials 18, no. 17: 4074. https://doi.org/10.3390/ma18174074
APA StyleSu, Q., & Chiang, K.-N. (2025). Multi-Algorithm Ensemble Learning Framework for Predicting the Solder Joint Reliability of Wafer-Level Packaging. Materials, 18(17), 4074. https://doi.org/10.3390/ma18174074






