Experimental and Numerical Investigations on the Influences of Target Porosity and w/c Ratio on Strength and Permeability of Pervious Concrete
Abstract
1. Introduction
2. Experimental Investigation
2.1. Raw Materials
2.2. Mix Design
- (i)
- Target Porosity and Aggregate Preparation. Specify the desired porosity, choosing a target value such as 15%, 20%, or 25%. Next, prepare the coarse aggregates (including crushed granite and steel slag, SS) according to established grading curves. The mass of these coarse aggregates required per cubic meter is initially calculated based on their close-packing density. To account for practical construction considerations, this calculated mass is then reduced by applying a factor of 0.98.
- (ii)
- Void Content Assessment. Determine the void volume inherent within the densely packed coarse aggregate. In the close-packed state, the aggregate particles in pervious concrete are envisioned to be uniformly coated with cement paste. Upon solidification, this process facilitates the formation of the desired porous structure, where the interstitial voids present in the packed state evolve into the interconnected pores within the hardened concrete.
- (iii)
- Cement and Water Calculation. Establish an initial water-to-cement (w/c) ratio for the intended mixture, selecting from suitable values such as 0.25, 0.28, 0.30, 0.33, and 0.35. Based on this ratio, compute the required quantities of cement and water. Given that the mixture design targets a specific porosity, these quantities can be determined using the following derivations. The determination of aggregate content, paste volume, water requirement, and admixture dosage is governed by Equation (1). Table 4 and Table 5 provide the detailed mixing ratios for the PCs and SSPCs, where the w/c ratio for the SSPC specimens is 0.30. Table 6 presents the physical and mechanical properties of the mixed aggregate using crushed granite and steel lag.
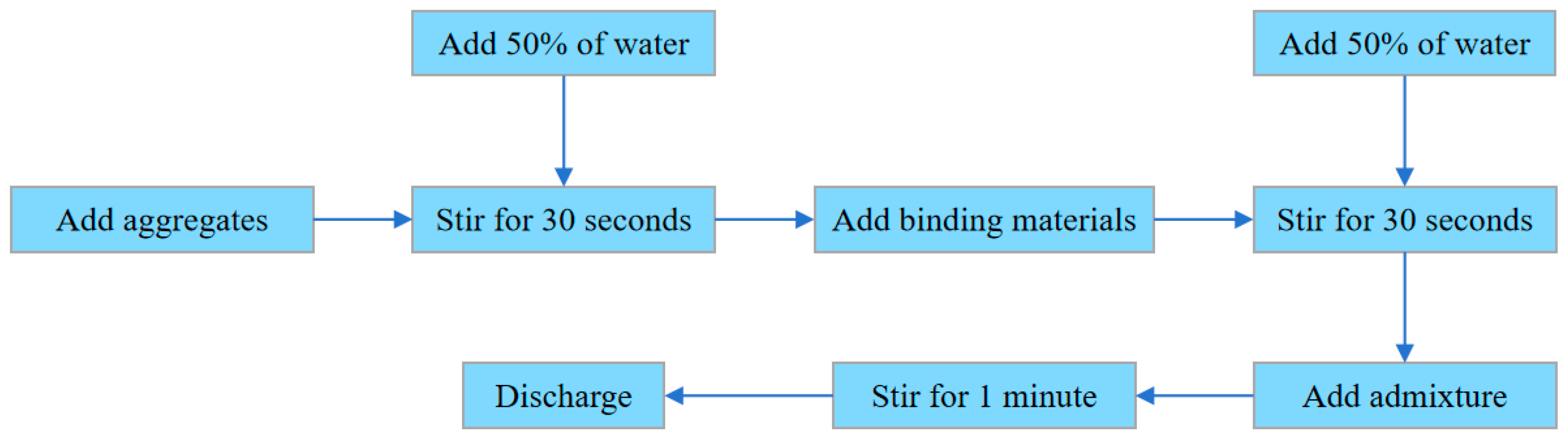
2.3. Specimen Preparation
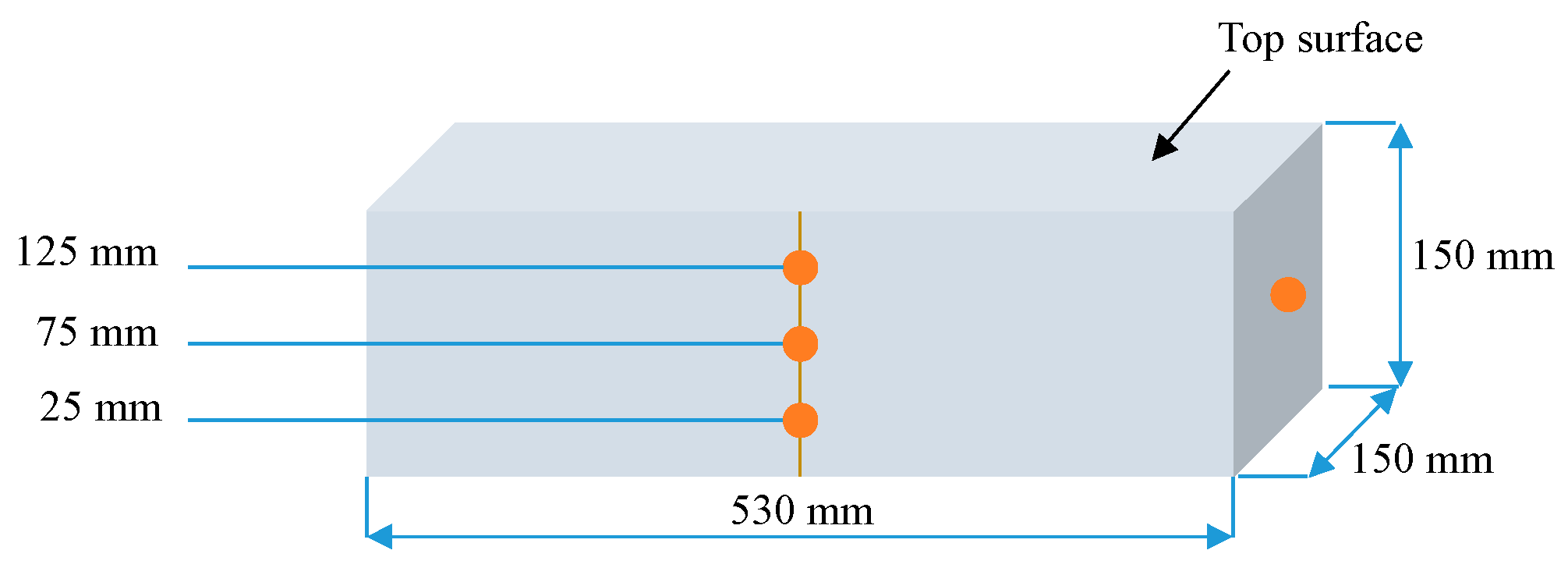
2.4. Test Methods
2.4.1. Strength Tests
2.4.2. Permeability Tests
3. Experimental Results and Discussion
3.1. Compressive Strength
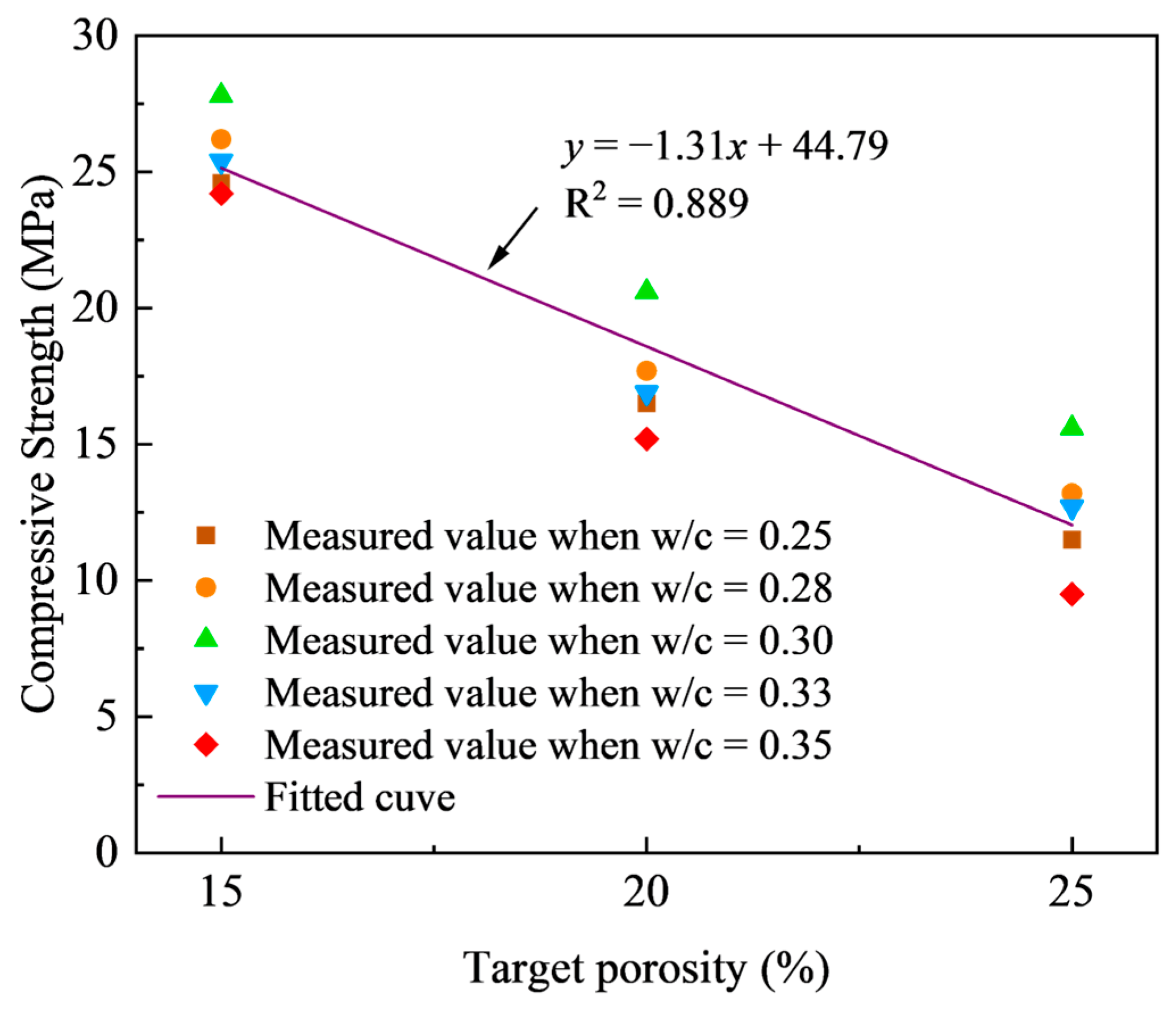
3.1.1. Effect of Target Porosity on Compressive Strength
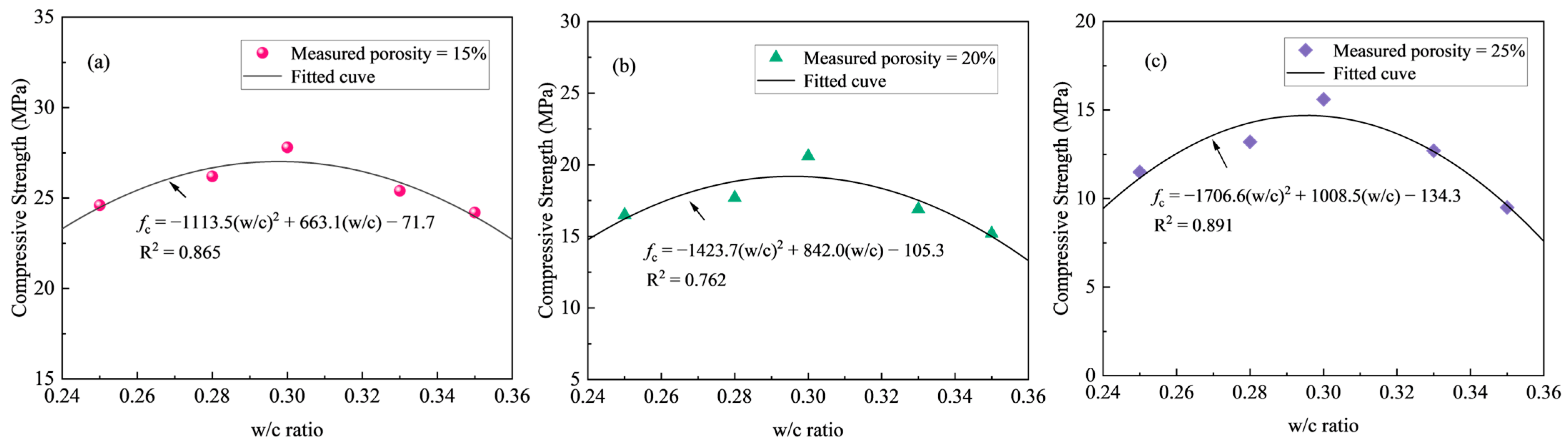
3.1.2. Effect of w/c Ratio on Compressive Strength
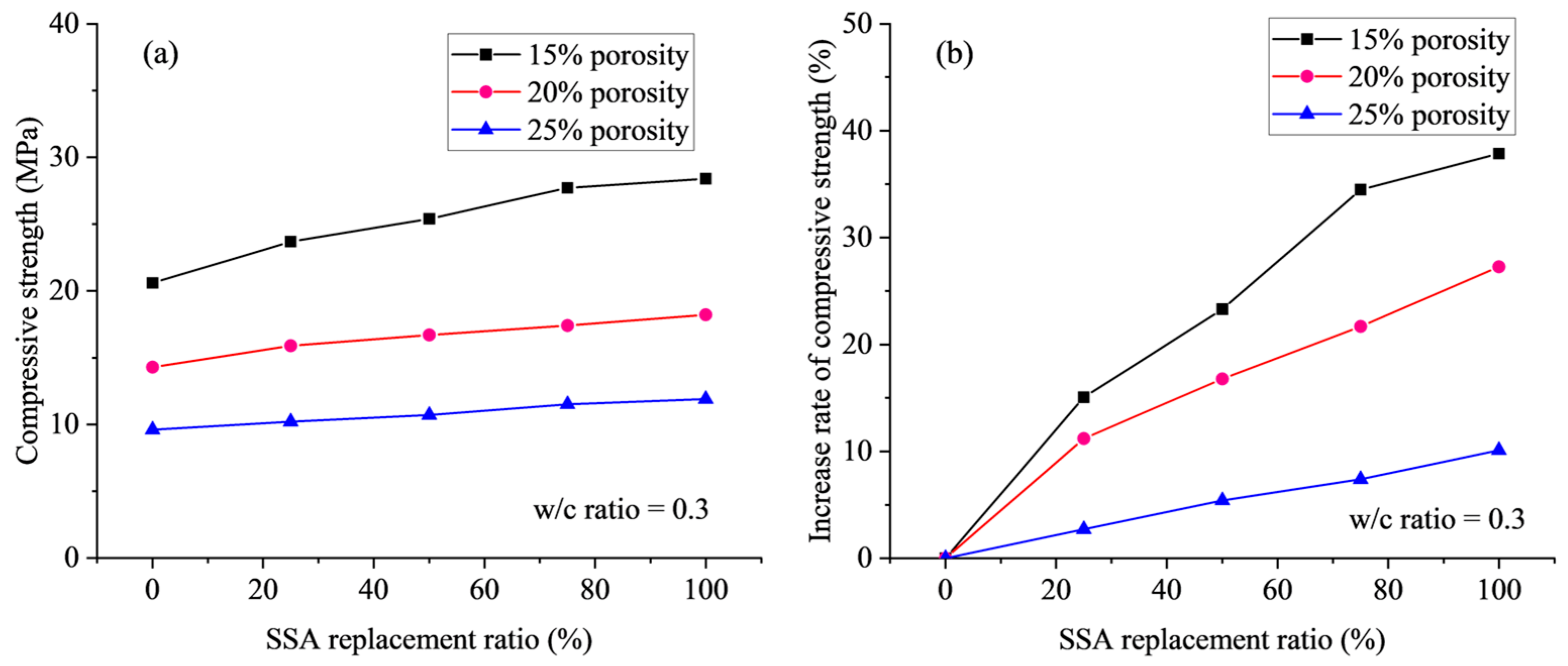
3.1.3. Effect of SSA Replacement Ratio on Compressive Strength
3.2. Permeability Coefficient
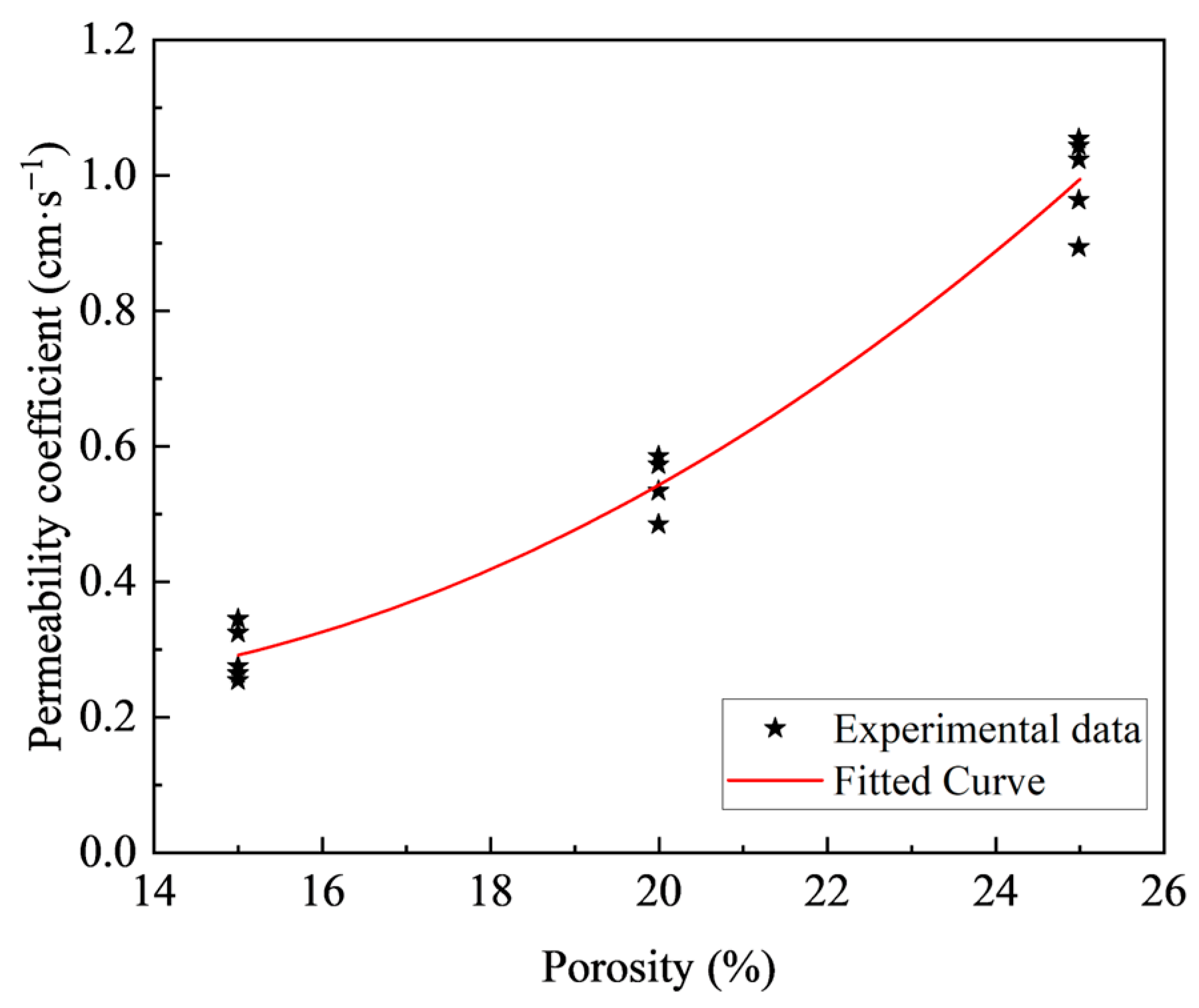
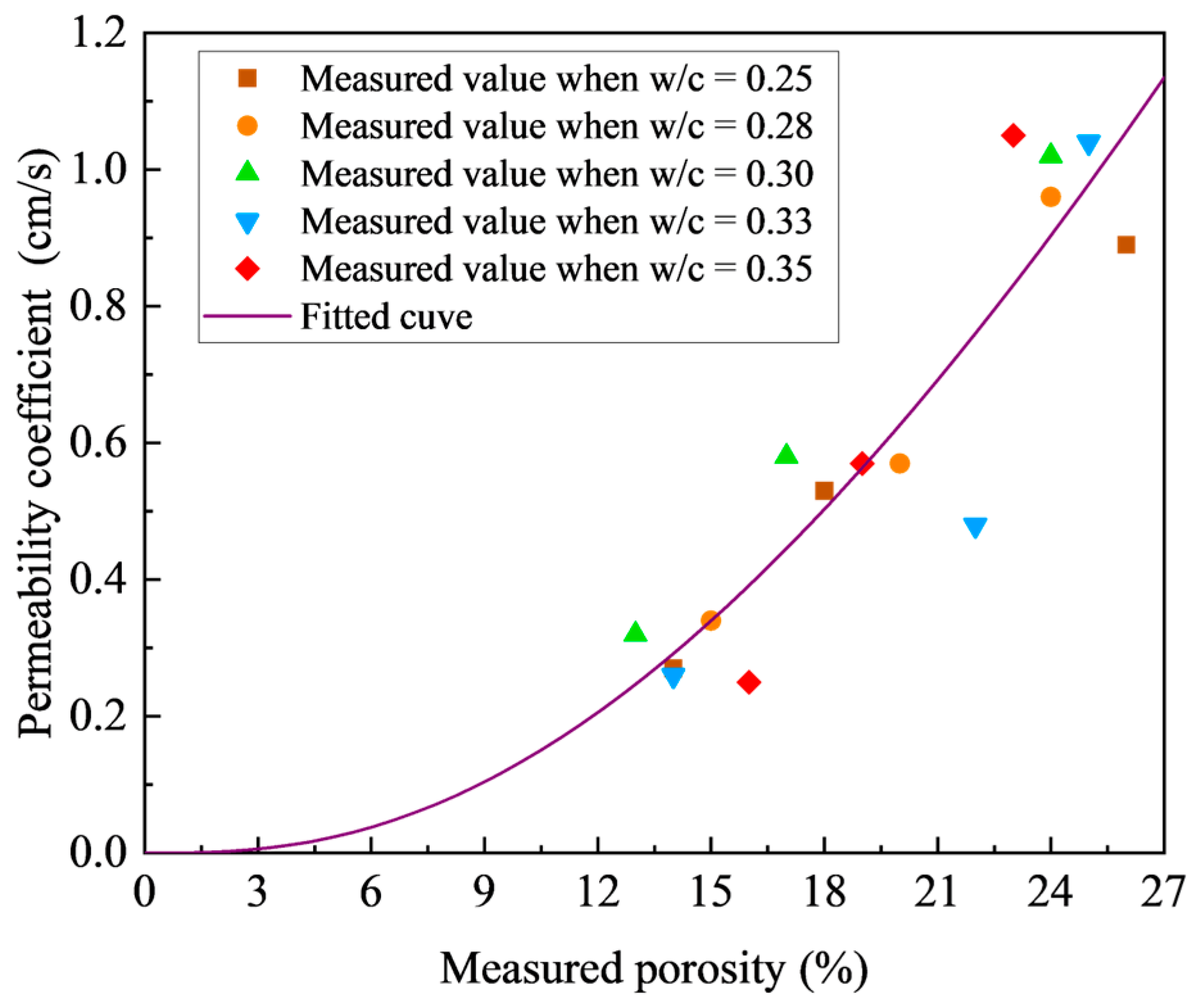
3.2.1. Effect of Target Porosity
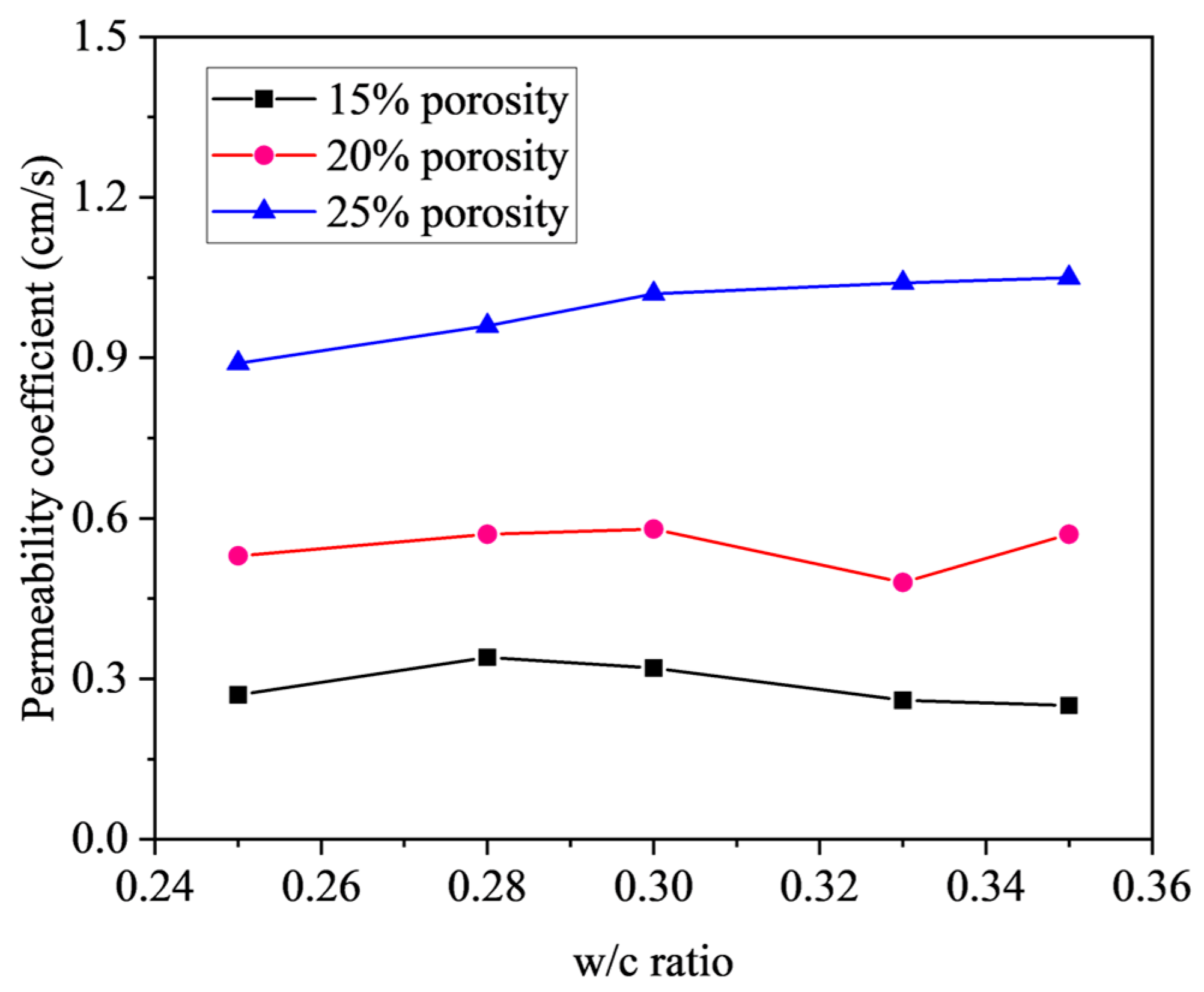
3.2.2. Effect of w/c Ratio
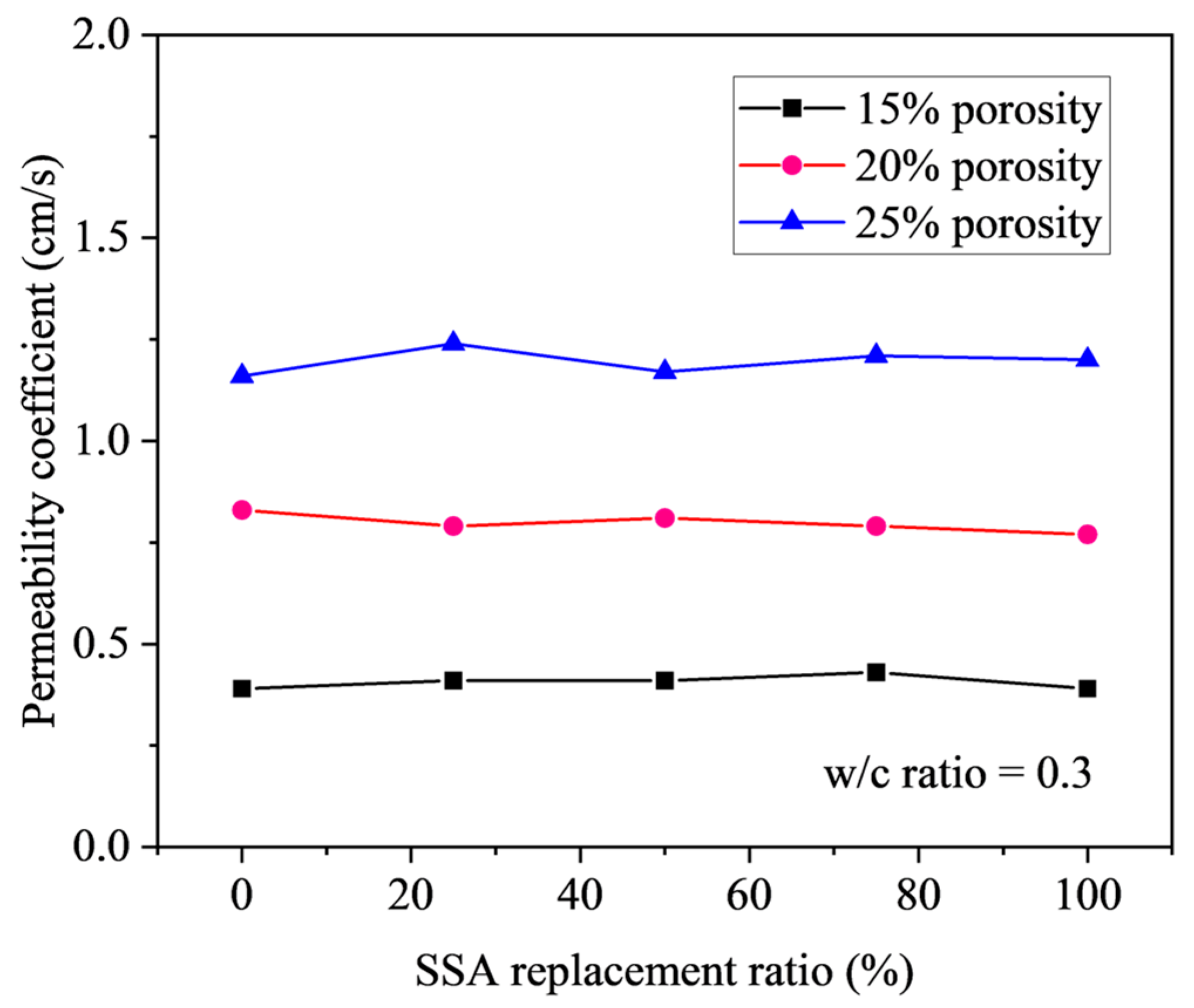
3.2.3. Effect of SSA Replacement Ratio
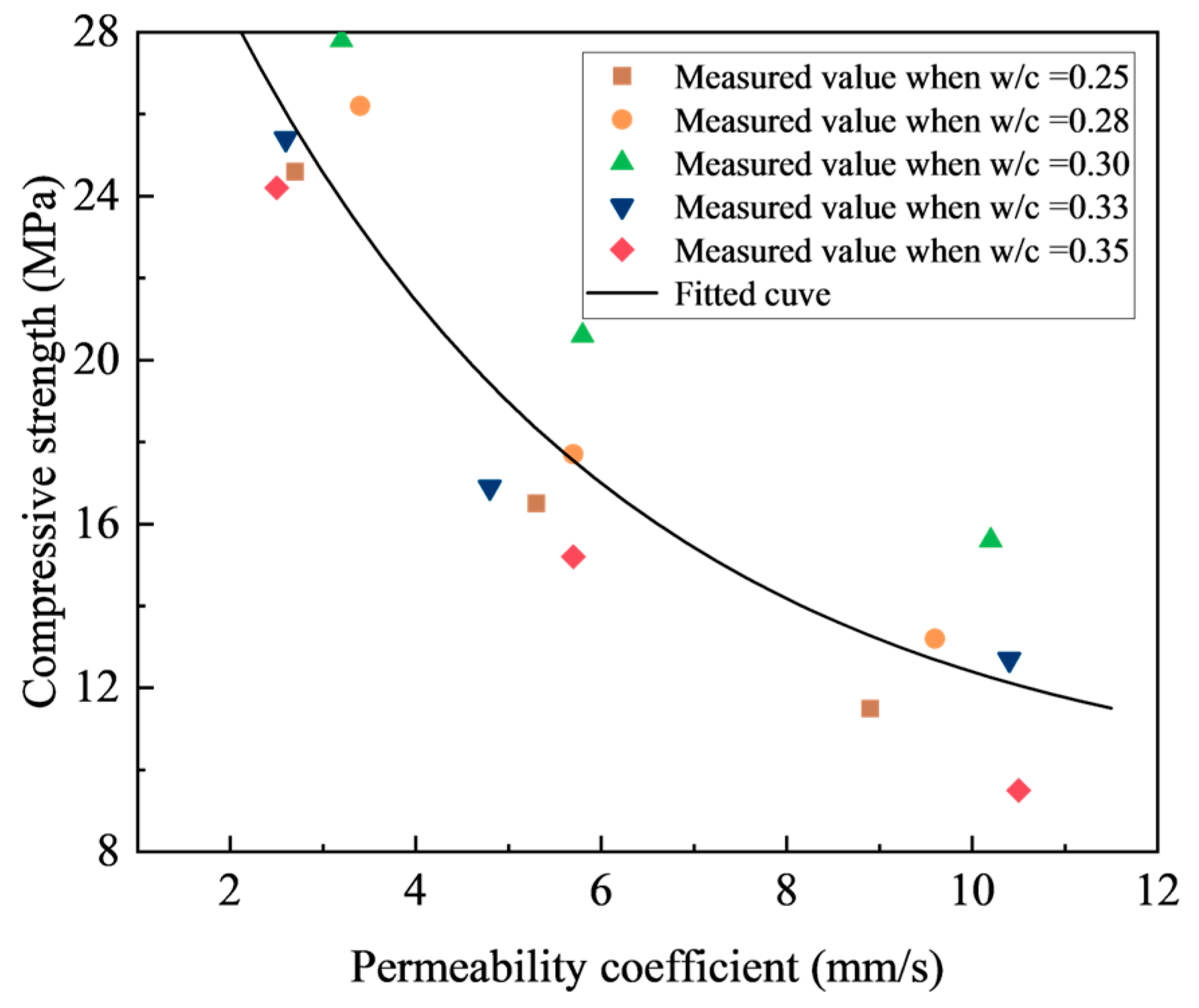
3.3. Relationship Between Porosity, Permeability and Strength
- (1)
- Specify the minimum required compressive strength (fc > A) and permeability coefficient (K > B) based on project-specific engineering requirements and quality control standards.
- (2)
- Utilize the empirical fc versus K relationship established in Figure 16 to derive the “effective interval”. This delimits the desired range for compressive strength [fc ∈ (A, C)] and permeability coefficient [K ∈ (B, D)].
- (3)
- Calculate the required porosity (P) corresponding to the mean target permeability coefficient (K) using the empirical relationship between K and P shown in Figure 15.
- (4)
- Identify the optimum w/c ratio that achieves the mean target compressive strength fc at porosity P, utilizing the empirical relationship between fc and w/c ratio presented in Figure 10.
- (5)
- Calculate the permeability coefficient (K) associated with the optimum w/c ratio using the empirical relationship in Figure 13. Confirm compliance with the target range [K ∈ (B, D)].
- (6)
- The preceding steps yield a mix design meeting specified engineering requirements.
4. Numerical Simulations
4.1. Finite Element Modelling
4.2. Parameter Calibration
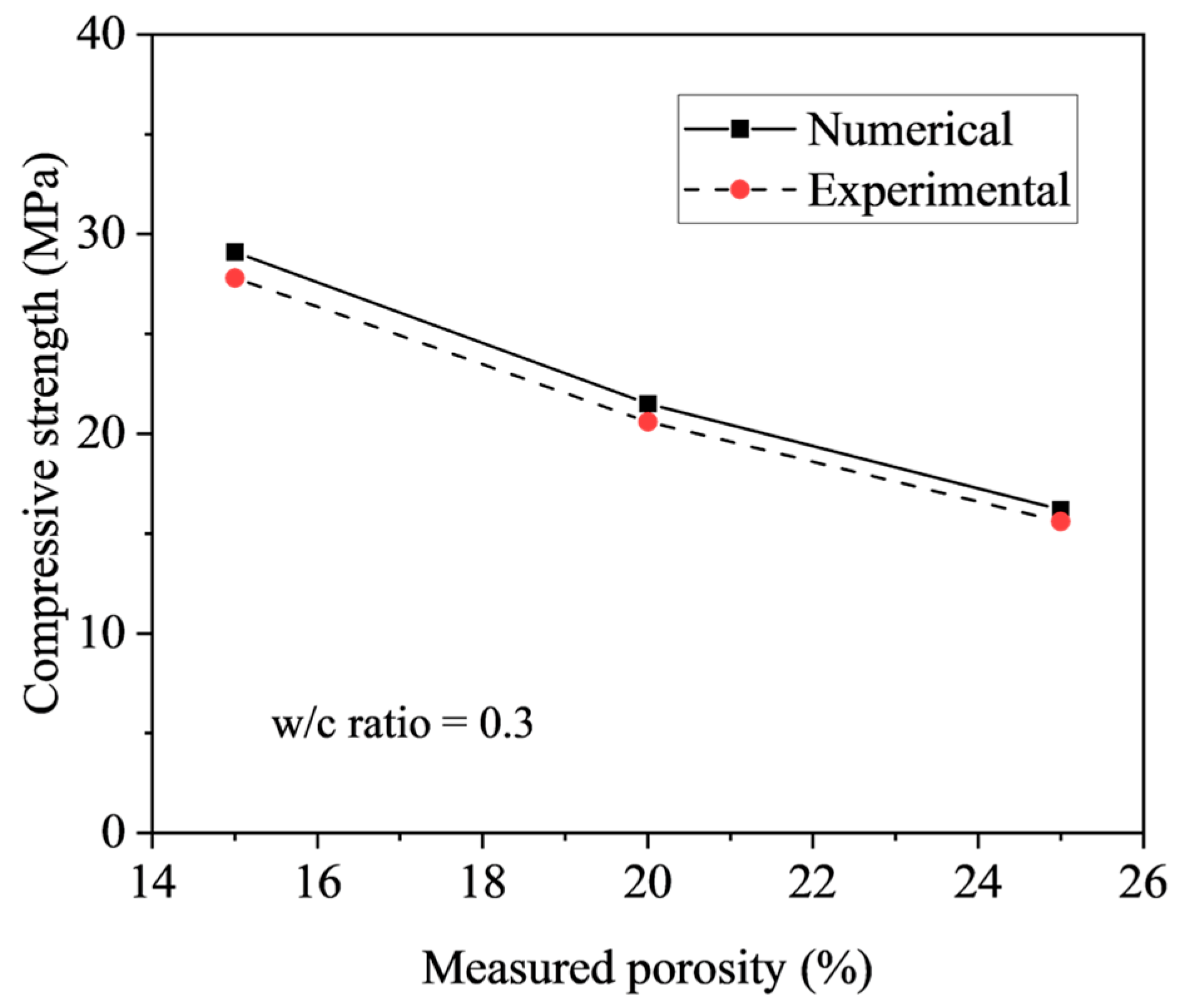
4.3. Comparison Between Numerical and Experimental Results
5. Conclusions
- (1)
- Pervious concrete cube specimens prepared with an optimal w/c ratio of 0.3 exhibit compressive strengths of 27.8, 20.6, and 15.6 MPa for target porosities of 15%, 20%, and 25%, respectively. Conversely, the permeability coefficients experience a significant increase with porosity, reaching 0.32, 0.58, and 1.02 cm/s for the respective porosity levels.
- (2)
- The porosity shows a significant influence on both the strength and permeability of pervious concrete, while the influence of w/c ratio is marginal. As the porosity increases from 15% to 25%, the permeability coefficient increases considerably from 0.228 to 0.992 cm/s on average, while the average compressive strength decreases from 25.64 MPa to 12.5 MPa.
- (3)
- The incorporation of steel slag aggregate (SSA) leads to an increase in the strength of pervious concrete but has no significant influence on the permeability. For a lower porosity of 15%, pervious concrete with the SSA replacement ratio of 100% exhibits a larger improvement in the compressive strength up to 37.86% compared to conventional pervious concrete.
- (4)
- Empirical models correlating the porosity, strength and permeability of pervious concrete were established and validated through comparison with the experimental results. As the permeability coefficient increases, the compressive strength decreases monotonously while the rate of this reduction diminishes gradually.
- (5)
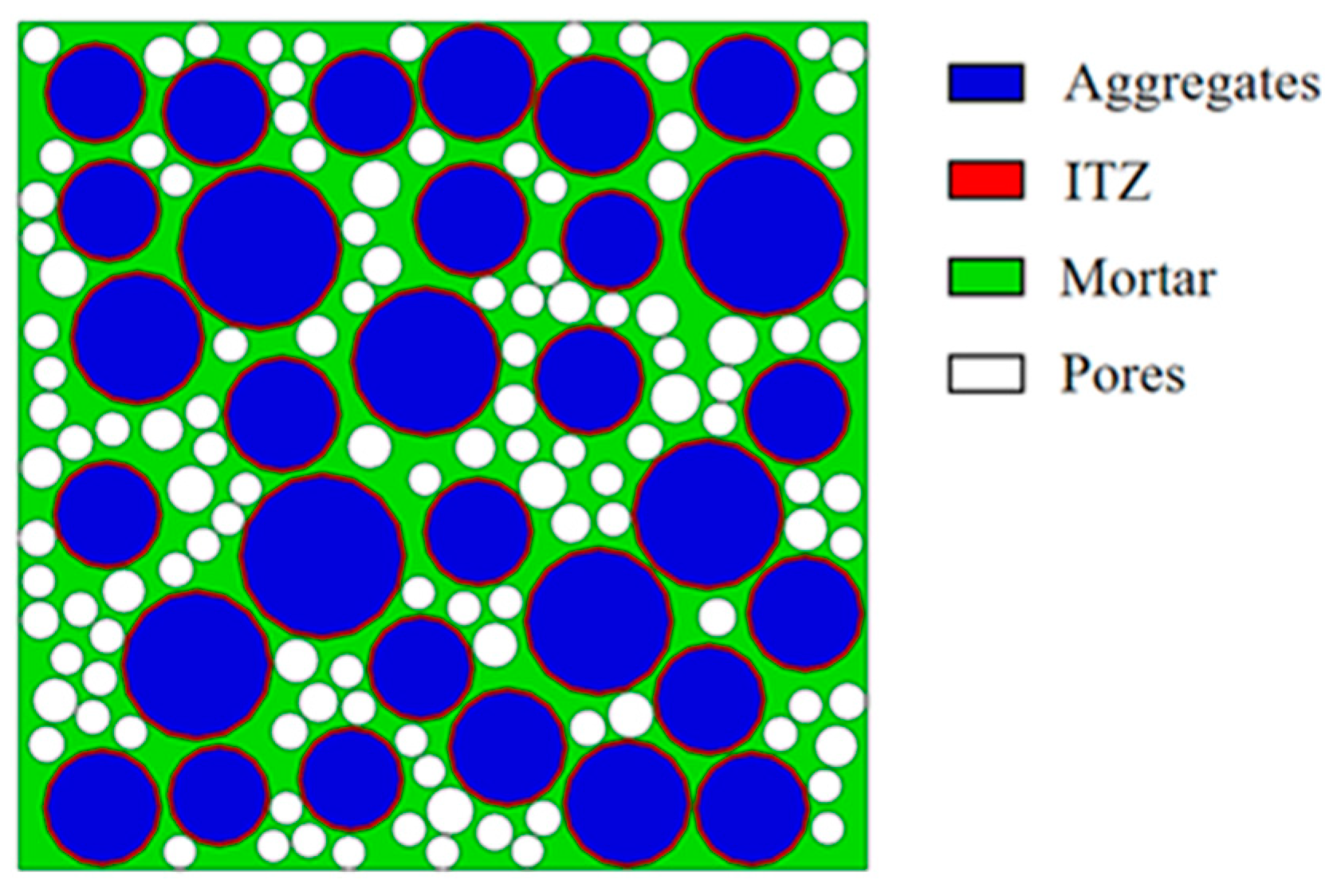
- A distinct relationship exists between porosity and the failure mechanism of pervious concrete. Lower porosities are associated with a higher propensity for aggregate fracture. As porosity increases from 15% to 25%, the failure mode progressively changes from aggregate penetration to ITZ interface debonding and mortar cracking, leading to strength reductions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chandrappa, A.K.; Biligiri, K.P. Pervious concrete as a sustainable pavement material–Research findings and future prospects: A state-of-the-art review. Constr. Build. Mater. 2016, 111, 262–274. [Google Scholar] [CrossRef]
- Elango, K.S.; Gopi, R.; Saravanakumar, R.; Rajeshkumar, V.; Vivek, D.; Raman, S.V. Properties of pervious concrete—A state of the art review. Mater. Today Proc. 2021, 45, 2422–2425. [Google Scholar] [CrossRef]
- Adresi, M.; Yamani, A.; Tabarestani, M.K.; Rooholamini, H. A comprehensive review on pervious concrete. Constr. Build. Mater. 2023, 407, 133308. [Google Scholar] [CrossRef]
- Zhang, Q.; Feng, X.; Chen, X.; Lu, K. Mix design for recycled aggregate pervious concrete based on response surface methodology. Constr. Build. Mater. 2020, 259, 119776. [Google Scholar] [CrossRef]
- Zhu, M.; Leo, C.; Zeng, Q.; Fanna, D.J.; Hsi, J.; Karimi, R.; Fabbri, A.; Liyanapathirana, S.; Hu, P.; Alzghool, H. Efficacy of expansive soil stabilisation using un-calcinated Kaolinite-Based Alkali-Activated binders. Clean. Mater. 2025, 16, 100315. [Google Scholar] [CrossRef]
- Govedarica, O.; Aškrabić, M.; Hadnađev-Kostić, M.; Vulić, T.; Lekić, B.; Rajaković-Ognjanović, V.; Zakić, D. Evaluation of solidified wastewater treatment sludge as a potential SCM in pervious concrete pavements. Materials 2022, 15, 4919. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Sebaibi, N.; Boutouil, M.; Leleyter, L.; Baraud, F. A modified method for the design of pervious concrete mix. Constr. Build. Mater. 2014, 73, 271–282. [Google Scholar] [CrossRef]
- Joshaghani, A.; Ramezanianpour, A.A.; Ataei, O.; Golroo, A. Optimizing pervious concrete pavement mixture design by using the Taguchi method. Constr. Build. Mater. 2015, 101, 317–325. [Google Scholar] [CrossRef]
- Yu, F.; Sun, D.; Sun, G.; Ling, S.; Hu, M.; Ma, J. A modified mix design method for pervious concrete based on Mohr-Coulomb failure criterion. Constr. Build. Mater. 2021, 269, 121801. [Google Scholar] [CrossRef]
- Chindaprasirt, P.; Hatanaka, S.; Chareerat, T.; Mishima, N.; Yuasa, Y. Cement paste characteristics and porous concrete properties. Constr. Build. Mater. 2008, 22, 894–901. [Google Scholar] [CrossRef]
- Brasileiro, K.P.T.V.; de Oliveira Nahime, B.; Lima, E.C.; Alves, M.M.; Ferreira, W.P.; Santos, I.S.D.; Filho, C.P.B.; Reis, I.C.D. Influence of recycled aggregates and silica fume on the performance of pervious concrete. J. Build. Eng. 2024, 82, 108347. [Google Scholar] [CrossRef]
- Yu, F.; Guo, J.; Liu, J.; Cai, H.; Huang, Y. A review of the pore structure of pervious concrete: Analyzing method, characterization parameters and the effect on performance. Constr. Build. Mater. 2023, 365, 129971. [Google Scholar] [CrossRef]
- AlShareedah, O.; Nassiri, S. Pervious concrete mixture optimization, physical, and mechanical properties and pavement design: A review. J. Clean. Prod. 2021, 288, 125095. [Google Scholar] [CrossRef]
- Chandrappa, A.K.; Biligiri, K.P. Comprehensive investigation of permeability characteristics of pervious concrete: A hydrodynamic approach. Constr. Build. Mater. 2016, 123, 627–637. [Google Scholar] [CrossRef]
- Wang, G.; Chen, X.; Dong, Q.; Yuan, J.; Hong, Q. Mechanical performance study of pervious concrete using steel slag aggregate through laboratory tests and numerical simulation. J. Clean. Prod. 2020, 262, 121208. [Google Scholar] [CrossRef]
- Rashad, A.M. Behavior of steel slag aggregate in mortar and concrete—A comprehensive overview. J. Build. Eng. 2022, 53, 104536. [Google Scholar] [CrossRef]
- Dong, Q.; Wang, G.; Chen, X.; Tan, J.; Gu, X. Recycling of steel slag aggregate in portland cement concrete: An overview. J. Clean. Prod. 2021, 282, 124447. [Google Scholar] [CrossRef]
- Brand, A.S.; Roesler, J.R. Interfacial transition zone of cement composites with steel furnace slag aggregates. Cem. Concr. Compos. 2018, 86, 117–129. [Google Scholar] [CrossRef]
- Liao, L.; Wu, S.; Hao, R.; Zhou, Y.; Xie, P. The compressive strength and damage mechanisms of pervious concrete based on 2D mesoscale pore characteristics. Constr. Build. Mater. 2023, 386, 131561. [Google Scholar] [CrossRef]
- Chen, X.; Wang, G.; Dong, Q.; Zhao, X.; Wang, Y. Microscopic characterizations of pervious concrete using recycled Steel Slag Aggregate. J. Clean. Prod. 2020, 254, 120149. [Google Scholar] [CrossRef]
- Chang, J.J.; Yeih, W.; Chung, T.J.; Huang, R. Properties of pervious concrete made with electric arc furnace slag and alkali-activated slag cement. Constr. Build. Mater. 2016, 109, 34–40. [Google Scholar] [CrossRef]
- Shen, W.; Liu, Y.; Wu, M.; Zhang, D.; Du, X.; Zhao, D.; Xu, G.; Zhang, B.; Xiong, X. Ecological carbonated steel slag pervious concrete prepared as a key material of sponge city. J. Clean. Prod. 2020, 256, 120244. [Google Scholar] [CrossRef]
- San-José, J.T.; Vegas, I.; Arribas, I.; Marcos, I. The performance of steel-making slag concretes in the hardened state. Mater. Des. 2014, 60, 612–619. [Google Scholar] [CrossRef]
- Akand, L.; Yang, M.; Gao, Z. Characterization of pervious concrete through image based micromechanical modeling. Constr. Build. Mater. 2016, 114, 547–555. [Google Scholar] [CrossRef]
- Pieralisi, R.; Cavalaro, S.H.P.; Aguado, A. Advanced numerical assessment of the permeability of pervious concrete. Cem. Concr. Res. 2017, 102, 149–160. [Google Scholar] [CrossRef]
- Elango, K.S.; Revathi, V. Fal-G binder pervious concrete. Constr. Build. Mater. 2017, 140, 91–99. [Google Scholar] [CrossRef]
- Li, L.G.; Feng, J.J.; Zhu, J.; Chu, S.H.; Kwan, A.K.H. Pervious concrete: Effects of porosity on permeability and strength. Mag. Concr. Res. 2021, 73, 69–79. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, G. Experimental study on properties of pervious concrete pavement materials. Cem. Concr. Res. 2003, 33, 381–386. [Google Scholar] [CrossRef]
- Alemu, A.S.; Yoon, J.; Tafesse, M.; Seo, Y.-S.; Kim, H.-K.; Pyo, S. Practical considerations of porosity, strength, and acoustic absorption of structural pervious concrete. Case Stud. Constr. Mater. 2021, 15, e00764. [Google Scholar] [CrossRef]
- Xie, X.; Zhang, T.; Wang, C.; Yang, Y.; Bogush, A.; Khayrulina, E.; Huang, Z.; Wei, J.; Yu, Q. Mixture proportion design of pervious concrete based on the relationships between fundamental properties and skeleton structures. Cem. Concr. Compos. 2020, 113, 103693. [Google Scholar] [CrossRef]
- Rehder, B.; Banh, K.; Neithalath, N. Fracture behavior of pervious concretes: The effects of pore structure and fibers. Eng. Fract. Mech. 2014, 118, 1–16. [Google Scholar] [CrossRef]
- Rangelov, M.; Nassiri, S.; Haselbach, L.; Englund, K. Using carbon fiber composites for reinforcing pervious concrete. Constr. Build. Mater. 2016, 126, 875–885. [Google Scholar] [CrossRef]
- Shan, J.; Zhang, Y.; Wu, S.; Lin, Z.; Li, L.; Wu, Q. Pore characteristics of pervious concrete and their influence on permeability attributes. Constr. Build. Mater. 2022, 327, 126874. [Google Scholar] [CrossRef]
- Montes, F.; Valavala, S.; Haselbach, L.M. A new test method for porosity measurements of Portland cement pervious concrete. J. ASTM Int. 2005, 2, 1–13. [Google Scholar] [CrossRef]
- da Costa, F.B.P.; Haselbach, L.M.; da Silva Filho, L.C.P. Pervious concrete for desired porosity: Influence of w/c ratio and a rheology-modifying admixture. Constr. Build. Mater. 2021, 268, 121084. [Google Scholar] [CrossRef]
- Wu, Y.; Pieralisi, R.; Sandoval, F.G.B.; López-Carreño, R.; Pujadas, P. Optimizing pervious concrete with machine learning: Predicting permeability and compressive strength using artificial neural networks. Constr. Build. Mater. 2024, 443, 137619. [Google Scholar] [CrossRef]
- ACI PCR-522-23; American Concrete Institute: Farmington Hills, MI, USA, 2023.
- GB 175-2007; AQSIQ (General Administration of Quality Supervision, Inspection and Quarantine), Common Portland Cement. AQSIQ: Beijing, China, 2007. (In Chinese)
- GB/T50146-2014; Technical Code for Application of Fly Ash Concrete. National Standard of the People’s Republic of China: Beijing, China, 2014. (In Chinese)
- NRMCA-Concrete in Practice-38 (CIP-38); National Ready Mix Concrete Association (NRMCA): Silver Spring, MD, USA, 2004.
- ASTM C469; Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete in Compression. Annual Book of ASTM Standard 04: West Conshohoken, PA, USA, 2002.
- GB/T 50081-2019; Standard for Test Methods of Physical and Mechanical Properties of Concrete. National Standard of the People’s Republic of China: Beijing, China, 2019. (In Chinese)
- ASTM C597/C597M-16; Standard Test Method for Pulse Velocity Through Concrete. ASTM: West Conshohoken, PA, USA, 2016.
- CJJ/T 135-2009; Technical Specification for Pervious Cement Concrete Pavement. China Construction Industry Press: Beijing, China, 2009. (In Chinese)
- Chockalingam, T.; Vijayaprabha, C.; Raj, J.L. Experimental study on size of aggregates, size and shape of specimens on strength characteristics of pervious concrete. Constr. Build. Mater. 2023, 385, 131320. [Google Scholar] [CrossRef]
- Lee, M.G.; Wang, Y.C.; Wang, W.C.; Chien, H.J.; Cheng, L.C. Experimental study on the mechanical properties of reinforced pervious concrete. Buildings 2023, 13, 2880. [Google Scholar] [CrossRef]
- Suksawang, N.; Wtaife, S.; Alsabbagh, A. Evaluation of elastic modulus of fiber-reinforced concrete. ACI Mater. J. 2018, 115, 239. [Google Scholar] [CrossRef]
- Ridengaoqier, E.; Hatanaka, S.; Palamy, P.; Kurita, S. Experimental study on the porosity evaluation of pervious concrete by using ultrasonic wave testing on surfaces. Constr. Build. Mater. 2021, 300, 123959. [Google Scholar] [CrossRef]
- Sonebi, M.; Bassuoni, M.T. Investigating the effect of mixture design parameters on pervious concrete by statistical modelling. Constr. Build. Mater. 2013, 38, 147–154. [Google Scholar] [CrossRef]
- Cui, X.; Zhang, J.; Huang, D.; Liu, Z.; Hou, F.; Cui, S.; Zhang, L.; Wang, Z. Experimental study on the relationship between permeability and strength of pervious concrete. J. Mater. Civ. Eng. 2017, 29, 04017217. [Google Scholar] [CrossRef]
- Montes, F.; Haselbach, L. Measuring hydraulic conductivity in pervious concrete. Environ. Eng. Sci. 2006, 23, 960–969. [Google Scholar] [CrossRef]
- Bin, S.; Li, Z. Multi-scale modeling and trans-level simulation from material meso-damage to structural failure of reinforced concrete frame structures under seismic loading. J. Comput. Sci. 2016, 12, 38–50. [Google Scholar] [CrossRef]
- Zhao, H.; Geng, Q.; Liu, X. Influence of freeze-thaw cycles on mechanical properties of pervious concrete: From experimental studies to discrete element simulations. Constr. Build. Mater. 2023, 409, 133988. [Google Scholar] [CrossRef]
- Yılmaz, O.; Molinari, J.F. A mesoscale fracture model for concrete. Cem. Concr. Res. 2017, 97, 84–94. [Google Scholar] [CrossRef]
- Gidrão, G.M.S.; Carrazedo, R.; Bosse, R.M.; Silvestro, L.; Ribeiro, R.; de Souza, C.F.P. Numerical modeling of the dynamic elastic modulus of concrete. Materials 2023, 16, 3955. [Google Scholar] [CrossRef] [PubMed]
- Jin, L.; Fan, L.; Li, P.; Du, X. Size effect of axial-loaded concrete-filled steel tubular columns with different confinement coefficients. Eng. Struct. 2019, 198, 109503. [Google Scholar] [CrossRef]






| Materials | Size (mm) | Apparent Density (kg/m3) | Compacted Bulk Density (kg/m3) | Clay Content (%) | Needle and Flake Content (%) | Compacted Bulk Porosity (%) | Crush Value (%) |
|---|---|---|---|---|---|---|---|
| Granite | 5–10 | 2870 | 1550 | 0.4 | 2.2 | 46 | 6.4 |
| Steel lag | 5–10 | 3290 | 1870 | - | - | 43 | 6.3 |
| CaO | Fe2O3 | SiO2 | Al2O3 | MgO | MnO | P2O3 |
|---|---|---|---|---|---|---|
| 37.53 | 22.32 | 19.45 | 6.24 | 6.04 | 1.90 | 1.38 |
| Density (kg/m3) | Water Reduction (%) | Solid Content (%) | Alkali Content (%) | Chlorine Ion Content (%) | PH |
|---|---|---|---|---|---|
| 1049 | 32 | 23.64 | 0.45 | 0.02 | 6.0 |
| Concrete Type | No. | Target Porosity (%) | w/c | Cement (kg/m3) | Water (kg/m3) | Crushed Granite (kg/m3) | Additive (%) |
|---|---|---|---|---|---|---|---|
| PC | PC15_0.25 | 15 | 0.25 | 569 | 142 | 1522 | 0.9 |
| PC15_0.28 | 15 | 0.28 | 540 | 157 | 1522 | 0.9 | |
| PC15_0.30 | 15 | 0.30 | 522 | 169 | 1522 | 0.8 | |
| PC15_0.33 | 15 | 0.33 | 498 | 120 | 1522 | 0.5 | |
| PC15_0.35 | 15 | 0.35 | 483 | 132 | 1522 | 0 | |
| PC20_0.25 | 20 | 0.25 | 480 | 120 | 1522 | 0.9 | |
| PC20_0.28 | 20 | 0.28 | 456 | 128 | 1522 | 0.9 | |
| PC20_0.30 | 20 | 0.30 | 441 | 132 | 1522 | 0.8 | |
| PC20_0.33 | 20 | 0.33 | 420 | 139 | 1522 | 0.5 | |
| PC20_0.35 | 20 | 0.35 | 408 | 143 | 1522 | 0 | |
| PC25_0.25 | 25 | 0.25 | 391 | 98 | 1522 | 0.9 | |
| PC25_0.28 | 25 | 0.28 | 371 | 104 | 1522 | 0.9 | |
| PC25_0.30 | 25 | 0.30 | 359 | 107 | 1522 | 0.8 | |
| PC25_0.33 | 25 | 0.33 | 342 | 113 | 1522 | 0.5 | |
| PC25_0.35 | 25 | 0.35 | 332 | 116 | 1522 | 0 |
| Concrete Type | No. | Target Porosity (%) | SSA Replacement (%) | Steel Lag (kg/m3) | Crushed Granite (kg/m3) | Cement (kg/m3) | Water (kg/m3) |
|---|---|---|---|---|---|---|---|
| SSPC | SSPC15_0 | 15 | 0 | 0 | 1519 | 522.0 | 157 |
| SSPC15_25 | 15 | 25 | 458 | 1139 | 507.8 | 152 | |
| SSPC15_50 | 15 | 50 | 916 | 760 | 507.8 | 152 | |
| SSPC15_75 | 15 | 75 | 1375 | 380 | 507.8 | 152 | |
| SSPC15_100 | 15 | 100 | 1833 | 0 | 475.1 | 143 | |
| SSPC20_0 | 20 | 0 | 0 | 1519 | 441.0 | 132 | |
| SSPC20_25 | 20 | 25 | 458 | 1139 | 426.1 | 128 | |
| SSPC20_50 | 20 | 50 | 916 | 760 | 426.1 | 128 | |
| SSPC20_75 | 20 | 75 | 1375 | 380 | 426.1 | 128 | |
| SSPC20_100 | 20 | 100 | 1833 | 0 | 393.5 | 118 | |
| SSPC25_0 | 25 | 0 | 0 | 1519 | 359.0 | 107 | |
| SSPC25_25 | 25 | 25 | 458 | 1139 | 344.5 | 103 | |
| SSPC25_50 | 25 | 50 | 916 | 760 | 344.5 | 103 | |
| SSPC25_75 | 25 | 75 | 1375 | 380 | 344.5 | 103 | |
| SSPC25_100 | 25 | 100 | 1833 | 0 | 312.5 | 94 |
| Aggregate Type | Apparent Density (kg/m3) | Compacted Bulk Density (kg/m3) | Compact Packing Porosity (%) | Crush Value (%) |
|---|---|---|---|---|
| Crushed granite | 2870 | 1550 | 46 | 12.6 |
| Granite:SS (3:1) | 2890 | 1590 | 45 | 11.2 |
| Granite:SS (1:1) | 3110 | 1710 | 45 | 9.5 |
| Granite:SS (1:3) | 3220 | 1770 | 45 | 7.8 |
| Steel slag | 3290 | 1870 | 43 | 6.4 |
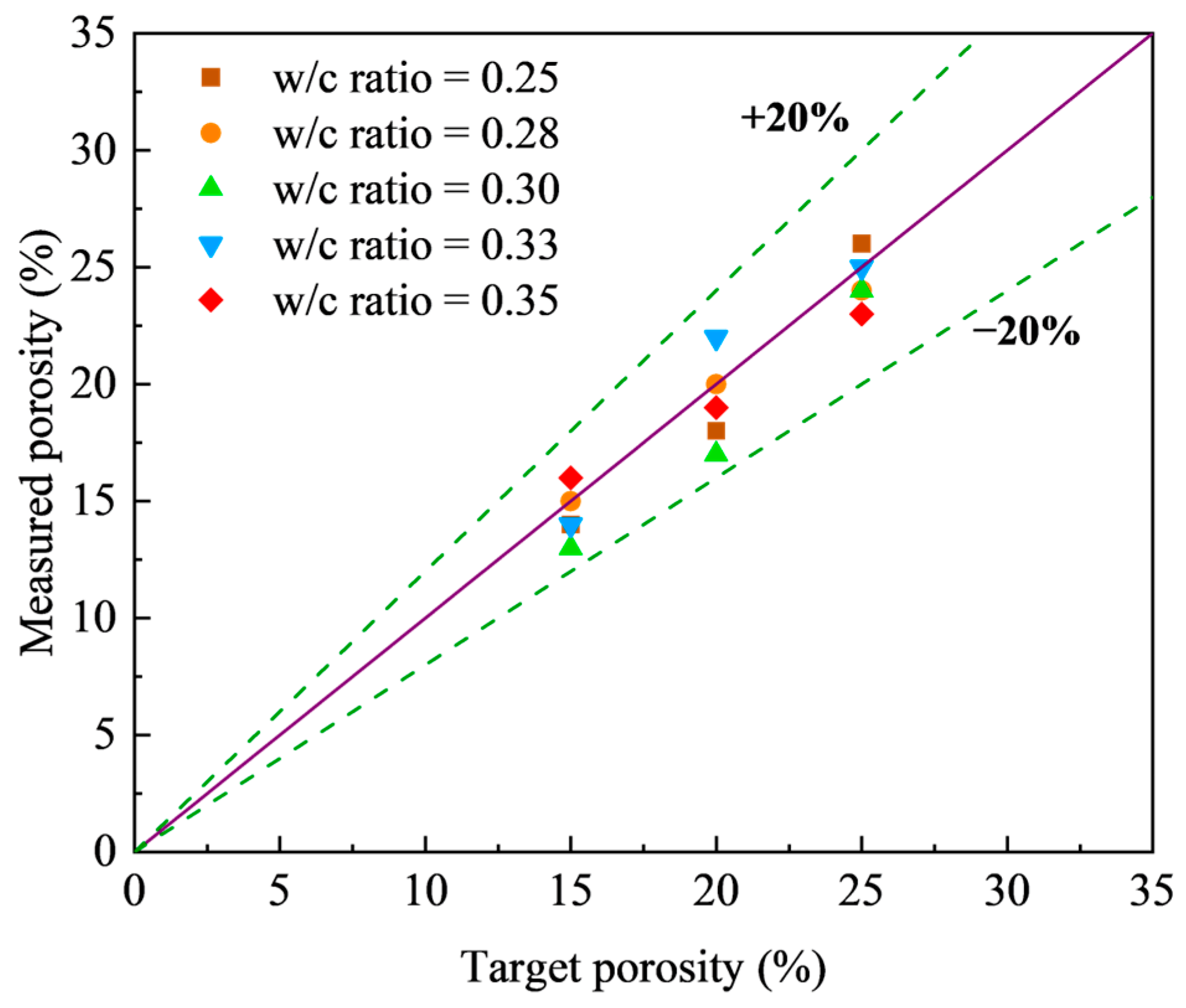
| Specimen No. | Target Porosity (%) | Measured Porosity (%) | w/c Ratio | Elastic Modulus (GPa) | Compressive Strength (MPa) | P-Wave Velocity (m/s) | Permeability Coefficient (cm/s) |
|---|---|---|---|---|---|---|---|
| PC15_0.25 | 15 | 14 | 0.25 | 24.2 | 24.6 | 4505 | 0.27 |
| PC15_0.28 | 15 | 15 | 0.28 | 25.0 | 26.2 | 4617 | 0.34 |
| PC15_0.30 | 15 | 13 | 0.30 | 25.7 | 27.8 | 4586 | 0.32 |
| PC15_0.33 | 15 | 14 | 0.33 | 24.6 | 25.4 | 4493 | 0.26 |
| PC15_0.35 | 15 | 16 | 0.35 | 24.0 | 24.2 | 4482 | 0.25 |
| PC20_0.25 | 20 | 18 | 0.25 | 19.8 | 16.5 | 4146 | 0.53 |
| PC20_0.28 | 20 | 20 | 0.28 | 20.5 | 17.7 | 4179 | 0.57 |
| PC20_0.30 | 20 | 17 | 0.30 | 22.1 | 20.6 | 4183 | 0.58 |
| PC20_0.33 | 20 | 22 | 0.33 | 20.1 | 16.9 | 4125 | 0.48 |
| PC20_0.35 | 20 | 19 | 0.35 | 19.0 | 15.2 | 4178 | 0.57 |
| PC25_0.25 | 25 | 26 | 0.25 | 16.5 | 11.5 | 3787 | 0.89 |
| PC25_0.28 | 25 | 24 | 0.28 | 17.7 | 13.2 | 3831 | 0.96 |
| PC25_0.30 | 25 | 24 | 0.30 | 19.3 | 15.6 | 3883 | 1.02 |
| PC25_0.33 | 25 | 25 | 0.33 | 17.4 | 12.7 | 3921 | 1.04 |
| PC25_0.35 | 25 | 23 | 0.35 | 14.9 | 9.5 | 3933 | 1.05 |
| Specimen No. | Target Porosity (%) | Measured Porosity (%) | SSA Replacement (%) | Compressive Strength (MPa) | Permeability Coefficient (cm/s) |
|---|---|---|---|---|---|
| SSPC15_0 | 15 | 15 | 0 | 20.6 | 0.39 |
| SSPC15_25 | 15 | 14 | 25 | 23.7 | 0.41 |
| SSPC15_50 | 15 | 14 | 50 | 25.4 | 0.41 |
| SSPC15_75 | 15 | 14 | 75 | 27.7 | 0.43 |
| SSPC15_100 | 15 | 16 | 100 | 28.4 | 0.39 |
| SSPC20_0 | 20 | 19 | 0 | 14.3 | 0.83 |
| SSPC20_25 | 20 | 21 | 25 | 15.9 | 0.79 |
| SSPC20_50 | 20 | 20 | 50 | 16.7 | 0.81 |
| SSPC20_75 | 20 | 19 | 75 | 17.4 | 0.79 |
| SSPC20_100 | 20 | 18 | 100 | 18.2 | 0.77 |
| SSPC25_0 | 25 | 25 | 0 | 9.6 | 1.16 |
| SSPC25_25 | 25 | 24 | 25 | 10.2 | 1.24 |
| SSPC25_50 | 25 | 26 | 50 | 10.7 | 1.17 |
| SSPC25_75 | 25 | 27 | 75 | 11.5 | 1.21 |
| SSPC25_100 | 25 | 24 | 100 | 11.9 | 1.20 |
| Particle Parameters | Linear Parallel Bonding Parameters (Aggregate) | Linear Parallel Bonding Parameters (Paste) | |||||
|---|---|---|---|---|---|---|---|
| Density (kg/m3) | Friction Factor | Parallel Bond Modulus (GPa) | Normal Bond Strength (MPa) | Shear Bond Strength (MPa) | Parallel Bond Modulus (GPa) | Normal Bond Strength (MPa) | Shear Bond Strength (MPa) |
| 2500 | 0.7 | 3.0 | 11.1 | 14.0 | 3.0 | 9.5 | 12.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Li, Z.; Liu, B.; Yu, Z.; Li, Z.; Zhu, M.; Wang, Y.; Ding, X. Experimental and Numerical Investigations on the Influences of Target Porosity and w/c Ratio on Strength and Permeability of Pervious Concrete. Materials 2025, 18, 3951. https://doi.org/10.3390/ma18173951
Liu F, Li Z, Liu B, Yu Z, Li Z, Zhu M, Wang Y, Ding X. Experimental and Numerical Investigations on the Influences of Target Porosity and w/c Ratio on Strength and Permeability of Pervious Concrete. Materials. 2025; 18(17):3951. https://doi.org/10.3390/ma18173951
Chicago/Turabian StyleLiu, Fei, Zhe Li, Bowen Liu, Zhuohui Yu, Zetong Li, Mengyuan Zhu, Yanjie Wang, and Xizhou Ding. 2025. "Experimental and Numerical Investigations on the Influences of Target Porosity and w/c Ratio on Strength and Permeability of Pervious Concrete" Materials 18, no. 17: 3951. https://doi.org/10.3390/ma18173951
APA StyleLiu, F., Li, Z., Liu, B., Yu, Z., Li, Z., Zhu, M., Wang, Y., & Ding, X. (2025). Experimental and Numerical Investigations on the Influences of Target Porosity and w/c Ratio on Strength and Permeability of Pervious Concrete. Materials, 18(17), 3951. https://doi.org/10.3390/ma18173951






