Experimental Investigation of Thermal Conductivity of Selected 3D-Printed Materials
Abstract
1. Introduction
2. 3D-Printing Technological Parameters and Sample Specification
3. Measurement Methodology
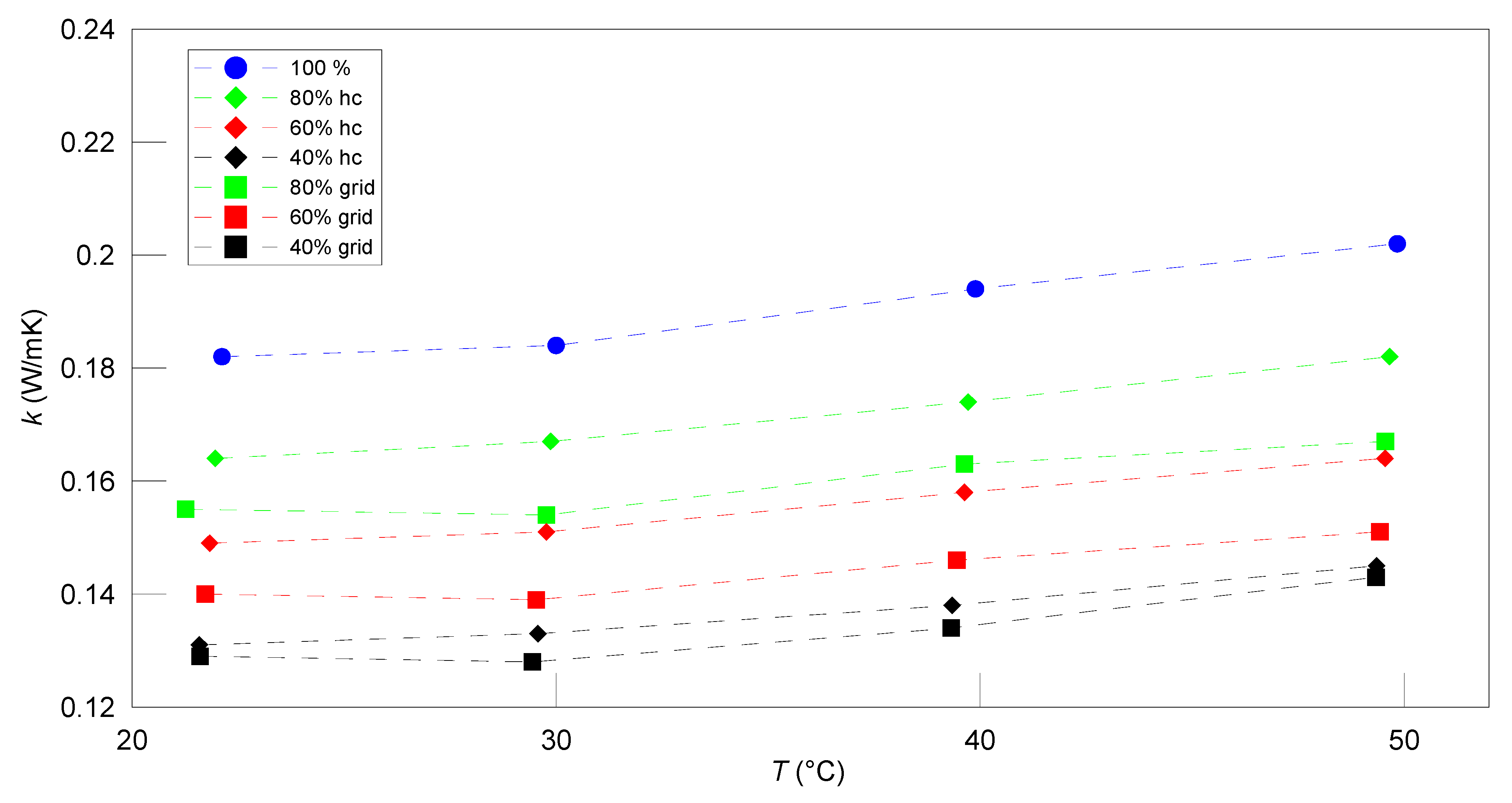
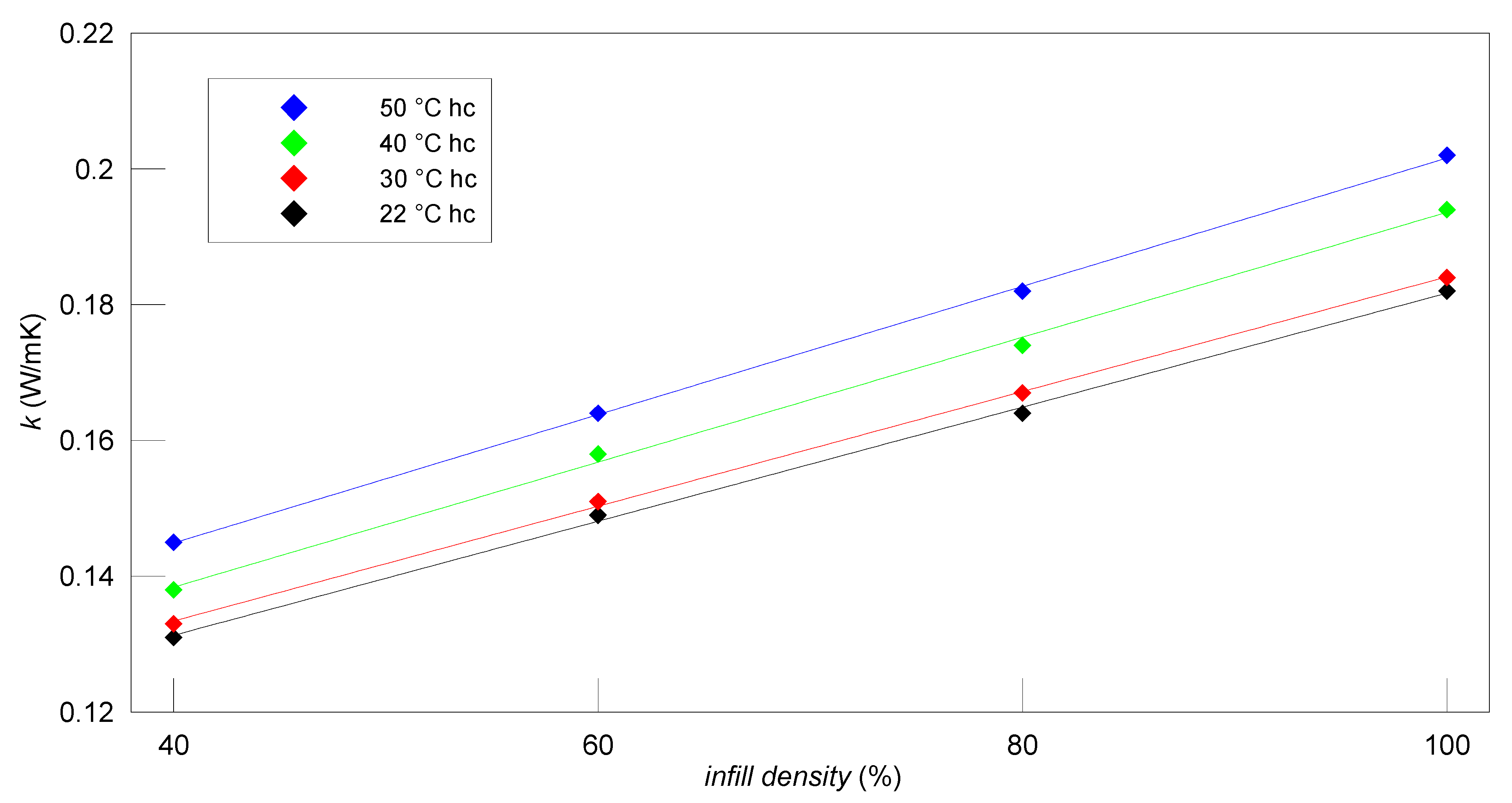
4. Results
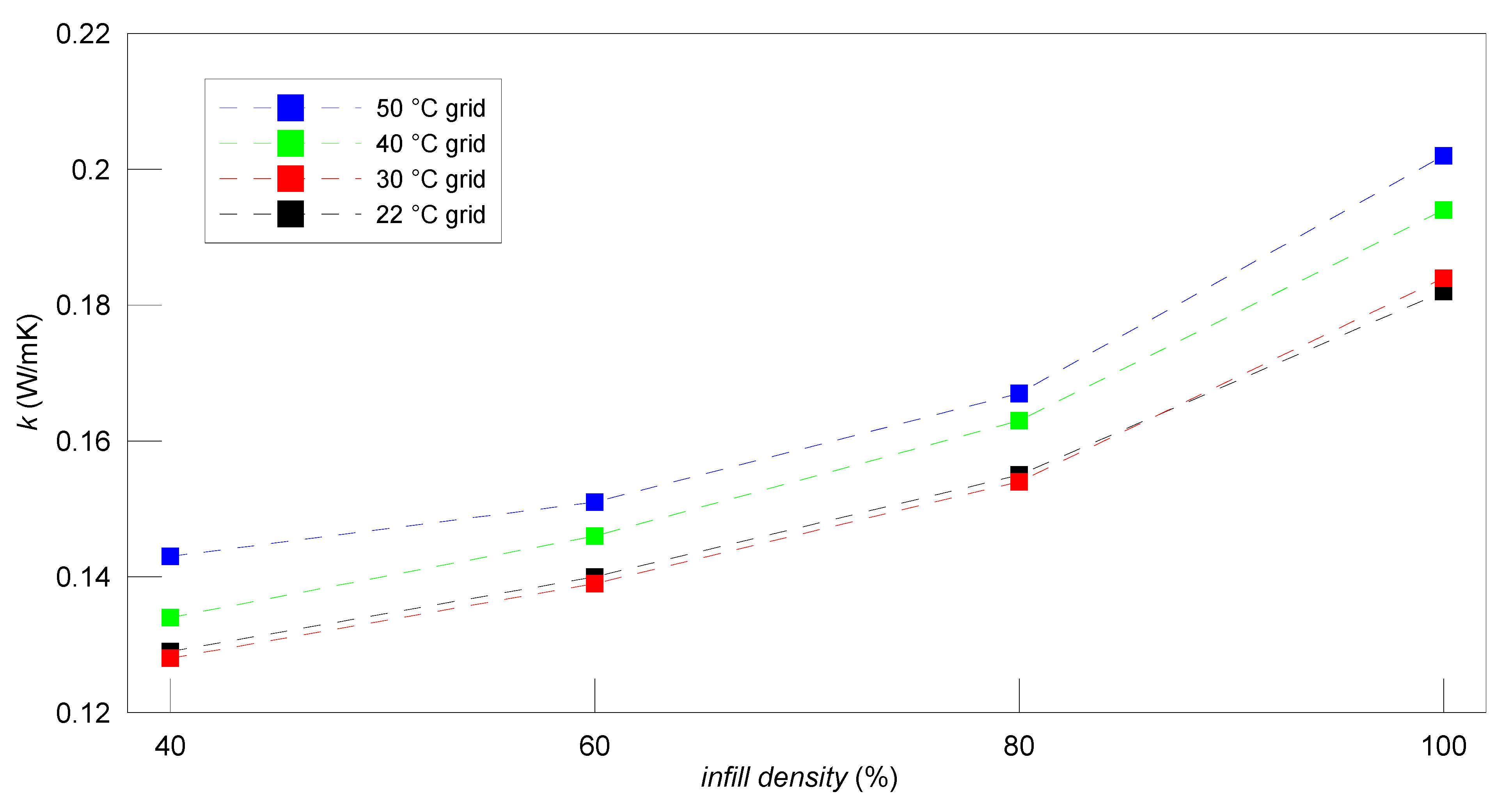
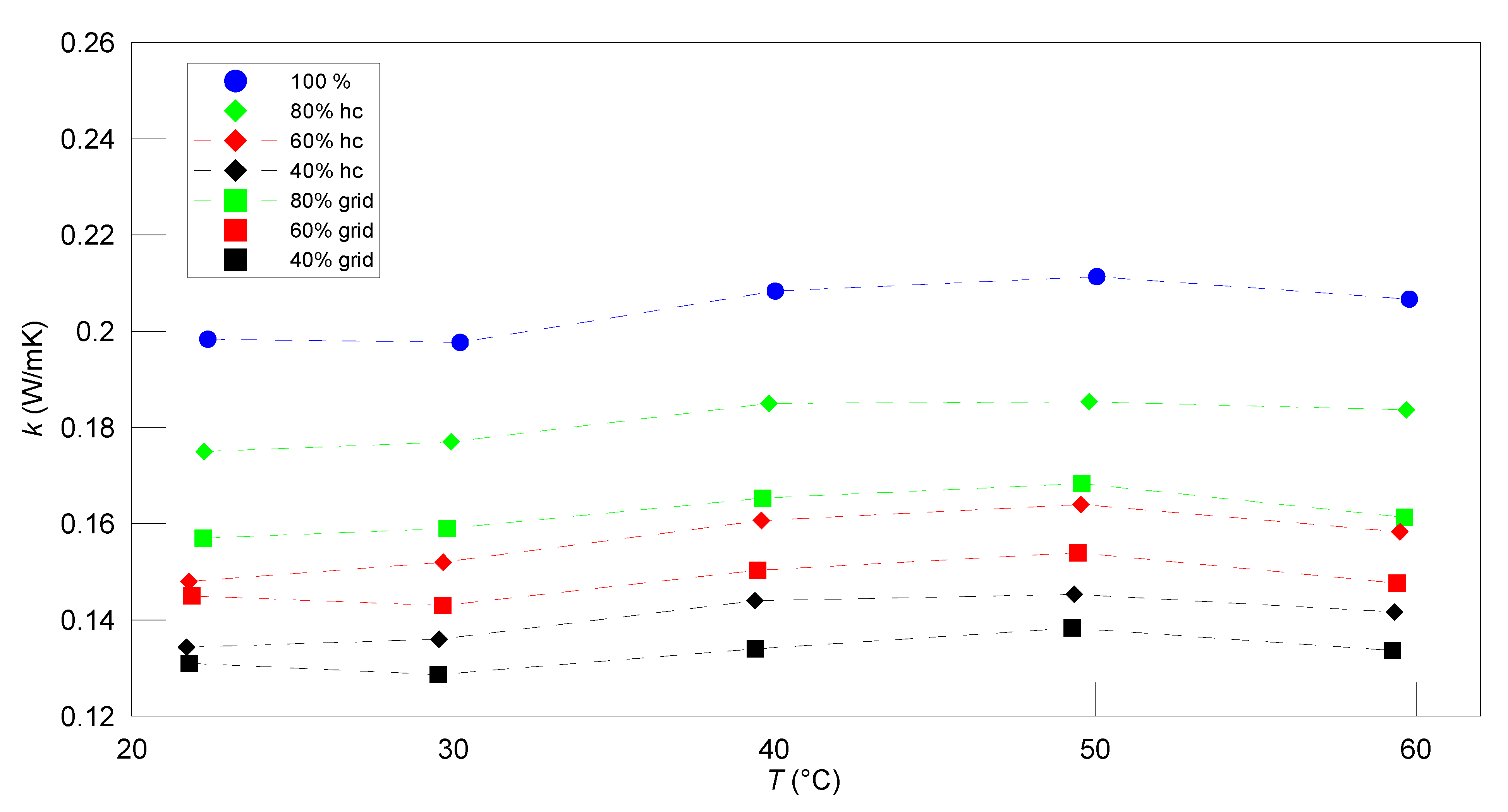
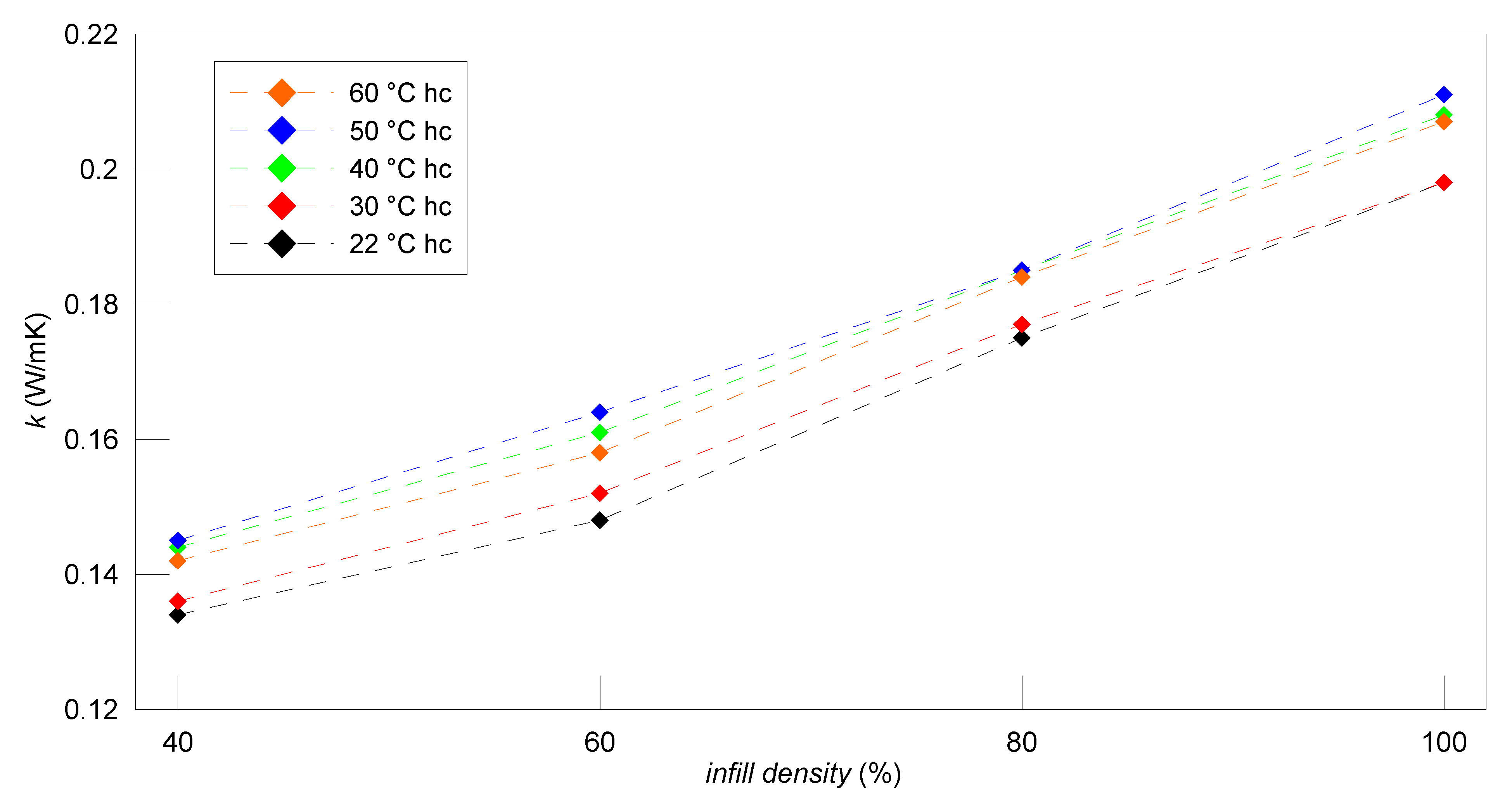
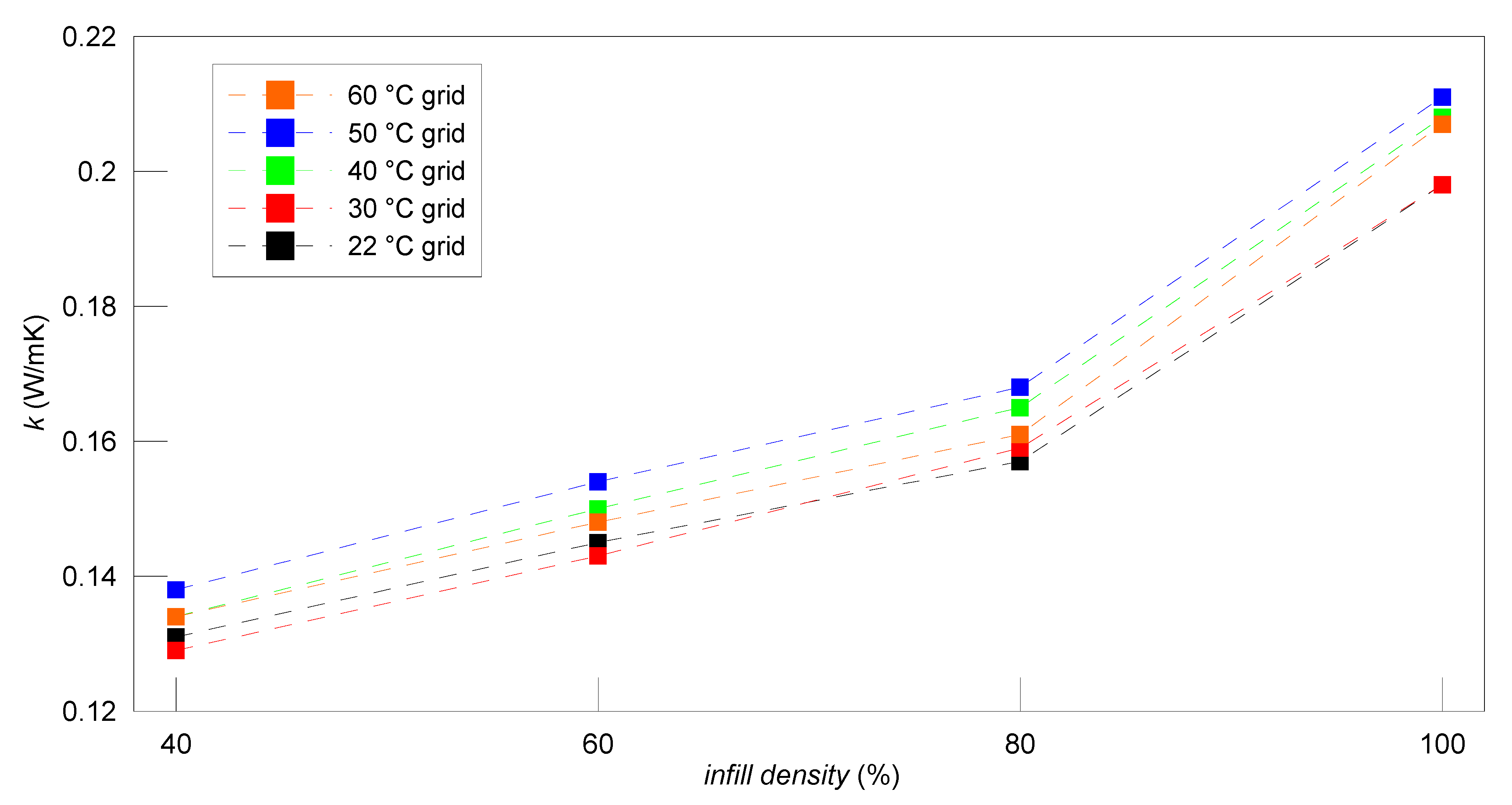
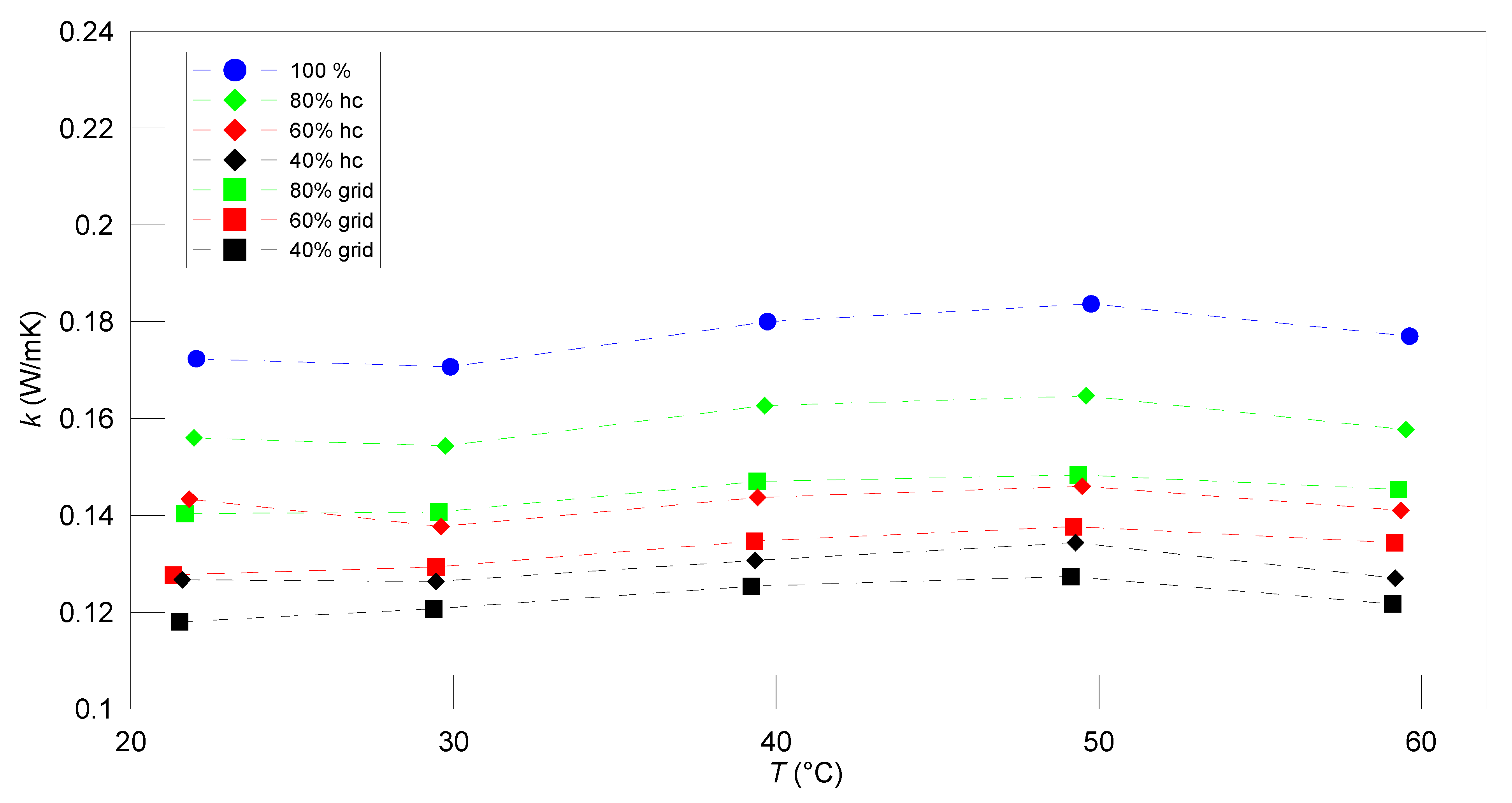
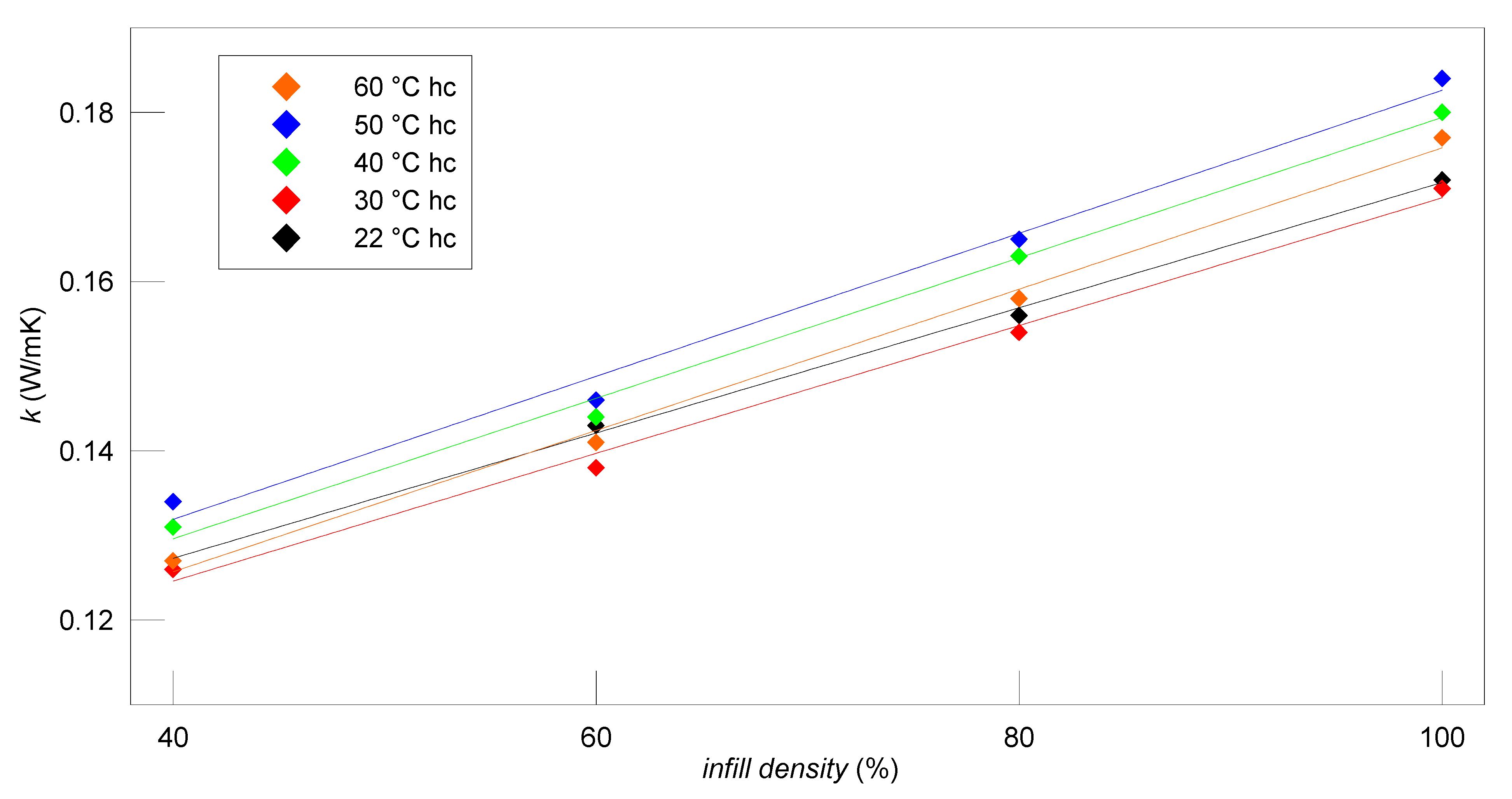
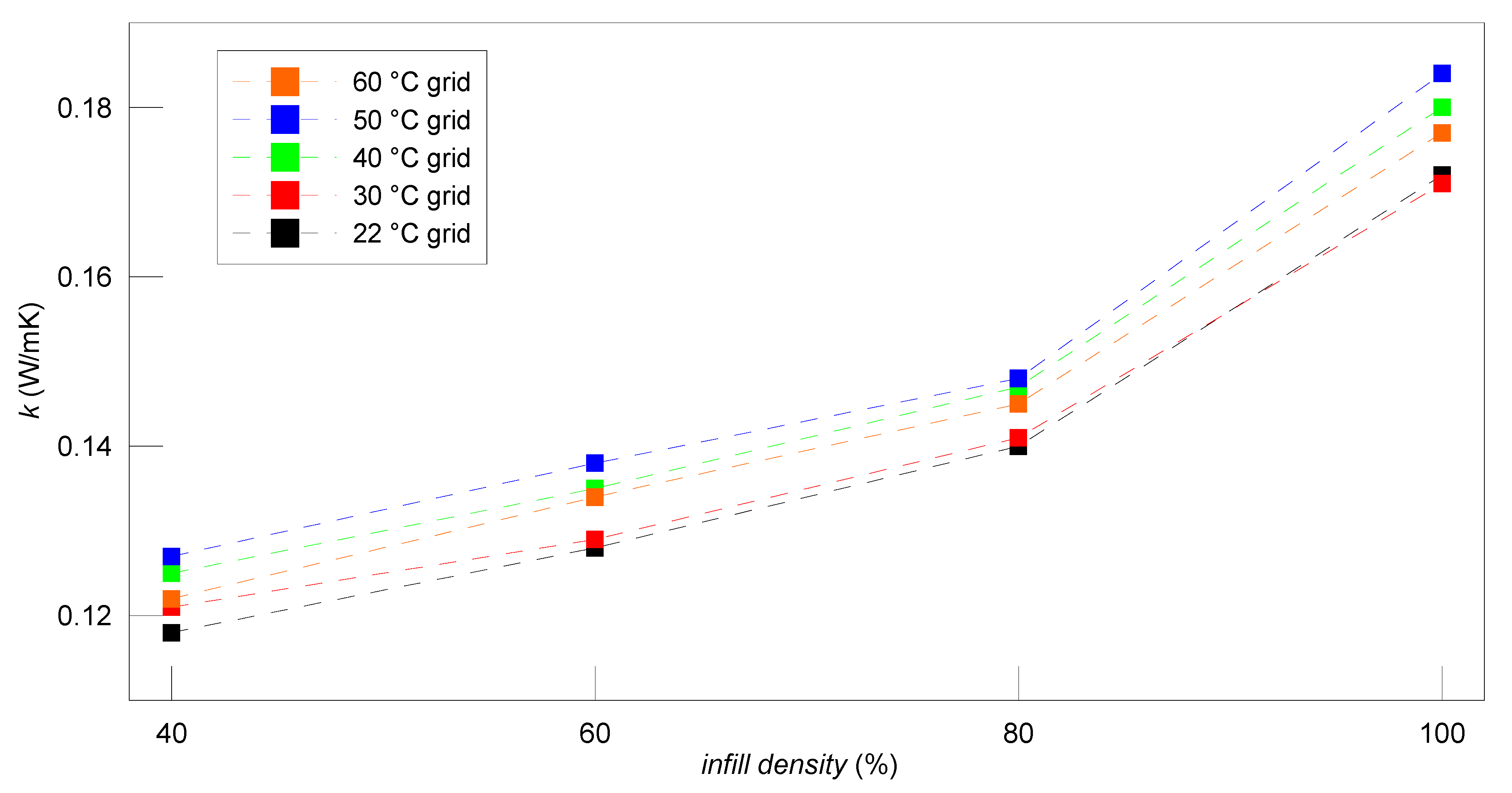
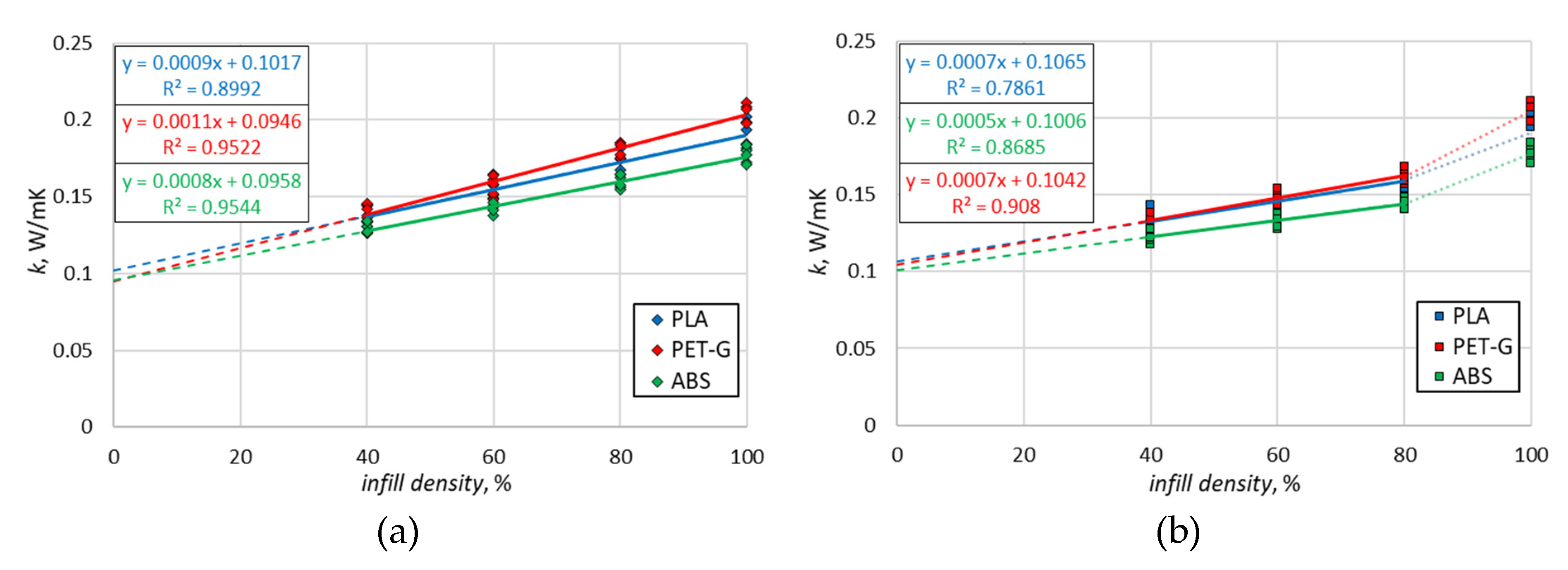
4.1. PLA Material
4.2. PET-G Material
4.3. ABS Material
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bute, I.; Tarasovs, S.; Vidinejevs, S.; Vevere, L.; Sevcenko, J.; Aniskevich, A. Thermal properties of 3D printed products from the most common polymers. Int. J. Adv. Manuf. Technol. 2023, 124, 2739–2753. [Google Scholar] [CrossRef]
- Parandoush, P.; Lin, D. A review on additive manufacturing of polymer-fiber composites. Compos. Struct. 2017, 182, 36–53. [Google Scholar] [CrossRef]
- Wong, K.V.; Hernandez, A. A review of additive manufacturing. Int. Sch. Res. Not. 2012, 2012, 208760. [Google Scholar] [CrossRef]
- Tychanicz-Kwiecien, M.; Smusz, R.; Gil, P. Performance of thermal insulation fabricated by rapid prototyping technology. Therm. Sci. 2019, 23 (Suppl. S4), 1079–1090. [Google Scholar] [CrossRef]
- Sonsalla, T.; Moore, A.L.; Meng, W.; Radadia, A.D.; Weiss, L. 3D printer settings effects on the thermal conductivity of acrylonitrile butadiene styrene (ABS). Polym. Test. 2018, 70, 389–395. [Google Scholar] [CrossRef]
- Hamzah, K.A.; Yeoh, C.K.; Noor, M.M.; Teh, P.L.; Sazali, S.A.; Aw, Y.Y.; Ibrahim, W.M.A.W. Effect of the Printing Orientation on the Mechanical Properties and Thermal and Electrical Conductivity of ABS-ZnFe2O4 Composites. J. Mater. Eng. Perform. 2019, 28, 5860–5868. [Google Scholar] [CrossRef]
- Kam, M.; İpekçi, A.; Saruhan, H. Investigation of 3D printing filling structures effect on mechanical properties and surface roughness of PET-G material products. Gaziosmanpaşa Bilimsel Araştırma Derg. 2017, 6, 114–121. [Google Scholar]
- Markowicz, M.; Gałek, R.; Gil, P.; Wilk, J.; Korzeniowski, M. Alternative experimental method in investigations of thermal diffusivity of 3D printing material. Exp. Therm. Fluid Sci. 2025, 168, 111512. [Google Scholar] [CrossRef]
- Bahar, A.; Belhabib, S.; Guessasma, S.; Benmahiddine, F.; Hamami, A.E.A.; Belarbi, R. Mechanical and thermal properties of 3D printed polycarbonate. Energies 2022, 15, 3686. [Google Scholar] [CrossRef]
- Rodriguez, A.; Fuertes, J.P.; Oval, A.; Perez-Artieda, G. Experimental measurement of the thermal conductivity of fused deposition modeling materials with a DTC-25 conductivity meter. Materials 2023, 16, 7384. [Google Scholar] [CrossRef] [PubMed]
- Flaata, T.; Michna, G.J.; Letcher, T. Thermal conductivity testing apparatus for 3D printed materials. In Proceedings of the Heat Transfer Summer Conference, Bellevue, WA, USA, 9–12 July 2017; American Society of Mechanical Engineers: New York, NY, USA, 2017; Volume 57892, p. V002T15A006. [Google Scholar]
- Roudný, P.; Syrový, T. Thermal conductive composites for FDM 3D printing: A review, opportunities and obstacles, future directions. J. Manuf. Process. 2022, 83, 667–677. [Google Scholar] [CrossRef]
- Trhlíková, L.; Zmeskal, O.; Psencik, P.; Florian, P. Study of the thermal properties of filaments for 3D printing. AIP Conf. Proc. 2016, 1752, 040027. [Google Scholar] [CrossRef]
- Olcun, S.; Ibrahim, Y.; Isaacs, C.; Karam, M.; Elkholy, A.; Kempers, R. Thermal conductivity of 3D-printed continuous pitch carbon fiber composites. Addit. Manuf. Lett. 2023, 4, 100106. [Google Scholar] [CrossRef]
- Ebrahimi, N.D.; Ju, Y.S. Thermal conductivity of sintered copper samples prepared using 3D printing-compatible polymer composite filaments. Addit. Manuf. 2018, 24, 479–485. [Google Scholar] [CrossRef]
- Tsekmes, I.A.; Kochetov, R.; Morshuis, P.H.F.; Smit, J.J. Thermal conductivity of polymeric composites: A review. In Proceedings of the 2013 IEEE International Conference on Solid Dielectrics (ICSD), Bologna, Italy, 30 June–4 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 678–681. [Google Scholar]
- Laureto, J.; Tomasi, J.; King, J.A.; Pearce, J.M. Thermal properties of 3D printed polylactic acid-metal composites. Prog. Addit. Manuf. 2017, 2, 57–71. [Google Scholar] [CrossRef]
- Ibrahim, Y.; Kempers, R. Effective thermal conductivity of 3D-printed continuous wire pol-ymer composites. Prog. Addit. Manuf. 2022, 7, 699–712. [Google Scholar] [CrossRef]
- Blanco, I.; Cicala, G.; Recca, G.; Tosto, C. Specific heat capacity and thermal conductivity measurements of PLA-based 3D-printed parts with milled carbon fiber reinforcement. Entropy 2022, 24, 654. [Google Scholar] [CrossRef]
- Ibrahim, Y.; Elkholy, A.; Schofield, J.S.; Melenka, G.W.; Kempers, R. Effective thermal conductivity of 3D-printed continuous fiber polymer composites. Adv. Manuf. Polym. Compos. Sci. 2020, 6, 17–28. [Google Scholar] [CrossRef]
- Parmaksiz, F.; Anaç, N.; Koçar, O.; Erdogan, B. Investigation of mechanical properties and thermal conductivity coefficients of 3D printer materials. Int. Adv. Res. Eng. J. 2023, 7, 146–156. [Google Scholar] [CrossRef]
- Shemelya, C.; De La Rosa, A.; Torrado, A.R.; Yu, K.; Domanowski, J.; Bonacuse, P.J.; Martin, R.E.; Juhasz, M.; Hurwitz, F.; Wicker, R.B.; et al. Anisotropy of thermal conductivity in 3D printed polymer matrix composites for space based cube satellites. Addit. Manuf. 2017, 16, 186–196. [Google Scholar] [CrossRef]
- ASTM E1530; Standard Test Method for Evaluating the Resistance to Thermal Transmission of Materials by the Guarded Heat Flow Meter Technique. ASTM International: Conshohocken, PA, USA.
- Guide to the Expression of Uncertainty in Measurement; ISO: Geneva, Switzerland, 1995.
- Dupaix, R.B.; Boyce, M.C. Finite strain behavior of poly(ethylene terephthalate) (PET) and poly(ethylene terephthalate)-glycol (PETG). Polymer 2005, 46, 4827–4838. [Google Scholar] [CrossRef]
- Slavković, V.; Hanželič, B.; Plesec, V.; Milenković, S.; Harih, G. Thermo-mechanical behavior and strain rate sensitivity of 3D-printed polylactic acid (PLA) below glass transition temperature (Tg). Polymers 2024, 16, 1526. [Google Scholar] [CrossRef] [PubMed]
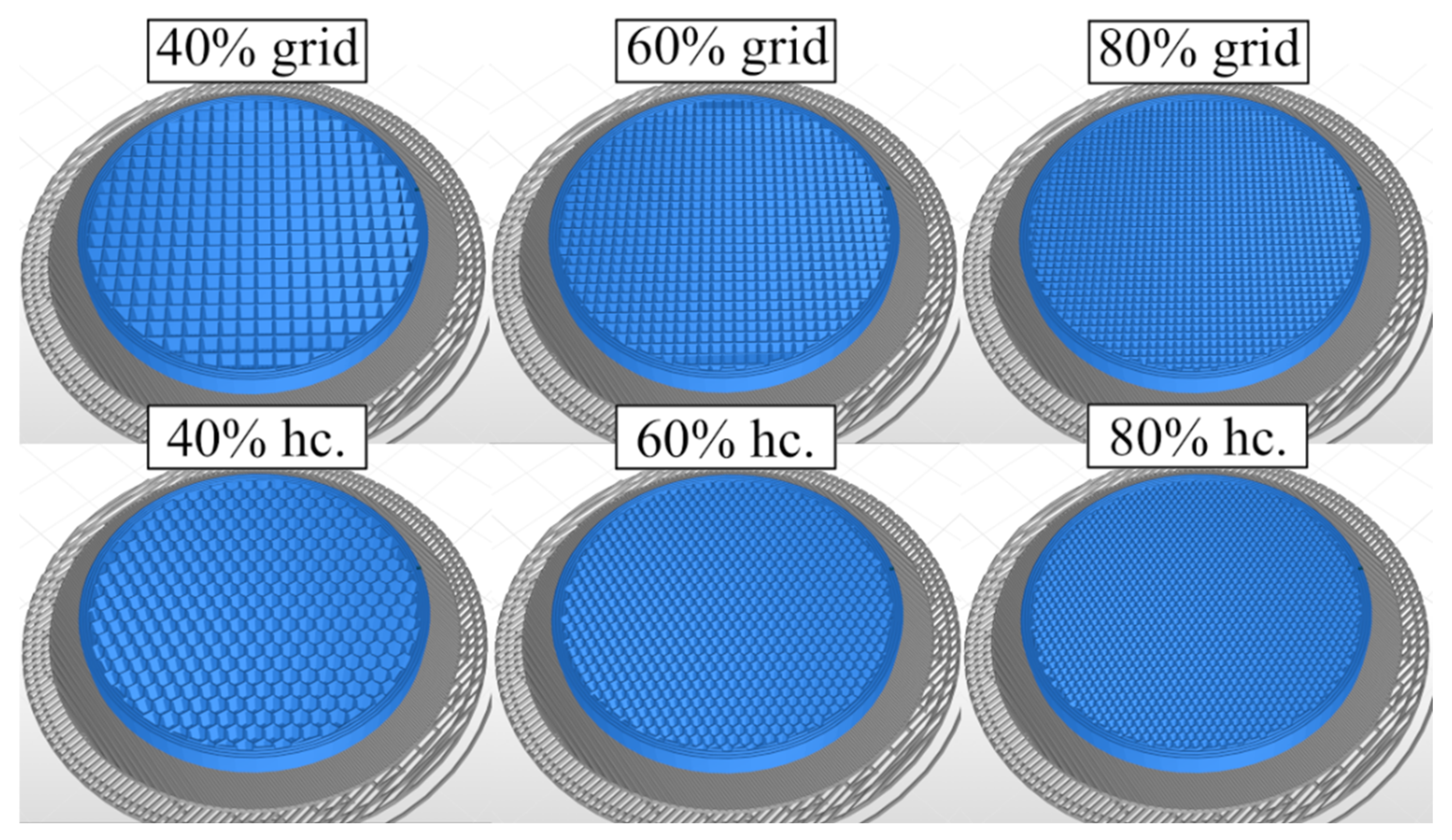



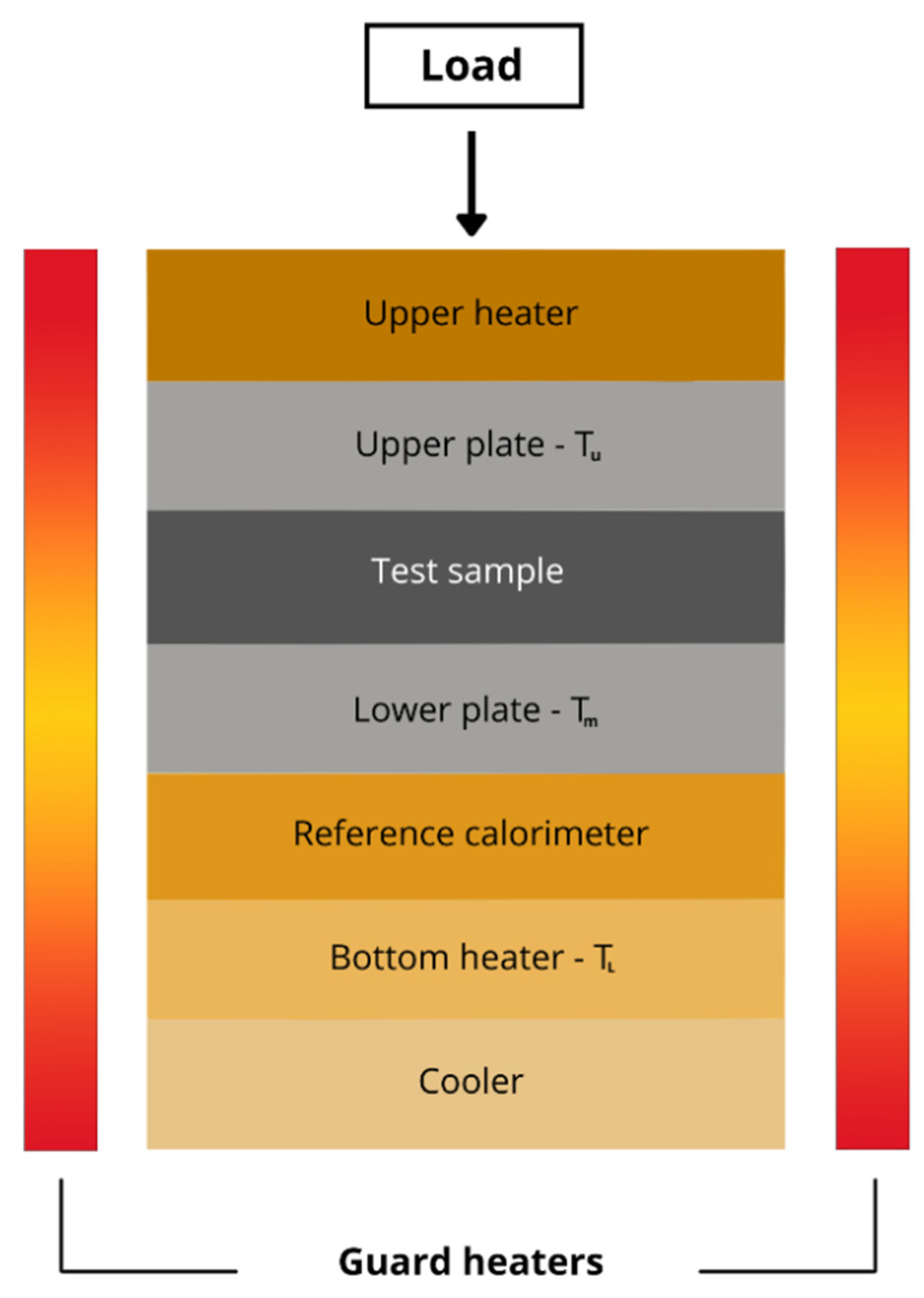
| Material | Temperature Set on Guard Heaters [°C] | Infill Pattern | Infill Density [%] |
|---|---|---|---|
| PLA PET-G * ABS * | 20 30 40 50 60 * | Honeycomb (hc.) | 40 |
| 60 | |||
| 80 | |||
| Grid | 40 | ||
| 60 | |||
| 80 | |||
| --- | 100 |
| PLA | ||||||
|---|---|---|---|---|---|---|
| 40% grid | 60% grid | 80% grid | ||||
| T ℃ | k W/mK | T ℃ | k W/mK | T ℃ | k W/mK | |
| 1. | 21.60 ± 0.25 | 0.129 ± 0.004 | 21.73 ± 0.27 | 0.140 ± 0.006 | 21.27 ± 0.66 | 0.155 ± 0.005 |
| 2. | 29.44 ± 0.26 | 0.128 ± 0.004 | 29,53 ± 0.26 | 0.139 ± 0.005 | 29.77 ± 0.25 | 0.154 ± 0.005 |
| 3. | 39.32 ± 0.25 | 0134 ± 0.005 | 39.45 ± 0.26 | 0.146 ± 0.005 | 39.63 ± 0.25 | 0.163 ± 0.005 |
| 4. | 49.34 ± 0.26 | 0.143 ± 0.004 | 49.43 ± 0.25 | 0.151 ± 0.005 | 49.56 ± 0.26 | 0.167 ± 0.005 |
| 40% hc. | 60% hc. | 80% hc. | ||||
| T ℃ | k W/mK | T ℃ | k W/mK | T ℃ | k W/mK | |
| 1. | 21.59 ± 0.26 | 0.131 ± 0.005 | 21.83 ± 0.25 | 0.149 ± 0.005 | 21.96 ± 0.25 | 0.164 ± 0.006 |
| 2. | 29.57 ± 0.25 | 0.133 ± 0.004 | 29.77 ± 0.25 | 0.151 ± 0.005 | 29.87 ± 0.25 | 0.167 ± 0.005 |
| 3. | 39.34 ± 0.25 | 0.138 ± 0.004 | 39.63 ± 0.25 | 0.158 ± 0.005 | 39.72 ± 0.25 | 0.174 ± 0.005 |
| 4. | 49.35 ± 0.25 | 0.145 ± 0.005 | 49.55 ± 0.25 | 0.164 ± 0.005 | 49.66 ± 0.25 | 0.182 ± 0.005 |
| PET G | ||||||
|---|---|---|---|---|---|---|
| 40% grid | 60% grid | 80% grid | ||||
| T ℃ | k W/mK | T ℃ | k W/mK | T ℃ | k W/mK | |
| 1. | 21.79 ± 0.28 | 0.131 ± 0.004 | 21.87 ± 0.25 | 0.145 ± 0.005 | 22.22 ± 0.27 | 0.157 ± 0.005 |
| 2. | 29.54 ± 0.26 | 0.129 ± 0.004 | 29.68 ± 0.25 | 0.143 ± 0.005 | 29.82 ± 0.25 | 0.159 ± 0.005 |
| 3. | 39.41 ± 0.25 | 0.134 ± 0.004 | 39.49 ± 0.26 | 0.150 ± 0.005 | 39.64 ± 0.25 | 0.165 ± 0.005 |
| 4. | 49.28 ± 0.25 | 0.138 ± 0.004 | 49.47 ± 0.25 | 0.154 ± 0.005 | 49.59 ± 0.25 | 0.168 ± 0.005 |
| 5. | 59.25 ± 0.25 | 0.134 ± 0.004 | 59.40 ± 0.25 | 0.148 ± 0.004 | 59.63 ± 0.26 | 0.161 ± 0.005 |
| 40% hc. | 60% hc. | 80% hc. | ||||
| T ℃ | k W/mK | T ℃ | k W/mK | T ℃ | k W/mK | |
| 1. | 21.70 ± 0.27 | 0.134 ± 0.004 | 21.77 ± 0.25 | 0.148 ± 0.005 | 22.25 ± 0.25 | 0.175 ± 0.005 |
| 2. | 29.56 ± 0.25 | 0.136 ± 0.004 | 29.70 ± 0.25 | 0.152 ± 0.005 | 29.95 ± 0.25 | 0.177 ± 0.005 |
| 3. | 39.40 ± 0.25 | 0.144 ± 0.004 | 39.61 ± 0.25 | 0.161 ± 0.005 | 39.85 ± 0.25 | 0.185 ± 0.006 |
| 4. | 49.35 ± 0.25 | 0.145 ± 0.005 | 49.56 ± 0.25 | 0.164 ± 0.005 | 49.82 ± 0.25 | 0.185 ± 0.006 |
| 5. | 59.32 ± 0.25 | 0.142 ± 0.004 | 59.49 ± 0.25 | 0.158 ± 0.005 | 59.70 ± 0.25 | 0.184 ± 0.006 |
| ABS | ||||||
|---|---|---|---|---|---|---|
| 40% grid | 60% grid | 80% grid | ||||
| T ℃ | k W/mK | T ℃ | k W/mK | T ℃ | k W/mK | |
| 1. | 21.51 ± 0.27 | 0.118 ± 0.004 | 21.32 ± 0.28 | 0.128 ± 0.004 | 21.69 ± 0.25 | 0.140 ± 0.004 |
| 2. | 29.38 ± 0.25 | 0.121 ± 0.004 | 29.45 ± 0.25 | 0.129 ± 0.004 | 29.55 ± 0.25 | 0.141 ± 0.004 |
| 3. | 39.22 ± 0.25 | 0.125 ± 0.004 | 39.32 ± 0,25 | 0.135 ± 0.004 | 39.41 ± 0.25 | 0.147 ± 0.005 |
| 4. | 49.13 ± 0.25 | 0.127 ± 0.004 | 49.22 ± 0.25 | 0.138 ± 0.004 | 49.36 ± 0.25 | 0.148 ± 0.005 |
| 5. | 59.10 ± 0.25 | 0.122 ± 0.004 | 59.17 ± 0.25 | 0.134 ± 0.004 | 59.29 ± 0.25 | 0.145 ± 0.004 |
| 40% hc. | 60% hc. | 80% hc. | ||||
| T ℃ | k W/mK | T ℃ | k W/mK | T ℃ | k W/mK | |
| 1. | 21.60 ± 0.25 | 0.127 ± 0.004 | 21.81 ± 0.25 | 0.143 ± 0.005 | 21.96 ± 0.26 | 0.156 ± 0.006 |
| 2. | 29.45 ± 0.25 | 0.126 ± 0.004 | 29.62 ± 0.25 | 0.138 ± 0.004 | 29.75 ± 0.25 | 0.154 ± 0.005 |
| 3. | 39.35 ± 0.25 | 0.131 ± 0.004 | 39.43 ± 0.25 | 0.144 ± 0.004 | 39.64 ± 0.25 | 0.163 ± 0.005 |
| 4. | 49.28 ± 0.25 | 0.134 ± 0.004 | 49.49 ± 0.26 | 0.146 ± 0.005 | 49.60 ± 0.25 | 0.165 ± 0.005 |
| 5. | 59.19 ± 0.25 | 0.127 ± 0.004 | 59.36 ± 0.25 | 0.141 ± 0.004 | 59.52 ± 0.26 | 0.158 ± 0.005 |
| PLA 100% | PET G 100% | ABS 100% | ||||
|---|---|---|---|---|---|---|
| T ℃ | k W/mK | T ℃ | k W/mK | T ℃ | k W/mK | |
| 1. | 22.12 ± 0.25 | 0.182 ± 0.006 | 22.36 ± 0.25 | 0.198 ± 0.006 | 22.03 ± 0.26 | 0.172 ± 0.006 |
| 2. | 30.00 ± 0.25 | 0.184 ± 0.006 | 30.22 ± 0.25 | 0.198 ± 0.006 | 29.90 ± 0.25 | 0.171 ± 0.005 |
| 3. | 39.89 ± 0.25 | 0.194 ± 0.006 | 40.04 ± 0.25 | 0.208 ± 0.006 | 39.73 ± 0.25 | 0.180 ± 0.005 |
| 4. | 49.84 ± 0.26 | 0.202 ± 0.006 | 50.05 ± 0.25 | 0.211 ± 0.006 | 49.76 ± 0.26 | 0.184 ± 0.006 |
| 5. | --- | --- | 59.78 ± 0.31 | 0.207 ± 0.006 | 59.63 ± 0.26 | 0.177 ± 0.005 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tychanicz-Kwiecień, M.; Grosicki, S.; Markowicz, M. Experimental Investigation of Thermal Conductivity of Selected 3D-Printed Materials. Materials 2025, 18, 3950. https://doi.org/10.3390/ma18173950
Tychanicz-Kwiecień M, Grosicki S, Markowicz M. Experimental Investigation of Thermal Conductivity of Selected 3D-Printed Materials. Materials. 2025; 18(17):3950. https://doi.org/10.3390/ma18173950
Chicago/Turabian StyleTychanicz-Kwiecień, Maria, Sebastian Grosicki, and Marek Markowicz. 2025. "Experimental Investigation of Thermal Conductivity of Selected 3D-Printed Materials" Materials 18, no. 17: 3950. https://doi.org/10.3390/ma18173950
APA StyleTychanicz-Kwiecień, M., Grosicki, S., & Markowicz, M. (2025). Experimental Investigation of Thermal Conductivity of Selected 3D-Printed Materials. Materials, 18(17), 3950. https://doi.org/10.3390/ma18173950






