Molecular Dynamics Simulation Study on the Cooling Behavior and Mechanical Properties of Silicone Carbide/Aluminum Composites
Highlights
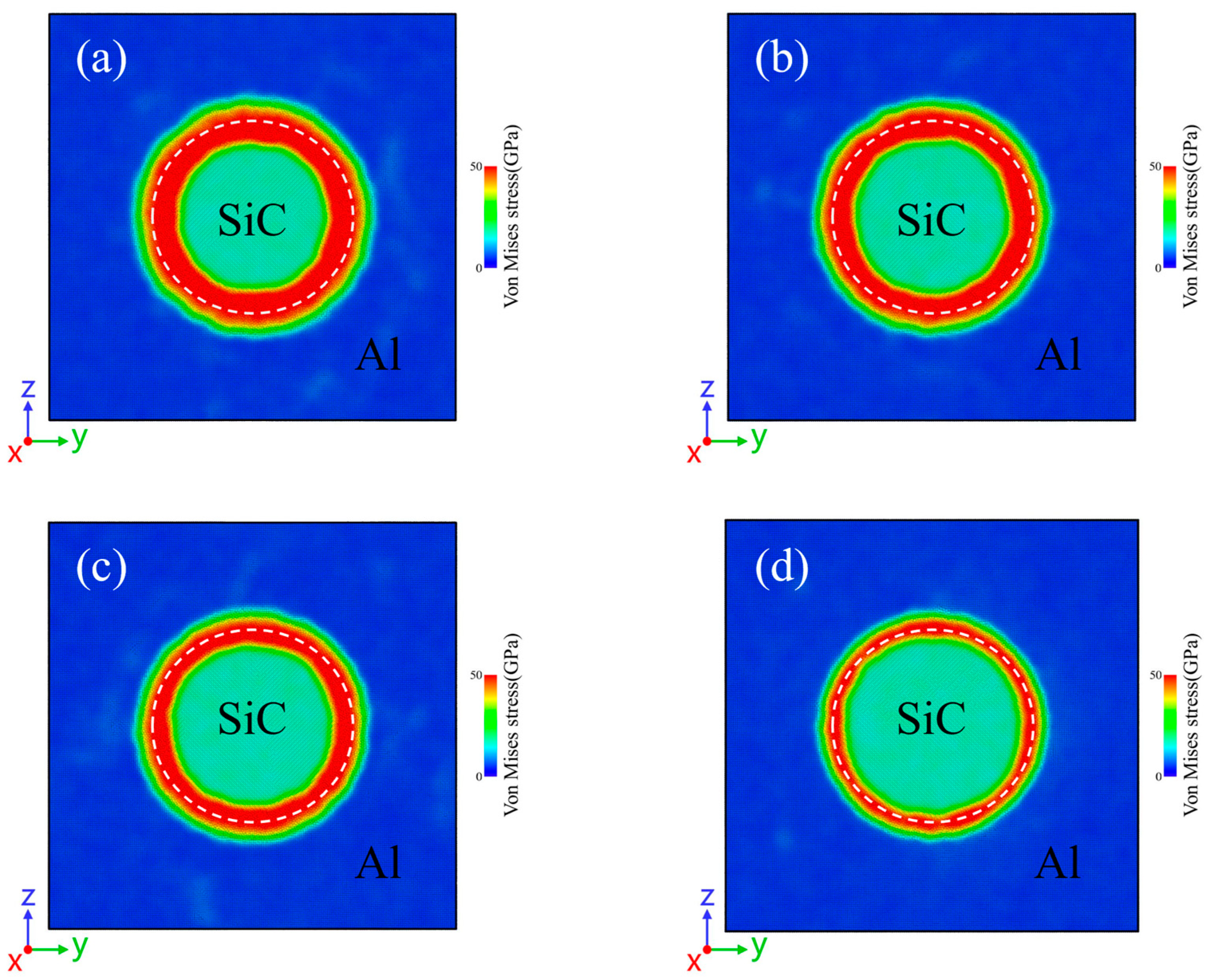
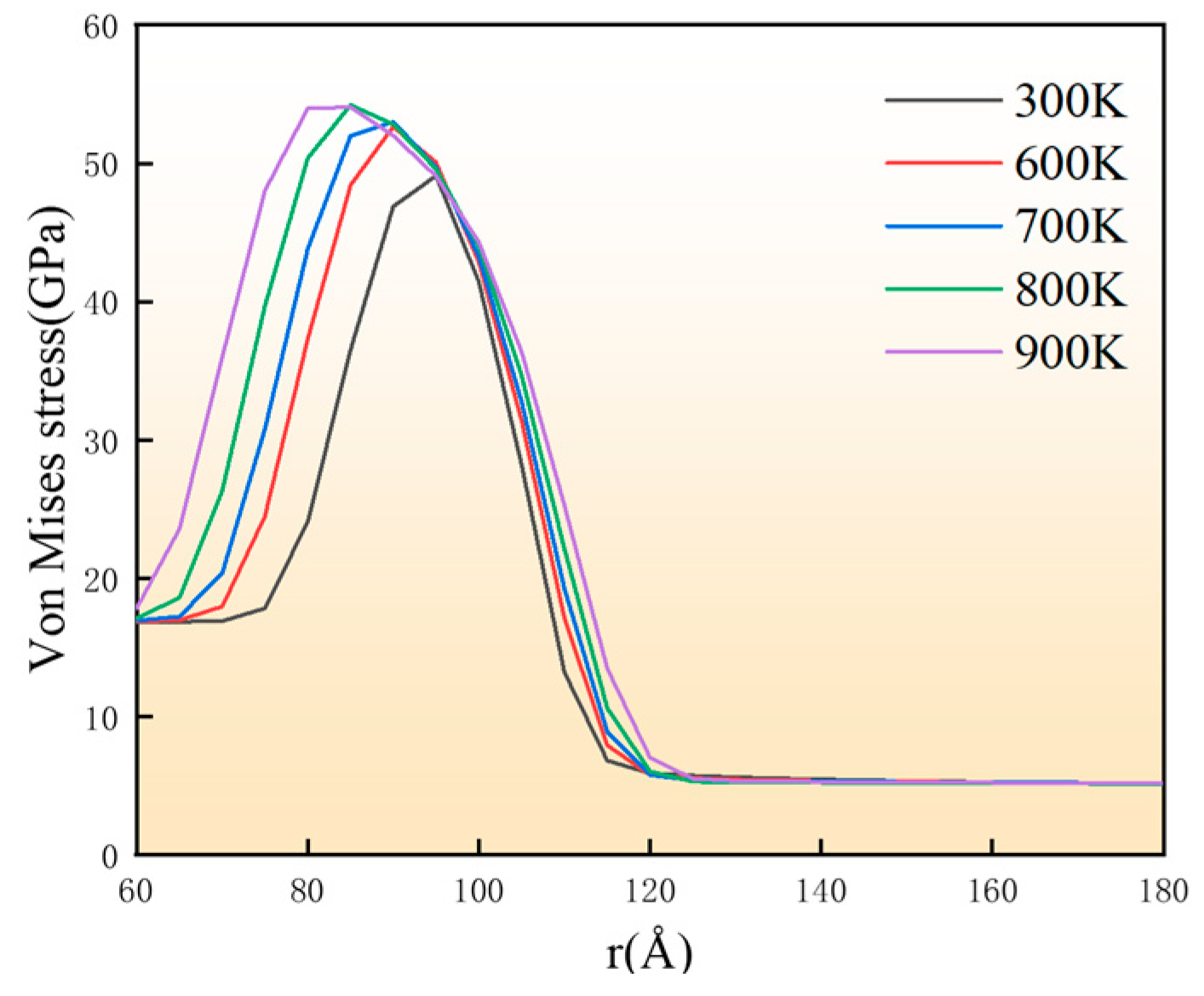
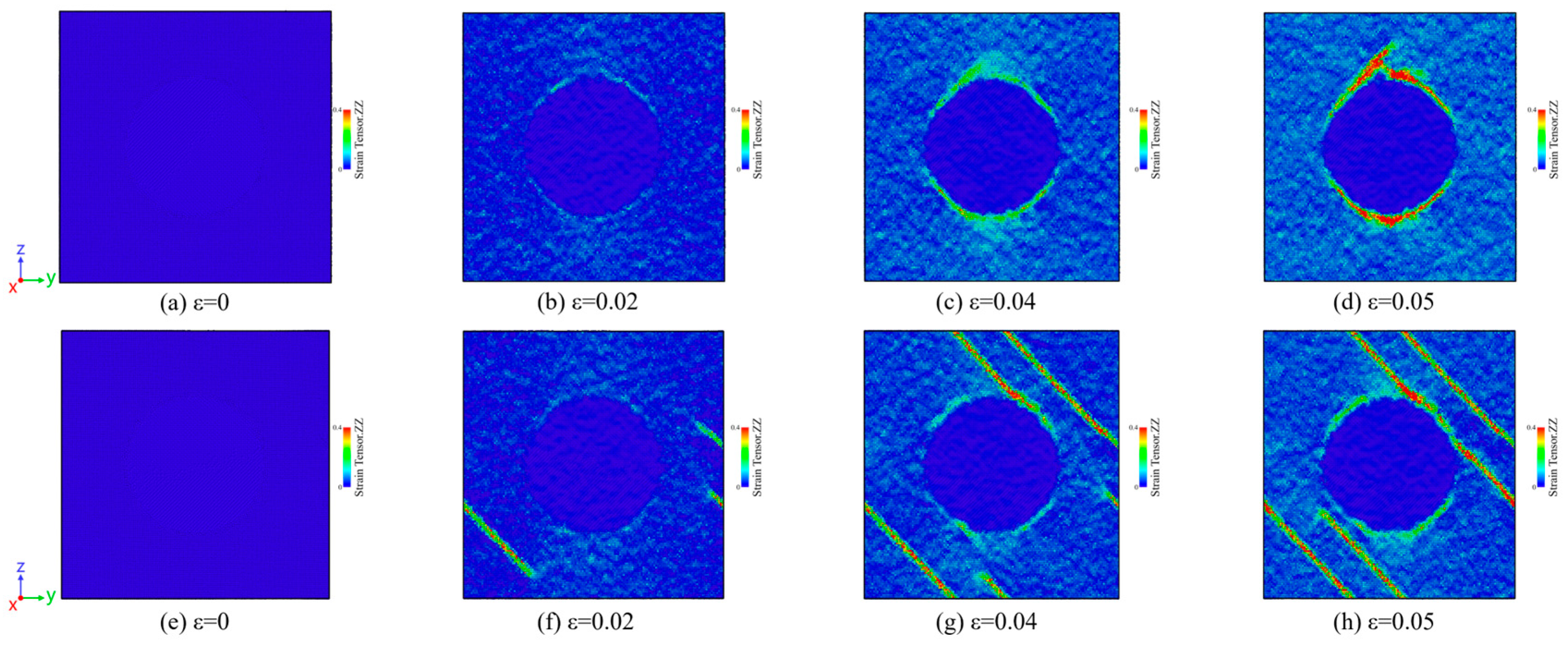
- Residual stresses are mainly distributed in the interface of SiC/Al composites after cooling, and the higher the initial temperature of cooling is, the higher the value of residual stresses.
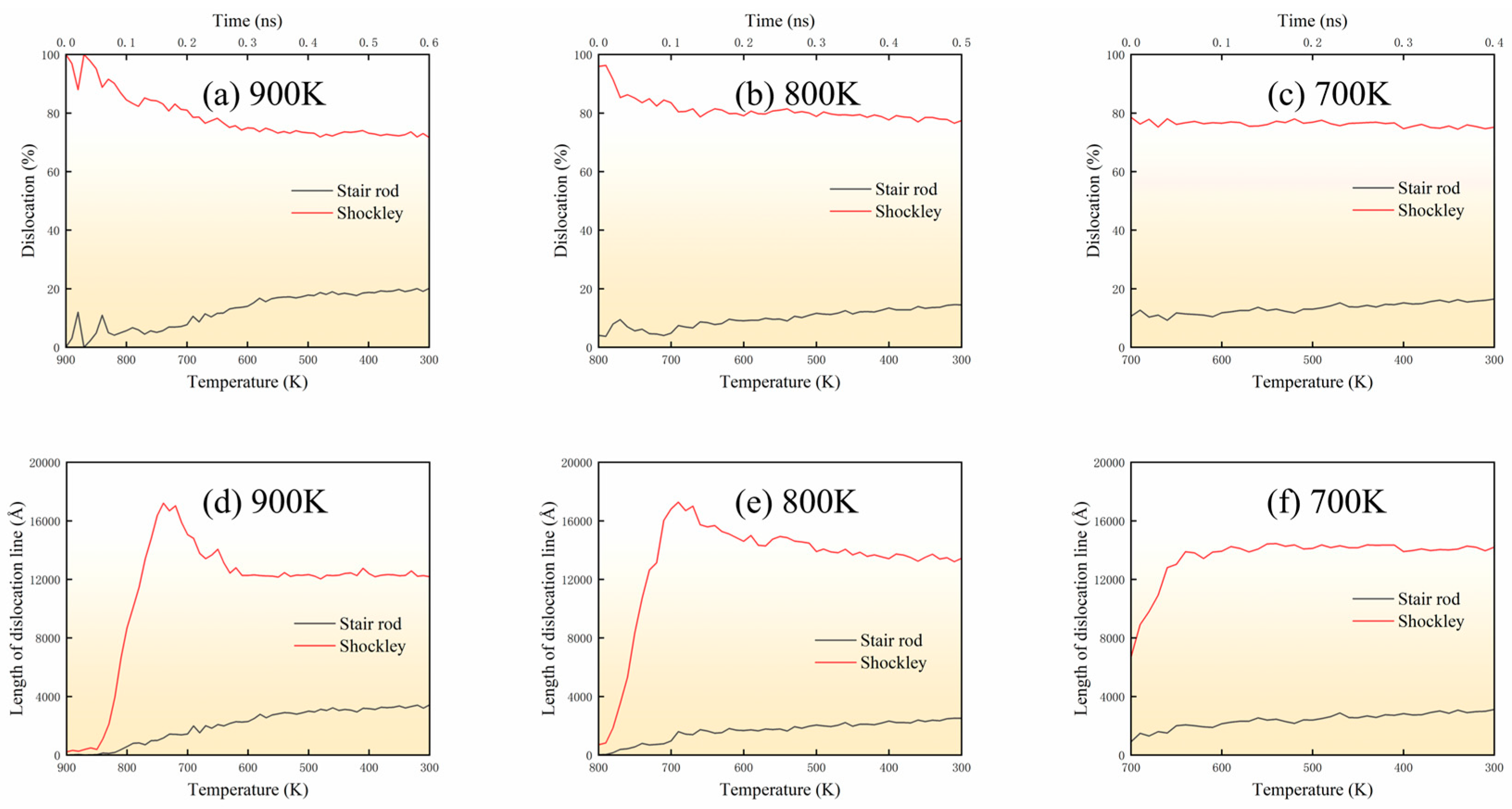
- Shockley partials and stair-rod dislocations were the two dominant dislocation types.
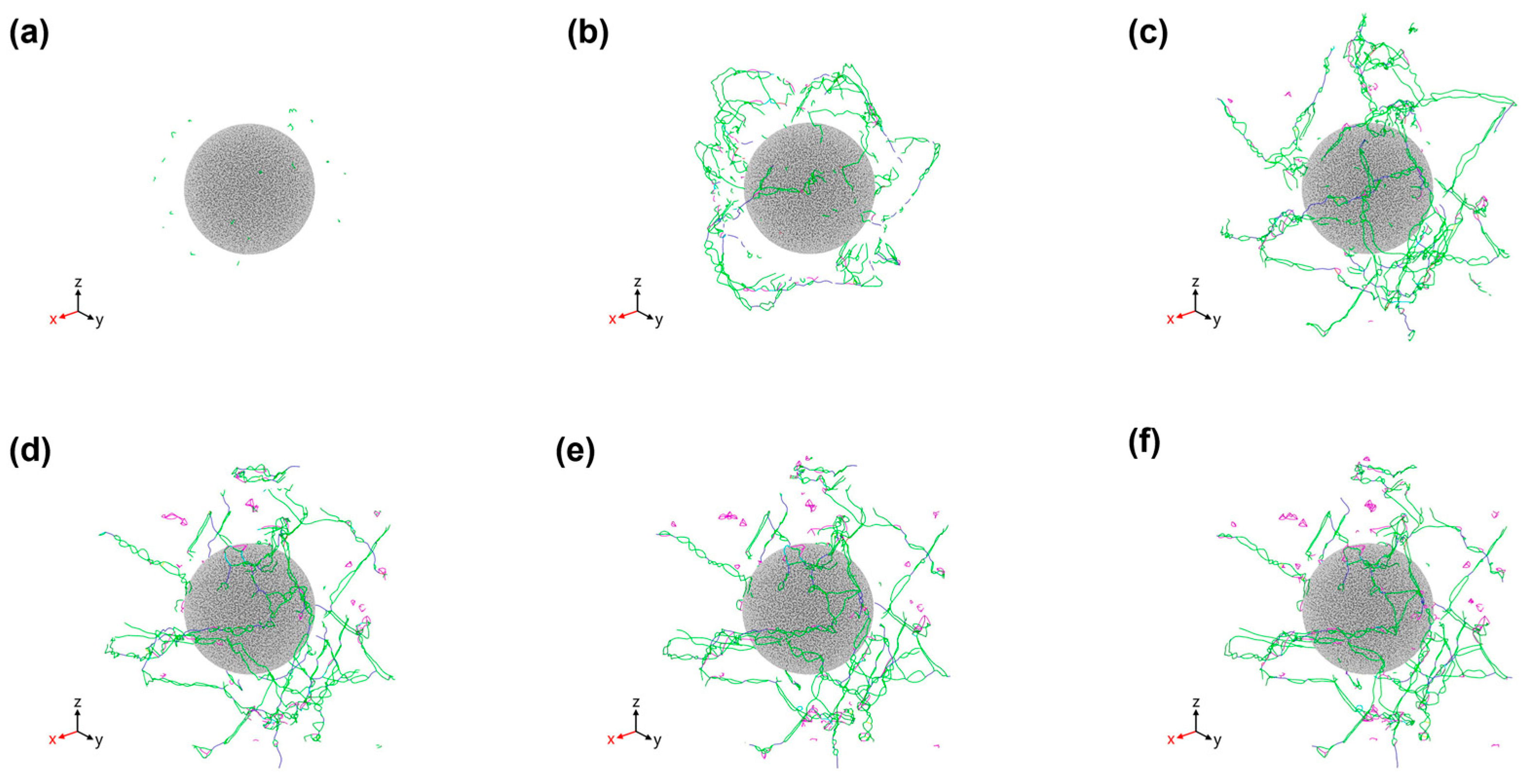
- Dislocations were first generated near the interface and gradually extended to the boundary region of the Al matrix.
- The higher the initial cooling temperature, the more significant the reduction in the tensile mechanical properties of the material.
Abstract
1. Introduction
2. Computational Models and Methods
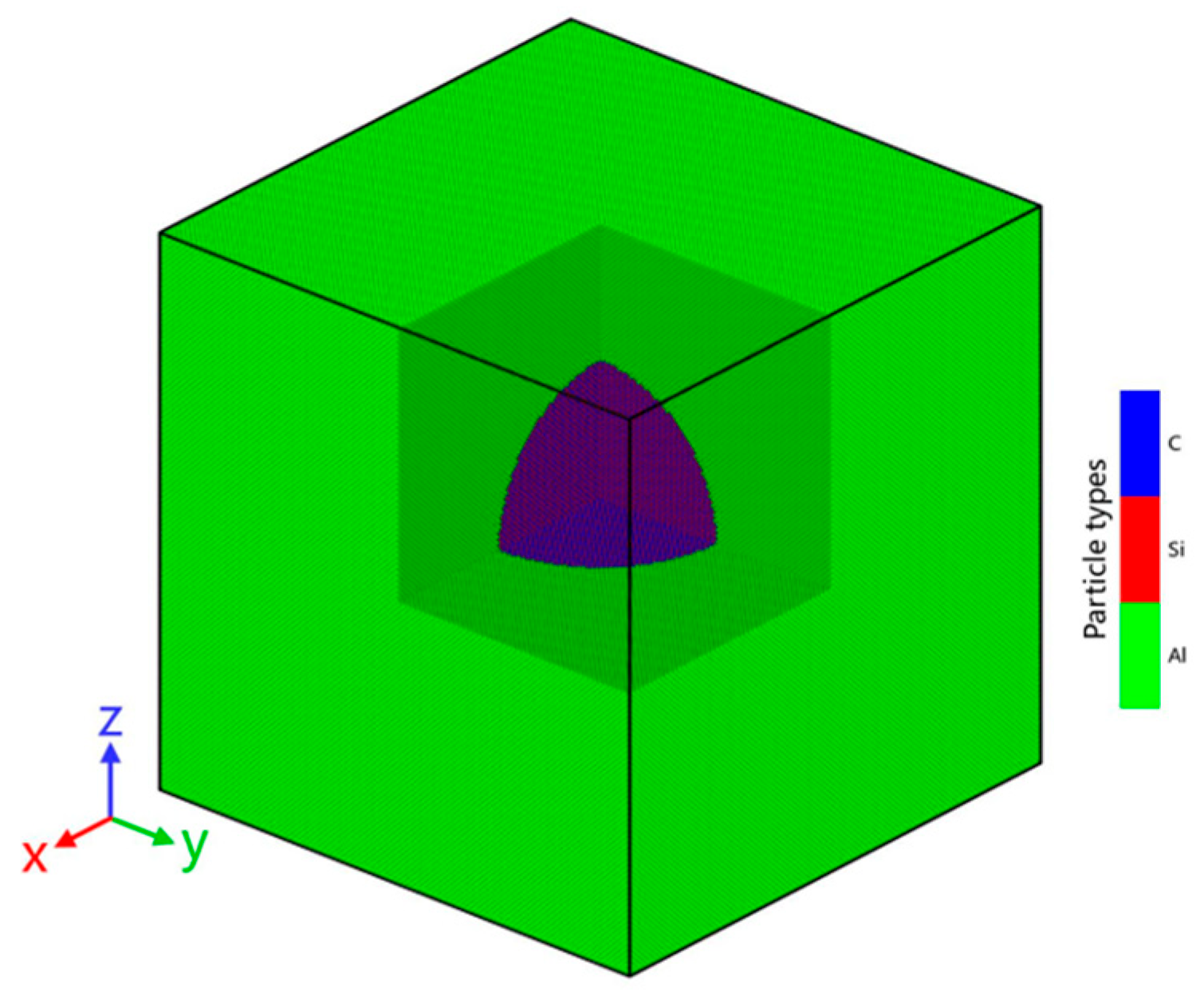
2.1. Simulation Details
2.2. Interatomic Potentials
3. Results and Discussion
3.1. Residual Stresses Distribution
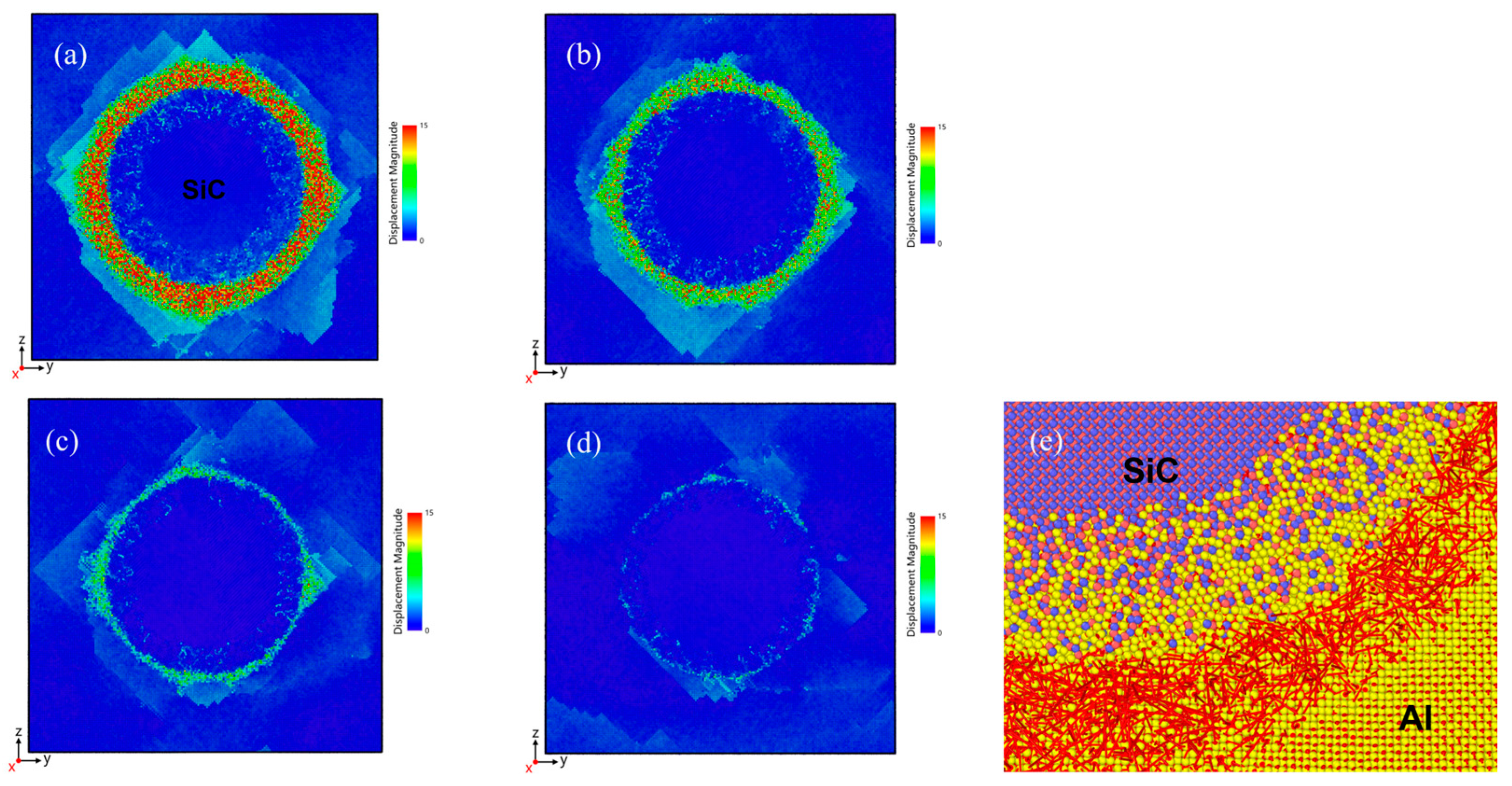
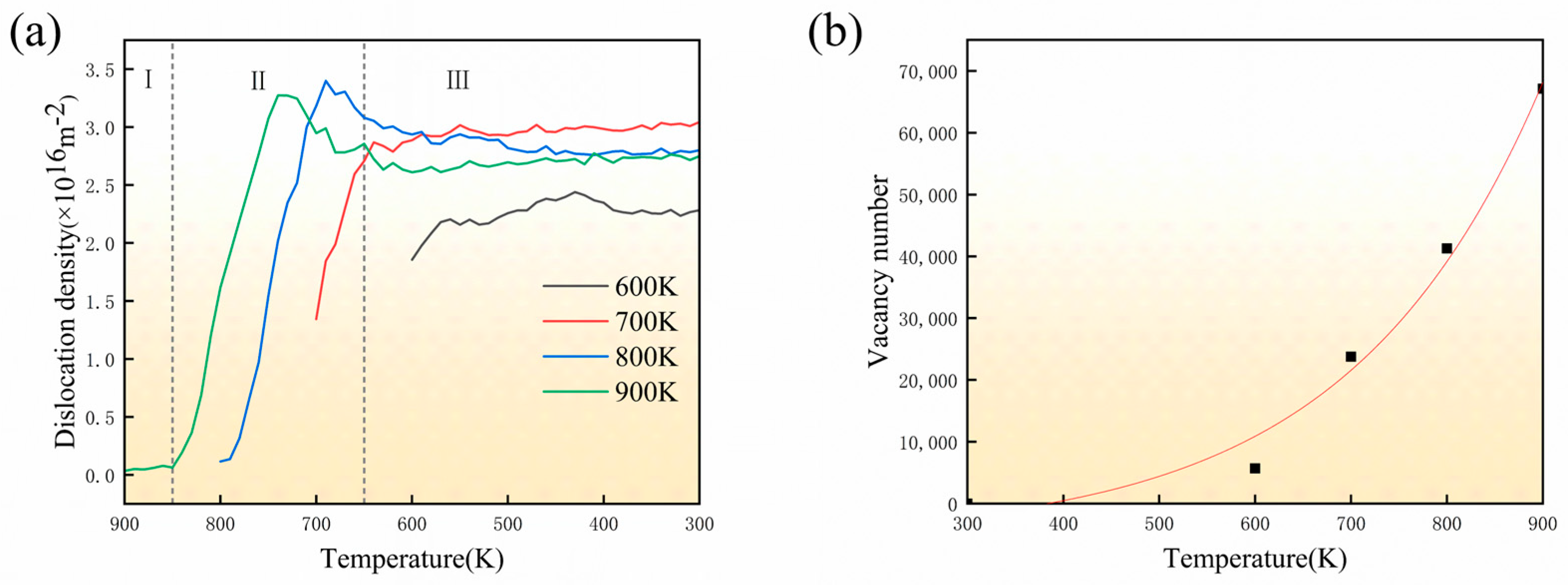
3.2. Evolution of Dislocation Density During Cooling
3.3. Dislocation Type
3.4. Effect of Cooling on Tensile Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Wang, Z.; Guo, Z. Preparation of SiC/Al composite material by supergravity infiltration method and its properties. Ceram. Int. 2024, 50, 28025–28036. [Google Scholar] [CrossRef]
- Wang, L.; Yang, S.; Wang, S.; Pan, Y. Microstructure and textile reinforcement mechanism of extruded 6H-SiC/6092Al composites. Vacuum 2025, 233, 114025. [Google Scholar] [CrossRef]
- Kot, P.; Baczmański, A.; Gadalińska, E.; Wroński, S.; Wroński, M.; Wróbel, M.; Bokuchava, G.; Scheffzük, C.; Wierzbanowski, K. Evolution of phase stresses in Al/SiCp composite during thermal cycling and compression test studied using diffraction and self-consistent models. J. Mater. Sci. Technol. 2020, 36, 176–189. [Google Scholar] [CrossRef]
- Gadalińska, E.; Baczmański, A.; Wroński, S.; Wróbel, M.; Scheffzük, C.; Bokuchava, G. Neutron Diffraction Study of Phase Stresses in Al/SiCp Composite During Tensile Test. Met. Mater. Int. 2018, 25, 657–668. [Google Scholar] [CrossRef]
- Li, J.; Zhang, W.; Zhao, X.; Lang, F.; Xing, Y. Experimental and mechanistic investigation of the residual stress in SiCP/Al composites at the multi scale. Mater. Des. 2025, 253, 113888. [Google Scholar] [CrossRef]
- Zhang, X.X.; Ni, D.R.; Xiao, B.L.; Andrä, H.; Gan, W.M.; Hofmann, M.; Ma, Z.Y. Determination of macroscopic and microscopic residual stresses in friction stir welded metal matrix composites via neutron diffraction. Acta Mater. 2015, 87, 161–173. [Google Scholar] [CrossRef]
- Zhang, W.; Dai, X.; Ding, D.; Gao, P.; Mingyuan, G. A monotonic loading approach for determining residual stresses of fiber reinforced metal matrix composites. Mater. Sci. Eng. A 2014, 616, 29–34. [Google Scholar] [CrossRef]
- Zhao, X.; Gong, Y.; Cai, M.; Han, B. Numerical and experimental analysis of material removal and surface defect mechanism in scratch tests of high volume fraction SiCp/Al composites. Materials 2020, 13, 796. [Google Scholar] [CrossRef]
- Zhou, L.; Cui, C.; Zhang, P.; Ma, Z. Finite element and experimental analysis of machinability during machining of high-volume fraction SiCp/Al composites. Int. J. Adv. Manuf. Technol. 2017, 91, 1935–1944. [Google Scholar] [CrossRef]
- Lin, J.; Fu, B.; Gu, Y.; Xi, Y.; Fu, L.; Wu, S.; Kang, M.; Liang, G. Experimental and MD simulation study of surface residual stress and surface quality of SiCp/Al in pulsed laser-ultrasonic assisted grinding. J. Mater. Res. Technol. 2024, 30, 7741–7755. [Google Scholar] [CrossRef]
- Bouafia, F.; Serier, B.; Bouiadjra, B.A.B. Finite element analysis of the thermal residual stresses of SiC particle reinforced aluminium composite. Comput. Mater. Sci. 2012, 54, 195–203. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Q.; Lu, C.; Xue, T.; Hu, B.; Zhang, C. Microscopic residual stress evolution at the SiC/Al interface during nanoindentation via molecular dynamics simulation. Surf. Interfaces 2022, 33, 102210. [Google Scholar] [CrossRef]
- Lu, Y.; Hao, L.; Pan, F.; Chen, J.; Hirohashi, M. A study of the residual stress and its influence on tensile behaviors of fiber-reinforced SiC/Al composite. Adv. Compos. Mater. 2013, 22, 255–263. [Google Scholar] [CrossRef]
- Xiong, Y.; Hu, W.; Shu, Y.; Luo, X.; Zhang, Z.; He, J.; Yin, C.; Zheng, K. Atomistic simulation on the generation of defects in Cu/SiC composites during cooling. J. Mater. Sci. Technol. 2022, 123, 1–12. [Google Scholar] [CrossRef]
- Dandekar, C.R.; Shin, Y.C. Molecular dynamics based cohesive zone law for describing Al–SiC interface mechanics. Compos. Part A Appl. Sci. Manuf. 2011, 42, 355–363. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Mishin, Y.; Farkas, D.; Mehl, M.J.; Papaconstantopoulos, D.A. Interatomic potentials for monoatomic metals from experimental data and ab initio calculations. Phys. Rev. B 1999, 59, 3393. [Google Scholar] [CrossRef]
- Vashishta, P.; Kalia, R.K.; Nakano, A.; Rino, J.P. Interaction potential for silicon carbide: A molecular dynamics study of elastic constants and vibrational density of states for crystalline and amorphous silicon carbide. J. Appl. Phys. 2007, 101, 103515. [Google Scholar] [CrossRef]
- Doan, D.Q.; Fang, T.H.; Tran, A.S.; Chen, T.H. Residual stress and elastic recovery of imprinted Cu-Zr metallic glass films using molecular dynamic simulation. Comput. Mater. Sci. 2019, 170, 109162. [Google Scholar] [CrossRef]
- Ji, W.; Wu, M.S. Nanoscale origin of the crystalline-to-amorphous phase transformation and damage tolerance of Cantor alloys at cryogenic temperatures. Acta Mater. 2022, 226, 117639. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Stukowski, A.; Sadigh, B.; Erhart, P.; Caro, A. Efficient implementation of the concentration-dependent embedded atom method for molecular-dynamics and Monte-Carlo simulations. Model. Simul. Mater. Sci. Eng. 2009, 17, 075005. [Google Scholar] [CrossRef]
- Stukowski, A.; Albe, K. Extracting dislocations and non-dislocation crystal defects from atomistic simulation data. Model. Simul. Mater. Sci. Eng. 2010, 18, 085001. [Google Scholar] [CrossRef]
- Stukowski, A.; Bulatov, V.V.; Arsenlis, A. Automated identification and indexing of dislocations in crystal interfaces. Model. Simul. Mater. Sci. Eng. 2012, 20, 085007. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, N. An inverse adhesion problem for extracting interfacial pair potentials for the Al (0 0 1)/3C–SiC (0 0 1) interface. Inverse Probl. 2008, 24, 035019. [Google Scholar] [CrossRef]
- González-Lezcano, R.A.; del Río-Campos, J.M.; Awad Parada, T. Influence of thermal residual stresses on the behaviour of metal matrix composite materials. Iran. J. Sci. Technol. Trans. Mech. Eng. 2023, 47, 1903–1922. [Google Scholar] [CrossRef]
- Fudger, S.; Sediako, D.; Karandikar, P.; Ni, C. Residual stress induced mechanical property enhancement in steel encapsulated light metal matrix composites. Mater. Sci. Eng. A 2017, 699, 10–17. [Google Scholar] [CrossRef]
- Huang, J.; Wang, Z.; Bian, K.; Jiang, C. Investigation for different peening techniques on residual stress field of SiCw/Al composite. J. Mater. Eng. Perform. 2013, 22, 782–786. [Google Scholar] [CrossRef]
- Wong, C.S.; Pramanik, A.; Basak, A.K. Residual stress generation in metal matrix composites after cooling. Mater. Sci. Technol. 2018, 34, 1388–1400. [Google Scholar] [CrossRef]
- Ho, S.; Saigal, A. Three-dimensional modelling of thermal residual stresses and mechanical behavior of cast SiC/A1 particulate composites. Acta Metall. Mater. 1994, 42, 3253–3262. [Google Scholar] [CrossRef]

| Temperature (K) | 300 | 600 | 700 | 800 | 900 |
| Al (Å) | 4.065 | 4.086 | 4.095 | 4.103 | 4.112 |
| 3C-SiC (Å) | 4.371 | 4.383 | 4.389 | 4.393 | 4.396 |
| Atom Pair | ||
|---|---|---|
| Al-Si | D0 (eV) | 0.4824 |
| α (1/Å) | 1.322 | |
| r0 (1/Å) | 2.92 | |
| Al-C | D0 (eV) | 0.4691 |
| α (1/Å) | 1.738 | |
| r0 (1/Å) | 2.246 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, G.; Hao, S.; Xie, J.; Huang, H.; Zhang, G.; Cai, B.; Shi, Y.; Wang, J.; Wang, J. Molecular Dynamics Simulation Study on the Cooling Behavior and Mechanical Properties of Silicone Carbide/Aluminum Composites. Materials 2025, 18, 3908. https://doi.org/10.3390/ma18163908
Zhou G, Hao S, Xie J, Huang H, Zhang G, Cai B, Shi Y, Wang J, Wang J. Molecular Dynamics Simulation Study on the Cooling Behavior and Mechanical Properties of Silicone Carbide/Aluminum Composites. Materials. 2025; 18(16):3908. https://doi.org/10.3390/ma18163908
Chicago/Turabian StyleZhou, Guanzhuo, Shiming Hao, Jingpei Xie, Hai Huang, Guopeng Zhang, Bin Cai, Yunjia Shi, Jing Wang, and Jiefang Wang. 2025. "Molecular Dynamics Simulation Study on the Cooling Behavior and Mechanical Properties of Silicone Carbide/Aluminum Composites" Materials 18, no. 16: 3908. https://doi.org/10.3390/ma18163908
APA StyleZhou, G., Hao, S., Xie, J., Huang, H., Zhang, G., Cai, B., Shi, Y., Wang, J., & Wang, J. (2025). Molecular Dynamics Simulation Study on the Cooling Behavior and Mechanical Properties of Silicone Carbide/Aluminum Composites. Materials, 18(16), 3908. https://doi.org/10.3390/ma18163908







