Study of the Scale Effect on the Mechanical Properties of High-Strength Concrete
Abstract
1. Introduction
- A 10% reduction in value in the case of limestone aggregate,
- A 30% reduction in value in the case of sandstone aggregate,
- A 20% increase in value in the case of basalt aggregate.
- —probability of brittle decohesion of a specimen of volume V subjected to uniform tensile stress σ,
- —specimen volume,
- —characteristic quantity for which the probability of survival is 1/e,
- —threshold value below which specimens cannot be destroyed,
- m—Weibull modulus.
2. Materials
3. Methods
- —dynamic modulus of elasticity;
- —wave velocity;
- —concrete density;
- ν—Poisson’s ratio.
- —stabilized secant modulus of elasticity;
- i —strains measured at the third cycle corresponding to the measured stress values i .
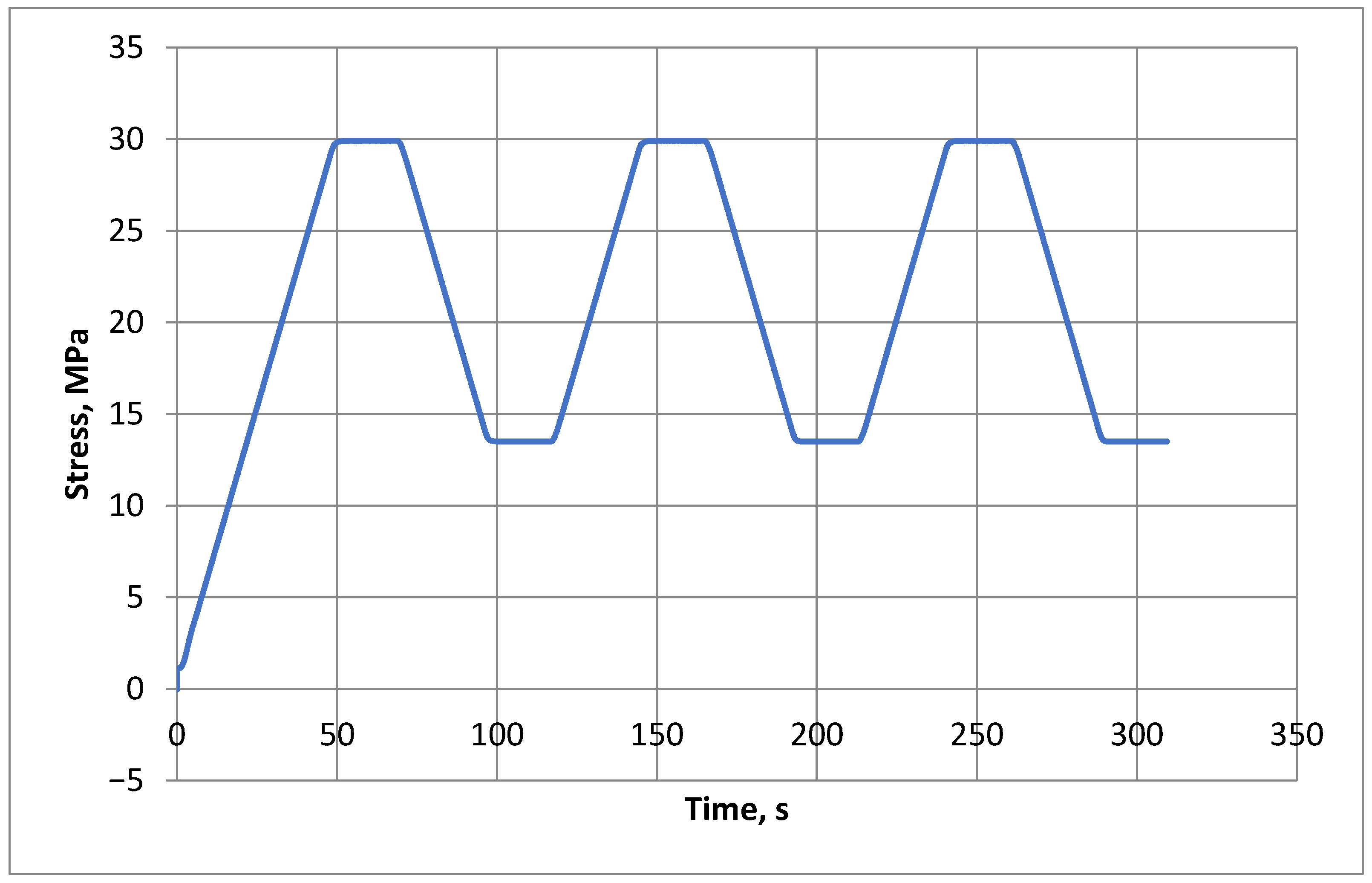
4. Results
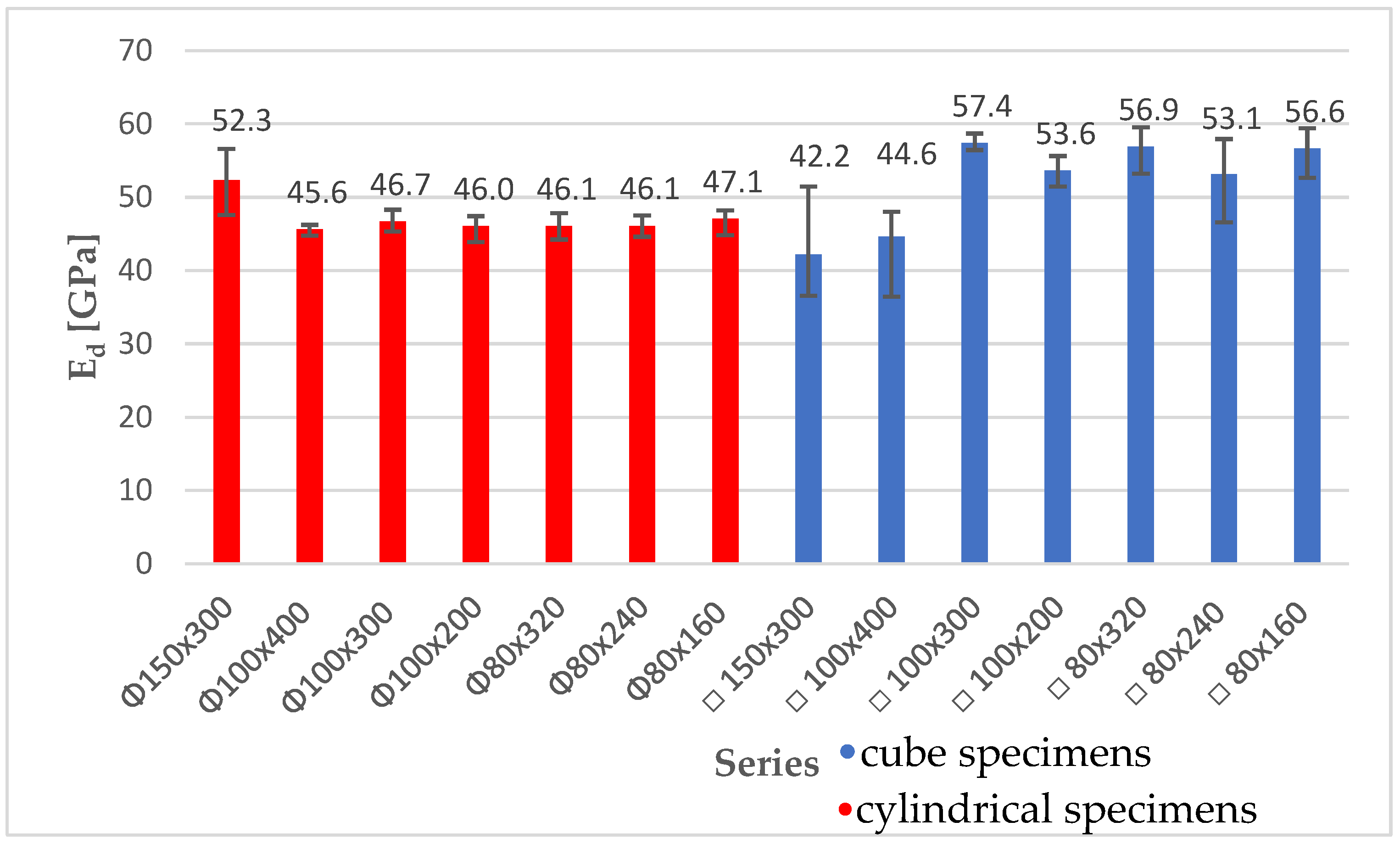
4.1. Dynamic Tests
- V—coefficients of variation;
- s—standard deviation;
- —arithmetic mean of the values obtained on specimens in a given series.
- s—standard deviation;
- —subsequent data values obtained for individual specimen of the series;
- —arithmetic mean of the values obtained on specimens in a given series;
- —number of specimens in a given series.
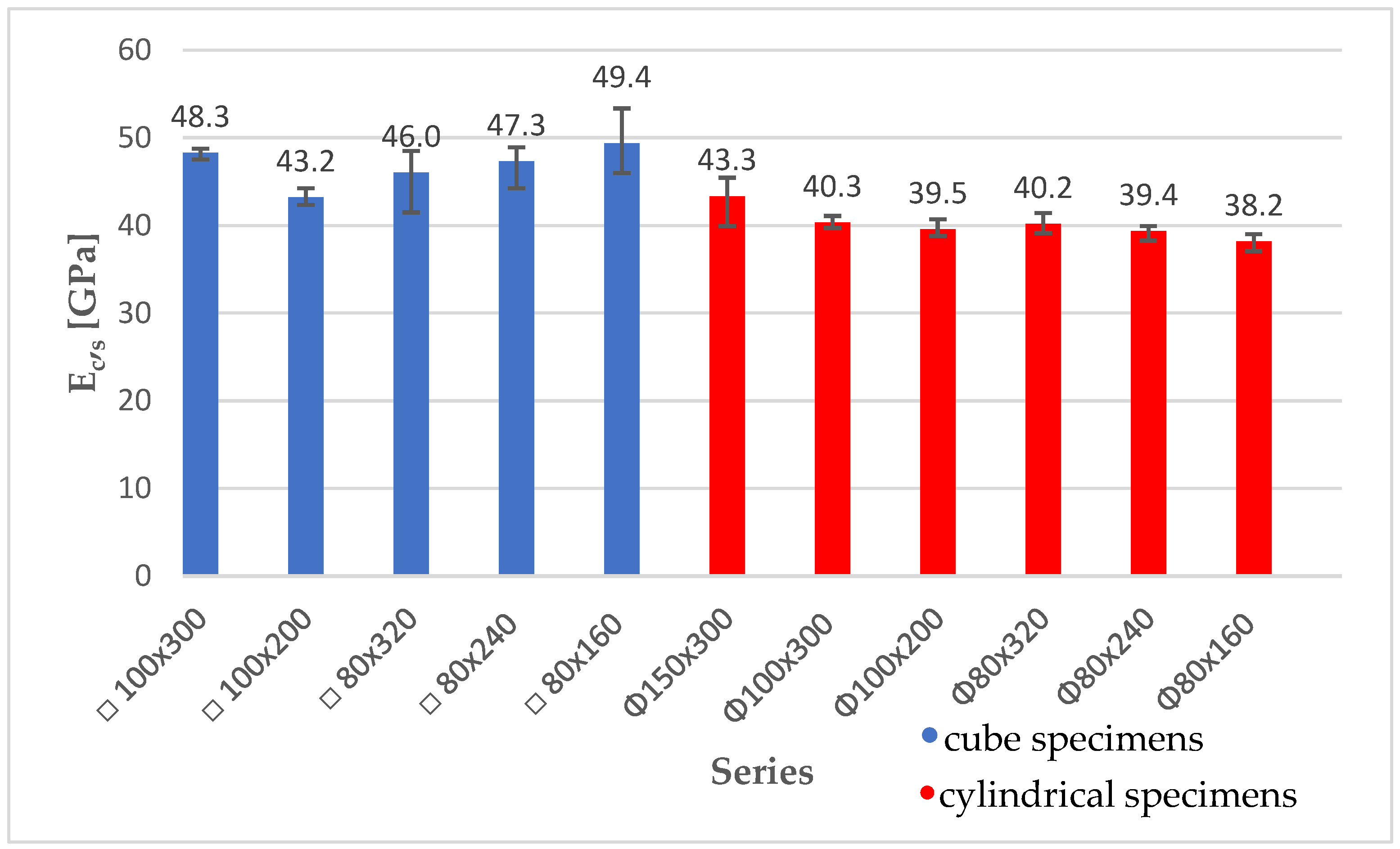
4.2. Static Tests
4.3. Compressive Strength Tests
5. Discussion
- For the high-strength concrete tested, no significant scale effect was observed either in the elastic modulus or compressive strength tests.
- The concrete used for the tests was characterized by particularly high strength. In its analysis, cracks appear only at a very high level of stress, while during tests, in accordance with the standard EN 12390-13:2021 [1], the specimen is subjected to maximum stresses equal to only 1/3 of the compressive strength. Therefore, when testing the secant modulus of elasticity, the scale effect for high-strength concretes may be less noticeable than in the case of ordinary concretes.
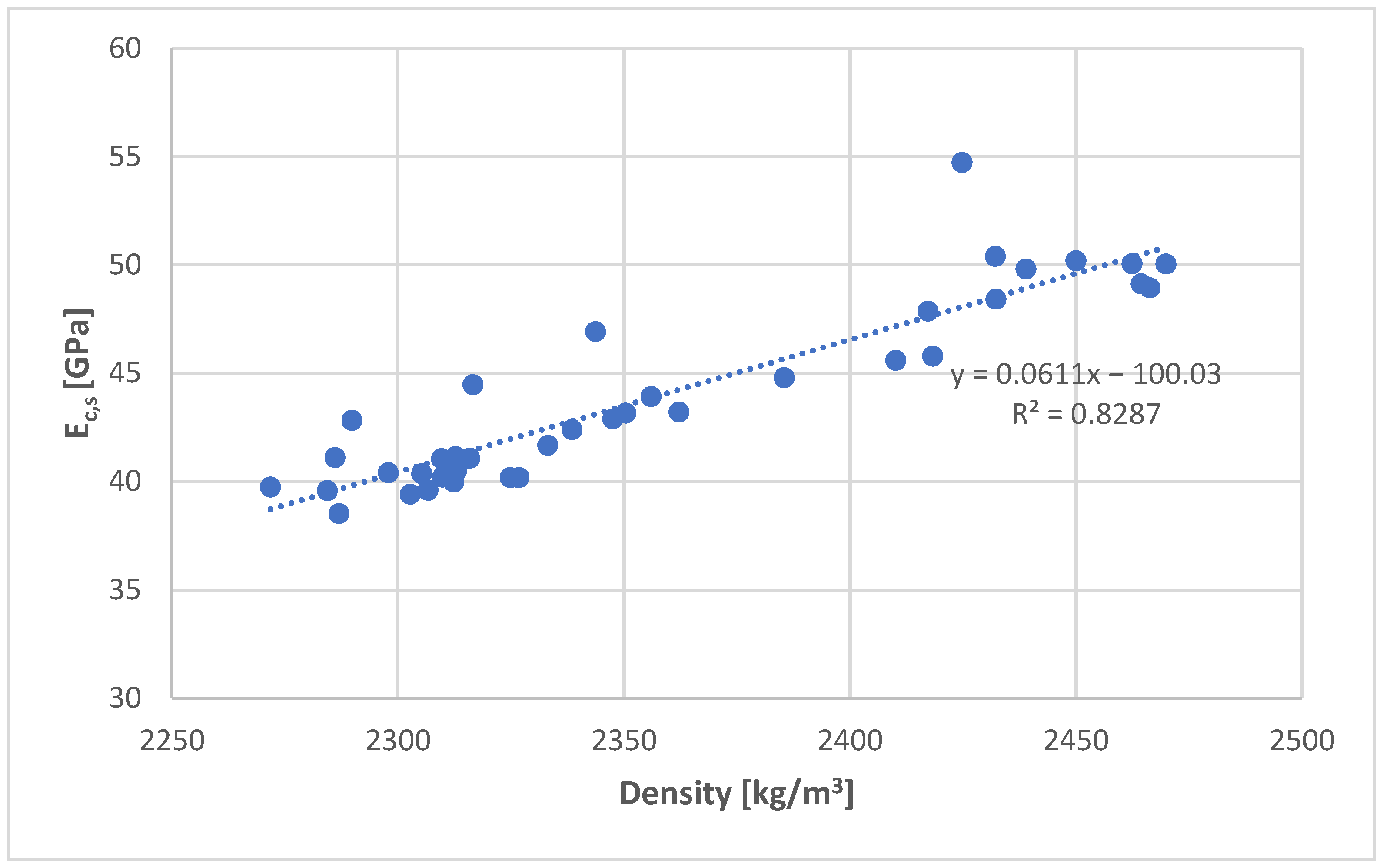
- The conducted studies have shown that the key factor influencing the value of the modulus of elasticity and the compressive strength of the specimens is concrete structure, which determines the density. In connection with this, due to the differences in the density of individual specimens, it is also difficult to identify the scale effect in the case of the compressive strength test.
- It is worth noting that the coefficient of variation in the density test was significantly lower than in the tests of the dynamic and secant modulus of elasticity. It turned out to be the highest in the compressive strength test.
- The authors intend to conduct further research in which they will standardize the specimens in terms of density by making prefabricated concrete elements themselves.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- EN 12390-13:2021; Testing Hardened Concrete—Part 13: Determination of Secant Modulus of Elasticity in Compression. European Committee for Standardization: Brussels, Belgium, 2021.
- Łapko, A.; Jensen, B. Podstawy Projektowania I Algorytmy Obliczeń Konstrukcji Żelbetowych; Arkady: Warszawa, Poland, 2015. [Google Scholar]
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. Committee for Standardization: Brussels, Belgium, 2004.
- Neville, A.M. Properties of Concrete, 5th ed.; Pearson Education Limited: London, UK, 2012. [Google Scholar]
- Mehta, P.K.; Monteiro, P.J.M. Concrete: Microstructure, Properties and Materials; McGraw-Hill Education: New York, NY, USA, 2014. [Google Scholar]
- Li, J.; Zhang, J.; Yang, X.; Zhang, A.; Yu, M. Monte Carlo Simulations of Deformation Behaviour of Unbound Granular Materials Based on a Real Aggregate Library. Int. J. Pavement. Eng. 2023, 24, 2165650. [Google Scholar] [CrossRef]
- Woyciechowski, P.P.; Adamczewski, G.; Adaszyńska, J.; Szklarczyk, M. Ocena wpływu charakterystyki kruszywa grubego na moduł sprężystości betonu wysokiej wytrzymałości. In Proceedings of the Concrete Days Conference: Tradition and Modernity, Wisła, Poland, 13–15 October 2014. [Google Scholar]
- Piasta, W.; Budzyński, W.; Góra, J. Wpływ rodzaju kruszywa grubego na odkształcalność betonów zwykłych. Przegląd. Bud. 2012, 83, 35–38. [Google Scholar]
- Kallel, H.; Carré, H.; La Borderie, C.; Masson, B.; Tran, N.C. Effect of Temperature and Moisture on the Instantaneous Behaviour of Concrete. Cem. Concr. Compos. 2017, 80, 326–332. [Google Scholar] [CrossRef]
- Wang, H.; Li, Q. Prediction of Elastic Modulus and Poisson’s Ratio for Unsaturated Concrete. Int. J. Solids. Struct. 2007, 44, 1370–1379. [Google Scholar] [CrossRef]
- Domagała, L. Structural Lightweight Aggregate Concrete/Konstrukcyjne Lekkie Betony Kruszywowe; CUT Publishing House: Cracow, Poland, 2014. [Google Scholar]
- Domagała, L.; Sieja, K. Effect of Moisture Condition of Structural Lightweight Concretes on Specifi ed Values of Static and Dynamic Modulus of Elasticity. Materials 2023, 16, 4299. [Google Scholar] [CrossRef] [PubMed]
- Popovics, S. Effects of Uneven Moisture Distribution on the Strength of and Wave Velocity in Concrete. Ultrasonics 2005, 43, 429–434. [Google Scholar] [CrossRef] [PubMed]
- Domagała, L.; Dobrowolska, J. The influence of an applied standard test method on a measurement of concrete stabilized secant modulus of elasticity. MATEC Web Conf. 2018, 163, 07001. [Google Scholar] [CrossRef][Green Version]
- Bazant, Z.; Planas, J. Fracture and Size Effect in Concrete and Other Quasi-Brittle Materials; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar][Green Version]
- Kremnev, L.S. Cyclic Strength and Nonlinear Material Fracture Mechanics. arXiv 2014, arXiv:1410.4177. [Google Scholar][Green Version]
- Weibull, W. A statistical theory of the strength of materials. Proc. Roy. Swed. Inst. Eng. Res. 1939, 151, 5–45. [Google Scholar]
- Bazant, Z.; Pang, S.; Vorechovsky, M.; Novak, D. Statistical size effect in quasibrittle materials: Computation and extreme value theory. Fract. Mech. Concr. Struct. 2014, 1, 189–196. [Google Scholar]
- Tokyay, M.; Özdemir, M. Specimen shape and size effect on the compressive strength of higher strength concrete. Cem. Concr. Res. 1997, 27, 1281–1289. [Google Scholar] [CrossRef]
- Li, M.; Hao, H.; Shi, Y.; Hao, Y. Specimen shape and size effects on the concrete compressive strength under static and dynamic tests. Constr. Build. Mater. 2018, 161, 84–93. [Google Scholar] [CrossRef]
- Domagała, L. Size effect in compressive strength tests of cored specimens of lightweight aggregate concrete. Materials 2020, 13, 1187. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.J.; Kee, S.H.; Oh, T.; Kim, Y.Y. Effect of Cylinder Size on the Modulus of Elasticity and Compressive Strength of Concrete from Static and Dynamic Tests. Adv. Mater. Sci. Eng. 2015, 2015, 580638. [Google Scholar] [CrossRef]
- Domagała, L.; Margańska, M.; Miazgowicz, M. Moisture Impact on Static and Dynamic Modulus of Elasticity in Structural Normal-Weight Concretes. Materials 2024, 17, 3722. [Google Scholar] [CrossRef] [PubMed]
- EN 12390-7:2019; Testing Hardened Concrete—Part 7: Density of Hardened Concrete. European Committee for Standardization: Brussels, Belgium, 2019.
- EN 12390-3:2019; Testing Hardened Concrete—Part 3: Compressive strength of Test Specimens. European Committee for Standardization: Brussels, Belgium, 2019.
- EN 12390-4:2020-03; Testing Hardened Concrete—Part 4: Compressive Strength—Specification for Testing Machines. European Committee for Standardization: Brussels, Belgium, 2020.
- EN 12504-4:2021; Testing Concrete in Structures—Part 4: Determination of Ultrasonic Pulse Velocity. European Committee for Standardization: Brussels, Belgium, 2021.
- ASTM C 215:2019; Standard Test Method for Fundamental Transverse. Longitudinal, and Torsional Resonant Frequencies of Concrete Specimens. American Concrete Institute: Washington, DC, USA, 2019.





| Series Number | Diameter (d) [mm] | Height (h) [mm] |
|---|---|---|
| Φ80 × 160 | 80 | 160 |
| Φ80 × 160’ | 80 | 160 |
| Φ80 × 240 | 80 | 240 |
| Φ80 × 320 | 80 | 320 |
| Φ100 × 200 | 100 | 200 |
| Φ100 × 300 | 100 | 300 |
| Φ100 × 400 | 100 | 400 |
| Φ150 × 300 | 150 | 300 |
| Series Number | Width (a, b) [mm] | Height (h) [mm] |
|---|---|---|
| □80 × 160 | 80 | 160 |
| □80 × 160’ | 80 | 160 |
| □80 × 240 | 80 | 240 |
| □80 × 320 | 80 | 320 |
| □100 × 200 | 100 | 200 |
| □100 × 300 | 100 | 300 |
| □100 × 400 | 100 | 400 |
| □150 × 300 | 150 | 300 |
| Series | Density [kg/m3] | Ed [Mpa] | Ed/Ed,cyl |
|---|---|---|---|
| Φ80 × 160 | 2310 | 47.1 | 90.1% |
| Φ80 × 240 | 2300 | 46.1 | 88.1% |
| Φ80 × 320 | 2320 | 46.1 | 88.1% |
| Φ100 × 200 | 2260 | 46.0 | 88.0% |
| Φ100 × 300 | 2280 | 46.7 | 89.3% |
| Φ100 × 400 | 2270 | 45.6 | 87.2% |
| Φ150 × 300 | 2370 | 52.3 | 100.0% |
| □80 × 160 | 2450 | 56.6 | 108.2% |
| □80 × 240 | 2390 | 53.1 | 101.5% |
| □80 × 320 | 2400 | 56.9 | 108.8% |
| □100 × 200 | 2400 | 53.6 | 102.5% |
| □100 × 300 | 2410 | 57.4 | 109.8% |
| □100 × 400 | 2330 | 44.6 | 85.3% |
| □150 × 300 | 2350 | 42.2 | 80.7% |
| Series | Density [kg/m3] | Ec,s [Mpa] | Ec,s/Ec,s,cyl |
|---|---|---|---|
| Φ80 × 160 | 2310 | 38.2 | 88.2% |
| Φ80 × 240 | 2300 | 39.4 | 91.0% |
| Φ80 × 320 | 2320 | 40.2 | 92.8% |
| Φ100 × 200 | 2260 | 39.5 | 91.2% |
| Φ100 × 300 | 2280 | 40.3 | 93.1% |
| Φ150 × 300 | 2370 | 43.3 | 100.0% |
| □80 × 160 | 2450 | 49.4 | 114.1% |
| □80 × 240 | 2390 | 47.3 | 109.2% |
| □80 × 320 | 2400 | 46.0 | 106.2% |
| □100 × 200 | 2400 | 43.2 | 99.8% |
| □100 × 300 | 2410 | 48.3 | 111.5% |
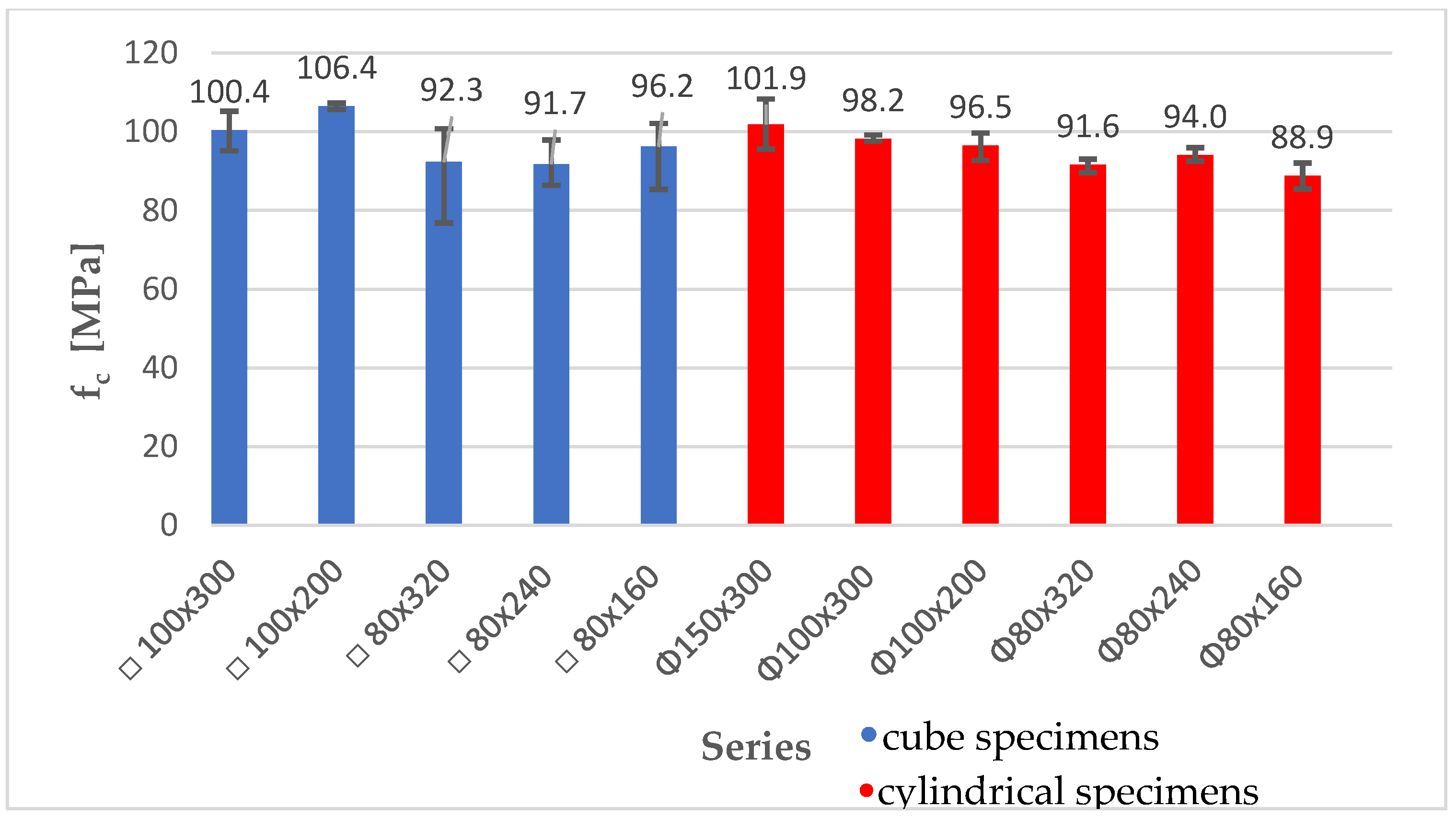
| Series | Density [kg/m3] | fcm | fcm/fcm,cyl |
|---|---|---|---|
| Φ80 × 160 | 2310 | 88.9 | 87.2% |
| Φ80 × 240 | 2300 | 94.0 | 92.2% |
| Φ80 × 320 | 2320 | 91.6 | 89.9% |
| Φ100 × 200 | 2260 | 96.5 | 94.7% |
| Φ100 × 300 | 2280 | 98.2 | 96.4% |
| Φ150 × 300 | 2370 | 101.9 | 100.0% |
| □80 × 160 | 2450 | 96.2 | 94.4% |
| □80 × 240 | 2390 | 91.7 | 90.0% |
| □80 × 320 | 2400 | 92.3 | 90.6% |
| □100 × 200 | 2400 | 106.4 | 104.4% |
| □100 × 300 | 2410 | 100.4 | 98.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miazgowicz, M.; Domagała, L. Study of the Scale Effect on the Mechanical Properties of High-Strength Concrete. Materials 2025, 18, 3795. https://doi.org/10.3390/ma18163795
Miazgowicz M, Domagała L. Study of the Scale Effect on the Mechanical Properties of High-Strength Concrete. Materials. 2025; 18(16):3795. https://doi.org/10.3390/ma18163795
Chicago/Turabian StyleMiazgowicz, Marek, and Lucyna Domagała. 2025. "Study of the Scale Effect on the Mechanical Properties of High-Strength Concrete" Materials 18, no. 16: 3795. https://doi.org/10.3390/ma18163795
APA StyleMiazgowicz, M., & Domagała, L. (2025). Study of the Scale Effect on the Mechanical Properties of High-Strength Concrete. Materials, 18(16), 3795. https://doi.org/10.3390/ma18163795





