Optimization of Tribological Properties of Shot-Peened Surfaces via Multi-Criteria Decision-Making Using TOPSIS and GRA
Abstract
1. Introduction
2. Materials and Methods
- Construction of the decision matrix.
- Normalization of the decision matrix:
- 3.
- Construction of the weighted normalized decision matrix:
- 4.
- Determination of the ideal solution (A+) and the anti-ideal solution (A−):
- 5.
- Calculation of the Euclidean distance from the ideal and anti-ideal solutions:
- 6.
- Calculation of the closeness coefficient (Ci), representing the relative proximity of each variant to the ideal solution:
- Data normalization.
- 2.
- Calculation of the deviation sequence.
- 3.
- Calculation of the grey relational coefficient (GRC).
- 4.
- Calculation of the grey relational grade (GRG).
- 5.
- Ranking
3. Results and Discussion
3.1. Surface Topography After the Shot Peening Process
3.2. Tribological Properties
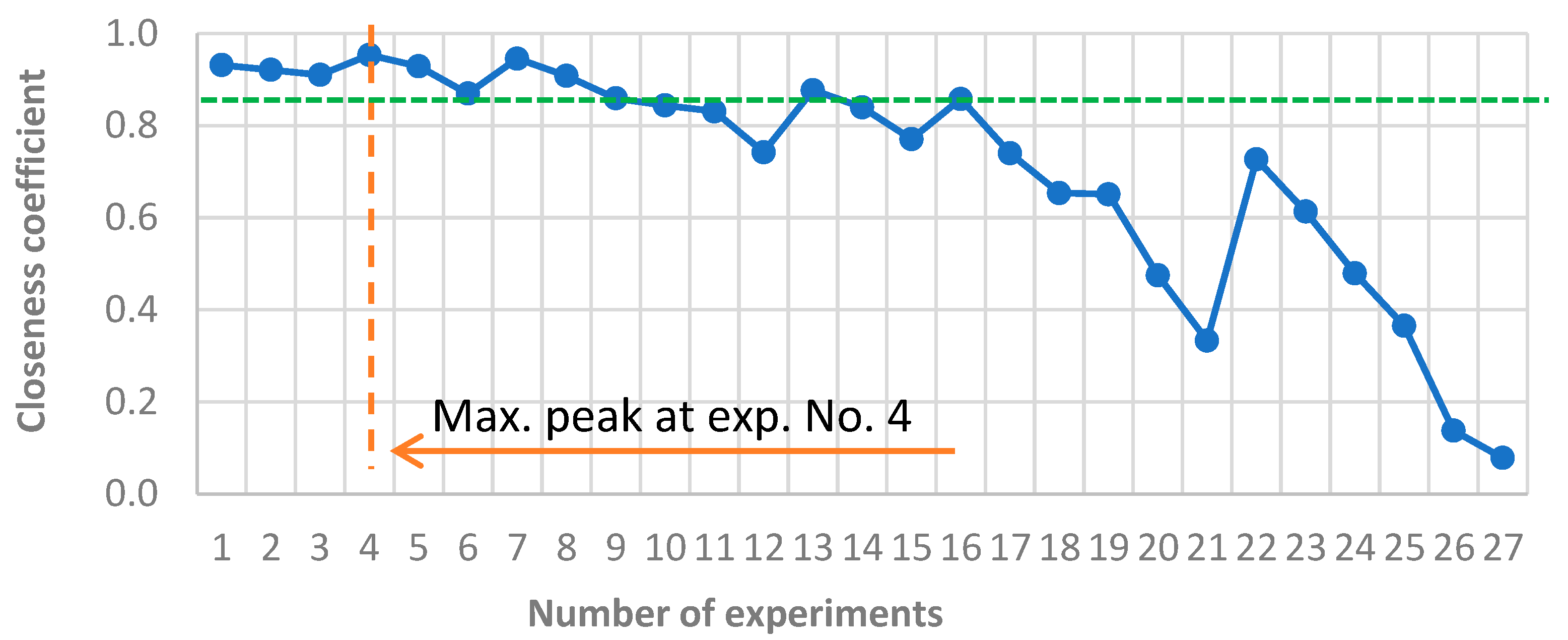
3.3. TOPSIS Analysis
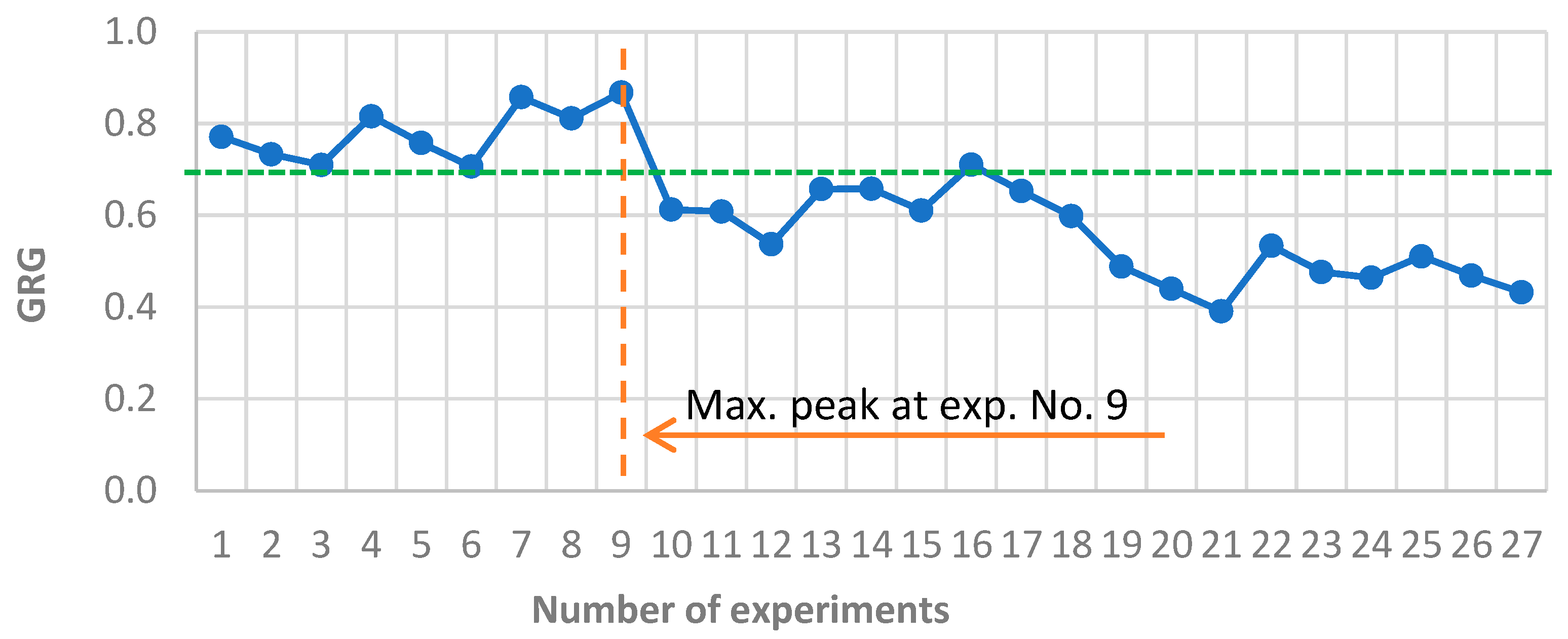
3.4. GRA Method
- The top-performing variants (GRG > 0.7) exhibited a low volumetric wear, low friction coefficient, and moderate mass loss. These configurations represent potentially optimal settings of input parameters for tribological testing.
- Middle-ranked variants (GRG between 0.5 and 0.7) demonstrated certain trade-offs; typically, at least one output parameter remained significantly less favorable, which lowered the overall efficiency rating.
- The lowest-ranked variants (GRG < 0.5) were associated with at least two unfavorable parameters—most often very high wear (VD > 2 mm3) and significant mass loss (>0.010 g)—which significantly penalized their final scores, particularly due to the weighted evaluation system.
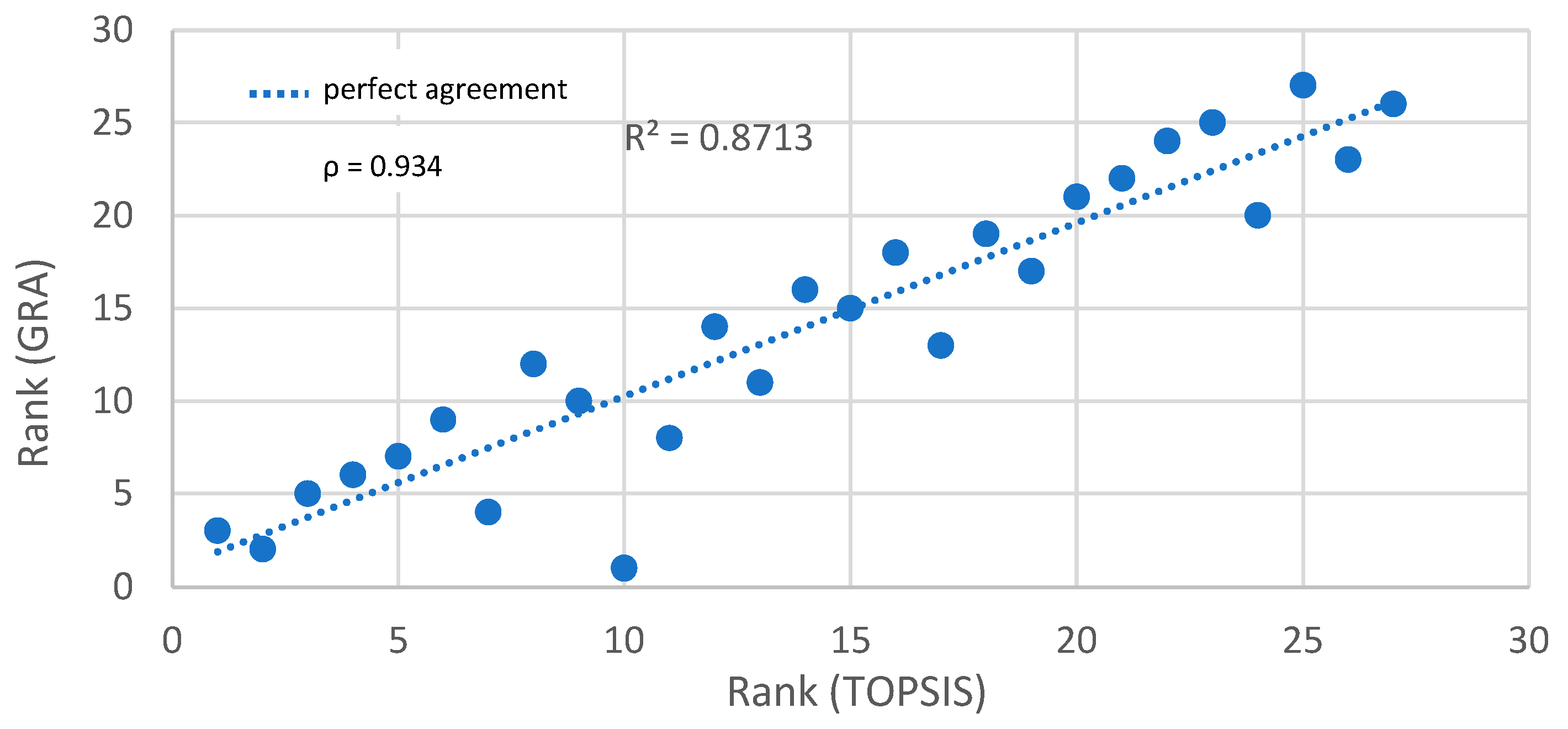
3.5. TOPSIS vs. GRA Comparison
- Variant No. 4 was ranked 1st in TOPSIS and 3rd in GRA;
- Variant No. 1 appeared in the TOP 5 for both methods;
- Variant No. 7 was ranked 2nd in both TOPSIS and GRA;
- Variants No. 2, 5, and 8 also consistently appeared in the top 7, confirming the reliability of the rankings.
3.6. Weight Sensitivity Analysis
- -
- Scenario A (Friction-prioritized): CoF = 0.5, VD = 0.3, WL = 0.2;
- -
- Scenario B (Balanced weights): CoF = 0.33, VD = 0.33, WL = 0.34;
- -
- Scenario C (Wear-prioritized): CoF = 0.3, VD = 0.5, WL = 0.2.
4. Conclusions
- ✓
- The shot peening process significantly modified the surface topography, increasing surface isotropy and enhancing load-bearing properties.
- ✓
- Tribological tests showed that load had the strongest influence on all output parameters (wear volume, coefficient of friction, and weight loss), followed by sliding distance and speed.
- ✓
- The application of multi-criteria decision-making (MCDM) methods—TOPSIS and GRA—enabled a comprehensive optimization of test conditions based on three conflicting output parameters. Both the TOPSIS and GRA methods provided consistent rankings, with Spearman’s rank correlation coefficient reaching 0.934, confirming the reliability of the selected solutions.
- ✓
- The best-ranked configurations, particularly variants No. 4, 1, and 5, which met all predefined threshold criteria (VD < 0.22 mm3; CoF < 0.57; WL < 0.005 g), are recommended as optimal. These limit values were selected based on percentile analysis of the results (approx. lower quartile), technical relevance to tribological systems, and engineering judgement to ensure a balance between friction reduction and wear resistance. Variant No. 7 also ranked highly in both methods and can be considered a near-optimal solution.
- ✓
- A weight sensitivity analysis confirmed the robustness of the top-performing variants across three different weighting scenarios.
- ✓
- GRA proved to be less sensitive to individual outliers, making it a valuable complementary tool to distance-based methods like TOPSIS.
5. Limitations and Future Work
- ✓
- The present study was limited to dry sliding conditions using a specific ball-on-disc configuration. The influence of lubrication, temperature variation, and environmental exposure (e.g., humidity, corrosion) was not considered.
- ✓
- Only one material pair (42CrMo4 steel vs. SiC) was investigated. Additional studies should include alternative substrate materials and counter-body types to generalize the findings.
- ✓
- The tribological behavior was assessed at macro scale. Micro- or nano-scale investigations could offer more detailed insights into the mechanisms of wear and friction.
- ✓
- The current weighting scheme in MCDM was based on assumed engineering priorities. Future work could integrate stakeholder-based preference modeling or machine learning techniques to dynamically adjust weights.
- ✓
- Future research should also explore the hybridization of optimization techniques (e.g., combining GRA or TOPSIS with genetic algorithms), as well as the use of AI-assisted modeling to predict tribological outcomes under a wide range of conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Skoczylas, A.; Zaleski, K. The Effect of the Chamber-Filling Ratio in Vibratory Shot Peening on Selected Surface Layer Properties of 30HGSA. Materials 2025, 18, 8. [Google Scholar] [CrossRef]
- Zając, G.; Michnej, J. Fatigue Strength Improvement of Steel Rollers in Conveyor Belts When Using Shot Peening. Tribologia 2019, 284, 143–149. [Google Scholar] [CrossRef]
- Zhu, W.; Liu, H.; Xing, S.; Jiang, C.; Ji, V. Effect of Dual Shot Peening on Microstructure and Wear Performance of CNT/Al-Cu-Mg Composites. Materials 2024, 17, 5066. [Google Scholar] [CrossRef] [PubMed]
- Calvo-García, E.; del Val, J.; Riveiro, A.; Valverde-Pérez, S.; Álvarez, D.; Román, M.; Magdalena, C.; Badaoui, A.; Pou-Álvarez, P.; Comesaña, R. The Influence of Shot Peening Media on Surface Properties and Fatigue Behaviour of Aluminium Alloy 6082 T6. J. Manuf. Mater. Process. 2024, 8, 192. [Google Scholar] [CrossRef]
- Raghuvaran, P.; Suresh, M.; Narasimharaj, V.; Rajesh, A. Enhancing the Fatigue Strength of Stir-Casted Al7075-SiC Composites through Heat Treatment and Shot Peening. Phys. Scr. 2023, 98, 125703. [Google Scholar] [CrossRef]
- Peng, R.; Vuoristo, T.; Bäckström, D.; Ahmad, M.; Lundberg, M.; Johansson, S. Fatigue Strength of Shot Peened Compacted Graphite Iron. In Proceedings of the ICSP-12, Goslar, Germany, 15–18 September 2014; pp. 74–79. [Google Scholar]
- Wu, M.-Z.; Zhang, J.; Mei, G.-M.; Li, X. Effects of Fine Particle Shot Peening Treatment on Fatigue Properties of Al-7Si-0.3Mg Alloy. J. Mater. Eng. Perform. 2019, 28, 2600–2609. [Google Scholar] [CrossRef]
- Maleki, E.; Unal, O. Optimization of Shot Peening Effective Parameters on Surface Hardness Improvement. Met. Mater. Int. 2021, 27, 3173–3185. [Google Scholar] [CrossRef]
- Koppula, V.R.; Vambabu, V.; Mrudula, G.; Prakash, P.; Venkatesh, D.J.; Mudunuri, R.; Satyanarayana, M. Effect of Shot Peening on Microstructural Features, Residual Stress Behavior, and Hardness of Aluminum Alloy 2014. Eng. Res. Express 2025, 7, 045012. [Google Scholar] [CrossRef]
- Si, C.; Song, Z.M.; Cao, Y. Effect of Peening Media Type on the High-Cycle Tensile–Tensile Fatigue Properties of Ti-6Al-4V Alloy by Ultrasonic Shot Peening. Fatigue Fract. Eng. Mater. Struct. 2024, 48, 1166–1182. [Google Scholar] [CrossRef]
- Moradi, A.; Heidari, A.; Amini, K.; Aghadavoudi, F.; Abedinzadeh, R. The Effect of Shot Peening Time on Mechanical Properties and Residual Stress in Ti-6Al-4V Alloy. Metall. Res. Technol. 2022, 119, 401. [Google Scholar] [CrossRef]
- Ravnikar, D.; Šturm, R.; Žagar, S. Effect of Shot Peening on the Strength and Corrosion Properties of 6082-T651 Aluminium Alloy. Materials 2023, 16, 4976. [Google Scholar] [CrossRef]
- Ciuffini, A.F.; Barella, S.; Peral Martinez, L.B.; Mapelli, C.; Pariente, I.F. Influence of Microstructure and Shot Peening Treatment on Corrosion Resistance of AISI F55-UNS S32760 Super Duplex Stainless Steel. Materials 2018, 11, 1038. [Google Scholar] [CrossRef]
- Liu, H.-B.; Yang, B.; Zhang, J.; Gan, J.S.; Wu, W.-F.; Wang, C.; Jiang, C. Surface Mechanical Property and Residual Stress Stability of Shot-Peened Mg-8Gd-3Y Alloy by In-Situ X-ray Diffraction. J. Mater. Res. Technol. 2023, 26, 3015–3024. [Google Scholar] [CrossRef]
- Wang, S.; Yang, X.; Zhang, Z.; Zhu, Y.; Song, F.; Dong, W.; Wu, M. Study on Shot Peening Strengthening 42CrMoA Steel and Its Fretting Wear Properties. Mater. Sci. Technol. 2024, in press. [CrossRef]
- Walczak, M.; Świetlicki, A.; Szala, M.; Turek, M.; Chocyk, D. Shot Peening Effect on Sliding Wear in 0.9% NaCl of Additively Manufactured 17-4PH Steel. Materials 2024, 17, 1383. [Google Scholar] [CrossRef] [PubMed]
- Żebrowski, R.; Walczak, M. Effect of the Shot Peening on Surface Properties and Tribological Performance of Ti-6Al-4V Alloy Produced by Means of DMLS Technology. Arch. Metall. Mater. 2019, 64, 377–383. [Google Scholar] [CrossRef]
- Khun, N.W.; Trung, P.Q.; Butler, D.L. Mechanical and Tribological Properties of Shot-Peened SAE 1070 Steel. Tribol. Trans. 2016, 59, 932–943. [Google Scholar] [CrossRef]
- Guan, H.; Zhang, J.; Zhang, X.; Sun, G.; Duan, C. Study on the Effects of the Shot Peening Intensity on the Microstructure, Friction and Wear Properties of High-Strength Steel. PLoS ONE 2024, 19, e0314561. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Lai, F.; Qu, S.; Ji, V.; Liu, H.; Li, X. Effect of Shot Peening on Residual Stress Distribution and Tribological Behaviors of 17Cr2Ni2MoVNb Steel. Surf. Coat. Technol. 2020, 386, 125497. [Google Scholar] [CrossRef]
- Thirumalvalavan, S.; Perumal, G.; Senthilkumar, N.; Selvarasu, S. Enhancing Tribological Characteristics of Titanium Grade-5 Alloy through HVOF Thermal-Sprayed WC–Co Nanocoatings Using TOPSIS and Golden Jack Optimization Algorithm. Recent Pat. Nanotechnol. 2025, 19, 4. [Google Scholar] [CrossRef]
- Sylajakumari, P.A.; Ramakrishnasamy, R.; Palaniappan, G. Taguchi Grey Relational Analysis for Multi-Response Optimization of Wear in Co-Continuous Composite. Materials 2018, 11, 1743. [Google Scholar] [CrossRef]
- Dharmalingam, S.; Subramanian, R.; Kök, M. Optimization of Abrasive Wear Performance in Aluminium Hybrid Metal Matrix Composites Using Taguchi–Grey Relational Analysis. Proc. Inst. Mech. Eng. Part J 2013, 227, 749–760. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, M.; Pandey, B. Investigations on Mechanical and Sliding Wear Performance of AA7075-SiC/Marble Dust/Graphite Hybrid Alloy Composites Using Hybrid ENTROPY-VIKOR Method. Silicon 2022, 14, 2051–2065. [Google Scholar] [CrossRef]
- Huang, Q.; Shi, X.; Xue, Y.; Zhang, K.; Wu, C. Assessment and Optimization of Tribological Parameters for Bionic Textured AISI 4140-SnAgCu Self-Lubricating Composite under Dry Sliding Conditions Using AHP and RSM. Tribol. Trans. 2022, 65, 479–491. [Google Scholar] [CrossRef]
- Rajesh, S.; Rajakarunakaran, S.; Suthakarapandian, R.; Pitchipoo, P. MOORA-Based Tribological Studies on Red Mud Reinforced Aluminum Metal Matrix Composites. Adv. Tribol. 2013, 2013, 213914. [Google Scholar] [CrossRef]
- Dašić, M.; Almog, R.; Agmon, L.; Yehezkel, S.; Halfin, T.; Jopp, J.; Ya’akobovitz, A.; Berkovich, R.; Stanković, I. Role of Trapped Molecules at Sliding Contacts in Lattice-Resolved Friction. ACS Appl. Mater. Interfaces 2024, 16, 44249–44260. [Google Scholar] [CrossRef] [PubMed]
- Dašić, M.; Ponomarev, I.; Polcar, T.; Nicolini, P. Tribological Properties of Vanadium Oxides Investigated with Reactive Molecular Dynamics. Tribol. Int. 2022, 175, 107795. [Google Scholar] [CrossRef]
- Gkagkas, K.; Ponnuchamy, V.; Dašić, M.; Stanković, I. Molecular Dynamics Investigation of a Model Ionic Liquid Lubricant for Automotive Applications. Tribol. Int. 2017, 113, 83–91. [Google Scholar] [CrossRef]
- PN-EN ISO 25178-2:2012; Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 2: Terms, Definitions and Surface Texture Parameters. International Organization for Standardization: Geneva, Switzerland, 2012.
- Trzepieciński, T.; Szpunar, M.; Dzierwa, A.; Żaba, K. Investigation of Surface Roughness in Incremental Sheet Forming of Conical Drawpieces from Pure Titanium Sheets. Materials 2022, 15, 4278. [Google Scholar] [CrossRef] [PubMed]
- DigitalSurf. TalyMap Software, version 6.2; DigitalSurf: Besançon, France, 2015.
- Kuo, T. A Modified TOPSIS with a Different Ranking Index. Eur. J. Oper. Res. 2017, 260, 152–160. [Google Scholar] [CrossRef]
- Panda, A.; Sahoo, A.; Rout, R. Multi-Attribute Decision Making Parametric Optimization and Modeling in Hard Turning Using Ceramic Insert through Grey Relational Analysis: A Case Study. Decis. Sci. Lett. 2016, 5, 581–592. [Google Scholar] [CrossRef]
- Behzadian, M.; Otaghsara, S.K.; Yazdani, M.; Ignatius, J. A State-of-the-Art Survey of TOPSIS Applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Dzierwa, A.; Reizer, R.; Pawlus, P.; Grabon, W. Variability of Areal Surface Topography Parameters Due to the Change in Surface Orientation to Measurement Direction. Scanning 2014, 36, 170–183. [Google Scholar] [CrossRef]
- Grochała, D.; Grzejda, R.; Józwik, J.; Siemiątkowski, Z. Improving the Degree of Surface Isotropy of Parts Manufactured Using Hybrid Machining Processes. Coatings 2025, 15, 461. [Google Scholar] [CrossRef]
- Gadelmawla, E.S.; Koura, M.M.; Maksoud, T.M.A.; Elewa, I.M.; Soliman, H.H. Roughness Parameters. J. Mater. Process. Technol. 2002, 123, 133–145. [Google Scholar] [CrossRef]
- Podulka, P. Fast Fourier Transform Detection and Reduction of High-Frequency Errors from the Results of Surface Topography Profile Measurements of Honed Textures. Ekspl. Niezawodn. 2021, 23, 84–93. [Google Scholar] [CrossRef]
- Whitehouse, D.J. Handbook of Surface and Nanometrology, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Archard, J.F. Contact and Rubbing of Flat Surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Stachowiak, G.W.; Batchelor, A.W. Engineering Tribology, 4th ed.; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Blau, P.J. The Significance and Use of the Friction Coefficient. Tribol. Int. 2001, 34, 585–591. [Google Scholar] [CrossRef]
- Holmberg, K.; Matthews, A. Coatings Tribology, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Gachot, C.; Rosenkranz, A.; Hsu, S.M.; Costa, H.L. A Critical Assessment of Surface Texturing for Friction and Wear Improvement. Wear 2017, 372–373, 21–41. [Google Scholar] [CrossRef]
- Al Mufachi, H.A.; Al Azawi, Z.H.; Abed, A.M. Tribological Behavior of Al7068/Si3N4 Reinforced Composites under Dry Sliding Conditions. Materials 2021, 14, 6871. [Google Scholar] [CrossRef]
- Bhushan, B. Introduction to Tribology, 2nd ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Wen, Q.; Liu, M.; Zhang, Z.; Sun, Y. Experimental Investigation into the Friction Coefficient of Ball-on-Disc in Dry Sliding Contact Considering the Effects of Surface Roughness, Low Rotation Speed, and Light Normal Load. Lubricants 2022, 10, 256. [Google Scholar] [CrossRef]
- Yin, C.; Li, N.; Wu, Y.; Liang, Y.; Yang, C.; Wu, J. Frictional Shear-Induced Nanolamellar Oxidation and Transformation to Oxide Nanoparticles during Pearlitic Steel Sliding. Mater. Des. 2023, 233, 112299. [Google Scholar] [CrossRef]
- Okonkwo, P.; Kelly, G.; Rolfe, B.F.; Pereira, M.P. The effect of sliding speed on the wear of steel–tool steel pairs. Tribol. Int. 2016, 97, 229–238. [Google Scholar] [CrossRef]
- Sun, K.; Peng, W.; Wei, B.; Yang, L.; Fang, L. Friction and Wear Characteristics of 18Ni(300) Maraging Steel under High-Speed Dry Sliding Conditions. Materials 2020, 13, 1485. [Google Scholar] [CrossRef] [PubMed]
- Hutchings, I.M. Tribology: Friction and Wear of Engineering Materials; Edward Arnold: London, UK, 1992. [Google Scholar]
- Gajević, S.; Marković, A.; Milojević, S.; Aćonja, A.; Ivanović, L.; Stojanović, B. Multi-Objective Optimization of Tribological Characteristics for Aluminum Composite Using Taguchi Grey and TOPSIS Approaches. Lubricants 2024, 12, 171. [Google Scholar] [CrossRef]
- Muthu, P. Multi Objective Optimization of Wear Behaviour of Aluminum MMCs Using Grey-Taguchi Method. Manuf. Rev. 2020, 7, 16. [Google Scholar] [CrossRef]
- Meng, H.C.; Ludema, K.C. Wear Models and Predictive Equations: Their Form and Content. Wear 1995, 181–183, 443–457. [Google Scholar] [CrossRef]


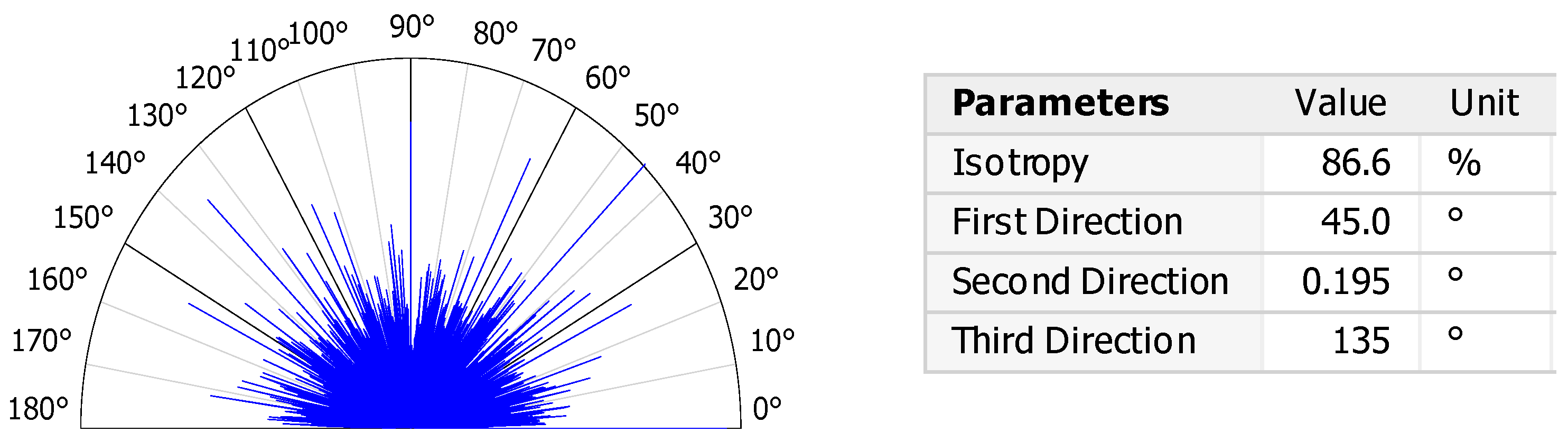
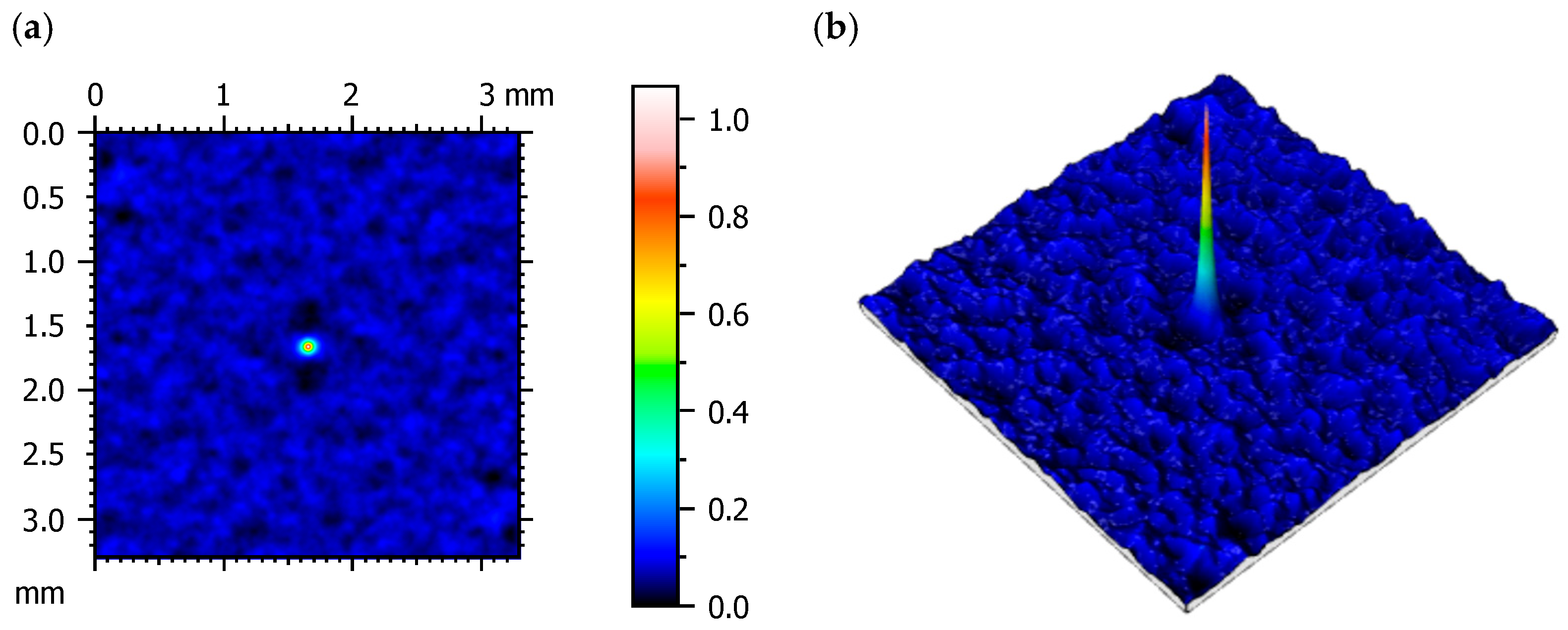
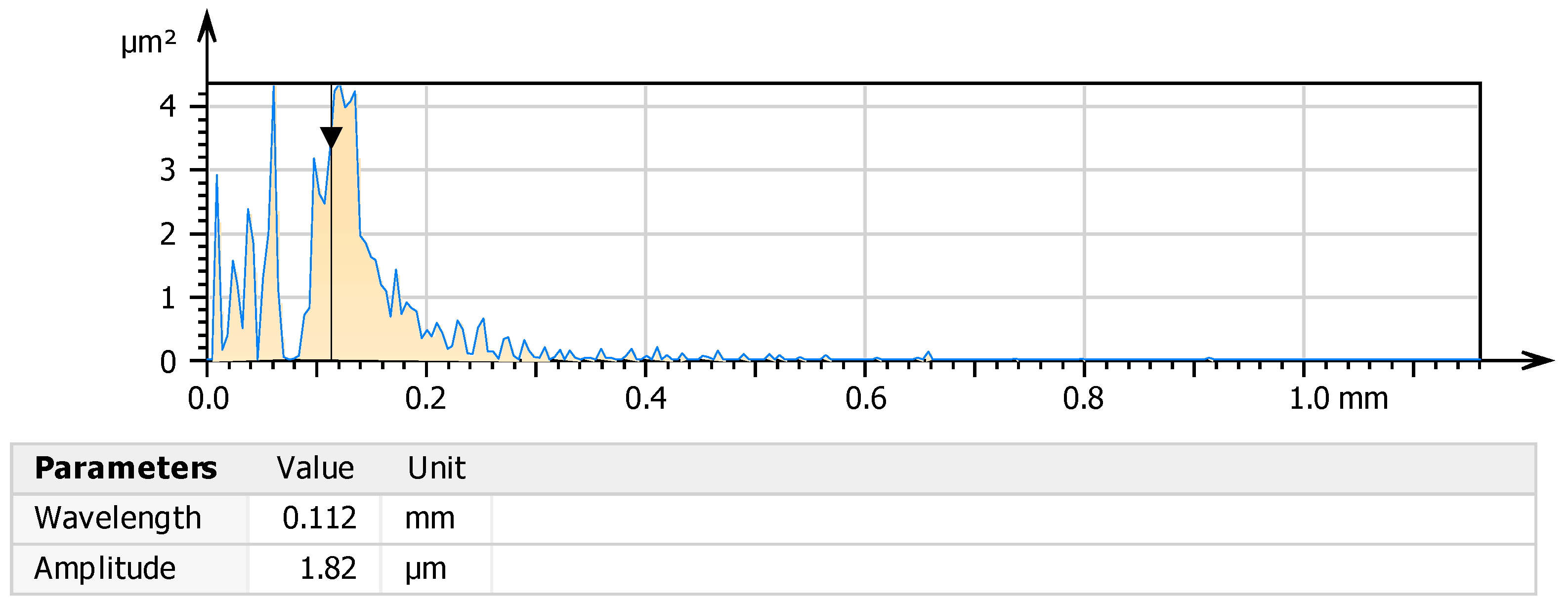

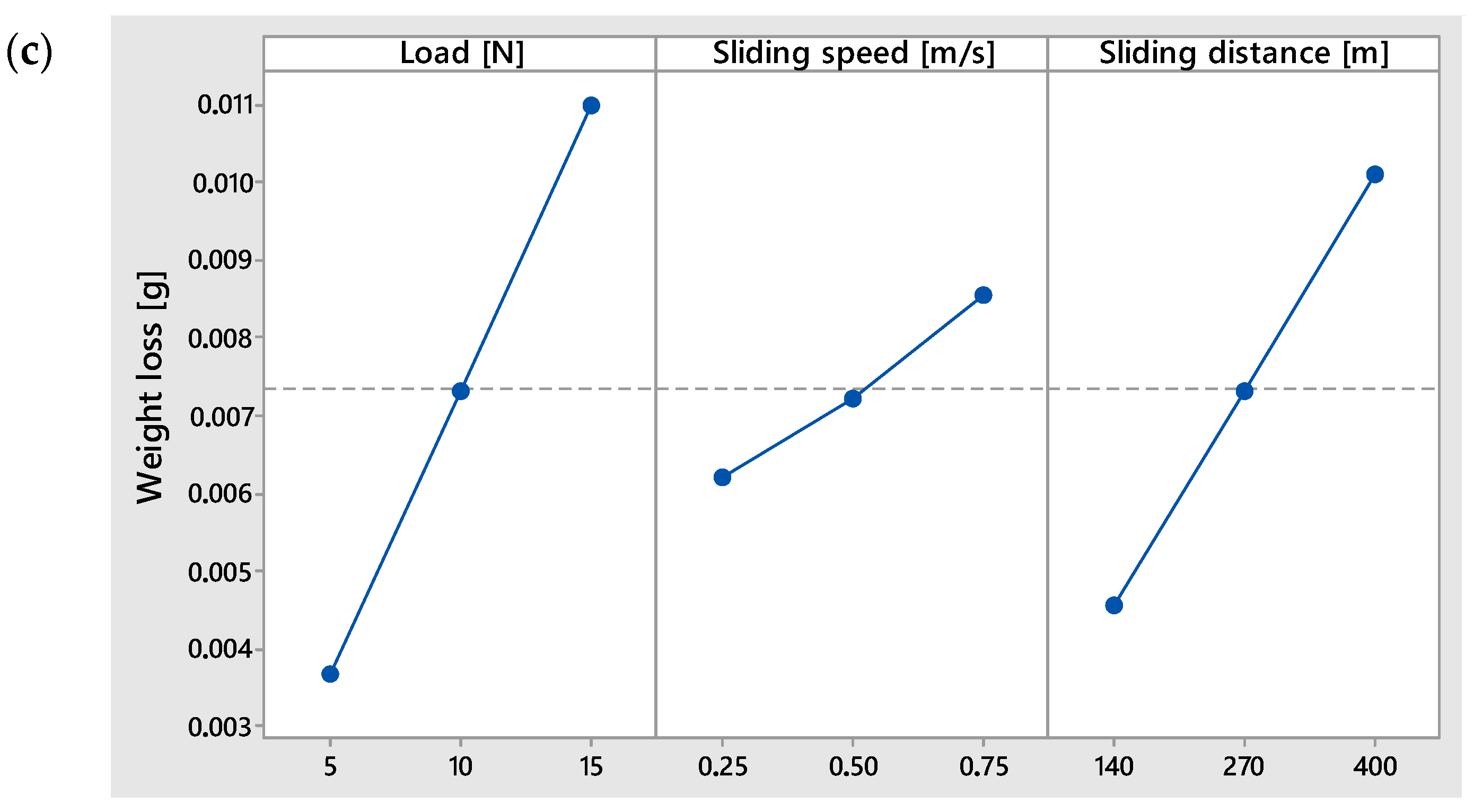

| Levels | Load [N] | Sliding Speed [m/s] | Sliding Distance [m] |
|---|---|---|---|
| 1 | 5 | 0.25 | 140 |
| 2 | 10 | 0.50 | 270 |
| 3 | 15 | 0.75 | 400 |
| No. | Input Parameters | Output Variables | ||||
|---|---|---|---|---|---|---|
| P [N] | v [m/s] | s [m] | VD [mm3] | CoF | WL [g] | |
| 1 | 5 | 0.25 | 140 | 0.169 | 0.565 | 0.002 |
| 2 | 5 | 0.25 | 270 | 0.201 | 0.572 | 0.003 |
| 3 | 5 | 0.25 | 400 | 0.233 | 0.571 | 0.004 |
| 4 | 5 | 0.5 | 140 | 0.174 | 0.536 | 0.002 |
| 5 | 5 | 0.5 | 270 | 0.212 | 0.541 | 0.004 |
| 6 | 5 | 0.5 | 400 | 0.571 | 0.532 | 0.005 |
| 7 | 5 | 0.75 | 140 | 0.357 | 0.499 | 0.003 |
| 8 | 5 | 0.75 | 270 | 0.477 | 0.502 | 0.004 |
| 9 | 5 | 0.75 | 400 | 0.584 | 0.479 | 0.006 |
| 10 | 10 | 0.25 | 140 | 0.568 | 0.622 | 0.004 |
| 11 | 10 | 0.25 | 270 | 0.607 | 0.589 | 0.006 |
| 12 | 10 | 0.25 | 400 | 0.868 | 0.606 | 0.009 |
| 13 | 10 | 0.5 | 140 | 0.474 | 0.585 | 0.004 |
| 14 | 10 | 0.5 | 270 | 0.531 | 0.549 | 0.007 |
| 15 | 10 | 0.5 | 400 | 0.653 | 0.555 | 0.01 |
| 16 | 10 | 0.75 | 140 | 0.642 | 0.526 | 0.005 |
| 17 | 10 | 0.75 | 270 | 0.972 | 0.519 | 0.009 |
| 18 | 10 | 0.75 | 400 | 1.216 | 0.526 | 0.012 |
| 19 | 15 | 0.25 | 140 | 1.459 | 0.645 | 0.006 |
| 20 | 15 | 0.25 | 270 | 2.168 | 0.621 | 0.009 |
| 21 | 15 | 0.25 | 400 | 2.635 | 0.633 | 0.013 |
| 22 | 15 | 0.5 | 140 | 1.088 | 0.606 | 0.007 |
| 23 | 15 | 0.5 | 270 | 1.429 | 0.609 | 0.011 |
| 24 | 15 | 0.5 | 400 | 1.914 | 0.575 | 0.015 |
| 25 | 15 | 0.75 | 140 | 2.783 | 0.544 | 0.008 |
| 26 | 15 | 0.75 | 270 | 3.762 | 0.536 | 0.013 |
| 27 | 15 | 0.75 | 400 | 3.957 | 0.546 | 0.017 |
| No | Weighted Normalized Value | Separation Values | Ci Value | Rank | |||
|---|---|---|---|---|---|---|---|
| VD [mm3] | CoF | WL [g] | A+ | A− | |||
| 1 | 0.0074 | 0.0867 | 0.0092 | 0.0132 | 0.1792 | 0.9314 | 3 |
| 2 | 0.0088 | 0.0878 | 0.0138 | 0.0151 | 0.1761 | 0.9212 | 5 |
| 3 | 0.0101 | 0.0877 | 0.0184 | 0.0171 | 0.1732 | 0.9102 | 6 |
| 4 | 0.0076 | 0.0823 | 0.0092 | 0.0088 | 0.1794 | 0.9535 | 1 |
| 5 | 0.0092 | 0.0830 | 0.0184 | 0.0134 | 0.1744 | 0.9288 | 4 |
| 6 | 0.0249 | 0.0817 | 0.0230 | 0.0237 | 0.1584 | 0.8697 | 9 |
| 7 | 0.0155 | 0.0766 | 0.0138 | 0.0099 | 0.1709 | 0.9454 | 2 |
| 8 | 0.0208 | 0.0771 | 0.0184 | 0.0166 | 0.1643 | 0.9080 | 7 |
| 9 | 0.0254 | 0.0735 | 0.0276 | 0.0258 | 0.1574 | 0.8602 | 10 |
| 10 | 0.0247 | 0.0955 | 0.0184 | 0.0295 | 0.1593 | 0.8439 | 12 |
| 11 | 0.0264 | 0.0904 | 0.0276 | 0.0314 | 0.1546 | 0.8311 | 14 |
| 12 | 0.0378 | 0.0930 | 0.0414 | 0.0484 | 0.1395 | 0.7424 | 16 |
| 13 | 0.0206 | 0.0898 | 0.0184 | 0.0229 | 0.1633 | 0.8769 | 8 |
| 14 | 0.0231 | 0.0843 | 0.0322 | 0.0299 | 0.1568 | 0.8399 | 13 |
| 15 | 0.0284 | 0.0852 | 0.0461 | 0.0440 | 0.1480 | 0.7708 | 15 |
| 16 | 0.0279 | 0.0807 | 0.0230 | 0.0258 | 0.1556 | 0.8577 | 11 |
| 17 | 0.0423 | 0.0797 | 0.0414 | 0.0479 | 0.1364 | 0.7400 | 17 |
| 18 | 0.0529 | 0.0807 | 0.0553 | 0.0652 | 0.1229 | 0.6535 | 19 |
| 19 | 0.0635 | 0.0990 | 0.0276 | 0.0643 | 0.1200 | 0.6509 | 20 |
| 20 | 0.0944 | 0.0953 | 0.0414 | 0.0953 | 0.0862 | 0.4750 | 23 |
| 21 | 0.1147 | 0.0972 | 0.0599 | 0.1210 | 0.0604 | 0.3331 | 25 |
| 22 | 0.0473 | 0.0930 | 0.0322 | 0.0501 | 0.1333 | 0.7268 | 18 |
| 23 | 0.0622 | 0.0935 | 0.0507 | 0.0716 | 0.1136 | 0.6134 | 21 |
| 24 | 0.0833 | 0.0883 | 0.0691 | 0.0978 | 0.0900 | 0.4792 | 22 |
| 25 | 0.1211 | 0.0835 | 0.0368 | 0.1175 | 0.0676 | 0.3653 | 24 |
| 26 | 0.1638 | 0.0823 | 0.0599 | 0.1646 | 0.0263 | 0.1377 | 26 |
| 27 | 0.1722 | 0.0838 | 0.0783 | 0.1791 | 0.0152 | 0.0782 | 27 |
| No | Normalized Values | GRC | GRG Grade | Rank | ||||
|---|---|---|---|---|---|---|---|---|
| VD [mm3] | CoF | WL [g] | VD [mm3] | CoF | WL [g] | |||
| 1 | 1.0000 | 0.4819 | 1.0000 | 1.0000 | 0.4911 | 1.0000 | 0.7710 | 5 |
| 2 | 0.9916 | 0.4398 | 0.9333 | 0.9835 | 0.4716 | 0.8824 | 0.7329 | 7 |
| 3 | 0.9832 | 0.4458 | 0.8667 | 0.9675 | 0.4743 | 0.7895 | 0.7100 | 9 |
| 4 | 0.9988 | 0.6566 | 1.0000 | 0.9976 | 0.5929 | 1.0000 | 0.8159 | 3 |
| 5 | 0.9887 | 0.6265 | 0.8667 | 0.9778 | 0.5724 | 0.7895 | 0.7577 | 6 |
| 6 | 0.8939 | 0.6807 | 0.8000 | 0.8249 | 0.6103 | 0.7143 | 0.7062 | 10 |
| 7 | 0.9504 | 0.8795 | 0.9333 | 0.9098 | 0.8058 | 0.8824 | 0.8575 | 2 |
| 8 | 0.9187 | 0.8614 | 0.8667 | 0.8601 | 0.7830 | 0.7895 | 0.8113 | 4 |
| 9 | 0.8904 | 1.0000 | 0.7333 | 0.8203 | 1.0000 | 0.6522 | 0.8675 | 1 |
| 10 | 0.8948 | 0.1386 | 0.8667 | 0.8262 | 0.3673 | 0.7895 | 0.6123 | 14 |
| 11 | 0.8845 | 0.3373 | 0.7333 | 0.8123 | 0.4301 | 0.6522 | 0.6083 | 16 |
| 12 | 0.8155 | 0.2349 | 0.5333 | 0.7305 | 0.3952 | 0.5172 | 0.5370 | 18 |
| 13 | 0.9197 | 0.3614 | 0.8667 | 0.8616 | 0.4392 | 0.7895 | 0.6571 | 12 |
| 14 | 0.9045 | 0.5783 | 0.6667 | 0.8397 | 0.5425 | 0.6000 | 0.6580 | 11 |
| 15 | 0.8723 | 0.5422 | 0.4667 | 0.7965 | 0.5220 | 0.4839 | 0.6105 | 15 |
| 16 | 0.8752 | 0.7169 | 0.8000 | 0.8003 | 0.6385 | 0.7143 | 0.7103 | 8 |
| 17 | 0.7881 | 0.7590 | 0.5333 | 0.7024 | 0.6748 | 0.5172 | 0.6529 | 13 |
| 18 | 0.7238 | 0.7169 | 0.3333 | 0.6441 | 0.6385 | 0.4286 | 0.5985 | 17 |
| 19 | 0.6596 | 0.0000 | 0.7333 | 0.5949 | 0.3333 | 0.6522 | 0.4887 | 21 |
| 20 | 0.4724 | 0.1446 | 0.5333 | 0.4866 | 0.3689 | 0.5172 | 0.4397 | 25 |
| 21 | 0.3490 | 0.0723 | 0.2667 | 0.4344 | 0.3502 | 0.4054 | 0.3907 | 27 |
| 22 | 0.7576 | 0.2349 | 0.6667 | 0.6734 | 0.3952 | 0.6000 | 0.5336 | 19 |
| 23 | 0.6674 | 0.2169 | 0.4000 | 0.6005 | 0.3897 | 0.4545 | 0.4764 | 22 |
| 24 | 0.5393 | 0.4217 | 0.1333 | 0.5204 | 0.4637 | 0.3659 | 0.4640 | 24 |
| 25 | 0.3101 | 0.6084 | 0.6000 | 0.4202 | 0.5608 | 0.5556 | 0.5105 | 20 |
| 26 | 0.0514 | 0.6566 | 0.2667 | 0.3452 | 0.5929 | 0.4054 | 0.4687 | 23 |
| 27 | 0.0000 | 0.5964 | 0.0000 | 0.3333 | 0.5533 | 0.3333 | 0.4323 | 26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dzierwa, A.; Miturska-Barańska, I. Optimization of Tribological Properties of Shot-Peened Surfaces via Multi-Criteria Decision-Making Using TOPSIS and GRA. Materials 2025, 18, 3733. https://doi.org/10.3390/ma18163733
Dzierwa A, Miturska-Barańska I. Optimization of Tribological Properties of Shot-Peened Surfaces via Multi-Criteria Decision-Making Using TOPSIS and GRA. Materials. 2025; 18(16):3733. https://doi.org/10.3390/ma18163733
Chicago/Turabian StyleDzierwa, Andrzej, and Izabela Miturska-Barańska. 2025. "Optimization of Tribological Properties of Shot-Peened Surfaces via Multi-Criteria Decision-Making Using TOPSIS and GRA" Materials 18, no. 16: 3733. https://doi.org/10.3390/ma18163733
APA StyleDzierwa, A., & Miturska-Barańska, I. (2025). Optimization of Tribological Properties of Shot-Peened Surfaces via Multi-Criteria Decision-Making Using TOPSIS and GRA. Materials, 18(16), 3733. https://doi.org/10.3390/ma18163733







