A Comprehensive Review of Numerical and Machine Learning Approaches for Predicting Concrete Properties: From Fresh to Long-Term
Highlights
- This paper reviews state-of-the-art predictive methods for estimating extensive properties of cementitious materials, highlighting key challenges and advances.
- Data variability strongly affects model accuracy, requiring careful handling of missing values, normalization, and outlier detection.
- Both large and small datasets can yield accurate predictions, though larger datasets often enhance reliability.
- Machine Learning frequently outperforms traditional models in predicting properties like workability, strength, elastic modulus, and shrinkage.
- Complex interactions among materials and environmental factors make modeling challenging, demanding sophisticated approaches.
Abstract
1. Introduction
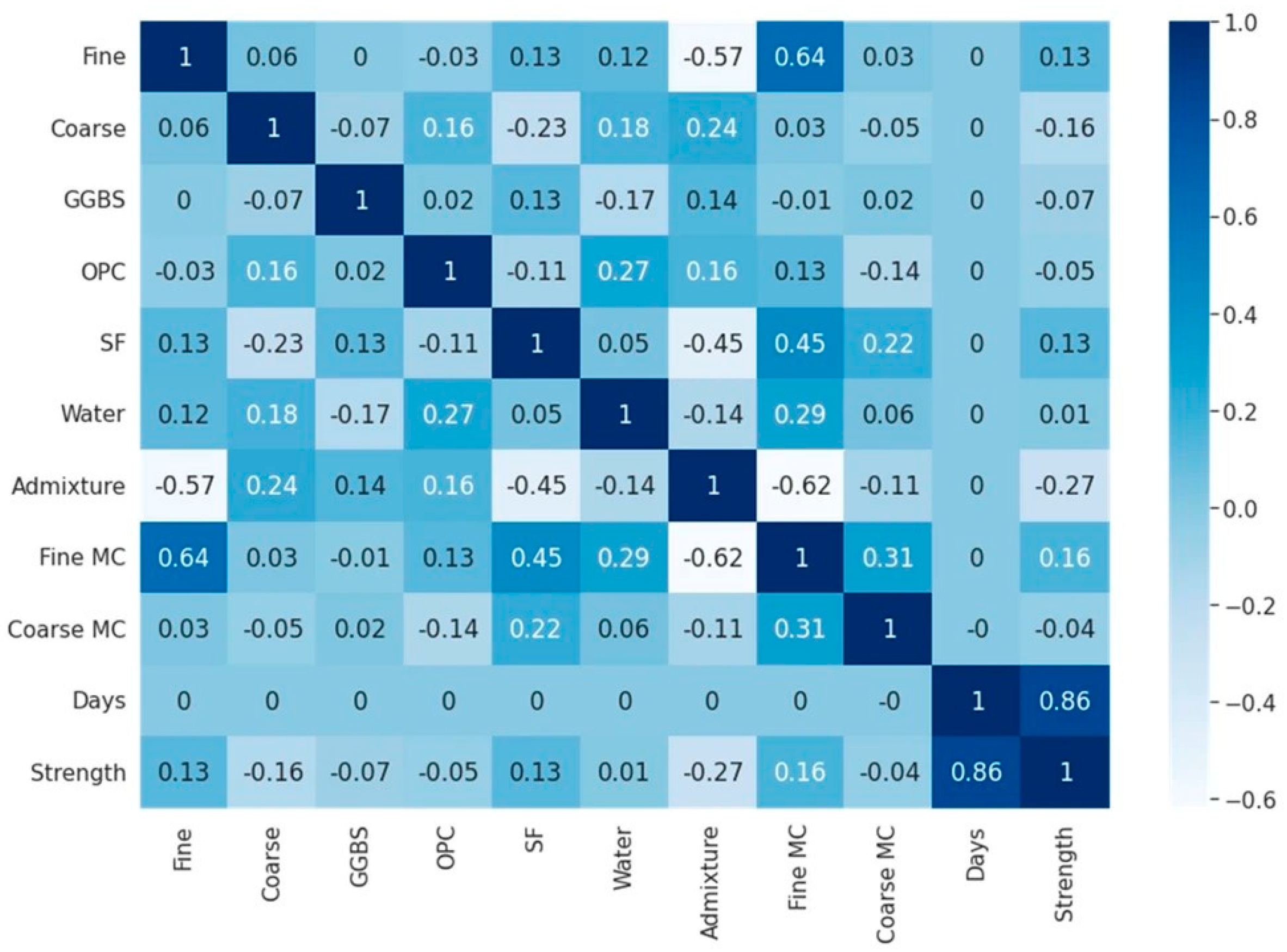
2. Methodology, Data Handling, and Data Processing Techniques

| Ref. | Type of Concrete | Input | Output | Model Evaluation Parameters | Dataset/Range | Model Interpretation and Modelling Technique |
|---|---|---|---|---|---|---|
| [4] | HPC | slump, w/b, W, FA, s/a, SF, and SP | 28D CS | R, PCC and MAPE, MSE, MAE | 77 | Generalized Regression Neural Network, Nonlinear Auto Regressive with exogenous inputs (NARX neural network), and RF, Radial Basis Function Neural Network |
| [7] | Concrete | C, fly ash, mineral powder content, FA, CA, W, and SP | 28D Cube CS | F1-score for classification tasks, MSE, RMSE, and MAE | 189 | Backpropagation Neural Network (BPNN), SVM, and RF, PSO algorithm |
| [9] | Concrete | C, BFS, Fly ash, W, SP, CA, FA, age | 28D CS | MAD, RMSE, CC, MAPE | 1030 | ANN, MLR, SVM, and a regression tree |
| [10] | HPC | C, FA, W, SP, CA, fly ash, age | CS | MAE, MSE, RMSE, and RMSLE | 471 | MLP, DT, RF and GBR |
| [12] | Nano-modified concrete | w/c, carbon nanotubes, nano-silica, nano-clay, nano-aluminum, C, CA, and FA | Uniaxial CS | R2, MAPE, RMSE, RSR, and NMBE | 94 | BPNN, RF, XGB, and HEStack |
| [19] | Pervious concrete | C, CA, minimum Agg. Dmin and maximum Agg. Dmax diameter of CA, CA type, sand, w/c, content of additions, content of additives, porosity | Permeability and CS | R2 | 3252 | ANN (MLP) |
| [55] | HSC | w/b, W, FA, fly ash replacement ratio, SF replacement ratio and SP | 28D CS | RMSE, MAE, R | 300 | Multilayer Perceptron (MLP), M5P Tree models and LR |
| [62] | Concrete | w/c, w/b, a/c, C, SF, Fly ash, BFS, MK, Filler, SP, SAP%, SAP size, SAP water uptake (%), time | AS | RMSE, R2, Overall Index of model performance, MAE, and 95% Uncertainty | 437 | Simple Average Ensemble, Snapshot Ensemble, and Stacked Generalization, integrated stacking model (ISM), SHAP, KNN, RF, Gradient Boosting (GB), and XGB |
| [66] | HPC | C, BFS, Fly ash, W, SP, CA, FA, age of testing | CS | R2, RMSE, MAE, MAPE, RRSE, RMSLE, R, KGE, NSE | 1133 | ELimination Et Choix Traduisant la REalité (ELECTRE), Recursive Feature Elimination (RFE), SHAP, logistic regression, SVM, RF, XGB, AdaBoost, CatBoost, LightGBM, and MLP |
| [70] | Normal concrete | C, BS, fly ash, water, SP, CA, FA, and age | 28D CS | R2, RMSE, MAE | 1030 | RFR and CatBoost, fivefold cross-validation technique |
| [71] | Aluminate cement pastes and concrete | Amount of SAP, Size of SAP (mesh), and C/W | CS, modulus of elasticity, and split TS | Standard deviation (SD) | 45 | Box–Behnken design |
| [72] | Cellular concrete | Density of fresh concrete, w/c, s/c, vol./weight of C, W, and air, degree of hydration | 28D CS | R2 | 96 | Duff Abrams Formula, Feret’s formula, Powers’ modified gel/space ratio formula |
| [80] | HPC | C, BFS, Fly ash, W, SP, CA, FA, Age of testing | 28D CS | MAPE, RMSE | 1030 | Linear regression (LR), ANN, SVR |
| [81] | HSC | w/b, W, FA, fly ash replacement ratio, air-entraining agent ratio, SF replacement ratio and SP | CS and slump | RMS, SSE, R2, MAPE | 132 | ANN (BPNN) |
| [82] | SCC and HPC | C, w/c, w/b, w/p (P = C + FA + MS), FA/P, CA/P, HRWR/P, VMA/P, FA/B, MS/B | Slump and 28D CS | R2, Error | 300 | ANN (Matlab Neural Network Toolbox and Alyuda NeuroIntelligence (2001)) |
| [83] | Porous concrete | Cement to aggregate, specific gravity of binder, aggregate density, sample density, total porosity, CS | Relation between porosity and CS | R2 | Approx. 42 | Griffith’s fracture theory, Multiple linear regression run by least square method |
| [90] | Cement paste with/without GGBS | RH, w/c, volume fraction of the aggregates, shrinkage of the paste, correlation parameter controlled by aggregate restraining effects | Drying (DS) and autogenous shrinkage (AS) | R2 | Approx. 40 | HYMOSTRUC model, Pickett model |
| [84] | HSC | C, sand, small CA, medium CA, W, and SP | 3-, 7-, and 28-day CS | RMSE, MAPE, R2 | 239 | Least Squares Support Vector Regression Firefly Algorithm (FFA) |
| [85] | concrete | C and NA | 28D CS | R2 | 618 | Abrams, Slater and ACI models, two modified models (Bolomey and Feret) |
| [86] | Pervious concrete | w/c, a/c, and aggregate size | Permeability coefficient and 28D unconfined CS (UCS) | RMSE, R | 270 | Evolved support vector regression (ESVR) tuned by beetle antennae search (BAS) |
| [87] | Concrete | C, BFS, fly ash, W, SP, CA, FA | Slump and 28D CS | R, MAE | 103 | LR analysis, classification and regression tree analysis, Chi-squared automatic interaction detection, ANN, and SVM |
3. Modelling Techniques
3.1. Fresh Properties
3.2. Internal Relative Humidity (IRH) and Degree of Hydration (DOH)
3.3. Porosity
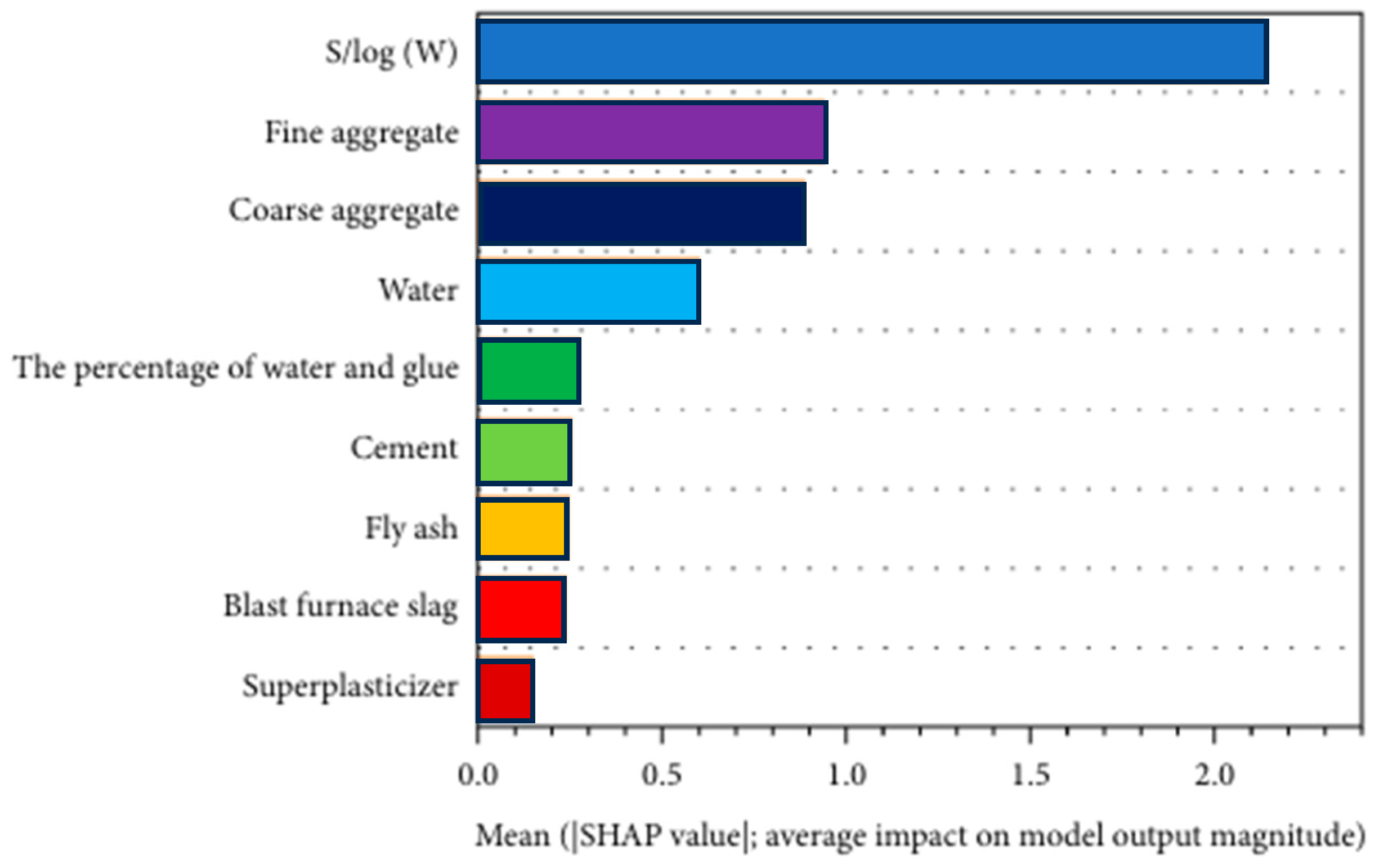
3.4. Compressive Strength (CS)
3.5. Tensile Strength (TS)
3.6. Flexural Strength (FS)
3.7. Elastic Modulus (EM)
3.8. Shrinkage
3.8.1. Autogenous Shrinkage (AS)
3.8.2. Drying Shrinkage (DS)
3.9. Creep
3.10. Permeability and Sulphate Attack Resistance
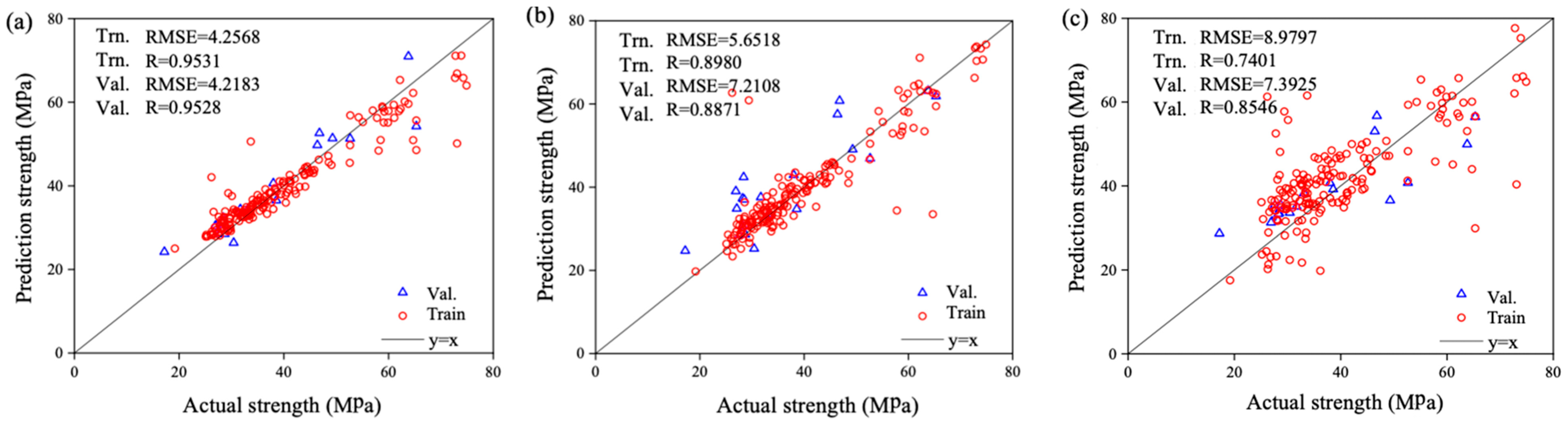
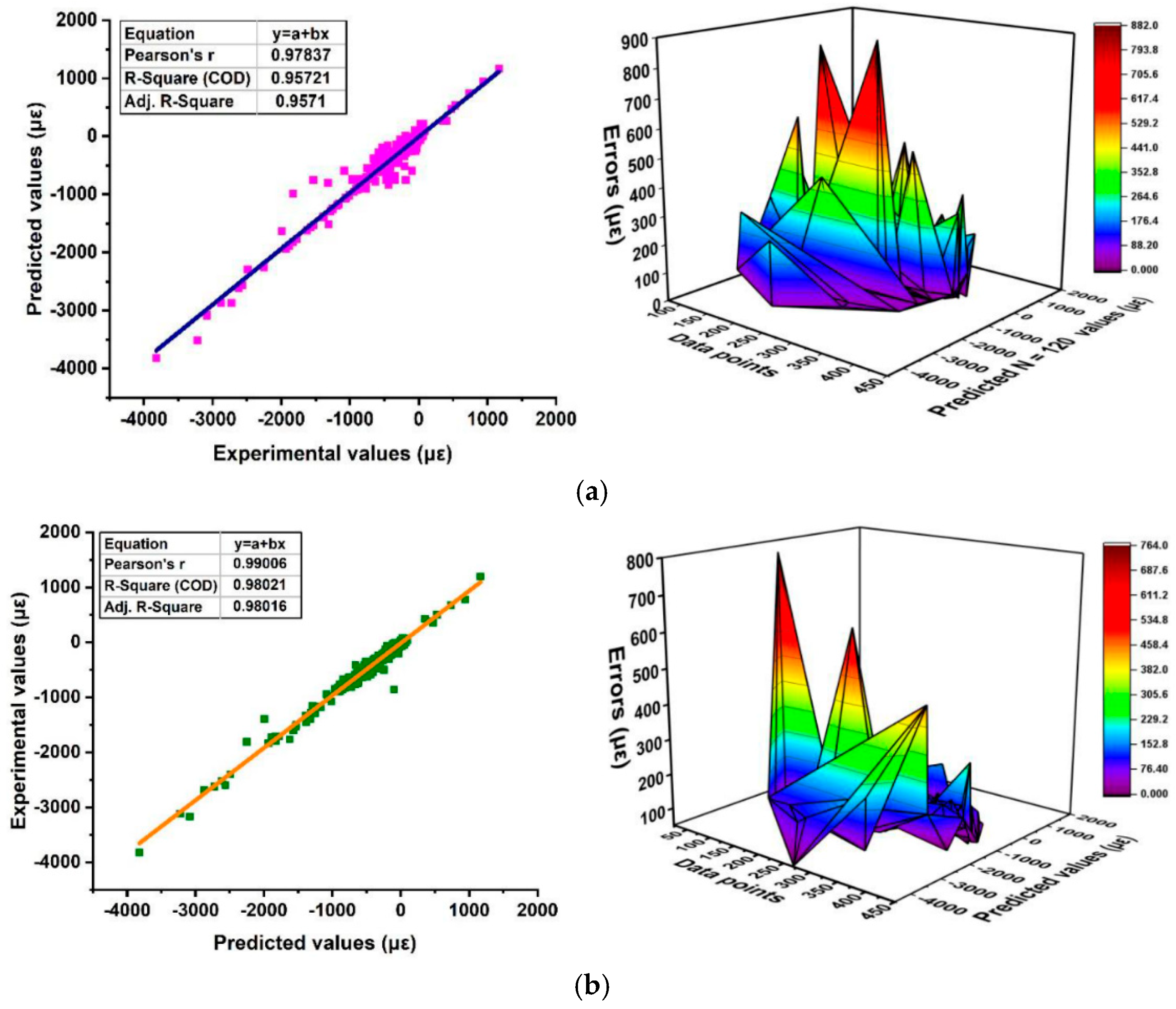
3.11. Model Validation Technique
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Van Damme, H. Concrete Material Science: Past, Present, and Future Innovations. Cem. Concr. Res. 2018, 112, 5–24. [Google Scholar] [CrossRef]
- Thapa, J. Concrete Compressive Strength Prediction by Ensemble Machine Learning Approach. J. Eng. Sci. 2024, 3, 66–73. [Google Scholar] [CrossRef]
- Elshaarawy, M.K.; Alsaadawi, M.M.; Hamed, A.K. Machine Learning and Interactive GUI for Concrete Compressive Strength Prediction. Sci. Rep. 2024, 14, 1–26. [Google Scholar] [CrossRef]
- Muhammad, U.J.; Aminu, I.I.; Mahmoud, I.A.; Aliyu, U.U.; Usman, A.G.; Jibril, M.M.; Malami, S.I.; Abba, S.I. An Improved Prediction of High-Performance Concrete Compressive Strength Using Ensemble Models and Neural Networks. AI Civ. Eng. 2024, 3, 21. [Google Scholar] [CrossRef]
- Naved, M.; Asim, M.; Ahmad, T. Prediction of Concrete Compressive Strength Using Deep Neural Networks Based on Hyperparameter Optimization. Cogent Eng. 2024, 11, 2297491. [Google Scholar] [CrossRef]
- Alsalman, A.; Dang, C.N.; Prinz, G.S.; Hale, W.M. Evaluation of Modulus of Elasticity of Ultra-High Performance Concrete. Constr. Build. Mater. 2017, 153, 918–928. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, X.; Chen, W.-Z. Advanced Predictive Modeling of Concrete Compressive Strength and Slump Characteristics: A Comparative Evaluation of BPNN, SVM, and RF Models Optimized via PSO. Materials 2024, 17, 4791. [Google Scholar] [CrossRef]
- Ulucan, M.; Gunduzalp, E.; Yildirim, G.; Alatas, B.; Alyamac, K.E. Optimizing Sustainable Concrete Compressive Strength Prediction: A New Particle Swarm Optimization-Based Metaheuristic Approach to Neural Network Modeling for Circular Economy and Disaster Resilience. Struct. Concr. 2024, 26, 1226–1244. [Google Scholar] [CrossRef]
- Sah, A.K.; Hong, Y.M. Performance Comparison of Machine Learning Models for Concrete Compressive Strength Prediction. Materials 2024, 17, 2075. [Google Scholar] [CrossRef]
- Song, Y.; Zhao, J.; Ostrowski, K.A.; Javed, M.F.; Ahmad, A.; Khan, M.I.; Aslam, F.; Kinasz, R. Prediction of Compressive Strength of Fly-Ash-Based Concrete Using Ensemble and Non-Ensemble Supervised Machine-Learning Approaches. Appl. Sci. 2021, 12, 361. [Google Scholar] [CrossRef]
- Li, Z.; Yoon, J.; Zhang, R.; Rajabipour, F.; Srubar III, W.V.; Dabo, I.; Radlińska, A. Machine Learning in Concrete Science: Applications, Challenges, and Best Practices. npj Comput. Mater. 2022, 8, 127. [Google Scholar] [CrossRef]
- Tao, X. Compressive Strength Prediction of Nano-Modified Concrete: A Comparative Study of Advanced Machine Learning Techniques. AIP Adv. 2024, 14, 075017. [Google Scholar] [CrossRef]
- Wang, X.; Munir, M.J.; Wu, Y.-F. Effect of Mix Design Parameters on the Behavior of Compression Cast Concrete. J. Build. Eng. 2023, 76, 107399. [Google Scholar] [CrossRef]
- Vellaichamy, P.; Kumar, J.M.W.V.; Elangovan, A.; Annadurai, H.; Veerachamy, S. kumar Material Aspects of High Performance Concrete. IOP Conf. Ser. Mater. Sci. Eng. 2020, 955, 012028. [Google Scholar] [CrossRef]
- Anand, P.; Singh, S.D.; Bhowmik, P.N.; Kontoni, D.-P.N. Optimizing Concrete Mix Proportions with Zeolite, GGBS, and CDW: A Data-Driven Approach Integrating Experimental Analysis and Machine Learning Models. Eng. Res. Express 2025, 7, 015105. [Google Scholar] [CrossRef]
- Ćurčić, G.T.; Grdić, D.; Ristić, N.; Grdić, Z. Impact of the River Aggregate Particle Size Distribution on the Quantity of Cement and Admixtures Required for Making of Concrete Mixes of the Same Properties. Rom. J. Mater. 2016, 46, 277–288. [Google Scholar]
- Meddah, M.S.; Zitouni, S.; Belâabes, S. Effect of Content and Particle Size Distribution of Coarse Aggregate on the Compressive Strength of Concrete. Constr. Build. Mater. 2010, 24, 505–512. [Google Scholar] [CrossRef]
- Ogunbayo, B.F.; Aigbavboa, C.O. Experimental Investigation of Coarse Aggregates Used for Concrete Production in the Construction of Higher Educational Institution (HEI) Buildings. J. Phys. Conf. Ser. 2019, 1378, 032012. [Google Scholar] [CrossRef]
- Wu, Y.; Pieralisi, R.B.; Sandoval, F.G.; López-Carreño, R.D.; Pujadas, P. Optimizing Pervious Concrete with Machine Learning: Predicting Permeability and Compressive Strength Using Artificial Neural Networks. Constr. Build. Mater. 2024, 443, 137619. [Google Scholar] [CrossRef]
- Gadve, S.; Jajodia, R. Development of Statistical Models for Prediction of Mechanical Properties of Plain Concrete. Inf. Construcción 2022, 74, e440. [Google Scholar] [CrossRef]
- Ghahremani, G.; Bagheri, A.; Zanganeh, H. The Effect of Size and Shape of Pores on the Prediction Model of Compressive Strength of Foamed Concrete. Constr. Build. Mater. 2023, 371, 130720. [Google Scholar] [CrossRef]
- Ben Youssef, M.; Miled, K.; Néji, J. Mechanical Properties of Non-Autoclaved Foam Concrete: Analytical Models vs. Experimental Data. Eur. J. Environ. Civ. Eng. 2020, 24, 472–480. [Google Scholar] [CrossRef]
- Schiller, K.K. Strength of Porous Materials. Cem. Concr. Res. 1971, 1, 419–422. [Google Scholar] [CrossRef]
- Ryshkewitch, E. Compression Strength of Porous Sintered Alumina and Zirconia. J. Am. Ceram. Soc. 1953, 36, 65–68. [Google Scholar] [CrossRef]
- Kiang, K.H. Development of Creep and Shrinkage Prediction Model for Malaysian Normal Strength Concrete; Universiti Teknologi Malaysia: Skudai, Malaysia, 2006. [Google Scholar]
- EN 1992-1-1:2004; Eurocode 2: Design of Concrete Structures Part1-1: General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- ACI 209R-92; Prediction of Creep, Shrinkage, and Temperature Effects on in Concrete Structures. ACI Committee: Québec, QC, Canada, 2000.
- CEB-FIP 1990; Evaluation of the Time Dependent Properties of Concrete, Bulletin d’Information No. 199. Comite European du Beton/Federation Internationale de la Precontrainte: Lausanne, Switzerland, 1990.
- Pan, Z.; Li, B.; Lu, Z. Re-Evaluation of CEB-FIP 90 Prediction Models for Creep and Shrinkage with Experimental Database. Constr. Build. Mater. 2013, 38, 1022–1030. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Baweja, S. Short form of creep and shrinkage prediction model B3 for structures of medium sensitivity. Mat. Struct. 1996, 29, 587–593. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Baweja, S. Creep and shrinkage prediction model for analysis and design of concrete structures—model B3. Mater. Struct. 1995, 28, 357–365. [Google Scholar] [CrossRef]
- Gardner, N.J.; Lockman, M.J. Design Provisions for Drying Shrinkage and Creep of Normal Strength Concrete. ACI Mater. J. 2001, 98, 159–167. [Google Scholar] [CrossRef]
- AS 3600-2009; Australian Standard for Concrete Structures by Committee BD-002. Standards Australia: Sydney, Australia, 2009.
- ACI 318-14; Building Code Requirements for Structural Concrete. American Committee Institute: Farmington Hills, MI, USA, 2014.
- CEB-FIP-2010; fib Model Code for Concrete Structures. International Federation for Structural Concrete: Lausanne, Switzerland, 2010. [CrossRef]
- JTG/T F30-2014; Technical Guidelines for Construction of Highway Cement Concrete Pavements. Ministry of Transport of the People’s Republic of China: Beijing, China, 2014.
- Xie, F.; Zhang, C.; Cai, D.; Ruan, J. Comparative Study on the Mechanical Strength of SAP Internally Cured Concrete. Front. Mater. 2020, 7, 588130. [Google Scholar] [CrossRef]
- Ali, A.; Mostafa, M. A Model for Prediction of Compressive Strength of Chemically Activated High Phosphorous Slag Content Cement. Int. J. Civ. Eng. 2014, 12, 481–487. [Google Scholar]
- Chen, W.F.; Suzuki, H. Constitutive Models for Concrete. Comput. Struct. 1980, 12, 23–32. [Google Scholar] [CrossRef]
- Marchand, J.; Samson, E. Predicting the Service-Life of Concrete Structures—Limitations of Simplified Models. Cem. Concr. Compos. 2009, 31, 515–521. [Google Scholar] [CrossRef]
- Mirela, G.; Pavao, M. An Overview of Some Characteristic Numerical Models for Concrete. Eng. Model. 2012, 25, 65–75. [Google Scholar]
- Mohtasham Moein, M.; Saradar, A.; Rahmati, K.; Ghasemzadeh Mousavinejad, S.H.; Bristow, J.; Aramali, V.; Karakouzian, M. Predictive Models for Concrete Properties Using Machine Learning and Deep Learning Approaches: A Review. J. Build. Eng. 2023, 63, 105444. [Google Scholar] [CrossRef]
- Tiwari, T.; Tiwari, T.; Tiwari, S. How Artificial Intelligence, Machine Learning and Deep Learning Are Radically Different? Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2018, 8, 1. [Google Scholar] [CrossRef]
- Ramprasad, R.; Batra, R.; Pilania, G.; Mannodi-Kanakkithodi, A.; Kim, C. Machine Learning in Materials Informatics: Recent Applications and Prospects. npj Comput. Mater. 2017, 3, 54. [Google Scholar] [CrossRef]
- Umehara, M.; Stein, H.S.; Guevarra, D.; Newhouse, P.F.; Boyd, D.A.; Gregoire, J.M. Analyzing Machine Learning Models to Accelerate Generation of Fundamental Materials Insights. npj Comput. Mater. 2019, 5, 34. [Google Scholar] [CrossRef]
- Himanen, L.; Geurts, A.; Foster, A.S.; Rinke, P. Data-Driven Materials Science: Status, Challenges, and Perspectives. Adv. Sci. 2019, 6, 1900808. [Google Scholar] [CrossRef]
- Han, T.; Ponduru, S.A.; Cook, R.; Huang, J.; Sant, G.; Kumar, A. A Deep Learning Approach to Design and Discover Sustainable Cementitious Binders: Strategies to Learn From Small Databases and Develop Closed-Form Analytical Models. Front. Mater. 2022, 8, 796476. [Google Scholar] [CrossRef]
- Rios, R.; Childs, C.; Smith, S.; Washburn, N.; Kurtis, K. Advancing Cement-Based Materials Design through Data Science Approaches. RILEM Tech. Lett. 2021, 6, 140–149. [Google Scholar] [CrossRef]
- Moradi, M.J.; Khaleghi, M.; Salimi, J.; Farhangi, V.; Ramezanianpour, A.M. Predicting the Compressive Strength of Concrete Containing Metakaolin with Different Properties Using ANN. Measurement 2021, 183, 109790. [Google Scholar] [CrossRef]
- Algaifi, H.A.; Bakar, S.A.; Alyousef, R.; Sam, A.R.M.; Alqarni, A.S.; Wan Ibrahim, M.H.; Shahidan, S.; Ibrahim, M.; Salami, B.A. Machine Learning and RSM Models for Prediction of Compressive Strength of Smart Bio-Concrete. Smart Struct. Syst. 2021, 28, 535–551. [Google Scholar] [CrossRef]
- Bandaru, M.D.; Kyle, S.; Priyadarshini, T.I.; Prasad Bokka, D.V.; Sai, U.G. Predicting the Compressive Strength of Concrete by Using Machine Learning Techniques. J. Phys. Conf. Ser. 2024, 2779, 012016. [Google Scholar] [CrossRef]
- Njoroge, M.W.; Abuodha, S.O.; Kabando, E.K.; Achieng, K.O. Modelling of Restrained Shrinkage Stresses in Mortar Using Artificial Neural Networks. Int. Res. J. Multidiscip. Technovation 2024, 6, 40–60. [Google Scholar] [CrossRef]
- Mohammed, A.; Rafiq, S.; Sihag, P.; Kurda, R.; Mahmood, W. Soft Computing Techniques: Systematic Multiscale Models to Predict the Compressive Strength of HVFA Concrete Based on Mix Proportions and Curing Times. J. Build. Eng. 2021, 33, 101851. [Google Scholar] [CrossRef]
- Salami, B.A.; Iqbal, M.; Abdulraheem, A.; Jalal, F.E.; Alimi, W.; Jamal, A.; Tafsirojjaman, T.; Liu, Y.; Bardhan, A. Estimating Compressive Strength of Lightweight Foamed Concrete Using Neural, Genetic and Ensemble Machine Learning Approaches. Cem. Concr. Compos. 2022, 133, 104721. [Google Scholar] [CrossRef]
- Deepa, C.; SathiyaKumari, K.; Pream Sudha, V. Prediction of the Compressive Strength of High Performance Concrete Mix Using Tree Based Modeling. Int. J. Comput. Appl. 2010, 6, 18–24. [Google Scholar] [CrossRef]
- Chaitanya, M.; Manikandan, P.; Prem Kumar, V.; Elavenil, S.; Vasugi, V. Prediction of Self-Healing Characteristics of GGBS Admixed Concrete Using Artificial Neural Network. J. Phys. Conf. Ser. 2021, 1716, 012019. [Google Scholar] [CrossRef]
- Alshihri, M.M.; Azmy, A.M.; El-Bisy, M.S. Neural Networks for Predicting Compressive Strength of Structural Light Weight Concrete. Constr. Build. Mater. 2009, 23, 2214–2219. [Google Scholar] [CrossRef]
- Keshavarz, Z.; Torkian, H. Application of ANN and ANFIS Models in Determining Compressive Strength of Concrete. J. Soft Comput. Civ. Eng. 2017, 2, 62–70. [Google Scholar]
- Paudel, S.; Pudasaini, A.; Shrestha, R.K.; Kharel, E. Compressive Strength of Concrete Material Using Machine Learning Techniques. Clean. Eng. Technol. 2023, 15, 100661. [Google Scholar] [CrossRef]
- Schapire, R.E. The Boosting Approach to Machine Learning: An Overview. In MSRI Workshop on Nonlinear Estimation and Classification; Springer: New York, NY, USA, 2003; pp. 149–171. [Google Scholar]
- Kalule, R.; Abderrahmane, H.A.; Alameri, W.; Sassi, M. Stacked Ensemble Machine Learning for Porosity and Absolute Permeability Prediction of Carbonate Rock Plugs. Sci. Rep. 2023, 13, 9855. [Google Scholar] [CrossRef]
- Barkhordari, M.S.; Ghavaminejad, S.; Tehranizadeh, M. Predicting Autogenous Shrinkage of Concrete Including Superabsorbent Polymers and Other Cementitious Ingredients Using Convolution-Based Algorithms. Period. Polytech. Civ. Eng. 2024, 68, 1098–1121. [Google Scholar] [CrossRef]
- Ninditha Silalahi, D.D.; Marsella; Valentino, A.A.; Edbert, I.S.; Suhartono, D. Bagging and Boosting for Predicting Bank Customer Churn. In Proceedings of the 2023 International Conference on Advanced Mechatronics, Intelligent Manufacture and Industrial Automation (ICAMIMIA), Surabaya, Indonesia, 14–15 November 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Duan, M. Innovative Compressive Strength Prediction for Recycled Aggregate/Concrete Using K-Nearest Neighbors and Meta-Heuristic Optimization Approaches. J. Eng. Appl. Sci. 2024, 71, 1–16. [Google Scholar] [CrossRef]
- Taiwo, R.; Yussif, A.M.; Adegoke, A.H.; Zayed, T. Prediction and Deployment of Compressive Strength of High-Performance Concrete Using Ensemble Learning Techniques. Constr. Build. Mater. 2024, 451, 138808. [Google Scholar] [CrossRef]
- Nguyen, X.H.; Phan, Q.M.; Nguyen, N.T.; Tran, V.Q. Interpretable Machine Learning Model for Evaluating Mechanical Properties of Concrete Made with Recycled Concrete Aggregate. Struct. Concr. 2024, 25, 2890–2914. [Google Scholar] [CrossRef]
- Li, D.; Tang, Z.; Kang, Q.; Zhang, X.; Li, Y. Machine Learning-Based Method for Predicting Compressive Strength of Concrete. Processes 2023, 11, 390. [Google Scholar] [CrossRef]
- Ziyad Sami, B.H.; Ziyad Sami, B.F.; Kumar, P.; Ahmed, A.N.; Amieghemen, G.E.; Sherif, M.M.; El-Shafie, A. Feasibility Analysis for Predicting the Compressive and Tensile Strength of Concrete Using Machine Learning Algorithms. Case Stud. Constr. Mater. 2023, 18, e01893. [Google Scholar] [CrossRef]
- Sapkota, S.C.; Saha, P.; Das, S.; Meesaraganda, L.V.P. Prediction of the Compressive Strength of Normal Concrete Using Ensemble Machine Learning Approach. Asian J. Civ. Eng. 2024, 25, 583–596. [Google Scholar] [CrossRef]
- Gao, D.; Heimann, R.B.; Alexandertll, S.D.B. Box-Behnken Design Applied to Study the Strengthening of Aluminate Concrete Modified by a Superabsorbent Polymer/Clay Composite. Adv. Cem. Res. 1997, 9, 93–97. [Google Scholar] [CrossRef]
- Tam, C.T.; Lim, T.Y.; Ravindrarajah, R.S.; Lee, S.L. Relationship between Strength and Volumetric Composition of Moist-Cured Cellular Concrete. Mag. Concr. Res. 1987, 39, 115. [Google Scholar] [CrossRef]
- Kearsley, E.P.; Wainwright, P.J. The Effect of Porosity on the Strength of Foamed Concrete. Cem. Concr. Res. 2002, 32, 233–239. [Google Scholar] [CrossRef]
- Hoang, N.-D.; Pham, A.-D. Estimating Concrete Workability Based on Slump Test with Least Squares Support Vector Regression. J. Constr. Eng. 2016, 2016, 1–8. [Google Scholar] [CrossRef]
- Li, F.X.; Yu, Q.J.; Wei, J.X.; Li, J.X. Predicting the Workability of Self-Compacting Concrete Using Artificial Neural Network. Adv. Mat. Res. 2010, 168–170, 1730–1734. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Q.-F.; Zhou, H.-D.; Song, Z.-M. Experimental Study and Prediction Model of the Flexural Strength of Concrete Containing Fly Ash and Ground Granulated Blast-Furnace Slag. Adv. Civ. Eng. 2021, 2021, 8773664. [Google Scholar] [CrossRef]
- Rathakrishnan, V.; Bt. Beddu, S.; Ahmed, A.N. Predicting Compressive Strength of High-Performance Concrete with High Volume Ground Granulated Blast-Furnace Slag Replacement Using Boosting Machine Learning Algorithms. Sci. Rep. 2022, 12, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Hussain, A.; Farooqi, M.U.; Deifalla, A.F. Artificial Intelligence-Based Estimation of Ultra-High-Strength Concrete’s Flexural Property. Case Stud. Constr. Mater. 2022, 17, e01243. [Google Scholar] [CrossRef]
- Fei, Z.; Liang, S.; Cai, Y.; Shen, Y. Ensemble Machine-Learning-Based Prediction Models for the Compressive Strength of Recycled Powder Mortar. Materials 2023, 16, 583. [Google Scholar] [CrossRef]
- Chou, J.S.; Tsai, C.F. Concrete Compressive Strength Analysis Using a Combined Classification and Regression Technique. Autom. Constr. 2012, 24, 52–60. [Google Scholar] [CrossRef]
- Öztaş, A.; Pala, M.; Özbay, E.; Kanca, E.; Çaǧlar, N.; Bhatti, M.A. Predicting the Compressive Strength and Slump of High Strength Concrete Using Neural Network. Constr. Build. Mater. 2006, 20, 769–775. [Google Scholar] [CrossRef]
- Prasad, B.K.R.; Eskandari, H.; Reddy, B.V.V. Prediction of Compressive Strength of SCC and HPC with High Volume Fly Ash Using ANN. Constr. Build. Mater. 2009, 23, 117–128. [Google Scholar] [CrossRef]
- Lian, C.; Zhuge, Y.; Beecham, S. The Relationship between Porosity and Strength for Porous Concrete. Constr. Build. Mater. 2011, 25, 4294–4298. [Google Scholar] [CrossRef]
- Pham, A.-D.; Hoang, N.-D.; Nguyen, Q.-T. Predicting Compressive Strength of High-Performance Concrete Using Metaheuristic-Optimized Least Squares Support Vector Regression. J. Comput. Civ. Eng. 2015, 132, 31–39. [Google Scholar] [CrossRef]
- de Brito, J.; Kurda, R.; da Silva, P.R. Can We Truly Predict the Compressive Strength of Concrete without Knowing the Properties of Aggregates? Appl. Sci. 2018, 8, 1095. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, J.; Gu, Y.; Huang, Y.; Sun, Y.; Ma, G. Prediction of Permeability and Unconfined Compressive Strength of Pervious Concrete Using Evolved Support Vector Regression. Constr. Build. Mater. 2019, 207, 440–449. [Google Scholar] [CrossRef]
- Prayogo, D.; Santoso, D.I.; Wijaya, D.; Gunawan, T.; Widjaja, J.A. Prediction of Concrete Properties Using Ensemble Machine Learning Methods. J. Phys. Conf. Ser. 2020, 1625, 012024. [Google Scholar] [CrossRef]
- Cao, C. Prediction of Concrete Porosity Using Machine Learning. Results Eng. 2023, 17, 100794. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Mousavi, S.S.; Dehestani, M. An Ensemble Learning-Based Prediction Model for the Compressive Strength Degradation of Concrete Containing Superabsorbent Polymers (SAP). Sci. Rep. 2024, 14, 1–21. [Google Scholar] [CrossRef]
- Wei, Y.; Hansen, W.; Biernacki, J.J.; Schlangen, E. Unified Shrinkage Model for Concrete from Autogenous Shrinkage Test on Paste with and without Ground-Granulated Blast-Furnace Slag. ACI Mater. J. 2011, 108, 13–20. [Google Scholar]
- Kovler, K.; Roussel, N. Properties of Fresh and Hardened Concrete. Cem. Concr. Res. 2011, 41, 775–792. [Google Scholar] [CrossRef]
- Singh, P.; Bhardwaj, S.; Dixit, S.; Shaw, R.N.; Ghosh, A. Development of Prediction Models to Determine Compressive Strength and Workability of Sustainable Concrete with ANN; Springer: Singapore, 2021; pp. 753–769. [Google Scholar]
- Agarwal, V.; Sharma, A. Prediction of Slump in Concrete Using Artificial Neural Networks. Int. J. Civ. Environ. Struct. Constr. Archit. Eng. 2010, 4, 279–286. [Google Scholar]
- Bai, J.; Wild, S.; Ware, J.A.; Sabir, B.B. Using Neural Networks to Predict Workability of Concrete Incorporating Metakaolin and Fly Ash. Adv. Eng. Softw. 2003, 34, 663–669. [Google Scholar] [CrossRef]
- Azimi-Pour, M.; Eskandari-Naddaf, H.; Pakzad, A. Linear and Non-Linear SVM Prediction for Fresh Properties and Compressive Strength of High Volume Fly Ash Self-Compacting Concrete. Constr. Build. Mater. 2020, 230, 117021. [Google Scholar] [CrossRef]
- Jiang, J.; Xin, C.; Wu, S.; Chen, W.; Li, H.; Ran, Z. Enhancing Concrete Workability Prediction Through Ensemble Learning Models: Emphasis on Slump and Material Factors. Adv. Civ. Eng. 2024, 2024, 4616609. [Google Scholar] [CrossRef]
- Karim, R.; Islam, M.H.; Datta, S.D.; Kashem, A. Synergistic Effects of Supplementary Cementitious Materials and Compressive Strength Prediction of Concrete Using Machine Learning Algorithms with SHAP and PDP Analyses. Case Stud. Constr. Mater. 2024, 20, e02828. [Google Scholar] [CrossRef]
- Jin, R.; Chen, Q.; Soboyejo, A. A Statistical Approach to Predicting Fresh State Properties of Sustainable Concrete. Ser. Built Environ. 2021, 2, 28–36. [Google Scholar]
- Ostwald, W. Ueber die rechnerische Darstellung des Strukturgebietes der Viskosität. Colloid Polym. Sci. 1929, 47, 176–187. [Google Scholar] [CrossRef]
- Eyring, H. Viscosity, plasticity, and diffusion as examples of absolute reaction rates. J. Chem. Phys. 1936, 4, 283–291. [Google Scholar] [CrossRef]
- Sisko, A.W. The flow of lubricating greases. Ind. Eng. Chem. 1958, 50, 12, 1789–1792. [Google Scholar] [CrossRef]
- Casson, N. Rheology of disperse systems. In Proceedings of the Conference Organized by the British Society of Rheology; Pergamon Press: New York, NY, USA, 1959. [Google Scholar]
- Williamson, R.V. The flow of pseudoplastic materials. Ind. Eng. Chem. 1929, 21, 1108–1111. [Google Scholar] [CrossRef]
- Tao, C.; Kutchko, B.G.; Rosenbaum, E.; Massoudi, M. A Review of Rheological Modeling of Cement Slurry in Oil Well Applications. Energies 2020, 13, 570. [Google Scholar] [CrossRef]
- Flatt, R.J.; Bowen, P. Yodel: A Yield Stress Model for Suspensions. J. Am. Ceram. Soc. 2006, 89, 1244–1256. [Google Scholar] [CrossRef]
- Flatt, R.J.; Bowen, P. Yield Stress of Multimodal Powder Suspensions: An Extension of the YODEL (Yield Stress MODEL). J. Am. Ceram. Soc. 2007, 90, 1038–1044. [Google Scholar] [CrossRef]
- Krieger, I.M.; Dougherty, T.J. A Mechanism for Non-Newtonian Flow in Suspensions of Rigid Spheres. Trans. Soc. Rheol. 1959, 3, 137–152. [Google Scholar] [CrossRef]
- De La Rosa, Á.; Ruiz, G.; Castillo, E.; Moreno, R. Calculation of Dynamic Viscosity in Concentrated Cementitious Suspensions: Probabilistic Approximation and Bayesian Analysis. Materials 2021, 14, 1971. [Google Scholar] [CrossRef]
- Rajagopalan, S.R.; Lee, B.Y.; Kang, S.T. Prediction of the Rheological Properties of Fresh Cementitious Suspensions Considering Microstructural Parameters. Materials 2022, 15, 7044. [Google Scholar] [CrossRef]
- Shafiq, N. Degree of Hydration and Compressive Strength of Conditioned Samples Made of Normal and Blended Cement System. KSCE J. Civ. Eng. 2011, 15, 1253–1257. [Google Scholar] [CrossRef]
- Bentz, D.P. A Review of Early-Age Properties of Cement-Based Materials. Cem. Concr. Res. 2008, 38, 196–204. [Google Scholar] [CrossRef]
- Jiang, Z.; Sun, Z.; Wang, P. Internal Relative Humidity Distribution in High-Performance Cement Paste Due to Moisture Diffusion and Self-Desiccation. Cem. Concr. Res. 2006, 36, 320–325. [Google Scholar] [CrossRef]
- Shen, D.; Wang, T.; Chen, Y.; Wang, M.; Jiang, G. Effect of Internal Curing with Super Absorbent Polymers on the Relative Humidity of Early-Age Concrete. Constr. Build. Mater. 2015, 99, 246–253. [Google Scholar] [CrossRef]
- Shen, D.; Wang, M.; Chen, Y.; Wang, T.; Zhang, J. Prediction Model for Relative Humidity of Early-Age Internally Cured Concrete with Pre-Wetted Lightweight Aggregates. Constr. Build. Mater. 2017, 144, 717–727. [Google Scholar] [CrossRef]
- Shen, D.; Wang, M.; Chen, Y.; Wang, W.; Zhang, J. Prediction of Internal Relative Humidity in Concrete Modified with Super Absorbent Polymers at Early Age. Constr. Build. Mater. 2017, 149, 543–552. [Google Scholar] [CrossRef]
- Dabarera, A.; Saengsoy, W.; Kaewmanee, K.; Mori, K.; Tangtermsirikul, S. Models for Predicting Hydration Degree and Adiabatic Temperature Rise of Mass Concrete Containing Ground Granulated Blast Furnace Slag. Eng. J. 2017, 21, 157–171. [Google Scholar] [CrossRef]
- Park, K.-B.; Noguchi, T.; Plawsky, J. Modeling of Hydration Reactions Using Neural Networks to Predict the Average Properties of Cement Paste. Cem. Concr. Res. 2005, 35, 1676–1684. [Google Scholar] [CrossRef]
- Lapeyre, J.; Han, T.; Wiles, B.; Ma, H.; Huang, J.; Sant, G.; Kumar, A. Machine Learning Enables Prompt Prediction of Hydration Kinetics of Multicomponent Cementitious Systems. Sci. Rep. 2021, 11, 3922. [Google Scholar] [CrossRef]
- Le, B.-A.; Vu, V.-H.; Seo, S.-Y.; Tran, B.-V.; Nguyen-Sy, T.; Le, M.-C.; Vu, T.-S. Predicting the Compressive Strength and the Effective Porosity of Pervious Concrete Using Machine Learning Methods. KSCE J. Civ. Eng. 2022, 26, 4664–4679. [Google Scholar] [CrossRef]
- Sathiparan, N.; Wijekoon, S.H.; Jeyananthan, P.; Subramaniam, D.N. Soft Computing to Predict the Porosity and Permeability of Pervious Concrete Based on Mix Design and Ultrasonic Pulse Velocity. Int. J. Pavement Eng. 2024, 25, 2337916. [Google Scholar] [CrossRef]
- Zavrtanik, N.; Prosen, J.; Tušar, M.; Turk, G. The Use of Artificial Neural Networks for Modeling Air Void Content in Aggregate Mixture. Autom. Constr. 2016, 63, 155–161. [Google Scholar] [CrossRef]
- EN 13108-1: 2006/AC:2008; Bituminous Mixtures-Material Specifications-Part 1: Asphalt Concrete. European Committee for Standardization: Brussels, Belgium, 2006.
- Mahajan, L.; Kirange, M.; Bhagat, S. Statistical Exploration for Enlargement of Reformed Water Cement Ratio Law for Fly Ash Concrete. Sigma J. Eng. Nat. Sci. 2024, 43, 269–281. [Google Scholar] [CrossRef]
- Pamfil, A.; Mihai, P. Compression Resistance of Concrete. Bull. Polytech. Inst. Iași. Construction. Archit. Sect. 2021, 67, 9–17. [Google Scholar] [CrossRef]
- Fu, Z. Review of Researches on Strength Model of Foamed Concrete. J. Phys. Conf. Ser. 2024, 2671, 012010. [Google Scholar] [CrossRef]
- Olawuyi, B.J. The Mechanical Behaviour of High-Performance Concrete with Superabsorbent Polymers (SAP); University of Stellenbosch: Stellenbosch, South Africa, 2016. [Google Scholar]
- Meera, M.; Gupta, S. Development of a Strength Model for Foam Concrete Based on Water—Cement Ratio. Mater. Today Proc. 2020, 32, 923–927. [Google Scholar] [CrossRef]
- Shen, D.; Liu, C.; Jiang, J.; Kang, J.; Li, M. Influence of Super Absorbent Polymers on Early-Age Behavior and Tensile Creep of Internal Curing High Strength Concrete. Constr. Build. Mater. 2020, 258, 120068. [Google Scholar] [CrossRef]
- Chidiac, S.E.; Moutassem, F.; Mahmoodzadeh, F. Compressive Strength Model for Concrete. Mag. Concr. Res. 2013, 65, 557–572. [Google Scholar] [CrossRef]
- Schindler Anton, K.; Folliard Kevin, J. Heat of Hydration Models for Cementitious Materials. ACI Mater. J. 2005, 102, 24–33. [Google Scholar] [CrossRef] [PubMed]
- De Larrard, F. Concrete Mixture Proportioning; CRC Press: Boca Raton, FL, USA, 1999; ISBN 9781482272055. [Google Scholar]
- Popovics, S. New Formulas for the Prediction of the Effect of Porosity on Concrete Strength. ACI J. Proc. 1985, 82, 136–146. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Song, Z.; Ding, Y. Predicting Compressive Strength of Cement-Based Materials Containing Water-Absorbent Polymers Considering the Internal-Curing Region. Constr. Build. Mater. 2022, 360, 129594. [Google Scholar] [CrossRef]
- Odler, I.; Rößler, M. Investigations on the Relationship between Porosity, Structure and Strength of Hydrated Portland Cement Pastes. II. Effect of Pore Structure and of Degree of Hydration. Cem. Concr. Res. 1985, 15, 401–410. [Google Scholar] [CrossRef]
- Hwang, K.; Noguchi, T.; Tomosawa, F. Prediction Model of Compressive Strength Development of Fly-Ash Concrete. Cem. Concr. Res. 2004, 34, 2269–2276. [Google Scholar] [CrossRef]
- Adresi, M.; Yamani, A.; Tabarestani, M.K.; Nalon, G.H. A Prediction Model for the Unconfined Compressive Strength of Pervious Concrete Based on Mix Design and Compaction Energy Variables Using the Response Surface Methodology. Buildings 2024, 14, 2834. [Google Scholar] [CrossRef]
- Younis, K.H.; Pilakoutas, K. Strength Prediction Model and Methods for Improving Recycled Aggregate Concrete. Constr. Build. Mater. 2013, 49, 688–701. [Google Scholar] [CrossRef]
- Ling, T.C. Prediction of Density and Compressive Strength for Rubberized Concrete Blocks. Constr. Build. Mater. 2011, 25, 4303–4306. [Google Scholar] [CrossRef]
- Rahimzadeh, C.Y.; Salih, A.; Barzinjy, A.A. Systematic Multiscale Models to Predict the Compressive Strength of Cement Paste as a Function of Microsilica and Nanosilica Contents, Water/Cement Ratio, and Curing Ages. Sustainability 2022, 14, 1723. [Google Scholar] [CrossRef]
- Ahmad, S.A.; Ahmed, H.U.; Rafiq, S.K.; Ahmad, D.A. Machine Learning Approach for Predicting Compressive Strength in Foam Concrete under Varying Mix Designs and Curing Periods. Smart Constr. Sustain. Cities 2023, 1, 1–17. [Google Scholar] [CrossRef]
- Lee, S.C. Prediction of Concrete Strength Using Artificial Neural Networks. Eng. Struct. 2003, 25, 849–857. [Google Scholar] [CrossRef]
- Zhang, Y.; Aslani, F. Compressive Strength Prediction Models of Lightweight Aggregate Concretes Using Ultrasonic Pulse Velocity. Constr. Build. Mater. 2021, 292, 123419. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhu, Z.; Yao, W.; Wang, Z.; Wang, C.; Wei, Y.; Wei, Z.; Guan, X. Accurate Prediction of Concrete Compressive Strength Based on Explainable Features Using Deep Learning. Constr. Build. Mater. 2022, 329, 127082. [Google Scholar] [CrossRef]
- Kang, M.C.; Yoo, D.Y.; Gupta, R. Machine Learning-Based Prediction for Compressive and Flexural Strengths of Steel Fiber-Reinforced Concrete. Constr. Build. Mater. 2021, 266, 121117. [Google Scholar] [CrossRef]
- Liu, G.; Sun, B. Concrete Compressive Strength Prediction Using an Explainable Boosting Machine Model. Case Stud. Constr. Mater. 2023, 18, e01845. [Google Scholar] [CrossRef]
- Ullah, H.S.; Khushnood, R.A.; Farooq, F.; Ahmad, J.; Vatin, N.I.; Ewais, D.Y.Z. Prediction of Compressive Strength of Sustainable Foam Concrete Using Individual and Ensemble Machine Learning Approaches. Materials 2022, 15, 3166. [Google Scholar] [CrossRef] [PubMed]
- Yaseen, Z.M.; Deo, R.C.; Hilal, A.; Abd, A.M.; Bueno, L.C.; Salcedo-Sanz, S.; Nehdi, M.L. Predicting Compressive Strength of Lightweight Foamed Concrete Using Extreme Learning Machine Model. Adv. Eng. Softw. 2018, 115, 112–125. [Google Scholar] [CrossRef]
- Shishegaran, A.; Varaee, H.; Rabczuk, T.; Shishegaran, G. High Correlated Variables Creator Machine: Prediction of the Compressive Strength of Concrete. Comput. Struct. 2021, 247, 106479. [Google Scholar] [CrossRef]
- Kashem, A.; Das, P. Compressive Strength Prediction of High-Strength Concrete Using Hybrid Machine Learning Approaches by Incorporating SHAP Analysis. Asian J. Civ. Eng. 2023, 24, 3243–3263. [Google Scholar] [CrossRef]
- Lan, W. Accurate Compressive Strength Prediction Using Machine Learning Algorithms and Optimization Techniques. J. Eng. Appl. Sci. 2024, 71, 1–20. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, R.; Lu, Y.; Huang, J.; Zhang, J.; Wang, R.; Lu, Y.; Huang, J. Prediction of Compressive Strength of Geopolymer Concrete Landscape Design: Application of the Novel Hybrid RF-GWO-XGBoost Algorithm. Buildings 2024, 14, 591. [Google Scholar] [CrossRef]
- Li, D.; Li, Z.; Lv, C.; Zhang, G.; Yin, Y. A Predictive Model of the Effective Tensile and Compressive Strengths of Concrete Considering Porosity and Pore Size. Constr. Build. Mater. 2018, 170, 520–526. [Google Scholar] [CrossRef]
- Cao, H.; Xiao, B.; Qin, F.; Yang, Q. A Mathematical Model for Predicting the Ultra-Early-Age Strength of Concrete. Coatings 2024, 14, 1140. [Google Scholar] [CrossRef]
- Glinicki, M.A. Effect of the Loading Rate on the Tensile Strength of Concrete. MRS Proc. 1985, 64, 93. [Google Scholar] [CrossRef]
- Sim, J.I.; Yang, K.H. A Proposal of Tensile Strength Prediction Models Considering Unit Weight of Concrete. J. Korea Inst. Struct. Maint. Insp. 2012, 16, 107–115. [Google Scholar] [CrossRef][Green Version]
- ACI 318-11; Building Code Requirements for Structural Concrete (ACI 318-11) and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2011.
- Balàzs, G.L.; Beeby, A.W.; Eibl, J.; Eligehausen, R.; Bigaj-van Vliet, A.; Lima, L.J.; Hilsdor, H.; Kordina, K.; König, G.; Soukhov, D.; et al. Fib Bulletin 1. Structural Concrete Textbook on Behaviour, Design and Perfomance Up Dated Knowledge of the CEB/FIP Model Code 1990 Volume 1; FIB The International Federation for Structural Concrete: Lausanne, Switzerland, 1999; ISBN 288394041X. [Google Scholar]
- Concrete Structures Standard NZS 3101:2006; The Design of Concrete Structures. New Zealand Standard: Wellington, New Zealand, 2006.
- Li, Q.; Ansari, F. High-Strength Concrete in Uniaxial Tension. ACI Mater. J. 2000, 97, 49–57. [Google Scholar] [CrossRef] [PubMed]
- Zheng, W.; Kwan, A.K.H.; Lee, P.K.K. Direct Tension Test of Concrete. ACI Mater. J. 2001, 98, 63–71. [Google Scholar] [CrossRef]
- Carniero, F.B.; Barcellos, A. Tensile Strength of Concretes. RILEM Bull. 1953, 13, 97–123. [Google Scholar]
- Slate, F.O.; Nilson, A.H.; Martinez, S. Mechanical Properties of High-Strength Lightweight Concrete. ACI J. 1986, 83, 606–613. [Google Scholar]
- Zhang, M.H.; Gjvorv, O.E. Mechanical Properties of High-Strength Lightweight Concrete. ACI Mater. J. 1991, 88, 240–247. [Google Scholar] [CrossRef]
- Zain, M.F.M.; Mahmud, H.B.; Ilham, A.; Faizal, M. Prediction of Splitting Tensile Strength of High-Performance Concrete. Cem. Concr. Res. 2002, 32, 1251–1258. [Google Scholar] [CrossRef]
- ACI 363R-92; State of the Art Report on High-Strength Concrete. American Concrete Institute: Farmington Hills, MI, USA, 1992.
- ACI 318-99; Building Code Requirements for Structural Concrete (ACI 318-99) and Commentary (318R-99). American Concrete Institute: Farmington Hills, MI, USA, 1999.
- Yan, K.; Xu, H.; Shen, G.; Liu, P. Prediction of Splitting Tensile Strength from Cylinder Compressive Strength of Concrete by Support Vector Machine. Adv. Mater. Sci. Eng. 2013, 2013, 1–13. [Google Scholar] [CrossRef]
- Behnood, A.; Verian, K.P.; Modiri Gharehveran, M. Evaluation of the Splitting Tensile Strength in Plain and Steel Fiber-Reinforced Concrete Based on the Compressive Strength. Constr. Build. Mater. 2015, 98, 519–529. [Google Scholar] [CrossRef]
- Alarfaj, M.; Qureshi, H.J.; Shahab, M.Z.; Javed, M.F.; Arifuzzaman, M.; Gamil, Y. Machine Learning Based Prediction Models for Spilt Tensile Strength of Fiber Reinforced Recycled Aggregate Concrete. Case Stud. Constr. Mater. 2024, 20, e02836. [Google Scholar] [CrossRef]
- Ullah, I.; Javed, M.F.; Alabduljabbar, H.; Ullah, H. Estimating the Compressive and Tensile Strength of Basalt Fibre Reinforced Concrete Using Advanced Hybrid Machine Learning Models. Structures 2025, 71, 108138. [Google Scholar] [CrossRef]
- Bagher Shemirani, A.; Lawaf, M.P. Prediction of Tensile Strength of Concrete Using the Machine Learning Methods. Asian J. Civ. Eng. 2024, 25, 1207–1223. [Google Scholar] [CrossRef]
- Wang, X.-Y. Prediction of Flexural Strength of Natural Pozzolana and Limestone Blended Concrete Using Machine Learning Based Models. IOP Conf. Ser. Mater. Sci. Eng. 2020, 784, 012005. [Google Scholar] [CrossRef]
- Lok, T.S.; Xiao, J.R. Flexural Strength Assessment of Steel Fiber Reinforced Concrete. J. Mater. Civ. Eng. 1999, 11, 188–196. [Google Scholar] [CrossRef]
- Al-Taan, S.A.; Wadie, R.N. Flexural Strength of Steel Fibrous Reinforced Concrete Beams. In Proceedings of the Conference on Building and Infrastructure Technology, World Engineering Congress 2010, Kuching, Sarawak, Malaysia, 2–5 August 2010; pp. 258–270. [Google Scholar]
- Awodiji, C.T.G.; Sule, S. A Multivariate Regression Model for Predicting the 28days Flexural Strength of Lime-Cement Concrete Beam. FUOYE J. Eng. Technol. 2021, 6, 401–407. [Google Scholar] [CrossRef]
- Khan, K.; Iqbal, M.; Salami, B.A.; Amin, M.N.; Ahamd, I.; Alabdullah, A.A.; Arab, A.M.A.; Jalal, F.E. Estimating Flexural Strength of FRP Reinforced Beam Using Artificial Neural Network and Random Forest Prediction Models. Polymers 2022, 14, 2270. [Google Scholar] [CrossRef]
- Shah, H.A.; Yuan, Q.; Akmal, U.; Shah, S.A.; Salmi, A.; Awad, Y.A.; Shah, L.A.; Iftikhar, Y.; Javed, M.H.; Khan, M.I. Application of Machine Learning Techniques for Predicting Compressive, Splitting Tensile, and Flexural Strengths of Concrete with Metakaolin. Materials 2022, 15, 5435. [Google Scholar] [CrossRef] [PubMed]
- Qian, Y.; Sufian, M.; Hakamy, A.; Farouk Deifalla, A.; El-said, A. Application of Machine Learning Algorithms to Evaluate the Influence of Various Parameters on the Flexural Strength of Ultra-High-Performance Concrete. Front. Mater. 2023, 9, 1114510. [Google Scholar] [CrossRef]
- Amin, M.N.; Alkadhim, H.A.; Ahmad, W.; Khan, K.; Alabduljabbar, H.; Mohamed, A. Experimental and Machine Learning Approaches to Investigate the Effect of Waste Glass Powder on the Flexural Strength of Cement Mortar. PLoS ONE 2023, 18, e0280761. [Google Scholar] [CrossRef] [PubMed]
- Das, P.; Kashem, A. Hybrid Machine Learning Approach to Prediction of the Compressive and Flexural Strengths of UHPC and Parametric Analysis with Shapley Additive Explanations. Case Stud. Constr. Mater. 2024, 20, e02723. [Google Scholar] [CrossRef]
- Ahmadi-Nedushan, B. Prediction of Elastic Modulus of Normal and High Strength Concrete Using ANFIS and Optimal Nonlinear Regression Models. Constr. Build. Mater. 2012, 36, 665–673. [Google Scholar] [CrossRef]
- ACI 318-95; Building Code Requirements for Reinforced Concrete. American Institute: Farmington Hills, MI, USA, 1995.
- TS 500; Requirements for Design and Construction of Reinforced Concrete Structures. Turkish Standardization Institute: Ankara, Türkiye, 2000.
- Felix, E.F.; Possan, E.; Carrazedo, R. A New Formulation to Estimate the Elastic Modulus of Recycled Concrete Based on Regression and ANN. Sustainability 2021, 13, 8561. [Google Scholar] [CrossRef]
- Ahmadi, M.; Kioumarsi, M. Predicting the Elastic Modulus of Normal and High Strength Concretes Using Hybrid ANN-PSO. Mater. Today Proc. 2023, in press. [Google Scholar] [CrossRef]
- ACI 318-19; Building Code Requirements for Structural Concrete. American Concrete Institute: Farmington Hills, MI, USA, 2019.
- ACI 363R-10; Report on High-Strength Concrete. American Concrete Institute: Farmington Hills, MI, USA, 2010.
- NS 3473; Norwegian Council for Building Standardization, Concrete Structures-Design and Detailing Rules. Standard Norge: Stockholm, Switzerland, 1998.
- BS 8110; British Standard, Structural Use of Concrete: Code of Practice for Design and Construction, Part1. British Standards Institution: London, UK, 1997.
- Qu, B. Estimation of elastic modulus of recycle aggregate concrete based on hybrid and ensemble-hybrid approaches. Struct. Concr. 2024, 25, 1364–1387. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, S.; Li, Z.; Wang, L.; Shi, Y.; Luo, Q. Machine Learning-Based Model for Prediction of Elastic Modulus of Calcium Hydroxide in Oil Well Cement Under High-Temperature High-Pressure Conditions. Processes 2025, 13, 344. [Google Scholar] [CrossRef]
- Mokarem, D.W.; Weyers, R.E.; Stephen Lane, D. Development of Performance Specifications for Shrinkage of Portland Cement Concrete. Transp. Res. Rec. J. Transp. Res. Board. 2003, 1834, 40–47. [Google Scholar] [CrossRef]
- Shen, D.; Wang, X.; Cheng, D.; Zhang, J.; Jiang, G. Effect of Internal Curing with Super Absorbent Polymers on Autogenous Shrinkage of Concrete at Early Age. Constr. Build. Mater. 2016, 106, 512–522. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Kim, M.-J.; Kim, S.; Ryu, G.-S.; Koh, K.-T. Effects of Mix Proportion and Curing Condition on Shrinkage Behavior of HPFRCCs with Silica Fume and Blast Furnace Slag. Constr. Build. Mater. 2018, 166, 241–256. [Google Scholar] [CrossRef]
- Tazawa, E.; Miyazawa, S. Effect of Constituents and Curing Condition on Autogenous Shrinkage of Concrete. In Proceedings of the Proceedings of International Workshop, Autogenous Shrinkage of Concrete, Hiroshima, Japan, 13–14 June 1998; Tazawa, E., Ed.; Japan Concrete Institute: Chiyoda City, Japan, 1999; pp. 269–280. [Google Scholar]
- Jonasson, J.; Hedlund, H. An Engineering Model for Creep and Shrinkage in High Performance Concrete. In Proceedings of the International RILEM Workshop on Shrinkage of Concrete, Shrinkage, RILEM, Paris, France, 16–17 October 2000; RILEM: Paris, France, 2000; pp. 173–178. [Google Scholar]
- Dilger, W.H.; Wang, C. Creep and Shrinkage of High-Performance Concrete. In Proceedings of the SP-194: The Adam Neville Symposium: Creep and Shrinkage-Structural Design Effects, Atlanta, GA, USA, 9 November 1997; American Concrete Institute: Farmington Hills, MI, USA, 2000. [Google Scholar]
- Lee, K.M.; Lee, H.K.; Lee, S.H.; Kim, G.Y. Autogenous Shrinkage of Concrete Containing Granulated Blast-Furnace Slag. Cem. Concr. Res. 2006, 36, 1279–1285. [Google Scholar] [CrossRef]
- Liu, J.; Farzadnia, N.; Khayat, K.H.; Shi, C. Effects of SAP Characteristics on Internal Curing of UHPC Matrix. Constr. Build. Mater. 2021, 280, 122530. [Google Scholar] [CrossRef]
- Graybeal, B.A. Material Property Characterization of Ultra-High Performance Concrete; FHWA-HRT-06-103; Federal Highway Administration: Washington, DC, USA, 2006. [Google Scholar]
- Shen, D.; Wen, C.; Zhu, P.; Wu, Y.; Wu, Y. Influence of Barchip Fiber on Early-Age Autogenous Shrinkage of High-Strength Concrete Internally Cured with Super Absorbent Polymers. Constr. Build. Mater. 2020, 264, 119983. [Google Scholar] [CrossRef]
- Dönmez, A.; Bažant, Z.P. Shape Factors for Concrete Shrinkage and Drying Creep in Model B4 Refined by Nonlinear Diffusion Analysis. Mater. Struct. 2016, 49, 4779–4784. [Google Scholar] [CrossRef]
- Technical Committee RILEM. TC-242-MDC (Zdeněk Bažant, chair), Model B4 for creep, drying shrinkage, and autogenous shrinkage of normal and high-strength concretes with multi-decade applicability. (RILEM draft recommendation: TC-242-MDC multidecade creep and shrinkage of concrete: Material model and structural analysis). Mater. Struct. 2015, 48, 753–770. [Google Scholar]
- Židanavičius, D.; Augonis, M.; Adamukaitis, N.; Fornes, I.V. Concrete Shrinkage Analysis with Quicklime, Microfibers, and SRA Admixtures. Materials 2023, 16, 2061. [Google Scholar] [CrossRef]
- Hubler, M.H.; Wendner, R.; Bažant, Z.P. Statistical Justification of Model B4 for Drying and Autogenous Shrinkage of Concrete and Comparisons to Other Models. Mater. Struct. 2015, 48, 797–814. [Google Scholar] [CrossRef]
- Li, Z.; Lu, T.; Chen, Y.; Wu, B.; Ye, G. Prediction of the Autogenous Shrinkage and Microcracking of Alkali-Activated Slag and Fly Ash Concrete. Cem. Concr. Compos. 2021, 117, 103913. [Google Scholar] [CrossRef]
- Qureshi, H.J.; Saleem, M.U.; Javed, M.F.; Al Fuhaid, A.F.; Ahmad, J.; Amin, M.N.; Khan, K.; Aslam, F.; Arifuzzaman, M. Prediction of Autogenous Shrinkage of Concrete Incorporating Super Absorbent Polymer and Waste Materials through Individual and Ensemble Machine Learning Approaches. Materials 2022, 15, 7412. [Google Scholar] [CrossRef] [PubMed]
- Hilloulin, B.; Quan Tran, V. Using Machine Learning Techniques for Predicting Autogenous Shrinkage of Concrete Incorporating Superabsorbent Polymers and Supplementary Cementitious Materials. J. Build. Eng. 2022, 49, 104086. [Google Scholar] [CrossRef]
- Zheng, Z.; Hu, D.; Liu, P.; Sha, F.; Liu, L.; Yu, Z. Considering the Effect of the Randomness of Concrete Strength and Relative Humidity on Concrete Creep. Struct. Concr. 2021, 22, E916–E930. [Google Scholar] [CrossRef]
- Pang, C.; Wu, J.; Fan, X. Modification of Shrinkage Prediction Model for Partially Enclosed Steel Reinforced Concrete Columns Based on Moisture Diffusion Analysis. Constr. Build. Mater. 2024, 416, 135164. [Google Scholar] [CrossRef]
- Zhang, J.; Li, S.; Zhai, J. Grey Prediction Model for Drying Shrinkage of Cement Concrete Made from Recycled Coarse Aggregate Containing Superabsorbent Polymers. Math. Probl. Eng. 2021, 2021, 1–9. [Google Scholar] [CrossRef]
- Bal, L.; Buyle-Bodin, F. Artificial Neural Network for Predicting Drying Shrinkage of Concrete. Constr. Build. Mater. 2013, 38, 248–254. [Google Scholar] [CrossRef]
- Khodabandeh, P.; Azarhomayun, F.; Shekarchi, M.; Kioumarsi, M. Predicting Dry Shrinkage Using Machine Learning Methods; Springer Nature: Cham, Switzerland, 2025; pp. 731–738. [Google Scholar]
- Ocak, A.; Bekdaş, G.; Işıkdağ, Ü.; Nigdeli, S.M.; Bilir, T. Drying Shrinkage and Crack Width Prediction Using Machine Learning in Mortars Containing Different Types of Industrial By-Product Fine Aggregates. J. Build. Eng. 2024, 97, 110737. [Google Scholar] [CrossRef]
- Bissonnette, B.; Pigeon, M.; Vaysburd, A.M. Tensile Creep of Concrete: Study of Its Sensitivity to Basic Parameters. ACI Mater. J. 2007, 104, 360–368. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, P.; Qun, X. Experimental Research on The Effect of Silica Fume on Tensile Basic Creep of Early-Age Concrete. Open Civ. Eng. J. 2015, 9, 997–1001. [Google Scholar] [CrossRef]
- ACI 209; ACI PRC-209.2-08 Guide for Modeling and Calculating Shrinkage and Creep in Hardened Concrete. ACI Committee: Québec, QC, Canada, 2008.
- Purba, L.H.; Supriyadi, B.; Suhendro, B. Effect of Creep on the Long-Term Deflection of Box Girder Balanced Cantilever Bridge Structure Using B3 Model and CEB 2010. J. Civ. Eng. Forum 2022, 9, 91–100. [Google Scholar] [CrossRef]
- Li, L.; Dabarera, A.G.P.; Dao, V. Basic Tensile Creep of Concrete with and without Superabsorbent Polymers at Early Ages. Constr. Build. Mater. 2022, 320, 126180. [Google Scholar] [CrossRef]
- Walraven, J. Fib Model Code for Concrete Structures 2010: Mastering Challenges and Encountering New Ones. Struct. Concr. 2013, 14, 3–9. [Google Scholar] [CrossRef]
- Delsaute, B.; Torrenti, J.-M.; Staquet, S. Modeling Basic Creep of Concrete since Setting Time. Cem. Concr. Compos. 2017, 83, 239–250. [Google Scholar] [CrossRef]
- Shen, D.; Jiang, J.; Zhang, M.; Yao, P.; Jiang, G. Tensile Creep and Cracking Potential of High Performance Concrete Internally Cured with Super Absorbent Polymers at Early Age. Constr. Build. Mater. 2018, 165, 451–461. [Google Scholar] [CrossRef]
- Østergaard, L.; Lange, D.A.; Altoubat, S.A.; Stang, H. Tensile Basic Creep of Early-Age Concrete under Constant Load. Cem. Concr. Res. 2001, 31, 1895–1899. [Google Scholar] [CrossRef]
- Bal, L.; Buyle-Bodin, F. Artificial Neural Network for Predicting Creep of Concrete. Neural Comput. Appl. 2014, 25, 1359–1367. [Google Scholar] [CrossRef]
- Zhu, P.; Cao, W.; Zhang, L.; Zhou, Y.; Wu, Y.; Ma, Z.J. Interpretable Machine Learning Models for Prediction of UHPC Creep Behavior. Buildings 2024, 14, 2080. [Google Scholar] [CrossRef]
- Ghasemzadeh, F.; Manafpour, A.; Sajedi, S.; Shekarchi, M.; Hatami, M. Predicting Long-Term Compressive Creep of Concrete Using Inverse Analysis Method. Constr. Build. Mater. 2016, 124, 496–507. [Google Scholar] [CrossRef]
- Tadros, M.K.; Al-Omaishi, N.; Seguirant, S.J.; Galt, J.G. Prestress Loses in Pretensioned High-Strength Concrete Bridge Girders. In National Cooperative Highway Research Program (NCHRP) Transportation Board; NCHRP Report 496; Transportation Research Record: Washington, DC, USA, 2003. [Google Scholar]
- Mazloom, M. Estimating Long-Term Creep and Shrinkage of High-Strength Concrete. Cem. Concr. Compos. 2008, 30, 316–326. [Google Scholar] [CrossRef]
- Huo, X.S.; Al-Omaishi, N.; Tadros, M.K. Creep, Shrinkage, and Modulus of Elasticity of High-Performance Concrete. ACI Mater. J. 2001, 98, 440–449. [Google Scholar] [CrossRef] [PubMed]
- Gilbert, R.I. AS3600 Creep and Shrinkage Models for Normal and High Strength Concrete. In Proceedings of the SP-227: Shrinkage and Creep of Concrete, New York, NY, USA, 10–15 April 2002; American Concrete Institute: Farmington Hills, MI, USA, 2005. [Google Scholar]
- CEB. Design and Performance. Updated Knowledge of the CEB/FIP Model Code 1990. In Structural Concrete—Textbook on Behaviour; Fib Bulletin 2; fib: Lausanne, Switzerland, 1999; Volume 2, pp. 37–52. [Google Scholar]
- Gardner, N.J. Comparison of Prediction Provisions for Drying Shrinkage and Creep of Normal-Strength Concretes. Can. J. Civ. Eng. 2004, 31, 767–775. [Google Scholar] [CrossRef]
- Bouras, Y.; Li, L. Utilisation of Machine Learning Techniques to Model Creep Behaviour of Low-Carbon Concretes. Buildings 2023, 13, 2252. [Google Scholar] [CrossRef]
- Abdelhady, A.; Hui, L.; Zhang, H. Comprehensive Study to Accurately Predict the Water Permeability of Pervious Concrete Using Constant Head Method. Constr. Build. Mater. 2021, 308, 125046. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, G.; Tong, Y.; Gu, C. Prediction on Permeability of Engineered Cementitious Composites. Crystals 2021, 11, 526. [Google Scholar] [CrossRef]
- Ahmad, S.A.; Ahmed, H.U.; Rafiq, S.K.; Jafer, F.S.; Fqi, K.O. A Comparative Analysis of Simulation Approaches for Predicting Permeability and Compressive Strength in Pervious Concrete. Low-Carbon. Mater. Green. Constr. 2024, 2, 1–20. [Google Scholar] [CrossRef]
- Ma, J.; Yang, Q.; Wang, X.; Peng, X.; Qin, F. Review of Prediction Models for Chloride Ion Concentration in Concrete Structures. Buildings 2025, 15, 149. [Google Scholar] [CrossRef]
- Huang, X.; Wang, S.; Lu, T.; Li, H.; Wu, K.; Deng, W. Chloride Permeability Coefficient Prediction of Rubber Concrete Based on the Improved Machine Learning Technical: Modelling and Performance Evaluation. Polymers 2023, 15, 308. [Google Scholar] [CrossRef] [PubMed]
- Hafidi, A.; Hilloulin, B.; Boudache, S.; Rejoice, U.; Loukili, A. Comparison of Machine Learning Algorithms for the Prediction of the External Sulphate Attack Resistance of Blended Cements. In International RILEM Conference on Synergising Expertise towards Sustainability and Robustness of Cement-Based Materials and Concrete Structures; Springer: Cham, Switzerland, 2023; p. 10. [Google Scholar]
- Qin, S.; Zhang, M.; Zou, D.; Liu, T. A Failure Thickness Prediction Model for Concrete Exposed to External Sulfate Attack. Constr. Build. Mater. 2024, 416, 135202. [Google Scholar] [CrossRef]
- DeRousseau, M.A.; Laftchiev, E.; Kasprzyk, J.R.; Rajagopalan, B.; Srubar, W.V. A Comparison of Machine Learning Methods for Predicting the Compressive Strength of Field-Placed Concrete. Constr. Build. Mater. 2019, 228, 116661. [Google Scholar] [CrossRef]
- Valbuena, R.; Hernando, A.; Manzanera, J.A.; Görgens, E.B.; Almeida, D.R.A.; Silva, C.A.; García-Abril, A. Evaluating Observed versus Predicted Forest Biomass: R-Squared, Index of Agreement or Maximal Information Coefficient? Eur. J. Remote Sens. 2019, 52, 345–358. [Google Scholar] [CrossRef]
- Kambezidis, H.D. The Solar Resource. In Comprehensive Renewable Energy; Elsevier: Amsterdam, The Netherlands, 2012; pp. 27–84. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adsul, N.; Choi, Y.; Kang, S.-T. A Comprehensive Review of Numerical and Machine Learning Approaches for Predicting Concrete Properties: From Fresh to Long-Term. Materials 2025, 18, 3718. https://doi.org/10.3390/ma18153718
Adsul N, Choi Y, Kang S-T. A Comprehensive Review of Numerical and Machine Learning Approaches for Predicting Concrete Properties: From Fresh to Long-Term. Materials. 2025; 18(15):3718. https://doi.org/10.3390/ma18153718
Chicago/Turabian StyleAdsul, Nilam, Yongho Choi, and Su-Tae Kang. 2025. "A Comprehensive Review of Numerical and Machine Learning Approaches for Predicting Concrete Properties: From Fresh to Long-Term" Materials 18, no. 15: 3718. https://doi.org/10.3390/ma18153718
APA StyleAdsul, N., Choi, Y., & Kang, S.-T. (2025). A Comprehensive Review of Numerical and Machine Learning Approaches for Predicting Concrete Properties: From Fresh to Long-Term. Materials, 18(15), 3718. https://doi.org/10.3390/ma18153718








