Determination of Quantum Yield in Scattering Media Using Monte Carlo Photoluminescence Cascade Simulation and Integrating Sphere Measurements
Abstract
1. Introduction
2. Theory
2.1. Radiative Transfer Equation
2.2. Monte Carlo Implementation
| Algorithm 1 Photon interaction: absorption vs. scattering |
| Require: Photon with wavelength and weight |
| Require: Absorption: , |
| Require: Scattering coefficient |
| Require: Random number |
|
| Algorithm 2 Absorption with fluorescence and isotropic re-emission |
| Require: Quantum yield , emission |
| Require: Random numbers |
|
| Algorithm 3 Wavelength-dependent scattering |
| Require: Scattering coefficients for each material component j |
| Require: Phase function (e.g. Henyey–Greenstein) for each j |
| Require: Random number |
|
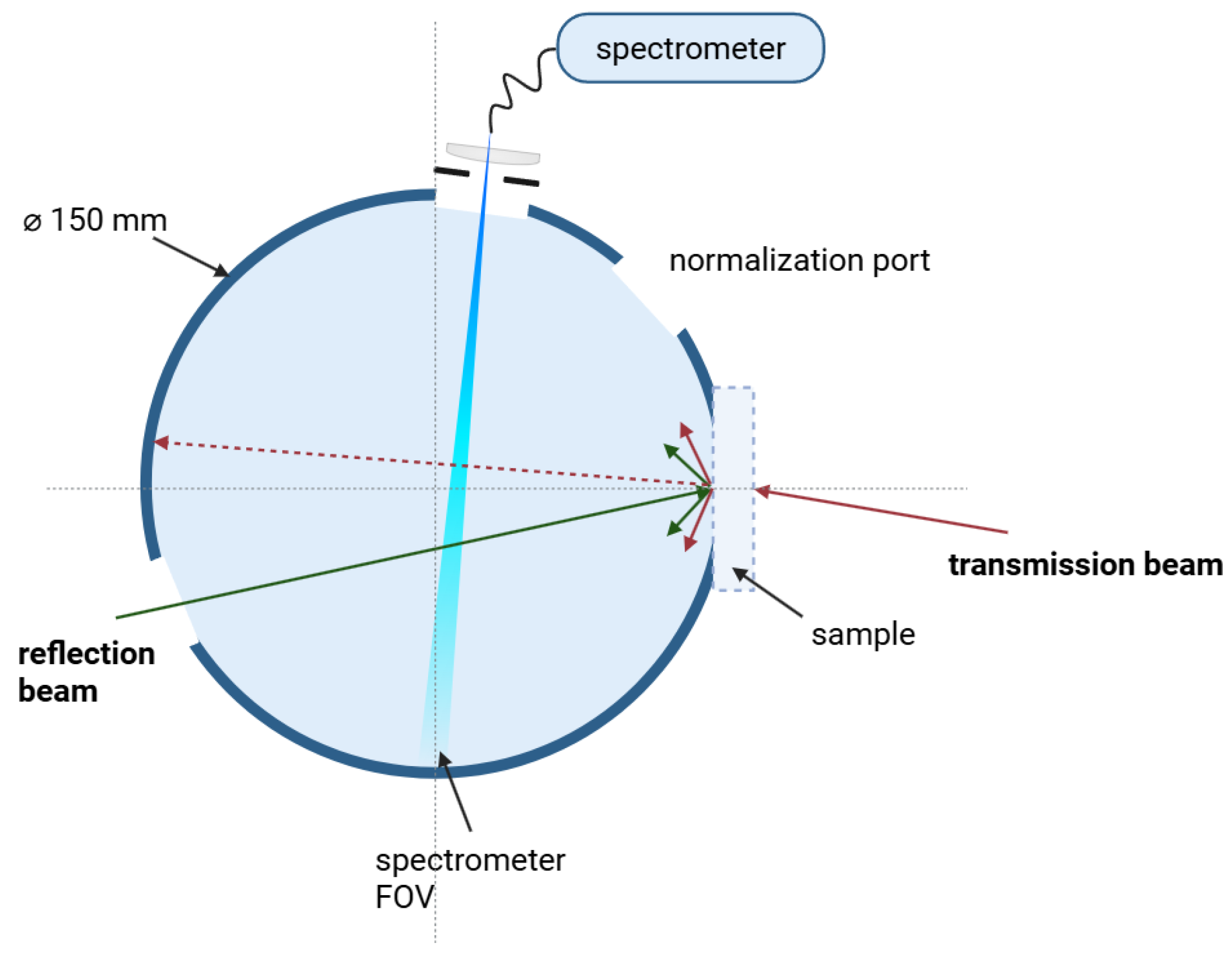
2.3. Integrating Sphere Model
2.4. Source Model
2.5. Sample Preparation and Reference Dye
3. Results
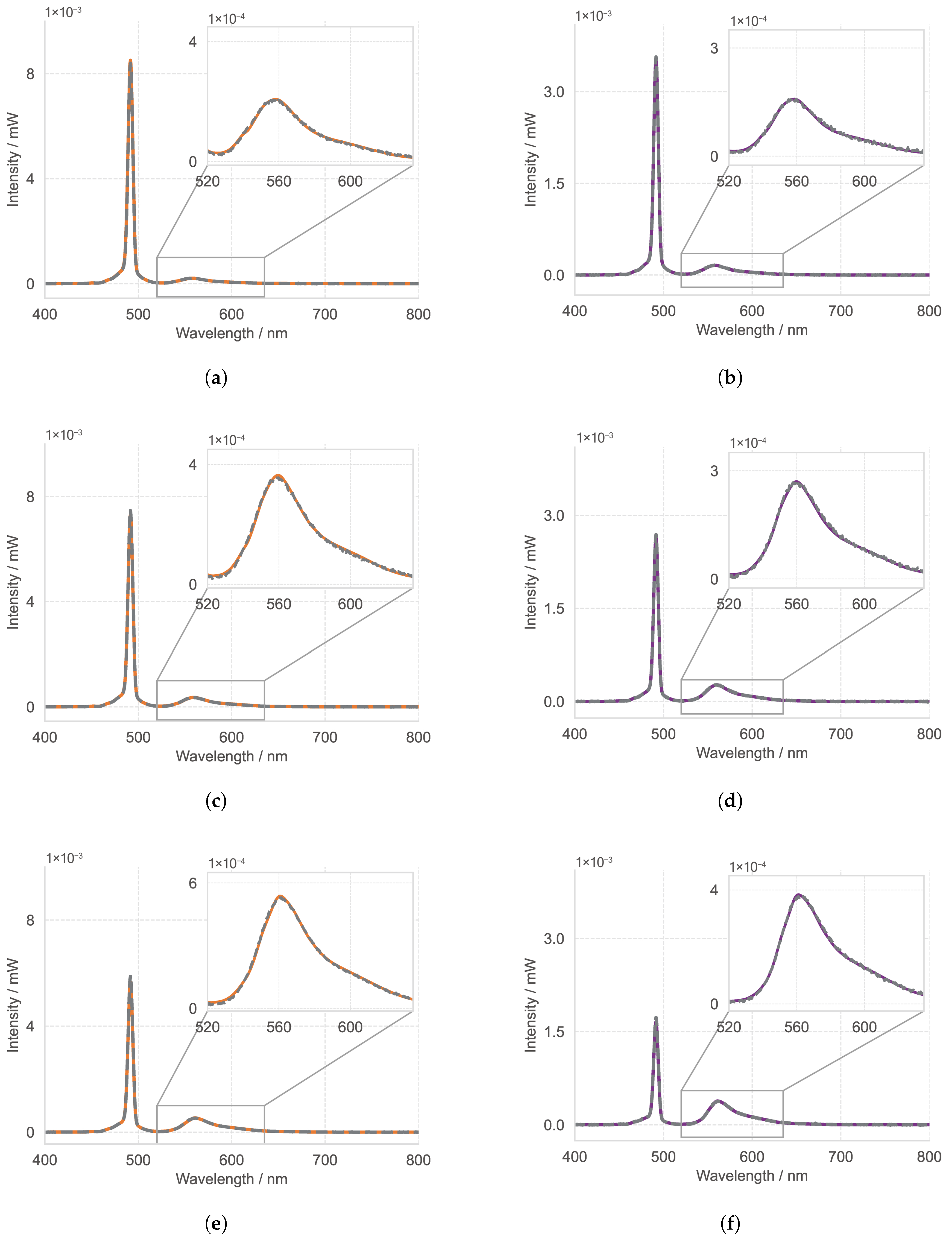
3.1. Quantum Yield in Ethanol
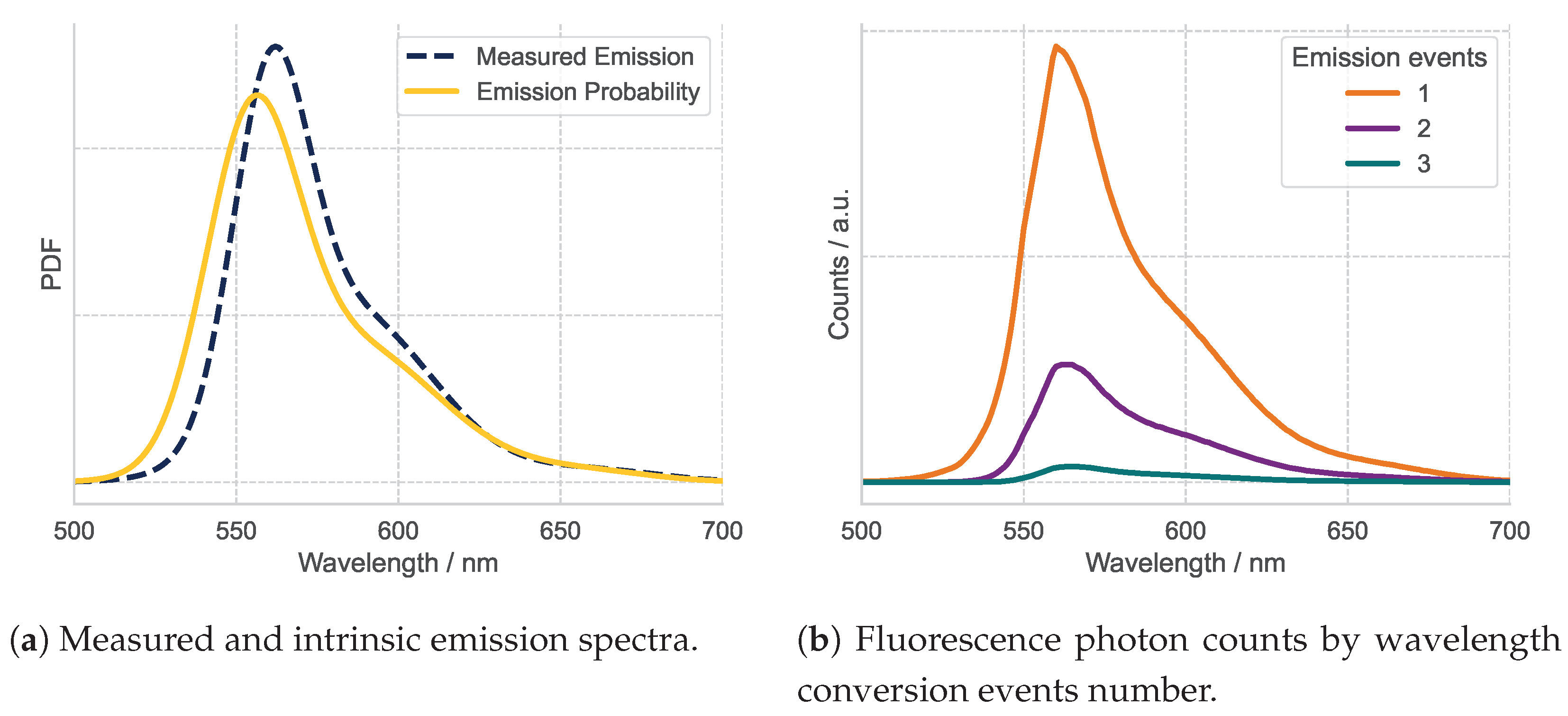
3.2. Effect of Re-Absorption on the Quantum Yield
3.3. Other Distortion Effects
3.4. Quantum Yield in PDMS
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lakowicz, J.R. Principles of Fluorescence Spectroscopy; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
- Rurack, K. Fluorescence Quantum Yields: Methods of Determination and Standards. In Standardization and Quality Assurance in Fluorescence Measurements I: Techniques; Resch-Genger, U., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 101–145. [Google Scholar] [CrossRef]
- Würth, C.; Grabolle, M.; Pauli, J.; Spieles, M.; Resch-Genger, U. Relative and absolute determination of fluorescence quantum yields of transparent samples. Nat. Protoc. 2013, 8, 1535–1550. [Google Scholar] [CrossRef] [PubMed]
- Martini, M.; Montagna, M.; Ou, M.; Tillement, O.; Roux, S.; Perriat, P. How to measure quantum yields in scattering media: Application to the quantum yield measurement of fluorescein molecules encapsulated in sub-100 nm silica particles. J. Appl. Phys. 2009, 106, 094304. [Google Scholar] [CrossRef]
- Fischer, M.; Georges, J. Fluorescence quantum yield of rhodamine 6G in ethanol as a function of concentration using thermal lens spectrometry. Chem. Phys. Lett. 1996, 260, 115–118. [Google Scholar] [CrossRef]
- Levitus, M. Tutorial: Measurement of fluorescence spectra and determination of relative fluorescence quantum yields of transparent samples. Methods Appl. Fluoresc. 2020, 8, 033001. [Google Scholar] [CrossRef]
- Brouwer, A.M. Standards for photoluminescence quantum yield measurements in solution (IUPAC Technical Report). Pure Appl. Chem. 2011, 83, 2213–2228. [Google Scholar] [CrossRef]
- Resch-Genger, U.; Hoffmann, K.; Nietfeld, W.; Engel, A.; Neukammer, J.; Nitschke, R.; Ebert, B.; Macdonald, R. How to Improve Quality Assurance in Fluorometry: Fluorescence-Inherent Sources of Error and Suited Fluorescence Standards. J. Fluoresc. 2005, 15, 337–362. [Google Scholar] [CrossRef]
- Parker, C.A.; Rees, W.T. Correction of fluorescence spectra and measurement of fluorescence quantum efficiency. Analyst 1960, 85, 587–600. [Google Scholar] [CrossRef]
- Ware, W.R.; Rothman, W. Relative fluorescence quantum yields using an integrating sphere. The quantum yield of 9,10-diphenylanthracene in cyclohexane. Chem. Phys. Lett. 1976, 39, 449–453. [Google Scholar] [CrossRef]
- Gaigalas, A.K.; Wang, L. Measurement of the Fluorescence Quantum Yield Using a Spectrometer with an Integrating Sphere Detector. J. Res. Natl. Inst. Stand. Technol. 2008, 113, 17–28. [Google Scholar] [CrossRef]
- Porrès, L.; Holland, A.; Pålsson, L.O.; Monkman, A.P.; Kemp, C.; Beeby, A. Absolute Measurements of Photoluminescence Quantum Yields of Solutions Using an Integrating Sphere. J. Fluoresc. 2006, 16, 267–273. [Google Scholar] [CrossRef]
- Leyre, S.; Coutino-Gonzalez, E.; Joos, J.J.; Ryckaert, J.; Meuret, Y.; Poelman, D.; Smet, P.F.; Durinck, G.; Hofkens, J.; Deconinck, G.; et al. Absolute determination of photoluminescence quantum efficiency using an integrating sphere setup. Rev. Sci. Instrum. 2014, 85, 123115. [Google Scholar] [CrossRef] [PubMed]
- Lagorio, M.G. Determination of Fluorescence Quantum Yields in Scattering Media. Methods Appl. Fluoresc. 2020, 8, 043001. [Google Scholar] [CrossRef] [PubMed]
- Ahn, T.S.; Al-Kaysi, R.; Mueller, A.; Wentz, K.; Bardeen, C. Self-absorption correction for photoluminescence quantum yields from integrating sphere measurements. Rev. Sci. Instrum. 2007, 78, 086105. [Google Scholar] [CrossRef] [PubMed]
- Würth, C.; Resch-Genger, U. Determination of Photoluminescence Quantum Yields of Scattering Media with an Integrating Sphere: Direct and Indirect Illumination. Appl. Spectrosc. 2015, 69, 749–759. [Google Scholar] [CrossRef]
- Lagorio, M.G.; San Román, E. How Does Light Scattering Affect Luminescence? Fluorescence Spectra and Quantum Yields in the Solid Phase. J. Chem. Educ. 2002, 79, 1362. [Google Scholar] [CrossRef]
- Liemert, A.; Reitzle, D.; Kienle, A. Analytical solutions of the radiative transport equation for turbid and fluorescent layered media. Sci. Rep. 2017, 7, 3819. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, M.; Sun, J.; Hu, R.; Luo, X. Phosphor modeling based on fluorescent radiative transfer equation. Opt. Express 2018, 26, 16442–16455. [Google Scholar] [CrossRef]
- Yalçın, R.A.; Ertürk, H. Monte Carlo method solution of the broadband fluorescent radiative transfer equation considering fluorescent cascade. Appl. Opt. 2021, 60, 1068–1077. [Google Scholar] [CrossRef]
- Leyre, S.; Ryckaert, J.; Acuna, P.; Audenaert, J.; Meuret, Y.; Hofkens, J.; Durinck, G.; Deconinck, G.; Hanselaer, P. Taking the spectral overlap between excitation and emission spectra of fluorescent materials into account with Monte Carlo simulations. In Optical Modelling and Design III; SPIE: Bellingham, WA, USA, 2014; Volume 9131, p. 913103. [Google Scholar] [CrossRef]
- Sandilands, L.J. Modeling fluorescence reemission in the one-dimensional radiative transfer problem using the P3 approximation. J. Opt. Soc. Am. A 2021, 38, 1631. [Google Scholar] [CrossRef]
- Martelli, F.; Binzoni, T.; Liemert, A.; Del Bianco, S.; Kienle, A. Light Propagation Through Biological Tissue and Other Diffusive Media: Theory, Solutions, and Validations, 2nd ed.; SPIE: Bellingham, WA, USA, 2022. [Google Scholar] [CrossRef]
- Jabłoński, A. Über den Mechanismus der Photolumineszenz von Farbstoffphosphoren. Z. Für Phys. 1935, 94, 38–46. [Google Scholar] [CrossRef]
- Franck, J.; Dymond, E.G. Elementary processes of photochemical reactions. Trans. Faraday Soc. 1926, 21, 536–542. [Google Scholar] [CrossRef]
- Condon, E.U. Nuclear Motions Associated with Electron Transitions in Diatomic Molecules. Phys. Rev. 1928, 32, 858–872. [Google Scholar] [CrossRef]
- Kasha, M. Characterization of electronic transitions in complex molecules. Discuss. Faraday Soc. 1950, 9, 14–19. [Google Scholar] [CrossRef]
- Jelken, J.; Brall, T.; Gelbing, P.; Foschum, F.; Kienle, A. Characterization of the Optical Properties of Photoluminescent Turbid Media Using an Integrating Sphere and Monte Carlo Simulations. Materials 2024, 17, 6072. [Google Scholar] [CrossRef] [PubMed]
- Foschum, F.; Bergmann, F.; Kienle, A. Precise determination of the optical properties of turbid media using an optimized integrating sphere and advanced Monte Carlo simulations. Part 1: Theory. Appl. Opt. 2020, 59, 3203–3215. [Google Scholar] [CrossRef] [PubMed]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Penzkofer, A.; Leupacher, W. Fluorescence behaviour of highly concentrated rhodamine 6G solutions. J. Lumin. 1987, 37, 61–72. [Google Scholar] [CrossRef]
- Rohwer, L.S.; Martin, J.E. Measuring the absolute quantum efficiency of luminescent materials. J. Lumin. 2005, 115, 77–90. [Google Scholar] [CrossRef]
- Würth, C.; González, M.G.; Niessner, R.; Panne, U.; Haisch, C.; Genger, U.R. Determination of the absolute fluorescence quantum yield of rhodamine 6G with optical and photoacoustic methods—Providing the basis for fluorescence quantum yield standards. Talanta 2012, 90, 30–37. [Google Scholar] [CrossRef]
- Magde, D.; Wong, R.; Seybold, P.G. Fluorescence Quantum Yields and Their Relation to Lifetimes of Rhodamine 6G and Fluorescein in Nine Solvents: Improved Absolute Standards for Quantum Yields. Photochem. Photobiol. 2002, 75, 327–334. [Google Scholar] [CrossRef]
- Zehentbauer, F.M.; Moretto, C.; Stephen, R.; Thevar, T.; Gilchrist, J.R.; Pokrajac, D.; Richard, K.L.; Kiefer, J. Fluorescence spectroscopy of Rhodamine 6G: Concentration and solvent effects. Spectrochim. Acta. Part A Mol. Biomol. Spectrosc. 2014, 121, 147–151. [Google Scholar] [CrossRef]
- Kumar, B.R.; Basheer, N.S.; Kurian, A.; George, S.D. Study of concentration-dependent quantum yield of Rhodamine 6G by gold nanoparticles using thermal-lens technique. Appl. Phys. B 2014, 115, 335–342. [Google Scholar] [CrossRef]
- Kubin, R.F.; Fletcher, A.N. Fluorescence quantum yields of some rhodamine dyes. J. Lumin. 1982, 27, 455–462. [Google Scholar] [CrossRef]
- Zhang, X.F.; Zhang, Y.; Liu, L. Fluorescence lifetimes and quantum yields of ten rhodamine derivatives: Structural effect on emission mechanism in different solvents. J. Lumin. 2014, 145, 448–453. [Google Scholar] [CrossRef]
- Zakerhamidi, M.S.; Moghadam, M.; Ghanadzadeh, A.; Hosseini, S. Anisotropic and isotropic solvent effects on the dipole moment and photophysical properties of rhodamine dyes. J. Lumin. 2012, 132, 931–937. [Google Scholar] [CrossRef]
- Amemori, S.; Kikuchi, K.; Mizuno, M. Poly(dimethylsiloxane) and oligo(dimethylsiloxane) solvent effects on aromatic donor–acceptor interactions. Chem. Commun. 2021, 57, 1141–1144. [Google Scholar] [CrossRef]
- López Arbeloa, F.; López Arbeloa, T.; López Arbeloa, I.; Costela, A.; García-Moreno, I.; Figuera, J.; Amat-Guerri, F.; Sastre, R. Relations between photophysical and lasing properties of rhodamines in solid polymeric matrices. Appl. Phys. B 1997, 64, 651–657. [Google Scholar] [CrossRef]
| Concentration | Statistical Error | 95% CI | |
|---|---|---|---|
| 0.91 | ±0.006 | [0.90, 0.92] | |
| 0.94 | ±0.005 | [0.93, 0.95] | |
| 0.93 | ±0.003 | [0.92, 0.94] |
| Concentration | Statistical Error | 95% CI | |
|---|---|---|---|
| 0.75 | ±0.003 | [0.74, 0.75] | |
| 0.78 | ±0.003 | [0.78, 0.79] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gelbing, P.; Jelken, J.; Foschum, F.; Kienle, A. Determination of Quantum Yield in Scattering Media Using Monte Carlo Photoluminescence Cascade Simulation and Integrating Sphere Measurements. Materials 2025, 18, 3710. https://doi.org/10.3390/ma18153710
Gelbing P, Jelken J, Foschum F, Kienle A. Determination of Quantum Yield in Scattering Media Using Monte Carlo Photoluminescence Cascade Simulation and Integrating Sphere Measurements. Materials. 2025; 18(15):3710. https://doi.org/10.3390/ma18153710
Chicago/Turabian StyleGelbing, Philip, Joachim Jelken, Florian Foschum, and Alwin Kienle. 2025. "Determination of Quantum Yield in Scattering Media Using Monte Carlo Photoluminescence Cascade Simulation and Integrating Sphere Measurements" Materials 18, no. 15: 3710. https://doi.org/10.3390/ma18153710
APA StyleGelbing, P., Jelken, J., Foschum, F., & Kienle, A. (2025). Determination of Quantum Yield in Scattering Media Using Monte Carlo Photoluminescence Cascade Simulation and Integrating Sphere Measurements. Materials, 18(15), 3710. https://doi.org/10.3390/ma18153710








