Hydrogen Cryomagnetic a Common Solution for Metallic and Oxide Superconductors
Highlights
- Liquid hydrogen enables efficient, low-cost cooling of LTS and HTS superconductors.
- Hydrogen cryomagnetic technology fuses superconductivity with clean energy.
- Indirect liquid hydrogen, i-LH2, systems offer scalable heat exchange cooling via pressurized helium loops.
- Boosted pinning of low temperature superconductors enables high-performance magnets in strong fields cooled by LH2.
- Applications include magnets, SMES, magnetic heating, fusion, cables and medical imaging.
Abstract
1. Introduction
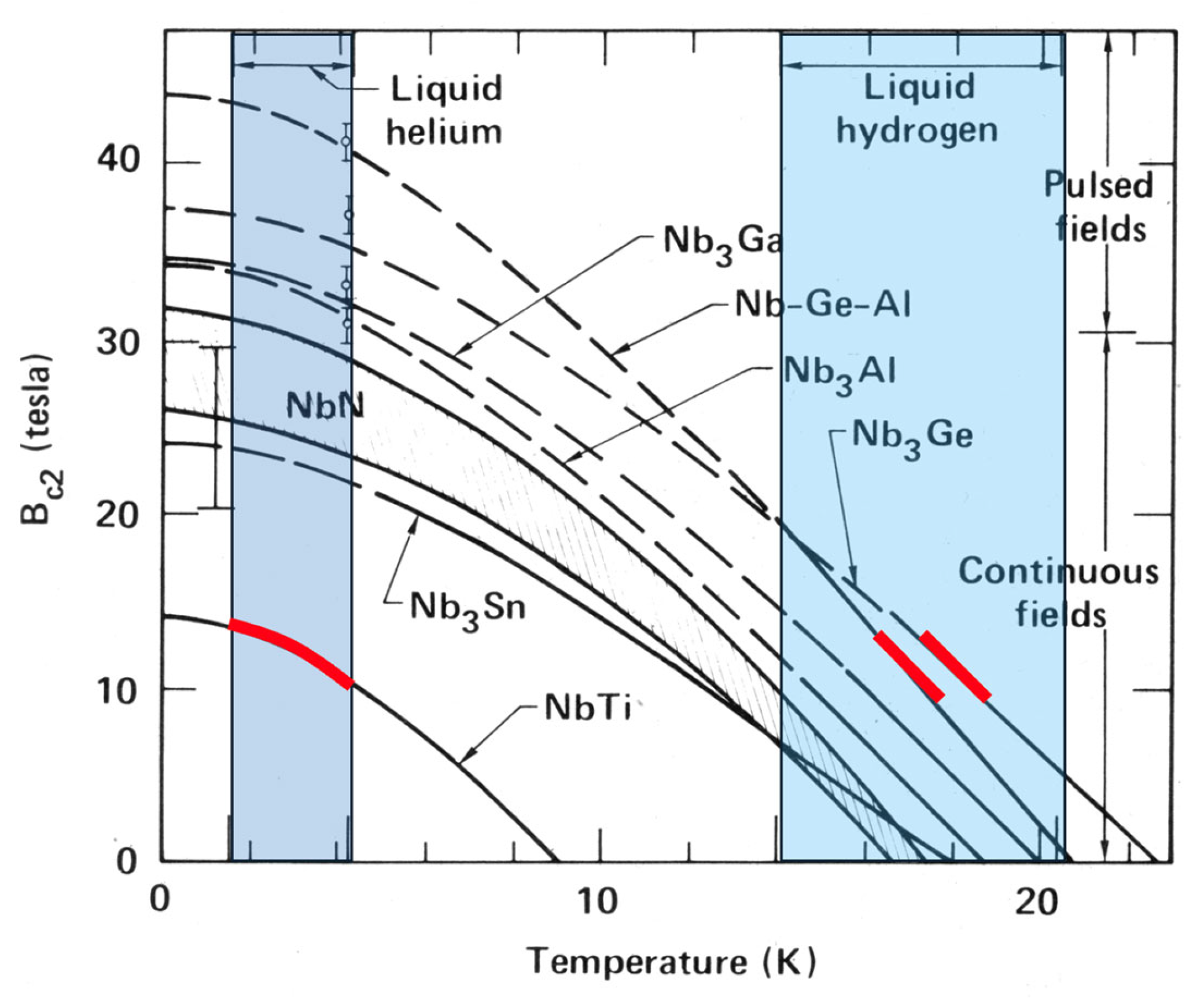
2. Hydrogen Cryomagnetic
Hydrogen Cryomagnetic Cooling: Indirect and Direct LH2 Approaches
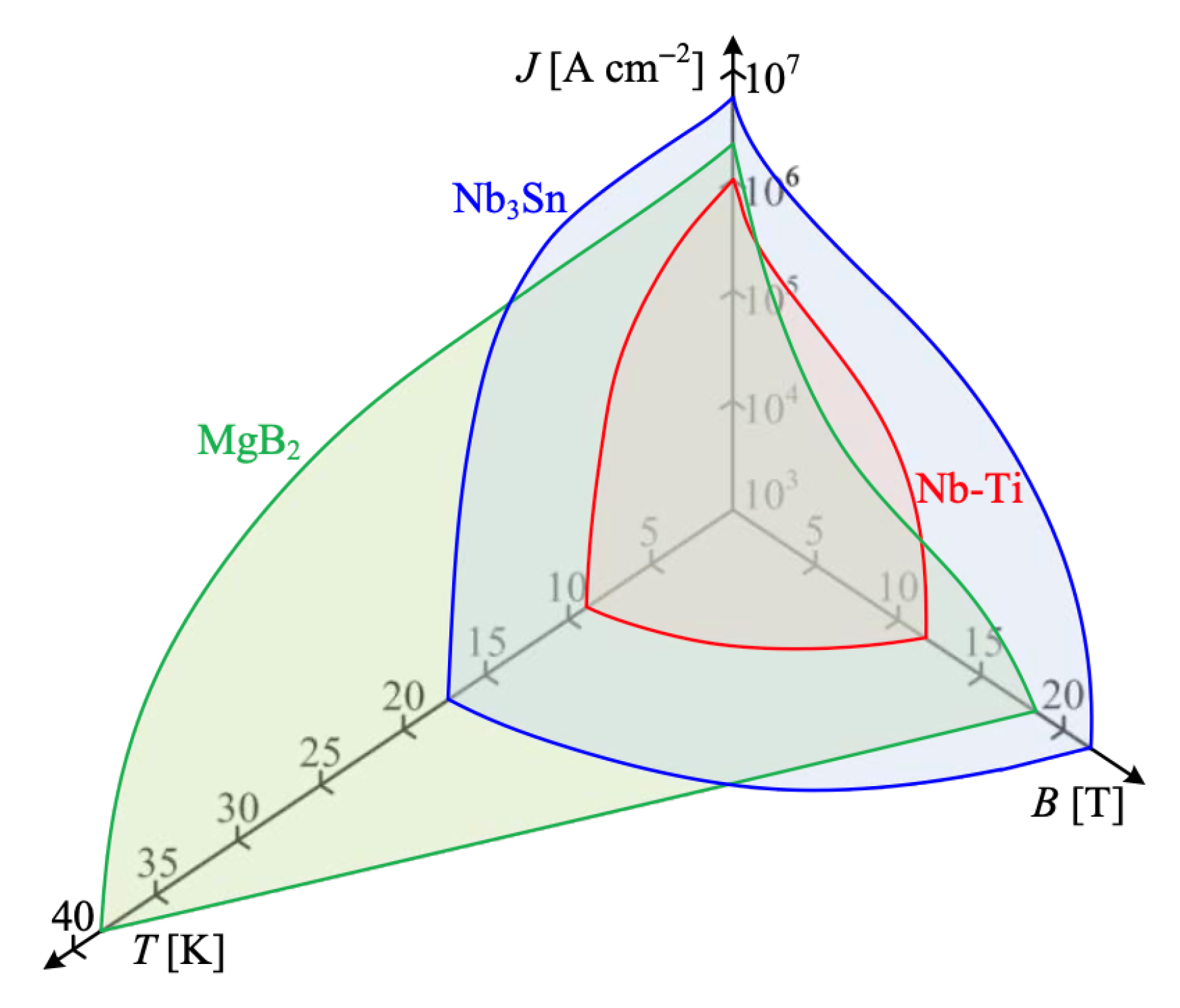
3. Superconductors Selection
4. Metallic Superconductors
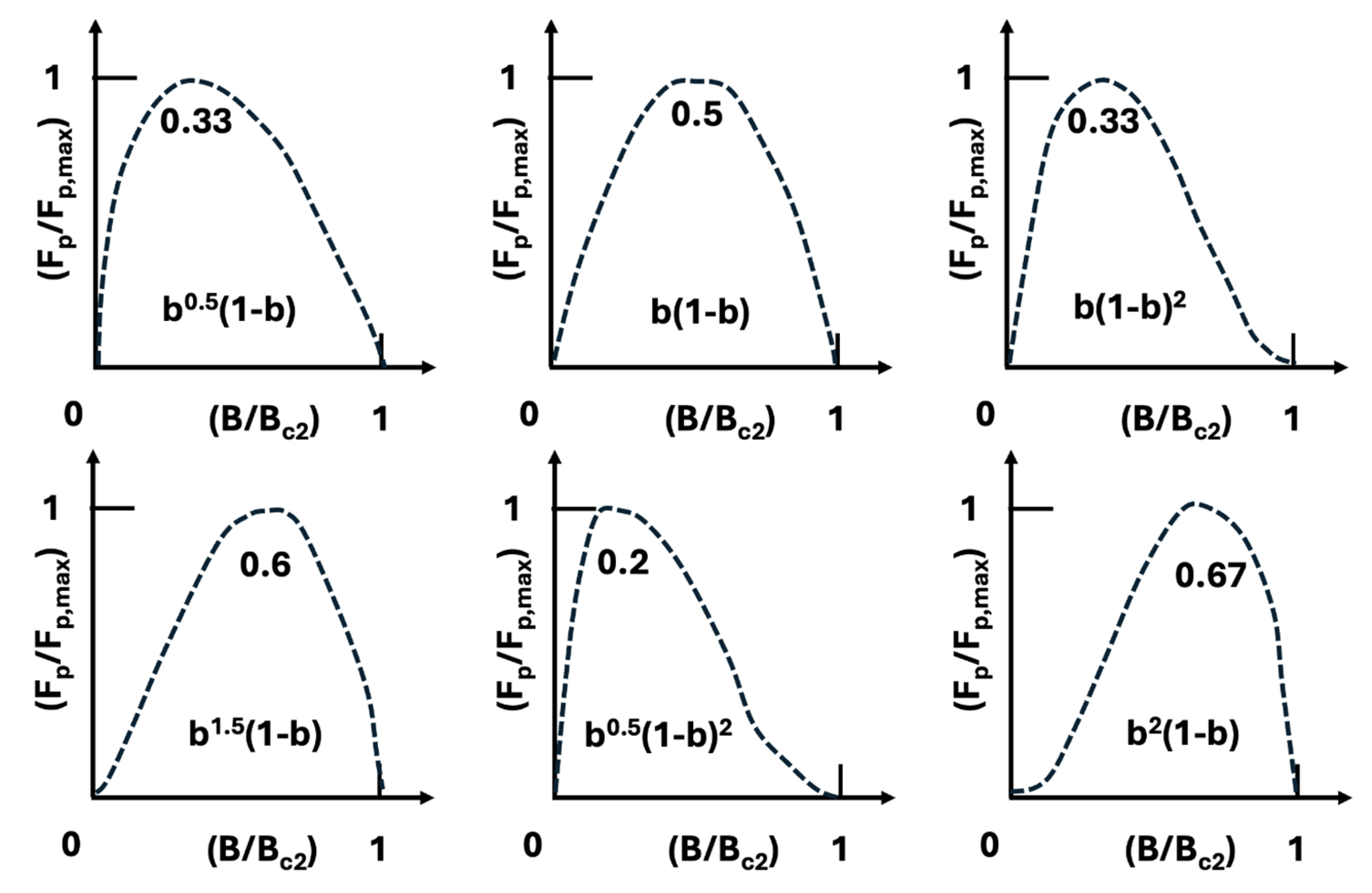
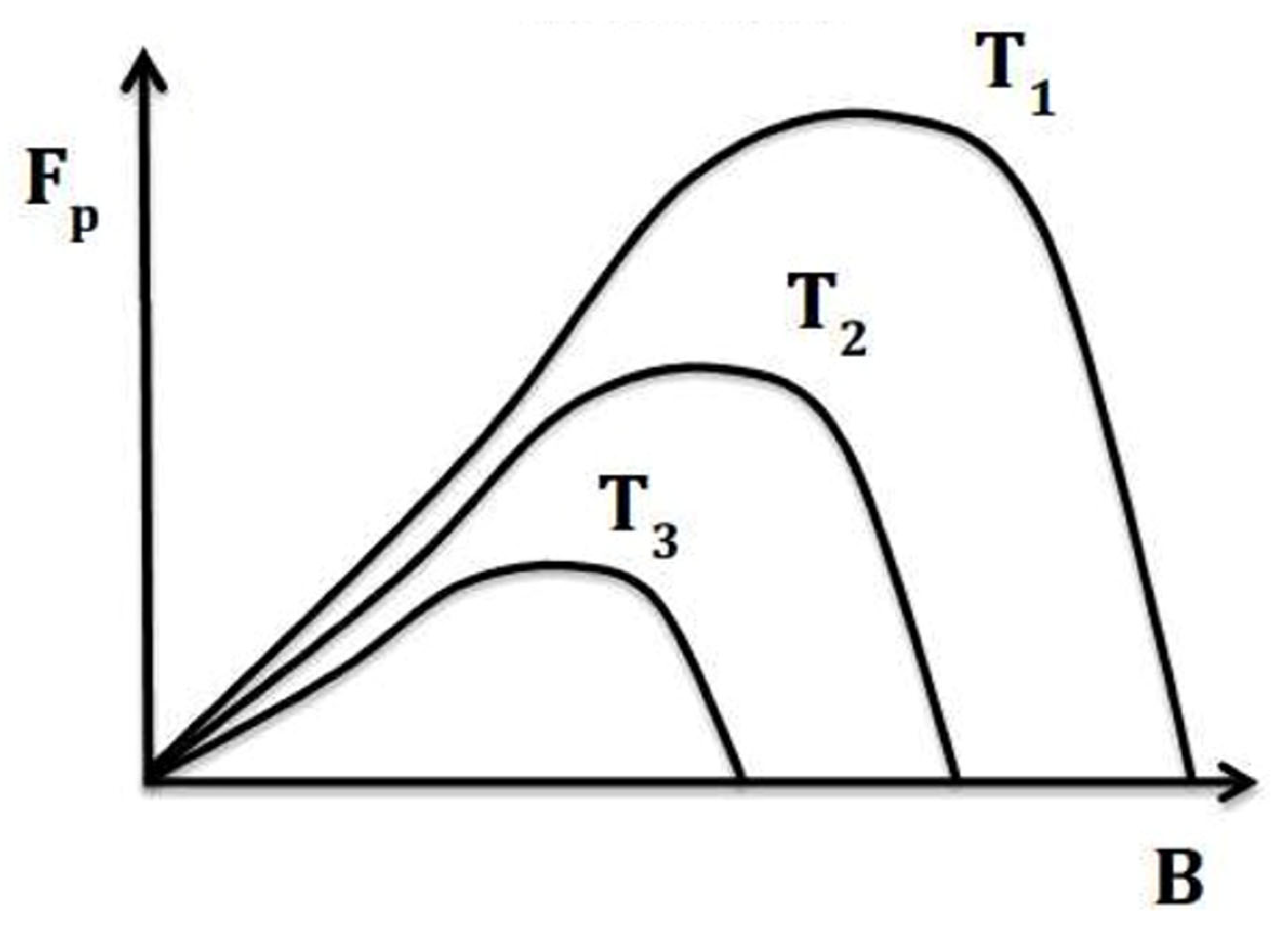
4.1. Nb3(Al, Ge)
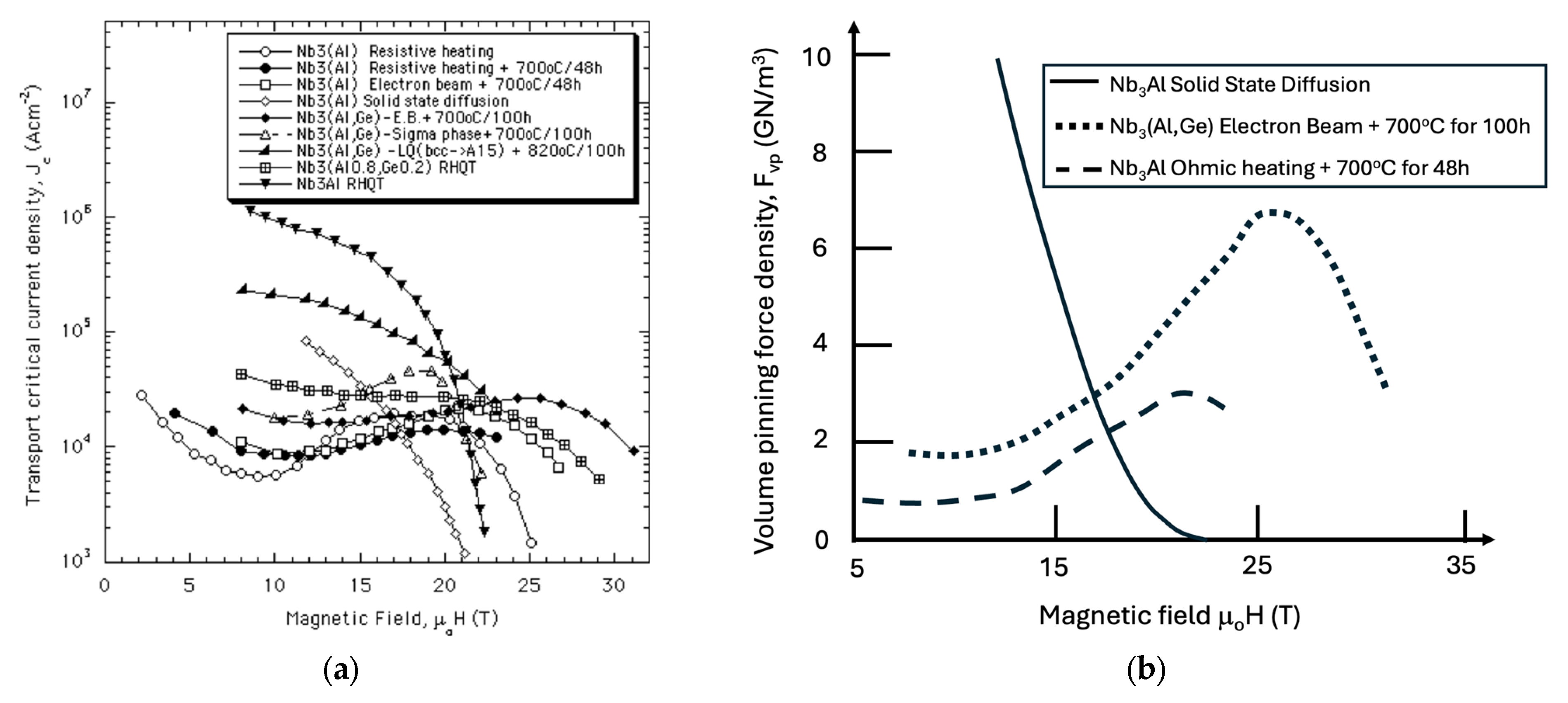
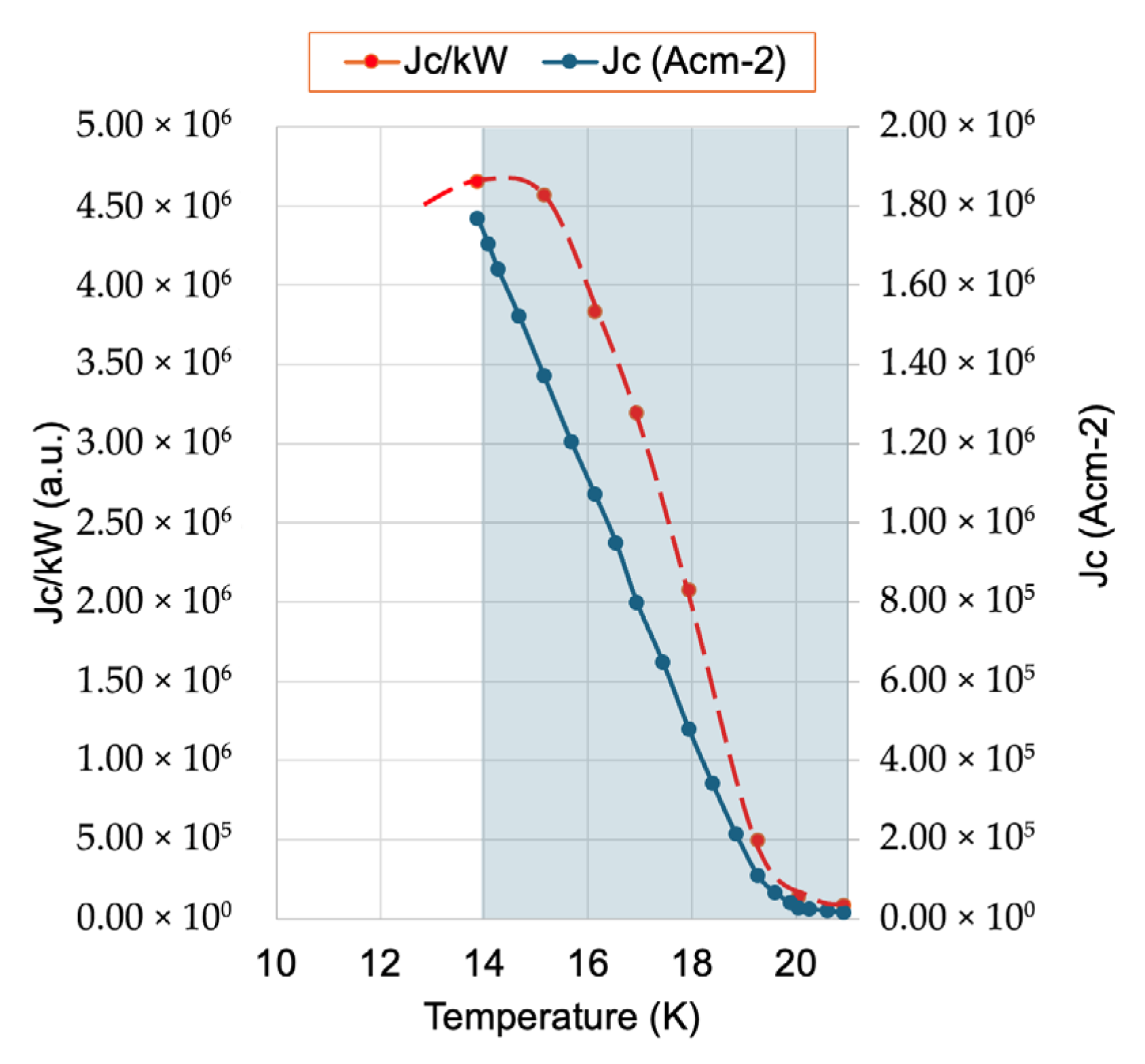
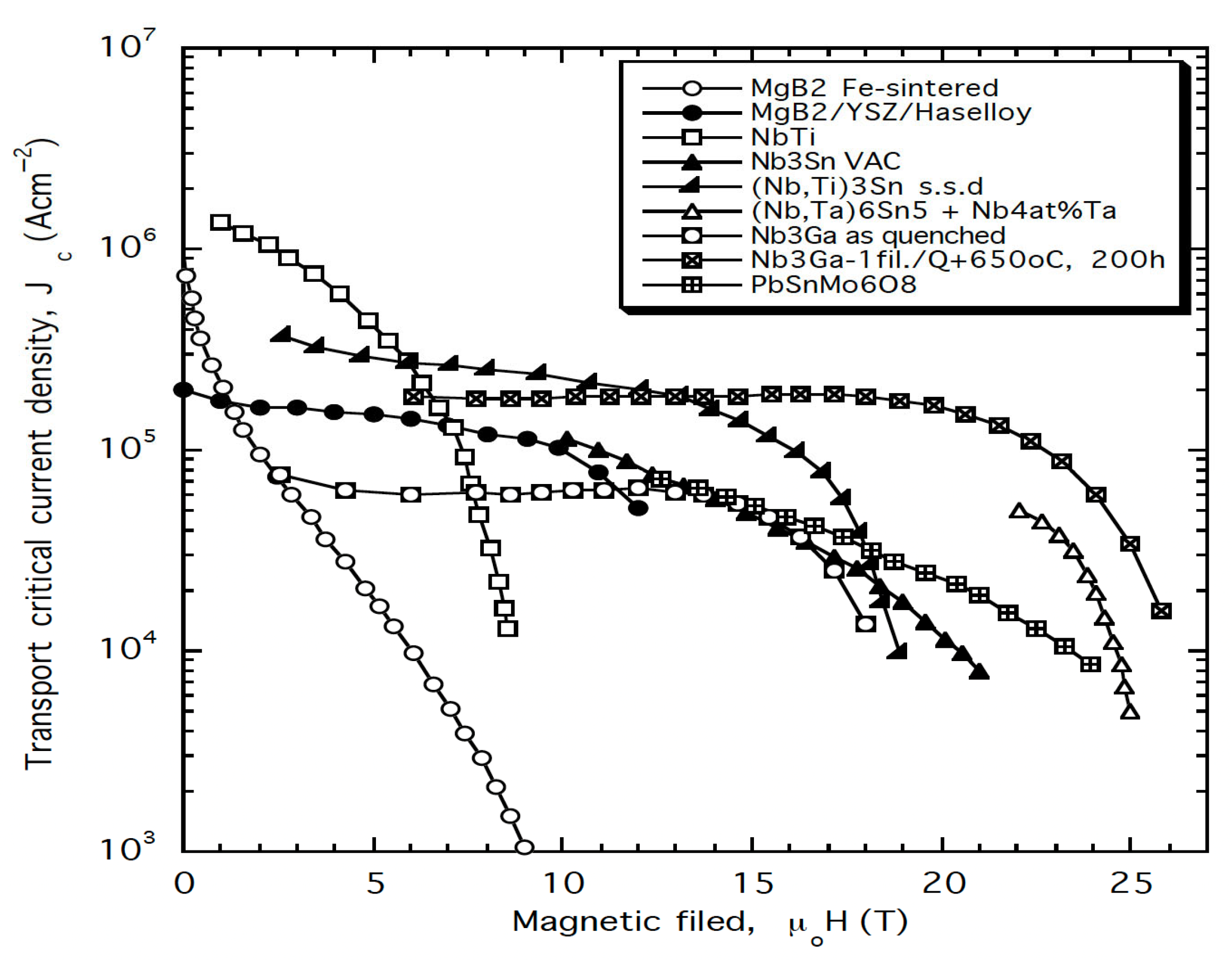
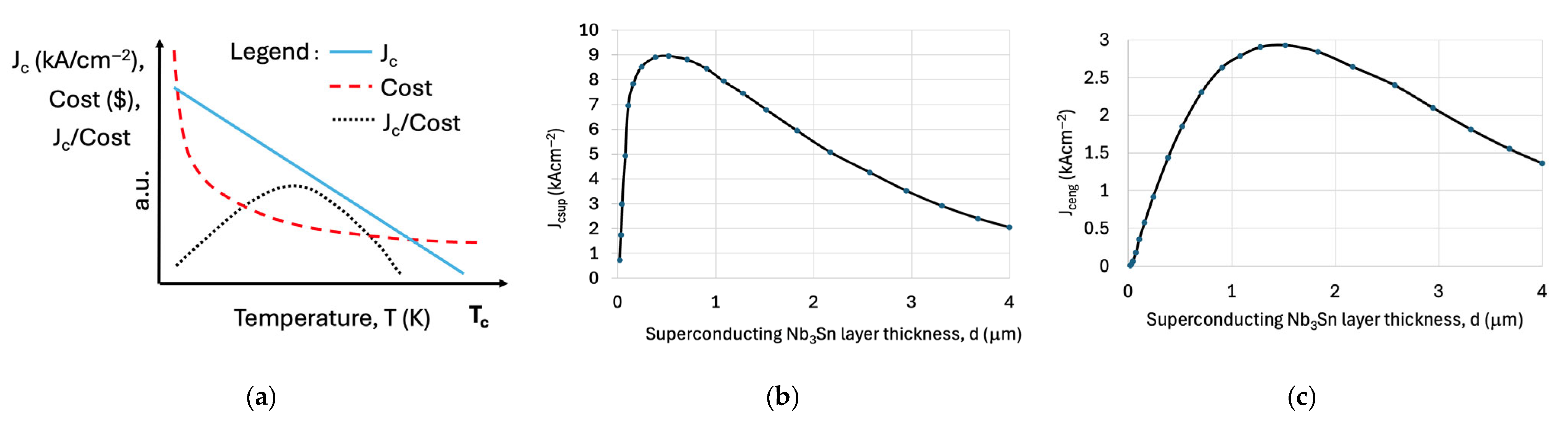
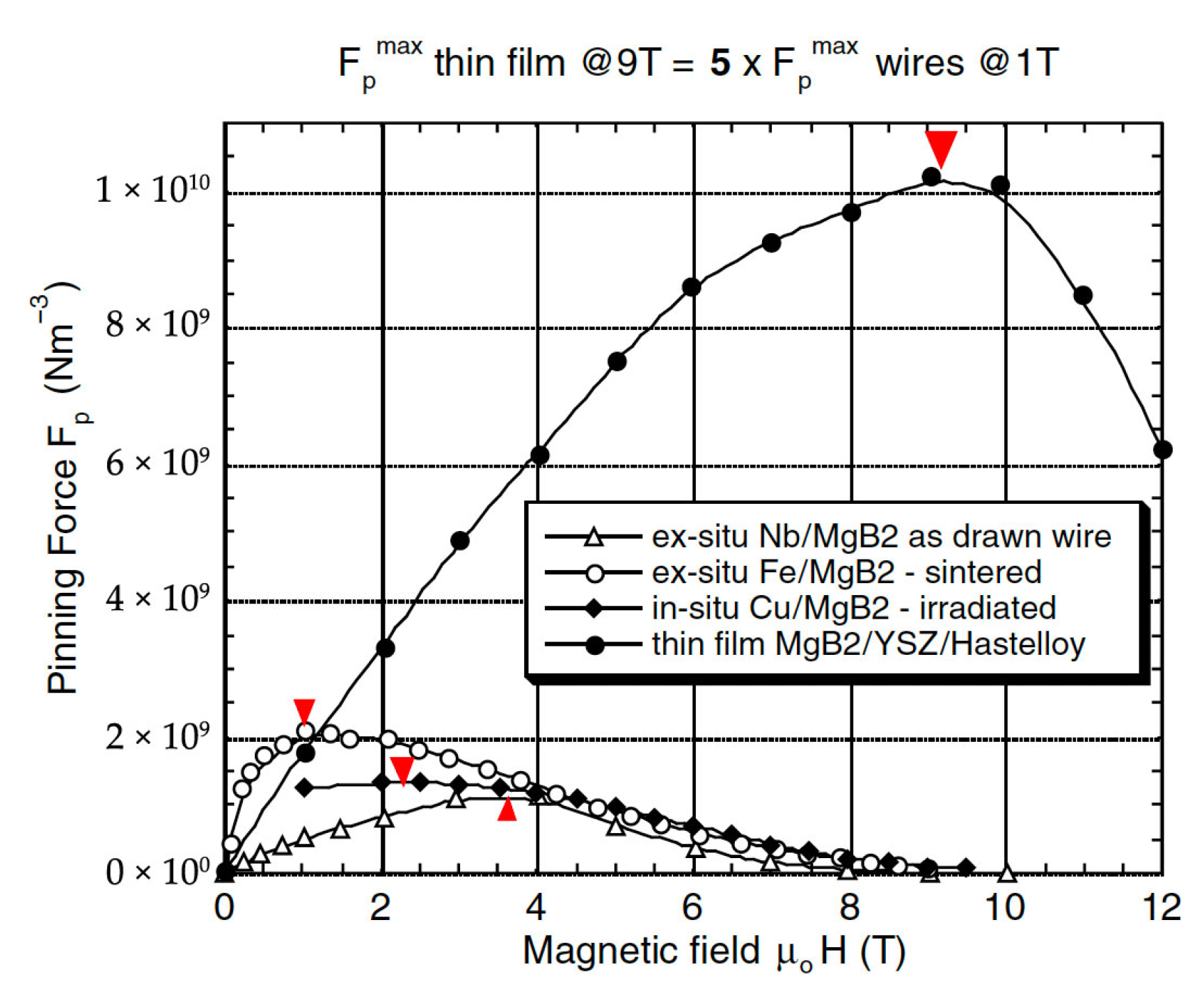
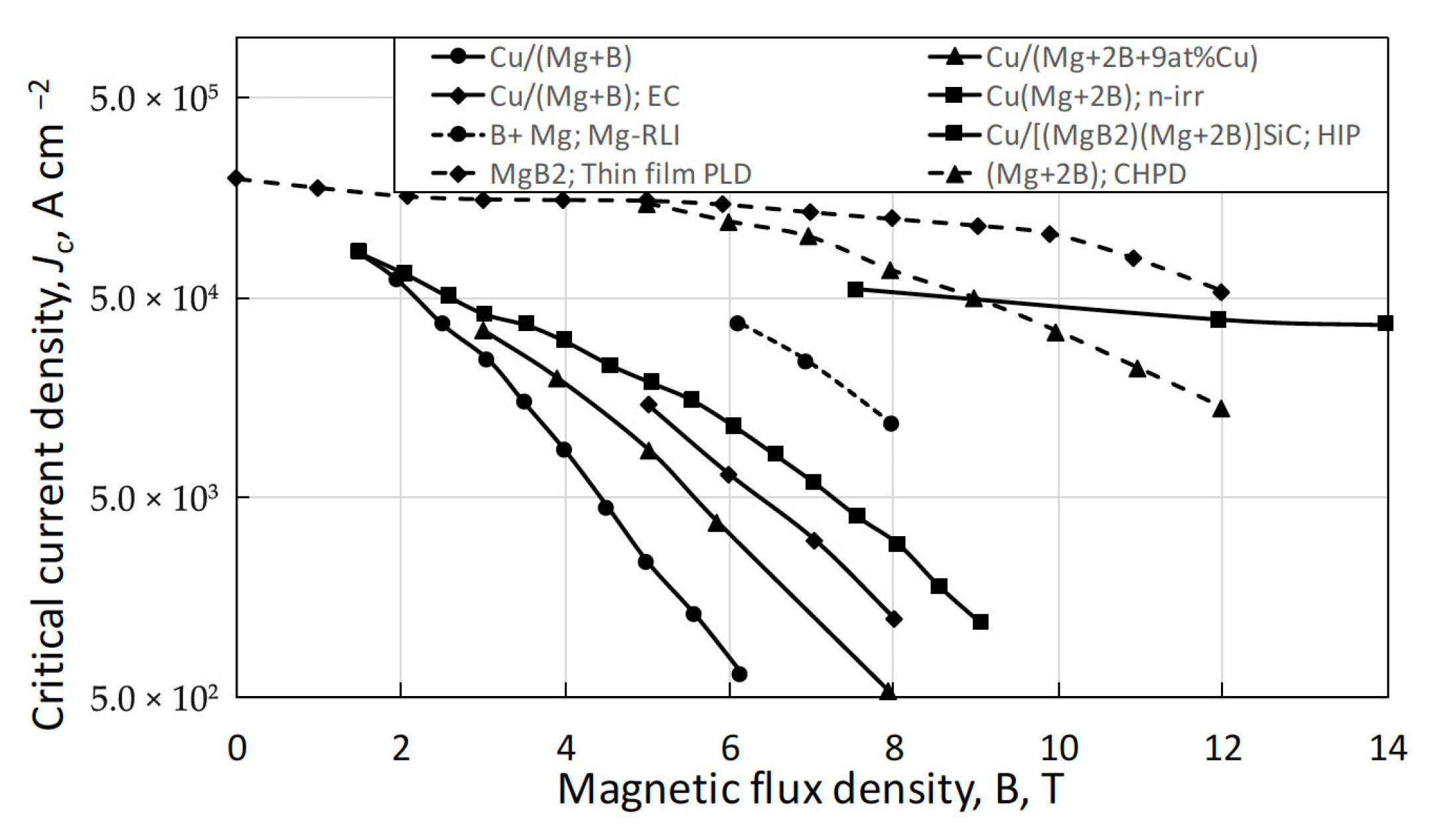
4.2. MgB2 Conductors
5. High Temperature Superconductors
- Dependence on rare-earth elements with concentrated and geopolitically sensitive supply chains.
- Relatively low irreversibility fields, which limit performance under high magnetic fields.
- Extremely complex and costly manufacturing processes, especially for REBCO tapes;
- Lack of scalable, wide-tape production infrastructure.
- Absence of multifilamentary or transposed technologically scalable configurations, which are essential for AC and dynamic current applications.
- And above all, their prohibitively high cost, which restricts their accessibility and scalability.
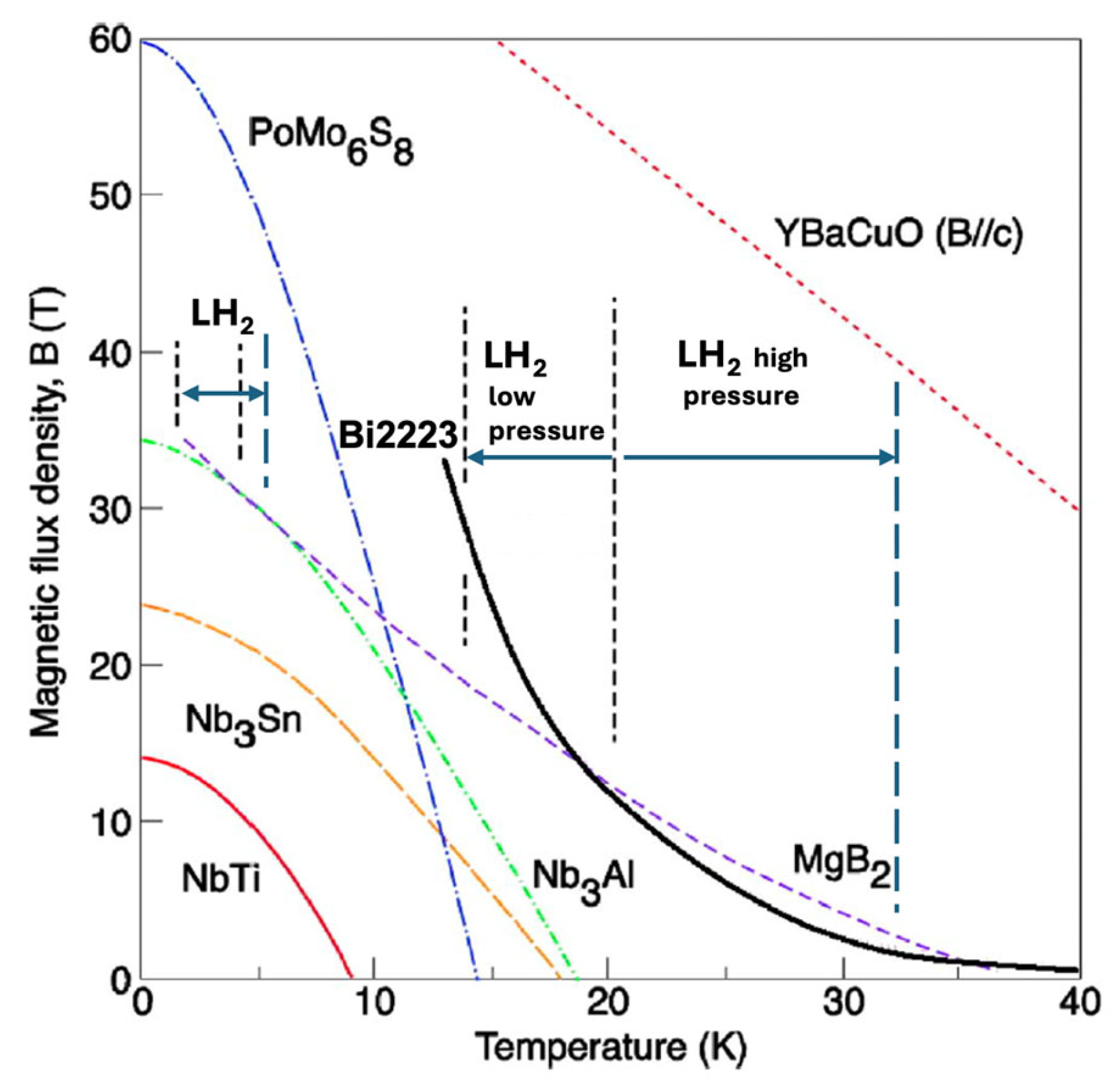
- Optimizing pinning defect structures at 20–40 K, especially under variable flux density conditions (Figure 19a).
- Tailored pinning architectures, which are not yet achievable with current fabrication technologies.
- And the development of low-cost, scalable, and highly reliable manufacturing techniques to replace today’s expensive and limited 2D coated conductor architecture.
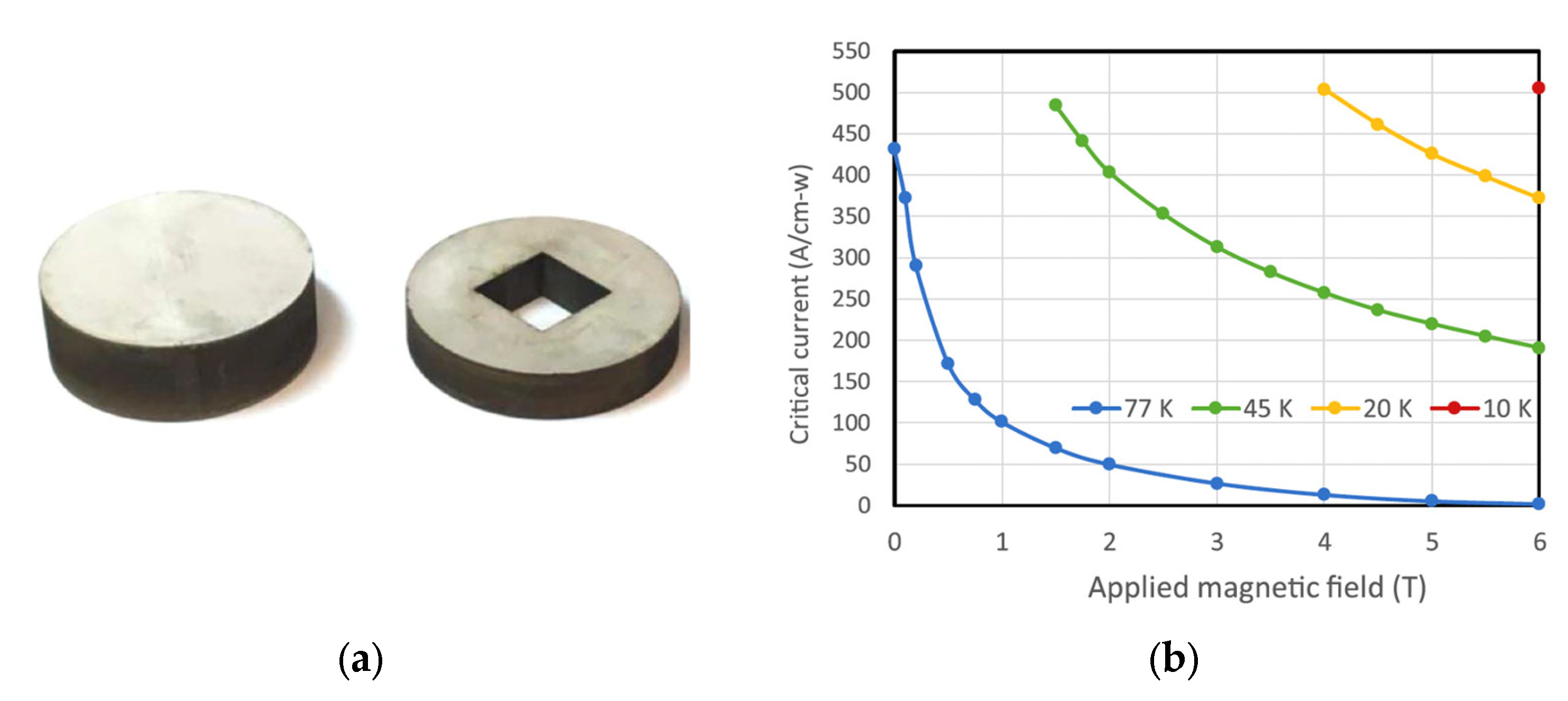
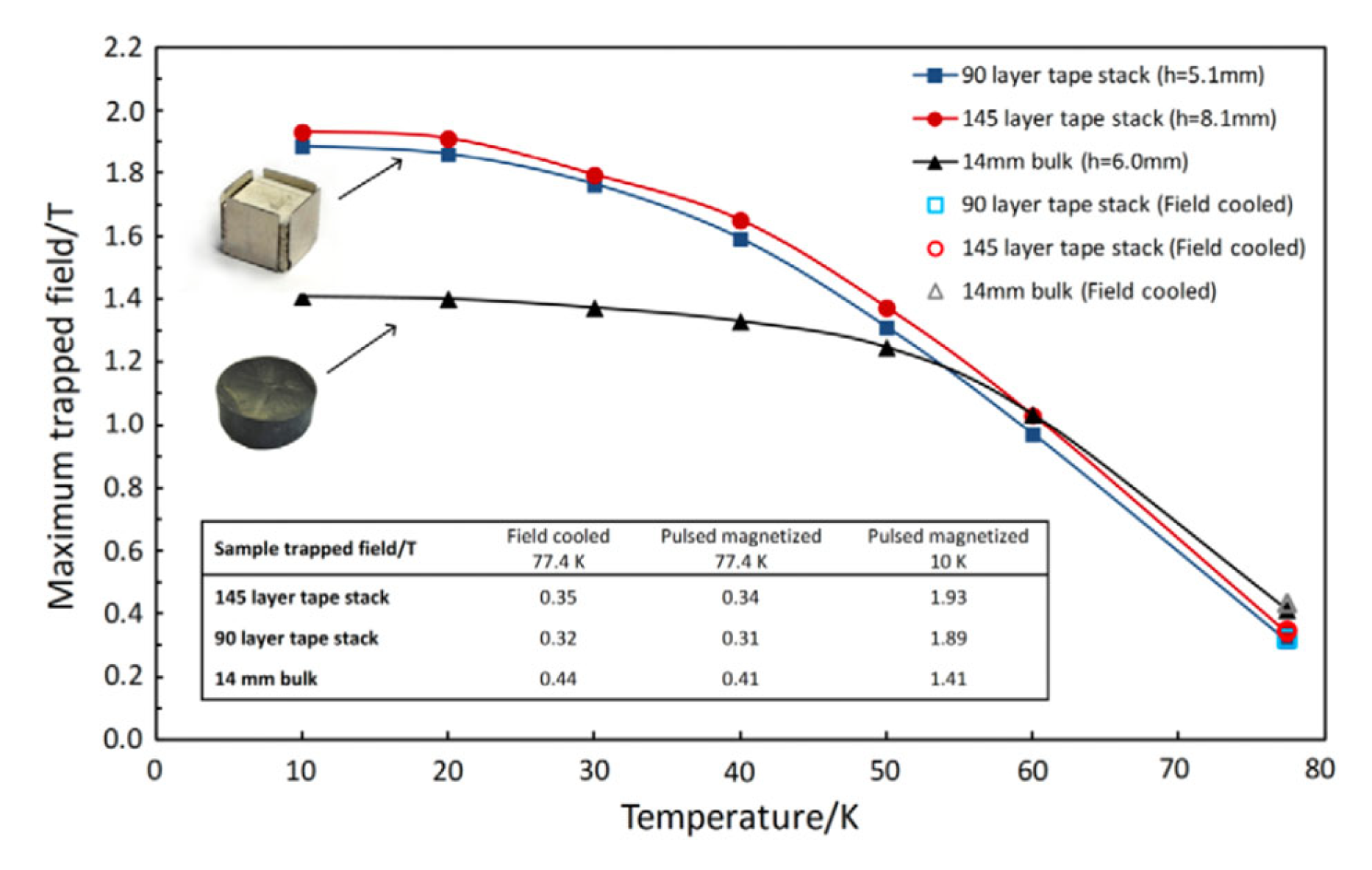

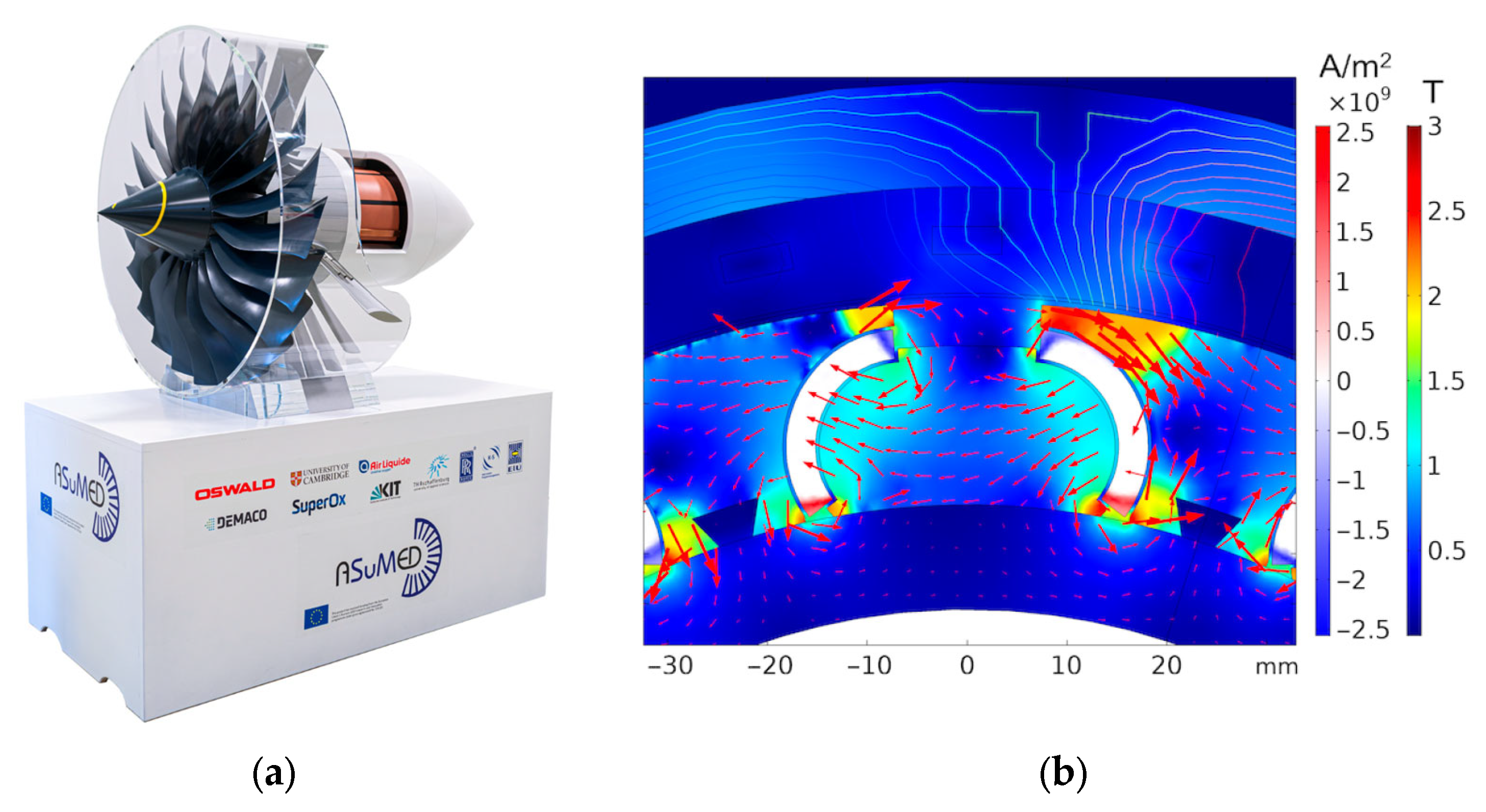
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Song, W.; Jiang, Z.; Staines, M.; Wimbush, S.; Fang, J.; Zhang, J.; Badcock, R. Superconducting traction transformer. Transformer Magazine, 20 August 2021; 10–21. [Google Scholar]
- Rostila, L.; Lehtonen, J.; Masti, M.; Lallouet, N.; Saugrain, J.-M.; Allais, A.; Schippl, K.; Schmidt, F.; Balog, G.; Marot, G. Design of a 30 m long 1 kA 10 kV YBCO cable. Supercond. Sci. Technol. 2006, 19, 418. [Google Scholar] [CrossRef]
- Sotelo, G.G.; Santos, G.; Sass, F.; França, B.W.; Dias, D.H.N.; Fortes, M.Z.; Polasek, A.; Andrade, R. A review of superconducting fault current limiters compared with other proven technologies. Superconductivity 2022, 3, 100018. [Google Scholar] [CrossRef]
- Fabbri, M.; Morandi, A.; Luigi Ribani, P. DC induction heating of aluminum billets using superconducting magnets. COMPEL—Int. J. Comput. Math. Electr. Electron. Eng. 2008, 27, 480–490. [Google Scholar] [CrossRef]
- Ohara, T.; Kumakura, H.; Wada, H. Magnetic separation using superconducting magnets. Phys. C Supercond. 2001, 357, 1272–1280. [Google Scholar] [CrossRef]
- Dondapati, R.S.; Kumar, A.; Kumar, G.R.; Usurumarti, P.R.; Dondapati, S. Superconducting magnetic energy storage (SMES) devices integrated with resistive type superconducting fault current limiter (SFCL) for fast recovery time. J. Energy Storage 2017, 13, 287–295. [Google Scholar] [CrossRef]
- Tixador, P. Superconducting electrical motorsMoteurs électriques supraconducteurs. Int. J. Refrig. 1999, 22, 150–157. [Google Scholar] [CrossRef]
- Kikuch, M. A Review of Fusion and Tokamak Research Towards Steady-State Operation: A JAEA Contribution. Energies 2010, 3, 1741–1789. [Google Scholar] [CrossRef]
- Yao, C.; Ma, Y. Superconducting materials: Challenges and opportunities for large-scale applications. iScience 2021, 24, 102541. [Google Scholar] [CrossRef]
- Wang, B.; Re, Y.; Deng, Z.; Zheng, J.; Zhang, W.; Zhang, J.; Zheng, X. A high-temperature superconducting maglev-evacuated tube transport (HTS maglev-ETT) test system. IEEE Trans. Appl. Supercond. 2017, 27, 3602008. [Google Scholar]
- Cai, Z.; Clarke, R.H.; Glowacki, B.A.; Nuttall, W.J.; Ward, N. Ongoing ascent to the helium production plateau—Insights from system dynamics. Resour. Policy 2010, 35, 77–89. [Google Scholar] [CrossRef]
- Glowacki, B.A.; Nuttall, W.J.; Clarke, R.H. Beyond the Helium Conundrum. IEEE Trans. Appl. Supercon. 2010, 23, 0500113. [Google Scholar] [CrossRef]
- Clarke, R.; Glowacki, B.A. Indirect hydrogen versus helium or nitrogen cooling for fusion cryogenic systems. In Proceedings of the 23rd International Cryogenic Engineering Conference and International Cryogenic Materials Conference 2010 ICEC 23/ICMC, Wroclaw, Poland, 19–23 July 2010; Advances in Cryogenic Engineering. pp. 347–352. [Google Scholar]
- McDonald, K.T.; Iarocci, M.; Kirk, H.G.; Mulholland, G.T.; Titus, P.H.; Weggel, R.J. Use of He Gas Cooled by Liquid Hydrogen with a 15-T Pulsed Copper Solenoid Magnet. In Proceedings of the ICEC23 ICMC10, Wroclaw, Poland, 20 July 2002; pp. 365–369. [Google Scholar]
- Hirabayashi, H.; Makida, Y.; Nomura, S.; Shintomi, T. Liquid Hydrogen Cooled Superconducting Magnet and Energy Storage. IEEE Trans. Appl. Supercond. 2008, 18, 766–769. [Google Scholar] [CrossRef]
- Chesneau, E.C.L.; Glowacki, B.A.; Kvitkovic, J.; Majoros, M.; van Beek, K.; Konczykowski, M. Comparison of magnetic field profiles of Ag/BSCCO-2223 tapes carrying AC and DC currents. IEEE Trans. Appl. Supercon. 1999, 9, 2557–2560. [Google Scholar] [CrossRef]
- Shamray, V.F.; Mikhailova, A.B.; Mitin, A.V. Crystal structure and superconductivity of Bi-2223. Crystallogr. Rep. 2009, 54, 584–590. [Google Scholar] [CrossRef]
- Wozniak, M. High Engineering Critical Current Density MgB2 Wires and Joints for MRI Applications. Ph.D. Thesis, Department of Materials Science and Metallurgy, University of Cambridge, Cambridge, UK, 2012. [Google Scholar]
- Coote, R.I. The Interaction of Abrikosov Vortices with Metallurgical Defects. Ph.D. Thesis, Department of Materials Science and Metallurgy, Cambridge University, Cambridge, UK, 1970. [Google Scholar]
- Campbell, A.M.; Evetts, J.E. Flux vortices and transport currents in type II superconductors. Adv. Phys. 1972, 21, 199–428. [Google Scholar] [CrossRef]
- Glowacki, B.A. Pinning Improvement of A15 Applied Superconducting Materials. Acta Phys. Pol. A 2016, 130, 531–536. [Google Scholar] [CrossRef]
- Glowacki, B.A.; Majoros, M.; Vickers, M.; Eisterer, M.; Toenies, S.; Weber, H.W.; Fukutomi, M.; Komori, K.; Togano, K. Composite Cu/Fe/MgB2 superconducting wires and MgB2/YSZ/Hastelloy coated conductors for ac and dc applications. Supercond. Sci. Technol. 2003, 16, 297–305. [Google Scholar] [CrossRef]
- Glowacki, B.A.; Yan, X.Y.; Fray, D.; Chen, G.; Majoros, M.; Shi, Y. Niobium based intermetallics as a source of high-current/high magnetic field superconductors. Phys. C 2002, 372, 1315–1320. [Google Scholar] [CrossRef][Green Version]
- Glowacki, B.A. Niobium aluminide as a source of high-current superconductors. Intermetallics 1999, 7, 117–140. [Google Scholar] [CrossRef]
- Summers, L.T.; Miller, J.R. The development of superconductors for applications in high-field, high-current-density magnets for fusion research. IEEE Trans. Mag. 1987, 23, 1552–1556. [Google Scholar] [CrossRef][Green Version]
- Kikuchi, A.; Iijima, Y.; Inoue, K.; Kosuge, M.; Itoh, K. Nb3(Al, Ge) multifilamentary wires made by the rapidly-heating/quenching process. IEEE Trans. Appl. Supercond. 2001, 11, 3984–3987. [Google Scholar] [CrossRef]
- Evetts, J.E.; Wade, J.M.A. Superconducting properties and the phase diagrams of the Pb–Bi and Pb–In alloy systems. Phys. Chem. Sol. 1970, 31, 973–982. [Google Scholar] [CrossRef]
- Pippard, A.B. A possible mechanism for the peak effect in type II superconductors. Phil. Mag. 1969, 19, 217–220. [Google Scholar] [CrossRef]
- Takeuchi, T.; Kuroda, T.; Itoh, K.; Kosuge, M.; Ijima, Y.; Kiyoshi, T.; Matsumoto, F.; Inoue, K. Development of Nb tube processed Nb3Al multifilamentary superconductor. J. Fusion Energy 1992, 11, 7–18. [Google Scholar] [CrossRef]
- Kosuge, M.; Iijima, Y.; Takeuchi, T.; Inoue, K.; Kiyoshi, T.; Irie, H.; Wtanabe, K. Multifilamentary Nb3Al wires reacted at high temperature for short time. IEEE Trans. Appl. Supercond. 1993, 3, 1010–1013. [Google Scholar] [CrossRef]
- Yamada, Y.; Ohmatsu, K.; Nagata, M.; Ando, T.; Tkahashi, Y.; Nishi, M. Development of Nb3Al Superconductor using the jelly-roll process. Sumitomo Elec. Tech. Rev. 1992, 33, 83–89. [Google Scholar]
- Tchikawa, K.; Sakinada, K.; Kobayashi, M. New A15 Nb3(Al, Ge) tape prepared from σ-phase powder. Cryogenics 1993, 33, 1091–1094. [Google Scholar] [CrossRef]
- Dukhovnii, I.S.; Fridman, A.A.; Korzhov, V.P.; Shmidt, V.V.; Zarubina, A.A. Flux pinning centres in solid-state diffusion processed superconducting Nb3(AlGe) alloyed with Cu. Phys. Stat. Sol. (A) 1980, 62, 123–128. [Google Scholar] [CrossRef]
- Togano, K.; Kumakura, H.; Yoshida, Y.; Tachikawa, K. Fabrication of superconducting composite tapes by a newly developed liquid quenching technique. IEEE Trans. Magn. 1985, 21, 463–466. [Google Scholar] [CrossRef]
- Takeuchi, T.; Togano, K.; Tachikawa, K. Nb3Al and its ternary A15 compound conductors prepared by a continuous liquid quenching technique. IEEE Trans. Magn. 1987, 23, 956–959. [Google Scholar] [CrossRef]
- Takeuchi, T.; Banno, N.; Fukuzaki, T.; Wada, H. Large improvement in high-field critical current densities of Nb3Al conductors by the transformation-heat-based up-quenching method. Supercond. Sci. Technol. 2000, 13, 11–14. [Google Scholar] [CrossRef]
- Wordenweber, R.; Kes, P.H. Dimensional crossover in collective flux pinning. Phys. Rev. 1986, 34, 494–497. [Google Scholar] [CrossRef] [PubMed]
- Bartlett, R.L.; Laquerh, H.L.; Taylor, R.D. Critical current densities in Nb3Ge between 14 and 21 K. IEEE Trans. Magn. 1975, 11, 405–407. [Google Scholar] [CrossRef]
- Sumption, M.D.; Collins, E.W.; Lee, E.; Wang, X.L.; Soltanian, S.; Dou, S.X. Reduction and elimination of external-field AC loss in MgB2/Fe wire by in situ magnetic shielding. Phys. C Supercond. 2002, 378, 894–898. [Google Scholar] [CrossRef]
- Komori, K.; Kawagishi, K.; Takano, Y.; Arisawa, S.; Kumakura, H.; Fukutomi, M.; Togano, K. A New Approach for the Fabrication of MgB2 Superconducting Tape with Large In-field Transport Critical Current Density. Appl. Phys. Lett. 2002, 81, 1047–1049. [Google Scholar] [CrossRef]
- Glowacki, B.A.; Majoros, M.; Vickers, M.; Evetts, J.E.; Shi, Y.; McDougall, I. Superconductivity of powder-in-tube MgB2 wires. Supercond. Sci. Technol. 2001, 14, 193–199. [Google Scholar]
- Glowacki, B.A.; Kutukcu, M.N.; Atamert, S.; Dhulst, C.; Mestdagh, J.; Van Vooren, W.; Nijhuis, A. Comparative Study of The Continuous and Batch Thermal Processing of MgB2 Wires. IEEE Trans Appl. Supercon. 2019, 29, 6200604. [Google Scholar] [CrossRef]
- Giunchi, G.; Ripamonti, G.; Perini, E.; Cavallini, T.; Bassani, E.; Gambardella, U.; Yangh, Y.; Young, E.A.; Bianchetti, M.; Beduz, C. Superconducting characteristics of MgB2 wires obtained by Reactive Liquid Mg Infiltration. MRS Online Proc. Libr. 2006, 946, 403. [Google Scholar] [CrossRef]
- Suo, H.; Beneduce, C.; Dhalle, M.; Musolino, V.; Genoud, J.Y.; Flukiger, R. Large transport critical currents in dense Fe- and Ni-clad MgB2 superconducting tapes. Appl. Phys. Lett. 2001, 79, 3116–3127. [Google Scholar] [CrossRef]
- Zhou, S.; Pan, A.V.; Ionescu, M.; Liu, H.; Dou, S. Influence of Ag, Cu and Fe sheaths on MgB2 superconducting tapes. Supercond. Sci. Technol. 2002, 15, 236–240. [Google Scholar] [CrossRef]
- Tarantini, C.; Segal, C.; Sung, Z.H.; Lee, P.J.; Oberli, L.; Ballarino, A.; Bottura, L.; Larbalestier, D.C. Composition and connectivity variability of the A15 phase in PIT Nb3Sn wires. Supercond. Sci. Technol. 2015, 28, 095001. [Google Scholar] [CrossRef]
- Kutukcu, M.N.; Atamert, S.; Scandella, J.-L.; Hopstock, R.; Blackwood, A.C.; Dhulst, C.; Mestdagh, J.; Nijhuis, A.; Glowacki, B.A. Composite Superconducting MgB2 Wires Made by Continuous Process. IEEE Trans Appl. Supercon. 2018, 28, 6200704. [Google Scholar] [CrossRef]
- Li, G.Z.; Reddy, K.M.; Zwayer, J.B.; Kuldell, M.A.; Susner, M.A.; Yang, Y.; Sumption, M.D.; Yue, J.J.; Rindfleisch, M.A.; Tomsic, M.J.; et al. Critical current density and current transfer length of multifilamentary MgB2 strands of various design. IEEE Trans. Appl. Supercond. 2013, 23, 6200204. [Google Scholar] [CrossRef]
- Brunner, B.; Kovác, P.; Reissner, M.; Hušek, I.; Melišek, T.; Pardo, E. Critical current density and pinning behaviour of mono-core MgB2 wires prepared by internal magnesium diffusion and in-situ powder-in-tube method. Phys. C. 2014, 505, 39–43. [Google Scholar] [CrossRef]
- Glowacki, B.A. Microstructurally Determined Electromagnetic Properties of Copper-Sheathed In Situ MgB2 Wires. In Proceedings of the 2017 International Conference on Electromagnetic Devices and Processes in Environment Protection with Seminar Applications of Superconductors (ELMECO & AoS), Naleczow, Poland, 3–6 December 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Schilling, A.; Cantoni, M.; Guo, J.D.; Ott, H.R. Superconductivity above 130 K in the Hg–Ba–Ca–Cu–O system. Nature 1993, 363, 56–58. [Google Scholar] [CrossRef]
- Scanlan, R.M.; Malozemoff, A.P.; Larbalestier, D.C. Superconducting materials for large scale applications. Proc. IEEE 2004, 92, 1639–1654. [Google Scholar] [CrossRef]
- Maeda, H.; Yamazaki, T.; Nishiyama, Y.; Hamada, M.; Hashi, K.; Shimizu, T.; Suematsu, H.; Yanagisawa, Y. Development of Super-High-Field NMR Operated Beyond 1 GHz Using High-Temperature Superconducting Coils. eMagRes 2016, 5, 1109–1120. [Google Scholar]
- Maeda, H.; Yanagisawa, Y. Recent Developments in High-Temperature Superconducting Magnet Technology (Review). IEEE Trans. Appl. Supercond. 2014, 24, 4602412. [Google Scholar] [CrossRef]
- MacManus-Driscoll, J.L.; Wimbush, S.C. Advances in processing and application of high temperature superconducting coated conductors. Nat. Rev. Mater. 2021, 6, 587–604. [Google Scholar] [CrossRef]
- Patel, A.; Baskys, A.; Mitchell-Williams, T.; Aoife McCaul, A.; Coniglio, W.; Hänisch, J.; Lao, M.; Glowacki, B.A. A trapped field of 17.7T in a stack of high temperature superconducting tape. Supercond. Sci. Technol. 2018, 31, 09LT01. [Google Scholar] [CrossRef]
- Durrell, J.H.; Dennis, A.R.; Jaroszynski, J.; Ainslie, M.D.; Palmer, K.G.B.; Shi, Y.-H.; Campbell, A.M.; J Hull, J.; Strasik, M.; Hellstrom, E.E. A trapped field of 17.6 T in melt processed, bulk Gd–Ba–Cu–O reinforced with shrink-fit steel. Supercond. Sci. Technol. 2014, 27, 082001. [Google Scholar] [CrossRef]
- Tomita, M.; Murakami, M. High-temperature superconductor bulk magnets that can trap magnetic fields of over 17 Tesla at 29 K. Nature 2003, 421, 517–520. [Google Scholar] [CrossRef]
- Patel, A.; Hopkins, S.C.; Glowacki, B.A. Trapped fields up to 2 T in a 12 mm square stack of commercial superconducting tape using pulsed field magnetization. Supercond. Sci. Technol. 2013, 26, 032001. [Google Scholar] [CrossRef]
- Patel, A.; Baskys, A.; Hopkins, S.C.; Kalitka, V.; Molodyk, A.; Glowacki, B.A. Pulsed-Field Magnetization of Superconducting Tape Stacks for Motor Applications. IEEE Trans. Appl. Supercon. 2015, 25, 5203405. [Google Scholar] [CrossRef]
- Grilli, F.; Benkel, T.; Hanisch, J.; Lao, M.; Reis, T.; Berberich, E.; Wolfstadter, S.; Schneider, C.; Miller, P.; Palmer, C.; et al. Superconducting motors for aircraft propulsion: The Advanced Superconducting Motor Experimental Demonstrator project. J. Phys. Conf. Ser. 2020, 1590, 012051. [Google Scholar] [CrossRef]
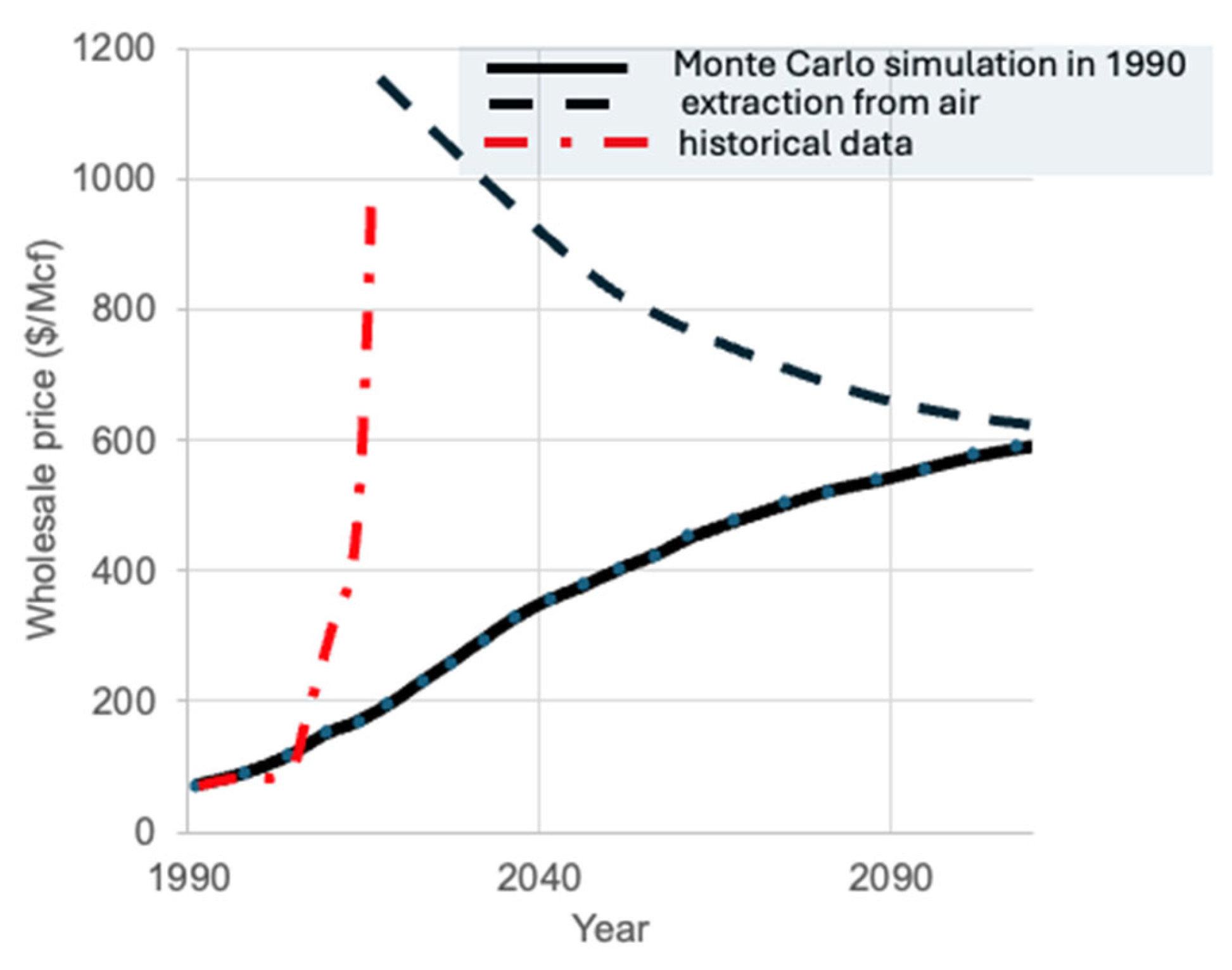
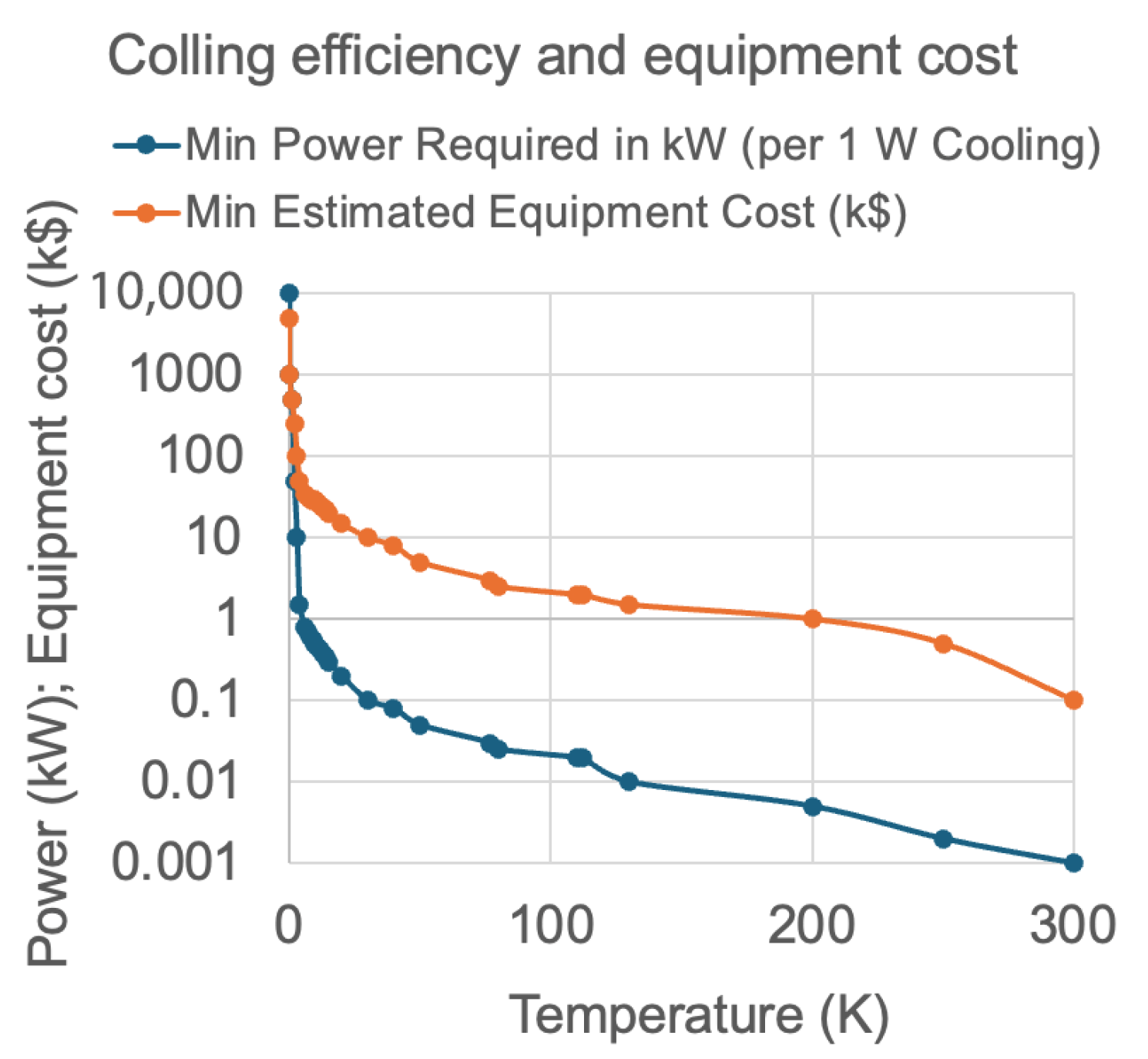
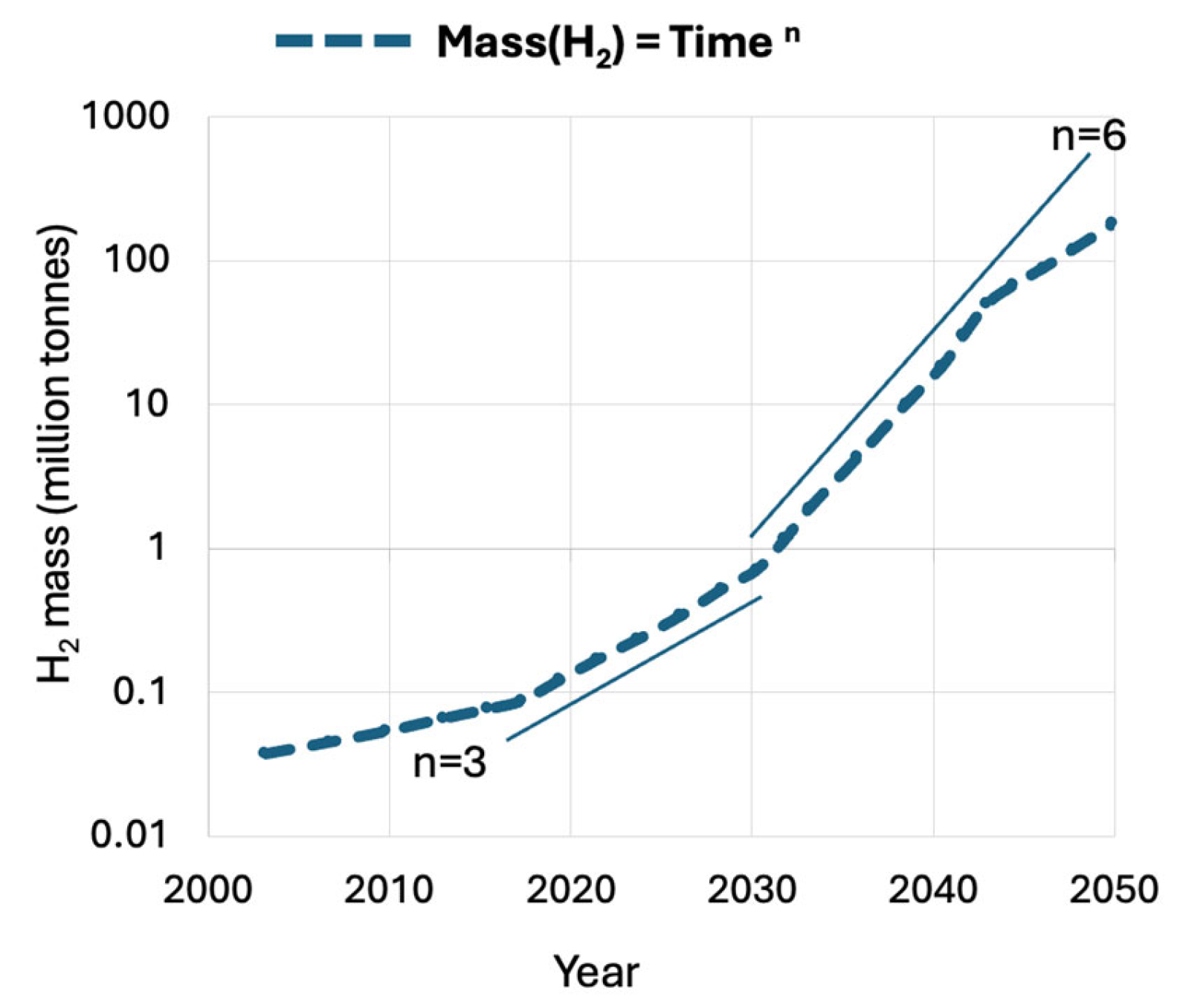
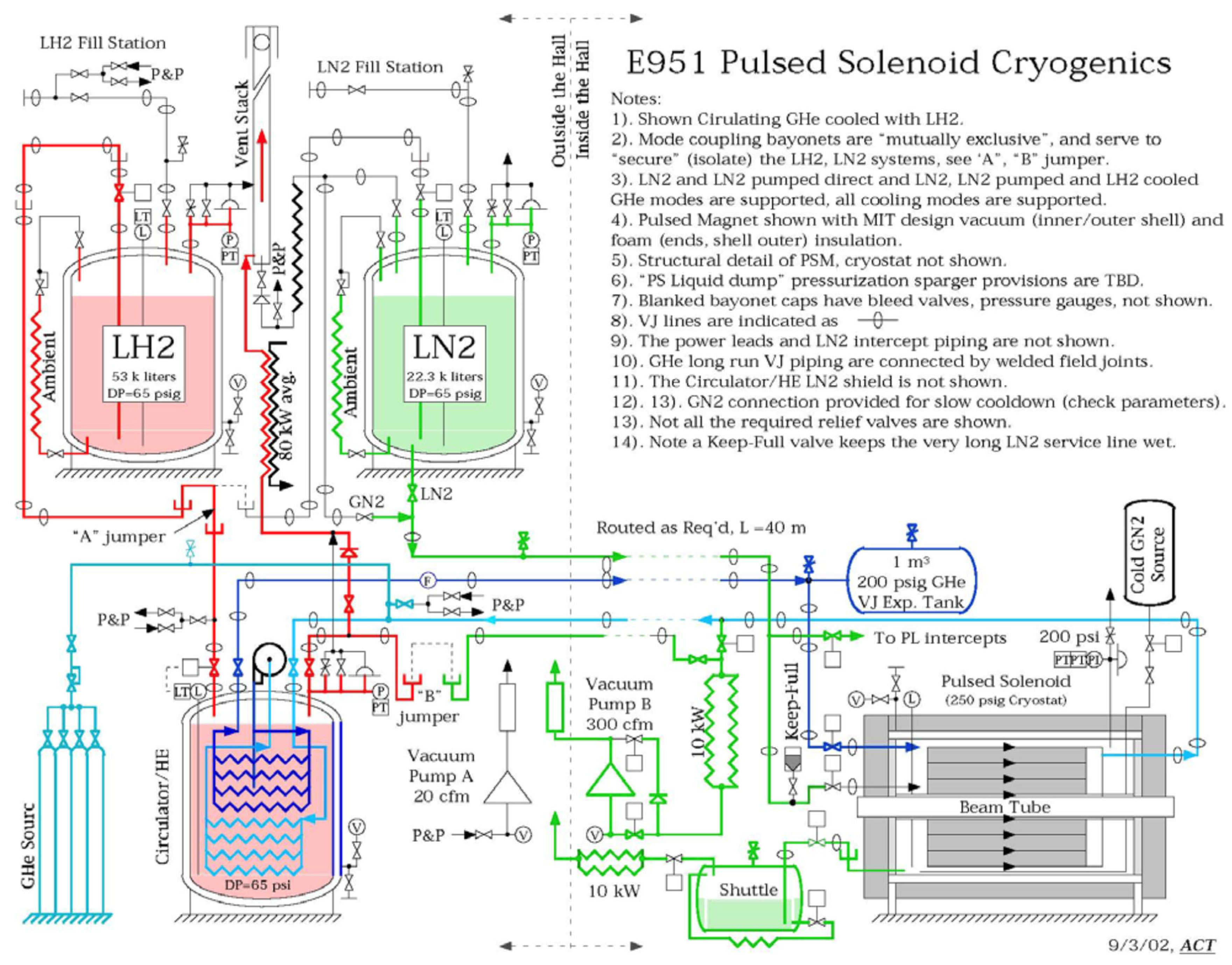
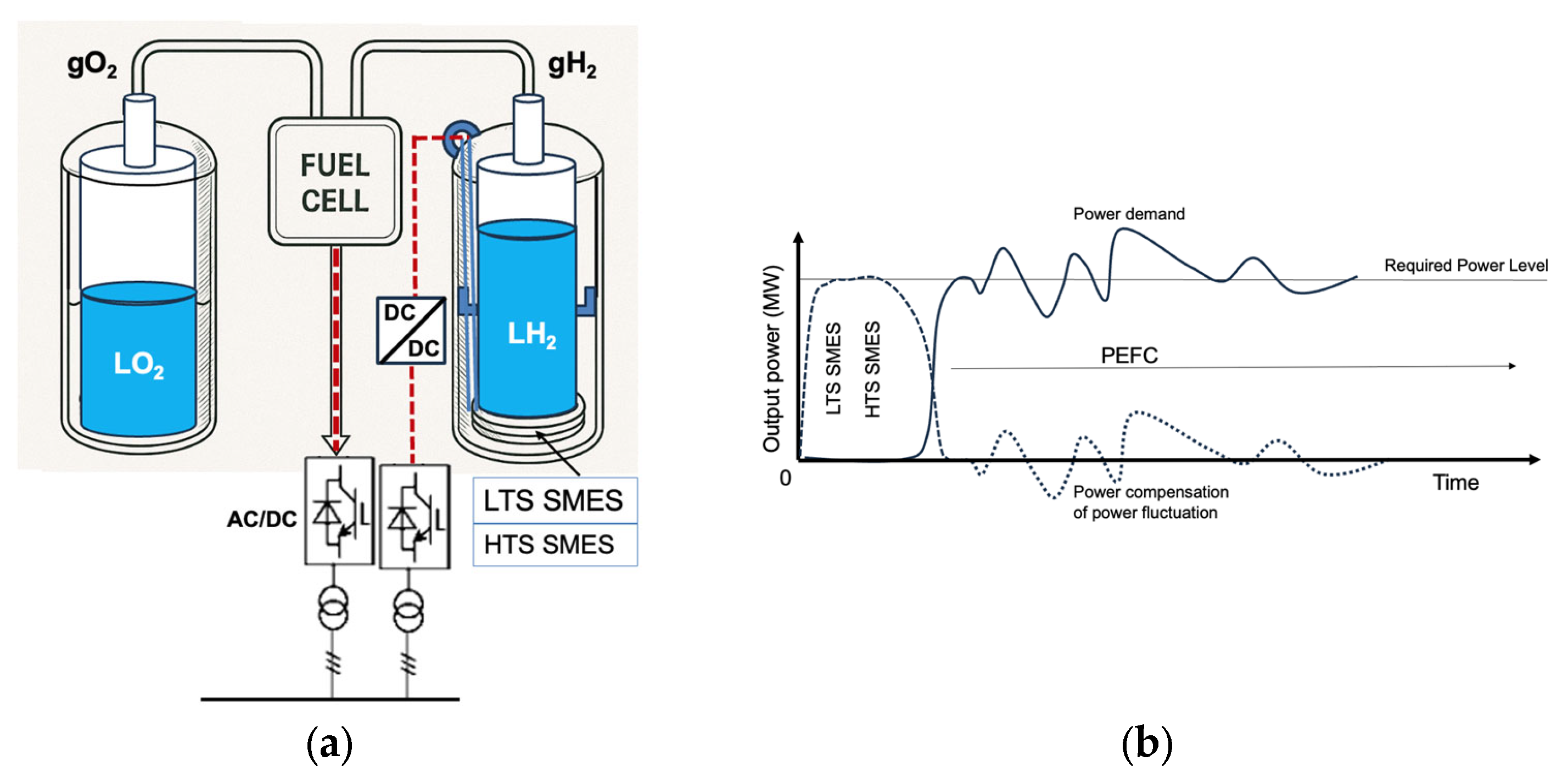
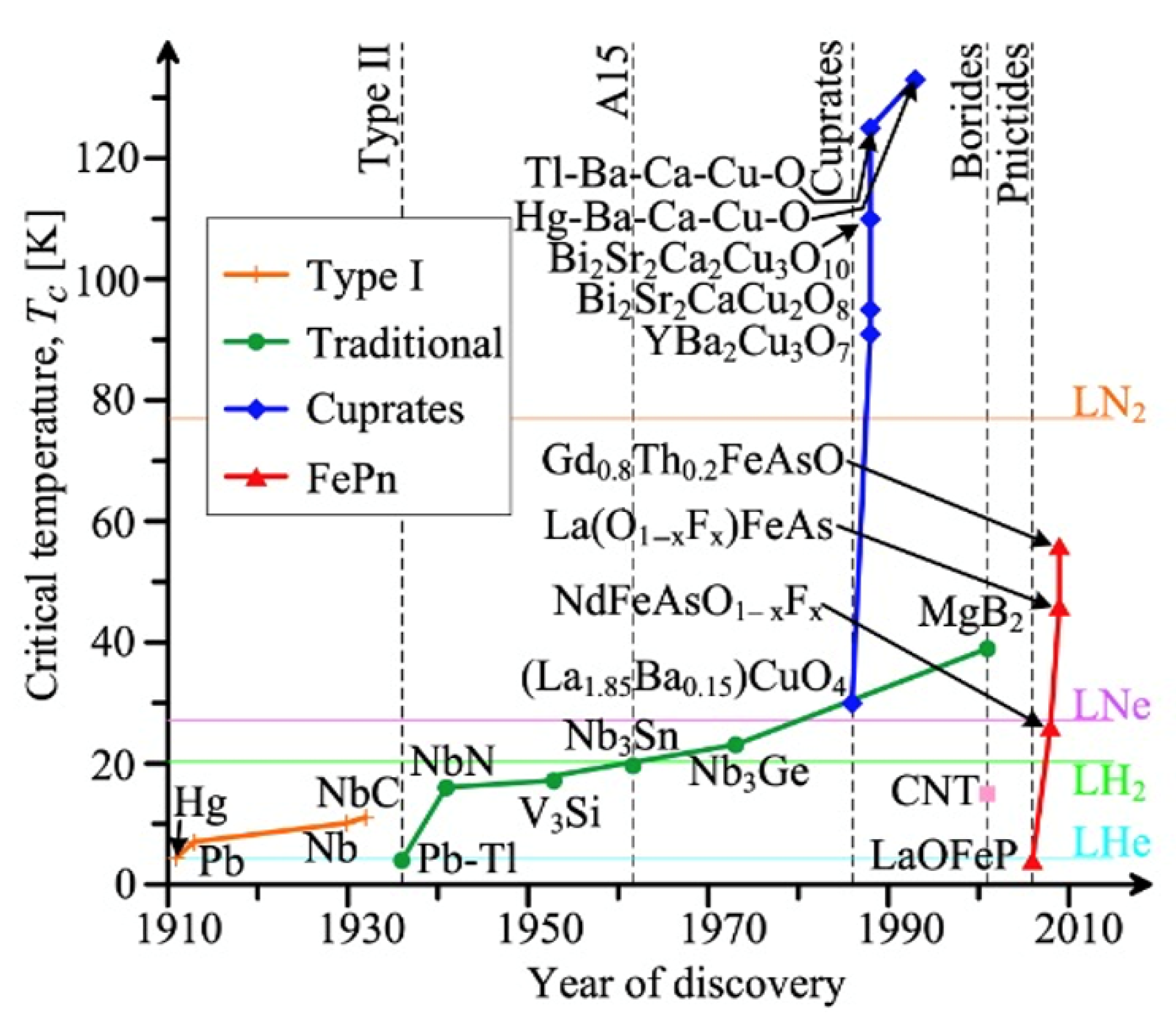
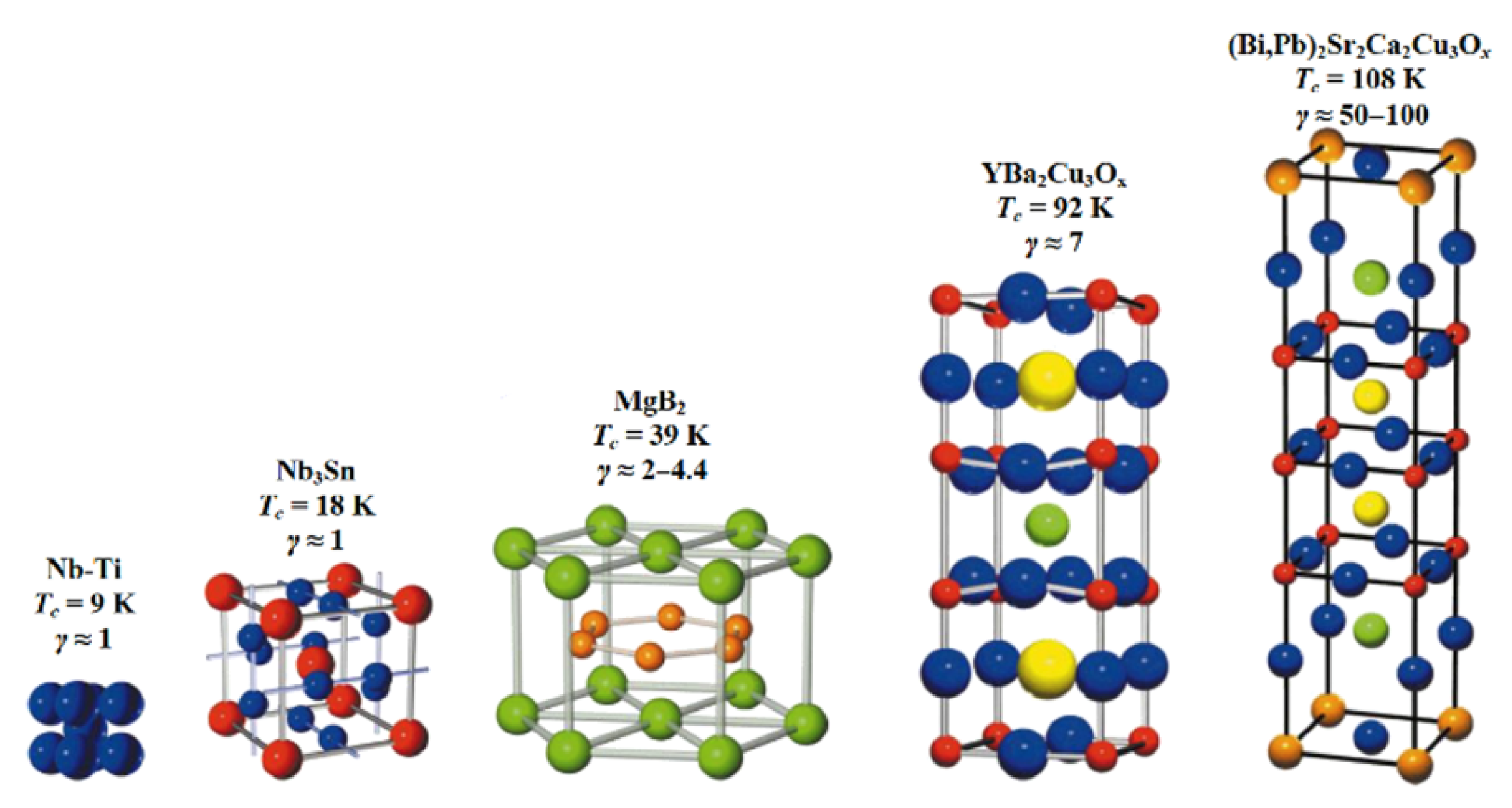
| Property | Helium (He) | Hydrogen (H2) | Nitrogen (N2) |
|---|---|---|---|
| Boiling Point @ 1 atm | 4.2 K | 20.3 K | 77.4 K |
| Latent Heat of Vaporization | 20.9 kJ/mol | 445 kJ/kg | 199 kJ/kg |
| ≈5.23 kWh/kg | ≈123.6 Wh/kg | ≈55.3 Wh/kg | |
| Liquid Density | 125 kg/m3 | 71 kg/m3 | 808 kg/m3 |
| Typical Market Price | 30–50 $/L | 4–6 $/L | 0.10–0.20 $/L |
| Energy Equivalent | — | ~33.3 kWh/kg (HHV) | — |
| Superconductor | Tc (K) | Cooling Medium | Material Dependency | Toxicity & Safety | Production Complexity |
|---|---|---|---|---|---|
| Hg-1223 (HTS) | 135 | LN2 (77 K) LH2 (20 K) | Mercury (Hg) | Extremely toxic (highly restricted) | Difficult (vapor-phase synthesis) |
| Tl-1223 (HTS) | 127 | LN2 (77 K) LH2 (20 K) | Thallium (Tl) | Extremely toxic (highly restricted) | Difficult (vapor-phase synthesis) |
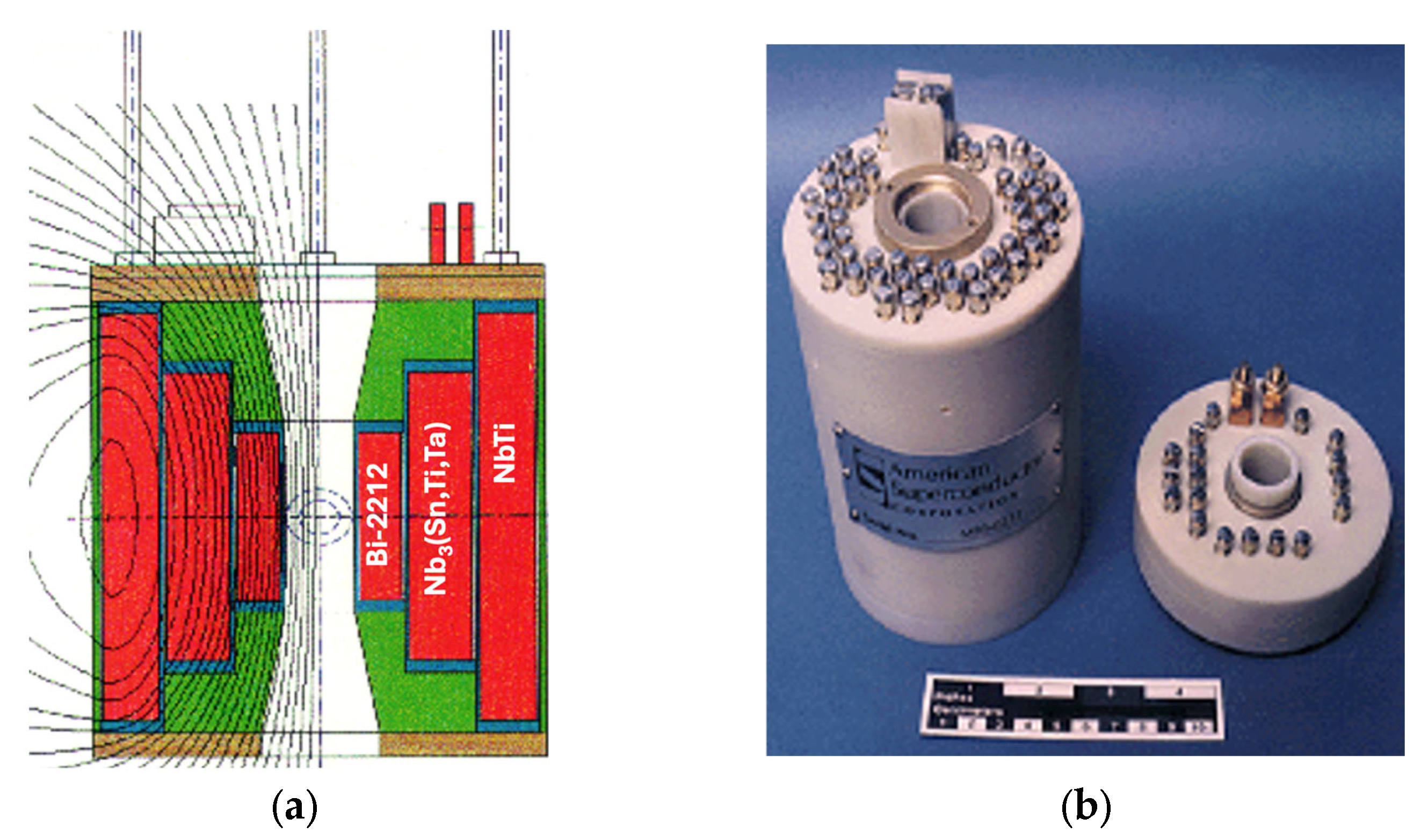
| Bi-2223 (HTS) | 110 | LH2 (20 K) | (Pb)-doped | Moderate toxicity | Complex (multi-phase sintering) |
| Bi-2212 (HTS) | 95 | LH2 (20 K) | Bismuth (Bi) | Safe | Complex (multi-phase sintering) |
| YBCO (HTS) | 92 | LN2 (64 K) LH2 (20 K) | Rare earth (Y, Sm, Nd) | Safe | Complex (coated conductor, slow deposition) |
| SmFeAs(O,F) (Iron Pnictide) | 55 | LH2 (20 K) | Arsenic (As) Sm, Fe, | toxicity risk | Difficult (thin films, complex doping) |
| MgB2 (HTS) | 39 | LH2 (14 K) | Boron (strategic) | Safe | Simple, but low high-field performance in PIT |
| Nb3Ge (LTS) | 23 | LH2 (14 K) | Nb, Ge (abundant) | Safe | Metallic synthesis, simpler than HTS |
| Compound | Tc [K] | Bc2 [T] |
|---|---|---|
| Nb3Sn | 18.5 | 24 |
| Nb3Al | 18.9 | 29.5 |
| Nb3(Al,Ge) | 21.0 | 44 |
| Nb3Ge | 23.2 | 38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Glowacki, B.A. Hydrogen Cryomagnetic a Common Solution for Metallic and Oxide Superconductors. Materials 2025, 18, 3665. https://doi.org/10.3390/ma18153665
Glowacki BA. Hydrogen Cryomagnetic a Common Solution for Metallic and Oxide Superconductors. Materials. 2025; 18(15):3665. https://doi.org/10.3390/ma18153665
Chicago/Turabian StyleGlowacki, Bartlomiej Andrzej. 2025. "Hydrogen Cryomagnetic a Common Solution for Metallic and Oxide Superconductors" Materials 18, no. 15: 3665. https://doi.org/10.3390/ma18153665
APA StyleGlowacki, B. A. (2025). Hydrogen Cryomagnetic a Common Solution for Metallic and Oxide Superconductors. Materials, 18(15), 3665. https://doi.org/10.3390/ma18153665








